Livre Mathématiques objectif agrégation pdf - Web Education

Objectif

Agrégation

deuxième édition Vincent BECK Jérôme MALICK Gabriel PEYRÉ

© H&K, 68 boulevard de Port-Royal, 75005 Paris Dépôt légal : aoû.t 2005

AVANT-PROPOS

Pour réussir l'agrégation de mathématiques, il ne suffit pas de connaître tous les résultats sur le bout des doigts ! L'année de préparation doit permettre à l'agrégatif d'acquérir du recul par rapport au programme c'est-à-dire, selon le rapport du jury de 2002, de « faire une synthèse (et de) mettre en perspective résultats et méthodes » .

Cette maturité peut s'acquérir par la fréquentation des mathématiques au fil

des années et au hasard des expériences. Mais elle peut également être activement recherchée pour elle-même et construite en quelques mois. C'est cet objectif que nous souhaitons vous aider à réaliser. Nul ne peut vous « apprendre » cette maturité, pas plus qu'on ne peut expliquer à un enfant comment marcher : il doit apprendre par lui-même. Nous pouvons néanmoins guider votre apprentissage en vous aidant à structurer vos connaissances, à faire votre chemin dans la jungle des références et à mettre en œuvre les mathématiques du programme.

Structurer les connaissances. Ce livre propose des synthèses de cours sur lesquelles

vous pouvez vous appuyer pour construire et justifier vos plans de leçons selon vos connaissances, vos préférences et vos objectifs.

Il propose aussi des exercices corrigés en détail pour préparer l'écrit et enrichir vot_re panoplie d'exemples pour l'oral. Certains exercices sont extraits des écrits, d'autres ont étés posés à l'oral lors des sessions précédentes.

Domestiquer les références. Pour bien préparer le concours, l'agrégatif a besoin

de « bonnes » références. Il doit aussi trouver un équilibre difficile : diversifier ses références en évitant de trop se disperser ...

Nous avons épluché la bibliographie pour vous et nous proposons, pour chacun des thèmes abordés dans ce livre, des références précises à des ouvrages classiques et accessibles que nous vous invitons naturellement à compléter selon vos goüts, vos besoins et vos objectifs.

Valoriser les exemples et les applications. Cet ouvrage rassemble des commentaires, remarques, exemples et illustrations autour de thèmes essentiels pour l'agrégation. Nous vous livrons ainsi notre expérience afin que vous puissiez vous en enrichir.

Ce livre a été organisé et structuré pour faciliter la préparation des leçons, notam­ ment en s'affranchissant d'une lecture linéaire. Des étoiles (*) signalent des exemples ou des applications qui utilisent des notions présentées dans la suite.

Ajoutons que vous trouvez en ligne à l'adresse

http://www.H-K.fr/publications/objectif-agregation

iv AVANT-PROPOS

Bon courage et bon travail 1 Nous espérons que ce livre vous aidera à façonner votre propre réservoir de savoir, de savoir-faire et de références fiables ainsi qu'à prendre du recul sur les mathématiques au programme de l'agrégation. Bon courage, bon travail et bonne réussite.

Vincent Beck Jérôme Malick Gabriel Peyré

Merci 1

Nous remercions tous nos lecteurs. Cette deuxième édi­ tion revue et corrigée tient compte des commentaires et des suggestions de ceux qui nous ont contactés pour poser des questions, pointer une erreur ou transmettre leurs remarques.

Nous adressons tous nos remerciements à l'équipe des Éditions H&K : Sébastien Desreux pour son accueil et ses conseils, Bérangère Condomines pour son œil acéré lors des relectures typographiques et Walter Appel et Manu Cornet pour leur travail sur la couverture. Les riches commentaires de Sylvain Brochard, Karel Pravda-Starov et Jean Starynkévitch nous ont permis d'éclaircir certains passages de ce livre. Pierre Bernard, Aris Daniilidis, Matthieu Gendulphe, Stef Graillat et Cyril Odasso nous ont également fait part de perti­ nentes remarques. Nous les remercions tous chaleureu­ sement pour leur aide et leur amitié.

Et surtout, merci à Carole, Sylvie et Marie-Noëlle, merci pour tout.

TABLE DES MATIÈRES

1 CALCUL DIFFÉRENTIEL 1 . 1 Différentiabilité . . 1 . 1 . 1 1 . 1 .2 1 . 1 .3 1 . 1 .4 Applications différentiables . . . . . Lemme fondamental de composition Inégalité des accroissements finis Utilisations de la différentielle . . 1.2 Inversion locale et fonctions implicites

1.2.1 Fonctions inverses, fonctions implicites . 1 .2.2 Applications .

1 .2.3 Généralisations

1.3 Optimisation . . . . 1.3.1 Existence et unicité

1 .3.2 Localisation et calcul différentiel 1 .3.3 Optimisation numérique . 1 .4 Développements de Taylor . 1 .4.1 Développement local . 1 .4.2 Développement global 1.5 Fonctions convexes . . . . 1.5.1 1 .5.2 1 .5.3 1 .5.4 Ensembles convexes Fonctions convexes .

Fonctions convexes différentiables . Fonctions convexes et optimisation

1 .6 Exercices corrigés . . . .

2 FONCTIONS D 'UNE VARIABLE COMPLEXE

2.1 Séries entières . . . . 2 . 1 . 1 Rayon de convergence . . . . 2.1.2 Au bord du disque de convergence

2.2 Fonctions analytiques . . . . 2.2.1 Fonctions développables en série entière

1 1 2 6 7 8 9 10 1 1 13 15 16 16 22 24 24 25 26 26 27 28 30 30 45 47 47 49 51 51

viii

2.2.2 2.2.3 2.2.4

TABLE DES MATIÈRES

Factorisation . . . . Théorème des zéros isolés . . Fonctions analytiques réelles

2.3 Fonctions holomorphes . . . . .

2.3.1 Holomorphie VS calcul différentiel réel 2.3.2 Applications conformes . . . . 2.3.3 Fonctions holomorphes et inversion locale

2.4 Conséquences de la théorie de Cauchy . . . . . 2.4. 1 Formule de Cauchy . . . . 2.4.2 Lien holomorphie - développements en série . 2.4.3 Résidus . . . . .

2.4.4 Holomorphie sous le signe somme .

2.4.5 Familles de fonctions holomorphes

2.5 Fonctions harmoniques . . . . 2.5.1 Harmonicité et holomorphie . . . . 2.5.2 Harmonicité et propriété de la moyenne 2.5.3 Principe du maximum . . . . . . . . 2.6 Compléments . . . . 2.6. 1 L'anneau des fonctions holomorphes

2.6.2 Algèbre de Banach complexe

2.6.3 Déterminations .

2. 7 Exercices corrigés . . . . .

3 ANALYSE FONCTIONNELLE

3.1 Analyse hilbertienne . . . . 3. 1 . 1 Espace muni d'un produit scalaire 3.1.2 Théorème de projection 3.1.3 Dualité . . . . . 3.1.4 Bases hilbertiennes . . . 3.1.5 Polynômes orthogonaux 3.1.6 Compléments . . . . . . 3.2 Convolution . . . . . 3.2. 1 3.2.2 3.2.3 Propriétés de la convolution . Convolution et régularisation Identités approchées 3.3 Séries de Fourier . . . . 3.3.1 Aspect hilbertien . . . . 3.3.2 Algèbre de convolution L1 {'Il')

3.3.3 Convergence au sens de Cesàro

3.3.4 Convergence ponctuelle 3.3.5 Régularité et estimation 3.3.6 Applications 3.4 Exercices corrigés . . . . . 51 53 54 56 56 58 61 62 62 63 66 67 69 71 71 72 72 73 73 74 74 77 91 91 91 95 103 107 1 10 1 1 2 1 13 114 1 16 1 19 122 123 125 127 129 131 132 133

TABLE DES MATIÈRES

4 ALGÈBRE LINÉAIRE

4.1 Théorie de la dimension

4. 1 . 1 Bases et dimension . . . . 4. 1 .2 Dimension et applications linéaires 4. 1 .3 Théorème du rang . . . . 4. 1 .4 Rang et matrices équivalentes . 4. 1 .5 Calcul du rang . . . . . . 4.2 Réduction des endomorphismes . . .

4.2.1 Sous-espaces stables . . . . 4.2.2 Polynômes et endomorphismes 4.2.3 Polynômes annulateurs et réduction 4.2.4 Réductions simultanées .

4.3 Endomorphismes remarquables . 4.3.1 Endomorphismes nilpotents 4.3.2 Endomorphismes cycliques 4.3.3 Endomorphismes diagonalisables

4.4 D'autres outils d'algèbre linéaire

4.4. 1 Déterminant . . . . 4.4.2 Opérations élémentaires 4.4.3 Une méthode

4.5 Codes Correcteurs . . . . 4.5.1 Notion de code correcteur

4.5.2 Distance et séparation des mots . 4.5.3 Codes cycliques . 4.6 Exercices corrigés . . 5 ALGÈBRE COMMUTATIVE 5.1 Quotient . . . . 5.1.l Surjection canonique . 5.1.2 Passage au quotient .

5.1.3 Quotients et structures algébriques .

5.2 Anneaux . . . . . 5.2.1 5.2.2 5.2.3 Morphismes d'anneaux . Anneaux euclidiens . Divisibilité . 5.3 Théorème chinois . . . . .

5.3.1 Autour du théorème chinois . 5.3.2 Factorisation de polynômes 5.4 Exercices corrigés . . . . ix 147 148 148 151 153 155 156 157 158 161 165 167 168 168 174 176 181 181 186 189 189 190 192 193 194 231 . 231 . 231 . 232 . 233 . 236 236 . 238 . 239 . 241 . 241 . 244 . 249

X TABLE DES MATIÈRES 6 MODULES 6.1 Structure de module . . . 6. 1 . 1 6.1.2 6.1.3 6.1.4

Modules sur un anneau . . Morphismes de A-modules . Sous-modules . . . . Module quotient . . . . .

6.2 Changement d'anneau de base 6.2. 1 Restriction des scalaires .

6.2.2 Lien entre A-modules et A/1-modules

6.2.3 A[X)-modules et A-modules . .

6.2.4 Lorsque A est un corps . . . .

6.3 Familles génératrices, familles libres 6.3.1 Définitions . . .

6.3.2 Modules de type fini . . . .

6.3.3 Modules libres . . . . .

6.4 Modules de type fini sur un anneau principal 6.4. 1 Approche théorique . . . .

6.4.2 Approche matricielle . . . .

6.4.3 Lien entre les deux approches . 6.5 Réduction des endomorphismes

6.5.1 Invariants de similitude 6.5.2 Réduction de Jordan . 6.6 Exercices corrigés . . . . 253 . 254 . 254 . 256 . 257 . 259 . 263 . 263 . 264 . 266 . 269 . 270 . 270 . 272 . 274 . 275 . 276 . 285 . 289 . 292 . 293 . 304 . 307 Bibliographie . . . 329 Index . . . 331

CHAPITRE 1

CALCUL DIFFÉRENTIEL

L'idée du calcul différentiel est d'approcher au voisinage d'un point une fonction f par une fonction plus simple (ou d'approcher localement le graphe de f par un espace plus simple).

Une fois les notations assimilées, les méthodes et les résultats du calcul différentiel sont naturels : ce sont les mêmes que pour l'étude des fonctions d'une variable réelle. On est ainsi amené

- à étudier la restriction des fonctions le long d'une droite comme, par exemple, pour démontrer les formules de Taylor.

- à généraliser les outils familiers en dimension 1 comme les changements de variables, l'inégalité des accroissements finis, etc.

Ce chapitre présente les résultats essentiels qui exploitent ces idées. Nous insistons sur leur mise en situation, en particulier en optimisation et pour l'étude des fonctions convexes. Nous nous appuyons régulièrement sur le livre de François Rouvière [RouJ qui est une excellente référence sur le sujet.

PRÉLIMINAIRES

Les définitions et les résultats sont valides dans les espaces de Banach réels.

Cependant, la dimension infinie amène des problèmes qui sont secondaires en cal­ cul différentiel (la dépendance vis-à-vis de la norme et la non-continuité automatique des applications linéaires) . On a alors besoin de résultats sur les espaces de Banach comme par exemple le théorème de l'inverse continue de Banach (voir [BRÉ, II.61) . Comme la plupart des illustrations et des exemples que nous proposons ont pour cadre la dimension finie, nous avons choisi de ne pas nous attarder sur ces questions. Dans cette section, E, F et G désignent des IR-espaces vectoriels normés. Sauf men­ tion explicite du contraire, ils sont supposés de dimension finie. La norme est notée

11 · li indépendamment de l'espace.

1.1 DIFFÉRENTIABILITÉ

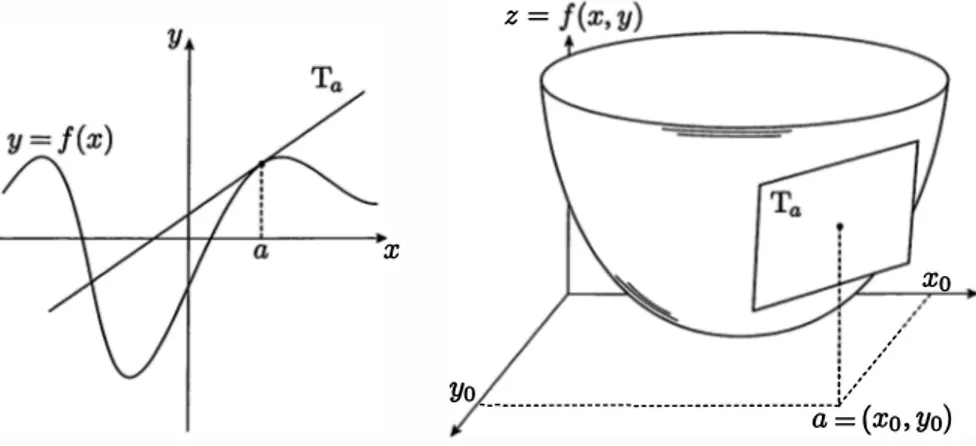
Les applications différentiables en un point a sont celles qui peuvent être appro­ chées au voisinage de a par une application affine. Intuitivement, le graphe de f « ressemble » localement à un espace affine Ta ·

2

y

CHAPITRE 1 - CALCUL DIFFÉRENTIEL

z =

f(x,

�y):---X

/ /

Xo

Yo

î,/ ---a = J (

xo,Yo

)

Fig. 1 . 1 Différentiabilité d'une fonction de lR dans lR et d'une fonction de IR.2 dans lR.

1 . 1 . 1 APPLICATIONS DIFFÉRENTIABLES

DIFFÉRENTIABILITÉ

1 . 1 . 1

Soient U un ouvert de E et f : U --+ F . On dit que f est différentiable en a

E

U s'il

existe l une .application linéaire

(

continue

)

de E dans F telle que

f(a +

h)

= f(a) +

l(h)

+ o

(llhll),

quand

h

tend vers O. Cette application lest unique

(

voir

[

RD03, 8. 1 . 1 . 1°]) : on l'ap­ pelle la différentielle de f en a. On choisit de la noter df

(

a

) (

d'autres notations courantes sont f'(a) ou Df(a)) . Insistons : df(a) est une application linéaire

(

conti­ nue

)

de E dans F. On note souvent df(a) ·

h E

F sa valeur prise en

h E

E.

Exemple 1.1 - Applications affines. Une application affine est la somme d'une application constante et d'une application linéaire.

Une application constante est différentiable partout et sa différentielle en tout point est l'application nulle. La réciproque est vraie si U est connexe

(

voir l'applica­ tion 1 . 14) . Ainsi l'application différentielle d'une application constante est elle-même constante et, par suite, une fonction constante est de classe <(?00 •

D'autre part, une application f linéaire

(

continue

)

est différentiable partout, et elle est sa propre différentielle en tout point :

V

h E

E, df

(

a

)

·

h

=

f(h).

L'application différentielle est ainsi l'application constante d

f

:

x

1-t f. Une applica­

tion linéaire

(

continue

)

est donc de classe <(/00• Bref, une application affine

(

continue

)

est de classe <(/00•

Exemple 1.2 - Différentielle d'un « produit ». Soit B une application bilinéaire

(

continue

)

d'un produit Ex F dans G. Alors B est différentiable en

(a, b) E

Ex F et

V

(h, k) E

Ex F, dB

(

a, b) ·

(h, k)

= B

(

a,

k)

+

B(h,

b).

En particulier, on peut différentier le produit scalaire d'un espace euclidien

(

voir l'exemple 1.12

)

.

1.1.1 DIFFÉRENTIABILITÉ 3

Exemple 1.3 - Dans les espaces de matrices. L'analyse matricielle regorge

d'exemples intéressants.

- Lors de la démonstration du lemme 1 .31 de Morse, on s'intéresse à la différentielle de l'application M E Mn{IR) i--+ tMAoM E Sn, où Ao E Sn.

- Le calcul de la différentielle de l'inverse sur GLn{IR) est fait directement dans l'exercice 16 de [Rou) ou via les dérivées partielles dans l'exercice 7 de [GOU2, p.309) . La première méthode présente l'avantage d'être valable en dimension infinie et a fait l'objet de la troisième partie du sujet d'analyse de 1999.

- la différentielle du déterminant M E Mn{IR) i--+ det{M) E lR est un autre exemple classique. (voir l'exercice 25 de [Rou) ou l'exercice 7 de [GOU2, p.309) ainsi qu'une application à l'exercice 1 .5).

Exemple 1.4 - Sandwich. Soient f : E - JR et a E E. Considérons deux applications

m : E - JR et M : E - JR

différentiables en a avec la même différentielle dm{a) = dM{a) en a et vérifiant

m(a) = f(a) = M(a) et m(y) � f(y) � M(y)

pour y proche de a. Alors f est différentiable en a, avec df(a) = dm{a) = dM{a).

M

Ce résultat exprime simplement ce qui est évident sur un dessin : une courbe prise « en sandwich » entre deux courbes ayant la même tangente admet cette même tangente. Démontrons ce résultat. Posons

f

= dm{a) = dM{a) et écrivons, pour tout

h

suffisamment petit,

m(a +

h)

� f(a +

h)

� M(a +

h).

D'où m(a +

h)

- m(a) � f(a +

h)

- f(a) � M(a +

h)

- M(a) c'est-à-dire

f(h)

+ o

(h)

� f(a +

h)

- f(a) �

f(h)

+ o

(h).

Finalement f(a +

h

₎ - f(a) =

f

(

h

) + o

(h),

ce qui permet de conclure.

Remarque 1.5 - Identifications. Ajoutons que deux identifications sont utilisées en

permanence en calcul différentiel : l'une concernant la différentielle seconde, l'autre les fonctions d'une variable réelle.

Soit f : E - F une application deux fois différentiable en a. Cette hypothèse im­ pose à f d'être différentiable dans un voisinage de a. Pour tout x dans ce voisi­ nage, df(x) appartient à 2'{E, F) , et donc la différentielle au point a de l'applica­ tion x i--+ df(x) appartient à 2'(E, 2'(E, F)) . Cet espace est identifié avec l'espace 2'2 (E, F) des applications bilinéaires de E dans F grâce à l'isomorphisme

{

2(E, 2'{E, F)) � 2'2 (E, F)

u

f-+ ((

h, k

) i--+

u(h)(k)) .

4 CHAPITRE 1 _- CALCUL DIFFÉRENTIEL 1.1.1 La deuxième identification précise pourquoi la différentiabilité est bien une exten­ sion de la dérivabilité. Soit f : lR -F. La différentiabilité en a équivaut (par définition) à la dérivabilité en a, et la différentielle est h 1--+ f'(a)h. Ainsi, avec l'isomorphisme

{

2'(1R, F) � F u 1----t u(l),

on identifie dérivée et différentielle. Notez que certains livres (comme ICIA)) parlent d'applications « dérivables » pour dire « différentiables » , et de « dérivées » pour dire « différentielles ».

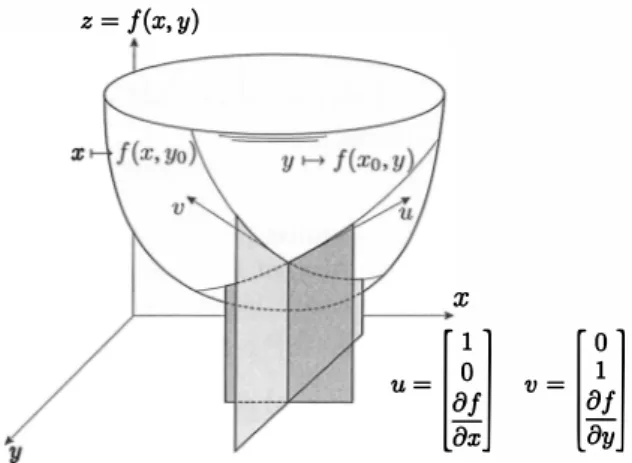
DÉRIVÉES DIRECTIONNELLES

Soit f une application d'un ouvert U de E dans F. On dit que f est dérivable en a E U selon h E E si la fonction partielle t 1--+ f(a + th) est dérivable en O. Sa dérivée

est la dérivée partielle ou la dérivée directionnelle de f dans la direction h. On la note

:�

(a) ou

:�

(a) si h = ei et (ei, ... , en) une base de E.

Certains ouvrages utilisent d'autres notations, comme âhf(a) ou Dhf(a).

z = f(x,y)

X

U=

[�]

V=

[f]

Fig. 1 . 2 Dérivées directionnelles d'une fonction de IR.2 dans IR

Si f est différentiable en a E U, alors les dérivées directionnelles en a existent et

on a l'égalité

âf

âh (a) = df(a) · h.

La réciproque est fausse : l'existence des dérivées partielles dans toutes les direc­ tions n'implique pas la différentiabilité. C'est bien naturel puisque la connaissance du comportement des fonctions partielles (même dans toutes les directions) ne donne d'information sur le comportement de f'que sur les droites issues de a. Or, dans la définition de la différentielle, h peut tendre vers 0 « en tournant autour ».

Contre-exemple 1 . 6 Soit l'application définie par f(x, y) = y2 /x si x # 0 et

f(O, y) = y sinon. Elle est dérivable en (0, 0) dans toute direction, mais elle n'est même pas continue. Cet exemple est proposé dans IRD03, 8.1.1.5°J et corrigé à l'exercice 1 de loou2, p.305J. L'idée géométrique est d'approcher (0, 0) en tournant (le long de la parabole x = y2) . On a f(y2,y) = 1 et donc f(y2,y) ne tend pas /(0, 0) = 0 quand

1.1.1 DIFFÉRENTIABILITÉ 5

Remarque 1.7 - Affine VS vectoriel. En calcul différentiel, l'espace de travail possède une structure d'espace vectoriel et donc aussi une structure d'espace af­ fine. Il n'est pas toujours désirable de distinguer vecteurs et points, mais il est bon de garder à l'esprit la cohabitation des deux en calcul différentiel. Par exemple, pour la dérivée directionnelle, on dérive une fonction en un point dans la direction d'un vecteur.

GRADIENT

Soient (E, ( ·, ·}) un espace euclidien (ou un espace de Hilbert) et

f:

E --+ lR une

application différentiable en a E E. Par définition, df(a) est une forme linéaire (conti­ nue) sur E. D'après le théorème 3.29, il existe un unique vecteur de E, noté \1

f(a),

tel que

df(a)

· h

=

(\/

f(a),

h} pour tout h E E.

On l'appelle gradient de

f

en a. Remarquez que le gradient dépend du produit scalaire choisi sur E.

z = f(x,y)

X

y

{(x,y), f(x,y)=zo}

\lf(ao)

Fig. 1.3 Gradient d'une fonction de IR2 dans lR

Si E

= Rn

muni de sa structure euclidienne canonique, il y a essentiellement deux méthodes pour calculer le gradient :

- en revenant à la définition, - via les dérivées partielles

(

âf

âf

)

\1

f(a) = âx1

(a), · · · '

ÔXn

(a) ·

Attention, ce n'est pas parce que toutes les dérivées partielles existent que le vecteur des dérivées partielles est égal au gradient. En effet, le gradient n'est défini que pour des applications différentiables. De plus, cette notion ne concerne que les fonctions à valeurs dans lR.

Remarque 1.8 - Interprétation géométrique. Géométriquement, le gradient en a (supposé non nul) peut s'interpréter de trois manières.

- \1

f(a)

indique la direction « de la plus forte pente » de

f

en a (voir !ROU, ex.27)). - Le graphe de la fonction

f

est une hypersurface de Ex lR dont l'espace tangent est

6 CHAPITRE 1 - CALCUL DIFFÉRENTIEL 1 . 1 .2

- 'V l(a) dirige la normale à « l'hyperplan tangent » en a à « l'hypersurface »

S = {x E E, l(x) = l(a)}.

Si l'on trace sur S une courbe dérivable 'Y qui passe par a en t = 0, son vecteur tangent -y'(O) est orthogonal à 'Vl(a) (pour le voir, dériver par rapport à t l'égalité 1 o -y(t) = l(a)).

Le cadre justifiant proprement tout ceci est celui des sous-variétés (auquel !Rou, Ch.5) est une bonne introduction) .

1 . 1 . 2 LEMME FONDAMENTAL DE COMPOSITION

Le lemme technique suivant est extrêmement important : il généralise la formule de dérivation des fonctions composées et il est d'usage permanent.

Lemme 1 . 9 - Différentiabilité d'une composée. Soient U un ouvert de E, V un ouvert de F et a un point de U tel que l(a) E V. Si 1 : U - _F et g : V - G sont différentiables respectivement aux points a et l(a), alors g o 1 est différentiable au point a et

d(g o f) (a) = dg (f(a)) · dl(a) .

Pour démontrer ce lemme, il suffit d'écrire le développement limité de g o 1 en a au premier ordre (voir !Rou, Ch.2) pour le schéma de la preuve et IRD03, 8.1 .2) pour les détails) .

L'identité d'Euler donne un exemple d'utilisation de ce lemme (voir !ROU, ex.20)). Par ailleurs, en appliquant ce lemme à une fonction bijective 1 et à son inverse, on obtient le résultat suivant.

Application 1 . 1 0 - Différentielle de la réciproque. Soit 1 : U c E - F une bijection de U sur l(U) . Si 1 est différentiable en un point a E U et si 1-1 est différentiable au point l(a) , alors dl(a) est un isomorphisme de E sur F et

d(f-1 ) (f(a)) = dl(a)-1 .

Sous ces hypothèses, dl(a) réalise donc un isomorphisme entre E et _F (qui sont ainsi de même dimension) .

L'inconvénient de cet énoncé est qu'il exige que de 1-1 soit différentiable en l(a), ce qui est difficile à vérifier. Pour y remédier, on ajoute des propriétés à 1 (que 1 soit de classe '!&' 1 et de différentielle inversible en a) pour se passer de celles sur 1-1 (que 1 soit différentiable en l(a)). Cela donne le premier théorème fondamental du calcul différentiel : le théorème d'inversion locale (voir la section suivante) .

Ajoutons que si 1 est simplement un homéomorphisme, E et F sont aussi de même dimension, mais c'est plus difficile à prouver (sauf si E =

R

car on dispose alors d'un argument de conn�xité, voir l'exercice 7 de laou2, p.46)).

Exemple 1 .11 - Restriction à un segment. Soit 1 différentiable sur un ouvert U de E. Pour tous a, b E U tels que le segment 1 a , b J soit dans U, l'application

{

I0 ,1) - F

cp ·

t �l(a+t(b - a))

est dérivable sur I0 , 1 ) et cp'(t) = dl(a + t(b - a)) · (b - a) pour tout t E IO , l). C'est une application directe du lemme de composition 1.9 que l'on retrouve très

1 . 1.3 DIFFÉRENTIABILITÉ 7

souvent, comme par exemple dans la démonstration de l'inégalité des accroissements finis IRD03, 8.1 .3. 1°J et celle des développements de Taylor IRD03, 8.3J .

Exemple 1.12 - Norme au carré. Soient (E, (·, ·)) un espace euclidien et g une

fonction de classe

'i&'1

sur un ouvert U de E. Posons N : x 1-+ llxll 2 et G = N o g. Alors G est de classe 'if

1

sur U et

'Vx E U, 'Vh E E, dG(x) · h = 2(g(x), dg(x) · h) .

On démontre ceci en appliquant deux fois le lemme 1 .9. Commençons par observer que N est la composée de l'application linéaire i : x 1-+ (x, x) avec l'application bilinéaire

b : (x,y) 1-+ (x,y) . D'après les exemples 1 . 1 et 1.2, N est différentiable et

dN(x) · h = db(i(x))(di(x) · h) = db(x, x) · (h, h) = (x, h) + (h, x) = (2x, h) .

On en déduit que G est différentiable et que

dG(x) · h = dN(g(x)) · (dg(x) · h) = 2(g(x), dg(x) · h) .

On retrouve notamment une fonction de ce type au cours de la preuve du théorème d'Hadamard-Lévy proposée dans IZQ, p.392J . Remarquez que cette preuve utilise une hypothèse supplémentaire de régularité justement pour pouvoir faire ce calcul.

1 . 1 . 3 INÉGALITÉ DES ACCROISSEMENTS FINIS

L'inégalité des accroissements finis (parfois appelée inégalité de la moyenne) per­ met de majorer l'accroissement de f entre deux points avec un majorant de la norme de sa différentielle.

Théorème 1.13 - Inégalité des accroissements finis. Soient U un ouvert de E et f : U -t F une application différentiable sur U. Soit [ a , b) un segment contenu dans U.

S'il existe M > 0 tel que lldf(x) ll � M pour tout x E la , b J , alors

llf(b) - f(a) ll � M ll b - all . Ce théorème généralise l'inégalité des

accroissements finis pour une unique variable réelle (voir IRD03, 4.2.1 . 1°1). D'ailleurs, l'inégalité en dimension su­ périeure se montre grâce à l'inégalité en une dimension via la fonction cp de l'exemple 1 . 1 1 (voir IRD03, 8.1 .3. 1°1). Nous renvoyons aux intéressants com­

mentaires de !ROU, chap.3J. _{d = IJ(b) -f(a)I}

D

d

b

D = M lb - al

Remarquons que si f est de classe

'i&'1,

l'existence du majorant M est assurée par la compacité du segment [ a , b) et la continuité de x 1-+ df(x). Soulignons qu'il

faut que U soit convexe pour appliquer l'inégalité entre deux points quelconques de U. Ajoutons aussi que la norme de df(x) qui apparaît dans l'énoncé est la norme d'application linéaire associée aux normes de E et F :

lldf( ) Il =

X ���

lldf(x) ll hllE · hllF .

Lorsque l'inégalité des accroissements finis est utilisée pour montrer que f est contrac­ tante, le choix des normes est primordial (voir !Rou, ex.32]).

8 CHAPITRE 1

-

CALCUL DIFFÉRENTIEL 1 . 1 .4 Application 1 .14 - Différentielle nulle. Soit U un ouvert connexe de E ; alors

V x E U, df(x) = 0 {::::==} f est constante sur U.

L'implication ( <=) est toujours vraie. L'hypothèse de connexité permet de démontrer ( =>) en exploitant l'équivalence suivante (voir [GOU2, 1.4.3]) pour un ouvert U

U connexe {::::==} U connexe par arc {::::==} U connexe par lignes brisées. Ajoutons que si la différentielle est nulle mais U n'est pas connexe, la fonction f est constante seulement sur chaque composante connexe de U.

Application 1 . 15 - Caractérisation des fonctions �1• Soient U un ouvert de

IR.n

et f : U--+ F une fonction dont les dérivées partielles existent en tout point de U. On ne peut pas en déduire que _f est différentiable sur U (voir le contre-exemple 1.6). Mais dès lors què les dérivées partielles existent et sont continues, alors f est de classe

'6'1

sur U, et donc notamment différentiable (voir [ROU, ex.37]). Comme la réciproque est vraie, c'est ainsi une caractérisation des fonctions

'6'1

(utilisée constamment). Application 1 . 1 6 - Théorème de Schwarz. Soit f une application d'un ouvert U de

IR.n

dans F. Si f est deux fois différentiable au point a E U alors, pour 1::;; i, j ::;; n,

on a

82! 82!

d2 f(a)(ei)(eJ) = 8Xi8Xj (a) = ÔXj8Xi (a) = d2 f(a)(eJ)(ei)·

Voir le théorème 6.1 dans [RouJ. Le théorème de Schwarz est parfois donné avec d'autres hypothèses (voir [GOU2, p.302J et l'exercice 1 de [GOU2, p.305]).

Ce théorème permet d'identifier la différentielle seconde d2 f(a) avec une applica­ tion bilinéaire symétrique sur E (via le premier isomorphisme de la remarque 1.5). En particulier, lorsque f est à valeurs réelles, d2 f(a) est identifiée à une forme bi­ linéaire symétrique et donc aussi à une forme quadratique. La matrice représentant cette forme quadratique dans la base canonique est appelée la hessienne de f en a.

On la note

(

82!

)

Hf(a) = �(a) _{Xi X3} .

i,j

Maintenant qu'on peut intervertir deux dérivées partielles, on peut faire de même pour toute permutation de plusieurs dérivées partielles (puisque les transpositions engendrent les permutations). Ainsi, l'ordre des dérivations partielles n'a pas d'in­ fluence. A priori, il y avait donc nP dérivées partielles p-ièmes. On sait maintenant

qu'il n'y en a en fait que C�-Hp (voir l'exercice 4.1).

Application 1 . 1 7 - Différentielle d'une limite. Il existe un théorème en plu­ sieurs variables analogue au théorème [RD04, 2.2.3.1°J de la variable réelle. Sous des hypothèses de convergence uniforme, la différentielle de la limite est la limite des dif­ férentielles (voir [ROU, ex.38J pour un énoncé précis, une preuve et une application) .

1 . 1 . 4 UTILISATIONS DE LA DIFFÉRENTIELLE

DIFFÉRENTIABILITÉ

La différentielle d'une fonction en un point approche cette fonction au premier ordre autour de ce point. En fait, une information sur la différentielle en un point permet d'obtenir des propriétés de la fonction elle-même au voisinage de ce point.

1 .2. 1 INVERSION LOCALE ET FONCTIONS IMPLICITES 9

Cette idée centrale se retrouve notamment :

- dans le théorème d'inversion locale (voir la section 1 .2),

- pour les conditions nécessaires du premier ordre vérifiées par les minima (voir la sous-section 1 .3.2),

- lors de l'étude qualitative des équations différentielles : la stabilité d'un point cri­ tique peut se lire sur la différentielle (voir le théorème !zQ, X.IV.4)) .

Lorsque l'approximation au premier ordre ne suffit pas, on peut la préciser par les différentielles supérieures : ce sont les formules de Taylor, étudiées au paragraphe 1 .4.

CHANGEMENT DE VARIABLES

Énonçons l'important théorème du changement de variables dans une intégrale.

Théorème 1.18 - Changement de variables. Soient U un ouvert de !Rn et cp : U --+ !Rn une application injective et différentiable sur U. Alors V = cp(U) est mesurable et une fonction f appartient à L1 {V) si, et seulement si, la fonction ldet dcpl f o cp est

dans L1 (U). Dans ce cas,

fv

f(x) dx =

L

f(cp(y)) ldet dcp{y) l dy.

La preuve de ce théorème est basée sur le théorème 4.83. Une fois de plus, l'idée est d'approcher autour de chaque point y la transformation cp par sa différentielle dcp{y). Ainsi localement, cp affecte le volume infini­ tésimal de la même manière que l'applica­ tion linéaire dcp{y) : en le multipliant par ldet dcp{y) I . Attention à ne pas oublier le déterminant et la valeur absolue dans la for­ mule de changement de variables.

f(xo

(y

ldet df{xo)IA

Signalons aussi que le résultat est encore vrai sous des hypothèses plus faibles (voir !RUD, 7.26]). Nous l'énonçons ici sous une forme plus pratique, que l'on peut encore simplifier en supposant que cp est un difféomorphisme de U sur V.

On utilise três souvent des changements de variables pour calculer ou ré-exprimer des intégrales (voir par exemple l'exercice 1 .4) .

Application 1.19 - Calcul de loi. En probabilité, ce théorème permet de calculer

la loi d'une variable aléatoire définie à partir d'autres variables aléatoires dont on connaît la loi (voir les exemples 8.3 et 8.4 ainsi que l'exercice 8.4 de !ouv)) .

1.2 INVERSION LOCALE ET FONCTIONS IMPLICITES

Le théorème d'inversion locale établit qu'une fonction de classe <6'1 est localement un <6'1-difféomorphisme dès lors que son premier ordre l'est. Le théorème des fonctions implicites exprime qu'une courbe définie implicitement par une équation du type f(x, y) = 0 peut être vue localement comme le graphe d'une fonction.

Les deux théorèmes servent à créer des fonctions. Comme ce n'est pas facile en général, ces théorèmes apportent un véritable plus. Pensez-y quand vous voyez une question du genre « montrer qu'il existe f de classe <6'1 telle que ... ».

10 CHAPITRE 1 - CALCUL DIFFÉRENTIEL

1 . 2 . 1 FONCTIONS INVERSES, FONCTIONS IMPLICITES

1.2.1

Théorème 1.20 - I nversion locale. Soient U un ouvert de E, a un point de U et f : U --+ F un application de classe C(lk

(

k

;;::: 1). Si df (a) est un isomorphisme de E

dans F, alors il existe un voisinage ouvert V C U de a et un voisinage ouvert W C F de f (a) tels que la restriction de f à V est un C(!k _difféomorphisme de V sur W.

f

Fig. 1.4 Inversion locale

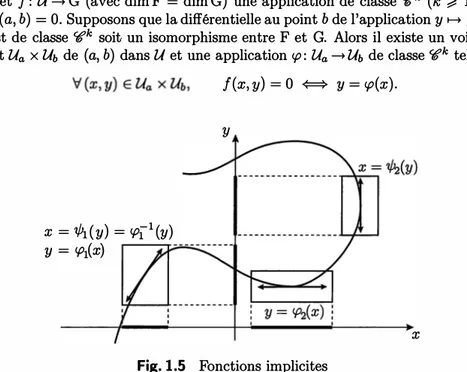
Théorème 1.21 - Fonctions implicites. Soient U un ouvert de Ex F, (a, b) un point de U et f : U --+ G (avec dim F

=

dim G) une application de classe C(lk

(

k

;;::: 1) telle

que f(a, b) = O. Supposons que la différentielle au point b de l'application

y

1-+ f(a,

y)

qui est de classe C(lk soit un isomorphisme entre F et G. Alors il existe un voisinage ouvert Ua X ub de (a, b) dans u et une application

<p:

Ua --+ ub de classe C(lk telle que

f(x, y) =

0 <=:::}

y = <p(x).

y

X

= 1/J1 ( y) = <p!1 ( y)

Y

= <pi(x)

X

Fig. 1.5 Fonctions implicites

Vous trouvez dans !Rou, Ch.5J des figures illustrant ces théorèmes et des re­ marques concernant les applications pratiques. Nous conseillons vivement la lecture de ce passage, en méditant sur cet extrait du rapport du jury de 2002

:

« L'importance du théorème des fonctions implicites et du théorème d'inversion locale du point de vue géométrique ne saurait apparaître si l'on se noie dans le formalisme analytique. Une étude illustrée par des figures en dimensions 2 ou 3 est plus adéquate ».

1.2.2 INVERSION LOCALE ET FONCTIONS IMPLICITES 1 1

Remarque 1.22 - Même dimension. Remarquez que F , l'espace d'arrivée de <p, est de même dimension que

G,

l'espace d'arrivée de f. Pour appliquer le théorème, on décompose l'espace de départ de f en deux blocs dont l'un a la même dimension que l'espace d'arrivée de f.

En particulier, si f :

IR.2-+ IR.,

on peut choisir quelle variable exprimer en fonction de l'autre (voir la figure 1 .5) : on peut appliquer le théorème pour obtenir

y= ip(x)

si

:�(a,

b) :f 0 ou

x

=

'l/J( y)

si

:�(a,

b) :f O.

Remarque 1.23 - Même régularité. Notez qu'une fonction créée par le théorème

d'inversion locale ou le théorème des fonctions implicites possède la même régularité que la fonction f de départ.

Par exemple, on obtient ainsi l'existence du développement limité de la fonction implicite <p du théorème 1.21. On peut alors le calculer explicitement (voir l'exer­ cice 2 de [GOU2, p.322), attention, les coefficients du développement donnés dans le

corrigé ne sont pas les bons). •

Ajoutons un mot à propos des démonstrations. La preuve du théorème d'inversion locale est un peu longue mais reste élémentaire. Elle illustre la méthode qui consiste à se mettre de toute force dans une situation canonique : ici celle du point fixe de Picard (voir [ROU, ex.70) ou [GOU2, V.3.1)). On en déduit ensuite le théorème des fonctions implicites en ajoutant une variable (voir [ROU, 5.3)). On peut aussi faire le chemin inverse : les deux théorèmes sont équivalents.

Soulignons que ces deux théorèmes sont obtenus à partir d'une hypothèse ponc­ tuelle sur la différentielle. Le fait que f soit au moins de classe '6'1 permet alors d'étendre cette hypothèse à un voisinage de

a.

1 . 2 . 2 APPLICATIONS

Application 1.24 - Racine k-ième d 'une matrice. Soient un entier k E N* et une matrice A E

Mn{IR.).

Si A est suffisamment proche de l'identité Id, alors A est une racine k-ième c'est-à-dire il existe B E

Mn{IR.)

telle que Bk = A. Pour démontrer ceci, considérons

. {

Mn{IR.)

---+

Mn{IR.)

f . B f----+ Bk .

Chaque fonction composante de f est une fonction polynomiale en les coefficients de B, donc f est de classe '6'00 • Observons que f(Id) = Id. Effectuons le dévelop­ pement {Id + H)k = Id + kH + o {H) avec la formule du binôme (puisque Id et H commutent) pour obtenir df{Id) = k ldMn(IR) · On applique le théorème d'inversion locale en Id pour assurer que f est un difféomorphisme entre deux voisinages U et V de Id. Bref, pour tout A E V, il existe B E U telle que Bk = A (et, de plus, la dépendance est '6'00) .

Application 1.25 - Algèbre linéaire. Le comportement en 0 de l'exponentielle matri­ cielle et le fait qu'il n'existe pas de « petits » groupes dans

GLn{IR.)

sont des exemples d'applications du théorème d'inversion locale en algèbre linéaire (voir [MT₎₎.

Application 1.26 - Régularité d'une racine simple d'un polynôme. Soient Po un polynôme de

IR.n(X)

et

xo

une racine simple de Po. Alors la racine dépend localement du polynôme de manière '6'00 • Précisément, montrons qu'il existe une application <p de

12 CHAPITRE 1 - CALCUL DIFFÉRENTIEL 1.2.3

classe <-(/00 définie sur un voisinage

U

de

Po

dans

IRn (X]

à valeurs dans un voisinage V

de

xo

dans

IR

telle que

'v'P

EU, Vx EV, x =

<p(P) <===>

P(x) = O.

Considérons pour cela l'application de classe <-(!00

{

IRn(X]

x

IR-+ IR

f

· ·

(P, x) �

P(x) .

On calcule sa dérivée partielle par rapport à la seconde variable : âf (P )-l· P

(x +

y

) -

P

(x)

_ P'

( )

â

X

,X

- lm y-O y -

X.

On a donc

��

( Po, xo)

=F 0 puisque la racine

xo

de

Po

est simple. Le théorème des fonctions implicites permet alors de conclure.

Application 1 .27 - Polynômes scindés à racines simples. Soit Yrs l'ensemble des

polynômes de

IRn(X]

scindés à n racines simples. Montrons que Yrs est un ouvert

de

IRn(X].

Soient Q

E

Yrs et

(x1, .. . , Xn)

ses racines. D'après l'application précédente, il existe pour chaque i

E

[ 1 , n B une application 'Pi de classe <-(/00 définie sur un

voisinage ui de Q dans

IRn (X]

à valeurs dans un voisinage Vi de Xi dans

IR

telle que

x =

'Pi(P) <===>

P(x) = O.

Les Xi sont distincts. On peut donc considérer, pour tout i

E

[1

,

n B, des voisinages

ouverts VI C Vi des Xi deux à deux disjoints. Posons

Uf =

'Pi

-l

(VD. Comme les fonctions 'Pi sont continues, les

U

f sont des voisinages ouverts de Q. Alors

n

U =

_i=nui

l

est un voisinage ouvert de Q. De plus, pour P

EU,

les 'Pi (P)

E

Vf sont des racines distinctes de P, d'où P

E

Sl;.8• Bref, on a exhibé un voisinage ouvert de Q inclus dans .51;.8• Ainsi Yrs est un ouvert de

IRn(X].

Application 1 .28 - Géométrie. L'interprétation géométrique de ces théorèmes en

fait des outils de base de la géométrie différentielle. En particulier, ils permettent de démontrer l'équivalence des différentes définitions d'une sous-variété (voir [ROU, 5.4] pour une introduction et des références) .

Contre-exemple 1 .29 - Sans théorème. Soit

f: IRn

-of

IR

de classe <-t!00• Montrons

qu'il existe un difféomorphisme <p de

JRn+l

qui « aplatit le graphe de

f

en un hyperplan de

JRn+l

» c'est-à-dire tel que

ip({(x,f(x)), xEIRn}) = {xeJRn+l, Xn+i = O}.

Une petite mise en garde : si le théorème d'inversion locale est très utile pour construire des fonctions, on peut parfois raisonner directement. On construit ici <p « à la main » en posant

)Rn

X

IR

�

JRn

X

IR

(x,t)

�

(x,t - f(x))

(u,v+f(u))� (u,v),

1.2.3 INVERSION LOCALE ET FONCTIONS IMPLICITES

1 . 2 . 3 GÉNÉRALISATIONS

On considère deux directions pour généraliser le théorème d'inversion locale : - ajout d'hypothèses pour avoir un résultat global,

- affaiblissement des hypothèses : que peut-on alors dire ?

VERSION GLOBALE

13

Commençons par un résultat que l'on rencontre souvent : si une application f est différentiable sur un ouvert U et que df(x) est inversible en tout point x E U, alors f est une application ouverte (voir l'exercice 1 .6). En fait, avec l'injectivité de f en plus, on obtient le résultat suivant.

Théorème 1 .30 - Théorème d'inversion globale. Soient U un ouvert de E et f : U --+ F de classe '6'1 . Alors f est un '6'1-difféomorphisme de U sur l'ouvert f (U) si, et seulement si, f est injective sur U et df(x) est un isomorphisme pour tout x E U.

f -l gi = 1

V

Fig. 1 .6 L'injectivité empêche de tels « recouvrements » : on a un résultat global

Le théorème global est une application directe du résultat local : on applique le théorème d'inversion locale en tout x E U pour obtenir autour de chaque f(x) des réciproques de f de classe '6'1 ; l'injectivité assure alors que ce sont les restrictions d'une même application définie sur f(U) . Ainsi, la situation de la figure 1.6 est exclue. Nous renvoyons aux commentaires de [ROU, Th.5.3] et à la démonstration de [RD03, 8.5.5.3°] . Ajoutons que f(U) doit être ouvert puisqu'un difféomorphisme a toujours lieu entre deux ouverts (la différentiabilité se définit sur des ouverts) .

Le théorème d'inversion globale n'est pas d'usage aisé à cause de la vérification de l'injectivité de f. Il est utilisé aux exercices 1 .4 et 1.7 ainsi qu'aux exercices 3, 5 et 6 de [aou2, V.3.3] par exemple. Un autre énoncé global qui caractérise les difféomorphismes de

!Rn

sur

!Rn

est le théorème d'Hadamard-Lévy (voir [zQ, p.392]). Par ailleurs, les versions holomorphes des théorèmes d'inversion sont présentées à la sous-section 2.3.3.

RANG DE LA DIFFÉRENTIELLE

L'utilisation du théorème d'inversion locale nécessite que l'espace de départ de f (de dimension n) et son espace d'arrivée (de dimension p) aient la même dimension

(n = p). La condition imposée sur la différentielle signifie que son rang est maximum.

14 CHAPITRE 1 - CALCUL DIFFÉRENTIEL 1 .2.3

différentielle garde cette propriété de rang maximum (c'est-à-dire injective si n < _p

ou surjective si n > _{p) ?}

- Premier cas : n < p . Soit une application f : U -JRP de classe 'if 1 telle que df (a)

est injective en a E U (on dit que f est une immersion en a) . La première chose à remarquer est que df(x) est alors injective dans tout un voisinage de a. En effet, le déterminant d'une matrice extraite de taille n x n est non nul en a et donc aussi dans un voisinage de a (par continuité du déterminant). D'après la caractérisation par déterminants extraits (voir la sous-section 4.1.5), df(x) est de rang n dans ce voisinage de a. Le théorème d'immersion [ROU, ex.72) dit qu'il n'y a localement qu'une seule immersion à un difféomorphisme près à l'arrivée : c'est l'injection canonique de IRn dans JRP

(xi , . . . , Xn) 1---t (x1 , . . . , Xn , 0, . . . , 0).

- Second cas : n > _{p .} On obtient un résultat analogue pour la surjectivité (voir [ROU, ex. 71)). Une application f : U -JRP de classe '6'1 telle que df (a) est surjective

en a E U (on dit que f est une submersion en a) est localement la projection 7r de

IRn sur JRP

7r : (xi , . . . , Xn) 1---t {xi , . . . , xp) ,

à un difféomorphisme près au départ.

En combinant les deux démonstrations, on obtient le théorème du rang constant (voir [ROU, ex.73)). Ces trois résultats sont d'intéressantes applications des méthodes d'algèbre linéaire (calcul du rang par le déterminant, théorème de la base incomplète, etc.). Par ailleurs, ces résultats sont des généralisations aux fonctions '6'1 de résultats connus pour les applications linéaires (voir théorème 4.19) : ceci illustre aussi le fait que f récupère les propriétés de son approximation au premier ordre.

Supposons à présent que f soit à valeurs dans IR. La surjectivité de l'application df(a) équivaut donc à sa non-nullité (voir application 4.10). Ainsi, si f : U -lR est

de classe '6'1 et telle que df(a) =f. 0, alors f est une forme linéaire à un difféomor­ phisme local près. Que se passe-t-il si df(a) = 0 ? On va chercher plus loin dans le

développement de Taylor : on démontre que f est une application quadratique, à un difféomorphisme local près, dès que sa hessienne en a est non dégénérée.

Lemme 1.31 - Lemme de Morse. Soient un ouvert U de IRn contenant 0 et f : U -JR une application de classe '6'3. Si d/ {O) = 0 et si d2 f (0) est une forme

quadratique non dégénérée de signature {p, n _{- p),} alors il existe un difféomorphisme cp = ('Pl , . . . , 'Pn) entre deux voisinages de 0 tel que cp(O) = 0 et

z

f(x) - f(O) = 'Pl 2(x) + · · · + 'Pv2 (x) - 'Pv+i 2(x) -· · · -'Pn 2 (x).

1.3.1 OPTIMISATION 15 Une première idée pour démontrer le lemme de Morse est de raisonner par ré­ currence sur la dimension en copiant la méthode de Gauss de réduction des formes quadratiques (voir [PHA, p.171). Une autre preuve s'appuie sur le théorème d'inversion locale (voir [ROU, ex. 1 101) .

Remarque 1.32 - Une condition suffisante d e minimalité. Soit une application f :

!Rn-+ lR

de classe 'if3 telle que df (0) = 0 et que d2 f (0) est définie positive (c'est­ à-dire de signature (n, 0)) . Alors 0 est un minimum local (strict) de f.

En effet, on a, pour tout x proche de 0,

f(x) - f(O) = <p1 2 (x)

+

· · ·

+ 'Pn

2 (x).

Ainsi J(x) - f(O) > 0 tout x non nul proche de 0 (puisque <p ne s'annule qu'en 0 sur un voisinage de 0) et donc 0 est un minimum local (strict) de f. En fait, ce résultat ne nécessite pas le lemme de Morse : il s'obtient sous des hypothèses plus faibles avec un développement de Taylor (voir le lemme 1.38) .

1.3 ÜPTIMISATION

Soient C une partie de E et f une application de E dans IR. On considère le problème d'optimisation minimiser f sous la contrainte que x reste dans C, ce qui s'écrit

inf {f(x) , x E C}.

La fonction f est appelée l'objectif et l'ensemble C la contrainte du problème. On ai­ merait connaître la valeur de cette borne inférieure f* et surtout trouver un point x* E C réalisant f(x*) = f* (s'il en existe). L'attaque d'un tel problème se fait en quatre temps :

- Existence : si f est minorée alors la borne inférieure existe dans IR. Existe-t-il un point de C qui atteigne cette valeur ?

- Unicité : y a-t-il unicité d'un point réalisant le minimum ? Sinon, l'ensemble de ces points est-il « structuré » (borné, fini, convexe ... ) ?

- Localisation : comment peut-on savoir qu'un point x E C réalise le minimum ?

Quelles sont les conditions suffisantes, nécessaires ou les caractérisations éventuelles d'un point minimum ?

- Calcul : existe-t-il une expression du minimum ? Sinon, dispose-t-on d'un algo­ rithme qui permette d'approcher un point réalisant le minimum ?

Les problèmes d'optimisation apparaissent souvent en mathématiques mais aussi dans des applications concrètes : minimiser le coüt de production d'une marchandise, minimiser le risque d'un placement en bourse, minimiser le temps d'attente d'un avion au sol, etc. Une fois modélisés, ces problèmes s'écrivent sous la forme d'un problème d'optimisation à résoudre numériquement. Le quatrième point est alors essentiel. Nous en touchons donc un mot à la sous-section 1 .3.3.

Dans le reste de cette section, on s'intéresse surtout au troisième point qui offre un terrain d'application du calcul différentiel. D'autres résultats d'optimisation se trouvent à la section 1.5 sur les fonctions convexes. Ajoutons que la section 2.5.3 étudie les propriétés d'optimalité des fonctions holomorphes.

16 CHAPITRE 1 CALCUL DIFFÉRENTIEL 1 .3.2

1 . 3 . 1 EXISTENCE ET UNICITÉ

Observons que les démonstrations des résultats d'existence utilisent fréquemment une suite minimisante, c'est-à-dire une suite (xk)keN de C telle que

f(xk)---+ f*.

k-++oo

Par définition de la borne inférieure, il existe toujours une suite minimisante. L'ob­ jectif est alors d'utiliser les propriétés de C et celles de f pour montrer que la suite

(xk)keN , ou une suite extraite, converge dans C. Si f est continue par exemple, la limite réalise alors le minimum.

En général, l'hypothèse-clé pour démontrer l'existence d'un point minimum est la compacité. On justifie souvent l'existence en écrivant « l'application est continue sur un compact donc atteint son minimum » . On dispose aussi d'extensions élémen­ taires de ce résultat en dimension finie (voir l'exercice 1.1). Dans les autres cas, on revient aux suites minimisantes.

En dimension infinie, la compacité des fermés bornés est mise en défaut (par exemple la boule unité fermée n'est jamais compacte, voir (RD03, 3.1 .5.5°)). On com­ pense alors ce manque par des arguments de compacité faible (voir IBRÉ, 111.20)).

Par ailleurs, la stricte convexité offre une condition suffisante pour démontrer l'unicité du point minimum (voir le lemme 1 .75).

Exemple 1.33 - Projection sur un convexe fermé. La minimisation de la distance

d'un point x à un convexe fermé non vide dans un espace de Hilbert est un problème agréable : il y a existence et unicité du point minorant. En plus, on dispose d'une condition nécessaire et suffisante de minimalité (la caractérisation angulaire de la projection) . Cette situation est commentée et illustrée dans la section 3.1.

1 . 3 . 2 LOCALISATION ET CALCUL DIFFÉRENTIEL

Les conditions vérifiées par un point minorant dépendent de la nature de C et de la régularité de f en ce point. Les outils pour démontrer les conditions d'optimalité sont les formules de Taylor. On suppose ici que f est suffisamment régulière et on considère trois cas pour C :

( i) C est ouvert, ( ii) C est convexe, ( iii) C est une « surface » .

CONDITIONS DU PREMIER ORDRE SUR UN OUVERT

Lemme 1.34 - Condition nécessaire de minimalité locale. Soient C un ouvert

de E et f une application de C dans R.. Si x* est un minimum local de f et si f est différentiable en x*, alors df (x*) = O.

On commence par démontrer le résultat en dimension 1 : le fait que l'on puisse approcher x* par chacun de ses deux côtés va assurer à la fois la positivité et la négativité du premier terme du développement limité. En dimension supérieure, on se place en x* E C, et comme C est ouvert, on peut appliquer le résultat de la dimension 1 sur toutes les directions issues de x* (voir ICIA, Th.7.2-1)).

Le lemme 1 .34 exige que f soit différentiable en x* . En pratique, on ne sait pas a priori si les candidats se trouvent dans la zone de différentiabilité de f. On doit

1 .3.2 OPTIMISATION

J'(x) = 0

df(xi) = 0

Fig. 1.8 Minima d'une fonction de

IR

dans

IR

et d'une fonction de

IR2

dans

IR

17

donc s'assurer en général que f est différentiable sur tout l'ouvert

U.

Mentionnons toutefois l'exemple 1 .37 où ce n'est pas le cas.

Les points x E C où df(x) = 0 s'appellent les points critiques (ou points station­ naires) de f : C -t

IR

; les valeurs prises en ces points s'appellent les valeurs critiques

de f. Il peut y avoir « beaucoup » de point critiques, mais il y a en revanche peu de valeurs critiques. Ceci est quantifié par le théorème de Sard (voir [ROU, ex.42) et les références s'y trouvant).

Contre-exemples 1.35 L'application t E

IR

1-+ t3 E

IR

montre que la condition n'est que nécessaire (la dérivée s'annule en 0 qui n'est pas un point minimum) . L'applica­ tion t E (0, 1] 1-+ t E

IR

montre que le résultat est faux si C n'est pas un ouvert.

En revanche, si C n'est pas ouvert mais qu'une condition supplémentaire permet d'assurer que le minimum est atteint dans l'intérieur de C, alors on peut appliquer le lemme 1.34 à la restriction de f à l'intérieur de C. Le théorème de Rolle illustre cette démarche.

Applications 1.36 - Fonctions d'une variable réelle. On a déjà des applications intéressantes du lemme 1 .34 en une dimension. Il s'écrit ainsi : si x* est un minimum local de f sur un intervalle ouvert et si f est dérivable en x* , alors f'(x*) =O. - Le théorème de Rolle donne un bon exemple de théorème d'optimisation (voir

[aou2, p.70]). La compacité et la continuité donnent l'existence d'un minimum et d'un maximum. La condition f(a) = f(b) permet de régler le cas du bord. On conclut avec le lemme. Notons que le théorème de Rolle se généralise à la dimension finie avec la même preuve (voir l'exercice 2 de [GOU2, p.312]).

- Le théorème de Darboux établit que « la dérivée d'une fonction vérifie la propriété des valeurs intermédiaires » . Sa preuve est du même acabit que celle du théorème de Rolle (voir l'exercice 4 de [aou2, p.76) , deuxième méthode) . La compacité donne l'existence d'un minimum puis la condition sur les dérivées au bord permet de s'en éloigner un peu : on est alors sur l'intérieur du segment et on applique le lemme. Exemple 1.37 - Fonction min. Soit

U

un ouvert de !Rn. Définissons

f :

{U --+

IR

x _{1--+ min{f1 (x), . . . ,fn(x)}.}

où chacune des fonctions fi :

U

1-+

IR

est différentiable sur

U.

Si x* est un minimum local de f, montrons que f est différentiable en x* (et donc df(x*) = 0).

Comme x* est un minimum local de f, il existe un voisinage V de x* sur lequel

18 CHAPITRE 1 - CALCUL DIFFÉRENTIEL

Posons I(x*) = {i E [ 1 , n _{J , fi(x*)} = _{f(x*)} et fixons i E I(x*). On a alors} V x E U, f(x) :::; fi (x) et f(x*) = fi(x*).

Ainsi V x E V, f (x*) :::; f (x) :::; fi(x) et f (x*) = fi (x*).

Pour conclure, appliquons le résultat de l'exemple 1 .4 avec m et M définis par

V x E U, m(x) = f(x*) et M(x) = fi (x).

1 .3.2

Attention ce résultat devient faux si l'on remplace min par max : par exemple la valeur absolue (qui est le max de x t--t x et x t--t -x) atteint son minimum en 0 où

elle n'est pas différentiable.

CONDITIONS DU DEUXIÈME ORDRE SUR UN OUVERT

Si f est suffisamment régulière et si a est un point critique, le deuxième ordre donne des informations sur la minimalité éventuelle de f au point a.

Lemme 1 .38 - Conditions de minimalité locale. Soient C un ouvert de E, a E E et f : C --+ lR. deux fois différentiable en a. Si df (x*) = 0, alors

- si x* est un minimum local de f, la forme quadratique d2 f(x*) est positive ; - si d2 f(x*) est définie positive, x* est un minimum local strict de f.

Exemples 1.39 Considérons l'application f: (x, y) t--t x2 - y3. Le calcul du gradient

montre que le seul point critique est (0, 0) . La hessienne en (0, 0) est positive mais pas définie positive. Ainsi f remplit les conditions nécessaires d'optimalité mais pas les conditions suffisantes du deuxième ordre. On observe que (0, 0) n'est pas un minimum (même local) de f (puisque pour y > 0, on a /(0, y) < 0) .

Par ailleurs, g : ( x, y) t--t x2 + y4 admet un minimum strict en ( 0, 0) mais ne vérifie

pas les conditions suffisantes du deuxième ordre.

Application 1.40 - Principes du maximum. La preuve du principe du maximum proposé à l'exercice 3 de [aou2, p.313) utilise les conditions nécessaires d'optimalité. Le lemme [zQ, Xl.1.4) et le théorème [zQ, XI.1. 1) qui établissent une version plus générale de ce principe se démontrent à l'aide des mêmes arguments. Notons que ces théorèmes s'appliquent notamment à l'équation de la chaleur.

Remarque 1 .41 - Ordre supérieur. Précisons à présent ce qui se passe lorsque les conditions nécessaires du deuxième ordre sont satisfaites mais que les conditions suffisantes ne le sont pas. Le cas de la dimension 1 est traité dans [RD03, 5.3. 1.2°) ; généralisons la démarche.

Plaçons-nous dans le cadre suivant : soient <.p : E --+ lR. de classe �00 et a E E tels que d<.p(a) = 0 et q = d2ip(a) est positive. Si q n'est pas définie positive (c'est le cas pour les fonctions f et g de l'exemple 1.39) , une condition de minimalité doit « aller se chercher aux ordres supérieurs ». En effet, il reste à étudier le comportement de <.p sur le noyau de q. On écrit la formule de Taylor-Young (proposition 1 .56) pour h dans le noyau de la forme quadratique q

t3 t4

V t E IR., ip(a + t h) - <.p(a) = 31 d3ip(a) (h3) + 41 d4ip(a)(h4) + o(t4).

Dans ce cadre, on obtient ainsi deux nouvelles conditions suivantes en adaptant le raisonnement effectué pour les premier et deuxième ordres.

- Si a réalise un minimum local, on est assuré que, pour tout h dans le noyau de q,

1.3.2 ÛPTIMISATION 19

- Une condition suffisante de minimalité est que, pour h :f. 0 dans le noyau de q,

d3<p(a) (h3) = 0 et d4ip(a) (h4) > O.

On peut évidemment continuer le raisonnement et aller chercher des conditions similaires aux ordres encore supérieurs en réduisant au fur et à mesure l'espace. Remarquez la dimension des espaces considérés peut ne pas diminuer strictement, comme dans l'exemple classique x 1--+ exp (- 1/x2) .

Exemples 1.42 Illustrons ces idées par l'étude en (0, 0) des applications

/ : (x, y) 1--+ x2 - y3 , g : (x, y) 1--+ x2 + y4 et h : (x, y) 1--+ x2 + x3 + y4•

Observons que les hessiennes de ces applications sont positives mais non définies positives et qu'elles ont pour noyau la droite IR(O, 1). L'application f ne satisfait pas la condition du troisième ordre, ce qui implique que (0, 0) n'est pas un minimum local. L'application g satisfait les conditions suffisantes d'ordre 4 et (0, 0) est un minimum strict. Enfin, l'exemple de h montre que les conditions d'ordre 3 et 4 se regardent sur le noyaux de la hessienne et non sur l'espace tout entier. Les conditions suffisantes d'ordre 3 et 4 sont vérifiées mais d3h(O, O) ((x, y)3) = x3 n'est pas nul sur JR2 (uniquement sur JR(O, 1)).

SI _C EST CONVEXE

Essayez d'adapter la preuve du lemme 1.34 quand C est un ensemble convexe (voir [CIA, 7.4-1)). Il y a deux re�trictions : d'une part, toutes les directions ne sont pas toujours admissibles et, d'autre part, parmi celles qui le sont, on ne peut a priori s'approcher de x* que « d'un côté » (on n'obtient donc qu'une inégalité) .

Lemme 1.43 - I négalité d ' Euler. Soient U un ouvert de E, C un convexe inclus

dans U et f une application de U dans

R

Si f admet un minimum local en x* E C et si elle est différentiable en x*, alors

df (x*) · (y - x*) � 0 pour tout y E C.

Remarque 1.44 - I nterprétation géométrique. Soit (E, (., ·}) un espace euclidien ;

l'inégalité d'Euler se réécrit

('V f (x*), y - x*} � 0 pour tout y E C.

Pour rendre f(y) plus petit que f(x*), il faudrait que le premier ordre de f(y) - f(x*) (c'est-à-dire ('Vf(x*) , y - x*}) soit négatif, ce qui n'est possible pour aucun y E C. La seule manière de rendre f plus petit serait de « sortir de C » .

Interprétons cette condition avec les no­ tions de la sous-section 3.1.2. Considé­ rons le convexe C - x* et son semi-cône polaire (C-x*)0 (voir la définition 3.26) . Alors l'inégalité d'Euler s'exprime

-'V f (x*) E (C - x*)0•

Application 1.45 - Projection sur un convexe fermé. Soient (H, (., ·}) un espace de Hilbert, C un convexe fermé de H et x E H. Posons, pour y E H,

1

20 CHAPITRE 1 - CALCUL DIFFÉRENTIEL 1.3.2

La fonction f est différentiable sur H et V f(x) = y - x. Observez que minimiser f(y) sous la contrainte y E C correspond à minimiser la distance de x à y E C (cette remarque est aussi utilisée à l'exercice 1.5) .

Supposons que f admette un minimum sur C noté x* . D'après le lemme 1.43, ce point minimum x* vérifie

(x* - x, y - x*) � 0

c'est-à-dire (x - x* , y - x*) � 0

pour tout y E C.

pour tout y E C.

On retrouve ainsi la caractérisation angulaire du théorème 3.11. Néanmoins, le théo­ rème 3.11 conserve tout son intérêt puisqu'il établit l'existence du point minimum.

MULTIPLICATEURS DE LAGRANGE

Supposons à présent que l'espace-contrainte C soit décrit par m équations

C = {x E

Rn,

g1 (x) = 0, . . . ,gm(x) =

O},

où les m fonctions 9i

: Rn

-+

R

sont de classe '16'1 sur

Rn.

Théorème 1.46 - Extremums liés. Soient U un ouvert de E contenant C et f : U -+

R

Si x* est un extremum local de f dans C, si f est différentiable en x* et si les différentielles dg1 (x*), . . . , dgm(x*) sont linéairement indépendantes, alors il existe .À = (.Xi , . . . , .Àm) E Rm tel que

m

df (x*)

+

L .Àidgi (x*) =

O.

i=l

La condition ( *) exprime l'appartenance de df (x*) au sous-espace vectoriel de

E* engendré par les dgi(x*). Les .Ài sont uniques puisque les dgi(x*) sont linéaire­ ment indépendantes. On les appelle les multiplicateurs de Lagrange. Dans ce cadre, on dispose aussi de conditions pour le deuxième ordre (voir [Hu, p.93]).

Par ailleurs, le résultat se généralise aux contraintes définies par des inégalités : ce sont les relations de Kuhn-Tucker (voir [Hu, p.63] ou [CIA, Ch.9] et le sujet d'ana­ lyse numérique de l'agrégation de 1992).

Remarque 1 .47 - Interprétation géométrique. Grâce à la condition d'indépen­ dance des dgi(x*), C est une sous-variété de

Rn

autour de x*. D'autre part, la condi­ tion ( *) est équivalente à

m

n Ker dgi(x*) c Ker df(x*),

i=l

ce qui signifie que df(x*) est nulle sur l'intersection des Ker dgi (x*) (voir l'exer­ cice 6.27 de [FRA]). Soulignons au passage que le rapport du jury de 1996 déplore que ce résultat ne soit pas connu. Or l'espace tangent en x* à la sous-variété

est justement

{x proche de x*, 91 (x) = 0, . . . ,gm₍x) =

O},

{h

E

Rn,

dg1 (x*) ·

h

= 0, . . . , dgm(x*) ·

h

=

O}.

Bref, la condition ( *) exprime simplement que df(x*) est nulle sur le plan tangent

à C en x* (voir [ROU, Ch. 7]) . Ceci équivaut aussi à ce que V f (x*) soit orthogonal à l'espace tangent à C en x* . Ainsi la seule manière de rendre f plus petit serait de « sortir de C » . Citons le rapport du jury de 1998 : « le caractère géométrique de la

1.3.2 OPTIMISATION 21

Dans [CIA, 7.2.3) et dans [aou2, p.311), on trouve des preuves analytiques du théorème 1.46. Ces preuves utilisent le théorème des fonctions implicites qui, de toute façon, est à la base de la �héorie des sous-variétés (voir [Rou, Ch.5) pour une intro­ duction et des références) .

Exemple 1.48 Comment utiliser le théorème 1.46 en pratique ? O n calcule les déri­ vées partielles pour former V' gi (x*) et V' f (x*). On cherche (x* , >.) E C x IRm tel que les gradients sont liés. On écrit les équations qui expriment ( *) et celles qui donnent

x* E C. On est donc amené à résoudre un système de n + m équations (non-linéaires) à n + m inconnues.

Les variables Ài ne sont en fait que des auxiliaires de calcul (c'est x* qui nous intéresse) , mais on ne peut pas éviter qu'elles interviennent. Voici des exercices d'ap­ plication : l'exercice 1.5, l'exercice 4 de [aou2, p.313) ainsi que l'exercice 126 de (Rou)

qui propose une démonstration de l'inégalité d'Hadamard.

Contre-exemple 1.49 Il ne faut pas oublier la condition de régularité géométrique :

les hypothèses du théorème 1.46 demandent que les dgi (x*) soient linéairement in­ dépendants.

Voici un contre-exemple si ce n'est pas le cas. Soit f(x, y) = x + y2 que l'on minimise sous la contrainte g(x, y) = x3 - y2 =O. On vérifie que le minimum (global)

de f SOUS cette contrainte se situe en (0, 0) (puisque la contrainte entraîne X ;;;:: 0).

La différentielle de g à l'origine est nulle et la relation ( *) n'est pas vraie. Application 1.50 - Diagonalisation des endomorphismes symétriques.

Soient E un espace euclidien et u E 2'(E) un endomorphisme symétrique (c'est-à-dire tel que u = u* , on dit aussi auto-adjoint). Alors il existe une base orthonormée de E formée de vecteurs propres de u.

Démontrons ce résultat à l'aide des multiplicateurs de Lagrange. Considérons pour cela les applications différentiables

{

E - IR f ·

x i---+ (u(x) , x)

et g :

{

E - IR

x i---+ _(x, x) ,

et S = { x E E, g(x) = 1} la sphère unité. Puisque S est fermée et bornée dans l'espace de dimension finie E, S est compacte. La fonction f continue sur E atteint donc son maximum sur S en un point que l'on note e1 . Par ailleurs, pour tout x E E et tout h E E

df(x) · h = 2(u(x) , h) et dg(x) · h = 2(x, h).

D'après le théorème 1.46 appliqué avec f et g en e1 , il existe une constante >.1 telle que df(e1 ) = À1dg(ei)

c'est-à-dire

Ainsi À1 est une valeur propre de u et e1 est un vecteur propre associé de norme 1. On peut à présent raisonner par récurrence. Soit F = e1 .L . D'après la proposition

[RD02, 1.3.2.3°) , F est stable par u* = u car e1 est stable par u (voir aussi la sec­ tion 4.2.1). La restriction de u à F est alors aussi un endomorphisme symétrique. De plus dim F = dim E - 1.

Ajoutons pour finir que le résultat est vrai si E est un espace hermitien et aussi que les endomorphismes auto-adjoints ne sont pas les seuls à être diagonalisables dans une base orthonormée. Dans un espace hermitien, on a même une caractérisa­ tion des endomorphismes qui sont diagonalisables dans une base orthonormée (voir

22 CHAPITRE 1 - CALCUL DIFFÉRENTIEL 1.3.3 1 . 3 . 3 ÜPTIMISATION NUMÉRIQUE

Dans un problème réel d'optimisation, on peut rarement obtenir explicitement une solution

x*.

Pour approcher cette solution, on construit une suite

(xn

)

nEN

qui converge vers

x*.

Concrètement, on met en œuvre des algorithmes qui calculent numé­ riquement des valeurs

(xnh:::;n,.;N

jusqu'à ce que

XN

soit une « bonne approximation » de

x*.

Décrivons une étape d'un algorithme d'optimisation, c'est-à-dire le passage de

Xn

à

Xn+i

(pour plus de détails, voir l'excellente introduction de [HULl, Ch.II)).

Considérons un problème d'optimisation sans contraintes inf {

J

₍

x

)

, x

E JRd } ,

où la fonction objectif f est suffisamment régulière et admet un unique minimum

x*.

O n se place ainsi dans une situation favorable. Le problème est plus difficile s'il y a des contraintes ou si f n'est pas différentiable (voir les sections 8.6 et 9.3 de [CIAJ et [HULl, Ch.III).

Supposons que

Xn

ne soit pas assez proche de

x*

{il ne satisfait pas le « critère d'arrêt » de l'algorithme). La recherche de

Xn+i

se décompose en deux étapes : - le choix d'une direction de descente

dn;

- le choix d'un pas de descente

tn.

On pose alors

Il y a plusieurs stratégies pour le choix de

dn

(voir les exemples ci-dessous) . Le cal­ cul d'un bon pas de descente est très technique (voir [HUL1, II.3)) et peu intéressant pour l'agrégation. Notez la particularité de la méthode de Newton pour laquelle le pas

tn

= 1 est toujours un bon choix (voir l'exemple 1.53).

!

Fig. 1 . 9 Méthode de descente pour une fonction de IR2 dans IR

Exemple 1.51 Soit (

e1, .. . , en

) une base de

!Rn.

On peut imposer à l'avance les

directions de descente comme les directions des vecteurs de la base pris successivement et de manière cyclique :

dk

=

er+l

où r est le reste de la division euclidienne de

k

par n. Cette méthode converge sous de bonnes hypothèses mais elle est à proscrire en pratique ! La direction de descente est imposée et donc elle ne tient pas compte des propriétés de f en

Xn.