Mouvement de l'ensemble de Julia des polynômes en itération aléatoire

MOUVEMENT DE L'ENSEMBLE DE JULIA DES

POLYNÔMES EN ITÉRATION ALÉATOIRE

Mémoire présenté

à la Faculté des études supérieures de l'Université Laval dans le cadre du programme de maîtrise en mathématiques

pour l'obtention du grade de Maître es sciences (M.Sc.)

FACULTÉ DES SCIENCES ET DE GÉNIE UNIVERSITÉ LAVAL

QUÉBEC

2010

L'ensemble de Julia d'une fonction rationnelle, issu de la théorie dite classique de l'itération, possède une généralisation à une théorie dite aléatoire, où les fonctions ap-pliquées peuvent être différentes d'une itération à l'autre. En restreignant notre étude de l'itération aléatoire aux cas où les suites de fonctions considérées sont des suites dites bornées de polynômes, plusieurs phénomènes de la théorie classique se généralisent, et on se demande jusqu'à quel point c'est le cas. On étudie donc les liens entre les deux théories via la question suivante : comment est modifié l'ensemble de Julia lorsque les coefficients des fonctions qui l'engendrent sont modifiés? Un théorème classique décrit ainsi l'ensemble de Julia comme ressemblant à une multifonction méromorphe, et on tente de généraliser celui-ci. Il faut donc, d'abord, décrire les grandes lignes de la théorie l'itération et de celle des multifonctions méromorphes.

Bienvenue, chère lectrice ou cher lecteur, à la porte de l'endroit où résident certaines des idées mathématiques qui meublèrent, un temps, mon esprit. Avant de débuter l'ex-ploration de celles-ci, ce qui nécessitera un formalisme digne du plus pointu théorème ainsi qu'une distance entre nous qui m'obligera à bannir des pronoms personnels tels que « je », « tu » et « vous », il est de coutume que je t'offre ces quelques paragraphes d'avant-propos, plus personnels. J'aurai ainsi le loisir de remercier les êtres qui ont fait en sorte que les lignes que tu t'apprêtes à lire sont aujourd'hui écrites. Car la recherche du savoir est, pour moi, bien loin d'être une quête qui puisse être faite de façon solitaire. Mes premiers remerciements vont, bien sûr, à ma directrice principale de recherches, Line Baribeau, pour toute son implication dans mon parcours mathématique. Elle a su me redonner espoir au terme de l'été 2008 lors duquel, en tentant de me résigner à passer ma maîtrise à explorer un sujet pointu d'analyse fonctionnelle ne m'intéressant guère, je feuilletais plutôt de belles images fractales colorées en me disant : « Pour-quoi n'étudierais-je pas ceci, à la place? » Line a alors su me proposer un sujet dont l'arborescence des idées qui y sont reliées continue encore à stimuler mon intérêt. Cet intérêt commun de Line, sa compréhension à mon égard, son érudition et la clarté de ses explications ont alors grandement suffi à me permettre de garder le cap.

Je tiens aussi à remercier mon co-directeur de recherches, Jérémie Rostand, de son efficacité, sa rigueur et son professionnalisme légendaires, qui ont permis de grandement rehausser la qualité de ce mémoire aux derniers temps de la rédaction de celui-ci. Sa contribution fut essentielle, tant à cet ouvrage qu'à mon intérêt et mes talents pour les mathématiques en général, grâce à ses cours auxquels j'ai eu le privilège d'assister.

Dans le reste du clan professoral, je tiens à témoigner tout particulièrement ma joie d'avoir côtoyé Bernard R. Hodgson, Frédéric Gourdeau, Javad Mashreghi et Thomas J. Ransford. Leur apport pédagogique à mon parcours est, pour moi, d'une importance qui n'est égalée que par leur apport humain. Je remercie également le professeur Mark Comerford de l'Université de Rhode Island pour son intérêt, son temps et ses précieux

commentaires relatifs à mon sujet de maîtrise.

Sur un plan moins académique, ma plus sincère reconnaissance va à mes parents. Fernand Fortier et Henriette Jobin, d'avoir fait de moi qui je suis et de la fierté qu'ils m'ont toujours témoignée. Leur apport financier n'est pas non plus à négliger, car ils ont épargné dès notre plus jeune âge pour offrir, à moi et mes frères, toutes les chances de pouvoir poursuivre des études et de choisir notre propre chemin dans la vie.

Outre ces derniers, sur le plan financier, je remercie sincèrement le Conseil de re-cherches en sciences naturelles et en génie du Canada (CRSNG), le Fonds québécois de la recherche sur la nature et les technologies (FQRNT), le groupe d'Analyse et le Département de mathématiques et de statistique de l'Université Laval. Ils m'ont permis de traverser en petit prince ce grand périple intellectuel qu'a constitué la maîtrise.

Au plan plus affectif, j'aimerais remercier tous les confrères et consoeurs avec qui j'ai eu le plaisir de me lier d'amitié lors de ces cinq dernières années à l'Université Laval. Il serait trop long et hasardeux de tenter d'établir une liste exhaustive, mais toute personne à qui j'ai déjà adressé un sourire, avec qui j'ai ri, travaillé ou entretenu des discussions plus personnelles peut se sentir visée. Sans eux, qui enduraient notamment mes jeux de mots mathématiques de mauvais goût ou me donnaient tout simplement le goût de continuer quand plus rien n'avait de sens, je n'aurais jamais traversé l'épopée universitaire.

Je remercie également mes amis de plus longue date ; ceux-ci se reconnaîtront car ils sont peu nombreux. Ils m'ont permis de demeurer moi-même dans la jungle des mathématiques, et je les en remercie. Parmi ceux-ci, j'ai une pensée particulière pour celle que j'ai, de surcroît, longtemps considéré comme étant la femme de ma vie : Stéphanie. Je la remercie de son amour comme de son amitié, alors que la science peut la remercier du mal qu'elle m'a fait. Car les mathématiques sont, pour moi, une activité très salutaire quand il s'agit de noyer ses peines. C'est donc beaucoup grâce à elle et en ne pensant qu'à elle que je conclus ce mémoire.

Te voici donc, lectrice ou lecteur, au pas de la porte qui mène de ma personne jusqu'à mon mémoire, où est contenu l'essentiel des mathématiques que j'ai faites lors de ma maîtrise. Franchis cette porte sans craintes, car pour t'accrocher à ce qui suit, il te suffira de vider ton esprit de tous les problèmes de la vie et de te poser, comme moi, l'obsédante question suivante : la régularisation semi-continue supérieurement de l'ensemble de Julia d'une famille analytique de suites bornées de polynômes est-elle une multifonction méromorphe ?

« Will the misty master break me ? Will the key unlock my mind ?

Will the following footsteps catch me ? Am I really dying ?

Julia dream, dreamboat queen, Queen of all my dreams. »

Résumé ii Avant-Propos iii

Table des matières vii Table des figures viii

1 Introduction 1 1.1 Structure du mémoire 5

2 L'itération aléatoire des fonctions rationnelles 6

2.1 Familles normales 6 2.1.1 Équicontinuité et normalité 8

2.2 Ensembles de Fatou et de Julia 8 2.2.1 Les cas d'ensembles vides 9

2.2.2 Invariance 10 2.2.3 Quoi d'autre ? 12 3 Dynamique des suites bornées de polynômes 14

3.1 Dynamique classique des polynômes 14

3.2 Généralisation des polynômes 16

3.3 Attraction vers l'infini 17 3.4 L'ensemble de Julia en tant que répulseur 19

3.5 Auto-similarité 22 3.6 Capacité de l'ensemble de Julia 23

4 Les fonctions multiformes 26 4.1 Topologie des ensembles compacts 27

4.2 Continuité et semi-continuité 29 4.2.1 Semi-continuité supérieure 31 4.2.2 Semi-continuité inférieure 33 4.3 Qu'en est-il de l'ensemble de Julia? 34

4.3.1 Continuité 34 4.3.2 Semi-continuité de /C 38

4.3.3 Semi-continuité de J 39 5 Les multifonctions méromorphes 43

5.1 Fonctions sous-harmoniques 43 5.1.1 Ensembles polaires 46 5.1.2 Fonctions pluri-sous-harmoniques 48

5.2 Multifonctions méromorphes 48 5.2.1 Premiers liens avec les fonctions méromorphes 50

5.2.2 Théorèmes des multifonctions implicites 53

5.2.3 Unions et intersections 54 6 Ensembles de Julia et multifonctions méromorphes 58

6.1 L'ensemble de Julia classique 58 6.2 L'ensemble de Julia rempli 61 6.3 L'ensemble de Julia des suites bornées de polynômes 62

6.3.1 Densifier une sous-multifonction 63 6.3.2 Les idées qui fonctionnaient pour le mouvement holomorphe . . 66

6.3.3 Une intersection de la bonne chose 68

6.3.4 Des cas où L = J * 72

7 Conclusion 77 A Rappels d'analyse complexe 79

A.l Fonctions holomorphes et méromorphes 79

A.1.1 Singularités 81 A.2 La sphère de Riemann 81 A.3 Fonctions harmoniques 84 B Mesure et capacité 86

B.l Mesures 86 B.2 Capacité logarithmique 88

1.1 Le disque unité 2

1.2 Domaines de stabilité pour f(z) := z2 — 1 3

1.3 Domaines de stabilité pour fn(z) :— z2 — £ 4

3.1 Ensemble de Julia rempli du polynôme P(z) = z3 + (1 + i)/2 15

3.2 Le triangle de Sierpinski 20 4.1 Distances maximales entre deux compacts 28

4.2 Ensembles de Julia remplis pour z2 + A, avec A G {0.30,0.28, 0.25} . . . 36

4.3 Ensembles de Julia pour euz + z2, avec t <E {0.27, 0.13, 0.00} 37

A.l Représentation géométrique de la sphère de Riemann 83

Toutes les figures présentées dans ce mémoire ont été produites par l'auteur. Les ensembles de Julia ont été générés sur Mat Lab® par l'algorithme décrit à la section 3.1 de cet ouvrage, à l'exception de ceux de la figure 4.2 qui ont été générés par une appli-cation Java de Mark McClure (University of North Carolina at Asheville) gratuitement disponible (avec son code source) sur internet.l

Introduction

Toute personne ayant déjà suivi un cours de mathématiques, c'est-à-dire toute per-sonne dans le monde occidental moderne, reconnaîtra le problème suivant. Étant donné une suite de nombres, disons la suivante :

2, 4, 16, 256, 65 536, 4 294 967 296,...

induire une règle permettant de passer d'un terme à l'autre de cette suite. Dans l'exemple ci-haut, la réponse est immédiate ; il suffit d'appliquer, à un terme z de la suite, la fonc-tion f(z) = z2 pour obtenir le terme suivant. Une fois cette règle obtenue, on peut alors

se poser la question suivante : quelle suite aurait-on obtenue si, tout en appliquant la même règle pour passer d'un terme à l'autre, on avait choisi un autre point de départ que le nombre 2? Notre règle / étant, dans ce cas-ci, une fonction rationnelle, rien n'empêche de choisir le point de départ ZQ comme étant un nombre complexe ou même un point de la sphère de Riemann C (voir annexe A). Ainsi, on s'intéresse à cartogra-phier C en fonction du comportement de la suite dont le point de départ est ZQ et la règle est d'itérer / . Cette suite sera dénommée par le nom d'orbite de z0. En gros, si

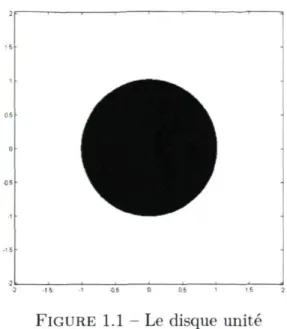
deux points de départ donnés engendrent des orbites qui se comportent, à long terme, de la même manière, on coloriera ces deux points de la même couleur. Un rien de travail conduira alors le mathématicien amateur à tracer la carte illustrée à la figure 1.1.

Dans cette figure, la région noire (le disque unité) représente l'ensemble des points de départ pour lesquels la suite obtenue à partir de la fonction f(z) = z2 converge vers

zéro, alors que la région blanche désigne l'ensemble des points de départ pour lesquels la suite obtenue de la même manière tend vers oc. On a toutefois omis de tracer la frontière séparant ces deux régions (le cercle unité) sur laquelle la suite ne convergera ni vers 0, ni vers oo. En fait, deux points donnés sur le cercle unité peuvent, même s'ils sont pris très près l'un de l'autre, donner lieu à des comportements radicalement différents.

FIGURE 1.1 - Le disque unité

Par exemple, si ZQ est une racine rationnelle de l'unité, son orbite sera éventuellement périodique, alors que sinon, son orbite sera dense dans le cercle. Ainsi, sur le long terme, l'orbite du point eî7rv^ n'aura rien de semblable à celle du point e"r'1'414. Le

cercle unité est donc l'ensemble sur lequel l'itération de / est dite chaotique, alors que sur son complément, l'itération sera dite numériquement stable, les orbites de deux points rapprochés s'y comportant éventuellement de la même manière. En l'honneur des mathématiciens Pierre Fatou et Gaston Julia qui, à l'instar de Newton et Leibniz pour le calcul différentiel, se disputèrent la paternité de la théorie de l'itération des fonctions rationnelles1, l'ensemble sur lequel l'itération d'une fonction rationnelle / est

stable sera désigné par le nom d'ensemble de Fatou de / , alors que son complément sera désigné par le nom d'ensemble de Julia de / .

Le problème de cartographier les domaines de stabilité d'une fonction rationnelle devient véritablement intéressant lorsqu'on complique un peu la fonction considérée. Ainsi, si, par exemple, on avait plutôt choisi d'itérer la fonction f(z) = z2 — 1, on aurait

obtenu la figure 1.2.

Ici, la région blanche représente l'ensemble des points dont l'orbite tend vers oo, alors que les régions opaques représentent les points dont l'orbite est bornée. Parmi ceux-ci, les points en noir ont une orbite tendant à se rapprocher du cycle (0, — 1,0, — 1,...), alors que les points en rouge ont une orbite se rapprochant du cycle ( — 1, 0, — 1,0,...) (voir [Bel, Section 1.5]). Il reste encore à discuter de la frontière entre toutes ces régions,

S 2

FIGURE 1.2 - Domaines de stabilité pour f(z) := z2 — 1

l'ensemble de Julia de / , qui décrit dans ce cas-ci une intrigante courbe fractale.11

Encore une fois, sur cette courbe, l'itération de / est chaotique.

Les figures fractales n'ayant pas leur pareil pour attirer les curieux vers les ma-thématiques, l'observation du fait général que les ensembles de Julia en sont presque toujours a grandement contribué à une recrudescence de la théorie de l'itération des fonctions rationnelles dans les années 1970 et 1980, avec l'avènement des techniques d'imagerie par informatique. Or, quand il s'agit de tracer une figure avec un ordina-teur, le problème de la stabilité numérique se pose encore : si on veut, par exemple, tracer l'ensemble de Julia de la fonction f(z) := z2 + y/2, en obtiendra-t-on une bonne

approximation en traçant plutôt celui de la fonction f(z) := z2 + 1,414?

On s'intéresse donc à déterminer si l'ensemble de Julia d'une fonction rationnelle dépend de façon continue des coefficients de cette fonction. Des exemples, dont certains seront vus dans ce mémoire, démontrent qu'en général, ce n'est malheureusement pas le cas. Or, dans l'article [MSS], Mané, Sad et Sullivan établissent que le mouvement de l'ensemble de Julia est continu sur au moins un ouvert dense dans l'espace des pa-ramètres, sur lequel le mouvement est même très lisse (on parle ici d'un mouvement holomorphe). En poussant plus loin l'analyse avec les outils de la théorie des multifonc-tions méromorphes, Baribeau et Ransford établissent dans [BR] que la régularisation semi-continue supérieurement de l'ensemble de Julia d'une fonction rationnelle, un en-semble qui coïncide avec l'enen-semble de Julia là où celui-ci bouge continûment et dont

II. Du latin « fractus » qui signifie « brisé » : une courbe irrégulière à toutes les échelles, mais dont chaque partie est semblable au tout. Lire, par exemple, [Barn] ou [Man] pour plus d'exemples et d'explications.

la différence avec ce dernier permet de mesurer les discontinuités, se déplace méromor-phiquement sur tout l'espace des paramètres. Ils donnent également une description topologique plus précise de l'ensemble des discontinuités, avec quelques applications.

Or le problème d'identifier les domaines de stabilité d'une suite de fonctions peut s'étendre à des contextes plus généraux. On peut considérer, par exemple, le cas où la règle pour passer d'un point à son successeur dans une suite dépend de la position de ce point. On peut ainsi se donner une suite (/n)neN de fonctions rationnelles, un point

de départ z0 E C, puis observer le comportement de l'orbite de z0, c'est-à-dire la suite

(2n)neN définie récursivement par la règle zn := fn(zn-i)- Alors, si au voisinage d'un

point z0 donné, tous les points ont une orbite éventuellement semblable à celle de ZQ, on

dira que l'itération est stable en ZQ et que z0 appartient à l'ensemble de Fatou de la

suite de fonctions (/n)neN- Dans le cas contraire, on dira que z0 appartient à l'ensemble

de Julia de {fn)neN- C'est ce qu'on appelle la théorie de l'itération aléatoire, introduite

par Fornaess et Sibony en 1991 (voir [FS]). À titre d'exemple, les régions de l'ensemble de Fatou de la suite de fonctions définies par fn(z) := z2 — - sont illustrées à la figure 1.3.

FIGURE 1.3 - Domaines de stabilité pour fn{z) := z2 — £

La région blanche de la figure correspond aux points dont l'orbite tend vers l'infini, la région noire correspond aux points dont l'orbite est bornée, et la frontière entre les deux correspond à l'ensemble de Julia de la suite (/„)n€N.

Il est naturel de vouloir transposer le problème de la continuité de l'ensemble de Julia au contexte de l'itération aléatoire. Or, il s'avère qu'en itération aléatoire, très peu de phénomènes de la théorie classique peuvent être transposés dans toute leur généralité. On restreindra donc notre étude de la théorie aléatoire à une catégorie particulière de suites de polynômes, qu'on appellera les suites bornées de polynômes. Sachant que ces

suites généralisent à merveille un grand nombre de résultats classiques sur l'itération des polynômes, notre objectif, proposé dans l'article non publié [BRR], sera de découvrir si le résultat de Baribeau et Ransford sur le mouvement de l'ensemble de Julia peut être généralisé à ces suites particulières.

1.1 Structure du mémoire

Le présent ouvrage est divisé en cinq chapitres de développement et deux annexes, organisés de façon à établir, de façon pyramidale, les outils nécessaires pour attaquer la généralisation du résultat de Baribeau et Ransford.

D'abord, le survol préalable de l'annexe A est recommandé au lecteur, car l'analyse complexe est utilisée dès le début du chapitre 2. Dans ce dernier, on établit les définitions fondamentales d'ensembles de Fatou et de Julia dans le contexte de l'itération aléatoire, tout en mentionnant les liens avec la théorie classique. Le chapitre se termine avec la constatation que très peu de phénomènes classiques demeurent vrais en itération aléatoire. C'est pourquoi on définit, au chapitre 3, les suites bornées de polynômes, tout en exhibant quelques-unes de leurs propriétés qui en font une réelle généralisation des polynômes, au plan de leur dynamique. La lecture de l'annexe B deviendra alors progressivement nécessaire au lecteur, car des liens entre la théorie du potentiel et celle des systèmes dynamiques commenceront à poindre.

L'étude du mouvement d'ensembles débute au chapitre 4 où, après avoir établi les bases topologiques nécessaires à une telle étude, on définit le concept de multifonction continue, via les deux concepts fondamentaux de semi-continuité inférieure et supé-rieure. On étudiera alors ce qu'il en est de la semi-continuité des ensembles de Julia classiques comme aléatoires, avec ces seuls outils. Pour décrire plus précisément ce mouvement, on introduira ensuite, au chapitre 5, les multifonctions méromorphes, qui généralisent essentiellement les fonctions méromorphes, pour le cas des fonctions dont les valeurs sont des ensembles compacts. C'est finalement au chapitre 6 que sera décrit le mouvement de l'ensemble de Julia en termes de multifonctions méromorphes. On y démontrera le résultat classique de Baribeau et Ransford, qu'on tentera également de généraliser aux suites bornées de polynômes.

L'itération aléatoire des fonctions

rationnelles

Rappelons le contexte de la théorie de l'itération aléatoire des fonctions rationnelles, brièvement abordé en introduction. Soit une suite (/n)neN de fonctions rationnelles

de C vers C. On s'intéresse à identifier, selon un point de départ ZQ G C donné, le comportement de la suite (zn)n e^, où pour tout n, on pose zn = fn(zn-i)- Il s'agit d'une

généralisation directe de la théorie dite classique de l'itération des fonctions rationnelles, dans laquelle la suite (/n)neN e s t constante par-rapport à n, c'est-à-dire qu'on n'y itère

qu'une seule fonction / (une infinité de fois!).

Bien que le lecteur n'ait nul besoin d'être familier avec la théorie classique pour aborder la lecture de ce chapitre, des liens avec cette dernière seront tout de même évoqués ponctuellement, en vue de mettre en évidence les différences entre les deux théories et surtout les difficultés présentées par la théorie aléatoire. Un survol du livre de Beardon [Bel] ou de celui de Steinmetz [St] serait donc un atout recommandable

(mais non nécessaire) pour apprécier les différences entre les deux théories.

2.1 Familles normales

L'idée derrière la définition des mystérieux ensembles de Fatou et de Julia est la suivante : on cherche à localiser les points z G C à partir desquels, si on itère certaines fonctions de façon algorithmique, cette itération sera numériquement stable. C'est-à-dire que deux points pris assez proches dans cet univers de stabilité (que l'on appellera

l'ensemble de Fatou) devraient se comporter essentiellement de la même manière entre eux, à long terme, lorsqu'on leur applique le processus itératif. En considérant les étapes de ce processus comme formant une suite de fonctions (Fn)n 6 N, on s'intéresse à la

convergence de celle­ci. Lorsqu'on parle de convergence en analyse complexe, la notion suivante est souvent la plus appropriée.

Définition 2.1.1. Soit X un espace topologique et soit (Y, d) un espace métrique. Soit F : X —>• Y et (Fn)n€N une suite de fonctions de X vers Y. On dit que (Fn)n6N

converge localement uniformément vers F sur X si, pour chaque x E X, il y a un voisinage ouvert V de x tel que

supd(Fn(,z), F(z)) —■> 0 lorsque n —> oo.

zev

L'une des raisons principales pour lesquelles la convergence localement uniforme nous intéresse particulièrement en analyse complexe, c'est parce que si une suite (Fn)n € N

de fonctions holomorphes, sur un domaine D de C, converge localement uniformément vers une fonction F , alors ou bien F est holomorphe sur D, ou bien F prend identi­ quement la valeur oo. En excluant ce dernier cas, la convergence localement uniforme préserve donc l'holomorphie (voir, par exemple, [Ah, section 5.5]). Ceci est également vrai dans la sphère de Riemann (en remplaçant le mot « holomorphe » par le mot « ana­ lytique »). Dans le cas particulier où le domaine D est toute la sphère de Riemann, alors si la suite (Fn)TieN est une suite de fonctions rationnelles, on peut même déduire que la

fonction limite F est également rationnelle, avec deg(Fn) = deg(F) à partir d'un cer­

tain rang (voir [Bel, théorème 2.8.2]). Mais la convergence localement uniforme nous permet surtout de définir ce qu'est une famille normale.

Définition 2.1.2. Une famille 5 de fonctions de X vers Y est une famille normale sur X si chaque suite (Fn)n €^ dans 5 admet une sous­suite qui converge localement

uniformément sur X.

Essentiellement, dire qu'une famille de fonctions est normale sur un domaine D signifie que les points qui se trouvent dans ce domaine ont un comportement prévisible, ou encore stable, lorsqu'on leur applique une suite de fonctions dans la famille. Le critère le plus fondamental (et certes l'un des plus puissants) visant à déterminer si une famille de fonctions analytiques est normale est le critère de normalité de Montel, dont la preuve peut être trouvée, par exemple, dans [Bel, Théorème 3.3.4].

T h é o r è m e 2.1.3 (Critère de normalité de Montel).

Soit D Ç C un domaine, et soient a,b,c trois points distincts dans C. Soit 5 une famille de fonctions analytiques sur D, à valeurs dans C \ {a,b,c}. Alors 5 est une famille normale sur D.

Le principal inconvénient du critère de Montel est le fait qu'il ne possède pas de réciproque. Pire encore : on ne connaît pas de critère aussi simple permettant de conclure qu'une famille n'est pas normale. C'est d'ailleurs, en quelque sorte, ce phénomène qui nous engendrera le plus de malheur, à la fin de ce mémoire.

2.1.1 Équicontinuite et normalité

Une autre façon pouvant s'avérer naturelle pour qualifier le comportement des fonc-tions d'une famille 5 comme étant semblable entre les individus de celle-ci est la notion d ' équicontinuité.

Définition 2.1.4. Soient (X, dx) et (Y, dy) deux espaces métriques. Une famille 5 de fonctions de X vers Y est une famille équicontinue sur X si, pour tout e > 0, il existe un 5 > 0 (ne dépendant que de e) tel que, pour tout F G # et X\,x2 G X, on a

dx(xi,x2) < S = * dY(F(x1), F(x2)) < e.

Autrement dit, les membres d'une famille équicontinue sont des fonctions uniformé-ment continues sur X, mais de plus, elles le sont toutes autant, puisque le ô ne dépend pas du choix de la fonction. Il ne s'agit toutefois pas véritablement d'une autre façon de qualifier la similitude entre les membres d'une famille de fonctions à variable com-plexe, puisque dans ce cas, équicontinuité et normalité sont deux concepts équivalents. Il s'agit là du théorème de Arzelà-Ascoli, dont la preuve peut être trouvée dans [Ah, Section 5.3].

Théorème 2.1.5 (Arzelà-Ascoli).

Soit U Ç C ouvert. Une famille # de fonctions continues de U vers C est normale sur U si et seulement si elle est équicontinue sur U.

2.2 Ensembles de Fatou et de Julia

Soit (fn)neN une suite de fonctions rationnelles sur C. On s'intéresse à la suite des compositions des fonctions de cette première suite, sur un voisinage de chaque z G C. Considérons donc la suite de fonctions (Fn)n 6 N définie par F0 = Id (la fonction identité),

et pour chaque n G N,

Il est facile de remarquer que, avec les notations données en préambule de ce chapitre, pour un point de départ zo donné, on a zn = Fn(z0)- On peut maintenant définir

l'ensemble de Fatou de la suite (fn)neN comme :

J : = { 2 6 C : {Fn}n € N est une famille normale sur un voisinage ouvert de z.}

et son complément, J := <C\ J-, se nomme l'ensemble de Julia de la suite (/n

)neN-Dans la théorie classique, puisque la suite (/n)neN est composée d'une seule fonction / ,

les fonctions Fn sont souvent dénotées fn (pour « / composée avec elle-même, n fois »),

et les ensembles T et J sont respectivement appelés les ensembles de Fatou et de Julia de la fonction / .

Une conséquence immédiate à la définition de J- est qu'il s'agit d'un ensemble ouvert. En effet, soit z G T et V un voisinage ouvert de z sur lequel la famille {Fn}n(-^ est

normale. Comme V est également un voisinage ouvert de chaque w € V, il suit que V Ç T, ce qui permet de conclure. Par conséquent, J est fermé dans C. Comme C est compact avec la métrique de la corde (voir annexe A), on déduit que J est toujours un ensemble compact. Dans les cas où J est borné dans C avec la métrique euclidienne, on peut également conclure que J est compact avec cette métrique.

2.2.1 Les cas d'ensembles vides

On peut se demander si, pour certaines suites de fonctions, il peut advenir que l'un des ensembles T ou J soit vide. La réponse est la même dans la théorie classique que dans la théorie aléatoire. Le premier exemple historique d'une fonction dont l'ensemble de Fatou est vide est dû à Lattes, qui l'a publié dans un article en 1918 (voir [L]). Il s'agit de la fonction

; , ; ' 4 4 * 2 - 1 ) '

et la preuve que T est vide peut être trouvée dans l'article original, ou encore dans [Bel, section 4.3]. Le même exemple s'applique également à la théorie aléatoire, en prenant une suite constante de cette même fonction.

À l'opposé, les cas où l'ensemble de Julia est vide sont rares et, dans un certain sens, dégénérés. Cela peut se produire, par exemple, lorsqu'une des fonctions fno est

constante. Alors, Fno est aussi constante, et le point de départ de l'itération n'a aucune

importance. À partir de cette étape n0, la suite (Fn)n e N est une suite de constantes

dans C, et comme C est compact, on peut y trouver une sous-suite convergente ; donc T = C. Les seuls autres cas où J peut être vide surviennent lorsque la suite (/n)neN ne

contient que des fonctions rationnelles de degré 1 à partir d'un certain rang n0. Dans ce

cas, on s'intéresse à la dynamique d'une suite de transformations de Môbius, à partir du point FnQ(z). Or, cette étude cadre dans sa propre théorie, différente de celle de Fatou

et Julia, et le lecteur intéressé est invité à se reporter à [PT] ou à [Be2] pour plus de détails. Dans tous les autres cas, J est non vide, et c'est l'objet du prochain théorème. Théorème 2.2.1. Soit (/n)neN une suite de fonctions rationnelles non constantes, dont

une infinité d'entre elles sont de degré > 2. Alors son ensemble de Julia est non vide.

Démonstration. Supposons qu'au contraire, la famille {Fn}n G N soit normale sur C. Alors

il existe une sous-suite {Fn j}je^ qui converge localement uniformément sur C vers

une certaine fonction F. Par la remarque qui suit la définition 2.1.1, cette fonction F est rationnelle, et pour tout j assez grand, deg(Fnj) = deg(F). Or, deux fonctions

rationnelles f et g ont toujours la propriété que

àeg(fog) = deg(f)deg(g). Par induction, on trouve que, pour tout j ,

deg(F„.) = ndeg(/

),

fc=i

n

et comme il existe une infinité de k pour lesquels deg(fk) > 2, alors lim J deg(/fc) = oo.

n _ >° ° fc=i

C'est une contradiction avec le fait que deg(Fnj) = deg(F) à partir d'un certain

rang. D

Dans tout ce qui suivra, on s'intéressera toujours à ce dernier cas où nos fonctions /„ sont non constantes, et une infinité d'entre elles sont de degré > 2. Pour éviter les interminables passages à des sous-suites, on supposera même, sans perte de généralité, que toutes les fonctions de nos suites (fn)nen seront de degré > 2. L'ensemble

de Julia sera donc toujours un compact non vide de la sphère de Riemann.

2.2.2 Invariance

Dans la théorie classique de l'itération, une propriété importante des ensembles de Fatou et de Julia est leur invariance complète sous l'action de / . Cela veut dire que pour tout n, les ensembles J et F satisfont les égalités suivantes (voir Beardon [Bel, théorème 3.2.4]) :

L'importance de cette propriété est telle qu'on l'utilise dans presque toutes les preuves des théorèmes sur les ensembles de Fatou et de Julia. Le fait que celle­ci n'ait pas d'équi­ valent dans la théorie de l'itération aléatoire rend souvent impossible l'adaptation des preuves classiques, dans les cas où les théorèmes classiques ne deviennent pas carrément faux.

Une version faible de la propriété d'invariance est tout de même vraie en itération aléatoire. Pour la formuler, on a besoin de définir, pour n G N et m > n, les composi­

tions partielles :

Fn,m := fm ° fm­l ° • • ' ° fn+i, si m > n,

Fn,n := Id.

Les compositions Fn définies à la section précédente correspondent donc aux composi­

tions F0iTl de cette définition­ci. On peut alors définir, pour n G N, le n­ième ensemble

de Fatou itéré :

•Fn := {z G C : {Fn,m)m=n est une famille normale sur un voisinage ouvert de 2.}

et le n­ième ensemble d e Julia itéré, Jn: = C \ Fn­ Encore une fois, ces définitions

coïncident avec les précédentes, avec F = J­Q et J = JQ. On peut maintenant citer le théorème d'invariance, qui justifie par ailleurs les noms d'ensembles itérés pour Tn

et Un­

T h é o r è m e 2.2.2. Pour tout n et m entiers tels que 0 < n < m, on a ( V ^ln,m\J~n) • ' m &t J~n = rn m{ J ~m)

(UJ C n , m \ U n ) = Um Ct Un = ■* n,mV«­'nV

(iii) les composantes connexes de Tn sont envoyées surjectivement sur celles de J­'m par

F

1 n,m­

Démonstration. Fixons n > 0 et m > n. Montrons d'abord que Tn = F~^l(Jrm). Pour

tout z 6 C, on sait que z G F"„ si et seulement s'il existe un voisinage ouvert Vz de z sur

lequel la famille {Fn^k}^Ln est normale. Or, comme l'ajout ou le retrait d'un nombre fini

d'éléments d'une famille ne change rien à la normalité, on peut commencer à considérer celle­ci seulement à partir du stade k = m. De plus, puisque, pour tout k > m, on a Fn,k = Fm,fe o Fn>m, dire que z G Tn est donc équivalent à dire que la famille {Frrltk}kxLm

est normale sur Fn,m(Vz). Ainsi, si z G ­Fn, l'ensemble Wz := Fn,m(I4) est un voisinage

de FniTn(z) sur lequel la famille {Fm^}kLm est normale. Réciproquement, si un tel Wz

existe pour un z donné, on peut prendre Vz := F ' ^ W z ) , et on obtient un voisinage

Fn,m(z) G Tm, d'où on obtient F*n = F~^(.Fm). En appliquant Fn,m de chaque côté, on

déduit immédiatement que Fn>m(F"n) = Tm et on obtient la conclusion (i).

La conclusion (ii) est une simple conséquence de (i) et de la formule de Hausdorff, selon laquelle, pour n'importe quels ensembles A et B et n'importe quelle fonction / , on a f~l(B \ A ) = f ~ \ B ) \ f ~ \ A ) . On obtient

F­m{Jm) = J £ j ( Ô \ Fm) = F ­m( Q \ F­m(J"m) = C \ f n = Jn­

En appliquant, encore une fois, Fn m de chaque côté de l'équation, on obtient que

■F n , m \ U n ) = Um­

Pour la conclusion (iii), on considère une composante connexe C de Tn, et on veut

montrer que Fn,m{C) est une composante connexe de Tm­ Comme Fn,m est continue,

alors Fn,m(C) doit être un ensemble connexe, et comme Fn>m(C) Ç F„im(.Fn) = Tm,

alors Fn}Tn{C) est contenu dans une seule composante connexe, disons D, de Tm­ On

veut montrer que D — Fn^m(C). Or, le théorème de l'application ouverte ainsi qu'un

peu de topologie conduisent à :

dFn t m(C) C Fn,m{dC) Ç Fn>m( Jn) = Jm = t \ F m Q t \ D .

Pourtant, si Fn^m(C) était strictement contenu dans D, un point de sa frontière devrait

se trouver à l'intérieur de D, et il y aurait une contradiction. D

2.2.3 Quoi d'autre ?

La liste des propriétés de T et de J qui sont communes aux deux théories s'arrête, malheureusement, essentiellement là (voir [BB, section 2]). Par exemple, dans la théorie classique, J est non seulement toujours non vide, mais c'est même un ensemble parfait, et par conséquent, il est infini non dénombrable (voir [Bel, théorème 4.2.4]). C'est faux dans l'itération aléatoire, où J peut être un ensemble fini. En effet, pour tout d > 2, la suite des fonctions définies par

zd

fn(z) = ­ ^

n

a comme ensemble de Julia le singleton {oo}. Pour le voir, il suffit de remarquer que pour tout n, on a Fn(oo) = oo, alors que pour tout z G C, en prenant R > \z\, on a

Rd n / R \d n

s u p | Fn( u / ) | < —­— = ( — J ­>■ 0 lorsque n ­ ^ oo.

Donc, Fn —> 0 localement uniformément sur C.

On définira toutefois, au prochain chapitre, un certain type de suites de fonctions dont les ensembles de Julia préservent une part appréciable des propriétés de la théorie classique. Par exemple, dans la théorie classique, l'ensemble de Julia d'une fonction rationnelle / est généralement une figure fractale. Il est, entre autres, auto-similaire. Géométriquement parlant, cela signifie que lorsqu'on agrandit n'importe quelle partie d'une représentation graphique d'un ensemble de Julia, on peut y reconnaître le même type de formes que celles de l'ensemble au complet (comme c'est le cas, par exemple, pour un brocoli ou une fougère). Donc, toute la structure géométrique d'un ensemble de Julia est répétée dans la moindre de ses parties.

Les fractales sont aussi souvent caractérisées par leur dimension de Hausdorff. Sans entrer dans les détails sur cette notion,! la dimension de Hausdorff d'un ensemble de

Julia classique est toujours strictement positive (voir [Bel, théorème 10.3.2]) ce qui signifie, dans un certain sens, que les ensembles de Julia sont plus gros que les nuages de points, sans nécessairement devoir contenir un arc (bien que ce puisse être le cas).

On verra donc, au prochain chapitre, un certain type de suites de fonctions qui préservent, entre autres choses, des propriétés d'auto-similarité et de relative grosseur, dans la théorie aléatoire.

Dynamique des suites bornées de

polynômes

On a déjà mentionné à quelques reprises que très peu de propriétés des ensembles de Fatou et de Julia classiques s'étendaient dans toute leur généralité à la théorie aléatoire. Il peut alors être utile de restreindre la classe des fonctions rationnelles auxquelles on s'intéresse. De cette façon, on peut espérer que certains résultats, propres à ces fonctions aux propriétés précises, s'adaptent à leur généralisation de la théorie aléatoire. Dans cette optique, les polynômes deviennent une avenue d'étude intéressante, car ils pré-sentent déjà bien des propriétés particulières dans la théorie classique. On s'intéressera donc à définir une classe de suites de fonctions dont la dynamique en théorie aléatoire présente des points communs avec la dynamique classique des polynômes. Par la suite, notre obsession sera d'explorer jusqu'à quel point c'est bien le cas.

3.1 Dynamique classique des polynômes

Soit P un polynôme de degré > 2, et T et J ses ensembles de Fatou et de Julia, au sens classique. On sait que F(oo) = oo, c'est-à-dire que le point oo est un point fixe de P. Plus encore : il s'agit d'un point fixe attractif. Cela signifie que sur un certain voisinage de oo, les fonctions itérées Pn convergent uniformément vers oo ; donc, oo G F .

Notons par A » la composante connexe de l'ensemble de Fatou qui contient le

point oo, et appelons-la le bassin d'attraction immédiat à l'infini du polynôme P. On peut montrer (voir [Bel, section 5.2]) que, dans le cas des polynômes, la relation

suivante est satisfaite

J = dAt x.

Cette caractérisation entraîne une application pratique immédiate, car l'ensemble Aoo, ou plutôt son complément /C qui est borné, est facile à tracer sur un ordinateur. Il suffit d'itérer P en chaque point d'une grille représentant une région de C suffisament grande, et si le module des itérés semble tendre vers l'infini, on le colorie en blanc ; sinon, on le colorie en noir. Comme on sait que l'ensemble de Julia se trouve à la frontière entre la région blanche et la région noire, on bénéficie alors d'un algorithme facile, rapide et efficace pour repérer l'ensemble de Julia des polynômes par ordinateur (voir la figure 3.1). Cette application justifie d'ailleurs que l'on donne habituellement à K. le nom d'ensemble de Julia rempli.

FIGURE 3.1 - Ensemble de Julia rempli du polynôme P(z) = z3 + (1 + ï)/2

Mais la caractérisation J = dAoo = dK nous donne également deux définitions alternatives de l'ensemble de Julia, qui sont en un certain sens plus pratiques et plus révélatrices de la dynamique de P que la définition avec les familles normales. On peut donc utiliser celles-ci pour obtenir des théorèmes qui sont propres aux polynômes (voir par exemple [Bel, sections 5.2 et 9.5]).

3.2 Généralisation des p o l y n ô m e s

On cherche à définir une classe de suites de fonctions pour lesquelles il existe une caractérisation de l'ensemble de Julia du type J = dAoc = dK., comme pour les poly­ nômes classiques.

Une première idée, pour s'assurer que oo soit fixé par tous les Fn, est de considérer

tout simplement les suites (Pn)neN, où chaque Pn est un polynôme de degré dn > 2

qu'on identifiera désormais comme étant de la forme

Pn(z) = an 4 nz ^ + an>dn_12rf»­1 + • • • + an>0. (3.2.1)

On posera, de plus, la n o r m e de chaque Pn comme étant :

||Pn|| := maxflonjl : j = 0 , . . . ,dn} ,

et le coefficient directeur de chaque Pn sera dénoté par :

[Pn] ■= an t d n.

L'exemple donné dans la section 2.2.3, d'une suite de polynômes dont l'ensemble de Julia contient seulement le point oo, laisse entendre qu'il faut exiger un peu plus de nos suites, pour au moins s'assurer que oo soit un point attractif et qu'il appartienne à l'ensemble de Fatou. On peut s'en assurer en bornant les membres de notre suite de polynômes de plusieurs façons. D'abord, on peut borner la suite (rf„)neN des degrés par

une constante d, ainsi que les normes des polynômes de la suite. On définit ainsi l'espace V{d) des suites de polynômes aux degrés < d, tels que supn e N ||F„|| < oo. Au risque

d'abuser de notations, on notera cette dernière quantité ||(Pn)neN||> qu'on appellera la

n o r m e de la suite (F„)neN­

Si on voit les coefficients des polynômes de V(d) comme formant un vecteur à d + 1 coordonnées, alors V(d) avec la norme || • || est précisément l'espace £°°(Cd+l, || • ||oo),

qui est bien connu. On privilégiera tout de même la notation V(d) car elle est plus compacte et parce qu'on parle de polynômes et non de vecteurs. Au risque de confondre encore davantage le lecteur par l'abus d'utilisation de la lettre « P », un élément d'un des espaces V(d) (qui est donc une suite de polynômes) sera dès maintenant représenté par le symbole P , qui signifie (Pn)neN avec chaque Pn comme dans l'équation (3.2.1).

Mais encore là, la restriction aux espaces V{d) n'est pas suffisante pour obtenir notre précieuse composante Aoo, car pour tout d > 2, l'exemple de la section 2.2.3 appartient à V(d). La clé se trouve dans les coefficients directeurs des Pn, qu'il faut

borner inférieurement pour nous assurer que notre suite de polynômes ne se comporte pas asymptotiquement comme une suite de polynômes linéaires ou constants. On dira donc qu'une suite P — (Fn)neN de polynômes de degrés > 2 est une suite bornée de

polynômes si P G V(d) pour un certain d, et si inf I FnJ > 0. On notera cette dernière

quantité [PJ, tout en recommandant au lecteur d'apposer un signet à cette page pour se souvenir de toutes ces notations.

3.3 Attraction vers l'infini

On peut maintenant généraliser la dynamique classique des polynômes à nos suites dites bornées. La première étape est de montrer que oo est un point attractif.

Définition 3.3.1. Soit (fn)neN une suite de fonctions rationnelles. S'il existe un R > 0

tel que pour tout n G N, on a Fn m —\> oo uniformément sur {\z\ > R} lorsque m —>■ oo,

alors R est un rayon d ' é c h a p p e m e n t pour la suite (/n)neN­

T h é o r è m e 3.3.2. Toute suite bornée de polynômes admet un rayon d'échappement R. De plus, on peut s'assurer que pour tout n G N et m > n, on ait \ Fn m\ > 2m~nR sur

l'ensemble {\z\ > R}.

Démonstration. Montrons qu'il suffit de prendre n'importe quel R tel que :

2+IIPII

* > i + ^ U

Fixons z E C avec \z\ > R, et n G N. D'abord, par l'inégalité triangulaire, on trouve

Y.

Or, comme \z\ — 1 > R — 1 > — ^—, on trouve que lan,dnl

V izP = ^ ­

< (l^l'"­

)!

»^!

On a donc

21^,^1 • k h + IIFnlI-KdJ

~ 11^11+2

On peut ainsi établir, par induction, que pour chaque n G N et m > n, \Fn>m(z)\ > 2m-n\z\ > 2m~nR.

Comme cette borne inférieure ne dépend pas de z, et qu'elle tend vers oo lorsque

m —ï oo, alors |F„im| —» oo uniformément sur {|z| > R}. D

Comme oo est fixé par chaque Fn, on conclut immédiatement, du précédent

théo-rème, que oc E J-. Notons par A ^ la composante connexe de T qui contient le point oo. Alors on a le résultat suivant.

Théorème 3.3.3. Soit P une suite bornée de polynômes. Alors : Aoo = {z G C : Fn(z) -)• oo}.

Démonstration. Soit R un rayon d'échappement pour P, et soit £> := {oc} U {,2 G C : \z\ > R).

On sait que D Ç A ^ , d'où on peut déduire que Fn —y oo localement uniformément

sur Aoo. En effet, si la famille {F„}neN possédait une autre fonction limite sur Aœ,

celle-ci devrait être analytique, ce qui est impossible car elle devrait prendre la valeur co sur tout D qui n'est pas un ensemble discret.

Réciproquement, soit z G C tel que Fn(z) —» oo. Fixons n G N tel que |F„(z)| > R.

Alors Fn(z) G A^n, où Aoo,n est la composante connexe de J-n qui contient oo. Par le

théorème 2.2.2, on doit donc avoir z E J-, car sinon, Fn(z) devrait se trouver dans Jn, ce

qui n'est pas le cas. Soit donc C la composante connexe de T qui contient z. Encore par le théorème 2.2.2, on sait que Fn(C) = Aoo,n- Donc, il existe w E C avec Fn(w) = oo.

Mais comme F„ est un polynôme, alors forcément, w = oo, ce qui veut dire que oo se

Comme dans le cas classique, on appelera A ^ le bassin d'attraction à l'infini de P, nomenclature désormais justifiée par le théorème 3.3.3. Son complément, K., sera dénommé l'ensemble de Julia rempli de P . et cette dernière dénomination est, cette fois-ci, méritée par le théorème suivant.

Théorème 3.3.4. Soit P une suite bornée de polynômes. Alors J = dK, =

dAoo-Démonstration. Comme Aoo est une composante connexe de T et T est ouvert, alors assurément, d A x Ç C \ Jr = J'.

Réciproquement, soit z G C \ A ^ . Comme C \ Aoo est ouvert, alors il existe un voisinage ouvert V de z qui est contenu dans celui-ci. En particulier, pour tout w G V, la suite (Fn(w))n(-N est bornée par un certain R (où R est un rayon d'échappement),

car sinon, elle convergerait vers oo et on aurait w G Aoo par le théorème 3.3.3. Ainsi, pour tout n, on a Fn(V) Ç 'BR. Par le critère de Montel (théorème 2.1.3), il suit que la

famille {Fn}n€N est normale sur V, et donc, z G J-'.

On a donc montré que C \ A » Ç F", ou par contraposition, que J Ç ^l^,. Comme J H Aoo = 0, on conclut que J Ç dAoo. Ainsi, J = dAoo, et puisque Aoo et K sont

complémentaires, alors nécessairement, dK = dAoo- D

3.4 L'ensemble de Julia en tant que répulseur

Dans la théorie des systèmes dynamiques, un objet abondamment étudié est l'at-tracteur d'un système de fonctions itérées. Il s'agit, en effet, d'une source de figures fractales très utilisée pour modéliser, par exemple, des arbres ou des montagnes. Sans entrer dans les détails1 : étant donné un certain système de fonctions, que l'on itère

dans un ordre aléatoire à partir d'un point de départ ZQ donné, si la suite ainsi obte-nue tend à se rapprocher d'un certain ensemble, pour n'importe quel choix de z0, alors

cet ensemble s'appelle l'attracteur du système. Par exemple, le triangle de Sierpinski (figure 3.2) est l'attracteur du système dynamique à trois fonctions suivant :

z 2 + 1 z + eiir/3

Dans le cas de l'itération d'une fonction rationnelle, les orbites ne se comportent pas toujours de la même manière, et c'est précisément pour cibler ces différences qu'on

0 01 0.2 0 3 0 4 0 5 0.6 07 08 0 9 1

FIGURE 3.2 - Le triangle de Sierpinski

s'intéresse aux ensembles de Fatou et de Julia. Cependant, les orbites arrière des points, à l'exception peut-être de deux points dits exceptionnels, tendent à se rapprocher de l'ensemble de Julia, d'où on dit qu'il est, à quelques détails près, le répulseur du système dynamique (ou l'attracteur du système de fonctions inverses).

Théorème 3.4.1. Soit f une fonction rationnelle telle que deg(f) > 2 et soit J son ensemble de Julia. Alors il existe un ensemble E, dit exceptionnel et contenant au plus deux points, tel que, pour tout z £ E , o n a J Ç - \ ^ f~n(z). De plus, pour tout

z E j , o n a J = \J f~n(z).

7i€N

Démonstration. Il s'agit du théorème 4.2.7 du livre de Beardon [Bel]. D

Le théorème 3.4.1 ne décrit pas exactement l'ensemble de Julia comme un répulseur, car il faudrait d'abord que le point de départ choisi ne se trouve pas dans E, et même si c'était le cas, il pourrait arriver que les orbites arrière s'accumulent en un ensemble strictement plus grand que J . C'est le cas par exemple lorsque le point de départ ZQ choisi est un point fixe pour / , qui se trouve dans l'ensemble de Fatou. En faisant toutefois quelques hypothèses supplémentaires sur les points de départ, l'ensemble de Julia devient alors un véritable répulseur (voir le théorème 4.2.8 du livre de Beardon [Bel]).

Le prochain théorème est un analogue au théorème 3.4.1 en itération aléatoire, pour le cas des suites bornées de polynômes. Il décrit l'ensemble de Julia comme un répulseur,

pourvu que le point de départ choisi se trouve à l'extérieur d'un rayon d'échappement. De plus, en choisissant deux points de départ plutôt qu'un seul, leurs orbites arrière s'accumulent sur tout l'ensemble de Julia.

Théorème 3.4.2. Soient P une suite bornée de polynômes, J son ensemble de Julia et R un rayon d'échappement. Alors, pour n'importe quels deux points a,b distincts tels que \a\, \b\ > R, on a

neN \k>n

Démonstration. Dénotons par E la partie droite de la relation que nous cherchons à établir. Montrons d'abord que E Ç. J . Pour k fixé, soit z G Fk~l{a, b}. Alors on a

|Fjfc(.z)| > R, donc, par le théorème 3.3.2, on a Fn(z) = Fk<n(Fk(z)) —> oo lorsque

n —> oo. On déduit, par le théorème 3.3.3, que z G Aoo- Donc, pour tout k, on a Fk~1{a,b} Ç Aoo, d'où on conclut que E Ç Aoo- Supposons maintenant qu'il existe

z E E d Aoo et fixons un voisinage ouvert V de z tel que V C Aoo- Alors comme z G E, il existe une infinité de k pour lesquels Fk(V) fl {a, b} ^ 0 , et ceci contredit le

fait que Fk —> oo uniformément sur V. Il n'existe donc pas de tel z, d'où on obtient

C J ^ "^Vx> \ *^oo U

-Pour montrer que J Q E, soit z G C \ E. Alors il existe un n G N et un voisinage ouvert V de z tels que, pour tout k > n, on ait Fk(V) Ç C \ {a,b}. Par le critère de

Montel (théorème 2.1.3), il suit que la famille {Fk}k>n est normale sur V, d'où on a

z E J- = C \ J , ce qui nous donne, contraposition faite, la conclusion recherchée. D

On peut également décrire K, l'ensemble de Julia rempli d'une suite bornée de polynômes, à l'aide des orbites arrière. Il ne sera toutefois plus suffisant, cette fois, de regarder les orbites arrière de quelques points, et il faudra plutôt itérer à rebours tout un disque, suffisamment grand pour recouvrir K.

Théorème 3.4.3. Soit P une suite bornée de polynômes, K son ensemble de Julia rempli, et R un rayon d'échappement. Alors :

K= n^oB*).

Démonstration. Soit z G C. On montre directement que z g K si et seulement si z $. flneN F ~1( P R ) . En effet, par le théorème 3.3.3, z £ K si et seulement si Fn(z) —» oo

lorsque n —> oo. Par le théorème 3.3.2, cela est équivalent à dire qu'il existe un no G N tel que |Fno(z)| > R, ou autrement dit, tel que z G" F~*(BR). Or, l'existence d'un tel

Notons au passage que K est non seulement une intersection dénombrable d'en-sembles simples, mais que ces end'en-sembles forment même une suite décroissante. En effet, pour tout n et z, si z 0 F ^ ^ D R ) , alors |Fn(z)| > R, et comme R est un rayon

d'échap-pement, par le théorème 3.3.2, on aura aussi |Fn + 1(z)| > R, donc z & F ' + ^ H R ) . Par

contraposition, on a donc toujours F ^ + ^ B R ) Ç F^^O/j). C'est une particularité qui

sera essentielle par la suite.

3.5 Auto-similarité

Tel que mentionné à la section 2.2.3, un ensemble est dit auto-similaire s'il est géométriquement similaire à chacune de ses parties. Plus mathématiquement parlant, en analyse complexe, cette idée peut être traduite par la définition suivante.

Définition 3.5.1. Un compact non vide K Ç C est dit auto-similaire si, pour tout ouvert U tel que U D K ^ 0 , il existe une fonction analytique 0 : U —> C telle que

K ç <j>(U D K ) .

Ainsi, dans un ensemble auto-similaire K, chaque région qui touche à K contient une copie (ou plutôt une préimage analytique) n de tout l'ensemble K. Dans la théorie

classique de l'itération, cette propriété d'applique aux ensembles de Julia sous la forme du théorème suivant, dont la preuve peut être trouvée dans [Bel, Théorème 4.2.5]. Théorème 3.5.2. Soit f une fonction rationnelle et J son ensemble de Julia. Alors pour tout ouvert U tel que UTl J ^ 0 , il existe un UQ tel que, pour tout n > UQ, on a

J = f

{unj).

Pour adapter ce théorème au cas aléatoire, il faut évidemment remplacer le terme « / " » par « Fn », mais il faut aussi remplacer l'ensemble de Julia J par son n-ième

itéré Jn = Fn( J ) (voir section 2.2.2) puisque l'ensemble de Julia n'est pas invariant

sous l'action des Fn. On formule ainsi le prochain théorème, dont la preuve est due à

Bùger (voir [Bu, Théorème 2]).

Théorème 3.5.3. Soit P une suite bornée de polynômes et J son ensemble de Julia. Alors, pour tout ouvert U tel que U ( 1 J ^ 0 , il existe un n§ tel que, pour tout n > n0,

on a Jn = Fn(U D J ) ou, de façon équivalente, J = F~1(Fn(U D J ) ) .

II. Il est à noter que certains auteurs exigent plutôt que la transformation 4> de la définition 3.5.1 soit affine ou encore bi-Lipschitz. La définition de l'auto-similarité dépend essentiellement du type d'ensembles que l'on étudie et dont on souhaite affirmer qu'il s'agit d'un type de fractales.

La démonstration du théorème 3.5.3 est plutôt longue et technique (elle fait tout de même l'objet d'un article!) et sa consultation dans l'article original est donc laissée à la discrétion du lecteur. Notons toutefois que les ensembles de Julia des suites bornées de polynômes ne sont généralement pas auto-similaires au sens de la définition 3.5.1. En effet, ce ne sont pas précisément des préimages analytiques de J que l'on retrouve dans chaque partie de lui-même, mais bien des préimages de ses ensembles itérés Jn.

Toutefois, le théorème 3.5.3 affirme que chaque région de J exhibe exactement le même comportement que tout J sous l'action des fonctions Fn, après un certain temps. Il

s'agit là, tout de même, d'une propriété qui évoque la notion intuitive recherchée dans une définition de l'auto-similarité. La distinction à faire vient du fait que les ensembles de Julia de la théorie aléatoire ne sont pas invariants sous l'action des fonctions qui le définissent, comme c'était le cas des ensembles de Julia classiques ou encore des attracteurs de systèmes de fonctions itérées.

On utilise le théorème 3.5.3 pour déduire le corollaire suivant, qui apporte un ana-logue aléatoire à la seconde partie du théorème classique 3.4.1 et qui nous sera concrè-tement utile plus tard.

Corollaire 3.5.4. Soit P une suite bornée de polynômes et soit J son ensemble de Julia. Fixons z0 G J . Alors J = [ j F-1(Fn(z0

))-neN

Démonstration. Soit w G J et fixons un voisinage ouvert V de w. On veut montrer que V n (UneN-^n~1(^n(2o))) 7^ 0- Or, par le théorème 3.5.3, il existe un no tel que

J = F~^(Fno(V n j ) ) . En particulier, il existe C G V tel que z0 G F ^ F ^ C ) ) ou, de

façon équivalente, tel que Ç G F^01(Fno(z0)). On a donc C G Vf](\JneNF~ 1(Fn(zQ))). D

3.6 Capacité de l'ensemble de Julia

À la section 2.2.3, on a mentionné que l'ensemble de Julia d'une fonction ration-nelle, dans la théorie classique, était de dimension de Hausdorff strictement positive, ce qui signifie essentiellement qu'un tel ensemble n'est, dans un certain sens, jamais trop petit. Une généralisation exacte de ce résultat, pour les ensembles de Julia des suites bornées de polynômes, n'est jamais parvenue jusqu'aux oreilles de l'auteur et, après quelques consultations, il est probable que ce soit une question qui est toujours ouverte. Cependant, une interprétation légèrement plus faible de la notion de « ne pas être trop petit » demeure vraie dans le cas des suites bornées de polynômes, et est traduite par la notion de capacité logarithmique (voir Annexe B). On calculera donc, dans cette section,

la capacité logarithmique des ensembles de Julia de suites bornées de polynômes. On interprétera ainsi que ces ensembles ne sont jamais trop petits.

T h é o r è m e 3.6.1. Soient P une suite bornée de polynômes et dn := deg(Pn). Soient J

et K, respectivement, l'ensemble de Julia et l'ensemble de Julia rempli de P . Alors : eap( J ) = cap(/C) = exp ­ £ r^­

\ neN " 1 ' " " «n

Démonstration. Premièrement, par la proposition B.2.1 de l'annexe B, puisque K est compact et J = dK, il suit immédiatement que cap( J ) = cap(/C), et on se concentrera à calculer la capacité de K.

Soit R un rayon d'échappement pour P . Par le théorème B.2.3 et la discussion qui le précède, pour tout n, on a :

/cap(B

)V

«

"»

cap(F­.(BR)) = ^

Or, on a cap(D/j) = R, deg(Fn) = d\ ■ ■ ■ dn, et on établit facilement par induction que,

pour tout n,

|_p |l/(<*i­dn) _ \ pi| l / ( d i ) i p , |l/(did2) . . . \ p 11/(dr­•<*„)_

En prenant le logarithme de chaque côté, on trouve donc :

lo

cap(^(«

)) = ^ ­ Ê M ^ .

«1 • • • «n k =x «1 ­ ­ ­ «fc

Enfin, puisque K = flneN F '1 (OR) et puisque ces ensembles forment une suite décrois­

sante, il suit de la proposition B.2.1 que :

logcap(£) = lim logcap(F­1(Dfl)) = ­ _T J ^ ,

fc=i i ' ' ' n

d'où le résultat. D

Il suit immédiatement du théorème que la capacité logarithmique de l'ensemble de Julia d'une suite bornée de polynômes n'est jamais nulle. Or, dans le contexte de la théorie du potentiel, les ensembles dits petits sont les ensembles de capacité nulle (ou ensembles polaires, voir la section 5.1.1). Ainsi, l'ensemble de Julia est toujours relativement gros, du moins, au regard de la théorie du potentiel.

En utilisant son auto­similarité, on arrive même à démontrer que l'ensemble de Julia est finement parfait. Un ensemble compact A" C C est dit finement parfait si, pour chaque ouvert U tel que U (1 K ^ 0 , on a cap(t/ n K) > 0. Un tel ensemble est donc relativement gros jusque dans ses moindres parties.

Théorème 3.6.2. Soit P une suite bornée de polynômes, et soient J et K, respecti-vement, son ensemble de Julia et son ensemble de Julia rempli. Alors J et K sont des ensembles finement parfaits.

Démonstration. Puisque J = dK, par la proposition B.2.1 de l'annexe B, il suffit de démontrer le résultat pour J . Soit donc U ouvert tel que U C \ J ^ 0 . Fixons z G UC\J ainsi qu'un disque D centré en z tel que D C U. Montrons que cap(F> PI J ) > 0 d'où il suivra, par la proposition B.2.1, que cap(£/ fl J ) > 0.

Supposons au contraire qu'on ait c&p(D fl J ) = 0. Par le théorème 3.5.3, il existe un n G N tel que J = F~l(Fn(D n J ) ) . O r , D r \ J est compact et F„ est Lipschitz

sur D par le théorème de la moyenne (voir par exemple [Mas, Théorème 11.1]). Il suit donc, par le théorème B.2.4, qu'on a cap(Fn(D D J ) ) = 0. Puisque Fn est un polynôme,

le théorème B.2.3 permet de conclure qu'on a cap(F~1(Fn(Z) n J ) ) ) = 0. On a donc

Les fonctions multiformes

Dans les cours de mathématiques donnés au secondaire, on introduit souvent le concept de fonction comme étant une chose (souvent illustrée par une machine ou, plus précisément, un processus) qui, à chaque point dans un domaine donné, associe une et une seule image. On évite ainsi prudemment de devoir introduire une terminologie pour parler des processus qui, à un point donné, associent plusieurs images.l Mais si

cette prudence est tout-à-fait défendable sur le plan pédagogique, il se trouve que pour nous, qui sommes désormais habitués à remettre en question toutes les définitions ma-thématiques apprises dans notre jeunesse, une terminologie de ce type de processus sera nécessaire dans l'étude de la variation d'un ensemble de Julia. On appellera donc fonc-tion multiforme, ou multifoncfonc-tion, une foncfonc-tion qui, à chaque point d'un domaine donné, associe un ensemble compact non vide de points dans un espace d'arrivée. n

L'objectif de ce chapitre est d'adapter les notions de continuité et de semi-continuité à ces fonctions généralisées. Rappelant que l'ensemble de Julia et l'ensemble de Julia rempli d'une suite bornée de polynômes peuvent être vus comme des multifonctions d'un certain espace de suites de polynômes vers C, on étudiera ensuite ce qu'on peut dire de leur continuité et de leur semi-continuité.

I. Par exemple, l'inversion d'un polynôme de degré n qui, à un point, associe n images (en comptant les multiplicités).

II. Les fonctions multiformes généralisent donc les fonctions uniformes, ou simplement « les fonc-tions », dont l'image est constituée de valeurs uniques, c'est-à-dire de singletons.

4.1 Topologie des ensembles compacts

Pour cette section, soit (X, d) un espace métrique quelconque. On note n(X) l'en-semble de tous les sous-enl'en-sembles compacts et non vides de X. Naturellement, chaque singleton fait partie de K(X), et pour chaque paire {{x}, {y}) de singletons, on peut dé-finir la distance entre eux comme étant simplement la distance d(x, y) entre x et y dans X. Notre objectif est de définir une métrique sur n(X) qui généralise cette dernière. Il s'agit de la métrique de Hausdorff.

Définition 4.1.1. Soit x G X et A G K(X). Alors la distance de x vers A est définie par

dist(x, A) := inîd(x,a).

aeA

Remarquons que le premier avantage au fait de tenter de définir une topologie sur les compacts de X plutôt que sur tous les sous-ensembles de X est que le a qui minimise la distance dans la formule ci-haut existe toujours, si A est compact (on aurait donc pu écrire 'min' au lieu de 'inf'). Cette particularité jouera un grand rôle dans les propriétés de l'objet défini ci-après.

Définition 4.1.2. Soient A, B G K(X). Alors la distance maximale de A vers B est définie par

SH(A, B) := sup dist(a, B).

a€A

Géométriquement parlant, S H (A, B) représente la plus courte distance r telle que chaque point de A soit contenu dans l'enveloppe de rayon r autour de l'ensemble B (voir figure 4.1). L'indice H est pour « Hausdorff », qui a eu l'idée de considérer la distance maximale de A vers B pour construire une métrique sur K(X). m

Il n'est donc jamais nécessaire de s'éloigner d'une distance supérieure à SH(A, B)

d'un point de A, pour atteindre B (d'où le nom). On peut donc déduire que si on a SH(A, B) — 0, alors A Ç B (ce qui ne serait pas forcément vrai si A et B n'étaient pas compacts). Par contre, le fait que 8H(A, B) = 0 n'implique aucunement que B Ç A, et

dans le cas général, 5H(A, B) ^ Ô H ( B , A ) . Par exemple, prenons X = R (ou C), avec

A = {0} et B = [—1,1]. Il est facile de vérifier que Su (A, B) = 0, alors que B (£. A et

6 H ( B , A ) = 1. Mais la fonction SH est tout de même positive et elle satisfait l'inégalité

triangulaire, comme on s'apprête à le voir. Cela justifie son intérêt dans la construction d'une métrique sur K(X).

F I G U R E 4.1 ­ Distances maximales entre deux compacts

Lemme 4.1.3. Soient x E X et A, B E K ( X ) . Alors dist(x, A) < dist(x, B ) + SH( B , A).

Démonstration. Soit b G B le point le plus près de x (qui existe, par compacité). Alors pour tout a E A,

d(x, a) < d(x, b) + d(b, a) = dist(.x, B) + d(b, a). En évaluant l'infimum sur A de chaque côté, on trouve

dist(x, A) < dist(x, B) + dist(6, A) < dist(x, B) + 5H(B, A).

D

T h é o r è m e 4.1.4. Soient A , B , C G K ( X ) . Alors SH(A, B) < 6H(A, C) + ÔH(C, B).

Démonstration. Pour tout a G A, en appliquant le lemme précédent, on trouve : dist(o, B) < dist(a, C) + 8H(C, B).

En prenant le supremum sur A de chaque côté de l'inégalité, on obtient exactement le

résultat voulu. D

Pour obtenir une métrique sur K ( X ) , il suffit donc de corriger le problème de la symétrie de 8H■ C'est ce qu'on fait dans la définition suivante :

Définition 4.1.5. Soient A, B G K ( X ) . Alors la distance de Hausdorff entre A et B est définie par

Il est désormais très simple, en se servant du théorème 4.1.4 et des remarques qui le précèdent, de démontrer que A# est une métrique sur K ( X ) , et qu'on a effectivement AH{{x}, {y}) = d(x, y) pour n'importe quels x, y G X. Ce qui est, de loin, moins simple

à démontrer (mais néanmoins d'un grand intérêt dont nous devrons nous priver ici) est que si (X, d) est complet, alors ( K ( X ) , A H ) est complet, et si (X,d) est compact, alors ( K ( X ) , A H ) l'est également (voir, par exemple, [BP]). La distance de Hausdorff sur K ( X )

préserve donc véritablement la structure topologique de l'espace X. Pour nos besoins, le résultat de convergence suivant sera suffisant.

Proposition 4.1.6. Soient K\ D K% 3 Kz 3 • • ■ des ensembles compacts non vides dans un espace métrique (X, d), et soit K := Ç\ Kn. Alors K est un compact non vide,

neN

et A H { KH, K) —> 0 lorsque n —> oo.

Démonstration. Puisqu'une intersection infinie d'ensembles fermés est fermée, et puis­ qu'un fermé dans un compact est compact, alors comme K Ç K\, on déduit que K est compact. Ensuite, pour tout n G N, fixons xn G Kn. Puisque (xn)n e^ Ç K\, alors une

sous­suite, disons {xnk)k(z^, converge, disons vers x G X. Or, pour tout k G N et / > k,

on a que xni G Knk, donc x G Knk également. Il suit que x G Ç\ Knk = K, donc, K est

fceN

non vide.

Enfin, puisque, pour tout n G N on K Ç Kn, alors 8H{K, Kn) = 0 et il n'y a plus

qu'à démontrer que 5H(Kn, K) —» 0. Or, supposons qu'au contraire, il existe e > 0 et des

entiers mi < m2 < ■ ■ ■ tels que, pour tout k, il existe yk G Kmk tel que dist(y/t, K) > e.

Par le même procédé qu'au paragraphe précédent, sans perte de généralité, la suite (?/fc)fceN converge, disons vers y € K. D existe donc un k tel que d(yk, y) < e, et donc,

dist(t/fe, K) < d(yk, y) + dist(y, K) < e + 0,

une contradiction. D

4.2 Continuité et semi­continuité

Commençons par définir formellement les fonctions multiformes, et les premières généralisations au cas multiforme des concepts habituels relatifs aux fonctions.

Définition 4.2.1. Soient X, Y deux espaces topologiques.

(i) Une multifonction de X vers Y est une fonction K : X ­> n(Y). On dit aussi que K est une fonction multiforme de X vers Y.

(ii) L'image par K d'un sous-ensemble F Ç X est l'ensemble K(E) := (J K(x).

xeE

(iii) Le graphe de K est l'ensemble Gr(K) :— {(x, y) E X x Y :y E K(x)}.

Dans le cas où Y est un espace métrique, une multifonction n'est, à toutes fins pratiques, rien d'autre qu'une fonction vers un espace que l'on peut munir de la métrique de Hausdorff. Il est donc naturel de définir (comme on le fera) la continuité d'une multifonction en utilisant cette métrique, puisqu'elle préserve la structure topologique de l'espace Y. Or, la métrique de Hausdorff est le maximum entre deux quantités (voir la définition 4.1.5) et il peut arriver (comme il nous arrivera!) que seulement l'une de celles-ci soit intéressante dans l'étude d'une multifonction donnée. Comme dans le cas des fonctions habituelles, on dira alors qu'on s'intéresse à la semi-continuité de la multifonction, et c'est ce qui nous conduit à la définition suivante :

Définition 4.2.2. Soient X un espace topologique, Y un espace métrique et K une multifonction de X vers Y. Fixons x G X et soit 5H comme dans la définition 4.1.2,

défini sur l'espace K(Y). Alors on dira que K est :

(i) semi-continue inférieurement (ou s.c.i.) en x si, pour toute suite (xn)n(:N Ç X

telle que xn —r x, on a ÔH(K(X), K(xn)) —> 0.

(ii) semi-continue supérieurement (ou s.es.) en x si, pour toute suite (x„)neN Ç X

telle que xn —> x, on a ÔH(K(xn), K(x)) —> 0.

(iii) continue en x, si K est à la fois semi-continue inférieurement et supérieurement en x.

Si, pour tout x G X, K est s.c.i., s.es. ou continue en x, alors on dira que K est, respectivement, s.c.i., s.c.s. ou continue sur X.

Il est de mise de présenter au lecteur une interprétation géométrique des multi-fonctions semi-continues qui permettrait de justifier l'emploi des termes « inférieure-ment » et « supérieureinférieure-ment ». Soit donc K une multifonction de X vers Y. Fixons une suite (xra)n6N Ç X qui converge vers un certain x G X et supposons que la suite

{K(xn))n e n de compacts dans Y admette une sous-suite qui converge, au sens de la

distance de Hausdorff, vers un certain compact H.I V En utilisant l'inégalité

triangu-laire du théorème 4.1.4, on obtient aisément que si K est semi-continue inférieurement en x, alors K(x) Ç H. L'ensemble K(x) est donc inférieur à toute limite éventuelle des images des xn. De même, si K est semi-continue supérieurement en x, on aura alors que

H Ç K(x) et donc que K(x) est supérieur à toute limite éventuelle des mêmes images.

IV. Une telle sous-suite existera assurément, par exemple, si Y est compact. Voir la discussion suivant la définition 4.1.5.

Les deux sous-sections qui suivent présentent, pour leur part, des interprétations topologiques des multifonctions semi-continues inférieurement et supérieurement.

4.2.1 Semi-continuité supérieure

Les multifonctions semi-continues supérieurement sont essentiellement celles dont le graphe est fermé. C'est ce que raconte le théorème suivant.

Théorème 4.2.3. Soit K une multifonction de X vers Y et soit d la métrique sur Y. Alors :

(i) Si K est s.es. sur X, alors Gr(K) est fermé dans X x Y.

(ii) Si C Ç X est compact et K est s.es. sur X, alors K(C) est compact.

(iii) Si Gr(K) est fermé dans X x Y, et s'il existe C Ç Y" compact tel que K(X) Ç C, alors K est s. es. sur X.

Démonstration.

(i) Soit ((xn,yn))n e N Ç Gr(K) et (x,y) G X x Y tels que xn ->• x et yn ->• y et

supposons K s.es. On veut montrer que (x, y) G Gr(K). Soit e > 0, et choisissons un n tel que

d(yn, y) < e/2 et 5H(K(xn), K(x)) < «s/2.

Alors, en utilisant l'inégalité triangulaire du théorème 4.1.4, on a dist(y,K(x)) = 8H({y},K(x))

< 8H({y}, {yn}) + 8H({yn}, K(xn)) + 6H(K(xn), K(x))

= d(y, yn) + dist(y„, K(xn)) + 5H(K(xn), K(x))

< e/2 + 0 + e/2 = e.

Comme cela fonctionne pour tout e > 0, on conclut que dist(y, K(x)) = 0. Comme K(x) est compact, on a donc y G K(x).

(ii) Supposons K s.es. et soit (yn)neN une suite dans K(C). Montrons que cette suite

admet une sous-suite convergente. Pour tout n, comme yn G K(C), alors il existe

xn E C tel que yn G K(xn). Puisque C est compact, alors la suite (xn)n e N admet

une sous-suite, disons ( xn) je N, qui converge vers un certain x E C.

Or, pour tout j , puisque ynj G K(xn j), on a dist(ynj, K(x)) < 8H(K{xnj),K(x)),