© Guy-Roger Kaba, 2019
Former les futurs enseignants de mathématiques du
secondaire gabonais à l'articulation
visualisation-raisonnements en géométrie
Thèse
Guy-Roger Kaba
Doctorat en didactique
Philosophiæ doctor (Ph. D.)
Québec, Canada
ii
Former les futurs enseignants de mathématiques du
secondaire gabonais à l’articulation
visualisation-raisonnements en géométrie
Thèse
Guy-Roger Kaba
Sous la direction de :
iii
RÉSUMÉ
La préparation des enseignants du secondaire gabonais à la prise en compte des erreurs des élèves en géométrie nous a conduits à questionner leur formation initiale. Ce questionnement a débouché sur la nécessité de concevoir et d’expérimenter une formation initiale à l’enseignement de la géométrie axée sur une articulation entre visualisation et raisonnements. La présente recherche vise l’étude des rapports aux savoirs de futurs enseignants au cours de cette formation. Pour atteindre cet objectif, nous nous sommes basés sur une articulation de plusieurs cadres théoriques. Ainsi, les rapports aux savoirs de ces futurs enseignants ont été appréhendés selon deux perspectives : les rapports à l’apprendre et les rapports à faire apprendre (Caillot, 2014). À ces deux perspectives, nous avons joint trois dimensions : identitaire, sociale et épistémique (Charlot et al., 1992). Nous avons choisi d’appréhender les dimensions identitaire et sociale à travers la dialectique outil-objet (Douady, 1986) et la dimension épistémique au moyen du modèle d’articulation visualisation-raisonnements inspiré de Duval (2005). Les rapports aux savoirs émergeant pendant la formation ont par la suite été expliqués par les interactions entre trois postures épistémologiques (DeBlois et Squalli, 2002). Ces explications se sont fondées sur le modèle de DeBlois (2012). Notre méthodologie s’est axée autour d’une expérimentation didactique (Steffe et D’Ambrosio, 1996). Ainsi, les rapports aux savoirs de cinq futurs enseignants ont été étudiés lors des différentes composantes de la formation. Il a été possible de mettre en lumière le fait que les futurs enseignants s’illustrent en début de formation soit par des rapports aux savoirs de nature heuristique, soit par des rapports aux savoirs de nature formelle. Les rapports aux savoirs de nature heuristique se caractérisent par une préoccupation pour la visualisation, alors que les rapports aux savoirs de nature formelle montrent une préoccupation pour le raisonnement déductif. La thèse montre par ailleurs que la formation a fait émerger des rapports aux savoirs de nature pragmatique. Ces rapports aux savoirs se caractérisent par une plus grande préoccupation pour l’articulation visualisation-raisonnements et favorisent une prise en compte des erreurs des élèves basée sur cette articulation. Les rapports aux savoirs de nature heuristique et de nature formelle s’expliquent par une tension entre les postures de l’ancien élève et de l’étudiant se soldant à l’avantage de la première. Les rapports aux savoirs de nature pragmatique résultent d’une synergie entre les postures de l’étudiant et de l’enseignant.
iv
ABSTRACT
The preparation of Gabonese teachers in secondary school to take into account the errors of students in geometry led us to question their pre-service training. This questioning has led to design and experiment a pre-service training in geometry teaching based on connection between visualization and reasoning. This research aims to study relationships to knowledge of pre-service teachers during this training. To achieve this goal we are based on several frameworks. Thus, these pre-service teachers's relationships to knowledge have been apprehended through two perspectives: relationships to learn and relationships to teach (Caillot, 2014). In these two perspectives, we have added three dimensions: identity, social and epistemic (Charlot et al., 1992). We chose to apprehend the dimensions of identity and social through the Dialectic Tool-Object (Douady, 1986) and the epistemic dimension using visualization-reasoning articulation model inspired by Duval (2005). The relationships to knowledge of pre-service teachers emerging during the training were later explained by the interactions between the three epistemological stances they adopted (DeBlois et Squalli, 2002). These explanations were based on the model of DeBlois (2012). Our methodology focused on a formative experiment (Steffe et D’Ambrosio, 1996). Thus, relationships to knowledge of five pre-service teachers were studied during the different components of the training. It has been possible to highlight the fact that pre-service teachers are illustrated at the beginning of training by heuristic or formal relationships to knowledge. Heuristic relationships are characterized by a concern for visualization, while formal relationships show a concern for deductive reasoning. The thesis also shows that the training has led to the emergence of pragmatic relationships to knowledge. These relationships to knowledge are characterized by a greater concern for the connection of visualization-reasoning and promote the taking into account of pupils’ errors based on this connection. The heuristic and formal relationships are explained by a tension between former-pupil stance and student stance, which resulted in advantage of the first. Pragmatic relationships to knowledge seems result from a synergy between student stance and teacher stance.
v
TABLE DES MATIÈRES
RÉSUMÉ iii
ABSTRACT iv
TABLE DES MATIÈRES v
LISTE DES FIGURES xv
LISTE DES TABLEAUX xxi
LISTE DES ABRÉVIATIONS ET DES SIGLES xxii
DÉDICACES xxiii REMERCIEMENTS xxiv INTRODUCTION 1 CHAPITRE 1 : PROBLÉMATIQUE 4 1.1 Cadre contextuel 4 1.1.1 Pertinence sociale 4
1.1.1.1 Système éducatif gabonais : accès universel vs échec massif 4 1.1.1.2 Programmes du 1er cycle et décrochages en géométrie 6 1.1.1.3 Dispositif de formation initiale des enseignants du secondaire au Gabon 10
1.1.2 Pertinence scientifique 12
1.1.2.1 Agir en formation initiale pour influencer les pratiques à leur installation 12 1.1.2.2 Promouvoir une fréquentation professionnelle des mathématiques 13 1.1.2.3 Viser des savoirs utiles à l’enseignement des mathématiques au secondaire 15 1.1.2.4 Baser le dispositif de formation initiale sur une stratégie de transposition 16
1.1.3 Synthèse du cadre contextuel 18
1.2 Cadre théorique 19
1.2.1 Rapports aux savoirs des futurs enseignants de mathématiques 19 1.2.1.1 Définition du concept et élargissement au ces des futurs enseignants 19 1.2.1.2 Intérêt de l’étude des rapports aux savoirs des futurs enseignants et des rapports à la
formation 20
1.2.1.3 Modélisation des rapports aux savoirs des futurs enseignants 22 1.2.1.4 Dialectique outil/objet, rapports traditionalistes, rapports formels et rapports
constructivistes 23
1.2.2.5 Rapports à l’erreur des futurs enseignants 25 1.2.2.6 Transformation des rapports aux savoirs des futurs enseignants 26 1.2.2 Postures épistémologiques des futurs enseignants 28 1.2.2.1 Définition du concept de « posture épistémologique » 28
vi
1.2.2.2 Postures de l’ancien élève, de l’étudiant et de l’enseignant 29 1.2.2.3 Adaptations, effets de contrat didactique et postures de futurs enseignants 29 1.2.2.4 Modèle de l’influence des préoccupations des futurs enseignants 31 1.2.2.5 Nouvel enjeu pour la formation initiale : décentrer la posture de l’ancien élève 33
1.2.3 Synthèse du cadre théorique 35
1.3 Cadre d’investigation 35
1.3.1 Exigences d’un apprentissage de la géométrie au secondaire 35 1.3.2 Modèle des modalités d’articulation visualisation-raisonnements en géométrie 38
1.3.3 Synthèse du cadre d’investigation 43
1.4 Questions et objectifs de la recherche 44
CHAPITRE 2 : MÉTHODOLOGIE 46
2.1 Choix méthodologiques 46
2.1.1 Recherche qualitative, descriptive, explicative et interprétative 46
2.1.2 Expérimentation didactique 46
2.1.3 Choix du milieu et des futurs enseignants participants à la recherche 47
2.1.3.1 Choix du milieu 47
2.1.3.2 Choix des futurs enseignants participants à la recherche 48
2.1.4 Considérations éthiques 49
2.2 Description du dispositif mis à l’épreuve 50
2.2.1 Composantes du dispositif à l’étude 50
2.2.1.1 Formation à l’interprétation 50
2.2.1.2 Formation à l’activité mathématique 53
2.2.1.3 Formation à l’intervention 55
2.2.2 Chronogramme et mise en œuvre du dispositif à l’étude 58
2.2.3 Séquence de formation 59
2.2.3.1 Objectifs et organisation de la séquence de formation 59
2.2.3.2 Contenu de la séquence de formation 60
2.3 Collecte des données 65
2.3.1 Productions écrites 65
2.3.1.1 Questionnaire 65
2.3.1.2 Analyses de productions d’élèves 66
2.3.1.3 Activité mathématique par la résolution de problèmes de recherche 71
vii
2.3.2.1 Planifications 72
2.3.2.2 Réalisations 73
2.4 Plan d’analyse des données 74
2.4.1 Retranscription des données 74
2.4.2 Analyse des données 76
2.4.2.1 Questionnaire 76
2.4.2.2 Analyse de productions d’élèves 79
2.4.2.3 Activité mathématique par la résolution de problèmes de recherche 81
2.3.2.4 Planification 82
2.3.2.5 Réalisation 84
2.4.3 Interprétation des données 85
2.4.4 Subjectivité du chercheur : ancien enseignant du secondaire, formateur d’enseignants et
superviseur de stagiaires 86
CHAPITRE 3 : ANALYSE DES RÉSULTATS 88
3.1 Alain 89 3.1.1 Questionnaire 89 3.1.1.1 Question I-1 89 3.1.1.2 Question I-2 89 3.1.1.3 Question I-3 89 3.1.1.3 Question I-4 89 3.1.1.4 Question II-1 91 3.1.1.5 Question II-2 91 3.1.1.6 Question II-3 92 3.1.1.7 Bilan 92
3.1.2 Analyse de productions d’élèves 93
3.1.2.1 Sans savoir de formation 93
3.1.2.2 Avec savoirs de formation 97
3.1.2.3 Bilan 102
3.1.3 Activité mathématique par la résolution de problèmes de recherche 103
3.1.3.1 Segments mobiles 103
3.1.3.2 Aires égales 105
3.1.3.3 Planètes cubiques 106
viii
3.1.3.5 Bilan 108
3.1.4 Planification 109
3.1.4.1 Concept à l’étude et savoirs préalables 109
3.1.4.2 Situations d’apprentissage 110 3.1.4.3 Situations d’évaluation 116 3.1.4.2 Bilan 126 3.1.5 Réalisation 127 3.1.5.1 Situations d’apprentissage 127 3.1.5.2 Situation d’évaluation 131 3.1.5.3 Bilan 132 3.1.6 Synthèse 133 3.2 Yannick 134 3.2.1 Questionnaire 134 3.2.1.1 Question I-1 134 3.2.1.2 Question I-2 134 3.2.1.3 Question I-3 134 3.2.1.4 Question I-4 134 3.2.1.5 Question II-1 136 3.2.1.6 Question II-2 136 3.2.1.6 Question II-3 137 3.1.1.7 Bilan 137
3.2.2 Analyse de productions d’élèves 137
3.2.2.1 Sans savoirs de formation 137
3.2.2.2 Avec savoirs de formation 139
3.2.2.3 Bilan 141
3.2.3 Activité mathématique 142
3.2.3.1 Segments mobiles 142
3.2.3.2 Aires égales 143
3.2.3.3 Planètes cubiques 143
3.2.3.4 Volume d’un solide composé de pavés droits imbriqués 144
3.2.3.5 Bilan 144
3.2.4 Planification 145
ix 3.2.4.2 Situations d’apprentissage 146 3.1.4.3 Situations d’évaluations 149 3.2.4.4 Bilan 156 3.2.5 Réalisation 157 3.2.5.1 Situations d’apprentissage 157 3.2.5.2 Situations d’évaluation 160 3.2.5.3 Bilan 156 3.2.6 Synthèse 157 3.3 Édouard 158 3.3.1 Questionnaire 158 3.3.3.1 Question I-1 158 3.3.3.2 Question I-2 158 3.3.3.3 Question I-3 158 3.3.3.4 Question I-4 159 3.3.3.5 Question II-1 160 3.3.3.6 Question II-2 160 3.3.3.5 Question II-3 160 3.3.3.5 Bilan 161
3.3.2 Analyse de productions d’élèves 161
3.3.2.1 Sans savoirs de formation 161
3.3.2.2 Avec savoirs de formation 163
3.3.2.3 Bilan 170
3.3.3 Activité mathématique 171
3.3.3.1 Segments mobiles 171
3.3.3.2 Aires égales 172
3.3.3.3 Planète cubique 175
3.3.3.4 Volume d’un solide composé de pavés droits imbriqués 176
3.3.3.5 Bilan 177
3.3.4 Planification 177
3.3.4.1 Concept à l’étude et savoirs préalables 177
3.3.4.2 Situations d’apprentissage 179
3.3.4.3 Situations d’évaluation 183
x 3.3.5 Réalisation 185 3.3.5.1 Introduction 185 3.3.5.2 Situations d’apprentissage 186 3.3.5.3 Bilan 190 3.3.6 Synthèse 190 3.4 Karl 192 3.4.1 Questionnaire 192 3.4.3.1 Question I-1 192 3.4.3.2 Question I-2 192 3.4.3.3 Question I-3 192 3.4.3.4 Question I-1 193 3.4.3.5 Question II-1 194 3.4.3.6 Question II-2 195 3.4.3.7 Question II-3 195 3.4.3.8 Bilan 195
3.4.2 Analyse de productions d’élèves 196
3.4.2.1 Sans savoirs de formation 196
3.4.2.2 Avec savoirs de formation 199
3.4.2.3 Bilan 203
3.4.3 Activité mathématique 204
3.4.3.1 Segments mobiles 204
3.4.3.2 Aires égales 206
3.4.3.3 Planète cubique 208
3.4.3.4 Volume d’un solide composé de pavés droits imbriqués 209
3.4.3.5 Bilan 211
3.4.4 Planification 212
3.4.4.1 Concept à l’étude et savoirs préalables 212
3.4.4.2 Situations d’apprentissage 212 3.4.4.3 Situations d’évaluation 219 3.4.4.4 Bilan 223 3.4.5 Réalisation 223 3.4.5.1 Situations d’apprentissage 223 3.4.5.2 Situations d’évaluation 233
xi 3.4.5.3 Bilan 240 3.4.6 Synthèse 241 3.5 Norbert 243 3.5.1 Questionnaire 243 3.5.1.1 Question I-1 243 3.5.1.2 Question I-2 243 3.5.1.3 Question I-3 243 3.5.1.4 Question I-4 244 3.5.1.5 Question II-1 245 3.5.1.5 Question II-2 245 3.5.1.5 Question II-3 245 3.5.1.6 Bilan 246
3.5.2 Analyse de productions d’élèves 246
3.5.2.1 Sans savoir de formation 246
3.5.2.2 Avec savoirs de formation 250
3.5.2.3 Bilan 254
3.5.3 Activité mathématique 255
3.5.3.1 Segments mobiles 255
3.5.3.2 Aires égales 257
3.5.3.3 Planète cubique 258
3.5.3.4 Volume d’un solide composé de pavés droits imbriqués 259
3.5.3.5 Bilan 261
3.5.4 Planification 261
3.5.4.1 Concept à l’étude et savoirs préalables 261
3.5.4.2 Situations d’apprentissage 262 3.5.4.3 Situations d’évaluation 268 3.5.4.4 Bilan 273 3.5.5 Réalisation 273 3.5.5.1 Situations d’apprentissage 273 3.5.5.2 Situations d’évaluation 285 3.5.5.3 Bilan 287 3.5.6 Synthèse 288
xii
4.1 Entrée dans la formation : Rapports aux savoirs et postures épistémologiques 298
4.1.1 Dimensions identitaire et sociale 298
4.1.1.1 Rapports à l’apprendre 298
4.1.1.2 Rapports à faire apprendre 298
4.1.1.3 Rapports aux savoirs de nature heuristique 300 4.1.1.4 Rapports aux savoirs de nature formelle 303 4.1.2 Modalités d’articulation visualisation-raisonnements en géométrie 304 4.1.2.1 Dimension épistémique de modalités 0/1 305 4.1.2.2 Dimension épistémique de modalités 2/3 306 4.1.3 Bilan des rapports aux savoirs à l’entrée dans la formation à l’étude 308
4.1.4 Postures épistémologiques 309
4.2 Durant la formation : Rapports aux savoirs et postures épistémologiques 311
4.2.1 Formation à l’interprétation 311
4.2.1.1 Rapports aux savoirs et modalités d’articulation 311
4.2.1.2 Postures épistémologiques 315
4.2.2 Formation à l’activité mathématique 318
4.2.2.1 Rapports aux savoirs et modalités d’articulation 318
4.2.2.2 Postures épistémologiques 322
4.2.3 Formation à l’intervention 323
4.2.3.1 Rapports aux savoirs et modalités d’articulation 323
4.2.3.2 Postures épistémologiques 325
4.3 Rapports à la formation 328
4.4 Synthèse de l’interprétation des résultats 331
CONCLUSION GÉNÉRALE 334
1. Rappel de la problématique 335
2. Rappel de la méthodologie 336
3. Réponses aux questions de recherche 336
3.1 Question 1 : Postures épistémologiques 336
3.2 Question 2 : Rapports aux savoirs 337
3.2.1 Dimensions identitaire et sociale des rapports à l’apprendre et des rapports à faire
apprendre 337
3.2.2 Modalités d’articulation visualisation-raisonnements 339
xiii
4. Limites de la recherche 340
5. Apports, retombées et perspectives 341
5.1 Apports et retombées 341 5.2 Perspectives 343 BIBLIOGRAPHIE 344 ANNEXES 363 ANNEXE 1 : Questionnaires 363 Alain 363 Yannick 365 Édouard 367 Karl 369 Norbert 371
ANNEXE 2 : Analyses de productions d’élèves (formation à l’interprétation) 373
Alain 373
Analyses sans savoir de formation 373
Analyses avec savoirs de formation 375
Yannick 380
Analyses sans savoir de formation 380
Analyses avec cadre théorique 380
Édouard 382
Analyses sans savoir de formation 382
Analyses avec savoirs de formation 384
Karl 388
Analyses sans savoir de formation 388
Analyses avec savoirs de formation 389
Norbert 392
Analyses sans savoir de formation 392
Analyses avec savoirs de formation 394
ANNEXE 3 : Résolution de problèmes (formation à l’activité mathématique) 398
Alain 398
Yannick 401
Édouard 402
xiv
Norbert 414
ANNEXE 4 : Planifications (Formation à l’intervention) 419
Alain 419
Yannick 426
Édouard 432
Karl 437
Norbert 444
ANNEXE 5 : Réalisations (Formation à l’intervention) 450
Alain 450
Yannick 459
Édouard 471
Karl 477
Norbert 493
xv
LISTE DES FIGURES
Figure 1 : Pyramide éducationnelle du Gabon (Fiche EPT Gabon, 2012) ... 5
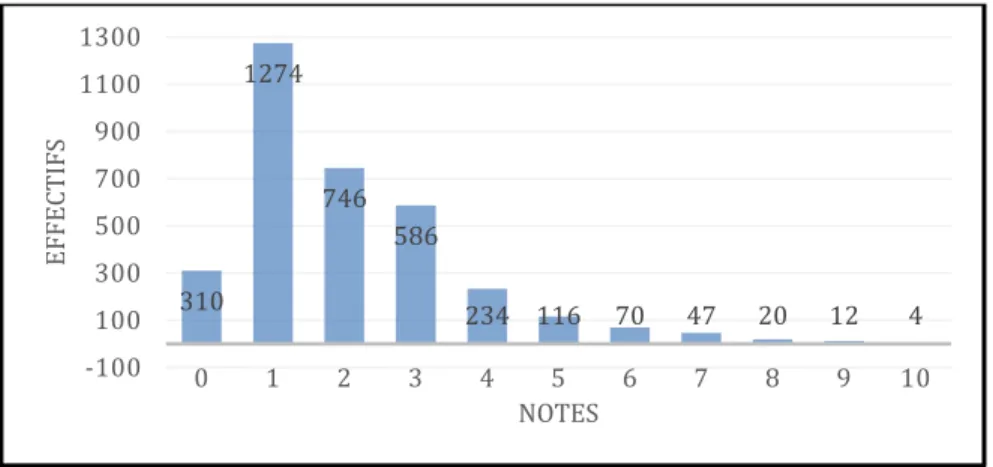
Figure 2 : Notes obtenues par 3419 élèves à l’exercice de géométrie du BEPC 2018 au Gabon ... 8
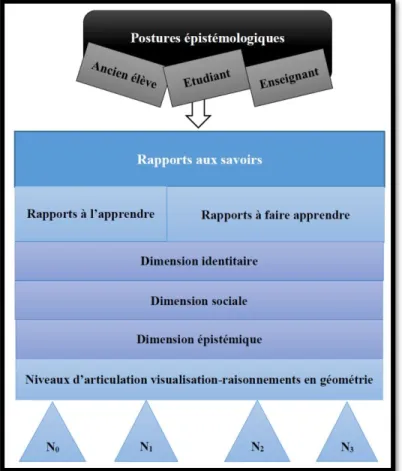
Figure 3 : modélisation des rapports aux savoirs de futurs enseignants de mathématiques du secondaire .... 22
Figure 4 : Modèle d’influence des préoccupations des futurs enseignants (DeBlois, 2012, p. 317) ... 32
Figure 5 : Division méréologique strictement homogène d’un parallélogramme (Duval, 2005:21) ... 41
Figure 6 : Division méréologique homogène d’un parallélogramme (Duval, 2005:21) ... 41
Figure 7 : Division méréologique hétérogène (Duval, 2005 : 22) ... 41
Figure 8 : Figure contre-exemple pour dépasser la confusion aire-périmètre (Balacheff, 1988 : 289) ... 42
Figure 9 : Déconstruction dimensionnelle d’un triangle pour aider à démontrer une égalité d’aires (Duval, 2005:27) ... 42
Figure 10 : Modèle d’analyse d’une formation à l’articulation visualisation-raisonnements en géométrie ... 44
Figure 11 : Un exemple d’analyse structurelle d’une démarche géométrique extrait de Cabassut (2005:62) .. 52
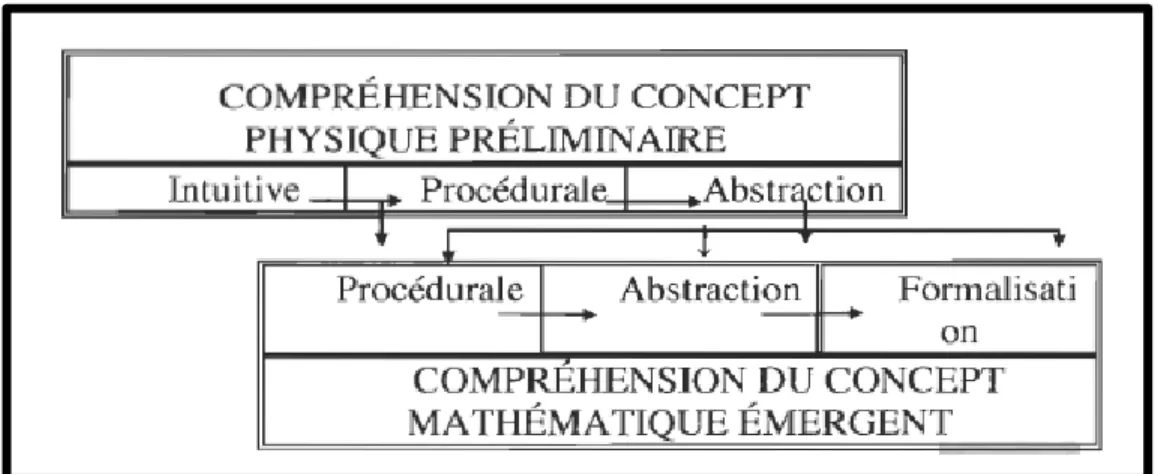
Figure 12 : Modèle de la compréhension mathématique de Bergeron et Herscovics (1989) repéré dans Jean (2014 : 20) ... 56
Figure 13 : Un exemple de question de réflexion durant la séquence de formation ... 59
Figure 14 : Découpage et recollement d’un disque (Cabassut, 2002 : 22) ... 63
Figure 15 : Modèle de planification inspiré de Barry (2011:10) ... 64
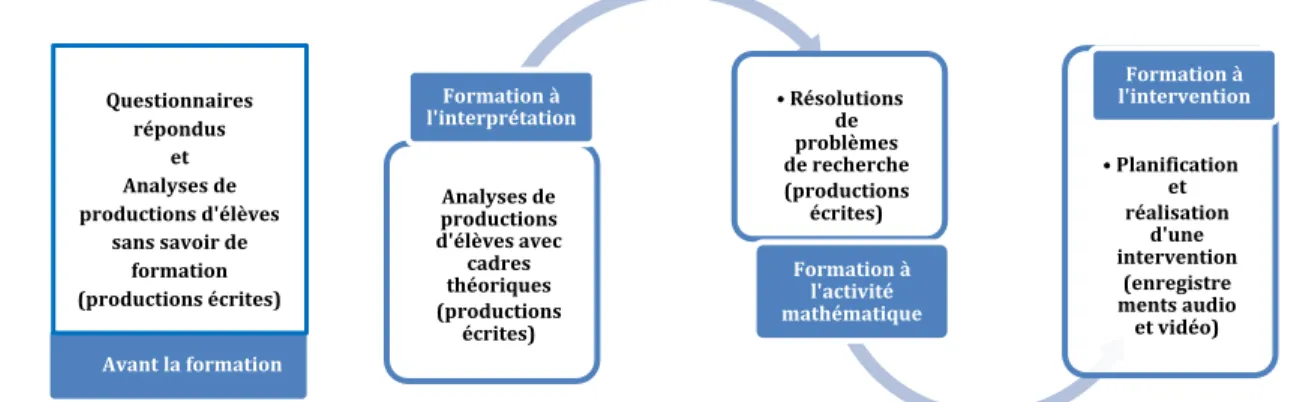
Figure 16 : Dispositif de collecte des données lors d’une formation à l’articulation visualisation-raisonnements ... 65
Figure 17 : Lunules d’Hippocrate (Delahaye, 1998) ... 66
Figure 18 : Production 1 ... 67
Figure 19 : Production 2 ... 68
Figure 20 : Production 3 ... 68
Figure 21 : Production 4 ... 69
Figure 22 : Problèmes soumis aux futurs enseignants lors de la formation à l’activité mathématique ... 71
Figure 23 : Plan d’analyse des données ... 74
Figure 24 : Extrait du verbatim de la planification d'Alain ... 75
Figure 25 : Extrait du verbatim de l'intervention de Norbert ... 75
Figure 26 : Étapes de l’interprétation des données ... 85
Figure 27 : Dessin construit par Alain (Annexe 1; questionnaire : question I-4) ... 90
Figure 28 : Preuve formelle d’Alain (annexe 1; questionnaire : question I-4) ... 90
Figure 29 : Analyse structurelle de la démarche géométrique d’Alain dans le questionnaire ... 91
Figure 30 : Déconstruction du solide de la production 1 dans le projet d’intervention d’Alain... 95
Figure 31 : Analyse structurelle de la démarche de l’élève dans la production 4 par Alain ... 98
Figure 32 : Déconstruction d’un solide en cubes par Alain ... 100
Figure 33 : Déconstruction d’un solide en cylindres et en pavé droit par Alain ... 100
Figure 34 : Dessins d’Alain dans la résolution du problème « segments mobiles » ... 103
Figure 35 : Dessins d’Alain dans la résolution du problème « aires égales » ... 105
Figure 36 : Dessins d’Alain dans la résolution du problème « planète cubique » ... 106
Figure 37: Dessin d’Alain dans le problème « volume d’un solide composé de pavés droits imbriqués » ... 107
Figure 38 : Intentions des situations d’apprentissage planifiées par Alain ... 110
xvi
Figure 40 : Parallélogramme décomposé en carrés dans la planification d’Alain ... 113
Figure 41 : Découpage/recollement d’un parallélogramme dans la planification d’Alain ... 113
Figure 42 : Recollement de deux triangles pour obtenir un parallélogramme dans la planification d’Alain ... 114
Figure 43 : Recollement de deux trapèzes pour obtenir un parallélogramme dans la planification d’Alain .... 115
Figure 44 Intentions des situations d’évaluation planifiées par Alain ... 116
Figure 45 : Calcul de l’aire d’un rectangle dans la planification d’Alain ... 117
Figure 46 : Calcul de l’aire d’une couronne rectangulaire dans la planification d’Alain ... 117
Figure 47 : Comparaison d’aire de différentes surfaces dans la planification d’Alain ... 118
Figure 48 : Calcul de l’aire d’un quadrilatère dans la planification d’Alain ... 119
Figure 49 : Comparaison d’aire de rectangles et de parallélogrammes dans la planification d’Alain ... 120
Figure 50 : Calcul de l’aire d’un triangle dans la planification d’Alain... 120
Figure 51 : Calcul d’une hauteur dans un triangle dans la planification d’Alain ... 122
Figure 52 : Calcul de l’aire d’un trapèze dans la planification d’Alain ... 124
Figure 53 : Calcul d’une des dimensions d’un trapèze dans la planification d’Alain ... 124
Figure 54 : Découpage d’un parallélogramme en deux trapèzes et calcul des aires de ces trapèzes dans la planification d’Alain ... 125
Figure 55 : Illustration de l’explication du découpage/recollement du parallélogramme dans l’intervention d’Alain ... 130
Figure 56 : Influence des préoccupations d’Alain comme prisme pour interpréter ses rapports aux savoirs (inspiré de DeBlois, 2012)) ... 133
Figure 57 : Preuve sans mot de Yannick (Annexe 1; questionnaire : Question I-4) ... 135
Figure 58 : Preuve formelle de Yannick (Annexe 1; questionnaire : Question I-4) ... 135
Figure 59 : Analyse structurelle de la démarche géométrique de Yannick dans le questionnaire ... 135
Figure 60 : Dessin de Yannick dans la résolution du problème « segments mobiles » ... 142
Figure 61 : Dessin de Yannick dans le problème « planète cubique » ... 143
Figure 62 : Intentions des situations d’apprentissage planifiées par Yannick ... 146
Figure 63 : Dessin servant d’appui à Yannick pour démontrer le théorème des angles d’un triangle ... 147
Figure 64 : Découpage d’un quadrilatère convexe en deux triangles dans la planification de Yannick ... 148
Figure 65 : Découpage d’un pentagone en trois triangles dans la planification de Yannick ... 149
Figure 66 : Intentions des situations d’évaluation planifiées par Yannick ... 149
Figure 67 : Situation d’évaluation sur le calcul d’un angle manquant dans un triangle dans la planification de Yannick ... 150
Figure 68 : Situation d’évaluation sur l’existence et la nature d’un triangle dans la planification de Yannick . 150 Figure 69 : Situation d’évaluation visant la détermination des angles d’un triangle dans la planification de Yannick ... 151
Figure 70 : Situation d’évaluation visant la détermination de deux angles d’un triangle dans la planification de Yannick ... 152
Figure 71 : Situation d’évaluation visant une démonstration de l’alignement de trois points dans la planification de Yannick ... 153
Figure 72 : Situation d’évaluation visant la discussion de l’existence d’un quadrilatère dans la planification de Yannick ... 154
Figure 73 : Situation d’évaluation visant la discussion sur la nature d’un quadrilatère dans la planification de Yannick ... 154
xvii
Figure 74 : Situation d’évaluation visant le calcul des angles d’un polygone planifié par Yannick... 155
Figure 75 : Situation d’évaluation visant le calcul des angles d’un pentadécagone planifié par Yannick ... 156
Figure 76 : Dessin réalisé au tableau par Yannick durant son intervention ... 158
Figure 77 : Dessin réalisé au tableau par Yannick durant son intervention ... 159
Figure 78 : Dessin réalisé au tableau par Yannick durant son intervention ... 160
Figure 79 : Dessin réalisé au tableau par Yannick durant son intervention ... 161
Figure 80 : Dessin réalisé au tableau par Yannick durant son intervention ... 149
Figure 81 : Dessin réalisé au tableau par Yannick durant son intervention ... 149
Figure 82 : Influence des préoccupations de Yannick pour interpréter ses rapports aux savoirs ... 157
Figure 83 : Dessin réalisé par Édouard (Annexe 1; questionnaire : question I-4) ... 159
Figure 84 : Preuve formelle d’Édouard (Annexe 1; questionnaire : question I-4) ... 159
Figure 85 : Analyse structurelle de la preuve formelle d’Édouard dans le questionnaire ... 159
Figure 86 : Analyse séquentielle effectuée par Édouard dans les analyses de productions d’élèves (Production 3) ... 165
Figure 87 : Analyse séquentielle effectuée par Édouard dans les analyses de productions d’élèves (Production 4) ... 166
Figure 88 : Dessin d’Édouard dans l’analyse de la production 4 ... 169
Figure 89 : Dessins d’Édouard dans la résolution du problème « segments mobiles » ... 171
Figure 90 : Dessins d’Édouard dans la résolution du problème "aires égales" ... 172
Figure 91 : Dessins d’Édouard dans la résolution du problème « aires égales » ... 173
Figure 92 : Dessins d’Édouard dans la résolution du problème "aires égales" ... 173
Figure 93 : Dessin d’Édouard dans la résolution du problème « planète cubique » ... 175
Figure 94 : Dessins d’Édouard dans la résolution du problème "volume d’un solide composé de pavés droits imbriqués" ... 176
Figure 95 : Intentions des situations d’apprentissage planifiées par Édouard ... 179
Figure 96 : Solide utilisé comme exemple de pavé droit dans la planification d’Édouard ... 181
Figure 97 : Collage de pyramides pour expliquer la formule de l’aire d’une pyramide dans la planification d’Édouard ... 182
Figure 98 : Collage de deux prismes en pavé droit pour expliquer la formule du volume d’un prisme dans la planification d’Édouard ... 182
Figure 99 : Intentions des situations d’évaluation planifiée par Édouard ... 183
Figure 100 : Objet représentant un cube présentant aux élèves par Édouard durant son intervention ... 187
Figure 101 : Objet représentant un pavé droit présentant aux élèves par Édouard durant son intervention .. 188
Figure 102 : Patron d’un cube dessiné au tableau par Édouard durant son intervention ... 188
Figure 103 : Patron d’un prisme droit dessiné au tableau par Édouard durant son intervention... 189
Figure 104 : Patron d’un pavé droit dessiné au tableau par Édouard durant son intervention... 189
Figure 105 : Influence des préoccupations d’Édouard pour interpréter ses rapports aux savoirs (Inspiré de DeBlois, 2012)) ... 190
Figure 106 : Dessin réalisé par Karl (Annexe 1; questionnaire : Question I-4) ... 193
Figure 107 : Preuve formelle de Karl (Annexe 1; questionnaire : Question I-4) ... 193
Figure 108 : Analyse structurelle de la démarche géométrique de Karl dans le questionnaire ... 194
Figure 109 : Dessin réalisé par Karl dans les analyses de productions d’élèves sans savoir de formation .... 198
Figure 110 : Dessin réalisé par Karl dans l’analyse de la production 3 ... 202
xviii
Figure 112 : Dessins au brouillon de Karl dans le problème « segments mobiles » ... 204
Figure 113 : Dessin de Karl dans la résolution du problème « aires égales » ... 206
Figure 114 : Dessin au brouillon de Karl dans la résolution du problème « aires égales » ... 206
Figure 115 : Dessins de Karl dans la résolution du problème « planète cubique » ... 208
Figure 116 : Dessins de Karl dans la résolution du problème « volume d’un solide composé de pavés droits imbriqués » ... 209
Figure 117 : Intentions des situations d’apprentissage planifiées par Karl ... 212
Figure 118 : Rectangle à décomposer en carrés unité dans la planification de Karl ... 213
Figure 119 : Parallélogramme à transformer en rectangle dans la planification de Karl ... 215
Figure 120 : Triangles à distribuer aux élèves dans la planification de Karl ... 216
Figure 121 : Situation sur la définition d’un trapèze dans la planification de Karl ... 217
Figure 122 : Intentions des situations d’évaluation planifiées par Karl ... 219
Figure 123 : Situation d’évaluation sur la comparaison d’aires planifiée par Karl ... 219
Figure 124 : Situation d’évaluation sur le calcul de l’aire d’une surface décomposable planifiée par Karl ... 220
Figure 125 : Situation d’évaluation sur le calcul de l’aire d’une surface décomposable planifiée par Karl ... 222
Figure 126 : Forme rectangulaire sur un fond de quadrillage distribuée aux élèves par Karl durant son intervention ... 223
Figure 127 : Dessin réalisé par Karl au tableau pour indiquer le carré-unité durant son intervention ... 224
Figure 128 : Dessin réalisé au tableau par Karl durant son intervention ... 229
Figure 129 : Dessin réalisé au tableau par Karl durant son intervention ... 230
Figure 130 : Dessin réalisé au tableau par Karl durant son intervention ... 230
Figure 131 : Dessin réalisé au tableau par Karl durant son intervention ... 233
Figure 132 : Dessin illustrant une situation d’évaluation dans l’intervention de Karl ... 234
Figure 133 : Surface décomposable dont les élèves doivent calculer l’aire durant l’intervention de Karl ... 235
Figure 134 : Dessin réalisé par Karl pour indiquer le découpage d’une figure décomposable durant l’intervention de Karl ... 235
Figure 135 : Dessin réalisé au tableau par Karl durant son intervention ... 239
Figure 136 : Dessin réalisé au tableau par Karl durant son intervention ... 239
Figure 137 : Influence des préoccupations de Karl comme prisme pour interpréter ses rapports aux savoirs (inspiré de DeBlois, 2012)) ... 241
Figure 138 : Dessin réalisé par Norbert (annexe 1; questionnaire : Question I-4) ... 244
Figure 139 : Preuve formelle de Norbert (annexe 1; questionnaire : Question I-4) ... 244
Figure 140 : Analyse structurelle de la démarche géométrique de Norbert dans le questionnaire ... 244
Figure 141 : Analyse structurelle que Norbert de sa démarche de résolution de la tâche relative à la production 3 ... 252
Figure 142 : Analyse structurelle que Norbert de sa démarche de résolution de la tâche relative à la production 4 ... 253
Figure 143 : Dessins de Norbert dans la résolution du problème "segments mobiles" ... 255
Figure 144 : Dessins au brouillon de Norbert dans la résolution du problème "segments mobiles" ... 255
Figure 145 : Dessin de Norbert dans l dans la résolution du problème « aires égales » ... 257
Figure 146 : Dessins au brouillon de Norbert dans la résolution du problème « aires égales » ... 257
Figure 147 : Dessins de Norbert dans la résolution du problème « planète cubique » ... 258
xix
Figure 149 : Dessins de Norbert dans la résolution du problème « volume d’un solide composé de pavés droits
imbriqués » ... 259
Figure 150 : Dessins au brouillon de Norbert dans la résolution du problème « volume d’un solide composé de pavés droits imbriqués » ... 259
Figure 151 : Intentions des situations d’apprentissage planifiées par Norbert ... 262
Figure 152 : Situation d’apprentissage sur la formule du volume d’un cube dans la planification de Norbert 262 Figure 153 : Situation hors évaluation sur la formule du volume d’un pavé droit dans la planification de Norbert ... 264
Figure 154 : Situation d’apprentissage sur la formule du volume d’une pyramide à base carrée dans la planification de Norbert ... 265
Figure 155 : Patrons de cubes à distribuer aux élèves dans la planification de Norbert ... 266
Figure 156 : Situation d’apprentissage sur collage de pyramides pour former un pavé droit dans la planification de Norbert ... 267
Figure 157 : Intentions des situations d’évaluation planifiées par Norbert ... 268
Figure 158 : Situation d’évaluation sur la formule du volume d’un cube dans la planification de Norbert ... 268
Figure 159 : Situation d’évaluation sur le volume d’un pavé droit dans la planification de Norbert... 269
Figure 160 : Situation d’évaluation sur le volume d’un pavé droit dans la planification de Norbert... 269
Figure 161 : Situation d’évaluation sur la comparaison de volumes de pavés droits dans la planification de Norbert ... 270
Figure 162 : Situation d’évaluation sur le calcul du volume d’une pyramide planifiée par Norbert ... 271
Figure 163 : Situation d’évaluation sur le volume d’une pyramide dans la planification de Norbert... 271
Figure 164 : Situation d’évaluation sur le calcul du volume d’une forme décomposable dans la planification de Norbert ... 272
Figure 165 : Cube découpé en cubes-unités dans l’intervention de Norbert ... 275
Figure 166 : Morceaux de sucre illustrant une rangée de cubes-unités dans l’intervention de Norbert ... 275
Figure 167 : Morceaux de sucre utilisés pour aider un élève dans l’intervention de Norbert ... 278
Figure 168 : Pavé droit découpé en cubes-unités dans l’intervention de Norbert ... 278
Figure 169 : Morceaux de sucre utilisés pour aider un élève dans l’intervention de Norbert ... 279
Figure 170 : Morceaux de sucre utilisés pour aider un élève dans l’intervention de Norbert ... 279
Figure 171 : Morceaux de sucre utilisés pour aider un élève dans l’intervention de Norbert ... 280
Figure 172 : Morceaux de sucre utilisés pour aider un élève dans l’intervention de Norbert ... 280
Figure 173 : Morceaux de sucre utilisés pour illustrer une couche de cubes-unités dans l’intervention de Norbert ... 282
Figure 174 : Situation d’évaluation dans l’intervention de Norbert ... 286
Figure 175 : Influence des préoccupations de Norbert pour interpréter ses rapports aux savoirs (Inspiré de DeBlois, 2012)) ... 288
Figure 176 : Dimensions identitaire et sociale des rapports à l’apprendre des futurs enseignants à leur entrée en formation ... 298
Figure 177 : Dimensions identitaire et sociale des rapports à faire apprendre des futurs enseignants à leur entrée en formation ... 299
Figure 178 : Dimension épistémique de modalités 0/1 des rapports aux savoirs des futurs enseignants à leur entrée en formation ... 306
xx
Figure 180 : Rapports aux savoirs des futurs enseignants à leur entrée en formation à l’articulation visualisation-raisonnements ... 308 Figure 181 : Tension entre les postures de l’ancien élève et de l’étudiant dans une formation à l’articulation visualisation-raisonnements en géométrie ... 316 Figure 182 : Transition de la posture de l’ancien élève vers celle de l’enseignant pendant une formation à l’articulation visualisation-raisonnements en géométrie ... 317 Figure 183 : Interactions entre postures épistémologiques et rapports aux savoirs de futurs enseignants lors d’une formation à l’articulation visualisation-raisonnements ... 332 Figure 184 : Rapports aux savoirs des futurs enseignants lors d’une formation à l’articulation visualisation-raisonnements ... 332 Figure 185 : Rapports aux savoirs et importance accordée à la démonstration ... 333
xxi
LISTE DES TABLEAUX
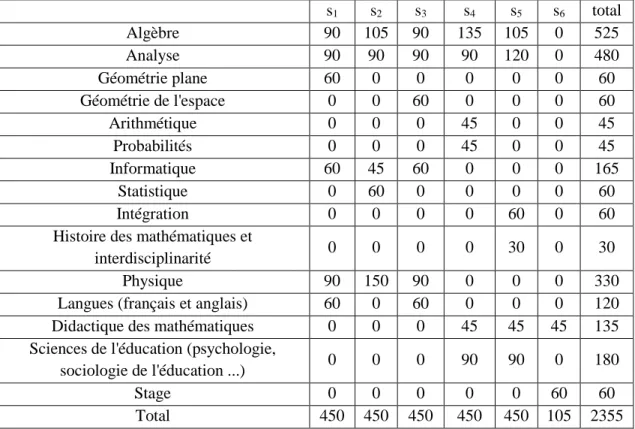
Tableau 1 : Répartition des cours selon la masse horaire pour la formation initiale à l’enseignement des
mathématiques ... 10
Tableau 2 : Types d’adaptations des futurs enseignants (DeBlois et Maheux, 2005:2) repérés dans Ndolly (2012:40) ... 30
Tableau 3 : Modèle des modalités d’articulation visualisation-raisonnements en géométrie ... 39
Tableau 4 : Analyse séquentielle d’une démarche géométrique ... 52
Tableau 5 : Chronogramme de la formation à l’articulation visualisation-raisonnements ... 58
Tableau 6 Contenu de la séquence de formation ... 60
Tableau 7 : Hypothèses sur l'origine des erreurs des élèves (DeBlois, 2011:211) ... 61
Tableau 8 : Codes des questions du questionnaire ... 76
Tableau 9 : Sous-grille d’analyse des questions I-1 et II-1 ... 76
Tableau 10 : Sous-grille d’analyse de la question I-2 ... 77
Tableau 11 Sous grille d’analyse de question I-3 ... 77
Tableau 12 Sous grille d’analyse de question I-4 ... 78
Tableau 13 : Sous-grille d’analyse de la question II-2 ... 78
Tableau 14 : Sous-grille d’analyse de la question II-3 ... 78
Tableau 15 : Codage des critères d’analyse des productions d’élèves ... 79
Tableau 16 :Sous-grille d’analyse du critère C1 ... 79
Tableau 17 : Sous-grille d’analyse du critère C2 ... 80
Tableau 18 : Sous-grille d’analyse du critère C3 ... 80
Tableau 19 : Sous-grille d’analyse du critère C4 ... 81
Tableau 20 : Grille d’analyse de la résolution des problèmes ... 82
Tableau 21 : Sous-grille d’analyse d’une situation d’apprentissage... 83
Tableau 22 : Sous-grille d’analyse d’une situation d’évaluation ... 84
Tableau 23 : Grille d’analyse des exigences des tâches d’une situation d’apprentissage ou d’évaluation ... 84
Tableau 24 : Grille d’analyse des évènements remarquables issus des réalisations d’interventions ... 85
Tableau 25 : Récapitulatif des grilles et des sous-grilles d’analyse des résultats ... 88
Tableau 26 : Analyse séquentielle de la démarche géométrique d’Alain dans le questionnaire ... 90
Tableau 27 : Analyse séquentielle de la démarche de l’élève dans la production 4 par Alain ... 98
Tableau 28 : Analyse séquentielle de la démarche géométrique de Yannick dans le questionnaire ... 135
Tableau 29 : Analyse séquentielle de la preuve formelle d’Édouard dans le questionnaire ... 159
Tableau 30 Analyse séquentielle effectuée par Édouard dans les analyses de productions d’élèves (Production 3) ... 165
Tableau 31 : Analyse séquentielle effectuée par Édouard dans les analyses de productions d’élèves (Production 4) ... 166
Tableau 32 : Analyse séquentielle de la démarche géométrique de Karl dans le questionnaire ... 193
Tableau 33 : Analyse séquentielle de la démarche géométrique de Norbert dans le questionnaire ... 244
Tableau 34 : Analyse séquentielle que Norbert de sa démarche de résolution de tâche relative à la production 3 ... 252
Tableau 35 : Analyse séquentielle que Norbert de sa démarche de résolution de la tâche relative à la production 4 ... 253
Tableau 36 : Rapports à la formation de futurs enseignants lors d’une formation à l’articulation visualisation-raisonnements ... 328
xxii
LISTE DES ABRÉVIATIONS ET DES SIGLES
Bac (série) C : Baccalauréat de l’enseignement secondaire général à dominante mathématiques
Bac (série) D : Baccalauréat de l’enseignement secondaire général à dominante Sciences expérimentales
Critère C1 : Décrire la démarche géométrique de l’élève : indiquer ce que l’élève a fait et
non ce qu’il aurait dû faire ou ce qu’il n’a pas réussi à faire
Critère C2 : Décrire les erreurs de l’élève : indiquer dans la démarche de l’élève ce qui
semble être erroné et expliquer pourquoi cela peut être considéré comme une erreur Critère C3 : Émettre une hypothèse sur les origines possibles de ces erreurs
Critère C4 : Proposer une intervention pour aider l’élève à prendre conscience de ses erreurs
et à les dépasser
ÉNS : École Normale Supérieure IPN : Institut Pédagogique National
Question I-1 : Que signifie apprendre la géométrie en 4e ?
Question I-2 : À quoi servent les dessins dans une démarche géométrique ?
Question I-3 : Que pensez-vous de la démarche présentée dans la figure ci-dessous appelée preuve sans mot ? Peut-elle être considérée comme une démonstration ?
Question I-4 : Donnez une preuve sans mot et une preuve formelle pour montrer que l’aire d’un carré inscrit dans cercle de rayon r est égale à 2r2, puis comparez ces deux preuves
Question II-1 : Que signifie enseigner la géométrie en 4e ?
Question II-2 : Comment expliquez-vous que des élèves de 4e utilisent l’évidence, des mesures ou des vérifications à l’aide d’instruments quand on leur demande de démontrer ? Question II-3 : Comment pourriez-vous intervenir auprès de tels élèves ?
SA : Situation d’apprentissage SÉ : Situation d’évaluation
SVT : Sciences de la Vie et de la Terre
UNESCO : Organisation des Nations unies pour l'éducation, la science et la culture UNICEF : Fonds des Nations unies pour l'enfance
xxiii
DÉDICACES
À Léandre À Théo À Aurélien
xxiv
REMERCIEMENTS
Cette thèse est l’aboutissement d’une longue aventure qui n’aurait pas pu aboutir sans la contribution de plusieurs personnes que la Providence a bien voulu placer sur mon chemin. Elles ont su m’apporter l’aide nécessaire au moment opportun. En premier lieu, je citerai Lucie DeBlois, ma directrice de recherche. Dès notre première rencontre, j’ai su qu’elle allait m’être d’un apport décisif pour l’aboutissement de ce projet. Par la suite, à chacune de nos discussions, j’ai noirci mon carnet de notes qui, en fin de compte, m’ont permis d’éviter de nombreux écueils. J’ai ainsi pu bénéficier de ses habiletés tant personnelles que professionnelles. Qu’elle reçoive ici toute ma gratitude et ma reconnaissance. En deuxième lieu, je tiens à remercier les membres de mon comité de thèse. Je commencerai par exprimer ma reconnaissance à Claudia Corriveau qui en plus de son rôle d’examinatrice a accepté de faire la pré-lecture de cette thèse. Il y a ensuite Frédéric Gourdeau qui n’a pas manqué d’apporter sa rigueur de mathématicien pour émettre des critiques toujours constructives. Enfin, j’exprime toute ma gratitude à Annette Bracone-Michoux pour son rôle de jury externe.
Je voudrais associer à ces remerciements Jacques Désautels et Marie Larochelle, professeurs émérites, pour avoir les premiers crus en mon aptitude à mener à bien des études doctorales. Il est clair que ce projet n’aurait pas vu le jour sans leurs encouragements notamment durant la période ayant précédé mon arrivée au Canada. Je n’oublie pas non plus les interventions décisives des professeurs Denis Savard et Guy-Martial Nkiet1 pour la
signature de la convention entre l’université Laval et l’École Normale Supérieure (ENS) de Libreville dans laquelle s’inscrit cette thèse. Merci aussi aux étudiants de l’ENS qui ont accepté de participer à cette recherche et à Gaël avec qui j’ai eu le plaisir à partager un même bureau pour son aide précieuse à chacune de mes sollicitations.
Je remercie également Octave pour son soutien discret, mais non moins précieux, je n’oublie pas Léa et Didier qui m’ont encouragé à vivre cette expérience québécoise. Pour finir, last but not least, je tiens à adresser toute ma gratitude à mon épouse Sabrina qui a accepté de me suivre dans cette aventure à l’issue incertaine. Elle aura été mon inspiratrice.
1
INTRODUCTION
L’enseignement de la géométrie au secondaire est souvent étudié sous l’angle de l’acquisition du raisonnement déductif (Balacheff, 1982; Houdebine, 1990; Barbin et al., 2001; Tanguay, 2002). Cela peut se justifier par l’importance de ce type de raisonnement dans la formation mathématique des élèves (Hanna, 1995; Houdebine, 1990). Comme dans plusieurs pays, les programmes du secondaire gabonais mettent donc l’accent sur l’apprentissage du raisonnement déductif dès le début du secondaire. C’est ainsi que la formation initiale à l’enseignement de la géométrie est essentiellement axée sur ce raisonnement. Mais les travaux de Duval (2005) montrent qu’une articulation entre visualisation et différents types de raisonnements apparaît comme une condition nécessaire à l’apprentissage de la géométrie au secondaire. On comprend la tendance observée chez les enseignants de mathématiques à ne se préoccuper que très peu des erreurs des élèves, source de difficultés et nombreux décrochages (Quentin de Mongaryas, 2013). Cette thèse part de l’hypothèse qu’agir en formation initiale en formant les futurs enseignants à l’articulation entre visualisation et raisonnements pourrait contribuer à favoriser une inversion de cette tendance.
C’est ainsi que nous avons conçu et expérimenté un dispositif de formation visant à promouvoir des savoirs sur l’articulation visualisation-raisonnements en géométrie. Ce choix justifie le titre de la thèse : « Former les futurs enseignants de mathématiques du secondaire gabonais à l’articulation visualisation-raisonnements en géométrie ». L’organisation de ce dispositif ne relève pas d’une stratégie d’homologie consistant à proposer aux futurs enseignants la résolution de situations d’apprentissage similaires à celle qu’ils proposeront à leurs élèves (Kuzniak, 1994). Le dispositif expérimenté est plutôt axé sur une stratégie de transposition (Houdement, 2013) à travers l’arrimage de trois composantes :
- une formation à l’interprétation à travers l’analyse de productions d’élèves;
- une formation à l’activité mathématique par la résolution de problèmes de recherche peu familiers aux futurs enseignants;
- une formation à l’intervention à travers des planifications et la réalisation de ces planifications en classe.
Cette articulation entre plusieurs composantes s’explique par une volonté de prendre en considération la non-transparence des savoirs de formation (DeBlois, 2012; Sayac, 2013). Ainsi, plusieurs recherches montrent la difficulté pour les futurs enseignants pour mobiliser
2
ces savoirs dans leurs interventions (Schram et al., 1988). Cette difficulté pourrait être en lien avec le sens et la valeur que les futurs enseignants confèrent à ces savoirs de formation (Raymond, 1997; Astolfi et Peterfalvi, 1993; Favre et Reynaud, 2000). L’organisation privilégiée dans le cadre de cette thèse permet donc de prendre en compte les rapports aux savoirs des futurs enseignants pendant la formation. Cela permet de comprendre pourquoi notre questionnement central renvoie aux types de rapports aux savoirs des futurs enseignants et à la recherche d’une explication de l’actualisation de ces rapports aux savoirs pendant la formation. Pour cela, nous avons convenus d’appréhender les rapports aux savoirs des futurs enseignants à travers :
- deux perspectives : les rapports à l’apprendre (Charlot et al., 1992) et les rapports à faire apprendre (Caillot, 2014);
- trois dimensions : identitaire, sociale et épistémique (Charlot et al., 1992; Charlot, 2003).
Alors que les dimensions identitaire et sociale ont été appréhendées à travers la dialectique outil-objet (Douady, 1986), la dimension épistémique a été étudiée au moyen du modèle des modalités d’articulation visualisation-raisonnements que nous avons développé en nous inspirant des travaux de Duval (2005). Ce modèle met en jeu quatre modalités d’articulation visualisation-raisonnements :
- la modalité 0 est celle dans laquelle la visualisation n’est pas requise et seul le raisonnement déductif et particulièrement la démonstration est valorisé;
- la modalité 1 est celle dans laquelle la visualisation est requise dans sa fonction d’illustration (Chaachoua, 1997) et seul le raisonnement déductif et particulièrement la démonstration est valorisé;
- la modalité 2 est celle dans laquelle la visualisation est requise dans ses fonctions « prise en charge d’hypothèses » et « expérimentation » (Chaachoua, 1997). Dans cette modalité, la validité des propositions est établie par les raisonnements inductif ou analogique. Mais une place importante est accordée aux raisonnements informels des élèves;
- la modalité 3 est celle dans laquelle la visualisation est requise dans ses fonctions « prise en charge d’hypothèses » et « expérimentation » (Chaachoua, 1997). Cette modalité prend en compte également les raisonnements formel, analogique et inductif. Mais la différence avec la modalité 2 réside dans le fait que la validité des propositions s’établit par le raisonnement déductif. Ici, la visualisation sert d’appui à la recherche d’une démonstration.
Le modèle explicatif de l’actualisation de ces rapports aux savoirs se fonde sur les recherches de DeBlois et Squalli (2002) sur les postures épistémologiques adoptées par les futurs enseignants en formation initiale : la posture de l’ancien élève, la posture de
3
l’étudiant et la posture de l’enseignant. Il met également à contribution le modèle de DeBlois (2012) relatif aux préoccupations des futurs enseignants lors d’une formation initiale à l’enseignement des mathématiques.
La thèse se structure en quatre chapitres. Le chapitre 1 est consacré à la problématique et se compose : d’un cadre contextuel, d’un cadre théorique, d’un cadre d’investigation et de la définition de nos questions et de notre objectif de recherche. Le cadre contextuel permet de montrer les particularités du système éducatif gabonais et de mettre à jour la pertinence sociale de la thèse. Le cadre théorique permet de présenter quelques théories de la didactique des mathématiques et de montrer leur pertinence pour analyser la formation à l’étude. Le cadre d’investigation permet d’expliciter quelques caractéristiques de l’enseignement et de l’apprentissage de la géométrie au secondaire. La présentation des cadres théoriques et d’investigation aboutit à la mise en évidence de nos questions et de notre objectif de recherche.
Le chapitre 2 est réservé à la méthodologie. Le chapitre 3 est consacré à l’analyse des résultats alors que le chapitre 4 consiste en l’interprétation de ces résultats. La dernière partie de cette thèse concerne la conclusion générale. Elle comporte en particulier la réponse à nos questions de recherche. La thèse comporte par ailleurs cinq annexes. L’annexe 1 contient les réponses des futurs enseignants au questionnaire. L’annexe 2 contient les analyses de productions d’élèves, l’annexe 3 contient les résolutions de problèmes de recherche, l’annexe 4 contient les verbatim des présentations orales des planifications et l’annexe 5 contient les verbatim des réalisations d’interventions des futurs enseignants. Dans l’annexe 6, nous avons regroupé tous les documents ayant servi de supports aux activités des futurs enseignants avant et pendant la formation, mais également ceux relatifs à l’information et au recrutement des futurs enseignants participants à la recherche. Cette thèse, ancrée en didactique des mathématiques, ambitionne de contribuer à la réflexion sur la résolution des problèmes qui se posent dans le système éducatif gabonais. La première partie du chapitre 1 consacrée au cadre contextuel, commence par une brève présentation de la situation globale de ce système puis se focalise sur la question des décrochages en mathématiques des élèves du secondaire qui montre la pertinence sociale de la thèse.
4
CHAPITRE 1 : PROBLÉMATIQUE
1.1 Cadre contextuel
1.1.1 Pertinence sociale
1.1.1.1 Système éducatif gabonais : accès universel vs échec massif
Au Gabon, l’enseignement obligatoire se compose du pré-primaire, du primaire et du 1er
cycle du secondaire appelé « collège ». Le secondaire comprend en plus du collège, un second cycle appelé « lycée ». Le collège dure quatre ans et se termine par un examen final : le Brevet d’Études du Premier Cycle (BEPC). Le lycée dure trois ans et se solde également par un examen national : le baccalauréat de l’enseignement secondaire2. La réussite à cet
examen conditionne l’entrée à l’université alors que l’obtention du BEPC ne permet pas l’admission au lycée. Seule l’obtention d’une moyenne de 10/20 des moyennes arithmétiques des disciplines pondérées par des coefficients permet la promotion d’une classe à la suivante. Il est important de noter que les quatre classes du collège sont : la 6e (élèves de 11/12 ans), la 5e (élèves de 12/13 ans), la 4e (élèves de 13/14 ans), et la 3e(élèves de 14/15 ans). Au lycée, les trois classes sont : la 2nde, la 1ère et la terminale. Les classes de 2nde se subdivisent en deux séries : S (dominante mathématiques et sciences expérimentales) et LE (dominante littérature et sciences économiques et sociales). Les élèves de 2nde S peuvent poursuivre en 1ère S (dominantes mathématiques et sciences expérimentales). La 1ère S leur donne par la suite la possibilité de continuer soit en terminale C3 (dominantes mathématiques), soit en terminale D (dominantes sciences expérimentales). Les élèves de 2nde LE peuvent poursuivre soit en 1ère puis en terminale A1 (dominantes français et philosophie), soit en 1ère A2 puis en terminale A2 (dominantes langues), soit en 1ère B puis en terminale B (dominantes sciences économiques et sociales).
Par ailleurs, le système éducatif gabonais est marqué par un paradoxe. D’une part, on observe un taux net de scolarisation d’environ 94% et un taux de parité garçon/fille quasi égalitaire
2 Diplôme inspiré du système éducatif français. Le baccalauréat est organisé en séries : A (dominantes langues et philosophie), B (dominantes sciences économiques et sociales), C (dominantes mathématiques), D (dominantes sciences expérimentales).
3 La voie scientifique à dominante mathématiques (2nde S, 1ère S et terminale C) est considérée dans les faits comme la voie d’excellence (Kouassi Assah, 2014), alors que les orientations dans les autres séries se font le plus souvent par défaut en particulier en série B qui est souvent perçue comme celle dans laquelle se retrouvent les élèves ne pouvant être orientés ailleurs (Quentin de Mongaryas, 2017).
5
de 0,974 traduisant un accès quasi universel. D’autre part, des taux de redoublement de
l’ordre de 40 % au primaire et de 30 % au secondaire en 20125 mettent à jour un échec
massif. Les données suivantes confirment ce paradoxe dans tous les ordres d’enseignement : Sur 1000 élèves inscrits en première année du primaire, 19 seulement arrivent en 6e sans reprendre de classe, 31 en reprenant une fois l’une des classes du primaire, 39 en reprenant deux fois et le reste, soit 911 élèves, aurait abandonné le système scolaire. Au secondaire, sur 1000 élèves admis en classe de 6e, 5e obtiennent le bac sept années plus tard sans redoubler, 12 après une reprise de classe, 161 au terme de deux reprises, 11 après trois reprises et le reste, soit 811 élèves, aurait décroché (Demba, 2011:211).
En outre, les taux de scolarisation nets sont de 64 % au collège6, de 27 % au lycée7 et de 698
étudiants universitaires pour 100 000 habitants8 ce qui montre une forte déperdition d’un
ordre d’enseignement à l’autre (Mackaya, 2014). Cette situation s’illustre par la figure 1 :
Figure 1 : Pyramide éducationnelle du Gabon (Fiche EPT Gabon, 2012)
Pour sortir de cet échec massif, le gouvernement gabonais a organisé en 2010 des États généraux de l’éducation et de la formation. Le rapport final de ces assises 9 indique que « […]
le système éducatif gabonais est placé devant l’urgence de se réformer en redonnant un
4 http://www.unicef.org/french/infobycountry/gabon_statistics.html. 5http://www.unesco.org/new/fileadmin/MULTIMEDIA/FIELD/Dakar/pdf/GabonprofileEPToct2012.pdf. 6 1er cycle du secondaire 7 2d cycle du secondaire 8 Rapport UNESCO de 2007.
9 Rapport final des États Généraux de l’Éducation, de la Recherche et de l’adéquation formation – emploi
6
nouveau souffle à l’école, à la formation et à la recherche, en vue de les rendre plus intégrales, inclusives, performantes et justes ; en somme, tendre vers une meilleure gouvernance » (p.23). Afin de mettre en œuvre ces réformes, une nouvelle loi d’orientation (loi 21/2011) a été promulguée en 2012. Il s’en est suivi l’adoption d’une loi de programmation précisant les objectifs de cette réforme : 1) lutter contre le redoublement, 2) parvenir à un taux de décrochage inférieur à 10 %, 3) viser des taux de réussite de plus de 60 % aux examens nationaux.
Par ailleurs, les mathématiques jouent un rôle central dans l’enseignement secondaire (ministère de l’Éducation nationale Gabon, 2015). Ce rôle central s’illustre par une masse horaire supérieure à celle des autres disciplines : 5 heures hebdomadaires comme le français, 2 ou 3 heures pour les autres disciplines. Une autre illustration de ce poids important est le coefficient 6 attribué aux mathématiques au même titre que le français dans le calcul de la moyenne, principal critère de passage en classe supérieure. Il n’est donc pas déraisonnable de vouloir questionner l’enseignement de cette discipline en vue de contribuer à une plus grande réussite scolaire au Gabon. Cela justifie l’intérêt porté dans le cadre de cette thèse à l’enseignement et à l’apprentissage des mathématiques et donc à la didactique de cette discipline. Dans la section suivante, après une description des programmes du 1er cycle, nous envisagerons des angles possibles sur lesquels pourrait s’articuler une réflexion menant à contribution à la réduction du décrochage des élèves gabonais en mathématiques.
1.1.1.2 Programmes du 1er cycle et décrochages en géométrie
Les programmes actuellement appliqués au secondaire gabonais ont été introduits en 1992. Ils résultent d’une collaboration d’experts d’une quinzaine de pays d’Afrique subsaharienne francophone et ont permis d’harmoniser les programmes de ces pays (Touré, 2002). Ces programmes ont été révisés en 2016 avec l’introduction, entre autres, des probabilités en classe de 3e (élèves de 15/16 ans) alors qu’elles n’étaient enseignées qu’en terminale (17/18 ans). Cette réforme s’est accompagnée d’une réorganisation de la progression des apprentissages marquée par une volonté de viser une plus grande continuité dans la manière d’aborder les concepts mathématiques d’une classe à l’autre. La poursuite de cette réforme devrait aboutir au basculement progressif d’une pédagogie par objectifs à une approche par
7
les compétences afin de s’arrimer à la réforme du primaire vieille d’une quinzaine d’années (Mackaya, 2014; Ndolly, 2012).
Le programme du 1er cycle se subdivise en deux parties : 1) les travaux numériques (algèbre, arithmétique, probabilités et statistique), 2) la géométrie (configurations du plan et de l’espace, transformations du plan et repérage). En géométrie, l’accent est mis sur l’apprentissage du raisonnement déductif. En effet, un des objectifs du programme stipule qu’il faut « initier le plus tôt possible l’élève au raisonnement déductif »10 (p.1). Ainsi, en
classes de 6e (10/11 ans) et de 5e (11/12 ans), le programme préconise une initiation aux
raisonnements à un seul pas de déduction (application directe d’une définition ou d’une propriété). En classes de 4e (13/14 ans) et de 3e (15/16 ans), le programme propose d’introduire des raisonnements à plus d’un pas de déduction selon les trois étapes suivantes : 1) la lecture de l’énoncé (construction d’une figure codée, repérage des données et de la conclusion), 2) la recherche d’une démarche et 3) la rédaction de la solution. Cette progressivité se traduit par l’apparition, en classe de 4e (13/14 ans), de l’exigence du raisonnement déductif.
Toutefois, la mise en œuvre de ce programme s’illustre par de nombreuses difficultés d’apprentissage et une recherche de Quentin de Mongaryas (2013) indique que :
La plupart des élèves ont fait ressortir la thèse selon laquelle les difficultés ont débuté dès la classe de 4e. Cela est évoqué par les élèves de 4e en terminale. Mais dans un premier temps, ces élèves s’expriment de façon générale : « mes difficultés en maths sont théoriques et pratiques depuis la classe de 4e » (fille, terminale A1); « il y a certains chapitres que je ne maîtrise pas depuis la classe de 4e » (garçon, terminale D); « mes difficultés sont que je n’arrive pas à
assimiler toutes les propriétés depuis la classe de 4e » (fille, 3e) (p.6).
Outre le fait de pointer la classe de 4e comme cadre de la naissance de leurs difficultés en mathématiques, ces élèves indexent particulièrement la géométrie :
Les élèves ajoutent aussi qu’elles sont les composantes les moins accessibles […] ainsi que l’indiquent les extraits suivants : « j’éprouve des difficultés en géométrie depuis la 4e » (garçon, 2nde S); « mes difficultés se situent au niveau
de la géométrie depuis la classe de 4e » (fille, 3e); « mes difficultés en maths ce sont les chapitres de géométrie, et ce depuis la 4e » (garçon, terminale B), « mes difficultés en maths sont les constructions et les démonstrations depuis la classe
10Ministère de l’Éducation nationale du Gabon (1996). Programme de mathématiques du premier cycle du secondaire. Institut Pédagogique National (IPN).
8
de 4e » (garçon, 2nde S), « mes difficultés se situent au niveau de la géométrie depuis la classe de classe 4e » (garçon, 2nde S (p.6).
Ces difficultés sont confirmées par les notes obtenues par les élèves à l’exercice de géométrie du BEPC 2018 portant essentiellement sur la production de démonstrations 11.
Figure 2 : Notes obtenues par 3419 élèves à l’exercice de géométrie du BEPC 2018 au Gabon
La répartition de ces notes présentées dans la figure 2 montre qu’un peu plus de 85% des élèves ont obtenu une note inférieure ou égale à 3/10. Ces difficultés pourraient être en lien avec l’exigence dès la classe de 4e du raisonnement déductif à des élèves peu familiers
jusqu’ici à ce mode de raisonnement. Cela met en évidence la nécessité pour les enseignants12 d’accompagner la construction progressive du raisonnement déductif en
géométrie à travers une prise en compte des difficultés d’apprentissage.
Or, ces difficultés pourraient le plus souvent déboucher sur de nombreux décrochages (Ella Mvé, 2009; Ikapi, 2012; Quentin de Mongaryas, 2013). Pour tenter d’expliquer ces décrochages, Quentin de Mongaryas (2013) pointe des rapports négatifs aux mathématiques chez les élèves qui pourraient être liés à l’engagement pédagogique des enseignants :
Dans ce sens les propos sont plus qu’évocateurs : « mon prof de maths de 4e est
responsable de ma faiblesse en géométrie » (garçon, 2nde S); « mes enseignants ont joué un rôle dans mes difficultés en géométrie » (garçon, terminale D); « mes enseignants ont joué un rôle dans mes difficultés en maths » (fille, 3e), « les enseignants ont joué un rôle négatif, celui de me faire détester les maths» (fille, 1ère A1), « les enseignants ont survolé certains chapitres » (fille, terminale A2),
« c’est lié à la paresse des profs ». De façon ramassée, ici, toutes les accusations
11 Le sondage réalisé par les encadreurs pédagogiques porte sur 3419 copies choisies de manière aléatoire dans plusieurs centres de correction de Libreville.
12Dans cette thèse, le masculin est utilisé à titre épicène.
310 1274 746 586 234 116 70 47 20 12 4 -100 100 300 500 700 900 1100 1300 0 1 2 3 4 5 6 7 8 9 10 EF FEC T IF S NOTES
9
formulées laissent présager un faible engagement pédagogique des enseignants (p.6).
À ce stade de la réflexion, un postulat émerge : les enseignants pourraient ne prendre que peu en compte les difficultés d’apprentissage de la géométrie. Pour explorer ce postulat, plusieurs pistes peuvent être envisagées. L’une d’entre elles conduit à questionner l’incidence des conditions dans lesquelles exercent souvent ces enseignants tels que des tailles des classes pouvant excéder le ratio de 100 élèves par classe (Quentin de Mongaryas, 2017). Ces conditions pourraient rendre problématique une telle prise en compte. Une seconde piste consiste à questionner la culture scolaire dans laquelle pourraient avoir baigné ces enseignants dans leur scolarité au secondaire et en formation initiale. Cette culture scolaire pourrait avoir conforté les enseignants dans l’idée qu’enseigner pourrait consister à exposer les savoirs mathématiques de la meilleure des manières et que les difficultés seraient dues à un travail insuffisant des élèves. L’exploration de cette seconde piste incite à s’interroger sur la capacité du dispositif de formation initiale à complexifier cette vision de l’enseignement des mathématiques. L’inclination de la thèse pour la didactique des mathématiques explique que la seconde piste ait été privilégiée. Dans la sous-section suivante, nous nous proposons donc d’analyser dans quelle mesure le dispositif actuel permet de préparer les futurs enseignants à la prise en compte des difficultés d’apprentissage de la géométrie.