La notion d'expression et ses origines mathématiques

HAL Id: hal-00984103

https://hal.archives-ouvertes.fr/hal-00984103

Submitted on 26 Feb 2017

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

La notion d’expression et ses origines mathématiques

Debuiche Valérie

To cite this version:

Debuiche Valérie. La notion d’expression et ses origines mathématiques. Studia Leibnitiana, Franz Steiner Verlag, 2009, 41 (1), pp.88-117. �hal-00984103�

La notion d’expression et ses origines mathématiques

Par

VALERIE DEBUICHE (AMIENS, FRANCE)

Summary

The notion of “expression”, which infuses the whole Leibnizian thought, originates, at least partially, from mathematics, for it appears explicitly in the corpus of the author, after his Parisian initiation to modern mathematics. The crucial point then consists in drawing the path that leads Leibniz from his first mathematical works about quadrature of the circle, differential calculus and series, and his discovery of perspective projection, to the notion of “expression”. Then, many mathematical elements seem to be inscribed in the very nature of “expression”: the idea of transformation and preservation, of relationship between finite and infinite, or still of envelopment and development. Now, it turns out that these elements, if they are considered merely in their mathematical dimension, are sometimes more problematic than enlightening when the question is grasping what “expression” means in its metaphysical instances, and consequently that “expression” cannot be reduced to a mere mathematical notion.

L’expression est une notion qui, chez Leibniz, est aussi souvent employée (dans presque tous les champs de sa pensée, mathématique, logique, gnoséologique, linguistique, physique, métaphysique) qu’elle est peu explicitée. La diversité et la quantité de ses occurrences est donc paradoxalement liée à une certaine imprécision conceptuelle, ou du moins à une trompeuse simplicité qui tend à la définir comme une analogie entre des rapports. Il semble cependant que, en dépit de cette applicabilité presque universelle, la notion d’expression entretienne un rapport privilégié avec les mathématiques D’une part, parce qu’elle n’apparaît pas nommément dans les textes avant 1673, année des premières et importantes découvertes mathématiques de Leibniz lors de son séjour parisien.1 D’autre part, parce que les emplois de la notion d’expression sont souvent accompagnés d’illustrations ou d’explicitations à teneur mathématique, telles la « loi » ou la « série » intra-monadique d’une substance qui préside aux changements qui font d’elle un miroir toujours « vivant » de l’univers, ou le « situs » monadique qui pose la substance dans un « point de vue » à partir duquel elle acquiert son unicité et pourtant participe à l’entr’expression. Enfin, parce que la fréquence de l’exemple de la projection perspective des sections coniques, dans les rares tentatives de Leibniz de définition de l’expression, laisse penser que la perspective conique recèle des éléments essentiels pour appréhender cette notion.

Deux articles de Mark A. Kulstad2 et Chris Swoyer3 vont dans ce dernier sens, puisqu’ils relèvent tous deux l’existence d’un paradigme perspectif. Ils éclaircissent la notion d’expression d’une façon précieuse parce qu’elle est rare, en cela qu’ils s’efforcent d’en proposer une conception à la fois synthétique et profondément ancrée dans l’analyse minutieuse des textes leibniziens. Aussi, ce sont ces articles et les éléments problématiques qu’ils font saillir au sujet de la nature mathématique de l’expression que nous présentons dans une première partie (I.) : en premier lieu, la question de l’isomorphisme de l’expression, en deuxième lieu, l’apparente identité de l’expression avec une certaine transformation et, en dernier lieu, la réduction de l’entr’expression à une sorte de transitivité de l’expression.

Ces différents problèmes nous conduisent à distinguer deux objets d’étude de nature mathématique mais dont les implications excèdent le champ mathématique. D’abord, en

1 _{Il s’agit comme nous le verrons de la méthode des métamorphoses, du triangle infinitésimal, de la quadrature}

du cercle, des séries et du calcul différentiel.

2 _{« Leibniz’s conception of expression », in : Studia Leibnitiana IX/1 (1977), pp. 55-76.} 3 _{« Leibnizian expression », in : Journal of the History of Philosophy 33/1 (1995), pp. 65-99.}

deuxième partie (II.), nous nous proposons d’analyser les méthodes mathématiques des transformations (la méthode des métamorphoses et la projection perspective), qui doivent permettre d’élucider le rapport entre expression et transformation, entre invariance et variation, entre unité et multiplicité, autant d’éléments qui jouent dans les usages non-mathématiques et plus métaphysiques de la notion. Ensuite, dans la partie suivante (III.), nous choisissons d’examiner les formes du rapport entre fini et infini qui intervient dans les séries et le calcul infinitésimal, car ces formes déterminent de façon importante les conditions de perfection de l’expression, perfection qui fonde à la fois la théorie leibnizienne de la connaissance et la variété infinie de substances singulières à l’œuvre dans la monadologie. Enfin, dans une dernière partie (IV.), nous concluons sur les apports des premiers modèles mathématiques pour penser l’expression, et sur notre idée selon laquelle la notion leibnizienne d’expression ne peut être considérée comme une notion toute mathématique.

I. Le paradigme perspectif en question

1. La projection perspective, un modèle pour l’expression : Lecture des articles de Mark A. Kulstad et Chris Swoyer

L’article de Mark A. Kulstad pose un certain ensemble d’éléments qui constituent le fond d’une analyse solide et renseignée de la façon dont Leibniz explicite et illustre ce qu’il entend par « expression d’une chose par un autre » ou par « une chose exprime une autre chose ». En plus d’une liste fournie de cas particuliers d’expression d’une chose par une autre, il propose trois citations qui font office de définitions de l’expression et dans lesquelles l’exemple perspectif apparaît, voire tient une place centrale.4 Chris Swoyer se fait le lecteur de Mark A. Kulstad et pose, comme lui, le caractère paradigmatique de la projection perspective pour déterminer la nature conceptuelle de l’expression leibnizienne. Cela les conduit cependant chacun à deux conclusions qui, sans être incompatibles, orientent la compréhension de la notion d’expression dans des voies distinctes.

4 _{Nous les reprenons ici de façon plus complète et pour deux d’entre elles dans leur traduction française.}

Définition 1. « Est dit exprimer une chose ce en quoi il y a des rapports qui répondent aux rapports de la chose à exprimer. Mais ces expressions sont variées ; par exemple le modèle exprime la machine, le dessin perspectif le volume sur un plan, le discours exprime les pensées et les vérités ; les caractères expriment les nombres, l’équation algébrique exprime le cercle ou toute autre figure : et ce qui est commun à ces expressions est qu’à partir du seul examen des rapports de l’exprimant nous pouvons parvenir à la connaissance des propriétés correspondantes de la chose à exprimer. On voit ainsi qu’il n’est pas nécessaire que ce qui exprime soit semblable à la chose exprimée, pourvu que soit préservée une certaine analogie de rapport. » (« Quid sit idea » ; GP VII, 263 ; traduit par J.-B. Rauzy : « Qu’est-ce qu’une idée ? », in : G. W. Leibniz : Recherches générales sur

l’analyse des notions et des vérités. 24 thèses métaphysiques et autres textes logiques et métaphysiques, Paris

2001, p. 445.)

Définition 2. « Une chose exprime une autre (dans mon langage) lorsqu’il existe un rapport constant et réglé entre ce qui se peut dire de l’une et de l’autre. C’est ainsi qu’une projection de perspective exprime son géométral. L’expression est commune à toutes les formes, et c’est un genre dont la perception naturelle, le sentiment animal et la connaissance intellectuelle sont les espèces. Dans la perception naturelle et dans le sentiment, il suffit que ce qui est divisible et matériel, et se trouve dispersé en plusieurs êtres, soit exprimé ou représenté dans un seul être indivisible, ou dans la substance qui est douée d’une véritable unité. » (GP II, 112) Définition 3. « Il suffit en effet pour l’expression d’une chose dans une autre qu’il existe une loi constante des relations par laquelle les éléments singuliers de la première pourraient être rapportés aux éléments singuliers qui leur correspondent dans la seconde, tout comme un cercle peut être représenté par une ellipse, c’est-à-dire par une courbe ovale dans une projection en perspective, et même par une hyperbole bien que cette courbe lui soit plus dissemblable et qu’elle ne revienne pas sur elle-même, car à tout point de l’hyperbole peut être assigné par la même loi constante un point correspondant du cercle dont elle est le projeté. » (C, 15 ; traduit par J.-B. Rauzy : « Sur le principe de raison », ibid., pp. 476-477.)

La conception de Mark A. Kulstad est de nature ensembliste qui, mettant l’accent sur la Définition 3., décrit l’expression comme une fonction qui envoie un ensemble d’éléments singuliers associé à la chose exprimant dans un ensemble d’éléments singuliers associé à la chose exprimée, c’est-à-dire comme une relation par laquelle chaque élément de la chose exprimant a un et un seul correspondant dans la chose exprimée. Ainsi, si l’on associe au cercle et à l’ellipse l’ensemble des points qui leur appartiennent, alors l’ellipse exprime le cercle parce qu’il existe une relation par laquelle on peut ramener chaque point de l’ellipse à un et un seul point du cercle. Or, dans la projection perspective, si une telle relation « point par point » existe bel et bien, elle n’est pas seulement une fonction, mais elle est une fonction bijective comme le note Chris Swoyer. À chaque point du cercle correspond un et un seul point de l’ellipse et réciproquement. Or, une telle spécificité n’est pas requise pour tous les cas particuliers de l’expression, ainsi que le prouve l’exemple de l’expression d’une aire géographique par un plan, dans lequel on ne retrouve pas chacun des détails du relief ou des éléments du paysage.

Aussi, pour Chris Swoyer, qui travaille surtout la Définition 1., ce qui est mis en relation dans l’expression n’est pas tant les singuliers qui composent les ensembles associés à des choses que des relations dans ces choses mêmes. Si une section conique est dite exprimer le cercle qui génère le cône, c’est en tant qu’il existe entre des propriétés du cercle et des propriétés des coniques une certaine relation par laquelle elles sont préservées en dépit de la transformation perspective. Ainsi l’est la propriété pour une droite d’être une tangente. Toutefois il note que, dans la plupart des cas d’expression, ces relations ne sont pas de même nature. Par exemple, la relation qui existe entre les points sur le plan n’est pas identique à celle qui existe entre les villes représentées par ces points, alors que le plan constitue une sorte d’expression de la ville. Aussi l’expression consiste-t-elle en une correspondance entre des relations éventuellement hétérogènes, en la préservation d’un ordre, d’une structure sous une certaine relation de corrélation.

Néanmoins, que l’exemple perspectif conduise à la conception ensembliste de Mark A. Kulstad ou à la conception structurelle de Chris Swoyer, que l’expression se comprenne comme une fonction « point par point » de l’exprimant dans l’exprimé ou comme la préservation de structures par la relation de projection centrale, apparaissent quelques éléments communs. D’une part, est en jeu la question fortement discutée par Chris Swoyer de la bijectivité de la fonction ou, encore, de l’isomorphisme des structures. Si Mark A. Kulstad n’évoque pas la nécessité que la fonction qui envoie un ensemble associé dans l’autre soit bijective, même si elle est « point par point », Chris Swoyer remarque à juste titre qu’elle l’est dans le cas de la projection perspective. Or l’expression d’une chose par une autre présente rarement une telle bijection. En revanche, la préservation des structures à l’œuvre dans la projection perspective ne présente pas la nécessité d’une telle complétude : de fait, les propriétés du cercle ne se retrouvent pas toutes dans l’ellipse qui l’exprime. Aussi n’est-elle pas un isomorphisme parfait et, pour cette raison, représente-t-elle pour Chris Swoyer un modèle plus adéquat de la notion d’expression, laquelle ne présente pas non plus un tel isomorphisme.

D’autre part, l’expression se joue apparemment dans une transformation, explicitée soit par le passage d’un ensemble à un autre comme chez Mark A. Kulstad, soit par la relation de corrélation entre des structures comme chez Chris Swoyer. Quoi qu’il en soit, elle est dans les deux cas à la fois existence d’une modification et préservation de quelque chose. L’exemple perspectif lui-même le dit cette fois mieux que l’idée de passage d’un ensemble à l’autre ou de morphisme des structures : l’ellipse exprime le cercle en tant qu’elle en est la figure projetée selon les lois de la perspective, c’est-à-dire la figure transformée sous une certaine relation. Mais il s’agit alors d’une transformation qui ne transforme pas tout, qui maintient une forme de communauté qui n’est cependant pas une ressemblance, mais sans laquelle

toutefois l’expression serait anéantie. Aussi l’expression se trouve-t-elle constituer le moyen de concilier altérité et identité, modification et invariance.

Enfin, les analyses de Mark A. Kulstad et Chris Swoyer tendent à délaisser la Définition 2. que pourtant ils retiennent et dans laquelle l’expression est cette fois-ci simplement illustrée par la projection perspective, mais explicitée plus longuement sur le mode la perception unifiée au sein d’une substance indivisible d’une multitude quant à elle dispersée. Dès lors, le modèle perspectif prend un nouveau tour, comme simple image, d’une activité expressive plus profonde : celle d’une perception qui, saisissant une multiplicité qui peut aller jusqu’à l’infinité, peut embrasser la totalité d’un univers. Alors, il s’inscrit davantage dans cette perspective visuelle qu’un observateur détermine quand il regarde une ville du haut d’une tour, exemple fréquent sous la plume de Leibniz et de façon très précoce, dans sa Dissertatio

de arte combinatoria de 1666.5 Dans cette infinité exprimée « immédiatement » apparaît alors

le ressort essentiel de l’entr’expression monadologique et la raison de son irréductibilité à la simple médiation transitive de l’expression qui œuvre entre les sections coniques.

Ce sont ces trois points que nous allons maintenant examiner : l’expression et son éventuelle isomorphie, le rapport problématique de l’expression et de la transformation, et la singularité de l’idée d’entr’expression.

2. L’isomorphisme de l’expression : Une question moins mathématique que philosophique L’exigence d’isomorphisme de l’expression qui apparaît lorsque l’on considère le modèle perspectif comme devant se retrouver tout entier dans l’expression elle-même n’est pas aussi générale qu’elle le semble. Elle se retrouve surtout dans la littérature consacrée aux usages logico-cognitifs de l’expression : l’expression symbolique bien constituée y doit en effet être celle qui correspond d’une façon parfaitement adéquate à ce qu’elle signifie. Les signes doivent être univoques, le passage des uns aux autres réglé de façon combinatoire, de sorte que, entre les signes et les idées, il n’existe qu’une manière d’aller des uns aux autres. La naissance du projet caractéristique dès 1666 dans le De arte combinatoria, ses nombreuses élaborations à partir de 1679 pour les travaux logiques et sa prégnance par la suite jamais démentie, comme projet d’une langue symbolique qui serait à la fois un instrument heuristique de découvertes de nouvelles vérités et l’organe de l’infaillibilité de la pensée et de sa communication, ont laissé à une tradition liée à Louis Couturat l’idée d’un transport du modèle isomorphe de la caractéristique universelle dans la notion de l’expression en général. Mais, si cette isomorphie de l’expression caractéristique constitue bel et bien un idéal du Leibniz-logicien, elle est aussi une qualité dont il reconnaît parfois qu’elle ne peut pas être atteinte par l’expression caractéristique.

Les raisons de l’imperfection de l’expression caractéristique sont multiples. D’abord, dans

ses Generales inquisitiones6 de 1686, Leibniz réduit explicitement ses recherches aux

propositions de forme prédicative, alors même que toutes les pensées ne se peuvent traduire de cette façon, même au prix de longues périphrases. Surtout, Leibniz choisit l’objet de son calcul rationnel de sorte qu’il s’accorde avec la nature combinatoire de ce calcul qu’il est en train d’élaborer dans l’esprit de ses premiers travaux de caractéristique numérique de 1677. En effet, les propositions prédicatives peuvent aisément s’exprimer par des relations méréologiques, d’inhérence des notions les unes dans les autres, et les raisonnements s’exprimer par des relations de substitution des notions les unes aux autres, qui permettent de passer d’une proposition à l’autre salva veritate. Ces deux types de relations se traduisent par

5 _{GM V, 9-79 ou GP IV, 27-104.}

6 _{« Generales inquisitiones de analysi notionum et veritatum » ; C, 356-399 ; traduit par J.-B. Rauzy, in : G. W.} Leibniz : Recherches générales sur l’analyse des notions et des vérités. 24 thèses métaphysiques et autres textes logiques et métaphysiques, op. cit., pp. 200-303.

suite avec facilité à l’aide des lois combinatoires d’un calcul grandement inspiré de l’arithmétique. Une caractéristique ainsi constituée ne saurait alors manquer de réussir là où elle garantit elle-même son application. Et Leibniz, en se restreignant aux propositions prédicatives et aux opérations de substitution, modélise la pensée, dans son objet comme dans sa forme, de manière à la rendre entièrement exprimable par la caractéristique combinatoire du calculus ratiocinator. Mais, ce faisant, si la caractéristique universelle peut prétendre être isomorphe à la pensée, ainsi que Leibniz l’affirme parfois, c’est alors à une pensée qu’il pré-modélise, et non à la pensée humaine en général.

De plus, selon une considération moins technique, la caractéristique est une création de l’homme, dont les expressions conventionnelles et imparfaites, sont la conséquence de son imperfection intrinsèque. En effet, comprise sur le modèle de la projection perspective, l’expression est quelque chose qui permet les transformations en même temps qu’elle veille au transport d’un invariant, certaines propriétés géométriques dans la projection perspective, une certaine forme de vérité (méréologique) dans la caractéristique universelle. Or, la fin que Leibniz assigne à la caractéristique universelle et à laquelle l’expression participe est le progrès des connaissances humaines. Et, dans cette perspective, l’expression a pour fonction heuristique essentielle de mettre à jour, par ce qu’elle transforme, un inaltéré, un inchangé, un invariant qu’elle permet alors de connaître. Aussi la nécessité de recourir à l’expression révèle-t-elle la confusion indépassable des connaissances humaines, en même temps que l’heureux enveloppement dans ce qui est connu de ce qui ne l’est pas. Par conséquent, l’isomorphie de l’expression caractéristique la rendrait vaine, parce qu’elle ne pourrait alors être que l’image d’une pensée déjà par elle-même entièrement distincte. En revanche, la possibilité même d’une entreprise caractéristique fondée dans l’expression laisse entrevoir une autre sorte d’expression : celle, au sein de la pensée humaine, de la réalité dans sa totalité, mais de façon partiellement confuse et pourtant entièrement enveloppée. Celle, donc, d’un homme qui, créature de Dieu, exprime l’univers d’une façon complète et imparfaite, alors que l’expression caractéristique, œuvre de cet homme, exprime la pensée de façon incomplète et (idéalement) parfaite.

Aussi nous semble-t-il que l’expression, dans sa dimension caractéristique, n’est pas une expression isomorphe à ce qu’elle exprime, ou alors, si elle l’est, c’est sur le mode d’un idéal régulateur et non d’une invention logique achevée. En revanche, au cœur de l’âme humaine se joue quelque chose d’une telle expression, à la fois pleine et imparfaite, qui appelle par conséquent les ressorts métaphysiques de la théorie leibnizienne de la connaissance, fondée à la fois dans l’idée d’une activité substantielle (toujours liée à une théodicée) et dans une théorie de l’idée fréquemment accompagnée de l’exemple perspectif. Mais ce sont là des considérations qui débordent le cadre de notre propos et que nous ne développerons pas plus avant.

3. Expression et transformation : Une origine mathématique problématique

Le modèle perspectif s’appuie sur une conception de la représentation inspirée du Quattrocento et des ses innovations picturales et architecturales. Le modèle du cône généré par un cercle à l’infini, tel celui à partir duquel les coniques sont engendrées par projection du cercle sur un plan à distance finie du sommet du cône, est l’analogue du cône visuel dont le tableau est le plan de projection sur lequel les éléments sont représentés selon le point de vue de l’artiste, c’est-à-dire selon son angle de vision. La circonférence d’une coupe, pourtant ronde, devient ovoïde lorsqu’elle est représentée sur le tableau, de même le cercle devient ellipse quand il est projeté sur un plan ayant une certaine inclinaison (il devient parabole, hyperbole, droite, voire point quand il est projeté sous d’autres angles ou à d’autres distances). Les sections coniques qui expriment le cercle générateur sont donc les figures transformées de

ce cercle suivant une certaine règle, ici suivant les lois de la projection perspective que les peintres et les sculpteurs ont maîtrisées avant les géomètres. Dès lors on pourrait admettre qu’une chose en exprime une autre lorsqu’elle en est la transformée, selon une certaine règle déterminée et constante, c’est-à-dire selon une règle unique et pourtant productrice d’une multiplicité.

Toutefois, considérer l’expression comme une transformation, c’est prendre le risque de voir la conception leibnizienne se confondre avec celle de Spinoza, dont pourtant il se distingue explicitement. En effet, les substances, qui expriment Dieu, pourraient dans ce cas être considérées comme des transformations de Dieu lui-même, des modifications de son être. Elles ne seraient plus alors à strictement parler des substances et la monadologie se dissoudrait dans un monisme que Leibniz rejette. Par ailleurs, le modèle perspectif pourrait également fonder une sorte de solipsisme substantiel, la monade seule avec Dieu. Une telle conception est rendue possible par la métaphore de Leibniz lui-même quand il présente la monade comme un point de vue sur l’univers, point de vue nécessairement d’origine divine, point de vue d’un œil divin qui se porte de l’infini sur l’univers et en tire une infinité de représentations qui, chacune, font une monade, mais nécessairement indépendante des autres. Ce serait alors la pluralité des monades qui risquerait d’être perdue.

Enfin, au-delà du risque du « spinozisme », confondre expression et transformation ne permet pas de répondre à la question, importante pour saisir ce qu’est l’expression leibnizienne, de la condition nécessaire et suffisante de l’expression d’une chose par une autre. Si l’expression est une transformation, elle est une transformation qui doit révéler quelque chose ou, du moins, qui transporte un élément commun de l’exprimé à l’exprimant. Est-ce alors parce que des choses portent en elles quelque chose de commun qu’il existe un invariant qui fonde la transformation de l’une en l’autre ? Ou bien est-ce parce que la transformation est toujours à la fois déformation et préservation que quelque chose passe de l’exprimé à son exprimant qui leur devient alors commun ? La question fait sens car l’expression est liée très étroitement à l’existence d’une correspondance, mais elle est en même temps ce qui distingue ce qu’elle relie : variation d’une identité, transformation d’un original, multiplication d’une unité.

Par conséquent, s’il est remarquable que cette question n’a pas de réelle importance en mathématiques, la communauté d’un ordre et l’existence d’une transformation déterminée étant deux propriétés réciproques, il n’en demeure pas moins que l’analyse des méthodes de transformation que Leibniz découvre ou emploie doit nous permettre de saisir quelque chose de la nature de l’expression. Elle donne notamment à voir la portée du modèle perspectif quand il est transposé à la sphère métaphysique du point de vue monadique. Car il faut alors saisir de quelle manière Leibniz parvient à appréhender la création divine sur le modèle de la transformation projective (incarnée par la monade considérée comme point de vue) sans toutefois réduire son système à celui de Spinoza. Elle permet aussi de mettre à jour comment la transformation offre sous certaines conditions une expression, conditions à la fois heuristiques et méthodologiques qui révèlent un élément essentiel de l’expression leibnizienne : un certain rapport entre le connaissable et l’inconnu, entre le déterminé et l’indéterminé, entre le fini et l’infini.

4. L’entr’expression : Au-delà de la transitivité mathématique de l’expression

Le terme d’entr’expression n’est pas aussi fréquent que certains autres termes, avec lesquels Leibniz le confond volontiers, tels que celui de « correspondance » ou celui d’« accord ». Les choses « s’entre-répondent » ou « s’accordent » plus souvent qu’elles ne « s’entr’expriment », encore que ces variations lexicologiques ne soient pas en elles-même problématiques. Elles marquent seulement le rapport étroit que la notion d’entr’expression

entretient avec celle d’harmonie ou d’accord, évidence des textes métaphysiques qui ne saillit pas vraiment dans les textes mathématiques. À cet égard, le modèle perspectif à la fois égare et oriente celui qui, par lui, s’efforce d’appréhender la notion d’expression dans sa totalité. Car il apparaît en premier lieu que les choses qui s’entr’expriment le font sur le mode d’une expression mutuelle et, qu’en ce sens, elles semblent réaliser en particulier ce que l’expression, qui n’est pas toujours réciproque, est de façon plus générale. Or, cette expression mutuelle se résout comme l’expression d’un troisième terme commun, qui fonde cette réciprocité de l’expression mutuelle et semble donc la précéder.

Ainsi, les sections coniques peuvent être considérées comme s’exprimant mutuellement, car elles expriment toutes une même chose : le cercle générateur du cône, cercle à l’infini, que toutes représentent sous un certain angle de projection et à une distance finie du sommet du cône. Une première difficulté se pose : si ce sont bien des choses différentes entre elles, un cercle, une ellipse, une parabole, etc., qui expriment une autre chose, qui leur est commune, le cercle à l’infini, comment saisir ce qui fait qu’elles représentent une telle chose commune ? Affirmées dans une variété première, quel est alors le fondement de leur identité ? Mais si l’on admet, à l’inverse, que les choses s’entr’expriment parce qu’elles en expriment une même autre, si l’expression précède l’entr’expression, pour quelle raison affirmer la multiplicité de ces expressions ? L’expression seule ne permet pas alors de rendre compte de l’entr’expression qui suppose une identité au cœur de la pluralité des choses exprimant, pluralité non requise par l’expression individuelle elle-même.

Il semble donc qu’il faille poser comme première l’entr’expression, à la fois comme existence préalable d’un ordre commun et comme multiplicité des expressions qui, dans le modèle perspectif comme dans la métaphysique de la monadologie, est toujours aussi une infinité. En effet, de même que les sections coniques sont en nombre infini, en raison de la continuité de la variation des angles de projection qui déterminent la représentation perspective, les substances qui s’entr’expriment constituent une multiplicité infinie. Surgit alors une autre difficulté. Si quelque chose comme un ordre commun détermine préalablement ce que sont les coniques, si on admet qu’une forme d’identité préexiste entre les substances, alors comment rendre compte de la variété de ces choses pensées d’abord comme identiques ? Comment, en effet, concevoir la variété infinie des monades expressives si la condition nécessaire de la création divine est l’entr’expression, ordre commun et universel, identité primordiale ? Faut-il alors la penser sur le mode de la transformation projective, productrice d’une infinité par la variation continue de l’angle de vision et l’uniformité de la loi de transformation ? Mais cela renverrait aux difficultés métaphysiques évoquées ci-dessus de la conception de l’expression comme transformation. C’est à ces questions que l’examen de la relation mathématique entre l’expression et la transformation doit pouvoir nous permettre de répondre, au moins en partie.

II. Les méthodes mathématiques de transformation

Son parisien, entre 1672 et 1676, est l’occasion pour Leibniz, non de se perfectionner, mais de se former aux mathématiques, et il appréhende avec une facilité étonnante les travaux de ses contemporains les plus brillants, Descartes évidemment, Pascal, Grégoire de Saint Vincent, Gregory, Fabri, Wallis, Mercator, etc. En 1675, il invente le calcul différentiel à partir de ses propres travaux combinatoires de jeunesse, des travaux sur les séries et de la découverte en 1673 du triangle caractéristique (né d’une lecture du Traité des sinus du quart

de cercle de Pascal) qui fonde la méthode des métamorphoses et la quadrature leibnizienne du

des travaux de Pascal sur les coniques7 et saisit avec acuité et rapidité la puissance de cette nouvelle géométrie projective dont il trouve les prémices chez Philippe de La Hire et Girard Desargues également. Ces méthodes nouvelles de métamorphose et de projection perspective font apparaître une relation étroite entre l’expression et la transformation : que ce soit l’expression d’une conique par une autre dans la méthode projective, d’une courbe par une autre dans la méthode des métamorphoses ou d’une grandeur finie par une grandeur infinie dans la quadrature du cercle, cela pose entre l’expression et ce qu’elle exprime une relation de transformation qui modifie autant qu’elle préserve, rendant alors possible la connaissance simplifiée et unifiée de ce qui jusqu’à présent était inconnaissable ou, du moins, peu aisément connaissable.

1. La méthode des métamorphoses et la quadrature du cercle

En 1673, Leibniz établit une première version de sa méthode des métamorphoses et rédige sa découverte en 1676 dans sa Quadratura arithmetica circuli ellipseos et hyperbolae cujus

corollarium est trigonometria sine tabulis.8 La quadrature du cercle est surtout pour le jeune

mathématicien l’occasion d’illustrer la puissance et l’originalité de la méthode qu’il a inventée, bien plus que de proposer une quadrature du cercle qui, d’une part, est déjà connue et, d’autre part, exprimée sous des formes bien plus satisfaisantes du point de vue mathématique (c’est-à-dire par des séries qui convergent plus vite que la sienne). Comme il l’avoue lui-même dans son Historia et origo calculi differentialis, la lecture de Pascal suscite en lui l’idée d’une transformation des courbes afin de mieux les pouvoir quarrer, notamment de la transformation qui consiste à calculer la superficie d’un solide de révolution à partir de « celle de la figure plane qui lui est proportionnelle ». Il s’agit alors d’une simplification du calcul en ce que la transformation permet de passer du calcul d’une intégrale double à celui d’une intégrale simple. Fort de cette découverte, nouvelle à ses yeux, il envisage avec confiance la possibilité de l’établissement d’une méthode générale par laquelle il serait possible de quarrer toutes sortes de courbes, y compris les courbes transcendantes, telles la courbe circulaire.

La première étape de la constitution de cette méthode de transformation des courbes consiste en la conception du « triangle caractéristique », triangle non nécessairement assignable et néanmoins semblable à des triangles quant à eux commensurables. À l’aide des rapports de proportionnalité entre ce triangle et d’autres triangles formés à partir des tangentes et des normales à la courbe, il devient possible de transformer la courbe à quarrer de sorte que le calcul soit grandement simplifié. Ainsi, dans la figure ci-dessous, le triangle caractéristique est Y1DY2 :

7 _{Ces éléments se trouvent dans le texte rétrospectif que Leibniz rédige en 1714 en réponse à ceux qui l’accusent}

de ne pas avoir inventé le calcul différentiel, mais de l’avoir repris à Newton : « Historia et origo calculi differentialis », GM V, 392-410 ; traduit Régine Szeftel-Zylberbaum, in : Les cahiers de Fontenay 1 (1975), pp. 58-98.

T X1 A X2 Z1 Z2 P H Y1 Y2 D Ω П θ N L

TΩ est la tangente à la courbe en Y, ΠP sa normale. (AX) et (AZ) sont les axes des ordonnées et des abscisses AX et AZ.

H est déterminé par la projection de Ω sur (AX). θ est l’intersection de la tangente avec (AZ). AN est la perpendiculaire à la tangente TΩ. XP est la sous-normale à la courbe en Y. Posons : x=AX, z=AZ=g(x), f(x)=XP, dz=Z1Z2,

dx=X1X2.

Par similitude entre le triangle caractéristique et le triangle Y2X2P, on a :Y_XX_{P Y}YD_D 2 1 2

2

2 _{= ,}

c’est-à-dire PX2·X1X2=AZ2·Z1Z2 ou encore f(x)dx=g(x)dg(x)=zdz, où f(x) désigne la

sous-normale à la courbe au point d’abscisse x. Or, si l’on considère que les z croissent et prennent pour valeur maximale g(a) (pour x égal à a), alors la somme des z·dz forme un triangle rectangle duquel il est aisé de voir que l’aire est égale à la moitié du carré de côté l’ordonnée maximale g(a). En symbolisme intégral, cela donne alors pour x allant de 0 à a, donc pour g(x) allant de 0 à g(a) : ∫f(x)dx=∫g(x)dg(x)=½g(a)². Leibniz peut alors conclure sur une méthode générale de quadrature d’une courbe : si l’on veut quarrer une courbe Cf, c’est-à-dire

si l’on veut calculer ∫f(x)dx pour x allant de 0 à a, alors il suffit de chercher une nouvelle courbe Cg telle que f(x) soit la sous-normale d’un point M de Cg à l’abscisse x, car dans ces

conditions l’aire sous la courbe Cf est égale à la moitié du carré de côté g(a). Le problème du

calcul de l’aire sous une courbe est par conséquent ramené à celui de la recherche d’une nouvelle courbe, inverse de la courbe déterminée par la sous-normale de la courbe à quarrer, c’est-à-dire inverse de la courbe déterminée par la tangente. Alors, avec une telle méthode générale de calcul des aires, Leibniz peut affirmer avec raison qu’il est possible, pour toutes sortes de courbes de réduire le problème des quadratures à un problème inverse de celui des tangentes.

Leibniz s’attache alors à appliquer cette nouvelle façon de faire à la quadrature du cercle, problème exemplaire en cela que cette quadrature ne se donne pas par les méthodes algébriques habituelles en raison de l’irrationalité de l’expression de ses ordonnées sous la forme y=f(x)= a²−x² . Réussir à quarrer cette courbe à l’aide de sa nouvelle méthode, c’est donc conférer à celle-ci, ad hoc, une valeur heuristique indéniable et en faire la méthode générale des quadratures. En plus de sa nouveauté, la spécificité de cette méthode réside dans son découpage de la superficie à quarrer, non selon les rectangles infinitésimaux des ordonnées comme cela est habituel, mais selon les triangles infinitésimaux pris tous à partir d’un des points de la circonférence du cercle. Ce triangle AYiYi+1 infinitésimal est néanmoins

semblable à d’autres triangles assignables et connus. L’emploi de ce premier triangle infinitésimal permet l’emploi d’un second triangle caractéristique DYiYi+1, tel que l’aire des

triangles infiniment petits AYiYi+1 peut être ramenée à l’aire des rectangles infinitésimaux

XiXi+1Zi : 2·Aire du triangle AY1Y2=X1Z1·X1X2, c’est-à-dire 2·Aire du triangle AYiYi+1=Aire

du rectangle XiXi+1Zi. 9

9 _{Ceci se montre aisément. AN étant la hauteur en A du triangle AY}

1Y2, on a :

Aire du triangleAY1Y2

2AN Y Y1 2⋅

N X1 X2 X3 O Xi B Z1 Z2 θ 2 θ 1 Z θ i Y1 Y3 You Q P θ Yi Y2 D A Zi θi est l’intersection de la

tangente à la courbe en Yi avec

l’axe passant par A et Z.

AN est la perpendiculaire à cette tangente menée à partir de A. Xi est la projection sur l’axe

(AB) de Yi., c’est-à-dire son

abscisse.

Zi est la projection de θi sur la

droite (XiYi).

Posons : x=AX, y l’ordonnée de Y sur l’axe (Aθ), z=XZ=Aθ,

Ainsi, du triangle infinitésimal on passe à un rectangle infinitésimal d’aire double, de sorte que les points Zi ainsi construits forment une nouvelle courbe. C’est cette transformation qui

rend possible une quadrature rationnelle du cercle selon la nouvelle courbe Cg décrite

ci-dessous : b _y A B g(b) g(z) 2 1 O X Z Q P Cg

Il s’agit alors d’une courbe rationnelle qui tend asymptotiquement vers l’axe des ordonnées et qui possède une aire de grandeur finie, bien qu’elle soit une figure non finie, préfigurant par ce biais le rapport qui existera à la fin de son raisonnement entre une grandeur finie (l’aire du quart de cercle) et une série infinie.

À ce stade de la quadrature, il s’agit alors de déterminer l’aire du quart de cercle de rayon pris comme l’unité, c’est-à-dire

_∫

₀1ydx=

_∫

₀1 1−x²dx. La somme des triangles infinitésimaux AYiYi+1 décrivant l’aire de la figure mixtiligne AYA, l’aire du quart de cercle est la somme

de l’aire du triangle AOQ rectangle en O et de la moitié de l’aire de la figure mixtiligne AQA (constituée par les rectangles infinitésimaux dont on sait que l’aire est double de celle des triangles infinitésimaux). L’aire du triangle rectangle AOQ est égale à ½ et, d’après nos conventions d’écriture z=XiZi et dx=XiXi+1, l’aire formée par les rectangles infinitésimaux

Comme les triangles Y1DY2 et ANθ1 sont semblables, on a : ANθ A D YY Y 1 1 2 1 _{= , d’où AN·Y}

s’écrit . On peut donc réécrire l’intégrale recherchée de la façon suivante :

∫

01zdx

∫

∫

₀1 = + ₀1zdx 2 1 2 1 ydx .

Par ailleurs, par les triangles rectangles semblables OAθ et YBA, puis XAY et OAθ, on a les relations suivantes :

ACOθ

AYAB= etAXAY=ACOθ , c’est-à-direAXAB=OAA²+θA² θ². Comme AX=x,

Aθ=z, et comme OA et AB sont respectivement les rayon et diamètre du cercle, on obtient :_x2=1+_z²z², c’est-à-dire x=₁2₊z_z²_²=g(z). Une nouvelle courbe est ainsi obtenue, dont l’ordonnée g(z), égale à x, est exprimée rationnellement en fonction de z.

Or, ∫zdx correspond à l’aire mixtiligne AXZA de la nouvelle courbe (Aire 2) qui a pour aire complémentaire dans le rectangle AθZX l’aire mixtiligne AθZA (Aire 1), dont l’intégrale est ∫xdz, c’est-à-dire que ∫zdx=XZ·AX-∫xdz. Pour le quart de cercle, on a ∫zdx=OQ.AO-∫xdz=1-∫xdz10 où AO et OQ sont les rayons du cercle, c’est-à-dire sont égaux à 1. L’intégrale devient donc :

_∫

₀1 = +

(

−

_∫

₀1

)

=− ₀1xdz 2 1 1 xdz 1 2 1 2 1

ydx

_∫

, puisque dans le quart de cercle lorsque x varie

de 0 à 1, z varie également de 0 à 1. Reste alors à faire le calcul suivant :

(

)

∫

₀1 = −

∫

₀1 ₊ =−

∫

₀1 ₊ = −

∫

₀1 − ₊ dz ² z 11 1 1 dz ² z 1z² 1 dz ² z 12z² 2 1 1

ydx . Leibniz s’inspire de la méthode de Mercator

qui se sert de la série infinie obtenue par division euclidienne de 1 par 1+z², et il trouve que

∑

∞ = + =− + − + − = 0 k k ... 7 1 5 1 3 1 1 1 k 2 ) 1 ( 4 π _.

Enfin, ce résultat est généralisé par Leibniz, selon une formulation qui comprend le cas du quart de cercle, dans lequel le « demi-axe » correspond au rayon (de longueur 1) et « la portion de tangente au sommet » (t) est égale à 1, puisque la tangente en Q est égale à AZ, c’est-à-dire est égale au rayon.

A θ Y t Z O B X

Analogiquement à la formule du quart de cercle de rayon 1, et si l’on prend comme unité le rectangle ayant pour côtés les deux demi-axes, on a :

∑∞ = + + − = 0 k 1 k 2 k 1 k 2 t ) 1 (

Aire , ce qui revient à calculer

“Arctan t”.

La méthode des métamorphoses offre donc une méthode générale pour trouver l’aire d’une portion de conique par le biais de la valeur « t », où « t » représente une certaine portion de la tangente au sommet de la conique, déterminée par l’arc dont on cherche à calculer l’aire. Ceci montre derechef que le problème de la quadrature est lié à celui des tangentes : la nouvelle courbe Cg a pour ordonnée en une certaine abscisse la grandeur de la tangente de l’ancienne

courbe en cette même abscisse. Trouver la quadrature d’une courbe revient à sommer les diverses valeurs prises par cette tangente ; pour les coniques à centre, ceci revient à déterminer l’arc dont la tangente est égale à t.

L’intérêt premier et immédiat, dans la compréhension du rapport entre l’expression et les travaux mathématiques de Leibniz et plus précisément de la relation étroite que la notion entretient avec l’idée de transformation, réside dans ce tour de force qui permet de passer

d’une intégrale incalculable, ydx=f(x)dx, à l’intégrale plus simple, xdz=g(z)dz, dans laquelle les ordonnées sont commensurables aux abscisses et, de ce fait, peuvent s’exprimer rationnellement en fonction de ces dernières. Une telle transformation est utile parce qu’elle change l’inconnaissable en connaissable. Mais elle est surtout intéressante pour les conditions sous lesquelles un tel changement peut s’effectuer. En effet, l’originalité de la méthode leibnizienne se trouve tout entière dans l’emploi de ce triangle caractéristique qui porte en lui, au cœur de son inassignabilité, des rapports invariants qui se trouvent à la fois dans la nouvelle et dans l’ancienne courbe. Telles sont les deux fonctions de ce triangle : déterminer une transformation et préserver quelque chose de ce qui doit être connu (sans quoi il ne le pourrait jamais être). C’est de la même façon l’invariance de certains rapports sous une transformation qui définit ce que peut être une projection perspective et produit en Leibniz une raison, mais certes pas la seule, de s’enthousiasmer pour cette nouvelle méthode géométrique.

2. La méthode projective

Leibniz découvre la perspective géométrique entre autres par le biais de l’abscons

Brouillon Project11 de Desargues daté de 1639, texte aussi ingénieux et novateur qu’éloigné

de tout formalisme mathématique, empreint de métaphores botaniques qui le rendent peu aisé d’accès. Desargues y déploie deux innovations centrales au sujet des sections coniques dont il traite essentiellement. D’abord, il identifie, avec une certaine audace pour une époque mal à l’aise avec l’infini mathématique, les droites parallèles et les droites concourantes, les premières étant conçues comme des droites d’une même ordonnance, mais en un point à l’infini. Le point à l’infini est alors en retour défini comme le point de concours de droites parallèles entre elles, à l’instar des points ordinaires qui sont les points de rencontre des droites concourantes. Dès lors, il devient possible de considérer les sections coniques, non à partir du cône, mais à partir du rouleau dont les génératrices sont toutes parallèles entre elles, et de confondre sections coniques et sections cylindriques, le cône devenant le cas particulier du cylindre. L’identification des points à l’infini et des points à distance finie permet également de considérer toutes les sections coniques comme des courbes unicursales se refermant sur elles-mêmes, à distance finie ou à distance infinie, en un point à l’infini ou en deux. Tout cela engage Desargues sur la voie de la possibilité d’une méthode une et simplifiée de l’étude des coniques, qu’il trouve, et telle est sa seconde innovation, dans la perspective elle-même. Cette méthode consiste à affirmer, au regard de l’invariance (grâce aux points à l’infini) de la relation d’incidence droite-point dans la projection centrale de la perspective et ainsi à poser l’invariance de la relation d’involution. Avec elle, ce sont toutes les propriétés qui en découlent, et notamment celles concernant les pôles et les polaires, c’est-à-dire en une certaine manière les tangentes, qui deviennent invariantes par projection perspective. Il est alors possible de démontrer les théorèmes concernant ces propriétés pour le cercle, figure plus simple, et d’en déduire leur validité pour les coniques en général.

Pascal se situe de lui-même dans la lignée des travaux de Desargues auquel il rend

hommage dans son Essai pour les coniques de 1640.12 Il emprunte à son prédécesseur

l’analogie des droites parallèles et des droites concourantes comme droites de même ordonnance, la caractérisation des sections coniques comme point, angle rectiligne, droite, cercle, ellipse, parabole et hyperbole, et son théorème d’involution. Il pressent l’élaboration d’une méthode nouvelle qui le pousse à produire en 1654 un traité sur les coniques dont seule la première partie, la Generatio conisectionum, nous est parvenue, grâce à Leibniz qui en a

11 _{Brouillon project d’une atteinte aux événements des rencontres du cône avec un plan, Paris 1639.} 12 _{In : L. Lafuma (éd.), B. Pascal : Œuvres complètes, Paris 1963, pp. 35-37.}

fait copie.13 La différence entre Pascal et Desargues se joue à deux niveaux. D’un point de vue formel, d’abord, le texte de Pascal est plus explicite et ordonné suivant une tradition tout euclidienne, en définitions, corollaires, scholies. À ce titre, il présente une plus grande modernité que celui de Desargues. Mais, à un second niveau, il délaisse la notion d’invariance des propriétés. Pascal insiste en effet sur la construction perspective des coniques, celles-ci étant alors considérées comme les projections point par point du cercle générateur du cône, chaque point projeté de ce cercle étant déterminé par la rencontre de la génératrice du cône passant par ce point avec le plan de projection.

Fig. 1 : Ellipse Fig. 2 : Parabole

Point sans image Fig. 3 : Hyperbole Point sans image Représentation d’une seule partie de l’hyperbole.

Si ce plan est parallèle à la génératrice, alors le point projeté est à l’infini (cas de la parabole), s’il est parallèle à deux génératrices, alors ce sont deux points qui se trouvent projetés en des points à l’infini (cas de l’hyperbole). Ce faisant toutefois, il postule plus qu’il n’établit la nature de la projection d’une droite, le passage des propriétés sur les droites sécantes aux propriétés sur les droites tangentes et, surtout, la préservation de certaines propriétés géométriques, comme la propriété pour une tangente projetée de demeurer tangente. Pour cette raison, le lecteur de Pascal, dont Leibniz lui-même, oscille entre la considération de la méthode projective comme une mise en rapports, selon une loi déterminée, des points entre eux, et sa considération comme une méthode fondée dans la règle de l’invariance de certaines structures. Néanmoins, la Generatio conisectionum de Pascal offre le moyen de penser une véritable continuité des coniques les unes par rapport aux autres, par l’analogie qu’il pose entre toutes les figures grâce à l’emploi des points et droites à l’infini. C’est à cette identité de genre, fondement d’une unification de la méthode, que Leibniz s’attache tout particulièrement.

Leibniz n’a pas en effet lui-même produit de travaux sur la géométrie perspective. Aussi est-ce dans sa réception des travaux arguésien et pascalien qu’on peut lire les idées nouvelles qu’il ne manque pas d’en faire surgir. L’importance de l’exemple perspectif dans l’illustration du concept d’expression prouve que les analyses que Leibniz tire de ces travaux ne sont pas seulement accidentelles, mais suscitent en son jeune esprit des conceptions aussi vivaces qu’elles seront pérennes. À cet égard, les notes qu’il rédige en juillet 1676 au sujet du Traité

sur les coniques de Pascal14 sont révélatrices. D’une part, elles montrent qu’il saisit avec un

intérêt tout particulier ce qui, dans la génération des coniques, les unit et les fait naître d’une seule et même transformation. La projection perspective se réalise de façon continue, selon le mouvement du plan de projection qui passe progressivement de l’angle droit avec l’axe du cône à l’angle nul. Ce faisant, les projetés du cercle peuvent être considérés comme les limites les uns des autres, sur l’exemple de la parabole qui peut être conçue comme un cas-limite de l’hyperbole quand le plan de projection est parallèle à deux génératrices qui sont

13 _{Ibid., pp. 38-42.}

14 _{LH, XXXV, 15, Bl. 11 ; traduit par P. Costabel : « Traduction française des notes de Leibniz sur les}

infiniment proches (ce qui équivaut à être parallèle à une seule génératrice). Cette possibilité d’un passage à la limite témoigne à la fois de la diversité et de l’identité des coniques : toutes les sections coniques ne sont que les espèces différentes d’un seul et même genre, celui de la projection perspective du cercle, en même temps que chacune des coniques est distinguée des autres par une loi de projection déterminée, en l’occurrence par l’angle de projection, encore appelé « angle de vue ». C’est, d’autre part, cette prégnance du modèle optique qui ressort des

notes de Leibniz, comme un modèle riche en lui-même de vertus heuristiques.15 On y voit

apparaître les termes de « point de vue » et de « plan de vision » et l’idée d’une méthode meilleure que les autres dans le traitement des coniques, en raison surtout de la fixité du centre de projection. Car, alors, le cône est fixe, déterminé par le centre de projection et le cercle générateur, de sorte qu’il est possible d’unifier l’étude des coniques parce qu’elles sont déterminées par des éléments communs et, de ce fait, sont comparables les unes aux autres, dans le sens d’une congruence qui fonde chez Leibniz la possibilité même d’une connaissance générale. La nature optique de la loi de projection porte donc, aux yeux de Leibniz, le ferment d’une théorie générale des coniques, c’est-à-dire d’une connaissance unifiée qui doit permettre de connaître le compliqué par le simple.

Mais Leibniz n’est pas sans être également fortement marqué par les travaux de Desargues, avec lequel on peut parfois lui trouver plus d’affinités qu’avec Pascal. En effet, ce dernier insiste sur la nature ponctuelle de la transformation perspective. Desargues, au contraire, propose une conception davantage ancrée dans la préservation de certaines propriétés. Il s’agit donc moins d’un rapport perspectif « point par point » que « propriété par propriété ». Or, le

Quid sit idea présente comme centrale cette idée d’une préservation, au sein de l’expression,

entre les propriétés du connu et de l’inconnu.16 Aussi, si la conception ponctuelle donne un moyen de construire la projection perspective, elle n’en présente pas toute la spécificité, du moins telle que Leibniz semble la concevoir. Car si le modèle perspectif est un modèle expressif, il semble que ce soit sur le mode d’une préservation des structures qui ne soit pas la simple conséquence d’un certain procès de construction, mais qui constitue l’élément essentiel de l’expression elle-même. Et alors que les textes de Pascal n’offre pas d’occurrence des termes de « réponse » ou de « correspondance » entre les propriétés, ces termes abondent au contraire dans le Brouillon project de Desargues comme dans de nombreux textes de Leibniz relatifs à la perspective comme à l’expression. Ce qui confère à l’héritage arguésien de Leibniz une force particulière.

3. Expression et transformation

Si Leibniz invente la méthode des métamorphoses et non la méthode projective, il n’en demeure pas moins qu’entre 1673 et 1676, son intérêt mathématique est tout porté sur ces méthodes qui sont essentiellement des méthodes de transformation. La méthode des métamorphoses permet de plus d’appréhender la méthode projective, qui œuvre dans le modèle perspectif de l’expression, sous un jour éclairant pour la notion d’expression elle-même. Elle consiste en effet en la transformation d’une courbe géométrique transcendante en une courbe algébrique, tandis que la méthode projective est une transformation optique, mais toutes deux transforment leur objet de sorte que la connaissance de l’une par l’autre soit possible. Il n’est toutefois pas possible d’attribuer un sens à cette transformation, au moins à l’égard de la connaissance. Car, dans la méthode projective, l’ellipse exprime le cercle parce qu’elle en est la transformée, mais c’est le cercle en tant que figure plus simple qui permet de

15 _{« Par cette manière optique de traiter, si l’on découvre un théorème particulier du cercle ou dans le cercle, on a}

aussitôt un répondant donc dans les autres sections coniques, grâce à cette considération, et on résout aussi des problèmes tels que mener des tangentes, etc. » (Ibid., p. 97.)

connaître l’ellipse, tandis que dans la quadrature du cercle, l’équation algébrique est une expression du cercle qu’elle permet toutefois de connaître. Et si, en mathématiques, il semble qu’il y ait un sens de l’expression du transformé qui est l’exprimant à la chose transformée qui est l’exprimé, ceci ne semble pas pouvoir être tenu pour une caractéristique de l’expression, puisque Leibniz la caractérise, non par la transformation, mais bien par la possibilité de la connaissance.

Se pose alors la question de ce qui est réellement transformé puisque quelque chose subsiste qui est assez fondamental pour que la connaissance reste possible. Ce qui revient à affirmer que la transformation porte moins sur les choses mêmes que sur la façon de les appréhender. Et, en effet, la méthode des métamorphoses consiste en un changement de variable, c’est-à-dire en un changement de repère par rapport auquel la courbe à quarrer est exprimée algébriquement ; la méthode projective consiste quant à elle en une variation de l’angle de projection, c’est-à-dire en une modification de l’angle sous lequel la figure est représentée. Là se trouve la raison de l’étroite relation qui existe entre l’expression et la transformation : dans l’une comme dans l’autre, quelque chose se trouve préservé de la nature profonde de ce dont l’apparence est affectée. Ceci implique donc l’existence d’un invariant qui ne se trouve pas modifié par la transformation elle-même et qui constitue le fondement de l’expression. Est-ce alors la nature même de la transformation qui produit une telle invariance, de sorte que l’expression serait la conséquence la transformation ? Ou bien est-ce l’existence d’un invariant préalable qui rend possible l’élaboration d’une loi de transformation qui modifie sans altérer ?

Si celui qui connaît l’expression leibnizienne ne peut croire que la transformation soit la cause de l’expression, alors même que l’idée d’une loi de transformation semble absente de la plupart des cas non-mathématiques de l’expression, tels l’expression des pensées par les mots ou de Dieu par les substances, le lecteur de ses textes mathématiques de la période parisienne peut légitimement se demander si la notion d’expression n’est pas originairement fondée dans l’idée de loi de transformation. (Ce qui impliquerait de comprendre comment Leibniz peut légitimement par suite l’abandonner afin d’éviter de tomber dans les écueils qu’il trouve au spinozisme.) Mais il s’agirait là d’une erreur méthodologique double. D’abord, ce serait transposer comme tout-puissant le modèle mathématique de l’expression, alors même que Leibniz affirme que sa métaphysique n’est pas toute mathématique. Ensuite, ce serait le transposer sans questionner quelles conclusions proprement mathématiques il porte avec lui, dans une spécificité qui ne peut alors être dite, en droit et sans prudence, généralité. En effet, dans les mathématiques, l’expression joue entre des choses analogues, semblables, simplement proportionnées : entre les sections des coniques, entre les coordonnées des points du cercle et le cercle lui-même, ou entre une courbe et sa métamorphosée par changement de repère. Et il est dit qu’il y a une loi de transformation parce que celle-ci est connaissable. Mais elle ne l’est que parce que les choses sont peu différentes les unes des autres, et si la loi de transformation se donne avec une facilité et une évidence qui semblent permettre de poser la transformation comme réelle et primordiale, c’est seulement parce qu’elle est ténue, légère, presque inefficace, si ce n’est à des fins heuristiques.

C’est donc parce qu’elle joue entre les objets mathématiques, abstraits, généraux, essentiellement semblables, au cœur d’une analogie qui fonde les mathématiques elles-mêmes, qu’elle apparaît comme première. Et il semble alors au contraire que l’expression comme forme préexistante d’une invariance, d’un ordre commun, est plus générale que la transformation qui requiert de connaître un moyen de passer d’une expression à l’autre. Ou, pour le dire en des termes moins radicaux, qu’une chose en exprime une autre parce qu’elle en est la transformation ne suffit pas pour affirmer que l’expression est nécessairement précédée d’une transformation, mais seulement que l’existence d’une transformation d’une chose en une autre est un critère suffisant pour dire d’une chose qu’elle en exprime une autre. Cela

suffit pour dire qu’elle exprime hic et nunc d’une certaine façon une certaine chose, mais non que ces choses ne possédaient pas préalablement quelques rapports communs. Et si la transformation, par exemple du cercle en ellipse, construit bel et bien un type d’expression, c’est-à-dire un rapport entre des propriétés du cercle et de l’ellipse, cela ne permet pas de dire que le cercle et l’ellipse ne possédaient pas ces rapports préalablement. Condition d’une expression donnée, la transformation, qui modifie et préserve, peut également sembler possible précisément en raison de la préexistence d’un ordre commun. Aussi est-ce plutôt l’expression, comme existence d’un ordre invariant, qui apparaît comme la condition de la transformation, même si toute transformation offre le cas d’une expression réalisée.

Un dernier élément fondamental qui se donne au travers des méthodes de transformation qui encadrent l’émergence du concept leibnizien d’expression est l’intervention, à chaque fois, d’une forme d’infini par lequel une chose est transformée en une autre, une chose est exprimée par une autre. Ainsi, dans la méthode des métamorphoses, le triangle est infinitésimal qui porte en lui les rapports invariants qui se portent de la courbe transcendante du cercle à la nouvelle courbe algébrisée ; dans la quadrature du cercle, c’est l’infinité de la série qui porte en elle les rapports qui se retrouvent dans le rapport fini du cercle à son diamètre (de π à 4) ; dans la méthode projective, c’est l’invariance du birapport harmonique du cercle générateur à l’infini qui se transporte dans toutes les coniques à distance finie du centre de projection. Ces éléments (de nature infinie) portent certes un ordre commun, déterminent la transformation dans sa loi et réalisent ce lien si difficile entre l’invariance et la modification, entre la multiplicité et l’unité, entre l’altérité et l’identité. Mais il est remarquable que, dans le même temps, ils engagent nécessairement la relation de l’infini au fini, forme si leibnizienne du rapport entre la multitude et l’un, forme si problématique pour les mathématiques du 17e siècle, et dont cependant Leibniz s’accommode avec inventivité.

III. Le fini et l’infini

À nos analyses précédentes, nous choisissons donc d’ajouter, pour éclairer cette question délicate du rapport entre le fini et l’infini, l’examen du calcul différentiel inventé en 1675, dans le décor conceptuel dessiné par les innovations du triangle caractéristique et de la méthode des métamorphoses, et par l’originalité de sa quadrature du cercle comme série infinie et rationnelle exprimant une grandeur finie non-rationnelle. De plus, c’est encore une fois la lecture de Pascal et de ses travaux sur le triangle arithmétique qui est évoquée comme prémices de cette découverte17, à laquelle vient s’ajouter l’impression très forte que firent sur Leibniz ses propres travaux de jeunesse relatifs à la combinatoire. Dans une telle inscription, les premiers pas de l’élaboration du calcul infinitésimal prennent appui sur des considérations au sujet des séries, éventuellement infinies de quantités finies, de sorte que ce calcul porte en son centre ce rapport particulier chez Leibniz du fini et de l’infini, entre identification méthodologique et distinction métaphysique.

1. De la combinatoire et du calcul des différences aux calculs différentiel et intégral

Le texte rétrospectif de l’Historia et origo calculi differentialis offre encore une fois un précieux témoignage de la façon dont Leibniz ancre l’invention des calculs infinitésimal et intégral aussi bien dans ses travaux sur les quadratures comme « problèmes inverses des tangentes » que dans ses recherches sur les séries. Ce sont en effet des études sur les séries numériques et les propriétés de leurs différences qui, sans être novatrices en elles-mêmes, le conduisent à élaborer ce calcul différentiel dont il note à bon droit qu’il se distingue du calcul

des fluxions inventé par Newton à la même époque. Ainsi qu’il le reconnaît, Leibniz fait remonter son intérêt pour les séries, fussent-elles alors finies, à l’époque du De arte

combinatoria de 1666. Il évoque explicitement la relation existant entre ces premiers travaux

et ceux de 1673, dont le point de départ est cette vérité très simple : a=a. De là vient que toute différence entre des termes peut s’exprimer comme la somme des différences des termes intermédiaires : soit une suite croissante de nombres (a, b, c, d, e, etc.), comme a–a=0, on a (a–a)+(b–b)+(c–c)+(d–d)+(e–e)=0, d’où a–e=(a–b)+(b–c)+(c–d)+(d–e). Leibniz illustre l’intérêt de cette propriété en calculant grâce à elle et aussi aisément que possible les différences d’ordre premier, deuxième, etc. des termes des suites de nombres entiers, par exemple (0, 1, 2, 3, 4, etc.) ou (0, 1, 4, 9, 16, etc.), en remarquant que les différences secondes des entiers naturels s’annulent, que les différences troisièmes des carrés s’annulent, les différences quatrièmes des cubes s’annulent, etc., tandis que les différences premières des entiers sont toutes égales à 1=1!, les différences secondes des carrés toutes égales à 2=2!, les différences troisièmes des cubes toutes égales à 6=3!, etc.

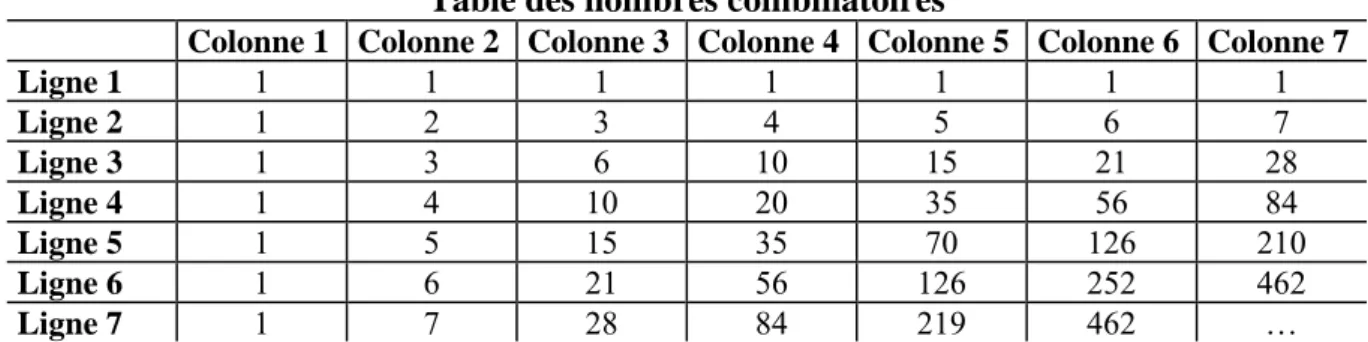
Puis, il s’intéresse avec intensité aux suites de nombres combinatoires, dont la table (qui est celle du triangle arithmétique de Pascal) est alors très utilisée et a pour particularité d’être formée de différences et de sommes.

Table des nombres combinatoires

Colonne 1 Colonne 2 Colonne 3 Colonne 4 Colonne 5 Colonne 6 Colonne 7

Ligne 1 1 1 1 1 1 1 1 Ligne 2 1 2 3 4 5 6 7 Ligne 3 1 3 6 10 15 21 28 Ligne 4 1 4 10 20 35 56 84 Ligne 5 1 5 15 35 70 126 210 Ligne 6 1 6 21 56 126 252 462 Ligne 7 1 7 28 84 219 462 …

Tout terme ui,j de la i-ème ligne, j-ème colonne est égal à la somme des termes de la ligne

précédente ( pour i>1), ou bien à la différence des termes de la ligne consécutive

( pour j>1). De surcroît, la constitution du tableau combinatoire implique une

symétrie (u

∑

= − j 1 k ui 1,k 1 j , 1 i j , 1 i u u₊ − _{+ −}

i,j=uj,i pour tous i et j), qui permet d’identifier les propriétés des lignes et des

colonnes. Ce qui pose au cœur des relations entre les nombres combinatoires la simplicité propre à tout élément dont la constitution est réglée par une loi de symétrie. Elle présente également une hérédité fondatrice de récurrence, toute ligne étant la différence de la ligne qui lui succède et la somme de la ligne qui la précède. Elle est donc la différence p-ème de la ligne qui lui succède en p-ème lieu et la somme p-ème de la ligne qui la précède en p-ème lieu. Enfin, entre la différence et la sommation, la relation est réciproque, puisque la ligne qui suit une autre en est la somme, de même que la deuxième est la différence de la première. Ainsi, les nombres combinatoires s’écrivent par des relations additives ou soustractives, fortes mais simples, qui ramènent les éléments de la table les uns aux autres. L’importance de ces relations est d’autant plus grande que Leibniz note une propriété remarquable : le rapport entre les différences et les nombres combinatoires.

En effet, il utilise ces relations soustractives et additives des nombres combinatoires dans le cadre de suites décroissantes de nombres entiers. Ce qui l’amène à formuler, sans les démontrer, les propriétés suivantes pour des différences finies d’entiers naturels ordonnés suivant une suite décroissant à l’infini.18 La première de ces propriétés affirme que toute

différence finie entre le premier terme et le dernier terme d’une suite d’entiers naturels peut être considérée comme la somme des différences premières de ces entiers, pondérées par les nombres combinatoires de la première ligne, ou la somme des différences secondes pondérées par les nombres combinatoires de la deuxième ligne, etc. Dans une propriété qu’il juge réciproque, il présente comme seconde propriété que cette différence est aussi égale la somme des nombres combinatoires de la première ligne pondérés par la différence première des deux premiers termes de la suite, moins la somme des nombres combinatoires de la deuxième ligne pondérés par la différence seconde des premiers termes de la suite, plus la somme des nombres combinatoires de la troisième ligne pondérés par la différence troisième des premiers termes de la suite, etc.19 Leibniz a ainsi trouvé des formulations de différences finies où interviennent les nombres combinatoires comme éléments de sommes pour leur part infinies.

La généralisation de la méthode de calcul permet alors une écriture elle aussi générale qui, plus qu’une simple traduction, est l’incarnation de ces relations de réciprocité et d’hérédité constatées dans le tableau combinatoire et qui se transposent dans cette nouvelle forme de calcul. Leibniz pose x = 1+1+1+1+1+1+…, entier naturel, tel que dx=1 en soit la différence première et ∫x la somme première, et note :

1 + 2 + 3 + 4 + 5 + etc. font ∫x, 1 + 3 + 6 + 10 + etc. font ∫∫x, 1 + 4 + 10 + 20 + etc. font ∫3x

1 + 5 + 15 + 35 + etc. font ∫4x, et ainsi de suite.

Il en déduit (sans le démontrer) que y – ω = dy·x – ddy·∫x + d³y·∫∫x – d4y·∫³x + etc., avec ω qui peut être égal à 0 quand on poursuit la différenciation à l’infini, et ∫y = yx – dy·∫x +ddy·∫∫x – d3y·∫³x + etc.Leibniz n’utilise pas à l’époque de ces découvertes les notations différentielle et intégrale, mais il les emploie tout de même dans son Historia, sans doute par souci de clarté.20 Surtout, à propos des deux formules générales de « y – ω » et de « ∫y », il écrit :

« Or, ces deux théorèmes ont pour propriété remarquable d’être également valides dans les deux calculs différentiels, aussi bien le Calcul différentiel numérique que le Calcul infinitésimal. »21

les termes a b c d e etc. les différences 1ères f g h i k etc.

2èmes l m n o p etc. 3èmes q r s t u etc. 4èmes v w x y z etc. etc.

On pose alors a comme terme premier et µ comme terme dernier. L’auteur trouvait alors : a - µ = 1f + 1g + 1h + 1i + 1k + etc., a - µ = 1l + 2m + 3n + 4o + 5p + etc., a - µ = 1q + 3r + 6s + 10t + 15u + etc., a - µ = 1v + 4w + 10x + 20y + 35z + etc., etc. » (Ibid., p. 68.) 19 « Et réciproquement : a - µ = 1f + 1f - 1l + 1f - 2l + 1q + 1f - 3l + 3q - 1v + 1f - 4l + 6q - 4β + etc. etc. » (Ibid., p. 68)

20 _{« Par conséquent, en adoptant la terminologie introduite plus tard par l’auteur, et en appelant “y” n’importe}

quel terme d’une suite (et dans ce cas a=y), on pourra noter la différence première “dy”, la différence seconde “ddy”, la différence troisième “d3_{y”, la différence quatrième “d}4_{y”, et en appelant “x” n’importe quel terme}

d’une deuxième suite, on pourra appeler la somme de ces termes “∫x”, la somme des sommes (ou somme seconde) “∫∫x”, la somme troisième “∫3_{x”, et la somme quatrième “∫}4_{x”. » (Ibid., page 69.)}