.
Aires, int´ egrales et primitives
dans l’enseignement secondaire, de 1902 ` a 2019
Daniel PERRIN
Table des mati` eres
1 Introduction 3
1.1 Pourquoi ce th` eme ? . . . . 3
1.2 Mes sources . . . . 4
2 Le programme de 1902 4 2.1 Les racines . . . . 4
2.2 Le point de vue de Louis Liard . . . . 5
2.3 Poincar´ e . . . . 7
2.4 Le programme de 1902 . . . . 7
2.5 Deux exemples de manuels . . . . 8
2.6 Conclusion . . . . 8
3 La p´ eriode interm´ ediaire : 1902-1972 9 3.1 Les programmes de 1945 . . . . 9
3.2 L’´ evolution dans les ann´ ees 1960 . . . . 9
4 La r´ eforme des math´ ematiques modernes 10 4.1 Les contextes de la r´ eforme . . . . 10
4.2 Le contenu des programmes, cˆ ot´ e analyse . . . . 12
5 La contre-r´ eforme des ann´ ees 1980 14 5.1 Les raisons de la col` ere . . . . 14
5.2 Le cadre de l’analyse dans le programme 1982 . . . . 15
5.3 L’int´ egrale . . . . 16
5.4 Commentaire . . . . 16
6 Le programme de 2002 ou le cul entre deux chaises 17 6.1 Les changements du programme d’analyse . . . . 17
6.2 Sur l’int´ egrale . . . . 17
7 Le programme 2011 : alleluia ! 20 8 Annexe : Les sommes de Riemann ou de Darboux 20
8.1 A quoi ¸ca sert ? . . . . ` 21
8.2 Montrer l’existence de l’aire ? . . . . 21
8.3 Les sommes de Riemann comme moyen de calcul ? . . . . 25
8.4 Interm` ede : Archim` ede et la quadrature de la spirale . . . . . 26
8.5 Les sommes de Riemann comme moyen d’approximation . . . 29
8.6 Les sommes de Riemann et la mod´ elisation . . . . 30
9 Extraits de manuels 35
1 Introduction
1.1 Pourquoi ce th` eme ?
De nombreuses raisons m’ont conduit ` a proposer ce sujet pour le colloque du cinquantenaire des IREM.
• La premi` ere raison tient ` a l’histoire des math´ ematiques. Je consid` ere que l’invention du calcul infinit´ esimal (c’est-` a-dire des notions de d´ eriv´ ee et d’int´ egrale) par Newton et Leibniz (vers 1680) est le plus grand progr` es accompli par l’humanit´ e en math´ ematiques
1. Avec cette invention, les plus grands r´ esultats des math´ ematiciens de l’Antiquit´ e : le calcul du volume de la pyramide (Euclide), la quadrature de la spirale, celle de la parabole, le calcul du volume de la boule (Archim` ede), sont maintenant des exercices faciles pour les lyc´ eens.
• C’est un sujet int´ eressant du point de vue de l’´ evolution des programmes et notamment des mouvements de balancier exag´ er´ es entre des options di- vergentes pour introduire l’int´ egrale : les aires, les sommes de Riemann, les primitives ... L’´ etude de ce cas, o` u l’on voit de fa¸con ´ eclatante combien la recherche de l’´ equilibre est difficile, devrait sans doute ˆ etre m´ edit´ ee par toute personne en charge d’´ elaborer des programmes.
• On peut suivre en filigrane dans l’´ evolution des programmes en ce do- maine les conceptions id´ eologiques (et parfois politiques) qui traversent la soci´ et´ e (tout un tas de mots en isme : positivisme, structuralisme, construc- tivisme etc.), ainsi que l’influence de certains acteurs, les math´ ematiciens, les professeurs (via l’APMEP) et ... les IREM.
• Ce th` eme est l’occasion d’aborder un certain nombre de questions qua- siment philosophiques qui tiennent ` a la pratique des math´ ematiques (le di- lemme entre d´ efinitions axiomatiques et constructions) et ` a leurs applications, notamment aux calculs de grandeurs, ainsi que les questions concernant la mod´ elisation.
• Enfin, c’est un sujet qui me tient personnellement ` a cœur. En effet, dans le travail effectu´ e au sein de la commission Kahane, j’ai beaucoup r´ efl´ echi sur les aires d’un point de vue g´ eom´ etrique. J’ai d’ailleurs enseign´ e ces ques- tions pendant sept ans en licence pluridisciplinaire, voir [10] ou [11]. Quant
`
a l’int´ egrale et aux primitives, outre que j’ai enseign´ e l’int´ egrale de Lebesgue en licence, c’est l’un des th` emes essentiels de l’oral du CAPES dont je me suis occup´ e pendant de nombreuses ann´ ees, voir [14] sur ce point.
1. Mon sentiment est que cette invention n’a pu ´ emerger que grˆ ace ` a celle des nombres
d´ ecimaux (Stevin, 1585) qui permet depuis ` a tous (ou presque) de calculer sans peine.
J’ai d’ailleurs d´ ej` a abord´ e ce sujet dans deux conf´ erences, en 2005 devant la commission Inter-IREM second cycle et en 2006 ` a l’IREM de Bordeaux, voir sur ma page web :
https://www.math.u-psud.fr/~perrin/conferences.html
1.2 Mes sources
Pour les questions historiques, je m’appuie essentiellement sur l’excellente
´
etude de J.-P. Daubelcour de l’IREM de Lille (voir [5], [6]), ainsi que sur nombre de manuels de chacune des ´ epoques ´ etudi´ ees. J’ai aussi utilis´ e le livre de Bruno Belhoste [2]. Pour les questions de fond, une r´ ef´ erence dont les positions sont tr` es proches des miennes, est le livre de Marc Rogalski [19].
2 Le programme de 1902
2.1 Les racines
2.1.1 Le contexte politique, social et philosophique de la r´ eforme de 1902
En 1902, la troisi` eme R´ epublique est bien install´ ee et peut-ˆ etre ` a son apog´ ee et la politique de scolarisation primaire de Jules Ferry a ´ et´ e une r´ eussite. En revanche, il faut ˆ etre conscient qu’` a l’´ epoque, les lyc´ eens ne repr´ esentent que 2 ` a 3 % d’une classe d’ˆ age : la d´ emocratisation de l’ensei- gnement se limite au primaire.
Les sciences n’occupent qu’une place limit´ ee dans les programmes avant 1902. Au contraire, la r´ eforme de 1890 a remis en avant les humanit´ es. Voil` a ce qu’en dit le ministre L´ eon Bourgeois : Les lettres, c’est ` a dire l’´ etude des langues et des litt´ eratures, avec l’histoire et la philosophie comme compl´ ement ou couronnement, garderont naturellement la premi` ere place. Cela signifie que dans l’enseignement secondaire classique, les ´ el` eves doivent suivre des
´
etudes de latin et grec jusqu’en classe de premi` ere, mˆ eme ceux qui choisiront ensuite la classe de math´ ematiques ´ el´ ementaires. Il y a bien un enseignement secondaire “moderne” avec des programmes all´ eg´ es, mais, s’il ouvre la porte des facult´ es des sciences et de pharmacie, il ne donne pas acc` es aux facult´ es des lettres, de droit et de m´ edecine.
Pourtant, l’id´ eologie philosophique dominante est sans doute le positi-
visme, doctrine philosophique d’Auguste Comte (1798-1857), qui met en
avant la science (et non la m´ etaphysique ou la th´ eologie) comme moteur
du progr` es de l’humanit´ e, les math´ ematiques y jouant un grand rˆ ole. Elle
influence profond´ ement les fondateurs de la troisi` eme R´ epublique et notam- ment Jules Ferry ou Marcellin Berthelot (chimiste et ministre de l’instruction publique en 1886). La refonte g´ en´ erale de l’enseignement de 1902 se place dans le cadre de ce que Bruno Belhoste appelle le triomphe de l’humaniste scientifique d’inspiration positiviste.
2.1.2 Le rˆ ole des math´ ematiciens
De nombreux math´ ematiciens de l’´ epoque, et non des moindres (Henri Poincar´ e, Gaston Darboux, Paul Appell, Jules Tannery, Henri Lebesgue) s’int´ eressent ` a la r´ eforme de l’enseignement. Par exemple Darboux dirige la publication d’un cours complet de math´ ematiques ´ el´ ementaires.
2.1.3 La structure de la r´ eforme
Cette r´ eforme est pr´ epar´ ee par le ministre de l’instruction publique Georges Leygues. La structure du lyc´ ees comprend quatre sections : A (latin-grec), B (latin-langues vivantes), C (latin-sciences), D (sciences-langues vivantes).
Cette structure va (pour l’essentiel) persister jusque dans les ann´ ees
21960.
2.2 Le point de vue de Louis Liard
La philosophie de la r´ eforme de 1902 me semble parfaitement d´ ecrite dans le remarquable texte suivant, extrait d’une conf´ erence (janvier 1904) de Louis Liard (1846-1917), philosophe, directeur des enseignements sup´ erieurs. Il y a d’abord un paragraphe sur la place de l’enseignement des sciences.
Dans l’enseignement secondaire, les ´ etudes scientifiques doivent, comme les autres, contribuer ` a la formation de l’homme. Elles sont donc, elles aussi,
`
a leur fa¸ con, des “humanit´ es”, au sens large du mot, les “humanit´ es scien- tifiques”.
Vient ensuite, une d´ efense d’un enseignement qui ne soit pas fond´ e sur la seule m´ emoire :
... l’enseignement des sciences doit surtout faire appel aux facult´ es ac- tives des esprits, ` a celles-l` a mˆ emes par lesquelles se fait la construction des sciences. La m´ emoire y joue sans doute un rˆ ole, mais non le principal. Ce qu’il s’agit de former c’est la vision exacte des choses, le discernement du r´ eel et de l’irr´ eel, du vrai et du faux, le sentiment de la certitude et la jus- tesse du raisonnement. ... Rien de plus contraire au v´ eritable enseignement
2. L’auteur de ces lignes peut en t´ emoigner, ` a ceci pr` es qu’il y avait aussi des sections
modernes M, voire M’, sections issues des cours compl´ ementaires.
Plus de détails Peinture de Louis Liard par André Rixens
CC BY-SA 4.0 File: Peinture de Louis Liard.jpg Création : 6 août 2014, 11:49:13
À propos de cette interface | Discussion | Aide Jean-André Rixens — Travail personnel
Peinture de Louis Liard - Louis Liard — Wikipédia file:///Users/perrin/Downloads/Louis Liard.html
1 sur 1 16/03/2019 à 17:37
Figure 1 – Louis Liard
(Image JPEG, 193!"!261 pixels) data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBxMTEhUTExMWFRUXFxoYGBcYGBgXGBodGBgYG...
Figure 2 – Henri Poincar´ e
scientifique que de verser dans des esprits passifs, soit par le livre, soit mˆ eme par la parole,une masse d’abstractions et de faits ` a apprendre par cœur. ... Ce qu’il faut, au contraire, c’est susciter la spontan´ eit´ e de l’´ el` eve, mettre en jeu ses activit´ es mentales, provoquer son effort personnel, en un mot le rendre capable d’agir.
La vieille formule du philosophe est toujours vraie, “savoir, c’est faire”.
... le vrai profit n’est pas ce que l’´ el` eve peut reproduire, mais ce qu’il peut produire.
Liard met ensuite en avant la m´ ethode :
Alors, qui nous empˆ eche, dans ces classes, de tout faire pour amener progressivement l’´ el` eve ` a juger personnellement des choses, ` a discerner les v´ erit´ es par lui-mˆ eme et non sur l’autorit´ e de celui qui les ´ enonce, livre ou professeur ? L’id´ eal serait que, dirig´ e par le maˆıtre, il trouvˆ at tout ce qu’il doit savoir. Assur´ ement, c’est impossible. Il n’y a pas un Pascal latent en chacun de nos ´ ecoliers. Mais sans viser ` a l’impossible, croyez-vous que la m´ ethode, qui est bien vieille, puisque c’´ etait d´ ej` a celle de Socrate, ne puisse, appliqu´ ee avec discernement, donner de bons effets ?
Il ajoute, un peu plus loin, prˆ onant la recherche de l’´ equilibre :
Mais ce qui est ` a sa place dans l’enseignement sup´ erieur ne l’est pas dans l’enseignement secondaire. Or on m’assure que l` a, sous l’influence des plus hautes sp´ eculations, il s’est introduit, depuis quelques ann´ ees, des fa¸ cons qui
6
ne seraient pas sans p´ eril. Ne perdons pas de vue que, dans nos classes, il s’agit de former, non des candidats ` a la section de g´ eom´ etrie de l’Acad´ emie des sciences, mais des esprits clairs, voyant juste, raisonnant juste.
2.3 Poincar´ e
Dans le mˆ eme esprit que Louis Liard, voici un extrait d’une conf´ erence d’Henri Poincar´ e (1904, mus´ ee p´ edagogique).
Pour d´ efinir une int´ egrale, nous prenons toutes sortes de pr´ ecautions ; nous distinguons les fonctions continues et celles qui sont discontinues, celles qui ont des d´ eriv´ ees et celles qui n’en ont pas. Tout cela est ` a sa place dans l’enseignement des Facult´ es ; tout cela serait d´ etestable dans les lyc´ ees.
L’´ el` eve, quelque d´ efinition que vous lui donniez, ne saura jamais ce qu’est une int´ egrale si on ne lui en a d’abord montr´ e. Toutes les subtilit´ es le laisseront indiff´ erent. Il croit savoir ce qu’est une surface et il ne comprendra qu’il ne le sait pas que quand il saura tr` es bien le calcul int´ egral.
Ce n’est donc pas au moment o` u il aborde ce calcul qu’il peut y avoir int´ erˆ et ` a le lui dire. Alors ce qui reste ` a faire est bien simple : d´ efinir l’int´ egrale comme l’aire comprise entre l’axe des x, deux ordonn´ ees
3et la courbe, montrer que quand l’une des ordonn´ ees se d´ eplace, la d´ eriv´ ee de cette aire est pr´ ecis´ ement l’ordonn´ ee elle-mˆ eme. C’est le raisonnement de New- ton, c’est comme cela que le calcul int´ egral est n´ e, et bon gr´ e mal gr´ e il faut repasser par o` u nos p` eres ont pass´ e.
Le lecteur pourra constater, tout au long de ce texte, que, sur ce point au moins
4, je suis un fid` ele disciple d’Henri Poincar´ e !
2.4 Le programme de 1902
La d´ eriv´ ee est introduite en seconde
5, avec le lien entre le signe de la d´ eriv´ ee et le sens de variation de la fonction (admis, sans doute). Voici le texte exact du programme :
Notion de la d´ eriv´ ee. Signification g´ eom´ etrique (coefficient angulaire de la tangente) et cin´ ematique (vitesse dans le mouvement rectiligne) de la d´ eriv´ ee ;
3. Ce mot, qui nous semble bizarre, est celui qu’on utilise ` a l’´ epoque et encore long- temps apr` es, voir le programme de 1962. L’ordonn´ ee d´ esigne ici le segment vertical et pas seulement la coordonn´ ee de son extr´ emit´ e. Merci ` a Dominique Tourn` es de m’avoir expliqu´ e ce point.
4. Le r´ esultat qui affirme que la d´ eriv´ ee de l’aire sous la courbe est ´ egale ` a la fonction est appel´ e Th´ eor` eme fondamental de l’analyse par les anglo-saxons, c’est dire son importance.
5. C’est une nouveaut´ e dans l’enseignement classique, mais elle ´ etait d´ ej` a apparue vers
1890 dans l’enseignement moderne.
le sens de variation d’une fonction est indiqu´ e par le signe de la d´ eriv´ ee.
D´ eriv´ ee d’une somme, d’un produit, d’un quotient, de la racine carr´ ee d’une fonction, de sin x, cos x, tan x, cot x. Sont ´ evoqu´ es ensuite des exemples d’´ etudes de fonctions (notamment ax
2+ bx + c
a
0x
2+ b
0x + c
0).
S’agissant des int´ egrales le programme (de terminale) est particuli` erement succinct :
D´ eriv´ ee de l’aire d’une courbe regard´ ee comme une fonction de l’abscisse (on admettra la notion d’aire).
2.5 Deux exemples de manuels
Le premier est le Cours d’alg` ebre ´ el´ ementaire de 1910, dont l’auteur est un religieux, le Fr` ere Georges-Marie, voir §9.
La d´ emonstration du fait que la fonction est la d´ eriv´ ee de l’aire sous la courbe, principale nouveaut´ e de ces programmes selon la requˆ ete explicite de Poincar´ e, est donn´ ee ici. Elle s’appuie sur une connaissance de la notion d’aire et de ses propri´ et´ es, notamment la croissance et l’aire du rectangle. De plus, la fonction est implicitement suppos´ ee croissante (pour avoir l’in´ egalit´ e d’aires annonc´ ee) et le cas h < 0 n’est pas ´ evoqu´ e. ` A cela pr` es, la d´ emonstration, mˆ eme si elle n’est pas exactement dite avec les mots que l’on utiliserait aujourd’hui, est essentiellement correcte. La notation R
ba
f (t)dt est introduite ensuite.
Le second est l’excellent Pr´ ecis d’alg` ebre de F. Brachet et J. Dumarqu´ e de 1930. Ce livre est r´ esolument moderne dans sa d´ efinition de la limite par rapport ` a ses contemporains
6voir §9. Sur les primitives, le th´ eor` eme fondamental est prouv´ e dans le cas croissant et il y a quelques applications au calcul d’aires et de volumes (en particulier une amorce de preuve du fait que la d´ eriv´ ee du volume est l’aire des sections, voir §9). Les auteurs donnent aussi la d´ efinition du logarithme n´ ep´ erien comme primitive de 1/x. On notera qu’ici, la notation R
ba
f (t)dt n’est pas utilis´ ee.
2.6 Conclusion
Ind´ eniablement, le programme de 1902, sur ce sujet de l’int´ egrale, consti- tue un progr` es important. Cela ´ etant, il est encore assez limit´ e. Si l’on regarde les sujets de Bac de l’´ epoque, les primitives n’y sont que peu pr´ esentes. On les trouve soit sous forme de questions de cours, soit, souvent ` a la fin des probl` emes, pour calculer l’aire comprise entre deux courbes, voir §9.
6. Mˆ eme dans les manuels d’apr` es 1945, par exemple le Lespinard et Pernet, on trouve
encore une “d´ efinition” de l’expression x tend vers a, voir [6] Chapitre 2 p. 3.
3 La p´ eriode interm´ ediaire : 1902-1972
3.1 Les programmes de 1945
Les programmes de 1902 restent essentiellement inchang´ es jusque 1945. Il y aura bien un projet de r´ eforme du r´ egime de Vichy qui visait ` a supprimer le calcul int´ egral mais il restera pratiquement lettre morte (les manuels traitent ce chapitre comme un compl´ ement au programme
7).
Juste apr` es la guerre, il faut mentionner l’importance, au moins dans l’imaginaire collectif, du plan Langevin-Wallon qui visait une d´ emocratisation de l’enseignement. Cependant ce plan n’a jamais ´ et´ e vraiment appliqu´ e (il
´
emanait de personnalit´ es proches du parti communiste et le contexte de la guerre froide l’a bloqu´ e). De plus, il ne s’occupe pas du d´ etail des pro- grammes.
Le programme de 1945 ne change pratiquement pas le contenu
8du th` eme des int´ egrales. Pour s’en rendre compte, on regardera l’extrait du manuel de Lespinard et Pernet de 1947 donn´ e au §9. On notera que la d´ emonstration du
“th´ eor` eme fondamental” prend en compte le cas non monotone (en admettant qu’une fonction continue sur un segment est born´ ee et atteint ses bornes).
3.2 L’´ evolution dans les ann´ ees 1960
Sous l’influence des math´ ematiciens (notamment Gustave Choquet), l’Uni- versit´ e a fait sa r´ evolution culturelle dans les ann´ ees 1950, avec l’apparition du vocabulaire de la th´ eorie des ensembles, de la topologie, de l’alg` ebre, etc.
Dans cette p´ eriode, on voit se d´ evelopper une r´ eflexion intense sur l’ensei- gnement des math´ ematiques, dans le cadre de l’APMEP, mais aussi, sur le plan international, au sein de la CIEAEM (Commission Internationale pour l’´ Etude et l’Am´ elioration de l’Enseignement des Math´ ematiques), autour de Caleb Gattegno notamment. En France, c’est en 1966 que voit le jour la com- mission Lichn´ erowicz, charg´ ee de proposer une r´ eforme de l’enseignement des math´ ematiques dans le secondaire.
Au lyc´ ee, dans les ann´ ees 1960, outre l’apparition du vocabulaire en- sembliste, on note un renforcement de l’analyse (le mot apparaˆıt pour la premi` ere fois) : th´ eor` eme de Rolle (admis), des accroissements finis, appa-
7. Dans le livre d’alg` ebre de A. Benoˆıt, il dit, ` a propose de primitives : Cette no- tion, bien que ne figurant pas au programme officiel, est utile aux ´ el` eves de la classe de Math´ ematiques.
8. En revanche il est plus novateur du cˆ ot´ e de la g´ eom´ etrie : introduction du produit
scalaire, des transformations du plan et de l’espace (y compris l’inversion).
rition des fonctions logarithme (vue comme primitive
9de 1/x) et exponen- tielle (r´ eciproque du logarithme), quelques ´ equations diff´ erentielles simples (y
0= ay, y
00+ ω
2y = 0).
Cˆ ot´ e rigueur et formalisation, les d´ efinitions des limites avec , η appa- raissent dans certains manuels (voir §9).
Le programme parle de fonctions primitives. Il dit (apr` es avoir pr´ ecis´ e qu’aucune difficult´ e ne sera soulev´ ee au sujet des notions d’aire et de volume) : Aire d’un domaine plan limit´ e par un arc de la courbe repr´ esentative d’une fonction f (x) continue (on pourra se limiter au cas d’une fonction mono- tone), positive ou nulle, par l’axe des abscisses, et par deux “ordonn´ ees”
10, l’une fixe, l’autre variable (abscisse x) ; cette aire repr´ esente une primitive de la fonction donn´ ee.
Suivent quelques mots sur les conventions de signe et les applications aux calculs d’aires et de volumes.
On trouvera au §9 un exemple de manuel de l’´ epoque (collection Cagnac et Thiberge).
En fait, les programmes et les manuels de cette courte p´ eriode sont par- ticuli` erement bons ! Ils n’ont pas les d´ efauts de ceux de l’´ epoque des maths modernes qui vont tomber dans la surench` ere et ils n’en subissent ´ evidemment pas les contre-coups comme ceux qui suivront. Le lecteur regardera par exemple avec envie les manuels de la collection Queysanne-Revuz de cette p´ eriode.
4 La r´ eforme des math´ ematiques modernes
4.1 Les contextes de la r´ eforme
Comme pour la r´ eforme de 1902, on ne peut dissocier la r´ eforme des maths modernes de son contexte, ou plutˆ ot de ses divers contextes, philosophique, politique, scientifique, noosph´ erique ...
4.1.1 Le contexte philosophique : le structuralisme
C’est un courant de pens´ ee important ` a cette ´ epoque, issu de la linguis- tique, et repr´ esent´ e notamment par Claude L´ evi-Strauss. Pour en r´ esumer l’id´ ee en un mot, il donne le pas aux structures sur les objets. Bien entendu
9. ` A mon avis, c’est un point essentiel car cela renforce beaucoup l’importance du chapitre sur l’int´ egrale qui ´ etait jusque l` a assez marginal.
10. On notera que le texte du programme utilise encore ce mot, comme Poincar´ e, mais
avec des guillemets.
ce mouvement a un large ´ echo en math´ ematiques, notamment via les th´ eories axiomatiques et il y a de fortes accointances entre Levi-Strauss et le groupe Bourbaki (essentiellement via Andr´ e Weil).
4.1.2 Le contexte scientifique : Bourbaki
Du point de vue proprement math´ ematique, l’´ epoque voit l’apog´ ee du groupe Bourbaki, ` a la fois sur le fond (il n’est qu’` a regarder les contenus des cours de DEA de l’´ epoque) et en termes de pouvoir (on disait expli- citement alors que seul un membre du groupe pouvait ˆ etre en charge des math´ ematiques ` a l’ENS de la rue d’Ulm par exemple). Les relais vers l’en- seignement secondaire de cette tendance (pas n´ ecessairement membres du groupe) ont noms Dieudonn´ e, Choquet, Revuz, etc. D’ailleurs les d´ ebats sont souvent vifs sur les questions d’enseignement, on se souvient de l’invective : A bas Euclide, plus de triangles ` de Dieudonn´ e ou de sa controverse avec Choquet sur la g´ eom´ etrie.
L’un des objectifs des promoteurs de la r´ eforme des maths modernes ´ etait en r´ eaction ` a une vision trop intuitive des math´ ematiques qui leur donnait le sentiment qu’elles reposaient sur du sable. L’auteur de ces lignes se souvient d’avoir eu, ` a la suite de l’´ ecriture du rapport sur la g´ eom´ etrie de la commission Kahane, donc au tout d´ ebut des ann´ ees 2000, une longue discussion avec Andr´ e Revuz (alors ˆ ag´ e de plus de quatre-vingts ans, mais toujours vif et pugnace) o` u il expliquait ses r´ eticences sur les justifications des cas d’´ egalit´ e des triangles qu’on lui proposait quand il ´ etait ´ el` eve. La cons´ equence de cette frustration a ´ et´ e la volont´ e de fonder toutes les math´ ematiques sur des bases solides, en gros sur la th´ eorie des ensembles, et de construire tout ` a partir de ces bases. En particulier on construisait alors Z, Q, voire R ` a partir des entiers avec des relations d’´ equivalence (d` es la classe de cinqui` eme pour Z !).
Dans le cas de la th´ eorie de l’int´ egration, il n’´ etait pas question de s’appuyer sur les aires, qui n’avaient pas ´ et´ e bien d´ efinies auparavant et le mot d’ordre a donc ´ et´ e : sans les sommes de Riemann, point de salut. Nous reviendrons plus loin sur ce th` eme.
4.1.3 Le contexte politique : le gaullisme et mai 68
La r´ eforme est soutenue par la partie marchante du gaullisme, les tenants de la n´ ecessaire mise ` a jour de notre enseignement pour rattraper les grandes puissances de l’´ epoque (USA, URSS). C’est la raison de la cr´ eation de la commission Lichn´ erowicz en 1967. On peut raisonnablement penser que la r´ eforme a ´ et´ e acc´ el´ er´ ee
11par le mouvement de mai 1968, avec sans doute
11. Comme la cr´ eation des IREM.
beaucoup d’illusions de tous cˆ ot´ es, mais aussi beaucoup d’enthousiasme.
4.1.4 La noosph` ere
J’emploie ce terme au sens d’Yves Chevallard, il s’agit de l’ensemble des acteurs intervenant ` a l’intersection du syst` eme d’enseignement et de la soci´ et´ e. Dans le cas pr´ esent, un acteur important de la r´ eforme est l’APMEP, avec des personnalit´ es aussi marqu´ ees que P. Vissio, G. Walusinski, A. Revuz, etc. L’association soutient fermement la r´ eforme et la cr´ eation des IREM et elle est partie prenante de la commission Lichn´ erowicz,
4.1.5 D´ emocratisation ?
Nombreux sont ceux, parmi les promoteurs de la r´ eforme, pour qui elle est synonyme de d´ emocratisation. Je cite G. Walusinski (voir Bull. APMEP 353 d’avril 1986) :
Pour certains coll` egues amants des belles math´ ematiques, c’est la r´ enovation des contenus qui primait. Alors que pour d’autres, la recherche didactique s’amor¸ cait et ils y voyaient un moyen de diminuer l’´ echec scolaire. Pour d’autres avec lesquels je me sentais en accord, la r´ enovation des programmes paraissait une occasion ` a saisir pour mettre en cause les m´ ethodes anciennes et d´ evelopper ce qu’on appelait les m´ ethodes actives.
La suite sera moins glorieuse et la d´ emocratisation esp´ er´ ee ne sera pas vraiment au rendez-vous. Au contraire, avec le recul, on a le sentiment que, si cette r´ eforme convenait bien ` a ceux des ´ el` eves qui avaient d´ ej` a un goˆ ut pour les maths
12, elle en a d´ egoˆ ut´ e beaucoup d’autres.
4.2 Le contenu des programmes, cˆ ot´ e analyse
Les modifications des programmes de 1970 sont consid´ erables, en analyse (et plus encore en g´ eom´ etrie). Voici quelques exemples :
4.2.1 Les r´ eels
Dans les programmes ils sont d´ efinis axiomatiquement (c’est bien) ` a l’aide de la borne sup´ erieure (c’est tr` es discutable, voir sur ce sujet le chapitre IV de Daubelcour ([6]), il eut ´ et´ e sans doute plus raisonnable d’utiliser les suites adjacentes comme axiome de continuit´ e). Dans les classes, il n’´ etait pas rare qu’on donne une construction de R, souvent par les suites de Cauchy
13.
12. Par exemple ceux qui sont devenus math´ ematiciens ...
13. Je suis tr` es hostile ` a cette option et, si l’on veut ` a tout prix construire les r´ eels, ce
qui ne me semble pas indispensable, je pr´ ef` ere une approche plus intuitive ` a l’aide des
4.2.2 L’int´ egrale
Je recopie le programme :
D´ efinition des sommes de Riemann d’une fonction num´ erique d’une va- riable r´ eelle sur un intervalle ferm´ e born´ e. Existence de l’int´ egrale pour une fonction monotone ; notation R
ba
f(t)dt ; premi` eres propri´ et´ es. On admettra que ces propri´ et´ es s’´ etendent ` a des fonctions continues, ou monotones par morceaux.
Moyenne d’une telle fonction sur un intervalle ferm´ e born´ e. Lien avec la d´ erivation en des points o` u la fonction est continue.
Primitives, ensembles des primitives ; ´ egalit´ e Z
ba
f (t)dt = F (b) − F (a), f
´
etant continue sur [a, b] et admettant F pour primitive. Calcul des primitives ; int´ egration par parties.
Viennent ensuite des applications au calcul de l’aire de l’hypographe d’une fonction, puis ` a des applications aux volumes, masses, moments d’inertie, etc.
Daubelcour donne comme exemple le livre de Terminale C de la collec- tion Queysanne-Revuz (´ ecrit par Marc Gourion) qui introduit l’int´ egrale au moyen des fonctions en escalier, voir §9 ci-dessous.
Dans ce livre, on commence par d´ efinir les fonctions en escalier et leur int´ egrale, puis on d´ efinit une fonction Riemann-int´ egrable en l’encadrant par des fonctions en escalier et en demandant que la borne sup´ erieure des int´ egrales minorantes soit ´ egale ` a la borne inf´ erieure de int´ egrales majorantes.
L’int´ egrabilit´ e des fonctions monotones est prouv´ ee, celle des fonctions conti- nues admise. On d´ efinit ensuite les primitives et on en montre l’existence pour une fonction continue. L’aire n’arrive qu’ensuite
14. L’int´ egration par parties est au programme. On donne d’autres applications du calcul int´ egral, notam- ment pour les calculs de volumes et de nombreuses grandeurs physiques.
Dans les exercices du Queysanne-Revuz, outre les applications ´ evoqu´ ees ci-dessus, on trouve les int´ egrales de Wallis, quelques int´ egrales impropres, et de nombreux calculs de primitives mettant en jeu les fonctions exponentielle et logarithme.
d´ eveloppements d´ ecimaux illimit´ es, voir [10].
14. Dans les 27 premi` eres pages de ce chapitre, le mot aire n’apparaˆıt nulle part. L’aire
sous la courbe est d´ efinie alors comme l’int´ egrale. On donne ensuite les propri´ et´ es des
parties quarrables et de la mesure (de fa¸ con un peu formelle, mais assez conforme ` a ce que
je pr´ econise.)
4.2.3 Discussion
Il est clair qu’` a l’´ epoque de la r´ eforme des maths modernes, on n’avait peur de rien ! Le niveau du cours d’analyse ressemble plus ` a celui du d´ ebut de l’universit´ e qu’` a celui d’une classe terminale de lyc´ ee et d’ailleurs, c’est le sentiment de beaucoup de professeurs, je cite Daubelcour :
... le choix des sommes de Riemann associ´ ees ` a la propri´ et´ e de la borne sup´ erieure pour d´ efinir l’int´ egrale au Lyc´ ee est pour moi une erreur. ... Il y a d’autres approches, plus en ad´ equation avec l’enseignement en terminale.
... La pratique de ce programme en classe m’a appris que le plus souvent les heures pass´ ees en cours ` a ces d´ eveloppements difficiles n’ont pas conduit l’´ el` eve ` a donner une certaine ´ epaisseur s´ emantique au terme“int´ egrale d’une fonction continue” : l’acquisition du sens est tr` es souvent un ´ echec.
Sur le fond, du point de vue math´ ematique, mon impression c’est que, dans ce programme, on parle le moins possible de Newton et Leibniz, c’est-` a- dire de primitives, et le plus possible de sommes de Riemann, ce qui constitue un retour aux m´ ethodes d’Eudoxe et d’Archim` ede
15, voir ci-dessous la dis- cussion du §8.
En revanche, il faut reconnaˆıtre que ce programme est le premier o` u l’analyse prend une place aussi cons´ equente (sans doute au d´ etriment de la g´ eom´ etrie). Mˆ eme si l’on est – comme moi – un ardent partisan de celle-ci, au vu de la place de ces domaines dans les math´ ematiques de l’´ epoque et dans les programmes, on doit bien reconnaˆıtre qu’il y avait l` a une certaine n´ ecessit´ e.
5 La contre-r´ eforme des ann´ ees 1980
5.1 Les raisons de la col` ere
Il est aujourd’hui admis par tout le monde ou presque que la r´ eforme des math´ ematiques moderne a ´ et´ e un ´ echec, plus encore sans doute sur la partie g´ eom´ etrie que sur la partie analyse. Pour r´ esumer de nombreuses critiques, cette r´ eforme a donn´ e l’impression d’une formalisation ` a la fois p´ edante et creuse qui mettait trop l’accent sur les structures et pas assez sur leurs conte-
15. Il est int´ eressant de voir comment on proc` ede dans [QR] pour le “calcul” du volume
de la pyramide ou celui de la boule : cela ressemble tr` es fort ` a Euclide, on utilise la m´ ethode
d’exhaustion, c’est-` a-dire les sommes de Riemann ou Darboux, ou les fonctions en escalier
et pas du tout la m´ ethode qui consiste ` a voir l’aire comme d´ eriv´ ee du volume. De plus, et
c’est vraiment absurde, faute d’accepter une d´ efinition axiomatique du volume, la formule
avec l’int´ egrale est donn´ ee comme d´ efinition du volume !
nus
16. Il y a eu aussi de vives protestations des utilisateurs de math´ ematiques qui n’y retrouvaient pas les notions qui leur ´ etaient indispensables et ont ´ et´ e, de ce fait, contraints (et contents ?) de traiter eux-mˆ emes les math´ ematiques qui leur ´ etaient n´ ecessaires.
Par ailleurs, dans la r´ eforme, la place du cours magistral ´ etait sans doute devenue trop importante. En r´ eaction, la p´ eriode des ann´ ees 1980 voit l’apog´ ee d’une nouvelle position id´ eologique issue du constructivisme (inspir´ ee notam- ment par les travaux de Piaget) et dont la traduction scolaire peut se r´ esumer en une formule dont le succ` es a ´ et´ e consid´ erable : l’´ el` eve au centre du syst` eme
´
educatif.
Enfin, par rapport ` a l’inspiration bourbachique de la r´ eforme, qui mettait souvent en avant des th´ eor` emes formels sans d´ evelopper leur aspect calcula- toire
17l’apparition d’outils de calcul performants, et notamment des calcu- latrices, conduira ` a un changement dans la perception des math´ ematiques et en particulier de l’analyse
18.
Tous ces aspects sont relay´ es par une implication forte des IREM (nou- veaux ` a l’´ epoque) dans la r´ eforme des programmes (on peut citer notamment Jean-Louis Ovaert, Daniel Lazet, Mich` ele Artigue, etc.) avec un recentrage de l’analyse sur ses fondements : majorer, minorer, encadrer. Un texte essentiel sur ces points est le bulletin Inter-IREM [8].
5.2 Le cadre de l’analyse dans le programme 1982
On bat en retraite sur l’usage des d´ efinitions en , η pour pr´ ef´ erer une approche par les “fonctions de r´ ef´ erence”, voir [8]. Un exemple significatif d’application de la doctrine majorer, minorer, encadrer est l’utilisation de l’in´ egalit´ e des accroissements finis, avec un exercice incontournable, notam- ment au Bac : l’´ etude des suites r´ ecurrentes
19en encadrant la distance au point fixe par l’in´ egalit´ e des accroissements finis.
16. Je cite une phrase de l’introduction de [8] : L’´ etude des structures n’est pas une fin en soi, elle doit ˆ etre au service d’une maˆıtrise plus efficace de probl` emes compliqu´ es.
17. On examinera de ce point de vue le cours de calcul diff´ erentiel d’Henri Cartan.
18. D` es qu’on utilise une calculatrice on se pose forc´ ement la question, ` a cˆ ot´ e de la convergence d’une suite, de la rapidit´ e de celle-ci.
19. La pr´ esence presque oblig´ ee des suites r´ ecurrentes dans les ´ epreuves de Bac a ´ et´ e ` a
l’origine de la suppression de ce point dans les programmes suivants. Pour avoir enseign´ e
ce th` eme pendant plus de vingt ans au CAPES, je ne peux que le regretter car cette ´ etude
est un excellent moyen d’entrer dans les probl´ ematiques de l’analyse.
5.3 L’int´ egrale
Sur ce sujet, le retour de balancier est particuli` erement brutal
20. On aban- donne les sommes de Riemann, mais aussi l’introduction plus intuitive par l’aire, et l’int´ egrale R
ba
f(t)dt d’une fonction continue
21est d´ efinie comme la diff´ erence des valeurs F (b) − F (a) d’une primitive F de f, l’existence des primitives ´ etant admise sans justification. Cette d´ efinition a le m´ erite de permettre de prouver rapidement les principales propri´ et´ es de l’int´ egrale (po- sitivit´ e, lin´ earit´ e, Chasles, in´ egalit´ e de la moyenne, ...) Deux autres points sont au programme : les changements de variables affines et l’int´ egration par parties. Le programme ´ evoque ensuite les calculs de valeurs approch´ ees d’int´ egrales (en 1982, seulement la m´ ethode des rectangles, mais avec majo- ration du reste, en 1997, sont cit´ ees les m´ ethodes des rectangles, trap` ezes et point milieu). C’est un point positif qui est tr` es pr´ esent dans les manuels de l’´ epoque.
L’utilisation de l’int´ egrale pour le calcul d’aires, de volumes, etc. est
´
evoqu´ ee ensuite, mais l` a, on se garde bien de dire comment on fait le lien entre l’aire et l’int´ egrale
22. La raison de ces choix est partiellement expliqu´ ee dans les commentaires des programmes de 1983. Je cite :
Il a toujours ´ et´ e malais´ e de pr´ esenter en Terminale l’int´ egration ; en ef- fet, ` a ce niveau, par souci des techniques de calcul, le concept de primitive pr´ edomine sur celui d’int´ egrale. Il a donc paru plus efficace et plus court de rattacher la d´ efinition de l’int´ egrale d’une fonction continue aux primitives de cette fonction ; il va de soi que cette d´ efinition d’aura rien d’abrupt, elle peut ˆ etre pr´ ec´ ed´ ee d’une sensibilisation au moyen de la notion d’aire.
5.4 Commentaire
Je suis en d´ esaccord avec cette fa¸con de d´ efinir l’int´ egrale, essentiellement parce que l’introduction par les primitives est parachut´ ee et d´ econnect´ ee de la notion d’aire
23. En contrepartie, il faut reconnaˆıtre que, l` a, on est capable
20. ` A la lecture du paragraphe consacr´ e ` a l’int´ egration dans [8], qui met en avant les approximations et la mod´ elisation, on ne peut pas en attribuer la responsabilit´ e ` a l’action des IREM.
21. Sur ce point, un stade avanc´ e du ridicule est atteint en 1997 o` u, le mot continu ayant disparu des programmes, seules les fonctions d´ erivables ont droit ` a une primitive !
22. Le programme de 1997 dit : Dans le cas d’une fonction positive, interpr´ etation gra- phique de l’int´ egrale ` a l’aide d’une aire mais cette interpr´ etation n’est nullement ´ evidente.
23. On voit bien cependant, en lisant les commentaires des programmes, que la notion
d’aire est pr´ esente dans l’esprit de leurs concepteurs. Pourquoi n’ont-ils pas saut´ e le pas
en revenant ` a une d´ efinition de l’int´ egrale comme celle de 1902 ? Peut-ˆ etre qu’on ´ etait trop
proche de l’´ epoque des maths modernes, o` u l’aire avait ´ et´ e s´ ev` erement bannie.
de donner des d´ emonstrations simples et correctes de toutes les propri´ et´ es.
En fait, si l’on regarde les manuels de l’´ epoque, beaucoup pr´ esentent une introduction de l’int´ egrale et des primitives par les aires, mais avec mauvaise conscience. Dans le Transmath TCE de 1987 on commence par une introduc- tion sur les aires, on propose en travaux pratiques d’approche la preuve du fait que la d´ eriv´ ee de l’aire est ´ egale ` a la fonction, mais on d´ efinit l’int´ egrale en se conformant au programme, i.e. comme F (b) − F (a) (en admettant l’existence de F ) et pour l’aire sous la courbe, on la d´ efinit comme l’int´ egrale ! Dans le Hachette TCE de la mˆ eme ann´ ee (par ailleurs tr` es riche), on commence par donner les propri´ et´ es de l’aire (exactement comme je propose de le faire), mais on passe sous les fourches caudines du programme pour la d´ efinition de l’int´ egrale (mˆ eme si l’existence de la primitive comme aire est prouv´ ee plus loin). On trouvera au §9 l’exemple du livre de la collection Terracher.
6 Le programme de 2002 ou le cul entre deux chaises
6.1 Les changements du programme d’analyse
On peut signaler deux points importants en ce domaine : la disparition de l’in´ egalit´ e des accroissements finis (et donc des exercices sur les suites r´ ecurrentes) et l’introduction de l’exponentielle via l’´ equation diff´ erentielle.
Plus g´ en´ eralement, l’accent est mis sur les ´ equations diff´ erentielles
24avec un remarquable document d’accompagnement r´ edig´ e par les GTD (Groupes Techniques Disciplinaires) de maths, de physique et de SVT.
6.2 Sur l’int´ egrale
6.2.1 Le programme
Pour une analyse d´ etaill´ ee de ce programme, je renvoie ` a mon texte : https://www.math.u-psud.fr/~perrin/conferences.html
La critique principale des programmes de 1982 c’est que l’entr´ ee par les primitives perd tout l’aspect g´ eom´ etrique li´ e ` a la notion d’aire. Prenant acte de ce fait, le programme 2002 commence par la d´ efinition de R
ba
f(t)dt, pour une fonction continue positive, comme l’aire sous la courbe.
24. Elles seront supprim´ ees dans les programmes de 2011, encore un bel exemple d’os-
cillation excessive !
Mais cette introduction est tout de suite temp´ er´ ee par une sorte de re- mords et l’on voit r´ eapparaˆıtre les sommes de Darboux de l’´ epoque des maths modernes :
On indiquera que l’aire sous la courbe peut ˆ etre approch´ ee en l’encadrant par deux suites adjacentes en quadrillant le plan de plus en plus finement.
Exemple o` u la fonction int´ egr´ ee est en escalier. Exemple de la parabole : on fera apparaˆıtre l’int´ egrale comme limite de sommes et on admettra que cette situation est g´ en´ eralisable.
Ce paragraphe est bien peu clair ! Il y a dans la premi` ere phrase quelque chose d’ambigu : qu’a-t-on en tˆ ete exactement ? Une d´ efinition de la notion d’aire pour toutes les parties du plan ? C’est ce qu’indiquerait le mot qua- drillage, car pour l’aire sous une courbe il suffit de prendre des rectangles.
L’exemple de la parabole, au contraire, semble aller dans le sens des rec- tangles donc des sommes de Darboux. On trouve plus loin :
Les ´ el` eves ont une notion intuitive d’aire (avec la propri´ et´ e d’additivit´ e) et savent calculer certaines aires ´ el´ ementaires ; l’objectif est de leur donner un aper¸ cu de la d´ efinition et du calcul de l’aire de domaines plans li´ es aux fonctions : tout d´ eveloppement th´ eorique est exclu.
Ici on aper¸coit un objectif plus ou moins avou´ e du programme : donner un aper¸cu de la d´ efinition de l’aire (et dans l’esprit des auteurs, il n’y a de d´ efinition qu’en construisant l’aire ` a l’aide de sommes de Riemann ou autres).
Il est clair que cela ne peut que semer le trouble chez les enseignants, comme le montre l’article [7] que nous ´ evoquerons plus loin. De plus, la mention du calcul d’aire par cette m´ ethode est pour le moins discutable. Nous revenons sur tous ces points au §8.
Outre cet aspect, l’autre critique essentielle de ce programme c’est l’ar- riv´ ee beaucoup trop tardive du lien entre int´ egrale et primitive. En effet, ce point n’apparaˆıt qu’au quatri` eme paragraphe, alors qu’entre temps, apr` es quelques contorsions pour d´ efinir l’int´ egrale dans le cas d’une fonction de signe quelconque, on ´ enonce toutes les propri´ et´ es de l’int´ egrale : lin´ earit´ e, positivit´ e, ordre, relation de Chasles, in´ egalit´ e de la moyenne, et ces pro- pri´ et´ es sont toutes admises (c’est dit explicitement), alors que la formule avec la primitive permet de les d´ emontrer sans peine.
On notera aussi qu’il n’y a pratiquement plus d’allusion aux m´ ethodes de
calcul approch´ e. Cela semble doublement incoh´ erent, d’abord avec l’accent
mis sur l’utilisation de la calculatrice dans le pr´ eambule du programme, et
ensuite, avec les multiples allusions aux sommes de Riemann.
6.2.2 Discussion
Le programme 2002 a eu le m´ erite essentiel de remettre la notion d’aire au cœur de la notion d’int´ egrale. Mais il avait cependant deux d´ efauts majeurs, que l’on peut tous deux interpr´ eter en termes des mouvements de balancier des programmes.
D’abord, on a vraiment l’impression en lisant ce programme, que les au- teurs sont en permanence le cul entre deux chaises, partag´ es qu’ils sont entre des soucis contradictoires :
• l’id´ ee, qui rel` eve de la nostalgie des math´ ematiques modernes, que sans les “sommes de Riemann” il n’est pas de th´ eorie rigoureuse de l’int´ egrale (voir [7] sur ce point),
• la crainte (justifi´ ee) que cette th´ eorie soit trop difficile pour des ´ el` eves de terminale.
Nous reviendrons sur cette question au paragraphe 8.
Ensuite, ce programme a voulu se d´ emarquer du programme pr´ ec´ edent qui d´ efinissait l’int´ egrale comme diff´ erence de deux valeurs d’une primitive et c’´ etait justifi´ e. Mais comme c’est souvent le cas, la r´ eaction a ´ et´ e trop brutale et la notion de primitive a ´ et´ e indˆ ument rejet´ ee ` a la fin, ce qui oblige
`
a admettre pratiquement toutes les propri´ et´ es de l’int´ egrale et notamment la lin´ earit´ e.
Cette fa¸con d’admettre toutes les propri´ et´ es essentielles d’une notion est tr` es discutable. Les auteurs du programme ont l’air d’oublier qu’ils font des math´ ematiques. Or, en math´ ematiques on est cens´ e justifier ses affirmations, c’est mˆ eme le propre de cette discipline, ce principe pouvant ˆ etre temp´ er´ e si les r´ esultats ` a admettre sont trop difficiles et/ou si l’on peut s’en convaincre intuitivement.
Mais ici, ces deux points sont battus en br` eche. D’abord, il n’est pas vrai que les choses soient claires intuitivement. Le lecteur se convaincra que la lin´ earit´ e, en particulier, n’est pas du tout ´ evidente, mˆ eme pour les fonctions positives, sauf ` a revenir aux indivisibles de Cavalieri.
Ensuite, au contraire, si l’on a ´ etabli que l’aire est une primitive de f, le r´ esultat devient ´ evident et c’est l’un des multiples aspects qui fait que la primitive est un progr` es !
Le r´ esultat est un programme mal fichu, o` u l’on ne d´ emontre rien, o` u le lien primitive-int´ egrale arrive trop tard et o` u l’aspect num´ erique est absent.
Mais il est facile de rem´ edier ` a ces inconv´ enients
25, avec des modifications somme toute mineures et c’est ce que fera le programme suivant.
25. Il y avait tout ce qu’il fallait pour cela dans le livre de Marc Rogalski ([19]) paru en
2001.
7 Le programme 2011 : alleluia !
Sur l’int´ egrale, le programme 2011 reprend
26pour l’essentiel les remarques pr´ ec´ edentes. Comme en 2002, l’int´ egrale est introduite par les aires dans le cas des fonctions positives (et on ´ evoque les axiomes d’additivit´ e et d’inva- riance par d´ eplacement des aires), mais on fait aussitˆ ot apr` es le lien avec les primitives comme le sugg´ erait Poincar´ e en montrant que la d´ eriv´ ee de l’aire sous la courbe est ´ egale ` a la fonction. Cela permet de d´ efinir l’int´ egrale d’une fonction de signe quelconque et de prouver les propri´ et´ es de lin´ earit´ e, etc.
Les seuls points n´ egatifs de ce programme sont la disparition de l’int´ egration par parties, outil essentiel s’il en est, mais aussi le peu de place que tiennent les calculs approch´ es et la pauvret´ e des exemples d’applications, notamment en physique. Mais, ` a mon sens, c’est tout de mˆ eme le meilleur programme sur ce th` eme, depuis longtemps. Comme aurait dit Boris Vian :
C’qui prouve qu’en protestant, quand il est encore temps, On peut finir par obtenir des m´ enagements !
8 Annexe : Les sommes de Riemann ou de Darboux
Je discute
27dans ce paragraphe le rˆ ole math´ ematique des sommes de Riemann, englobant sous ce nom aussi bien les vraies sommes de Riemann que celles de Darboux
28voire une approche ´ equivalente par les fonctions en escalier. On a vu que, depuis l’´ epoque des maths modernes, les auteurs de programmes sont tiraill´ es entre leur envie d’introduire ces notions en termi- nale, parce qu’elles seraient les seules ` a en assurer la rigueur, et le sentiment frustrant que ces questions sont trop difficiles pour les lyc´ eens.
Pour avoir enseign´ e l’int´ egrale de Riemann ` a l’universit´ e, je partage en tous cas l’id´ ee que cette th´ eorie n’est pas ´ evidente, surtout ` a ce niveau, no- tamment en raison de difficult´ es techniques (on a besoin de la notion de
26. J’ai eu un ´ echo de ce programme, quand il n’´ etait encore qu’en projet, dans le cadre des consultations alibis qui pr´ ec´ ed` erent sa mise en place (j’´ etais pr´ esent au titre du comit´ e scientifique des IREM). Les auteurs du programme me dirent d’ailleurs explicitement ` a cette occasion qu’ils s’´ etaient inspir´ es de mon texte. Ma vanit´ e en fut ´ evidemment flatt´ ee, et tout ` a la joie d’ˆ etre entendu ( A ces mots le corbeau ne se sent plus de joie ...), je laissai ` passer alors sans r´ eagir l’introduction de la loi normale en terminale S. Depuis, j’ai r´ eagi vivement sur ce th` eme, voir [15]. Mais le mal ´ etait fait ...
27. Ce paragraphe est essentiellement issu du texte que j’avais ´ ecrit en r´ eaction aux programmes de 2002. J’y exprime mon opinion, que le lecteur n’est pas tenu de partager.
28. En v´ erit´ e, si l’on avait deux sous de reconnaissance, ces sommes devraient s’appeler
sommes d’Eudoxe ou d’Archim` ede.
borne sup´ erieure, il y a des difficult´ es li´ ees aux subdivisions
29, pour montrer l’int´ egrabilit´ e d’une fonction continue on a besoin de l’uniforme continuit´ e, etc.). Ce que je veux contester ici c’est l’id´ ee que cette th´ eorie doit, sinon ˆ
etre enseign´ ee au niveau du lyc´ ee, du moins ˆ etre sous-jacente dans les pro- grammes, sous peine de l` ese-math´ ematique. Pour r´ esumer mon opinion, je reprendrai la phrase de Poincar´ e ´ evoqu´ ee ci-dessus :
Tout cela a sa place dans l’enseignement des facult´ es, tout cela serait d´ etestable dans les lyc´ ees.
8.1 A quoi ¸ ` ca sert ?
Au travers de leurs apparitions dans la litt´ erature, on peut attribuer aux sommes de Riemann quatre fonctions essentielles :
• Elles permettent de d´ efinir l’int´ egrale et l’aire ( ?) et de montrer leur existence.
• Elles permettent de les calculer.
• Elles permettent de les approcher.
• Elles permettent de mod´ eliser des situations physiques.
A mon avis, en terminale, les deux premiers points sont inutiles, voire ` nocifs. Le troisi` eme est important (mais il ne n´ ecessite pas vraiment l’intro- duction des sommes de Riemann et il a malheureusement presque disparu dans les programmes actuels). Enfin le quatri` eme est essentiel aussi mais m´ erite ` a tout le moins une discussion approfondie.
8.2 Montrer l’existence de l’aire ?
Entendons-nous bien. Je suis fondamentalement d’accord avec mes coll` e- gues sur la n´ ecessit´ e de donner des d´ efinitions pr´ ecises des objets dont on s’oc- cupe. Mais, lorsqu’il s’agit, comme ici avec les aires, de notions compl` etement intuitives, avec lesquelles les ´ el` eves travaillent ` a l’´ ecole primaire et au coll` ege, la n´ ecessit´ e d’une construction ne me semble pas essentielle, une d´ efinition axiomatique me semblant suffisante.
Ainsi, ce que je conteste dans le programme 2002, c’est qu’apr` es avoir introduit l’int´ egrale par les aires, il jette aussitˆ ot une sorte de suspicion sur cette notion dans la phrase : Les ´ el` eves ont une notion intuitive d’aire (avec la propri´ et´ e d’additivit´ e) et savent calculer certaines aires ´ el´ ementaires ; l’ob- jectif est de leur donner un aper¸ cu de la d´ efinition et du calcul de l’aire de domaines plans li´ es aux fonctions. J’ai ´ et´ e confort´ e dans la crainte que j’avais que cette lecture du programme n’induise une d´ erive par la lecture
29. ` A cause de Chasles, on ne peut pas se limiter aux subdivisions r´ eguli` eres.
de l’article de Sophie Dupuy-Touzet et Pierre Lopez [7] paru en 2006 dans le bulletin de l’APM. En effet, les auteurs, soucieux de se conformer au pro- gramme, r´ epercutent dans cet article cette n´ ecessit´ e de la d´ efinition de l’aire via l’int´ egrale. Je cite, en vrac :
Or (est-il besoin de le rappeler), le calcul int´ egral ... montre (et on pourrait rajouter “surtout”) que l’on peut d´ efinir l’aire de ces surfaces.
Le calcul int´ egral n’est pas un calcul d’aire parce que sans le calcul int´ egral, les aires n’existent pas.
C’est le calcul int´ egral qui va permettre de parler de la notion d’aire.
Le calcul int´ egral devient un calcul d’aire car on dira que “l’aire sous la courbe” est d´ efinie par l’int´ egrale de la fonction ...
En lisant cet article, ´ ecrit par des gens de bonne foi, j’ai ´ et´ e catastroph´ e, car je suis en d´ esaccord total avec tout cela. Je m’explique.
8.2.1 Un premier argument : l’histoire
Les anciens ne se posaient pas la question de l’existence des aires planes, consid´ er´ ee comme allant de soi et l’on a fait des math´ ematiques jusqu’au XIX-` eme si` ecle sans s’en inqui´ eter et sans rencontrer de difficult´ e essentielle.
Comme le niveau des classes de lyc´ ee ne d´ epasse gu` ere le d´ ebut du XIX-` eme si` ecle, on doit pouvoir aussi y admettre cette existence. C’est, je pense, ce que Poincar´ e avait en tˆ ete, et je partage son point de vue. C’est d’autant plus vrai que cette notion est famili` ere aux ´ el` eves qui la manipulent depuis l’´ ecole pri- maire
30. Ce qui est important, en revanche, c’est d’expliciter les propri´ et´ es de l’aire : additivit´ e, invariance par isom´ etrie, ´ eventuellement homog´ en´ eit´ e, voir par exemple [10]. Je signale que cela n’a rien de bien nouveau : les deux premiers axiomes sont ´ enonc´ es dans Euclide !
8.2.2 Un second argument : les math´ ematiques
En v´ erit´ e, ce n’est que lorsqu’on a commenc´ e ` a manipuler des fonctions un peu bizarres qu’est apparue la n´ ecessit´ e d’une formalisation. L` a encore, Poincar´ e le dit : Pour d´ efinir une int´ egrale, nous prenons toutes sortes de pr´ ecautions ; nous distinguons les fonctions continues et celles qui sont dis- continues, celles qui ont des d´ eriv´ ees et celles qui n’en ont pas. C’est dans cette perspective que le travail de Riemann et celui de Lebesgue s’inscrivent.
N’oublions pas que l’exemple le plus simple de partie non quarrable du plan
30. C’est le mˆ eme argument qui a men´ e, pour justifier les bases de la g´ eom´ etrie
´
el´ ementaire, ` a introduire les espaces vectoriels et affines des maths modernes avec le succ` es
que l’on sait, voir §4.1.2 ci-dessus.
est l’ensemble des points ` a coordonn´ ees rationnelles du carr´ e : ce n’est pas du tout une question qui se pose pour des ´ el` eves de lyc´ ee.
J’ajoute qu’il y a une arnaque manifeste ` a pr´ etendre que les sommes de Riemann d´ efinissent les aires. Ce qu’elles montrent, c’est seulement l’exis- tence de l’aire de l’hypographe d’une fonction. Si l’on veut ˆ etre complet, il reste ` a voir l’existence de l’aire des parties du plan qui ne sont pas de ce type.
C’est essentiel du point de vue g´ eom´ etrique. D´ ej` a, il n’est pas ´ evident avec cette d´ efinition de dire ce qu’est l’aire d’un rectangle de cˆ ot´ es non parall` eles aux axes, et pourquoi elle est ´ egale au produit de ses dimensions. En parti- culier, on a besoin pour cela de l’additivit´ e de l’aire, nullement ´ evidente. De mˆ eme, pour calculer l’aire d’un segment de parabole quelconque, on effectue un changement d’axes, qui n’est justifi´ e que si l’on admet l’invariance de l’aire par isom´ etrie. Or ce point n’est pas abord´ e dans le point de vue fonctionnel (sauf pour les translations horizontales et verticales).
Ce qui pr´ ec` ede montre que, si l’on veut vraiment d´ efinir les aires planes, on ne peut pas faire l’´ economie d’une approche du type de celle que proposait Lebesgue aux professeurs de lyc´ ee de l’entre deux guerres, voir [9]. Cette d´ efinition, quand on a compris les propri´ et´ es de l’aire fournies par les axiomes, est tout ` a fait naturelle. On choisit un rep` ere, qui donne un quadrillage du plan, que l’on raffine ensuite en divisant en 10, 100, 10
n, etc. On sait d´ ej` a mesurer les aires d´ elimit´ ees par le quadrillage. Pour les autres on compte les carreaux qui sont ` a l’int´ erieur d’une partie et ceux qui la rencontrent et on a une mesure int´ erieure et une mesure ext´ erieure, qui doivent encadrer la mesure cherch´ ee (` a cause des axiomes). La d´ efinition s’impose alors : il suffit de prendre la limite commune quand n tend vers l’infini (si elle existe).
Ce qui est moins ´ evident c’est de montrer que la construction ainsi produite v´ erifie bien les axiomes voulus, mais Lebesgue le fait, voir [9].
8.2.3 Un troisi` eme argument : la logique
Le programme de 2002 a ´ et´ e ´ ecrit par des math´ ematiciens ´ eminents, mais qui, me semble-t-il, continuent ` a entretenir des illusions sur les math´ ematiques.
Il reste en filigrane dans leur d´ emarche un peu du “programme de Hilbert” de fonder rigoureusement les math´ ematiques. Pour eux, donner une d´ efinition de la notion d’aire ne signifie pas seulement en donner une d´ efinition axio- matique (c’est ce que je propose, avec l’appui de l’intuition), mais n´ ecessite de la construire. Ce souci de construction est d’ailleurs partag´ e par nombre de coll` egues de l’enseignement sup´ erieur, qui ont l’impression qu’ils ont manqu´ e
`
a leur devoir s’ils ont donn´ e aux ´ etudiants une d´ efinition axiomatique des
r´ eels, mais pas une construction de R ` a partir de Q. Je pense, au contraire,
qu’on n’a pas mieux compris les r´ eels quand on en a vu une construction par
les coupures de Dedekind ou les suites de Cauchy. De plus, je pr´ etends que cela ne peut ˆ etre, en dernier ressort, qu’une illusion. Bien sˆ ur on peut fonder les aires sur les r´ eels (via les fonctions ou les espaces vectoriels), bien sˆ ur on peut construire les r´ eels sur les rationnels, ´ elaborer ces derniers ` a partir des entiers, mais l` a, on doit bien finir par se contenter d’une th´ eorie axiomatique (sauf ` a faire appel ` a Dieu, comme Kronecker), soit qu’on s’appuie sur les axiomes de Peano, soit sur la th´ eorie des ensembles
31de Zermelo-Fraenkel.
De plus, on se heurte au th´ eor` eme d’incompl´ etude de G¨ odel : on ne peut prouver la consistance
32ni de la th´ eorie des ensembles, ni de l’arithm´ etique de Peano, au moins ` a l’int´ erieur de ces th´ eories. Au bout du compte, la quˆ ete du Graal d’une construction inattaquable des math´ ematiques se r´ ev` ele assez vaine.
Fort de cette constatation, il devient pertinent de proposer, ici comme ailleurs, l’usage d’axiomes interm´ ediaires comme ceux des aires
33. 8.2.4 Ce que je propose
Je propose donc d’adosser le programme ` a une d´ efinition axiomatique de l’aire comme application d´ efinie sur certaines parties “raisonnables” du plan et v´ erifiant additivit´ e, invariance par isom´ etrie et homog´ en´ eit´ e. Un math´ ematicien mauvais coucheur
34peut ´ evidemment m’objecter qu’il faut encore savoir ce qu’on entend par parties “raisonnables”. Je r´ epondrai qu’elles contiennent ´ evidemment les polygones, disques, segments de parabole, etc.
et, en fait, toutes les parties qu’un ´ el` eve de terminale pourra ˆ etre amen´ e ` a consid´ erer. Si le mauvais coucheur insiste, je le renverrai sans m´ enagement
`
a un th´ eor` eme (non trivial) de Banach qui affirme qu’il existe une mesure simplement additive et invariante par isom´ etrie d´ efinie sur toutes les parties born´ ees du plan
35(et qui co¨ıncide avec l’aire sur les parties quarrables). On
31. Pour une fois que je suis d’accord avec Dieudonn´ e, je ne r´ esiste pas au plaisir de le citer : Mais il convient ici comme ailleurs de d´ ebarrasser l’enseignement de la superstition consistant ` a vouloir ` a n’importe quel prix tout rattacher ` a une source axiomatique unique.
Les math´ ematiciens professionnels ont de bonnes raisons de tenir ` a ce qu’il en soit ainsi, mais ces raisons ne concernent qu’eux ; ce qui est par contre d’une importance universelle, c’est de savoir faire des d´ eductions logiques correctes ` a partir de pr´ emisses qui n’ont pas besoin d’ˆ etre n´ ecessairement sanctifi´ ees par un arbre g´ en´ ealogique remontant ` a la Th´ eorie des ensembles !
32. C’est-` a-dire montrer qu’il en existe un mod` ele ou qu’elle est non contradictoire, ce qui revient au mˆ eme par un autre th´ eor` eme de G¨ odel.
33. Cela vaut non seulement pour les aires, mais aussi pour les volumes, les moments d’inertie, etc. et aussi les cas d’´ egalit´ e des triangles !
34. J’en connais.
35. En revanche c’est faux dans l’espace ` a cause du paradoxe de Hausdorff-Banach-
Tarski.
peut donc sans aucun inconv´ enient admettre l’existence de l’aire pour les parties usuelles du plan.
Au lyc´ ee on se contentera de donner une liste de propri´ et´ es naturelles admises dont on d´ eduira les autres. Je propose une telle approche dans [10].
Elle a ´ et´ e essentiellement reprise dans le programme de 2011.
8.3 Les sommes de Riemann comme moyen de calcul ?
Le programme de 2002 sugg` ere : Exemple de la parabole : on fera ap- paraˆıtre l’int´ egrale comme limite de sommes et on admettra que cette situa- tion est g´ en´ eralisable et les manuels lui emboˆıtent le pas avec docilit´ e.
Cette proposition, pr´ esent´ ee sans discussion
36, me semble une absurdit´ e
´
epist´ emologique. Ce que propose le programme, et que pratiquaient aussi les livres de l’´ epoque maths modernes, consiste ` a revenir ` a la m´ ethode d’exhaus- tion d’Eudoxe, Euclide et Archim` ede, m´ ethode qui a men´ e ` a ces sommets des math´ ematiques de l’antiquit´ e que sont le calcul du volume de la pyramide ou la quadrature de la spirale et du segment de parabole, mais qui a ´ et´ e supplant´ ee depuis par le calcul infinit´ esimal.
Je m’explique. Si l’on m` ene le calcul dans le cadre propos´ e par le pro- gramme, disons pour calculer R
10
x
2dx, on obtient l’encadrement :
n−1
X
k=0
k
2n
3≤
Z
10
x
2dx ≤
n
X
k=1
k
2n
3. Il reste essentiellement ` a calculer la somme P
nk=1
k
2qui vaut n(n + 1)(2n + 1) et on obtient bien la limite 1/3 comme pr´ evu. Je dis que c’est exactement ce 6 que fait Archim` ede, non pas pour la quadrature de la parabole, pour laquel- le il a une autre m´ ethode, plus g´ eom´ etrique, voir [10] ou [12] mais pour la quadrature de la spirale (voir interm` ede ci-dessous ou [19]).
Qu’oublient nos auteurs de programmes ? Qu’entre temps, Newton et Leibniz sont pass´ es par l` a, avec l’invention du calcul diff´ erentiel et int´ egral et le lien entre primitive et int´ egrale qui rend trivial ce type de calcul puisqu’il le ram` ene au calcul de la primitive de x
2. D’ailleurs, ce qui ´ etait un sommet des math´ ematiques de l’antiquit´ e (la quadrature de la parabole) est maintenant un exercice pour ´ el` eves de terminale. Le fait essentiel qui explique cela, c’est que le calcul de la primitive d’une fonction continue est bien plus facile que le calcul de la somme finie analogue comme on le voit sur l’exemple pr´ ec´ edent.
36. C’est-` a-dire sans annoncer qu’on verra une m´ ethode beaucoup plus efficace pour
faire ce calcul avec les primitives.
Et ce cas n’est que le plus simple, on pensera au cas de l’int´ egrale de x
k, de
√ x, de x
α, de sin x, de ln(x) etc.
Comme je l’ai dit dans l’introduction, je consid` ere que l’invention du calcul infinit´ esimal est un des progr` es essentiels de l’humanit´ e et on aurait grand tort de s’en priver. En un mot : le continu c’est plus simple que le discret
37.
Pour revenir au programme de 2002, je trouve que prˆ oner, d` es les premi` eres lignes du programme sur le calcul int´ egral, un calcul comme celui de l’aire de la parabole par les sommes de Darboux, sans au moins un regard critique, est pour le moins maladroit. Je vois effectivement un int´ erˆ et ` a ce calcul, essentiellement historique et ´ epist´ emologique : c’est justement de servir de repoussoir et de montrer combien l’entr´ ee par les primitives est plus efficace.
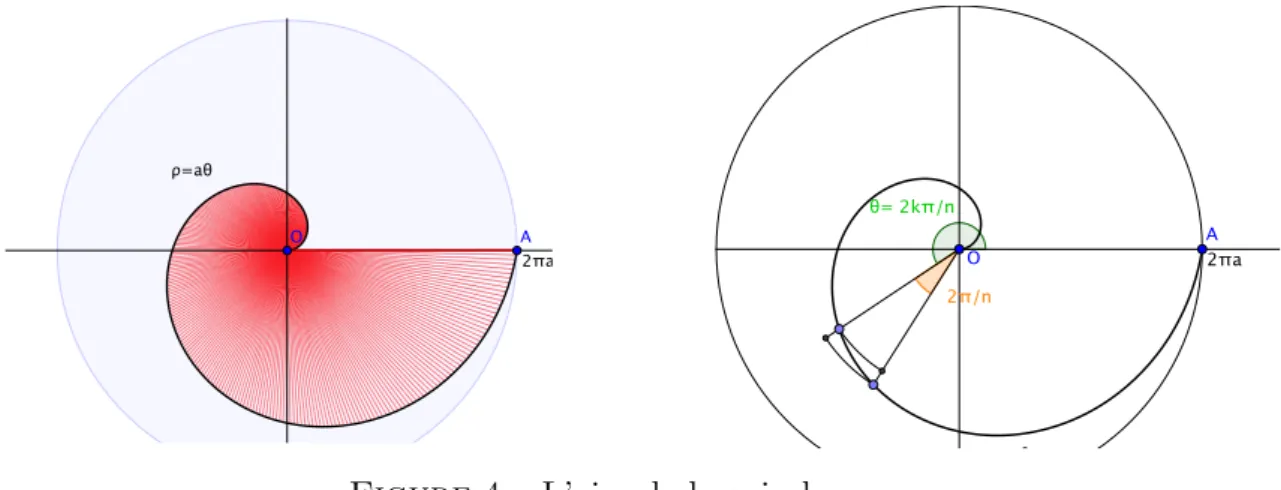
8.4 Interm` ede : Archim` ede et la quadrature de la spi- rale
8.4.1 La somme des carr´ es
Pour effectuer la quadrature de la spirale
38d’´ equation polaire ρ = aθ (ap- pel´ ee aujourd’hui spirale d’Archim` ede), Archim` ede calcule la somme S
n= P
nk=1
k
2que nous avons utilis´ ee dans le calcul de l’aire du segment de para- bole. Voil` a l’´ enonc´ e de la proposition X de son livre Des spirales (cf. [1]) :
Si des lignes en nombre quelconque, se d´ epassant l’une l’autre d’une mˆ eme grandeur, sont dispos´ ees les unes ` a la suite des autres, l’exc´ edent ´ etant d’ailleurs
´
egal ` a la plus petite ; et si on dispose un mˆ eme nombre d’autres lignes, dont chacune est aussi grande que la plus grande des premi` eres, les carr´ es des lignes ´ egales ` a la plus grande, ajout´ es au carr´ e de la plus grande ainsi qu’au rectangle d´ elimit´ e sous la plus petite et sous une ligne ´ egale ` a la somme de celles qui se d´ epassent l’une l’autre d’une mˆ eme grandeur, valent le triple des carr´ es de toutes les lignes se d´ epassant l’une l’autre d’une mˆ eme grandeur.
Il n’est d´ ej` a pas si facile de comprendre de quoi il s’agit. Le lecteur se convaincra qu’` a partir d’une suite, 1, 2, . . . , n il s’agit de montrer :
(∗) n × n
2+ n
2+ (1 + 2 + · · · + n) = 3(1
2+ 2
2+ · · · + n
2) ce qui donne la formule bien connue S
n= n(n + 1)(2n + 1)
6 .
37. Un exemple tr` es convaincant sur ce th` eme : comparer l’´ equation diff´ erentielle logis- tique et la suite du mˆ eme nom.
38. Voir l’excellent m´ emoire de M1 de Paloma Cabeza-Orcel et Da¨ ena L´ eauva [4].
La preuve est astucieuse et diff´ erente de toutes celles que je connaissais.
Bien entendu, Archim` ede l’exprime uniquement en termes g´ eom´ etriques, et sans formules, mais il est incomparablement plus commode pour nous de la donner sous forme alg´ ebrique. Voil` a ce que devient l’argument.
On ´ ecrit d’abord, pour k = 0, 1, . . . , n : n = (n − k) + k d’o` u n
2= (n − k)
2+ k
2+ 2k(n − k). En sommant, on obtient :
(n + 1) n
2= 2S
n+ 2U
navec U
n=
n
X
k=0
k(n − k) =
n−1
X
k=1
k(n − k).
On ajoute ` a 2U
nla somme T
n= 1 + 2 + · · · + n = P
nk=0
(n − k) : 2U
n+ T
n= 2
n
X
k=0
k(n − k) +
n
X
k=0
(n − k) =
n
X
k=0
(2k + 1)(n − k).
Il reste ` a montrer l’´ egalit´ e S
n=
n
X
k=0