Etude de l'effet du champ cristallin aléatoire sur des systèmes magnétiques complexes et semi-infinis

1

UNIVERSITÉ MOHAMMED V – AGDAL

FACULTÉ DES SCIENCES

Rabat

THÈSE DE DOCTORAT D’ETAT

Présentée par

Nom et Prénom : BEN AYAD MOHAMMED REDA

Discipline : Physique………

Spécialité : Physique Statistique…….………

Titre :

Etude de l’effet du champ cristallin

aléatoire sur des systèmes magnétiques

complexes et semi-infinis

Soutenue le 9/6/2012………..

Devant le jury

Président

: Benyoussef Abdelilah PES à la faculté des sciences de Rabat

Examinateurs :

Youssef El Amraoui PES et Doyen à la faculté des sciences d’ Errachidia

Mohamed Kerouad PES et Doyen à la faculté des sciences de Meknès

Lahoucine Bahmad PES à la faculté des sciences de Rabat

Hamid Ez-zahraouy PES à la faculté des sciences de Rabat

Mohammed Loulidi PES à la faculté des sciences de Rabat

Directeur de la thèse d’état :

2

Avant-Propos

Les travaux présentés dans cette thèse d’état ont été effectués dans le

laboratoire LMPHE à la faculté des sciences de Rabat sous la direction du

Professeur Abdallah El Kenz (PES, LMPHE).

Cette thèse d’état a été aussi préparée en codirection avec le Professeur

Abdelilah Benyoussef directeur du laboratoire LMPHE à la faculté des sciences

de Rabat, membre de l’Académie des sciences et technologies Hassan II et de

l’Institut de Nanomatériaux et Nanotechnologie (INANOTECH), Rabat, Maroc.

Tout d’abord je tiens à exprimer ma grande reconnaissance et ma gratitude au le

Professeur Abdallah El Kenz qui a par sa bien vaillance et son savoir a bien

voulu encadrer ma thèse d’état.

Je ne sauré oublier les concertations multiples et fructueuses. Sa

supervision professionnelle envers l’avancement des étapes des travaux a permis

à aboutir à des résultats probants.

Mes remercîments vont aussi au codirecteur le Professeur Abdelilah

Benyoussef pour son humilité et son engagement. Ces brillons conseils m’ont

été d’une grande aide pour la finalisé ce travail. Aussi je lui sais grée de me

faire l’honneur d’accepter de présider le jury de ma thèse d’état.

Mes remercîments vont aussi à la dynamique équipe des professeurs qui

forment les membres du jury :

Je tiens à saluer leurs générosités à savoir ainsi que leurs compétences :

Lahoucine

Bahmad

PES à la faculté des sciences de Rabat, Hamid Ez-zahraouy

PES à la faculté des sciences de Rabat et Mohammed Loulidi PES à la faculté

des sciences de Rabat.

Je tiens absolument à remercier les professeurs Youssef El Amraoui PES

et Doyen à la faculté des sciences d’Errachidia et Mohamed Kerouad PES et

Doyen à la faculté des sciences de Meknès d’avoir accepté d’être les rapporteurs

de ma thèse d’état.

3

Remerciements

:

Toute la grâce et louange à Allah pour m’avoir donné la force afin de

mener et achever ce travail.

.

A

ABDOU

Mes remercîment vont à Mes parents, ainsi que Ma femme et Mes

enfants, Mes beaux-parents, à toute Ma belle famille, à tous mes

amis, EL YADARI Mourad , El Filali Ahmed, Lahbib et El Harfaoui

Mohammed.

4

TABLE DE MATIERE

Introduction générale………..6

I-CHAPITRE 1 : Effet d’un champ cristallin aléatoire sur les systèmes …………..15

doubles décorés (article 1) I.1-Introduction……….……15

I.2-Formulation………16

I.3-Diagramme de phase de l’état fondamental………18

I.4-Les résultats numériques et discutions……….19

A-diagrammes de phase………19

B-courbes d’aimantation ………….……….….23

I.5-Conclusion……….28

II-CHAPITRE 2 :L’effet d’un champ cristallin aléatoire sur un modèle mixte d’Ising à spins (1/2, 3/2) (Article2)……….……….….45

II.1-Introduction………...…..45

II.2-Formulation………..……..46

II.3-Les résultats numériques et discutions………..………49

II.4-Conclusion………..………60

III-CHAPITRE 3 : L'effet du champ cristallin aléatoire sur les propriétés magnétiques d’un système semi-infini (article 3).67……….……..70

III.1-Introduction……….70

III.2-Formulation………71

III.3-Les résultats numériques et discutions……….73

III.4-Conclusion……….84

IV-CHAPITRE 4 : Etude dynamique du modèle Blume - Capel cinétique (article 4)..98

IV.1-Introduction………..…..98

IV.2- Comportements asymptotiques d’un système dynamique………..…..99

IV.2.1 Equation maitresse……….….100

IV.3-Modèle et équation de mouvement……….….102

IV.4-Discussions des résultats numériques………...104

5

IV.4.2 Diagramme de phase………..109

IV.5 Conclusion………...113

CONCLUSION GENERALE……….127

Liste des publications & des communications………..130

6

7

L'étude théorique des matériaux magnétiques est apparue avec succès à la fin du XIXe siècle et le début du XXe.

C’est Pierre Curie (1859 - 1906) introduisit ces classes des matériaux en fonction de leur comportement sous le champ H. Ainsi, l’histoire des transitions de phase paraît avec la thèse de Pierre Curie intitulée : « propriétés magnétiques des corps à diverses températures ».Pierre Curie a fait des recherches sur une vingtaine de substances différentes dans un domaine de température allant près de 1400°C. Il arrive à une conclusion que les propriétés des corps paramagnétiques sont intimement liées. Les expériences de Pierre Curie montrent qu’une substance ferromagnétique se transforme progressivement quand on la chauffe, en une substance faiblement magnétique. Ce passage appelé transition de phase a bouleversé en particulier les expérimentateurs et les théoriciens pendant cette décennie. Maintenant reste à définir, à étudier et différencier ces transitions de phases par les physiciens théoriciens et les expérimentateurs.

Chose qui a était entamé par, Ehrenfest, Ising et Landau pour essayer d’étudier les types des transitions de phase possibles. En 1933, Ehrenfest a généralisé le concept du changement de phase. Il proposa d’appeler transition du premier ordre les transitions qui s’accompagnent de discontinuité dans les dérivés premières de l’énergie libre et celle du deuxième ordre qui s’accompagnent de discontinuités dans les dérivés seconds de l’énergie libre. Landau introduit, suivant la valeur de la température, l’idée d’une brisure de symétrie dans le paramètre d’ordre qui est nul à haute température et non nul à basse température. Il donna aussi la nature d’une transition à la continuité du paramètre d’ordre de ce paramètre (transition de phase de second-ordre) ou à la discontinuité (transition de phase de premier ordre). Pour expliquer le ferromagnétisme Ising en 1925 a introduit un modèle sur réseau carré. Depuis, différents modèles ont été introduits (Blume Capel, Ashkin -Teller, Blume-Emery-Griffiths, Potts..). Onsager a réussis à résoudre exactement en 1944 le modèle d’Ising [1] et Baxter a résolu le modèle de Potts à deux dimensions [2].

La complexité des calculs exacte pose problème. Pour remédier à cet obstacle il faut passer par des méthodes d’approximations. En 1907, P. Weiss en s’appuyant sur la théorie de Langevin proposa la plus ancienne de ces méthodes. Cette méthode suppose que tout atome paramagnétique est porteur d’un moment magnétique permanent qui a toutes les orientations possibles sauf en présence d’un champ extérieur qui l’oriente, donne une forme mathématique

8

aux idées qualitatives de P. Curie en inventant la théorie du champ moyen. Cette méthode est la plus simple des approximations. Elle consiste à considérer un seul spin en remplaçant les interactions avec le reste du système, par un champ effectif [3].

Récemment, N. Boccara 1983 a mis en évidence une technique, portant le nom de la méthode de l’amas fini (MAF) [4,5], qui est basée sur l’idée du champ effectif. C’est une méthode qui a la simplicité de la méthode du champ moyen mais qui donne de meilleurs résultats qualitatifs et quantitatifs. Elle est aussi assez simple et systématique et permet de calculer les diagrammes de phase des modèles étudiés. Elle s’applique aussi à une vaste classe de système dans lesquels le désordre est décrit par des variables aléatoires discrètes. La méthode de l’amas fini a été utilisée avec succès dans l’étude de plusieurs modèles d’Ising désordonnés et pour différentes valeurs de spins définis sur des réseaux infinis et semi-infinis. A. Benyoussef et N. Boccara [5] ont calculé, à différents ordres d’approximation, diverses grandeurs telles que des températures critiques, des seuils de percolation et ils ont montré qu’ils convergent vers les résultats exacts connus. T. Kanesyoshi [6, 7,8] a proposé une méthode d’approximation, appelé théorie du champ effectif, qui donne les mêmes équations d’état que celles données par la méthode de N. Boccara. On utilise l’opérateur différentiel comme outil mathématique en l’introduisant dans l’identité de Callen [9].

Autres que les méthodes du type champ moyen, K.G Wilson, en 1971, a introduit une méthode très puissante [10] utilisant le groupe de renormalisation pour les comportements critiques. Par la suite Th. Nieumeijer et J.M.J Van Leuwen ont introduit la méthode du groupe de renormalisation dans l’espace réel, généralisée par différents auteurs, pour étudier les systèmes désordonnés. Elle consiste à transformer l’Hamiltonien qui décrit le système en un autre par une transformation qui laisse invariante la fonction de partition [10]. Ainsi, plusieurs techniques de calcul en découlent telles que la décimation, transformation par Bloc [11,12], transformation de Megdal-Kadanoff [13,14]. Beaucoup d’autres méthodes de normalisation ont été définies. En particulier la renormalisation phénoménologique [15], qui ressemble aux méthodes du groupe de normalisation. Seulement cette méthode utilise les lois d’échelles de la longueur de corrélation des systèmes de différentes tailles et ne permet de déterminer le flot dans l’espace des paramètres de l’Hamiltonien comme dans le cas des méthodes du groupe de normalisation.

Pour tenir compte des fluctuations négligées par ces méthodes de type champs moyen, on applique d’autres méthodes numériques qui tiennent compte des fluctuations tel que : Finite-Size –Scaling, la simulation Monte-Carlo…

9

L'étude expérimentale d'une transition de phase ne se distingue pas fondamentalement de celle d'un matériau : on étudie les propriétés d'un matériau, sa structure et les relations entre les propriétés et la structure. Dans une transition de phase, on pourra donc étudier les propriétés d'un matériau de part et d'autre du point de transition de phase, le changement de structure à la transition et les relations entre ce changement de structure et l'évolution des propriétés.

Il existe une très grande diversité de méthodes physiques pour étudier les propriétés d'un matériau : mesures calorimétriques pour mesurer les chaleurs spécifiques, analyse thermique différentielle pour détecter la fusion, rhéologiques pour mesurer la viscosité et le module d'élasticité, optiques pour mesurer la biréfringence, etc.

Les études de structure des matériaux, et par conséquent de leur modification au cours des transitions de phases, peuvent être réalisées par des méthodes classiques de microscopie, en particulier par microscopie électronique, par diffraction des rayons X mais aussi par Résonance Magnétique Nucléaire (RMN) et diffusion des neutrons. On peut également mettre en évidence et suivre les phénomènes de nucléation par certaines de ces méthodes, comme la cristallisation d'un liquide à l'aide de la microscopie électronique.

On obtient aussi de très nombreuses informations sur un matériau subissant une transition de phase, en particulier une transition du deuxième ordre (ou continue), à l'aide d'expériences de diffusion de particules. Ces particules peuvent être des électrons, des photons (lumière visible ou rayons X), des phonons (ondes acoustiques), des neutrons.

Les neutrons sont des particules particulièrement intéressantes car ils pénètrent dans la plupart des matériaux ce qui n'est pas le cas des photons (du moins ceux associés à la lumière visible).

Depuis plusieurs années, les recherches en sciences des matériaux visent à élaborer de matériaux constitués par les composés intermétalliques lanthanide/fer afin de se servir pour le stockage d’information. Ce sont des composés où le couplage magnétique entre le fer et la terre rare est antiparallèle, conduisant à un système ferrimagnétique. Par conséquent, un sérieux intérêt a été destiné, récemment, à l’étude des propriétés magnétiques des systèmes ferrimagnétique. Etant donné leur importance dans des applications technologique [16].

Un système réel étudié expérimentalement est limité dans l’espace par des surfaces et des volumes. Dans les surfaces, les propriétés physiques peuvent être différentes de ces systèmes physiques où le volume et la surface coexistent. Ces types de systèmes sont appelés

10

des systèmes semi-infinis. Leurs propriétés magnétiques ont été largement étudiées par des techniques expérimentales et théoriques en particulier des études ont été faites sur les systèmes d’Ising-1/2 semi-infini.

Actuellement, la physique des transitions de phase à l’équilibre est bien comprise dans le cadre de la physique statistique à l’équilibre. Cependant, les mécanismes derrières les phénomènes hors équilibre ou les transitions des phases dynamiques n’ont pas encore été explorés rigoureusement et une théorie appropriée pour aborder ces mécanismes reste toujours non développer. D’où, plus d’efforts doivent être déployé sur l’analyse et l’investigation de ces phénomènes dynamiques. Particulièrement, la détermination des transitions de phase dynamiques et la construction des diagrammes de phase doivent être effectué dans le futur. Les transitions de phase dynamiques ont été initialement trouvées en utilisant MFA, pour le modèle d’Ising cinétique spin-1/2 sous l’effet du champ oscillant dépendant du temps via la dynamique stochastique type Glauber [17].

Ces dynamiques stochastiques fournie une façon simple pour introduire la cinétique hors équilibre dans les modèles comme Ising et les systèmes d’Ising mixtes, qui n’ont pas une dynamique déterministe. Plusieurs études ont indiqué que les dynamiques stochastiques, malgré leurs simplicités, peuvent décrire d’une manière correcte les phénomènes hors équilibre. Les transitions de phase dynamique ont été trouvées dans des systèmes réels [18]. Le modèle d’Ising cinétique a été appliqué avec succès dans les ferromagnétiques nanométriques [19].

L’objectif de cette thèse est donc l’étude théorique et numérique de divers phénomènes physique induits par la présence d’un champ cristallin aléatoire, d’un champ magnétique oscillant externe, et d’autres interactions dont les détails seront exprimés et analysés le long du manuscrit. Dans toute la première partie, nous nous plaçons dans le cadre de la physique statistique et dans chacun des cas, nous avons choisi des descriptions énergétiques (Hamiltonien), principalement à base d’interactions de paires à courte portée sur un réseau. Les intérêts de cette description simplifiée sont multiples. D’une part, il est possible, dans un cadre simple, d’obtenir des résultats pour les différents paramètres de contrôles et ainsi de comprendre comment la présence de ces variétés de paramètre influent sur les propriétés critiques, tricritiques et magnétiques du système. D’autres part, lorsque les interactions sont à court portée, nous pouvons analyser le comportement d’un grand nombre d’atomes ce qui n’est pas précise dans le cadre d’une description plus précise des interactions (mécanique quantique et calcul ab-initio).Cette description phénoménologique du magnétisme

11

localisé exposée le long de la première partie à 1'avantage d'être pédagogique et relativement simple. Cependant, il est intéressant d’évoquer que divers substances relèvent d'une autre représentation, à savoir le modèle du magnétisme itinérant: ce sont des électrons partiellement ou totalement délocalisés qui sont alors responsables du magnétisme de la substance. Ce modèle sera décrit dans la deuxième partie de ce mémoire de thèse. Toutefois, qu'il s'agisse de magnétisme localisé ou itinérant, les phénomènes de base seront les mêmes.

Ce manuscrit est reparti de la façon suivante :  Etude statiques des systèmes magnétiques  Etude dynamiques des systèmes magnétiques La partie statique contient trois chapitres de cette thèse :

I. une étude théorique globale des transitions de phases dans le modèle d’Ising modélisant un système ferrimagnétique double décoré. Pour des valeurs des spins σ = ± 1/2 et S = ± 1.0 nous avons obtenu une variété de diagrammes de phase, à l’aide des outils d’investigation de la physique statistique, notamment la théorie du champ moyen….

II. Le but de ce travail est d’étudier, en utilisant l’approximation de champ moyen (MFA), l’influence de désordre de champ cristallin sur les diagrammes de phase et l’aimantation d’un système ferrimagnétique d’Ising-spin mixte, dans lequel les deux sous réseaux interpénétrant ont des valeurs de spin σ = ±½ et S = ± 3/2, ±½. Le résultat le plus intéressant ressortent de cette étude est l’apparition de trois types différents de diagrammes de phase.

III. Dans le troisième chapitre nous avons étudié les systèmes semi-infinis(MAF).

Le but de ce travail est d’étudier, en utilisant l’approximation de champ moyen (MFA), l’influence de désordre de champ cristallin sur les diagrammes de phase et l’aimantation d’un système semi-infini qui est un système réel étudié expérimentalement. Ce système est limité dans l’espace par une surface et un volume. La surface a des propriétés physiques qui peuvent être différentes de celles à l’intérieur du système. Donc on est obligé d’avoir des systèmes physiques où le volume et la surface coexistent (surface spin = ½ et volume spin = 1).

12

IV. Dans la deuxième partie dynamique, nous avons étudié l’effet du champ cristallin sur les états stationnaires du modèle Blume -Capel cinétique spin-1, sous l’effet d’un champ externe dépendant du temps en utilisant la dynamique stochastique de Glauber.

13

Références:

[1] L. Onsager, Phys. Rev.65, 117(1944) [2] P. J. Baxter, J. Phys.6, L445 (1973) [3] P. Weiss, J. Phys. Radium 4,661(1907) [4] N. Boccara, Phys. Lett. : 94A, 185(1983)

[5] A. Benyoussef and N. Boccara, J. App, Phys.55, 6, (1985)

[6] R. Honmura and T. Kaneyoshi, J. Phys.C: Solid State Phys.Vol.12, 3979(1979) [7] T. Kaneyoshi, I.P. Fittilpaldi, R. Honmura and T.Manbe, Phys.Rev.B24, 481(1981).

[8] T.Kaneyoshi, Z.Phys.B60, 35(1985)

[9] H.B. Callen, Phys.Lett, Vol.4, b°3, 161(1963) [10] K.G.Wilson, Phys. Rev. B4, 3184(1971) [11] L.P.Kadanoff, Phys.Rev.Let 34, 1005(1975)

[12] T.H.Niemeijer and J.M. Van Leuwen, Phase transition and critical phenomena, Vol.6, eds. Dom and Green (London Academic Press 1976)

[13] L.P.Kadanoff, Ann.Phys.NY 100,359(1976) [14] A. Migdal, Sov. Phys. JETP 42, 743(1976)

[15] A. El Kenz, thèse de 3ème _{Cycle (1986)}

[16] J.T. Dawley, and B.J.J Zelinski, Intergrated Ferroelectrics, 17, 339 (1997)

[17] Magnetic Molecular Materials, in: D. Gatteshi, O. Kahn, J. S. Miller, F. Palacio (Eds.), NATO ASI Series, Kluwer Academic, Dordrecht, 1991.

[18] R.J. Glauber, J. Math. Phys. 4, 294 (1963).

[19] M. Acharyya and B. K. Chakrabarti, in Annual Reviews of Computational Physics I, edited by D. Stauffer ~World Scientific, Singapore (1994); W. S. Lo and R. A. Pelcovits, Phys. Rev. A 42, 7471 (1990);

14

15

CHAPITRE-I : EFFET D’UN CHAMP CRISTALLIN

ALEATOIRE SUR LES SYSTEMES DOUBLES

DECORES

I.1-Introduction

L’étude des propriétés magnétiques des systèmes ferrimagnétiques ont eu beaucoup d’attention récemment vu leur importance dans des applications technologiques et industrielles [1]. Tout d’abord on va aborder les systèmes magnétiques décorés. On définit le cas ferrimagnétique une substance antiferromagnétique dans laquelle les différents sous réseaux ne se composent pas exactement de sorte qu’il en résulte une aimantation spontanée. Un tel arrangement magnétique peut exister lorsque les sous-réseaux ne sont pas identiques du fait que le nombre d’atomes de chaque sous réseau est différent et/ou qu’ils sont constitués d’atomes différents (et donc de moments différents).

Le ferrimagnétisme a été prévu par Louis Néel avant d’être confirmé par l’expérience. La magnétite, Fe3O4 ou Fe2+O2-, 2 Fe3+3O2- est une substance ferrimagnétique : la moitié des ions Fe3+ et les ions Fe2+ qu’elle comporte formant le premier sous-réseau, tandis que les ions Fe3+ restant formant le second. Des avancés expérimentales ont été réalisées dans la synthèse des ferrimagnétiques [2]. Théoriquement, les propriétés magnétiques de ces systèmes ont été largement étudiées par différentes techniques, à savoir, approximation du champ moyen (MFA) [3], théorie du champ effectif [4,5] finite cluster approximation [6], groupe de renormalisation [7,8] et simulation Monte-Carlo [9,10].

Néanmoins, dans un matériau ferrimagnétique comme le YIG (Yttrium Iron Garnet), deux moments inégaux et interagissant de manière antiferromagnétique, peuvent donner lieu à une aimantation totale nulle en dessous de la température de Curie. Un tel point est appelé point de compensation [11,12]. Ainsi, ce point particulier apparait lorsque les aimantations des sous-réseaux s’annulent exactement. Un tel cas est observé dans le composé Gd3Fe5O12. Cela survient en raison des dépendances différentes des sous-réseaux magnétiques vis-à-vis de la température. Des études théoriques récentes ont prouvé la possibilité de plusieurs points de compensation dans des systèmes ferrimagnétiques différents [13-15].

16

Ainsi, les auteurs ont montré que ce modèle révèle deux températures de compensation si le spin décoré S est entier [16, 17,19]. Cependant, une seule température de compensation et présente lorsque le spin S est demi-entier. Ces résultats ont été aussi trouvés dans d’autres travaux où les auteurs ont étudiés exactement des modèles d’Ising ferrimagnétiques [18,20]. Les modèles de spin des systèmes décorées ont été originalement introduits dans la littérature par Syozi [21] et ont été étudiés durant des années comme des modèles montrant le ferrimagnétisme [22]. En effet, les systèmes d’Ising décorés ferrimagnétiques sont composés de deux sous réseaux L1 et L2, où le sous réseau L1 est occupé par les atomes A de spin le sous réseau L2 est composé d’un point de décoration sur chaque lien du réseau L1, est composé par les atomes B de spin S (S>1/2). Le comportement de plusieurs modèles décorés a été examiné par différentes techniques mathématiques, et aussi avec quelques résultats exacts [21-31].

Le but de ce chapitre est d’examiner les propriétés magnétiques (les températures critiques, les températures de compensation, les diagrammes de phases et les courbes d’aimantations) pour un système ferrimagnétique double décoré dans lequel les deux atomes magnétiques A et B ont respectivement des spins σ = ± 1/2 et s = ± 1.0. Nous étudions ces propriétés magnétiques en utilisant l’approximation du champ moyen.

I.2- Formulation

L’Hamiltonien, dans ce cas, est défini comme suit :

H= -J1Σ(i,j) σiσj + J2Σ(i,j) σiSj - J3Σ(i,j) SiSj - Σ4Ni=1 Δi Si2 (1) N est le nombre total d’atomes. Les spins

2 1  

i

 et S=1,0 sont localisés, respectivement, sur les sous réseaux L1 et L2. J1 (J1>0), J2 (J2>0) et J3 (J3>0) sont les interactions d’échange entre les atomes, respectivement A-A, A-B et B-B. La sommation est considérée uniquement sur les spins pairs proches voisins et  est le champ cristallin aléatoire obéissant à la loi de _i probabilité [32-35] :



 







17

Figure 1: Le schéma représente le double décoré carrée. Les cercles pleins et vides désignent respectivement les atomes (atome A) spin -1/2 et spin-1 (atome B).

Une distribution de probabilité analogue a été utilisée pour étudier le comportement critique des mélanges 3He – 4He dans les médias aléatoires (aerogel) modélisé par le spin -1 Blume –Capel modèle. Dans ce modèle, une valeur négative du champ cristallin représente le champ à l’interface pore-grain et pour une valeur positive est un champ essentiel qui contrôle la concentration des atomes 3He [36-38]. Le principe variationel est basé sur l’inégalité de Gibbs-Bogoliubov pour l’énergie libre par site il est décrit par [39-41]:

F G= -T LogZ0 + <H –H0>0 (3) Les aimantations mσ et ms et l’énergie libre g par site g = (G/N) sont données, après l’intégration en utilisant la loi de probabilité définie dans l’équation (eq.2):

mσ = (1/2) tanh[2ß(J1mσ –J2ms )] (4) ms= -(1/2){[ 2sinhß(J2mσ-J3ms)/(2coshß(J2mσ – J3ms) + e-ßΔ(1+α)))]

+[2sinhß(J2mσ-J3ms)/(2coshß(J2mσ – J3ms) + e-ßΔ(1-α)))} (5) g=G/N= -T{Ln(2cosh2ß(J1mσ – J2ms)+ 2 [Ln(1+2eßΔ(1+α) coshß(J2mσ-J3ms)) +Ln(1+2eßΔ(1-α) coshß(J2mσ –J3ms))]} + 2J1mσ2 -4J2mσms +2J3ms2 (6)

18

Les solutions des équations (Eq.4) et (Eq.5) ne sont pas uniques. Les plus stables sont ceux en minimisant l’énergie libre (Eq.6), tandis que les autres paramètres sont instables. Si les paramètres d’ordres sont continués (discontinues), les transitions sont de seconde (première) ordre.

I.3-Diagramme de phase de l’état fondamental :

La comparaison des différentes valeurs de l’énergie correspondant aux différentes configurations nous permet d’avoir le diagramme de phase à T=0°K. Quatre cas ont été distingués en fonction de la valeur α.

i /– Pour α≤ (s/2(r+s)), une transition du premier ordre entre les phases (mσ = -1/2, ms = 0) et (mσ = -1/2, ms = 1) apparait pour d= -(r + s)/2. La transition du premier ordre linéaire disparait pour α = 0 si s = 0. Le dernier cas correspond au modèle Ising ferrimagnétique décoré [5]. D’autre par, quand s augmente, la valeur de α atteint le maximum α=1/2. ii/ Pour s/2(r + s) < α <1, la phase ferrimagnétique partielle (mσ = -1/2, ms =1/2) apparait. Par

conséquence, deux lignes de transitions de premier ordre entre les phases (mσ = -1/2 , ms =0 ) les (mσ = -1/2 , ms = 1/2 ) et les phases (mσ = -1/2 , ms = 1/2 ) et la phase (mσ = -1/2 , ms = 1 ) apparaissent respectivement pour d= -( r + s/2)/2(1-α) et d= -( r + 3α/2)/2( 1 + α ). iii/ Pour α=1 , la phase ( mσ = -1/2 , ms = 0 ) disparait et après il y a l’apparition d’une ligne

transition pour d= - ( r + 3s/2)/(2( 1 + α )) et une séparation des phases ferrimagnétiques (mσ = -1/2, ms = 1/2) et (mσ = -1/2, ms = 1).

iv/ Pour α _> 1, la phase partiellement ferrimagnétique survient à des les valeurs positives de d et deviennent stable pour une grande valeur du champ cristallin et la région de contact de la phase ferrimagnétique. Cependant, on obtient deux lignes de transitions: la première est entre les phases (mσ = -1/2 , ms = 1/2 ) et (mσ = -1/2 , ms = 1 ) sur la ligne d=-( r + 3α/2)/(2( 1 + α )) suivis par la ligne d=-( r + 3s/2)/2( 1 – α ) séparant les phases (mσ = -1/2 , ms = 1) et (mσ = -1/2 , ms = 1/2 ). Dans la Fig.2, on observe le diagramme de l’état fondamental (d, α) plane pour r = 0.5 et s = 0.2.

19 0 0.5 1 1.5 2 2.5 -5 -4 -3 -2 -1 0 1 2 3 4 5  d Fig.2 (1/2,0) d=-(2r+3s)/4(1+) (1/2,-1/2) (1/2,-1/2) d=-(2r+3s)/4(1-) (1/2,-1) d=-(r+s)/2 d=-(2r+s)/4(1-) r=0.5 s=0.2

Figure 2: le digramme de phase de l’état fondamental est établi dans le plan ( d , α ) pour r = 0.5 et s = 0.2. Les

20

I.4- Les résultats Numériques et discutions

4-1- Diagrammes de Phase

Dans cette partie nous allons présenter des résultats du modèle d’Ising ferrimagnétique double décoré à deux dimensions. Pour cela nous avons fait une résolution numérique des eqs.4-6. Nous avons obtenu des résultats très intéressants donnant plusieurs variétés de digrammes de phase dans le plan ( tc = Tc/J1 , d = Δ/J1 ). En effet, la température critique en fonction du champ cristallin pour r = 0.5 et s= 0.2 est donnée pour des valeurs sélectionnées α = 0.15 (Fig.3a), α = 0.7 (Fig.3b), α = 1. (Fig.3c) et α = 1.5 (Fig.3d). Dans la Fig.3a, la phase (mσ = -1/2, ms = 0 ) et la phase ferrimagnétique (mσ = -1/2 , ms = 1 ) apparaissent à basse température et sont séparées par une ligne du premier ordre. Cette ligne se termine par un point critique isolé ( tic = 0.049 ,dic = -0.35). Un passage continu, entre les deux phases, apparait à une température supérieure à tic. La ligne de transition de second ordre séparant les phases paramagnétiques (mσ = 0 , ms =0 ) qui est représentée à haute température. En plus, Il faut remarquer que la température de transition de phase de second ordre à gauche de la ligne de transition du premier ordre est plus basse que celle donnée par celle à la droite. Effectivement, la température de transition augmente avec la valeur du spin. Dans la Fig.3b, le diagramme de phase présente la phase ferrimagnétique partielle (mσ = -1/2, ms = 1/2) à basse température, entre deux phases (mσ = -1/2, ms = 0) et (mσ = -1/2, ms = 1). Ces dernières phases sont séparées par deux lignes de transitions du premier-ordres. La première les phases (mσ = -1/2 , ms =0 ) et (mσ = -1/2 , ms = 1/2) et la deuxième sépare les phases (mσ = -1/2 , ms =1/2 ) et (mσ = -1/2 , ms =1). Ces deux lignes se terminent par des points critiques isolés respectivement ( tic = 0.032, dic = -1. ) et ( tic= 0.053, dic= -0.23 ). La région de la phase ferrimagnétique s’allonge quand α croit, alors que la phase (mσ = -1/2, ms = 0) disparait pour α = 1 (Fig.3c). Cependant, la ligne de transition du premier-ordre apparait entre les phases

21

( mσ = -1/2 , ms = 1/2 ) et (mσ = -1/2 , ms = 1 ) et se termine par le point critique isolé ( tic = 0.025, dic = -0.2 ).

Pour α > 1, la phase partiellement ferrimagnétique apparait quand les valeurs du champ cristallin sont positives. Ensuite, la phase ferrimagnétique est inséré, à basse température, dans la phase partiellement ferromagnétique comme il est indiqué dans la figure 3d. Par ailleurs, la région de la phase (mσ = -1/2, ms = 1) se rétrécit si α augmente et les deux lignes de transition du premier ordre entre les deux phases ( mσ = 1/2 , ms = 1/2 ) et (mσ = -1/2 , ms = 1 ) s’approchent. Dans la Fig.3d, les points critiques isolés sont indiqués, pour α = 1.5, par ( tic = 0.1 , dic= -0.16 ) et ( tic = 0.055 , dic = 0.8 ).

22

Figure 3: La température critique tracée en fonction de d pour r = 0.5 et s = 0.2 et les valeurs sélectionnés de α = 0.15 (a), α = 0.7 (b), α = 1 (c) et α = 1.5 (d). Les lignes pointillés et lignes pleins représentent respectivement les lignes de transitions du second-ordre et les lignes de transitions du

premier-ordre. Les cercles vides et pleins représentent points critiques isolés et les températures de compensations.

A haute température, une ligne de transition du second-ordre apparait et sépare la phase ferrimagnétique de la phase paramagnétique (mσ = 0, ms = 0). On peut remarquer, que cette ligne a un maximum sur la région de la phase (mσ = -1/2, ms = 1). Afin de localiser la région où apparait le phénomène de compensation, nous avons tracés dans la Fig.3 la température de compensation en fonction du champ cristallin.

La température de compensation tcomp = Tcomp/J1, qui se trouve en dessous de la température réduite critique tc , est déterminée à partir de la condition m=0 ( m = mσ + 2 ms

-8 -6 -4 -2 0 2 4 6 8 10 0,0 0,2 0,4 0,6 0,8 1,0 1,2 o =0.15 r=0.5 s=0.2 (0,0) (-1/2,1) (-1/2,0) Fig.3a tc d -10 -5 0 5 10 0,0 0,2 0,4 0,6 0,8 1,0 1,2 (0,0) (-1/2,1) (-1/2,1/2) (-1/2,0) o o Fig.3b tc d =0.7 r=0.5 s=0.2 -15 -10 -5 0 5 10 15 0,0 0,5 1,0 (0,0) (-1/2,1) (-1/2,1/2) o Fig.3c tc d =1.0 r=0.5 s=0.2 -4 -3 -2 -1 0 1 2 3 4 0,0 0,2 0,4 0,6 0,8 1,0 1,2 Fig.3d (-1/2,1/2) (-1/2,1) (-1/2,1/2) (0,0) o o tc d =1.5 r=0.5 s=0.2

23

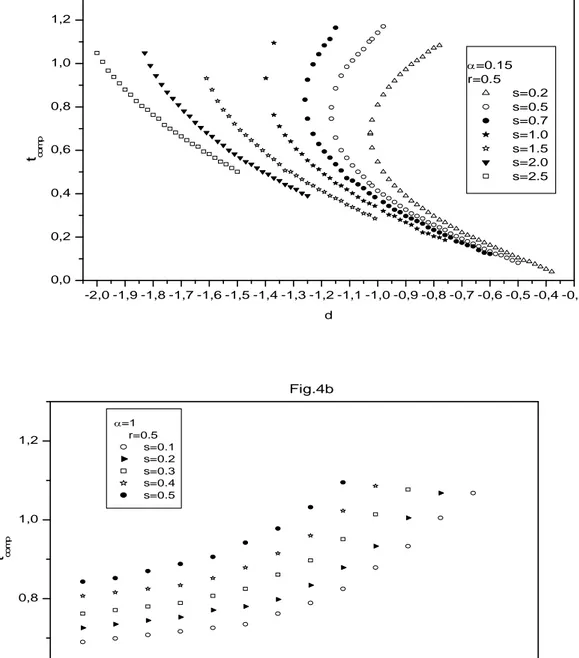
)/3. La figure 4 montre la température de compensation réduite tcomp comme fonction du champ cristallin d pour r=0.5 pour des valeurs de α=0.15 Fig.4a et α=1 Fig4b. Nous pouvons distinguer deux cas. Le premier correspond à 0<α<1 (Fig.4a). Dans ce cas, deux points de compensation peuvent se produire pour de petites valeurs de s. Lorsque le paramètre s augmente, une seule compensation de température apparaît. Le phénomène de compensation disparaît pour de très grandes valeurs de s. Par ailleurs, en conformité avec les systèmes décorés, la température de compensation disparaît lorsque r croit. Il est important de noter que le phénomène de double compensation apparaît dans une région de la phase (mσ=-1/2 ,mS=0) dans une région séparant cette phase et les phases ferromagnétiques (mσ= -1/2 , mS=1 ) ou (mσ= -1/2 , mS=1/2 ). Par conséquent, pour 0<α< 1, les deux pics de champ cristallin réduit, surtout d(1+α) et d(1-α) sont positifs et, par conséquent favorisent le (mσ= -1/2 ,mS=0).

Dans le second cas où α≥1 Fig.4b, Le phénomène de compensation se produit, mais un seul point de compensation apparaît pour les petites valeurs de s. S’il devient grand le phénomène disparaît. Ces résultats sont également donnés pour α>1. En fait, pour α≥1, il existe une concurrence entre les valeurs positives d (1+α) et la valeur négative d (1-α) du champ cristallin. Les valeurs d (1+α) et d (1- α) favorisent les états S=1et S=0, d’une manière respective, et par conséquence l'état s=1/2 apparaît et il est plus stable. Ainsi, la phase (mσ= -1/2 ,mS=0) disparaît et aussi le phénomène de double compensation.

4-2 Les propriétés magnétiques

Le comportement de l'aimantation mσ, mS et m, en fonction de la température réduite et le champ de cristal réduit, sont obtenues en résolvant numériquement les équations 10-12. Par conséquent, la Fig.5, tracée pour α=0.15, r=0.5et s=0.2, représente l’aimantation en fonction de la température pour d=0.88 . Dans la Fig.5a les aimantations mσ et mS commencent respectivement par -1/2 et 0, et disparaissent à une température de transition de second ordre. Alors, l'aimantation totale m présente deux points de compensation. Ces résultats sont en accord avec ceux donnés dans (les figures 3 et fig4a).

24 -2,0 -1,9 -1,8 -1,7 -1,6 -1,5 -1,4 -1,3 -1,2 -1,1 -1,0 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3 0,0 0,2 0,4 0,6 0,8 1,0 1,2 Fig.4a t co m p d =0.15 r=0.5 s=0.2 s=0.5 s=0.7 s=1.0 s=1.5 s=2.0 s=2.5 -2,0 -1,5 -1,0 -0,5 0,6 0,8 1,0 1,2 Fig.4b t com p d =1 r=0.5 s=0.1 s=0.2 s=0.3 s=0.4 s=0.5

Figure 4: La température de compensation tracée en fonction du champ cristallin réduit pour r = 0.5, α = 0.15 (a), α =1 (b) et les valeurs sélectionnées de s.

A basse température, (fig5b) montre que m saute de 0 à 1 et ensuite donner l'essor à une température de transition du premier ordre entre les phases (mσ=-1/2, mS=0) et (mσ= -1/2, mS=1) à une température t=0.023 inférieure à la valeur correspondant au point critique isolé tic. Un passage continu entre ces deux phases se produit pour les t=0.05 ce qui est supérieur à tic. La fig6, les aimantations mσ, mS et m sont représentés pour α =0.7, r=0.5 et s=0.2. La

25

( fig7a) tracée pour d= -1.3, le phénomène double compensation de température se produit. Par ailleurs, les aimantations mσ et mS commencent respectivement pour -1/2 et 0 .

0,5 1,0 1,5 -0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 m  m s m Fig.5a M a g n e ti z a ti o n t =0.15 r=0.5 s=0.2 =-0.88 -3,0 -2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 -0,6 -0,4 -0,2 0,0 0,2 0,4 0,6 0,8 1,0 Fig.5b m  m s M a g n e ti z a ti o n d =0.15 r=0.5 s=0.2 t=0.007 t=0.05

Figure 5: Les aimantations mσ, ms, et m en fonction de la température réduite et du champ cristallin réduit pour α = 0.15, r = 0.5, s = 0.2 et d = -0.88 (a), t = 0.02 et t = 0.05 (b).

26

Ce comportement est en conformité dans la fig3a. Cependant, à basse température, la dépendance des aimantations mσ et mS en fonction du champ cristallin réduit sont représentés pour t=0.0226, 0.035 et 0.06 (fig6b). En fait, dans le premier cas pour une température de (t=0.0226) inferieure que les deux points critique isolés (voir fig3b), nous pouvons montrer une transition du premier ordre successive entre les phases (mσ= -1/2, mS=0 ) et (mσ= -1/2 ,mS=1/2 ) et entre les phases (mσ= -1/2 , mS=1/2 ) et (mσ= -1/2 ,mS=1 ). Un passage continu se produit entre les phases ( mσ= -1/2 , mS=0 ) et (mσ= -1/2 , mS=1/2 ) à la température supérieur au premier point critique isolés.

0,5 1,0 1,5 -0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 m_ ms m Fig.6a M a g n e ti z a ti o n t =0.7 r=0.5 s=0.2 d=-1.3

Figure 6a: Les aimantations mσ, ms et m en fonction de la fonction de T et d pour α = 0.7, r = 0.5, s = 0.2 et d = -1.3 (a), t = 0.0226, t = 0.035 et t = 0.06 (b).

27 -1,6 -1,4 -1,2 -1,0 -0,8 -0,6 -0,4 -0,2 0,0 0,2 0,4 -0,6 -0,4 -0,2 0,0 0,2 0,4 0,6 0,8 1,0 =0.70 r=0.5 s=0.2 t=0.0226 t=0.0350 t=0.060 m_ m_s Fig.6b M a g n e ti z a ti o n d

Figure 6b: Les aimantations mσ, ms et m en fonction de la fonction de T et d pour α = 0.7, r = 0.5,

s = 0.2 , t = 0.0226, t = 0.035 et t = 0.06 (b).

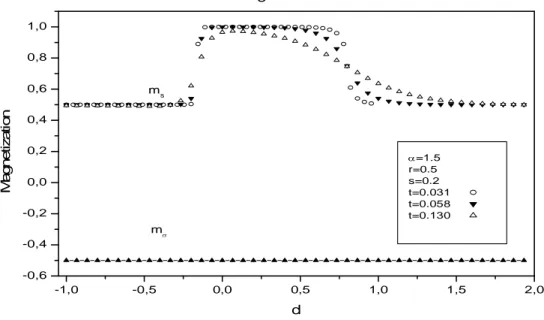
Pour la température t=0.06. Un passage continu apparaît entre les phases (mσ= -1/2 , mS=1/2 ) et (mσ= -1/2 , mS=1 ). Ces résultats sont également donnés dans fig7 pour α=1.5, r= 0.5 et s=0.2. En effet, une température de transition successifs de premier ordre, un passage continu et deux passages successifs continu, entre le (mσ= -1/2 , mS=1/2 ) et (mσ= -1/2 , mS=1) apparaît pour t=0.031, 0.058 et 0.13 d’une manière respective.

-1,0 -0,5 0,0 0,5 1,0 1,5 2,0 -0,6 -0,4 -0,2 0,0 0,2 0,4 0,6 0,8 1,0 =1.5 r=0.5 s=0.2 t=0.031 t=0.058 t=0.130 m m_s Fig.7 M a g n e ti z a ti o n d

Figure 7: Les aimantations mσ et ms, la dépendance de la réduction du champ cristallin d pour α = 1.5, r = 0.5, s = 0.2 et t = 0.031, t = 0.058 et t = 0.13

28

I.5- Conclusion

Les effets de champ cristallin aléatoire sur les propriétés magnétiques du modèle d'Ising ferrimagnétique doublement décorées sont étudiés en utilisant l'approximation de champ moyen. Nous avons étudié en détail le diagramme de phases de l'état fondamental où la phase partiellement ferrimagnétique (mσ= -1/2 ,mS=1/2) apparaît.

L'existence de cette phase présente les différents types de diagrammes de phase à température finie qui sont représentés pour s=0.2 et r=0.5. Par ailleurs, les points critiques isolés critiques sont également donnés.

Le phénomène de compensation apparaît dans ce système et en particulier le système présente des points double compensation pour r et s inférieur à un (r , s < 1). Notre discussion a été complété par l’étude de la dépendance des aimantations mσ, mS et m en fonction de t et d.

29

References:

[1] Magnetic Molecular Materials, in : D. Gatteshi, O. Kahn, J. S. Miller, F. Palacio (Eds.), NATO ASI Series, Kluwer Academic, Dordrecht, 1991.

[2] H. Tamaki, Z.J. Zhong, N. Mastsumoto, S. Kida, M. Koikawa, N. Achiwa, Y. Hashimoto, H. Okawa, J. Am. Chem. Soc. 114 (1992) 6974;

H. Okawa, N. Matsumoto, H. Tamaki, S. Kida, M. Ohba, Mol. Cryst. Liq. Cryst. 233 (1993) 257.

[3]T. Kaneyoshi, J. C. Chen, J. Magn. Magn. Mater. 98 (1991) 201.

[4]I. P. Fittipaldi, A. F. Siqueira, J. Magn. Magn. Mater. 54-57 (1986) 694. [5]T. Kaneyoshi, Solid State Commun, 70 (1989) 975.

[6] N. Benayad, A. Klumper, J. Zittartz, A. Benyoussef, Z. Phys. (B) 77 (1989) 339. [7]S. L. Schofield, R.G. Bowers, J. Phys. A 13 (1980) 3697.

[8]N. Benayad, Z. Phys. (B) 81 (1990) 99.

[9]G. M. Buenda, M. A. Novotny, J. Zhang, Computer simulations in condensed matter physics VII,, in: D. P. Landau, K.K. Mon, H. B. Schuttler(Eds.), Springer, Berlin, 1994;

G. M. Zhang, C. Z. Yang, Phys. Rev. (B) 48 (1993) 9452.

[10]G. M. Buenda, M. A. Novotny, J. Phys. : Condens. Matter 9 (1997) 5951. [11]L. Néel, Ann. Phys. Paris 3 (1948) 37.

[12]A. Herpin, Thèorie du magnétisme, Saclay, Presses Universitaire de France, 1968. [13]T. Kaneyoshi, J. Phys. : Condens. Matter 5 (1993) L501.

[14]T. Kaneyoshi, J. Phys. : Condens. Matter 6 (1994) 10691. [15]T. Kaneyoshi, Phys. Rev. (B) 52 (1995) 7304.

[16] A. Dakhama, Physica A 252, 225 (1998). [17] M. Jascur, Physica A 252, 207 (1998).

[18]J. Strecka and M. Jascur, J. Magn. Magn. Mater. 260, 415 (2003). [19]S. Lackova and M. Jascur, Acta, Phys. Slovaca. 48, 623 (1998). [20]M. Jascur and J. Strecka, Phys. Lett. A 258, 47 (1999).

30

[22]I. Syozi, in: C. Domb, M. S. Green (Eds.), Phase Transition and Critical Phenomena, vol. 1, Academic Press, New York, 1972, pp. 269-329.

[23] M. E. Fisher, Phys. Rev. 113 (1959) 969. [24]A. Dakhama, Physica (A) 252 (1998) 225. [25]M. Jascur, Physica (A) 252 (1998) 207.

[26]J. Strecka, M. Jascur, J. Magn. Magn. Mater. 260 (2003) 415. [27]S. Lackova, M. Jascur, Acta Phys. Slovaca 48 (1998) 623. [28] M. Jascur, J. Strecka, Phys. Lett. A 258 (1999) 47.

[29] A. Benyoussef, A. El Kenz and M. El yadari M. J. Condensed matter (2007) 71-77.

[30] A. Benyoussef, A. El Kenz and M. El yadari, Physica B 393 (2007) 204–212. [31] A. Benyoussef, A. El Kenz, M. El Yadari and M. Loulidi, Int. J. Mod. Phy. B Vol. 23, No. 24 (2009) 4963-4976.

[ 32 ] N. Boccara, A. El Kenz and M. Saber, J. Phys: Condens. Matter 1, 5721(1989) [ 33 ] L. Bahmad, A. Benyoussef and A. El Kenz ,Phys.Rev. B 76, 094412(2007) [ 34 ] L. Bahmad, A. Benyoussef and A. El Kenz ,Physica A 387,825 (2008)

[ 35 ] A. P. Vieira, J.X. de Carvalho and S.R. Salinas , Phys. Rev. B 63, 184415 (2001) [ 36 ] A. Maritan, M. Cieplak, M.R. Suift , F. Toigo and J.R. Banavar, Phys.Rev. let. 69,221(1992)

[ 37 ] C. Buzano , A Maritan and A Pelizzola J. Phys. Condens. Matter. 6, 327 (1994) [ 38 ] N.S. Branco and B.M. Boechat, Phys. Rev. B 56,11673 (1997)

[ 39 ] N.N. Bogoliubov , J. Phys. (USSR) 11, 23 (1947) [ 40 ] R-P- Feynmann, Phys. Rev. 97 ,660 ( 1955)

[ 41] J.J. Binney, N.J. Dowrick, A. J. Fischer and M.E.J. Newman “ the theory of Critical phenomena”, Clarendon Press (1992)

45

CHAPITRE II

ALEATOIRE SUR UN MODELE MIXTE D’ISING A SPINS (1/2, 3/2)

II.1- Introduction

Dans cette partie nous avons abordé l’étude des propriétés magnétiques des systèmes d’Ising ferrimagnétiques mixtes. Où les spins  = ±½ et S= (±3/2, ±1/2) sont placés,

respectivement, sur les sous réseaux L1 et L2.

Nous étudions les propriétés magnétiques d’un système d’Ising Ferrimagnétique¸ dans laquelle les deux sous-réseaux L1 et L2 sont occupés par des spins , ±1/2 et des spins S,

(±3/2, ± 1/2) ; en présence d’un champ cristallin aléatoire en utilisant l’approximation du champ moyen et la méthode de simulation Monte Carlo.

Récemment, de nombreux auteurs ont étudié, expérimentalement et théoriquement, les propriétés magnétiques des spins mixtes et des spins S>1/2 de système d’Ising sous l’effet du champ cristallin.

Ainsi, les effets du champ cristallin sur la température de transition ont été étudiés par plusieurs méthodes, telles que la théorie du champ effectif [1-4] l’approximation de l’amas fini [5] la théorie du champ moyen[6], la méthode de groupe de renormalisation Migdal Kadanol [7] et la méthode variationnelle [8]. Néanmoins, certains désaccords entre les études théoriques, tels que l’existence de points tricritiques ont eu lieu. Des études expérimentaux ont montré que les composés Mn Ni (EDTA)- 6H2O est un bon exemple d’un système du spin mixte [9].

D’autre part, d’importants progrès ont été réalisés dans la synthèse de deux et trois dimensions ferrimagnétiques, tels que 2d ferrimagnétiques organométalliques [10,11] et des réseaux 2d des matériaux métalliques mixtes [p(phéryl)] [Mncr(oxales)3]r [12]. D’autres intérêts dans les modèles de spins mixtes d’Ising peuvent être liés à la modélisation des structures magnétiques appropriés pour décrire un ferrimagnétisme de certaines classes des matériaux isolants. En effet, les systèmes mixtes offrent des modèles simples mais très intéressants pour étudier les matériaux magnétiques moléculaires et les matériaux d’enregistrement magnéto-optique [13,14]. En plus, l’apparition de plusieurs points de compensation dans une variété de systèmes ferrimagnétiques a été soulignée théoriquement [15,16]. Puisque l’ordre ferrimagnétique joue un rôle important dans ces matériaux, l’investigation sur le ferrimagnétisme dans des systèmes des spins mixtes est rapidement devenue un domaine d’intérêt. Puisque ces systèmes se composent de deux sous-réseaux interpénétrant et non équivalents, ils ont une symétrie transrationnelle inférieure a leurs homologues à spin-unique.

D’autre part, de nombreuses méthodes différentes ont été employées dans l’étude du système mixte à spin 1/2 et spin 1 [17,18] et ce système a été résolu exactement dans des cas particuliers. Toutefois, de nouvelles propriétés magnétiques et des comportements de

46

compensation sont trouvés pour les spins mixtes en présence d’un champ cristallin [19] comme ils ont été prédits par la théorie de ferrimagnétisme de Néel [20].

L’approche de la théorie du champ-moyen, basé sur l’inégalité de Bogolyoubov pour l’énergie libre des Gibbs ont montré que les diagrammes de phase obtenue présentent une variété de points multi critiques, tels que les points tri critiques et les points critiques isolées. D’autre part, nous avons montré dans certains travaux récents [22,23] l’existence des propriétés intéressantes dans le comportement d’aimantation et les diagrammes de phase en présence d’un champ cristallin aléatoire.

II.2- Méthode et Modèle

La méthode MFA est utilisée pour étudier le comportement des systèmes spin complexes tels que dans notre cas les modèles d’Ising mixtes ferrimagnétiques. Dans cette étude le modèle mixte se compose de deux réseaux interpénétrant. L’un de ces sous-réseaux a des spins  prend les valeurs ± ½ et l’autre sous-réseau a des spins S qui peuvent

prendre quatre valeurs : ±3/2 et ±½. Les spins S ont seulement comme proches voisins les spins  et vice versa. L’interaction entre spin S et  est supposé être un échange

antiferromagnétique

L’Hamiltonien, dans ce cas, est défini comme suit : N/2





N est le nombre total des sites du réseau. Le paramètre d’échange d’interaction J est supposé, être positif. La première sommation n’est effectuée que sur les paires proches voisins de spins et Δi est un champ cristallin aléatoire distribué selon la loi de probabilité [22,25] .



 







Où α est une constante positive.

Le principe variation el basé sur l’inégalité de Gibbs-Bogolyubov pour l’énergie libre par site est décrit par [29,31]

(3)

On peut désigner par h0 et hs les champs moléculaires associés à des paramètres d’ordre mσ = (σ)0 et ms = (S)0, respectivement, exprimés comme :

47

(4)

(5)

Où z est le nombre des voisins les plus proches.

L’Hamiltonien effectif du système est donnée par

(6)

La fonction de partition générée par l’ Hamiltonien ci-dessus est donnée par : (7)

Où T est une température absolue et β = 1/T. La constante de Boltzmann a été fixée à l’unité.

Après l’intégration sur la distribution de probabilité l’énergie libre par spin est exprimée en :

(8) Afin d’étudier l’aimantation du système, m_et ms sont définis en minimisant l’énergie libre.

(9) Et

(10) Où

48

Dans les équations ci-dessus, et dans toutes celles qui suivent, t et d désignent respectivement la température réduite T/J et le champ cristallin réduit Δ/J. Le nombre de coordination z est fixé à 4 (réseau carré).

Les solutions des équations (9) – (10) ne sont pas uniques, les solutions stables sont ceux qui minimisent l’énergie libre de l’équation (7), tandis que les solutions ne sont pas stables. Si l’ordre des paramètres sont continués (discontinues), les transitions dont de second (première) ordre.

Le diagramme de phase de l´état fondamental du système sous investigation est illustré dans Fig. 1. En effet, en fonction des valeurs de α ≥0 et le champ cristallin réduit d. les équations 10 et 11 conduisent à trois solutions : (mσ = -1/2, ms = 3/2), (mσ = -1/2 , ms = 1/2 ) et (mσ = -1/2 , ms = 1). En comparant les énergies de toutes les configurations, nous avons établi le diagramme de phase à l´état fondamental. Ce diagramme de phase est établi dans le plan réduit de (d, α). On peut distinguer quatre cas :

Figure 1 : diagramme de phase de l’état fondamental établi dans le plan (d,α). Pour les basses températures les phases suivantes sont stables (

m

m

49

1- Pour α = 0, un point de transition du premier ordre entre la phase (mσ = -1/2 , ms = 1/2 ) (mσ = -1/2 , ms = 3/2 ) et la phase (mσ = -1/2 , ms = 1/2 ) suivant à d = + 1.

2- Pour 0 < α < 1, deux lignes de transition du premier ordre apparaissent : l´une est entre la phase (mσ = -1/2, ms = 3/2) et la phase (mσ = -1/2, ms = 1) séparées par la ligne d´équation

d = z/[4(1 + α)] et l´autre entre la phase (mσ = -1/2, ms = 1) et la phase (mσ = -1/2, ms = 1/2) séparées par la ligne d´équation d = z/[4(1 - α)] .

3- Pour α = 1, un point de transition du premier ordre entre la phase (mσ = -1/2, ms =3/2) et la phase ferrimagnétique (mσ = -1/2, ms = 1) et apparaît à d= 1/2.

4- Pour α > 1, deux lignes de transition du premier ordre entre la phase (mσ = -1/2, ms =1) et la

phase (mσ = -1/2 , ms = 3/2 ) et la phase (mσ = -1/2 , ms = 1 ) apparaissent respectivement à

d = z/[4(1 - α)] et d = z/[4(1 + α)] ,

Il est intéressant de noter que pour d = 0, seule la phase (mσ = -1/2 , ms = 3/2) est stable à T=0 K, et α = 0 correspond au modèle de spin mixte (mσ = 1/2, ms = 3/2) avec un champ

cristallin constant.

II.3-Les résultats numériques et discussions :

Dans cette section, une discussion détaillée traitant les diagrammes de phase à température finie est présentée. A cet effet, les équations (9), (10) et (11) sont résolues numériquement. Une riche variété de diagrammes de phase est observée à la fois en faisant varier α dans le plan ( tc = Tc/j , d ), et d dans le plan (tc, α). La température critique est tracée en fonction de d pour α = 0 (fig.2a), α =0.5 (fig.2b), α = 1 (fig.2c) et α = 2 (fig.2d) dans la figure 2a, la phase paramagnétique (mσ = 0 , ms = 0) et les phases ferrimagnétiques

(mσ = -1/2 , ms = 3/2) et (mσ = -1/2 , ms = 1/2) sont séparées par une ligne de transition du second ordre.

Une ligne de transition du premier ordre qui sépare les phases ci-dessus est observée à une température très basse. Cette ligne de transition du premier ordre est terminée par un point critique isolé situé à (dtr =1 , ttr =0.06). Au-dessus de ce point, un passage continu se produit entre les deux phases ferrimagnétiques. Tandis que pour α = 0.5 (fig.2b) deux lignes de transition du premier ordre apparaissent à basse température. La première sépare les phases (mσ = -1/2 , ms = 3/2) et (mσ = -1/2 , ms = 1) et se termine à un point critique isolé situé à

50

ferrimagnétiques (mσ = -1/2 , ms = 1) et (mσ = -1/2 , ms = -1/2) et se termine en un point

critique isolé situé à : (dtr = 2 , ttr = 0.04)

Dans la figure 2c, tracée pour α = 1 , la phase (mσ = -1/2 , ms = 1/2) est absent à basse température et la seule ligne de transition du premier ordre, présente dans cette région,

Figure 2. La température critique est tracée en fonction de d pour α = 0 (a), α =0.5 (b), α = 1 (c) et α = 2 (d) Les transitions de phases du second ordre sont tracées en ligne pleines, du premier ordre en pointillés

et les cercles qui représentent les points critiques isolés.

sépare les phases (mσ = -1/2 , ms = 3/2) et(mσ = -1/2 , ms = 1) et se termine en un point critique isolé situé au (dtr = 0.5 , ttr = 0.09).

Dans la figure 2d, le système présente deux lignes de transition du premier ordre, à très basse température, se terminant par deux points critiques isolés : la première à (d = -1, t = 0.11) et la deuxième situé à (d =1/3, t = 0.19). Les deux lignes séparent respectivement les phases (mσ = -1/2 , ms = 1) et (mσ = -1/2 , ms = 3/2) , et les phases (mσ = -1/2 , ms = 3/2) et (mσ = -1/2 , ms = 1).

C´est très intéressant de noter que nos résultats concernant l´apparence de la ligne de transition du premier ordre à basse température terminée par un point critique isolé est en accord avec d´autres travaux tels que MFA [6] et Monte Carlo [32,33].

L´énergie libre et l´ entropie sont tracées en fonction de d pour t = 0.035 et les deux valeurs α = 0 et 1 respectivement dans les figs.3a et b respectivement. Pour les lignes de

51

transition de second ordre, l´énergie libre totale et l´entropie sont tracées en fonction de la température, pour α = 0.25 et d = -3 (voir Fig., 3c). L´entropie varie d´une façon discontinue à une température de transition du second-ordre.

Figure 3. L´énergie libre et l´ entropie sont tracées en fonction de d pour t = 0.035 et les deux valeurs α = 0 et 1 respectivement dans (a) et (b). Pour les lignes de transition de second ordre, l´énergie libre totale et l´entropie sont tracées en fonction de la température, pour α = 0.25 et d = -3 (c). L´entropie varie d´une façon

52

Par conséquent, la chaleur spécifique présentera une discontinuité à cette température de transition. Effet, afin de décrire l´effet du paramètre α, nous traçons dans la fig.4, les températures de transition pour plusieurs valeurs du champ cristallin. L´énergie libre et l´ entropie sont tracées en fonction de d pour t = 0.035 et les deux valeurs α = 0 et 1 respectivement dans les figs.3a et b respectivement. Pour les lignes de transition de second ordre, l´énergie libre totale et l´entropie sont tracées en fonction de la température, pour α = 0.25 et d = -3 (voir Fig., 3c). L´entropie varie d´une façon discontinue à une température de transition du second-ordre. Par conséquent, la chaleur spécifique présentera une discontinuité à cette température de transition. Afin de décrire l´effet du paramètre α, nous traçons dans la fig.4, les températures de transition pour plusieurs valeurs du champ cristallin.

En effet, pour d =2 (fig.4a) montre l´existence d´une ligne de transition du second ordre entre les phases paramagnétique et ferrimagnétiques et une transition du premier ordre entre les phases ferrimagnétiques (mσ = - 1/2, ms = 1/2 )et (mσ = - 1/2, ms = 1 ) terminé à un point critique isolé, (α = 1.5, t = 0.055).

53

Tandis que pour d = 0 (fig.4b) la ligne de transition du second ordre séparant la phase ferrimagnétique de la phase paramagnétique est indépendante de α en raison de l´absence du champ cristallin. Une ligne de transition du premier ordre qui sépare les phases (mσ = -1/2 , ms = 3/2), et (mσ = -1/2 , ms = 1) est obtenue pour d = -1 comme il est montré

dans la fig.4c, et se termine à un point critique isolé (α =2, t =0.09).

Dans cette section, nous concentrons notre intérêt sur les aimantations en fonction de la température et du champ cristallin qui caractérisent les différentes phases. Pour des valeurs des températures fixes. La figure 6a-c montre la dépendance des aimantations en fonction de d pour α= 0, α= 0.5 et α=1. Dans la figure 6.a, l’aimantation ms montre, respectivement un saut et un passage continu de 3/2 à 1/2 à des températures inférieurs et supérieurs à la température qui correspond au point critique isolé. La figure 6b. montre un double saut dans l’aimantation ms, à une température très basse, de 3/2 à 1 et de 1 à 1/2 , et un passage continu à une température supérieur à la température qui correspond aux points critiques isolées. Le même comportement ms, trouvés dans les Figures 6a et 6b, est représenté aussi dans la Fig. 6c pour α=1. Ceci est en accord avec la figure 2c. Le comportement réentrant indiqué dans Fig. 2d est bien illustré dans Figs. 7a et 7b, où les aimantations mσ et ms sont tracées, pour α =2 à deux températures t = 2.2 et t= 2.3 respectivement.

54 .

Figure 5.Diagrammes de phases tracés dans le plan (Δ, J ) pour une très basse température t = 0.025 pour α = 0.5 (a), α = 1 (b) et α = 2 (c).

55

La figure (8a, b) montre les aimantations mσ , ms et M= (mσ + ms )/2 comme une

fonction de α respectivement pour d= 2, t=2 et d=-1, t=2.5. La figure 8a montre que pour les valeurs positives du champ cristallin, l´effet de l´augmentation des valeurs α est de favoriser la phase ordonnée dans une région de température inférieure à tc. Pour une valeur négative du champ cristallin, ce phénomène est inversé comme il est montré dans la figure 8b, tracée pour d=-1. On peut noter que les résultats trouvés dans Fig. 8a et b sont en bon accord avec celles illustrées dans Fig.4a et c respectivement.

Afin de confirmer l´apparition de la phase partiellement ferrimagnétique (mσ = -1/2 , ms = 1 )trouvés à partir des calculs de MFA, les simulations de Monte Carlo mis

en œuvre sous l´algorithme de Métropolies, ont été utilisé.

En effet, un réseau carré de taille linéaire L=180 avec des conditions aux limites périodiques ont été envisagées. Les premières 20.000 MCS (Les étapes de Monte Carlo) jusqu´à que le système entre dans un régime stationnaire sont jetés.

Puis plus de 10.000 MCS ont été utilisées pour calculer les moyennes des quantités d´intérêt, notamment les aimantations des sous-réseaux par spin, (mσ) = (1/N) Σiσi et

56

57

Figure 7. Les aimantations mσ , ms et M= (mσ + ms )/2 en fonction de d pour α = 2 pour les températures t = 2.2 (a) et t= 2.3 (b) respectivement.

58

Figure 8. Les aimantations mσ , ms et M= (mσ + ms )/2 en fonction de α pour des valeurs fixes de d (d= 2, t = 2) (a) et( d = -1, t= 2.5) (b) respectivement.

59

La figure 9 montre les aimantations des sous réseaux pour α= 0.5 et d= 0.5 (a), d=1(b) et d= 3(c). On voit clairement sur la figure 9a-c que les aimantations des sous- réseaux ms commence à T=0 K à ms=3/2 et1 et 1/2 respectivement.

Figure 9. Les aimantations mσ et ms en fonction de t pourune valeur fixe α = 0.5 pour les valeurs de (d = 0.5) (a) ,( d = 1 ) (b) et ( d = 3) (c) respectivement.

Ceci est en accord avec le diagramme de phase de l´état fondamental (Fig.1) et avec les résultats de données par le calcul MFA.

60

II.4

- C o n c l u s i o n

Nous avons étudié les propriétés magnétiques d’un système d’Ising Ferrimagnétique¸ dans laquelle les deux sous-réseaux interagissant ont des spins σ, ±1/2 et des spins S, (±3/2, ± 1/2) dans la présence d’un champ cristallin aléatoire dans le cadre de l’approche de champ moyen. Les résultats obtenus, en utilisant l’approche de champ moyen et la méthode de simulation de Monte Carlo, montrent l’apparition d’une nouvelle phase ferrimagnétique. (mσ = - 1/2, ms = 1). Par conséquent¸ trois types, de diagramme de phase ont été donnés.

D´autre part, le phénomène de compensation apparait dans le système. Cela est du au fait le spin ferrimagnétique mixte σ = 1/2, s = 1 présente un phénomène de compensation comme indiqué dans d´autres travaux est également investigué. Les comportements de l’aimantation comme une fonction des paramètres α et d, sont également étudiées.

61

References:

[1] T. Kaneyoshi, Physica A 153, 556 (1988) [2] T. Kaneyoshi, J. Magh. Mater. 92, 59 (1990)

[3] A. Benyoussef, A. El Kenz, T. Kaneyoshi, J. Magn. Magn. Mater. 131, 173, (1994) [4] A. Benyoussef, A. El Kenz, T. Kaneyoshi, J. Magn. Magn. Mater. 131, 179 (1994) [5] N. Benayad, A. Klumper, J. Zittartz, A. Benyoussef, Z. Phys. B 77, 333 (1989) [6] O.F. Abubrig. D. Horvath. A. Bobak, M. Jascur, physica A. 296, 437 (2001). [7] N. Benayad, J. Zittartz, Z. Phys. B. 81, 107 (1990)

[8] J. W. Turcker, J.Magn. Magh. Mater. 237, 437 (2001)

[9] M. Drillon, E. Coronado, D. Beltran, R. Georges, J. Chem. Phys. 79, 440 (1983). [10] H. Tamaki, Z. J. Zhong, N. Matsumoto, S. Kida, M. Korkawa, N. Archiwa, Y. Yashimoto, H. Okawa, J. Ann. Chem. Soc. 114, 6974 (1992).

[11] H. Okawa, N. Matsumoto, H. Tamaki, S. Kida, M. Ohba, Mol, Cryst. Lig. Cryst, 223, 257 (1993)

[12] C. Mathoniere, C.I, Nutall, S.G. Carlin, P, Day, Inorg. Chem, P. Day, Inorg. Chem 351, 201 (1996)

[13] E. albayrak, Physica A 375, 174 (2007)

[14] J. Li, G. Wei, A. Du, Physica, B. 368, 121 (2005) [15] T. Kaneyoshi, Phys. Rev. B 52, 7304 (1995) [16] M. Jascur, Physica A 252, 217 (1998)

[17] A. Dahama, Physica A 252, 225 (1998)

[18] J. Octman, W. Zheng, Physica A 328, 185 (2003)

[19] S. Yana. L. Liua, J. Magh. Magn. Mater ; 312, 285 (2007) [20] A. Bobak, M. Jascur, Phys, Rev. B 51, 11533 (1995) [21] A. Bobak, F.O. Abubrig, Phys. Rev. B 68, 224405 (2003)

[22] L. Bahmad, A. Benyoussef, A. El Kenz, Phys. Rev. B 76, 094412 (2007). [23] L. Bahmad, A. Benyoussef, A. El Kenz, Physica. A 387, 825 (2008)

[24] N. Boccara, A. El Kenz, M. Saber, J. Phys. Condens. Matter 1, 5721 (1980) [25] A.P. Vieira, J.X. de Carvalho, S.R. Salinas, Phys. Rev. B 63, 184415 (2001) [26] A. Maritan, M. Cieplak, M.R. Swift, F. Toigo, J.R. Banavar, Phys. Rev. Lett. 69, 221 (1992).

62

[27] C. Buzano, A. Maritan, A. Pelizzola, J. Phys. Condens. Matter 6, 327 (1994). [28] N.S. Branco, B.M. Boechat, Phys. Rev. B 56, 11673 (1997)

[29] N.N. Bogliubov, J. Phys (USSR) 11, 23 (1947) [30] R.P. Feynmann, Phys, Rev. 97, 660 (1955).

[31] J.J. Binney, N.J. Dowrick, A.J. Fisher, M.E.J. Newman, The Theory of Critical Phonomena, Clarendon, Press, 1992.

[32] D. Peno Lara, J.A. Plascak, Physica A 260, 443 (1998) [33] G. Wei, Q. Zhang, Y. Gu, J. Magn. Magn, 301 ; 245 (2006).