Analyse / 3e  / 20-21

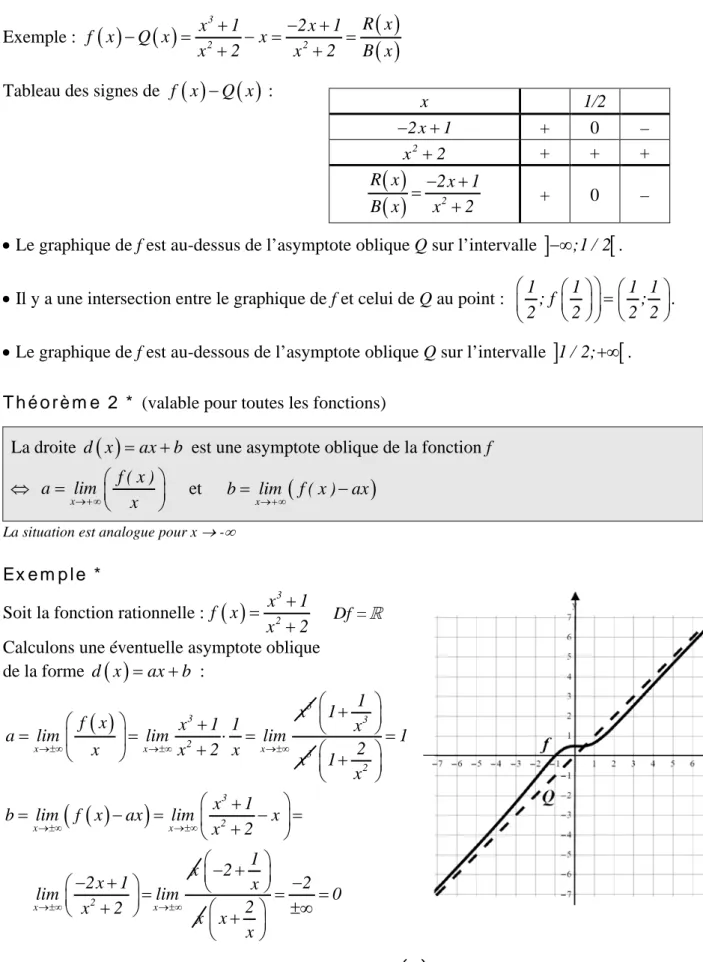
ANALYSE

3

ème

_année

1.1 Introduction

1

1.1.1 Rappels sur les fonctions

1

1.1.2 Fonctions par morceaux

4

1.1.3 Terminologie et symboles utilisés en lien

avec les énoncés Mathématiques

7

1.1.4 Ce qu’il faut absolument savoir

12

1.2 Limite d'une fonction

13

1.2.1 Introduction

13

1.2.2 Propriétés des limites

18

1.2.3 Calculs de limites

20

1.2.4 Ce qu’il faut absolument savoir

30

1.3 Asymptotes

31

1.3.1 Asymptotes verticales

31

1.3.2 Asymptotes horizontales

32

1.3.3 Asymptotes obliques

33

1.3.4 Ce qu’il faut absolument savoir

40

1.4 Fonctions continues

41

1.4.1 Introduction

41

1.4.2 Propriétés des fonctions continues

45

1.4.3 * Approximation des zéros d’une fonction *

52

1.5 Calcul différentiel

55

1.5.1 Introduction

55

1.5.2 Approximation polynomiale du premier ordre

59

1.5.3 Relation entre continuité et dérivabilité

62

1.5.4 Fonction dérivée

65

1.5.5 Règles de dérivation

68

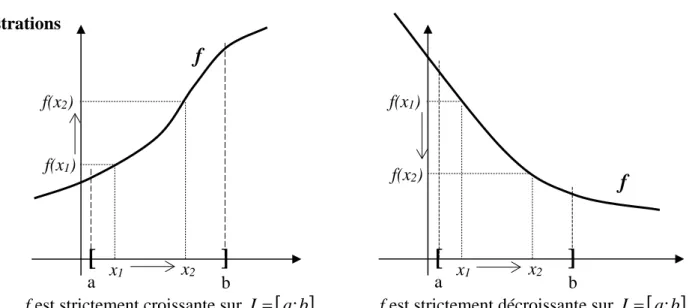
1.5.6 Croissance, décroissance et extremums

d'une fonction

85

1.5.7 *Concavité, convexité, points d’inflexions

et dérivées d’ordre supérieur *

89

1.5.8 Étude de fonctions

93

1.5.9 Les théorèmes de Rolle et de Lagrange

106

1.5.10 Problèmes d'optimisation

112

1.5.11 Ce qu’il faut absolument savoir

122

AVANT-PROPOS

• Ce document a été conçu pour l’enseignement des mathématiques dispensé au Collège de

Genève en troisième année ; il traite de l’analyse. Cela dit, il peut servir de support de cours

pour d’autres filières d’enseignement.

• Vous trouverez dans ce chapitre de la théorie (définitions, théorèmes, démonstrations, etc.) et des exercices qui vous permettront progressivement de vous familiariser et de maîtriser les diverses notations et concepts mathématiques. À la fin du chapitre se trouvent les solutions des exercices.

• Les exercices accompagnés d’un astérisque (*), sont des exercices supplémentaires de

développement destinés, par exemple, aux élèves ayant choisi l’option, niveau avancé (MA2). • Pour mieux repérer les points importants de la théorie, les définitions sont dans un encadré

blanc et les théorèmes dans un encadré grisé.

• Pour vérifier votre niveau de compréhension à la fin de l’étude d’un sous chapitre, vous pouvez vous référer à la section : « Ce qu’il faut absolument savoir ».

• Des QR CODES apparaissent à certains endroits du cours. Une fois scannés avec l’appareil photo de vos smartphones, ils donnent (aux personnes ayant un compte EDUGE) accès à la lecture de vidéos dont le contenu est en lien avec certains sujets du cours.

• Vous pouvez télécharger ce document au format PDF à l’adresse suivante :

http://www.sismondi.ch/disciplines/mathematiques/espace-perso-profs/serge-picchione

• Pour finir, un grand merci aux collègues de divers établissements scolaires qui ont partagé leurs cours : Nicolas Chabal, Yves Drevous, Bernard Gisin, Alain Klopfenstein, Maurizio Lalicata, Bernard Lenggenhager, Romanita Nagy Gauxachs, Adrien Schleining et Serge Zoutter.

1.1 Introduction

1.1.1 Rappels sur les fonctions

Définition Une fonction f est définie par : 1) Un ensemble A appelé ensemble de départ. 2) Un ensemble B appelé ensemble d'arrivée.

3) Une règle de correspondance, qui à chaque élément de l'ensemble de départ x ∈A fait correspondre

zéro (aucun) ou un élément de l'ensemble d'arrivée y ∈ B. Remarques

a) On désigne souvent une fonction par les lettres f, g ou h.

b) Nous étudierons surtout les fonctions réelles, c'est-à-dire les fonctions dont l'ensemble de départ et l'ensemble d'arrivée sont des sous-ensembles des nombres réels .

Exemples f f 2 : x x 5 x 6 = (x) → → + +  

f est une fonction de  dans  . C'est une fonction réelle. • L'image de -4 est

( ) ( )

2

( )

f − = −4 4 + ⋅ − + =5 4 6 2

• L'image de l’intervalle

[

−2;0

]

est f

(

[

−2;0

]

)

=

[ ]

0;6

• L'ensemble des préimages de 2 est 1

( ) {

}

f− 2 = − −4; 1 , car f

( )

− =4 2 et f 1

( )

− =2

Ce sont les solutions de l'équation : 2

f(x)= x +5x+ = 6 2

• Le domaine de définition de f est D_f =

• L'ordonnée à l'origine de f est f 0

( )

=6

• Les zéros de f est l'ensemble 1

( ) {

}

f− 0 = − −3; 2 car f

( )

− =2 0 et f

( )

− =3 0

Ce sont les solutions de l'équation : f(x)= x2+5x+ = 6 0

• Le graphique de f sur l'intervalle [−7;5] est : • Tableau des valeurs de f :

x préimages f(x) images -5 6 -4 2 -3 0 -2 0 -1 2 0 6 1 12

•

•

•

•

f A B x2 x1 x3 x4 y1 y2 y3

•

y4

________________________________________________________________________________ Définitions

• Si un nombre x ∈ A est en correspondance avec un nombre y ∈ B, alors :

- y est appelé image de x par f et on note y = f(x) (x possède au plus une image) - x est appelé préimage de y par f et on note f -1_{(y)={x,…} (y peut posséder zéro,}

une ou plusieurs préimages)

préimage image

f : A B

x f (x)= y

→

→ On parle d'une fonction f de A dans B. • Le domaine de définition (ou ensemble de définition) d'une fonction f est l'ensemble des nombres appartenant à  qui ont une image par f. Cet ensemble est noté D_f . • L'ordonnée à l'origine d'une fonction réelle f est l'image de 0. Elle se note : f (0) • Les zéros d'une fonction réelle f est l'ensemble des préimages de 0. Elle se note : f -1₍₀₎ Autrement dit, c'est l'ensemble des nombres x ayant 0 (= y) comme image.

• Le graphique de f est la représentation géométrique des couples de coordonnées

(

x; f x

( )

)

où x∈D_f .

Exercice 1

Déterminer le domaine de définition Df , les zéros et l'ordonnée à l'origine des fonctions suivantes.

1) f x

( )

=3x+2 2) f x

( )

=x2−9 3) f x

( )

=x3−2x2+x 4) f x

( )

=

x

5) f x

( )

= x 5+ 6) f x

( )

5 x 3 = + 7)

( )

2 x f x x 1 = − 8)

( )

2 x 2 f x x 4 − = − 9)

( )

2 f x = x 10)

( )

( )

2 f x = x 11) f x

( )

x 2 x 2 − = + 12)

( )

x 1 2 f x x 3 + − = + Exercice 2

Considérons les trois fonctions définies par : f x

( )

=x2+7 , g x

( )

= 2x+5 et h x

( )

= −3

Effectuer les opérations suivantes entre les fonctions et simplifier le résultat :

(

f h+

)( )

x = f

(

− h

)( )

x = g

(

+ h

)( )

x = f

(

+ g + h

)( )

x =

(

f g⋅

)( )

x =

(

f g

)( )

x =

(

g f

)( )

x =

(

g g

)( )

x =

(

f + −g h

)( )

x =

(

f g h⋅ ⋅

)( )

x = g

(

 g g

)( )

x =

(

g f g x

)( )

=

Exercice 3 (décomposition de fonction)

On appelle fonction élémentaire une fonction ne faisant intervenir qu’une seule opération. Exemples n * 1 2 3 4 5 1 f ( x ) x a , f ( x ) bx , f ( x ) x n , f ( x ) x et f ( x ) x = + = = ∈_ = = sont élémentaires.

A l'aide des fonctions élémentaires vues précédemment et de la composition de fonctions, on peut construire beaucoup d'autres fonctions réelles.

Par exemple, la fonction g définie par

( )

(

)

6 1 g x =

x - 5

peut être vue comme la composition des fonctions définies par : f₁

( )

x =x – 5 , f₃

( )

x = x6 et f₅

( )

x = 1

x. En effet, on a:

(

)( )

(

(

( )

)

)

(

(

)

)

(

(

)

)

(

)

( )

6 5 3 1 5 3 1 5 3 5 6 1 f f f x f f f x f f x 5 f x 5 g x x 5 = = − = − = = −   Illustration :

(

)

(

)

( )

3 5 1 f 6 f f 6 1 x 5 g x x 5 x→x – 5→ − → = −

On peut donc imaginer que, grâce à la composition de fonctions, la plupart des fonctions réelles puissent se construire à l’aide d’un petit nombre de fonctions élémentaires.

a) Énoncé

Considérons les fonctions élémentaires définies par :

2 1

f ( x )=x f ( x )₂ =2x f ( x )₃ = + x 1 f ( x )₄ 1

x

=

Écrire chacune des fonctions g sous forme d’une composition de fonctions de type f :

1 g ( x )=2x+ 1 2 2 g ( x )=2x g ( x )_{3 2}1 x 1 = + 2 4 g ( x )=2x +1 5 2 g ( x ) x =

(

)

6 2 1 g ( x ) 2x 1 = +

(

)

4 7 g ( x )= 2x+2 2 8 g ( x )=2x +4 x+2 b) Énoncé

Considérons les fonctions élémentaires définies par :

5 1

f ( x )=x f ( x )₂ =3x f ( x )₃ = + x 1 f ( x )₄ 1

x

= f ( x )5 = x

Écrire chacune des fonctions g sous forme d’une composition de fonctions de type f :

(

)

5 1 g ( x )= x+1

(

)

2 5 1 g ( x ) x 1 = +

(

)

5 3 g ( x )= x+1 g ( x )4 =

(

x+1

)

5 5 1 g ( x ) 3x = 5 6 1 g ( x ) 3x 3   = _{ +} _ 7 1 g ( x ) x =

(

)

25 8 g ( x )= 3x+3 g

________________________________________________________________________________

1.1.2 Fonctions par morceaux

Définition

Une fonction par morceaux est une fonction définie sur une réunion d’intervalles réels.

Exemple

Soit la fonction f définie par

( )

2

x 1 si x 0 f x x 1 si 0 x 2 1 x 1 si x 3 2  − + ≤   =_ − < <   − ≥  • Graphique de f sur l'intervalle

[

−5;10

]

:

• Explications :

Sur l’intervalle

]

−∞;0

]

la fonction f est définie par l’expression algébrique − + . x 1

Sur l’intervalle

] [

0;2 la fonction f est définie par l’expression algébrique x2− . 1

Sur l’intervalle

[

3;+∞ la fonction f est définie par l’expression algébrique

[

1x 1

2 − .

• Le domaine de définition de f est une réunion d’intervalles réels : Df = −∞

]

;2

[ [

∪ 3;+∞ .

[

• Calculs de quelques images : f

( )

− = − − + = 2

( )

2 1 3 f 0

( )

= −

( )

0 + = 1 1

( ) ( )

2 f 1 = 1 − = 1 0 f 4

( )

1 4 1 1 2 = ⋅ − =

[

]

(

)

]

] [ ]

f −1;1 = −1;0 ∪ 1;2 f

(

[ ]

4;8

)

=

[ ]

1;3 . • L’ensemble des préimages de 1 par f est : 1

( )

{

}

Exercice 4

Soit la fonction f définie par f x

( )

2x 1 si x 1

x 2 si x 1

+ ≤



= _{− + >} 

a) Déterminer le domaine de définition de f . b) Calculer l'image de 1 par f .

c) Calculer f

( )

− et 2 f 2 .

( )

d) Tracer le graphique de f sur l'intervalle

[

−3;6

]

. e) Déterminer f

(

[

−1;1

]

)

et f

(

[ ]

2;5 .

)

f) Calculer les préimages de -1 par f. g) Calculer le(s) zéro(s) de f.

h) Calculer l'ordonnée à l'origine de f .

Exercice 5

a) Considérons la fonction « valeur absolue » définie par : f x

( )

x x si x 0 x si x 0 ≥  = _{= } − <  1) Que valent 7 ; −7 ; 0 ; 17−29 ?

2) Que représente géométriquement le calcul a b avec a,b− ∈ ? 3) Tracer le graphique de la fonction f sur l'intervalle

[

−5;5

]

.

4) Déterminer le domaine de définition, le(s) zéro(s) et l'ordonnée à l'origine de f . b) Soit f x

( )

= x et g x

( )

= x2 deux fonctions. Est-ce que f x

( )

=g x

( )

∀ ∈x  ? c) Soit la fonction h définie par h x

( )

= − . x 3

1) Compléter l'écriture suivante : h x

( )

x 3 ... si ... ... si ...

 = − =  

2) Tracer le graphique de la fonction h sur l'intervalle

[

−10;10

]

.

3) Déterminer le domaine de définition, le(s) zéro(s) et l'ordonnée à l'origine de h . d) Même question qu'au point c) mais pour la fonction k x

( )

= + . x 4

Exercice 6

Soient f , g et h trois fonctions de  dans  et définies par :

( )

1 si x 0 f x 1 si x 0 + ≤  = _{− >}  ;

( )

1 si x 0 g x 1 si x 0 − ≤  = _{+ >}  ; h( x )= f ( x )+g( x ) Représenter le graphique des fonctions f , g et h (utiliser des couleurs différentes).

________________________________________________________________________________ Exercice 7

Définition

Deux fonctions f et g d'ensembles de définition respectifs Df et Dg sont égales

si D D _f = _g et pour tout réel x de Df , f x

( ) ( )

= g x . On note alors f = g .

Le fonctions f et g sont-elles égales ? Justifier a) f x

( )

= + et x 1

( ) (

)(

)

(

)

x 1 x 1 g x x 1 + − = − b) f x

( )

= + et x 2

( )

(

)(

)

(

)

x 2 x 1 si x 1 x 1 g x 3 si x 1  + − ≠  ₋ =   ₌  c) f x

( ) (

= x−3

)

2 − et 9 g x

( )

=x x

(

−6

)

d) f x

( )

= + et x 1 g x

( )

1

(

2x 2

)

2 = + e) f x

( )

= 9 x et g x

( )

=3 x f) f x

( )

1 x = et

( )

1 si x 0 g x x 0 si x 0  _≠  =   ₌  g)

( )

x si x 0 f x 1 si x 0 x si x 0 >   =_ = − <  et g x

( )

= x h)

( )

x si x 0 f x 0 si x 0 x si x 0 >   =_ = − <  et g x

( )

= x Exercice 8

Soit la fonction f définie par

( )

1 si x 0 x f x x 1 si x 0 − <  =   _{− >} 

a) Déterminer le domaine de définition de f . b) Calculer f

( )

− et 2 f 4 .

( )

c) Tracer le graphique de f sur l'intervalle

[

−5;5

]

. d) Déterminer f

(

[

− −2; 1

]

)

et f

(

[ ]

1;4 .

)

e) Calculer les préimages de -2 par f. f) Calculer le(s) zéro(s) de f.

g) Calculer l'ordonnée à l'origine de f .

Exercice 9

Soit la fonction g définie par

( )

(

)(

)

(

)

x 2 x 1 si x 1 x 1 g x 1 si x 1  − + ≠ −  ₊ =   _{= −} 

1.1.3 Terminologie et symboles utilisés en lien

avec les énoncés Mathématiques

De nombreux théorèmes seront énoncés et démontrés dans ce cours. Voici quelques rappels pour vous aider.

Définition

Un axiome est un énoncé admis comme vrai sans justification, ou règle arbitraire ne menant à aucune contradiction, une sorte de « règle du jeu ».

Exemples

a) « Par deux points distincts, il ne passe qu’une seule droite ».

b) « Deux droites parallèles n'ont aucune intersection ou conservent une même distance ». Remarques

i) Un énoncé est vrai si il est toujours vrai.

ii) Un énoncé est faux si il n’est pas toujours vrai. « Si n est un nombre entier relatif alors 2

n est un nombre entier naturel non nul » est un énoncé faux.

Cherchons un contre-exemple : 0 est un nombre entier relatif mais 2

0 n'est pas un nombre entier naturel non nul.

La recherche d'un contre-exemple est une méthode utilisée pour prouver que certains énoncés sont faux.

En mathématique, on n’admet pas d’exception : un énoncé qui est parfois vrai et parfois faux est mathématiquement faux.

Définition

Une conjecture est un énoncé dont on a l’intuition qu’il est vrai mais qui ne connaît pas encore de démonstration.

Exemples

a) Conjecture de Goldbach

« Tout nombre entier pair strictement supérieur à trois peut être écrit comme la somme de deux nombres premiers (le même nombre premier pouvant être utilisé deux fois) ».

b) Conjecture de Legendre

« Pour tout entier npositif, il existe un nombre premier entre 2

n et

(

n+1

)

2 ». Remarque

Il existe des milliers de conjectures mathématiques. Certaines font l’objet de recherche de la part de chercheurs (en mathématiques, physique, etc.) qui travaillent dans des universités ou des écoles d’ingénieurs.

________________________________________________________________________________ Définition

Un théorème est un énoncé que l'on peut démontrer être vrai. C'est en général l'énoncé d'un résultat important.

Exemples

a) « Dans un triangle la somme des angles vaut 180° ». b) « Si m est divisible par 9, alors m est divisible par 3. » Remarques

i) Un théorème est toujours composé d’une hypothèse et d’une conclusion.

L'hypothèse est constituée des données et de leurs propriétés connues. Elle doit permettre de démontrer la conclusion du théorème. La conclusion d’un théorème est la propriété

découlant logiquement des hypothèses.

Exemple a) : Hypothèse : « Dans un triangle » .

Conclusion : « La somme des angles vaut 180° » Exemple b) : Hypothèse : « m est divisible par 9 » .

Conclusion : « m est divisible par 3 »

ii) La formulation mathématique habituelle d'un théorème est de la forme : « Si hypothèse alors conclusion » ou « hypothèse

⇒

conclusion ».

iii) Une démonstration est une suite de raisonnements logiques justifiés par les hypothèses, des axiomes et définitions.

Exemple b) : Si m est divisible par 9 alors m= ⋅k 9 k∈ mais 9= ⋅3 3 donc donc _

p

m= ⋅ ⋅ = ⋅k 3 3 p 3 p∈ . Autrement dit, m est divisible par 3.

iv) La négation de l'hypothèse n'implique pas forcément la négation de la conclusion. Exemple b) :

Si m n’est pas divisible par 9 cela ne veut pas forcément dire que m n’est pas divisible par 3. 12 n’est pas divisible par 9 mais 12 est divisible par 3.

Mathématiquement : A⇒B ⇔ NA⇒NB

v) Un théorème qui a une portée moins importante (ou secondaire) sera appelé proposition. « Si m est divisible par 9, alors m est divisible par 3. » peut-être subjectivement être appelé : proposition.

Définition

Un corollaire est un théorème qui est la conséquence immédiate ou un cas particulier d'un autre théorème.

Exemples

« Dans un quadrilatère la somme des angles vaut 360° » est un corollaire du théorème suivant : « Dans un triangle la somme des angles vaut 180° ».

Définition

La réciproque d’un théorème est un énoncé obtenu en inversant hypothèse et conclusion. Exemple

La réciproque du théorème « Si m est divisible par 9, alors m est divisible par 3. » est : « Si m est divisible par 3, alors m est divisible par 9. »

Remarques

i) Mathématiquement : La réciproque de A⇒ B est B⇒ A

ii) La réciproque d’un théorème n’est pas toujours vraie ce qui est le cas dans l’exemple ci-dessus. Contre-exemple : 6 est divisible par 3 mais 6 n'est pas divisible par 9.

iii) La réciproque du théorème de Pythagore et de Thalès est vraie.

iv) Dans le cas d'un théorème, la négation de la conclusion implique toujours la négation de l'hypothèse.

Cet énoncé s'appelle la contraposée d'un théorème. Mathématiquement : A⇒B ⇔ NB⇒NA

Exemple : « Si m n’est pas divisible par 3 alors m n’est pas divisible par 9 » est un énoncé vrai. 11 n’est pas divisible par 3 et 11 n'est divisible par 9.

Formulation

Il existe aussi des théorèmes énoncés sous l'une des formes suivantes : 1) Si hypothèse alors conclusion et si conclusion alors hypothèse. 2) Si hypothèse alors conclusion et réciproquement.

3) hypothèse si et seulement si conclusion. 4) hypothèse

⇔

conclusion.

Chacun de ces énoncés indique que l'hypothèse est équivalente à la conclusion. Exemple (théorème de Pythagore)

Dans un triangle de côtés a, b et c, c étant le côté le plus long,

1) Si a2 + b2 = c2, alors le triangle est rectangle et si le triangle est rectangle, alors a2 + b2 = c2. 2) Si a2 + b2 = c2, alors le triangle est rectangle et réciproquement.

3) a2 + b2 = c2 si et seulement si le triangle est rectangle. 4) a2 + b2 = c2

⇔

le triangle est rectangle.

Remarque

[

]

[

]

________________________________________________________________________________ Liste de symboles

Les mathématiciens utilisent de nombreux symboles pour noter leurs énoncés. En voici quelques-uns.

symbole se lit exemples

∈ "appartient à" 2∈ 2 appartient aux nombres réels.

∉ "n'appartient pas à" 2∉ 2 n'appartient pas aux nombres rationnels. ⊂ "est inclus dans"  ⊂ ⊂ ⊂

 est inclus dans  qui est inclus dans qui est ... ⇒ "implique" ou "donc" ou

"si ... alors ..."

"n est divisible par 4 ⇒ n est divisible par 2".

"n est divisible par 4 implique n est divisible par 2" ou "Si n est divisible par 4 alors n est divisible par 2". ⇔ "si et seulement si" ou

"est équivalent à"

"n ∈_ et n2 _{est divisible par 2} ⇔ _{n est divisible par 2".}

"n ∈ et n2 _{est divisible par 2 si et seulement si n est divisible par 2".}

∀ "pour tout" ∀ x ∈, x

2 ∈

+  .

Pour tout nombre réel x, x2 _{appartient aux réels positifs ou nul.}

∃ "il existe" ∃ x ∈_{Il existe un nombre réel x, tel que x} tel que x2 = 2. 2 _{= 2.}

∞ "l'infini" x tend vers _{x tend vers l'infini. x devient de plus en plus grand.} ∞. −∞ "moins l'infini" x tend vers _{x tend vers moins l'infini. x devient de plus en plus négatif.} −∞.

± "plus ou moins" x tend vers ± ∞.

x tend vers plus l'infini ou moins l'infini.

< "est plus petit que" 3,14 < π. _{3,14 est plus petit que π.} > "est plus grand que" 3,15 > π. _{3,15 est plus grand que π.} ≥ "est plus grand ou égal à" ∀ x ∈ , x2 ≥ 0.

Pour tout nombre réel x, x2 _{est plus grand ou égal à 0.}

≤ "est plus petit ou égal à" ∀ x ∈[0;1], x_{Pour tout nombre x entre 0 et 1, x}2 ≤ x. 2 _{est plus petit ou égal à x.}

≈ "est environ égal à" 3,14 ≈ π. _{3,14 est environ égal à π.} {...} "l'ensemble" {−1;0;1}.

L'ensemble contenant -1, 0 et 1.

\ "sauf" ou "diff"

 \ {−1;0;1}.

L'ensemble des réels, sauf l'ensemble {-1, 0 ; 1}.  \ [2 ; 3].

L'ensemble des réels, sauf l'intervalle [2;3]. α, β,... alpha, beta, ...

L'utilisation de lettres grecques est courante en mathématiques. En voici la liste :

symbole signification

 l'ensemble des nombres entiers naturels plus grands ou égaux à 0.

 l'ensemble des nombres entiers relatifs. Ils peuvent être positifs ou négatifs.

 l'ensemble des nombres rationnels. Correspond aux nombres s'écrivant sous

forme de fraction.

 l'ensemble des nombres réels. Correspond aux nombres avec ou sans virgules. +

 l'ensemble des nombres réels positifs ou nuls. −

 l'ensemble des nombres réels négatifs ou nuls.

*

 l'ensemble des nombres réels sauf le zéro.

[a ; b] l'intervalle fermé de a à b. Correspond à tous les nombres entre a et b,

a et b compris.

]a ; b[ l'intervalle ouvert de a à b. Correspond à tous les nombres entre a et b,

a et b non compris.

]−∞; b] l'intervalle de moins l'infini à b. Correspond aux nombres plus petits ou égaux à b. [a ; ∞[ l'intervalle de a à plus l'infini. Correspond aux nombres plus grands ou égaux à a.

Exercice 10

Tous les énoncés suivants sont vrais ; ce sont donc des théorèmes.

a) Pour chacun des énoncés ci-dessous, indiquez quelle est l'hypothèse et quelle est la conclusion en les reformulant, si nécessaire, sous la forme : « Si……alors…….. ».

b) Construire la négation, la réciproque et la contraposée de chaque énoncé. c) Que constate-t-on ?

1) Si un quadrilatère est un carré alors ce quadrilatère est un rectangle. 2) Si ABC est rectangle en A alors AB² + AC² = BC².

3) ABC est un triangle isocèle si AB = AC. 4) Si il pleut alors il y a des nuages.

5) B est le milieu du segment [AC] ⇒ AB = BC.

6) Si un côté d'un triangle est un diamètre de son cercle circonscrit alors ce triangle est rectangle. 7) S'il fait nuit alors il n'y a pas de lumière.

8) Le carré d'un nombre pair est un multiple de quatre.

9) La somme de trois nombres entiers consécutifs est un multiple de trois. 10) Un nombre entier est pair, si son carré est pair.

11) Dans un parallélogramme, les diagonales se coupent en leur milieu. 12) Tout triangle équilatéral est un triangle isocèle.

________________________________________________________________________________ Exercice 11

Construire :

1) Un énoncé vrai dont la réciproque soit fausse. 2) Un énoncé faux dont la réciproque soit vraie. 3) Un énoncé vrai dont la réciproque soit vraie. 4) Un énoncé faux dont la réciproque soit fausse. 5) Un énoncé vrai dont la contraposée soit fausse.

6) Un énoncé vrai dont la contraposée soit vraie et la réciproque soit fausse.

1.1.4 Ce qu’il faut absolument savoir

1♥ Connaître la définition rigoureuse d’une fonction f ok

2♥ Connaître la définition rigoureuse d’une fonction par morceaux ok 3♥ Connaître la définition rigoureuse du domaine de définition de f ok 4♥ Connaître la définition rigoureuse de l’ordonnée à l’origine et des zéros de f ok

5♥ Connaître la définition rigoureuse du graphique de f ok

6♥ Dessiner le graphique d’une fonction d’après son expression algébrique ok 7♥ Lire une image et les préimages à partir du graphique d’une fonction ok 8♥ Calculer une image et les préimages à partir de l’expression algébrique d’une fonction ok 9♥ Calculer les zéros et l'ordonnée à l'origine d’une fonction ok 10♥ Maitriser les opérations sur les fonctions (addition, multiplication, composition, etc.) ok

11♥ Composer et décomposer plusieurs fonctions ok

12♥ Savoir reconnaître l’hypothèse et la conclusion dans l’énoncé d’un théorème ok

13♥ Savoir formuler la réciproque d’un théorème ok

14♥ Savoir formuler la contraposée d’un théorème ok

15♥ Connaître les ensembles numériques et la notation avec les intervalles ok 16♥ Connaître les principaux symboles mathématiques (ensemblistes, d’inégalités, etc.) ok 17♥ Connaître les principales lettres grecques minuscules (écriture et prononciation) ok

1.2 Limite d'une fonction

1.2.1 Introduction

Activité I

a) Prenons la fonction f définie par f x

( )

x 1

x 1 − = − • Questions 1) Calculer f 1

( )

= ……….. 2) Domaine de définition de f : ……..

3) Comment se comporte la fonction f pour des valeurs de x proche de 1 (à gauche comme à droite de 1) ?

x 0,9 0,99 0,999 ... 1 ... 1,001 1,01 1,1

f(x) ∉

• Réponse Lorsque x se rapproche de 1 , f(x) se rapproche aussi près qu'on veut de ... • Graphique de f

• On écrira :

( )

x 1 lim f x

→ = ... mais cela ne veut pas dire que f 1

( )

=2 . b) Prenons la fonction f définie par

( )

2 x 2x 3 f x x 1 − − = + 1) Calculer f

( )

− =1 ……….. 2) Domaine de définition de f : ……..

3) Pouvez-vous prédire la valeur de

( )

xlim f x→ −1 ? ……….. x ... -1 ... f(x) ∉ 1 2 3 4 x 1 2 3 y f x x f(x) f(x)

________________________________________________________________________________ Définition intuitive de la notion de limite

Soit f une fonction définie au voisinage de a (proche de a, mais pas forcément en a).

On dit que la limite de f ( x ) lorsque x tend vers a est égale à L ⇔ f x s'approche "aussi près ( ) qu'on veut" de L à condition de prendre x "suffisamment près" de a, mais différent de a. Dans ce cas on note :

x a lim f ( x ) L → = Remarques • x a lim f ( x ) L

→ = ne veut pas forcément dire que f(a) = L.

• La valeur a ne doit pas nécessairement appartenir au domaine de définition de f. Dans la majorité des cas, a ∉ D_{f .}

La notion de limite nous permet, entre autres, de "voir" comment se comporte une fonction pour des valeurs de x qui sont proches d'une valeur "insolite" ; autrement dit pour déterminer la limite d'une fonction, cette fonction doit exister dans un voisinage de a, mais pas obligatoirement au point a lui-même.

• Il existe une définition mathématique plus formelle de la limite d’une fonction mais, nous ne l’aborderons pas dans ce cours (sauf en MA2).

Limite à gauche, limite à droite

Exemple Prenons la fonction f ( x ) x 1 si x 1 x 4 si x 1 + ≤  = _{− + >}  Df =

Lorsque x se rapproche de 1 par des valeurs inférieures à 1 (par la gauche), f(x) se rapproche de 2. Lorsque x se rapproche de 1 par des valeurs supérieures à 1 (par la droite), f(x) se rapproche de 3. On notera alors : -x 1 lim f ( x ) 2 → = xlim f ( x )→1+ 3 =

Que peut-on dire de la valeur de

x 1 lim f ( x )

→ ? lim f ( x )x→1 ∃ (la limite n’existe pas)

Remarque : f ( 1 )= 2

Plus généralement 1)

x a lim f ( x )₋

→ est la limite de f(x) lorsque x tend vers a par la gauche (par des valeurs inférieures à a). 2)

xlim f ( x )→a+ est la limite de f(x) lorsque x tend vers a par la droite (par des valeurs supérieures à a).

1 2 3 x y a x x x < a x > a x a– x a+

3)

x a

x a x a

lim f ( x )₋ lim f ( x )₊ L lim f ( x ) L

→

→ = → = ⇔ = (la limite existe)

Autrement dit : « Si la limite de f(x) lorsque x tend vers a par la gauche est égale à la limite de f(x) lorsque x tend vers a par la droite et vaut L alors la limite de f(x) pour x tendant vers a existe, est égale à L et réciproquement ».

4)

x a

x a x a

lim f ( x )₋ lim f ( x )₊ lim f ( x )

→

→ ≠ → ⇔ ∃ (la limite n’existe pas)

Extension de la notion de limite

1) Soit f une fonction définie sur un intervalle ouvert

]

a;+∞ . Alors

[

xlim f ( x )→+∞ =L signifie que si x est arbitrairement grand, alors f(x) est arbitrairement proche de L.

2) Soit f une fonction définie au voisinage de a. Alors x a

lim f ( x )

→ = +∞ signifie que si x est arbitrairement proche de a, alors f(x) est arbitrairement grand.

Exemples a) f ( x ) 1 x = f ( 0 ) 1 0 = ∉_ D_f =* x 0 1 1 lim x 0 − − → = = − ∞ x 0 1 1 lim x 0 + + → = = + ∞ x 0 1 lim x → ∃ x 1 1 lim 0 x →+∞ =+∞ = x 1 1 lim 0 x →−∞ = −∞ = b) g( x ) 1₂ x = g( 0 ) 1₂ 0 = ∉_ D_g =* ₂ x 0 1 1 lim x 0 − + → = = +∞ 2 x 0 1 1 lim x 0 + + → = = +∞ 2 x 0 1 lim x → = +∞ 2 x 1 1 lim 0 x →+∞ = +∞ = 2 x 1 1 lim 0 x →−∞ = +∞ =

________________________________________________________________________________ Exercice 12

On considère la fonction f définie par

2 x 4 f ( x ) x 2 − = − . a) Déterminer le domaine de définition de f .

b) Calculer f 1,8 , f 1,9 , f 1,99 , f 1,999 .

( ) ( ) (

) (

)

c) Calculer f 2,2 , f 2,1 , f 2,01 , f 2,001 .

( ) ( ) (

) (

)

d) Sans autre calcul, prédire les valeurs suivantes : 1)

x 2 lim f ( x ) + → 2) x 2 lim f ( x ) − → 3) x 2 lim f ( x ) → Exercice 13

Soit la fonction f déterminée par

2 x x 6 f(x) = x 2 − + − .

a) Déterminer le domaine de définition de f .

b) Calculer f(x) pour x = 1,9 ; 1,99 ; 1, 999 puis pour x = 2,1 ; 2,01 ; 2,001. c) Sans autre calcul, prédire les valeurs suivantes : 1)

x 2 lim f ( x ) + → 2) x 2 lim f ( x ) − → 3) x 2 lim f ( x ) → Exercice 14

Considérons les fonctions f et g définies par leur graphique.

a) Déterminer : 1) • f 1

( )

•

( )

x 1 lim f x₊ → • x 1

( )

lim f x₋ → • lim f xx→1

( )

2) • f 3

( )

•

( )

x 3 lim f x₊ → • x 3

( )

lim f x₋ → • lim f xx→3

( )

3) • f 4

( )

•

( )

x 4 lim f x + → • x 4

( )

lim f x₋ → • lim f xx→4

( )

4) •

( )

xlim f x→+∞ • xlim f x→−∞

( )

0 x y 1 1 -1 0 x y 1 1 -1 0 x y 1 1 -1 0 x y 1 1 -1 0 x y 1 1 -1 0 x y 1 1 -1 0 x y 1 1 -1 0 x y 1 1 -1 Exercice 15

Dans chacun des cas suivants, dessiner le graphique d’une fonction satisfaisant les conditions données. x 3 f ( 3 ) 4 et lim f ( x ) 4 → = = _f

{ }

x 3 x 3 D \ 3 , lim f ( x )₋ et lim f ( x )₊ → → =_ = +∞ = −∞

{ }

f x 3 D \ 3 et lim f ( x ) 2 → =_ = − _f

{ }

x 3 x 3 D \ 3 , lim f ( x )₋ 3 et lim f ( x )₊ 1 → → =_ = = − x 3 f ( 3 ) 3 et lim f ( x ) 1 → = = −

( )

x 3 x 3 f 3 1 , lim f ( x )₋ 1 et lim f ( x )₊ f ( 3 ) → → = = − =

( )

x 3 f 3 2 et lim f ( x ) → = = +∞ x 3 x 3 f ( 3 ) 0 , lim f ( x )₋ 1 et lim f ( x ) 1₊ → → = = − =

________________________________________________________________________________ Exercice 16

Tracer, sur un repère orthonormé, l’esquisse du graphique possible d’une fonction f vérifiant toutes les conditions suivantes :

•

{

}

f D =\ −1;1 • f ( 4 )− = f ( 3 )=0 • x 1 lim f ( x )₊ → = +∞ • x 1 lim f ( x )₋ → = −∞ •

xlim f ( x )→− ∞ = − 2 • xlim f ( x )→+ ∞ = −∞ • xlim f ( x )→−1 = +∞ • x 2

lim f ( x ) 3₊

→ =

•

xlim f ( x ) 3→2− = • f ( 2 )=1

1.2.2 Propriétés des limites

Soit f , g et h trois fonctions et a, k∈_ , alors :

1) x a lim k k → = 2) x a lim x a → = Si x a lim f ( x )

→ et lim g( x )x→a existent alors :

3)

(

)

x a x a lim k f ( x ) k lim f ( x ) → ⋅ = ⋅ → 4)

(

)

x a x a x a

lim f ( x ) g( x ) lim f ( x ) lim g( x )

→ ± = → ± →

( la limite d'une somme est égale à la somme des limites )

5)

(

)

x a x a x a

lim f ( x ) g( x ) lim f ( x ) lim g( x )

→ ⋅ = → ⋅ →

( la limite d'un produit est égale au produit des limites )

6) x a x a x a lim f ( x ) f ( x ) lim g( x ) lim g( x ) → → →  ₌     si lim g( x )x→a ≠0

( la limite d'un quotient est égale au quotient des limites )

7) n _n

x a x a

lim f ( x ) lim f ( x )

→ = → n≥ 2

8) Si f ( x )>g( x ) dans un voisinage de a, alors

x a x a

lim f ( x ) lim g( x )

→ ≥ → .

Si f ( x )<g( x ) dans un voisinage de a, alors

x a x a lim f ( x ) lim g( x ) → ≤ → . 9) Si f ( x )≤h( x )≤g( x ) dans un voisinage de a et si x a x a lim f ( x ) lim g( x ) L → = → = alors x a lim h( x ) L → = .

Exemples Calculons : 1) _ ( P1 ) x 4 f ( x ) lim 10 10 → = ( f(x) = 10 ne dépend pas de x.) 2)

(

)

( )

( )

( P1 ) ( P 2 ) ( P4 ) ( P3 ) x 1 x 1 x 1 x 1 x 1 f ( x )

lim 2x 1 lim 2x lim 1 2 lim x lim 1 2 1 1 1

→− + = →− + →− = ⋅ →− + →− = ⋅ − + = −

Dans cet exemple, si on calcule f ( 1 )− = −1 on obtient le même résultat que la limite.

3)

(

)

(

)

( ) ( )

( P4 ) ( P5 ) ( P 2 )

2

x 4 x 4 x 4 x 4 x 4 x 4

f ( x )

lim x x lim x x lim x lim x lim x lim x 4 4 4 20

→ + = → ⋅ + → = → ⋅ → + → = ⋅ + =

Dans cet exemple, si on calcule f 4

( )

=20 on obtient le même résultat que la limite.

4)

( )

(

)

( P6 ) x 3 x 3 x 3 f ( x ) lim x x 3 3 lim ... 2x 1 lim 2x 1 2 3 1 5 → → →  _{ = = = =}  ₋  _{− ⋅ −}   

Dans cet exemple, si on calcule f ( 3 ) 3 5

= on obtient le même résultat que la limite. Remarque

Pour une fonction polynomiale (somme de monômes) ou rationnelle (quotient de deux polynômes), calculer une limite au point d’abscisse x = a, lorsque a n’est pas une valeur particulière de cette fonction c'est-à-dire a∈D_f , revient simplement à évaluer f en a, c'est-à-dire calculer f(a).

Autrement dit :

Si f est une fonction polynomiale ou rationnelle et a∈D_f alors x a

lim f ( x ) f ( a )

________________________________________________________________________________

1.2.3 Calculs de limites

Calculs de limites contenant l'infini a) ( P3 )

(

)

( P 2 )

( )

xlim 5 x→+∞ = ⋅5 xlim x→+∞ = ⋅ +∞ = +∞5

( P3 )

(

)

( P 2 )

( )

xlim 5 x→−∞ = ⋅5 xlim x→−∞ = ⋅ −∞ = −∞5

Remarque :

( ) ( )

± ⋅ ±∞ = ±∞a

( ) ( )

±∞ ⋅ ±∞ = ±∞ (le signe est donné par la règle des signes) b) Soit la fonction f, définie par f ( x ) 1

x 1 = − . Df =\ 1

{ }

i) x 1 1 1 lim x 1 0 + + → − = = +∞ x 1 1 1 lim x 1 0 − − → − = = −∞ x 1 1 lim x 1

→ − ∃ (la limite n’existe pas) ii) x 3 1 1 lim x 1 2 + → − = x 3 1 1 lim x 1 2 − → − = x 3 1 1 lim x 1 2

→ − = (la limite existe) iii) x 1 1 lim 0 x 1 →+∞ − = +∞= x 1 1 lim 0 x 1 →−∞ − = −∞ = Remarque : a a 0 0± a ± ± ±∞ = ±∞ = = ±∞

±∞ ± (le signe est donné par la règle des signes) Calculs de limites contenant des indéterminations

On dit qu'une limite est indéterminée si l'application des propriétés des limites ne permet pas de prévoir sa valeur. Dans ce cas, il faut avoir recours à des manipulations algébriques pour se ramener à des cas déterminés. Les différents types d'indéterminations sont (liste non exhaustive):

Voici quelques méthodes permettant de lever une indétermination : a) Méthode : factorisation et simplification.

Cas où l’indétermination est de type 0

0 avec des polynômes.

1)

(

)

(

)

x 3 2 2 x 3 x 3 lim x 3 x 3 0 lim x 9 lim x 9 0 → → → − − _{= =} − − (Indétermination) ₂ x 3 x 3 x 3 x 3 lim lim x 9 → → − ₌ − −

₍

x−3

₎

(

)

x 3 1 1 lim x 3 6 x+3 = → + = 2)

(

)

(

)

2 2 x 1 2 2 x 1 x 1 lim x 3x 2 x 3x 2 0 lim x 4 x 3 lim x 4 x 3 0 →− →− →− + + + + _{= =} + + + + (Indétermination) 2 2 x 1 x 1 ( x 1 ) x 3x 2 lim lim x 4 x 3 →− →− + + + ₌ + + ( x 2 ) ( x 1 ) + + x 1 ( x 2 ) 1 lim ( x 3 ) 2 ( x 3 ) →− + = = + + +∞ − ∞ ±∞_±∞ 0 0 0·

( )

±∞ 0 0 0∞

b) Méthode : mise en évidence forcée

Cas où l’indétermination est de type +∞ − ∞ et ±∞

±∞ avec un polynôme

1)

(

2

)

2

xlim 3x→+∞ − +x 1 =xlim 3x→+∞ −xlim x→+∞ +xlim 1→+∞ = +∞ − ∞ + (Indétermination) 1

(

)

( )

( )

( )

2 2 2 2 2 2 x x x x 1 1 1 1

lim 3x x 1 lim x 3 lim x lim 3 3

x x x x 3 →+∞ →+∞ →+∞ →+∞     − + = ⋅_ − + _= ⋅ _ − + _= +∞ ⋅     = +∞ ⋅ = +∞ 2)

(

3 2

)

xlim→−∞ −7 x −2x +4 = +∞ − ∞ + (Indétermination) 4

(

)

( ) ( )

( ) ( )

3 3 2 3 3 3 3 x x x x 2 4 2 4

lim 7 x 2x 4 lim x 7 lim x lim 7 7

x x x x 7 →−∞ →−∞ →−∞ →−∞     − − + = ⋅ − − +_{ }= ⋅ _− − + _= −∞ ⋅ −     = −∞ ⋅ − = +∞ Proposition

Le comportement d'une fonction polynomiale (somme de monômes) à l'infini est le même que celui du terme de plus haut degré et on obtient ± ∞.

Démonstration *

(

)

(

)

n n n-1 2 n n-1 2 1 0 x x n n-1 2 1 0 n n-2 n-1 n x Pr opriétés des lim ites

n n-1 1 n n-1 x x x x a _{0 0} lim P( x ) lim a x a x ... a x a x a a a a a lim x a ... x x x x a a

lim x lim a lim ... lim

x x →±∞ →±∞ → ±∞ → ±∞ →±∞ →±∞ →±∞ = + + + + +    = _ ⋅_ + + + + + _     = ⋅ + + + +   

(

)

( )

0 n x 0 n n n n x a lim x lim x a a →±∞ → ±∞           = ⋅ = ±∞ ⋅ = ±∞  3) 3 2 2 x 3x x 1 1 lim x 3x →−∞ + + ₌ −∞ + ∞ + + +∞ − ∞ (Indétermination) 3 3 2 2 x x x 3x x 1 lim lim x 3x →−∞ →−∞ + + = + x 3 2 1 1 3 x x x   ⋅_ + + _   3

( )

3 1 1 x ⋅ −∞ = = −∞   ⋅_ + _   4) 4 2 4 x 2x x 1 lim x 1 →+ ∞ + + ₌ +∞ + +∞ (Indétermination) 4 4 2 4 x x x 2x x 1 lim lim x 1 →+ ∞ →+ ∞ + + ₌ + 2 4 4 1 1 2 x x x   ⋅_ + + _   4 2 2 1 1 1 x = =   ⋅_ + _  

________________________________________________________________________________ 5) 2 3 x x 1 lim x 1 →−∞ + ₌ +∞ − −∞ (Indétermination) 2 2 3 x x x x 1 lim lim x 1 →−∞ →−∞ + ₌ − 2 3 1 1 x x   ⋅_ + _    3

( )

x 1 1 0 1 1 1 x = = = −∞ ⋅ −∞   ⋅_ − _   Proposition

Le comportement d'une fonction rationnelle (quotient de deux polynômes) à l'infini dépend du degré du numérateur et du dénominateur.

On distingue 3 cas :

• Si le degré du numérateur est plus grand que le degré du dénominateur, on obtient

± ∞.

• Si le degré du numérateur est égal au degré du dénominateur, on obtient un nombre réel différent de zéro.

• Si le degré du numérateur est plus petit que le degré du dénominateur, on obtient 0. Démonstration *

(

)

(

)

(

)

(

)

n n-1 2 n n-1 2 1 0 m m-1 2 x x m m-1 2 1 0 n n-1 2 n n-1 2 1 0 x m m-1 2 m m-1 2 1 0 x n n x n m m x P( x ) a x a x ... a x a x a lim lim Q( x ) b x b x ... b x b x b lim a x a x ... a x a x a lim b x b x ... b x b x b lim x a _a lim x b →±∞ →±∞ →±∞ →±∞ →±∞ →±∞  + + + + +  = _{ } + + + + +   + + + + + = + + + + + ⋅ = = ⋅

( )

( )

( )

( )

n n m n m x x m m n n m n m m n n n m m m n n m m n m x a lim lim x b x b a si n m a _{b si n m} si n m 0 b a a 1 si n m si n m a _{b b} 1 si n m 0 b a 0 si n m 0 si n m a 1 _b si n m 0 b − →±∞ →±∞ − −   ⋅ _{ }= ⋅    _{⋅ ±∞ >}  _ ±∞ >  ⋅ ±∞ − >  _   _   _{ ⋅ = =}    =_ ⋅ − = =_ =_    _<   _{⋅ <}   ⋅ − <  _  ±∞   _

Cas où l’indétermination est de type +∞ − ∞ avec un radical.

6*)

(

2

)

x lim x x x →∞ + − = ∞ + ∞ − ∞ (Indétermination)

(

)

2 2 x x x x 1 1 1

lim x x x lim x x 1 lim x x 1 lim x x 1

x x x 1 →+∞ →+∞ →+∞ →+∞  _{ }     + − = _ + ⋅ −_{ }_=  + ⋅ − =  + ⋅ −        = +∞ + ∞ ⋅ = +∞

c) Méthode : multiplication par le facteur 1 Cas où l’indétermination est de type : 0

0 avec un radical.

(

)

(

)

x 3 x 3 x 3 lim x 3 x 3 0 lim 0 x 3 lim x 3 + + + → → → − − _{= =} − − (Indétermination)

(

)

x 3 x 3 x 3 1 x 3 x 3 x 3 x 3

lim lim lim

x 3 x 3 x 3 + + + → → → = − − ₌ − _⋅ − ₌ − − _−

(

)

x 3 x 3 ⋅ − − x 3 lim₊ x 3 0 → = − =

d) Méthode : Multiplication par le conjugué

Cas où l’indétermination est de type +∞ − ∞ ou 0

0 avec un radical.

1)

(

2

)

2

x x x

lim x x 1 lim x lim x 1

→∞ − + = →∞ − →∞ + = ∞ − ∞ (Indétermination)

(

) (

)

2

(

2

)

2 2 2 2 2 2 x x x 1 x x 1 x x 1

lim x x 1 lim x x 1 lim

x x 1 x x 1 →∞ →∞ →∞ = − + + + − + = − + ⋅ = + + + +  2 x x lim →∞ = −x2 2 x 2 1 1 1 lim 0 x x 1 →∞x x 1 − ₌ − ₌ − ₌ +∞ + + + + 2) x 0 x 1 1 0 lim x 0 → + − ₌ (Indétermination)

(

)

x 0 x 0 x 0 x 0 1 x 1 1 x 1 1 x 1 1 x 1 1

lim lim lim lim

x x x 1 1 x x 1 1 x 1 1 2 → → → → = + − ₌ + − _⋅ + + _{= = =} + + + + + + 

Remarque : x+ x2+ est le conjugué de 1 x− x2+ et réciproquement. 1

x 1 1+ − est le conjugué de x 1 1+ + et réciproquement. Plus généralement : A B+ est le conjugué de A B− et réciproquement.

Nous avons :

(

A+B

)(

A−B

)

=A2 −B2

Remarques

Pourquoi ne pouvons-nous pas conclure pour les indéterminations 0

0 , ∞ ∞ et 0⋅ ∞ ? • x 0 2x 0 lim 2 x 0 → ₌ ₌     et x 0 3x 0 lim 3 x 0 → ₌ ₌     • 2 x x lim x 1 →+∞ ∞ ₌ _{= +∞}   −  ∞ et _x 2 x 1 lim 0 x →+∞ − ₌ ∞₌  _∞   •

(

)

x 0 1 lim x 0 1 x + → ⋅ = ⋅ ∞ = et

(

)

2 x 0 1 lim x 0 0 x + → ⋅ = ⋅ ∞ =

________________________________________________________________________________ Proposition

Si f est la fonction définie par f x

( )

sin( x ) x = alors x 0 sin( x ) lim 1 x → = Remarque Df =\ 0

{ }

et x 0 sin( x ) sin( 0 ) 0 lim x 0 0 →   = _{=  }   « indétermination » Démonstration

Etape 1 : Calcul de la limite à droite Soit x 0;

2

π

 

∈_ _ la détermination d’un angle dans le premier quadrant du cercle trigonométrique. Pour tout x 0; 2 π   ∈_ _ on a : sin x

( )

> 0 et cos x

( )

> 0

On constate en observant la figure que :

Aire du triangle OQS < Aire du secteur OQS < Aire du triangle OQR

⇔ OQ PS 2 ⋅ < 2 x r 2 ⋅ (*) < OQ QR 2 ⋅ ⇔ 1 sin( x ) 2 ⋅ < 2 x 1 2 ⋅ < 1 tan( x ) 2 ⋅ On multiplie par

( )

2 0

sin x > les deux inégalités sans changer l’ordre :

⇔ 1 < x

sin( x ) <

1 cos( x )

Les trois nombres sont tous positifs, leurs inverses sont ordonnés de manière décroissante :

⇔ 1 > sin( x )

x > cos( x )

En utilisant les propriétés des limites : ⇔ x 0 lim 1 + → ≥ x 0 sin( x ) lim x + → ≥ x 0 lim cos( x ) + → ⇔ 1 ≥ x 0 sin( x ) lim x + → ≥ 1 Finalement : x 0 sin( x ) lim 1 x + → = . (*) 2 2 2

Aire du secteur OQS x x r xr

Aire du secteur OQS

r 2 2 2 π π = π ⇒ = π = x O P Q R S 1 1

•

•

•

•

•