Ecole Nationale Sup´ ´ erieure de l’A´ eronautique et de l’Espace D´ epartement ´ Energ´ etique et Propulsion

Ecole Nationale Sup´ ´ erieure de l’A´ eronautique et de l’Espace D´ epartement ´ Energ´ etique et Propulsion

Equilibre radial : ´

Application au calcul d’´ etages de turbomachines

J. Gressier Mai 2002

Le calcul des ´ ecoulements dans les turbomachines est fort complexe. En effet, la prise en compte de tous les ph´ enom` enes, sans hypoth` ese particuli` ere, nous obligerait ` a consid´ erer des

´ ecoulements tridimensionnels instationnaires visqueux. Le caract` ere instationnaire est princi- palement dˆ u aux interactions rotor/stator (compresseur/redresseur ou distributeur/turbine).

Mais il existe aussi les interactions pales/carter et des ´ eventuelles distorsions amont.

La premi` ere hypoth` ese simplificatrice est de consid´ erer un ´ ecoulement moyen “´ equivalent”

stationnaire. On peut alors penser que celui-ci est axisym´ etrique, pour autant que les conditions amont le soient aussi (pas d’effet de distorsion). Il suffit ensuite de calculer l’´ ecoulement dans un plan m´ eridien du corps. N´ eanmoins, cette approche n´ ecessite un certain nombre de donn´ ees, que seul le calcul de l’´ ecoulement inter-aubes peut donner (d´ eviation, perte de pression g´ en´ eratrice, etc). L’approche doit donc n´ ecessairement ˆ etre coupl´ ee : un calcul dans un plan m´ eridien qui d´ efinit les surfaces de courant ´ equilibr´ ees, et un certain nombre de calculs aube ` a aube pour chacune de ces surfaces ´ equilibr´ ees.

Dans cet esprit, nous nous int´ eressons ` a l’´ equilibre radial. Il s’agit d’extraire une ´ equation d’´ equilibre, plan par plan dans une surface m´ eridienne, qui permet de calculer l’orientation des tubes de courant dans la turbomachine. Apr` es un bref rappel sur les ´ equations en rep` ere absolu et en rep` ere tournant, les ´ equations seront d´ etaill´ ees pour un rep` ere axisym´ etrique. Puis, la m´ ethode d’obtention de l’´ equilibre radial sera donn´ ee pour ensuite pouvoir s’attarder sur les applications possibles.

1 Equations d’Euler en rep` ´ ere absolu et rep` ere tournant

Lorsque les effets de viscosit´ e et de conduction thermique sont n´ egligeables, les ´ equations de Navier-Stokes se simplifient et deviennent les ´ equations d’Euler. Ces ´ equations sont ´ etablies sous forme conservative. Peu adapt´ ee ` a la manipulation d’´ equations, cette forme est pourtant

`

a la base de toute m´ ethode conservative (m´ ethode volumes finis, approche avec bilans, etc). La forme compacte est :

∂

∂t







ρ ρ~ V ρE





 + div









ρ~ V ^T ρ~ V ⊗ V ~ + p~~I

ρ~ V ^T H









= 0 ( 1)

o` u E et H sont respectivement l’´ energie massique totale et de l’enthalpie d’arrˆ et. On rappelle les relations

ρE = ρe + 1

2 ρ~ V ² = p γ − 1 + 1

2 ρ~ V ² ( 2a)

ρH = ρE + p = γp γ − 1 + 1

2 ρ~ V ² ( 2b)

o` u e = C _v T est l’´ energie interne massique. On a bien sˆ ur H = h + 1/2ρ~ V ² avec ρh = ρe + p et h l’enthalpie massique.

Dans ces relations, on utilise implicitement une relation de fermeture qui est une ´ equation d’´ etat du fluide, p = (γ −1)ρe, par exemple. Elle permet de relier la pression aux autres variables thermodynamiques. On peut aussi l’´ ecrire

p = ρ rT ( 2c)

avec r = 287.14 J·kg ⁻¹ ·K ⁻¹ .

Ces ´ equations peuvent aussi s’´ ecrire sous forme non conservative. Ce ne sont plus des

´ equations de bilan ; le choix des variables est quasiment arbitraire et c’est pourquoi il en existe de nombreuses variantes. Dans la plupart des cas, l’obtention d’une forme non conservative se fait en d´ eveloppant la forme conservative, et en simplifiant certains termes ` a l’aide de l’´ equation de continuit´ e. Une des formes classiquement rencontr´ ees est la suivante :

∂ρ

∂t + divρ~ V = 0 ( 3a)

∂ ~ V

∂t + − →

rot V ~ ∧ V ~ + −−→

grad V ~ ²

2 = − 1

ρ

−−→ gradp ( 3b)

dH

dt = ∂H

∂t + −−→

gradH · V ~ = ∂p

∂t ( 3c)

Notons que l’´ equation d’´ energie peut ˆ etre remplac´ ee par une ´ equation pour l’entropie S, dS/dt = 0. Cette ´ equation signifie la conservation de la variable sur une trajectoire (ou sur une ligne de courant en ´ ecoulement stationnaire).

Pour obtenir les ´ equations d’Euler dans un rep` ere tournant, d´ efini par un vecteur rotation

~

ω, il suffit de d´ evelopper ces mˆ emes ´ equations ` a l’aide de V ~ = ~ ω ∧ −−→

OM + W ~ ( 4)

o` u W ~ est la vitesse relative dans le rep` ere tournant. Il n’est nul besoin d’ajouter les termes d’inertie (acc´ el´ eration d’entraˆınement et acc´ el´ eration de Coriolis) : les d´ eriv´ ees particulaires des membres de gauche les feront naturellement apparaˆıtre. Par contre, le rep` ere tournant est choisi tel que l’´ ecoulement relatif soit stationnaire.

Notons que les op´ erateurs diff´ erentiels div et −−→

grad ne sont pas identiques dans le rep` ere absolu et dans le rep` ere relatif. Leurs formulations d´ ependent du syst` eme de coordonn´ ees utilis´ e.

Nous garderons les notations identiques par souci de simplicit´ e.

2 Formulation du probl` eme en rep` ere axisym´ etrique

Nous pouvons consid´ erer cette section comme un pr´ ealable math´ ematique ` a l’´ etablissement

de l’´ equation d’´ equilibre radial. Nous allons d´ etailler la formulation des ´ equations dans le rep` ere

axisym´ etrique ( u ~ _x , ~ u _r , ~ u _θ ). L’´ equation de quantit´ e de mouvement s’´ ecrit, dans le rep` ere relatif,

∂ ~ W

∂t + − →

rot W ~ ∧ W ~ + −−→

grad W ~ ² 2

| {z }

acc´ el´ eration relative

= ω ² ~ r

| {z } acc´ el´ eration d’entraˆınement

− 2~ ω ∧ W ~

| {z } acc´ el´ eration

de Coriolis

− 1 ρ

−−→ gradp

| {z } bilan des efforts

volumiques

( 5)

Les relations qui suivent vont ˆ etre d´ evelopp´ ees dans le rep` ere absolu. On retiendra qu’il suffit de remplacer les vitesses par la relation ( 4 ) pour obtenir l’´ equation dans le rep` ere relatif.

L’´ equilibre radial s’´ ecrit dans un plan m´ eridien de la g´ eom´ etrie axisym´ etrique. C’est pour- quoi nous d´ etaillons ici quelques notations propres au calcul dans ce plan m´ eridien. L’angle

x r

θ V r

α ϕ V _θ

V

Vx

m V

α m

x r

s Rm

ϕ ϕ

Fig. 1 – Notations associ´ ee ` a une trajectoire dans un rep` ere axisym´ etrique

α est l’angle de d´ eviation absolu dans le plan azimuthal. On d´ efinit aussi l’angle de d´ eviation α _m dans la plan de la nappe de courant (voir figure 1). Le changement de rep` ere agit sur la vitesse orthoradiale V <sub>θ</sub> . Ainsi, il est n´ ecessaire de d´ efinir deux angles de d´ eviation, l’un absolu appliqu´ e ` a V ~ , l’autre relatif appliqu´ e ` a W ~ . On choisit les notations α et β pour les vitesses respectivement absolues et relatives.

Les relations de projections entre V , V _θ , V _m , V _r , V _x sont simples ` a retrouver. Citons par exemple :

V m = V cos(α m ) ( 6a)

V _x = V _m cos(ϕ) ( 6b)

V _r = V _m sin(ϕ) ( 6c)

V _θ = V sin(α _m ) ( 6d)

On pourrait ˆ etre tenter d’utiliser la d´ eviation α dans le plan projet´ e. La d´ eviation α _m dans le plan de la nappe de courant axisym´ etrique a cependant plus de signification physique. En particulier, α _m garde sa signification lorsque l’angle de conicit´ e ϕ tend vers 90 ^o . Ces angles sont reli´ es par

tan(α m ) = tan(α) cos(ϕ) ( 7)

Par contre, nous d´ etaillons ci-dessous les relations entre les d´ eriv´ ees de ϕ selon x, r et l’abscisse curviligne s, elle-mˆ eme reli´ ee au rayon de courbure de la trajectoire, dans la surface m´ eridienne.

Ces relations sont :

ds = R _m dϕ et dx = cos ϕ ds = ⇒ C _m = 1

R _m = dϕ

ds ( 8a)

dϕ dx = ∂ϕ

∂x + tan ϕ ∂ϕ

∂r = C _m

cos ϕ ( 8b)

3 Equation de l’´ ´ equilibre radial

Pour ´ etablir l’´ equation de l’´ equilibre radial, il faut chercher ` a ´ eliminer les d´ ependances selon l’axe x et arriver ` a une ´ equation qui ne fait intervenir que des d´ eriv´ ees radiales. Faisons d’abord

´ etat des hypoth` eses :

– le fluide est suppos´ e parfait (effet de viscosit´ e et de conduction thermique n´ egligeables), et le gaz id´ eal (gaz parfait et calorifiquement parfait),

– l’amont n’est pas n´ ecessairement homentropique car le fluide peut avoir subi des pertes de pression g´ en´ eratrice non homog` enes dans la direction radiale (selon la section ` a laquelle on s’int´ eresse),

– l’´ ecoulement est suppos´ e stationnaire,

– l’´ ecoulement est axisym´ etrique ; cela signifie que les quantit´ es ne d´ ependent pas de θ, mais uniquement de x et r. La vitesse orthoradiale V _θ , elle, n’est pas forc´ ement, et mˆ eme rarement nulle.

Dans le cadre de ces hypoth` eses, on note que la d´ eriv´ ee particulaire s’exprime seulement sous la forme

d

dt = V ~ · −−→

grad = V _x ∂

∂x + V _r ∂

∂r = V _x ∂

∂x + tan ϕ ∂

∂r

!

( 9)

3.1 Equation de continuit´ ´ e

Le d´ eveloppement de l’´ equation de continuit´ e donne V ~ · −−→

gradρ + ρ div V ~ = 0 ( 10)

A partir de l’´ ` ecriture diff´ erentielle de la fonction d’´ etat p = p(ρ, S) et de la d´ efinition de la vitesse du son, on peut ´ ecrire

−−→ gradp = a ² −−→

gradρ + ∂p

∂S

!

ρ

−−→ gradS ( 11a)

En effectuant le produit scalaire par V ~ , et en utilisant le fait que l’entropie se conserve sur une ligne de courant ( V ~ · −−→

gradS = 0), on obtient V ~ · −−→

gradρ = 1 a ²

V ~ · −−→

gradp ( 11b)

Sous ces hypoth` eses, l’´ equation de continuit´ e devient alors V ~ · −−→

gradp + ρa ² div V ~ = 0 ( 12)

On d´ eveloppe V ~ · −−→

gradp en ´ eliminant le gradient de pression longitudinal ` a l’aide de l’´ equation de quantit´ e de mouvement longitudinale

∂p

∂x + ρ dV x

dt = 0 ( 13a)

On obtient

V ~ · −−→

gradp = −ρV _x dV _x

dt + V _r ∂p

∂r ( 13b)

que l’on peut substituer dans l’´ equation de continuit´ e ( 12 ) :

−ρV x

dV _x dt + V r

∂p

∂r

!

+ ρa ² ∂V _x

∂x + ∂V _r

∂r + V _r r

!

= 0 ( 14a)

En d´ eveloppant quasiment tous les termes V _r en V _x tan ϕ, on voit apparaˆıtre des combinaisons

´ egales ` a dV _x /dt, et l’´ equation de continuit´ e modifi´ ee devient

1 − M _x ² dV _x

dt + M _x ² tan ϕ ρ

∂p

∂r + V _x ² ∂ tan ϕ

∂r + V _r V _x

r = 0 ( 14b)

avec M _x = V _x /a.

3.2 Equation de quantit´ ´ e de mouvement radiale L’´ equation de quantit´ e de mouvement radiale s’´ ecrit

1 ρ

∂p

∂r + dV _r dt − V _θ ²

r = 0 ( 15)

On peut aussi d´ evelopper, en utilisant l’expression de la d´ eriv´ ee particulaire ( 9 ), dV _r

dt = tan ϕ dV _x

dt + V _x d tan ϕ

dt ( 16a)

= tan ϕ dV _x

dt + V _x cos ² ϕ

dϕ

dt ( 16b)

= tan ϕ dV _x

dt + V _m ²

cos ϕ C _m ( 16c)

On obtient l’´ equation de quantit´ e de mouvement radiale suivante : 1

ρ

∂p

∂r + tan ϕ dV _x

dt + V _m ²

cos ϕ C _m − V _θ ²

r = 0 ( 17)

3.3 Equation de l’´ ´ equilibre radial

Pour obtenir l’´ equation de l’´ equilibre radial, il suffit d’´ eliminer le terme dV x /dt entre l’´ equation de continuit´ e ( 14a ) et l’´ equation de quantit´ e de mouvement ( 17 ). On obtient alors

1 ρ

∂p

∂r

h 1 − M _x ² 1 + tan ² ϕ ⁱ + 1 − M _x ² V _m ²

cos ϕ C m − V _θ ² r

!

− tan ϕ V _x ² ∂ tan ϕ

∂r + V _x V _r r

!

( 18a)

On peut r´ e´ ecrire cette ´ equation en remaniant quelques termes ; on obtient alors l’´ equation de l’´ equilibre radial, d´ ecrivant l’´ evolution du profil de pression statique dans une section en fonction de quantit´ es locales ou de d´ eriv´ ees partielles selon la mˆ eme section :

1 ρ

∂p

∂r

1 − M _m ² = 1 − M _x ² V _θ ² r

| {z } effet centrifuge

− 1 − M _x ² V _m ² cos ϕ C _m

| {z }

effet de courbure

+ tan ϕV _m ² ∂ϕ

∂r + V _r ² r

| {z } effet de conicit´ e

( 18b)

o` u l’on peut, dans le second membre, donner la signification physique de chacun des termes. Il existe d’ailleurs l’´ equation de l’´ equilibre radial simplifi´ ee qui ne tient uniquement compte que du terme centrifuge. L’´ equation peut aussi se mettre sous forme sans dimension :

1 γp

∂p

∂r

1 − M _m ² = 1 − M _x ² M _θ ²

r − M _m ² cos ϕ C m

!

+ tan ϕM _m ² ∂ϕ

∂r + M _r ²

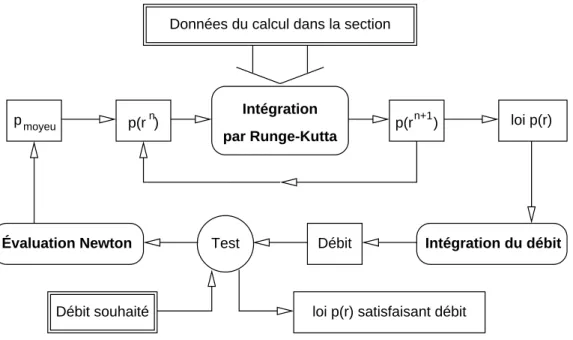
r ( 18c) Sous cette forme, l’´ equation ne fait intervenir que la pression statique et le nombre de Mach (ainsi que ses composantes). La donn´ ee de la pression d’arrˆ et suffit donc pour poser correctement le probl` eme de Cauchy et permettre l’int´ egration. En particulier, la temp´ erature d’arrˆ et n’est pas utile. Elle le devient lorsque l’on veut calculer, voire mˆ eme optimiser le d´ ebit dans la veine.

4 Applications

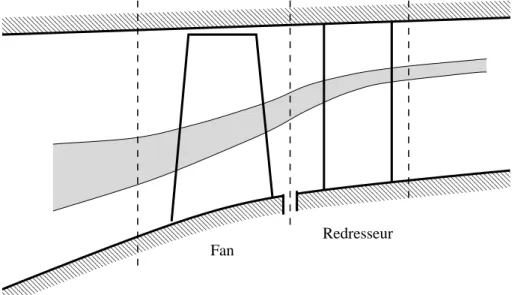
Les applications de l’´ equilibre radial sont multiples : v´ erifications de mesures exp´ erimentales, conception de turbomachines en utilisant le couplage avec des m´ ethodes de calcul du canal inter- aubes plus ou moins ´ elabor´ ees. On applique l’´ equation dans diff´ erentes sections de la veine, en amont et en aval de chaque roue comme cela est montr´ e sur la figure 2.

Fan

Redresseur

Fig. 2 – G´ eom´ etrie de la veine et ´ evolution des nappes de courant, sections de calcul de

l’´ equilibre radial.

4.1 Int´ egration de l’´ equation

L’int´ egration de l’´ equation de l’´ equilibre radial n´ ecessite un certain nombre de donn´ ees.

Ce sont en g´ en´ eral des quantit´ es g´ en´ eratrices. En effet, elles sont soit connues car provenant directement de l’amont, soit recalcul´ ees ` a partir des coefficients de pertes ou d’efficacit´ e locaux.

La connaissance des angles est elle aussi n´ ecessaire. On pourra se placer suffisamment loin en amont pour les prendre petits voire nuls, ou directement imposer des d´ eviations en sortie d’aubages, par exemple. De fa¸con g´ en´ erale, les quantit´ es que l’on consid` ere impos´ ees ici pour l’int´ egration de l’´ equation de l’´ equilibre radial peuvent ˆ etre corrig´ ees dans le cadre du couplage avec un calcul inter-aubes. En r´ esum´ e, on consid` ere que l’on dispose, dans toute la section de calcul, des donn´ ees suivantes :

– le profil de temp´ erature totale T _i , – le profil de pression totale p _i ,

– les donn´ ees g´ eom´ etriques ¹ locales de la ligne de courant, – l’angle de d´ eviation β (direction orthoradiale),

– l’angle ϕ dans le plan m´ eridien (conicit´ e locale), – la courbure C m dans le plan m´ eridien ;

– soit une autre quantit´ e locale (nombre de Mach, pression statique, etc) en un point de la section (g´ en´ eralement ` a une des parois), soit une quantit´ e int´ egrale telle que le d´ ebit.

Int´ egration de la pression dans une section

Nous nous attachons tout d’abord ` a d´ ecrire le calcul d’une section. Nous supposons que la donn´ ee du point (pression ou nombre de Mach) est au moyeu. Cette hypoth` ese n’est en rien restrictive puisque l’int´ egration n’a pas de direction privil´ egi´ ee. L’´ equation ` a int´ egrer peut tout simplement s’´ ecrire comme une ´ equation diff´ erentielle ordinaire

dp

dr = F (p, r) ( 19)

o` u la d´ ependance en r de F est due ` a l’ensemble des donn´ ees dans la section. En effet, tout le second membre de l’´ equation ( 18c ) peut ˆ etre calcul´ ee comme une fonction de la pression et des autres donn´ ees, fonctions elles-mˆ emes d´ ependantes de r. On cite bien sˆ ur la d´ efinition de la pression totale

p _i (r) = p(r)

1 + γ − 1 2 M ² (r)

_γ−1 ^γ

( 20) La donn´ ee d’une condition initiale permet la formulation du probl` eme en probl` eme de Cau- chy, dont la solution est unique. Cette ´ equation peut alors s’int´ egrer par une simple m´ ethode d’Euler ou, plus g´ en´ eralement une m´ ethode de Runge et Kutta (Annexe B).

Supposons que la donn´ ee initiale est celle de la pression ² au rayon du moyeu r _min . Alors on peut int´ egrer l’´ equation num´ eriquement, de fa¸con explicite, jusqu’` a r _max et obtenir le profil complet de pression dans la section ´ etudi´ ee.

Optimisation du d´ ebit

Il se peut que le probl` eme ne soit pas formul´ e initialement avec la donn´ ee d’une quantit´ e locale. Il sera alors n´ ecessaire d’it´ erer sur la condition initiale pour remplir la condition sou-

1 donn´ ees g´ eom´ etriques d´ efinies sur la figure 1.

2 ou toute autre valeur permettant de remonter ` a la pression via les autres quantit´ es, donn´ ees du probl` eme.

hait´ ee. Dans ce cas, du point de vue th´ eorique, la solution n’est pas unique. Il est utile de poser le probl` eme correctement sur le plan physique, et de commencer le calcul it´ eratif avec une estimation correcte de la condition initiale. Le sch´ ema de la figure 3 montre les deux boucles, l’une de l’int´ egration, l’autre du processus it´ eratif. Il faut bien diff´ erencier la condition initiale du processus it´ eratif global, que nous nommerons estimation initiale, et la condition initiale du probl` eme de Cauchy pour l’int´ egration de l’´ equation diff´ erentielle.

loi p(r)

moyeu

p

Test Débit

Données du calcul dans la section

Débit souhaité loi p(r) satisfaisant débit

Intégration par Runge-Kutta

Intégration du débit Évaluation Newton

p(r ) ⁿ p(r ) ⁿ⁺¹

Fig. 3 – Sch´ ema du processus it´ eratif global, incluant l’int´ egration de l’´ equation diff´ erentielle de la pression (´ equilibre radial).

Ce processus it´ eratif consiste donc ` a optimiser l’estimation de la condition initiale pour obte- nir une quantit´ e globale. Nous allons traiter l’exemple du d´ ebit : celui-ci d´ epend compl` etement du profil de pression r´ esultant de l’int´ egration (on pourra utiliser une m´ ethode des trap` ezes ou de Simpson).

D = 2π

Z r max

r min

ρV _x r dr ( 21)

Le profil de pression ayant ´ et´ e d´ etermin´ e ` a l’aide de l’estimation de la pression au moyeu, on peut consid´ erer que le d´ ebit est uniquement une fonction de p <sub>m</sub> , la pression statique au moyeu. On cherche alors ` a r´ esoudre D(p _m ) = D o` u D est le d´ ebit recherch´ e. On r´ esout cette

´ equation par la m´ ethode de Newton ou par la m´ ethode de la s´ ecante (Annexe A). ` A partir de l’estimation p <sup>n</sup> <sub>m</sub> et de son d´ ebit associ´ e D <sup>n</sup> (voire des valeurs aux it´ erations pr´ ec´ edentes), ces m´ ethodes donnent une nouvelle estimation du param` etre p ⁿ⁺¹ _m qui permettra de calculer un d´ ebit plus proche du d´ ebit recherch´ e D.

Une approche est possible : plutˆ ot que d’it´ erer sur le d´ ebit en int´ egrant sur une hauteur de veine constante [r _min ; r _max ], on peut int´ egrer sur une hauteur [r _min ; r ⁿ ] variable qui permet de satisfaire le d´ ebit. L’it´ eration sur le rayon du carter r ⁿ se d´ eroule de la mˆ eme mani` ere que pour le d´ ebit.

Les m´ ethodologies adopt´ ees diff` erent selon le type de section que l’on analyse : section amont

d’un rotor ou d’un stator, dite section d’entr´ ee, ou section aval de cette mˆ eme roue, dite section

de sortie.

4.2 Calcul d’un plan d’entr´ ee

Dans une section d’entr´ ee, des consid´ erations physiques nous poussent ` a imposer les quan- tit´ es d’arrˆ et. En effet, elles ont le bon goˆ ut d’ˆ etre des grandeurs caract´ eristiques de l’´ ecoulement et, avec les bonnes hypoth` eses, se conservent le long de trajectoire. Ainsi, on peut les impo- ser en consid´ erant la conservation depuis l’infini amont, voire en tenant compte d’´ eventuels chocs pour des entr´ ees d’air supersoniques. On peut aussi tout simplement utiliser des mesures exp´ erimentales.

En ce qui concernent les angles (ϕ pour les effets de conicit´ e, et la d´ eviation β) et la courbure, on peut soit commencer ` a imposer une progression lin´ eaire coh´ erente avec celle de la g´ eom´ etrie de la veine (pour ϕ et la courbure C m ), soit utiliser des donn´ ees exp´ erimentales.

Pour la d´ eviation β, selon la proximit´ e de la roue, on peut imposer l’angle d’attaque de la pale (approche triangle des vitesses) ou directement utiliser les sorties d’un calcul inter-aubes (attention aux changements de rep` ere).

Lorsque l’on dispose de toutes les donn´ ees n´ ecessaires, on applique directement la m´ ethode d´ etaill´ ee dans la section pr´ ec´ edente. En g´ en´ erale, la donn´ ee est celle du d´ ebit. Le calcul est alors it´ eratif.

4.3 Calcul d’un plan de sortie

Du point de vue des donn´ ees ` a imposer, sauf dans le cas o` u elles sont directement donn´ ees par des mesures exp´ erimentales, on dispose surtout de coefficients d’efficacit´ e qui d´ efinissent les pertes subies ` a la travers´ ee de la roue. Il faut alors prendre ` a garde ` a leurs d´ efinitions, qui n´ ecessitent parfois de se placer dans le rep` ere tournant.

Comme pour le plan d’entr´ ee, on d´ efinira souvent les angles soit par mesure, soit par consid´ erations g´ eom´ etriques (interpolation de la g´ eom´ etrie de la veine pour ϕ, d´ eviation β par le triangle des vitesses).

Le point o` u la m´ ethodologie diff` ere est celui du lien entre le plan de d’entr´ ee et le plan de sortie. On pourrait ´ evidemment it´ erer sur la valeur de la pression au moyeu pour respecter le d´ ebit impos´ e (g´ en´ eralement le mˆ eme que pour la section d’entr´ ee). Cette m´ ethode est tout ` a fait suffisante pour d´ eterminer le plan de sortie. Mais on recherche aussi ` a d´ eterminer l’´ evolution des nappes de courant dans la veine. Cette ´ evolution peut ˆ etre donn´ ee par la d´ etermination de la fonction r ^out (r ⁱⁿ ) : une nappe de courant issue du rayon r ⁱⁿ en entr´ ee arrive en r ^out dans la section de sortie (figure 2).

On a a priori le choix d’int´ egrer la pression dans la section de sortie et d’effectuer ensuite un post-traitement des donn´ ees calcul´ ees dans les deux sections, ou d’int´ egrer simultan´ ement les ´ equations de d´ ebit et de l’´ equilibre radial.

Dans les deux cas (post-traitement ou int´ egration simultan´ ee), on utilise la conservation du d´ ebit qui s’exprime, en axisym´ etrique,

h ρ r V x dr ⁱ

in = ^h ρ r V x dr ⁱ

out ( 22a)

o` u le terme ρV _x peut s’´ ecrire ρV _x =

r γ r

p _i

√ T _i M _x

1 + γ − 1 2 M ²

⁻ _2(γ−1) ^γ+1

( 22b)

Dans le cas de l’int´ egration simultan´ ee, on choisit alors la variable r ⁱⁿ du plan d’entr´ ee. On

int` egre sur [r <sup>in</sup> <sub>min</sub> ; r <sup>in</sup> <sub>max</sub> ]. Le probl` eme de Cauchy pour l’´ equilibre radial s’´ ecrit de la mˆ eme fa¸con

que pour le plan d’entr´ ee. La seule diff´ erence est que le pas ∆r ^out dans le plan de sortie est d´ etermin´ e par l’´ equation de conservation du d´ ebit ( 22a ) au lieu d’utiliser un pas constant.

Ainsi, l’int´ egration compl` ete assure la conservation du d´ ebit, mais rien n’assure que l’int´ egra- tion de la fonction r ^out (r ⁱⁿ ) donne r ^out (r _max ⁱⁿ ) = r _max ^out . C’est pourquoi on doit it´ erer sur l’estima- tion de la pression au moyeu dans le plan de sortie pour retrouver r ^out (r _max ⁱⁿ ) = r _max ^out .

L’int´ erˆ et de l’int´ egration simultan´ ee est de calculer les quantit´ es dans le plan de sortie au lieu exact de l’arriv´ ee de nappes issues du plan d’entr´ ee. Ainsi, on peut effectivement d´ efinir les quantit´ ees g´ en´ eratrices aval en fonction des quantit´ es amont, via des coefficients de perte ou des rendements. Par contre, la conservation du d´ ebit n’est assur´ ee qu’` a la pr´ ecision de la m´ ethode d’int´ egration pr` es.

Seul le cas o` u on connaˆıt explicitement les quantit´ es g´ en´ eratrices dans la section permet de d´ ecoupler le calcul de la section de sortie et celui de l’´ evolution des lignes de courant.

Enfin, pour calculer les diff´ erents ´ etages, on peut ´ eventuellement utiliser les donn´ ees du plan

de sortie de la premi` ere roue pour calculer la roue suivante (figure 2, grille de compression et

grille de redresseurs).

Annexes

A Recherche de solution par m´ ethode it´ erative

La recherche de racines d’une fonction quelconque se fait en g´ en´ eral de mani` ere it´ erative.

Cette approche est ` a la base de la recherche de param` etres o` u la fonction n’est pas connue mais d´ ecoule d’un processus de calcul complexe. On s’int´ eresse ici ` a calculer p telle que F (p) = 0.

Deux m´ ethodes it´ eratives sont pr´ esent´ ees : la m´ ethode de la s´ ecante et la m´ ethode de Newton. Elles consistent toutes les deux ` a approcher localement la fonction par une droite (` a d´ efinir selon la m´ ethode), utiliser la solution donn´ ee par cette droite et recommencer le processus jusqu’` a convergence.

On note x ₀ l’estimation initiale et x _n les estimations suivantes. On note F _n la valeur associ´ ee

`

a F (x _n ).

f(x)

x x

f(x)

Fig. 4 – Sch´ ema de fonctionnement des m´ ethodes it´ eratives, m´ ethode de la s´ ecante ` a gauche, m´ ethode de Newton ` a droite.

A.1 M´ ethode de la s´ ecante

La m´ ethode de la s´ ecante consiste ` a utiliser deux points connus de la fonction pour d´ efinir la droite approchant localement la fonction (figure 4, gauche). Le processus ´ etant cens´ e converger, le choix des deux derniers points calcul´ es est le meilleur. L’´ equation de la droite est

y = F _n − F _n−1 x _n − x n−1

(x − x n ) + F n ( 23)

L’estimation suivante de la solution est l’intersection de la droite avec l’axe des x. On a donc x _n+1 = x _n − F _n x _n − x n−1

F n − F n−1

( 24)

Le point particulier de la m´ ethode est de d´ emarrer le calcul : il faut deux ´ evaluations pour

pouvoir faire une estimation. On peut, soit prendre deux points arbitraires, soit imposer ` a la

premi` ere it´ eration une pente tr` es importante de la droite, ce qui conduit ` a estimer le point

x ₁ tr` es proche de x <sub>0</sub> . On peut aussi estimer le deuxi` eme point x ₂ selon (1 + ε)x ₁ . Les deux premi` eres it´ erations de la m´ ethode de la s´ ecante sont alors ´ equivalentes ` a une it´ eration par la m´ ethode de Newton (section A.2).

A.2 M´ ethode de Newton

Dans la m´ ethode de Newton, la droite approchant localement la fonction est la tangente ` a la courbe au dernier point calcul´ e (figure 4, droite). L’´ equation de la droite est donc

y = dF dx

_x

n

(x − x n ) + F n ( 25)

L’estimation suivante de la solution est toujours l’intersection de la droite avec l’axe des x. On a donc

x _n+1 = x _n − F _n

dF dx

_x

n

( 26) La difficult´ e est ici d’´ evaluer la d´ eriv´ ee en x _n . Soit la forme analytique de la d´ eriv´ ee est connue et on calcule directement sa valeur en x _n . Soit il est impossible ou bien trop coˆ uteux de la calculer et on a recours ` a une ´ evaluation approch´ ee par diff´ erences finies :

dF dx

_x

n

' F (x _n + ε) − F (x _n )

ε ( 27)

On remarque que le coˆ ut de cette ´ evaluation est le double de celui de l’´ evaluation d’un point de F (x). On retiendra que dans ce cas, la m´ ethode de Newton est, par it´ eration, deux fois plus coˆ uteuse que la m´ ethode de la s´ ecante. Par contre, on peut esp´ erer que la convergence soit plus rapide.

B M´ ethode d’int´ egration explicite de type Runge et Kutta

A partir du probl` ` eme de Cauchy compos´ e d’une ´ equation diff´ erentielle ordinaire et d’une condition initiale,



 

 

dp

dr = F (p, r) p(r _c ) = p _c

( 28) on peut int´ egrer num´ eriquement cette ´ equation en calculant un ensemble de points (r _n , p ⁿ ) avec (r ₀ , p ⁰ ) = (r _c , p _c ) et une discr´ etisation par la m´ ethode de Runge et Kutta de l’´ equation diff´ erentielle ordinaire. La formulation g´ en´ erale du pas de calcul pour ce type de m´ ethode explicite est, pour un point donn´ e (r _n , p ⁿ ),



 

 

 

 

 

 

 

 



 

 

 

 

 

 

 

 



δp ^(n,1) = ∆r F p ⁿ , r _n

δp ^(n,2) = ∆r F p ⁿ + κ ₂ δp ^(n,1) , r _n + κ ₂ ∆r .. . .. .

δp ^(n,N) = ∆r F p ⁿ + κ _N δp ^(n,N−1) , r _n + κ _N ∆r p ⁿ⁺¹ = p ⁿ +

N

X

i=1

K _i δp ^(n,i)

( 29)

o` u les coefficients κ _n et K _n sont habilement ajust´ es pour atteindre l’ordre de pr´ ecision souhait´ e.

On r´ esume dans le tableau 1 les sch´ emas d’int´ egration les plus connus et utilis´ es.

M´ ethode Euler Euler am´ elior´ e Euler-Cauchy RK4

N/ordre 1 2 2 4

κ ₂ 1/2 1 1/2

κ ₃ 1/2

κ ₄ 1

K ₁ 1 0 1/2 1/6

K 2 1 1/2 1/3

K ₃ 1/3

K ₄ 1/6

Tab. 1 – D´ efinitions des coefficients pour les m´ ethodes type Runge et Kutta.