Université d’Aix-Marseille
Mémoire de Master 2 - Recherche en didactique des mathématiques Sous la direction de Teresa Assude
Les raisons d’ˆetre de l’´etude des grandeurs
(longueur et aire)
Comment elles ont vécu au collège
entre 1900 et 2019
par Didier Auroy
Jury :
Pierre Arnoux, Professeur des universités, Aix-Marseille Université, Examinateur, Michèle Artaud, Maître de conférences, Aix-Marseille Université, Examinatrice,
Teresa Assude, Professeur des universités, Aix-Marseille Université, Directrice de mémoire Yves Chevallard, Professeur des Universités, Aix-Marseille Université, Examinateur,
Yves Matheron, Professeur des Universités, Institut Français de l’Éducation – ENS de Lyon, Examinateur.
Remerciements 5
1 Introduction 6
2 Cadre théorique de cette étude et problématique 9
2.1 Cadre théorique . . . 9
2.1.1 L’échelle des niveaux de codétermination didactique . . . 9
2.1.2 Sur la transposition didactique et l’approche écologique . . . 10
2.1.3 Sur l’organisation mathématique . . . 12
2.1.4 Sur le rapport à un objet du savoir . . . 13
2.2 Problématique de l’étude . . . 14
3 Méthodologie de l’enquête 15 3.1 Le choix des grandeurs à étudier . . . 15
3.2 Recherche des instructions officielles . . . 16
3.3 Les documents théoriques sur les grandeurs . . . 17
3.4 Les documents sociologiques et historiques . . . 17
3.5 Les documents épistémologiques sur les mathématiques . . . 18
3.6 Les manuels scolaires . . . 18
4 Les questions . . . et les réponses obtenues 19 4.1 Quelle est l’origine de l’intérêt porté aux grandeurs ? . . . 19
4.1.1 Une approche cognitive . . . 19
4.1.2 Un début d’approche mathématique . . . 20
4.2 Qu’est-ce qu’une grandeur ? (approche mathématique) . . . 21
4.2.1 Définition(s) . . . 21
4.2.2 Axiomes relatifs aux grandeurs . . . 22
4.2.3 Des axiomes aux types de taches . . . 24
4.3 Des grandeurs aux mesures des grandeurs . . . 25
4.4 Quelles praxéologies chez A.C. Clairaut ? . . . 27
4.4.1 La société du XVIIIe siècle . . . 27
4.4.2 Introduction à son ouvrage . . . 27
4.4.3 Les types de tâches chez Clairaut . . . 29
4.4.4 Clairaut, pas seulement le vulgarisateur d’Euclide du XVIIIe siècle . . . 30
4.5 La réforme de 1902 : absence ou refus d’une transposition didactique ? . . . 31
4.5.1 La société au début du XXe siècle . . . 31
4.5.2 L’école au début du XXe siècle . . . 32
4.5.3 Les mathématiques au début du XXe siècle . . . 33
4.5.4 La dialectique ancien/nouveau en géométrie . . . 34
4.5.5 Les ouvrages et manuels de cette réforme . . . 35
4.5.6 La victoire de l’ancien sur le nouveau monde . . . 36
SOMMAIRE
4.6.1 La société au milieu du XXe siècle . . . 37
4.6.2 L’école en 1970 . . . 37
4.6.3 Les mathématiques en 1970 . . . 38
4.6.4 La "réforme des mathématiques modernes" . . . 39
4.6.5 Les programmes de la réforme des mathématiques modernes . . . 41
4.6.6 La réforme des mathématiques modernes : un échec traumatisant . . . 41
4.7 La réforme de 1977 : le début d’une longue convalescence ? . . . 43
4.7.1 Contenus des documents . . . 43
4.7.2 Le manuel "Mathématiques 6ème" de 1977 ( Editions Istra) . . . 44
4.8 La réforme de 1985 : le nettoyage par le vide ? . . . 50
4.8.1 L’école en 1985 . . . 50
4.8.2 Le programme du collège en 1985 . . . 51
4.8.3 La prise en charge du rapport des grandeurs . . . 53
4.8.4 Quel rôle pour les transformations du plan ? . . . 53
4.9 Les programmes du XXIe siècle . . . 54
4.9.1 L’école au XXIe siècle . . . 54
4.9.2 Les programmes de 2004 à 2018 . . . 55
4.9.3 Le programme 2019, une nouvelle régression ? . . . 56
4.9.4 Bilan sur ces programmes . . . 56
5 Comparatif sur l’utilisation des grandeurs en géométrie 58 5.1 Dans les Eléments d’Euclide . . . 58
5.2 Dans les Eléments de Clairaut . . . 58
5.3 L’ouvrage de Vacquant et Macé . . . 59
5.4 Dans le manuel Sesamath de 2019 . . . 59
6 Conclusion et suites possibles à cette étude 61 6.1 Bilan de cette étude . . . 61
6.2 Grandeurs commensurables ou non : en parler ou pas ? . . . 63
6.2.1 Le choix actuel . . . 63
6.2.2 Grandeurs et fonctions . . . 64
6.2.3 Grandeurs et fractions . . . 65
6.3 Les trois âges des grandeurs dans les instructions officielles . . . 65
6.4 D’où vient la légitimité de l’utilisation des transformations du plan ? . . . 66
6.5 Une piste à suivre ? . . . 67
6.5.1 L’ouvrage de N. Rouche . . . 67 6.5.2 L’article de R. Bkouche . . . 68 6.5.3 Problématique de l’égalité . . . 69 6.5.4 Problématique de la forme . . . 69 Bibliographie 71 7 Annexes 73 1 Eléments de Clairaut . . . 73
2 La réforme des mathématiques de 1902 . . . 75
2.1 Le programme de géométrie plane dans la réforme de 1902 . . . 75
2.2 Les grandeurs dans l’ouvrage de C. Meray de 1874 . . . 76
2.3 Géométrie élémentaire de Vacquant et Macé - Édition 1903 . . . 77
3 La réforme des mathématiques modernes . . . 78
3.1 A l’école élémentaire . . . 78
3.2 Au collège . . . 80
4 La contre réforme de 1977 . . . 82
4.2 Arrêté du 16 novembre 1978 . . . 84 4.3 Circulaire 77-157 du 29 avril 1977 . . . 88 5 La réforme de 1985 . . . 97 5.1 Niveau 6ème . . . 97 5.2 Niveau 5ème . . . 98 5.3 Niveau 4ème . . . 98 5.4 Niveau 3ème . . . 99
6 Le programme de 1998 sur les grandeurs au collège . . . 100
7 Les programmes du XXIe siècle . . . 101
7.1 Les programmes antérieurs à 2019 . . . 101
Remerciements
Je remercie la providence qui a fait que j’ai pu suivre, un jour de l’année 2017, sans l’avoir demandé, un stage animé par S. Velon et Y. Matheron. C’est suite à ce stage que je me suis lancé dans ce Parcours d’Etude et de Recherche en Didactique. Merci donc à ces deux chercheurs pour l’inspiration qu’ils ont pu m’apporter.
Je tiens aussi à remercier les enseignants qui sont intervenus pendant ces deux années du Master 2 - Parcours de Recherche en Didactique des Mathématiques, à savoir M. Artaud, T. Assude, T. Bloor, K. Millon-Fauré, P. Arnoux, J-P Bourgade, Y. Matheron, avec une pensée toute particulière pour C. Mauduit, qui, à notre grand regret, nous a hélas prématurément quitté récemment. Deux années n’ont pas été de trop pour que nous, les étudiants, quittions les rapports que nous avions envers les mathéma-tiques en notre qualité d’enseignants , et que nous adoptions ceux de chercheurs en didactique. Le travail acharnés de tous a permis que cette alchimie fonctionne et aboutisse, j’en suis persuadé, aux objectifs fixés. Je remercie Teresa Assude pour son soutien et pour la confiance qu’elle m’a accordé dans la réalisation de cette étude.
Enfin, je remercie chaleureusement Costanza Alfierri, Emmanuelle Thomas, Juliette Ménard et Del-phine Paul, ces quatre drôles de dames avec qui j’ai eu plaisir et honneur de travailler. Je crois pouvoir affirmer que nous avons formé un groupe dynamique dans lequel ont régnés travail, solidarité et amitié. Avec elles, la compétence du groupe que nous avons formé a dépassé la somme des compétences de chacun de ses éléments. Une constatation qui est un comble pour un mémoire sur les grandeurs calculables. . .
En 1975, année vraisemblablement déjà très marquée à la fois par la précédente réforme des mathéma-tiques modernes, qui commençait sérieusement à montrer ses limites, et par la prochaine contre-réforme qui allait véritablement débuter deux années plus tard, j’entrais au collège. Mes enseignants m’ont en-seigné des notions de mathématiques dans une période pour le moins troublée du point de vue des programmes scolaires. Leur attitude oscillait entre deux positions : continuer sur le programme en cours (la réforme des mathématiques modernes), ou bien entamer une contre réforme à leur manière. Cette lutte entre les deux réformes, je la retrouverai, curieusement, à nouveau un peu plus tard au lycée, no-tamment en classe de première, lorsqu’on m’enseigna les nombres complexes par exemple. Pendant toutes ces années, je ne me rappelle pas que le mot « grandeur » fit partie du vocabulaire des mes enseignants, tant au collège qu’au lycée, autrement que dans l’expression « ordre de grandeur », qui donc concernait davantage les nombres et les mesures.
Pour moi, et sans doute pour beaucoup d’autres élèves, les grandeurs n’ont pas existé pendant très longtemps en tant que telles, mais uniquement sous forme de mesures et de calculs avec un paradoxe que je ne comprenais pas à l’époque : on n’indiquait jamais les unités dans les calculs, à l’exception du résultat final ! Cela a-t-il été problématique du point de vue scolaire en mathématiques, ou du point de vue de la formation du citoyen que j’étais, concernant mon rapport aux mathématiques et à leur rôle dans la société ? A première vue, je dirai que non : du point de vue scolaire, le « tout numérique » qui a sévi depuis les années 1970 a continué sur sa lancée, pour des raisons que j’ignorais à l’époque, privilégiant les mesures, négligeant les grandeurs qui les sous-tendaient. Quant au point de vue de ma formation de citoyen au regard de ce que pouvaient être les mathématiques, comme beaucoup d’autres là-encore, j’ai bien vite intégré que « faire des maths » c’était « apprendre des réponses à des questions
qu’on ne se posait pas ». Apprendre des réponses suffisait à satisfaire l’Institution, quand bien même vous
ne compreniez pas le sens de ce que vous faisiez.
A contrario, les raisons d’être des sciences physiques apparurent plus clairement dans mes apprentis-sages dès l’année de 5ème, puisqu’elles étaient enseignées à ce niveau à l’époque. Cet intérêt, absent en mathématiques, m’a conduit à des « hautes » études universitaires, jusqu’à la maîtrise de physique. Mais, si la physique apprise en 5ème avait pu susciter en moi de l’intérêt, je dois avouer que la physique ensei-gnée jusqu’en maitrise a considérablement tempéré cette ardeur, car elle se heurtait au même problème de « perte de sens » à un niveau plus élevé cette fois : enseignées de manière très dogmatique et hautement mathématisée, la mécanique quantique, la physique des solides ou même la physique nucléaire devinrent davantage des sources d’ennui plutôt que des tremplins vers des travaux de recherches. Cela a marqué la fin de mes études de physique. Je suis allé voir ailleurs si l’on s’intéressait au « sens » des notions de mathématiques et de sciences. Par chance, l’université de Nantes possédait un pôle d’Histoire et Phi-losophie des Sciences dirigé par l’illustre et très occupé Jean Dhombres. Ce fut un réel soulagement de voir qu’enfin, en étudiant l’histoire de certaines disciplines (optique, astronomie, mécanique, etc.), on pouvait rencontrer des questionnements qui étaient à la base de découvertes majeures et qui justifiaient les réponses obtenues. Ce fut une année mémorable qui m’amena, plus tard, à utiliser l’épistémologie dans les cours de mathématiques que je donnais aux élèves qu’on me confiait.
En tant qu’enseignant en mathématiques, j’ai fait ce que font tous les collègues ne bénéficiant pas de formation en didactique : j’ai utilisé des manuels, essayé de suivre des instructions officielles et des programmes mis en place par des réformes successives, en tentant d’appliquer des « recettes », essen-tiellement pédagogiques, données par des collègues plus anciens, séduis par leur potentielle efficacité,
souvent illusoire. Car s’occuper de "pédagogie" ne pouvait pas remédier à des problèmes d’ordre "didactique" ! Ça, je l’ai appris bien plus tard.
En 2017, en tant qu’enseignant, j’ai suivi une formation sur les PER (Parcours d’Etudes et de Recherches) destinés aux élèves. Elle m’a ouvert la voie vers d’autres manières d’enseigner les mathéma-tiques. J’ai alors décidé de suivre le parcours de recherche en didactique des mathématiques en intégrant le Master 2 de l’Université de Marseille Provence.
Au cours de ce Master, une lecture d’un article de Y. Chevallard1 m’a conforté dans l’analyse que j’avais faite de ma scolarité et de mes années d’enseignement. Notamment le passage suivant que je ne peux m’empêcher de citer malgré sa longueur :
« La lettre X désignant le collectif des « étudiants », Y celui des « aides à l’étude » et le signe
ª(« cœur ») marquant la place de l’enjeu de l’étude, on y observe des systèmes didactiques
S(X, Y ; ł) qui ont une vie non éphémère, qui, par exemple, commencent à vivre en septembre pour se dissoudre en juin, etc. Ce qui va se passer dans S(X, Y ; ł) est (sous-)déterminé par
ª et par l’organisation de l’étude ou organisation didactique OD(ª) qui sera mise en œuvre.
Qu’est-ce donc que cet « enjeu de l’étude » au cœur du fonctionnement d’un système didac-tique ? Sur un point évident, l’état historique des systèmes didacdidac-tiques scolaires apparaissait – et apparaît encore très largement – comme profondément marqué par un processus historique qu’on peut reconstruire sommairement ainsi. Au départ, dans une histoire des enseignements scolaires que je brosse en la stylisant, l’enjeu didactiqueª est une question Q – une question en Comment ? (« Comment effectuer mentalement la division d’un entier par un entier que l’on sait décomposer en facteurs plus petits que 10 ? »), qui appelle en réponse une technique, ou une question en Pourquoi ? (« Pourquoi peut-on "laisser tomber" les restes dans les divisions successives d’un entier par les différents facteurs d’une décomposition donnée du diviseur ? »), qui appelle une réponse technologico-théorique. Un programme scolaire P se compose alors, ty-piquement, d’un certain nombre de telles questions, en sorte qu’on peut l’écrire sous la forme P = (Qi)1≤i≤n. L’étude de la question Q conduit à une réponse R validée par la culture, par
la société, par l’école ; si X est le groupe des élèves de la classe, y son professeur, la chose s’écrira : S(X, y; Q)åR, « formule » que l’on retouchera un peu plus loin. Le programme d’études, lui, s’écrit alors véritablement sous la forme P = (Qi; Ri)1 ≤ i ≤ n. Mais bientôt,
par un court-circuit culturel et didactique, « étudier Q » est regardé comme un synonyme in-utile d’une expression qui la supplante : « apprendre R ». Alors, sans encore que R perde tout à fait son statut de réponse, les questions commencent à s’effacer : le programme d’études P doit désormais s’écrire plutôt sous la forme P = (?; Ri)1 ≤ i ≤ n. C’est ensuite que, en une involution sans doute différenciée (elle n’atteint pas également toutes les disciplines scolaires ni, en leur sein, toutes les praxéologies à enseigner), un refoulement s’opère : les réponses R cessent d’être regardées comme telles et se trouvent hypostasiées en œuvres de la culture ayant valeur en soi et pour soi, œuvres dont les raisons d’être – d’être là, dans la culture, mais aussi dans le programme scolaire – se sont perdues. Un programme scolaire devient ainsi une suite
<1, <2, . . . , <nd’œuvres à étudier : on doit l’écrire désormais sous la forme P = (<i)1 ≤ i ≤ n.
Alors que la réponse R était socialement précieuse parce que, précisément, elle répondait à la question Q, l’œuvre < est considérée maintenant pour elle-même : on la visite avec déférence comme un monument qui a perdu sa fonctionnalité, que l’on honore formellement, et qui n’a plus que de rares emplois, adventices, opportunistes, minuscules. C’est là une tendance que j’ai nommée la monumentalisation des savoirs (et, plus largement, des praxéologies), qui, de la part des institutions comme des personnes, peut aller jusqu’à une passion sombrement fétichiste.»
La mise en mots, et en théorie, de ce que j’ai pu vivre comme beaucoup de mes concitoyens à l’école (au sens large du mot) a pris une force inattendue en 2018 avec cette lecture. Du même coup, la prise de recul par rapport à ce que j’ai pu vivre en a été facilitée, me permettant d’avoir une vue plus large
de la dialectique constante qui oppose les différentes institutions qui ont façonné et façonnent encore le système éducatif français.
Par ailleurs, l’analyse des programmes, anciens et plus récents, montre un thème d’étude qui a attiré mon attention : celui des « grandeurs et mesures ». Mes observations sur l’absence de la notion de grandeur pendant ma propre scolarité, ainsi que les recoupements faits par Y. Chevallard, notamment sur la perte de sens en mathématiques, m’ont logiquement conduit à m’intéresser aux « conditions et contraintes qui
ont fait que les grandeurs, et leurs raisons d’être, aient pu figurer, ou non, dans les différents curricula proposés par les différentes Institutions jouant un rôle dans les notions, qui doivent, ou non, apparaitre dans ces derniers ».
Le présent mémoire est le résultat de cette recherche portant sur la période de 1901 à 2019, avec une excursion au XVIIIe siècle suite à l’ouvrage d’A. C. Clairaut paru en 1743, et une autre au XIXe siècle pour, en quelque sorte, planter le décor de l’époque tant d’un point de vue social que mathématique. La première partie de ce mémoire porte sur le cadre théorique dans lequel se situe cette étude. J’y reprends la question centrale sur la perte de sens et sur les raisons d’être des grandeurs afin de clarifier la problématique, et exposer ensuite les outils, essentiels à ce type d’enquête curriculaire, que sont la théorie des niveaux de codétermination didactique, celle de la transposition didactique et l’approche écologique, et la théorie de l’organisation mathématique. Je la termine en énonçant la formulation de la question principale de ce mémoire ainsi que les questions secondaires qui en découlent. Dans la deuxième partie j’expose la méthodologie que j’ai suivi pour cette enquête curriculaire, en expliquant mon choix des grandeurs à étudier. J’expose aussi comment se sont déroulées les recherches d’instructions officielles, de documents théoriques sur les grandeurs et leurs enseignements, de documents sociologiques et historiques sur la période envisagée (1900 - 2019). A cela se sont ajoutés des documents épistémologiques sur les mathématiques afin d’être le plus complet possible, sans oublier certains manuels scolaires liés aux programmes étudiés.
La troisième partie qui constitue l’essentiel de ce mémoire, porte sur les questions principales et secondaires issues de la problématique envisagée, et sur les réponses obtenues. Je pose d’abord la question de ce qu’est une grandeur et de ce que peuvent être les raisons d’être de son étude. J’examine ensuite l’ouvrage de Clairaut qui, dans le reste de mon étude, représentera un élément de comparaison par rapport à d’autres œuvres étudiées. J’examinerai les programmes de 1901, de 1970, de 1977, de 1985, de 1998 (sommairement), de 2004, 2008, 2015 et 2019, afin d’étudier l’impact qu’ils ont pu avoir sur les grandeurs enseignées, en fonction de quelles transpositions didactiques, sous l’influence de quelles Institutions.
La dernière partie conclura cette étude en faisant le point sur les réponses obtenues et en examinant quelles conséquences possibles on pourrait en tirer sur l’enseignement des grandeurs et sur la pertinence, ou non, de l’exposition de certaines de leurs raisons d’être.
2
Cadre théorique de cette étude et
probléma-tique
2.1
Cadre théorique
Une telle étude curriculaire ne concerne pas des comptes rendus de ce qui se passe en classe. Elle porte essentiellement sur les instructions officielles et sur les ouvrages théoriques et pratiques destinés aux enseignants ou aux élèves. La théorie anthropologique du didactique(TAD) est l’outil idéal pour ce type d’étude. En effet, l’étude des instructions officielles y trouve un outil parfaitement adapté dans ce que Y. Chevallard a nommé "l’échelle des niveaux de codétermination didactique". De plus, pour chaque époque étudiée, il convient d’étudier l’impact du savoir savant et la manière dont il a été décidé de l’enseigner. Ce sera le volet traitant de la "transposition didactique". Enfin,pour que cet ensei-gnement puisse avoir lieu dans les classes, il faut en étudier ce qui, en TAD, porte le non d’organisation
mathématique. Cette organisation mathématique n’est pas innocente. Elle dépend de l’Institution dans
laquelle elle a lieu et donc l’objectif est que ses "sujets" aient, au final, un certain rapport au savoir qui leur a été enseigné. Détaillons ces quatre points de la TAD avant de passer à la problématique de cette étude.
2.1.1 L’échelle des niveaux de codétermination didactique
Selon Y. Chevallard et M. ArtaudChevallard et Artaud (2015), on pourrait définir cet échelle de la manière suivante :
Notons d’emblée que, dans l’univers des types d’objets de la TAD, figurent celui des personnes x et celui des institutions I. Le mot « institution » a ici un sens extensif : une classe est une institution, une famille aussi, une société – la société française, par exemple – également, et il en va de même d’une langue, d’une activité sportive, d’une danse, d’une science, etc. Un personne est n’importe quel spécimen d’être humain, dans la mesure où il ou elle a contracté des assujettissements à des institutions, dont il ou elle devient ainsi le sujet, dans une certaine position p, celle de dernier-né d’une fratrie, de père dans une famille, d’élève dans une classe, de locuteur d’une langue, etc. Cela posé, on introduira ici un premier outil important : l’échelle des niveaux de codétermination didactique. Cette échelle (voir figure 2.1) nous permettra de « trier » les conditions sous lesquelles les personnes x et les institutions I « vivent » et opèrent. On précisera au fur et à mesure, en fonction des besoins, les « étiquettes » qui apparaissent dans ce schéma : « Système didactique », « Pédagogie », « École », etc. Notons seulement, dès maintenant, que ces étiquettes doivent être entendues au pluriel – il y a des systèmes didactiques, des pédagogies, des écoles, etc. –, à une exception près : il n’y a plus aujourd’hui qu’une humanité, depuis la disparition d’Homo neanderthalensis – l’homme de Néandertal – il y a environ 30 000 ans.
Humanité ↑ ↓ Civilisation ↑ ↓ Société ↑ ↓ École ↑ ↓ Pédagogie ↑ ↓ Système didactique
Figure 2.1 – Echelle de codétermination simplifiée
La double flèche placée entre chacun des termes de cette échelle indique que chaque niveau peut exercer ou recevoir une influence de la part de ceux qui l’entourent. Pour en illustrer la pertinence, considérons une partie de cette échelle :
Société ↑ ↓ École ↑ ↓ Pédagogie ↑ ↓ Système didactique
Il va de soit que l’Ecole a pour objet de délivrer un ensemble de savoirs fortement recommandé par son niveau supérieur, la Société. Mais il se peut aussi qu’au sein de cette Ecole, des problèmes surviennent à n’importe quel niveau inférieur. L’Ecole peut essayer d’y remédier "localement" dans un premier temps, mais il se peut que les remèdes trouvés ne soient pas efficaces. A ce moment là, l’Ecole va faire remonter les problèmes à son niveau supérieur qui, en retour, modifiera, par exemple, ses exigences, etc. Sans entrer dans les détails, on peut penser à ce qui a pu se faire, depuis quelques dizaines d’années, dans quelques réformes structurelles de l’enseignement, notamment concernant l’aide aux élèves en difficulté.
L’intérêt majeur de cette échelle de codétermination réside dans le fait qu’elle permet, quasi instanta-nément, de prendre du recul sur les différentes conditions et contraintes issues de ses différents niveaux. Ce découpage, autorise le chercheur à cibler ce qui peut se passer à un certain niveau, et en étudier les conséquences sur les niveaux qui l’entourent.
2.1.2 Sur la transposition didactique et l’approche écologique
2.1.2.1 La transposition didactique
L’usage s’est imposé, en français, de parler de la transmission d’un savoir, comme si un savoir était une réalité ou entièrement matérielle (tel un bien que l’on cède à autrui), ou entière-ment symbolique (comme l’est un droit dont on hérite). Cette apparente simplicité, pourtant, ne résiste pas à l’analyse : la métaphore de la transmission est, en vérité, le symptôme par excellence de la réduction pédagogique du didactique – laquelle, on l’a suggéré, ne s’intéresse que d’assez loin au destin du savoir. De fait, une organisation praxéologique ne saurait être simplement « transmise ». Même lorsque cette organisation existe déjà en mille institutions, on ne saurait la « transporter » en une nouvelle institution à la manière dont on déménage un meuble – par simple transfert. Il convient au contraire de l’y reconstruire, de la recréer en cet habitat nouveau, à l’écologie peut-être fort différente.
"Les savoirs enseignés et leurs formes scolaires de transmission : un point de vue didactique", page 8
2.1. CADRE THÉORIQUE
Cette citation de Y.Chevallard, datant de 1997, illustre qu’il est illusoire de penser qu’on peut passer, de manière binaire, de "ceux qui ne savent pas" à "ceux qui savent". L’étude de la transmission sociale du savoir, qui est l’objet de la didactique, a mis en évidence la nécessité de reconstruire localement, au sein des écoles, des habitats qui vont permettre, à "ceux qui ne savent pas", de rencontrer des situations qui vont les amener à changer de statut, c’est à dire à avoir le rapport au savoir enseigné souhaité par l’Institution dont ils sont les sujets. Dans ces "situations", les savoirs vont vivre avec un double objectif : assurer la transposition du savoir, et s’intégrer en même temps à un curriculum scolaire dont ils vont assumer, avec d’autres savoirs transposés, une partie de la cohésion.
La théorie de la transposition didactique représente un outil indispensable au chercheur en didactique des mathématiques. D’après Y. Chevallard2, son objet est de donner à voir une certaine "distance" entre le savoir savant et le savoir enseigné :
Il convient, en d’autres termes, que le savoir enseigné et le savoir qui lui sert, en quelque sorte, de caution épistémologique au regard de la Société, se ressemblent suffisamment
Les processus de transposition didactique et leur théorisation, page 7
Cette distance s’expliquerait de la manière suivante, dans laquelle on peut distinguer les influences de certains niveaux de l’échelle de codétermination didactique :
L’enseignement d’un savoir, en effet, est toujours la réalisation d’un projet social, plus ou moins largement partagé, porté par au moins certains groupes sociaux. Or un tel projet, lorsqu’il n’est encore que projet, se formule essentiellement hors de l’École, et toujours à l’adresse de la Société, afin de gagner son consentement. C’est que l’École est la chose de la Société ; et que, pour cela, elle n’a pas de véritable autonomie politique
Les processus de transposition didactique et leur théorisation, page 8
L’École n’a pas la liberté de choisir les savoirs qu’elle va enseigner. Les savoirs, objet du débat réfor-mateur, doivent exister hors de l’École !
Plus tard, en 2005, Y. Chevallard précisera ce qu’il entend par cette "distance" :
« L’ordre scolaire tolère mieux, en effet, le regard « forain » lorsqu’il s’en tient au folklore de sa ceinture « pédagogique » et s’interdit de toucher au cœur didactique de l’institution. De là sans doute que la mise en circulation de l’idée de transposition didactique ait suscité émois et résistances : comment peut-on ainsi interroger ce qui doit aller de soi, par exemple l’algèbre que l’école enseigne, et chacun des « objets » qui s’y logent ? Il n’y a pas, s’indigne-t-on, l’algèbre enseignée, mais l’algèbre, tout court ! Telle est la fiction scolaire, et malheur à qui se met en tête d’en révéler tout à la fois l’arbitraire et la nécessité. Contre cette fiction, l’analyse de la transposition didactique fait apparaître les tours et détours par lesquels il a fallu passer pour aller de l’algèbre « savante » (par exemple) à l’algèbre « enseignée ».
"Passé et présent de la didactique", Chevallard, 2005b, page 3
Mais, si distance il y a, ressemblance il doit y avoir aussi !
Cette ressemblance, qui est le but des « manœuvres transpositives », et qui fonde le jugement de conformité du savoir enseigné au savoir à enseigner, ne peut être qu’assez grossièrement mesurée ; elle s’évalue à la présence de certains emblèmes, et d’abord d’un certain lexique. . .
"Les processus de transposition didactique et leur théorisation", Chevallard, 1991, page 10
Mais cette volonté de ressemblance porte en elle des risques : 2. Chevallard,1991
Il arrive même que l’effet contraire à celui recherché soit obtenu. À trop viser la ressemblance, on engendre de la dissemblance.
Chevallard, 1991 page 14
Ainsi peuvent s’expliquer certaines réformes, des contenus enseignés, mises en place dans le monde édu-catif. Nous verrons que la place des grandeurs dans ces enseignements variera en fonction de ces réformes. 2.1.2.2 Sur l’approche écologique
La notion d’habitat constitue un autre élément essentiel à la TAD, et donc au chercheur. Car décider de la transposition d’un savoir sans lui procurer un habitat dans lequel il va vivre sera forcément voué à l’échec. Par ailleurs, dans cet habitat, ce savoir va devoir jouer un rôle qui lui sera propre. Il appartient au chercheur de l’expliciter.
Ainsi, le fait que le "jeu" des institutions poussent en avant ou retirent certaines notions de l’enseigne-ment va poser la question de l’écologie dans laquelle ces notions ont vécu, vivent ou vont pouvoir vivre, ou survivre, ou bien disparaitre. Se poseront aussi les questions de savoir en quoi elles ont pu, peuvent ou pourront être utiles à d’autres savoirs au sein du curriculum dans lesquelles elles se trouvent ?
Pour répondre à ces questions, l’analyse des praxéologies (cf. section "Sur l’organisation mathé-matique") mises en place est vitale.
À l’origine d’une praxéologie se trouvent une ou plusieurs questions qui, génétiquement, appa-raissent comme les raisons d’être de l’organisation praxéologique, parce que celle-ci est censée leur apporter réponse.
"Les savoirs enseignés et leurs formes scolaires de transmission : un point de vue didactique", page 3
Ces questions trouveront leurs réponses dans l’analyse des organisation mathématiques telles qu’elles sont décrites dans les instructions officielles.
2.1.3 Sur l’organisation mathématique
Une des composantes de la TAD, l’organisation mathématique (OM), permet de rendre compte uni-quement des questions qui ont motivé la recherche d’une solution et donc d’un nouveau savoir, et sur la théorie qui en est le support et donc la justification. Cette OM regroupe ce qu’en TAD nous nommons les praxéologies3 mises en place par l’enseignant, ou par les instructions officielles, ou par des "institutions diverses", afin que le rapport des élèves au savoir soit conforme à celui qui est attendu.
Ainsi, pour un objet de savoir, il faudra définir :
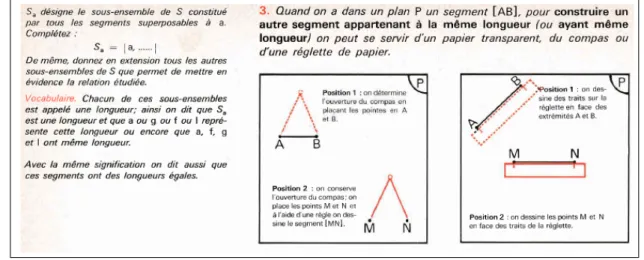
Le type de tâche précis auquel il se rapporte, présenté sous la forme d’une injonction commençant par un verbe d’action à l’infinitif. Par exemple, s’agissant de grandeurs, un type de tâche pourrait être "Comparer deux longueurs sans utiliser de règle graduée" ;
La technique qu’il faudra utiliser pour réaliser ce type de tâche précis. Dans l’exemple précédent, cela pourrait être "En utilisant du papier calque", ou "Par superposition", ou encore "En utilisant
un compas", ou bien "En utilisant une troisième longueur comme référence", etc. ,
La technologie (discours) qui justifie l’utilisation de celle technique. Dans le cas envisagé ci-dessus, une technologie pourrait être "La symétrie axiale et ses propriétés" ;
La théorie (discours) qui justifie la technologie. Dans notre exemple, ce pourrait être "La théorie
des transformations du plan et ses invariants".
Pour diverses raisons , les instructions officielles ne mentionnent que très exceptionnellement ces quatre composantes. Généralement, dans le meilleur des cas, seules les deux premières composantes ap-paraissent, la première de ces composantes étant plutôt exprimée à la manière d’une suggestion. Par
2.1. CADRE THÉORIQUE
exemple, ce que donne à voir le programme de 2019 du cycle 3, pour l’année de CM1, sur le thème "grandeurs et mesures" :
Les élèves comparent des surfaces selon leur aire
| {z }
Le type de tâche
par estimation visuelle, par superposition ou découpage et recollement
| {z }
La technique
.
Changement de niveau d’abstraction oblige, les instructions du niveau 6ème pour la même année donnent ceci : Le type de tâche :
Selon l’avancement du thème « nombres et calcul », les élèves réinvestissent leurs acquis de CM pour calculer des périmètres simples ou complexes.
La technique :
Ils apprennent la formule de la longueur d’un cercle et l’utilisent après consolidation du produit d’un entier par un décimal, dans un premier temps, puis du
produit de deux décimaux.
Nous ne pouvons que constater l’absence de toute référence au groupe "technologico-théorique". Pour notre étude, nous mentionnerons donc, a minima, les types de tâches et les techniques quand elles seront indiqués dans les instructions officielles. L’analyse de la transposition didactique, réalisée ou non, nous permettra parfois de montrer la théorie qui sous-tend ces deux composantes. Mais gardons à l’esprit que ce groupe praxéologique constitué des types de taches, techniques, technologies et théories, reste soumis aux aléas des interactions entre les différents niveaux de l’échelle de codétermination didactique, comme le rappelle Y. Chevallard dans plusieurs de ses articles :
« la didactique se voue à étudier les conditions et contraintes sous lesquelles les praxéologies se mettent à vivre, à migrer, à changer, à opérer, à dépérir, à disparaître, à renaître, etc., au sein des institutions humaines. »
"La didactique dans la cité avec les autres sciences", Chevallard, 2005a, page 3
2.1.4 Sur le rapport à un objet du savoir
Pour en rester à un niveau élémentaire, nous savons que la notion de "carré" sera différente selon que l’on est un élève de cours préparatoire (où l’on s’intéressera surtout à la forme) ou élève en 5ème en collège (où l’on envisagera toutes ses propriétés et ses liens avec le parallélogramme). Ce rapport au savoir est donc relatif à l’institution qui le délivre.
"[...]la notion de rapport – d’une personne x à un objet o, R(x, o), ou d’une institution I à cet objet, ou plus exactement des sujets (idéaux) de l’institution I en position p dans I à cet objet o, RI(p, o). Il s’agit, par cela, d’une part de subsumer sous une unique entité tout ce que la culture, dans sa frénésie « psychologique », a élaboré autour de la vie de l’esprit, d’autre part d’objectiver l’infinitude bigarrée des postures personnelles ou institutionnelles pouvant coexister au sein d’un espace cognitif culturellement partagé. Il y a par exemple la notion supposée de logarithme, qu’aucune personne ni aucune institution ne saurait « posséder » ; et il y a le rapport que j’ai, personnellement, à cette notion, comme il y a le rapport que l’on devrait avoir à elle quand on occupe légitimement telle position en telle institution – rapport qui, au lycée, ne sera pas le même pour le professeur de mathématiques et pour le professeur de physique et chimie par exemple. La notion supposée est celle qu’on évoque lorsque, par exemple, tel sujet de telle institution me demande si je connais cette notion : la notion supposée est alors le référent d’un jeu d’évocations ; elle n’est pas sa notion à lui ni ma notion à moi. Elle est ce qu’il faut que nous supposions ensemble, pris que nous sommes dans une culture commune, pour échapper au solipsisme. Elle est la condition de l’intersubjectivité et de l’inter-institutionnalité."
"Passé et présent de la didactique", Chevallard, 2005b, page 4
Y. Chevallard indique que, pour un même objet de savoir, les attentes des institutions diffèrent en fonction de leurs besoins. Les rapports des élèves au savoir enseigné seront donc multiples. Mais aucune de ces institutions ne pourra s’arroger le droit d’avoir la vérité sur cet objet. Autrement dit, la connaissance est relative à l’Institution dans laquelle elle est dispensée. L’Homme étant constamment le sujet de plusieurs institutions, il se peut qu’en lui coexistent des rapports différents relativement au même objet. Pour prendre l’exemple des grandeurs, la notion intuitive de ce que peut être une grandeur sera à mettre en parallèle avec la notion enseignée de mesure d’une grandeur qui, elle-même, pourra être liée aux mesures rencontrées dans la vie quotidienne, ou à des notions scolaires de calculs, etc.
Dans notre étude, il faudra donc que nous interrogions le rapport aux grandeurs que les Institutions, impliquées dans la mise au point des programmes scolaires, entendent faire adopter à leurs sujets, et ce aux différentes époques étudiées.
2.2
Problématique de l’étude
En prenant en compte, dans ce qui précède, la période historique sur laquelle l’étude porte, la question de la perte de sens dans l’enseignement des mathématiques, les difficultés rencontrées lors de la la transposition des savoirs savants, la problématique principale qui se dégage de l’enseignement des grandeurs peut s’exprimer de la manière suivante :
Problématique principale
Entre 1900 et 2019, quelles sont les conditions et les contraintes qui ont pesé sur l’enseignement des grandeurs, et notamment sur
l’enseignement de leurs raisons d’être ?
Cette problématique principale, de facto, en pose beaucoup d’autres, parmi lesquelles :
Problématiques secondaires
Quelles sont les raisons d’être des savoirs sur les grandeurs ? Comment ces raisons d’être ont-elles vécu sur la période étudiée ? Comment ces raisons d’être ont-elles été impactées par les différentes
3
Méthodologie de l’enquête
Cette étude "curriculaire" sur les grandeurs, et leurs raisons d’être, au sein de l’enseignement des mathématiques au collège, porte sur plus d’un siècle. Une telle étude, sur une période de temps aussi longue, a soulevé quelques contraintes qu’il faut énoncer dès maintenant afin de clarifier son objet.
3.1
Le choix des grandeurs à étudier
A l’origine, l’école devait s’isoler des pressions de la vie courant afin de prendre en charge la partie "didactique" des apprentissages des petits de l’homme. Voici par exemple ce que rappelle Y. Chevallard4 à l’occasion du Master M1, en 2009 :
Le mot « école » vient d’un terme grec, schole, qui veut dire loisir, entendu au sens de libre activité. Le latin schola reprend cette acception, d’abord donnée au terme ludus, qui veut dire aussi « jeu ». Évoquant l’école (schola) comme lieu d’enseignement, Festus précise que les enfants doivent s’y adonner aux études libérales, toutes choses étant par ailleurs suspendues (ceteris rebus omissis, vacare liberalibus studiis pueri debent). L’idée essentielle tient déjà dans cette maxime : l’école est inventée pour que le petit homme puisse cultiver ses facultés par des études délivrées des contraintes du moment. C’est que de telles études ont pour seule fin l’épanouissement des potentialités de chacun en authentiques facultés. Reposant sur ces facultés, le sort des activités qui conditionnent la vie et la survie n’en sera pas pour autant négligé : il sera au contraire mieux assuré. Le succès d’une telle entreprise requiert que le lieu et le temps de ces études soient préservés des urgences de la vie, qui sinon les marqueraient de leurs limites. Ainsi naît l’idée d’un espace et d’un temps de loisir consacré à l’étude. On tient ici l’idée fondatrice de l’école.
page 191
En réalité, élèves et enseignants appartiennent à des institutions extra scolaires (famille, groupes d’amis, associations, etc.). Ainsi, concernant les grandeurs, élèves et enseignants baignent, dans la vie quotidienne, dans des environnements où les grandeurs les plus diverses coexistent sans aucun question-nement particulier : les débits, les volumes, les prix, les longueurs, les aires, les vitesses instantanées ou moyennes, la pression atmosphérique, etc. La liste est trop longue pour être exhaustive. On peut alors espérer que l’étude des grandeurs, dans les instructions officielles ou les manuels scolaires, soit plus ciblée. Mais la lecture de n’importe quel programme de primaire ou de secondaire, de n’importe quel manuel scolaire de mathématiques, montre clairement que ce n’est pas le cas : les longueurs côtoient très vite les aires, les volumes, les monnaies, les durées, les masses, les capacités, etc. Et l’introduction précoce de la proportionnalité, sous forme d’une simple division ou multiplication entre deux grandeurs, peut engendrer des grandeurs composées qui peuvent très vite interférer avec les grandeurs simples déjà connues5. Sans parler de l’apparition d’une grandeur scalaire en cas de rapport entre deux grandeurs de même espèce.
4. Chevallard,2009
5. Il est difficile de faire dire à des élèves de 6ème que le quotient de la division d’un gâteau pesant 200g en 4 parts est égal à "50 grammes par part".
On l’aura compris, il fallait trancher afin de simplifier notre propos sur le rôle joué par les raisons d’être des grandeurs au collège. Revenir à l’essentiel était le plus simple. Or, les notions de longueurs et d’aires sont les premières à apparaitre : tout être humain, par sa condition "d’être prématuré", apprend de son environnement d’abord. Les mots "loin", "proche", "plus grand", "plus petit", etc. sont parmi les premiers mots appris et compris par les enfants en bas âge.
Nous avons donc choisi de n’étudier principalement que ces deux grandeurs afin de minimiser les conditions et les contraintes à étudier. On peut raisonnablement inférer que si l’enseignement de ces deux grandeurs "simples" a déjà été impacté par les différentes réformes, il a dû en être de même pour les autres, qu’elles aient été simples ou composées.
3.2
Recherche des instructions officielles
On pourrait penser que nos sociétés de "communication" nous permettent d’accéder aisément à des sources d’informations officielles, comme les programmes scolaires, qu’ils soient actuels ou éloignés dans le temps. Pour ce qui concerne cette étude, la recherche d’instructions officielles de l’enseignement secondaire a rencontré quelques contraintes, liées à diverses institutions dont les rôles ne sont pas toujours explicites. Le site web du ministère de l’Education et de la Jeunesse6 permet, en théorie, l’accès aux programmes de 1998 à 2019, par l’intermédiaire d’une liste déroulante présente sur la page d’accueil de son site Internet. Seulement, deux inconvénients majeures freinent, ou empêchent, la recherche des numéros du Bulletin Officiel traitant de la question des programmes scolaires :
1. en l’absence de connaissance de la date exacte où un programme officiel de mathématiques a été établi et diffusé, l’utilisateur de ce site devra passer en revue tous les résultats fournis par le moteur de recherche ; Avec un peu de patience, on peut alors retrouver une bonne partie des programmes officiels de 1998 à nos jours, mais, pour l’année 1998, seul est disponible le programme du niveau 3ème. Pour les programmes des niveaux précédents, il faut chercher ailleurs. . .
2. si on cherche des programmes officiels antérieurs à 1998, le même site semble avoir le remède, comme en témoigne la figure 3.1 :
Figure 3.1 – Quand Canopée n’est d’aucune aide. . .
et c’est là que de nouvelles difficultés surviennent : selon le site du réseau Canopé, leur objectif est de "développer la refondation de l’école et de conjuguer innovation et pédagogie pour faire
entrer l’École dans l’ère du numérique". Questionnés afin d’obtenir les B.O. antérieurs à 1998,
leur réponse a été :
3.3. LES DOCUMENTS THÉORIQUES SUR LES GRANDEURS
- "Nous sommes désolés, nous n’assurons plus ce genre de services et nous ne pouvons pas vous
aider dans vos recherche. Le site du ministère de l’Education n’est pas à jour. C’était un service qui était délivré par les anciens CRDP.".
Le site Eduscol7 n’est pas en reste de ce point de vue. Censé permettre aux enseignants de s’informer,
on peut lui faire confiance pour se procurer le programme actuel en mathématiques, et il dispose même de documents d’accompagnement sur l’enseignement du thème "grandeurs et mesures". Mais curieusement, dans ce dernier document, très approximatif, il n’est pas fait mention du document d’accompagne-ment de 20078, portant sur le même sujet, et qui était beaucoup plus complet, tellement même qu’il était d’une lecture plutôt difficile pour les enseignants. Ce dernier document, de 2007, semble donc "perdu" et ceux qui n’en n’ont jamais eu connaissance n’ont quasiment aucun espoir de se le procurer. Les documents officiels antérieurs à 1998 doivent donc être cherchés ailleurs. Mais où ?
Le réseau des réseaux : Internet ! En fait, il s’agit avant tout d’essayer de voir si des particuliers, des associations, etc. mettent en ligne certains de ces programmes, parfois volontairement, parfois par hasard. Un site a été d’une aide certaine. Il s’agit du sitehttps://manuelsanciens.blogspot.com/qui, comme son nom l’indique, est alimenté de manuels et autres ouvrages anciens, par des personnes qui souhaitent simplement les partager, quelles que soient les disciplines concernées. Nous avons pu y trouver certains ouvrages, notamment celui de L. Leterrier9, contenant entre autres, les instructions officielles de la réforme des années 1970 (niveaux élémentaires et secondaires) comparées avec celles de 1945.
3.3
Les documents théoriques sur les grandeurs
Compte tenu de notre problématique, il fallait nous procurer une documentation liée à la fois à la didactique et à la théorie des grandeurs, en gardant à l’esprit que les grandeurs apparaissent aussi dans d’autres disciplines (sciences physiques, mécanique, etc.). En utilisant les mots "grandeurs" et "collège", un moteur de recherche permet d’obtenir les noms de chercheurs ayant travaillés sur le sujet comme Y. Chevallard et M. Bosch10, N. Rouche11 , R. Bkouche12 .
Sans oublier d’autres auteurs et d’autres lectures, comme "les actes de la 11ème école d’été de didactique
des mathématiques" (textes parus en 2002), exclusivement consacrée aux grandeurs dans l’enseignement.
3.4
Les documents sociologiques et historiques
La recherche du programme de la réforme de 1902 nécessita des investigations plus longues. L’ouvrage de H. Gispert13, sur la réforme de l’enseignement de 1902, contenait quelques pistes intéressantes dans sa bibliographie. De fil en aiguille, le programme de cette réforme se matérialisa sous la forme d’ouvrages comme celui de Vacquant et Macé14, fortement inspirés de l’ouvrage de C. Meray15. Les trous importants
dans la recherche des programmes se comblaient peu à peu.
Est venu s’ajouter l’ouvrage de L. Heurdier16sur les politiques de l’éducation en France qui a permis d’avoir une vue d’ensemble sur les réformes successives à partir de 1800.
Enfin, l’ouvrage de A. Corbin17sur "L’avènement des loisirs entre 1850 et 1960 " a permis de dresser un schéma plus complet sur les modifications sociales, pendant cette période, et sur l’expansion croissante
7. https://eduscol.education.fr/ 8. Grandeurs et mesures au collège 2007
9. Leterrier,1971
10. Chevallard et Bosch,2001et Chevallard et Bosch,2002
11. Rouche,1994et Rouche et al.,2008
12. Lehman et Bkouche,2003et Bkouche,2009
13. Gispert,2007
14. Vacquant et Macé de Lepinay,1903
15. Meray,1874
16. Heurdier et Prost,2014
de la culture au sein des différentes catégories sociales.
3.5
Les documents épistémologiques sur les mathématiques
Selon Y. Chevallard18, la double transposition didactique du savoir savant nécessite que les ensei-gnants soient confrontés à cette problématique. Il nous fallait donc rechercher des documents, épistémo-logiques ou fondateurs, concernant certains savoirs savants qui ont émergés comme reflétant à la fois des
avancées majeures en mathématiques, et la nécessité sociale de les intégrer à l’enseignement, dès le plus
jeune âge. Pour les besoins de cette étude, notre choix s’est porté sur les ouvrages suivants : 1. les mathématiques d’Euclide ;
2. les éléments de géométrie de Clairaut19; 3. le programme d’Erlangen de F. Klein(1872) ;
4. les éléments de mathématiques du groupe Bourbaki (1950).
Nous verrons que selon le savoir savant transposé, les instructions officielles donneront aux grandeurs, et à leurs raisons d’être, des importances parfois fort différentes.
3.6
Les manuels scolaires
Les instruction officielles ayant été parfois difficiles, voire impossible à obtenir, le recours à certains manuels scolaires s’est parfois avéré nécessaire pour y chercher les types de tâches et les techniques associées, généralement visibles dans ces ouvrages.
Nous avons déjà cité le manuel de Vacquant et Macé20 , pour la réforme de 1902.
Pour la réforme de 1977, nous avons choisi les manuels Mauguin (Mauguin, 1977) , parus aux éditions Istra, notamment le manuel de niveau 6ème.
Pour les suites de la réforme de 1985, nous avons choisis plusieurs manuels qui courent jusqu’en 2018 : — Maths 6ème (Barra et al.,1990, Nathan) ;
— nouveau Transmath 6ème (Denux et al., 1996, Nathan) ; — Math 6ème (Pène et Depresle,1996, Belin) ;
— Maths 6ème (Delord et al.,2000, Hachette) ;
— Maths 6ème (Charmarty, Merlier et Freycenet,2005collection Diabolo, Hachette) ; — et Sesamath 6ème (Sesamath 6ème 2018).
18. Chevallard,1991
19. Clairaut,1743
4
Les questions . . . et les réponses obtenues
Afin de clarifier l’objet de ce mémoire, il nous a fallu chercher les raisons d’être "originelles" de l’étude des grandeurs. Les cours de Master 2 de recherche en didactique des mathématiques nous ont apporté quelques pistes, confirmées par l’étude de quelques documents historiques et théoriques.
4.1
Quelle est l’origine de l’intérêt porté aux grandeurs ?
4.1.1 Une approche cognitive
L’étude, réalisée au tout début de notre recherche, des "Eléments" de Clairaut, contient un passage important :
"J’ai pensé que cette science, comme toutes les autres, devait s’être formée par degrés ; que c’était vraisemblablement quelques besoins qui avaient fait faire les premiers pas et que ces
premiers pas ne pouvaient pas être hors de portée des commençants puisque c’était des commençants qui les avait faits."
Clairaut, 1743, préface, page iij
Le passage, mis en gras par nous, montre une idée très chère à Clairaut : la progressivité des ap-prentissages ! On doit présenter aux "commençants" des observations qui sont à leur portée.
Plus tard, la logique de l’argument de Clairaut se trouva confortée lors des lectures faites pour la réalisation de cette étude, notamment l’ouvrage de Rouche et al.,2008 :
Constatant que les objets géométriques les plus simples tels que les traits rectilignes, les carrés, les rectangles, les cubes, les boîtes à faces rectangulaires, les boîtes cylindriques et quelques autres sont familiers à tout un chacun et ne requièrent dans l’immédiat aucune définition, nous nous concentrons plutôt sur des phénomènes que sur des objets. Les phénomènes, en l’occurrence, sont des situations ou des relations que l’on observe autour de soi ou que l’on peut aisément faire apparaître, qui sont dignes d’attention et parfois intrigantes.
"Du quotidien aux mathématiques", page 4
La progressivité qui transparait dans les deux citation précédentes permet de clarifier l’objet de la géo-métrie avec, au final, une définition plus complète :
Définition : La géométrie, c’est toujours la science de l’espace mais ce n’est pas toujours le même espace (passage de l’espace sensible à l’espace abstrait)
Cette dernière définition a trouvé, par ailleurs, un nouvel écho lors du premier cours sur les "Images
Le mot "Abstraire" a pour origine "tractio" qui signifiait "tirer de ...
En l’occurrence, on tire quelque chose (qui nous parait significatif) d’un objet concret. Cette abstraction va nous servir à modéliser l’objet initial en éliminant les détails non pertinents. Cette modélisation nous permettra ensuite de travailler sur elle, plutôt que sur l’objet lui même.
Cours du 3 octobre 2018
L’enseignement de la géométrie (mais on pourrait en dire autant pour le calcul) doit donc se faire par étapes successives, chacune ayant son importance21. Nous pouvons les résumer succinctement par le
schéma suivant :
Enseignement de la géométrie
Concret (action sur l’environne-ment/usage des sens)
Abstraction (on extrait quelque chose du concret) L’abstraction comme objet d’étude Découvertes d’invariants
Figure 4.1 – Enseignement de la géométrie Mais qu’allons-nous extraire du concret ?
Une réponse à cette question apparait dans le texte de N. Rouche :
Cette géométrie étudiera ce qui, dans l’univers quotidien des grandeurs et des formes, intrigue ou embarrasse le sens commun. . .
"Comment repenser l’enseignement de la géométrie ?", Rouche, 2000, page 611
C’était là, à n’en pas douter, l’objectif des Euclide, Clairaut, Meray et F. Klein dans son pro-gramme d’Erlangen, précise N. Rouche à la fin de l’article cité.
Les grandeurs sont à la source de l’enseignement de la géométrie, et leur étude permet de s’af-franchir des limites imposés par nos sens. A un moment donné, le "cognitif" doit intervenir pour dépasser ces limites.
4.1.2 Un début d’approche mathématique
L’œuvre d’Euclide, les "Eléments", document fondateur des mathématiques savantes et enseignées pendant plus de 1500 ans, se compose de plusieurs livres. Les cinq premiers concernent la géométrie, et les grandeurs apparaissent dès qu’il s’agit de comparer des segments de droites, ou des angles. Les livres V et VI terminent cette série par l’étude des rapports de grandeurs appliqués aux longueurs et aux aires.
On peut se demander quels problèmes "concrets" ont poussé les hommes à étudier ces "objets" nommés "grandeurs".
Quelques éléments de réponses nous sont apparus en plusieurs occasions.
Quand on parle "géométrie", l’étymologie du mot nous revient vite en mémoire : "la mesure de la terre". Cette expression proviendrait23 de la nécessité d’effectuer des mesures afin que, suite aux débor-dements du Nil, chaque personne récupère son terrain sans être lésée par rapport aux autres.
21. Pour reprendre les mots de N. Rouche22, nous pourrions écrire : « [. . . ]pour enseigner les mathématiques, il ne faut
pas se précipiter vers la science constituée, et surtout pas vers ses fondements. Il faut plutôt aller avec une lenteur calculée et par étapes motivées, de la pensée commune et des situations particulières vers des structures de plus en plus générales. »
4.2. QU’EST-CE QU’UNE GRANDEUR ? (APPROCHE MATHÉMATIQUE)
En laissant de côté une potentielle polémique sur les origines de la géométrie, nous pouvons conserver l’idée qu’elle véhicule : il y aurait une problématique de comparaison qui serait intimement liée à une problématique de la mesure.
Examinons ces deux problématiques un instant.
La comparaison entre, par exemple, deux longueurs, ne va pas de soi. D’abord va se poser la question quel(s) moyen(s) utiliser pour comparer deux grandeurs. Bien sûr, notre premier réflexe va nous amener à utiliser nos sens, notamment la vue. Pourtant celle-ci est limitée et ce dans de multiples circonstances : — si nous pouvons comparer aisément les longueurs de deux bâtons quand elles sont très différentes l’une de l’autre, le problème devient en revanche plus difficile si leurs longueurs sont très légèrement différentes ;
— comment pouvons-nous comparer des longueurs quand l’une d’elle, ou les deux, nous sont inac-cessibles24?
— mêmes choses pour ce qui concerne les comparaisons d’aires, d’angles, etc.
Par ailleurs, une comparaison ne peut aboutir qu’à deux résultats : soit les deux grandeurs, de même espèce, sont différentes l’une de l’autre, soit elles sont semblables ou égales. Dans le deuxième cas, il faudra expliquer et définir l’égalité entre deux grandeurs. Dans le premier cas, de nouvelles questions vont naturellement apparaître. En effet, on pourra se demander :
— quelle longueur faut-il ajouter à la plus petite pour égaler la plus grande ? — quelle longueur faudrait-il enlever à la plus grande pour égaler la plus petite ?
— est-il possible de recouvrir une longueur donnée au moyen de ces deux longueurs différentes ? — ou encore combien de bâtons, tous de même longueur, faut-il pour égaler un bâton plus grand ?
Est-ce toujours possible ? et si cela ne l’est pas, que faire ?
Nous avons donc débouché naturellement sur une problématique d’addition ou de soustraction entre des grandeurs de même espèces, la dernière question posant par ailleurs la problématique de la multiplication ou de la division d’une grandeur.
La mesure, quant à elle, intervient à la suite de la parfaite compréhension de ce qui se passe lors du produit d’une grandeur par un nombre, ou lors du rapport de deux grandeurs. A l’origine, le nœud du problème réside dans l’étude des rapports de grandeurs. Celle-ci doit aboutir à ce que nous pouvons appeler, de manière impropre mais suffisante pour l’instant, la réduction des grandeurs à des nombres. L’abstraction va alors s’opérer en substituant des nombres aux grandeurs. A ce mo-ment là seulemo-ment, le concret "physique" devient un "concret numérique". La mesure est donc une construction humaine issue d’une abstraction des grandeurs depuis une réalité physique et matérielle.
4.2
Qu’est-ce qu’une grandeur ? (approche mathématique)
4.2.1 Définition(s)
La littérature théorique sur les grandeurs propose plusieurs définitions d’une "grandeur". Cette section en montre quelques unes.
L’article de N.Rouche25, paru en 1994, montre les grandeurs, sous leur aspect axiomatique (cf. sous-section "Axiomes relatifs aux grandeurs"), en utilisant les classes d’équivalences. Il abouti à la défi-nition suivante :
Une grandeur est, par définition, un élément de l’ensemble quotient de X par la relation d’équi-valence ∼.
"Qu’est-ce qu’une grandeurs ?", page 33 24. Cette problématique inscrit les grandeurs dans le cadre de la géométrie dans l’espace tout autant que dans la géométrie plane.
Peu claire pour un non initié au lexique des mathématiques ensemblistes, nous pouvons l’interpréter de la manière suivante :
Quand des "objets" sont extraits d’un ensemble plus vaste du fait d’une caractéristique commune, le sous-ensemble obtenu est une grandeur.
Concrètement, par exemple, si nous considérons un ensemble de buchettes de bois en tous points iden-tiques à l’exception de leurs longueurs, nous pouvons en extraire différents sous-ensembles contenant chacun des buchettes la même longueur. Chacun de ces sous-ensembles sera alors une grandeur, et tous ces sous-ensembles seront des grandeurs de même espèce. Nous serons alors à même d’effectuer des "opé-rations" sur les éléments de ces sous-ensembles comme :
— comparer des longueurs de buchettes extraites de différents sous-ensembles ; — ajouter des buchettes de même longueur ;
— ajouter des longueurs différentes ;
— soustraire une longueur plus petite à une plus grande ; — établir un classement par ordre croissant de longueurs ; — etc.
En 2001, Y. Chevallard et M. Bosch26 évoquent une définition de ce qu’est une grandeur en citant
un ouvrage paru en 1958, la "Nouvelle Encyclopédie autodidactique Quillet" :
[une grandeur est] tout ce qui peut être diminué au augmenté, sachant que les grandeurs ma-thématiques sont celles pour lesquelles on peut définir l’égalité et la somme.
"Les grandeurs au collège : une Atlantide oubliée", pages 8 et 9
Dans cette deuxième définition, il semble qu’il y ait des grandeurs "mathématiques" et d’autres qui ne le seraient pas.
C’est qu’en effet, certaines grandeurs, comme les températures, ne sont pas calculables bien qu’elles soient mesurables. C’est d’ailleurs la raison pour laquelle, comme nous le verrons avec l’étude de la réforme de 1902, la 1ère moitié du XXe siècle correspond à une séparation entre les disciplines : les sciences physiques s’écartent du giron des mathématiques. Le cloisonnement disciplinaire va entrainer un cloisonnement des grandeurs. Ce cloisonnement persiste encore aujourd’hui.
Ainsi, pour les mathématiques élémentaires, on gardera les grandeurs qu’on peut voir, sentir, toucher, et donc, sans appareil de mesure, comprendre le sens que peuvent avoir les actions de "com-paraisons" de "soustractions" et "d’additions" sur ces grandeurs. Autrement dit, aux mathéma-tiques "élémentaires" sont affectées
— les "grandeurs simples" comme la longueur (terme pris ici dans le sens de la grandeur "lon-gueur"), la masse, les angles, les monnaies, et le temps,
— les grandeurs composées comme l’aire et le volume.
Notons que les grandeurs "quotients" comme les vitesses, les masses volumiques, les débits, etc., si elles apparaissent en mathématiques durant le collège, sont à la frontière des sciences physiques. Elles obéissent à d’autres règles, ce qui explique notamment les difficultés rencontrées dans l’enseignement de la proportionnalité ou lors des opérations avec les fractions.
4.2.2 Axiomes relatifs aux grandeurs
En mathématiques, au moment de la théorisation, une règle générale consiste à partir d’évidences partagées par tous que l’on nomme "axiomes"27 Dans les sous-sections "Une approche cognitive" et "Un début d’approche mathématique", nous avons donné les versions littérales des axiomes sur les grandeurs. Il reste à leur donner un formalisme mathématiques, la fameuse "abstraction" dont nous avons déjà parlé.
26. Chevallard et Bosch,2001
27. D’après le Trésor de la Langue Française Informatisé (TLFI) : "Un axiome est un énoncé évident, non démontrable et universel."
4.2. QU’EST-CE QU’UNE GRANDEUR ? (APPROCHE MATHÉMATIQUE)
N. Rouche28 a dressé une liste exhaustive et réfléchie de ces axiomes, en prenant en compte, et en le contournant subtilement, l’aspect peu "naturel" de la comparaison d’une grandeur à elle même. En considérant un ensemble X contenant les grandeurs de même espèce a, b et c, il a obtenu les onze axiomes suivants, numérotés de (i) à (xi)29 :
L’équivalence ou la non équivalence
(i) ∀a, b ∈ Xa ∼ b ⇔ b ∼ a ; ici, on traduit simplement le fait expérimental de l’équivalence de deux baguettes en les plaçant l’une sur l’autre.
(ii) ∀a, b, c ∈ Xa ∼ b et b ∼ c ⇔ a ∼ c ; ici aussi, c’est un fait qu’on peut facilement expérimenter dans la prime enfance. C’est la transitivité, tandis que la première était la symétrie. (iii) ∀a ∈ X∃b ∈ Xa 6= b et a ∼ b ; cet axiome a pour but de contourner l’axiome de réflexivité
a ∼ a qui n’est pas naturel : il ne fait pas partie de la réflexion des enfants de comparer une
baguette à elle-même ! Cet axiome permet de réaliser des ensembles de baguettes similaires, et les baguettes seules, s’il en existe, sont alors comparées à elles-mêmes "naturelle-ment", sans qu’on ait recours à une sorte de dédoublement "mental" permettant de comparer une baguette à elle-même.
La relation d’ordre total
Si nous munissons X d’une relation d’ordre total <, nous pourrons énoncer deux nouveaux axiomes qui correspondent encore à des acquis nés d’expériences chez de jeunes enfants :
(iv) ∀a, b ∈ Xa < b ou a ∼ b ou a > b ; (v) ∀a, b, c ∈ Xa < b et b < c ⇒ a < c ;
On évite ainsi la relation d’ordre ≤ qui est inutile et perturbante dans toutes les circonstances où l’on est en contact direct avec les choses : en présence de deux baguettes, on constate facilement qu’elles sont de tailles différentes.
L’addition
Si on munie X de l’opération addition ⊕, nous pouvons définir cette opération de la manière suivante, qui dépend fortement du choix de l’axiome (iii) qui "interdit" la réflexivité :
(vi) ∀a, b ∈ Xa ⊕ b est défini ⇔ a 6= b ; ici, l’opération n’est pas définie partout sur X car additionner deux baguettes, c’est les mettre bout à bout, ce qui est impossible à faire si l’addition est a ⊕ a. Par contre, grâce à l’axiome (iii), on sait qu’on peut additionner deux baguettes similaires !
(vii) ∀a, b, c ∈ X, si a ∼ b et a ⊕ c et b ⊕ c sont définies alors a ⊕ b ∼ b ⊕ c ; (viii) ∀a, b ∈ X, si a ⊕ b est définie alors a ⊕ b ∼ b ⊕ a ;
(ix) ∀a, b, c ∈ Xsi (a ⊕ b) ⊕ c et a ⊕ (b ⊕ c) sont définies alors (a ⊕ b) ⊕ c ∼ a ⊕ (b ⊕ c) ;
Les axiomes (vii) à (ix) se passent d’explication car ils correspondent à des expériences sensibles partagées par une grande partie des jeunes enfants.
Bien évidemment, on s’interdit l’addition a ⊕ a du fait qu’une baguette ne peut matériellement pas s’ajouter à elle-même. Par contre, on peut trouver b ∼ a et du coup définir l’addition a ⊕ b qui sera l’équivalent, sans le dire, à a ⊕ a.
L’addition et la relation d’ordre mélangée
(x) ∀a, b ∈ Xa < b ⇔ ∃c ∈ Xa ⊕ c est défini et b ∼ a ⊕ c ; La division par un nombre naturel
(xi) ∀a ∈ X ∀n ∈ N n > 0 ∃b1, b2, . . . , bn (. . . ((b1⊕b2)⊕b3)⊕. . .⊕bn) est défini et équivalent à a 28. Rouche,1994