Modélisation et Simulation par la DFT des Propriétés Magnétiques et Structures Electroniques des Oxydes Magnétiques Dilués

UNIVERSITÉ MOHAMMED V

FACULTE DES SCIENCES

Rabat

N° d’ordre :2767

THÈSE DE DOCTORAT

Présentée par

Abdelmajid FAKHIM LAMRANI

Discipline : Physique Informatique

Spécialité : Matière condensée et modélisation des systèmes

Titre :

Modélisation et Simulation par la DFT des Propriétés

Magnétiques et Structures Electroniques des Oxydes

Magnétiques Dilués

Soutenue le 16/05/ 2015, Devant le jury :

Président :

Abdelilah BENYOUSSEF : PES, Faculté des Sciences de Rabat.

Examinateurs :

Mohamed BELAICHE : PES, Ecole Normale Supérieure de Rabat Abdallah EL KENZ : PES, Faculté des Sciences de Rabat

Mohamed KEROUAD : PES, Faculté des Sciences de Meknès

Mohammed LOULIDI : PES, Faculté des Sciences de Rabat

Hamid EZ-ZAHRAOUY : PES, Faculté des Sciences de Rabat

Lahoucine BAHMAD : PES, Faculté des Sciences de Rabat

Faculté des Sciences, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat-Maroc

i

Les travaux de recherches développés dans cette thèse ont été réalisés au sein du Laboratoire de Magnétisme et Physique des Hautes Energies de l’Université Mohamed V, RABAT, Faculté des Sciences, sous la direction des Professeurs Abdelilah BENYOUSSEF et Mohammed BELAICHE.

J’aimerais tout d’abord remercier mes directeurs de thèse, Monsieur Abdelilah BENYOUSSEF, Professeur à l’Université Mohamed V, RABAT, Faculté des Sciences, et Monsieur Mohammed BELAICHE, Professeur à L’école Normale Supérieure de Rabat, pour la confiance qu’ils m’ont accordée en acceptant d’encadrer ce travail de thèse. Leurs multiples conseils et leurs vastes connaissances de la physique m’ont permis d’accomplir ce travail dans de très bonnes conditions. Enfin, j’ai été extrêmement sensible à leurs qualités humaines, d’écoute et de compréhension tout au long de ce travail.

J’exprime ma reconnaissance à Monsieur le Professeur Abdelilah BENYOUSSEF, qui a bien voulu accepter de présider le jury de cette thèse. Je souhaite aussi lui exprimer ma profonde reconnaissance et gratitude pour les efforts qu’il a déployé depuis ma première année de DESA jusqu'à la fin de ma thèse, afin de me permettre d’acquérir une bonne formation et me faire aimer la recherche scientifique. Les mots ne suffisent pas pour décrire les qualités humaines d’une telle personnalité

Je remercie vivement Monsieur Abdallah EL KENZ, Professeur à l’Université Mohamed V, RABAT, Faculté des Sciences pour sa participation très active à ce travail de thèse. Encore je le remercie infiniment en tant que rapporteur et examinateur de ce travail. C'est un honneur pour moi d'avoir pu compter sur sa présence dans mon jury de soutenance.

Je remercie sincèrement Monsieur Mohamed KEROUAD, Professeur à L'Université Moulay Ismail, Faculté des Sciences de Meknès pour avoir accepté d’être rapporteur de cette thèse. Je suis sensible à l’honneur qu’il m’a fait en acceptant de participer à ce jury de thèse malgré ses nombreuses occupations.

ii

Je tiens à exprimer mes sincères remerciements, à nos trop chers professeurs qui ont accepté d’être membres de jury d’évaluation de cette thèse :

A ce titre, je souhaite exprimer mon estime et mon profond respect à Monsieur Mohammed LOULIDI, Professeur à la Faculté des Sciences de Rabat, pour tout l'intérêt qu'il a manifesté pour ce travail de doctorat.

Ma gratitude va également à Monsieur Hamid EZ-ZAHRAOUY, Professeur à l’Université Mohamed V, RABAT, Faculté des Sciences, qui m’a encouragé, soutenu et conforté tout au long de mon parcours doctoral.

De même je remercie chaleureusement Monsieur Lahoucine BAHMAD, Professeur à l’Université Mohamed V, RABAT, Faculté des Sciences, pour ses encouragements, ses conseils et sa gentillesse.

Je tiens à remercier aussi Monsieur El hassane SAIDI, Professeur à l’Université Mohamed V, RABAT, Faculté des Sciences pour m’avoir accueilli dans son unité de recherche en physique des hautes énergies, je le remercie encore pour ses encouragements et ses conseils qui m’ont aidé à faire le premier pas en recherche scientifique en physique.

Mes remerciements vont, aussi, à mes collègues, pour leur amitié et la bonne ambiance qu’ils font régner au laboratoire. C'est une chance d'avoir pu évoluer dans un groupe aussi pluridisciplinaire, dynamique, et soudé.

Bien entendu, il ne m'est pas possible d'oublier de remercier infiniment M. EYERT Volker, Professeur à l’Université, Augsburg, Allemagne, tant pour son coup de main technique que pour les discussions qui m'ont beaucoup aidé pour bien maîtriser son code ASW.

Je témoigne enfin toute ma reconnaissance à ma petite famille particulièrement ma chère mère avec son soutien moral constant durant toutes les années de la préparation de cette thèse, et toutes celles et tous ceux que je n’ai pas cité ici, et ils sont nombreux, dont la présence et le soutien m’ont donné la volonté d’aller jusqu’au bout de ce travail.

iii

This thesis presents a modeling and simulation study of diluted magnetic semiconductors based on oxide: TiO2 Rutile, SnO2 Rutile and the double perovskite Sr2FeMoO6, using Ab initio

method, namely the augmented spherical wave method (ASW) in the context of the density functional theory. These are of interest to both fundamental and applied research, which is very interesting in the field of spintronics.

Generally, oxide semiconductors, and particularly TiO2 and SnO2 rutile doped with Co,

become ferromagnetic after creating oxygen vacancies in these systems. The present work is aimed at studying oxide-based semiconductors doped with double transition metal impurities rather than the traditional single impurities. A special interest is placed on the competitive role of double impurity to realize the half-metallic antiferromagnets, i.e, systems with 100% spin polarization of the conduction electrons at the Fermi level without showing a net magnetization. These materials are suitable for the fabrication of spin-polarized scanning tunneling spectroscopy (SPSTM).

Keywords: Spintronic, Oxide semiconductors, double perovskite, Ab initio calculations, ferromagnetic coupling, Half-metallic ferromagnetic, Half-metallic Antiferromagnets, ASW Method.

iv

Cette thèse présente une étude par modélisation et simulation des semi-conducteurs magnétiques dilués à base d’oxyde : TiO2 Rutile, SnO2 Rutile et la double pérovskite

Sr2FeMoO6, en utilisant une méthode Ab initio dite méthode des ondes sphériques augmentée

(𝐴𝑆𝑊) dans le cadre de la théorie de la fonctionnelle de la densité (𝐷𝐹𝑇). Ces derniers présentent un intérêt à la fois fondamental et appliqué, ce qui est très intéressant dans le domaine de la spintronique.

En général, les semi-conducteurs d'oxyde, et notamment TiO2 et SnO2 dopés avec Co,

deviennent ferromagnétiques après la création des lacunes d'oxygène dans ces systèmes. Le présent travail vise à étudier les semi-conducteurs à base d'oxydes dopés avec double impuretés de métaux de transition 𝑀₁ , 𝑀₂ (différents) au lieu de la traditionnelle simple impureté. Un accent particulier est mis sur le rôle compétitif de la double impureté pour réaliser des matériaux antiferromagnétiques demi-métalliques : la polarisation en spin des porteurs est de 100 % au niveau de Fermi avec une aimantation totale égale à zéro. Ces matériaux sont souhaitables pour la fabrication des microscopes à effet tunnel polarisé en spin.

Mots-clefs

: Spintronique, Oxyde semi-conducteurs, double pérovskite, Calcul Ab initio, Couplage ferromagnétique, Ferromagnétisme métallique, antiferromagnétique demi-métallique, Méthode ASW.

v

1 A. Fakhim Lamrani, M. Belaiche, A. Benyoussef, A. ElKenz, E.H. Saidi Exchange mechanism of half-metallic ferromagnetism of TiO2 doped with double impurities: A

first-principles ASW study Journal of Magnetism and Magnetic Materials 322 (2010) 454–458.

2 A. Fakhim Lamrani , M. Belaiche , A. Benyoussef , A. ElKenz , E.H. Saidi First-principles study of electronic structure and magnetic properties of doped SnO2 (rutile)

with single and double impurities. Journal of Magnetism and Magnetic Materials 323 (2011) 2982–2986.

3 A. Fakhim Lamrani, M. Belaiche, A. Benyoussef, A. ElKenz, E.H. Saidi Ferromagnetism In Mo-doped TiO2 Rutile from Ab Initio Study. J Supercond Nov

Magn DOI 10.1007/s10948-011-1317-z.

4 A. Fakhim Lamrani, M. Ouchri, A. Benyoussef, M. Belaiche and M. Loulidi Half-metallic antiferromagnetic behavior of double perovskite Sr2OsMoO6 : First principle

calculations. Journal of Magnetism and Magnetic Materials 345 (2013) 195–200.

5 A. Fakhim Lamrani, M. Belaiche, A. Benyoussef and A.El Kenz Half-metallic behaviour in doped TiO2 (rutile) with double impurities: ab initio caclculation. Phase

Transitions, 2013 Vol. 86 No. 12, 1178-1185.

6 A. Fakhim Lamrani, M. Belaiche, A. Benyoussef, and El Kenz. Electronic structures and ferromagnetism of SnO2 (rutile) doped with double-impurties: First-principal

calculations Journal of Applied Physics 115, 013910 (2014); doi: 10.1063/1.4852475. 7 A. Fakhim Lamrani, M. Ouchri, M. Belaiche , A. El Kenz , M. Loulidi a, A. Benyoussef

Half metallic antiferromagnetic behavior in doped TiO2 Rutile with doubles impurities

(Os, Mo) from Ab initio calculations Thin Solid Films 570 (2014) 45–48.

8 A. Fakhim Lamrani, M. Ouchri, M. Belaiche, A. El Kenz, M. Loulidi, A. Benyoussef The effect of fluorine doping on electronic and magnetic properties of Os-doped TiO2

rutile phase from ab initio calculation. Submitted to Journal of Magnetism and Magnetic Materials.

9 A. Fakhim Lamrani, M. Ouchri, M. Belaiche, A. El Kenz, M. Loulidi, A. Benyoussef Half metallic ferromagnetism semiconductors of TiO2 Rutile doped with doubles

impurities (V,Tc): First principle calculations. Submitted to Journal of Computational Materials Science.

vi

Abréviations les plus couramment utilisées :

DFT Théorie de la fonctionnelle de la densité (Density functional theory) ASW Onde sphérique augmentée (Augmented spherical wave)

ASA Approximation de la sphère atomique (Atomic sphere approximation) LDA Approximation de la densité locale (Local density approximation)

GGA Introduction d’un gradient a l’approximation LDA (Generalized gradient

approximation)

GGA+U Gradients généralisée combiné avec le terme d’Hubbard

DMS Semi-conducteurs magnétiques dilué (Diluted magnetic semiconductors)

DMO Semi-conducteurs magnétiques dilué à base d’oxydes (Oxyde semiconductors dilue) RKKY Couplage Ruderman-Kittel-Kasuya-Yoshida

B0 Module de compressibilité (Bulk modulus)

DOS Diagramme de densités d’états (Density of states) FM Ferromagnetique (ferromagnetic)

AFM Antiferromagnetique (Antiferromagnetic)

HMAFM Demi-metal antiferromagnetique (Half metallic antiferromagnetic) BC Bande de conduction (Conduction band)

BV Bande de valence (Valence band) BZ Zone de Brillouin (Brillouin zone)

Ec Electrons de conduction (conduction electrons) EF Energie de Fermi (Fermi energy)

NM Non-magnétique (Non-magnetic) NSP Spin non polarise (Non spin polarized) SP Spin polarise (Spin polarized)

vii

Titre . . .

Remerciements . . . i

Abstract . . . . iii

Résumé . . . iv

Publications dans des périodiques à comité de lecture . . . v

Nomenclature . . . vi

Table des matières . . . vii

1 Introduction . . . 1

1.1 Contexte général . . . 3

1.2 Objectifs de la thèse . . . 5

1.3 Structuration de la thèse . . . 7

2 Aperçu sur le cadre théorique. . . . 8

2.1 L’approche de Hartree. . . 10

2.2 Approximation de Hatree-Fock . . . . 12

2.2.1 Le principe d’exclusion de Pauli et l’échange . . . 12

2.2.2 Problème de la corrélation, trou de Coulomb . . . 13

2.3 Les débuts de la 𝐷𝐹𝑇 . .. . . 14

2.4 Théorie de la fonctionnelle de la densité . . . 16

2.4.1 Note sur les équations de Kohn-Sham . . . 19

2.4.2 Formulation de l’échange-corrélation . . . 20

2.5 Les fonctionnelles de la 𝐷𝐹𝑇 . . . 21

2.5.1 L’approche locale de la densité . . . 21

2.5.2 L’introduction du spin dans l’approche locale de la densité . . . 22

2.5.3 Implications de la 𝐿𝑆𝐷𝐴 . . . 23

2.5.4 Schémas de paramétrisation de la 𝐿𝑆𝐷𝐴 . . . 23

2.5.4.1 Description d’un schéma de paramétrisation . . . 24

2.5.5 Améliorations sur l’approximation locale . . . 25

2.5.5.1 Introduction d’un gradient (𝐺𝐺𝐴) . . . 25

2.5.5.2 L’approximation 𝐿𝑆𝐷𝐴 + 𝑈 . . . 25

2.6 Méthodes de calculs . . . 26

2.6.1 La méthode 𝐴𝑆𝑊. . . 26

2.6.2 L’approximation 𝐴𝑆𝐴 et ses implications . . . 27

2.6.3 Solution de la fonction d’onde . . . 27

2.6.4 Développement du formalisme de la méthode 𝐴𝑆𝑊 . . . 27

2.6.5 Le processus mathématique d’augmentation . . . 29

viii

3 Les Semi-Conducteurs Magnétiques Dilués . . . 33

3.1 Familles de semi-conducteurs magnétiques . . . 34

3.2 Semi-conducteursoù les éléments magnétiques forment un réseau périodique . . . 34

3.3 Semi-conducteurs où les éléments magnétiques substituent aléatoirement les cations (𝐷𝑀𝑆) . . . 35

3.4 Les oxydes Magnétiques dilués (𝐷𝑀𝑂) . . . 35

3.5 Les couplages ferromagnétiques : oxydes, 𝐷𝑀𝑆 𝑒𝑡 𝐷𝑀𝑂 . . . 36

3.5.1 Le cas des oxydes . . . 36

3.5.1.1 Superéchange . . . .36

3.5.1.2 Double échange . . . .37

3.5.2 Le cas des 𝐷𝑀𝑆 𝑒𝑡 𝑑𝑒𝑠 𝐷𝑀𝑂 . . . 39

3.5.2.1 Le couplage Ruderman-Kittel-Yoshida (𝑅𝐾𝐾𝑌) . . . 41

3.5.2.2 Modèle de Zener . . . 42

3.5.2.3 Modèle de polarons magnétiques . . . 43

4. Etudes du Complexe 𝑻𝒊𝟏−𝟐𝒙𝑨𝒙𝑩𝒙𝑶𝟐 𝑨 ≠ 𝑩 Structure Electronique et Propriétés Magnétiques . . . 44

4.1 Dioxyde de Titane . . . 46

4.1.1 Phase Rutile . . . 46

4.1.2 Optimisation de la Structure . . . ..47

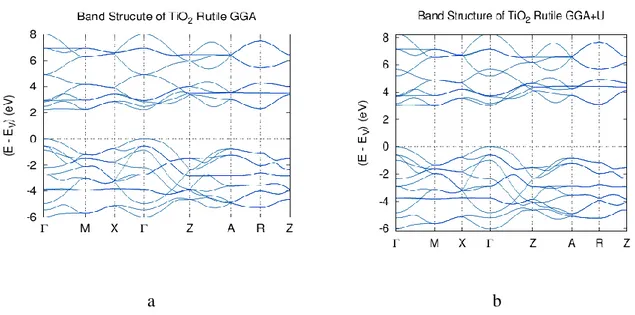
4.1.3 Structure Electronique . . . 50

4.2 Etudes des propriétés électroniques et magnétique de TiO2 rutile dopé par double impuretés. . . .52

4.2.1 Introduction . . . 52

4.2.2 Méthodes de Calcul . . . .53

4.3 Etude du Complexe 𝑇𝑖1−2𝑥𝐴𝑥𝐵𝑥𝑂2 𝐴 ≠ 𝐵 . . . 54

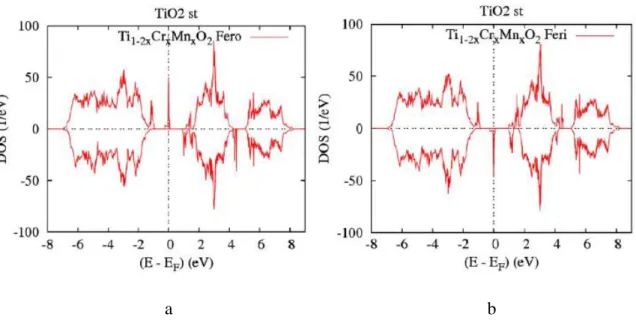
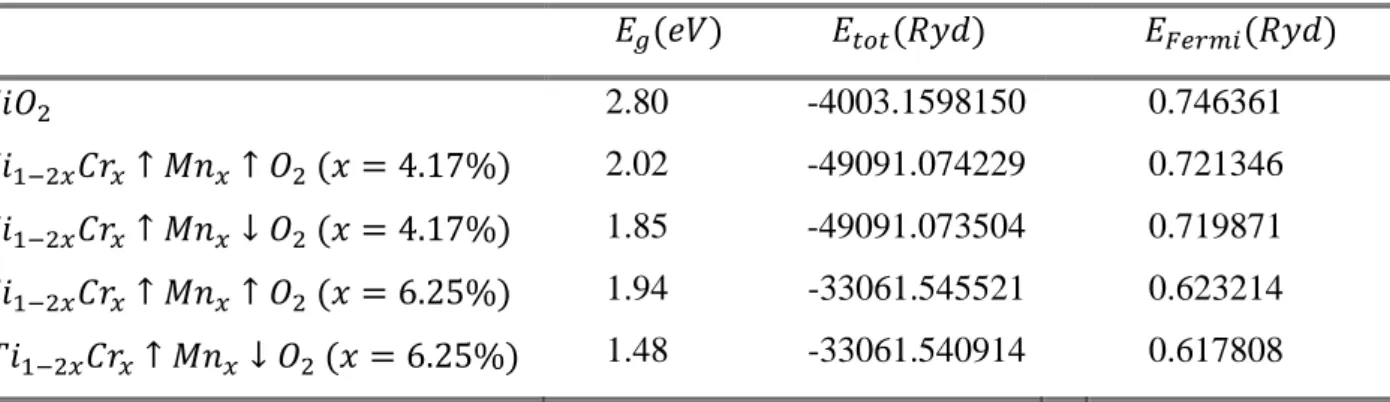
4.3.1 Cas du complexe 𝑇𝑖1−2𝑥𝐶𝑟𝑥𝑀𝑛𝑥𝑂2 (3𝑑 − 3𝑑) . . . 55

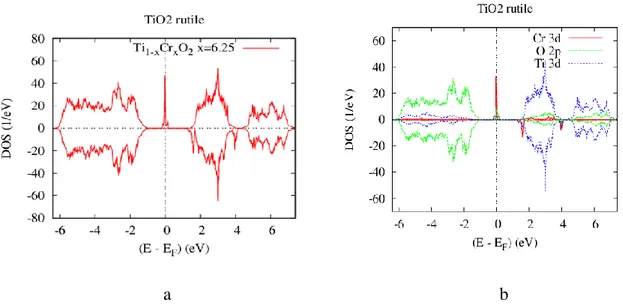
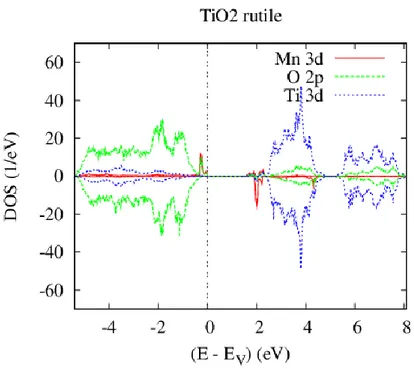
4.3.1.1 Propriétés Electronique et Magnétique du complexe 𝑇𝑖_1−2𝑥𝐶𝑟_𝑥𝑀𝑛_𝑥𝑂₂ . . . 55

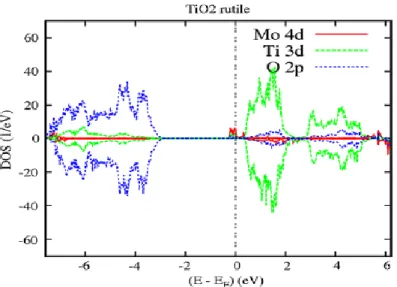
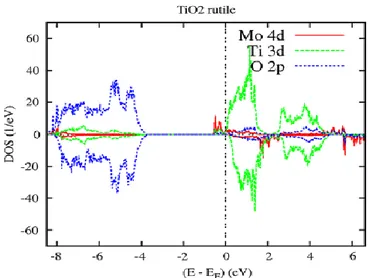
4.3.2 Cas du complexe 𝑇𝑖_1−2𝑥𝐶𝑟_𝑥𝑀𝑜_𝑥𝑂₂ (3𝑑 − 4𝑑) . . . 63

4.3.2.1 Etudes de TiO2 dopé par Molybdène . . . 63

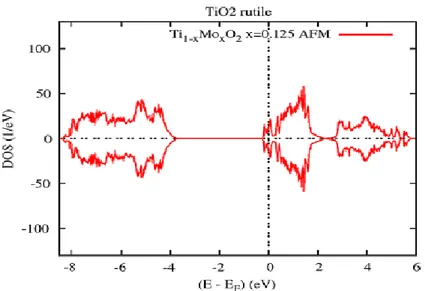
4.3.2.2 Propriétés Electronique et Magnétique de 𝑇𝑖1−𝑥𝑀𝑜𝑥𝑂2 . . . 63

4.3.2.3 Propriétés Electronique et Magnétique du complexe 𝑇𝑖_1−2𝑥𝐶𝑟_𝑥𝑀𝑜_𝑥𝑂₂ . . . .68

4.4 Conclusion . . . .. 73

4.5 Article . . . 4.5.1 Article 1 . . . .75

4.5.2 Article 2 . . . ..76

4.5.3 Article 3 . . . 77

5 Etudes Des Propriétés Electroniques et Magnétiques des Oxyde : 𝑺𝒏_{𝟏−𝟐𝒙}𝑨_𝒙𝑩_𝒙𝑶_𝟐 𝑨 ≠ 𝑩 5.1 L’oxyde d’étain 𝑆𝑛𝑂₂ . . . 80

ix

5.1.1 Résultats de l’optimisation . . . 80

5.2.2 Structure de bande et densité d’états (𝐷𝑂𝑆) . . . 84

5.2 Etude d’oxyde magnétique dilué SnO2 dopé par double imputetés : 𝑆𝑛_1−2𝑥𝐴_𝑥𝐵_𝑥𝑂₂ . . 87

5.2.1 Introductions . . . . . . 87

5.2.2 Cas du complexe 𝑆𝑛_1−2𝑥𝑀𝑛_𝑥𝑊_𝑥𝑂₂ (3𝑑 − 5𝑑) . . . 88

5.2.2.1 Propriétés électronique et magnétique . . . 88

5.2.3 Cas du complexe 𝑆𝑛_1−2𝑥𝐶𝑟_𝑥𝑅𝑒_𝑥𝑂₂ (3𝑑 − 5𝑑) . . . 94

5.2.3.1 Propriétés électronique et magnétique . . . 94

5.2.4 𝑆𝑛_1−2𝑥𝐶𝑟_𝑥𝑀𝑛_𝑥𝑂₂ (3𝑑 − 3𝑑) . . . 98

5.2.4.1 Propriétés électronique et magnétique . . . 99

5.3 Conclusions . . . . . . 101

5.4 Articles . . . 5.4.1 Articles 1 . . . 103

5.4.2 Articles 2 . . .. . . 104

6 Matériaux Antiferromagnétiques demi-métalliques . . . 105

6.1 Introductions . . . 107

6.2 Méthodes de Calcul. . . 109

6.3 Le 𝑆𝑟₂𝐹𝑒𝑀𝑜𝑂₆ . . . 110

6.3.1 Structure . . . 110

6.3.2 Propriétés électronique et Magnétiques . . . 111

6.4 Le demi-métal antiferromagnétique 𝑆𝑟₂𝑂𝑠𝑀𝑜𝑂₆ . . . 113

6.4.1 Propriétés électronique et magnétique . . . 114

6.4.2 Effet des interactions du coulomb sur les propriétés magnétique du composé𝑆𝑟₂𝑂𝑠𝑀𝑜𝑂₆ . . . 119

6.5 Le demi-métal antiferromagnétique 𝑇𝑖1−2𝑥𝑂𝑠𝑥𝑀𝑜𝑥𝑂2 . . . .121

6.5.1 Propriétés électronique et magnétique . . . .121

6.6 Conclusion . . . .128 6.7 Articles . . . 6.7.1 Article 1 . . . .130 6.7.2 Article 2 . . . .131

Conclusion générale

. . . 132

Bibliographie

. . . . . . 135

1

CHAPITRE 1

2

Sommaire

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 1.1 Contexte général . . . 1.2 Objectif de la thèse . . . 1.3 Structuration de la thèse . . . = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

3

1.1 Contexte général

En août 2006, alors que Samsung met sur le marché les premiers ordinateurs sans disque dur, Freescale vend ses premières MRAM (Magnetic Random Access Memories). Les premiers reposent sur une mémoire flash, où une grille flottante qui manipule la charge de l'électron. Les secondes sont en revanche l'aboutissement de vingt ans d'efforts de recherche pour utiliser le spin de l'électron pour stocker et manipuler l'information : l'espoir de créer des composants à courant (de spin) non dissipatif, donc à très basse consommation, mais aussi celui de trouver une solution à la fin du CMOS (Complementary Metal Oxide Semiconductor) annoncée par la loi de Moore.

Après les premières mises en évidence à la fin des années 1980 d'un transport électronique dépendant du spin dans des multicouches ferromagnétiques à barrières métalliques ou isolantes [1, 2], il a rapidement été envisagé d'incorporer ces effets à des structures semi-conductrices. L'objectif était entre autres de profiter du temps de vie des porteurs plus longs que dans les métaux, pour faciliter la manipulation du spin [3]. Deux domaines se trouvent ainsi combinés la physique des semi-conducteurs et le magnétisme - avec pour objectif de réaliser le stockage, la manipulation et la détection de l'information sur un même composant. Trois voies sont actuellement explorées : les semi-conducteurs non-magnétiques, où l'on exploite l'interaction spin-orbite (transistor Datta et Das [4]), les structures hybrides semi-conducteur/ ferromagnétique, et enfin, les matériaux multifonctionnels, à la fois semi-conducteurs et ferromagnétiques.

Parallèlement aux progrès de l'électronique de spin dans les semi-conducteurs usuels, s'est donc engagée la recherche d'un matériau ferromagnétique à température de Curie bien supérieure à 300 K, à polarisation de spin élevée [5], et intégrable aux technologies semi-conducteur existantes. Différents types d'électrodes ont ainsi été proposées : des métaux de transition ou oxydes ferromagnétiques [6], ou encore des semi-conducteurs magnétiques. Ces derniers ont des propriétés magnétiques variées, et ont l'avantage de ne pas présenter les problèmes de réactivité chimique, ou d'adaptabilité d'impédance rencontrés dans les structures hybrides métal/semi-conducteur.

Les semi-conducteurs magnétiques ont commencé à être étudiés bien avant les débuts de l'électronique de spin. Ainsi, c'est plus d'une vingtaine d'alliages différents qui ont été envisagés depuis les années 1960, comme par exemple des matériaux à base de terres rares ou de chrome (EuS, CdCr2Se4) ordonnés selon un réseau périodique [7]. Dix ans plus tard, une nouvelle

4

famille de matériaux, les semi-conducteurs magnétiques dilués (DMS) voyait le jour, où les dopants magnétiques (Mn, Fe, Co, Cr) substituent de façon aléatoire les cations de matrices semi-conductrices II-VI (CdTe, ZnTe, HgTe, ZnS, CdS). Cette approche permet une bonne adaptation aux composants semi-conducteurs, mais cette voie n’a pas abouti, car les chalcogénures à base de terres rares, donnaient majoritairement des phases antiferromagnétiques, paramagnétiques, ou verres de spin à cause de la compétition entre interactions de super-échange anti- ferromagnétique, et interactions de double échange ferromagnétique.

Un vif regain d'intérêt de la communauté scientifique a été suscité par la découverte en 1989 et 1996 d'une phase ferromagnétique homogène dans les semi-conducteurs magnétiques III-V (In,Mn)As et (Ga,Mn)As [8, 9]. La mise en évidence du fait que cette phase résultait d'une interaction entre les spins des manganèses induite à travers les trous apportés par les dopants [10] a déclenché une série de percées expérimentales, comme le contrôle du ferromagnétisme par un champ électrique externe [11], la détection optique du taux de polarisation jusqu'à 85% [12], des magnéto-résistances tunnel (TMR) de plus de 1000% dans des nano constructions [13] ou encore l'obtention pour (Ga,Mn)As de températures de Curie supérieures à 170 K pour des couches fines [14], et proches de l'ambiante pour des structures à modulation de dopage [15]. Différents outils théoriques [16, 17] ont par ailleurs permis de rendre compte d'effets originaux dans ces matériaux, comme la TMR anisotrope, ainsi que la forte dépendance des propriétés magnétiques, en particulier de l'anisotropie magnétique, sur la forme et le remplissage de la bande de valence hébergeant les porteurs. Malgré une température de Curie faible, ces calculs continuent de stimuler les travaux expérimentaux sur (Ga,Mn)As, matériau modèle grâce auquel d’autres propriétés ont été explorées ; comme les propriétés de transport, la dynamique des porteurs et de l'aimantation, ou encore, les effets de confinement quantique dans les DMS. Dans ce contexte, Dietl et al. Prévoyaient que GaN et ZnO dopés au manganèse seraient ferromagnétiques au-delà de la température ambiante si on parvenait à en faire des semi-conducteurs de type p [18]. Cette prédiction théorique a donné lieu à d’intenses recherches expérimentales sur ZnO dopé par des éléments de transition mais aussi par extension sur de nombreux autres oxydes dopés « magnétiquement ». Les oxydes magnétiques dilués (DMO, « Dilute Magnetic Oxides ») constituent maintenant un champ de recherche à part entière. A la suite des travaux de Dietl et al. Beaucoup d’´équipes ont étudié les DMO expérimentalement. La première découverte importante dans ce domaine date de 2001 avec la fabrication de couches minces de TiO2 dopé au Co ferromagnétiques à température ambiante

5

[19]. En 2001 toujours, des couches minces de ZnO dopé au Co ferromagnétiques à température ambiante ont également été produites [20]. Depuis, on a observé du ferromagnétisme dans de nombreux DMO (en couches minces dans la grande majorité des cas) dont :

– TiO2 dopé au V, Cr, Fe, Co ou Ni [19, 21, 22] ;

– SnO2 dopé au V, Cr, Mn, Fe ou Co [23, 24, 25] ;

Néanmoins, des incertitudes persistent concernant la nature du ferromagnétisme dans ce type d’oxydes. Il est en effet très difficile de démontrer sans ambiguïté que le comportement ferromagnétique observé est une caractéristique intrinsèque du matériau et non un effet extrinsèque lié à la présence de phases magnétiques parasites. Donc Il est intéressant de voir quels sont les mécanismes de couplage à l’œuvre dans les oxydes magnétiques (ferromagnétique, antiferromagnétique ou ferrimagnétique) classiques et les DMS [26, 27]. Ainssi nous verrons dans quelle mesure ils peuvent ou ne peuvent pas s’appliquer au cas des DMO doublement dopés.

1.2 Objectifs de la thèse

Cette thèse présente une étude par modélisation et simulation des semi-conducteurs magnétiques dilués à base d’oxyde : TiO2 Rutile, SnO2 Rutile et la double pérovskite

Sr2FeMoO6, en utilisant une méthode Ab initio dite méthode des ondes sphériques augmentée

(ASW) dans le cadre de la théorie de la fonctionnelle de la densité (DFT). Le choix des oxydes est justifié par le fait qu’ils sont plus appropriés pour la fabrication de dispositifs de spintronique en comparaison avec le DMS non-oxyde, en raison de leurs nombreuses caractéristiques avantageuses, y compris la largeur de la bande interdite, la concentration des porteurs de charge type n et la haute température de transition Tc. D’un autre côté, Matsumoto et al. Rapportent

l’existence d’un ordre ferromagnétique à longue portée dans des couches minces d’anatase TiO2

dopées au cobalt, ceci a ouvert la voie à une recherche complètement nouvelle [Matsumoto 2001a]. Cet ordre ferromagnétique qui se maintient à la température ambiante est observé pour des concentrations en cobalt inférieures à 8 %.

Depuis l’article de Matsumoto et al. De nombreuses équipes ont commencé à travailler sur ce type de systèmes ; une grande majorité des chercheurs s’est intéressée aux couches minces de TiO2 faiblement dopées par différents métaux de transition, les plus utilisés étant le

cobalt et le fer. L’existence d’un ferromagnétisme intrinsèque à la température ambiante dans ces matériaux est un sujet très controversé.

6

Dans notre recherche sur des Semi-conducteurs magnétiques dilués à base d'oxydes nous avons choisi d’utiliser deux types de méthodes complémentaires construites dans le cadre quantique de la 𝐷𝐹𝑇 : (𝑖) celles qui font appel à tous les électrons : la méthode de l’onde sphérique augmentée 𝐹𝑃𝐴𝑆𝑊 adaptée aux optimisations de la géométrie des systèmes avant l’accès aux propriétés électronique et magnétique, et (𝑖𝑖) celles qui permettent essentiellement d’écrire la structure électronique (densités d’états, structure de bande d’énergie) ainsi que les propriétés magnétiques. (Ici la méthode 𝐴𝑆𝑊) [28, 29].

Ces méthodes ont démontré leur efficacité à donner des résultats précis et fiables s’agissant de la simulation de la structure électronique et des propriétés magnétiques des oxydes magnétiques dilués. Un nombre important de publications sur des travaux réalisés au 𝐿𝑀𝑃𝐻𝐸 en témoigne [30-38]. Les résultats obtenus montrent la contribution de chacun des constituants atomiques des systèmes étudiés à différents apports. Le comportement magnétique et la configuration de l’état fondamental sont soulignés. Les propriétés magnétiques sont extraites suivant différentes approches.

L’apport attendu de l’étude théorique de ces systèmes, menée dans cette thèse, se résume dans les points suivants :

En général, les semi-conducteurs d'oxyde, et notamment TiO2 et SnO2 dopés avec

Co, deviennent ferromagnétique après la création de lacunes d'oxygène dans ces systèmes [39]. Le présent travail vise à étudier les semi-conducteurs à base d'oxydes dopés avec double impuretés de métaux de transition 𝑀₁ , 𝑀₂ (différents) au lieu de la traditionnelle simple impureté, pour les raisons suivantes : la possibilité d’éviter les lacunes en oxygène qui peuvent être à l’origine de la distorsion du matériau. Il est possible que la double impureté forme avec l’oxygène un complexe M1-O-M2 de large

dimension, qui donne une section efficace de diffusion plus élevée.

La simulation de la structure électronique et magnétique des composées 𝑇𝑖_1−2𝑥𝐴_𝑥𝐵_𝑥𝑂₂ (𝑟𝑢𝑡𝑖𝑙𝑒), 𝑆𝑛_1−2𝑥𝐴_𝑥𝐵_𝑥𝑂₂ (𝑅𝑢𝑡𝑖𝑙𝑒) 𝑒𝑡 𝑙𝑎 𝑑𝑜𝑢𝑏𝑙𝑒 𝑝𝑒𝑟𝑜𝑣𝑠𝑘𝑖𝑡𝑒 𝑆𝑟₂𝐹𝑒𝑀𝑜𝑂₆ afin de comprendre l’intérêt des propriétés magnétiques rapportées dans le domaine de la spintronique.

Savoir dans quelle mesure les couplages proposés pour expliquer le ferromagnétisme des DMS peuvent ou ne peuvent pas s’appliquer au cas des oxydes semi-conducteurs dopés avec double impuretés.

Avec un choix convenable de la double impureté il est possible de réaliser des matériaux demi-métalliques antiferromagnétiques : la polarisation en spin des porteurs est de 100 % au niveau de Fermi, avec une aimantation totale égale à zéro. Ces

7

matériaux sont souhaitables pour la fabrication des microscopes à effet tunnel polarisé en spin, il permet de caractériser à une échelle sub-atomique la forme et l’état électronique des nanostructures. En fait, ils sont utilisés pour la fabrication des sondes d’ordre magnétique local sans perturber le caractère magnétique global du système.

1.3 Structure de la thèse

Dans le cadre de cette thèse, le chapitre 2 est consacré à des généralités sur la méthode ab initio qui sera utilisée pour étudier la structure électronique et les propriétés magnétiques des oxydes magnétiques dilués. La théorie de la fonctionnelle densité et les différentes approximations utilisées dans cette thèse seront décrites. L’état de l'art théorique des oxydes semi-conducteurs dilués, la description des semi-conducteurs hôtes, et les différents couplages magnétiques d'échange présents dans les DMS et les DMO seront présentés dans le chapitre 3. Le chapitre 4 est dédié à l’étude de l’optimisation structurale du semi-conducteur hôte et les propriétés électroniques et magnétiques du dopage simple et double du dioxyde de titane TiO2

rutile. Une attention particulière est donnée au système 𝑇𝑖_1−2𝑥𝑀1_𝑋𝑀2_𝑥𝑂₂ , 𝑀₁ ≠ 𝑀₂ . Le moment total du système, les moments magnétiques locaux des impuretés, et leurs états d'oxydation sont également discutés. Cela nous donne une vision sur l’optimisation de la phase magnétique et la nature des interactions magnétiques (le mécanisme qui contrôle le ferromagnétique). Dans le chapitre 5, Le succès du double dopage de SnO2 rutile apparait

clairement dans l’optimisation de la structure électronique et la phase magnétique. En effet, elle est plus performante que le simple dopage. Les matériaux demi-métalliques antiferromagnétiques font l’objet des recherches du chapitre 6. Ce dernier traite deux types de matériaux : double pérovskite et oxyde semi-conducteurs, en utilisant deux types de méthodes complémentaires.

8

CHAPITRE 2

9

Sommaire

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

2.1 L’approche de Hartree

2.2 Approximation de Hartree-Fock

2.2.1 Le principe d’exclusion de Pauli et l’échange 2.2.2 Problème de la corrélation, trou de Coulomb

2.3 Les débuts de la DFT

2.4 Théorie de la fonctionnelle de la densité

2.4.1 Note sur les équations de Kohn-Sham 2.4.2 Formulation de l’échange-corrélation

2.5 Les fonctionnelles de la 𝑫𝑭𝑻

2.5.1 L’approche locale de la densité

2.5.2 L’introduction du spin dans l’approche locale de la densité 2.5.3 Implications de la LSDA

2.5.4 Schémas de paramétrisation de la LSDA 2.5.4.1 Description d’un schéma de paramétrisation 2.5.5 Améliorations sur l’approximation locale 2.5.5.1 Introduction d’un gradient (𝐺𝐺𝐴) 2.5.5.2 L’approximation 𝐿𝑆𝐷𝐴 + 𝑈

2.6 Méthodes de calculs

2.6.1 La méthodes 𝐴𝑆𝑊

2.6.2 L’approximation 𝐴𝑆𝐴 et ses implications 2.6.3 Solution de la fonction d’onde

2.6.4 Développement du formalisme de la méthode 𝐴𝑆𝑊 2.6.5 Le processus mathématique d’augmentation

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

10

Les propriétés physiques d’un système solide, illustré par l’image d’électrons légers en mouvement autour de noyaux lourds, dépendent du comportement de sa structure électronique. La mécanique quantique fournit le cadre idéal à cette étude. Une description complète d’un système quantique à 𝑁 électrons requiert le calcul de la fonction d’onde correspondante : Ψ(𝑟1, 𝑟2, … … , 𝑟𝑁) (le spin est omis ici pour raison de simplicité). En principe ceci peut être

obtenu à partir de l’équation de Schrödinger indépendante du temps, 𝐻Ψ = ΕΨ; mais en pratique le potentiel subi par chaque électron est imposé par le mouvement, non seulement des plus proches voisins mais également par l’ensemble des autres électrons du système réel. Ceci nécessiterait la solution d’une équation de Schrödinger avec ∼ 1023 _{équations Différentielles}

simultanées. En général, il n’est pas possible de résoudre cette équation et le recours à des approximations s’impose. Dans la suite du chapitre nous nous efforcerons de suivre avec le lecteur le cheminement des différentes approches conduisant in fine à la formulation et la mise en œuvre de la théorie de la fonctionnelle densité -électronique- (𝐷𝐹𝑇).

2.1 L’approche de Hartree

Partant du constat -presque trivial- qu’un atome avec un cortège électronique pouvant atteindre une centaine d’électrons est un système complexe à étudier, et sachant que l’on ne sait exactement traiter que le cas d’un atome avec un seul électron (l’atome d’hydrogène), il devient presqu’intuitif de chercher une méthode permettant de résoudre le problème de l’atome réel et complexe sur la base du cas mono-électronique: 𝐻₁ 1. Une des premières tentatives fut celle de Hartree qui exprima la fonction d’onde globale comme un produit de fonctions mono-électroniques. Dans l’approximation de Born Oppenheimer découplant le mouvement des électrons de celui des noyaux, la fonction d’onde électronique s’écrit :

Ψ(r

1

, r

2

… r

N

) = 𝜓

1

(r

1

)𝜓

2

(r

2

)...𝜓

N

(r

N

) (2.1)

Les équations de Schrödinger mono-électroniques dans l’approche de Hartree s’écrivent :

-

_2𝑚ℎ2

∇

2

𝜓

_𝑖

(r)+ 𝑣

𝑒𝑓𝑓

(𝑟)= 𝜖

𝑖

𝜓

𝑖

(r) (2.2)

Dans ce qui suit les vecteurs 𝑟 et 𝑅 expriment les positions spatiales de l’électron et du noyau respectivement.

11

Dans l’équation 2.2 le premier terme correspond à l’énergie cinétique et 𝑣_𝑒𝑓𝑓(𝑟) est le potentiel que subit l’électron, dit effectif. Le choix de ce potentiel est tel que L’équation 2.2 a une solution. Celle-ci est basée sur le principe 𝑣𝑎𝑟𝑖𝑎𝑠𝑖𝑜𝑛𝑛𝑒𝑙1 _{. En outre, ce potentiel doit tenir}

compte de l’interaction électron-noyau :

𝑉

_𝑁

(𝑟)=-𝑍𝑒

2

∑

1

|𝑟−𝑅|

𝑅

(2.3)

et de l’action des autres électrons. Ce dernier effet est plus délicat à prendre en compte et dans l’approximation de Hartree on considère que les autres électrons forment une distribution de charge négative 𝜌(𝑟′_{). En outre, l’électron se déplace dans un potentiel électrostatique moyen}

𝑉_𝐻(𝑟) provenant de l’ensemble des électrons voisins exprimé par :

𝑉

_𝐻

(𝑟) = −𝑒 ∫ 𝑑

3

_{𝑟′𝜌(𝑟}

′

₎

1

|𝑟−𝑟′|

(2.4)

Enfin on exprime le potentiel effectif comme la somme de ces deux contributions :

𝑉

_𝑒𝑓𝑓

= 𝑉

_𝐻

(𝑟) + 𝑉

_𝑁

(𝑟) (2.5)

Il est important de signaler que le terme (2.3) est à un seul centre, en 𝑟, alors que (2.4) est à deux centres, en 𝑟 et 𝑟′. Nous en verrons la conséquence dans les approches suivantes. Les fonctions propres résultant de la solution de l’équation 2.2 permettent de calculer une nouvelle densité électronique :

𝜌(𝑟) = ∑ 𝜓

_{𝑖 𝑖}∗

(𝑟)𝜓

_𝑖

(𝑟) (2.6)

La relation ≪ densité-potentiel ≫ est obtenue par l’équation de Poisson :

Δ𝑉

_𝐻

(𝑟) = −

𝜌(𝑟)

𝜀0

(2.7)

Où 𝑉_𝐻(𝑟) est le potentiel de Hartree en 𝑟 et 𝜌(𝑟) est la densité électronique. 𝜀₀ est la constante diélectrique du vide. Ceci sous-tend bien le cycle auto-cohérent, puisque la fonction d’onde et la densité électronique (et donc le potentiel) sont inter-dépendantes. Un grand mérite de cette

1 . _{Le principe variationnel est un concept mathématique puissant communément utilisé en chimie théorique. Il} stipule que si un système donné peut être décrit par un ensemble de paramètres représentant son état fondamental, c’est cet ensemble qui minimise l’énergie totale

12

approche est donc d’avoir proposé une solution auto-cohérente au problème du système électronique.

2.2 Approximation de Hartree-Fock

Le système électronique dans l’approximation de Hartree est incomplètement décrit. Ainsi peut-on présenter la différence entre l’énergie du système multiélectronique réel et celle obtenue dans l’approximation de Hartree comme celle qui représente le restant des interactions électroniques. Une des interactions manquantes est l’échange. C’est l’effet qui exprime l’antisymétrie de la fonction d’onde par rapport à l’échange des coordonnées de n’importe quels deux électrons menant à décrire le système à 𝑁 corps (électrons) par l’égalité

Ψ(𝑟

₁

, … . 𝑟

_𝑎

, … 𝑟

_𝑏

, … . 𝑟

_𝑁

) = −Ψ(𝑟

₁

, … . 𝑟

_𝑏

, … . 𝑟

_𝑎

, … . . 𝑟

_𝑁

) (2.8)

dans laquelle ont été interverties les positions de a et de b. Ψ(𝑟₁, … . 𝑟_𝑏, … . 𝑟_𝑎, … . . 𝑟_𝑁) est la fonction d’onde du système à 𝑁 corps résultant du produit de fonctions mono-électroniques. Ceci est parce que les électrons sont des Fermions (spin 1

2 ) et obéissent à une distribution de

Fermi-Dirac.

2.2.1 Le principe d’exclusion de Pauli et l’échange

Le principe d’exclusion de Pauli est la conséquence directe de cette antisymétrie. La conséquence essentielle en est que le mouvement des paires d’électrons de même spin est corrélé. On peut montrer l’antisymétrie de la fonction d’onde par une séparation spatiale entre les électrons de même spin. Elle est illustrée par un espace (dont la forme reste à définir mais que nous considérons ad hoc comme sphérique) entourant l’électron dans la distribution des spins parallèles qualifié de trou de Fermi. C’est une sphère de densité électronique constante équivalente à la charge d’un électron. De cet espace vide autour de l’électron une charge équivalente a +1

2𝑒 est exclue. Ce trou qui accompagne l’électron dans son déplacement rend

donc bien compte de l’échange. Sur le plan du bilan énergétique, ceci conduit à une réduction de l’énergie électrostatique de Coulomb d’une quantité appelée énergie d’échange : 𝐸𝑒𝑐ℎ . Elle

rend compte du fait que deux électrons de même spin ne peuvent pas se rapprocher indéfiniment. 𝐸_𝑒𝑐ℎ est incluse dans les calculs tels que ceux basés sur l’approximation de Hartree-Fock (HF).

13

L’approximation de Hartree-Fock constitue la base de presque toutes les méthodes de chimie quantique, ab initio et semi-empiriques, d’où son succès confirmé dans ce domaine depuis plusieurs décennies [40]. Tout comme dans l’approche de Hartree, la fonction d’onde d’un système à 𝑁 electrons est décrite par un produit de fonctions mono-électroniques avec en plus la prise en compte de l’antisymétrie de l’ensemble. Ceci ne peut être obtenu avec un produit de fonctions comme celui donné dans l’équation (2.1). Une généralisation permettant d’incorporer l’antisymétrie est assurée en remplaçant les fonctions d’onde de Hartree par un déterminant de Slater. Ce déterminant comprend des fonctions d’onde mono-électroniques comme un produit de toutes les fonctions de Hartree dans lesquelles des permutations de 𝑟_𝑖 modulées des poids ±1 sont effectuées de manière à obéir au principe d’exclusion de Pauli (2.8). Suivant une procédure variationnelle (cf. plus haut) la meilleure fonction satisfait les équations de Hartree-Fock :

-

_2𝑚ℎ2

∇

2

𝜓

_𝑖

(𝑟) + 𝑉

_𝑁

(𝑟)𝜓

_𝑖

(𝑟)+ 𝑉

𝐻

(𝑟)𝜓

𝑖

(𝑟) − ∑ [∫

𝑑3𝑟 |𝑟−𝑟′_|

𝑗

𝜓

𝑗∗

(𝑟

′

). 𝜓

𝑖

(𝑟

′

)]𝜓

𝑗

(𝑟) =

𝜖

_𝑖

𝜓

_𝑖

(r) (2.9)

Les équations de Hartree-Fock (2.9) diffèrent de celles de Hartree par le terme d’échange (dernier terme avant le signe d’égalité). Avec une forme intégrale d’opérateur, il est non linéaire en 𝜓_𝑖 : la complexité ajoutée par la prise en compte de l’échange est considérable. Elle rend les calculs de type Hartree-Fock difficiles à mener pour des systèmes dépassant les petits ensembles de molécules.

2.2.2 Problème de la corrélation, trou de Coulomb

Nous venons de décrire l’échange par une séparation spatiale entre les électrons de même spin, i.e. entre spins ↑ −↑ ou ↓ −↓, illustrée par le trou de Fermi. Qu’en est-il des électrons de spins opposés, i.e. entre spins ↑ et ↓ ? Dans l’approximation de Hartree-Fock rien ne s’oppose à leur présence dans la même région de l’espace. En outre, les électrons se déplacent comme si leurs mouvements étaient indépendants. Par conséquent, ils peuvent pénétrer le trou d’échange de Fermi. Ainsi les paires d’électrons de même spin et celles de spins opposés sont traitées d’une manière dissymétrique. Les corrélations ne sont donc pas bien prises en compte (quoique dans des méthodes HF plus récentes les corrélations soient extrapolées à partir de calculs de dynamique moléculaire). De ce qui a été formulé plus haut, la contribution à l’énergie totale due à la corrélation (𝐸_{𝑐𝑜𝑟𝑟}) apparaît comme la différence entre l’énergie totale exacte du système électronique 𝐸𝑒𝑥𝑎𝑐𝑡𝑒 et celle de Hartree-Fock (calculs non relativites) :

14

𝐸

𝑐𝑜𝑟𝑟

=𝐸

𝑒𝑥𝑎𝑐𝑡𝑒

-𝐸

𝐻𝐹

(2.10)

𝐸_𝐻𝐹 Étant toujours supérieure à l’énergie exacte, 𝐸_{𝑐𝑜𝑟𝑟} est une quantité négative. Donc tout comme on a postulé un trou d’échange (de Fermi) excluant les électrons de spins parallèles (↑ ou ↓) dans une même région de l’espace, un trou de corrélation doit être ≪ imaginé ≫ pour les électrons de spins opposés (↑, ↓) car les mouvements de ceux-ci sont corrélés par des interactions Coulombiennes. Intuitivement le trou de corrélation doit être plus petit que celui d’échange puisque la règle d’exclusion de Pauli est déjà satisfaite mais on parlera d’un même trou d’échange-corrélation dont on exclura les autres électrons de même spin ainsi que de spin opposé. Ayant précisé que l’approximation de Hartree rend compte du système sans échange ni corrélations, et en stipulant que l’on peut mettre toute l’information sur ces deux dernières quantités dans un terme que l’on qualifiera de 𝐸_𝑋𝐶 (énergie d’échange et de corrélation), on peut donner l’expression de l’énergie totale 𝐸_{𝑒𝑥𝑎𝑐𝑡𝑒} que l’on souhaite atteindre :

𝐸

_{𝑒𝑥𝑎𝑐𝑡𝑒}

= 𝐸

_{𝐻𝑎𝑟𝑡𝑟𝑒𝑒}

+ 𝐸

_𝑋𝐶

(2.11)

En écrivant ad hoc, pour l’instant, que la variable est la densité électronique 𝜌, qui elle-même dépend de la position 𝑟, on en arrive à l’expression de l’énergie telle qu’elle est proposée dans la théorie de la 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛𝑛𝑒𝑙𝑙𝑒 2 _{de la densité électronique (DFT) :}

𝐸

_{𝐸𝑥𝑎𝑐𝑡𝑒}

[𝜌(𝑟)] = 𝐸

_{𝐻𝑎𝑟𝑡𝑟𝑒𝑒}

[𝜌(𝑟)] + 𝐸

_𝑋𝐶

[𝜌(𝑟)] (2.12)

La tâche de la DFT est donc de proposer la meilleure fonctionnelle possible pour exprimer 𝐸_𝑋𝐶[𝜌(𝑟)] .

2.3 Les débuts de la DFT

Le concept fondamental de la DFT est que l’énergie d’un système électronique peut être exprimée en fonction de sa densité. C’est en fait une idée ancienne datant principalement des travaux de Thomas [41] et Fermi [42]. L’utilisation de la densité électronique comme variable fondamentale pour décrire les propriétés du système a toujours existé en leitmotive depuis les

2_{. C’est la fonction d’une fonction : On peut décrire l’action d’une fonctionnelle comme la transformation d’une} fonction en un nombre ; tout comme la surface sous une courbe est une fonctionnelle de la fonction qui définit la courbe entre deux points. Pour une fonctionnelle universelle 𝐹 dépendant de la densité 𝜌, on a 𝐹[𝜌(𝑟)], la quantité entre les crochets droits est la densité électronique 𝜌 = 𝜌(𝑟) qui dépend des coordonnées spatiales

15

premières approches de la structure électronique de la matière mais n’a obtenu de preuve que par la démonstration des deux théorèmes de Kohn et Sham [43].

L’intérêt d’utiliser la densité électronique provient du fait qu’elle ne dépend que des 3 coordonnées spatiales ou à la limite de 6 coordonnées si l’on considère deux populations de spins (↑ et ↓) pour décrire les systèmes magnétiques. En revanche si l’on s’en tient à la description d’un système avec une fonction d’onde à plusieurs électrons, pour 𝑁 électrons celle-ci dépendrait de 3𝑁 variables pour un système à spin dégénéré et de 6𝑁 variables pour un système magnétique, tâche impraticable.

La théorie de Thomas et Fermi est une véritable théorie de la fonctionnelle de la densité (DFT) dans la mesure où toutes les contributions à l’énergie électronique totale (cinétique aussi bien qu’électrostatique) sont exprimées en termes de la densité électronique. Elle consiste à subdiviser le système inhomogène en ≪ petites boîtes ≫ de volumes élémentaires 𝑑3𝑟 où les électrons ont un comportement d’un gaz homogène de densité 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒 3_{. Dans ce contexte,}

le potentiel effectif 𝑣𝑒𝑒 (𝑟1, 𝑟2) décrivant un terme 𝑏𝑖 − é𝑙𝑒𝑐𝑡𝑟𝑜𝑛𝑖𝑞𝑢𝑒 4 est exprimé de la

manière suivante :

𝑣

_𝑒𝑓𝑓

= 𝑣

_𝑒𝑥𝑡

(𝑟) + 𝑣

_𝑒𝑒

(

𝑟

₁

, 𝑟

₂

)

2.13

Le terme monoélectronique 𝑣_𝑒𝑥𝑡(𝑟) définit le potentiel obtenu par l’action des noyaux et 𝑣_𝑒𝑒(𝑟₁, 𝑟₂) l’action électrostatique des électrons en r2 sur ceux en r1. La complexité de la

solution de Thomas-Fermi provient du terme de répulsion interélectronique :

𝑣

_𝑒𝑒

(𝑟

₁

, 𝑟

₂

)=∫

_{|𝑟1−𝑟2|}𝜌(𝑟2)

𝑑

3

𝑟

₂

2.14

Difficile à calculer. Thomas et Fermi ont tenté de résoudre ce problème en remplaçant ce terme par une intégrale de Coulomb traduisant l’interaction de deux densités électroniques :

3_{. Pour un tel gaz idéalisé appelé également jellium, l’énergie cinétique est facilement calculée puisque sa} population est caractérisée par des électrons libres, i.e. ne subissant pas le potentiel dû aux noyaux, et indépendants entre eux, 𝑉𝑒𝑒 = 0, ignorant ainsi toute corrélation. C’est en somme un système de référence, d’où

son importance.

16

𝐽

₁₂

[𝜌] =

1 2

∬ 𝜌(𝑟

1

)

1 |𝑟1−𝑟2|

𝜌(𝑟

2

)𝑑

3

_𝑟

1

𝑑

3

𝑟

2

2.15

C’est un pas de plus par rapport au terme direct de Hartree (cf. l’équation 2.4). Néanmoins, cette astuce ne fournit pas une solution parce que 𝐽₁₂[𝜌] ne tient pas compte de l’influence réciproque de la position instantanée des électrons, i.e. les effets d’échange-corrélation.

2.4 Théorie de la fonctionnelle de la densité

La théorie de la fonctionnelle de la densité électronique (𝐷𝐹𝑇) a été développée en deux temps, en 1964 et en 1965, par Hohenberg, Kohn et Sham [42 ,43]. Elle consiste en la réduction du problème à plusieurs corps en un problème à un seul corps dans un champ effectif prenant en compte toutes les interactions. La DFT fournit une base théorique principale pour le calcul de structure de bandes d’énergie. Comme on l’a exprimé plus haut, l’idée fondamentale est que les propriétés exactes de l’état fondamental d’un système fermé, i.e. sans réactions chimiques, formé de noyaux positionnés dans des sites fixes et d’électrons les entourant, sont des fonctionnelles de la seule densité électronique. Malgré sa formulation exacte du système électronique, la DFT ne fournit que l’existence d’une preuve que des résultats fiables seront obtenus si l’on sait établir les relations nécessaires entre la densité et l’énergie. Néanmoins, cette tâche n’est pas aisée dans la mesure où la fonctionnelle de l’énergie totale n’est pas connue pour sa partie multicorps. A cette fin, la communauté scientifique tente depuis plus d’une vingtaine d’années de proposer et de tester des fonctionnelles afin de les éprouver en confrontant les résultats qu’elles donnent avec des propriétés physiques observées expérimentalement. A titre d’exemple la fonctionnelle originelle de la DFT, la LSDA (Local

Spin Density Approximation), construite sur la base d’un gaz d’électrons homogène donne de

bons résultats pour une grande diversité de systèmes : des molécules, des oxydes magnétiques des éléments de transition, des alliages et des intermétalliques. Elle est néanmoins capable de fournir une description erronée des propriétés observées pour des systèmes simples comme l’état fondamental du fer, le magnétisme de certains alliages binaires simples, etc (cf. la section 2.5.5).

L’hamiltonien non-relativiste et indépendant du temps (2.16) est écrit dans l’approximation de Born-Oppenheimer [44], i.e. en négligeant les interactions entre les coeurs d’atomes. Il est composé de trois parties relatives respectivement aux énergies cinétique (2.17), potentielle (2.18) et d’interaction de Hartree (2.19).

17

𝐻 = 𝑇 + 𝑉 + 𝑈

avec

(2.16)

𝑇 = − ∑

𝑁_𝑖=1

∇

_𝑖2

(2.17)

𝑉 = ∑

𝑁_𝑖=1

𝑣

_𝑒𝑥𝑡

(𝑟

_𝑖

)

(2.18)

𝑈 = ∑

𝑁_{𝑖≠𝑗=1}

𝑣

_{𝑒𝑙−𝑒𝑙}

(𝑟

_𝑖

− 𝑟

_𝑗

)

(2.19)

Où

𝑣

_{𝑒𝑙−𝑒𝑙}

(𝑟

_𝑖

− 𝑟

_𝑗

) =

1 |𝑟𝑖−𝑟𝑗|

=

1 𝑟𝑖𝑗

(2.20)

Les deux premiers termes (cinétique et potentiel) sont à un seul centre alors que le troisième terme (interaction Coulombienne) est à deux centres

.

Théorème 1 :

L’énergie totale de l’état fondamental 𝐸 est une fonctionnelle unique de la densité des particules 𝜌(𝑟) pour un potentiel externe 𝑣𝑒𝑥𝑡(𝑟) donné.

La conséquence de ce théorème fondamental de la DFT est que la variation du potentiel externe implique alors une variation de la densité :

𝐸[𝜌(𝑟)] = 𝐹[𝜌(𝑟)] + ∫ 𝜌(𝑟)𝑣

𝑒𝑥𝑡

(𝑟)𝑑

3

𝑟 (2.21)

Où

𝐹[𝜌(𝑟)] = 𝑇[𝜌(𝑟)] +

1 2

∬

𝜌(𝑟)𝜌(𝑟,) |𝑟−𝑟,_|

𝑑

3

_𝑟𝑑

3

_𝑟

,

_{+ 𝐸}

𝑥𝑐

[𝜌(𝑟)] (2.22)

𝐹[𝜌(𝑟)] est une fonctionnelle universelle inconnue à cause du 3𝑒 _{terme de l’égalité, i.e.}

𝐸_𝑥𝑐[𝜌(𝑟)]. En fait tel qu’on a exprimé l’énergie totale précédemment, toutes les autres quantités peuvent être calculées exactement parce qu’elles correspondent à un système d’électrons sans interactions. Le troisième terme de l’égalité dans l’équation 2.22, i.e. l’énergie d’échange-corrélation 𝐸𝑥𝑐[𝜌(𝑟)], apparaît comme la différence entre la vraie énergie cinétique et celle

18

d’un gaz d’électrons sans interaction d’une part et la différence entre la vraie énergie d’interaction et celle de Hartree, d’autre part, comprenant ainsi toutes les contributions multicorps.

Malgré le fait que 𝐸_𝑥𝑐[𝜌(𝑟)] représente une petite partie de l’énergie totale, elle regroupe néanmoins toute l’information manquante sur les interactions. En outre, on peut lui attribuer l’important rôle de ≪ liant ≫ ou de ≪ colle ≫ [45] dans le système physico-chimique réel qui est mal décrit dans l’approximation de Hartree. Par conséquent, son évaluation est à la base

même de la solution à une particule dans un champ effectif des méthodes modernes de calcul ab initio de structure électronique.

Ainsi, dans sa formulation la DFT est exacte, puisque tous les effets multicorps sont sous-jacents dans le terme 𝐸𝑥𝑐[𝜌(𝑟)]. Mais nous n’avons pas encore l’outil pour résoudre le

problème tant qu’on n’a pas le moyen d’évaluer l’énergie 𝐸_𝑥𝑐[𝜌(𝑟)] qui devra être approchée. Un aspect essentiel du premier théorème est que l’énergie totale et les propriétés physiques qui en découlent sont indépendantes de la base de fonctions d’ondes utilisées pour construire la densité.

Théorème 2

La fonctionnelle de l’énergie totale de tout système à plusieurs particules possède un minimum qui correspond à l’état fondamental et à la densité de particules de l’état fondamental.

Ce théorème sous-tend le principe variationnel. L’équation d’onde des fonctions monoélectroniques est alors décrite par l’expression :

[-

_2𝑚ℎ2

∇

2

𝜓

_𝑖

(r) + 𝑣

𝑒𝑓𝑓

(𝑟) - 𝜖

𝑖

]𝜓

𝑖

(r) = 0 (2.23)

Dans laquelle le potentiel effectif est exprimé par :

𝑣

_𝑒𝑓𝑓

(𝑟) = 𝑣

_𝑒𝑥𝑡

(𝑟) + ∫

_|𝑟 1

𝑖−𝑟𝑗|

𝜌(𝑟

𝑗

) + 𝑣

𝑥𝑐

(𝑟) (2.24)

C’est l’ensemble (pour tous les 𝑖) des équations dites de Kohn-Sham. La densité de charge 𝜌 est donnée par :

19

Le facteur 2 précédant la sommation sur les états i rend compte de la double occupation de chaque orbitale (spatiale) due à la dégénérescence de spin. Le terme 𝑓_𝑖 correspond à l’occupation partielle de l’orbitale (0 ≤ 𝑓𝑖 ≤ 1).

Le potentiel corrélation est obtenu par différentiation de l’énergie d’échange-corrélation par rapport à la densité 𝜌(𝑟) :

𝑣

_𝑥𝑐

(𝑟) =

𝛿𝐸𝑥𝑐[𝜌]

𝛿𝜌(𝑟)

(2.26)

Par suite le terme 𝑣_𝑥𝑐(𝑟) est égale à 𝑣_𝑥𝑐(𝜌(𝑟)) . Le potentiel d’échange-corrélation, contenant tous les effets multicorps est alors uniquement fonction de la densité de charge 𝜌. Par ailleurs, dans la mesure où le potentiel effectif dépend de la densité des particules qui, elle-même dépend de l’état 𝜓_𝑖 d’une particule, on est face à un problème dit autocohérent ou self consistent.

2.4.1 Note sur les équations de Kohn-Sham

L’objectif atteint est celui d’avoir substitué au système réel à plusieurs particules en interaction un autre système modèle où les particules sont sans interaction mais dont la densité est la même que celle du système réel. L’équation de Schrödinger est donc reformulée en termes de ce que l’on convient d’appeler l’équation de Kohn-Sham (2.23) qui est en fait une équation de Schrödinger avec un potentiel effectif dans lequel des quasi-particules se déplacent. Les équations de Kohn-Sham sont couplées par la densité électronique :

𝜌(𝑟) = ∑ 𝜓𝑖 _𝑖∗(𝑟)𝜓𝑖(𝑟)

(2.27)

Ce couplage est alors inclus dans la solution obtenue d’une manière itérative. Pour le développement d’orbitales en termes de base de fonctions d’ondes, différentes bases peuvent être utilisées en fait le choix de la base n’est pas aussi crucial que celui de la fonctionnelle pour l’énergie d’échange-corrélation. Une fois ce choix fixé, les orbitales sont utilisées pour trouver une meilleure densité ρ au travers du cycle auto-cohérent. Un premier exemple de base est un ensemble d’ondes planes. Son efficacité n’est certes pas la meilleure car il y a un besoin d’un grand nombre de fonctions planes pour le développement. Cela présente tout de même l’avantage de permettre l’utilisation de transformées de Fourier rapides entre les espaces direct et réciproque. Une base plus efficace serait bien entendu les orbitales de Kohn-Sham elles-mêmes mais elles présentent le grand inconvénient de ne pas être connues au début du calcul. Une alternative est l’utilisation d’une combinaison linéaire d’orbitales atomiques (LCAO) [40].

20

2.4.2 Formulation de l’échange-corrélation

Le principe d’exclusion de Pauli et la corrélation inter-électronique jouent le rôle d’interdire la présence d’électrons de spin 𝜎 (𝜎 =±1

2) dans une même région de l’espace au

moyen du trou d’échange-corrélation (XC). Cette section qui précède le détail des fonctionnelles est destinée à expliciter davantage les propriétés de cet espace d’échange-corrélation.

En termes de ≪ probabilité ≫ d’occupation spatiale, ceci s’écrit :

𝜌(𝑟

₂𝜎,

, 𝑟

₁𝜎

) = 𝜌(𝑟

_{2 1}⁄

) (2.28)

signifiant que la probabilité de trouver l’électron désigné par l’indice ≪ 2 ≫ de spin 𝜎, _{en r} 2

est affectée -en fait diminuée- de celle de trouver l’électron d’indice ≪ 1 ≫ de spin σ en r1 par

rapport à un gaz d’électrons indépendants. Si l’on développe 𝜌(𝑟_{1 2}⁄ ) on obtient la matrice

densité à deux corps, i.e. impliquant deux centres d’intégration.

𝜌(𝑟

2 1⁄

) = 𝜌(𝑟

1

)[𝜌(𝑟

2

) + 𝜌

𝑥𝑐𝑡𝑟𝑜𝑢

] (2.29)

= 𝜌(𝑟

₁

)𝜌(𝑟

₂

) + 𝜌(𝑟

₁

)𝜌

_𝑥𝑐𝑡𝑟𝑜𝑢

_(2.30)

Dans l’équation (2.30) on reconnaît dans le premier terme un produit des densités électronique. Ce dernier, multiplié par le terme 1

|𝑟1−𝑟2| , peut être lié à l’interaction

Coulombienne entre deux densités électroniques comme celle décrite dans l’approximation de Thomas-Fermi. La nouveauté est dans le deuxième terme qui de par sa formulation, traduit l’interaction d’une densité électronique avec celle d’un trou appelé trou d’échange-corrélation. Tout en étant moins aisé à imaginer que le premier terme, nous introduisons par-là l’expression mathématique du trou d’échange-corrélation. La matrice densité ainsi définie est normalisée pour les paires d’électrons dont la désignation est généralisée à r et r’ de spins 𝜎 et 𝜎, _:

∑

_𝜎,𝜎,

∬ 𝑑

3

𝑟𝑑

3

𝑟

,

𝜌(𝑟

_𝜎

,𝑟

_𝜎,,

) = 𝑁(𝑁 − 1) (2.31)

En toute rigueur il faut formuler la densité du trou d’échange-corrélation comme suit : 𝜌_𝑥𝑐𝑡𝑟𝑜𝑢_(𝑟

1, 𝑟2) ou bien 𝜌𝑥𝑐𝑡𝑟𝑜𝑢(𝑟, 𝑟,) pour généraliser, car il tient compte des deux centres. A

partir de cette écriture on peut exprimer à nouveau l’énergie interélectronique pour deux centres r et r’ de la manière suivante :

21

𝑉

_𝑒𝑒

=

1 2

∬ 𝑑

3

_𝑟𝑑

3

_𝑟

, 𝜌(𝑟,𝑟,) |𝑟−𝑟,_|

(2.32)

=

1 2

∬ 𝑑

3

_𝑟𝑑

3

_𝑟

, 𝜌(𝑟)𝜌,(𝑟) |𝑟−𝑟,_|

+

1 2

∬ 𝑑

3

_𝑟𝑑

3

_𝑟

, 𝜌(𝑟)𝜌𝑥𝑐𝑡𝑟𝑜𝑢(𝑟,𝑟,) |𝑟−𝑟,_|

(2.33)

= 𝑈 + 𝐸

𝑥𝑐

(2.34)

On voit apparaître le terme attendu d’énergie électrostatique 𝑈 et un nouveau terme, celui d’échange-corrélation que l’on peut définir comme l’interaction d’une densité électronique avec celle probabiliste d’un trou d’échange-corrélation. Les propriétés d’un tel trou font encore l’objet de plusieurs travaux de recherche.

De plus nous introduisons un paramètre λ supplémentaire, susceptible de mieux aider à définir l’amplitude de la corrélation. Dans la limite λ = 0 la corrélation est nulle et le système ne subit que l’interaction d’échange ; en revanche pour λ = 1 le système est entièrement corrélé. Ceci permet de réécrire la densité probabiliste en reprenant le premier terme de (2.28), généralisé à r et r’ de spins σ et σ′, et en introduisant le paramètre de corrélation λ :

𝜌

_𝜆

(𝑟

_𝜎

, 𝑟

_𝜎,,

) = 𝜌(𝑟

_𝜎

)𝑛

_𝜆

(𝑟

_𝜎

, 𝑟

_𝜎,,

) (2.35)

Le terme 𝑛𝜆(𝑟𝜎, 𝑟𝜎,,) représente la probabilité de trouver un électron de spin σ′ dans le volume

élémentaire d3_{r′ en r’ pourvu qu’un électron de spin σ soit dans le volume d}3_{r en r.}

2.5 Les fonctionnelles de la DFT

La première fonctionnelle propre-DFT ayant permis la résolution du problème est l’approximation locale (LSDA : local spin density approximation). Elle est en fait basée sur des idées de Félix Bloch (cf. par exemple [46]) considérant une statistique de Fermi d’un gaz d’électrons uniforme pour exprimer l’échange. Ces développements ont été ensuite étendus à la prise en compte de la corrélation.

2.5.1 L’approche locale de la densité

Dans une densité électronique variant ≪ lentement ≫, Kohn et Sham ont proposé un développement de l’énergie d’échange-corrélation :

22

𝐸

_𝑥𝑐

[𝜌(𝑟)] = ∫ 𝜌𝜖

𝑥𝑐

(𝑟)𝑑

3

𝑟 + ∫[|∇

𝜌

|]

2

𝜖

_𝑥𝑐

(𝑟)𝑑

3

𝑟 + ⋯ (2.36)

Où 𝜖𝑥𝑐(𝑟) est la contribution à l’énergie d’échange-corrélation par électron dans un gaz

homogène. Notons qu’elle est fonction de 𝑟 d’où la localité (contrairement à l’échange non local dans HF). La LDA consiste à considérer 𝐸_𝑥𝑐[𝜌(𝑟)] comme une fonctionnelle locale de la densité électronique ρ(r), c’est-à-dire qu’elle dépend de la densité en 𝑟 :

𝜖

_𝑥𝑐

(𝑟)=𝜖

ℎ𝑜𝑚

[𝜌(𝑟)] (2.37)

Le terme en gradient au premier ordre ainsi que ceux d’ordre supérieur sont alors omis, conduisant à la formulation :

𝐸

_𝑥𝑐

[𝜌(𝑟)] = ∫ 𝜌𝜖

𝑥𝑐

(𝑟)𝑑

3

𝑟 (2.38)

2.5.2 L’introduction du spin dans l’approche locale de la densité

La généralisation de la 𝐿𝐷𝐴 au cas où une polarisation des spins est prise en compte conduit à la 𝐿𝑆𝐷𝐴 où 𝑆 désigne le spin électronique. L’introduction de ce dernier consiste à considérer deux populations 𝜌(↑) et 𝜌(↓) dans la matrice de densité et à formuler le potentiel dépendant du spin (𝛼) pour l’échange et la corrélation : 𝑣_𝑥𝑐𝛼(𝑟) (où α désigne l’orientation ↑ ou ↓). Le système est décrit par deux fonctions dans un espace à 3 dimensions. Le terme 𝜖𝑥𝑐 est

maintenant fonction des deux spins : 𝜖_𝑥𝑐[ρ↑(r), ρ↓(r)]. Il existe pour cette énergie différents schémas de paramétrisation comme on le verra plus loin. Ainsi définit-on l’approximation de la 𝐿𝑆𝐷𝐴 à l’énergie d’échange-corrélation de la manière suivante :

𝐸

𝑥𝑐𝐿𝑆𝐷𝐴

[𝜌

↑

, 𝜌

↓

] = ∫ 𝑑

3

𝑟𝜌(𝑟)𝜖

𝑥𝑐ℎ𝑜𝑚

(𝜌

↑

, 𝜌

↓

) (2.39)

𝐼𝑐𝑖 𝜖_𝑥𝑐ℎ𝑜𝑚(𝜌↑, 𝜌↓) est l’énergie d’échange-corrélation par particule d’un gaz d’électrons homogène. L’équation d’onde est réécrite pour les deux canaux de spins :

[−∇

2

+ 𝑣

_𝑒𝑓𝑓↑

(𝑟) − 𝜖

_𝑖↑

]𝜓

_𝑖

(𝑟) = 0 (2.40)

[−∇

2

+ 𝑣

_𝑒𝑓𝑓↓

(𝑟) − 𝜖

_𝑖↓

]𝜓

_𝑖

(𝑟) = 0 (2.41)