Le model Auto-régressive moyenne Mobile intègre arima (p,d,q)

"

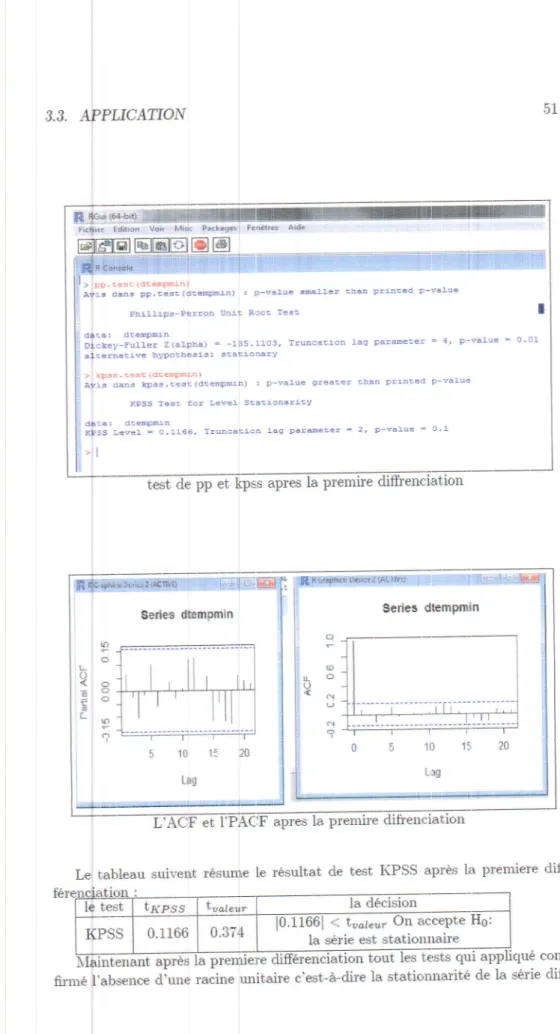
Atg6ti"*"

Ddmocratique

et

F'opulaire

t,rlinistdre de

Jt'EnsEignement

Sup6rieur

et de

la

RechLerc'he

t/ljr

u"

tt

Scientifique

[Jniversitd

I

Mai

1945

Guelma

Facult{

des

Mattrdrnatiques

et

de

l'Inrfonnatiqurl

et

des

liciences

de la

Matidre

D6Parternent

de

Mathdmatiques

M6.mo-ire"

Prtise,nt6

en vue

de

l'obtention du

diplome

de

Master Acad6mique en Math6maticlues

Option

:

F

robabilit6

et

application

Par

.

ry1elre

Kouarta Asma

;Ylerre

hadjoudji

mounira

;Ylerre

Azzedinne Habiba

lntitul6

P'ITEISI]DEF{T

P51P'PIJI]RTBU

R

[])KA.MI][]\ATBUR

Diriq€ Par

:

Dr.

Otmani

I

Devant

le

jurY

Dr"Rallai

MCA

Univ-Guelrna

Dr.

Otmani MCA

Univ-tGuelmat

Dr.

Bakhouche

MCA

Univ-Guehna

Le

nnudBle

Auturfgressive

Moyenrne Mnbiful lrutBlpre

ARIMA(p,d,q)

JFJFgg}

ffi

F

g

s

#

g

w

#

g

g

#

6

g

#

I

g

#

#

#

#

#

#

#

#

g

#

#

#

#

#

#

#

#

tr

#

#

s

#

g

s

g

#

w

#

g

H

#

#

#

tr

#

g

#

tr

#

ff

#

#

F

#

#

#

F

#

sS#SrSj

t#

# # fr # g fr # # tr 6 # g g fr # g g fr # tr

9'

#

Pf sr'#s

#

frir se

s

p

^lc

t,

'lF

#

"]F

F

,#

-#r

f

,#

$F

lf

.tf

JF

-#

,

IW

iff

a i

i#

$F

,l

'l

3F

ftr

i

s#

#f

I As

€f

F &

st

#+

F &

sF

s{

s

1Pn

€r

s-js

s

fllr-F

fi

#l

#'-,#

,#

,#

,#-#

'iff

Jff

-J#

JF

jff-#

,tr

cF_

lil

rt

,lf

*S-I$ff

_{?'. +}

nf

*

ii

.1j ;1;.;;:'.-r;: u1,..

*;

i3'

(7n,tnmil

e

_*e

dalidi

fuD'#rU{#

te

faat

p^rua,amt

_W

_ryt{l-

_{drt &ard}

_dr4

_{/ia4dtsrta'ftl,}

?lh*

@

_d

r+acrc e$eadnccst,

e&

h

p#unq*rc

dE

%#B

:

0t

nasi

tua*t,

?tuar

ozo

_fnia:(nx

car4asle,

c&t

t&aerffi.ta*sdanaw

e:,t

o@

ottce:ofrl4,lch$A.

_Fa4tr

_FtzuTnAAat,

drtaL

0&,

_dnwtat)to,

C{d a{a

44itnri4,

kfu*rc

,w??tsrcd00r+

_{ilfalstrternt}

_taaa

_{sa

_auttfqattta

_dz

h

D,pnndta*a+t

_P4at,

{'eort*tc

dtlar&f/f

ataa,a

td

ttuuwrtu&ta

deq,

oar,to6w, d.(hdi

_W

d

tara

ta,.

pnuwaata

_dqnat

_u"ctpaetr*

_d

h

,rca/A,aAiaot

_dn

_outaa

t-'i Srl; !" -"-.-,*;,i

**rii5.$

'

(D6fiicace

d6&e

ce

mimoire

&

toute

ma

6eliteJami$e,

pire

_0q6[e

atfraft)

pour

s&

dductrtisn

qu'if

rn'a

e

{es

_,ye'ines

qu'i{

s'est

donnrfe

_pour

Tfta

rdussite.

],t

wa

Ttu,i

m'o

(fr[assaouc{a)

qui

m'*

6c{ak6,e

tn$n

cfremin

et:

our*gd

et soutenue

tsute

au

fan6

{e

mes

dtufes.

Mesfrdres

_flmar

et

gk{.ofiamnfe,

%.a

tie$e

seur

Safrrc.

J'e

ltt

i

tou:s mes

onc{es:

touframi

_%rtfrg,

W{,

St{at:ii{

e,t

{eur

mes

S\{a$ime,

Lirda,

Nadia,

t%eriim,

Lin{a.

te:

,{e

dt

particw{iireffient ma tstfie Soria et

_son

_{ipou.X,{Fares.}

J$

rue

wi terminer

$&?ts

citer

mes

amis Sousou,

!T{ada,

fiartr,

t\fadjat,

I{frnrrce,

S{a{a, lMoufida.

{e

dddie

d

tous

mes

awis

que

je

n'ai

pas

citds

et

d.

t,aus

ceu"gqui me

conttn"issent.

lEt

tn

ts

fisfoni{fx:

Kp*arta

rt$o&

svfusi

:q

if

"t t : i' h

ffio,'ffi

:ffiP'ffi

_{&ffiffi&%KffktrtuffiffiK€mil}

6ieu

_ft

tout

puissant

{e

m'ar,,sk dcnne

f

fionneur

fe

caur*g,t

tlnTrf t/17

rvw, Jwe

{ake

#

trs.,s'i!"

ftf.r'

'lP. flP.d.1e

fe

tnctn.ol.re

.fr-

rnon

(tutofrpmeQ

pour

sa

€ducatian

qu''i{m'a

incu{qune

iles

peiruzs

qu'i{

s'est donnie

_f;our

ma

i'ffissiie.

*),rn /flf^rnn"r*n\

_iia'itiV

n*i nnta 6rfair6o

tr!t-r!!

r6ttain o! nti mtn

irtLJl,ili'ii44j

alrr,

iia. ai'

ra.i4n,'toe it.,r'tte {,rt*/t,et"r'

ve

rTtr'e

tr.'

w

ens*u/ggi st s*uteru$ tsttte

au

krg

de #tes

ftu6es.

A

mon

ehers

frires:

Noure:ddine.

A

tnan chers

Scr'urs

:

Samia,

AbIa,

Neims.

qu'e

tous

ieurs epoax: Ghuni,

wainsb. Aussi

qu'e

toaw

ieurs

:

Nsdire, Chaimu,

S€if, Mouhsrne'd,

y4rwu

et ma

grande

mdre{hmama}

A

enfi

amie\ surtout :Asm*,

N#diet, AmeI,

M*aftda

,

Ilham

,,Sihem,

Ifds@

toas

lu

promo

de

probabititi:

2013-2014

.

ma

ch/rs:

Soahilu,

Foufa,

Habiba,

)Tinna,

Imane,

Amtina,

H*$s,Mareim,

Nadai,

Aieha,

AhlemrS*brin*

tous

lelftmilles:

Hadioadji,

Djouide,,

Djamaa,

Gemihi,,

Mousasui

_,sellnoui

$

taus ceux

que

j'aiwe

et

qui **'siment

t -^-Tt ?rD ,

lWUUIVTITA

nte

1.1.1 1.1.2 1.1.3 1.1.4 Ires Quelque s€ries

chronologiques.

. al6atoires

stationnarite

. .

.

foncti'ons

ACV. ACF et

PACF

!.J

Le us

bruit

blanc (white

noise)

1.2.1

retard

1.3.1 1.3.2 1.3.3 1.3.4

ARMA(p,q)

autor6gressif

AR(p)

de moyenne

mobile

MA{d

ARMA(p,q)

conditions de

stationnarit6 et d'inversibilit6

.

{e

La moyenne,

ACV, ACF et PACF

de

la fonction

d'autocolaniance

des fonctions

d'autocorrdlation

.

.

par la

m6thode Moindres

Carr(b

Ordinakes a Moiadree Cars€es Conditionnels

imation

du

maximum

de waisemblance .

test

de r€sidus)

central

limite pour

rdsidus

1 1 1 3 3 6 8

I

I

9 L2 15 16 l-9 20 2A 20 2L ?3 28 31 31 34 34 36

.19

2.1.1 de

la

movenne

19 2.1.2 2.1.5 2.2.r 2.2.2

v

2.3.1 2.2.3 2.2.4 2.2.5

des proceesus

ARMA

manuelle

IY 3 3

CONTEMTS

rrtodCle

ARIMA

(p,drq)

D6finition

de

la

non

stationnarite

.

.

.

tlpes

de non

stationnarit6

.

.

.

3.2.1

Non

stationnarit€ d6terministe (Stationnaritd

en tendance)

3.2.2

Non

stationnaritd

stochastique

(Stationnaritd

en diffErence)

3.2.3

D6tection de la non

stationnarit6

en

utilisant

les fonctiorrs

ACF et PCAF

3.2.4

Ddtection

de Ia non

stationnaritd

en

utilisant

les tests tle Dickey-frrller

3.2.5

D€tection

de

la

non

stationnaritd

en

utilisant

les

tmts

tle

Philips-Perron

3.2.6

Confirmation

d.u non

stationnarit6

en

utilisant

le

tests de

KPSS (Kwiatowski, Phillips,

Schmidt,

Shitt)

.

3.2.7

Stationnarisation

en diff€rence

3.2.8

Moddlisation de processus stationnaire

Application

tl

3.3.1 s.ghilation

3.3.2

IntroductionsurR

.

.

.

3.3-3 Etapc

de

la

modalisation

d'une

s6rie des donu€es

(I,x

temp€ratures de

notre wilaya

Guelma)

Conclusion 46 47 47 56

37

37 37 37 38 39 40 45 .46 46 46

I

I

I

I

I

I

ro

ion

g6n6rale

effec

U serie

est

une succession

d'obsenations d'une

grandeur

al

r6guliers au cours

du temps.

Les s6ries temporelles

con-tres

importent dont I'objet est l'6tude

des r'ariables au cours u temps. 'importance de ce dornaine est illustrde

par

les nombreux

do'

d'

:

(M6teorologie

:

analyse de donn6es climatiques, Eeonomie 6conomiques, Finance

:

€r.olution des cours de

la

bourse,

de lo€l'olution d'r:ne

population,

\{6deciD€, _{. '}

.ext..

Nous

travaille

de donner

un

compte syst6matique de moddle de

lin€aire

et

leur application

d la

mod€lisation

des donn6es

sequentielle dans

le temps. Le

processtrs

ARNIA ont joud

darx

de nombreux

nouveatx

d€veloppements dans I'analyse

par exemple

la simulation

de moddle non stationnaire Le

but

de

fournir

une technique specifique

pour la simuiation de;

le

logiciet

R et

en m€me temps

ii fownir

une

compr6hen-base rnath6matique

pour

cette techniqrre

et pour

ce

la

nous en

trois

chapitres.

chapitre, nous introduisons une classe extr€mement

impor-ues

(

Xr,

t

e

V'

₎

ddfini en

terrnes

d'6quations

aux

avec des coeffi.cients constants.

L'imposition

de cette struc-dEfinit une famille param6trique de processus stationnaires.

avons selle , un des

AR

sion divir serle ldmes

, apris

.

Dans der slls

AR

en

utili

tant

ce f,fa

,le

pr, s6ries

twe

I'Au

moyenne mobile ou processus

ARMA.

d'un

moddle approprid

ARMA

(p,

q) pour

representer un

stationnaire

observ6

implique un certain

nombre de

prob-trl

s'agit

notamment du choix de p et q, et

I'estimation

de des

j:1

...,

ql

et

q). de

I'

du modBle doib 6galement €tre v6rifi€e d€pend d'une de

la

de

tests

d'ajustement,

m€me

si la

s6lection

finale

des plus

peut €tre

syst6matis6 dans une large mesure

par I'utilisation

tels

I'AIC.

Nous allons discuter ces principes dans le deuxidme la classe des mod€les

ARMA,

qui intdgre une large gafirme

est

fourni

1mr le processus

ARIN{A,

i

savoir }es

proces-iation un

nombre

fini

de

fois,

de

r6duire aux

plocessrr's

le nidre

chapitre

nons abordons

de d6finir le logiciel R,

puis

s, c'est d

dire la

moyenne: les coeffficients

_{f

,r

8,:

i

:

1, ..., Pi

les

notre

ARINIA

qui

ann€es en

INTTRODUCTIOJV

GEMfRAIE

la

mod6lisation de eette processus' Finalement

i{/par

une

simulation d'un

ens€mble des don.n€es de

kh

degr€s de temp6rature de

notre

n'ilaya

Gutima

les

I

l

I

I

-l

I

-t

I

pr

cessus

stationrlaire

est

d'introduire la notion

de procesisus temporel et plus

classe des processus

ARI{A

(famille

de processus lin6aires

processus sont trds g6n6raux et sp6cialement Ie

modile

clas-srque

Le de ce

par

iirement

).

1.1

Ia s6rie _, qui sont particulidrement utiles

pour

d6c.rire le

com-des temporelles unirariEes. Cette presentation suppose que I'on

un certain

nombre de notions essentielles

d

I'analyse des

et

en

particulier la notion

de

stationnarit6.

Les

s6rie

d6finition

chronologiques

(Xt,

t

g

Jn)

est une suite d'obserrations

d'une

Xt

ddfinies

sur un

espace de

probabilitE d

diff€rentes dates

n

est un

.T)

et

T

de temps

qui peut €tre

discret,

(dans ce cas,

fn:

le nornbre

d'obsenations)

ou

continu.

Habituellement

fn

able _).

temporelles:

La

partiti

de musique est

un

exemple de s€rie temporelle, m6me s'i1

de la math€matiquement {si on excepte

la

musique s6rielle :

:

modifier

I'emplacement d'une note a des cons€quences

La

s€rie

r.1).

reprdsente

la

population

des

Etats Unis de

1890

d

1950,

nombre de decdes accidente en USA (197&1979), (figure 1.2).

1 d€fini series

r.

on

{1,2,

. est

I

l

I

I

I

I

I

I

I

I

I

T

I

I

I

I

I

I

I

I

I

CHAPTER

1.

LE

PROCI'SSUS

S?i{?IONNA]RE AHMA

/

) Populatic,n de

geglAa

2008-201'1,

(figure

1.3).

(

o e c

8s

fe TiEne

figure 1.1:

population

des Etahs-Unis 189G1950

I

6 oQ 5O 6 a 1975 1976 19'rf Tine

figule

i.2

:

Nombre mersuel

,1\rI9P/

DEFII\TITION

2010 2011 2012 2013

2014 Tin€ iste. U du _Ps, Ia

I

figure

1.3:

population

de geulma 2008-201{

al6atoires

utilise

le

rme

cle processus al€atoire

pour d'€crire

une variable

dont

le,

peut pas €tre exprfun6 entidrement

par

une

relation d6termin{

proc€ssufi

toire

est une suite de

reriables

al6atoires indexdes dans le

d€liniesr un espace des 6tats de

la nature. Ainsi

pour chaque

instant

de

la quantit6

6tudi6e

Xt

est appel6e rrariable alEatoire et

des

Xi

quand

f

nie

est appel€ processus alEatoire.

profil

temporel d'une s6rie chronologique

r6vile:

tendance globale plus ou moins 6videtrte(Evolution polyge. ) un aspect local trds

irr€gulier,

impossitrle une courbe simple

d'un

tit

nombre de paramdtres,

A

(

Xt'

est i ue. vue de la

e ?')

par la sui

de recommenger la suite des mesules dans des conditions

ii),

on tente

de mod6liser

la suite

des obserlatiorus processlls al6atoire

X :

(Xt,

t

€

T),

ce

qui revient

i

af-Xr,

t

€

T)

est une trajectoiyd typique du processus, D'aprds pou\rou

Quand

N

---+ oa, la loi du processus.

ll faui

donc se restreindre

( Xt,

t

€

T)

est une

trajectof#

typique du processus, D'aprds

rl-pire le

modile

des

donneell

f/t

que

la donnee (Xr,

t

€

f),

tY7

CHAPTEN

L

LE

PROCESSUS

SIi{TIONNAIREIAR]VIA

sur

la loi

P

du

processus.

La

La

vt€

que

trois

s6rie dans dans

ag4ens

strict (

la

stationnarit6 forte)

(

Yle

he

d,e

r

un

processns temporel al6atoire

(Xr,t

e

Z).

I

Le

prvceaws X7 est d,it strietenzent ou

_fortement

stati,onnaire si

-uplet

du

ternps

tr

{

tz

aaec

t;

+

h e

Z,

Vi,,i,

: lr...rfl

_{la suite t*rr*o,...,}

rr_*^)

d,

la

nt€me loi,

que Ia suite

(str,...,#r.).

autre

fagon 6quivalente de

d6finir la stationnarit€ forte

:

2

Un

processl.rs est

dit

stationna'ire

au sens

strict

si,

pouir toutes

jt,jzr....rjn

lad,istributionjointed,elasuite

_{{*r,*r+jr,...,rt+j*)}

d*pend, des i,nter"ualles ile ternps

jt,

j2r....,

j*

et est ind,Cpend,ante d,e la

pEri-3

Une.

suite de aariable

aldatoir.es

(Xr,te Z)

ind€pendantes

et

d,e

loi

est stat'ionnai,rc.

au

sens

strict"

porte sur

les moments

d'ordre

un

et

signifie

tout

simplernent que les

itions,

il

existe alors une

ou

plusieurs repr6sentations possibles _{de la}

X6, ces repr€sentations ou processus ayant la m€me

distriibution

temps (m6me _{mornents). Cette hypothdse d'invar.iance de la distrjitrution}

temps permet ainsi de se

limiter

d une certaine classe de processru.s"

totl

:

dtordre deux

(la

stationnaire

faible)

Un stochastique (X1) est

dit

lbiblement stationnaire ou stati,onnaire

du

oldre

si:

eZ,E

(xf)

S

_"".

e

Z,

E (X*)

:

m

,inddpendant de

t.

(f,

h) €

Zzcw

_{X1,X.+a)

:

_T

(h)

inddpendant d.e

t.

premidre condition

E (Xrt)

{

oo

garantit

tout

simplement I'existence (ou

la

₎

des moments

d'ordre deux. La

seconde

coudition E

(&,)

: *,

allatoires

Xt

doivent

avot

la

mdme esp€rance quelle qne

soit la

date

f.A

t dit,

I'esp6rance

du

pfoce$sus

Xr

cloit 6tre ind6pendante

du

temps.

d'

la

troisidme condition 'y(h) ind€pendant de

t,

porte sur les

uroments deux rersum6s par la fonction

d'autocorariance.

Cette condition irnplique

monrents doivent €tre ind€pendants de

la

date consid6r6e

et

ne doivent uniquement que

de I'ordre

des

retards.

Autrement

dit

la

fonction

d'a

ance

du

processns

X;

doit €tre

ind6pendante

du temps.

S,rus ces

processus

_{{ Xr,}

t

e

_{Q te\p}

que poru presque

tout

r,r toute portionL

su-ffisa-longue de la

trajectoire

(X)

t

e T),

fournisse des indications su-ff.snmment

tury(r,

/'

oErrnrrrrow

io'n 4

nEsumE, an procesllrs est stat'isnna'irc au second srdre si l'ensemblet

d,e fixonlents ind4pend,ants du temps-

Par la

su'ite le ter"rne stati,onnaire fem,, at at'i ann arit E

_f

aib I e.

Ex

ple

5

odA

et

,B sont

ua,r\

:

L amec

€

_[-r,

r],

on uEri,fi,e que

X1

est

un

proceEslus

stationnaire

du

ordre put:,

(

*oo,

Vt

eZ,.

(dh)

ne d€pant pas de

t.

B1)

X1

est Jortement stati,onnai,rc

et

E

_tX?)

K.

x,

alora

X1

est

it

Le

rec'iproque est _fausse en g6,n|ml.

7e)

X1 _{est fai,blement} stati,onnai,re

et

gaussienne, alors

Xx

est

telle

que Ie pweessts gauss'iens

dtfinie par

:

8{

gaussierzs)

ll

lea

gaussienne

reelle).

On

dit

que

X

est une variabie al6atoire

reell[e sa

loi

de

probabilit6

a

pour fonction

caract6ristique :

E

E

"v

le processus

(Xt,

t

e

Z)

def,ni

par

X1:

Acos (d*)

+ Bsin

(0t)

deu,x

v.a non

contl,IEes

et

E

(d)

: E(B) :

0, uar(A)

:

€IRettr

en d6duil;

E[X]

:

_;,r,

et

que

uor(X)

:

02.

Si

o

_*

O,la

loi

possdde

de qur a

pour

expresslon :

<bx(*)

: zll"*t]

/.

o2r2\

: exp\?pu-

2 ).

R+.

px@):#"*(-%#)

(tx,t''

r(Xr)

₌

(h):c

iorn

I

_f$

gaussien

reel).

Un aecteur al€ato'ire yreel _de

_dirtension

_n

(xr'.

,

X"")

est aecteur gaussien s'i toute combi,naison lin1ai,re de

X1,...,Xn

est zsuriqble gaussienne r6elle.

10[

gaussi,en

{eel).

On di,t qu'un

prvcessus r€el

X

₌

tx

{t

t e,T)

gau,ss'i,en si,

pour toute

suite

_finie

_{d'instants {t1rtzr...rtn!-}

,

X

(fr))

est

un

uecteur gaussien.

(x

(tr

_,X

(tz)

'

:11 P, oppos:ition,

un

prrl.ces*tls non stationna'ire est un

ptcessus

qui

pas I

oil

l'autre

d,e ces condi;ti,ons _{de stationnari,t€ faible.Nous}

un

qu€

CHilPTER

1.

LE

PROCESSUS

STA.?IONNAIREIARJ!fA

12

(prvcessus non stat'ionnaire

:

nzarche aleatiore)

Ss le processus

d6flni

sw

f

€ N

p*

&

:

Xo

*

Xr

*...

*

Xt,

oh

Xt

est

it

blanc. Un tel

processus est appel€ une marehe

al6atoire.

On e:n

dduit

,sr]

:0,

que

_"y(t;t)

:.8

_[xf]

:

toz et pour

que,

h>0,

on

a

:

'v(t

+

n,4:

"E

K&

*

&+r

+

.'.

+

x41")sr|

:162

processus

_{,$}

n'est donc pas

stationnaire

au second ordre.

Les

fnnctions

ACV, ACF et

PACF

d?autocovariance

(

ACV)

ion d'autocovariance d'un processus

(Xr, t

e Z),

de moyenne

J4(Xr)

:

1{h) ou.y6,

est d€finie

par

:

VIr

e

Z:

I (h):

cw(X1,,Xt+il: Ei(Xr

_-

m)

(Xt+r.

_-

O(Xr+r,)))

rtrice

d'autocovariance

(de dimension

m.)

est d€finie de

la

mani€re

| 'l(o)

'i(1)

?(h-1)

I r(t)

?(0)

1&*2)

Fl'

ra: I

I

:

: I

\

r

(t,

_{- t)}

_1(h

_-2)

_{? (0)}

ion

d'autocorr€lation (ACF)

La

ion

d'autocorr€lation

d'u:r processus

(Xr

_,t

e Z)

de rnoyenne

lt(&) :

n-Lt

p{h)

ori

pr

ffit

d6finie par Yh

e

Z

:

p(h):oo:

_#

p(ft)

e

_[-1;1],

et

"y

(h)

-'yu

designe

la

foacti,on d'autocovariance :

1

p(1)

p{2)

p (3)

p(n

_-

1) p (1) 1 p (1)

p(2)

.-.

p(2)

p(3)

p(1)

p(2)

1

p(1)

p(r)

1

oirr

,irt

p(n

*

r)

p("

_-

2)

p(n-3)

p(n-

a)

prit

i

NI Un de fagon,

ition

13 I'es _foncti,ont p

(h)

_{et 7}

(h)

sont sym€triques Yh

e

Z

;

p(h):

p(-a)

r(h):r(-i,)

partielle

(PACF)

i

un lien

entre des donnees observ6es

d

diff6rents instants.

de Iien co4siste d mesurer La relation entre deux observations,

aux

obeilratione intermdiafues.

Il

s'agit

de

I'application

de

aux s€ries chronologiques.

p!

(notee aussi

_{pLr )}

designe

la projection

orthogonale dans

form€ des combinaisons lin6aires des

Xr,

orl

s

(

r

(

t.

(xr)r.,

proceasus stationnaire centr€, de

fonction

d'autocorr€lation. est d€finie par:

corr

(X1,X2)

:

p(1)

corr (x1,a1

_-

P*(xo+r),&

_-

P*

(xt))

I'autocorr6lation

entre deux

instants,

une fois

tir€ partie

lin6aire disponible entre ces deux instarrts. D'une certaine

les observations

faites

en ces

deux instants

de

tout

ce les obserr,ations

intermffiaires.

def

CHAPTER

1.

LE

PROCESSUS

STATIONNAIRE ARMA

-t

"tr*,:..t1.

figure

1.4:

Autocorrlation

entre deux instants

statinnnaire

S.

accroissernents

ind6pendants

pf,oc€ssus

(X*,t

g

V,)

*f

un

processus

stationnaire d

accroissenrents

in-si la loi de

probabilitd

des accroissements (4111, 116) est ind6pendante

Yh

e

Z:

C'est

donc une classe

particulidre

des processus stationnaires d.

dans

la

pratique

on retient plus

g€n€ralement

la

d6finiti,on suivante du

blanc.

Le

processus

bruit

blanc (white

noise)

processus le plus simple mais veritable atome de ba"se de tous nos modiles

processun

dit

rtbruit

blanc",

(v'hite noise). Le processus (et)tes cornpos6 de

bles al€atoires rGelles

_{v.a.r)

centr€es de rrariance

flnie o2'

sans corr6lation

un

bruit

blanc (0,o2) not6

BB(0,o2;'

Btoit

blanc

est

un

proc€ss's

ii

accroissements inddpendants.

'exemple Ie plus classique est celui form6 de suites de

v.a.r

de variarnce

finie

it t it r*

1.3

1.3.

AEMA(P,Q)

ll:t::*it

figure 1.5

:

graphe de

bruit

blanc

retard

B

(

Backward) est d6finB

par la relation

suir,ante :

BX2:X;1

VteZ

permet de dEfinir une application

qui d

toute variatrle

Xg

retardde.

Cet

op6rateur

_{

les propri€tes

suilantes

:

i

Yj,t eZ.

*i

Vj,t

eV,.

=

Xt-i-r

Yi,i,t eZ.

sont trds g€n€raux, appellent

le

model

ARN{A(p,q).

ARJvtA(p,q)

us

_{autoregressif ARIA)}

&1,APU

rporel

(X1)s€z

est.un

proc€ssus autorF.gresif

d'ordre p

not6

prOce6$uff

_{) s'iiegtdrend,tes}

conditions suirantes :

| _-r)

la

varia

-ll.

:;g

B_]Xt:

Bi{Bi

Xt

si

_lol

<

1, intenant Crs

L€S

X1 rest

stat

du

seconde ordre.

*

aB)-1*

:

$frt

:;!f*

(r +

"r

+

at*z

+

a5B3

+

...

+ oi

gi)

xt.

station-10

CHAPTER

1.

LE

PROCESSUS

STAflONNA]R.E AR]!fA

Existe un processuc

("r)te"

est

B.B(0,os)

et p nombres rdels _@1...@o, telle

proces€us (X1) v6rifie

l'6quation

de r€currence

i

second membre al6atoire

Xt

*

6tXt-1

_-

...

_-

_flpXt-p:

e1 (1)

d'un

procesars AR' p

₎

(Xr,

t

€:

L4

La

_fonction

d'autoccaariance _{1 (h)}

une rrelati,sn de rdeunence de

la

forrne :

2 que

(Xt,

o(B

[dfln;-t-

dz"tn_z

Qpln-r-t

fi

I

dt'yo-t

*

6z]n-z +

...

₊

_6p'ta-r

si h:0

si

h>0

(2)

.

On coneiddre

la

d6bition

de

X1

:

& :

c+

_f.rt-r

+...

+

$"'et-p*

eg apres

la d(ftrition

de

la fonction

?h, on a Vh

>

0

:

r

.Et(-{r

_-

rrz)

(Xt-n

_-

.E(&-r")))

E'(cxn-a)

*

hE

(J(r-rxr-r)

+

...

+ 6pE

_lxt-"Xt-o)

*

E

(e,Xr-r)

dr?r_r

-t

6z",tn_z+ ...

+

&o"ya_p

E(6r&-1,)

:0

cat

Xt-t

ne ddpend que

des

€t-h-i

avec

j )

0.

la

m6me fbgon :

nlrx,

_{t' '}

_-*\2f

J

("x.-a)

*

6tE

{Xr-rxr)

+

...

+

6"8

(Xt-"Xt)

+.8

(€rXr)

$fln-t

*

fiz'Yn-z

+

..'

+

6p7n-p

+.8

(e6X1)

dftn-t*

6z"Ya-z+

..'

+

_6e1n--u+ 62

E

(erxr)

:

d2 puisque

Xt

peut s'6crire

sous

la

forme d'une

sotnme

des cho-cs passes.

LE

La foneti,on

d'autocontlation

notee

p1

d'un

processus

AR(p),

7,)

satisJait une velut'i,an d,e r{cuvvenre, de la

_forme:

L - " r&

[drPr,-r

*

fuzPn-z

+

...'

+

6pPp-n

Yh _'e

L

relations sont conrures sous le nom

d'iquations

de Yul+.Walker.

tQ

Les

autrcantlations paftielles,

not6.s

a6,

d'un

ptocesstts

AR(p),

X1

:

(4).

II

suftt

et

celle

ARI/LAe,q)

11

identifier

fnembres

d

membres les termes de

la d€finition

de

L p:ocessu$

Xr.

r

X,

: t*

_drer-r

+...

+

&net-p

*

e1

r€arire soqs

la

forme:

ier

coeffiqient 6gal

a

dup tt l=: a! I E T :l

**

.:,

₌ J

$u

processus

Aftt1)

:

Xt

:

0.7&-r

*

et

et

fonction d'autocorrlation,

Tr

:

6t

_{6t

_-

m}

+...

+

6ptXt-ea1

-

rn)

*e6'

de Ia

projection

lin6aire cle

Xt+r

sur les p plus

partielle d'un

A.R(p) s'arrnule &

I'ordre p

+

1.

CHAPTER

1.

LEPROCESSUS

S"ATIOI{IVAIREI

AR.I!tA :J ri "I ,'

:r.a 1t.t:

':rJ

h:0

o<h<g

h>q

Calculons les

autocovariance pour

le processus

MA(q)

:

Xr :

et*dret-r+...+Os€t-c

.T

E--:

et

l-

_{Lfli€t_,}

.

i:1

-trJ (5) (6)

;:W

o.,l

u

Itr 1 ng Average)

t

Xa est

stationnaireTu

seconde

ordre

.

_\

Existe un processus

_tur)r.,

est

BB(0oot)

"t

p

nombres r€els

01,.'.,du, tel

(t +af

+ol+...+e?)6?

(-0n

+

0t0n+r

+

...

₊

0q-n0q)

o!

Thc

1.7

:

Tlajectoire du

processus

Ai?(l)

: X1

:

0.7Xt-r

*

e1 et; sa

fonetion

d'autocorrlation

partielle.

Procpssus

de

moyenne

mobile

M

A{q)

processus

(Xr)

of

un processus de moyenne rnobile

d'ordre

g not{i

MA{q)

proc€ssus

(X1)

v6rife

la relation

:

X;

:

sr

*

9tet-t+...

+

0c€t-s

LT

La

fonction

d'aucsuari,&nre

_{1k d'un}

processu's

MA(q)

lirXr,t

e &)

AR+IIAg,a)

13 .6.

{xtx.ta)

+

_(*

*

E'"--,)

(*-"

*

*r,"--,)

r

(h)

E((

E(

-0qo2 si

h:Q

0 ei

hlq

h:0

o<h<g

o

h>q

rcstrltat,

il

sufrt

de rappeler que .E(es,es-5i

*

_*\

(Xr+u

_-

a(Xr-a)))

-

0ret-r

-r

...

_-

Acet-q)

(t.*r.

_{- 96t-r-n}

flcet-c-n)1

cette

expression

on retrouve le resultat

g6n6ral 6noncd ci-La _fonctiolt,

d'autocontlatian

notde p7"

il'un

p"oeessus

MA(B)

it

une rcIation de r€cunvnce de Ia

_farrne:

o<h<g

q

h>q

ffi *

'v

(h)

d'un

MA(q)

pour

hcq

donn6e par

blle est d6montr€ ci-deesu6.

I

o(o):

t!91

:

t

? (u)

r

(h)

-

-

?

i0)

-on*D3:o*.

oiai-6)o2

-@

01*

Q$na1+

...

₊

0q-n0q

tw

(1

₊

f,lr

0l)o"

si

h:0

(-Pr.1+

_{D3:u*r0;0;-Vlo2}

si

1(

h<g-1

(t

+ af

+

e?r+ ...

+

eZ) o?

(-0r,

+

0106ar

+."

+

Lq-n|qlo!

p(h)

:

iai-n)oz

p(h)

,n:

{

Ona:

*

El=r+r

14 CHAPTEP-

1.

LE

PROCESSUS

STATTONNAIRE'ARMA

) pour

h>$:

aa

{a

s

fl

T

p(h)

:

?

(h)

? (0) 0

t(o)

0

1

_|

_,--;-;'i

6

s

l; { {-r I

I

ll 1$ l$t

IX{ Tir

r

Tlajectoire du procesus M,4(1)

:

Xr

:

€6

*

0.761*1 ret

sa

fonction

dnautocorrlation

partielle'

figFr€ 1.9

_{]Ttalectoire du}

processus

MAtl)

:

X1:

e6

*

0.7e1-1

et

sa

fonction d'autocorrlation

partielle. Lrr r +t

€

a "l fforrre 1 li t. l' {? *d

e-{:

W

I.3.

1"3.

De

en di

(Xt't

q

ARMA(P,Q)

ARpIA(p,q)

19 med,ile agtordgressif et rnoyenne-mobile

d'adrcs (p,q)

(abrdge

tl(p,d)

wn procq"sslts ternporel discrv,t

(Xt,

*

e

V')

uerifi*r&

les

con-Eutivantes

15

{Xsi

est

il

existe

rh-ionnaire

du

seconde ordrc.

processuq

_{rr}r.z

est

un

BB(0,o2)

et p

nombres r€els _S1... r6els 01...@o,

tel

que le

processus

(Xr)*ez

v6ri-fie

l'dquation

Xt--r-

z

-ds

Xr+r-..'.-drXr-o

:

et*dr

€t-r 1-9zsr-z*".*

0 _s€t-.

q

(B) Clti les _{S; et 0; sont constants} avec 0s,

_6e+A

et les termee

€i; SOIrt

iion

2O La

_fonctioq

d'autocoaariance,y

(h)

d'un prvcestus

ARMA(p,q)

Z)t est

par la

relati,on suiaante:

p

0{t

&-

i)

+

E

(Xt-aet)

_-

_{Dtr"(Xr-r,at-a)}

i:1

s

iil _Li il B

rf

.+

+

ltnr

1.10:

Tl4jectoire du

processus

_ARMA(l,l)

: Jis

:

g.

_r-r

*

0.6$r-t

*

er

et

sa

fonction d'autoeorrlation.

autqrfgressi,f

,4nb)

est

un

AnMAftr,0).

rnayten$Le mnbil.e

MA(S)

est

un

ARMA{A,d.

21

Un

il?

Un !l

-l

-l---{---1,1",'l

j'i---

----'----CHA?TER

1.

LEFROCESSUS

STATIONNTAJRET ARtLfA

uilJ-.

1_.

/7

pouT sdrie l',i d,e

lusion

2& II

se trvuue egalement't'i,mgtortance de la _foncti,on d.au,trt-cor"rtlatirtn

le modile

d,e

la

sErie Etudi,€e

telle

que

:

_la

stat'ionnamiti, de la

e n1cgigfrg; que les coefficients de p7, d,'ou €tre egales d,

0.

En

tl,autres

il

fau\Ies coffici,ents

d,'auto-eort€.Iat'ian sont s'itu€s d,ans les liyn,ites d,e de canfi.ance,

S'iI

eviste d.ans I'estEriewe" d,es linzi.tes cle I'iruteraalle

poLtr

une

longue

piriode,

Ies coeffici,ents

d'auto-con{lation

d,onc

fdrentes d,e z1ro et sa im,pkque que la

sirie

est non stationnai,re.

On

sa,it

coefficients de p1,

sudl6

loi norrnale centgE de aariance Egale

it

_1|),

aonc,*--t(

alle de confi,ance

_Wur

un

Echantillon de |-mnde

taille

est,

P

d,

_{= 5}

J

.

rc:

f-r.oo

. +1.96 {e)

hypothise H1

Qui

_{WAu" pn*0}

(la sdrie

est

nan

stat'ionnairc

_).

on ua

r

cea tests

largemint

d,ans

le trois'iime

chapitre.

.24

Si, Ies coeffic'ients de

p6

dans

IC

en

arnepte l,hgpothise

Hs

qui

pl

₌

0

(la

sirie

est stationna,ire) sinan

en

rejet

H6

et

en

acrcpte le

Les

conditions

de

stationnaritG

et

d'inversib

de

stationnarit6

de

AR(p)

25

Un

procesllas

_tXr,t

_e

Z)

_{satisfaisant une} repr€sentat'ion

_AR(p)

inuervi,ble.

Il

est stat'ionnairv lorsque toutes les rac,ines d,u po/ynime

not€es

_{A; € C,3}

1.

p

_{sant de mod,ule}

_strictement

_{sup€ri,eur d, t'anit6.}

pp

o(.\i):Idn^t:o

,

_ff

(r-.r;1r):o

,l)il >1.vj

t:0

t:0

indique

tout d'abord

que

tout

processus

AR

peut €tre ooinversr4,' sous la forme

d'un

processus

trIA.

Le second

point,

plus

fon<ilamen-be sur

la stationnarit6

du processus.

ce

th6ordme indique que lors,que les

dt

polyn6me autor6gressif

sont

boubes sup€rieures d

I'unit€

en rnodule,

satisfait lm

3 eonditions de

_{la stationnarit6 du}

second ordre.

ions de

d'inversibilit6

de

MA(q)

26

Un

processlts

(Xr,t

_e

_Z)

satisfa,isant une repr4sentati,on .MA(q) stati,onnaire.

Il

est inaers'ible lorsque tsutes les rac'ines d,u polt,ynilme que I'dn est

Q@),

etr

tal,

Concl

linrh*oo p{h',1

:

h)

:

oYhls

limh*6., p(lz)

:

0

Les

d,

d'un Dans not6 SC

le

cas

(r)

a _{Ar) th€ordme u'ume p,artie s€rUs

la

s€6

itions

27

ta

retard

avec _{A6 Ie

r:asp:

A>

A(0,

A8/ldA(P,Q)

Z=FZ

_I

i

:1,2

17

*,,^r

=

o

*,t

(,

-;")

:,

r.\,t>

1vj

us

indique

tout

d'abord. que

tout

processus

_MA,

_qui

_n,est

:

pond6r$e _de

_bruits

_{blancs, est}

toujours stationnaires.

Ce

I aisemertt _{compte tenu des}

_propri6tl

_ao

u*it"

blancs.

La

h{"ttr

qu'un

processus

_N,

_{d6fini cornme}

""

UIA

peut

€tre

te

d'un

_dR

si le

pollrrdme

associ€ g

_{g)

est inversible, c,est

sont toutes sup€rieures

_d

_I

_{en moduie.'}

stationqarit6

et

d'inversibilitd

_des

_processus

_ARMA

d,ts

conditimts d,e

stationnarit|

(o*,

des

ttnditions

les cas) yeaient _{d d,6,terrniner}

_Ia

_{position'relatiue}

d,es racines

i

en

l'opSrateur

retard

_{par rappart ou}

_*rnl"

_unit6

d,u plan

n

polyndrnre !D

(B)

_d,ordre

p d

_{coeffcients r6els, d6fini}

en

B,

_:lo

_dq

:

_1.

_{Soit (A;),}

_I'ensembte -Jes

racines

_de

_ce

€cp

*

("),8

_$iBi

:g

_(,

_-

ir)

:

o

les racinqs _{du polyndme s'obtierurent}

d.irectement _d

_partir

4\z

*

rbzFz:

_(t

- ;) {t - ;) :

o de

la quantitE:

_A

:

_d7

_-

_A6z,on

_{montre que}

:

At:z$z[-*,

_*

les

raqines

_du

pol5.n6me

_d

_{coefficients r6els d,ordre}

ent

aqx

_{rmleur propres de}

_la

_matrice

_F

;tBss

t/s s?t{Tr0-tu't{-,[rRr;

AR-{.IA )l t), ,rp \

10

0l

I I

0... r 0/

18

CHAPTER,L LEPRO(

La AF I'e:

qI

dte

2.1

Er*i

cette

ARMA

2.1.L

_Esti

Pour emprrrq Si le nrombres $n mrlable

rxiste

les

pte

tp,q)

on

dr-'l'

critdres lee

PACF

fil; ,,', fin

suite

dq

T

observations

_{produites par un}

_{processus sta_}

&:

de

_{p et}

Se fonetion d'atrtocovariance .y(h).

nous gstimons

_{les paramitres}

_inconnues

_d'un

moddle

p

_,1(hj

p(h).

de

l4

moyenne

(theprique)

_p,

_{un estimateur}

_naturel

_est

_la

moyenne (10)

pr. : sans

biais

E'(/r)

:

pr

1g

:TL*,

t:1

r6alisat

tio

determinef

tion

dp

la

moyenne,

_AC\/,

_ACF

_et

est simplelnent un

bruit

blanc, alors la

loi

forte eles grands

N'erg-enc:

_{e

_1,c vers

p

presque sorement, en

probabilite

et

*',I"_l:t

_ftrte

des-grands nombres n'est g6n6ralement _pas

de

Xi

nF sont plus

iid.

Cependant, urr

i6".,ltut

analogue correl6$s, d

condition

_{de supposer indEpendance faible}

oo).

C'IIAPTER

2.

ESNN,fATION

les

variablp

(c'est-i-dire

en imposant une

condition du

tlpe

_[ll,I,yol

<

Estirfration

de

la fonction

dtautocovariance

construire un

estimateur

de la fonction

d'autocovaniance th€orique

_7(lr),

r que

si (Xr,Y1)r..., (Xz,

l'7)

sont

d.es obserrations bir.anierx

iid

de

flni,

un eetimat€ur de

la

cotari.ance entre

X et

Y

eet donn€

par

:

**e-'t

(v,-v'l

ime donc [raturellement

la fonction

d'autocovaniance

par

:

t L!/

_-\/

_-\

i

(h)

: r4}(x,

_-

x,)

_(x+"

_-

i")

(12)

2.1

( 11)

t

pour

0

< Il <

T

_-

1,

il

est appelE I'autocovariance empirique.

les valpurs negatives

de

h

on utilise la sym6trie de

l,autocor,ariance

ue _7(iz),

_{t

on

d66nie

_r{tr)

: i (-h)

pour

V

fr,

<

0.)

estimaterfr a l'avantage d'€tre un estimateur sans bi;ais de I'autoccrr,rariance ^v{h)

{'est-i-dire

son esp6rance est exactement 6gal a

.f{ft).

2.1.

Estir4ation

des

fonctions

d'autocorr€lation

On

natur{lleurent

la fonction d'autocorr6lation d

partir

de I'autocovariance

de

_{la ftgon}

suivante:

p(h):

"ffi

I

t'n-po'

I

w(0"-*)

_-N-(0,o2)

t13) appel€ lflautocorr6lation empirique.

rrem€

_.:

:

soit

soit

Xr

Xr

un un processus processus ,41?

AR(p)

(r causal

or

€6

*

BA

(0, a2), et soit

{4r,".- ,ro}

de

taille

n.

note

S, 1 R;t?,

et

&f;: I

_tol

₍₁

_-

_6a;tpr).

_Alors

_, quand

n

--.---+ _oo, (14)

2.2

Estirrfation

des processus AR.,MA

nou{ nous irrt6ressons aux probldmes de I'estimation des parcrm€tres ts

_-4ffllfA(p,

g)

*

partir

d'une suite de n

obsenations. L'estimation

tres d'frn procesrius

ARM

A@, q) comprend aussi, en principe, ,l,estimatiom

p et

q.

L'estimation

de

paramdtres

d'un modile

ARMA(p,g)

peut

par

dilprentes m6thodes dans le domaine

temporel

:

I

2T

2.2.L

l/Iod6ltisation

manuelle

choix

de ltordr,e

dtun

modele

par

les

fonctions

d'autoco,rr6lation:

Au

chapitre

I,

nous avons

vu

comment estimer

la

fonction d'autocovariance d'un

pro.urr.tr. Le

theordme central

limite

(1.1)

a

permis de d6r'elopper

un

test sur la foncbion d'autocorr€lation empirique afin de voir si un processus de type

rrbruit _{blancrr pouvait €tre ajust€ aux donn6es.}

L'objectif

de cette section est de g6n6rali,ser cette proc6dure de test d la classe des processus ARMA.

Poururrm<rdOleMA(q):Lorsqu'onobserveunes6riechronologique,

la fonctionL d'autocorr6lation empirique est un premier

outil

pour selectionner l,ordre du moddle qui

doit

6tre ajust6 aux donn6es.Nous avons observ6 sur un exemple d,e procelssus d, moyenne mobile qu'un test pouvait pratiquement €tre mis en plar:e-pour d6terminei si les coefficients d'autocorr6latio' empiriques sont n6gligeabl:s _{_Cetexenrpleestg6n6ralisabledtoutelaclassedesprocessusA,moyenne}ou significativement difi6rents de z6ro'

mobile.

Soit X6 un processus stationnaire de modele M A(q) est de Ia forme:

Xt:

et

*

?:.t-r

*

.'.

*

?qeFt

Nous avions o,bserv6 que sa fonction d'autocorr6lation p6 s'a'nnule pour h

>

q

(voir la formule (7), figure:

(t.9))'

Oe pl.Ytl

.oott

avons montr6 que' pour touf,

;t;;";;t;

I'€airr:, ia

fJnction d'autocorr6lation empirique

p'

est un estimateur

sans biais de p6, et on a Ie th6ordme central limite :

2.2.

ESTIMAI'ION

DES PROCESSUS ARNIA

,fftpi'

--

_p{,...,p{

-

pI)

₄

n(o,f)

to"ou'?

*

oo (15)

ori

lesl 6l6ments de Ia

matrice!

de covariance sont donn6s par Ia formule

(*).

E;

cons6quence,

,i

ot

obse,'oi"n

6chantillon

(X''

"''X1)'

cette propri6t6

po-*

de const:ruire un intervalle de confiance pour Ie test :

(Ho,

{X,}

*

MA(q)

t

rrt

:

non Hs

Sous l'hypothdse 116, le processus

Xt

est un

YA(d '

So-us.l?6'

ladistribution

d";#; jii"

i.""e"

p*

(ir),

et les 6l6ments diagonaux de la' matrice sommme de covarirance sont donn€s Par:

t --t2 t -t2

I

=

1

+

z

(o{)

+,...'+2

_{\B; )}

hlr

End'autrestermes'sous'[16,lescoefficientsd'autocorr'6lationempirique

lr.

>

q

sont distribu6s

lJt-"""

fti

norlgle

de moyenne zlito

et

de variance

t" /? .

Cela

'ignifi"

'iu",

t"*

Ao'

pf

avec

ft'

>

q doit

se situer dans

l'#!tu"tl"

de confi ance:

22

I

I

I

I

T

I

I

I

I

I

1

I

T T T

t-I I CTIAPTER

2.

ESTIMATION

confi.ance Plus

strict

:

[-r.so.f,

r.e6/fl

Pour un

modOle

AR(p)

Dans ce paragraphe' nous allons voir commernt

e6n6raliser Ie test

pr6c6dt"i-u''

cas des

pto""""u

autor6gressifs' Quelle est la

F.;;;;,;to.orretution

d,un processus autor6gressif consid6rons le processus

AR(1) suivant :

X1=

$7X1a*

e1

' {e1} ^^'

BB(0'

1)

(16)

.La fonction d'autocorr6lation th6orique de ce processus est donn6e par:

pI

:

(d)n

et est repr6sent6e d la figure (1'6) 'Nous c:ns,taton$ que la fonction d'autocorrblation

de ce processus ne

_''uit'ul"

pas'mais tend vers zero lorsque I'horizon

h

aug-mente.Essayonsdevoirpourquoicettefonctionnes,annulepas.L,6quation('16) montre une

corr6lation'ti"eui'"

entre X1

et

it'-t

6gale

d /1'Par

ailleurs'(i16)

s'applique egalement

-

xt-l

,*

qui.permet

_l'6crire

xt-r:

Qlx;2 *

et-t

En

ins6rant."tt" i*rricr"'equation

dans (1.6), on obtient alors

Xt-r

:

(Qr)'Xr-,

*

QrXt-t

)-

€+r

*

€t-t

et on observe qu'il existe une corr6lation linOaire

d" (d')2

entre X1

et

Xt'-z

'

On peut bie,t

"nt""J"

r6p€ter ce raisonnement

pour comprendre que la

struc-ture de l,equation

autffieisive

implique que la correlation lin€aire entre toutes les donn6es ne s'annule pas'(pourquoi ce pndnomd n'apparait-il

pas pour: les

processus

MA)'

Proposition2SLaJoncti,ond',autocorr(Iati'onpartielled,,unprocessus.Xll*

ARI(P) est telle que

P{

=A

Pour

tout

h

)

q'

Cettepropositionmontrequel,autocorrdlationoartielle(figure1'.7)d'un.proces.

sus AR joue Ie

*u*"';;;;;;ll"io*"erution

d'un precessus

MA'En

effet :

"*';

.i;

:

MAk),alors

Pf

=

Q Pour

tout

h

)

q'

;i

;; *

ARdI

,alors

Pf

=

o

Pwr tout

h

>

P'

Cetteobservationcr,-.clat[nouspermettradeconstruiredestestssurlafonc-tion

d,autocorr6lation parielle

?T

1"

d6terminer I'ordre d'un

moddle

AI;l'

ex-actement comme

f'ou'"1'""iio"

de la fonction Ji'notoco"6lation

I

f 'a

I

T

T-

l-2,2,

ESTTMATION DES PROCESSUS

ARNIA

23

I'ordre d,un moddle

MA.

Mais

ll

nous faut

tout

d'abord etablir un th60rdme de normalit6 asmptotique pour la fonction d'autocorrOlation parielle'

par

_{le th6ordme} de normalite asymptotique des 6quations de Yule-walker, on a directement; , pour un processus AR(p), un th6ordme centrale limite pour

les pacf elnpirique

t0on

₄

N(0'1)

T'a'

On peut donc d pr6sent construire des intervalles de confizrnce pour le test

'

f

H6:{Xt}-AR(p)

t

rrr

:

non

Hs'

En efiet, sous

/{g,

fa probabilite que

la

suite des autocorr6lation partielles

empiriques se tr,cuvent, pour

h

)

p, dans I'intervalle:

l--1,961\/T;1,96v"1

.

CasclesmoddlesmixtesARMAPourchoisirl'ordre<l'unmoddlemixte

ARMA,ladoubleobservationdeI'ACFetdelaPACFserontnecessaires'

D'ailleurs, rema,rquons de nouveau qu'en pratique

il

est tou;iours. judicieux de

;;;;*

ces deuxiunctions,

I'ACF

etla

PACF

empirique' ensemble-pour

pou-uoi. u;rrrt",, le rnoddle le plus parcimonieux possible'

c'a'd'

(iventuellement un

moddle

/-R ou MAPrlr.

Prenons quelques exemples' La figure (11) reor6sente I'acf

et

Ia pacf d'un processurl observ6. L'observation

del'ACF

montre que

pf

et

pf.

sont

significa-tivement non nuls,

d ;f ;"

sont pas significativement non nuls

pour h

>

1' Par aille,urs, on oberve une d6croissance rapide de la pacf'

On cleoisit ctonc un modele

MA(l),

puisque

I'ACF etla PACF

th6oriques

d,un

M/(1)

,u

.,o*po.t",'t

th6oriquement de cette fagon' La ligure (12) pr6sente

u* acr""l

une

pACF

qui d6croissent tous deux lentemenl;

On c,onclut donc en rrn ,l'Rtvt'L1t,1), puisque l'acf et la pacf th6oriques d'un

ARMA(l,l)

,"

.ornpo't"ttt

theoriquement de cette fa'qon' (Ce sont les parties

decesdr:uxfon'ctionsacfetpacfquid6croissentlepluslente.ment,lapartieAR

pour l'acf et la partie

Wfl

qtl"t

a fu

p"i'

qui dominent alors le comportement)' Observez €galement

ft

nd*

dg)

_'

qt'"t

*oaote d' ajuster ch'oisiriez-vous

?

2.2.2

Moddlisation automatique

Le critOre

FPE

(processus

autor6gressifs

p::")t

,t::

::il*es

6tudi6es

jusqu'd, pr€sen't pou,

'cttttionner

I'ordre d'un

moddle autor6gressif se basent sur

I'observation au tu

ronltLn

d,autocorr6lation partielle empirique-,

cette

m6th-ode ne consisttr

"n

ftit

;;;;;gg?t"t

i"ta*

des mod.les et nous allons d' pr6sent

d6velopper des critdres automatiques pour le

choisir' En outre' la

qualit6 de

l'ajustement d6pend

d;;;;;;htisi'

En effet' en ne consid6rant que I'erreur

d,ajustr:ment, on ne

p"-*i

qJ",ooi, de meilleurs rdsultats en prenant un ordre p

plus grand. On sera ainsi

tlnte

de sur param6trer le moddle ajust6' D'un autre

c6t6, la qualit6

a'""

ti"'t"*"*

lcp""i

6galement du nombre de paramdtres du

T_ T* T I

t-

f-.A :IHAPTER

2.

IISTL&nTATI'|IN

:') {)rla'J'tiart*;rt }"!tF ; t'a}f:-:.;lrl:

figure:2.1

2.2. A DES AHMA 25 2'pr

;t

,l

t, lts: *rr

t-*,{*-,

llti 4*rF*{t*1tt|1t n+rtw,s nm$l' -:i.':y

tllr

I .: rttF4d|*t|,\u fll ot

AI

uel

il

lmdtr de sd

unr

plus men 1 enc Ia sr A

E

le ajust6 : s oddle

AR(l

e moddle cc e$ critdres t firrissant un --^-<r-:-un ajusten 00) dans k rtient de Pe 2.3: flgure:2.3

l(2) convient,

il

n'est pas conseill6 d'ajuster

froart

estimer 1001 paramdtres, m€me si'

es, et plus la vraisemblance du mod0le

aug-lection de moddles rem6dien

i

ce probldme r fopction d

bion est 6vi

dre

FPE

(i lnne de la tr p _{lton obser} € lQs estima

lui

ajuste

Xt-ru temps

T

*r

qugdratiqu

rl :

pax

a:

erreur d'ajustement modifi€e de telle manicre que ;6e.

\nal

Prediction

Error)

est de consid6rer I'erreur

r6diction d'une valeur de la s6rie'

,e _{les r6alisations}

X1,.", X1

d'un processus AR(p)'

;eurs de Yule-Walker de

_4,

₌

(dr,

_{"', Qr)''(vecteur}

e moddle

6rXr-r+

...

+

&oXt-o

+

e1

*

1 est donn6e Par :

=

\rXr

*

.'.

*

6oXr+r-p

, moyenne est :

,

₊

nl(ar-

_or)

_{lXya-v;xr+t-il!,i=r(a,- or)}

,*

"

[(a"

-

6o)'$

(a"-

d')]

(

i).

Par le th6ordme de normalit€ des €quations de id6e

du

cr '4,tique mo1 rPposons qr i a,voir calcr ne) et

ol

o n pr6vision ; son erreu:

ir+.t

_-

xr

i

rf;

est Walker,

l

17)

I

1

I

1"

I

I

L

1

CHAPTER

2.

ESTIMATION

dt,(A,-

oo)

*

ff{o,ol

(rf)-tl

qr{e

si

Z

:

_\Zt,

..., ZF)t

suit

une

distribution et Np

(p,

f

₎ (18)

r

(-fr*,

_{- xr*r)'}

:

_'31r11r

+

_$)

Le

AI

,"ry

*x?-p

remplagapt

dans (19)

ol

par I'estimateur

fe?b4ltf

-

P),

on obtient

rteur de

_!'*rreor

quadratique mo)'enne de

pr$iction

de

Y;a1

:

FFE

(p)

:

e2(|)##

(20)

'il

tbut

miirimiser eu _P.

dtEre

AIC

Darx le n6me ordre

d'id€es que

le

critire

FPE,le

critdre

prcpse

d4

mininis€r

Ia

fonction

NC{p):

los,6':k})

+

?#

une

version

p6nali#

la

fonctio

t21)

€

:

(Fp+r, ...,

ar)

les rdsidus

d'un

proceesus

Afi{p)

gaussien

p

Et:

rt-

_Ido"*-o

^^+

N(0,r1)

k:l

calcrildr

h

fonction

de r'laisemblance, on

part

de

ptolo!.,)

_{e}:

(zaol.o}-E

_"*

(ff)

si

r

>

P

(x

_-

p)'(I)-'(x

_-

p)

**

x3

'

utilisant

de

reultat

et

(18), on

peut

appraxiurer (17)

par

:

(1e)

p

version

p6nali#

la

fonction de

waisemblance des r6sidus de plus, si dJ est

l'estimateur

de Yule-'Walker de

alon

ar

pou'

?

asse:z grand,

On En vrai et le CHAPTER

2.

ESTIMATION

(p)

₌

_-z-te

(A,a?,r)

*

2p

₌

rros@!,r)

+

2p

?-1 , on retrouve bien (2.3). (Par ailleurs, dans la litt6ra-q logiciels, on utilise aussi souvent cette forme nonnormalis6e

En ture et

du cr de I'A

une ipition

asym

tend 1 si? vers I'infini).

naires

c4s de d

.

Cela dans 'expression de la

0<h<p

en consid6rant log

FPE(p),

que les critdres

_'FPII

uement dquivalents.

constate que le critdre

AIC

atendance d choisir

p

>

po si

R(po). On a m€me calcul6 I'approximation suivante I

PW>-polln(po)l13*

1

PW:

po _l.a.R(ps)l

₌

0.8

qbtenir u estimateur consistant de p0, on modi e le critdre

AIC

en

une ion plus importante en cas de surparam6trisation :

Brc(e)=

toe63h) +

_$nsr

ntre qu'un moddle AR(p) choisi par le crit€re _'r{/C permet une plus

petite

erreur

al(e)

(on

dit

que ce crit0re est

e cace

:

le rapport entre l'erreur de pr6diction 6valu€e au

et I'erreur se basant sur Ia valeur choisie par le critdre AIC

n

par

la

m6thode Moindres

Cam6s

Ordi-Lation d'un processus AR(p), on verra que, pour. obtenir de

6n,L

1

n

i

p\

et o2,

il

sufit de

partit

*tQ

l

1)

l*TL::'

,olr*iurr""

empiiique

et

de r6soudre les 6oyations de

Yule-rifie que,

q,r"i

qnu soit

n,

les observatioyy'n 'interviennent' de l'estimateur, que

par un

nombre fi7de, egal A' p

*

1'

de 'iance empirique

:

t

n-h

i"(h)

=

_;

l!{',*o

-i,,)(rr-i,*)

t:L , n-h

n-en for d'au or) En pre (st)teiv est It

d*E

(Xt-*

longueur Les uations En

i

(h), Cer colonne et o2

l/

AHMA

tout

d'bord un procesus autor€gressif

s'eprire

p fprm6

:(;;l

Yule- ont pour expression matricielle :

t

(p)

₌

todo

0):

dot(d

+

"?

forme matricielle, en notont

_f

(p) _{.le vecteur}

(r

(1) _, ...,

_r

_@))

t et

(6

₀₎

_, ..,,4

(d)"

29 d'ordre

nulle:

Xt-dt

t-r-.'.-doXt-r-6,

tsB(0, ) et les

_/6

sont des nombers r6els.

de cette 6quation par

Xt-n

_, 0

(

h

1p

et de cot6, on obtient pour le premier membre la

tanpe :

XrXt-a)

:

"y (h) sl

h:1..,p

r--,r,)

*

E (

si h:0

dn&-h)

si h=

l'..P

6xl&)*o2

si

h.=0

p

tia , t'

,L6ot@

-

h)

,xr-n): jolt

'foot@)+o2

k:t

{.,

ces ions, les covariances

_I

(h)par les covariances

lin6aire qui fournit les estimateurs @t obfient un

de:

{'

i

@)

= io6o

qrfe, si

_i

(

{e

i[o)

et

[tion

CHAPTER

2.

ESTIMATION

) >

0,alors

io

est de rang plein. En divisant alors les deux

i

@)

:io6o

introduisant I'autocorr6lation empirique

?(h):

deux €quations :

i

(h)

m

p (0)

uP

?(p)

n29

note

n.

On

(

el-'P62

\rnto"-

o)

''

Ne

(o'd2r;1)

Soit

Xt un

processus AR(1) causal

et

soit un |chantillon {X'7'

"'

Xnl,de'

d*

=

it-r']?t*

od m

)

p

Alors'quand' n-+

a

on a:

Ja@^-

d^)'

N-

(0,

_"'t*)

S oit

Xt un

processus AR(1) cousat et s oit

un

lchantillon {a 1

"''

a _n} de

tn

₌

it;r?,

et of;

_=t

(0) (1

- ;;0;'br)

Alors, quand' ??'--' oo

rus allons pr6senter ici bridvement la d€marche de I'estimation

il

iltir"*uft"."'

Cetie ma'ximisation est r€alis6e

d

I'aide

timisationnonlin6aire(Newton.Rahpson,m6thodedusim.

pax

d'a

ple: