Livre Calcul intégral pdf - Web Education

calcul

intégral

Bernard Candelpergher

CALCUL INTÉGRAL

Enseignement des mathématiques

1. J.-Y. Ouvrard, Probabilités I

3. M. Cottrell, V. Genon-Catalot, Ch. Duhamel, Th. Meyre, Exercices de probabilités

4. F. Rouvière, Petit guide de calcul différentiel à l'usage de la licence et de l'agrégation 5. J.-Y. Ouvrard, Probabilités II

6. G. Zémor, Cours de cryptographie 7. A. Szpirglas, Exercices d'algèbre

8. B. Perrin-Riou, Algèbre, arithmétique et Maple

10. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Algèbre I 11. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Analyse I 12. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Algèbre 2

13. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Analyse 2 14. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Algèbre 3

15. H. Krivine, Exercices de mathématiques pour physiciens

16. J. Jacod, Ph. Protter, L'essentiel en théorie des probabilités 17. M. Willem, Analyse fonctionnelle élémentaire

18. É. Amar, É. Matheron, Analyse complexe

19. B. Randé, Problèmes corrigés. Concours 2002 et 2003 (MP)

20. D. Perrin, Mathématiques d'école

21. B. Randé, Problèmes corrigés. Concours 2004 (MP)

22. P. Bourgade, Olympiades internationales de mathématiques 1976-2005

23. V. Prasolov, Problèmes et théorèmes d'algèbre linéaire

24. R. Sa Earp, E. Toubiana, Introduction à la géométrie hyperbolique et aux surfaces de Riemann

25. L. Di Menza, Résolution numérique des équations aux dérivées partielles 26. B. Candelpergher, Calcul intégral

27. J. Hubbard, B. West, Équations différentielles et systèmes dynamiques, vol. 1

28. J. Hubbard, B. West, Équations différentielles et systèmes dynamiques, vol. 2

BERNARD CANDELPERGHER

Calcul intégral

CASSINI

BERNARD CANDELPERGHER _{est maître de conférences à l'université de Nice. Il est} l'auteur de Fonctions d'une variable complexe (Armand Colin, 1995).

ISBN 978-2-84225-053-9

© Cassini, Paris, 2009.

Table des matières

Avant-propos XI

Notations et terminologie I

Introduction 5

Chapitre 1. L'intégrale des fonctions continues II

1.1. _{Propriétés élémentaires} . . . 11

1.1.1. _{Premières propriétés} . . . 13

1.1.2. _{Intégrales et primitives} . . . 14

1.1.3. _{Deux formules indispensables} . 18

1.1.4. _{La formule de Taylor avec reste intégral} 20

1.2. Les intégrales impropres . . 22

1.2.1. _Définitions . . . 22

1.2.2. Quelques propriétés . . . . 23

1.2.3. _{Lien entre série et intégrale} 26

1.2.4. _{Intégrales absolument convergentes} 26

1.3. _{Permutation des symboles lim,} L _et J . . . . ₃₂ 1.3.1. _{Le cas des intégrales de fonctions continues sur} [a , b] 32 1.3.2. Le _{cas des intégrales impropres} . . . 35

1.3.3. _{Théorèmes de permutation de Lebesgue 37}

1.3.4. _{Permutation dans le cas semi-convergent 39}

1.4. _{Fonctions définies par une intégrale 41}

1.4.1. _{Les théorèmes de Lebesgue 42}

1.4.2. _{Un théorème} « classique » . 49

1.5. _{La fonction} r . . . ₅₀

1.6. Intégrales de Laplace . . . . 52

1.6.1. _{Lemme de Watson} . 52

1.6.2. _{Méthode de Laplace 56}

1.6.3. _{La méthode de la phase stationnaire} 61

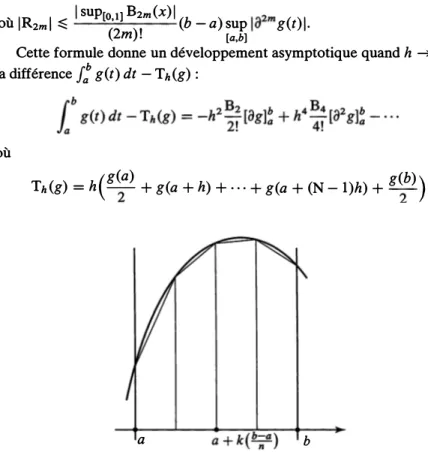
1.7. _{La formule d'Euler-MacLaurin} . . . 64

1.7.1. _{Les polynômes de Bernoulli} . . . 65

1.7.2. _{La formule d'Euler-MacLaurin} . . . 66

1.7.3. _{Développement asymptotique des sommes partielles}

d'une série . . . . 1.7.4. _{La constante de Ramanujan d'une série .}

V

70 75

VI TABLE DES MATIÈRES

Appendice : continuité uniforme et existence de l'intégrale . 76

Exercices . . . 80

Chapitre 2. Intégrales et résidus 85

2.1. _{Analyticité et dérivabilité} . . . 85 2.1.1. _{Définitions et propriétés} . . . 85

2.1.2. _{Construction de fonctions analytiques} 96

2.2. _{Intégrale curviligne} . ₉₉

2.2.1. _Définition . . . 99

2.2.2. _Homotopie . . . 102

2.2.3. _{Le problème des primitives} 107

2.3. _{Prolongement analytique et points singuliers} . 109

2.3.1. _{Prolongement analytique} 109

2.3.2. _{Points singuliers} . . . 113 2.3.3. Théorème des résidus . . . 118

2.3.4. _{Logarithme et puissances complexes} 121

2.4. _{La fonction Gamma dans le plan complexe} 126

2.5. _{Calculs d'intégrales} . . . 129 2.6. Calculs de sommes . . . 140 2.6.1. _{Utilisation de la cotangente} 140 2.6.2. _{Formule de Plana} . 143 2.7. _{La méthode du col .} . . . 148 2.7.1. _{Le choix du chemin} 148

2.7.2. _{Étude locale au col} . 152

2.7.3. _{Application : Comportement en} +oo de la fonction

d'Airy . . . 154

Exercices . . . . 157

Chapitre 3. L'intégrale de Lebesgue I6I

3.1. _{Un première extension de l'intégrale} . 161

3.2. _{La mesure de Lebesgue sur} lR . . . 164

3.3. _{Les fonctions mesurables} . . . 169

3.4. _{Intégration des fonctions mesurables} . 174

3.4.1. _{Intégration des fonctions étagées positives} 174 3.4.2. _{Intégration des fonctions mesurables positives} 176 3.4.3. _{Intégration des fonctions intégrables quelconques} 180 3.4.4. _{Presque partout} . . . 182

3.4.5. _{La relation intégrale� primitive} 183

3.5. _{Théorèmes de permutation} . . . 185

3.6. _{Lien avec l'intégrale usuelle} . . . 190

3.7. Fonctions définies par une intégrale . . . 193

3.8. _{Intégration par rapport à une autre mesure} 193

Exercices . . . 197

TABLE DES MATIÈRES VII

Chapitre 4. Intégrales multiples 2ox

4.1. _{L'intégrale de Lebesgue sur} !Rn . . . 201 4.1.1. La mesure de Lebesgue sur !Rn . . . 202 4.1.2. _{Intégration des fonctions définies sur} !Rn 207

4.1.3. Intégrabilité et calcul des intégrales 208

4.2. Changement de variables dans !Rn . . . 216

4.3. _{Intégrales liées aux courbes et aux surfaces} 226

4.3.1. _{L'intégrale sur une courbe de IR2} 226

4.3.2. _{L'intégrale sur une surface de} lR ₃ 230

4.4. _{Formule de Stokes} . . . 233

4.5. _{Les fonctions harmoniques sur IR2} 237

Exercices . . . 242

Chapitre 5. Espaces LP et convolution 249

5.1. _{Préliminaires topologiques} . 249

5.1.1. _{Espaces normés} . . . 249

5.1.2. _{Espaces de Hilbert} . . . . 256

5.1.3. _{Le théorème de Stone-Weierstrass} 258

5.2. _{L'espace des fonctions intégrables} . . . 259

5.2.1. _{Définition de L 1 (A). L 1 (A) est complet} . 259 5.2.2. _{Lien entre convergence presque partout et convergence}

L1 . • • • • • . . . • • • • . • • • . • 264

5.3. _{L'espace des fonctions de carré intégrable} . . . . 266

5.3.1. _{Définition de L2(A). L2(A) est complet} . 266

5.3.2. _{L1 , L2 et convergence presque partout} 270

5.4. _{Sous-espaces denses} . . . 272 5.5. _{Les polynômes de Legendre} . . . 275

5.6. _{Fonctions <l'Hermite et espace de Bargmann} . 280

5.7. Espaces U, p > 1 . . . 284

5.8. _{Convolution sur} lR . . . 286

5.8.1. _{Définitions et propriétés} . 286

5.8.2. Régularisation gaussienne 295

Exercices . . . 299

Chapitre 6. Les séries de Fourier ₃₀₃

6.1. _{Position du problème} +oo 6.2. _{Les séries} L Un n=-oo 6.3. _{Convergence L2} • • 6.4. _{Convergence ponctuelle} . 6.5. _Convolution . . . . 6.6. _{La transformation :Fpér .} 303 304 307 312 323 324 www.bibliomath.com

VIII TABLE DES MATIÈRES

6.7. Procédés de sommation des séries de Fourier 329

6.7.1. _{Sommation de Cesàro} 329

6.7.2. _{Noyaux réguliers} . . . ₃₃₁

6.7.3. _{Sommation d'Abel} . . . 335

6.8. _{L'intervention de l'analyse fonctionnelle 340}

Exercices . . . 346

Chapitre 7. Transformation de Fourier 35I

7.1. _{Des séries de Fourier à la transformation de Fourier} . ₃₅₁

7.2. _{Transformation de Fourier sur L1 (IR)} . . . ₃₅₂

7.3. _{Transformée de Fourier des gaussiennes} . ₃₅₆

7.4. _{Inversion de la transformation de Fourier 359}

7.5. _{Formule d'inversion ponctuelle} . . . ₃₆₂

7.6. _{L'espace .S(IR)} . . . ₃₆₅

7.7. _{Transformation de Fourier et convolution 366}

7.8. _{La transformation de Fourier sur L2(JR)} . ₃₆₈

7.8.1. _{Définition et propriétés de :F sur L2(JR) 368}

7.8.2. Calcul pratique de :F f . . . ₃₇₆ 7.9. _{Noyaux de sommation pour les intégrales de Fourier 378}

7.10. _{Fourier dans l'espace de Bargmann} . . ₃₇₉

7.11. _{Propriétés de localisation et de support 382}

7.11.1. _{L'inégalité de Heisenberg} . . ₃₈₃

7.11.2. _{Le théorème de Paley-Wiener 385}

7.12. Un point de vue unificateur : les distributions . ₃₈₉ 7.12.1. _{Les distributions} . . . ₃₈₉

7.12.2. _{Transformation de Fourier dans .S'(IR) 391}

Exercices . . . ₃₉₇

Chapitre 8. De l'équation de la chaleur aux nombres premiers. 40I

8.1. _{L'équation de la chaleur} . . . 401

8.2. _{La formule de Poisson} . . . ₄₀₆

8.2.1. _{La formule de Poisson sur} lR . . . 406

8.2.2. _{Développement de la cotangente} 410

8.3. _{La fonction zêta} . . . ₄₁₂ 8.3.1. _{La formule d'Euler} . . . ₄₁₂

8.3.2. _{Expression intégrale et équation fonctionnelle pour la}

fonction s . . . ₄₁₃

8.4. _{Fonctions entières et produits infinis} . . . ₄₁₆

8.4.1. _{Convergence d'un produit infini} . 416

8.4.2. _{Produit infini de fonctions} . . . . ₄₁₈

8.4.3. _{Factorisation d'une fonction entière} . ₄₂₀

8.4.4. _{Les fonctions} r _{et sinus comme produits infinis 421} 8.5. _{Les zéros de} s . . . 423

8.5.1. _{Les zéros triviaux . . .} . 8.5.2. _{Les zéros non triviaux} . . . . 8.5.3. Le _{développement de s en produit infini} 8.6. _{La répartition des nombres premiers .} . . . . . _.

8.6.1. _{Fonctions de comptage . . .} .

8.6.2. _{La fonction 1/t et la dérivée logarithmique de s} 8.7. _{Transformation de Mellin . . .} .

8.7.1. _{Définition et prolongement analytique} 8.7.2. _{L'inversion de Mellin . . .} . 8.7.3. La formule explicite de von Mangoldt 8.8. _{L'article de Riemann sur les nombres premiers}

Petits sujets de réflexion . . . . . . _. . . . .

Bibliographie Index 423 424 426 427 427 430 431 431 433 437 439 447 455 457

Avant-propos

L'un des buts de ce livre est de définir rapidement l'intégrale de Lebesgue et d'apprendre à l'utiliser. Dans la pratique de l' Analyse, la quasi-totalité des fonctions que l'on considère sont suffisamment régulières pour que la notion de mesurabilité ne pose pas de problème, aussi j'ai évité les développements abstraits sur la Théorie de la mesure et ses préliminaires ensemblistes. Je me suis limité à introduire la mesure de Lebesgue d'abord sur lR _{et ensuite sur} !Rn,

en admettant le minimum de propriétés nécessaires pour définir l'intégrale de Lebesgue et démontrer ses résultats essentiels, comme la construction des espaces complets de fonctions intégrables et les diverses possibilités de permutation des signes lim, I:;, a, avec le signe f . _{Ces résultats seront mis en}

pratique dans l'étude de l'analyse de Fourier.

Mais pour utiliser pratiquement ces résultats encore faut-il savoir tra­ vailler avec les intégrales des fonctions usuelles. Il m'a donc semblé néces­ saire de commencer ce livre par la définition et les propriétés de l'intégrale des fonctions continues, et ceci sans imposer au lecteur la notion fort peu utile de « fonction Riemann-intégrable ». On ne lui infliger pas non plus les

calculs fastidieux de primitives par d'astucieux changements de variables. Les logiciels de calcul formel permettent aujourd'hui de confier à des composants électroniques ces tâches sans intérêt. Dans les exercices situés à la fin de chaque chapitre, le lecteur est convié à se livrer à des calculs lui permettant de se familiariser avec la théorie. Ces exercices contiennent souvent des indi­ cations qui facilitent leur résolution et ne doivent pas être considérés comme

des épreuves pénibles, mais comme des occasions de se confronter calme­ ment à quelques petites difficultés. C'est par cette confrontation que l'on peut comprendre une théorie et non en récitant machinalement des théorèmes ou des démonstrations. La vérification méticuleuse de tous les points d'une démonstration est nécessaire si on veut s'assurer que « ça tient la route »,

mais elle ne garantit en rien qu'on l'a assimilée. Pour arriver à la retrouver par soi-même, il est indispensable d'en avoir dégagé les idées essentielles. Le lecteur s'apercevra alors que derrière une terminologie sophistiquée ne se cachent bien souvent que quelques idées simples. Cette constatation permet de garder un peu de liberté d'esprit et de sens critique, ce qui peut d'ailleurs être utile dans d'autres domaines que les Mathématiques.

L'autre but de ce livre est de mettre l'accent sur un point fondamental qui a été mis en évidence par les mathématiciens du x1xe siècle : la plupart des

fonctions usuelles ne sont pas seulement définies pour des valeurs réelles de

XII AVANT-PROPOS

l'argument mais aussi pour des valeurs complexes. Ce n'est qu'en considérant cette extension dans le complexe que l'on peut bien comprendre leurs pro­ priétés. D'ailleurs, même d'un point de vue utilitaire, on peut remarquer que beaucoup d'intégrales usuelles pour lesquelles on a des formules explicites, sont calculées « en passant dans le complexe ». C'est ce que l'on appelle la « méthode des résidus », les résultats qu'elle fournit sont spectaculaires et il me semble déraisonnable de se priver d'un tel outil.

Malheureusement dans le découpage de l'enseignement en« modules semestriels » ces considérations font souvent l'objet d'un module étiqueté « fonctions analytiques » qui se veut plus ou moins indépendant du reste. Contrairement à cette fâcheuse tendance au morcellement nous montrerons comment le « point de vue complexe » est intimement lié à diverses branches des Mathématiques comme l' Analyse de Fourier ou la Théorie des nombres. Le dernier chapitre de ce livre montre que l'on peut ainsi obtenir de magni­ fiques résultats sur la répartition des nombres premiers. Il se termine par une traduction de l'article de Riemann sur les nombres premiers qui date de 1859, _{article historique par l'énorme avancée qu'il a provoqué dans la}

Théorie analytique des nombres et par l'énoncé de la fameuse Hypothèse de Riemann, qui reste encore aujourd'hui une conjecture. Souhaitons que malgré l'idéologie absurde de la « rentabilité-productivité-compétitivité », qui domine notre époque y compris dans les Mathématiques, le lecteur trouve encore le temps et l'envie de s'intéresser à ces choses pour leur simple beauté. Ce dernier chapitre est écrit dans un style plus libre permettant au lecteur de s'évader de la routine « théorème-démonstration-exercices » qui permet d'ingurgiter rapidement des mathématiques, mais qui donne une vision to­ talement fausse de la manière dont elles ont été crées. Celles-ci sont le fruit d'un travail artisanal avec ses hésitations et ses erreurs, les théorèmes et démonstrations que l'on lit dans les livres ne sont qu'une étape de ce travail et il est bon d'avoir à l'esprit une vision plus humaine des Mathématiques.

Ce livre est issu d'un cours de Calcul Intégral que j'ai fait pendant plu­ sieurs années à l'Université de Nice.

Je remercie toutes les personnes avec qui j'ai eu la chance de partager cet enseignement, plus particulièrement Thierry Goudon, Vladimir Kostov, Marie-Christine Pérouème, Martine Smolders-Junca.

Merci aussi à Jean-François Burnol, Michel Miniconi, Michel Merle et Jean-Pierre Kahane pour toutes les agréables et instructives discussions que nous avons eues.

Un grand merci à André Bellaïche pour sa lecture attentive du manuscrit et ses remarques judicieuses, à Catherine Bellaïche pour le soin apporté à la finition du texte et des figures et à Rached Mneimné pour ses encourage­ ments.

AVANT-PROPOS XIII

cours de François Rouvière avec qui j'ai partagé divers enseignements et en particulier celui d'Intégration. Ses conseils, toujours prodigués avec gen­ tillesse, ont été pour moi un grand soutien, qu'il trouve ici l'expression de ma profonde gratitude.

Ce livre est dédié à André Cerezo. Sa passion pour les mathématiques, son désintéressement vis-à-vis de la « carrière » et son amour pour l'enseignement ont été pour nous un exemple. �

Notations et terminologie

Si n est un entier positif, on pose n! =--t:.Z _{. . . n (O!} = 1), et pour tout entier

k = 0, . . . 'n on pose c� _{= k!}(:�_{k)! .}

Si z = x + iy (x, y réels) est un nombre complexe, on pose x = Re(z),

y = lm(z) et lzl = (x2 + y2)112•

On note (un)n'1oO la suite Uo, u1 , . . . , Un, . . . et limn-++oo Un la limite de cette suite, si elle existe.

Une suite extraite de la suite (un) est une suite (uk(n>) où l'application n --+

k(n) de N _dans N _{est strictement croissante. On note aussi} (unk) _{une suite}

extraite de la suite (un)· Dans ce cas c'est l'application k --+ nk de N dans N

qui est strictement croissante.

Soit (an)n'1oo une suite de nombres, ou de fonctions, ou de vecteurs. On dit que la série L:,o an converge, ou que la série de terme général an converge, si la suite des sommes partielles

N

Lan = ao + a1 + · · · + aN

n=O

a une limite (s'il s'agit de nombres réels, on précise : limite finie) quand N tend vers l'infini. Dans le cas contraire, on dit que la série diverge. Lorsque la limite existe, on la note L:,o an et on l'appelle somme de la série. En résumé, l'expression L::O _{an a un sens et a pour valeur limN-+oo L� an}

quand cette limite existe, elle n'est pas définie dans les autres cas.

Lorsque les an sont des réels positifs la somme partielle L�=o an a soit une limite finie (et la série converge), soit pour limite +oo (et la série di­ verge). Dans ce dernier cas, on écrit par exception à la définition précédente

L:,o an = +oo. On peut donc écrire L:,o an < +oo pour dire que la série

converge.

Une partie A de R est dense si pour tout intervalle non vide ]a, b[, l'intersec­ tion A n ]a, b [ est non vide.

Si une quantité A E [O, +oo], on note A < +oo pour dire que A est finie.

Si f est une fonction, on note [/]� = f(b) - f(a).

2 NOTATIONS ET TERMINOLOGIE ôf(x) = J'(x) = lim _h-+0 f(x + h) - f(x) . _h

Pour une fonction f de deux variables (x et t), on pose

Ô f( t t, x )_1. - im f(t + h, x) - f(t, x) h

h-+O

a _x !( ) _{t, x} = li _m f(t, x + k) - f(t, x) _{k .}

k-+O

On note supxeI f(x) le plus petit majorant dans ] -oo, +oo] des nombres réels f(x) lorsque x parcourt

1.

On dit que SUPxeI f(x) est la borne supé­ rieure de f sur

1.

On note infxeI f(x) le plus grand minorant dans [-oo, +oo[ des nombres réels f(x) lorsque x parcourt

1.

On dit que infxeI f(x) est la borne inférieure de f sur

1.

f +(x) = max(f(x), O) et f-(x) = - min(f(x), O), on a

f = !+ - f-1!1 = !+ + f-·

'e(E, OC) est l'espace des fonctions continues sur E à valeurs dans JI{ où JI{ = lR

ou C.

'eb(E, OC) est l'espace des fonctions continues bornées sur E à valeurs dans OC

où JI{ = lR ou c.

'e0(E, OC) est l'espace des fonctions continues tendant vers 0 à l'infini sur E à valeurs dans JI{ où JI{ = lR ou C.

'eP(E, OC) est l'espace des fonctions p fois continûment dérivables sur E à

valeurs dans OC où JI{ = lR ou C.

'epér(IR) est l'espace des fonctions périodiques de période 1 et continues sur IR .

.V(JR) est l'espace des fonctions indéfiniment dérivables sur lR et nulles en

dehors d'un intervalle borné .

.S(JR) est l'espace des fonctions g E 'e00(JR) qui vérifient pour tous k et p

entiers positifs SUPxeR lxP ôk g(x) 1 < +oo.

s(Z) est l'espace des suites (en) telles que Cn ₌ 0(1/nk) pour tout k � O .

.S' (JR) est l'espace des distributions.

f ,...., g en x0 (on dit que f et g sont équivalentes en x0) s'il existe un voisinage V de x0 tel que f(x) = a(x)g(x) pour tout x E V où a(x) 4 1

NOTATIONS ET TERMINOLOGIE 3

f = O(g) en x0 s'il existe C > 0 et un voisinage V de x0 tel que lf(x)I :::::

Clg(x)I pour tout x E V.

f = o(g) en x0 (on dit que f est négligeable devant g, ou infiniment petite

par rapport à g en x0) s'il existe un voisinage V de x0 tel que f(x) =

e(x)g(x) pour tout x E V où e(x) --+ 0 quand x --+ x0•

XA est la fonction indicatrice de A, qui vaut 1 sur A et 0 sur le complémentaire

de A.

[x] est la partie entière de x, c'est-à-dire le plus grand entier inférieur ou égal à x.

D(z, r) où r > 0 et z E C, est le disque ouvert de centre z et de rayon r,

D(z, r) = {z E C l lzl < r}.

D(z, r) où r > 0 et z E C, est le disque fermé de centre z et de rayon r,

D(z, r) = {z E C 1 lzl::::: r}.

det(M) désigne le déterminant de la matrice carrée M. Id désigne l'application identité.

Introduction

Il y a sur lR _{une théorie très simple de l'intégration, c'est celle de Cauchy.}

Elle définit l'intégrale des fonctions continues, ou plus généralement des fonctions qui sur tout intervalle borné de lR _{n'ont qu'un nombre fini de}

discontinuités.

Elle se développe de la façon suivante :

a) On intègre les fonctions continues sur des intervalles fermés bornés

[a, b] en sommant les valeurs de fen des points régulièrement espacés de l'intervalle [a, b] multipliées par l'espacement entre deux points, et en faisant tendre cet espacement vers O. Autrement dit on pose

lb

f(x) dx = lim -- L., f a + kb - a ;..., ( b - a--) .

a N-+oo N _k=l N

b) On intègre les fonctions continues sur les intervalles du type [a, b [ (ou

[a, +oo[) en prenant la limite des intégrales sur les intervalles fermés bornés

[a, c] lorsque c --+ b (ou c --+ +oo), ce qui donne la notion lieu à la notion d'intégrale impropre convergente ou divergente.

c) Pour finir, on intègre les fonctions discontinues en découpant quand c'est possible l'intervalle d'intégration en intervalles où la fonction est conti­ nue.

La principale propriété de l'intégrale des fonctions continues est son lien avec la dérivation :

Si f est continue sur [a, b] , la fonction

x --+

lx

f(u) du

est dérivable et sa dérivée est la fonction f.

On en déduit que si F est une fonction dont la dérivée est f, alors

lb

f(x) dx

=

F(b) - F(a).

Ceci fournit un moyen simple de calculer des intégrales. On dispose aussi d'autres outils de calcul, comme la formule d'intégration par parties et la formule de changement de variable.

Si la fonction f est m fois dérivable, on a une formule remarquable per­ mettant un calcul numérique de l'intégrale, la formule d'Euler-MacLaurin à

6 INTRODUCTION

l'ordre m. Cette formule permet aussi une étude du comportement asympto­ tique des sommes partielles d'une série (cf. chap. 1).

En fait, les fonctions classiques que l'on manipule en Analyse, comme les polynômes et fractions rationnelles, la fonction exponentielle, les fonctions trigonométriques et bien d'autres, sont souvent analytiques, ce qui veut dire qu'elles sont non seulement continues sur des intervalles de IR, mais qu'elles sont définies et indéfiniment dérivables sur des domaines du plan complexe <C.

La définition de l'intégrale sur le segment [a, b], donnée ci-dessus, s'étend

facilement en celle de l'intégrale le long de courbes dessinées dans le plan complexe. Cette intégrale curviligne possède la propriété remarquable que si la fonction est analytique sauf en certains points (points singuliers) et que la courbe est fermée, l'intégrale sur ce contour fermé ne dépend que de certaines valeurs liées à la fonction, qu'on appelle les résidus, et qui sont cal­ culées aux points singuliers situés à l'intérieur du contour. C'est la « méthode des résidus », qui permet le calcul pratique de beaucoup d'intégrales clas­

siques : par exemple l'intégrale d'une fonction sur lR _{est vue comme limite de}

l'intégrale sur [-A, A] lorsque A tend vers l'infini et l'étude de cette dernière se ramène à _{celle de l'intégrale sur la courbe fermée obtenue en fermant le}

segment grâce à un demi-cercle complexe (cf. chap. 2).

La théorie présentée ci-dessus est le cadre de travail habituel lorsqu'on fait de l'analyse avec des fonctions régulières, elle est très pratique du point de vue du calcul, mais on rencontre quelques difficultés lorsqu'on veut dé­ montrer des théorèmes de passage à la limite dans les intégrales. Cela tient au fait que si une suite (fn) de fonctions continues converge en tout point de

[a, b] vers une fonction f, rien n'assure que f est continue et que l'intégrale de f existe. On ne peut donc espérer que

1

b fn(x) dx �

1

b f(x) dx

sans faire des hypothèses qui assurent que la fonction f est continue. La difficulté vient donc du fait que la régularité (ici la continuité) des fonctions à intégrer n'est pas conservée par la convergence simple. Pour remédier à cet inconvénient on doit essayer de définir une notion d'intégrale pour des fonctions moins régulières.

Une première tentative est celle de l'intégrale de Riemann, qui consiste à remplacer le découpage� de l'intervalle [a, b] de la forme a + k b;t , k = 1, ... , N, par n'importe quelle subdivision a

=

x0 < x1 < x2 < · · · <

XN = b et à considérer les sommes

N-1

L(X;+1 - X;)f(t;) où t; E ]x; , x;+1 [. i=O

Si ces sommes tendent vers une limite finie lorsque les subdivisions de­ viennent de plus en plus fines, c'est-à-dire lorsque sup; lx;+i -x; 1 � 0, on dit

INTRODUCTION ₇

que

f

est Riemann-intégrable sur [a, b] et on note J:

f(x) dx

_{cette limite.}

Cette définition permet d'intégrer des fonctions très discontinues, mais on a toujours l'inconvénient suivant : si une suite

(fn)

de fonctions Riemann­ intégrables converge simplement vers une fonction

f

rien n'assure que

f

soit Riemann-intégrable. Par rapport à l'intégrale des fonctions continues, la situation ne s'est donc pas arrangée du point de vue du passage à la limite, mais elle s'est détériorée du point de vue des calculs : le lien dérivée-intégrale n'est plus aussi simple, et il en est de même pour d'autres formules classiques. En fait l'espace des fonctions Riemann-intégrables est suffisamment grand pour contenir des fonctions très irrégulières, ce qui complique les énoncés classiques de calcul intégral, mais il n'est pas suffisamment grand pour as­ surer des théorèmes simples de passage à la limite (en particulier il n'est pas complet pour la norme définie par l'intégrale de

If

I). Il existe d'autres tentatives (dues à Kurzweil et Henstock) basées sur des raffinements concer­ nant les subdivisions de l'intervalle [a, b]. Nous avons pris le parti de ne pas développer l'intégrale de Riemann, ni aucun de ses raffinements, pour pas­ ser directement à la théorie simple et pratique de l'intégration prolongeant l'intégrale des fonctions continues, qui est celle de l'intégrale de Lebesgue et qui permet de définir les espaces complets de fonctions intégrables utilisés partout en Analyse (cf. chap. 3).

L'idée de Lebesgue consiste à se placer d'emblée sur un « très grand » es­

pace de fonctions, stable par limite simple, l'espace des fonctions mesurables, et à ne plus sommer les valeurs de

f

à l'aide des subdivisions du domaine de définition de

f

(c'est-à-dire de l'axe des

x)

mais plutôt en utilisant des découpages du domaine des valeurs de

f

(c'est-à-dire de l'axe des y).

Plus précisément, une fonction f de lR dans lR est mesurable si pour tout intervalle

1

de lR l'ensemble

A =

f-1(1)

=

{x

E lR i

f(x)

E I}

est une partie de lR « mesurable au sens de Lebesgue », ce qui veut dire qu'on

peut lui attribuer une « mesure » À(A), qui n'est autre que la longueur de

A lorsque A est un intervalle. Pratiquement toutes les parties de lR qui se présentent naturellement sont mesurables au sens de Lebesgue, et les calculs de mesures se font à l'aide de la formule

À(A) = L À(An) si A = LJ A

n

où les An sont deux à deux disjoints.

n

n

Il s'ensuit que pratiquement toutes les fonctions de lR dans lR qui se présentent naturellement sont mesurables (au sens de Lebesgue) et aussi que la limite simple d'une suite de fonctions mesurables est encore une fonction mesurable.

La notion d'intégrale d'une fonction mesurable positive est très simple, on fait des découpages de plus en plus fins de l'axe des y en intervalles

8

lk = [Yb Yk + .ô.y[, on mesure les f-1fü) et on pose :

r

1

d}..

= lim L: J(yk)À(f-1 (1k)).

JR �y-+O k

INTRODUCTION

Une fonction mesurable quelconque f est dite intégrable (au sens de Lebesgue) si JR If 1

d}..

est finie.

Cette théorie permet d'obtenir des théorèmes de passage à la limite très pratiques. En particulier, pour permuter les signes lim et f , _{nul besoin de}

convergence uniforme, il suffit d'une « convergence dominée », c'est-à-dire d'une convergence simple fn(x) � f(x) _{pour tout} x, _{et « dominée » en ce}

sens qu'on a une fonction intégrable g, indépendante de n, telle que lfn 1 :::; g

pour tout n.

Cette théorie englobe la théorie de l'intégrale des fonctions continues (et aussi l'intégrale de Riemann) sur un intervalle fermé borné, mais elle n'englobe pas complètement la théorie des intégrales impropres. En effet dans sa définition même, elle pose

f est intégrable sur lR #-

l

1f1

d

À est finie #- 1f1 est intégrable sur IR.

Les fonctions qui ont des intégrales impropres convergentes mais non abso­ lument convergentes ne pourront donc pas être Lebesgue-intégrables.

La caractéristique remarquable de l'intégrale de Lebesgue est sa simpli­ cité ! En effet cette notion d'intégrale ne fait appel dans sa définition qu'à une chose : la possibilité de mesurer les 1-1 (Ik)·

Elle peut donc se généraliser à des fonctions mesurables définies sur n'importe quel ensemble E muni d'une notion de mesure. On obtient ainsi une théorie simple de l'intégration sur !Rn et des théorèmes très pratiques pour calculer des intégrales multiples à l'aide d'intégrations successives (cf. chap. 4).

Une des caractéristiques de l'Analyse du xxe siècle a été le changement

de point de vue qui consiste à ne pas se focaliser sur l'étude des fonctions en tant qu'objets individuels, mais à définir des espaces de fonctions doués de propriétés qui en font des cadres agréables pour y chercher (ou y construire) des solutions de problèmes concrets. Ce qui a fait le succès de l'intégrale de Lebesgue n'est pas tant le fait de pouvoir intégrer des fonctions très irrégu­ lières, mais l'énorme avantage que présentent les espaces normés complets de fonctions intégrables qu'elle permet d'obtenir. Le fait de travailler avec des espaces de fonctions complets est très agréable, car on peut montrer la convergence d'une suite de fonctions uniquement en prouvant que c'est une suite de Cauchy, c'est-à-dire que limp,q-+oo Il fp - fq Il = O. Il n'est donc

pas nécessaire de construire explicitement une fonction limite f telle que limp-+oo Il fp - f Il = O. Comme on construit le plus souvent les solutions

INTRODUCTION ₉

équations aux dérivées partielles, problèmes de minimum) comme limites de solutions approchées, le fait que l'espace dans lequel on travaille soit complet joue un rôle essentiel dans la preuve de l'existence de solutions.

L'espace L 1 des fonctions intégrables sur JR, muni de la norme

Il

f

Il

1 =

JR If 1 dÀ, est un espace normé complet, il en est de même des espaces LP (p � l) des fonctions dont la puissance p-ième est intégrable (cf. chap. 5).

L'un d'entre eux, l'espace L2, joue un rôle essentiel en Analyse car il est

naturellement _muni d'un produit _{scalaire qui en fait un espace de Hilbert,}

qui est l'analogue en dimension infinie des espaces

]Rn

ou

en :

(fig) =

1

f(x)g(x) dx B-

(vlw)

=

tViw;.

lR _i=I

On peut définir dans l'espace L2 la notion de projection orthogonale d'une fonction f de L2 sur un sous-espace fermé G, ce qui permet de donner une représentation géométrique de la notion de meilleure approximation de

f par des fonctions de G. Les bases orthonormées dans JRn ou

en

ont pour analogue les bases hilbertiennes dans L 2•

L'exemple le plus classique est celui de la base hilbertienne de L2([0, 1]) (espace des fonctions de carré intégrable sur [O, 1]) formée des fonctions

en : x -+ e2i:n:

n

x, n E 'll. Le développement d'une fonction f E L2([0, 1]) en

série de Fourier

nez

Cn(j)

=

{

en(x)f(x) dx 110,1]

s'interprète simplement comme la décomposition de f dans cette base or­ thonormée et l'application

qui à une fonction associe la suite de ses coefficients de Fourier, est un isomorphisme entre L2((0, 1]) et l'espace /2(Z) des suites complexes

(cn)neZ

telles que

Lnez lcnl2

< +oo (cf. chap. 6).

L'analogue de cet isomorphisme est réalisé sur L2(JR) par la transforma­ tion de Fourier, qui à une fonction f associe la fonction

:Ff(�) =

l

e-2i:n:�x f(x) dx.

On peut en effet montrer que cette formule, qui n'a de sens a priori que pour les fonctions f qui sont intégrables sur JR, permet de construire (à l'aide d'un sous-espace dense de L2(JR)) l'isomorphisme de Fourier :F de L2(JR) sur lui-même (cf. chap. 7).

IO INTRODUCTION

L'analyse de Fourier est l'une des branches les plus passionnantes et les plus difficiles de l' Analyse, elle donne naissance à _{de très belles formules}

se rattachant à des domaines a1:1ssi divers que l'équation de la chaleur ou la

Chapitre 1

L'intégrale des fonctions continues

Dans ce chapitre nous allons donner une définition simple de l'intégrale des fonctions continues sur un intervalle et nous allons énoncer ses prin­ cipales propriétés. Pour définir l'intégrale des fonctions continues sur un intervalle [a, b], il n'est pas nécessaire de faire appel à la définition classique de l'intégrale de Riemann obtenue à partir des subdivisions quelconques

a � x1 < x2 < · · · < Xn � b, on peut se contenter des rectangles construits à

l'aide de subdivisions régulières de [a, b]. On a donc donné dans ce cadre les démonstrations des propriétés élémentaires de l'intégrale, à partir desquelles on peut déduire les théorèmes classiques.

La plupart des formules et énoncés de ce livre feront appel à des intégrales sur des intervalles non nécessairement fermés bornés. Il est donc essentiel d'avoir bien assimilé la notion d'intégrale impropre, on en donne la définition et les principales propriétés.

Il nous a semblé utile aussi de pouvoir disposer dès le début des théorèmes de Lebesgue, même si on les doit les démontrer dans un cadre plus général dans le chapitre 3. _{Ainsi le lecteur peut se familiariser avec leur maniement}

et constater immédiatement leur efficacité.

1.1. Propriétés élémentaires

Théorème et définition. Soit f une fonction à valeurs réelles ou complexes,

définie et continue sur un intervalle [a, b], a < b. Alors la suite (SN(f))N�I

définie par

b - a N-i b - a SN(f) = -L:J(a + k-)

N k=O N

tend vers une limite finie lorsque N tend vers +oo. Cette limite est appelée

l'intégrale de f _sur [a, b] et est notée J: f(x) dx. On a donc

lb

f(x)dx = lim -b - a N-i L:J(a + k-b - a ).

a N-+oo N _k=O N

12 CHAPITRE 1. L'INTÉGRALE DES FONCTIONS CONTINUES

a a + k(b-;;-a) b Fig. 1.

Démonstration. Voir appendice, p. 77.

Remarques. 1) Le signe J provient d'une écriture ancienne du s, initiale du

« summa omnium » introduit par Leibniz en 1686. Pour Leibniz, l'intégrale

était la somme de toutes les valeurs f(x) affectées des coefficients infiniment petits dx. _{La définition moderne et rigoureuse considère l'intégrale comme}

une limite de sommes finies.

2) La lettre x figurant dans l'intégrale n'a aucune importance, et on peut la remplacer par n'importe quelle autre :

l

b f(x) dx =

l

b f(y) dy =

l

b f(t) dt .

3) _{La valeur b�a} J: f(x) dx _{est la limite quand N} � +oo des moyennes

des valeurs f (a + k b"t:/), _car

1

l

b 1 N-1 b - a

-b-- a a f(x) dx = N-+oo N lim -_k=O " f� (a + k--)N . On l'appelle la moyenne de f sur [a, b].

4) La définition ci-dessus permet d'intégrer toute fonction continue par morceaux sur un intervalle [a, b]. On dit que f est continue par morceaux sur [a, b] s'il existe une subdivision finie t0 = a < t1 < · · · < tn

=

b telle que

f soit continue sur tout ]t; , t; + 1 [ et possède une limite à gauche finie en t; + 1

et une limite à droite finie en t;. On pose alors

fb n-1

1

'i+I

la a f(x) dx = L . _{i=O t,} g; (x) dx , où g; est la fonction continue sur [t; , t; + 1] définie par

1.1. PROPRIÉTÉS ÉLÉMENTAIRES g; (t;) = _x�t; lim f(x) x>t; g; (x) = f(x) si x E]t; , t;+I [ g; (t;+1) = _x-+t;+1 lim f(x). x<t;+1 1.1.1. Premières propriétés

(i) Linéarité. Si f et g sont continues sur [a, b], on a

l

b (af(x) ₊ f3g(x)) dx = a

l

b f(x) dx ₊ /3

l

b g(x) dx

(a et f3 étant des constantes réelles ou complexes). En particulier, si f est à valeurs complexes, on a

l

b f(x) dx =

l

b Re f(x) dx ₊ i

l

b lm f(x) dx

(ii) Positivité. Si f est continue sur [a, b ], à valeurs réelles et f _{:;:::: 0,} alors

l

b f(x) dx :;:::: O.

13

Ceci implique que J: f(x) dx ::S J: g(x) dx si f et g sont réelles et f ::S g

sur [a, b].

En particulier on a

(b - a) inf f(x) ::::: rb f(x) dx ::::: (b - a) sup f(x) .

xE[a,b) la _xE[a,b]

De plus, si f est:;:::: 0, mais n'est pas identiquement nulle sur [a, b], alors

l

b f(x) dx >O.

(iii) Inégalité de la moyenne. Si f est continue sur [a, b], on a

1

fb f(x) dx

l

::::: { b

if(x)I dx ::::: (b - a) sup if(x)I .

la la xe[a,b)

(iv) Formule de la moyenne. Soit g une fonction continue sur [a, b ], réelle et positive sur [a, b], et f une fonction continue sur [a, b], à valeurs réelles. Il

existe 13 E [a, b] tel que

14 CHAPITRE I. L'INTÉGRALE DES FONCTIONS CONTINUES Cette formule doit son nom au fait que le nombre

b 1 f

b

f(x)g(x) dx fa g(x) dx la

n'est autre que la moyenne de f pondérée par la fonction g. ( v) Relation de Chasles.

l

b f(x) dx

= le

f(x) dx +

[

b f(x) dx si a < c < b .

Démonstration. Les trois premières propriétés sont des conséquences di­ rectes de la définition, par passage à la limite dans des égalités ou inégalités.

Pour montrer que si f � 0 mais f non identiquement nulle sur [a, b] alors

f: f(x) dx > 0, il suffit de prendre un point x0 de [a, b] tel que f(x0) > O.

Par continuité de f, il existe un intervalle [x0 -a, x0 + a] (avec a > 0) sur

lequel f > 0, et on a

l

b f(x) dx �

1

xo+a f(x) dx � 2a inf f(x) > 0 .

a xo-a xe[xo-a,xo+a]

Pour démontrer la formule de la moyenne, on peut supposer que

f: g(x)dx =fa 0, sinon on aurait g

=

0 car g est positive et continue sur

[a, b], et dans ce cas il n'y a plus rien à démontrer. D'autre part, comme g est positive, on a

. f f( ) < f: f(x)g(x) dx < f( ) m x ... _b ... sup x .

xE[a,b] _{fa g(x) dx xE[a,b]}

Et pour conclure, il suffit d'appliquer le théorème des valeurs intermédiaires à la fonction f.

Il reste à _{démontrer la relation de Chasles. Pour cela, voir p.} 79. D

Remarque. En général, l'intégrale d'un produit n'est pas égale au produit des intégrales :

l

b f(x)g(x) dx f:.

l

b f(x) dx

l

b g(x) dx .

Pas plus que le produit de deux sommes n'est la somme des produits : en général

Exemple. f

=

g

=

1 et 0 < b - a f:. 1. 1.1.2. Intégrales et primitives

Théorème. Soit f une fonction continue sur un intervalle [a, b ]. La fonction

1.1. PROPRIÉTÉS ÉLÉMENTAIRES 15 est dérivable sur [a, b], c'est-à-dire dérivable en tout point de ]a, b[ et dérivable à droite en a et à gauche en b, et vérifie

F'(x) = f(x) pour tout x E [a, b] F(a) =O.

Démonstration. Pour commencer supposons f réelle.

Soit x E [a, b[. Pour tout h > 0 tel que x + h E [a, b[, on peut expliciter

l'accroissement F(x + h) _{- F(x) à l'aide de la relation de Chasles : on a}

F(x + h) -_F(x) =

lx+h

f(t) dt -

lx

f(t) dt =

ix+h

f(t) dt .

Ce qui permet d'obtenir en appliquant la formule de la moyenne F(x +

�

-F(x) =

� ix+h

f(t) dt =

f(ex,h),

où

ex,h

E [x, X + h]. Comme f est continue ceci implique

�l;)\t !.._"""� F(x + h) - F(x) f( ) d _h

h --+ x quan --+ 0 .

On a donc montré que la dérivée à droite de F existe en x et vaut f(x). On montrerait de même que la dérivée à gauche de F existe en x et vaut aussi f(x).

Ce qui précède prouve la dérivabilité de F sur ]a, b[. Le fait que F est dérivable à droite en a et à gauche en b se démontre de la même manière.

Si f est à valeurs complexes, on utilise l'écriture

F(x) =

lx

f(t) dt =

lx

Re f(t) dt + i

lx

lm f(t) dt .

Les fonctions Re f et lm f étant réelles et continues, on voit que F est la somme de deux fonctions dérivables, et on a pour tout x E [a, b]

F'(x) = Re f(x) + i lm f(x) = f(x). D Remarque. Soit f une fonction continue sur un intervalle [a, b], et soit H la fonction définie sur [a, b] par

H : X --+

ib

f(t) dt .

En reprenant la démonstration ci-dessus, on voit que H est dérivable et que H'(x) = -f(x) pour tout x E [a, b] .

Ceci justifie le fait que l'on pose pour x :::; b

16 CHAPITRE 1. L'INTÉGRALE DES FONCTIONS CONTINUES

Définition. Si a > b, on pose par définition

lb

f(x) dx =

-1a

f(x) dx .

On pose aussi

la

f(x) dx = O .

Ce qui précède démontre donc le théorème suivant, qui est à la base du lien entre intégrales et primitives.

Théorème fondamental. La fonction définie sur [a, b J par

F : X -+

lx

J (t) dt ,

où c est un point quelconque de [a, b], est dérivable sur [a, b] et vérifie F'(x) = f(x) pour tout x E [a, b]

F(c) =O.

Définition. Soit f une fonction définie sur un intervalle [a, b]. On appelle

primitive de f sur [a, b] toute fonction F dérivable sur [a, b] (c'est-à-dire dérivable en tout point de ]a, b [ et dérivable à droite en a et à gauche en b)

telle que F' = f sur [a, b].

Remarque. Il n'est pas dit que toute fonction f définie sur [a, b] possède une primitive sur [a, b]. Ainsi la fonction indicatrice

(x) -

1

1 six E [O, 1/2]

X[o,1/2J - O . _smon

n'a pas de primitive sur [O, 1], car une primitive F devrait vérifier

F(x) =

l

x + C1

C2 sur sur][O, 1/2] l/2, 1]

où C1 et C2 sont deux constantes, et une telle fonction F ne peut être dérivable en 1/2.

Plus généralement, on peut montrer que la condition F' = f impose à f

de posséder la propriété des valeurs intermédiaires :

si c E f([a, b]) et d E f([a, b]) alors [c, d] C f([a, b]) .

Ainsi la fonction XQ ne peut avoir de primitive sur aucun intervalle de JR.

Existence et unicité des primitives. Remarquons d'abord que s'il existe une

1.1. PROPRIÉTÉS ÉLÉMENTAIRES 17

F + C est une primitive de f sur [a, b]. Il y a donc une infinité de primitives de f, mais on a là toutes les primitives de f. En effet si G est une primitive de f sur [a, b], on a

G'- F' = f-f = O

donc

G - F = C , où C est une fonction constante sur [a, b].

En particulier, si on se donne a E [a, b], il ne peut exister qu'une seule primitive F de f sur [a, b] telle que F(a) = O.

D'après le théorème fondamental, si f est continue sur [a, b], si a E [a, b],

la fonction

F : X �

lx

f(t) dt

est la primitive de f nulle en a.

On a donc existence d'une primitive F d'une fonction continue f sur

[a, b] et unicité de cette primitive si on impose à F une valeur fixée en un point de [a, b].

Calcul des intégrales. Si f est continue sur [a, b], et si F est une primitive de

f sur [a, b], on a

id

f(x) dx = F(d) - F(c). pour tout c et tout d dans [a, b].

Démonstration. La fonction

G : X �

lx

J (t) dt

est la primitive de f nulle en c.

La fonction F - G est donc constante sur [a, b] et on a F - G = F(c) - G(c) = F(c), ce qui donne bien

F(d) - G(d) = F(c), c'est-à-dire

G(d) = F(d) - F(c). D Notation. La fonction logarithme, notée log ou ln, est la primitive nulle en 1

de la fonction x � I/x sur ]O, +oo[, on a donc

lx

1

log x = ln x = -dt .

18 CHAPITRE I. L'INTÉGRALE DES FONCTIONS CONTINUES 1.1.3. Deux formules indispensables

Intégration par parties. Soient f et g deux fonctions continûment dérivables

sur [a, b].

La fonction (f g)' est continue sur [a, b] et a pour primitive la fonction

fg, on a donc

1b

(fg)'(x) dx = f(b)g(b) - f(a)g(a) .

La formule de dérivation d'un produit

(fg)'(x) = f'(x)g(x) + f(x)g'(x)

a alors pour conséquence immédiate la formule d'intégration par parties

1b

f(x)g'(x) dx = [f(b)g(b) - f(a)g(a)]

-1b

f'(x)g(x) dx . La formule précédente possède un analogue discret, la formule de « somma­

tion par parties »

n-1 n-1

Eak(bk+l - bk) = anbn - a1b1 -Ebk+•<ak+I - ak) .

k=I k=l

Exemple d'application : la seconde formule de la moyenne. Soient f une

fonction continûment dérivable et décroissante sur [a, b] et g une fonction continue sur [a, b]. Il existe c E [a, b] tel que

1b

f(x)g(x) dx = f(a)

1c

g(x) dx

(seconde formule de la moyenne). Pour démontrer cette formule, on considère la fonction G _{définie par}

G(x) =

1x

g(t) dt .

On a d'après la formule d'intégration par parties

1b

f (x )g(x) dx = f (b )G(b) +

1b

(-f')(x )G(x) dx .

Comme f est décroissante, on a -f' ::=:: 0 et donc

( _�� inf G) _L

fb

(-f')(x)

�lb

(-f')(x)G(x) dx

�

(sup G)

lb

(-f')(x) ,

a �� a

1.1. PROPRIÉTÉS ÉLÉMENTAIRES

(inf G)f(a) - (inf G )f(b) �

l

b f(x)g(x) dx - f(b)G(b)

�� �� a

On en déduit que

� (sup G )f(a) -(sup G )f(b) .

[a,b] [a,b]

( inf a) f (a) �

l

b f (x )g(x) dx � (sup _a) f (a) .

�� a ��

19

La fonction G étant continue sur [a, b], on en déduit, par le théorème des valeurs intermédiaires, l'existence de c tel que

l

b f(x)g(x) dx = G(c)f(a). D

Changement de variable. Soit cp une fonction continûment dérivable sur

[a, b], à valeurs réelles, et soit f continue sur l'intervalle I = cp([a, b]).

La fonction f possède une primitive F sur I et on peut former la fonction composée _{F o cp : [a, b] --+ 1 --+ <C.}

Cette fonction est dérivable et on a

(F 0 cp)'(t) = F'(cp(t))cp'(t) = f(<p(t))cp'(t) .

On voit donc que la fonction (F o cp) est une primitive sur [a, b] de la fonction

(f 0 <p )cp'.

On peut donc écrire

l

b f(cp(t))cp'(t) dt = F(cp(b)) - F(cp(a))

et comme F est une primitive de f, on a

1

rp(b)

F(cp(b)) - F(cp(a)) = f(x) dx .

rp(a)

On obtient donc la formule de changement de variable

l

b f(cp(t))cp'(t) dt = {"'(b) f(x) dx .

a }_rp(a)

Remarque. Dans la formule ci-dessus, il n'est pas nécessaire de supposer que

<p est bijective. Mais notons que si l'on veut calculer l'intégrale J! f(x) dx

en posant x = cp(t) on est amené à chercher a et b tels que a = cp(a) et

f3 = cp(b) et donc tout naturellement à « inverser » <p.

Exemple. En posant x = sin t on a

r1 r'2

20 CHAPITRE 1. L'INTÉGRALE DES FONCTIONS CONTINUES

en utilisant la fonction bijective sin : [O, Jr /2] --+ [O, l]. Mais on peut aussi

écrire

11

.J1 - x2 dx =

111:/2

1 cos t l cos t dt .

0 -11:

en utilisant la fonction non bijective sin : [-Jr, Jr/2]--+ [O, 1]. Le lecteur est

invité à représenter ces deux changements de variable -à l'aide d'un petit dessin.

1.1.4. La formule de Taylor avec reste intégral

Soit une suite de polynômes (Pn) telle que

Po = 1

Ôpn = Pn-1 pour tout n � 1.

Lemme. Pour toute fonction N + 1 fois continûment dérivable f on a

f

)Pn(x)ân f(y) - Pn(y)ân f(x)) =

1y-x

PN(x + t)âN+I f(y - t) dt .

n=O 0

Démonstration. En intégrant par parties on obtient

1y-x

PN(x + t)aN+l f(y - t) dt

= -pN(y)âN f(x) + PN(x)âN f(y) +

1y-x

PN-1 (x + t)âN f(y - t) dt

En répétant cette opération N fois, on obtient

1y-x

PN(x + t)aN+l f(y - t) dt

=

t.

(Pn(x)ân f(y) - Pn(y)ân f(x)) +

1y-x

Po(X + t)âf(y - t) dt N

= L(Pn(x)ân f(y) - Pn(y)ân f(x)) . D

n=O

Si on impose à la suite (Pn) de vérifier Pn(a) = 0 pour tout n � 1, où

a E IR, on a

( ) (x - a)n Pn X = n!

En effet les conditions

Po = 1 ,

I.I. PROPRIÉTÉS ÉLÉMENTAIRES 21

déterminent une unique suite (Pn) et on vérifie que les (x-�)n _n. satisfont bien ces conditions.

En faisant x = a dans la formule du lemme on obtient

N

r-a

f(y) - L Pn(y)ôn f(a)

=

_Jo PN(a + t)ÔN+I f(y - t) dt ,

n=O 0

ou encore par changement de variable

N

1

y

f(y)

=

L Pn(y)ôn f(a) + PN(a + y - t)aN+i f(t) dt .

n=O

a

C'est la classique formule de Taylor avec reste intégral :

j(x)

= t

Ôn j(a) (x - a)n +

1

x (X - t)N ÔN+I f(t) dt .

n=O n!

a

N!

Remarque. On peut obtenir d'autres formules du même type en imposant d'autres conditions pour définir la suite (Pn) que la condition Pn (a)

=

0 pour tout n ;:::

1.

Par exemple on peut imposer

ou

1

2.(Pn(a) + Pn(b))

=

O pour tout n ;:::

1

-

1-

1

b

Pn (x) dx = 0 pour tout n ::=::

1

. b - a

a

Plus généralement si v est une forme linéaire

telle que

V : 't' (JR) --+ C : f --+ v(f)

v(p0) = v(l)

=

1,

alors il existe une unique suite (Pn) telle que

v(pn)

=

0 pour tout n ;:::

1

(l'existence se voit en prenant une suite qn telle que q0 =

1

et ôqn

=

qn-I

et en posant Pn

=

qn - v(qn)l, quant à l'unicité on la démontre simplement par récurrence sur n).

En appliquant la forme linéaire v à la relation (entre fonctions de x) du lemme, on a

f(y) =

t

Pn(y)v(ôn f) + v(x --+

1

y-x PN(x + t)ôN+i f(y - t) dt) .

22 CHAPITRE 1. L'INTÉGRALE DES FONCTIONS CONTINUES

Exemple. Si

v(f)

= �(f(O)

+

f(I))

alors les Pn sont les polynômes d'Euler,

notés En , définis par E0

=

1 et pour tout n � 1 d_En

=

_En-

1

,

En(O)

+

En(I)

=

o.

Dans ce cas la formule de Taylor devient

f

(y)

= t !(anf(O)

+

anf(l))

En

(

Y

)

+

! (Y

E

N

(t)

aN+Ij

(y - t) dt

n=O 2 n! 2 }0

+

- EN

₂ 1

1

₀ y-l (1 + t)

aN+11

(y - t) dt . 1.2. Les intégrales impropres

1.2.1. Définitions

Il s'agit d'intégrer des fonctions

f

continues sur un intervalle non fermé borné, donc de la forme ]a, b], [a, b[ ou ]a, b[, l'extrémité a ou b étant éven­ tuellement égale à +oo ou -oo. On dit qu'on considère l'intégrale impropre

J: f(x) dx.

Définition. Soit

f

une fonction continue sur un intervalle [a, b[ avec b fini

ou +oo. On dit que l'intégrale J: f(x) dx est convergente si

le f

(x) dx tend vers une limite finie quand c

�

b ( c < b ).

Dans le cas contraire, on dit que l'intégrale est divergente.

a c b a c b

=

+oo

Fig. 2.

Soit une fonction

f

continue sur ]a, b[ avec a ou b éventuellement égal à

1 .2. LES INTÉGRALES IMPROPRES 23 c E ]a, b[ les intégrales f; f(x) dx et f: f(x) dx sont toutes deux conver­ gentes. En fait, il suffit qu'elles le soient pour un c E ]a, b[.

Exemples. 1) L'intégrale _{f1+00 x�} dx est convergente si a > 1, car la fonction

x � x�::11 est une primitive de la fonction x � _x� sur [1, +oo[, et donc

f c

_{- dx} 1 ₌ c-a+l - 1 _� --1 quand c � +oo. 1 xa -a + 1 a - 1

On voit aussi que f1+00 _x� dx est divergente si a < 1.

2) L'intégrale f1+00 � dx est divergente, car la fonction x � log x est une primitive de la fonction � sur [1, +oo[, et donc

fc

_{- dx} 1 _{= log e - 0 � +oo quand c � +oo.} 1 X

3) _{L'intégrale f01 x�} dx _{est convergente si et seulement si} a < 1. L'inté­

grale f0+00 _x� dx est divergente pour tout réel ex .

4) L'intégrale f01 log x dx est convergente, car la fonction x � x log x - x

est une primitive de la fonction log sur ]O, +oo[, et donc

1

1 _log x dx = -1 + e - e log e � -1 quand e � O.

5) _{On a}

l

+A X

---2 dx = 0 pour tout réel A,

-A 1 + x

mais l'intégrale {�= 1_;x2 dx est divergente. Pour le voir, il suffit de remar­

quer que fa+oo 1_{_;}x2 dx est divergente. 1.2.2. Quelques propriétés

Voici quelques critères permettant de montrer qu'une intégrale impropre est convergente ou divergente, la démonstration de ces critères est une conséquence immédiate des définitions.

On va se placer dans le cas d'une fonction continue sur un intervalle [a, b[ où b est fini ou +oo.

Cas où b est fini et f a une limite en b. Si f est continue sur [a, b[ où b est

fini et si f a une limite finie en b alors f: f (x) dx est convergente.

En fait, la fonction f peut se prolonger en une fonction continue g sur

24

On a alors

CHAPITRE 1. L'INTÉGRALE DES FONCTIONS CONTINUES g(x) = f(x) six E [a, b[ ,

g(b) = lim f(x) .

x-+b

lim

1

_c

_{f(x) dx} = lim

1

c

g(x) dx =

1

b

g(x) dx ,

c-+b

c<b

a

c-+b

_c<b

a a

car J: g(x) dx -+ 0 quand c -+ b (comme on le voit en utilisant l'inégalité de la moyenne).

0 . .

Exemple. J_1 si�x dx est convergente car si�x -+ 1 quand x -+ O.

Cas où b = +oo et f a une limite en b. Si f est continue sur [a, +oo[ et si

f a une limite l non nulle (ou si f -+ oo) en +oo, alors fa+oo f(x) dx est

divergente.

En effet on a pour A et B suffisamment grands

r f(x) dx � r � dx si l > 0

}A }A 2

� (8 � dx si l < O

}A 2

et il suffit de faire tendre B vers +oo.

Attention ! Si f -+ 0 en +oo, ceci n'implique pas que fa+oo f(x) dx est convergente.

Exemple. J1+00 � dx est divergente.

Remarque. Si fa+oo f (x) dx est convergente, ceci n'implique pas que f -+ 0 en +oo. Exemple où f est positive et continue : la fonction affine par morceaux représentée ci-dessous.

1

0 1 2 3

1 .2. LES INTÉGRALES IMPROPRES 25 Si f est 't'1 sur [a, +oo[ et si la+oo f(t) dt et la+oo f'(t) dt sont conver­

gentes alors f -+ 0 en +oo. En effet, f a une limite finie en +oo, car on a

f(x) = f(a) +

l

x f'(t) dt -+ f(a) +

1

+oo f'(t) dt ,

et comme on suppose que la+oo f(t) dt est convergente, cette limite ne peut être que nulle.

Critère de comparaison. Si f est positive sur [a, b [et si f ::::: g, la convergence

de 1: g(x) dx implique la convergence de 1: f(x) dx.

Ceci vient du fait que la fonction F : x -+ 1: f(t) dt est dans ce cas

croissante et majorée par 1: g(x) dx, elle a donc une limite finie en b.

On voit aussi que la divergence de 1: f(x) dx implique la divergence de

1: g(x) dx.

Exemple. L'intégrale 11+00 si:� x dx est convergente.

Règle des équivalents. Soit g une fonction positive sur un voisinage de b

et f une fonction telle que f ,...., g en b. Alors la convergence de 1: g(x) dx implique la convergence de 1: f(x) dx et la divergence de 1: g(x) dx implique la divergence de 1: f(x) dx. On dit que les intégrales sont de même nature.

Ceci est une conséquence du critère précédent, car la convergence de

J: f(x) dx est équivalente à celle de J: f(x) dx (a ::::: c < b). _Pour c _suffi­

samment proche de b (ou suffisamment grand si b = +oo) on a sur [c, b[ 0 ::::: (1 -e)g ::::: f ::::: (1 + e)g avec 0 < e < 1 .

Exemple. L'intégrale f1+00 �+1 . dx est convergente.

x sm x

Critère de Cauchy. L'intégrale 1: f (x) dx est convergente si et seulement si

pour toute suite (bn) qui tend vers b, on a

l

1bq

f (x) dx

1

-+ 0 quand p et q tendent vers + oo .

bp

Ceci vient du fait que la fonction F : x -+ 1: f(t) dt a une limite finie en

b si et seulement si pour toute suite (bn) qui tend vers b, la suite (F(bn)) est convergente. Ceci est équivalent à dire que (F(bn)) est de Cauchy, c'est-à-dire à la condition

l

1bq

f(x) dx

-1bp

f(x) dx

l

-+ 0 quand p et q tendent vers + oo . Ce critère n'est pas très utile en pratique, mais il servira dans la démonstration de certains théorèmes.

26 CHAPITRE I . L'INTÉGRALE DES FONCTIONS CONTINUES

1.2.3. Lien entre série et intégrale

Théorème. Soit a un entier � 0 et f une fonction continue, positive et décrois­

sante sur [a, +oo� l'intégrale fa+oo f(x) dx est de même nature que la série

L:�� f(n).

Démonstration. Il suffit d'utiliser la positivité de f et les inégalités

f (a) f(a + 1 ) f(a + 2) t [c] la f(x) dx

::S?;

f(n) N N

?;

f(n) ::=: f(a) +

1

f(x) dx . f(n) - - - _ _::_1-:s;:1:s;;;;;::i...._ 0 a a + 1 Fig. 4. n - 1 n n + l

Si la série converge, les sommes L��af(n) sont majorées par L��f(n) et on en déduit la convergence de l'intégrale. Si l'intégrale est convergente les sommes L�=a f(n) sont majorées par f(a) + fa+oo f(x) _{dx et on en déduit}

que la série converge. D

Exemple. La série L�� n I�gn a même nature que l'intégrale /2+00 x l�gx dx,

qui est divergente, car

1c

-1 1 -dx ₌ log(log c) - log(log 2) --+ +oo

2 x og x quand c --+ +oo.

1.2.4. Intégrales absolument convergentes

On va toujours se placer dans le cas d'une fonction continue sur un inter­ valle [a, b[ où b est fini ou +oo.

1.2. LES INTÉGRALES IMPROPRES 27

Définition. On dit que l'intégrale l: f (x) dx est absolument convergente si

l'intégrale l: lf(x)I dx est convergente.

Théorème. Si l'intégrale l: f(x) dx est absolument convergente, alors elle est

convergente et on a

Démonstration. Si la fonction f est à valeurs réelles, elle peut s'écrire comme différence f = f + - f- de deux fonctions positives

car Et on a !+ = sup(f, 0) et f-= sup(-f, 0), f(x) = f+(x) - 0 si f(x) � 0 = 0 - f-(x) si f(x) � O . !+ = sup(f,O) � Il l f- = sup(-f, 0) � If 1

-Par le critère de comparaison on en déduit que les intégrales l: f+(x) dx et l: f-(x) dx sont convergentes, et donc aussi l: f(x) dx. Et on montre l'inégalité en passant à la limite quand c � b dans l'inégalité de la moyenne

ile

f(x) dx

\

� le

lf(x)I dx.

Si f est à valeurs complexes, on écrit f = Re(f) + i Im(f) et on utilise le

fait que 1 Re(f)I � If 1_et1 _{Im(f)I � lfl.}

Le lecteur qui voudrait démontrer ce théorème en se passant des fonctions f + et f- peut avoir recours au critère de Cauchy en utilisant l'inégalité de la

moyenne. D

Exemple. L'intégrale impropre lo+oo si:�2 dx est convergente car elle est

absolument convergente.

Remarques. 1) La réciproque est fausse. On verra dans la suite que lo+oo si� x dx est convergente alors que lo+oo 1 si�x 1 dx n'est pas convergente (voir p. 30).

2) L'intégration par parties peut parfois permettre de se ramener à des intégrales absolument convergentes.

Exemple. Étudions la convergence de l'intégrale lo+oo cos x2 dx. Pour tout

CHAPITRE I . L'INTÉGRALE DES FONGnONS CONTINUES cos x2 dx = -2x cos x2 dx

le

le

1 o o _2x sin c2

le

sin x2 = -- + --dx . 2c 0 2x2

Quand c --+ +oo, on a si��2 --+ 0 _et l; s�x�2 _{dx tend vers une limite finie}

puisque l'intégrale impropre lo+oo s�x�2 _{dx est absolument convergente.}

Définition. Soit 1 un intervalle de IR, et f une fonction continue sur 1 (1 =

[a, b] ou [a, b[ ou ]a, b] ou ]a, b[ avec a < b, a _et b _finis ou non). _{On dit que}

f est intégrable sur 1 _si

l

b _{lf(x)I dx}

est convergente.

On résume par la notation li If 1 dx < +oo le fait quel: lf(x)I dx est

convergente. Et on note

[

! dx =

l

b _{f(x) dx .}

Remarque. Dans la notation ci-dessus peu importe que les points a ou b

appartiennent à 1.

et Si 1 = [a, b] fermé borné, toute fonction continue sur 1 est intégrable sur 1 { f dx = { f dx = { f dx = { f dx .

J[a,b] J[a,b[ J]a,b] J]a,b[

Si 1 = [a, b[ est borné, toute fonction continue sur 1 et qui a une limite

finie en b est intégrable sur 1.

Attention ! La fonction x --+ si�x n'est pas intégrable sur 1 = [O, +oo[ car

lo+oo 1 si�xl _{dx n'est pas convergente (voir p.} 30), _{bien que lo+oo si�x dx soit}

convergente.

Remarque. Les conventions concernant la notation des séries sont analogues à celles qui gouvernent l'emploi des notations li et l:. _{On n'écrit}

+oo L un _{au lieu de} L un

nEN n=O

que quand la série :L;t� Un _{est absolument convergente, c'est-à-dire quand}

la série :L;t� !un 1 _{est convergente. L'idée sous-jacente est que dans ce cas}

l'ordre sur les indices ne joue aucun rôle : une permutation des termes de la série ne change pas la valeur de la somme. Roger Godement écrit de façon imagée qu'on prend les termes « en vrac » au lieu de les prendre l'un après

I.2. LES INTÉGRALES IMPROPRES 29

série reste divergente après permutation des termes. C'est ce qui autorise d'écrire dans ce cas LneN Un = +oo.

Ces conventions valent aussi bien entendu pour Lnez Un, Ln;;:oa Un, etc.

Le lemme d'Abel. Soit f une fonction continûment dérivable sur [a, +ooL

positive et décroissante, tendant vers 0 en +oo, et soit g une fonction définie sur [a, +ooL à valeurs réelles ou complexes. On suppose que les intégrales de g sur les intervalles bornés sont bornées, c'est-à-dire qu'il existe un réel positif M tel que

11d

g(x) dx

l

� Mpour tous c et d dans [a, +oo[ .

Alors l'intégrale fa+oo f(x)g(x) dx est convergente et on a la « majoration du r+oo

IJd

f(x)g(x) dx

l

� Mf(d) pour tout d � a . reste »

Démonstration. D'après le critère de Cauchy, montrer que l'intégrale

fa+oo f(x)g(x) dx est convergente revient à montrer que pour toute suite

(bn) qui tend vers +oo, on a

1

Jbp

{bq

j(x)g(x) dx

l

-+ Ü quand p et q tendent vers + OO .

Pour majorer l'intégrale J:; f(x)g(x) dx, on va intégrer par parties en intro­ duisant la fonction G définie par

On a

G(x) = r g(t) dt .

Jbp

{bq

f(x)g(x) dx = f(bq)G(bq) +

{bq

(-f')(x)G(x) dx .

Jbp

Jbp

Comme f est décroissante, on a -f' � 0, et donc

-M

_Jbp

{bq

(-f')(x) �

_Jbp

{bq

(-f')(x)G(x) dx � M

_Jbp

{bq

(-f')(x) .

On en déduit que

-M(f(bp)-f(bq)) + f(bq)G(bq) �

_Jbp

{bq

f(x)g(x) dx

� M(f(bp)-f(bq)) + f(bq)G(bq). Comme f est positive on peut majorer et minorer le terme f(bq)G(bq)

30 CHAPITRE I . L'INTÉGRALE DES FONCTIONS CONTINUES

et on obtient finalement

1bq

Mf(bp) � f(x)g(x) dx � Mf(bp) .

bp

Ce dernier terme tend vers 0 quand p et q tendent vers +oo. La majoration

du reste est une conséquence de l'inégalité précédente, en prenant bp

=

d et

en faisant tendre bq vers

+oo.

D

Exemple. L'intégrale

JI+oo

si�x dx est convergente (f(x)

=

� et g(x)

=

sin x). Comme l'intégrale

/01

si�x dx est aussi convergente puisque si�x a une limite finie en 0, on en déduit que l'intégrale

/0+00

si�x dx est convergente. On ne peut appliquer le lemme d'Abel à l'intégrale

/1+00

l si�xl dx (en effet dans ce cas la fonction g : x --+ 1 sin xi n'est plus à intégrales bornées). Pour voir que l'intégrale

/0+00

1 si�xl _{dx est divergente on écrit}

et

1Nn

1 _{sin xi}

N-l 1(k+I)n

1 sin xi

--dx = L.: --dx

0

X

k=O kn

X

1(k+l)n

1 _{sin xi}

1"'

1 sin xi -- dx

=

dx

kn

x

0 x + br

?::

1,..

=

- -- sm x x 1 _{sin xi dx}

1 1

1"'

_{I . I d}

0

7r

+ krr

7r

k + 1

0

2

;k + 1 ,

et on conclut en utilisant le fait que

N-1

l

N

l

I: k + 1 = I: k � +00

k=O

k=l

(divergence de la série harmonique, voir §1.2.3).

On voit que ce qui fait la différence entre

/0+00

si�x dx et

/0+00

l si�xl dx est que dans le premier cas les intégrales

_Ji!+i)n

si�x dx _{changent de signe}

lorsque l'on passe de

k

à

k + 1

ce qui introduit des compensations entre les termes de la série alternée L:t�

Ji!+I)n

si�x dx alors que ceci ne se produit Plus avec les termes

_Jkn

r<k+i)n

l sinxl X dx.