Sur le point de Fermat d’un triangle

.

Sur le point de Fermat d’un triangle

Pascal GAMBLIN et Daniel PERRIN

Introduction

Dans ce texte, on se propose de d´ eterminer les points M du plan qui r´ ealisent le minimum de la somme des distances M A + M B + M C aux trois sommets d’un triangle donn´ e. C’est un probl` eme c´ el` ebre qui a ´ et´ e pos´ e pour la premi` ere fois par Fermat en 1636 et dont des solutions ont ´ et´ e propos´ ees par de nombreux math´ ematiciens (Torricelli, Cavalieri, Viviani, Simpson, Heinen, Steiner, etc.) Le lecteur trouvera plusieurs approches, toutes plus s´ eduisantes les unes que les autres, dans le livre de Berger [1] et sur de tr` es nombreux sites Internet, notamment :

http://www.ai.univ-paris8.fr/~audibert/tra/TORRICELLI.pdf

http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Torricel.

htm

Ce sujet a ´ et´ e propos´ e durant l’ann´ ee 2015-2016 comme th` eme d’ex- pos´ e dans le module de M2 pour futurs professeurs que nous encadrons ` a l’universit´ e Paris-Sud et en r´ efl´ echissant sur ce probl` eme nous avons pro- duit une preuve

tr` es simple qui n’est pas – nous semble-t-il – aussi connue que les autres. Elle consiste pour l’essentiel ` a se ramener au cas du triangle

´

equilat´ eral. Son int´ erˆ et essentiel est qu’elle peut ˆ etre d´ eclin´ ee ` a plusieurs niveaux du coll` ege et du lyc´ ee.

Dans ce qui suit, lorsqu’on parle d’un triangle, il est suppos´ e non aplati et quand on parle de ses points il s’agit des points du triangle plein (cˆ ot´ es compris). Nous utiliserons plusieurs fois le r´ esultat suivant :

0.1 Lemme. Dans un triangle ABC, si l’angle A b est obtus ou droit, le cˆ ot´ e BC est plus grand que AB et AC.

D´ emonstration. On peut soit invoquer Pythagore (si A b est obtus en utilisant les hauteurs issues de B et C), soit le vieux r´ esultat d’Euclide qui affirme que dans un triangle le plus grand angle fait face au plus grand cˆ ot´ e.

1 Le cas ´ equilat´ eral

On va commencer par montrer le r´ esultat suivant :

1. Avec plusieurs variantes.

1.1 Th´ eor` eme. Soit ABC un triangle ´ equilat´ eral, G son centre de gravit´ e, M un point du triangle. On a M A + M B + M C ≥ GA + GB + GC avec

´

egalit´ e si et seulement si M = G.

On conjecture facilement la propri´ et´ e avec un logiciel de g´ eom´ etrie en faisant afficher la somme M A + M B + M C . D’ailleurs, si l’on pense qu’il y a un unique point qui r´ ealise le minimum, il est clair qu’il est sur les trois axes de sym´ etrie du triangle, donc en G (sinon ses sym´ etriques r´ ealisent aussi le minimum). Le paragraphe suivant montre qu’en tous cas le minimum est n´ ecessairement sur les hauteurs.

1.1 La somme est plus courte sur les hauteurs

Pr´ ecis´ ement on montre :

1.2 Proposition. Soit M un point du triangle ´ equilat´ eral ABC . On appelle H le pied de la hauteur issue de A. Soit N l’intersection de (AH) avec la parall` ele ` a (BC) passant par M . Alors, on a M A + M B + M C ≥ N A + N B + N C avec ´ egalit´ e si et seulement si M = N .

D´ emonstration. On a d’abord M A ≥ N A car M A est l’hypot´ enuse du tri- angle rectangle AM N dont N A est un cˆ ot´ e de l’angle droit.

A

B C

H G M N

C'

Figure 1 – Le minimum ne peut ˆ etre que sur la hauteur

A

B C

G

M N

P R Q S

Figure 2 – Mais peut-on l’at- teindre ?

Montrons ensuite qu’on a M B + M C ≥ N B + N C . Bien sˆ ur, c’est

clair quand on connaˆıt les ellipses

, mais voici une preuve ´ el´ ementaire. On consid` ere le point C

sym´ etrique de C par rapport ` a (M N). On a donc M C

= M C et N C

= N C. De plus, B, N, C

sont align´ es (par exemple parce que N , qui est l’intersection de deux des m´ ediatrices du triangle rectangle BCC

, se trouve au milieu de l’hypot´ enuse [BC

]). On a donc N B +N C = N B+N C

= BC

et cette longueur est plus petite que M B + M C

= M B + M C par l’in´ egalit´ e triangulaire.

1.3 Remarque. Attention, cette proposition ne prouve pas l’existence d’un point qui r´ ealise le minimum de M A + M B + M C mˆ eme si l’on voit bien qu’on va pouvoir s’en approcher en recommen¸cant l’op´ eration avec une autre hauteur, voir figure 2. Cette remarque est ´ evidemment un point d´ elicat ` a faire comprendre ` a des lyc´ eens

.

1.2 Le cas o` u M est sur la hauteur

Le point G est encore le centre de gravit´ e du triangle et H le pied de la hauteur issue de A. Pour un point M de [AH], il s’agit de montrer qu’on a M A + M B + M C ≥ GA + GB + GC. On en propose quatre preuves, pouvant se d´ ecliner ` a diff´ erents niveaux du lyc´ ee ou du coll` ege.

1.2.1 Par l’´ etude de fonctions, terminale S

On choisit un rep` ere orthonorm´ e adapt´ e ` a la situation : H = (0, 0), B = (−a, 0), C = (a, 0), A = (0, a √

3). Le fait que G est au tiers des m´ edianes donne aussitˆ ot GA + GB + GC = 2a √

3. Soit M = (0, y) un point de la hauteur. On calcule M A + M B + M C = a √

3 − y + 2 p

a

+ y

et il n’y a plus qu’` a ´ etudier la fonction correspondante. Elle admet un minimum pour y = a/ √

3 et ce minimum vaut 2a √

3, d’o` u le r´ esultat.

1.2.2 Les outils des preuves g´ eom´ etriques

D’abord on note qu’on connaˆıt tous les angles de la figure : 60˚en A, B, C, 30˚ en ces mˆ emes points de part et d’autre des hauteurs-bissectrices et donc 120˚ en G pour \ BGC, CGA [ et AGB. [

2. Si l’on consid` ere l’ellipse E de foyers B, C qui passe par N , la droite (M N ) est tangente ` a E, donc M est ` a l’ext´ erieur de E et la somme des distances ` a B, C est plus grande en M qu’en N.

3. Dans ce genre de situation, personne ne doute de l’existence d’un minimum. Cela

montre que la propri´ et´ e de compacit´ e du triangle est bien naturelle !

30°

120°

A

B C

H G

M

Figure 3 – La figure de base

On sait aussi que G, qui est le point de concours des m´ edianes, est au tiers de [AH]. En particulier, on a GB = GA = 2GH .

Par la sym´ etrie d’axe (AH), on est ramen´ e ` a voir M A

2 +M B ≥ GA 2 +GB.

Il y a deux cas selon que M est dans [AG] ou dans [GH ]. Dans le premier cas il faut montrer M B ≥ GB +

M G, dans le second M B ≥ GB −

M G.

1.2.3 Par la g´ eom´ etrie, premi` ere S

En premi` ere S on dispose du produit scalaire, donc de la formule d’Al- Kashi

. On l’applique dans BM G : BM

= BG

+ M G

− 2BG × GM × cos BGM \ . L’angle BGM \ vaut 120˚dans le premier cas et 60˚dans le second donc son cosinus vaut −1/2 ou 1/2 et on a BM

= BG

+ M G

+ BG × GM ou BM

= BG

+ M G

− BG × GM . Il faut montrer que cette quantit´ e est

≥ GB

+

M G

+ GB × GM ou ≥ GB

+

M G

− GB × GM selon les cas, mais c’est ´ evident car on a M G

≥

M G

, avec ´ egalit´ e si et seulement si M est en G.

1.2.4 Par la g´ eom´ etrie, coll` ege 1

Une variante de la preuve pr´ ec´ edente consiste ` a utiliser le th´ eor` eme de Pythagore. L` a encore il est n´ ecessaire de distinguer selon la position du point M par rapport ` a G. Traitons le cas o` u M est dans [AG]. On calcule M B

=

4. Que l’on peut d´ emontrer aussi avec des arguments de coll` ege, bien entendu.

M H

+HB

= (M G+GH )

+HB

= M G

+GH

+2×M G×GH +HB

. Il faut voir que cette quantit´ e est ≥ (GB +

M G)

= GH

+HB

+GB ×M G+

1

4

M G

. En divisant par M G, on est ramen´ e ` a montrer

M G + 2GH ≥ GB.

Mais, comme on a GB = 2GH , c’est ´ evident.

Le cas o` u M est dans [GH ] est tout ` a fait analogue.

1.2.5 Par la g´ eom´ etrie, coll` ege 2

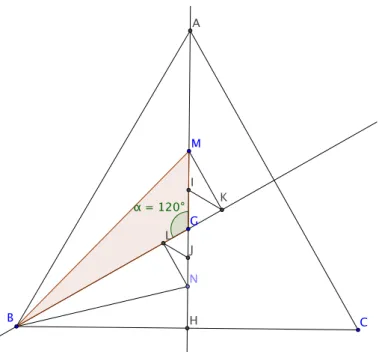
α = 120°

M

G

B

I K

N J L

C A

H

Figure 4 – La preuve g´ eom´ etrique Premier cas : M ∈ [AG[

Comme il s’agit de montrer M B ≥ GB +

M G on introduit le milieu I de [M G] (voir figure 4) et il faut prouver M B ≥ GB + GI. Cela incite ` a prolonger [GB] de la longueur GI et l’on obtient ainsi le point K. Comme l’angle BGM \ = BGA [ vaut 120 degr´ es, l’angle IGK [ vaut 60 degr´ es et le triangle isoc` ele IGK est ´ equilat´ eral. Mais alors, le point K est sur le cercle de diam` etre [GM], de sorte que M KG est rectangle en K, donc aussi M KB.

On en d´ eduit bien BK = BG + GK = BG + GI ≤ BM puisque le cˆ ot´ e de l’angle droit est plus court que l’hypot´ enuse.

Deuxi` eme cas : N ∈ [GH ]

Le raisonnement est identique en consid´ erant le milieu J de [N G].

2 L’´ enonc´ e g´ en´ eral

On a vu que, dans le cas ´ equilat´ eral, le minimum de M A + M B + M C est atteint en le centre de gravit´ e G. L’exp´ erience avec un logiciel montre clairement que ce n’est plus le cas pour un triangle quelconque

. Cependant, dans le cas ´ equilat´ eral, le point G est tel que les angles \ BGC, CGA [ et AGB, [ angles sous lesquels on voit les cˆ ot´ es depuis G, sont tous trois ´ egaux ` a 120˚

et c’est cette condition angulaire qui va se g´ en´ eraliser. On d´ efinit donc : 2.1 D´ efinition. Soit ABC un triangle. On appelle point de Fermat du triangle un point F tel que les angles \ BF C, CF A [ et AF B [ soient tous trois

´

egaux ` a 120 degr´ es.

On a alors le r´ esultat suivant :

2.2 Th´ eor` eme. Soit ABC un triangle dont les angles sont tous plus petits que 120 degr´ es. Il existe un unique point de Fermat F du triangle. Si M est un point du triangle distinct de F on a M A + M B + M C > F A + F B + F C .

2.1 Existence et unicit´ e du point de Fermat

2.1.1 Condition n´ ecessaire

On note d’abord que, si le point de Fermat existe, les angles du triangle sont plus petits que 120 degr´ es. En effet, si AF B [ et AF C [ valent tous deux 120˚, les angles BAF [ et CAF [ qui sont avec eux dans les triangles AF B et AF C sont < 60˚, donc l’angle en A, BAC [ = BAF [ + CAF [ est < 120˚.

2.1.2 Unicit´ e

Notons ensuite que si le point de Fermat existe, il est unique. En effet, si on a un point de Fermat F et si G est un point du triangle, distinct de F , il est par exemple dans le triangle F BC. Mais alors, on a \ GBC ≤ \ F BC et \ GCB ≤ \ F CB et l’un au moins des in´ egalit´ es est stricte. La somme des angles dans les triangles GBC et F BC montre qu’on a BGC > \ \ BF C = 120˚

et G n’est pas un point de Fermat.

5. En utilisant la preuve de 2.3, le lecteur montrera que le point de Fermat n’est ´ egal

au centre de gravit´ e que dans le cas ´ equilat´ eral.

2.1.3 Existence

Il y a plusieurs mani` eres de montrer l’existence du point de Fermat, mais aucune n’est tout ` a fait ´ evidente, surtout si l’on veut rester dans le cadre des programmes du secondaire. La plus simple

est la suivante :

2.3 Proposition. Soit ABC un triangle dont tous les angles sont < 120 ˚. On construit deux triangles ´ equilat´ eraux ABD et ACE ` a l’ext´ erieur du triangle ABC . Soit F le point d’intersection

de (CD) et (BE ). Alors F est le point de Fermat du triangle ABC.

60°

60°

A

B

C D

E

F

G

Figure 5 – Construction du point de Fermat

D´ emonstration. Voir figure 5. Les triangles CAD et EAB sont isom´ etriques

. En effet on a AC = AE, AD = AB et les angles en A sont tous deux ´ egaux

`

a BAC [ + 60˚. On en d´ eduit que les angles en E et C de ces triangles sont

´

egaux. Soit G le point d’intersection de (BE) et AC). Les triangles AGE et F GC sont semblables (outre les angles en E et C, ils ont les angles en G oppos´ es par le sommet). On en d´ eduit d’abord

que les angles EAG [ et CF G [

6. On a choisi ici une preuve dans l’esprit des programmes de coll` ege 2016, c’est-` a-dire avec les triangles isom´ etriques et semblables, mais sans l’angle inscrit.

7. Il est int´ erieur au triangle parce que A b est < 120˚.

8. Si l’on connaˆıt les rotations, on peut noter qu’on passe de l’un ` a l’autre par la rotation de centre A et d’angle π/3.

9. Ici, on peut se contenter d’invoquer la somme des angles de ces triangles.

sont ´ egaux, donc ce dernier angle vaut 60˚, ce qui donne \ BF C = 120˚. De plus, la similitude des triangles donne AG

F G = GE

GC donc aussi GA

GE = GF GC . Avec en plus l’´ egalit´ e des angles AGF [ et EGC [ , cela montre que les triangles AGF et EGC sont semblables, de sorte qu’on a

AF G [ = ECG [ = 60˚.

On a donc AF C [ = AF G [ + GF C [ = 120˚et le troisi` eme angle en F , AF B [ vaut aussi 120˚.

2.2 Le point de Fermat r´ ealise le minimum

A

B

C F

A'

B'

M

Figure 6 – R´ eduction au cas ´ equilat´ eral

Soit F le point de Fermat de ABC et montrons qu’on a M A + M B + M C ≥ F A + F B + F C pour tout point M du triangle. On se ram` ene au cas

´

equilat´ eral. Pour cela on choisit le sommet le plus ´ eloign´ e de F , disons C, et on prolonge les segments [F A] et [F B] en [F A

] et [F B

] avec F A

= F B

= F C, voir figure 6. Le triangle A

B

C est ´ equilat´ eral. En effet, F A

C, par exemple, est isoc` ele en F avec un angle de 120˚, donc ses angles ` a la base valent 30˚. Il

10. Si l’on dispose du th´ eor` eme de l’angle inscrit et de sa r´ eciproque, on voit que

E, A, F, C sont cocycliques grˆ ace ` a l’´ egalit´ e AEF [ = ACF [ et on en d´ eduit l’´ egalit´ e des

autres angles ` a 60˚.

en r´ esulte que les angles de A

B

C valent tous 60˚. Si M est un point de ABC distinct de F , on a M A ≥ M A

− AA

et M B ≥ M B

− BB

par l’in´ egalit´ e triangulaire, donc M A + M B + M C ≥ M A

+ M B

+ M C − AA

− BB

>

F A

+ F B

+ F C − AA

− BB

en vertu du cas ´ equilat´ eral et on conclut en utilisant F A = F A

− AA

et F B = F B

− BB

.

3 Compl´ ements

3.1 Les points ext´ erieurs

La proposition suivante montre qu’on peut se limiter aux points du tri- angle pour chercher le minimum.

3.1 Proposition. Soit ABC un triangle. Si M est un point ext´ erieur au triangle, il existe N dans le triangle tel que N A + N B + N C ≤ M A + M B + M C .

D´ emonstration. Il faut distinguer deux cas de figure.

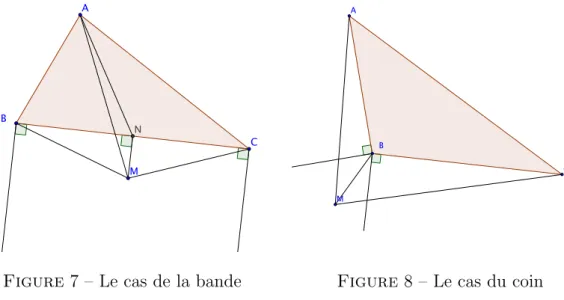
Le point M est dans une bande

On suppose que M est, par exemple, dans la (demi)-bande limit´ ee par le segment [BC] et les demi-droites perpendiculaires ` a (BC) en B et C, de l’autre cˆ ot´ e de A par rapport ` a (BC), voir figure 6. Soit N le projet´ e orthogonal de M sur (BC). L’hypoth` ese assure que N est dans [BC]. Alors, on a N A + N B + N C ≤ M A + M B + M C . En effet, on a N B ≤ M B car le triangle M N B est rectangle en N et de mˆ eme N C ≤ M C . On a aussi N A ≤ M A. En effet, dans le triangle M N A, comme A et M sont de part et d’autre de (BC) et que BN M \ est droit, l’angle en N est obtus. Le cˆ ot´ e M A qui fait face ` a cet angle est donc plus grand que N A par 0.1.

Le point M est dans un coin

On suppose que M est, par exemple, dans le secteur d´ efini par les deux demi-droites d’origine B, perpendiculaires ` a (BA) et (BC), ` a l’ext´ erieur du triangle, voir figure 7. Alors, on a M A + M B + M C ≥ BA + BB + BC. En effet, l’hypoth` ese montre que le triangle AM B a un angle obtus en B, donc que l’on a M A ≥ BA, toujours par 0.1. De mˆ eme, on a M C ≥ BC et on en d´ eduit le r´ esultat.

3.2 Corollaire. Dans le cas d’un triangle dont les angles sont tous < 120 ˚,

le minimum de la fonction M 7→ M A + M B + M C pour M variant dans le

plan, est atteint au point de Fermat du triangle.

A

B

C M

N

Figure 7 – Le cas de la bande

A

B

C M

Figure 8 – Le cas du coin

3.2 Le cas d’un triangle avec un angle de plus de 120 ˚

Dans ce cas on a le r´ esultat suivant :

3.3 Proposition. Soit ABC un triangle dont l’angle en A est ≥ 120 ˚. Alors, le minimum de la fonction M A + M B + M C pour M variant dans le plan est atteint au point A.

D´ emonstration. On peut se limiter au cas o` u M est dans le triangle en vertu de 3.1. Si le triangle est isoc` ele en A, le mˆ eme raisonnement qu’en 1.2 permet de supposer que M est sur la hauteur [AH]. Il s’agit alors de montrer

qu’on a AB < BM +

AM . On pose α = BAM \ et β = ABM \ avec α > 60˚. On a la relation des sinus dans ABM :

AB

sin(α + β) = AM

sin β = BM sin α .

La relation ` a prouver se ram` ene ` a 2 sin(α + β) ≤ 2 sin α + sin β, soit encore 2 sin α cos β + 2 sin β cos α ≤ 2 sin α + sin β. Mais comme on a α > 60˚ donc cos α < 1/2, on a le r´ esultat.

On se ram` ene ensuite au cas isoc` ele en prolongeant le plus petit des cˆ ot´ es AB et AC, disons AC, en AC

, voir figure 9. En vertu du cas isoc` ele, on a M A + M B + M C

≥ AB + AC

= AB + AC + CC

. Si l’on ajoute M C aux deux membres on a M A + M B + M C + M C

≥ AB + AC + CC

+ M C ≥ AB + AC + M C

, la derni` ere in´ egalit´ e provenant de l’in´ egalit´ e triangulaire et on a le r´ esultat.

11. Une premi` ere version de ce r´ esultat ´ etait radicalement fausse. Merci ` a Akil Zaimi de

nous avoir signal´ e cette erreur.

A

B

M C

C' H

Figure 9 – Le cas d’un grand angle

R´ ef´ erences

[1] Berger Marcel, G´ eom´ etrie, Nathan, 1990.