HAL Id: tel-00011911
https://tel.archives-ouvertes.fr/tel-00011911
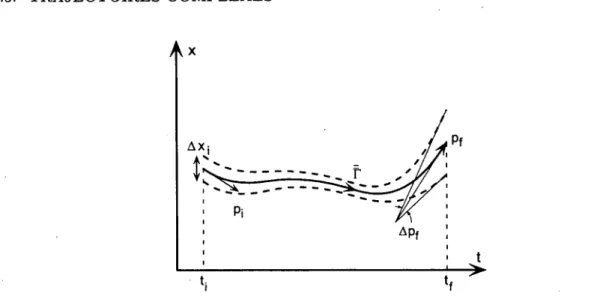
Submitted on 10 Mar 2006
HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
temps : étude semi-classique
Pipa Storey
To cite this version:
Pipa Storey. Ondes de matière dans des potentiels périodiques en temps : étude semi-classique. Physique Atomique [physics.atom-ph]. Université Pierre et Marie Curie - Paris VI, 1996. Français. �tel-00011911�
DE
L’ECOLE NORMALE
SUPÉRIEURE
THÈSE
DE
DOCTORAT
DE
L’UNIVERSITÉ
PARIS
VI
spécialité: Physique Quantique
présentée
par
Elizabeth
Pippa
STOREY
pour
obtenir le
titre
de
Docteur
de
l’Université Paris
VI
Sujet
de la thèse:
Ondes
de
matière dans des
potentiels
périodiques
entemps :
étude
semi-classique
Soutenue
le 13 décembre 1996 devant le
jury composé
de :
MM. Yvan
CASTIN,
Jean-Yves
COURTOIS,
Claude
FABRE,
Christian
MINIATURA,
Klaus
MØLMER,
Rapporteur
Andrew
STEANE,
Rapporteur
DE
L’ECOLE NORMALE
SUPÉRIEURE
THÈSE
DE
DOCTORAT
DE
L’UNIVERSITÉ
PARIS
VI
spécialité: Physique
Quantique
présentée
par
Elizabeth
Pippa
STOREY
pour
obtenir le
titre
de
Docteur
de
l’Université Paris
VI
Sujet
de la thèse:
Ondes de matière
dans
des
potentiels
périodiques
entemps :
étude
semi-classique
Soutenue le
13
décembre
1996
devant
le
jury composé
de :
MM. Yvan
CASTIN,
Jean-Yves
COURTOIS,
Claude
FABRE,
Christian
MINIATURA,
Klaus
MØLMER,
Rapporteur
Andrew
STEANE,
Rapporteur
Table des matières
Introductiongénérale
1 1 Présentation duproblème
5 Introduction ... 5 1.1Approches
existantes ... 6 1 1.1 Simulationnumérique
... 6 1.1.2Approximation
de Born ... 91.1.3 La méthode de
Floquet
et l’atome habillé ... 121.1.4 La méthode du réseau de
phase
mince ... 141.2 Considérations
expérimentales
... 171 2 1 Réalisation
expérimentale
... 171.2 2 Calcul des
paramètres
du modèle ... 191.2.3 Pertes dues à l’émission
spontanée
... 211.2.4 Effet du bruit
expérimental
... 22Conclusion ... 24
2 La méthode
d’intégrale
de chemin 25 Introduction ... 252.1 Le
propagateur
deFeynman
... 252 1.1 Définition ... 25
2 1.2 Idées menant à la formulation
d’intégrale
de chemin ... 262.1.3 Obtention de la formulation
d’intégrale
de chemin ... 282.2 La limite
semi-classique
... 312.2.1
Analogie
avec la construction deHuygens
... 312.2.2 Les rayons
optiques
... 332.2.3 Les
trajectoires classiques
... 342.2.4 La forme BKW du
propagateur
... 342.3
Propagateurs généralisés
... 362 3.1
Propagateurs dépendant
del’impulsion
... 362.3.2
Propagateurs dépendant
del’énergie
... 402.4 Calcul de
l’amplitude semi-classique
... 412.4.1 Démonstration directe à
partir
del’intégrale
de chemin ... 422.4.2
Interprétation
en termes d’un ensembleclassique
... 482.5
Trajectoires
complexes
... 512.5.1 L’onde évanescente ... 53
2.5.3 Traitement
géométrique
de la diffraction ... 57Conclusion ... 59
3
Caustiques
61 Introduction ... 613.1 La méthode de la
phase
stationnaire ... 613.1.1
Exemple
d’un calcul par la méthode de laphase
stationnaire .... 623.1.2 Observations sur la méthode de la
phase
stationnaire ... 643.1.3 Extension de la méthode de la
phase
stationnaire ... 653.2
Concepts
de la théorie descatastrophes
... 663.2.1 Stabilité
topologique ...
673.2.2
Systèmes
avecsymétrie
... 743.3
Approximations
uniformes ... 753.3.1 Le choix d’une forme
générique
pour laphase ...
753.3.2 Obtention
heuristique
desapproximations
uniformes ... 783.3.3
Comparaison
de résultats ... 843.4 La détermination des indices de Maslov ... 86
3.4.1 Variation des indices au cours de l’évolution du
système ...
863.4.2 Obtention des indices à
partir
dudiagramme
espacephase ...
92Conclusion ... 94
Conclusion
générale
95 A Normalisation des états propresd’énergie
96 B Calcul d’un déterminant par récurrence 101 CAmplitudes semi-classiques
104 C.1 Lepropagateur
K(x
f
,t
f
;p
i
,t
i
)
... 104C.2 Le
propagateur
K(x
f
,t
f
;p
i
,t
i
)
... 106D Réflexion par un
puits
depotentiel
108 D.1 Traitement de Stokes ... 108D.1.1 Point de rebroussement d’ordre un ... 108
D.1.2 Puits de
potentiel
... 111D.2 Calcul d’un
intégrale
de contour ... 114E Définitions de stabilité
topologique
117F Le théorème de Thom 119
G Forme
générique
del’amplitude
121Introduction
générale
Les
développements
récents dans le refroidissement laser ontpermis
d’atteindre destem-pératures
au-dessous de la ’limite’ derecul,
c’est-à-dire desdispersions
enimpulsion
atomiqueplus
faibles quel’impulsion
d’un seulphoton.
A de tellestempératures
lalongueur
d’onde de deBroglie
de l’atome estplus grande
que lalongueur
d’onde de lalumière,
et peut être considéréecomme
macroscopique.
La réalisation delongueurs
d’ondes de deBroglie
aussiimportantes
aredoublé l’intérêt
porté
à l’interférométrieatomique
[1],
analogue
de l’interférométrieoptique,
mais où des ondes de matière
jouent
le rôle d’ondes lumineuses. Un autredéveloppement
qui
a contribué à cet intérêt est la mise au
point
decomposants
d’optique atomique
analogues
aux
miroirs,
lentilles et lamesséparatrices
del’optique
traditionnelle.Le point de
départ
du travail décrit dans ce mémoire est unproblème
de diffusion danslequel
unjet
monocinétique
d’atomes traverse unpotentiel
modulépériodiquement
dans letemps.
Le spectred’énergie
dujet
sortantprésente
des bandes latéralesséparées
del’énergie
initiale par desmultiples
entiers de012703C9,
où 03C9 est lafréquence angulaire
de la modulation Ceproblème
est une variante du miroiratomique
vibrant[2],
la différence étant que lesystème
fonctionne en transmissionplutôt
qu’en
réflexion.Les situations
physiques
dans de tellesexpériences
restent souventproches
de la limiteclassique,
dans le sens que lalongueur
d’onde de deBroglie,
bien queplus
grande
que lalongueur
d’onde de lalumière,
reste petite devant les autreslongueurs
caractéristiques
duproblème,
telles que les dimensions dupotentiel.
Dans cerégime
lesystème
seprête
à uneanalyse
par destechniques semi-classiques.
Une telleapproche
permet d’éclairer le contenuphysique
mieuxqu’une
évolutionnumérique
del’équation
deSchrodinger
La limite
semi-classique
de lamécanique quantique
estanalogue
à la limite despetites
longueurs
d’ondes del’électromagnétisme
De même que lapropagation
d’ondesélectroma-gnétiques
peut être décrite en termes de rayonsoptiques,
l’évolution d’états quantiques peut être décrite en termes detrajectoires
departicules
classiques.
Dans les deux cas il faut unefamille de
trajectoires
pour décrire lesystème.
Enmécanique
quantique,
lamultiplicité
detrajectoires
vient duprincipe d’incertitude, puisque
pourchaque
variable de l’étatquantique
qui est définie
précisément,
la variableconjuguée
est entièrement inconnue.Représenter
unétat
quantique
nécessite donc un ensemble departicules
classiques
couvrant toutes les valeurspossibles
des variablesconjuguées.
Parexemple,
pour décrire unsystème
dontl’impulsion
in-itiale est bien définie il faut un ensemble de
particules classiques
dontl’impulsion
estidentique
mais dont les
positions
prennent
toutes les valeurspossibles.
Pour leproblème
considéré danscette
thèse,
il est commode d’utiliser un ensemble departicules
qui
entrent dans lepotentiel
avec uneénergie
identique
mais à des instants différents.On peut étendre
l’analogie
entrel’optique
et lamécanique quantique
en considérant laphase
etl’amplitude
duchamp
électromagnétique
et celles de la fonction d’onde. Dans la limitedéterminée par l’action le
long
de latrajectoire classique
qui
arrive en cepoint;
dans lelangage
de
l’optique
géométrique,
latrajectoire classique correspond
donc aux rayons lumineux etl’action à la
longueur
de cheminoptique.
Tandis que l’intensité lumineuse est donnée par ladensité de rayons, le module carré de la fonction d’onde est
proportionnel
à la densité detrajectoires classiques.
Dans les deux cas, des effets d’interférence seproduisent
auxpoints
oùarrivent
plus
d’unetrajectoire.
Pour sommer les contributions des différentestrajectoires
il estimportant
de déterminer leursphases
relatives(ou
plus
généralement
leurspoids
complexes),
et de traiter correctement les
caustiques,
c’est-à-dire lespoints
de focalisation destrajectoires,
en
lesquels
les densités de chemins deviennent infinies.Cette
approche s’applique
auproblème
de diffusion considéré dans cemémoire,
bien quedans ce cas on s’intéresse au
spectre
d’énergie plutôt qu’à
la fonction d’onde.L’énergie
finale dechaque
particule
de l’ensemble s’obtient en calculant satrajectoire
à travers lepotentiel
selon leséquations
de mouvementclassiques.
L’énergie
finaledépend
de l’instantauquel
laparticule
est entrée dans lepotentiel,
et peutadopter classiquement
une valeurquelconque
dans unegamme continue avec une distribution de
probabilité
P(E
f
)
(voir
figure ci-dessous).
Notonsque cette distribution contient des
caustiques
aux limites de la gammepermise
classiquement
La structure discrète du vrai spectre
03A9(E
f
)
provient
d’interférences entre destrajectoires
quitraversent le
potentiel
à des instantsséparés
par desmultiples
d’unepériode temporelle
dupotentiel
203C0/03C9.
Laprésence
de bandes latérales dans larégion
interditeclassiquement
est uneffet
quantique
analogue
à l’effet tunnel. En utilisant un traitement correct descaustiques,
l’approche
semi-classique
reproduit
avecprécision
le spectrequantique,
aussi bien dans larégion
permise
que dans larégion
interdite.Le
problème
desapproximations semi-classiques
ou des petiteslongueurs
d’onde a étéabordé sous
plusieurs angles
différents. Ilenglobe
plusieurs
branches desmathématiques,
ets’applique
à de nombreux domaines de laphysique.
Uneapproximation semi-classique
desétats propres
d’énergie
del’équation
deSchrôdinger
indépendante
du temps a été obtenueindépendamment
par Wentzel[3]
et Brillouin[4]
en 1926. Elle consiste en une somme desolutions
propageant
en sensopposés,
dont laphase
dépend
de l’actionclassique,
et dontl’amplitude
contient le facteur|p|
-1/2
,
qui
peut
êtreinterprété
comme la racine carrée dela densité
spatiale
d’unjet
departicules
de flux constant enchaque
point.
L’approximation
est valable sauf au
voisinage
despoints
de rebroussementclassique
du mouvement dans lepotentiel,
oùl’impulsion
p s’annule et la densitéclassique diverge.
Ceci estanalogue
à l’échecde
l’optique
géométrique
auxpoints
focaux,
où les rayonsconvergent
et leur densité devient infinie. En obtenant une solution locale autour d’unpoint
derebroussement,
Kramers[5]
acalculé la
phase
relative aveclaquelle
il faut sommer les solutions sepropageant
vers la droiteet vers la
gauche.
En utilisant uneapproximation
asymptotique
il aégalement
estimé la valeurde la fonction d’onde
exponentiellement
décroissante dans larégion
interdite au-delà dupoint
derebroussement,
oùl’énergie
potentielle
excèdel’énergie
totale dusystème.
Une méthode
plus générale
pour obtenir lesamplitudes complexes
relatives des ’solutionsBKW’ a été inventée par Zwaan
[6]
en 1929(et
résumée parLanger
[7]).
Au moyen de sa’méthode
complexe’,
lesrégions
séparées
par despoints
de rebroussement sont reliées par unchemin dans le
plan
complexe
despositions qui
passe assez loin despoints
de rebroussementpour que les solutions BKW restent valables. Les formules de raccordement obtenues sont
souvent suffisantes pour déterminer tous les facteurs
d’amplitude
et dephase
aveclesquels
ilfaut sommer les solutions BKW dans
chaque
région.
La méthode ne résout paspourtant
leproblème
de la valeur de la fonction d’onde auvoisinage
despoints
de rebroussement.Un
jet
d’atomesd’énergte
initiale E
i
entre dans unpotentiel
modulépériodiquement
dans letemps.
Après
avoir traversé lepotentiel
la distributionclassique d’énergie
P(E
f
)
des atomes est non nulle dans unerégion
dite’permise’.
Dû à lapériodicité
de lamodulation,
lespectre
exacte03A9(E
f
)
prend
uneforme
discrète. Les bandes latérales seproduisent
auxénergies
E
f
=E
i
+n012703C9,
et ont unpoids
exponentiellement
décroissant dans larégion
interditeclassiquement
espaces de
configuration
en 1928 par Van Vleck[8].
Uneanalyse
différente a étéprésentée
par Dirac
[9],
qui
a montrél’analogie
entrel’équation
surl’amplitude
de la fonction d’ondeet
l’équation
de continuité d’un fluidecompressible.
Commel’approximation
BKWstandard,
cette méthode échoue aux
caustiques,
où elleprédit
uneamplitude
infinie.La formulation en termes
d’intégrale
de chemin de lamécanique
quantique
parFeynman
en 1948
[10]
a été suivie aussitôt parplusieurs
articles obtenant la valeursemi-classique
del’intégrale
de chemin. Le rôleprépondérant
destrajectoires classiques apparaît explicitement
dans la formulation deFeynman, puisque
ce sontprécisément
lestrajectoires classiques
qui rendent l’actionstationnaire,
et donc contribuent leplus
àl’intégrale
de chemin. Morette[11]
en 1951 a été lapremière
àreproduire
les résultats de Van Vleck àpartir
del’approche
d’intégrale
de chemin. D’autres méthodes ont étépubliées
depuis
(voir
parexemple
Papa-dopoulos
[12]).
Commel’approximation
BKWgénéralisée,
ces méthodes échouent dans levoisinage
descaustiques.
Leproblème
de laphase
de la solution(analogue
auproblème
deraccordement de la méthode BKW
standard)
peut
être résolu en faisantappel
à un théorèmedû à Morse
[13, 14]
concernant desaspects
globaux
du calcul de variations. Le résultat est quequi
nepeut
changer
quelorsque
latrajectoire
traverse unecaustique.
Dans le casgénéral
d’espaces
deconfiguration
arbitraires,
Levit et al.[15]
ont montré que lechangement
dépend
dusigne
des dérivées secondes du hamiltonien à lacaustique.
Le
problème
de l’obtention de solutionssemi-classiques
auvoisinage
descaustiques
estrésolu par la méthode de
l’approximation
uniforme. La méthode a étédéveloppée
par deuxapproches complémentaires.
Lapremière,
établie par Miller et Good[16]
etDingle
[17]
estune extension de la méthode BKW
standard,
oùl’équation
deSchrôdinger
exacte estrem-placée
par uneéquation
qui
conduit à la même structure depoints
derebroussement,
maisdont les solutions sont connues exactement. La deuxième
approche,
due à Chester et al.[18]
et
Berry
[19],
utilise une formulationintégrale,
et est utile pour dessystèmes dépendant
dutemps et des
problèmes
de diffusion. Près d’unecaustique,
où les expressions BKWgénéralisée
échouent,
il estpossible
de trouver unereprésentation
intégrale
duchamp
ondulatoire,
ana-logue
à la ’somme d’ondelettes’ deHuygens
etFresnel,
etqui
reste finie à lacaustique.
Une méthodegénérale
pour trouver de tellesreprésentations intégrales
a été donnée par Maslov[20].
Puisque
l’intégrand
contient unephase
qui
oscillerapidement,
la contribution laplus
importante
àl’intégrale
provient
despoints
où laphase
est stationnaire. Par un choixjudi-cieux de la variable
d’intégration,
laphase
peut
être mise sous une formecanonique,
d’unefaçon
qui
préserve
la structure depoints
stationnaires. Les formescanoniques possibles
ontété classifiées par Thom
[21, 22],
et constituent la base d’une branche de latopologie appelée
la théorie descatastrophes.
Comme lesexpressions
BKWgénéralisées,
les solutions obtenuespar
l’approximation
uniforme nedépendent
que destrajectoires
classiques
dusystème.
Laméthode
s’applique
aussi bien à larégion
permiseclassiquement qu’à
larégion
interdite, oùles
trajectoires
sontcomplexes.
Les résultats obtenus sont trèsprécis
dans la limitesemi-classique.
Ces méthodes sont discutées en détail dans un excellent article de revue de
Berry
et al[23]
Elles sont universelles de la même
façon
que la théorie des ondes estuniverselle,
et trouventleurs
applications
dans des domaines aussi variés que laphysique
atomique
etmoléculaire,
l’optique, l’acoustique
et laphysique
des vaguesocéaniques.
Le mémoire est divisé en deux
parties parallèles
etcomplémentaires.
Lapremière partie
du manuscrit est unesynthèse
de matérielexplicatif
et d’autres méthodes etapplications,
qui
a pour but deplacer
le travail dans le contexte dessujets
mentionnésau-dessus,
enparticulier
le formalisme
d’intégrale
de chemin et la théorie descatastrophes.
L’intention n’est pas defournir une
présentation rigoureuse
de chacun dessujets
maisplutôt d’indiquer
les relationsentre eux, et de renvoyer le lecteur à des revues
plus
détaillées.L’application
de méthodessemi-classiques
auproblème
considéré estprésentée
en détail dans l’articlequi
constitue laseconde
partie
de la thèse. Il décrit enparticulier
une version del’approximation
uniformeadaptée
auxproblèmes périodiques.
Les résultatss’appliquent
à dessystèmes
qui
présentent
unepériodicité spatiale
outemporelle.
Chapitre
1
Présentation
du
problème
Introduction
On cherche à calculer les
poids
des bandes latérales créées par l’interaction d’un faisceauatomique
avec unpuits
depotentiel
modulépériodiquement
dans letemps.
On limitel’analyse
à une
dimension,
et on considère enparticulier
lepotentiel
où
V
0
(x)
est unprofil
localisé enposition,
supposé
gaussienet V est
positif.
Lesystème
se caractérise par troisparamètres
sans dimensionoù
V
et sontrespectivement
laprofondeur
dupotentiel
et la différenced’énergie
entre desbandes latérales
voisines,
exprimées
en unités del’énergie
initiale de l’atome. est lalargeur
du
potentiel
en unités de1/k,
où 0127k =03B4p
est la différenced’impulsion
entre les bandeslatérales au
premier
ordre en .Ce
chapitre
présente
quelques approches
existantes pour obtenir lespoids
des bandeslatérales,
etexplique
la motivation pour un calculsemi-classique
en termesd’intégrales
de chemin. On discute aussi certainsaspects
de la réalisationexpérimentale
dusystème.
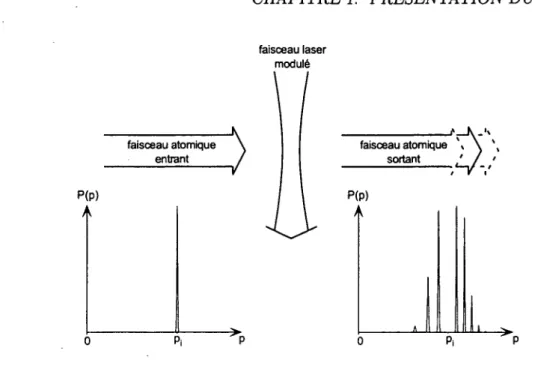
FIG. 1.1 - Le schéma de
l’expérience.
Des atomesd’impulsion
biendéfinie
traversent unfaisceau
laser dont l’intensité est modulée à lafréquence
03C9. La distributiond’impulsion
des atomes sortant contient des bandes latérales auximpulsions
p
2
i
+
2mn012703C9.1.1
Approches
existantes
Dans cette section
je
vais discuterl’application
dequelques
méthodes bien connues aucalcul des bandes latérales. On commence par la simulation
numérique
de la fonctiond’onde,
qui est une méthode
quantique,
valable dans tous lesrégimes
deparamètres
duproblème.
Onprésente
ensuite deux méthodesperturbatives: l’approximation
deBorn,
etl’approche
du réseau de
phase
mince. La méthode deFloquet
est mentionnéebrièvement,
mais s’avèredifficile à
appliquer
à cesystème.
1.1.1 Simulation
numérique
On
peut
calculer l’évolution de la fonction d’onde03C8(x, t)
enintégrant
numériquement
l’équation
deSchrodinger
où H est le hamiltonien
La fonction d’onde initiale
03C8(x, t
i
)
est unpaquet
d’ondes,
situé endeça
dupotentiel,
etdont la distribution
d’impulsion
est unpic
étroit centré en pi. L’évolution est déterminéejusqu’à
ce que lepaquet
d’ondes,
ayant
interagi
avec lepotentiel,
en soit sorti. Lespoids
desbandes latérales s’obtiennent alors en
intégrant
chacun despics
discretsapparaissant
dans laL’intégration
del’équation
deSchrôdinger
est effectuée sur des pas de durée03B4t,
enutili-sant la
technique
desplitting.
Puisque
le hamiltoniendépend
dutemps,
la méthode reposesur deux
approximations.
Lapremière provient
de l’utilisation d’une valeur constante pourle hamiltonien
pendant chaque
intervalle detemps.
La deuxième résulte de ladécomposition
del’opérateur
d’évolution pourchaque
intervalle en troisfacteurs,
de sorte que les termesd’énergie
cinétique
etd’énergie potentiel
soientséparés.
Les deuxapproximations
sontcor-rectes au second ordre en 03B4t.
L’équation
deSchrödinger
possède
la solution formelleoù T
indique
leT-produit
(la
mise des facteurs dechaque
terme dans l’ordrechronologi-que).
Numériquement
il faut discrétiser l’évolution en intervalles de tempsfinis,
et utiliserl’approximation
On
peut
facilement démontrer que l’erreur~
1
(03B4t)
associé àl’approximation
(1.8)
estoù H
et H sontrespectivement
les dérivéespremière
et seconde du hamiltonien par rapportau temps, évaluées à l’instant t.
Pour chacun des termes
(1.8),
on peut utiliser la méthode desplitting,
qui consiste à écrirel’opérateur
d’évolution sous forme d’unproduit
de trois facteursL’erreur
~
2
(03B4t)
associé à cetteapproximation
estEn
remplaçant
A et B par lesopérateurs d’énergie cinétique
etd’énergie
potentielle
respec-tivement, on obtient
l’algorithme
suivante pour calculer la fonction d’onde finalePuisque
lesopérateurs
qui
contiennent lepotentiel
sontdiagonaux
enposition,
on lesapplique
dans
l’espace
despositions.
De même lesopérateurs qui
contiennentl’énergie
cinétique
sontappliqués
dansl’espace
desimpulsions.
Numériquement
on bascule entrel’espace
despositions
etl’espace
desimpulsions
entrechaque opération
successive par une transformée de Fourier.Notons que cette méthode
préserve
exactement la normalisation de la fonction d’onde.On
peut
estimer de lafaçon
suivante la dimension destableaux,
le nombre de pas dedimension = kx où k est défini dans
l’équation
(1.4),
il faut que la valeur maximum dedans le tableau de
position
soitsupérieure
àDe
même,
en utilisantl’impulsion
sans dimension =p/p
i
,
on trouve que la valeur maximum de dans le tableaud’impulsion
doit êtresupérieure
àPuisque max
détermine la taille des divisions 0394 du tableau deposition
on trouve que la dimension N des tableaux est donné par
En insérant les valeurs de
max
etmax
on arrive à la conditionDe même on
peut
estimer le nombre de pas de tempsrequis.
En utilisant le temps sansdimension
=
03C9t on trouve que letemps
d’évolution estLe pas de temps doit être suffisamment
petit
pour que lesexposants
des facteurs dansl’équation
(1.12)
soient très inférieurs à 1. En termes desparamètre
sans dimension ceciimplique
Le nombre de pas de
temps
est doncPuisque
le temps de calculrequis
pour effectuer une transformée de Fourier sur un tableau1.1.2
Approximation
de BornDans le cas où les
poids
despremières
bandes latérales sontfaibles,
onpeut
les calculerpar la méthode de
Born,
en traitant comme uneperturbation
lapartie
dupotentiel
(1.1)
qui
dépend
dutemps.
Le hamiltonien est divisé en deux termes de lafaçon
suivanteoù
V
1
est laperturbation,
etH
0
est le hamiltoniennon-perturbé
Le
paramètre
~ est introduit dans le hamiltonien(1.22)
pour tenircompte
de l’ordre de laperturbation
dans lecalcul,
et on posera ~ = 1 à la fin.On suppose connus les états propres du hamiltonien
non-perturbé,
et on ne considère queles états
non-liés,
c’est-à-dire les étatsd’énergie
positive
Ep =
p
2
/2m.
Pourchaque énergie
E
p
,
il existe deux états propres deH
0
.
Loin dupotentiel
ils ressemblent à dessuperpositions
d’états propres
d’impulsion
|p> et |-p>.
Pour cette raisonje
lesappelle
|03C8
p
>
et|03C8
-p
>
Pour p >
0,
l’état|03C8
p
>
représente
uneparticule
incidente de lagauche
avecl’énergie
E
p
et|03C8
-p
>
est l’état d’uneparticule
incidente de la droite Si on normalise les états de tellefaçon
que
l’amplitude
de l’ondeplane
incidente vaille(203C00127)
-1/2
,
les états propres deH
0
satisfontaux mêmes relations d’orthonormalité que les états propres
d’impulsion
(voir
l’AnnexeA)
Etant donnés les états propres
non-perturbés,
on cherche les solutions|~
p
(t)>
del’équation
de
Schrodinger
pour le hamiltonienperturbé
Si on
développe
|~
p
(t)>
enpuissances
duparamètre
deperturbation
~le terme d’ordre zéro
|~
0
p
(t)>
est une solution del’équation
deSchrodinger
pour le hamiltoniennon-perturbé
On choisit la solution stationnaire
et on suppose que p > 0. On va s’intéresser en effet à une
petite
gammed’impulsions
p autourdont la solution est
où on
prend
la limite où lepotentiel
V
1
est branché et débranché très lentement.Supposant
qu’à
l’instant initial t = -~ lesystème
est dans l’état propre|03C8
p
>
du hamiltoniennon-perturbé,
on cherchel’amplitude
deprobabilité
cp(q)
pourqu’il
se trouve dans l’état|~
0
q
(t)> =
e
-iE
q
t/0127
|03C8
q
>
à l’instant final t = +~En insérant
l’équation
(1.29)
dans(1.31),
et en posant ~ =1,
on obtientqui
s’écrit en termesd’impulsion
commeoù
Notons
qu’on
a omis les termesd’impulsion négative
dansl’équation
(1.35).
Ceci est valabledans la limite
perturbative
si pi »~2m012703C9,
parcequ’en
ce cas leproduit
scalaireC
q
p
de cestermes dans est
négligeable .
Pour calculer le
poids
despremières
bandeslatérales,
il faut considérer un état|~(t)>
quiest initialement un
paquet
d’ondesoù
~(p)
est une distributionétroite,
située autour de pi. Laprobabilité
pour quel’impulsion
finale se trouve dans lapetite
gammedp
±
f
autour dep
±
f
,
oùLes
poids
despremières
bandes latérales sont alorsEn calculant la valeur de
dp
±
f
/dp
i
àpartir
del’équation
(1.38)
on obtientqui
estl’approximation
de Born aupremier
ordre. Engénéral
il faut calculer leproduit
scalairenumériquement.
Pourvu que lalargeur
dupotentiel
soit suffisammentgrande
par rapport à lalongueur
d’onde de deBroglie,
on peut évaluer les fonctions d’ondes des états|03C8
p
>
en utilisantla méthode BKW.
L’approximation
(1.41)
est en bon accord avec les résultats exacts dans lerégime
de faible diminution de la bande centrale(voir
laFigure
1.2).
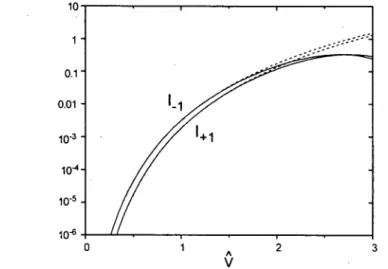
FIG 1.2 - Les
poids
despremières
bandes latéralesI
±1
,
calculés par la méthode de Bornau premier ordre
(pointillé),
etcomparés
avec lespoids
exacts, obtenus par une évolutionnumérique
del’équation
deSchrödinger
(trait continu).
Laprofondeur
dupotentiel V
estvarié entre 0 et
3,
et les autresparamètres
sontsfixés
=6.0,
= 0.1Si la
profondeur
dupotentiel
estbeaucoup
plus petite
quel’énergie
initiale del’atome,
les états propres du hamiltoniennon-perturbé Ho
peuvent êtreremplacés
par des états propresd’impulsion.
En ce cas on peut calculer lespoids
despremières
bandes latéralesanalytique-ment. En effet le
produit
scalairequi
figure
dansl’expression
(1.41)
vaut1.1.3 La méthode
de
Floquet
et l’atome habilléPour un
système
décrit par un hamiltonienpériodique
tel que(1.22),
l’équation
deSchro-dinger
possède
des solutions de la formeoù les états
|~
n
>
sontindépendants
du temps. En termes des cesétats,
l’équation
deSchro-dinger
s’écrit commeEn définissant un
spineur
on peut réduire le
problème
périodique
à unproblème indépendant
du temps. Lespineur
|03A6>
est la solution de
l’équation
H étant
l’opérateur
matricieloù
et I est la matrice d’identité. Pour calculer les
poids
des bandes latérales il faut trouverles états propres du hamiltonien H. Pour
chaque
valeur del’énergie
il existe une infinité despineurs
propres|03A6>.
On cherche lesspineurs
d’énergie
Eproche
deE
i
pourlesquels
seulondes
planes
sortants).
En recombinant cesspineurs
onpeut
construire unpaquet
d’onde etsimuler son évolution. Dans la limite où
l’énergie
dupaquet
d’onde est biendéfinie,
seul lespineur
d’énergie
E
i
estrequis.
Enprincipe
onpeut
le calculernumériquement.
Enpratique
les
exigences
sur la troncature et la discrétisation conduisent à des difficultés considérables. Dans la limiteperturbative
on peutpourtant
effectuer un calcul de Bornindépendant
dutemps
pour obtenir lepoids
des bandes latérales. On utilisel’expression
suivante de la matriceS
où
|03A6
0
>
et|03A6’
0
>
sont des états propres du hamiltoniennon-perturbé H
0
d’énergie E
et E’respectivement,
et T estl’opérateur
de transitionComme
spineur
initial|03A6
0
>
on choisit unspineur
d’énergie
Eproche
deE
i
pourlequel
seull’élément n = 0 est non-nul
où p ~
2mE.
Lespineur
final est unspineur
d’énergie
E’ pourlequel
seul l’élément n estnon-nul
où q ~
2m(E’ -
n012703C9).
Pour obtenirl’amplitude
de transition il faut calculer les éléments de matrice del’opérateur
T. Aupremier
ordre ils sontégaux
àoù 03B4 est une fonction delta de Kronecker. En
reportant
cetteexpression
dansl’équation
(1.49),
Ce résultat est
identique
à celui obtenu par la formulationdépendant
dutemps
(1.35).
Les fonctions delta de Kronecker donne des informations concernant
l’énergie
échangé
entrel’atome et
l’environnement,
informationsqui
n’étaient pasprésentes
dans la formulationdépendant
dutemps.
Cette observation nous mène à
l’interprétation
de la formulation deFloquet
comme lalimite des
grands
nombres dephotons
de la formulation d’atome habillé. Eneffet,
onpeut
supposer que le
potentiel
modulé est dû à l’interaction de l’atome avec deux modes optiques aet b
qui
diffèrent enfréquence
de 03C9. En effet l’atomepeut
absorber unphoton
d’une mode et l’émettre soit dans la mêmemode,
sans aucunchangement
de sonénergie
cinétique,
soit dans l’autremode,
avec unchangement
de sonénergie cinétique
de 012703C9. Dans la limite degrand
désaccord 0394 on
peut
élimineradiabatiquement
tous les niveaux internes excités del’atome,
et on arrive à
l’expression
suivante pour le hamiltonienoù on a
supposé
que la constante decouplage
atome-champ
g, et leprofil
spatial
f(x),
sontidentiques
pour les deux modes. Sichaque
mode contient ungrand
nombre moyen N dephotons,
et de faibles fluctuations 0394N «N,
ce hamiltonien devient formellementéquivalent
à
(1 47)
enposant
On peut chercher des états propres sous la forme
où le
premier
ketreprésente
l’état del’atome,
et le deuxième l’état des modesoptiques.
En substituantl’expression
(1.57)
dansl’équation
(1.46),
et enprojetant
sur l’état|N+n, N2014n),
on retrouvel’équation
(1.44),
cequi
démontrel’équivalence
des deux formulations.En
appliquant
le modèle de l’atome habillé à ceproblème
il estimportant
de noter quela différence 2n entre le nombre de
photons
danschaque
mode n’est pas biendéfinie,
mêmeavant le passage de l’atome. En
effet,
pour que la modulation dupotentiel
ait unephase
biendéfinie
1
,
il faut que laphase
relative entre les modes a et b soit elle aussi bien définie. Ceciimplique
une incertitude sur la différence entre le nombre dephotons
danschaque
mode.1.1.4 La méthode du réseau de
phase
minceLe calcul de Born
s’applique
aurégime
où lespoids
despremières
bandes latérales sontpetits.
Un autrerégime perturbatif qu’on
peut
étudier est celui où le transfertd’énergie
à1 Que la phase de la modulation du potentiel soit bien définie est nécessaire pour assurer la cohérence entre
les bandes latérales En utilisant ce fait, on peut expliquer l’incertitude sur la différence initiale entre le nombre de photons dans chaque mode de la façon suivante Supposons au contraire qu’on connaissait exactement la
valeur de n avant l’interaction En ce cas, on pourrait, en principe, déterminer l’énergie finale de l’atome en
mesurant le nombre de photons transférés d’un mode à l’autre Le fait que l’information concernant l’énergie
finale de l’atome est sauvegardée dans le champ optique détruirait toute cohérence entre les bandes latérales
On peut donc conclure que la supposition initiale est fausse, c’est-à-dire que la valeur de n n’est pas bien
l’atome
E
f
-
E
i
dû à son interaction avec lepotentiel
estpetit.
Les deuxrégimes
ne sontpas
identiques,
comme on le voit surl’exemple
suivant. Si lafréquence
d’oscillation 03C9 estpetite,
la différenced’énergie
entre les bandes latérales estpetite
aussi. L’interactionpeut
donc transférer une fractionsignificative
de lapopulation
atomique
aux bandes latérales sanspour autant transférer
beaucoup
d’énergie
aux atomes. Dans une telle situation le calcul deBorn au
premier
ordre n’est pas valable. Onpeut pourtant
utiliser la méthode du réseau dephase
mince,
présentée
ci-dessous.Cette méthode utilise une
approximation semi-classique
trèssimplifiée
de latechnique
d’intégrale
dechemin,
où onintègre
laphase
quantique
accumulée par l’atome lelong
de satrajectoire.
Dans la limitesemi-classique
on peutremplacer l’opérateur d’énergie
cinétique
dans le hamiltonien par un terme
approché
où v ~
v(x, t)
est la vitesse de l’atome considérée comme une fonctionclassique.
Notonsque le hamiltonien
(1.58)
esttoujours hermitien,
et satisfait àl’équation
de mouvement deHeisenberg
L’approximation
(1.58)
estéquivalente
à uneapproximation
detype
BKWdépendant
dutemps
(voir
leChapitre
2),
etremplace
l’équation
deSchrodinger
par uneéquation
différen-tielle de
premier
ordre enposition
Le terme de
gauche
est une dérivée totale de la fonction d’onde parrapport
au temps. Pourrésoudre
l’équation
il faut alorsexprimer
laposition x
en fonction detemps,
c’est-à-diretrouver la
trajectoire
de l’atome.Puisqu’on
considère lerégime
où la modulation dupotentiel
ne
change
pas le mouvement de l’atome defaçon
significative,
onpeut
remplacer
la vraietrajectoire
de l’atome par latrajectoire
qu’il
aurait suivie dans lepotentiel
non modulé. Onsuppose une
énergie
totale deE
i
,
et on choisit latrajectoire
x
0
(t)
qui
arrive à laposition x
f
àl’instant
t
f
.
De même la vitesse v de l’atome estremplacée
par sa valeur v0 dans lepotentiel
non moduléV
0
(x)/2.
Puisque
v0 nedépend
que de laposition
de l’atomeon trouve
où
t
i,0
est l’instantauquel
latrajectoire non-perturbée
(t)
0
x
part
de laposition
initiale xi. Enremplaçant
la fonction d’onde endeça
dupotentiel
par une ondeplane,
et en utilisant le fait que
f
)
(x
0
v
=v
0
(x
i
),
on trouveOn
peut
simplifier l’intégrale
en utilisant la relation(1 61)
où C est une constante. En
reportant
ce résultat dansl’équation
(1.65)
on obtientoù
1
estl’intégrale
dupotentiel
V
1
lelong
dutrajectoire non-perturbée
(c’est-à-dire
la tra-jectoire dans lepotentiel
non-modulé)
Pour effectuer cette
intégrale
il fautprendre
en compte ladépendance
de la fonctionx
0
(t)
vis-à-vis du
temps
finalt
f
.
Cettedépendance
s’écrit commeoù x est une fonction
qui
estindépendant
det
f
,
et satisfait à la relationx(0)
=0, c’est-à-dire,
x(t)
est latrajectoire non-perturbée
qui
passel’origine x
= 0 à l’instant t = 0. Letemps
T
f
est l’instantauquel
cettetrajectoire
arrive à laposition finale,
x(T
f
)
= x f. De même on
dénote par
T
i
l’instantauquel
latrajectoire
x(t)
part
de laposition
initialex(T
i
) =
xi. Ainsion peut récrire
l’équation
(1.68)
commeoù on a
remplacé
03C9T
f
par sonexpression
en fonction de xfk est défini dans
(1.4)
et C’ est une constantequi dépend
desparamètres
dupotentiel
nonmodulé. L’indice de
modulation 03B6
est la transformée de Fourier dupotentiel
vu par l’atomequand
il sedéplace
lelong
de latrajectoire
non-perturbée
x(t)
Elle est réelle parce que la fonction
V
0
[x(t)]
estsymétrique.
Notonsqu’il
est valable d’étendre les limitesd’intégration
à±~,
puisque
l’atome ne subit aucunpotentiel
avant l’instantT
i
niaprès
l’instantT
f
.
En insérantl’expression
(1.71)
dans(1.67)
on obtientLa fonction d’onde finale est donc une onde
plane,
dont laphase
est modulée sinusoidalement. En prenant une transformée de Fourier par rapport à la position del’expression approchée
(1.74),
on trouve des bandes latérales auximpulsions
dont les
poids
sontoù
J
n
sont des fonctions de Bessel. Le fait que la fonction d’ondeapprochée
(1.74)
ne satisfaitpas aux relations de
dispersion
exactes,
maisplutôt
aux relations du premier ordre en(1.75),
est dû auremplacement
destrajectoires
exactes par destrajectoires
non-perturbées
dans le calcul. Ceci estégalement
l’origine
de lasymétrie
du spectre calculé(1.76).
Lesapproximations
(1.75)
et(1.76)
sont en bon accord avec les résultats exacts dans lerégime
de validité de laméthode,
à savoir lerégime
où le transfertd’énergie
à l’atomeE
f
-
E
i
est faible devantE
i
(voir
laFigure
1.3).
1.2
Considérations
expérimentales
Dans cette section
je
vais discuterquelques
aspects de la réalisationexpérimentale
dusystème,
y compris le calcul desparamètres
du modèle et l’effet du bruitexpérimental
et de l’émissionspontanée.
1.2.1
Réalisation
expérimentale
On
peut
réaliser lepotentiel
V(x,t)
avec un faisceau laser dont l’intensité est modulée dans le temps. Le laser est focalisé avec unedemi-largeur
du colégale
à 03C3(voir
laFigure
1.4).
La hauteur du col et lalongueur
deRayleigh
doivent être suffisammentgrandes
pourque le
plus
grand
nombre d’atomespossible
subissent unpotentiel
qui
ressemble à celui del’équation
(1.1).
Il faut que le laser doit être désaccordé sur le rouge pour que lepotentiel
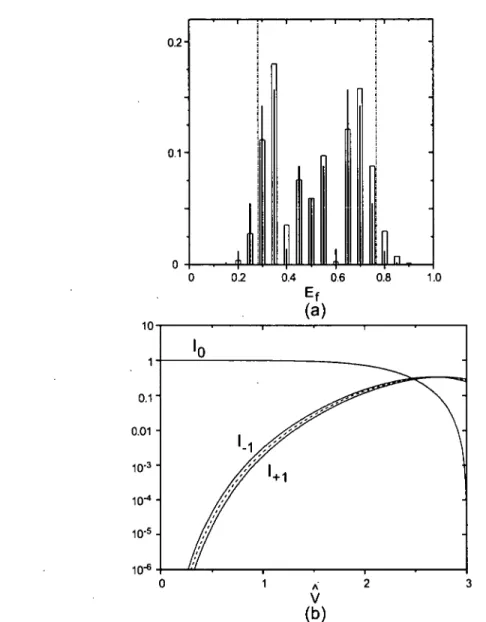
soitFIG. 1.3 -
(a)
Lespectre
exact(barres vides),
et les résultats de la méthode du réseau dephase
mince
(traits solides),
pour lesparamètres
=0.05,
= 6.0 et = 3.0. Les deuxlignes
enpointillé indiquent
les limites de larégion
permise.L’énergie
E
f
est
en unités dep
2
i
/m
(b)
Les
poids
exacts(lignes continues)
de la bande centraleI
0
et despremières
bandes latéralesI
±1
enfonction
deV,
pour = 6.0 et = 0.1. Les résultats de la méthode du réseau dephase
mince sont en
pointillé.
Les atomes
qui
ne passent pas au centre du col sontlégèrement
défléchis(voir
laFigure
1.5).
A cetélargissement
du faisceauatomique
s’ajoute
l’incertitude surl’impulsion
initiale desatomes. Pour avoir une idée de la distribution
d’impulsion
finale on peutappliquer
la méthodedu réseau de
phase
mince lelong
destrajectoires classiques non-perturbées,
c’est-à-dire lesFIG. 1.4 - Le schéma de
l’expérience
en trois dimensions.1.2.2 Calcul des
paramètres
du modèleLe modèle
théorique
se caractérise par les troisparamètres
sans dimensionV,
et,
définis par leséquations
(1.3).
Lesparamètres
et s’obtiennent directement à partir desquantités expérimentalement
mesurables 03C3, 03C9 et pi. Leparamètre ~
Vm/p
2
i
se calcule entermes du désaccord et de l’intensité de la lumière de la
façon
suivante.Le
potentiel
V s’écrit commeoù c est le coefficient de Clebsch-Gordon de la
transition,
03B4 < 0 est le désaccord enfréquence
entre le laser et la résonance
atomique,
et s est leparamètre
desaturation,
Dans cette
expression
0393 est le taux d’émissionspontanée,
et 03A9 est lafréquence
de Rabioù d dénote le
dipôle électrique.
03B5
0
estl’amplitude
duchamp électrique
qui
oscille à lafréquence optique
03C90. En utilisant le fait que lafréquence
de Rabi estpro-portionnelle
à la racine de l’intensité lumineuseI,
on trouvequ’à
grand
désaccord 03B4 » 0393 leFIG 15 - Les
trajectoires
classiques
d’atomes qui traversent lepotentzel
en absence demodu-lation. La
forme
dupotentiel
estindiquée
par deslignes
de contour. Lafigure
(a)
montre une section dufaisceau
laser transverse, et lafigure (b)
une sectionlongitudinale.
Leslignes
enpointillés
dans(b)
indique
la mode optiquelongitudinale.
Ce sont des contours où l’intensitéatteint une certaine
fraction
de sa valeur sur l’axe z.où
I
sat
est l’intensité desaturation,
définie comme l’intensité pourlaquelle
leparamètre
desaturation vaut un à désaccord nul. On
peut
la calculer de lafaçon
suivante. L’intensité lumineuse s’écrit en termes duchamp électrique
03B5(t)
commeoù
<···>
représente
la moyenne sur unepériode
duchamp.
En utilisantl’équation
(1.79),
eten déterminant la valeur du
dipôle électrique
d àpartir
du taux d’émissionspontanée
on trouve
On obtient la valeur du