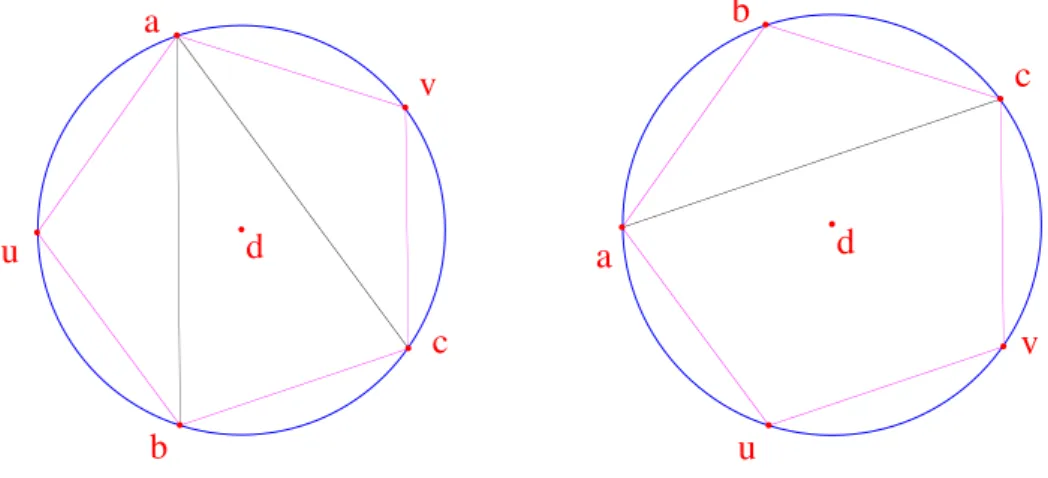
.
La question qui suit m’a ´ et´ e pos´ ee par Patrick Billot 1 . Elle ´ emanait semble-t-il d’un jury d’agr´ egation. La solution que j’en donne ici n’est peut- ˆ
Texte intégral
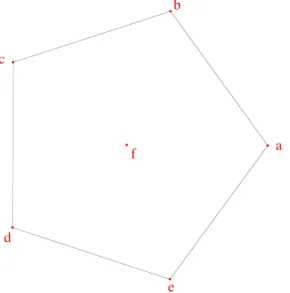
Figure


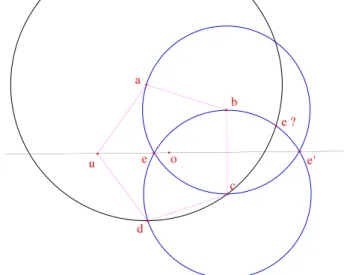
Documents relatifs
Colorie ²de ²la même ²couleur ²le$ étiquette$ ²qui ²désignent ²le
Des piles au magnésium équipent certains gilets de sauvetage, mais aussi
Das genau gleiche System entsteht durch die Reduktion der s~tmtlichen Geraden Uk'V~ (k g~nz). nicht zusammenh~tngende Bereieh heisse 9 ilL,.. fiber den Bereich
Die Bedeutung der Abel'sehen Abhandlung fiber die binomische Reihe. Die directe Behandlung und allgemeine LSsung der Aufgabe (III) finder man im
Le détail de ces pauses est communiqué à titre indicatif et peut faire l’objet de modifications sans préavis.. Pauses incluses dans nos forfaits restauration Pauses incluses dans
[r]
a) représenter graphiquement cette fonction affine pour x positif et inférieur à 6 (on prendra 2 cm pour unité sur l’axe des abscisses et 1 cm pour 100 unités sur l’axe
V´erifier que ces deux valeurs sont