INTRODUCTION AUX METHODES DE LA
MECANIQUE CELESTE
Introduction - Objectifs
•
Ce n’est pas un cours complet de mécanique céleste
ü
Présentation des outils de mécanique générale pour des
applications de la mécanique céleste
ü
Beaucoup d’applications en mécanique céleste ne nécessitent
pas ce formalisme
•
Présentations d’applications
ü
Importance de la modélisation des phénomènes de « chute
libre » et de « pendule » dans l’étude de la mécanique céleste
Plan du cours
•
C1-C2 : Introduction – problème à deux corps–
Formulation Hamiltonienne
•
PC1-PC2 : Trajectoires Képlériennes– Hamiltonien et
pendule harmonique
•
C3 : Problème à trois corps restreint
•
PC3 : Points de Lagrange L3/L4
•
C4-C5 : Résonances dans le système solaire
-500 AV JC : Les 7
“
objets
”
(Soleil, 5 planètes et la Lune) sont attachés
à 7 sphères concentriques transparentes
Modèle Aristotélicien
-384 -322 AV JC
•
Le philosophe Grec Aristote pense que les cieux
sont composés de 55 sphères cristallines
concentriques
ü
A chacune de ces sphères sont attachés des objets
célestes tournant à des vitesses différentes
Le système Ptolémaïque
150 après JC
•
La théorie qui prévalut en Europe
pendant de longs siècles été proposée
par Ptolémée dans son Almagest vers
150 après JC
ü
La terre est stationnaire au centre de
l
’
Univers
ü
Les étoiles sont piquées sur une large
sphère externe qui tourne rapidement
Mouvement rétrograde de Mars
•
Toutefois, pour décrire précisément le mouvement des planètes,
celles-ci ne décrivent pas des trajectoires exactement circulaires,
mais des épicycles
Cette théorie a
duré 1500 ans
Le modèle de Ptolémée
-150 av JC
•
De manière à rendre compte des observations, ce modèle nécessitait plus de
80 épicycles . Et la Terre devait être légèrement décalée …
Equant Déférent
Epicycle Terre
Centre
Calendrier Métonique
•
Cette incertitude sur le modèle n’empêchait pas ailleurs de connaître
précisément les cycles astronomiques. Le cycle dit de Méton ou cycle
métonique est un commun multiple approximatif des périodes orbitales de la
Terre et de la Lune.
ü Au bout de dix-neuf ans, les mêmes dates de l'année correspondent avec les mêmes phases
de la Lune. Cela est du au fait que dix-neuf années tropiques et 235 mois synodiques ne diffèrent que de deux heures
ü L'astronome grec Méton avait déjà remarqué cette coïncidence aux environs de -432,
comme le fit l'astronome chaldéen Kidinnu vers -380
•
Le cycle de Méton est employé dans les calendriers luni-solaires. En effet,
dans un calendrier luni-solaire typique, la plupart des années sont des années
lunaires de douze mois, mais sept des dix-neuf années possèdent un mois
Mécanisme d’Anticythère
La révolution Copernicienne
•
En 1543, Copernic formula un autre modèle d’Univers, dans lequel la terre
tournait autour du soleil, le modèle Héliocentrique.
•
Les orbites des planètes sont toujours circulaires, mais dans ce modèle il ny a
plus de problème de mouvement rétrograde.
Tycho Brahe
•
Tycho Brahe était un astronome danois au service du roi
Frédéric II de Danemark
ü
Il cherchait à combiner le système géocentrique de Ptolémée et
héliocentrique de Copernic.
•
Tycho Brahe établit le catalogue d'étoiles le plus complet et le
plus précis de son époque
Galilée
•
Invention de la lunette
astronomique
ü
Dessin de la Lune
ü
Phases de Vénus
ü
Satellites Galiléens
Johannes Kepler (1571 –1630)
•
Canoniquement, les fondements de la mécanique céleste
sont attribués à Kepler qui fonda ses fameuses trois lois
sur les observations de Tycho Brahe
Le modèle de Kepler du
système solaire incluait
les orbites terrestres dans
des sphères pouvant
Lois de Kepler (1)
•
Première loi de Kepler
ü
La trajectoire d’une planète est une ellipse dont l
’
un des
foyers est le soleil.
ü
Résout enfin le problème du mouvement rétrograde
apparent de Mars
Terre
Apoastre Périastre
•
Deuxième loi de Kepler dite
“loi des aires”
•
Une planète balaye des aires égales en des temps égaux
Loi de Kepler (3)
•
Troisième loi de Kepler (période)
ü
Le carré de la période d’une planète est
proportionnel au cube de sa distance au soleil
ü
T est la période, a le demi grand-axe de l’ellipse et
µ
Loi de Titius Bode (1766)
•
La loi de Titius-Bode, est une relation empirique entre les rayons des orbites des
planètes et du système solaire
•
R en UA. n est le numéro de la planète
•
Au début simple loi mnémonique, elle fut popularisée par Titius en 1766.
ü Triomphe de la découverte de Cérès et Uranus
•
Ne marche pas …mais des relations numériques remarquables
Rang Calcul Demi-grand axe Erreur absolue Erreur relative
Mercure 0 0,4 0,39 0,01 2,60% Vénus 1 0,7 0,72 0,02 2,80% Terre 2 1 1 0 0% Mars 3 1,6 1,52 0,08 5,30% Cérès 4 2,8 2,77 0,03 1,10% Jupiter 5 5,2 5,2 0 0% Saturne 6 10 9,54 0,46 4,80% Uranus 7 19,6 19,2 0,4 2,10% Neptune - - 30,1 - -Pluton 8 38,8 39,5 0,7 1,80% Sedna 9 77,2 505,8 1,2 1,60% (périhélie 76,1)
Le système solaire
Mouvements dans le système solaire
•
Le soleil et les planètes tournent chacun autour de leur axe.
Les centres de masse des planètes décrivent quant à eux une
ellipse dont l’un des foyers est le soleil.
•
Le Soleil et les planètes sont issus du même nuage
primordial en rotation,
ü
Les planètes, la plupart de leurs satellites, les astéroïdes, tournent
autour du soleil dans la même direction que leur rotation propre
par rapport aux étoiles, dans des orbites presque circulaires.
ü
Elles partagent le même plan, appelé écliptique (sauf Pluton 17
Le système solaire en perspective
•
Distances typiques
Distribution de moment angulaire
Planet Masse (x1027 kg) Periode (years) MA (gcm2s-1) Mercure 0.33 0.24 8.6x1045 Venus 4.87 0.61 1.9x1047 Terre 5.97 1 2.6x1047 Mars 0.64 1.88 3.4x1047 Jupiter 1898.8 11.86 1.9x1050 Saturne 568.41 9.5 7.8x1049 Uranus 86.97 19.31 1.7x1049 Neptune 102.85 30 2x10490.4% AM
99.2% AM
Axes de rotation des planètes
•
L’obliquité est l’angle de l’axe de otation des
Aux limites : données d’accélération Pioneer
Sanders & Verheijen 1998, tous types, toutes masses
Les Outils de la Mécanique Céleste
•
Principe de déterminisme
•
Equation de Newton
•
Exemple de systèmes mécaniques : chute libre
d’un corps, pendule, systèmes potentiels
•
Problème à deux corps
•
Equations de Lagrange, applications
•
Equations de Hamilton
Hypothèses
•
Les théories développées dans ce cours reposent
sur les postulats de la mécanique classique
ü
On ne considérera pas la mécanique non
newtonienne
•
Principe de déterminisme
ü
L’état d’un système (l’ensemble des positions et des
vitesses de ses points et leurs accélérations une date
quelconque) définit de manière unique le futur de
Théorème de Newton (1/2)
D'après le principe de déterminisme de Newton,
l'ensemble du mouvement d'un système est déterminé
par sa position initiale r(t
0)
∈
Net ses vitesses initiales
r(t
0)
∈
ND'après le principe de déterminisme de Newton,
(interprétation de Laplace) l'ensemble du mouvement
d'un système est déterminé par sa position initiale r(t
0)
∈
Net ses vitesses initiales
r(t
0)
∈
NIl existe donc une fonction
F :
N×
N×
N→
Ntelle que
:
r
= F(r, r,t) (E1)
Ce mouvement est défini de manière univoque (théorème
d'existence et d'unicité des équations différentielles)
Théorème de Newton (2/2)
•
L’équation (E1) permet de définir le mouvement de
manière nécessaire et suffisante
•
On a donc obtenu le théorème suivant :
•
En pratique, la forme de F est définie
empiriquement
(cf théorème de la dynamique
)
24/02/12 © ISAEDavid Mimoun
l’ensemble du mouvement. C’est ce qui explique son importance: cette ´equation a ´et´e
pos´ee `a la base de la m´ecanique par Newton. On l’appelle ´equation de Newton. On a
donc obtenu le th´eor`eme suivant:
Th´
eor`
eme: Soit (r(t
0) ∈ R
N) le vecteur position, ( ˙r(t
0) ∈ R
N) le vecteur vitesse d’un
syst`eme `a une date quelconque t
0alors le mouvement du syst`eme `a une date t > t
0est
d´ecrit de mani`ere univoque par l’´equation de Newton:
¨
r = F (r, ˙r, t).
(2)
Dans la pratique, la fonction F dans l’´equation (2) est d´etermin´ee empiriquement
pour chaque syst`eme m´ecanique concret. D’un point de vue math´ematique, la forme de
F d´efinit en soit le syst`eme.
2.1.3
Exemples de syst`
emes m´
ecaniques
La forme de F ´etant donn´ee par l’exp´erience pour chaque syst`eme m´ecanique, donnons
quelques exemples de syst`emes:
• Chute libre d’un corps sur la Terre
On appelle chute libre d’un corps sur la Terre , le mouvement libre d’un corps de
masse m, n´egligeable devant la masse de la Terre, dans le champs de gravit´e de la
Terre. En vertu d’une loi empirique ´etablie par Newton encore une fois, l’acc´el´eration
d’un objet en chute libre sur la Terre est inversement proportionnelle au carr´e de la
distance au centre de la Terre.
Exemples de systèmes dynamiques
•
La forme de F étant donnée par l’étude de
chaque système mécanique, nous allons donner
quelques exemples utiles en mécanique céleste
ü
Chute libre d’un corps (problème à deux corps)
ü
Pendule simple
•
On va tout d’abord retrouver rapidement les lois
Chute libre (problème à 1 corps)
•
On appelle « chute libre » d’un corps le mouvement d’un point
mécanique de masse m dans un champ de gravité
.
En vertu d’une loi
empirique l’accélération d’un objet en chute libre est inversement
proportionnelle au carré de la distance au centre de masse
•
F
= −
µ
.
m.
r
2.
u
Si l'on appelle E
3l'espace euclidien des configurations (ie espace
des positions) et r la fonction r(t):
→ E
3qui décrit son mouvement
r
= OM
u
=
OM
OM
Chute libre (Rappels)
•
On ne considère que la force de gravitation sur
le système
ü
L’expression du moment cinétique H en O de M est
la suivante
ü
D’où sa dérivée
H
= m.OM
∧ ∂
.OM
∂t
R= mr ∧ r
R∂.H
∂t
= mr ∧ r + mr ∧ r
= m.OM
∧
F
=
0
Chute libre d’un corps (Rappel)
•
Donc c.à.d le mouvement est plan
•
En coordonnées polaires, il vient :
H
= m.r ∧ r = Cste
v(M )
R=
r
r
θ
⎛
⎝⎜
⎞
⎠⎟
a(M )
=
r
− r
θ
2
⎛
⎜
⎞
⎟
Lois de Kepler : loi des Aires
•
Si l’on reprend l’équation fondamentale de la dynamique, il vient :
•
D
’
où
•
Pendant un temps dt
ü
L’aire parcourue est
ü
D’où la « loi des aires »
F
= m.a = m
r
− r
θ
2r
θ + 2r. θ
⎛
⎝
⎜
⎞
⎠
⎟
R= −G.
m.M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
Rr
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
⇒ r
θ
+ 2r
θ
= 0 ⇒ r
2θ
= C
dA
=
1
2
r.(rd
θ
)
A
t 1→t2=
r.(r
θ
)
2
t2∫
dt
= C(t
2− t
1)
dA
d
θ
r
rd
θ
(Constante)
Equation du mouvement
•
Equation fondamentale + loi des aires
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
= −
1
u
2.
du
dt
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
= −
1
u
2.
du
dt
= −
C
d
θ
.dt.
du
dt
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(2)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
=
−1
u
2.
du
dt
=
−C
d
θ
.dt.
du
dt
= −C.
du
d
θ
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(2)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
=
−1
u
2.
du
dt
=
−C
d
θ
.dt.
du
dt
= −C.
du
d
θ
r
=
d
r
dt
=
d
r
d
θ
d
θ
dt
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(2)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
=
−1
u
2.
du
dt
=
−C
d
θ
.dt.
du
dt
= −C.
du
d
θ
r
=
d
r
dt
=
d
r
d
θ
d
θ
dt
=
d
d
θ
(
−C.
du
d
θ
)
d
θ
dt
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(2)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
=
−1
u
2.
du
dt
=
−C
d
θ
.dt.
du
dt
= −C.
du
d
θ
r
=
d
r
dt
=
d
r
d
θ
d
θ
dt
=
d
d
θ
(−C.
du
d
θ
)
d
θ
dt
= −C
d
2u
d
θ
2.
d
θ
dt
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(2)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
=
−1
u
2.
du
dt
=
−C
d
θ
.dt.
du
dt
= −C.
du
d
θ
r
=
d
r
dt
=
d
r
d
θ
d
θ
dt
=
d
d
θ
(−C.
du
d
θ
)
d
θ
dt
= −C
d
2u
d
θ
2.
d
θ
dt
Equation du mouvement
•
Equation fondamentale + loi des aires
(1)
(2)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
=
dr
dt
=
d
dt
(
1
u
)
=
−1
u
2.
du
dt
=
−C
d
θ
.dt.
du
dt
= −C.
du
d
θ
r
=
d
r
dt
=
d
r
d
θ
d
θ
dt
=
d
d
θ
(−C.
du
d
θ
)
d
θ
dt
= −C
d
2u
d
θ
2.
d
θ
dt
r
= −C
d
2u
.Cu
2r
= −C
2u
2d
2u
Equation du mouvement
•
Equation fondamentale + loi des aires
•
(3)
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
θ
2= r. Cu
( )
2 2=
1
u
C
2u
4= C
2u
3Equation du mouvement
•
Equation fondamentale + loi des aires
•
(3)
•
(E1) devient
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
θ
2= r. Cu
( )
2 2=
1
u
C
2u
4= C
2u
3r− r
θ
2= −GMu
2Equation du mouvement
•
Equation fondamentale + loi des aires
•
(3)
•
(E1) devient
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
θ
2= r. Cu
( )
2 2=
1
u
C
2u
4= C
2u
3r− r
θ
2= −GMu
2d
2u
Equation du mouvement
•
Equation fondamentale + loi des aires
•
(3)
•
(E1) devient
(E2) r
2.
θ
= C
(E1)
r
− r
θ
2r
θ
+ 2 r.
θ
⎛
⎝⎜
⎞
⎠⎟
= −G.
M
r
21
0
⎛
⎝⎜
⎞
⎠⎟
u
=
1
r
r
θ
2= r. Cu
( )
2 2=
1
u
C
2u
4= C
2u
3r− r
θ
2= −GMu
2−C
2u
2d
2u
d
θ
2− C
2u
3= −GMu
2µ
Equation du mouvement - 1ère loi
•
Avec en passant par le changement de variables
•
Equation d
’
une conique constantes
d
’
intégration
ü
Si e=0 , il s
’
agit d
’
un cercle
ü
Si e<1 , il s
’
agit d
’
une ellipse
r
=
p
(1
+ ecos(
θ
−
θ
0))
1
ère
loi de Kepler
p
=
C
2µ
e,
θ
0u
=
1
r
3 RAPPELS DE MÉCANIQUE
F
IGURE
27 –
Les coniques
O
F
F
Ellipse
ae
!
M
r
b
a
P
Péricentre ApocentreA
!
0 Direction RéférenceF
IGURE
28 –
Géométrie des ellipses
3.3.2 Géométrie de l’ellipse
On rappelera un certain nombre de relations importantes pour la géométrie des ellipses :
⇢
a
2= b
2+ c
2e =
ac⇢
p = a 1
e
2b = a
p
1
e
2⇢
r
p= a (1
e) =
1+epr
a= a (1 + e) =
1 epavec les notations de la figure
28
, on peut écrire :
r =
p
(1 + e cos(✓
✓
0))
==
a 1
e
2
(1 + e cos(✓
✓
0))
(24)
24/02/12 © ISAEDavid Mimoun
Rappel: Ellipses
•
a demi grand axe, 2a = AP.
•
A est l'apogée, point le plus éloigné du foyer F.
•
P est le périgée, point le plus rapproché du foyer F.
•
b demi petit axe.
Cas particulier d’une ellipse - 3è loi
•
Appelons T la période mise pour parcourir une orbite
d’aire S
•
D’après la loi des aires on a
•
Les relations dans les ellipses donnent
r
2.
θ
= C
r
2θ
dt
O T∫
= C.T
r
2θ
dt
O T∫
= 2.S = C.T = 2.
π
.a.b
C
2=
µ
a 1
(
− e
2)
⇒ C
2.T
2= 4.
π
2.a
2.b
2Chute libre d’un corps
•
•
On retrouve là un résultat habituel, que l’on peut appliquer
également au cas du pendule.
On note au passage que si l'on introduit la fonction énergie potentielle
U :
3→ telle que U(r) = −m
µ
r
alors l'équation r
= −
µ
r
r
3(E3) peut
être mise sous la forme habituelle des systèmes potentiels:
mr
= - ∂
U
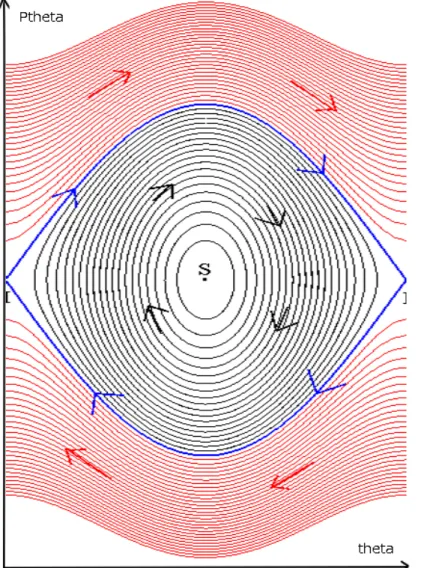
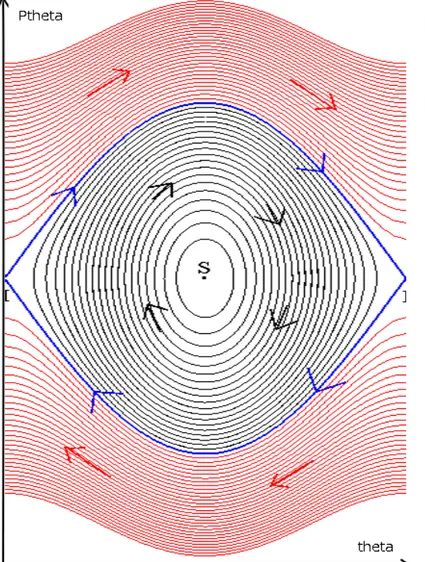
Le pendule simple
•
Pendule de longueur l, point massique de masse m
ü
Son mouvement est paramétré par un seul angle θ
∈[0,2π]
ü
L
’
espace de configuration du système est de dimension 1
ü
Projeter (E3) sur la droite de direction u
θpermet de retrouver
θ
u
r
Systèmes potentiels
•
•
Le mouvement de n points de masses respectives m
1,m
2, …m
ndans
un champ d’énergie potentielle U est régi par le système d’équations
différentielles
•
C’est ce que l’on appelle un
système potentiel
: la plupart des
systèmes mécaniques utilisés en mécanique céleste sont de cette
Soit E
3n= E
3× ...× E
3l'espace de configuration d'un système de n points
dans un espace Euclidien E
3. Soit U : E
3n→ une fonction différentiable
et m
1, m
2,...m
ndes nombres positifs
m
ir
i= −
∂U
Problème à deux corps, à trois corps
•
Problème à deux corps
•
Problème à trois corps
U
= −
m
1m
2r
1− r
224/02/12 © ISAEDavid Mimoun
Problème à deux corps
•
M
1et M
2sont deux corps de masses m
1et m
2, de centre d'inertie G.
•
Pour un système isolé, le centre d'inertie G a un mouvement
rectiligne uniforme.
ü
Le principe de relativité de Galilée permet de choisir G comme origine d'un
repère inertiel R
G.
ü
En général on préfère un des corps….
4 PROBLÈME À DEUX CORPS
4 Problème à deux corps
Le problème à deux corps s’intéresse à l’interaction de deux corps massiques se mouvant sous l’influence d’une attraction mutuelle. Il s’agit du problème techniquement le plus simple que l’on puisse envisager en mécanique céleste, avec des équations dynamiques qui sont in-tégrables en fonction du temps. La répartition de masse dans le Système Solaire fait que l’on peut utiliser l’approximation à deux corps dans un nombre très important de cas, le plus souvent quand un corps de faible masse orbite autour d’un corps ayant une masse plus importante (Soleil et Planète, Jupiter et ses satellites ...)
Bien évidemment, c’est dans l’approximation à deux corps que l’on démontre le mouvement elliptique des planètes, en une application simple des lois de la dynamique de Newton.
4.1 Approche Képlérienne
M1 et M2 sont les deux corps de masses m1et m2, de centre d’inertie G. Pour un système
isolé, le centre d’inertie G a un mouvement rectiligne uniforme. Le principe de relativité de Galilée permet de choisir G comme origine d’un repére inertiel RG. En général on préfère pour
simplifier choisir comme origine du système de référence un des deux corps.
O
!
!1 M1, m1 M2, m2 !2 !G GFIGURE33 –problème à deux corps
On note
⌦r =M1M⇥2 ⌦r1 =M1⇥G ⌦r2 =GM⇥2 (105)
Si l’on applique le principe fondamental de la dynamique : m1d 2OM⇥ 1 dt2 = ⌦f12 ⇤ ⌃ ⇧ d2 ⇥ ⇥⇥ d2OG⇥
4 PROBLÈME À DEUX CORPS
4 Problème à deux corps
Le problème à deux corps s’intéresse à l’interaction de deux corps massiques se mouvant sous l’influence d’une attraction mutuelle. Il s’agit du problème techniquement le plus simple que l’on puisse envisager en mécanique céleste, avec des équations dynamiques qui sont in-tégrables en fonction du temps. La répartition de masse dans le Système Solaire fait que l’on peut utiliser l’approximation à deux corps dans un nombre très important de cas, le plus souvent quand un corps de faible masse orbite autour d’un corps ayant une masse plus importante (Soleil et Planète, Jupiter et ses satellites ...)
Bien évidemment, c’est dans l’approximation à deux corps que l’on démontre le mouvement elliptique des planètes, en une application simple des lois de la dynamique de Newton.
4.1 Approche Képlérienne
M1 et M2 sont les deux corps de masses m1 et m2, de centre d’inertie G. Pour un système
isolé, le centre d’inertie G a un mouvement rectiligne uniforme. Le principe de relativité de Galilée permet de choisir G comme origine d’un repére inertiel RG. En général on préfère pour
simplifier choisir comme origine du système de référence un des deux corps.
O
!
!
1M
1, m
1M
2, m
2!
2!
GG
FIGURE 33 – problème à deux corps
On note
⌦r = M1M⇥2 ⌦r1 = M1⇥G ⌦r2 = GM⇥2 (105)
Si l’on applique le principe fondamental de la dynamique : m1d 2OM⇥ 1 dt2 = ⌦f12 m2d 2OM⇥ 2 dt2 = ⌦f21 ⇤ ⌃ ⇧ ⌃ ⌅ d2 dt2 m1 ⇥ OM1 + m2OM⇥2 ⇥ = (m1 + m1) d 2OG⇥ dt2 = ⌦f12 + ⌦f21 = ⌦0 (106)
24/02/12 © ISAEDavid Mimoun
Problème des 2 corps
•
Equations du mouvement
ü
Principe fondamental de la dynamique
ü
R
Gest galiléen
ü
Tout se passe comme si chaque particule matérielle était en
mouvement dans un champ de force centrale, où le corps
central est situé au barycentre des deux masses.
donc
4 PROBLÈME À DEUX CORPS
4 Problème à deux corps
Le problème à deux corps s’intéresse à l’interaction de deux corps massiques se mouvant
sous l’influence d’une attraction mutuelle. Il s’agit du problème techniquement le plus simple
que l’on puisse envisager en mécanique céleste, avec des équations dynamiques qui sont
in-tégrables en fonction du temps. La répartition de masse dans le Système Solaire fait que l’on
peut utiliser l’approximation à deux corps dans un nombre très important de cas, le plus souvent
quand un corps de faible masse orbite autour d’un corps ayant une masse plus importante (Soleil
et Planète, Jupiter et ses satellites ...)
Bien évidemment, c’est dans l’approximation à deux corps que l’on démontre le mouvement
elliptique des planètes, en une application simple des lois de la dynamique de Newton.
4.1 Approche Képlérienne
M
1et M
2sont les deux corps de masses m
1et m
2, de centre d’inertie G. Pour un système
isolé, le centre d’inertie G a un mouvement rectiligne uniforme. Le principe de relativité de
Galilée permet de choisir G comme origine d’un repére inertiel R
G. En général on préfère pour
simplifier choisir comme origine du système de référence un des deux corps.
O
!
!
1M
1, m
1M
2, m
2!
2!
GG
F
IGURE33 –
problème à deux corps
On note
⌦r =
M
1M
⇥
2⌦r
1=
M
1⇥
G ⌦r
2=
GM
⇥
2(105)
Si l’on applique le principe fondamental de la dynamique :
m
1d 2OM⇥ 1 dt2= ⌦
f
12m
2d 2OM⇥ 2 dt2= ⌦
f
21⇤
⌃
⇧
⌃
⌅
d
2dt
2m
1⇥
OM
1+ m
2OM
⇥
2⇥
= (m
1+ m
1)
d
2OG
⇥
dt
2= ⌦
f
12+ ⌦
f
21= ⌦0
(106)
Eléments de Mécanique Céleste V0.9
47
ISAE - SUPAERO
4 PROBLÈME À DEUX CORPS
RG est galiléen donc
m2d 2GM⇤ 2 dt2 = ⌦f21 (107) d’où m1m2 m1 + m2 d2M1M⇤2 dt2 = m1m2 m1 + m2 d2⇤r dt2 = ⌦f21 (108)
Tout se passe comme si un référentiel d’origine M1, de directions fixes par rapport au référentiel
d’origine O était galiléen pour le mobile M2.
On appelle µ = m1m2
m1+m2 la masse réduite. Si m2 ⇥ m1 alors le référentiel barycentrique se
confond avec M1.
Tout se passe comme si le mouvement de chaque particule matérielle était en mouvement dans un champ de force centrale, où le corps central est situé au barycentre des deux masses. On s’est donc ainsi ramené au cas traité au (3.3), pour chacune des particules considérées.
4.2 L’orbite dans l’espace
A un instant t, la trajectoire est complètement déterminée par trois coordonnées de position et trois coordonnées de vitesse. Le vecteur d’état comprend donc 6 paramètres. Dans le cas du mouvement Képlérien, il est plus adapté de décrire la trajectoire du mobile en fonction des caractéristiques géométriques de la conique décrite.
La trajectoire d’un satellite est décrite dans un repère galiléen (non tournant) centré au centre de gravité du corps autour duquel il orbite :
– La Terre pour les satellites terrestre
– Le Soleil pour les sondes interplanétaires durant leur croisière – Mars pour les sondes martiennes, etc ...
On utilisera donc :
– Un repère géocentrique équatorial pour décrire le mouvement des satellites terrestre – Un repère héliocentrique écliptique pour celui des sondes interplanétaires
4.3 Rappels sur les coniques
Ce paragraphe rappelle les principales propriétés caractéristiques des coniques, utiles pour comprendre ce qui suit.
4 PROBLÈME À DEUX CORPS RG est galiléen donc
m2d 2GM⇤ 2 dt2 = ⌦f21 (107) d’où m1m2 m1 + m2 d2M1M⇤2 dt2 = m1m2 m1 + m2 d2⇤r dt2 = ⌦f21 (108)
Tout se passe comme si un référentiel d’origine M1, de directions fixes par rapport au référentiel
d’origine O était galiléen pour le mobile M2.
On appelle µ = m1m2
m1+m2 la masse réduite. Si m2 ⇥ m1 alors le référentiel barycentrique se
confond avec M1.
Tout se passe comme si le mouvement de chaque particule matérielle était en mouvement dans un champ de force centrale, où le corps central est situé au barycentre des deux masses. On s’est donc ainsi ramené au cas traité au (3.3), pour chacune des particules considérées.
4.2 L’orbite dans l’espace
A un instant t, la trajectoire est complètement déterminée par trois coordonnées de position et trois coordonnées de vitesse. Le vecteur d’état comprend donc 6 paramètres. Dans le cas du mouvement Képlérien, il est plus adapté de décrire la trajectoire du mobile en fonction des caractéristiques géométriques de la conique décrite.
La trajectoire d’un satellite est décrite dans un repère galiléen (non tournant) centré au centre de gravité du corps autour duquel il orbite :
– La Terre pour les satellites terrestre
– Le Soleil pour les sondes interplanétaires durant leur croisière – Mars pour les sondes martiennes, etc ...
On utilisera donc :
– Un repère géocentrique équatorial pour décrire le mouvement des satellites terrestre – Un repère héliocentrique écliptique pour celui des sondes interplanétaires
4.3 Rappels sur les coniques
Ce paragraphe rappelle les principales propriétés caractéristiques des coniques, utiles pour comprendre ce qui suit.
– a le demi grand axe, 2a = A
– A est l’apogée , point le plus éloigné du foyer O.A – P est le périgée , point le plus rapproché du foyer O – b demi petit axe, b = IB, I est le centre.
Problème à deux corps
•
On appelle souvent la masse réduite
•
Si m
2
<<
m
1
alors le référentiel barycentrique se
confond avec M
1
µ
=
m
1m
2Problème à deux corps
Problème à deux corps
•
Orbites elliptiques
Problème à deux corps
Repères de l’espace , du temps et autres
hypothèses
Repères et coordonnées
•
On assimile une particule matérielle à un point de l’espace
physique, auquel on associe un scalaire positif appelé masse du
point. On parle alors aussi de point matériel.
•
On assimile un système matériel à un ensemble de points
matériels. Ces points sont en interaction (ou soumis à des
forces). La force agissant sur un point est représentée par un
vecteur lié à ce point, dirigé dans le sens de la force et de
module égal à son intensité.
•
La signification physique de la masse et des forces est donnée
Eléments orbitaux
•
A un instant t, une trajectoire est complètement
déterminée par trois coordonnées de position et
trois coordonnées de vitesse.
ü
Le vecteur d’état comprend donc 6 paramètres.
ü
Dans le cas du mouvement Képlérien, il est plus
« adapté » de décrire la trajectoire du mobile en
fonction des caractéristiques géométriques de la
conique décrite.
Eléments orbitaux
•
La trajectoire d
’
un satellite est décrite dans un repère
galiléen (non tournant) centré au centre de gravité du
corps autour duquel il orbite
ü
La Terre pour les satellites terrestres
ü
Le Soleil pour les sondes interplanétaires durant leur croisière
ü
Mars pour les sondes martiennes, etc ….
•
On utilisera donc
Repères usuels
•
Repère géocentrique tournant (lié à la Terre)
•
Repère géocentrique équatorial non tournant
•
Repère géocentrique écliptique non tournant
Repérage d
’
un satellite dans l
’
espace
•
Plan Equatorial - Ecliptique - Point vernal
Nœud
ascendant de
l’écliptique
ε
Point vernal
•
Par définition, le soleil se trouve toujours sur le
Point Vernal
•
Le point vernal ne définit pas une direction strictement
inertielle, en effet
ü
La Terre n’est pas un corps sphérique, l’attraction
luni-solaire, induit une nutation et une précession de son axe de
rotation
ü
Les résonances des planètes du système solaire font varier
l’inclinaison de l’écliptique
•
On peut donc définir :
Coordonnées Ecliptiques
Eté (N)
Hiver
(N)
•
Géocentriques
•
Héliocentriques
Coordonnées du soleil
•
Le point vernal est le point nodal ascendant du soleil,
càd la direction du soleil au printemps
Printemps Eté
Automne Hiver
α
0h
6h
12h
18h
δ
0°
23°27’
0°
-23°27’
λ
0°
90°
180°
270°
Plan de
référence :
équateur
Plan de
référence :
-
a : demi grand axe de l
’
orbite
-
e : excentricité de l
’
orbite
-
i : inclinaison de l
’
orbite
-
Ω: argument du nœud ascendant
-
ω : argument du périgée
-
t0 : instant de passage au périgée (ou τ)
-
ϒ: point vernal (direction du soleil le 21 mars à 0h)
Ω
ω
ϒ
i
A
N
S,T
Eléments orbitaux
Plan orbital
Equateur (orbite terrestre)
Ecliptique (orbite solaire)
Conventions
-
Angles positifs dans le sens direct
-
L
’
orbite est décrite dans le sens direct
-
Le nœud est le nœud ascendant
-
0°<i<180° et si i>90°, l
’
orbite est
rétrograde
Elements orbitaux
•
a : demi grand-axe de l
’
orbite
ü
p dans le cas d’parabole
ü
Définit l
’
énergie mécanique liée à l
’
orbite
•
e excentricité
Excentricité = c/a
e = 0.75
Eléments orbitaux
Eléments orbitaux
•
ω : argument du périgée
ü
C
’
est la position angulaire , dans le plan d
’
orbite, du périgée
par rapport au nœud ascendant
ü
Il est orienté par la normale à l
’
orbite
•
t
0
ou τ définit l
’
instant de passage au périgée
•
La connaissance de a et de t0 (ou τ) permet de
déterminer l’anomalie moyenne M, et donc l
’
anomalie
Mouvement de la Terre
•
Le terme "Rotation" se réfère au mouvement d’un objet autour
de son axe propre, tandis que le terme « révolution » se réfère au
mouvement de son centre de masse autour d’un autre objet.
•
La rotation de la Terre autour de son axe par rapport aux étoiles
a une période de 86164 secondes, soit 236s moins que le jour
solaire moyen
ü
Son inclinaison par rapport au plan de l’écliptique est de 23,45°
•
La révolution de la Terre autour du soleil dure 365,25 jours
Mouvement de la Terre autour du
soleil
•
La Terre parcourt son orbite en 365 jours, 6 heures, 9 minutes (par
rapport aux étoile) sa vitesse varie entre 29.29 et 30.29 km/s.
ü
Les 6 heures, 9 minutes et quelques donnent un jour supplémentaire tous les
quatre ans.
Tilt de 23,4° Nord Ecliptique
Equinoxe de printemps Solstice d'été
Soleil au plus haut dans l'hémisphère Nord ETE
Solstice d'hiver
Soleil au plus bas dans l'hémisphère Sud HIVER
24/02/12 © ISAEDavid Mimoun
La rotation de la Terre
•
Par rapport aux étoiles, la Terre fait
un tour sur elle même en 86164s
(Jour Sidéral)
•
Après un jour, le mouvement de la
Terre sur son orbite autour du
Soleil décale le moment où il est
midi en un méridien donné.
•
Le jour solaire moyen de 24 h =
86400 secondes, est le temps
moyen, au cours de l'année qui
sépare deux passages consécutifs
du soleil au zénith d’un méridien
donné.
Impression LeKiosque http://www.lekiosque.fr/reader.print.html?pages=1&l=http://l...
Impression LeKiosque http://www.lekiosque.fr/reader.print.html?pages=1&l=http://l...
1 sur 1 21/02/12 12:54
La rotation de la Terre
•
Analemne (trajectoire du Soleil dans le ciel)
•
Jour solaire vrai
ü
Deux passages au zénith
•
Jour solaire moyen
ü
Deux passages au zénith corrigé des variations de l’orbite terrestre : 86400 s
© ISAEDavid Mimoun
Impression LeKiosque http://www.lekiosque.fr/reader.print.html?pages=1&l=http://l...
Précession de l’axe de la Terre
•
Les forces associées à la rotation
de la Terre impliquent une
déformation à l’équateur (bourrelet
équatorial)
ü
Impact des forces de marée (Lune,
soleil)
ü
Couple gyroscopique
•
Précession de l’axe de la Terre de
période 26000 ans
Pôle Nord