La corrélation appliquée dans un contexte bayésien

LA CORRÉLATION APPLIQUEE DANS UN

C O N T E X T E BAYÉSIEN

Mémoire présenté

à la Faculté des études supérieures de l'Université Laval

dans le cadre du programme de maîtrise en statistique

pour l'obtention du grade de Maître es sciences (M.Sc.)

FACULTE DES SCIENCES ET DE GENIE

UNIVERSITÉ LAVAL

QUÉBEC

2010

Résumé

Bien que largement utilisée, la corrélation n'est pas souvent abordée dans un contexte bayésien. À l'aide de formules simples, on calcule ici la corrélation de Pearson entre un paramètre 9 et son estimation bayésienne ou par la méthode du maximum de vraisem-blance. Ceci nous permet alors d'examiner le comportement de la corrélation de Pearson selon la taille de l'échantillon et le choix des paramètres de la loi a priori. On compare ensuite son comportement avec celui des corrélations de Spearman, de Kendall et de Blomqvist obtenues à l'aide de simulations effectuées avec le logiciel R. Plusieurs cas sont considérés faisant notamment intervenir des lois conjuguées.

Voici mes remerciements les plus sincères à tous ceux qui m'ont aidée et encouragée, chacun à leur façon.

Je voudrais tout d'abord remercier mes co-directeurs Christian Genest et Claude Bélisle, tous deux professeurs au Département de mathématiques et de statistique de l'Université Laval. Merci Christian de m'avoir présenté ce projet avec votre passion débordante et contagieuse. J'ai appris mille et une choses grâce à votre patience et votre générosité. Vos nombreux encouragements m'ont permis de persévérer dans ce projet tout en me dépassant. Merci Claude d'avoir embarqué dans notre projet. Vous m'avez permis d'améliorer la qualité de mon travail grâce à vos nombreuses corrections et suggestions. Vos idées d'exemples pathologiques ont également beaucoup contribué à ma compréhension du sujet.

Un merci plus personnel à mon conjoint Alexandre qui a su me soutenir et m'encou-rager tout au long de mes études en statistique. Tu m'as toujours écoutée attentivement et répété que j'étais la meilleure, malgré le fait que tu n'aies jamais compris de quoi je parlais. De plus, je veux profiter de ce moment pour te remercier de m'avoir offert Batman pour me tenir compagnie durant mes nombreuses heures de travail à la maison. Merci également à ma mère qui m'a toujours encouragée et soutenue à sa façon. Qui d'autre m'aurait laissé refaire mes livres de mathématiques en plein été à l'âge de 7 ans? Un dernier merci pour Shany qui a bien voulu utiliser ses talents de graphiste pour me construire une figure sur mesure.

Finalement, je tiens à remercier encore une fois Christian Genest et Claude Bélisle pour m'avoir soutenue financièrement tout au long de ma maîtrise, ce qui m'a permis de profiter pleinement de mes études au deuxième cycle. Je tiens également à dire merci au Département de mathématiques et de statistique pour tout le soutien financier qu'il m'a apporté, tant sous la forme de bourses ou de contrats de travail. Vous m'avez permis de vivre de belles expériences. À tous ces gens, merci de m'avoir aidée à réaliser mon rêve.

A Xavier, une pensée toute spéciale pour ton premier anniversaire.

D'un point de vue strictement aérodynamique, le bourdon ne devrait pas être capable de voler, mais il ne le sait pas, alors il vole quand même. -Mary Kay

Ash-R é s u m é ii

A v a n t - P r o p o s iii

Table des m a t i è r e s vi

Table des figures x

1 I n t r o d u c t i o n ]

2 La corrélation d a n s un c a d r e bayésien 3 2.1 Rapide survol de la notion de copule

2.2 Définitions et propriétés de divers coefficients de corrélation 2.2.1 Le r de Pearson

2.2.2 Le p Spearman

2.2.3 Le r de Kendall C 2.2.4 Le fi de Blomqvist

2.3 Brève introduction à l'inférence bayésienne 8 2.4 Corrélation de Pearson entre un paramètre et son estimateur

2.5 Corrélation de Pearson entre l'estimateur de Bayes et un estimateur sans

biais 13 2.6 Concept d'estimateur à corrélation maximale 15

3 Applications d a n s u n c o n t e x t e d e lois conjuguées continues 16 3.1 Normale-Normale avec précision connue

3.1.1 Calcul des corrélations r, p et T 18 3.2 Normale-Gamma avec moyenne connue 21

3.2.1 Calcul des corrélations r, p, r et /5 mesurées entre le paramètre 6

et l'estimateur du maximum de vraisemblance 22 3.2.2 Calcul des corrélations r, p, T et (3 mesurées entre le paramètre 6

et l'estimateur de Bayes 25

3.3 Uniforme-Pareto 2s*

VI

3.3.2 Calcul du p de Spearman il 3.3.3 Calcul du r de Kendall 34 3.3.4 Calcul du 0 de Blomqvist 36

3.4 Gamma-Gamma 38 3.4.1 Calcul du r de Pearson mesuré entre le paramètre 9 et l'estimateur

du maximum de vraisemblance

3.4.2 Calcul du p de Spearman, du r de Kendall et du 8 de Blomqvist mesurés entre le paramètre 9 et l'estimateur du maximum de vraisemblance

3.4.3 Calcul du r de Pearson, du p de Spearman, du r de Kendall et du 8 de Blomqvist mesurés entre le paramètre 9 et l'estimateur de Bayes

4 Applications d a n s u n c o n t e x t e de lois conjuguées avec u n e loi discrète 50 4.1 Lois Conjuguées : Bernoulli-Bêta

4.1.1 Calcul du r de Pearson 52 4.1.2 Calcul du p de Spearman, du r de Kendall et du 3 de Blomqvist

4.2 Lois Conjuguées : Poisson-Gamma 57 4.2.1 Calcul du r de Pearson 59 4.2.2 Calcul du p de Spearman 61 4.2.3 Calcul du r de Kendall 64 4.2.4 Calcul du 8 de Blomqvist 65 4.3 Lois Conjuguées : Géométrique-Bêta 68

4.3.1 Calcul du r de Pearson 69 4.3.2 Calcul du p de Spearman

4.3.3 Calcul du r de Kendall 4.3.4 Calcul du 0 de Blomqvist

5 Exemples pathologiques 78

5.1 Premier exemple pathologique 7X

5.2 Deuxième exemple pathologique 80

6 Conclusion 84

Bibliographie 86

A E x e m p l e de p r o g r a m m a t i o n R 87

2.1 Représentation du plan xy tel que divisé par Blomqvist v

3.1 Illustration des différentes corrélations en fonction de la taille

d'échan-tillon n dans un contexte Normale-Normale 1 !) 3.2 Illustration des différentes corrélations en fonction de la taille

d'échan-tillon n selon la précision a priori dans un contexte Normale-Normale . 20 3.3 Illustration des différentes corrélations en fonction de la taille

d'échan-tillon n selon la précision des observations dans un contexte

Normale-Normale 2(1 3.4 Illustration des corrélations entre le paramètre de variance et son

estima-tion à vraisemblance maximale telles qu 'observées dans des échantillons

de taille n dans un contexte Normale-Gamma 23 3.5 Illustration des corrélations entre le paramètre de variance et son

es-timation à vraisemblance maximale en fonction de la moyenne p telles qu 'observées dans des échantillons de taille 50 dans un contexte

Normale-Gamma 23 3.6 Illustration des corrélations entre le paramètre de variance et son

esti-mation à vraisemblance maximale en fonction du paramètre d'échelle 8 telles qu'observées dans des échantillons de taille 50 dans un contexte

Normale-Gamma 24 3.7 Illustration des corrélations entre le paramètre de variance et son

esti-mation à vraisemblance maximale en fonction du paramètre de forme a telles qu'observées dans des échantillons de taille 50 dans un contexte

Normale-Gamma 24 3.8 Illustration des corrélations entre le paramètre de variance et son

estima-tion de Bayes telles qu'observées dans des échantillons de taille n dans

un contexte Normale-Gamma 20 3.9 Illustration des corrélations entre le paramètre de variance et son

esti-mation de Bayes en fonction de la moyenne p telles qu'observées dans

vm

3.10 Illustration des corrélations entre le paramètre de \~ariance et son esti-mation de Bayes en fonction du paramètre de forme a telles qu'observées

dans des échantillons de taille 50 dans un contexte Normale-Gamma . . 27 3.11 Illustration des corrélations entre le paramètre de variance et son

esti-mation de Bayes en fonction du paramètre d'échelle 8 telles qu'observées

dans des échantillons de taille 50 dans un contexte Normale-Gamma . . 27 3.12 Corrélation r(0, 6MV(X-)) en fonction du paramètre a selon la taille

d'échan-tillon n dans un contexte Uniforme-Pareto

3.13 Corrélation r(<?, 5(X)) en fonction de la taille d'échantillon n selon

l'es-timateur et le paramètre a dans un contexte Uniforme-Pareto 32 3.14 Corrélation p(0,(5,(X)) en fonction de la taille d'échantillon n dans un

contexte Uniforme-Pareto 33 3.15 Corrélation pi&, <$„(X)) en fonction du paramètre de localisation xQ selon

la taille d'échantillon n dans un contexte Uniforme-Pareto 33 3.16 Corrélation p(#,cV,,(X)) en fonction du paramètre de forme a selon la

taille d'échantillon n dans un contexte Uniforme-Pareto 34 3.17 Corrélation r(<?, <5*(X)) en fonction de la taille d'échantillon n dans un

contexte Uniforme-Pareto 35 3.18 Corrélation r(0, <J*(X)) en fonction du paramètre de localisation x0 selon

la taille d'échantillon n dans un contexte Uniforme-Pareto 35 3.19 Corrélation r(^, <5*(X)) en fonction du paramètre de forme a selon la

taille d'échantillon n dans un contexte Uniforme-Pareto 36 3.20 Corrélation /?(<?, 5*(X)) en fonction de la taille d'échantillon n dans un

contexte Uniforme-Pareto 37 3.21 Corrélation 8i9, <5*(X)) en fonction du paramètre de localisation x0 selon

la taille d'échantillon n dans un contexte Uniforme-Pareto 37 3.22 Corrélation 8i9, &»(X)) en fonction du paramètre de forme a selon la

taille d'échantillon n dans un contexte Uniforme-Pareto 38 3.23 Corrélation r(<?, # M V ( X ) ) en fonction de la taille d'échantillon n dans un

contexte Gamma-Gamma

3.24 Corrélation r(<?, <5MV(X)) en fonction de la taille d'échantillon n selon les

paramètres de forme Q et 7 dans un contexte Gamma-Gamma

3.25 Comparaison des corrélationspi9, £A/y(X)), r(0, ôMv(X-)) et 8i9, <5MV'(X))

en fonction de la taille d'échantillon n dans un contexte Gamma-Gamma 15 3.26 Comparaison des corrélations pi9, <5A/\/(X)), T ( 0 , <5A/V(X)) et 8i9, ^ M V ( X ) )

en fonction du paramètre de forme a priori a dans un contexte

Gamma-Gamma 15 3.27 Comparaison des corrélations pi9, ÔMVÇX-)), r(<?, <5A/V(X)) et /?(<?, ÔMVÇX))

en fonction du paramètre d'échelle a priori 8 dans un contexte Gamma-Gamma

3.28 Comparaison des corrélationspi9, # A / V ( X ) ) , T ( 0 , <5AA'(X)) et 0i9, 6 M V ( X ) )

en fonction du paramètre de forme 7 dans un contexte Gamma-Gamma 3.29 Comparaison des corrélationspi9, JA/V(X)), T ( 0 , <$A/V(X)) et 8i9, 5 A / V ( X ) )

en fonction de la taille d'échantillon n dans un contexte Gamma-Gamma 7 3.30 Comparaison des corrélationspi9, <$A/V(X)), T ( 0 , ^A/ V ( X ) ) et 3i9, £A/V(X))

en fonction du paramètre de forme a priori a dans un contexte

Gamma-Gamma Iv

3.31 Comparaison des corrélations pi9, <5A/V(X)), T ( 0 , £ A / V ( X ) ) et /3(0, # A / V ( X ) )

en fonction du paramètre d'échelle a priori 8 dans un contexte

Gamma-Gamma 4!) 3.32 Comparaison des corrélations pi9, # A / V ( X ) ) , T ( 0 , 6 M V ( X ) ) et 0i9, <5A/V(X))

en fonction du paramètre de forme 7 dans un contexte Gamma-Gamma

4.1 Corrélation r(#, J A / V ( X ) ) en fonction de la taille d'échantillon n pour le

cas Bernoulli-Beta 53 4.2 Corrélation r(i9, <5A/V(X)) en fonction du paramètre de forme a priori a

selon différentes tailles d'échantillon n pour le cas Bernoulli-Beta . . . . 4.3 Comparaison des corrélations de Spearman, de Kendall et de Blomqvist entre l'estimateur du maximum de vraisemblance et le paramètre 9 en

fonction de la taille d'échantillon n pour le cas Bernoulli-Beta 56 4.4 Comparaison des corrélations de Spearman, de Kendall et de Blomqvist

entre l'estimateur du maximum de vraisemblance et le paramètre 9 en

fonction du paramètre a priori a pour le cas Bernoulli-Beta 56 4.5 Comparaison des corrélations de Spearman, de Kendall et de Blomqvist

entre l'estimateur du maximum de vraisemblance et le paramètre 9 en

fonction du paramètre a priori 8 pour le cas Bernoulli-Beta 57 4.6 Corrélation r(é?, <5A/V(X)) en fonction de 8 selon la taille d'échantillon n

pour le cas Poisson-Gamma 60 4.7 Corrélation pi9, C5AIV(X)) en fonction de la taille d'échantillon n dans un

contexte Poisson-Gamma 62 4.8 Corrélation pi9, (5A/V(X)) en fonction du paramètre de forme a selon la

taille d'échantillon n dans un contexte Poisson-Gamma 63 4.9 Corrélation P(#,<5A/V(X)) en fonction du paramètre d'échelle 8 selon la

taille d'échantillon n dans un contexte Poisson-Gamma 63 4.10 Corrélation r(#, (5A/V(X)) en fonction de la taille d'échantillon n dans un

contexte Poisson-Gamma 64 4.11 Corrélation T ( 0 , 6 A / V ( X ) ) en fonction du paramètre de forme a selon la

taille d'échantillon n dans un contexte Poisson-Gamma 65 4.12 Corrélation T(#, <5A/V(X)) en fonction du paramètre d'échelle 8 selon la

4.13 Corrélation 3(0, <5A/V(X)) en fonction de la taille d'échantillon n dans un

contexte Poisson-Gamma 67 4.14 Corrélation 8i9, 6 A / V ( X ) ) en fonction du paramètre de forme a selon la

taille d'échantillon n dans un contexte Poisson-Gamma 07 4.15 Corrélation 5(0,T5A/V(X)) en fonction du paramètre d'échelle 3 selon la

taille d'échantillon n dans un contexte Poisson-Gamma 08 4.16 Comparaison des corrélations r(0, <5A/V(X)) et r(0, ô^(X)) en fonction du

paramètre a priori a dans un contexte Géométrique-Beta 70 4.17 Comparaison des corrélations Î~(0,<5A/V(X)) et r(0,<5„.(X)) en fonction du

paramètre a priori 8 dans un contexte Géométrique-Beta

4.18 Comparaison des corrélations p(0, £ A / V ( X ) ) et p(0, ôn(X)) en fonction de

la taille d'échantillon n dans un contexte Géométrique-Beta 72 4.19 Comparaison des corrélations p(0,5Mv(X)) et p(0, <5^(X)) en fonction du

paramètre a priori a selon deux tailles d'échantillon n dans un contexte

Géométrique-Beta 72 4.20 Comparaison des corrélations p(0, <$A/V(X)) et p(0, S^{X.)) en fonction du

paramètre a priori 3 selon deux tailles d'échantillon n dans un contexte Géométrique-Beta

4.21 Comparaison des corrélations T ( 0 , <5A/V(X)) et r(0, Jff(X)) en fonction de

la taille d'échantillon n dans un contexte Géométrique-Beta 74 4.22 Comparaison des corrélations T ( 0 , <5A/V(X)) et r(0, ^ ( X ) ) en fonction du

paramètre a priori a selon deux tailles d'échantillon n dans un contexte

Géométrique-Beta 74 4.23 Comparaison des corrélations r(0, S M V ( X ) ) e t r( 0 , <^r(X)) en fonction du

paramètre a priori 3 selon deux tailles d'échantillon n dans un contexte Géométrique-Beta

4.24 Comparaison des corrélations 0(0, SM V(K)) et /3(0, £*(X)) en fonction de

la taille d'échantillon n dans un contexte Géométrique-Beta 76 4.25 Comparaison des corrélations /?(0, <5MV(X)) et /3(0, ^ ( X ) ) en fonction du

paramètre a priori a selon deux tailles d'échantillon n dans un contexte

Géométrique-Beta 70 4.26 Comparaison des corrélations /3(0, <5A/V(X)) et /3(0, J^(X)) en fonction du

paramètre a priori 3 selon deux tailles d'échantillon n dans un contexte

Introduction

La corrélation est une notion fondamentale pour l'évaluation de la relation entre deux variables aléatoires. Qu'elle soit mesurée par le r de Pearson, le p de Spearman ou bien le r de Kendall, la corrélation est bien connue et largement utilisée dans le domaine de la statistique. En outre, le coefficient de Pearson est de loin le plus populaire.

D'abord étudié par le scientifique britannique Francis Galton (1822-1911) et ensuite popularisé par le mathématicien britannique Karl Pearson (1857-1936), le coefficient de corrélation de Pearson mesure l'intensité de la liaison linéaire entre deux variables aléa-toires X et Y. Fréquemment employé, ce coefficient est par contre rarement utilisé dans un cadre bayésien. Le présent mémoire met donc en évidence les propriétés de plusieurs coefficients de corrélation, dont celui de Pearson, dans un contexte non-fréquentiste.

Le chapitre 2 regroupe différentes connaissances au sujet des coefficients de corréla-tion. Tout d'abord, un bref rappel de leurs définitions ainsi que de courtes introductions à l'inférence bayésienne et aux copules amorcent le chapitre. On y présente ensuite di-verses formules permettant de calculer la corrélation de Pearson entre le paramètre à estimer et différents types d'estimateurs. On étudie également la corrélation r entre l'estimateur de Bayes et un estimateur sans biais et on discute finalement de la notion d'estimateur à corrélation maximale.

Le chapitre 3 présente plusieurs applications des propositions du chapitre 2 dans un cadre où les lois sont conjuguées et continues. On y présente quatre exemples illustrant chacun des situations différentes : Normale avec précision connue, Normale-Gamma avec moyenne connue, Uniforme-Pareto et finalement, Normale-Gamma-Normale-Gamma. Pour chacun de ces exemples, on compare les différentes corrélations entre elles en analysant leur comportement respectif.

Chapitre 1. Introduction 2

Le chapitre 4 contient également plusieurs exemples d'applications des concepts du chapitre 2 dans un cadre de lois conjuguées où les données suivent une loi discrète. L'intérêt de ce chapitre est d'étudier le comportement des corrélations dans un contexte où la copule n'est pas unique. On y travaille les cas Bernoulli-Bêta, Poisson-Gamma et Géométrique-Bêta.

Le chapitre 5 conclut ce mémoire avec deux exemples pathologiques pour lesquels la corrélation obtenue ne se comporte pas aussi bien que dans les exemples des chapitres 3 et 4. En effet, la corrélation de Pearson tend habituellement vers 1 lorsque la taille de l'échantillon tend vers l'infini. Les exemples pathologiques présentent, quant à eux, des comportements bien différents.

La corrélation dans u n cadre

bayésien

Ce chapitre présente plusieurs résultats permettant, dans un cadre bayésien, de calculer le coefficient de corrélation de Pearson entre un estimateur et le paramètre à estimer dans différentes situations. Tout d'abord, les sections 2.1, 2.2 et 2.3 offrent respectivement un rapide survol de la notion de copule, de divers coefficients de corré­ lation et de l'inférence bayésienne. La section 2.4 présente diverses formules permettant de calculer le coefficient de corrélation de Pearson selon la situation. La section 2.5 introduit la notion de corrélation entre un estimateur de Bayes et un estimateur sans biais, tous deux estimant bien sûr le même paramètre. Finalement, la section 2.6 met un bémol à la définition d'estimateur à corrélation maximale.

2.1 Rapide survol de la notion de copule

Largement utilisée dans le domaine de la finance, la copule est un objet mathéma­ tique qui caractérise la dépendance entre deux variables aléatoires sans égard aux lois marginales.

Soit iX, Y) une paire de variables aléatoires continues. Considérons la distribution conjointe H(x.y) = P[X < x , Y < y] et les distributions marginales F i x ) — P [ X < x] et Giy) = P[Y < y}. On dit que les variables X et Y sont indépendantes si et seulement si H i x , y ) = F i x ) ■ Giy) pour tout x , y G R. Si les variables X et Y ne sont pas indépendantes, il est alors intéressant de qualifier et de quantifier leur relation. Pour ce

Chapitre 2. La corrélation dans un cadre bayésien 4

faire, on peut avoir recours à la copule C liant les marges de X et de Y. La copule du couple iX, Y) est définie implicitement par la relation

H(x,y) = C[F{x),G(y)]

postulée pour l'ensemble des valeurs de x, y G R. La copule C n'est autre que la fonction de répartition du couple (£/, V) = (P(X),G(F)). Voici quelques unes de ses propriétés.

P r o p o s i t i o n 2.1.1. Si C est une copule, alors

max(« + v — 1,0) < C(u, v) < min(it, v)

pour tout u,v G [0,1].

Lorsque la loi du couple (X, Y) est absolument continue, la densité conjointe et les densités marginales sont respectivement données par hix,y) = -^g-Hix,y) et fix) = F'ix) et giy) = G'iy). Alors, on peut exprimer la densité conjointe comme

h(x,y) = f{x)-g(y)-c[F(x),G(v)]

où c(w, v) = faîhjCiu, v). Il existe un grand nombre de copules. Parmi celles-ci, la copule d'indépendance C(w, v) = uv où u, v G (0,1) lie les variables X et Y lorsque ces dernières sont indépendantes.

2.2 Définitions et propriétés de divers coefficients

de corrélation

Les sous-sections qui suivent regroupent différentes mesures de corrélation. On y présente les définitions ainsi que certaines propriétés des coefficients suivants : le r de Pearson, le p Spearman, le r de Kendall et le 0 de Blomqvist. On suppose partout dans la suite que les variables X et Y d'intérêt sont continues.

2.2.1 Le r de Pearson

La première corrélation étudiée dans le présent mémoire est celle popularisée par le mathématicien britannique Karl Pearson (1857-1936). La corrélation théorique r

mesurée entre les variables aléatoires continues X et Y est donnée par :

r(X, Y) = . . (2.1) ^/VarLY^Var^]

Le coefficient de corrélation de Pearson r(A", Y) est une statistique mesurant l'in-tensité de la relation linéaire entre X et Y. Il est toutefois inapproprié lorsque le lien entre les variables n'est pas linéaire. Voici quelques propriétés de cette corrélation. P r o p o s i t i o n 2.2.1. Soit r(X, Y) la corrélation selon Pearson mesurée entre les va-riables aléatoires continues X e t Y .

(a) r ( X , Y ) e

[-1,1]-(b) \riX,Y)\ = 1 si et seulement si il existe a,b G R, où a ^ 0, tel que

P[Y = aX + b] = l. S i a > 0 , alors r i X , Y ) = 1. Autrement, r i X , Y ) = - 1 . (c) Si les variables X et Y sont indépendantes, alors r(X, Y) = 0. Par contre,

r(X, Y) = 0 n'implique pas nécessairement que X e t Y soient indépendantes.

La corrélation selon Pearson présente plusieurs inconvénients. En effet, cette mesure de corrélation n'existe pas toujours. De plus, le coefficient r est très sensible aux valeurs aberrantes ou extrêmes et perd de son intérêt lorsque les données sont très hétérogènes. Finalement, l'inconvénient majeur de cette mesure est que r dépend des lois marginales de X et Y.

2.2.2 Le p Spearman

Pour contrer l'effet des lois marginales, il suffit de travailler avec des mesures de dépendance utilisant la notion de copule. En effet, rappelons que la copule caractérise la dépendance sans égard aux marges.

Proposé par le psychologue anglais Charles Spearman (1893-1945), le p de Spearman est une première mesure de corrélation liée à la notion de copule. Le p de Spearman théorique n'est en fait qu'une variante du coefficient de corrélation de Pearson.

p(X,Y) = r(U,V)

= - 3 + 12 f f C(u, v)dudv Jo Jo

Chapitre 2. La corrélation dans un cadre bayésien 6

où U = F i X ) et V = G(Y) ont pour loi conjointe la copule C. On remarque que le p de Spearman est une mesure de corrélation uniquement fonction de la copule. Il permet d'évaluer la relation entre les variables aléatoires X et Y et est parfaitement adapté au cas où celle-ci est monotone. Alors, contrairement au r de Pearson, la relation entre X et Y n'a pas besoin d'être nécessairement linéaire. Voici quelques propriétés de p.

P r o p o s i t i o n 2.2.2. Soit p le coefficient de corrélation de Spearman. (a) p G [-1,1].

(b) Si \p\ = 1, alors il existe une fonction tiy) tel que X = t(Y). Cette fonction est croissante si p = 1 et décroissante si p = — 1.

(c) Si X e t Y sont indépendants, alors p = 0.

Finalement, il est important de noter que, tout comme le coefficient de corrélation de Pearson, le fait que p(X, Y) = 0 n'implique pas nécessairement que les variables aléatoires X et Y soient indépendantes.

2.2.3 Le r de Kendall

Élaboré en 1938 par le statisticien britannique Maurice Kendall (1907-1983), le r de Kendall est une deuxième mesure de dépendance uniquement fonction de la copule. Le coefficient de Kendall théorique est donné par

T ( X , Y )

= P [ ( X

- X

) ( Y

- Y

) > 0 ] - P [ ( X

- X

) { Y

- Y

) < 0 ]

= - 1 + 4 /" / C(u,v)dC(u,v)

Jo Jo

où (Xi, Yi) et iX2,Y2) sont deux paires de variables aléatoires indépendantes issues de

\a\oiHix,y) = C[Fix),Giy)].

Tout comme le p de Spearman, le r de Kendall permet de mesurer l'intensité d'une relation fonctionnelle entre les variables aléatoires X et Y. Finalement, le r de Kendall possède exactement les mêmes propriétés que celles du p de Spearman énoncées à la proposition 2.2.2.

Pour une version empirique, on écrit le coefficient T comme suit : c — d

T ( X , Y ) =

G)

où c est le nombre de paires de points concordants, d est le nombre de paires de points discordants et n est le nombre de points. On dit que deux paires (A^Yj) et iX2,Y2)

sont concordantes lorsque (Xi — X2)(Yi — Y2) > 0. À l'opposé, on dit que deux paires

(Xi, Yi) et iX2,Y2) sont discordantes lorsque (Xj - X2)(YX - Y2) < 0.

2.2.4 Le (3 de Blomqvist

Le 0 de Blomqvist a été proposé en 1950 par le Suédois Nils Blomqvist. Bien que les coefficients de corrélation basés sur les rangs soient toujours valides même sous de faibles hypothèses concernant la distribution de la population, leur utilisation représentait un défi considérable en 1950. En effet, les calculs devenaient rapidement fastidieux lorsque la taille de l'échantillon était grande. Le 0 de Blomqvist a donc été élaboré pour contrer cet inconvénient.

Considérons un échantillon bivarié de variables aléatoires continues ( £ i , y i ) , . . . , (^n) yn) provenant d'une fonction de répartition conjointe i/(x, y). Soit Fix) et Giy) les

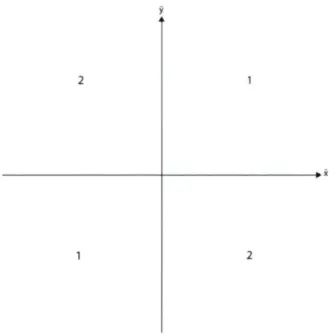
distributions marginales et x = x et y = y les médianes échantionnales correspondantes. Le plan xy est divisé en quatre régions délimitées par les droites x = x et y = y tel qu'illustré à la figure (2.1).

À partir de cette représentation, Blomqvist a déduit une corrélation utilisant ni, le nombre de points appartenant au 1er quadrant, en les comparant à n2, le nombre de

points dans le 2e quadrant. Le coefficient sous sa forme empirique s'écrit alors comme

suit :

3ix,Y) =

^ ^ = - ^ ^ - i .

nx + n2 ni + n2

Prendre note que 0 i X , Y ) G [—1,1]- De plus, on remarque que si n est impair, le calcul de 0 peut devenir ambigu. En effet, par définition de la médiane, on risque d'avoir un ou même deux points situés exactement sur les droites x = x et y = y. Pour contrer ce problème, Blomqvist a proposé les règles suivantes :

(1) Si un seul point tombe sur les droites x = x et y = y, on ne le compte pas. (2) Si deux points tombent sur les droites x = x et y = y, on considère que le premier

point appartient au quadrant touché par les deux points mais on ne tient pas compte du deuxième point.

Chapitre 2. La corrélation dans un cadre bayésien

y 4

2 1

1 2

FIGURE

2.1 - Représentation du plan xy tel que divisé par Blomqvist

Prendre note que ce problème d'ambiguité ne se présente pas si n est pair.

Pour la version théorique, on écrit le 0 de Blomqvist en fonction de la copule.

0iX,Y) = 4-(7(1/2,1/2)-1

= 4 - P [ X < p -

( l / 2 ) , Y < G

( l / 2 ) ] - l

Finalement, cette mesure de corrélation possède exactement les mêmes propriétés que

celles du p de Spearman énoncées à la proposition 2.2.2.

2.3 Brève introduction à l'inférence bayésienne

Considérons maintenant un problème d'inférence. À partir d'un échantillon de

don-nées X, on cherche à inférer sur le paramètre inconnu 9. Pour utiliser une approche

bayésienne, on doit premièrement connaître le modèle liant le paramètre 0 aux

don-nées X, soit la densité conjointe des variables X \ , . . . , X

sachant 0, qu'on note /(x|0).

Deuxièmement, une connaissance a priori des valeurs possibles de 0 est essentielle. On

quantifie l'incertitude sur 0 en utilisant une loi a priori 7r(0). Finalement, en combinant

les deux distributions avec la règle de Bayes, on obtient la loi a posteriori de 0 étant

donné x comme suit :

/ ( X | 0 ) T T ( 0 ) 7T(0|X)

J7(x|0')7r(0')d0'

Comme le dénominateur ne dépend pas de 0, on peut exprimer 7r(0|x) comme suit :

TT(0|X) OC / ( X | 0 ) T T ( 0 ) . (2.2)

Dans le paradigme bayésien, la loi a posteriori 7r(0|x) est à l'origine de toutes les infe-rences sur 0. On utilise généralement l'espérance a posteriori E[0|X] comme estimateur mais il est également raisonnable d'utiliser la médiane ou bien le mode a posteriori.

La notion de lois conjuguées simplifie beaucoup l'emploi de l'équation (2.2). En effet, si la loi a priori 7r(0) et la loi a posteriori 7r(0|x) sont de la même famille de lois, on dit que 7r(0) est conjuguée à /(x|0). Par exemple, une loi a priori Gamma et une distribution conjointe Poisson conduisent invariablement à une loi a posteriori Gamma. En sortant du cadre restrictif des lois conjuguées, plusieurs choix de lois a priori 7r(0) sont possibles. Lorsqu'il y a peu d'informations disponibles a priori sur le paramètre 0, on utilise une loi a priori non-informative. Ce type de loi est plate sur l'espace paramètre, suggérant alors une faible connaissance a priori du comportement du paramètre 0. Il arrive parfois qu'une loi non-informative soit également impropre. Prendre note qu'une loi est généralement impropre lorsque l'espace paramétrique est non-borné. L'utilisation d'une telle loi est appropriée à condition que la loi a posteriori soit propre, c'est-à-dire que J/(x|0)7r(0)d0 < oo. Si ce n'est pas le cas, il est toujours possible d'utiliser une loi a priori pratiquement plate sur l'espace paramétrique, comme par exemple une loi normale avec une très grande variance. On parle alors d'une loi a priori diffuse ou vague.

2.4 Corrélation de Pearson entre un paramètre et

son estimateur

Soit (0, X) la paire de variables aléatoires représentant respectivement le paramètre à estimer et l'échantillon. Toujours dans le cadre bayésien décrit à la section précédente, considérons <Î(X) un estimateur arbitraire de 0 qui est fonction de l'échantillon X.

Sous l'erreur quadratique moyenne, le risque de Bayes est une fonction de l'esti-mateur £(X) et de la loi a priori 7r(0) donnée par P(7r.£(X)) = E[(J(X) — 0)2]. En

Chapitre 2. La corrélation dans un cadre bayésien 10

inference bayésienne, on cherche un estimateur minimisant ce risque. Parmi tous les estimateurs possibles du paramètre 0, l'estimateur de Bayes S„iX) = E[0|X] est celui qui minimise le risque. On représente le risque de l'estimateur de Bayes <5^(X) par P(7r).

P r o p o s i t i o n 2.4.1. Soit S(X.) un estimateur quelconque du paramètre 9. Considérons le biais 6(0) = E[<5(X)|0] — 9. La corrélation entre cet estimateur et le paramètre 9 est alors donnée par

r{9, SiX)) = Var[0] + Cov[0,6(0)]

y/Wax[d]y/Vax[9 + 6(0)] + R(n, 6(X)) - E[62(0)]

Comme on peut le constater, la corrélation entre le paramètre 0 et un estimateur quelconque oLX) est une fonction de la variance a priori du paramètre 0, de la cova-riance entre 0 et le biais 6(0), du biais 6(0) et du risque P(7r, £(X)) associé à la loi a priori TT. On remarque également que, caeteris paribus, la corrélation diminue lorsque le risque bayésien de l'estimateur augmente.

D é m o n s t r a t i o n 2.4.1. Sans perte de généralité, on suppose que E[0] = 0. Calculons d'abord les différentes quantités composant l'équation (2.1).

Premièrement, par définition de la covariance, on sait que

Cov[M(X)] = E[06'X)] - E[9]E[SiX)}

et puisque nous supposons que E[0] = 0, on en déduit

Cov[9,ôiX)} = E[9ôiX)\.

En conditionnant sur le paramètre 9, on a

Cov[0,<5(X)] = E[0E[5(X)|0]].

Ensuite, par définition du biais 6(0), on a

Cov[0,(5(X)] = E[0(0 + 6(0))] = E[02 + 06(0)]

Puisqu 'on suppose que E[0] = 0, on obtient finalement

Cov[0, SiX)} = Var[0] + Cov[0,6(0)]. (2.4)

Deuxièmement, en conditionnant sur 9, le terme Var[<5(X)] devient

Var[<S(X)] = E[Var[£(X)|0]] + Var[E[<J(X)|0]].

Par définition du biais 6(0), on obtient

Var[<5(X)] = E[Var[*(X)|0]] + Var[0 + 6(0)]

et puisque E[(<J(X) - 0)

|0] = Var[<S(X)|0] + 6

(0), on trouve

Var[<5(X)] = E[E[(<5(X) - 0)

|0] - 6

(0)] + Var[0 + 6(0)]

= E[(<5(X) - 0)

] - E[6

(0)] + Var[0 + 6(0)]

= i?(7r,<5(X))-E[6

(0)] + Var[0 + 6(0)]. (2.5)

En réunissant les expressions (2.4) et (2.5) dans l'équation (2.1), on obtient bel et

bien que

ri9,SiX))= Var[0] + C o v [

) ]

JVax[0]y/Vfn[6 + 6(0)] + P(TT,<5(X)) - E[6

(0)]'

Proposition 2.4.2. Soit Ô(X) un estimateur sans biais arbitraire du paramètre 9. La

corrélation entre cet estimateur et le paramètre 9 est alors donnée par

r(M(X)) =

* > (2.6)

\Vav[9] + Rin,ôiX)Y

Comme on peut le remarquer, la corrélation est non-négative et est strictement

posi-tive à condition que la loi a priori 7r(0) ne soit pas dégénérée, c'est-à-dire que Var[0] ^ 0.

Chapitre 2. La corrélation dans un cadre bayésien 12

Démonstration 2.4.2. Sans perte de généralité, on suppose que E[0] = 0. Il suffit

d'utiliser l'équation (2.3) et de remarquer que 6(0) = 0. On trouve

Var[0] + Cov[0,6(0)]

r(0,6(X)) =

^/Varffl^Varp + 6(0)] + P(TT, 5(X)) - E[6

(0)]

Var[0] + Cov[0,O]

Var[0]

^Varffl^Varffl + ^ M C X ) )

Var[0]

\ Var[0]+iî(7r,(5(X))'

Proposition 2.4.3. Soit ^ ( X ) = E[0|X], l'estimateur de Bayes du paramètre 9 sous

la fonction de perte quadratique. La corrélation entre cet estimateur et le paramètre 9

est alors donnée par :

r(0A(X)) = I-*®- (27)

Y Var[0]'

On remarque que la corrélation entre le paramètre 0 et l'estimateur de Bayes ô^(X)

est non-négative. Elle est même strictement positive à condition que l'estimateur ô^iX)

ne soit pas une constante.

Démonstration 2.4.3. On suppose sans perte de généralité que E[0] = 0. Le risque

bayésien est donné par

P(TT) = E [ ( ^ ( X ) - 0 )2] .

Par manipulations algébriques, on obtient

P(TT) = E[6*(X)(Ô*(X) - 0)] - E[0(<MX) - 0)].

En conditionnant le premier terme sur X et le deuxième terme sur 9, on a

Ri*) = E[^(X) • (MX) - E[0|X])] - E[0 • (E[(5

(X)|0] - 0)].

Par définition du biais 6(0), de l'estimateur <5

(X) et de la covariance, on a

P(TT) = E[<MX)(MX)-MX))]-E[06(0)]

= -E[06(0)]

Le numérateur de l'équation (2.1) se réduit alors à

Var[0] + Cov[0,6(0)] = Var[0] - R(n). (2.8)

Par ailleurs, au vu de la définition de la variance, on remarque que

Var[0 + 6(0)] - E[6

(0)] = Var[0] + Var[6(0)] + 2Cov[0,6(0)] - E[6

(0)].

Puisque E[6(0)] = 0, on a

Var[0 + 6(0)] - E[6

(0)] = Var[0] + E[6

(0)] + 2E[06(0)] - E[6

(0)]

= Var[0] + 2E[06(0)]

et par définition du risque bayésien, on obtient

Var[0 + 6(0)] - E[6

(0)] = Var[0] -

(2.9)

En réunissant les équations (2.7) et (2.8), l'équation (2.1) devient finalement

Var[0] - P(TT)

r(0A(X)) =

y/Vax[d]y/V8ir[6] -

+

Var[0] - Rjir)

y/Var[6]JVa.T[0] - R(ir)

Var[0] - Rjrr)

\\ ~ Var [9]

1 _

W

\ Var[0] '

2.5 Corrélation de Pearson entre l'estimateur de

Bayes et un estimateur sans biais

Examinons maintenant la corrélation entre deux estimateurs du même paramètre

9 : l'estimateur de Bayes ô

iX) et un estimateur sans biais arbitraire Ô(X).

Chapitre 2. La corrélation dans un cadre bayésien 14

Proposition 2.5.1. Si £(X) est un estimateur sans biais arbitraire pour le paramètre

9, alors

r(<S(X)A(X)) =

*r[0]

^

yjSmX\0\ - P(7r)^/Var[0] + E[Var[«5(X)|0]]

On remarque que cette corrélation est non-négative et strictement positive sauf si

la loi a priori 7r(0) est dégénérée, c'est-à-dire si Var[0] = 0. De plus, la corrélation sera

maximale si l'estimateur sans biais arbitraire â(X) est à variance minimale. En effet,

puisque les termes Var[0] et P(7r) ne dépendent pas de l'estimateur 5(X), il suffit de

minimiser le terme E[Var[J(X)|0]] afin de maximiser la corrélation entre l'estimateur de

Bayes et l'estimateur #(X). On choisit donc l'estimateur sans biais à variance minimale

appelé estimateur UMVU.

Démonstration 2.5.1. Il suffit de développer l'équation (2.1).

Par définition de la covariance, le numérateur devient

Cov[5(X)A(X)] = E[*(X)k(X)] - E[Ô(X)]E[6*{X)].

En conditionnant sur X, on a

Cov[<5(X)A(X)] = E[5(X)E[0|X]] - E[J(X)]E[^(X)].

Par définition de la covariance et de la variance, on obtient

Cov[6(X),6*{X)] = Cov[0,6(X)]

= E[06{X)] - E[0]E[6{X)]

= E[0

]-E

[0]

= Var[0].

En remplaçant le numérateur de l'équation (2.1) et en conditionnant sur 9, on obtient

finalement

Var[0]

r(*(X)A(X)) =

V/

Var[<5(X)]

/Var[<5.(X)]

Var[0]

v

/Var[E[(5(X)|0]] + E[Var[£(X)|0]]^/Var[0] - R(ir)

Var[0]

2.6 Concept d'estimateur à corrélation maximale

Il pourrait paraître intéressant d'avoir recours à un estimateur à corrélation maxi-male. En effet, la corrélation entre un paramètre et son estimateur pourrait être un critère de choix dans la sélection de l'estimateur. Parmi un ensemble d'estimateurs quelconques, il semble intéressant de choisir celui dont la corrélation avec le paramètre est maximale. Par contre, il est évident que l'utilisation unique de ce critère pourrait mener à des choix erronés. En effet, deux estimateurs qui seraient une combinaison linéaire l'un de l'autre auront exactement la même corrélation.

Soit SiX) un estimateur sans biais. Considérons un nouvel estimateur 5*(X) = côiX) + d où c,d G R et c > 0. Le biais de l'estimateur <5»(X) est donné par 6,(0) = (c — 1)0 + d. Ainsi construit, on pourrait croire que la corrélation r(0,5(X)) soit plus près de 1 que la corrélation r(0, <5»(X)). Prouvons le contraire en calculant la corrélation r(0,<5*(X)) à l'aide de l'équation (2.3). On a

r(0A(X)) =

y/yfor]0]y/Vai[0 + 6,(0)] + P(TT, <S,(X)) - E[62(0)]

Var[0] + Cov[0, (c - 1)0 + d]

^War[0]yjYai[0 + (c - 1)0 + d] + E[Var[c5(X) + d] + 62(0)] - E[62(0)]

Var[0] + (c-l)Var[0]

y V a r ^ ^ V a r ^ ] + c2E[Var[6(X)]] + E[62(0)] - E[62(0)]

cVar[0]

^Var[0]^/c2Var[0] + C2P(TT, <Î(X)) Var[0]

^Var[0] + P(7r,£(X))

r(M(X)).

Prendre note que, si c < 0, alors r(0,<5*(X)) = —r(0,<5(X)). On conclut que la no-tion de corrélano-tion maximale entre un paramètre et son estimateur est intéressante à condition de ne pas l'utiliser pour comparer deux estimateurs qui sont une combinai-son linéaire l'un de l'autre. Cette notion est également utile lorsqu'on se restreint aux estimateurs sans biais. En effet, à l'aide de l'équation (2.6), on sait que, si on cherche un estimateur tel que la corrélation entre ce dernier et le paramètre est maximale, cet estimateur sera nécessairement celui ayant le risque le plus faible.

Chapitre 3

Applications dans un contexte de

lois conjuguées continues

On présente dans ce chapitre plusieurs applications des propositions du chapitre 2 dans un contexte de lois conjuguées continues. Parmi une dizaine de lois conjuguées continues possibles, ce chapitre illustre quatre cas pour lesquels le calcul des corrélations et leur comportement diffèrent les uns des autres. Les sections 3.1 et 3.2 contiennent les exemples des cas Normale-Normale et Normale-Gamma dans lesquels on considère respectivement la précision et la moyenne comme des constantes connues. La section 3.3 présente en détails le cas Uniforme-Pareto tandis que la section 3.4 conclut le chapitre avec le cas Gamma-Gamma.

3.1 Normale-Normale avec précision connue

Soit X = ( X i , . . . , X „ )T, le vecteur contenant les données tel que X i , . . . ,Xn|0 sont

indépendantes et identiquement distribuées selon une loi normale de moyenne 0 et de précision v. On suppose que le paramètre v est une constante connue strictement supé-rieure à 0 représentant l'inverse de la variance. Avec cette paramétrisation, la densité de la loi conjointe s'écrit

/(x

=(^)"

.e¥^.<-»>'.

Afin d'obtenir une loi a priori 7r(0) conjuguée à /(x|0), on suppose que 0 ~ Normale(po, ir) c'est-à-dire

. „ / ^ o \1 / 2

• e

Prendre note que les paramètres p0 et vo s o nt des constantes connues telles que po G R et u0 est strictement supérieure à 0. Dans le but d'étudier le comportement des

corrélations décrites au chapitre 2, calculons l'estimateur du maximum de vraisemblance ainsi que l'estimateur de Bayes. Premièrement, on trouve l'estimateur du maximum de vraisemblance ÔMviX) à l'aide de la dérivée partielle de la log­vraisemblance. On a

u m = (£)■"*■ e?zu«­»\

«»M =

n

­^(£)­t.±

{ x t

­er

>*> - -i

=

f

l o g

(é)-i'

^ >

­ 2 0 ] > > + n0

En égalant l'équation (3.1) à 0 et en isolant le paramètre 0, on trouve que (5A/V(X) =

X = (Xi + • • • + Xn) / n . Autrement dit, l'estimateur du maximum de vraisemblance

n'est nul autre que la moyenne des observations. On remarque que cet estimateur est sans biais puisque E X|0 —9.

Pour calculer l'estimateur de Bayes S^iX), il faut d'abord trouver la loi a posteriori 7r(0|X). Pour ce faire, on utilise la règle de Bayes tel que présentée à l'équation (2.2). On trouve

,f l|v, ­ ^ ( O ­ M Q )2 _ i i V ­ " (X i­ 0 )2

7r(0|X) oc e 2 ­e 2 Z­i=iW °>

x e­l/2(#a(Mo+ni/)­2*(MOW)+«'Eteia:<)).

La loi a posteriori 7r(0|X) est donc une loi normale de moyenne (l'oPo + v Y,7=i xi ) l iuo +

nu) et de précision UQ + nu. On en déduit que l'estimateur de Bayes est c rv^ ^oPo + ^ E L i ^ i

à*(X) = ; •

UQ + nu

On remarque que l'estimateur de Bayes peut s'écrire comme une transformation linéaire de l'estimateur du maximum de vraisemblance comme suit :

c /Vx ^ 0 + nvôMv(X)

à*{X) = ; •

UQ + nu

La sous­section suivante présente les calculs relatifs aux différentes corrélations mesurées entre le paramètre 0 et son estimateur dans le cadre Normale­Normale avec précision connue. Ces différentes mesures sont ensuite comparées entre elles. Puisque l'estimateur de Bayes est une combinaison linéaire de l'estimateur du maximum de vraisemblance, on ne calcule que la corrélation p(0, <5A/V(X)) pour connaître le comportement des deux

Chapitre 3. Applications dans un contexte de lois conjuguées continues IS

3.1.1 Calcul des corrélations r, p et r

Puisque les lois conjuguées sont Normale-Normale, la copule sous-jacente aux don-nées est de type normale, ce qui facilite le calcul des corrélations. En effet, il suffit maintenant de connaître la corrélation de Pearson afin de déduire les corrélations de Spearman, de Kendall et de Blomqvist. Tout d'abord, puisque l'estimateur du maximum de vraisemblance est sans biais, on utilise l'équation (2.6) pour calculer la corrélation de Pearson entre le paramètre 9 et son estimateur <5A/V(X). Puisque Var[0] = l/u0, on

a

ri9,ô

viX)) =

Par définition de l'estimateur, on a

" 0

^ +

E[Var[<W(X)|0]]-r(0,<W(X)) = _{^ + E[Var[X|0]]-}" 0

Puisque Var[X|0] = 1/u, on obtient donc que

r(0,<W(X)) = "o

\ ± + ± \

1

1 + ^

On remarque que la corrélation de Pearson T(0,<5A/V(X)) est croissante en fonction de la précision des données u et de la taille d'échantillon n. Autrement dit, plus la loi des observations est variable, moins la corrélation est forte. De plus, plus la taille de l'échantillon est grande, plus la corrélation r(0, # M V ( X ) ) est grande. Finalement, on note

que la corrélation de Pearson r(0,^A/v(X)) est décroissante en fonction de la précision a priori UQ, c'est-à-dire que plus la loi a priori est diffuse, plus la corrélation est forte.

Puisque la copule est normale, l'équation suivante lie la corrélation de Spearman à celle de Pearson. Ces relations sont entre autres rapportées dans l'article de Kruskal (1958). On a donc ta x / v w 6 • / r ( 0 , < W ( X ) ) p(0,(5A/v(X)) = -arcsin

6

• { l \

Vy/Ï+¥J

Il en est de même pour la corrélation de Kendall qui peut s'écrire r(0,<5A/v(X)) = - arcsin (r(0, ôMv(X)))

TT

= — arcsin

Prendre note que, puisqu'on travaille avec une loi normale bivariée, le coefficient de corrélation de Kendall théorique est égal à la version théorique de celui de Blomqvist. Ainsi, on ne considère pas le 0 de Blomqvist et on travaille plutôt avec le r de Kendall en gardant à l'esprit que ceux­ci sont égaux.

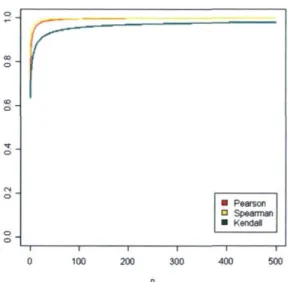
La figure 3.1 présente les différences entre ces trois corrélations en fonction de la taille d'échantillon n. Les précisions u0 et u ont été fixées à 1 pour simplifier la figure.

On remarque que les corrélations de Pearson et de Spearman sont très semblables et qu'elles se confondent à mesure que la taille d'échantillon n augmente. La corrélation de Kendall est, quant à elle, toujours inférieure aux deux autres mais cette différence tend à diminuer lorsque n augmente.

r

■ Pearson n Spearman ■ Kendall

i i i i 1

FIGURE 3.1 ­ Illustration des différentes corrélations en fonction de la taille d'échantillon n dans un contexte Normale­Normale

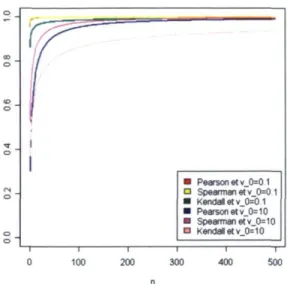
La figure 3.2 montre ensuite que si la précision a priori u0 augmente, les corrélations

tendent plus lentement vers 1. De plus, la différence entre celles­ci est plus marquée lorsque la précision a priori u0 est élevée. Prendre note que la précision u est fixée à

1. Par contre, si on augmente la précision des observations v, les corrélations tendent toutes plus rapidement vers 1, comme illustré à la figure 3.3. Prendre note que cette fois­ci la précision a priori u est fixée à 1.

Chapitre 3. Applications dans un contexte de lois conjuguées continues

20

FIGURE 3.2 - Illustration des différentes corrélations en fonction de la taille d'échantillon n selon la précision a priori dans un contexte Normale-Normale

■ Pearson et v=0 1 n Spearman et v=0 1 ■ Kendall e! v=0 1 ■ Pearson et v= 10 ■ Spearman et v= 10 D Kendall et v= 10 — i — 300 1— 400 100 200 500

FIGURE 3.3 - Illustration des différentes corrélations en fonction de la taille d'échantillon n selon la précision des observations dans un contexte Normale-Normale

3.2 Normale­Gamma avec moyenne connue

Dans cette section, on considère encore une fois que les observations proviennent d'une loi Normale. Par contre, on cherche cette fois­ci à estimer la précision au lieu de la moyenne.

Soit X = ( X i , . . . , X „ )T, le vecteur contenant les données tel que X \ , . . . , X„\0 sont

indépendantes et identiquement distribuées selon un loi normale de moyenne p et de précision 9. On suppose que le paramètre p est une constante réelle connue. Ainsi paramétrisée, la densité de la loi conjointe s'écrit

n/2

/(x|0) = (£) .«*£>»-* >

Dans le but de travailler avec des lois conjuguées, on suppose que 9 ~ Gamma(a,/?) c'est­à­dire

m = £ ­ ■ 0*­

e­f»

Tia)

pour tout 0 > 0. Prendre note que les paramètres a et 0 sont des constantes connues strictement supérieures à 0.

Considérons encore une fois deux estimateurs distincts, soit l'estimateur du maxi­ mum de vraisemblance et celui de Bayes. Tout d'abord, l'estimateur du maximum de vraisemblance 5 M V ( X ) est calculé à partir de la dérivée partielle de la log­vraisemblance.

On a n/2

t(«|x) = ( £ ) .e*E,".,<^)',

em = i*(5)­5Ê<*­ri'.

pm = è­îp»­* <w>

En égalant à 0 et en solutionnant l'équation (3.2), on conclut que 5 M V ( X ) = n j Y^=i(^i~

»?-Pour trouver l'estimateur de Bayes, il faut premièrement connaître la loi a posteriori 7r(0|X). Pour ce faire, on travaille avec l'équation (2.2) et on trouve

TT(0|X) OC 0<*-1e-/3e-05e-§£:=1(*.-M)2

0(°+i)-

.e V /,

Chapitre 3. Applications dans un contexte de lois conjuguées continues 22

y^n iX i-u)2

Puisque la loi a posteriori est de la forme Gammafa + | , 0 + ^ '= 1 2' ), on conclut

nue l'estimateur de Baves est que l'estimateur de Bayes est

a + ?

MX) =

0

T L ^ l

Les sous-sections qui suivent présentent le comportement des quatre types de corrélation en fonction de la taille d'échantillon n, de la moyenne p et des deux paramètres de la loi a priori 7r(0). Ces corrélations sont mesurées premièrement entre le paramètre 0 et l'estimateur du maximum de vraisemblance (5A/V(X) et ensuite entre le paramètre 0 et

l'estimateur de Bayes f5ff(X).

3.2.1 Calcul des corrélations r, p, T et P mesurées entre le

pa-ramètre 6 et l'estimateur du maximum de vraisemblance

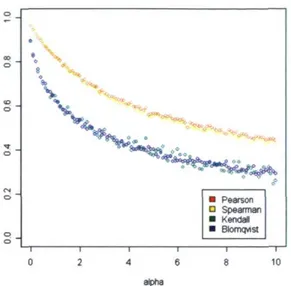
Puisque le calcul de la corrélation de Pearson effectué avec les formules du chapitre 2 présente quelques difficultés d'intégration, on analyse le comportement des quatre corrélations par simulations à l'aide du logiciel R. Pour ce faire, on simule d'abord le paramètre 0 selon une loi Gamma(a,/3). À partir de ce résultat, on génère les obser-vations X selon une loi Normale(p,0). On calcule finalement l'estimateur ÔMVÇX). On

itère ces trois étapes et on les répète 10 000 fois, ce qui permet d'estimer la corrélation entre 0 et <5A/V(X) selon r, p, r et 0. Prendre note que, puisque le r de Kendall compare

deux à deux toutes les paires de points, on itère seulement 1000 fois les étapes pour estimer cette corrélation.

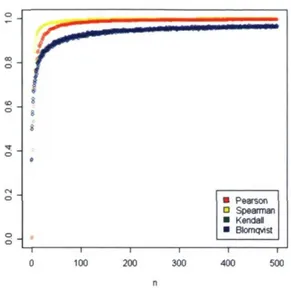
Commençons par analyser le comportement des corrélations selon la taille d'échan-tillon n. On fixe d'abord la moyenne p à 0 et les paramètres a et 0 à 1. On fait ensuite varier la taille de l'échantillon de 1 jusqu'à 500 pour finalement obtenir la figure 5.4. Peu importe la corrélation, on remarque que, plus la taille d'échantillon n est grande, plus la corrélation est près de 1. De plus, on note que la corrélation de Spearman est celle qui tend le plus rapidement vers 1 tandis que celle de Pearson est celle qui est la moins près de 1 et la plus variable. Par contre, les corrélations de Spearman, de Kendall et de Blomqvist sont assez similaires lorsque n est assez grand.

Analysons maintenant le comportement des corrélations en fonction de la moyenne des observations p. On fixe la taille d'échantillon n à 50 et les paramètres a priori a et 0 à 1. En observant la figure 3.5, il est évident que le paramètre p n'a aucun effet sur les corrélations mesurées entre le paramètre 0 et son estimateur. Il en est de même pour le paramètre d'échelle a priori 0. Tel que le montre la figure 3.G, ce paramètre n'a

■ Pearson O Spearman ■ Kendall ■ Blomqvist — I — 300 100 200 400 500

FIGURE 3.4 ­ Illustration des corrélations entre le paramètre de variance et son esti­ mation à vraisemblance maximale telles qu'observées dans des échantillons de taille n dans un contexte Normale­Gamma

pas plus d'effet sur le comportement des corrélations.

mm+mmm+mmmm»mmmW' ''tm* ■ Pearson D Spearman ■ Kendal ■ Blomqvist ~ r

FlGURE 3.5 ­ Illustration des corrélations entre le paramètre de variance et son esti­ mation à vraisemblance maximale en fonction de la moyenne p telles qu'observées dans des échantillons de taille 50 dans un contexte Normale­Gamma

Chapitre 3. Applications dans un contexte de lois conjuguées continues 24

■ Pearson n Spearman ■ Kendall ■ Blomqvist

F I G U R E 3.6 ­ Illustration des corrélations entre le paramètre de variance et son estima­

tion à vraisemblance maximale en fonction du paramètre d'échelle 0 telles qu'observées dans des échantillons de taille 50 dans un contexte Normale­Gamma

V> *~V. • ^ ^ ^ ■ Pearson D Spearman ■ Kendall ■ Blomqvist alpha

F I G U R E 3.7 ­ Illustration des corrélations entre le paramètre de variance et son estima­

tion à vraisemblance maximale en fonction du paramètre de forme a telles qu'observées dans des échantillons de taille 50 dans un contexte Normale­Gamma

En ce qui concerne le paramètre de forme a priori Q, la figure 3.7 montre que, plus celui-ci augmente, plus les corrélations diminuent. Autrement dit, plus la loi a priori 7r(0) est symétrique, plus la corrélation diminue et ce, pour les quatre types de corrélations. On remarque que cet effet semble plus prononcé pour les corrélation de Kendall et de Blomqvist.

3.2.2 Calcul des corrélations r, p, r et (3 mesurées entre le

paramètre 9 et l'estimateur de Bayes

Tout comme à la sous-section précédente, la corrélation de Pearson mesurée entre le paramètre 0 et l'estimateur de Bayes <5Tr(X) présente quelques problèmes d'intégration

lorsqu'on tente d'utiliser l'équation (2.7). On procède donc par simulation pour étudier le comportement des corrélations selon la taille d'échantillon n, la moyenne p et les paramètres a priori a et 0.

Pour commencer, examinons le comportement des corrélations lorsqu'on fait varier la taille de l'échantillon n de 1 jusqu'à 500. Prendre note qu'on fixe la moyenne p à 0 et les paramètres a priori a et 0 & 1. A l'aide de la figure 3.8, on remarque que la corrélation de Spearman est celle qui tend le plus rapidement vers 1 en fonction de la taille d'échantillon n. La corrélation de Pearson est légèrement inférieure à celle de Spearman pour de faibles tailles d'échantillon mais tend également rapidement vers 1. Les corrélations de Kendall et de Blomqvist sont, quant à elles, parfaitement superposées et tendent un peu plus lentement vers 1 que celle de Spearman.

La figure 3.9 illustre le comportement des corrélations en fonction de la moyenne p. Les paramètres de forme et d'échelle a priori sont fixés à 1 et la taille d'échantillon n à 50. Tout comme pour l'estimateur du maximum de vraisemblance, la moyenne p n'a aucun effet sur les corrélations : celles-ci demeurent constantes peu importe la valeur de p.

La figure 3.10 permet de juger du comportement des corrélations en fonction du paramètre de forme a priori a. Le paramètre de moyenne p est fixé à 0, le paramètre d'échelle a priori 0 à 1 et la taille d'échantillon n à 50. On remarque qu'une augmentation du paramètre a induit une diminution de la corrélation. De plus, cet effet semble plus marqué pour les corrélations de Kendall et de Blomqvist.

Finalement, la figure 3.1 1 illustre le comportement des corrélations en fonction du paramètre d'échelle 0 pour p = 0, a = 1 et n = 50. On remarque que 0 ne semble pas

Chapitre 3. Applications dans un contexte de lois conjuguées continues 26 ■ Pearson D Spearman ■ Kendall ■ Blomqvist —|-500 100 400

F I G U R E 3.8 ­ Illustration des corrélations entre le paramètre de variance et son esti­

mation de Bayes telles qu 'observées dans des échantillons de taille n dans un contexte Normale­ Gamma ûGzjc&Tcoj&xi&jc&B&ri ixCar<K«ar.'>^3Dïoyfccrïjwr:œ»'1 i < W » » ■'<*■ ■ Pearson n Spearman ■ Kendall ■ Blomqvist ~r

FIGURE 3.9 ­ Illustration des corrélations entre le paramètre de variance et son esti­ mation de Bayes en fonction de la moyenne p telles qu 'observées dans des échantillons de taille 50 dans un contexte Normale­Gamma

■ Pearson D Spearman ■ Kendall ■ Blomqvist 1 1 1 1 1 1 alpha

FIGURE 3.10 ­ Illustration des corrélations entre le paramètre de variance et son es­ timation de Bayes en fonction du paramètre de forme a telles qu'observées dans des échantillons de taille 50 dans un contexte Normale­Gamma

■ ■ . ,.!.>.: ... ... I ­ ­ I l|l . . I . I I

■ Pearson D Spearman ■ Kendall ■ Blomqvist

FIGURE 3.11 ­ Illustration des corrélations entre le paramètre de variance et son es­ timation de Bayes en fonction du paramètre d'échelle 0 telles qu'observées dans des échantillons de taille 50 dans un contexte Normale­Gamma

Chapitre 3. Applications dans un contexte de lois conjuguées continues 28

avoir d'effet sur les corrélations de Spearman, de Kendall et de Blomqvist.

3.3 Uniforme­Pareto

Soit X = (A"i,... , Xn)T, le vecteur contenant les données tel que X i , . . . ,Xn\9

i.i.d. Uniforme sur l'intervalle [0,0]. Alors

/ ( x | 0 ) = 0­".I[ o,0 ](x( 1 )).I1o,„(a:( n ))

où X(i) représente la première statistique d'ordre tandis que X(n) représente la dernière.

Afin d'obtenir une loi a priori 7r(0) conjuguée à / ( x | 0 ) , on suppose que 0 ~ Pareto(a;o, a ) ,

c'est­à­dire a

On peut en déduire l'espérance a priori E[0] et la variance a priori Var[0]. On trouve

m ­ ­ ^ «>ii

a — 1

«•M = i a ­ W ­ * ) ' "

On utilise la statistique exhaustive T(X) = X<n) pour trouver un estimateur de 0 sans

biais. Puisque la loi du maximum est /„(#) = n • xn~1/ 9n, calculons l'espérance de la

statistique exhaustive. On trouve

p u 77 . i»** *■

E[X

] = l x • ^ | ^ d 0

n0"

( n + l ) 0 "

n

n + 1

On choisit donc <5*(X) = (n + \ ) X in) / n comme estimateur sans biais pour 0.

Considérons en outre un autre estimateur qui n'est pas une combinaison linéaire de X'n), à savoir l'estimateur de la méthode des moments <5A/A/(X) = 2X. On remarque

que cet estimateur est sans biais pour le paramètre 0 puisque E[2X|0] = 0. Par contre, il n'est pas très pratique puisqu'il peut s'avérer inférieur au maximum des observations provenant de la distribution conjointe / ( x | 0 ) . Par exemple, en simulant trois obser­ vations provenant d'une loi uniforme sur l'intervalle [0,12], on peut obtenir Xi = 1, x2 = 2, et x3 — 12. L'estimateur des moments est donc <5MM(X) = 10. Cet estimateur

Les sous­sections suivantes présentent les calculs des différentes corrélations étudiées

au chapitre 2. On y examine le comportement des diverses corrélations mesurées entre

le paramètre 0 et les estimateurs f5(X) et

en variant les différents paramètres

de la loi a priori Pareto(a,a:o). On suppose partout que a > 2.

3.3.1 Calcul du r de Pearson

Commençons d'abord par calculer la corrélation de Pearson r(0,<5,(X)) à l'aide de

l'équation (2.4), soit

r(M.(X)) =

Var[0]

\Vax[0] + R(ir,5*(X)Y

Puisque i?(7r,<5*(X)) = E[Var[r5„(X)]], calculons d'abord la variance de l'estimateur

<5»(X). On trouve

Var[«5.(X)] = ( ^ ± 2 ) ' • (E[X

\ ­ E

[X

}) .

n9

n

9

Puisque la loi du maximum X<

) est /„(x) =

^ , on a

VarW,(X)] = ( — V ■ (

\ n J \ n + 2 (n + 1)

/ n + l \

n0

i n J ' (n + 2)(n + l)

0

n(n + 2)'

Calculons maintenant le risque i?(7r, <5*(X)). On trouve

nin

Puisque 0 ~ Pareto(a,xo), on a

^ • ( V a r [ 0 ] + E

[0]).

R(ir,6.{X)) = , * • f

^ —

" n i n + 2) V ( a ­ l )

( a ­ °

2) ( a ­ l )

,

n(n + 2 ) ( a ­ 2 ) '

Chapitre 3. Applications dans un contexte de lois conjuguées continues 30

On obtient finalement que

r(M.(X)) =

^ ( Q ­ 1 )2( Q ­ 2 ) T n(n+2)(o­2) \ 11 ^ n(n+2) + («­D2

Contrairement à la corrélation de Pearson dans le cas Normale­Normale qui n'était fonction que de n, cette corrélation possède un facteur n2 au dénominateur. De plus,

on remarque que r(0, <S*(X)) ne dépend pas du paramètre Xo provenant de la loi a priori mais seulement des paramètres n et a. De plus, elle tend vers 1 lorsque n tend vers l'infini. En observant la figure 3.12, on remarque que, plus la taille de l'échantillon n est petite, plus la corrélation diminue rapidement lorsque le paramètre Q augmente. De plus, si la taille de l'échantillon n est assez grande, le paramètre a n'a que peu d'influence. ■ n=10 O n=50 ■ n=100 ■ n=250 ■ n=500 1 1 1 1 4 6 alpha 10

F I G U R E 3.12 ­ Corrélation r(0, <5A/V(X)) en fonction du paramètre a selon la taille

d'échantillon n dans un contexte Uniforme­Pareto

Commençons par calculer le risque i?(7r, »5A/A/(X)). R(*,6M M(X)) = E[Var[«WX)]] = E[4Var[X]] 02

= E[4

' 12n^

1

3n

• (Var[0] + E

M)

1

3n

\i<*-m<*

- 2 )

ctxl

On obtient finalement la corrélation suivante :

ri9,ôM M(X)) = ai£L (a-l)2(a-2) \ ( a - l )2( a - 2 ) "•" 3n(a-2)

\l +

Encore une fois, cette corrélation ne dépend que des paramètres Q et n mais possède par contre un facteur n au dénominateur et non n2. De plus, elle tend vers 1 lorsque n tend

l'infini. Finalement, on remarque que r(0,<5*(X)) > r(0,f5MAf(X)) lorsque n > 1 et que

Q est fixe. Ce résultat est plutôt rassurant puisque l'estimateur SMMÇX) n' a pas grand

intérêt. Finalement, en utilisant la figure 3.13, on remarque que la différence entre les deux corrélations est beaucoup plus marquée lorsque le paramètre a est grand et qu'elle est presque nulle lorsque a est petit.

3.3.2 Calcul du p de Spearman

Examinons maintenant le comportement du coefficient de corrélation de Spearman p(0,<5*(X)) selon les paramètres n, x0 et a. Pour ce faire, on simule des observations

selon le contexte Uniforme-Pareto décrit ci-dessus et on calcule p de façon empirique. On génère premièrement 0 à l'aide du logiciel R selon une loi Gamma(x0,a). Selon

la situation, on peut choisir de faire varier x0 et a ou bien de les fixer de telle sorte

que la loi a priori 7r(0) soit la plus non-informative possible. Ensuite, à partir du 0 obtenu, on simule un échantillon X de taille n = 500 selon une loi Uniforme d'intervalle [0,0]. On itère N = 10000 fois ces deux étapes pour finalement obtenir 10000 paires

Chapitre 3. Applications dans un contexte de lois conjuguées continues 32 ■ exhaustive et alpha=2 ■ moment et alptia=2 ■ exhaustive et alpha= 10 o moment et alpha= 10 — i — 400 100 200 300 500

F I G U R E 3.13 ­ Corrélation r(0, <5(X)) en fonction de la taille d'échantillon n selon

l'estimateur et le paramètre a dans un contexte Uniforme­Pareto

d'observations (0,, ( n+" y.)> c e Qui nous permet alors d'estimer les corrélations de façon

assez précise.

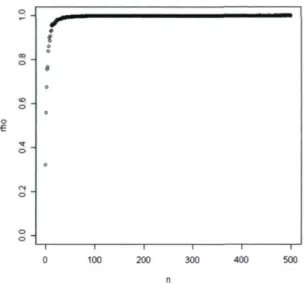
Commençons par regarder le comportement de la corrélation p(0, <5*(X)) en fonction de la taille de l'échantillon. Pour avoir une loi a priori la plus plate possible sur l'espace des paramètres tout en ayant une espérance et une variance finies pour 0, on fixe le paramètre de forme Q = 3. De plus, pour couvrir le plus de valeurs possibles de 0, on choisit le paramètre de localisation XQ = 0.001. La figure 3.14 illustre la corrélation p(0, <5*(X)) en fonction de la taille d'échantillon n. Comme on pouvait s'y attendre, plus l'échantillon est grand, plus la corrélation s'approche de 1.

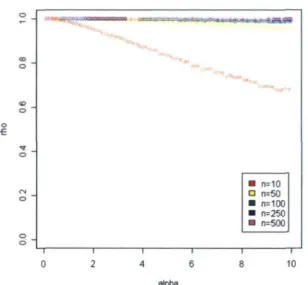
Regardons maintenant le comportement du coefficient p(0, <5*(X)) lorsque le para­ mètre de localisation x0 augmente. Puisque la variation simultanée du paramètre x0 et

de la taille d'échantillon n est intéressante, la figure 3.15 illustre le comportement de p(0, f5*(X)) selon la valeur de Xç, et ce, pour quelques valeurs de n. Prendre note que le paramètre de forme a est toujours fixé à 3. On remarque que, tout comme le coefficient de corrélation de Pearson, la corrélation de Spearman n'est pas du tout influencée par le paramètre de localisation x0. En effet, peu importe la taille de l'échantillon n, le

graphique présente des droites horizontales.

FIGURE 3.14 - Corrélation p(0,<5*(X)) en fonction de la taille d'échantillon n dans un contexte Uniforme-Pareto W^o+vrwKc ^ ^ ■ n=10 n n=50 ■ n=100 ■ n=250 ■ n=500 10 x_0

FIGURE 3.15 - Corrélation p(0, <5*(X)) en fonction du paramètre de localisation x0 selon

la taille d'échantillon n dans un contexte Uniforme-Pareto

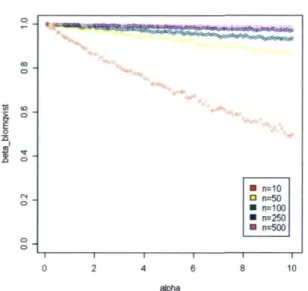
fonction du paramètre de forme a en fixant le paramètre de localisation XQ = 0.001 et ce, pour quelques valeurs de n. La figure 3.16 illustre une dimimution de la corrélation de Spearman lorsque le paramètre a augmente. De plus, on voit que le paramètre de

Chapitre 3. Applications dans un contexte de lois conjuguées continues 34

forme Q a de moins en moins d'influence sur la corrélation de Spearman lorsque la taille d'échantillon augmente. m n=10 □ n=50 ■ n=100 ■ n=250 ■ n=500 alpha

FIGURE 3.16 Corrélation p(0,<5»(X)) en fonction du paramètre de forme a selon la taille d'échantillon n dans un contexte Uniforme­Pareto

3.3.3 Calcul du r de Kendall

Pour évaluer le comportement du coefficient de corrélation de Kendall, on simule un échantillon des paires (0j, ( wi"M.) et on calcule r à l'aide de sa forme empirique. Puisque le r de Kendall compare les f™) paires de points (0,, ("„^")).); on se restreint

à N = 1000 itérations.

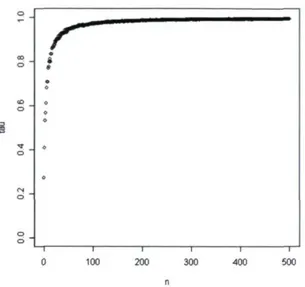
Pour commencer, on s'intéresse au comportement de la corrélation T(0,<5*(X)) en

fonction de la taille de l'échantillon n. Pour rester le plus neutre possible, on fixe les paramètres de la loi a priori tel que Xo = 0.001 et a = 3. À l'aide de la figure 3.17, on note que la corrélation r se rapproche de 1 lorsque la taille de l'échantillon n augmente. Par contre, en comparant la courbe à celle de la figure 3.14, on remarque que la corrélation de Kendall tend plus lentement vers 1 que celle de Spearman.

Observons ensuite le comportement de la corrélation r(0,t5»(X)) en fonction du paramètre de localisation x0 selon quelques tailles d'échantillons n. Prendre note que le

F I G U R E 3.17 ­ Corrélation T(0,<5»(X)) en fonction de la taille d'échantillon n dans un

contexte Uniforme­Pareto

le paramètre de localisation xo n'a pas plus d'influence sur le coefficient de corrélation de Kendall que sur les deux précédents. Finalement, la figure 3.19 illustre le comportement

I I I I »V»eS«** I I I I ■ n=10 D n=50 ■ n=100 ■ n=250 ■ n=500 I I I I i *_o

FIGURE 3.18 ­ Corrélation r(0, f5*(X)) en fonction du paramètre de localisation x0 selon

la taille d'échantillon n dans un contexte Uniforme­Pareto

Chapitre 3. Applications dans un contexte de lois conjuguées continues 36

d'échantillon n. Encore une fois, on remarque que lorsque le paramètre de forme a augmente, la corrélation diminue. De plus, cet effet est beaucoup plus prononcé lorsque la taille de l'échantillon n est faible. Finalement, le coefficient de corrélation de Kendall est plus sensible aux changements du paramètre a que le coefficient de corrélation de Spearman. c°**www—CB ^ ■ ? ^ % n=10 n=50 n=100 n=250 n=500 alpha

FIGURE 3.19 ­ Corrélation r(0,f5*(X)) en fonction du paramètre de forme a selon la taille d'échantillon n dans un contexte Uniforme­Pareto

3.3.4 Calcul du (3 de Blomqvist

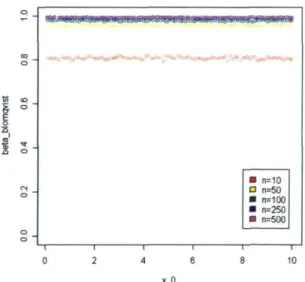
On utilise le logiciel R pour examiner le comportement du coefficient de Blomqvist /?(0, (5„(X)) tout en variant la taille d'échantillon n et les paramètres XQ et a. On simule 10 000 paires d'observations (0j, maxXj). On dénombre ensuite les points compris dans le premier quadrant formé par la jonction des médianes 0 et X .

La figure 3.20 illustre le comportement de la corrélation ,5(0, <5A/V(X)) en fonction de

la taille d'échantillon n. Le coefficient de Blomqvist augmente lorsque la taille d'échan­ tillon n augmente. Par contre, on remarque encore une fois que le 0 de Blomqvist tend moins rapidement vers 1 que le r de Pearson ou le p de Spearman.

La figure 3.21 montre le comportement de 0 en fonction du paramètre de localisation XQ selon quelques tailles d'échantillon. Sans surprise, le paramètre XQ n'a aucun effet