LE PROBL`EME P ´ERIODIQUE DE TOURN ´EES SUR LES ARCS AVEC CONTRAINTES DE CAPACIT´E ET DE GESTION DE STOCKS
JUAN PABLO RIQUELME RODR´IGUEZ
D´EPARTEMENT DE MATH´EMATIQUES ET DE G´ENIE INDUSTRIEL ´
ECOLE POLYTECHNIQUE DE MONTR´EAL
TH`ESE PR´ESENT´EE EN VUE DE L’OBTENTION DU DIPL ˆOME DE PHILOSOPHIÆ DOCTOR
(G ´ENIE INDUSTRIEL) JUIN 2014
c
´
ECOLE POLYTECHNIQUE DE MONTR´EAL
Cette th`ese intitul´ee :
LE PROBL`EME P ´ERIODIQUE DE TOURN ´EES SUR LES ARCS AVEC CONTRAINTES DE CAPACIT´E ET DE GESTION DE STOCKS
pr´esent´ee par : RIQUELME RODR´IGUEZ Juan Pablo en vue de l’obtention du diplˆome de : Philosophiæ Doctor a ´et´e dˆument accept´ee par le jury d’examen constitu´e de : M. GENDREAU Michel, Ph.D., pr´esident
M. GAMACHE Michel, Ph.D., membre et directeur de recherche M. LANGEVIN Andr´e, Ph.D., membre et codirecteur de recherche M. ROUSSEAU Louis-Martin, Ph.D., membre
D´EDICACE
`
A mes parents, Maria Dolores et H´ector, ma sœur Elisa, et mes amis.
REMERCIEMENTS
Je tiens `a remercier mes directeurs de recherche, les professeurs Michel Gamache et Andr´e Langevin, pour leurs observations, leur disponibilit´e corrections et leur orientation tout au long de ces quatre ann´ees. Mes remerciements aussi `a tous les membres du jury pour avoir accept´e de lire ce travail.
Je tiens `a remercier au Conseil National de Science et Technologie (CONACYT) du Gouvern-ment du Mexique et au Groupe d’´Etudes et de Recherche en Analyse de D´esisions (GERAD).
Mes remerciements s’adressent, enfin, `a ma soeur Elisa, mes parents H´ector et Mar´ıa Do-lores, mes amis Trish, Marcela, Olivier, Aurora, Caro, Lalo, Tere et Francisco pour leur appui. Un sp´ecial merci `a Elspeth Adams pour son support et encouragement.
R´ESUM´E
Dans cette th`ese, on introduit le probl`eme p´eriodique de tourn´ees sur les arcs avec contraintes de capacit´e et de gestion de stocks. Les arˆetes d’un r´eseau repr´esentent les clients qui n´ e-cessitent une certaine quantit´e de mat´eriel. Ce mat´eriel est mis en inventaire et consomm´e au cours du temps. Les besoins de r´eapprovisionnement indiquent la nature p´eriodique du probl`eme. Les exemples d’applications de ce probl`eme sont l’arrosage des chemins de terre dans les mines `a ciel ouvert pour supprimer la poussi`ere, l’arrosage des routes dans les r´eseaux forestiers et l’arrosage des plantes sur les trottoirs des rues. On prend l’application de l’arro-sage des routes dans les mines `a ciel ouvert. Un camion-citerne se d´eplace le long des routes en arrosant de l’eau pour supprimer la poussi`ere. `A cause de sa capacit´e limit´ee, le camion doit retourner au d´epˆot avant de commencer une nouvelle tourn´ee. `A cause de l’´evaporation de l’eau, l’humidit´e sur les routes diminue en fonction du temps. Les routes ont besoin d’un certain niveau d’humidit´e pour retenir efficacement les particules de poussi`ere. Une p´enurie arrive lorsque le niveau d’humidit´e se trouve en dessous du niveau requis. L’objectif de cette ´
etude est de trouver un ensemble de tourn´ees qui d´ebutent et finissent au d´epˆot de telle fa¸con que les coˆuts de p´enalit´e li´es `a la p´enurie, ainsi que les coˆuts de routage soient minimi-s´es. Parce que l’ordre dans lequel les arˆetes sont travers´ees et arros´ees affecte le moment o`u l’humidit´e est restaur´ee, des d´ecisions sur le routage et la gestion de l’inventaire sont prises simultan´ement. Ce probl`eme a ´et´e trait´e pour les tourn´ees sur les nœuds, i.e., les clients sont situ´es aux nœuds du r´eseau, et il est appel´e Inventory Routing Problem. Cependant, il n’a pas ´
et´e trait´e dans le domaine de tourn´ees sur les arcs. ´Etant donn´e la capacit´e limit´ee du camion et la nature p´eriodique du remplissage, on consid`ere cette application comme un probl`eme p´eriodique de tourn´ees sur les arcs avec contraintes de capacit´e (PCARP).
Au d´ebut, on consid`ere le cas du probl`eme d’arrosage o`u il n’existe qu’un seul d´epˆot (r´ e-servoir d’eau) dans le r´eseau et un seul camion citerne. On travaille sur un r´eseau mixte dans lequel, pour chaque arˆete, il y a deux arcs, un dans chaque direction de traverse. Il y a aussi une boucle artificielle au d´epˆot qui repr´esente le remplissage du camion. L’horizon de temps est divis´e en p´eriodes de temps de mˆeme dur´ee. Les coˆuts et les quantit´es en inventaire sont calcul´es pour chaque p´eriode de temps. On ´elabore un mod`ele de programmation lin´eaire en nombres entiers qui est test´e pour des exemplaires connus du probl`eme de tourn´ees sur les arcs avec contraintes de capacit´e (CARP). La solution indique la s´equence optimale de traverse et d’arrosage des arˆetes, le remplissage du camion au d´epˆot, s’il a lieu, et les coˆuts totaux de routage et de p´enalit´e pour la p´enurie sur le niveau d’humidit´e. Les limites de ce
mod`ele sont ´etablies en fonction de la taille des r´eseaux et de la longueur de l’horizon de temps qu’on est capable de r´esoudre. On est capable de trouver la solution optimale pour des r´eseaux avec 40 `a 55 arˆetes pour 20 `a 30 p´eriodes de temps. Ce qui correspond `a un horizon de temps de 30 minutes en r´ealit´e. Deux situations sont test´ees, lorsque la quantit´e d’eau arros´ee aux arˆetes est variable ou constante. Les r´esultats sont pr´esent´es pour valider les deux situations. La contribution de cette premi`ere approche est le mod`ele math´ematique pour r´esoudre le probl`eme d’arrosage des routes dans les mines `a ciel ouvert.
La deuxi`eme approche a pour objectif de r´esoudre des exemplaires de plus grande taille et pour un horizon de temps plus long. On modifie le mod`ele math´ematique pour inclure plus d’un v´ehicule et un seul d´epˆot. Avec ces modifications on est capable de trouver la solution optimale pour un exemplaire de petite taille, 11 arˆetes, pour un horizon de temps de 20 minutes. Pour r´esoudre des exemplaires de plus grande taille et incr´ementer l’hori-zon de temps, on utilise un algorithme heuristique appel´e adaptive large neighborhood search (ALNS). L’ALNS se compose de huit op´erateurs de destruction et de r´eparation choisis au hasard pour modifier la solution existante `a chaque it´eration. La performance des op´erateurs d´etermine la probabilit´e d’ˆetre choisi aux it´erations suivantes. Une meilleure performance de l’op´erateur, en termes d’am´elioration de la solution existante, correspond `a une plus grande probabilit´e d’ˆetre choisi. On utilise un ensemble d’exemplaires du CARP et un ensemble d’exemplaires cr´e´e `a partir des r´eseaux de mines `a ciel ouvert r´eels. Cette heuristique est capable de trouver une solution r´ealisable pour un horizon de temps de 300 minutes. Les op´erateurs sont test´es individuellement et en les combinant entre eux en utilisant un crit`ere d’arrˆet de 25000 it´erations. On trouve la combinaison qui obtient la meilleure am´elioration du coˆut total pour chaque ensemble d’exemplaires. Les contributions de cette approche sont la modification du mod`ele math´ematique afin d’inclure plus d’un v´ehicule et l’application de l’heuristique ALNS pour obtenir une solution `a ce nouveau probl`eme.
Finalement, un dernier probl`eme est abord´e. Il consiste `a localiser un ou plusieurs d´epˆots (r´eservoirs d’eau) le long des nœuds du r´eseau pour r´eduire les coˆuts de p´enurie et de routage du probl`eme d’arrosage des routes dans les mines `a ciel ouvert. Comme l’activit´e principale se trouve sur les arˆetes du r´eseau, ce probl`eme correspond `a un probl`eme de localisation et de tourn´ees sur les arcs (LARP) avec une composante p´eriodique. Ce probl`eme a ´et´e trait´e pour les tourn´ees sur les nœuds. Cependant, il n’y a pas une autre application dans laquelle la localisation des d´epˆots est faite dans le domaine des probl`emes p´eriodiques de tourn´ees sur les arcs. On prend des d´ecisions `a long terme telles que la localisation des d´epˆots et des d´ eci-sions `a court terme telles que le routage et la gestion des stocks. Pour cette raison, plusieurs
sc´enarios sont test´es et leur coˆut moyen est ajout´e aux coˆuts de localisation des d´epˆots afin d’obtenir un coˆut total pour le probl`eme. Les sc´enarios sont le r´esultat de changements dans les param`etres du probl`eme qui peuvent se produire sur un horizon de planification `a long terme. Trois algorithmes de localisation sont utilis´es pour obtenir une solution initiale `a la localisation d’un et de plusieurs d´epˆots. Ces algorithmes suivent le processus Location, allo-cation and Routing (L-A-R), une m´ethode divis´ee en trois parties : premi`erement, on place les d´epˆots sur les nœuds du r´eseau, puis on affecte les arˆetes aux camions et finalement on trouve une tourn´ee. L’heuristique ALNS d´evelopp´ee pour l’approche pr´ec´edente est adapt´ee et utilis´ee pour am´eliorer la solution. On compare la localisation d’un d´epˆot `a diff´erents en-droits. On compare aussi les trois algorithmes de localisation. La contribution de cette partie est le d´eveloppement d’un algorithme appliqu´e `a la localisation de d´epˆots pour un probl`eme p´eriodique de tourn´ees sur les arcs avec contraintes de capacit´e.
ABSTRACT
This dissertation introduces the periodic capacitated arc routing problem with inventory con-straints. The edges of a network act as customers that require a certain quantity of material. It is then held as inventory and consumed over time. The need for replenishment of the con-sumed material explains the periodic nature of the problem. Some examples of applications of this problem are the road watering in open-pit mine roads to suppress dust, road watering in forest roads and plant watering on street medians and sidewalks. This work focuses on the application of road watering in open-pit mines. A water truck travels along the roads of a mine spraying water to suppress dust. Because of its limited capacity, the truck needs to replenish at a water depot before starting a new route. Due to water evaporation, the humidity on the roads decreases over time. Roads require a certain amount of humidity to effectively retain dust particles. A shortage happens when the humidity level drops below the required level. The objective of this thesis is to find a set of routes that start and end at the depot so that the penalty costs associated with shortage, as well as the routing costs are minimized. Because the order in which roads are traversed and watered affects their humidity level, routing and inventory decisions are made simultaneously. This problem has been treated for node routing, i.e., the customers are located at the nodes of the network, and it is called the Inventory Routing Problem. However, it has not being addressed in the arc routing domain. This problem is modeled as a periodic capacitated arc routing problem due to capacity constraints and the frequency of service.
The first case studied is where there is only one water depot and one vehicle to travel along the network. A mathematical model is developed using a mixed network. For each edge, there are two arcs that correspond to the direction in which the edge can be traversed. There is an artificial loop at the depot that represents the refill of the truck. The time horizon is divided in time periods of equal duration. Costs and inventory levels are calculated for each time period. The model is tested for known instances of the capacitated arc routing problem (CARP). It is able to solve to optimality networks of 40 to 55 edges for a time horizon of 20 to 30 periods. Two situations are considered where the quantity of water delivered to the edges is variable and constant. Results are reported to validate both situations. The con-tribution of this first approach is the mathematical model to solve the road watering problem.
The mathematical model is then modified to include more than one vehicle. As the number of variables increases, it is capable of solving to optimality a network of 11 edges for a time
horizon of less than 30 time periods. An adaptive large neighborhood search (ALNS) heuristic is developed to solve larger networks for a longer time horizon. It is able to provide a feasible solution for networks up to 55 edges and a time horizon of 300 time periods. The ALNS con-sists of an initial solution obtained using a construction algorithm and eight destroy-repair operators that are randomly selected to modify the initial solution at each iteration of the algorithm. The performance of these operators determines the probability of being selected for the next iteration. A better performance of the operator, in terms of improving the exist-ing solution, corresponds to a higher probability of beexist-ing selected. The operators are tested individually and in different combinations. The best combination is selected for each set of instances. Apart from the CARP instances, ten instances are created to test the algorithm. These new instances correspond to road networks of real open-pit mines. The contributions of this approach are the modification of the mathematical model to include more than one vehicle and the application of the ALNS to obtain a solution for this new problem.
Finally, a new problem is addressed. It consists in the location of one or more water de-pots along the nodes of the network to reduce the shortage and routing costs. Because the solution is obtained by servicing the edges of a network, this problem corresponds to a loca-tion arc routing problem (LARP) with a periodic component. This problem has only been treated in the node routing domain. No other application has been studied for location in the arc routing domain. Long term decisions, such as depot location, are combined with short term decisions, such as routing and inventory replenishment. Several scenarios are tested and their average cost is added to the depot placement costs in order to obtain a total cost. These scenarios are the result of changes in the parameters of the problem that can occur over a long planning horizon. Three location algorithms are used to obtain an initial solution to the location of one and several depots. The algorithms follow a location, allocation and routing (L-A-R) approach in which, first the depots are placed, then the edges are assigned to the service trucks and finally, a route is formed. The ALNS developed for the previous approach is adapted and used to improve the solution. The contribution is an algorithm applied to the location of depots for a periodic capacitated arc routing problem.
TABLE DES MATI`ERES
D´EDICACE . . . iii
REMERCIEMENTS . . . iv
R´ESUM´E . . . v
ABSTRACT . . . viii
TABLE DES MATI`ERES . . . x
LISTE DES TABLEAUX . . . xiii
LISTE DES FIGURES . . . xv
LISTE DES SIGLES ET ABR´EVIATIONS . . . xvi
CHAPITRE 1 INTRODUCTION . . . 1
1.1 D´ecisions de routage et gestion de stocks . . . 2
CHAPITRE 2 REVUE DE LITT´ERATURE . . . 7
2.1 Probl`emes de tourn´ees sur les arcs avec contraintes de capacit´e . . . 7
2.1.1 Classement de probl`emes de CARP . . . 8
2.1.2 M´ethodes de r´esolution du CARP . . . 11
2.1.3 M´etaheuristiques pour le CARP . . . 15
2.2 CARP avec contraintes de p´eriodicit´e (PCARP) . . . 19
2.2.1 Mod`eles de programmation lin´eaire pour le PCARP . . . 21
2.2.2 Heuristiques et m´etaheuristiques pour le PCARP . . . 27
2.2.3 Autres applications du PCARP . . . 31
2.3 Discussion . . . 31
CHAPITRE 3 ARTICLE 1 : PERIODIC CAPACITATED ARC ROUTING PROBLEM WITH INVENTORY CONSTRAINTS . . . 34
3.1 Abstract . . . 36
3.2 Introduction . . . 36
3.3 Literature review . . . 37
3.5 Mixed integer programming model . . . 39
3.5.1 Inventory cost . . . 40
3.5.2 Routing cost . . . 42
3.5.3 Mathematical model . . . 42
3.5.4 Fixed-rate spraying . . . 46
3.5.5 Different vehicle speeds . . . 46
3.6 Test results . . . 47
3.6.1 Limits on the number of periods . . . 48
3.6.2 Comparison of models with fixed-rate and variable-rate spraying . . . . 49
3.6.3 Computational time . . . 56
3.7 Conclusion and future work . . . 58
CHAPITRE 4 ARTICLE 2 : ADAPTIVE LARGE NEIGHBORHOOD SEARCH FOR THE PERIODIC CAPACITATED ARC ROUTING PROBLEM WITH INVENTORY CONSTRAINTS . . . 61
4.1 Abstract . . . 63
4.2 Introduction . . . 63
4.3 Problem definition . . . 64
4.3.1 The problem of watering roads in open-pit mines . . . 64
4.3.2 Mathematical model . . . 65
4.4 Adaptive large neighborhood search . . . 70
4.4.1 Initial solution . . . 71
4.4.2 Improvement phase . . . 77
4.4.3 The problem of inventory constraints . . . 79
4.5 Computational results . . . 79
4.5.1 Individual performance of the operators . . . 80
4.5.2 Parameter tuning . . . 83
4.5.3 Combinations of operators . . . 84
4.5.4 Networks with low percentage of improvement . . . 85
4.6 Conclusions and future work . . . 88
4.7 Acknowledgements . . . 88
CHAPITRE 5 ARTICLE 3 : LOCATION ARC ROUTING PROBLEM WITH INVEN-TORY CONSTRAINTS . . . 89
5.1 Abstract . . . 91
5.2 Introduction . . . 91
5.2.2 Periodic capacitated arc routing problem . . . 92
5.3 Mathematical model . . . 93
5.3.1 Problem definition . . . 93
5.3.2 Mathematical model . . . 94
5.4 Location and routing algorithms . . . 100
5.4.1 Location algorithms . . . 100
5.4.2 Allocation . . . 102
5.4.3 Routing . . . 103
5.4.4 Adaptive large-neighborhood search . . . 104
5.5 Test results . . . 105
5.5.1 Parameters . . . 105
5.5.2 Alternative location of one depot . . . 107
5.5.3 Comparison of one and several depots . . . 108
5.5.4 Comparison of the depot-location methods . . . 109
5.6 Conclusion . . . 111
CHAPITRE 6 DISCUSSION G ´EN´ERALE . . . 112
CHAPITRE 7 CONCLUSION ET RECOMMANDATIONS . . . 114
7.1 Synth`ese des travaux . . . 114
7.2 Limitations de la solution propos´ee . . . 115
7.3 Am´eliorations futures . . . 115
LISTE DES TABLEAUX
Tableau 2.1 Exemple de combinaisons pour une fr´equence de 2 et 3 jours par semaine. 22
Tableau 2.2 Exemple de d´efinition de sous-p´eriodes. . . 25
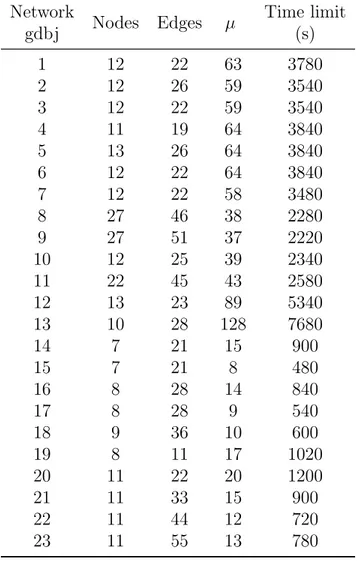
Tableau 3.1 Values of µ and time limit for gdbj instances. . . 50
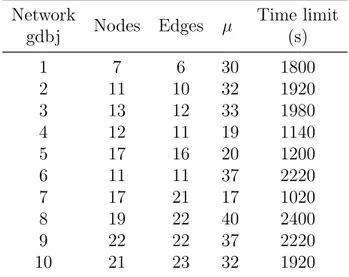
Tableau 3.2 Values of µ and time limit for jpr instances. . . 51
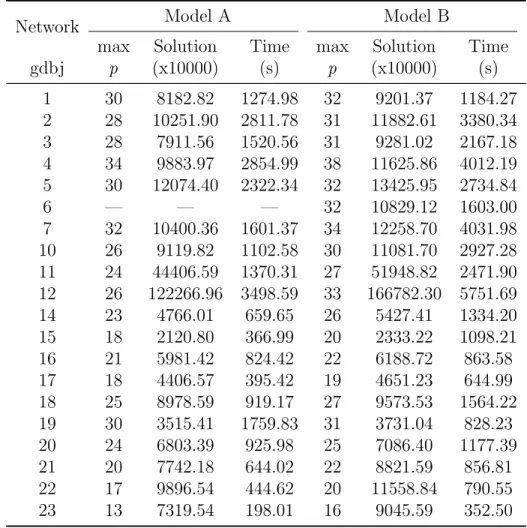
Tableau 3.3 Computational results for gdbj instances. . . 52
Tableau 3.4 Computational results for jpr instances. . . 53
Tableau 3.5 Computational results for gdbj instances after distance transformation. 53 Tableau 3.6 Maximum number of periods for which models A and B find an optimal solution within the time limit for gdbj instances. . . 54
Tableau 3.7 Maximum number of periods for which models A and B find an optimal solution within the time limit for jpr instances. . . 55
Tableau 3.8 Comparison of routes for gdbj20 network from models A and B. . . 55
Tableau 3.9 Comparison of routes for gdbj19 network from models A and B. . . 56
Tableau 3.10 Comparison of routes for jpr8 network from models A and B. . . 56
Tableau 3.11 Comparison of different vehicle capacities for jpr6 instance using model B. . . 57
Tableau 3.12 Percentage reduction in computational time when stopping criterion set to 2% relative gap for gdbj instances. . . 58
Tableau 3.13 Percentage reduction in computational time when stopping criterion set to 2% relative gap for jpr instances. . . 59
Tableau 4.1 Best solution from running the eight operators separately for gdbj ins-tances. . . 82
Tableau 4.2 Best solution from running the eight operators separately for mine instances. . . 82
Tableau 4.3 Percentage of improvement on the initial solution and computation time for the combinations of operators used for gdbj instances. . . 84
Tableau 4.4 Percentage of improvement on the initial solution and computation time for the combinations of operators used for mine instances. . . 85
Tableau 4.5 Percentage of improvement of the combinations against the best solu-tion for gdbj instances. . . 86
Tableau 4.6 Percentage of improvement of the combinations against the best solu-tion for gdbj instances. . . 86
Tableau 4.7 Comparison between three different vehicle capacities : Restricted, re-gular and unlimited. . . 87 Tableau 5.1 General information on the mine instances tested. . . 106 Tableau 5.2 Value of the objective function with one depot located at node 0 and
at node n. . . 107 Tableau 5.3 Comparison of the objective function values for one and N depots. . . . 108 Tableau 5.4 Comparison of the objective function values for one and N depots after
ALNS. . . 109 Tableau 5.5 Comparison of the objective function values for the three depot-location
methods without ALNS improvement. . . 110 Tableau 5.6 Comparison of the three depot-location methods after the ALNS
LISTE DES FIGURES
Figure 1.1 Repr´esentation d’un r´eseau. . . 2
Figure 1.2 Niveau d’humidit´e dans une arˆete de la mine `a ciel ouvert. . . 3
Figure 1.3 Niveau d’humidit´e et livraison d’eau sans p´enurie. . . 4
Figure 1.4 Niveau d’humidit´e sur les arˆetes A, B et E, a) si on choisit le trajet D-1-2-4-5-D ; b) si on choisit le trajet D-5-4-2-1-D. . . 5
Figure 2.1 Classement des probl`emes du domaine des CARP. . . 10
Figure 2.2 Deux trajets pour le CARP. . . 20
Figure 2.3 Diff´erence entre utiliser une solution pour un jour et une solution pour une semaine compl`ete. . . 20
Figure 2.4 Mod`ele M1 pour le PCARP. . . 23
Figure 2.5 Mod`ele M2 . . . 26
Figure 2.6 a. Augmentation de la quantit´e de mat´eriel dans les applications du PCARP. b. R´eduction de la quantit´e de mat´eriel dans le probl`eme PCARP avec contraintes de gestion de stocks. . . 33
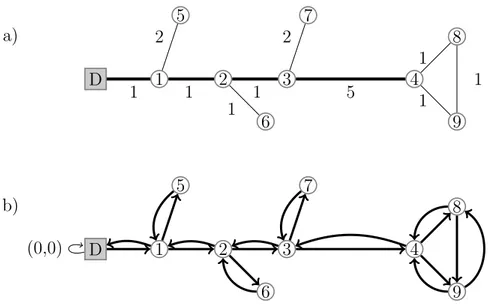
Figure 3.1 a) Representation of the road network in an open-pit mine. b) Directed network with the artificial arc (0, 0) at the depot. . . 40
Figure 3.2 Humidity inventory of edge (i, j). . . 41
Figure 3.3 Discretization of time. . . 41
Figure 3.4 Example of different truck speeds . . . 47
Figure 3.5 Representation of network gdbj19. . . 49
Figure 4.1 a) Humidity level of edge [i, j] in a continuous time horizon. b) Hu-midity level of edge [i, j] after the time horizon is discretized in equal periods. . . 67
Figure 4.2 a. Satellite view of one of the mines used to determine instances mine. b. The network that correponds to the pit shown in a. . . 80
Figure 4.3 Percentage of improvement of the cost of the initial solution when using the eight operators separately for gdbj instances. . . 81
Figure 4.4 Percentage of improvement of the cost of the initial solution when using the eight operators separately for mine instances. . . 83
Figure 5.1 Humidity level of edge [i, j] . . . 94
LISTE DES SIGLES ET ABR´EVIATIONS
ALNS Adaptive Large Neighborhood Search ARP Arc Routing Problem
CARP Capacitated Arc Routing Problem
CARPIF Capacitated Arc Routing Problem with Intermediate Facilities CARP-RP Capacitated Arc Routing Problem with Refill Points
CARPTW Capacitated Arc Routing Problem with Time Windows CPP Chinese Postman Problem
CVRP Capacitated Vehicle Routing Problem DCARP Directed Capacitated Arc Routing Problem IRP Inventory Routing Problem
LARP Location Arc Routing Problem LRPP Location Rural Postman Problem
MCARP Mixed Capacitated Arc Routing Problem M-CARP Multi-depot Capacitated Arc Routing Problem OCARP Open Capacitated Arc Routing Problem PCARP Periodic Capacitated Arc Routing Problem
PCARP IC Periodic Capacitated Arc Routing Problem with Inventory Constraints RPP Rural Postman Problem
SCARP Stochastic Capacitated Arc Routing Problem UCARP Undirected Capacitated Arc Routing Problem VND Variable Neighborhood Descent
VNS Variable Neighborhood Search VRP Vehicle Routing Problem
CHAPITRE 1
INTRODUCTION
Les particules de poussi`ere qui se retrouvent dans l’air posent un grave probl`eme de sant´e pour les travailleurs des mines et les personnes vivant dans les r´egions voisines. Les plus petites particules atteignent les voies respiratoires, et sont donc tr`es nocives (Tian et al., 1996). D’autre part, les particules plus grosses r´eduisent la dur´ee de vie des machines et des v´ehicules et peuvent aussi causer des accidents en raison de la visibilit´e r´eduite. La poussi`ere peut nuire sensiblement `a la v´eg´etation et affecter l’agriculture locale (Greening, 2011). Les pr´eoccupations environnementales augmentent lorsqu’on retrouve des particules m´etalliques m´elang´ees `a la poussi`ere. D’o`u l’importance de supprimer la poussi`ere dans les activit´es mi-ni`eres comme le forage, le dynamitage, le d´epˆot des mat´eriaux et le transport.
Nous nous concentrons sur la suppression, dans les mines `a ciel ouvert, de la poussi`ere due `a la circulation des v´ehicules le long des chemins de terre.
Les techniques de suppression de la poussi`ere comprennent des solutions `a long terme comme le pavage des chemins ou l’addition de gravier. Leur coˆut ´elev´e peut ˆetre justifi´e par l’utili-sation `a long terme des routes. Cependant, le caract`ere temporaire des routes dans les mines `
a ciel ouvert ne permet pas une telle solution.
Parmi les substances utilis´ees dans la suppression de la poussi`ere, comme le chlorure de calcium ou le chlorure de magn´esium, l’eau reste la moins ch`ere et la plus facile `a utiliser (FCM, 2005). Le seul inconv´enient est qu’elle doit ˆetre appliqu´ee p´eriodiquement en raison de sa faible r´etention au sol et de l’´evaporation continue.
L’eau s’applique en utilisant des camions-citerne qui parcourent les chemins d’une mine. Ils se remplissent `a un d´epˆot central pour commencer un nouveau trajet. L’objectif est de trouver un itin´eraire le moins coˆuteux pour les camions de telle sorte que l’efficacit´e de r´ e-tention des particules de poussi`ere soit maximis´ee. Parce que l’activit´e principale a lieu sur les chemins d’un r´eseau, et comme on utilise un v´ehicule pour r´ealiser l’activit´e principale, ce probl`eme d’application appartient `a la branche de la recherche op´erationnelle appel´ee pro-bl`emes de tourn´ees de v´ehicules. D’autre part, la gestion du niveau d’humidit´e dans les routes joue un rˆole important dans la r´eduction des coˆuts de p´enurie associ´es `a une quantit´e r´eduite
d’humidit´e. On a donc un probl`eme qui exige deux types de d´ecisions : d´ecider quelles sont les routes `a desservir et la quantit´e d’eau `a fournir `a chacune. La premi`ere d´ecision est li´ee aux probl`emes de tourn´ees sur les arcs et implique l’´elaboration d’un itin´eraire `a suivre par le camion-citerne pour atteindre les arˆetes choisies. La seconde d´ecision est un probl`eme de gestion des stocks, dans laquelle, chaque arˆete du r´eseau est un client avec un niveau d’in-ventaire qui correspond `a la quantit´e d’humidit´e et qui doit ˆetre r´eapprovisionn´e.
Mˆeme si on se concentre sur les deux principales d´ecisions, il y a d’autres consid´erations impliqu´ees dans le probl`eme de l’arrosage des chemins, telles que le nombre de camions-citerne `a utiliser, le nombre de d´epˆots d’eau `a installer et le choix des sites o`u les placer dans le cas o`u il y en a plus d’un.
1.1 D´ecisions de routage et gestion de stocks
La combinaison de deux d´ecisions, gestion de stocks et routage, a ´et´e ´etudi´ee pour des pro-bl`emes de tourn´ees sur les nœuds. Cependant, il n’existe pas d’applications dans la litt´erature concernant les probl`emes de tourn´ees sur les arcs. Pour illustrer comment la gestion de stocks et le routage sont combin´es pour obtenir une solution au probl`eme d’arrosage des routes, consid´erer la figure 1.1. Le nœud «D» repr´esente le d´epˆot et les arˆetes A `a H repr´esentent les segments de routes d’une mine `a ciel ouvert.
5 4 3 2 1 D A B C D E F G H
Figure 1.1 Repr´esentation d’un r´eseau.
Chaque arˆete a un niveau d’humidit´e qui peut ˆetre repr´esent´e avec un mod`ele de gestion de stocks tel qu’on montre dans la figure 1.2. Q repr´esente la quantit´e d’eau `a livrer et hm repr´esente le niveau d’humidit´e requis pour assurer la r´etention de la poussi`ere. Si le niveau d’humidit´e se trouve sous la ligne hm, il existe une p´enurie. Le niveau d’humidit´e ne peut pas ˆ
Figure 1.2 Niveau d’humidit´e dans une arˆete de la mine `a ciel ouvert.
On pose les hypoth`eses suivantes qui correspondent `a un mod`ele de r´eapprovisionnement par quantit´e ´economique de Silver et al. (1998) :
– La demande peut ˆetre estim´ee `a l’aide des lectures d’´evaporation d’eau dans un bac. Se-lon Neulicht et Shular (1998), l’´evaporation dans un bac est la meilleure fa¸con d’estimer l’´evaporation de l’eau au sol, mais les lectures sont effectu´ees une fois par jour. Molina-Mart´ınez et al. (2006) ont d´evelopp´e un moyen de simuler l’´evaporation horaire du bac. Ces taux d’´evaporation s’appliquent `a toutes les routes de la mine et d´ependent du moment de la journ´ee. La consommation d’eau est ´egalement affect´ee par le volume du trafic. `A chaque arˆete est attribu´ee un facteur d’´evaporation diff´erent selon le nombre de camions circulant sur la route correspondante. Les deux facteurs, l’´evaporation et le volume du trafic, sont utilis´es pour estimer le taux de consommation de l’humidit´e. – La quantit´e d’eau `a livrer ne doit pas forc´ement ˆetre un nombre entier et peut ˆetre
diff´erente `a chaque visite. Il existe une quantit´e minimum d’humidit´e sur les arˆetes quand le niveau est 0. Il existe un niveau d’humidit´e maximum qui correspond `a la quantit´e d’eau qui rend les routes boueuses et glissantes.
– Il n’y a pas un coˆut de possession de mat´eriel pour la quantit´e d’humidit´e dans les routes. Les coˆuts `a consid´erer sont les coˆuts de livraison qui correspond aux coˆuts de routage et les coˆuts de p´enurie. Les coˆuts ne changent pas par rapport au temps. – Il existe un seul mat´eriel livr´e, soit l’eau.
– On consid`ere que le r´eapprovisionnement est fait sans d´elai au d´ebut du remplissage. – On consid`ere un horizon de temps qui correspond `a un quart de travail divis´e en p´eriodes
de temps de dur´ee identique. Une p´eriode de temps est la quantit´e de temps qu’un camion-citerne prend afin de couvrir une distance constante `a une vitesse constante.
Par exemple, un camion roulant `a 20 km/h peut couvrir une distance constante de 300 m en environ 1 minute (54 secondes).
– La p´enurie est consid´er´ee et p´enalis´ee.
L’objectif de ce mod`ele de gestion de stocks est de r´eduire le coˆut de p´enurie et de trouver la fa¸con de livrer l’eau de telle sorte que le niveau d’humidit´e soit au-dessus du niveau hm. On montre cette situation `a la figure 1.3. On montre, dans cet exemple, que la quantit´e d’eau peut varier et peut ˆetre livr´ee `a diff´erents intervals de temps, mais le nievau d’humidit´e est toujours inf´erieur `a la quantit´e maximale d’humidit´e, hmax.
Figure 1.3 Niveau d’humidit´e et livraison d’eau sans p´enurie.
En consid´erant les arˆetes de la figure 1.1, on peut montrer l’implication de choisir un trajet parmi les arˆetes qui minimisent le coˆut de p´enurie `a cause du niveau d’humidit´e sur les routes. Supposons qu’on d´esire arroser les arˆetes A, B et E. Le niveau d’humidit´e est montr´e `a la figure 1.4. On peut parcourir les arˆetes dans la direction D-1-2-4-5-D ou dans la direction D-5-4-2-1-D. La figure 1.4a montre le premier trajet o`u l’arˆete A est arros´ee au temps t1, l’arˆete B est arros´ee au temps t2 et apr`es travers´e l’arˆete H sans l’arroser, on arrose E au temps t3. Au temps t3, l’humidit´e a ´et´e d´ej`a ´evapor´ee sous le niveau hm ce qui r´esulte en une p´enurie pour E. `A la figure 1.4b, on consid`ere le deuxi`eme trajet qui commence par traverser l’arˆete D sans l’arroser. On arrose E au temps t1, on traverse H et finalement on arrose B au temps t2 et A au temps t3. Au moment d’arroser B et A, on a d´ej`a une p´enurie. On va choisir le trajet en fonction de l’aire totale sous hm pour les trois arˆetes et de la priorit´e de chacune de ce trois arˆetes. Dans les deux trajets, la quantit´e livr´ee `a chacune des arˆetes est diff´erente.
d’inven-Figure 1.4 Niveau d’humidit´e sur les arˆetes A, B et E, a) si on choisit le trajet D-1-2-4-5-D ; b) si on choisit le trajet D-5-4-2-1-D.
taire. D’autres d´ecisions qui peuvent ˆetre prises sont le nombre de camions n´ecessaires pour arroser les arˆetes du r´eseau, la quantit´e d’eau `a arroser sur chacune d’elles et la localisation des d´epˆots d’eau, dans le cas o`u y en a plus d’un. Tous ces ´el´ements peuvent affecter le trajet des camions et le niveau d’humidit´e des arˆetes.
Le r´eapprovisionnement de l’inventaire sur chaque arˆete montre la nature p´eriodique de ce probl`eme. Quand on finit un trajet, il faut remplir le camion et d´ecider quelles arˆetes arroser sur le trajet suivant. `A la figure 1.4a, par exemple, l’arˆete E vient d’ˆetre arros´ee, il ne sera pas n´ecessaire de l’arroser de nouveau apr`es le remplissage du camion au d´epˆot. Par contre, les arˆetes A et B peuvent ˆetre arros´ees ainsi qu’une autre arˆete du r´eseau prenant en compte la capacit´e du camion. L’arrosage continuera jusqu’`a la fin de l’horizon de temps.
Ce probl`eme est une application des probl`emes p´eriodiques de tourn´ees sur les arcs, avec la caract´eristique que chaque arˆete a besoin d’une quantit´e de mat´eriel plus d’une fois durant l’horizon de temps, ce qui ressemble `a un probl`eme de gestion de stocks. On fait l’hypoth`ese
qu’il est possible de programmer une tourn´ee sur le r´eseau, qui d´ebute et finit au d´epˆot, pour servir les arˆetes de telle fa¸con qu’on minimise les coˆuts de routage et de la p´enurie du niveau d’humidit´e. Le nombre de combinaisons possibles augmente en raison de la taille du r´eseau. Dans les chapitres suivants, on d´ecrit les approches pour trouver une ou plusieurs tourn´ees possibles pour ce probl`eme.
Le chapitre 2 pr´esente une revue de la litt´erature qui porte sur les probl`emes de tourn´ees sur les arcs avec contraintes de capacit´e. On porte une attention particuli`ere aux probl`emes p´eriodiques et `a leurs applications. Le chapitre 3 d´ecrit le mod`ele math´ematique cr´e´e pour le probl`eme de suppression de la poussi`ere dans les mines `a ciel ouvert. Le chapitre 4 pr´esente un algorithme heuristique qui est capable de r´esoudre le probl`eme d’arrosage de chemins de terre pour des r´eseaux de grande taille. Le chapitre 5 examine la fa¸con de distribuer des r´eservoirs d’eau le long de la mine pour favoriser l’arrosage des chemins. Finalement, nos conclusions sont pr´esent´ees au chapitre 6.
CHAPITRE 2
REVUE DE LITT´ERATURE
Dans le domaine des probl`emes de tourn´ees, ceux dont l’activit´e principale se produit sur les arcs du r´eseau sont connus comme Arc Routing problems (ARP). Un r´esum´e de l’histoire de la recherche sur les ARP se trouve dans Assad et Golden (1995). Une revue des ARP est divis´e en deux parties : Eiselt et al. (1995b) pr´esentent une ´etude sur le probl`eme de postier chinois (CPP), un ARP qui vise `a trouver la tourn´ee de longueur minimale qui visite chaque arˆete d’un r´eseau au moins une fois, et Eiselt et al. (1995a) pr´esentent une revue sur le probl`eme du postier rural (RPP), un ARP similaire au CPP o`u seulement un sous-ensemble d’arˆetes ont besoin de service. Une bibliographie annot´ee a ´et´e present´ee dans Laporte et Osman (1995). Les premi`ers probl`emes d’ARP avaient pour objectif de trouver la fa¸con de parcourir les arˆetes d’un r´eseau. Des applications r´eelles telles que la collecte de d´echets ou l’´epandage sur les rues en hiver ont men´e `a l’incorporation de contraintes de capacit´e sur les v´ehicules. Ces derni`eres exemples font partie des probl`emes de tourn´ees sur les arcs avec contraintes de capacit´e (CARP).
2.1 Probl`emes de tourn´ees sur les arcs avec contraintes de capacit´e
On appelle CARP l’ensemble des probl`emes de tourn´ees sur les arcs avec contraintes de capacit´e. Ils ont ´et´e introduit par Golden et Wong (1981). Les arcs d’un r´eseau ont une demande sp´ecifique tandis que les v´ehicules qui donnent le service ont une capacit´e limit´e. Lorsque la somme des ressources accumul´ees lors de la visite des arcs d’une tourn´ee d’un v´ehicule atteint la capacit´e maximale du v´ehicule, ce dernier doit retourner au d´epˆot. Les caract´eristiques du CARP sont :
– Les arcs ont une demande qij ≥ 0. Chaque arc avec qij > 0 doit ˆetre visit´e par un v´ehicule. Les arcs sans demande peuvent ˆetre travers´es pour se d´eplacer vers des arcs qui ont besoin de services.
– La somme de la demande des arcs dans une tourn´ee ne doit pas d´epasser la capacit´e Qv du v´ehicule, i.e.,
P
ijqij ≤ Qv.
– L’objectif est de minimiser le coˆut total des trajets d’un ou plusieurs d´epˆots vers les arcs avec retour aux d´epˆots `a la fin.
Dans cette section, une revue g´en´erale de litt´erature sur le CARP sera pr´esent´ee. Certains mod`eles et m´ethodes propos´es par des auteurs du CARP sont utilis´es ´egalement par des auteurs du PCARP, d’o`u l’importance de les pr´esenter et d’en donner une br`eve explication. Deux revues de litt´erature sur le sujet du CARP ont ´et´e publi´ees r´ecement, l’une par Wohlk (2008) et l’autre par Corber´an et Prins (2010).
2.1.1 Classement de probl`emes de CARP
La figure 2.1 montre un classement des probl`emes CARP existants. Ce classement et les d´ e-finitions sont tir´es de la revue des probl`emes CARP effectu´ee par Corber´an et Prins (2010).
Classement par type de graphe
Le CARP non orient´e, ou UCARP, est bas´e sur un graphe G = (N, E) o`u N est l’ensemble de nœuds et E est l’ensemble d’arˆetes, qui peuvent se traverser dans les deux sens. Par contre, le CARP orient´e, ou DCARP, est bas´e sur un graphe orient´e G = (N, A), o`u A est l’ensemble des arcs qui peuvent ˆetre travers´es dans un seul sens. Le CARP mixte, ou MCARP, est une approche plus r´ealiste, car il combine des arcs et des arˆetes dans un graphe G = (N, E ∪ A). Le MCARP peut ˆetre utilis´e pour mod´eliser une situation o`u certains segments de rue peuvent se traverser dans un seul sens et d’autres dans les deux sens.
Pour le UCARP, DCARP et MCARP, on a un ensemble d’arcs ou arˆetes qui ont besoin de service identifi´e par Ar ⊆ A ou Er ⊆ E. L’objectif est de trouver la fa¸con la moins ch`ere de parcourir le r´eseau pour servir les ´el´ements de Er ou Ar.
Classement par type d’application
Le CARP stochastique ou SCARP (Fleury et al., 2004) ; (Fleury et al., 2005), a ´et´e d´ eve-lopp´e pour des probl`emes o`u la demande sur chaque segment de route est al´eatoire et on utilise des variables al´eatoires pour calculer la valeur de la fonction objectif. Les auteurs ont d´evelopp´e un algorithme genetique qui sera expliqu´e dans la section suivente. Des exemples plus r´ecents incluent le CARP avec incertitude (Mei et al., 2010), o`u la demande et le coˆut de parcours sont des variables al´eatoires, et le CARP avec demandes stochastiques (Laporte et al., 2010), qui est une application `a la collecte des d´echets avec des quantit´es al´eatoires. Les auteurs ont d´evelopp´e un algorithme Adaptive Large Neighborhood Search (ALNS) qui permet de modifier la solution par un processus it´eratif dans lequel on utilise un ensemble d’op´erateurs d’´elimination et d’insertion.
Dans le probl`eme multi-d´epˆot ou M-CARP (Amberg et al., 2000), le r´eseau a M d´epˆots desquels un ensemble de v´ehicules partent, servent les arˆetes requises une seule fois et fi-nissent le trajet au mˆeme d´epˆot. Une variante du probl`eme M-CARP est le CARP avec d´epˆots interm´ediaires, ou CARPIF, (Ghiani et al., 2001) dans lequel les v´ehicules visitent plusieurs stations pour charger ou d´echarger leur contenu. Une autre variante est le CARP avec points de recharge, CARP-RP, (Amaya et al., 2007). Dans cette application, des v´ ehi-cules de service tracent les lignes sur les rues et sont recharg´es `a certains nœuds du r´eseau par des v´ehicules de recharge. Ces derniers retournent vers le d´epˆot. Donc il faut programmer des rendez-vous entre les deux types de v´ehicules. Une application similaire est le CARP avec d´epˆots mobiles (Del Pia et Filippi, 2006). C’est une application de collecte des d´echets o`u on a deux types de camions : de gros camions qui ne peuvent traverser toutes les rues et de petits camions qui ont une faible capacit´e. Pour ´eviter le retour des petits camions vers le d´epˆot, il faut organiser des rendez-vous avec les grands camions qui peuvent servir de d´epˆots.
Le CARP ouvert, OCARP, a ´et´e introduit par Usberti et al. (2011) pour des applications o`u il n’existe pas de d´epˆot dans le r´eseau et il n’est pas n´ecessaire de cr´eer des trajets qui forment un cycle. Les v´ehicules peuvent d´ebuter et finir `a diff´erents nœuds du r´eseau. Deux applications sont mentionn´ees et mod´elis´ees comme un CARP : le probl`eme de lecture de compteurs, qui a ´et´e trait´e dans (Moreira et al., 2007) comme un probl`eme de postier chinois et le probl`eme de d´eterminer un chemin de coupe de diff´erents pi`eces `a partir d’une grande plaque m´etallique en utilisant plus d’un outil (Stern et Dror, 1979). Ce dernier probl`eme est trait´e comme un probl`eme de postier rural.
Le probl`eme de CARP avec fenˆetres de temps, ou CARPTW, a des contraintes pour d´ebuter et finir le service sur chacun des arcs (Mullaseril, 1997). Un probl`eme similaire a ´et´e trait´e par Tagmouti et al. (2007), o`u il existe une p´enalit´e dans le coˆut total si le service d´ebute plus tˆot ou plus tard que le temps souhait´e.
Le CARP avec demande au dead-heading a ´et´e introduit par Kirlik et Sipahioglu (2012) pour mod´eliser des situations o`u les arˆetes qui n’ont pas besoin de service (dead-heading) ont une demande qui doit ˆetre consid´er´e pour la contrainte de capacit´e du v´ehicule. On retrouve des applications dans la d´etection des mines terrestres, les activit´es de recherche et sauvetage, et la patrouille faite par des robots qui utilisent une quantit´e d’´energie en traversant les arcs qui ne sont pas desservis. On consid`ere l’´energie du robot comme la contrainte de capacit´e.
Figure 2.1 Classement des probl`emes du domaine des CARP.
Le CARP p´eriodique ou Periodic Capacitated Arc Routing Problem (PCARP) par ses ini-tiales en anglais, est le probl`eme o`u les segments de route Ar ou Er n´ecessitent une fr´equence de service et il faut les visiter une fois ou plus pendant un horizon de temps.
Classification des applications du PCARP
Cette classification a ´et´e faite par Lacomme et al. (2005). Les applications du PCARP peuvent ˆ
etre divis´ees en deux types :
Type A. Ce sont les probl`emes dont la demande est ind´ependante de la p´eriode. C’est-` a-dire que chaque fois qu’un arc est visit´e, la demande, la dur´ee et le coˆut de service sont les mˆemes. Ils ne changent pas, mˆeme si le temps entre chaque visite est diff´erent. Un exemple d’application est l’inspection de lignes ´electriques.
Type B. Ce sont les probl`emes dont chaque arc g´en`ere une certaine quantit´e de demande pour chaque p´eriode. Ainsi, la dur´ee et le coˆut de service peuvent ˆetre diff´erents chaque fois qu’on visite un arc.
Les probl`emes de type B peuvent ˆetre divis´es en : non cycliques (B1) et cycliques (B2). Dans le premier cas, l’horizon de planification peut commencer ind´ependamment de ce qui s’est pass´e `a la fin du dernier horizon, par exemple, couper la v´eg´etation le long des rues. Dans les probl`emes cycliques, l’horizon de planification doit prendre en compte la planification du dernier horizon, comme dans la collecte de d´echets.
R´ecemment, Monroy et al. (2011) ont ajout´e une deuxi`eme division pour les probl`emes de type A et B : ceux avec une fr´equence constante qui ont un besoin de services r´eguliers et ceux avec une fr´equence diff´erente pour lesquels il est n´ecessaire de calculer la fr´equence des services.
2.1.2 M´ethodes de r´esolution du CARP
Le premier mod`ele math´ematique pour le CARP a ´et´e pr´esent´e par Golden et Wong (1981). L’objectif est de minimiser la distance totale parcourue. Les auteurs montrent que le probl`eme est NP-dur et proposent un algorithme heuristique qui sera expliqu´e `a la section suivante.
Comme il sera montr´e dans les chapitres suivants, cette th`ese se concentre principalemnet sur l’utilisation de m´ethodes heuristiques et m´etaheuristiques. D’o`u l’importance d’exposer ces m´ethodes pour le CARP. N´eanmoins, il est important de souligner le travail qui a ´et´e r´ealis´e en termes d’algorithmes exacts. Un algorithme de Branch and Bound a ´et´e propos´e dans Hirabayashi et al. (1992). Cet algorithme a ´et´e test´e pour 10 exemplaires de probl`emes avec 15 `a 50 arcs qui n´ecessitent du service. Un algorithme de plans de coupe (cutting plane) a ´et´e propos´e par Belenguer et Benavent (2003) pour trouver la borne inf´erieure de quatre ensembles connus d’exemplaires CARP. Amaya et al. (2007) ont formul´e un mod`ele de pro-grammation lin´eaire en nombres entiers pour le CARP-RP. Ils ont utilis´e une m´ethode de plans de coupe pour r´esoudre ce nouveau probl`eme. Diff´erentes m´ethodes pour trouver des bornes inf´erieures pour le CARP incluent une m´ethode de coupe et de g´en´eration de colonnes combin´ees avec un probl`ene de partition d’ensembles par pour le CARP (Bartolini et al., 2013b) ; un algorithme cut first, branch-and-price second (Bode et Irnich, 2012). Martinelli et al. (2013) ont d´evelopp´e des algorithmes pour trouver des bornes inf´erieures et sup´erieures pour des exemplaires de grande taille du CARP (200 nœuds et 300 arˆetes). Un algorithme
exact pour le CARP avec demande au dead-heading a ´et´e propos´e par Bartolini et al. (2013a).
Afin d’utiliser les m´ethodes d´evelopp´ees pour les probl`emes de tourn´es sur les nœuds avec contraintes de capacit´e (CVRP), Baldacci et Maniezzo (2006) et Longo et al. (2006) ont propos´e la transformation du probl`eme CARP en un probl`eme CVRP ´equivalent en chan-geant le r´eseau G = (N, E) par un r´eseau ´equivalent G0 = (N0, E0). Ces deux m´ethodes sont bas´ees sur la transformation propos´ee par Pearn et al. (1987) dans laquelle le graphe r´esultant a 3R + 1 sommets, o`u R est le nombre d’arˆetes requises dans le graphe original. La transformation propos´ee par Baldacci et Maniezzo consiste `a r´epliquer en G0 les sommets de G autant de fois que le nombre d’extr´emit´es des arˆetes E requises et ajouter un sommet pour le d´epˆot. Pour avoir 2R + 1 sommets. Ensuite, les arˆetes E’ sont ajout´ees pour rendre le graphe G0 connexe. Le coˆut des arˆetes E0 est calcul´e en utilisant les plus courts chemins sur le graphe G et une solution r´ealisable du probl`eme comme borne sup´erieure. Le probl`eme est ensuite r´esolu en utilisant un algorithme de Branch and Cut. Cette m´ethode a ´et´e utilis´ee pour r´esoudre des probl`emes ayant jusqu’`a 98 arˆetes requises. La transformation propos´ee par Longo et al. (2006) r´esulte en un graphe G0 avec 2R + 1 sommets et les arˆetes R0 requises qui correspondent aux arˆetes R du graphe G et qui doivent ˆetre travers´ees dans la solution. Ensuite les auteurs, r´esolvent le probl`eme en utilisant un algorithme de type Branch and cut and price. Ils ont obtenu la solution optimale pour des exemplaires d´ej`a connus du CARP.
M´ethodes heuristiques et m´etaheuristiques pour le CARP ´
Etait donn´e la complexit´e du CARP, les auteurs qui ont trait´e ce probl`eme ont d´evelopp´e des m´ethodes heuristiques pour r´esoudre des exemplaires de grande taille. On pr´esentera les principaux algorithmes.
Algorithme Construct and Strike (Christofides, 1973).
Cet algorithme a ´et´e formul´e pour le probl`eme du postier chinois avec contraintes de capacit´e. Dans un graphe :
1. Construire un cycle qui sert un sous-ensemble d’arˆetes en tenant compte de deux pro-pri´et´es :
(a) La contrainte de capacit´e doit ˆetre respect´ee.
2. R´esoudre un probl`eme du couplage entre les nœuds de degre´e impair de telle fa¸con que tous les nœuds du graphe aient un degr´e pair.
3. R´ep´eter l’algorithme jusqu’`a ce que tous les arˆetes se trouvent dans un cycle.
Apr`es l’introduction du CARP (Golden et Wong, 1981), plusieurs algorithmes heuristiques ont ´et´e utilis´es pour traiter des applications sp´ecifiques. La plupart des algorithmes r´ ecem-ment d´evelopp´es sont bas´es sur les premi`eres heuristiques propos´ees. On va les d´ecrire pour pouvoir y r´ef´erer dans la description des algorithmes plus complexes. Une br`eve description de ces algorithmes se trouve dans Wohlk (2005).
Algorithme Augment Merge (Golden et Wong, 1981).
1. Construire un cycle qui relie le d´epˆot `a chaque arˆete qui a besoin de service, appel´ee tˆache, et trier en ordre d´ecroissant des coˆuts de routage.
2. D´eterminer, parmi les cycles trouv´es, et en commen¸cant par le cycle le plus grand, s’il est possible de servir un petit cycle dans un grand cycle. On appelle cette phase augmentation.
3. Si la capacit´e du v´ehicule est suffisante, fusionner deux cycles qui occasionnent la plus grande ´economie. Cette phase est r´ep´et´ee jusqu’`a ce qu’on atteigne la capacit´e du v´ e-hicule. On appelle cette phase unification.
Algorithme Path Scanning (Golden et al., 1983)
On d´ebute avec une route vide et on ajoute un arc (i, j) `a la route en utilisant un des cinq crit`eres suivants :
1. Minimiser la distance par unit´e de demande (coˆut/demande). 2. Maximiser la distance par unit´e de demande (coˆut/demande). 3. Minimiser la distance du nœud j au d´epˆot (cycles plus courts). 4. Maximiser la distance du nœud j au d´epˆot (cycles plus longs).
5. Si la capacit´e du v´ehicule est inf´erieure `a la moiti´e, maximiser la distance du nœud j au d´epˆot, sinon, minimiser la distance.
Si la demande de l’arc suivant d´epasse la capacit´e du v´ehicule, on trouve le plus court che-min au d´epˆot et on commence la route suivante. Finalement, on construit une solution avec chacun des crit`eres 1 `a 5 et on choisit celle de coˆut minimum comme solution finale.
Algorithme Route first-cluster second pour le CARP (Ulusoy, 1985)
Cet algorithme est appliqu´e sur un graphe G = (N, A) o`u Ar ⊆ A, est l’ensemble des arcs qui ont besoin de service. G se transforme comme suit :
1. Trouver un graphe GE qui contienne un tour d’Euler g´eant sans prendre en compte les contrainte de capacit´e. S’il y a des arcs r´ep´et´es de Ar, ils se transforment en arcs sans service.
2. `A partir de GE, trouver un graphe G∗ comme suit :
(a) Le premier nœud est le premier nœud de GE et les nœuds suivants sont les arˆetes de GE.
(b) Si le dernier arc de G∗ est r´ep´et´e dans GE, il est ´elimin´e.
(c) Les arcs de G∗ sont des trajets r´ealisables dans le graphe original G.
3. Calculer les coˆuts cij des arcs de G∗ en ajoutant les coˆuts des arcs correspondants dans G.
4. Calculer le plus court chemin du nœud 1 au dernier nœud dans G∗.
5. D´eterminer les trajets de chaque arc dans le plus court chemin. ´Eliminer les trajets qui n’ont pas d’arcs de Ar.
Une adaptation de cet algorithme a ´et´e utilis´e dans Kirlik et Sipahioglu (2012) pour le pro-bl`eme du CARP avec demande au dead-heading. La principale diff´erence est que les arcs non servis doivent ˆetre consid´er´es pour calculer les arcs r´ealisables dans G∗, et ce processus est fait apr`es le calcul de chaque trajet.
Algorithme insertion parall`ele (Chapleau et al., 1984) 1. D´eterminer le nombre de routes n´ecessaires.
2. Pour chaque route, trouver un arc pour d´ebuter.
3. Construire les routes en parall`ele en utilisant les processus suivants de mani`ere alter-native :
– Pour un arc donn´e, trouver la route o`u il peut ˆetre ins´erer de mani`ere `a minimiser le coˆut d’insertion.
– Pour une route donn´ee, d´eterminer l’arc `a ins´erer. 4. Arrˆeter quand tous les arcs ont ´et´e utilis´es.
Algorithme Cluster first-route second (Benavent et al., 1990). Dans un graphe G = (N, A) `a ˆetre parcouru par k v´ehicules :
1. D´eterminer k nœuds, appel´es centres, les plus ´eloign´es les uns des autres et les plus ´
eloign´es du d´epˆot.
2. Pour chaque centre, s´electionner les arˆetes les plus proches de fa¸con s´equentielle sans d´epasser la capacit´e du v´ehicule. Ces ensembles d’arˆetes sont appel´es clusters.
3. Si toutes les arˆetes requises ont ´et´e s´electionn´ees, avancer `a l’´etape de formation de trajets, sinon faire des ´echanges d’arˆetes d’un cluster `a l’autre jusqu’`a avoir toutes les arˆetes affect´ees `a un cluster.
4. Pour chaque cluster, cr´eer un trajet qui d´ebute et finit au d´epˆot.
2.1.3 M´etaheuristiques pour le CARP
Dans cette section on d´ecrit les m´etaheuristiques utilis´ees pour le CARP. On n’inclure pas les m´ethodes pour le CARP p´eriodique qui seront pr´esent´ees de fa¸con d´etaill´ee dans la section suivante.
Recherche tabou
La recherche Tabou utilise des techniques de recherche locale pour explorer un voisinage de solutions. Pour ´eviter de rester dans une r´egion r´eduite de l’espace de solution, certains mouvements sont interdits et conserv´es dans une liste tabou. Seulement une petite partie des mouvements sont inclus dans la liste tabou et sont conserv´es l`a pendant un temps relative-ment courts (Glover, 1986).
Hertz et al. (2000) ont d´evelopp´e un m´ethode de recherche tabou pour le CARP appel´ee CARPET. L’objectif est de minimiser la distance parcourue mais des solutions non r´ealisables sont admises avec une p´enalit´e. Le processus d’am´elioration (POSTOPT et SHORTEN) des solutions permet de r´eduire le nombre d’arcs sans demande et de grouper les arcs de service dans chaque cycle. Le voisinage est construit par l’addition ou la suppression d’un arc qui a besoin de service (processus ADD et DROP). Tous ces processus ont ´et´e pr´esent´es par Hertz et al. (1999).
Un algorithme de type Route First – Cluster Second a ´et´e utilis´e par Amberg et al. (2000) pour le CARP avec d´epˆots multiples. Ils cr´eent une route g´eante sans prendre en compte la contrainte de capacit´e et pour la phase de Cluster, ils utilisent une m´ethode d’arbre de poids minimal avec contraintes de capacit´e pour chaque v´ehicule disponible dans chaque d´epˆot. La
solution est am´elior´ee en utilisant des heuristiques de recuit simul´e et de recherche tabou. La liste tabou, au lieu de contenir solutions d´ej`a utilis´ees, garde les mouvements qui ont form´e de telles solutions.
Brandao et Eglese (2008) ont propos´e un algorithme de recherche tabou compl`etement d´ e-terministe pour le CARP. Ils utilisent deux m´ethodes d’insertion et une m´ethode d’´echange pour la recherche locale. La longueur de la liste tabou passe de E/2 pour E/6, dans une phase subs´equente, o`u E est le nombre d’arˆetes du r´eseau. Ils ont test´e cet algorithme sur des exemplaires d’environ 250 sommets et 375 arˆetes.
Recherche `a voisinage variable (VNS)
Cette technique vise `a effectuer une recherche dans un voisinage sp´ecifique pour trouver le minimum local et utilise une strat´egie pour effectuer la recherche sur un voisinage diff´erent. Une variante est la descente `a voisinage variable (VND) qui effectue une recherche locale dans un voisinage jusqu’`a trouver un minimum local, puis le voisinage est chang´e et le processus est r´ep´et´e. La VND applique une m´ethode de descente dans diff´erents voisinages afin de trouver l’optimum local pour chacun d’eux (Hertz et Mittaz, 2001).
Une m´ethode de descente `a voisinage variable (VND) a ´et´e propos´ee par Hertz et Mittaz (2001). La VND appliqu´ee au CARP vise `a minimiser la distance totale. L’espace S de solutions contient toutes les combinaisons qui servent les arrˆetes requises et respectent la contrainte de capacit´e. Le voisinage N (s) d’une solution s ∈ S a ´et´e trouv´e en applicant les processus SWITCH (modification de l’ordre pour servir les arcs requis), CUT (division d’un trajet non r´ealisable en trajets r´ealisables), et SHORTEN (r´eduire les trajets sans arcs requis) dans cet ordre `a un ensemble de trajets fusionn´es. Les r´esultats ont ´et´e compar´es avec deux m´ethodes de recherche tabou et les algorithmes heuristiques d´ecrits `a la section pr´ec´edente.
Un algorithme de recherche locale guid´ee a ´et´e propos´e par Beullens et al. (2003). L’al-gorithme utilise une recherche locale compos´ee de six mouvements dans la mˆeme route et dans des routes diff´erentes. Une proc´edure de recherche locale guid´ee s´electionne les arˆetes avec le coˆut de dead-heading le plus ´elev´e pour effectuer la prochaine recherche locale. La proc´edure est r´ep´et´ee jusqu’`a ce qu’un nombre maximum d’it´erations soit atteint.
le probl`eme du CARP avec d´epˆots mobiles. L’algorithme a un processus de rendez-vous pour les deux types de camions (gros et petits) de telle fa¸con qu’on respecte la contrainte de capa-cit´e pour les gros camions et on minimise le temps pris par les camions pour d´evier de leur route originale. Les voisinages ont ´et´e trouv´es par l’´echange d’arcs d’un trajet `a l’autre et par le processus SWITCH - CUT -SHORTEN de Hertz et Mittaz (2001).
Un algorithme VNS pour le CARPIF a ´et´e pr´esent´e par Polacek et al. (2008). L’algorithme utilise alternativement une heuristique gloutonne et Route first - cluster second pour g´en´erer la solution initiale. Les diff´erents voisinages sont g´en´er´ees par l’´echange de deux segments de route diff´erents choisis au hasard. L’algorithme effectue ensuite une recherche locale jusqu’`a ce qu’un crit`ere d’arrˆet soit atteint.
Algorithmes ´evolutifs
Ces algorithmes sont bas´es sur le concept de s´election naturelle. Il existe un ensemble de solutions qui forme une population initiale. Un certain nombre de solutions (parents) sont choisies de cette population et combin´ees (crois´ees) afin de cr´eer de nouvelles solutions (des-cendants). Ces derni`eres sont ensuite modifi´ees (mutation). Le processus est r´ep´et´e avec des solutions nouvellement cr´e´ees jusqu’`a ce qu’un crit`ere d’arrˆet soit atteint.
Un algorithme g´en´etique pour r´esoudre des exemplaires du CARP a ´et´e propos´e dans La-comme et al. (2001). Une partie de la population initiale est construite de fa¸con al´eatoire et l’autre partie est construite en utilisant les m´ethodes heuristiques de «Path-scanning», «Augment-Merge» et la m´ethode d’Ulusoy, d´ecrites dans la section pr´ec´edente. Ensuite, deux parents, P1 et P2, sont choisis parmi ceux de la population initiale afin de produire deux en-fants, C1 et C2. Le processus de croisement est fait en prenant une s´equence de tˆaches du P1. La s´equence est ins´er´ee dans C1 en gardant la mˆeme position qu’elle avait dans P1. Le reste des tˆaches sont ins´er´ees en C1 `a partir de P2 en gardant le mˆeme ordre qu’elles avaient dans P2. Les tˆaches qui sont d´ej`a ins´er´ees sont ´evit´ees. Le processus est similaire pour C2 en ´ echan-geant les rˆoles de P1 et P2. Un des enfants est donc s´electionn´e al´eatoirement pour suivre un processus de mutation par recherche locale, et enfin, remplacer l’un des parents. L’algorithme s’arrˆete quand on atteint un nombre maximum d’it´erations. Pour les exemplaires test´es en utilisant cet algorithme g´en´etique, on a obtenu des r´esultats de qualit´e comparable `a ceux obtenus avec la m´ethode de recherche tabou, CARPET.
a ´et´e d´ecrit dans Fleury et al. (2005). La quantit´e de demande sur chaque arc/arˆete est une variable al´eatoire normale N (qij, σij) avec une borne sup´erieure ´egale `a la capacit´e Qk des v´ehicules. Les mˆemes auteurs ont propos´e un algorithme m´em´etique pour r´esoudre le SCARP (Fleury et al., 2004). Cet algorithme travaille de fa¸con similaire `a l’algorithme g´en´etique mais avec un processus de recherche locale pour am´eliorer le croisement. Les auteurs ont aussi utilis´e des m´ethodes math´ematiques pour traiter les ´el´ements al´eatoires du probl`eme comme la demande sur chaque segment de route, le coˆut total de chaque route et la possibilit´e de s’arrˆeter avant de finir le service sur un segment de route lorsque la demande exc`ede la ca-pacit´e du v´ehicule.
Hongtao et al. (2013) ont utilis´e un algorithme g´en´etique avec un processus de perturbation pour le CARP-MD. L’algorithme est similaire `a celui propos´e par Lacomme et al. (2001), sauf que, quand un enfant s´electionn´e au hasard remplace un parent, il est soumis `a un m´ecanisme de perturbation par un double ´echange (´echange de deux arˆetes avec une autre solution), si l’enfant est un clone de l’une des solutions dans le bassin de parents. Ils mettent aussi en place une recherche locale pour les descendants s´electionn´es.
Liu et al. (2012) ont d´evelopp´e un algorithme g´en´etique pour le CARP avec plusieurs d´epˆots et v´ehicules ayant diff´erentes capacit´es. Les algorithmes utilis´es pour former la population ini-tiale (partition, path scanning) doivent ˆetre modifi´es pour inclure des d´epˆots multiples et des v´ehicules h´et´erog`enes. Apr`es que le croisement et la recherche locale soient termin´es, l’algo-rithme recommence avec les deux meilleures solutions et les solutions nouvellement g´en´er´ees. Cette deuxi`eme phase est faite avec une probabilit´e plus ´elev´ee d’appliquer la recherche locale.
Liu et Ray (2012) ont propos´e un algorithme m´em´etique pour le CARP. L’ensemble des solutions initiales est form´e en utilisant l’algorithme path scanning. Le croisement est fait en affectant des nombres al´eatoires aux tˆaches de deux parents. Pour les enfants, ces nombres repr´esentent l’ordre d’ex´ecution des tˆaches. Ensuite, ils utilisent un processus de recherche locale en utilisant des m´ethodes d’insertion et d’´echange.
Liu et al. (2013) ont d´ev´elop´e un algorithme m´em´etique avec une nouvelle forme de croisement dans laquelle, on prend la s´equence de tˆaches la plus longue pour le plus petit deadheading, qui est similaire dans les deux parents P1 et P2 et on l’ajoute aux deux enfants C1 et C2 au mˆeme endroit. Le reste des tˆaches est copi´e dans le mˆeme ordre de P1 `a C2 et de P2 `a C1. Une processus de recherche locale it´er´ee est utilis´e si la solution est tr`es proche de celle du meilleur parent dans la population.
Autres algorithmes
Dans Greistorfer (2003) on trouve un algorithme de recherche tabou combin´e avec un algo-rithme de recherche dispers´ee. Ce dernier algorithme combine les processus de diversification et intensification de fa¸con systematique et non al´eatoire (Mart´ı et al., 2006). Un ensemble de solutions initiales est obtenue `a l’aide d’une heuristique de construction. Le voisinage est obtenu par une combinaison des op´erations d’insertion et d’´echange de s´equences de tˆaches. Une liste tabou conserve un certain nombre d’it´erations dans lequel un mouvement d’inser-tion / ´echange ne peut pas ˆetre invers´e. Le processus de diversification est fait `a l’aide de la recherche dispers´ee en utilisant un nombre aleatoire de solutions obtenu de l’ensemble initial. Apr`es un nombre d’it´erations, l’op´erateur qui a donn´e les meilleurs r´esultats est utilis´e pour continuer la recherche.
2.2 CARP avec contraintes de p´eriodicit´e (PCARP)
Le PCARP est une extension du CARP auquel on ajoute des contraintes de p´eriodicit´e des visites, c’est-`a-dire, les arcs d’un r´eseau peuvent ˆetre visit´es plus d’une fois dans un horizon de temps. La demande de chaque arc dans le r´eseau est diff´erente. Quelques arcs ont une demande tr`es grande, d’autres ont une demande tr`es petite. La solution est de g´en´erer un horizon qui permet de laisser de cˆot´e les arcs `a faible demande pour une ou plusieurs p´eriodes et se concentrer sur les arcs `a forte demande. Cependant, `a la fin de l’horizon chaque arc sera servi au moins une fois. Certains seront servis plus d’une fois.
Afin d’illustrer l’importance du PCARP et sa diff´erence avec le CARP, on va utiliser l’appli-cation de la collecte de d´echets. La figure 2.2 montre deux trajets qui peuvent ˆetre r´ealis´es par un ou deux v´ehicules. Certains arcs (ceux en plus fonc´e) ont besoin de service. La figure 2.3 montre les mˆemes trajets r´ep´et´es pour un horizon de temps d’une semaine. Si on applique une approche CARP, la mˆeme solution est utilis´ee chaque jour (p´eriode). Cependant certains arcs ne g´en`erent pas une quantit´e suffisant de d´echets pour ˆetre servis et on peut seulement les traverser. L’approche PCARP comprend une solution pour la semaine compl`ete plutˆot que pour un seul jour, de telle fa¸con qu’on modifie les trajets pour accommoder seulement les arcs qui ont besoin de service.
Figure 2.2 Deux trajets pour le CARP.
Figure 2.3 Diff´erence entre utiliser une solution pour un jour et une solution pour une semaine compl`ete.
aux probl`emes de tourn´ees sur les arcs avec capacit´es pour d´eterminer la tourn´ee des v´ ehi-cules `a chaque jour plutˆot que d’avoir une solution g´en´erale donn´ee par le CARP. De plus, les applications du CARP trouv´ees dans la litt´erature consid´eraient des r´eseaux non orient´es
et un seul horizon de temps (Lacomme et al., 2005). Toutefois les applications r´eelles comme la collecte des d´echets se font g´en´eralement sur un r´eseau mixte.
Il est important d’´etablir les caract´eristiques g´en´erales du PCARP d´ecrites dans Lacomme et al. (2002), Chu et al. (2005) et Lacomme et al. (2005).
– Le PCARP est d´efini sur un horizon de temps H. Cet horizon peut changer d’une application `a l’autre mais est toujours compos´e de p´eriodes de temps. On a un total de P p´eriodes de temps de mˆeme dur´ee.
– On a un ensemble de V v´ehicules, chacun avec une capacit´e Q. Dans les applications trouv´ees, tous les v´ehicules ont la mˆeme capacit´e. N´eanmoins, il est possible d’avoir une flotte de v´ehicules avec des capacit´es diff´erentes.
– Les v´ehicules doivent d´ebuter la tourn´ee au d´epˆot initial et finir au mˆeme d´epˆot ou `a un autre.
– Le r´eseau G = (N, E ∪ A) est d´efini par N , l’ensemble des intersections de rues ; E, l’ensemble des segments de route non orient´es et A, l’ensemble de segments de route orient´es. C’est ainsi que le graphe devient mixte.
– Les arˆetes et les arcs ont un coˆut de travers´ee Cij, une demande qij et une activit´e avec une fr´equence fij qui repr´esente le nombre de services que le segment (i,j) n´ecessite dans l’horizon T . La fr´equence est born´ee par le nombre des p´eriodes, ainsi, 1 ≤ fij ≤ P mais au plus une fois par p´eriode.
– On parle de p´eriodicit´e lorsque les activit´es de service se d´eroulent `a intervalles r´eguliers. – On appelle espacement le temps ´ecoul´e entre chaque visite.
Le PCARP est NP-dur (Lacomme et al., 2002) parce qu’il inclut le cas principal du CARP avec une seule p´eriode. Golden et Wong (1981) ont d´emontr´e que le CARP ´etait NP-dur.
2.2.1 Mod`eles de programmation lin´eaire pour le PCARP Mod`ele de combinaisons jour-tˆache
Le premier mod`ele de programmation lin´eaire en nombres entiers pour le PCARP a ´et´e propos´e par (Chu et al., 2005). Quelques consid´erations importantes pour ce mod`ele :
– Le mod`ele est bas´e sur un graphe non orient´e G = (X, E) o`u X repr´esente l’ensemble de nœuds et E l’ensemble d’arˆetes.
– Un ensemble R ⊆ E repr´esente les tˆaches (arˆetes `a servir). Chaque tˆache a une fr´equence de r´ealisation fij. Un sous-ensemble ER(S) ⊆ E, o`u S ⊆ X repr´esente les arˆetes qui
sont coup´ees par la coupe (S,X-S).
– Tous les v´ehicules sont identiques et ils ont la mˆeme capacit´e W .
– Il existe un ensemble de combinaisons possibles K des p´eriodes p = 1, 2, . . . , P . Le nombre de p´eriodes dans chaque combinaison est reli´e `a la fr´equence fij.
On a une matrice A (0 ou 1) de taille K × P , o`u K est le nombre de combinaisons possibles et P est le nombre de p´eriodes sur un horizon T. La matrice A s’´elabore avant de r´esoudre le mod`ele en consid´erant les bornes sup´erieure et inf´erieure d’espacement entre deux visites sur la mˆeme arˆete. Par exemple, si la fr´equence pour une certaine arˆete est fij = 2, et l’horizon est d’une semaine, une combinaison peut ˆetre (lundi, jeudi) ou (mardi, vendredi). Un exemple de combinaisons possibles est montr´e au tableau 2.1 pour des combinaisons de 2 et 3 visites par semaine.
Tableau 2.1 Exemple de combinaisons pour une fr´equence de 2 et 3 jours par semaine.
P´eriode f (u) = 2
K / p Lundi Mardi Mercredi Jeudi Vendredi
1 x x 2 x x 3 x x 4 x x 5 x x . . . f (u) = 3 1 x x x 2 x x x . . .
Mod`ele M1 (Chu et al., 2005).
Soit la variable xijvp = 1 si l’arˆete (i, j) est travers´ee du sommet i vers j par le v´ehicule v durant la p´eriode p, 0 sinon ; lijvkp = 1 si la tˆache (i, j) s’effectue du sommet i vers j par le v´ehicule v, `a la p´eriode p en utilisant la combinaison k ; 0 sinon ; et zijk = 1 si la tˆache (i, j) utilise la combinaison k ; 0 sinon. Soit aussi le param`etre Cij, le coˆut de traverser l’arˆete (i, j), Qijkp, la demande de l’arˆete (i, j) pour la combinaison k durant la p´eriode p, et W , la capacit´e des v´ehicules. On suppose que tous les v´ehicules ont la mˆeme capacit´e. On pose Akp = 1 si la combinaison k couvre la p´eriode p, 0 sinon. La figure 2.4 montre ce mod`ele.
min X (i,j)∈E V X v=1 P X p=1 Cij(xijvp+ xjivp) (2.1) s.c : X k∈comb(i,j) zijk = 1 ∀(i, j) ∈ R (2.2) X (i,j)∈E xijvp = X (i,j)∈E xjivp ∀i ∈ X, v = 1, . . . , V, p = 1, . . . , P (2.3) xijvp ≥ X k∈comb(i,j) lijvkp ∀(i, j) ∈ R, v = 1, . . . , V, p = 1, . . . , P (2.4) xjivp ≥ X k∈comb(i,j) ljivkp ∀(i, j) ∈ R, v = 1, . . . , V, p = 1, . . . , P (2.5) V X v=1
(lijvkp+ ljivkp) = AkpZijk ∀(i, j) ∈ R, k ∈ comb(i, j), p = 1, . . . , P (2.6) X
(i,j)∈R X k∈comb(i,j)
Qijkp(lijvkp+ ljivkp) ≤ W ∀p = 1, . . . , P, v = 1, . . . , V (2.7) X
i∈S X
j /∈S
xijvp ≥ (lijvkp+ ljivkp) ∀S ⊆ {2, . . . , n}, (r, s) ∈ ER(S),
p = 1, . . . , P, k ∈ comb(i, j), v = 1, . . . , V (2.8) xijvp, xjivp, zijk, lijvkp, ljivkp ∈ {0, 1} ∀(i, j) ∈ R, p = 1, . . . , P, v = 1, . . . , V
(2.9)
Figure 2.4 Mod`ele M1 pour le PCARP.
La fonction objectif (2.1) permet de minimiser le coˆut Cij de traverser le r´eseau en trouvant une combinaison de p´eriodes pour executer chaque tˆache fij fois dans l’horizon de temps. Les contraintes (2.2) permettent qu’une seule combinaison k soit affect´ee `a chaque tˆache (i, j). Les contraintes (2.3) sont les contraintes de conservation de flux. Les contraintes (2.4) et (2.5) permettent d’assurer qu’on puisse servir l’arˆete (i, j) si et seulement si on la traverse. Dans les contraintes (2.6), une arˆete est servie durant la p´eriode p si et seulement si p fait partie de la combinaison k qui a ´et´e s´electionn´ee pour la tˆache (i, j). Ces contraintes permettent