j3c75
Université de Montréal
Réduction de dimensionnalité
non linéaire et vorace
par Marie Ouimet
Département d’informatique et de recherche opérationnelle Faculté des arts et des sciences
Mémoire présenté à la faculté des études supérieures en vue de l’obtention du grade de
Maîtrise en Informatique
jr. décembre, 2004
Zo05
Oh
Université
de Montréal
Direction des bibliothèques
AVIS
L’auteur a autorisé l’Université de Montréal à reproduire et diffuser, en totalité ou en partie, par quelque moyen que ce soit et sur quelque support que ce soit, et exclusivement à des fins non lucratives d’enseignement et de recherche, des copies de ce mémoire ou de cette thèse.
L’auteur et les coauteurs le cas échéant conservent la propriété du droit d’auteur et des droits moraux qui protègent ce document. Ni la thèse ou le mémoire, ni des extraits substantiels de ce document, ne doivent être imprimés ou autrement reproduits sans l’autorisation de l’auteur.
Afin de se conformer à la Loi canadienne sur la protection des renseignements personnels, quelques formulaires secondaires, coordonnées ou signatures intégrées au texte ont pu être enlevés de ce document. Bien que cela ait pu affecter la pagination, il n’y a aucun contenu manquant.
NOTICE
The author of this thesis or dissertation has granted a nonexciusive license allowing Université de Montréal to reproduce and publish the document, in part or in whole, and in any format, solely for noncommercial educational and research purposes.
The author and co-authors if applicable retain copyright ownership and moral rights in this document. Neither the whole thesis or dissertation, nor substantial extracts from it, may be printed or otherwise reproduced without the author’s permission.
In compliance with the Canadian Privacy Act some supporting forms, contact information or signatures may have been removed from the document. While this may affect the document page count, it does flot represent any loss of content from the document.
Université de Montréal
Faculté des études supérieures
Ce mémoire intitulé:
Réduction de dimensionnalité
non linéaire et vorace
présenté par: Marie Quimet
a été évalué par un jury composé des personnes suivantes:
Pierre Poulin (président-rapporteur) Yoshua Bengio (directeur de recherche) Ba1zs Kégi (membre du jury)
$ommaire
Les méthodes spectrales de réduction de dimensionnalité et les méthodes de segmentation spectrale exigent le calcul des vecteurs propres principaux d’une ma trice de taille n x n où n est le nombre d’exemples. Des techniques ont été pro posées dans la littérature pour accélérer les méthodes à noyau en se concentrant sur un sous-ensemble de in exemples. Nous proposons une procédure vorace pour la sélection de ce sous-ensemble, qui est basée sur la distance dans l’espace des ca ractéristiques entre un exemple candidat et le sous-espace généré par les exemples précédemment choisis. Dans le cas de l’ACP à noyau ou de la segmentation spec trale, nous obtenons un algorithme en O(nz2n), où ni « n, qui, contrairement aux techniques précédemment proposées, peut se formuler de façon en-ligne. Pour la même complexité en temps, nous pouvons également calculer la projection des exemples non choisis sur le sous-espace engendré par les exemples choisis dans l’espace des caractéristiques. En représentant ainsi les exemples par leur projection nous obtenons une approximation de plus faible rang de la matrice de Gram sur toutes les données. Nous pouvons également borner l’erreur correspondant à cette approximation de la matrice de Gram.
Mots-clés: apprentissage non-supervisé, réduction de dimensionnalité, méthodes spectrales, noyaux, algorithmes voraces.
$ummary
Spectral methods for dimensionnality reduction and methods for spectral dus tering require the calculation of the principal eigenvectors of a matrix of size nx n where n is the number of examples. Techniques were proposed in the literature to accelerate kernel methods by focusing on a subset of ni examples. We propose a greedy procedure for the selection of this subset, which is based on the distance in the feature space between a candidate example and the subspace spanned by the previously selected examples. In the case of kemel PCA or spectral clustering, we get an algorithm in O(m2n), where in < n, which can be formulated in an online
setting. For the same complexity in time, we can also calculate the projection of the non-selected examples on the subspace spanned by the chosen examples in the feature space. By representing the examples by their projection we obtain a lower rank approximation of the Gram matrix on ail the data. We can also bound the error corresponding to this approximation of the Gram matrix.
Keywords : unsupervised learning, dimensionnality reduction, spectral me thods, kemels, greedy algorithms.
Table des matières
Sommaire iii
Sumrnary iv
Table des matières vi
Liste des figures ix
Liste des tableaux xi
Liste des algorithmes xii
Introduction 1
1.1 Aperçu du mémoire 2
1.2 Notation et vocabulaire 4
2 Le fléau de la dimensionnalité 5
2.1 Manifestations du fléau de la dimensionnalité 6
2.1.1 Distance euclidienne 6
2.1.2 Augmentation de la capacité 6
2.1.3 Distribution des exemples 7
2.2 Vaincre le fléau de la dimensionnalité $
2.2.1 Restreindre la classe de fonctions . . . $
2.2.2 La sélection de variables 9
2.2.3 La réduction de dimensionnalité 9
3 Méthodes de réduction de dimensionnalité non linéaire 11
3.1 Réduction linéaire de dimensionnalité 12
TABLE DES MATIÈRES vii
3.2 L’analyse en composantes principales non linéaire 14
3.2.1 Deuxième version de I’ACP 15
3.2.2 L’astuce du noyau 17
3.2.3 Centrer les points dans l’espace des caractéristiques . . . 1$
3.3 Quelques méthodes à noyaux 20
3.3.1 La segmentation spectrale 21
3.4 Limitations de ces méthodes 22
3.5 Solutions proposées 23
4 Méthode vorace pour la reduction non linéaire de dimensionnalité 26
4.1 La technique du dictionnaire 27
4.1.1 Mise à jour du dictionnaire 28
4.1.2 Mise à jour des coefficients at 30
4.1.3 L’approximation de la matrice de Gram 31 4.1.4 Décomposition en vecteurs et valeurs propres généralisée . 31
4.2 Qualité de l’approximation 32
4.3 Intuition de la méthode 34
4.4 Normalisation du noyau 34
4.4.1 Normaliser avant ou après l’approximation‘ 34
4.4.2 Normaliser après l’approximation 36
4.4.3 Invariance à la translation dans l’espace des caractéristiques 38
4.5 Analyse de la complexité 40
5 Cadre expérimental 44
5.1 Comparer les algorithmes de réduction de dimensionnalité . . . . 44
5.1.1 Intervalles de confiance 45
5.2 Données utilisées 46
5.3 Version de l’algorithme utilisée 48
5.3.1 Choix des hyper-paramètres 48
6 Expériences 49
6.1 Description des expériences 49
6.2 Résultats 50
6.2.1 Évaluation de la technique du dictionnaire en comparaison avec lorsqu’on utilise la matrice de Gram complète . . . 50
6.2.2 Temps d’exécution 51
6.2.3 Comparaison avec d’autres techniques d’approximation 53
7 Conclusion 56
TABLE DES MATIÈRES viii
Liste des figures
2.1 Les trois figures rouges (la ligne, le carré et le cube) ont une lon gueur, une surface ou un volume correspondant à la moitié des fi gures noires qui les contiennent. Plus la dimensionnalité augmente, plus le côté de la figure rouge doit grandir pour que la proportion
reste 1/2 7
2.2 Longueur du côté c du sous-hypercube nécessaire pour occuper une fraction r du volume de l’hypercube unité. Cette longueur aug mente rapidement lorsque la dimensionnalité d augmente. Tiré de (HAs11E, TIBsHIRANIetFRIEDMAN 2003, p. 23) $
3.1
À
partir d’une spirale dans un espace en trois dimensions, l’algo rithme de réduction de dimensionnalité trouve un système de coor données dont la première dimension correspond à un déplacement le long de la spirale du centre vers l’extérieur et la deuxième di mension, à un déplacement de l’avant vers l’arrière. En (A), on représente la variété, en (B), des points tirés de cette variété et en (C), les mêmes points dans le nouveau système de coordonnées.Tiré deRowEls etSAuL(2000) 12
3.2 L’ACP appliquée à une gaussienne en deux dimensions. (A) est le système de coordonnées original et (B) correspond aux directions de principale variation des données. Ces directions sont données par les vecteurs propres trouvés par l’ACP et les longueurs des axes, par les valeurs propres et correspondent aux variances dans
ces directions 14
3.3 L’ACP classique comparée à l’ACPà noyau. Les lignes pointillées correspondent aux points ayant la même projection sur le premier vecteur propre. Dans le cas de l’ACP à noyau, ces lignes sont des courbes dans R2. Tiré de (ScH&KoPf, SM0LA etMULLER 1998). . 15
LISTE DES FIGURES x
3.4 L’effet de différents noyaux sur l’ACP à noyau. On affiche les lignes de projection constante sur les 3 premiers vecteurs propres. Les trois premières colonnes correspondent au noyauK(x, y) = (x• y)’,
pour c = 1,2, 3. Dans la quatrième colonne on a utilisé le noyau
gaussien et dans la dernière colonne, le noyau sigmoïdal. L’ACP classique, dans la première colonne, ne parvient pas à une bonne réduction de dimensionnalité, tandis qu’avec tous les autres noyaux on parvient à extraire de l’information pertinente. Images tirées de
(ScHôLK0PF, SM0LA etMtjLLER 1998) 18
3.5 Avec la décomposition en vecteurs propres du Laplacien d’un graphe on peut trouver une coupe qui permet de bien segmenter le graphe 22 4.1 Dans l’espace des caractéristiques, l’exemple hors dictionnaire (x,)
est approximé par une combinaison linéaire des exemples du dic tionnaire (Xd(i)), i = 1,... ,nz1_j si sa distance à sa projection sur le sous-espace généré par les exemples du dictionnaire, n’est
pas trop grande 27
4.2 En gris on représente le sous-espace généré par les 3 gros points noirs dans l’espace des caractéristiques (on suppose que ce sous-espace passe par l’origine). Les flèches bleues représentent les di rections de principale variation estimées par l’ACP. Dans notre tech nique, plutôt que d’estimer les directions de principale variation sur un sous-ensemble de points (a), on les estime sur la projection (b) de tous les points sur le sous-espace généré par le sous-ensemble
de points (c) 35
5.1 Cinq cents points tirés d’une spirale avec un bruit gaussien 47 5.2 Quelques images tirées des classes O et 1 des données MNIST. . . 47
6.1 Les deux premières dimensions de la représentation obtenue avec l’ACP à noyau sur les classes O (+) et 1 (x) des données MNIST (o = 3 1.6, n = 1300). L’image à gauche a été obtenue avec la ma
trice de Gram complète et les deux autres, avec la technique du dic tionnaire. Les points du dictionnaire sont désignés par le symbole •. On obtient une représentation presque identique avec 34 points dans le dictionnaire. Même avec seulement 4 points, le résultat est
LISTE DES FIGURES xi
6.2 Même avec de très petits dictionnaires, l’erreur de généralisation est comparable à celle obtenue avec la matrice de Gram corres pondant à l’ensemble d’entraînement au complet. Les courbes cor respondant à la méthode du dictionnaire sont étiquetées avec o-, l’écart-type du noyau gaussien, E, le paramètre d’exactitude et ni, le nombre maximal de points dans le dictionnaire pour cette courbe (obtenu pour lenmaximal). Les courbes correspondant aux méthodes sans dictionnaire sont étiquetées aveco-seulement. On a gardé trois composantes principales pour MNIST et deux pour la spirale. Les expériences individuelles correspondant aux symboles . et ont le même temps d’exécution, mais l’erreur de généralisation est bien plus faible pour la méthode du dictionnaire. Nous observons le même phénomène pour des symboles o et o correspondant à un plus long temps d’exécution. Plus de détails sur la relation entre le temps d’exécution et l’erreur de généralisation sont donnés au
Tableau 6.1 52
6.3 Comparaison de la méthode du dictionnaire avec la méthode de Nystrôm où la décomposition est faite seulement sur la matrice de Gram correspondant à un sous-ensemble aléatoire de l’ensemble d’entraînement en ignorant les autres exemples de cet ensemble. Nous montrons deux stratégies de choix de sous-ensemble pour la méthode du dictionnaire le sélection vorace proposée et un choix aléatoire simple. Ces expériences ont été exécutées sur les données MNIST avec un ensemble d’entraînement de la taille 3365 en gar
Liste des tableaux
6.1 Comparaison entre les erreurs de généralisation pour la technique du dictionnaire et la technique classique pour un temps d’exécution fixe. Les erreurs et lesncorrespondent à ceux donnés à la figure 6.2 pour MNIST. Certains de ces résultats y sont rapportés par des cercles et des carrés sur les courbes. Des résultats semblables ont
Liste
des algorithmes
3.1 Analyse en composantes principales 13 3.2 Analyse en composantes principales à noyau 20 3.3 La segmentation spectrale telle que présentée dans(BENGI0, DELAL
LEAU,Li Roux, PAIEMENT, VINCENT etOuJMET2004) 23 4.1 Algorithme vorace de plongement spectral 33 4.2 Algorithme vorace de plongement spectral invariant à la translation
dans l’espace des caractéristiques 41 4.3 Construit un dictionnaire de la taille spécifiée in,, avec un niveau
n
À
ma famille et à SimonCHAPITRE
1
INTRODUCTION
L’objectif de l’apprentissage statistique est de tirer de l’information d’un en semble de données. Alors que dans l’apprentissage supervisé à chaque exemple est associée une étiquette qu’on essaye de prédire, dans l’apprentissage non-supervisé
(HINT0N etSEJN0w5KI 1999) oncherche de façon générale à caractériser les données.
On se pose des questions comme : Où se répartissent les données dans l’espace? Quelle distribution aurait pu générer ces données? Quelles sont les zones de haute densité? Les données se retrouvent-elles dans des groupements différents? On peut aussi chercher àreprésenter les données de façon plus compacte, par des at tributs statistiquement indépendants, à éliminer la redondance dans les variables, à découvrir les véritables degrés de liberté ou à débruiter les données. Dans ce mémoire, nous nous intéressons à un domaine de l’apprentissage non-supervisé l’apprentissage de variétés. On utilise souvent des exemples tirés du domaine de la vision pour présenter ce type de problèmes. Prenons l’exemple d’une caméra numérique qui photographie un objet fixe sous plusieurs angles. Les images ainsi obtenues sont représentées par quelques milliers de pixels alors qu’on pourrait résumer chacune de ces images simplement par trois valeurs correspondant à la position de la caméra. Ces coordonnées constituent les seuls véritables degrés de
1.1 Aperçu du mémoire 2
liberté dans ce problème (si on suppose qu’à chaque position, la caméra ne peut avoir qu’une seule orientation, soit de viser l’objet bien au centre de son objectif). Dans l’espace de quelques milliers de dimensions où chaque point correspond à une image possible, les images qui correspondent à cet objet fixé se retrouveront sur une variété repliée dont la dimensionnalité intrinsèque est de 3.
Les méthodes spectrales de réduction de dimensionnalité peuvent découvrir de telles variétés. Elles ont fait l’objet ces dernières années d’un grand intérêt et plu sieurs variantes ont été développées. Ces techniques sont toutefois coûteuses à la fois en temps et en mémoire. Or, de nos jours, à l’ère de l’informatisation, nous retrouvons de plus en plus de bases de données de très grande taille. I] est donc important que les algorithmes d’apprentissage soient très efficaces. Dans cette op tique, nous avons cherché à développer une technique qui, en un espace mémoire et un temps fixé, obtiendrait de meilleurs résultats que les techniques de réduction non-linéaire de dimensionnalité originales.
1.1
Aperçu du mémoire
Ce mémoire se présente comme suit. Dans un premier temps, au chapitre 2, nous cherchons à motiver l’utilisation d’algorithmes spectraux de réduction de di mensionnalité en présentant un problème important en apprentissage statistique le fléau de la dimensionizalité. Ce terme réfère au fait qu’un grand nombre d’al gorithmes voient leurs performances se dégrader lorsque les exemples sont repré sentés par un grand nombre de variables. En effectuant une réduction de dimension nalité sur les données, nous tentons de conserver l’information pertinente dans un espace beaucoup plus compact. Cette représentation des données peut être utilisée pour améliorer les performances de plusieurs algorithmes.
Au chapitre 3, nous introduisons une méthode de réduction linéaire de dimen sionnalité : l’analyse eîz composantes principales.
À
partir de cet algorithme, nous montrons comment obtenir différents algorithmes de réduction non-linéaire de di mensionnalité. Plusieurs de ces algorithmes peuvent être vus comme des méthodes à noyau avec un noyau adaptatif et dépendant des données (BENGI0, DELAILEAu, LE1.1 Aperçu du mémoire 3
Roux, PA;EMEr.n-, VINCENTet OuIMET2004); les techniques comme LLE (RowEls et
SAut. 2000), Isomap (TENENBAuM, DESILvA et LANGF0RD 2000), l’analyse de Compo santes principales (ACP) à noyau (ScHÔLK0PF, SM0LA et Mt]LLER 199$), le Laplacian
Eigenmaps (BELKIN etNIY0GI 2003) et la segmentation spectrale (WEIss 1999; NG,
J0RDAN et WEIss 2002) nécessitent toutes une décomposition en vecteurs et valeurs
propres d’une matrice de tailleizxn,n étant le nombre d’exemples dont on dispose,
et peuvent toutes être formulées dans un même cadre.
Ces méthodes de réduction non-linéaire de dimensionnalité prennent toutes un
temps d’au moins 0(pn2),où p est le nombre de dimenions voulues, et nécessitent
un espace mémoire de taille 0(n2). Dans ce mémoire, nous nous intéressons aux techniques pour rendre ces algorithmes moins coûteux. Nous présentons d’abord
quelques techniques d’approximation en 0(m2n) (avec ni « n) qui ont été pro
posées pour les méthodes à noyau (SM0LA et ScHÔLK0PF 2000; SM0LA et BARTLETr
2001; WtLLTATIs et SEEGER 2001; HARMEuNG, ZIEHE, KAWANABE et MULLER 2002;
LAwRENcE, SEEGER et HERBRICH 2003; ENGEL, MANN0R etMEIR 2004), puis au cha
pitre 4, nous proposons une nouvelle technique plus spécifique aux algorithmes spectraux de réduction de dimensionnalité. Comme dans les méthodes précédem ment proposées, l’accélération est obtenue en se concentrant sur un sous-ensemble des exemples choisi en utilisant un algorithme vorace. Nous appelons l’ensemble
d’exemples choisis ledictiomzaire.Le critère utilisé pour le choix vorace est la dis
tance dans l’espace des caractéristiques entre un exemple candidat et sa projection sur le sous-espace généré par les exemples choisis. La projection des exemples hors dictionnaire peut être employée pour approximer la matrice de Gram sur tous les exemples. L’algorithme résultant a un temps de calcul de 0(m2n) et nécessite un
espace mémoire de taille 0(m2), où niest la taille du dictionnaire. Nous montrons
comment, en utilisant un algorithme généralisé de décomposition en vecteurs et valeurs propres, il est possible de tirer profit du fait que la matrice de Gram soit de plus faible rang. Nous montrons également une manière efficace d’obtenir la nor malisation du noyau utilisée dans l’ACP à noyau (normalisation additive) et dans la segmentation spectrale (normalisation divisive). L’algorithme proposé se distingue
des autres approches par le fait qu’il puisse se formuler comme un algorithme en
1.2 Notation et vocabulaire 4
l’eneur d’approximation de la matrice de Gram obtenue par l’algorithme proposé. Nous avons comparé cet algorithme à d’autres algorithmes de la littérature pour vérifier son efficacité. Nous présentons la technique de comparaison utilisée au cha pitre 5. Au chapitre 6, nous décrivons tes expériences puis rapportons et analysons les résultats obtenus. Nous montrons par plusieurs expériences que l’approximation vorace fonctionne bien et fonctionne mieux que (a) le même algorithme avec un dictionnaire aléatoirement choisi (mais en projetant tous les exemples sur le sous-espace associé au dictionnaire), et (b) en utilisant seulement ni points aléatoires pour estimer les vecteurs propres.
1.2
Notation et vocabulaire
Nous donnons ici quelques indications sur la notation mathématique utilisée dans ce mémoire. Nous donnons également la traduction de termes anglais spéci fiques au domaine.
— T
la transposition d’un vecteur ou d’une matrice
— A1. : la e ligne de la matrice A — A. la
f’
colonne de la matrice A — a : le 1e élément du vecteur a— O : un vecteur composé uniquement de zéros — x y le produit scalaire entre x et y
— K(x,y), çb(x), M noyau, fonction et matrice de Gram indépendants des
données
— KD(x,y), (x), ]t noyau, fonction et matrice de Gram dépendants des
données
— variable chacune des dimensions d’un exemple — espace des caractéristiques :feature space
— segmentation : cÏustering
CHAPITRE
2
LE
FLÉAU DE LA DIMENSIONNALITÉ
Dans la plupart des problèmes pour lesquels on recourt aux techniques d’ap prentissage on représente les données par un très grand nombre de variables. Par exemple, on représente en général une image par un vecteur dont chaque élément correspond à l’intensité d’un pixel; une image minuscule de taille 10 x 10 pixels en tons de gris correspond donc déjà à un vecteur de dimension 100. Malheureu sement, plusieurs algorithmes d’apprentissage ne fonctionnent pas bien en haute dimensionnalité. Ce phénomène est connu sous le nom de “fléau de la dimension nalité”. Dans ce chapitre nous nous intéresserons à quelques-unes de ses manifes tations : la perte de signification de la distance euclidienne, l’augmentation de la capacité et la réduction de la densité. Nous énumérerons ensuite des solutions à ce fléau, notamment la réduction de dimensionnalité qui fera l’objet du reste de ce document.
2.1 Manifestations du fléau de la dimensionnalité 6
2.1
Manifestations du fléau de la dimensionnalité
2.1.1
Distance euclidienne
Plus la dimensionnalité augmente, moins la distance euclidienne a de sens. En effet, en dimension d, la distance entre les exemples x et y est
Wx,yII
= (xj_yj)2.Par conséquent, plus d est grand, plus les dimensions dans lesquelles les deux exemples sont proches deviennent négligeables par rapport au total de celles dans lesquelles ils sont loins. Ce sont seulement les très petites distances qui sont in formatives en haute dimension on peut alors dire que les exemples sont proches dans toutes les dimensions. Ainsi, les méthodes basées sur la distance entre les exemples comme lek-pttis proches voisinsfonctionnent en faible dimension, mais
elles verront leurs performances se dégrader rapidement en haute dimension.
2.1.2
Augmentation de la capacité
La tâche de l’apprentissage statistique consiste à chercherparmi un ensemble de
fonctions celles qui modélisent bien le problème à résoudre à partir d’un ensemble
fini d’exemples. Dans le cas de l’apprentissage supervisé, où à chaque exemple
est associée une valeur réelle, on voudra que la fonction donne la bonne valeur lorsqu’on lui présente un exemple qu’elle n’a encore jamais rencontré, c’est-à-dire qu’ellegénéralise bien. De façon générale, lorsque le nombre de dimensions aug mente, la taille de l’ensemble de fonctions possibles grandit exponentiellement.
Si on veut conserver la même précision dans l’approximation de notre fonction le nombre d’exemples devra aussi croître exponentiellement (HAsTIE, TIB5HIRANI
et FRIEDMAN 2003, p. 24). Si la taille de l’ensemble de fonctions dans lequel on
cherche est trop grande par rapport au nombre d’exemples disponibles, on risque de sur-apprendre les exemples et donc de mal généraliser.
2.1 Manifestations du fléau de la dimensionnalité 7
2.1.3
Distribution des exemples
Supposons qu’on ait n points répartis uniformément dans un hypercube de di
mension d ayant un côté de taille 1. On voudrait placer un autre hypercube à
l’intérieur de celui-ci de sorte qu’il couvre une fraction r des exemples. Plus on
aura de dimensions, plus le côtécde l’hypercube couvrant cette fraction sera grand.
En fait, il est facile de voir qu’il faudra un hypercube de côté e = r pour couvrir
une fraction r du volume de l’hypercube de côté 1. Les figures 2.1 et 2.2 illus
trent ce phénomène. On remarque que lorsque la dimensionnalité augmente, une plus en plus grande proportion d’exemples sera située près des bords. Ceci est problématique car pour ces exemples, nous devrons extrapoler à partir des exemples
du centre, or l’extrapolation est beaucoup moins fiable que l’interpolation.
o
z
U=3
c =I/21;3
Figure 2.1 — Les trois figures rouges (la ligne, le carré et le cube) ont une lon
gueur, une surface ou un volume correspondant à la moitié des figures noires qui
les contiennent. Plus la dimensionnalité augmente, plus le côté de la figure rouge
doit grandir pour que la proportion reste 1/2.
d=1 U=2
c=1/2 c1/2”2
2.2 Vaincre le fléau de la dimensionnalité 8 D G) D O) o -J
Figure 2.2 — Longueur du côté e du sous-hypercube nécessaire pour occuper une
fraction r du volume de l’hypercube unité. Cette longueur augmente rapidement lorsque la dimensionnalité d augmente. Tiré de (HAsTIE, TIBsmRANI et FRIEDMAN
2003, p. 23).
2.2
Vaincre le fléau de la dimensionnalité
Si les données sont réellement réparties uniformément dans l’espace, il n’existe pas de moyen de vaincre le fléau de la dimensionnalité. Cependant, en général ce n’est pas le cas. Les quelques techniques que nous présentons dans cette section vont tirer parti du fait que les données vont se concentrer dans certaines régions de l’espace.
2.2.1
Restreindre la classe de fonctions
À la section 2.1.2 nous avons mentionné qu’une des raisons pour lesquelles les algorithmes d’apprentissage fonctionnent mal en haute dimension est que l’espace des fonctions parmi lesquelles on doit choisir est énorme. Une solution naturelle est de se limiter à certaines classes de fonctions.
À
titre d’exemple, considérons la classe des surfaces de séparation linéaires dans un problème de classification bi naire. En dimension d, pour toute affectation d’étiquettes, il est toujours possibleo (D à d1 0 d=3 d=2 tl= 1 0.0 0.2 0.4 0.6 Fraction du volumer
2.2 Vaincre le fléau de la dimensionnalité 9
de séparer linéairement d+ 1 points non colinéaires. Dans ce cas la taille de notre
ensemble d’entraînement ne doit donc croître que linéairement avec le nombre de dimensions. Nous pouvons ainsi vaincre le fléau de la dimensionnalité en impo sant des hypothèses fortes quant à la distribution de nos données. Cette façon de procéder est toutefois limitative car dans la plupart des cas nous n’avons pas de connaissances a priori sur nos données. De plus, si nous imposons un modèle qui n’est pas le bon, nous introduisons un biais, c’est-à-dire que la véritable fonction qu’on essaie d’approximer ne fait pas partie de la classe dans laquelle nous cher chons, ce qui augmentera notre erreur de généralisation.
2.2.2
La sélection de variables
Une alternative possible est de sélectionner un sous-ensemble de variables (di mensions) et d’ignorer les autres. Nous souhaiterions ne garder que les variables les plus pertinentes à notre problème. Un exemple de telles techniques est lefor ward seÏectio,t. On débute avec un ensemble de variables vide. On ajoute ensuite une à une les variables qui font le plus diminuer l’erreur de généralisation. On peut trouver un résumé des techniques récentes de sélection de variables dans (GuYoN
et EUssEEFf 2003). Ces approches présentent l’avantage de l’interprétabilité on
découvre quelles variables sont corrélées avec la tâche à apprendre. Toutefois, elles sont en général coûteuses et pas globalement optimales.
2.2.3
La réduction de dimensionnalité
Comme la sélection de variables, cette stratégie vise à exprimer les exemples par un plus petit nombre d’attributs. Toutefois, chacun de ces attributs peut être une fonction non linéaire de toutes les variables des exemples originaux; par exemple, un produit de variables. De plus, contrairement aux techniques de sélection de va riables, les algorithmes de réduction de dimensionnalité sont en généralnonsuper visés; ils se basent simplement sur la distribution des exemples dans l’espace pour déterminer quels attributs sont pertinents. Ils font l’hypothèse que les données se retrouvent sur une variété (pas nécessairement linéaire) de plus faible dimension. L’objectif est de trouver un changement de coordonnées qui fait en sorte qu’on
2.2 Vaincre le fléau de la dimensionnalité 10
obtienne les coordonnées le long de la variété. Nous nous pencherons davantage sur ces techniques dans le reste de ce document. Les algorithmes de réduction de dimensionnalité que nous décrirons à la section 3.3 découvrent un tel système de coordonnées en effectuant la décomposition en vecteurs propres et valeurs propres d’une matrice de similarité sur les données. Le résultat ainsi obtenu est globalement optimal au sens où les vecteurs propres sont les vecteurs qui, lorsqu’on projette les données sur le sous-espace généré par ceux-ci, donnent la meilleure approxima tion possible en terme d’erreur quadratique moyenne (DIAMANTRAs et KUNG 1996). Notons que ce résultat est optimal pour les données d’entraînement et ne donne au cune garantie sur la généralisation. On sait toutefois qu’asymptotiquement les va leurs propres estimées tendent vers celtes du problème continu associé à la véritable densité des données(SHAwE-TAYL0R et W;LL;AMs 2003).
CHAPITRE
3
MÉTHoDEs DE RÉDUCTION DE
A A
DIMENSIONNALITE NON LINEAIRE
Pour effectuer une réduction de dimensionnalité sur des données, on va suppo ser que les exemples se trouvent sur une variété de plus faible dimension. On va ensuite chercher à caractériser cette variété. Plus précisément, on souhaiterait trou ver un nouveau système de coordonnées dont chacun des axes correspondrait à un déplacement le long d’une des dimensions de la variété. La figure 3.1 illustre cette idée : les données en trois dimensions se trouvent initialement le long d’une spirale. On obtient le nouveau système de cordonnées en deux dimensions en déroulant la spirale.
Pour introduire les algorithmes de réduction de dimensionnalité non linéaire, nous allons d’abord présenter à la section 3.1 un algorithme de réduction de di mensionnalité linéaire très connu l’analyse en composantes principales.
À
la section 3.2 nous montrerons comment obtenir une version non linéaire de cet al gorithme $ l’analyse en composantes principales à noyau.À
la section 3.3 nousmontrerons comment nous pouvons reformuler plusieurs techniques de réduction de dimensionnalité non linéaire dans un même cadre que l’ACP à noyau. Nous insisterons davantage sur une de ces méthodes : la segmentation spectrale.
À
la3.1 Réduction linéaire de dimensionnalité 12
C
Figure 3.1 —
À
partir d’une spirale dans un espace en trois dimensions, l’algorithme de réduction de dimensionnalité trouve un système de coordonnées dont la première dimension correspond à un déplacement le long de la spirale du centre vers l’extérieur et la deuxième dimension, à un déplacement de l’avant vers l’arrière. En (A), on représente la variété, en (B), des points tirés de cette variété et en (C), les mêmes points dans le nouveau système de coordonnées. Tiré de RowEts etSAuL(2000).
section 3.4 nous attirerons l’attention du lecteur sur le fait que les méthodes de réduction de dimensionnalité non linéaire sont coûteuses en espace mémoire et en temps, les rendant difficilement applicables sur de gros ensembles de données. Nous terminerons ce chapitre en énumérant quelques techniques proposées dans la littérature pour obtenir des approximations moins coûteuses de ces méthodes.
3.1
Réduction linéaire de dimensionnalité
Supposons que les données se retrouvent sur une variété linéaire de plus faible dimension. Pour obtenir le nouveau système de coordonnées, il suffirait de trans later la variété de sorte qu’elle passe par l’origine et de prendre comme nouvel espace le sous-espace généré partoutes les données. Cette stratégie ne fonctionne évidemment pas si les points sont bruités, ce qui est le cas pour pratiquement toutes les vraies données. Dans ce cas, l’analyse en composantes principales peut être uti
3.1 Réduction linéaire de dimensionnalité 13
usée pour trouver un système de coordonnées correspondant à la variété linéaire. Ainsi, l’ACP peut être employée non seulement pour faire de la réduction de di mensionnalité, mais pour débruiter les données.
3.1.1
L’analyse en composantes principales
Pour extraire le système de coordonnées correspondant à la variété, on devra être capable de distinguer ce qui représente vraiment une dimension de la variété de ce qui n’est que du bruit. Pour ce faire, on va supposer que les directions où on retrouve seulement une petite variance sont du bruit. Après avoir centré les données autour de l’origine, on va construire la matrice de covariance de ces données. On va ensuite chercher les p plus grandes valeurs propres et les vecteurs propres cor respondants. Ces p vecteurs propres seront les axes du nouveau système de co ordonnées et nous obtiendrons une représentation des données en plus faible di mension en les projetant sur ces vecteurs. Cette procédure est décrite par l’algo rithme 3.1.
Algorithme 3.1 Analyse en composantes principales.
Arguments: ensemble de données D = {x1 ,...,x,,}, nombre de dimensions
désirées p
1: n =
DI
2:
-3: Construire la matrice X telle que X. x —, i = 1,... 4: C =
5: Trouer les p plus grandes valeurs propres il de C et les vecteurs propresy1qui
y sont associés
6: Le plongement d’un exemple x est donné par e = (x
— v ou par
-i=1,...,p.
Le premier vecteur propre obtenu est la direction dans laquelle les données ont la plus grande variance. La valeur de cette variance est donnée par la valeur propre correspondant à ce vecteur. Le deuxième vecteur est orthogonal au premier et correspond à la deuxième direction principale de variation. En terme d’erreur quadratique, si on projette toutes les données sur les p vecteurs propres principaux,
3.2 L’analyse en composantes principales non linéaire 14
nous obtenons la meilleure approximation qu’il est possible d’obtenir en projetant
surp vecteurs. La figure 3.2 illustre tes deux directions de principale variation de
données tirées d’une gaussienne.
-A
Figure 3.2 — L’ACP appliquée à une gaussienne en deux dimensions. (A) est le
système de coordonnées original et (B) correspond aux directions de principale variation des données. Ces directions sont données par les vecteurs propres trouvés par l’ACP et les longueurs des axes, par les valeurs propres et correspondent aux variances dans ces directions.
3.2
L’analyse en composantes principales non linéaire
L’ACP est un algorithme utilisé dans un très grand nombre de domaines. Ce pendant, en général, les variétés ne sont pas linéaires. Il est alors possible de faire mieux. L’ACPànoyau (ScHÔLK0PF, SM0LA et MtLLER 1999) est une généralisation de l’ACP qui permet de faire de la réduction de dimensionnalité non linéaire. L’idée est de projeter les données dans un espace de beaucoup plus haute dimension de sorte que la variété devienne linéaire et d’effectuer l’ACP dans cet espace. On dénotera la projection par
3.2 L’analyse en composantes principales non linéaire 15
où F est appelé l’espace des caractéristiques. Un exemple de projection est «5(x) =
(x, x1x2, x, x1x3, x, x2x3) qui correspond aux produits de deux variables du vec teur original x = (X1,x2, x3). En général, nous ne connaissons pas le type de pro
jection qui rendrait notre variété linéaire, donc on voudra que F soit de très haute dimension de sorte à pouvoir contenir plusieurs interactions différentes entre les variables. La figure 3.3 illustre l’idée de l’ACP à noyau.
ACP linéaire k(x,y) = (x.y)
ACPà novait e.g. k(x,y) = (x.y)d
/ R2
Figure 3.3—L’ACP classique comparée à l’ACP à noyau. Les lignes pointillées cor
respondent aux points ayant la même projection sur le premier vecteur propre. Dans le cas de l’ACP à noyau, ces lignes sont des courbes dans R2 Tiré de (ScHÔLK0PF, SM0LA etMULLER 1998).
3.2.1
Deuxième version de 1’ACP
En étudiant l’algorithme 3.1 on remarque qu’on doit construire une matrice de taille dXd (étape 4) si on effectue J’ACP dans W’. Typiquement on veut un F dont
la dimension est beaucoup plus grande que n; il serait donc plus avantageux d’ef fectuer les calculs sur une matrice de taille nXn. Il se trouve qu’on peut reformuler l’ACP de sorte qu’on cherche à résoudre le système
!XXTa = ila
3.2 L’analyse en composantes principales non linéaire 16
plutôt que le système
XTXv = Àv,
n
où X est la matrice dont les n lignes sont les points de notre ensemble de données qu’on suppose centrés pour l’instant, i.e. x1 = O. Pour reformuler l’ACP de
cette façon, on doit d’abord remarquer que y peut être exprimé comme une combi
naison linéaire des lignes de X. On a en effet que
y = LXTXV . v)x
XV
x.
Si onnommeale vecteur tel que a, = i = 1 n, on a
y = ojxj = XTo. Par conséquent, XTXv = lv XXXv = ,lXy xxTxxT=11xxT. (3.1)
On peut trouver les solutions de ce problème en résolvant _XXTy = la
‘z
pour n’ O. Pour obtenir la projection d’un point x sur le vecteur propre y il suffit
de faire
e = vTx n’TXX =
.x)
3.2 L’analyse en composantes principales non linéaire 17
3.2.2
L’astuce du noyau
Si nous voulons appliquer cette version de l’ACP dans l’espace des caracté ristiques, nous devons remplacer toutes les occurrences de x par ç5(x) et toutes les occurrences de X par I, la matrice telle que Ij. (x1). La matrice xT est
connue sous le nom de matrice de Grain M et peut aussi être obtenue en calculant
= «x1) «xi) pour ï,
j
= 1 n. Puisque F est de très grande dimension,calculer explicitement le produit scalaire (x) . (x1) serait très coûteux. L’astuce du noyau nous permet d’éviter ce problème. Elle consiste à exprimer le produit scalaire par une expression qui se calcule en 0(d) au lieu d’en 0(TÏ). Pour ce faire, nous introduisons un noyau K tel que K(x1, x) = (x1) . (x). En utilisant un tel noyau, l’ACP à noyau pourra se calculer en 0(pn2). L’ordre d’exécution ne dépend pas de FI car les (x1) ne se retrouvent qu’à l’intérieur de produits scalaires dans cet algorithme. La projection (x1) n’aura jamais à être calculée ni définie explicitement; on définira plutôt le noyau K qui implicitement définira une projection. On appelle noyaux de Mercer la classe de tels noyaux pour lesquels il
existe un espace dans lequel ils correspondent à un produit scalaire (CRI5TIANINI et SHAwE-TAYL0R 2000; ScHÔLK0PF et SM0LA 2002).
Cette astuce a été utilisée dans de nombreuses méthodes linéaires pour les rendre non linéaires efficacement. Un exemple notoire est la machine à vecteur de support (VAPNIK 1995) qui trouve une surface de séparation linéaire dans l’espace
des caractéristiques. Parmi les noyaux fréquemment rencontrés dans la littérature, nous trouvons: — le noyau gaussien: = exp(_ x-y 112) — le noyau polynomial: K(x,y) = (x y +b)< — le noyau sigmoïdal: K(x, y) = tanh (b(x .y) +c).
3.2 L’analyse en composantes principales non linéaire 18
Figure 3.4—L’effet de différents noyaux sur l’ACP à noyau. On affiche les lignes
de projection constante sur les 3 premiers vecteurs propres. Les trois premières colonnes correspondent au noyau K(x,y) = (x .y)t,
pour c = 1,2,3. Dans la qua
trième colonne on a utilisé le noyau gaussien et dans la dernière colonne, le noyau sigmoïdal. L’ACP classique, dans la première colonne, ne parvient pas à une bonne réduction de dimensionnalité, tandis qu’avec tous les autres noyaux on parvient à extraire de l’information pertinente.Ititages tirées de(ScHiILK0PF, SM0LAetMOLLER
1998).
3.2.3
Centrer les points dans l’espace des caractéristiques
Soit (x1), les points avant d’avoir été centrés. Nous voulons obtenir les points centrés h(x) = cb(x)—EJ(x)], oùE[b(x)J correspond à ‘p(x), la moyenne
sur l’ensemble de données D. Le noyau centré obtenu à partir d’une telle fonction (x.y)2 (x•y)3 l’ACP à noyau. (x .y) VI V2 V3 tanh(2(x.y)+ 1)
I’
n
3.2 L’analyse en composantes principales non linéaire 19
sera
KD(xj, x) = (xj)
= (b(x1) — Ekb(x)1) ((x)—
= K(x1,x1)— E1[K(x1,x)J — E[K(y,x)J +E[Ey[K(x,y)11. (3.2)
Montrons que si KD(xI, x) est donné par cette équation, alors pour tout
(.)
tel que KD(xj, x) = (x1) (x) on aEJch(x)] = O sur les données D, où O est un vecteurne contenant que des 0.
PreuveProcédons par contradiction. Supposons qu’il existectel que =i (x1)(. 0. En utilisant cette hypothèse, nous trouvons que
Z Z
KD(xj,x1) 1=1 j=I , =Z
Z
(x) (x) =Z Z
«xi)k(xJ)k 1=1 j=I I I k= I 2 2 2 =Z Z
(xj)k = (x + k=I I 1 k= I ,kc i1 >0. Or,Z Z
KD(xj, x) i=1 j=1 =Z Z
(K(xi x) —!
K(x1, x) — K(x,, x) + -Z Z
K(x11, x)] z=1 j=1 v=l 11=1 u=t v=1 =(z z
K(x1, xi)] —(z
Z
K(x, x) —(
K(x, x)i=t j=l i=1 v=1 j=t j=1 u=1 i=t
+(ÊÊKxxÊ
]
u=1 1=1 i=1 j=I
=0.
Nous appelons KD le noyau de l’équation 3.2 pour mettre l’emphase sur le fait
3.3 Quelques méthodes à noyaux 20
qu’il dépend de l’ensemble de données D, contrairement àK. Avec ce noyau nous avons tout ce qu’il faut pour effectuer 1’ACP dans l’espace des caractéristiques. L’algorithme 3.2 en résume les étapes. La matrice t’ de cet algorithme (étape 5) est la matrice de Gram associée au noyau KD
= KD(x, x) = M1— E[M1J — E[M] +EJE[M]] (3.3)
où E[M1j correspond à M. Dans le reste de ce document, nous référerons à ces opérations de centrage (éq. 3.2 et éq. 3.3) par le termenormalisation additive.
Algorithme 3.2 Analyse en composantes principales à noyau.
Arguments: ensemble de données D = x1,...,x,,), nombre de dimensions
désirées p, noyau indépendant des donnéesK
1: n
IDI
2: Construire la matrice M telle que M1 = K(x1, xi), j,
j
Ï,.. . ,n3: Construire le vecteur S tel que S = 1 M11, i = l,.,n
4: tzJZiSj
-5: Construire la matrice M telle que M1 = M1
—S —S
+ t
6: Trouver les p plus grands vecteurs propres v et valeurs propres de ]. 7: Le plongement d’un exemple x est donné par .
Z7=1
‘lJKD(xJ, x),l,...,p, où KD est donné par l’éq. 3.2.
3.3
Quelques méthodes à noyaux
En définissant différents noyaux nous pouvons exprimer divers algorithmes de réduction de dimensionnalité tels la segmentation spectrale (WEIss 1999; NG,
J0RDAN et WEIss 2002), le taplacian eigemnaps (BELKIN et NIY0GI 2003), le mtdti
dimensional scating (Cox et Cox 1994), isomap (TENEAuM, DESILvA et LANGF0RD
2000) etLLE (RowEIs et SAuL 2000) dans le même cadre que l’ACP à noyau. On peut tous les formuler ainsi
3.3 Quelques méthodes à noyaux 21
une matrice de Gram Mtelle que M1, = K(x1, x). On normalise en
suite M pour obtenir i?î et on calcule les p plus grandes (ou plus petites) valeurs propres À et les vecteurs propres y1 associés. Le plongement (la projection dans l’espace de plus faible dimension) de x E D est donné par le jième élément de chacun des vecteurs propres v multiplié par (et possiblement multiplié par
La plupart de ces méthodes ne fournissaient à l’origine qu’un plongement pour les points d’entraînement. En les formulant dans un même cadre comme l’appren tissage des fonctions propres d’un noyau, BENGI0, DELALLEAu, LE Roux, PAIEMENT,
VINCENT et OuIMET (2004) ont pu donner une formule pour obtenir le plongement
d’un point de test. Chacune des p composantes de la projection d’un nouveau point xpeut être obtenue par la formule de Nystriim:
J(x) = vK(x, x1) (3.4)
1=1
ou bien par Çf(x). Comme dans le cas de l’ACP à noyau, KD est un noyau dépendant des données obtenuàpartir deKqui est défini pour que KD(xj, x1) =
Il est facile de montrer que dans le cas des exemples d’entraînement, la formule de Nystrôm se réduitàf(x1) = v,.
Nous avons vu qu’en appliquant une normalisation additive sur M, nous obte nions l’ACPànoyau. Si nous utilisons plutôt la normalisation divisive, nous obte nons la segmentation spectrale.
À
la section suivante nous décrivons plus en détail cet algorithme.3.3.1
La segmentation spectrale
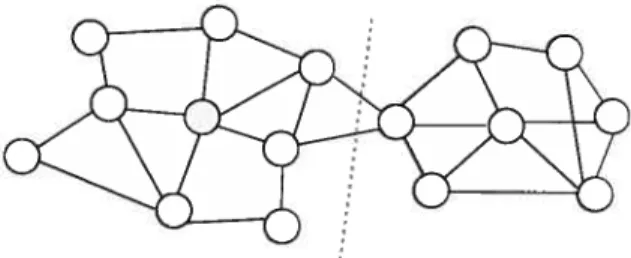
Même s’il effectue un type de réduction de dimensionnalité, la motivation à l’originede la segmentation spectrale est plutôt, comme son nom l’indique, la seg mentation. Il existe quelques variantes de cet algorithme (WEIss 1999). L’idée qui les a motivées origine de la théorie des graphes : il s’agit de former un graphe en reliant les voisins de chaque point. On voudrait ensuite trouver la coupe à coût minimum de ce graphe nous permettant de séparer le graphe en sous-graphes tel
3.4 Limitations de ces méthodes 22
Figure 3.5—Avec la décomposition en vecteurs propres du Laplacien d’un graphe
on peut trouver une coupe qui permet de bien segmenter le graphe.
qu’illustré à la figure 3.5. En prenant les vecteurs propres principaux du Laplacien du graphe, on obtient la solution d’une version relaxée de ce problème (SPIELMAN et
TENG 1996; CHuNG 1997). Pour obtenir la segmentation, on applique l’algorithme des k-moyennes sur le plongement donné par ces vecteurs propres (NG, J0RDAN et
WEIss 2002).
L’algorithme 3.3 décrit les étapes d’une version de la segmentation spectrale. La matrice i1 qu’on retrouve à l’étape 4 est obtenue en appliquant lanormalisation
divisive (WE;ss 1999;NG, JORDAN et WEIss 2002)surla matrice de GramM associée au noyau gaussien: M1 M1 = ______________ . (3.5)
Nous pouvons également définir directement le noyau normalisé KD qui aurait pu générerM: K(x1, x) KD(xI, x) = ______________________ . (3.6) JE[K(x1, x)JE[K(x, x)]
3.4
Limitations de ces méthodes
Nous avons vu que l’ACP à noyau revient à l’ACP ordinaire si on prend le
noyauK(x,y) = x y. Toutefois, au niveau algorithmique, les deux techniques sont
3.5 Solutions proposées 23
Algorithme 3.3 La segmentation spectrale telle que présentée dans (BENGI0, DE
LALLEAU, LERoux, PAIEMENT, VINCENT etOuIMET2004).
Arguments: ensemble de données D = {xj, . . .,x}, nombre de dimensions désirées p, noyau K(souvent le noyau gaussien)
1: n =
[Dl
2: Construire la matrice Mtelle que M1 = K(x1, x1), j,
j
= 1, . ..,n3: Construire le vecteur S tel que S = 1 M, j = 1,...,n
4: Construire la matrice i1t telle queA111 =
5: Trouver les p plus grands vecteurs propres v et valeurs propres d de i1?.
- in
6: Le plongement d un exemple xest donne par T 2=1 VJIKD(x, xi), t = 1, .. .,n,
où KD est donné par ]‘éq. 3.6.
7: Pour obtenir la segmentation, appliquer l’algorithme des k-moyennes sur le plongement.
n x n dont on doit calculer la décomposition en vecteurs et valeurs propres, dans l’ACP classique on effectue en général les calculs sur une matrice de taille dx d puisque la plupart du temps d est plus petit que n. Sachant qu’il en coûte O(pn2) en temps de calcul pour trouver les p valeurs et vecteurs propres principaux d’une matrice de taille iz x n, si n est très grand par rapport à d, l’ACP à noyau sera donc beaucoup plus coûteuse que l’ACP classique. De plus, cette matrice doit être gardée en mémoire. Ces considérations constituent des limitations importantes aux méthodes énumérées à la section 3.3.
3.5
Solutions proposées
Supposons qu’on dispose d’un très grand nombre d’exemples et qu’on veuille obtenir un plongement pour chacun des exemples, que peut-on faire si lamatrice de
Gram est trop grande pour être gardée en mémoire ou s’il est trop long de calculer sa décomposition? Avant de décrire la technique que nous proposons pour remédier à ce problème, nous décrivons les techniques proposées dans la littérature. Leurs temps d’exécution sont tous de O(m2n), où m «n.
Dans(SM0LA etScH&K0PF2000), le cadre est très général. On veut approximer une matrice K par
R,
une matrice de plus faible rang, en minimisant la norme de3.5 Solutions proposées 24
Frobenius du résidu K—1. On itère sur un sous-ensemble aléatoire des n colonnes
du résidu courant en choisissant chaque fois la colonne qui arrive le mieux à ap proximer les autres colonnes jusqu’à ce qu’on atteigne une erreur inférieure à E
sur la norme du résidu, Eétant une constante fixée d’avance. Dans la même veine, SM0LA et BAwIlErr (2001) et LAwRENcE, SEEGER et HERBRIcH (2003) proposent des
algorithmes pour les processus gaussiens. Encore ici, l’idée est de parcourir ni fois un sous-ensemble aléatoire des données en choisissant à chaque fois l’exemple qui réduit le plus un critère de coût. Alors que dans (SM0LA et BARTLETF 2001) on détermine un seuil d’erreur € à atteindre, dans (LAwRENcE, SEEGER et HERBRIcH
2003), on spécifie directement la valeur de ni désirée.
Une approche alternative est d’appliquer l’algorithme de réduction de dimen sionnalité sur un sous-ensemble de ni exemples et d’utiliser la formule de Nystrôm pour obtenir le plongement des n — in autres points, suivant les travaux de BEN
Gb, PAIEMENT, VINcENT, DELALLEAu, LE Roux et OuIMET (2004). Cette approche
a été employée par FowLKEs, BEL0NGIE, CHuNG et MALIK (2004) et WILuAM5 et SEEGER (2001) dans le but d’accélérer les méthodes à noyau. WILLIAivIS et SEEGER
(2001) affirment que bien que leur méthode soit moins précise que celle de SM0LA et SCHiLKoPF (2000), elle est beaucoup plus rapide. Au chapitre 6 nous compare
rons notre technique à celle de WWLIAMs et SEEGER (2001), montrant que pour le même temps d’exécution, l’erreur de généralisation obtenue avec notre algorithme
est moins grande.
Dans l’article deHARMELING, ZIEHE, KAwANABE et MÛLLER (2002), on cherche le
plus grand sous-ensemble aléatoire d’exemples pour lequel la matrice de Gram est de plein rang et on projette tous tes exemples sur le espace généré par ce sous-ensemble dans l’espace des caractéristiques. Cette technique est plus précise que celle deWrnIAMs et SEEGER (2001) car elle utilise l’information de chaque exemple
disponible lors de la décomposition en vecteurs et valeurs propres. Toutefois, bien qu’elle soit aussi en O(in2n), elle est assez coûteuse caron doit effectuer un grand nombre de décompositions de matrices afin de calculer leur rang.
La technique que nous proposons utilise aussi la projection des exemples sur
un sous-espace généré par un sous-ensemble d’exemples dans l’espace des ca ractéristiques, maisla principale différence avec les méthodes proposées est qu’on
3.5 Solutions proposées 25
peut le formuler comme un algorithme en-ligne. Le sous-ensemble de ni points formant une matrice de Gram de plein rang est choisi en un seul parcours des données. Le critère utilisé pour ce faire est celui présenté dans (ENGEL, MANN0R
etMEIR 2004), alors utilisé dans un contexte supervisé pour faire du moindre carré
récursif à noyau. On obtient un algorithme très rapide qui n’occupe qu’un espace mémoire de 0(m2); il est donc possible de l’utiliser pour de très grands ensembles de données.
CHAPITRE
4
MiTHoDE VORACE POUR LA REDUCTION
NON LINIAIRE DE DIMENSIONNALITI
Les méthodes spectrales pour la réduction de dimensionnalité étant coûteuses en temps et en mémoire, nous avons développé une version vorace de l’ACP à noyau et de la segmentation spectrale prenant un temps de 0(m2n) et un espace mémoire de taille 0(m2).
À
la différence des techniques précédemment proposées, elle peut être formulée comme un algorithme en-ligne. Elle convient donc bien pour de très grands ensembles de données et, en permettant d’ajouter des données sans avoir à refaire tous les calculs, elle s’avère utile dans les cas où de nouvelles données sont régulièrement disponibles.À
la section 4.1, après avoir décrit en détail la technique, nous montrons qu’on peut borner l’erreur faite sur la matrice de Gram. Nous présentons ensuite une justification intuitive de la méthode à la section 4.3.À
la section 4.4, nous décrivons comment obtenir, dans le cadre de cet algorithme, les normalisations additives et divisives de l’ACP à noyau et de la segmentation spectrale présentées au chapitre précédent. Finalement, à la section4.5 nous analy sons la complexité de cet algorithme. Nous donnons également le pseudo-code de différentes variantes de la technique.4.1 La technique du dictionnaire 27
4.1
La technique du dictionnaire
Pour développer un algorithme moins coûteux, nous allons utiliser un sous-ensemble des exemples comme prototypes sur tous les points de notre ensemble de donnéesD = {xi, ...,x,j, nous en gardonsni «npour former ce que nous appe lons undictionnaire. Soit P, le sous-espace généré par les exemples du dictionnaire dans l’espace des caractéristiques. Tous les points de notre ensemble de données seront alors approximés par leur projection sur P. Le dictionnaire est construit de façon itérative, suivant une idée présentée dans (ENGEL, MANN0R et MEIR 2004) on y ajoute un nouveau point si, dans l’espace des caractéristiques, il est loin de sa projection sur P; autrement dit, s’il est mal approximé par sa projection. Cette tech nique nous permet de trouver une approximation de moindre rang de la matrice de Gram dont nous pourrons trouver les vecteurs et les valeurs propres efficacement. figure 4.1 — Dans l’espace des caractéristiques, l’exemple hors dictionnaire
(x() est approximé par une combinaison linéaire des exemples du dictionnaire
(xJ(1)), i = 1 in, si sa distanceàsa projection sur le sous-espace généré par les exemples du dictionnaire, n’est pas trop grande.
4.1 La technique du dictionnaire 28
4.1.1
Mise à jour du dictionnaire
Supposons que nous ayons déjà considéré t—1 exemples et que nous disposions d’un dictionnaire2t—i = {xI(1),.. .,xj(,fl )). Nous dirons que(Xt)est approximati
vement linéairement dépendant de (xI(i)), . . ., (donc bien approximé par
sa projection sur
)
si,flI_I
= min aI,çb(XI()) —(xi)II2 E (4.1)
où a, = (aie,.. . ,a,,1,11)etEest un paramètre contrôlant l’exactitude de la dépendance
linéaire.
SoitA1,_i la matrice de Gram desiz_i exemples du dictionnaire et soit k,_1(x) le
vecteur (KD(x,Xd(i)),.. . ,KD(x,X(I(,fl, I))).En utilisant l’astuce du noyau, nous trou
vons que ttl. a(x,)) -(xt)lI2 =
(z
aI,(x,,(I)) -(xt)](z
aI(x(I(I)) -,fl,_I !IiI ,fl,_I =Z Z
a,aJI(xd(I)) . (x,j) —2 aI,(xd(I)) . (x,) + (x) . 1=1 j=i i=i ,fl,_I tfl,_I ,fl,_ =Z
a17aj,KD(xd(j»X,j(J)) —2)
aIKD(xd(I), x,)+ KD(xt, x1) 1=1 •j=I 1=1 = ai11_ia, — 2kt_i(xt)Tat+ KD(xt,X1), (4.2) donc= min (aMi_ia,— 2k1_i(x1)Ta1+ KD(x,, x,)). (4.3)
Le vecteur a, qui minimise 4.3 est trouvé en dérivant:
d(a]I,_iat— 2k,_i(xt)Ta, + KD(Xt,X)
= 2aM1_1 —2k1_1(x1)T = OT
da
4.1 La technique du dictionnaire 29
Avec ce a, l’expression de 6 donnée à l’équation 4.3 se simplifie à
ôt = x,) —k,_j(X,)Tat. (4.5)
Si 5, E, l’approximation est bonne; (Xt) n’est pas trop loin de sa projection
sur le sous-espace généré par les exemples du dictionnaire. Le dictionnaire reste donc le même : = e_i, = 171i1 et AJ Me_1. Parcontre, si 6 > e, on ajoute
x au dictionnaire : U {r},m = in_i + 1 et
flt—1 k_i(x)
M = . (4.6)
k1_i(xt)T KD(xI, x1)
Pour l’équation 4.4, nous avons aussi besoin de
M*
Afin d’obtenir un algorithme en 0(1,12,1), nous devons pouvoir faire la mise à jour de i11’ en 0(m2),il n’est doncpas question de recalculer l’inverse à chaque fois. Nous utilisons plutôt l’approche présentée dans (ENGEL, MANN0R etMEIR 2004), ce qui nous donne:
1 ‘
6A’ + aaT a
M1 = —
I
. (4.7)—a 1
Pour l’initialisation, il suffit de prendre 2 = {x1}, i1j (KD(xl,xI)) et =
(1/KD(xi,xi)).
Preuve II est facile de prouver ce résultat si on voit la matrice ?I comme une matrice en blocs
AB A1 =
BTC
oùA = ilt_i, B = k1_i(x)et C = KD(x, X,).
Décomposons tout d’abord cette matrice en 3 matrices bloc-triangulaires et bloc-diagonales de la façon suivante:
A B I O A O 1A’B
BT C — BTA’ I O SA O I
4.1 La technique du dictionnaire 30
chacune des trois matrices bloc-triangulaires
A 3 1 —A’B (A-’
o
io
3T
c
)
=o
io
s
—BTA’ IA-1 +A’BS1BTA’ —A’BS’
= —S’BTA’
Étant donné quea X1,z’1k_,(x,) = A’Bet que 5, = KD(xt,xt) —kt_,(xt)Ta, =
C— BTA_lB SA,nous obtenons
- A’+A’BS’BTA’ -A’BS’ A A — +a16’a7 —a15’ — —5’a + aa —a t1 t —a 1
4.1.2
Mise à jour des coefficients a
Une fois tous les exemples parcourus, nous avons un dictionnaire de taille in,,. Pour alléger la notation, nous utiliserons égalementnipour désignerrn.Nous pou vons mettre àjour les coefficients de la combinaison linéaire associés aux exemples qui ne sont pas dans le dictionnaire. Nous construisons la matriceA de taillen xni
dont les lignes sont
A. = a7 = k,1(x)T]’. (4.8)
Ceci donnera des coefficients différents de ceux précédemment calculés à l’équa tion 4.4 car on utilise la matrice ]1
correspondant au dictionnaire final et non Autrement dit, l’approximation de (x) sera meilleure car au lieu d’être ap proximé par ‘ a/Ib(xd(I)), il sera approximé par , aI(x1j()) (par abus de no
tation on utilise le symbole a1 dans les deux cas même si ces coefficients ne sont pas les mêmes). Cette étape n’est toutefois pas obligatoire; si nous désirons un
ai-4.1 La technique du dictionnaire 31
gorithme purement en-ligne, nous pouvons nous contenter des at déjà calculés pour former la matriceA. Ceci équivaut à obliger les coefficients a,1 à a,,, à être O pour l’exemple x.
4.1.3
L’approximation de la matrice de Gram
En utilisant le fait que
Z-1
aIl(xa(I)), nous trouvons que la matrice deGram ] sur tous les exemples est approximée parAAI,,AT. En effet,
(Pt),,,, — (x,,) . in in
Z
a,,(x)) . aj,b(xu) = a M a, =A,,. ,, (AT).,,Nous souhaiterions donc trouver les vecteurs propres et les valeurs propres de la matriceAM,,AT, et ce enO(,n2n).Si nous trouvons les vecteurs propres du problème
M,,ATAv = /1v, nous avons ceux deA],,AT. En effet, M,,ATAv = ilv = AAf,,AAv = ÂAv
Donc les valeurs propres sont les mêmes pour les deux problèmes et les vec teurs propres de A,,AT sont donnés par Av. Puisque la matrice MATA n’est pas symétrique, nous utilisons une décomposition en vecteurs propres et valeurs propres généralisée (voir la section 4.1.4) sur la matrice semi-définie positive ?I,, et la matrice symétriqueATA, toutes deux étant de taille ni X ni. L’algorithme 4.1 résume les étapes de la méthode du dictionnaire.
4.1.4
Décomposition en vecteurs et valeurs propres généralisée
Soit la matrice semi-définie positiveFet la matrice réelle et symétrique
Q.
Soit le problème de décomposition en vecteurs et valeurs propresPQz = Az. Étant donné4.2 Qualité de l’approximation 32
que le produit des matrices P et
Q
n’est en général pas symétrique, il s’agit d’un problème de vecteurs et valeurs propresgénéralisé(G0uRLAY et WATs0N 1973). Pour résoudre un tel problème, on va le transformer de sorte qu’on puisse le résoudre par une décomposition en vecteurs et valeurs propres ordinaire de forme Ry=
ly, où R est une matrice semi-définie positive. Si on décompose P à l’aide d’une factorisation de Cholesky, on obtient P=
LLT, où L est une matrice triangulaire inférieure. On a doncPQz
=
Az LUQz=/lz=
U’LLTQ(LL’)z=
/lLtz (LTQL)(L1z) A(L’z)Il suffit de résoudre le problème (LTQL)y Àyet les vecteurs propres désirés seront
donnés parLy, les valeurs propres restant les mêmes.
À
cause de la factorisation de Cholesky, cette méthode prend un temps de in étant le nombre de Lignes de la matriceP.4.2
Qualité de l’approximation
À l’aide du paramètre Econtrôlant l’exactitude de la dépendance linéaire, il est
aussi possible de borner l’erreur faite sur chaque entrée de la matrice de Gram en l’approximant parAAAT:
Proposition 4.1 Pour tout x, x E D, IKD(xt, x,,) — (AAI,1AT),111 E.
Preuve Soitr,
=
(x,)—Z
aI,(xd()). On remarque que si x, E alorslirtil
=
O,sinon,
lirtil
= sJ
etrtest orthogonal au sous-espace générépar (xd()), i=
1,...,in.On a donc
KD(x,, x)
=
(x,) (x11)=
(r, + aIt(xd(I))) . (r1, + aIl(xd(I)))4.2 Qualité de l’approximation 33
= r, . r + aI,(xd()))
(Z
aI,,(x,(Ï)))= r, r + (A,,AT)tu.
Par conséquent, IKD(x,,x,) — (A],7AT),,1I = !r,r,I E.
Algorithme 4.1 Algorithme vorace de plongement spectral.
Arguments : ensemble de données ordonnées aléatoirement D, tolérance E,
nombre de dimensions désirées p, noyau normalisé KD donné par l’éq. 3.2 ou l’éq 3.6
1: n =
jDj
2: initialiser .V = {x1
1
= (KD(xI, x1)), = (J<D(XI xi)_I), m1 = 1.3: fort = 2 to n do
4: fori = ltonz,_1 do
5: calculer(k,(x,))1 = KD(x,,Xd(j))
6: end for
7: calculer les poids de projection a, = i1k,(x,)
8: calculer l’erreur de projectioni5 = KD(x,, x,) —k,.1(xt)Ta,.
9: if,>Ethen
10: ni, 111t—l + 1, D = 2
u
{x,}11: JI est calculé suivant I’éq. 4.7. 12: else
13: in, nz_1, M =
14: end if 15: end for
16: construire la matrice A dont chaque ligne A,. est donnée par l’éq. 4.8, t =
1,.. .,n
17: calculerB= ArA
18: Trouver les p vecteurs propres principaux tt et les valeurs propres Àk du problème généralisé avec la matrice B à gauche et la matrice It àdroite. 19: Les k-ièmes coordonnées des plongements des exemples d’entraînement sont
données par sJïvk = ‘4JïAuk ou .JAuk.
20: Le plongement d’un exemple de test x est donnépar fk(x)ou -sJfk(x), oùfk(x) est calculé avec l’éq. 3.4 en utilisant1k = Auk.
4.3 Intuition de la méthode 34
4.3
Intuition de la méthode
Pourquoi ne pas simplement appliquer les méthodes spectrales sur un sous-ensemble de points et généraliser avec la formule de Nystriim? La figure 4.2 nous donne une intuition géométrique de la raison pour laquelle notre technique de vrait donner de meilleurs résultats. En a), on estime les directions de principale variation de nos données dans l’espace des caractéristiques sur seulement 3 points avec une ACP. On remarque qu’on sur-apprend les données. En b), les gros points représentent les points de l’ensemble de données les points noirs constituent le dictionnaire et les rouges sont situés à l’extérieur du sous-espace généré par les exemples du dictionnaire. Les petits points noirs représentent la projection des points rouges sur le sous-espace. Dans la technique du dictionnaire, pour obtenir de meilleures directions de principale variation, on tire parti de l’information donnée par tous les points en faisant l’ACP sur la projection des points en plus des 3 points du dictionnaire. C’est ce qu’on voit en c). Même si ces directions ne sont pas exac tement celles qu’on aurait trouvées en considérant tous les vrais points, elles s’en rapprochent certainement plus que celles trouvées en a).
4.4
Normalisation du noyau
Comme nous l’avons vu à la section 3.3, nous obtenons différents algorithmes de réduction de dimensionnalité en appliquant une normalisation à la matrice de Gram correspondant à utiliser un noyau dépendant des données. En particulier, la normalisation additive (éq. 3.3) est utilisée pour obtenir l’ACP à noyau et la normalisation divisive (éq. 3.5), pour la segmentation spectrale. Dans cette section nous décrivons comment ces normalisations peuvent être faites dans la cadre de notre algorithme sans que le coût ne dépasse O(m2n).
4.4.1
Normaliser avant ou après l’approximation?
Dans l’ACP à noyau et la segmentation spectrale ordinaires, nous obtenons le même résultat si nous construisons directement la matrice de Gram ] telle que
4.4 Normalisation du noyau 35
a)
.
!
Figure 4.2—En gris on représente le sous-espace généré par les 3 gros points noirs
dans l’espace des caractéristiques (on suppose que ce sous-espace passe par l’ori gine). Les flèches bleues représentent les directions de principale variation estimées par l’ACP. Dans notre technique, plutôt que d’estimer les directions de principale variation sur un sous-ensemble de points (a), on les estime sur la projection (b) de tous les points sur le sous-espace généré par le sous-ensemble de points (c).
4.4 Normalisation du noyau 36
= KD(xj, xi), où KD(x,x) est un noyau dépendant des données, ou si nous
construisons d’abord la matrice de Gram M à partir d’un noyau indépendant des données pour ensuite obtenir AI en normalisant M par rapport à la moyenne de ses lignes. Toutefois, d’un point de vue algorithmique, il est plus avantageux de normaliser la matrice pour ne pas avoir à effectuer de calculs redondants.
Avec la technique du dictionnaire, nous ne calculons jamais explicitement la matrice de Gram M, mais il est quand même possible de faire une transformation qui reviendrait à normaliserAM,AT.Toutefois, cette approche n’est pas équivalente à utiliser un noyau déjà normalisé dans l’algorithme 4.1. La différence tient au fait que l’approximation (le calcul des coefficients a1) n’est pas faite dans le même es pace des caractéristiques. En effet, si nous voulons que les coefficients a, soient op timaux dans l’espace de caractéristique correspondant au noyau de I’ACP à noyau ou à celui de la segmentation spectrale, nous devons utiliser un noyau déjà norma lisé (éq. 3.2 ou 3.6) dans l’algorithme 4.1. Toutefois, si dans ces équations nous effectuons les moyennes E[K(x1, x)] = 1 K(x,x) sur tous les n exemples,
nous nous retrouvons avec un algorithme en O(n2m), car l’étape 5 de l’algorithme 4.1 est exécutée O(nm)fois. Pour garder un algorithme enO(m2n) on peut effectuer la normalisation en choisissant un sous-ensemble aléatoire de taille inférieure àin2 sur lequel on va effectuer les moyennes.
Pour l’ACP à noyau, il existe aussi une façon valable d’effectuer la normalisa tion après I “approximation, sur la matriceAMAT.Il s’agit d’imposer une contrainte aux coefficients a qui rendent la combinaison linéaire invariante à une translation dans l’espace des caractéristiques. Comme la normalisation additive de l’ACP à noyau correspond justement à une translation dans l’espace des caractéristiques, elle peut être effectuée après l’approximation avec la technique décrite à la section suivante.
4.4.2
Normaliser après l’approximation
Les normalisations additive (équation 3.3) et divisive (équation 3.5) peuvent être appliquées sur la matrice impliciteAM,7ATde façon peu coûteuse, en effectuant une transformation sur la matriceA.