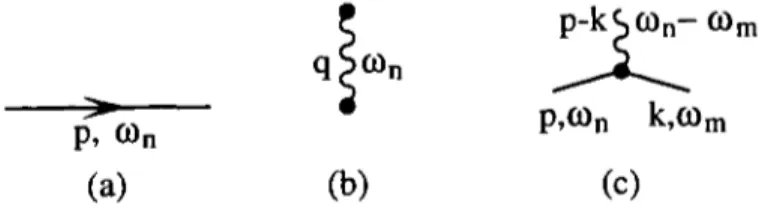HAL Id: tel-00011774
https://tel.archives-ouvertes.fr/tel-00011774
Submitted on 7 Mar 2006
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of
sci-entific research documents, whether they are
pub-lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diffusion de documents
scientifiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
To cite this version:
Markus Holzmann.
La transition de Bose-Einstein dans un gaz dilué.
Physique Atomique
[physics.atom-ph]. Université Pierre et Marie Curie - Paris VI, 2000. Français. �tel-00011774�
THÈSE
DE
DOCTORAT
DE
L’UNIVERSITÉ
PARIS
VI
pour
obtenir
le
titre
de
Docteur
de
l’Université Paris VI
présentée
par
Markus
HOLZMANN
SUJET de
la
thèse :
La Transition de
Bose-Einstein
dans
un
gaz
dilué
Soutenue
le 23
juin
2000
devant le
jury composé
de :
M.
Jean
ZINN-JUSTIN
Rapporteur
M.
Henk
STOOF
Rapporteur
M.
Jacques
TREINER
Examinateur
M.
Jean DALIBARD
Examinateur
M.
Werner KRAUTH
Directeur de thèse
THÈSE
DE
DOCTORAT
DE
L’UNIVERSITÉ
PARIS
VI
pour
obtenir le
titre
de
Docteur de
l’Université
Paris VI
présentée
par
Markus
HOLZMANN
SUJET
de la thèse:
La
Transition
de
Bose-Einstein
dans
ungaz
dilué
Soutenue
le 23
juin
2000 devant le
jury
composé
de :
M. Jean
ZINN-JUSTIN
Rapporteur
M.
Henk STOOF
Rapporteur
M.
Jacques
TREINER
Examinateur
M.
Jean DALIBARD
Examinateur
M.
Werner KRAUTH
Directeur de
thèse
M.
Claude COHEN-TANNOUDJI
Invité
Table des matières
Remerciements 5
Introduction 7
1 Le gaz
parfait
11Encadré 1 : Gaz
parfait
auvoisinage
de la transition ... 162 Gaz en interaction : calculs
analytiques
21 2.1 Hamiltonien du modèle ... 232.2
Approximation
duchamp
moyen ... 24Encadré 2 :
Approche
variationelle, champ
moyen ... 262.3
Développement
de la fonction departition ...
272.3.1 Calcul de la fonction de
partition
au deuxième ordre ena/03BB
28 Encadré 3 :Développement
enopérateurs
d’Ursell ... 29Encadré 4. Méthode de la théorie des
champs ...
352.3.2 Au-delà du deuxième ordre en
a/03BB
... 362.4
Développement
del’opérateur
densité à un corps ... 382 5 Formalisme des fonctions de Green ... 42
Encadré 5 : La fonction de Green à
température
finie ... 452.5.1 Théorie auto-cohérente pour calculer
0394T
c
/T
c
...
482.6 Annexe ... 52
2 6.1 Calcul de
U
2
en théorie deperturbation ...
522.6.2 Calcul de
U
3
en théorie deperturbation ...
533 Calcul de Monte-Carlo
quantique
55 3.1 Méthodegénérale
de Monte-Carloquantique
... 56Encadré 6: Conditions aux limites ... 58
3.2
Approche
dans la limite du gaz dilué ... 593.2.1 Action exacte ... 60
3.2.2
Longueur
de diffusion ... 603.2.3 Influence des interactions sur la fraction
superfluide ...
613.2.4
Algorithme
degénération
desconfigurations
du gazparfait
62 Encadré 7: Loi d’échelle ... 643.2.5 Taille finie et résultat de
0394T
c
/T
c
... 653.3 Annexe ... 66
3 3.1 Calcul de g2 avec
l’approximation
primitive ... 663.3.2 Calcul
analytique
de g2 ... 684.2 Gaz
piégé
en interaction ... 754.3 Fraction condensée ... 77
Bibliographie
81Publications Commentées 87
Publication I.
Bose-Einstein condensation in
interactmg
gasesM Holzmann, P Gruter, and F Laloe, Eur Phys J B 10, 739 (1999) ... 87
Publication II:
The Transition
Temperature
of the DiluteInteracting
Bose Gas G Baym, J -P Blaizot, M Holzmann, F Laloe, and D Vauthenn,Phys Rev Lett 83, 1703 (1999) ... 111
Publication III :
Transition
Temperature
of theHomogeneous,
Weakly
Interacting
Bose GasM. Holzmann and W. Krauth, Phys Rev Lett 83, 2687 (1999) ... 117
Publication IV :
Precision Monte Carlo test of the Hartree-Fock
approximation
for atrapped
Bose gasM Holzmann, W. Krauth, and M Naraschewski, Phys Rev A 59, 2956
(1999) 123
Publication V :Pair correlation function of an
inhomogeneous interacting
Bose-Einstein condensateRemerciements
Cette thèse a été réalisée au Laboratoire de
Physique
Statistique
et auLabo-ratoire Kastler Brossel à l’Ecole Normale
Supérieure.
Je remercie ses directeurssuccessifs,
Sébastien Balibar etJacques
Meunier,
ainsi que Michèle Leduc etElisabeth Giacobino pour
m’y
avoir accueilli.Mon premier contact avec le
Département
dePhysique
date du mois deseptembre 1996,
quand j’ai
rencontré Yvan Castin à l’occasion d’une conférencesur
l’optique quantique.
Je lui suisprofondément
reconnaissant d’avoir lu mademande de thèse
quelques
moisplus
tard et d’avoir cherché lapossibilité
de faire une thèse avec Werner Krauth et Franck Laloë dans(et
pasentre)
les deuxlaboratoires.
Je dois
beaucoup
à Werner Krauthqui
m’aguidé
pendant
ces années avecbeaucoup
d’enthousiame. Il m’aappris
la"physique
théorique pratique
surl’or-dinateur" avec
beaucoup
de patience etj’ai profité
de sonimagination incroyable
pour trouver des moyens pour résoudre presque
n’importe quel problème.
Je remercie
egalement
FranckLaloë,
avec quij’ai
eu des discussionsquoti-diennes Son
intuition,
saprécision
et sa connaisancegénérale
de laphysique
m’ontapporté
énormément.Tous les travaux
présentés
dans cette thèse sont les fruits de collaborationsavec des
personalités exceptionnelles ·
GordonBaym,
Jean-PaulBlaizot,
YvanCastm,
WernerKrauth,
Franck Laloë etDomimque
Vautherin Par ailleursj’ai
profité
de travailler avec GoraShlyapnikov
et de discuter avecChristophe
Salo-mon, Jean Dalibard et Maxim Olshanir.
Je dois
beaucoup
à DavidGuery-Odelin
et EmmanuelCourtade,
sans eux lathèse serait
probablement
illisible. Ils sont sacrifiébeaucoup
de leur temps pourm’aider à la formuler en francais. Ces nombreuses discussions m’ont aidé aussi
à former
plus précisement
mes idées. Je remercieégalement
Jean Vannimenus d’avoir bien voulucorriger
attentivement la version finale "enurgence".
Mes remerciements vont à toutes les personnes
qui
ontaccepté
de fairepartie
de mon jury, Claude
Cohen-Tannoudji,
JeanDalibard, Jacques
Treiner et enparticulier
Henk Stoof et Jean Zinn-Justin au titre de rapporteurs.Je remercie mes voisins dans mes divers bureaux pour une
athmosphére
trèsagréable.
Lionel Pérennes(Yo),
PatrickGiron,
NathaliePiegay,
KarenSauer,
François Marion,
EmmanuelCourtade,
XavierMuller,
DavidGuery-Odelin,
ChrisHerzog, Iacopo Carusotto,
AnnaMinguzzi,
ErichMüller,
XavierMaître,
François Treussart,
NicolasDureuil,
PierreDesbiolles,
HervéHenry,
Chi-Toung
Pham,
EricBrunet,
AlbertoRosso,
CécileAppert.
J’ai bénéficié de nombreuxéchanges scientifiques
avec eux comme avec MichaBaranov,
IsabelleBouchoule,
RolandCombescot, Philippe Cren, Ralph
Dum,
PeterFedichev,
GabrieleFer-rari,
VincentHakim,
DidierHerschkowitz,
ChristianHuepe,
TomHijman,
UnniDima
Petrov,
Ludger
Santen,
Franck Pereira DosSantos,
Pedro Patricio daSilva,
AliceSmatra,
GenevièveTastevin,
Jean Vanmmenus et tous les autres membres dans ledepartement
dephysique.
Je remercieégalement
leséquipes
dessecrétariats,
Angelique
Manchon,
CarolePhilippe,
NoraSadaoui,
MichèleSanchez,
Geneviève Piard et ZohraOuassyoun
comme les membres de l’Ateliergénéral
pourbeaucoup
d’aidepratique
etl’équipe
informatique
Zaire Dissi etThierry
Besançon.
Enfin mais surtout,
je
veux remercier ceuxqui
m’ontsupporté
mêmeen-dehors des heures
passées
au laboratoire. ErnstRasel,
Wolf vonKlitzing,
Ia-copo
Carusotto,
ClaudiaIsola,
DidierHerschkowitz,
AlbertoRosso,
RaoulSan-tachiara,
Yo pour m’avoirappris
la"langue
et civilisation" francaise et AnnaMmguzzi
pour la "cucina italiana" et pourbeaucoup
d’autres choses.Je remercie le "Deutscher Akademischer Austauschdienst
(DAAD)".
Diese Doktorarbeit wurde mittels eines DAADDoktorandenstipendiums
im Rahmendes
gemeinsamen Hochschulsonderprogramms
III von Bund und LändernIntroduction
Une transition de
phase
d’un gazparfait
2014comme
prédit
par Einstein[1]
pour unsystème
de bosons en trois dimensions 2014 contredit l’intuitionphysique :
en absence de toute interaction entre des atomes, les corrélations
quantiques
forcent à elles seules lesparticules
à former un condensat de Bose-Einstein en dessous d’unetempérature
critique T
c
> 0. Ces corrélationsquantiques
viennent de lastatistique bosonique
departicules
indiscernables.L’objectif
de cette thèse est d’étudierquantitativement
l’influence des interactions mutuellessur ce étonnant
phénomène
à bassetempérature
àpartir
desparamètres
micro-scopiques d’un gaz dilué.
La variation de la
température
critique T
c
avec l’interaction dans unsystème
homogène
a une histoire controversée dans la littérature(voir figure 1).
Mêmedans la limite d’un gaz très
dilué,
desprédictions théoriques
différentes abondent[2-11].
Parmi les calculsanalytiques
lesplus
récents,
le comportement deT
c
en fonction du diamètre a des
sphères
dures varie soit linéairement enan
1/3
[7, 8]
soit en racine carré(a
1/2
n
1/6
)
[6, 11],
où n est la densité du gaz. Un cal-culnumérique
de Monte-Carloquantique
pour différentes densitésna
3
proposeune augmentation de la
température
critique
linéairement avec le diamètre dessphères
dures[10].
Avec mon travail de
thèse, j’ai
contribué à une meilleurecompréhension
de ce
problème
en le clarifiant deplusieurs
points de vue. D’une part, undéveloppement
de la fonction departition
enagrégats
2014l’approche
d’Ursell[I]2014
et les méthodes de la théoriequantique
deschamps
àtempérature
non nulle 2014l’approche
en fonctions de Green[II]
2014permettent de
prédire
uncom-portement linéaire en
an
1/3
de latempérature critique
(chapitre
2)
Contrai-rement aux calculs
antérieurs,
nous avons considéré la structuregénérale
descorrections au spectre
énergétique
à tous les ordres ena/03BB,
où 03BB ~n
-1/3
estla
longueur
d’ondethermique.
La linéarité de la variation de latempérature
critique en
an
1/3
représente
un résultatnon-perturbatif
et non-trivial. Nousmontrons aussi
qu’un
calcul de la valeur absolue deT
c
pour un gaz dilué repose engénéral
sur desapproximations
incontrôlables 2014qui ne peuvent pas être contrôlées par un
paramètre
arbitrairement petit 2014,l’origine
desprédictions
qualitativement
etquantitativement
différentes dans la littératureUne
approche complémentaire
à ceproblème
est fournie par la méthodede Monte-Carlo
quantique
(chapitre 3)
qui
permet des calculsnumériquement
exactes pour un
système
de bosons en interaction. En associant la méthode deMonte-Carlo
quantique
avec la théorie deperturbation,
nous avonsoptimisé
cette
approche numérique
pour calculer de manière efficace desquantités
dansla limite d’un gaz dilué. Contrairement à
[10],
un calcul direct de latempérature
dynamique.
Nous déterminons ainsi latempérature
critique dans l’ensemblecanonique
1
.
Dans la deuxième
partie
(chapitre 4)
de cettethèse, je
résume mes calculs deMonte-Carlo
quantique
concernant desparamètres plus proches
desexpériences
sur la condensation de Bose-Einstein sur les vapeurs des alcalins[14,
15,
16]
et sur
l’hydrogène
[17].
Dans cessystèmes,
lepotentiel
extérieur dupiège
et le nombre fini desparticules jouent
un rôleimportant
Les résultats dusystème
homogène,
parexemple
la modification de latempérature
critique,
nes’ap-pliquent
pas directement. Nous avons mené des calculs de Monte-Carloquan-tique
avec N = 10 000 bosons dans unpiège harmonique
et unelongueur
de diffusion des atomesadaptée
aux experiences sur87
Rb
[IV,V].
Ces calculsper-mettent de tester
précisément
la validité desapproximations
simples,
utiliséesfréquemment
pourinterpréter
les résultatsexpérimentaux,
2014comme
l’approxi-mation de Hartree-Fock et
l’approximation
deBogoliubov
2014 avec ce choix desparamètres.
Finalement, j’aborde
laquestion
de la déterminationrigorouse
du condensat et de la fraction condensée dans unsystème
inhomogène
avec des interactions.Contrairement au
système homogène,
où la fonction d’onde du condensat estconnue par raison de
symétrie,
la formespatiale
du condensat n’est pas à prioriconnue dans un
potentiel
extérieur. Pour étudier l’ordrenon-diagonal
àlongue
portée qui
caractérise laprésence
d’uncondensat,
l’information sur les élémentsnon-diagonaux
de la matrice densité à un corps est nécessaire. Par un calcul deMonte-Carlo
quantique,
nous avons déterminé la fonction d’onde du condensatet la fraction condensée dans ce
système inhomogène
en utilisantuniquement
ceconcept fondamental. Le calcul permet de tester de manière directe la validité de
l’équation
de Gross-Pitaevskir pour décrire la fonction d’onde ducondensat,
mais aussi d’étudier
numériquement
la relationquantitative
entre lacondensa-tion de Bose-Einstem et
l’apparition
deslongs cycles d’échanges,
observables avec le calcul de Monte-Carlo Lastatistique
descycles
d’échanges
et leurre-lation avec le
phénomène
de la condensation de Bose-Emstein sont introduites dans le premierchapitre
pour le cassimple
du gazparfait
En tête de
chaque chapitre
le lecteur trouvera un résuméplus
détaillé. Parailleurs,
un certain nombre de méthodes ettechniques
utilisées tout aulong
decette thèse sont rassemblées dans des "encadrés". L’essentiel de mon travail de
thèse est
publié
dans les articles[I-V]
reproduits
et annotés àpartir
de la page 87.1 Plus recemment une augmentation linéaire en an1/3 de la température critique de la transition superfluide dans un systeme de
4
He-vycor
a éte mesuré dans[13]
Cependant, lesysteme de vycor est très complexe et il reste à verifiér si l’interprétation par un gaz dilué en
trois dimensions 2014
proposé dans cet article 2014
est quantitativement possible pour décrire la
FIG. 1 - Les
prédictions
théoriques
etexpérimentales proposées
dans la littérature pour lamodification
de latempérature
critiquec
0394T
/T
c
=c(na
3
)
03B3
dans la limite d’un gaz dilué
na
3
~
0. Je n’ai tracé que les résultats ou la limiteasymptotique était donnée
explicitement
dans les articles J’ai aussi inclu lesChapitre
1
Le
gaz
parfait
Pendant
plusieurs
décennies,
la nature de la condensation de Bose-Einsteinen
présence
d’interactions aposé
degrands
problèmes conceptuels.
Lacom-préhension
moderne de cephénomène
spectaculaire
est fournie par le conceptde l’ordre
non-diagonal
àlongue
portée, proposé
initialement par Penrose etOnsager
[18].
Le lien entre la condensation de Bose-Einstein et lasuperfluidité
a été
également
élucidé[19].
Bien avant ces travaux,
Feynman
avaitproposé
que leslongs cycles
d’échanges,
présents
dans un gazquantique,
jouaient
un rôle crucial pour ladescription
de lacondensation de Bose-Einstein
[20]
Cescycles d’échanges
apparaissentnaturel-lement en
première
quantification
via lasymétrisation
des états dans la fonctionde
partition
Cette image, basée surl’intégrale
dechemin,
a étébeaucoup
uti-lisée par
Feynman
pour unecompréhension
intuitive de la transitionsuperfluide
dans
4
He
liquide
[21,
22,
23].
La
description
deFeynman
a été fondamentale pour lesapproches numériques
aux
liquides
quantiques du type Monte-Carloquantique qui,
au cours des 15dernières
années,
ont permis unedescription
quantitative
de la transition lambdapartant des
premiers principes
[24]
Dans ce
premier chapitre,
j’introduis
ladescription
deFeynman
pour le cas du gazparfait.
J’établis ensuite le lienexplicite
entre lastatistique
descycles
d’échanges
et ladescription
habituelle en termes de nombred’occupa-tion d’états. Les
formules, présentées
dans cechapitre,
donnent ladescription
complète
dusystème
sans interaction à nombre fini desparticules.
La connais-sance détaillée du gazparfait
est essentielle pour les calculsnumériques
d’un gazen interaction au
chapitre
3 et auchapitre
4. Le formalismeprésente
en outredes liens étroits avec le
description
enopérateurs
d’Ursell auchapitre
2.En
particulier,
uneformule,
que nous avons établie dans[III],
donne lacor-respondance
précise
entre la distribution deslongueurs
descycles
et la fraction condensée Dans lechapitre
4 nous étudierons la relation entre ladéscription
de Penrose etOnsager
etl’image
deFeynman
enprésence
des interactions dans untionnelle à l’élément
diagonal 03C1
D
(R, R)
del’opérateur
densitéLa fonction de
partition
Z
D
N
pour desparticules
de Boltzmann s’obtient àpartir
des éléments
diagonaux
del’opérateur
densité03C1
D
(R,
R)
selonPour des
particules
quantiquesindiscernables,
les états dusystème
diffèrent à bassetempérature
de ceux de l’ensemble de Bolzmann. Pour lesbosons,
l’in-discernabilité limite les états accessibles à ceux
qui
sontsymétriques,
|R>
S
~
1 N’
03A3
{P}
|P(R)>.
Ongarde
explicitement
l’action dusymétriseur
Squi
s’ex-prime
dans la somme sur toutes lespermutations
possibles
{P}.
AvecP(R) ~
(r
P(1)
, r
P(2)
, ..., r
P(N)
),
on obtientLa fonction de
partition
ZN dusystème
bosonique
s’obtient àpartir
de lama-trice densité 03C1B
(R,
R’)
parPuisque
l’hamiltonien commute avecl’opérateur
desymétrisation
S,
il suffit dene
garder
ce dernierqu’une
seule fois enéquation
(1.3).
Exception
faite de lapermutation
identitéP(i)
= i(i
=1,..,
N),
la sommesur toutes les
permutations
{P}
dansl’expression (1.5)
pour03C1
B
(R, R)
faitin-tervemr les éléments
non-diagonaux
03C1
D
(R,
P(R) )
de la matrice densité despar-ticules discernables
(voir figure 1.1).
Enreprésentation "position",
les élémentsnon-diagonaux
de la matrice densité décroissent sur une distance de l’ordre de lalongueur
d’onde de deBroglie 03BB ~
(mT)
-1/2
Pour unsystème
avec une den-sité moyenne n =N/V
à hautetempérature,
seule l’identité contribue : ainsi les effetsd’échange
déviennentnégligeables
On retrouve dans cette limite lerésultat
classique
pour desparticules
discernables(
=0).
Les effetsstatis-tiques quanstatis-tiques commencent à intervenir dès que la
longueur thermique
estde l’ordre de la distance moyenne entre les
particules n
-1/3
~
03BB,
d’où onob-tient un
paramètre
sans dimensionn03BB
3
,
qui
décrit ledegré
dedégénérescence
quantique
dusystème
FIG 1.1 - Les
permutations
font
intervenir engénéral
les élémentsnon-diagonaux
del’opérateur
densité desparticules
discernables. Le termecorrespon-dant à la
permutation
P àgauche
estgraphiquement
représenté
à droite :après
une évolution en
"temps
imaginaire"
=03B2
lesparticules
2,3,4
ontéchangé
leurs rôles. Cette
permutation
P =(1)(243)
peutégalement
être décrite entermes de
cycles
{m
k
}
par m1 = 1 et m3 = 1(m
2
= m4 =0).
Comme l’hamiltonien H est
symétrique,
de nombreusespermutations
nediffèrent que par
l’étiquetage
desparticules
et contribuent avec unpoids
statis-tique
identique.
C’est le cas, à titred’exemple,
de toutes lespermutations
qui
n’échangent
le rôle que de deuxparticules :
P(i) = j, P(j)
=i, P(k)
=k,
i ~ j ~
k. La contribution de ce sous-ensemble de
permutations
se réduit au calcul dela matrice densité pour la
permutation,
P(1)
=2,
P(2)
=1,
P(i)
= z, i~
1, 2,
multipliée
par le nombre de ces permutations, à savoirN!/2(N - 2)!.
Cesper-mutations sont des
cycles
delongueur
2,
où lalongueur
k d’uncycle
est définiepar
P
k
(i)
= i.Plus
généralement,
on peut donc reformuler le comptage en termes decycles
d’échange.
Il suffit de connaître le nombred’occupation
mk d’uncycle
delon-gueur k donné. La somme sur les
permutations
peut alors êtreremplacée
parune somme sur les distributions
{m
k
}.
Notons quechaque configuration
{m
k
}
vérifie la conservation du nombre total de
particules
Pour une distribution
(m
k
)
donnée,
il y a N!mk
-1
)
03A0
!k
k
(m
k
possibilités
dedis-tribuer les indices des
particules.
Ce facteur de comptagecorrespond
au nombrede
permutations
différentes,
qui conduisent à la même distribution encycles.
On obtient
l’expression
de la matrice densité pour des bosons :où
03C1
D
(R, P
{mk}
(R))
est la valeur de la matrice densité desparticules
discer-nables pour une permutationP
{mk}
arbitraire
correspondant
à cetteconfigura-tion en
cycles
{m
k
}.
Appliquons
dans unpremier
temps ce formalisme au cas d’un gazpar-fait L’hamiltonien
H
0
correspondant
est la somme des hamiltoniens individuelsHo
=03A3
i
h
0
(i),
oùh
0
(i)
=p
2
i
/2m
estl’énergie cinétique
d’uneparticule.
Il estd’une
grande
importance que les contributions desparticules qui
ne sont pasconnectées par un
cycle
d’échange
se factorisent dans03C1
D
(R,
P
{mk}
(R)).
FIG. 1.2 - Un
cycle
delongueur
3(à gauche)
correspond
à uneparticule
quiévolue entre = 0 et =
303B2
(à droite).
L’intégration
sur deuxparticules
(r
2
,
r
3
)
montrequ’une particule
dans uncycle
delongueur
3 se comporte en moyenne comme une seuleparticule
à unetempérature
3 foisplus petite. Puisque
l’hamiltonien nedépend
pasexplicite-ment de la
température
(c’est-à-dire
du"temps
imaginaire"
),
l’évolution entemps
imaginaire
d’uncycle
delongueur
k estéquivalent
à l’évolution d’une seuleparticule
entre = 0 et= k03B2
(voir figure
1.2 etl’application
page62).
Dans la trace de la fonction departition
(1.6),
chaque
cycle
delongueur
k contribue avec unpoids
sk, qui s’écritAinsi,
uncycle
delongueur
k se comporte comme uneparticule
àtempérature
1/(k03B2).
La fonction de partition s’écrit alors sous laforme,
obtenue parFeynman
[20],
avec la contrainte
03A3
k
km
k
= NCette dernière contrainte est
imposée
par l’ensemblecanonique.
On peut la contourner via le formalismegrand-canonique
qui,
grâce
aupotentiel
chimique
03BC, ne conserve le nombre de
particules
qu’en
moyenne. La fonction departition
grand-canonique
Z
GC
est reliée à la fonction departition canonique Z
N
par :où z =
e
03B203BC
est lafugacité.
On peut ainsi sommerindépendamment
sur tous lesnombres
d’occupation
descycles,
soit finalement.Pour un
système homogène
on obtient à la limitethermodynamique
où l’on a introduit la
longueur
d’ondethermique 03BB
=203C0
2
03B2/m.
On obtientalors
l’expression
de la densité dansl’espace
desphases :
Pour un gaz
classique
(03B203BC
=log(z)
«0),
seuls lespremiers
termes de la sommedans
l’équation
(1.16)
sontimportants.
Rappelons
que k fait référence à unelon-gueur de
cycle.
Dans la limiteclassique,
on voit que leslongs cycles
d’échange
ne contribuent presque pas à la densité. Mais dès que le
potentiel
chimique
s’ap-proche
del’énergie
de l’état fondamental d’une distance de l’ordre de1/N,
tous les termes deviennentimportants.
On retrouvel’interprétation
deFeynman
se-lon
laquelle
lephénomène
de condensation de Bose-Emstein estintrinsèquement
lié à l’occurence des
longs cycles
d’échange
dans lesystème.
La densité aupoint
de transition est donnée par :
Une formulation
plus quantitative
del’interprétation
deFeynman
peut être obtenuegrâce
àl’équation
(1.11),
où la fonction departition
est écrite comme une somme sur tous les nombresd’occupation
descycles
{m
k
}.
Elle permetégalement d’expliciter
laprobabilité
P({m
i
})
de la distribution des nombresd’occupation
{m
i
}
dans lesystème.
Cette dernière relation permet de déduire
l’expression
de la valeur moyenned’occupation
mk d’uncycle
delongueur
k dans l’ensemble canonique[III] :
La somme sur toutes les
partitions
{m
l
,m
k
~
1}
correspond
aux deuxcondi-tions,
03A3
l
lml = N et la conditionque le
cycle
delongueur
k soit au moinsoccupé
unefois,
mk ~ 1. Cette sommeéquivaut
à une somme sur toutes lespartitions
{m
l
}
avec une seule condition03A3
l
lm
l
= N - k.avec 03B5k =
2
k
2
/2m.
Puisque
la fonction de Bosedéveloppe
unesingularité
(infrarouge)
à k = 0 au pointcritique
(03BC
=0),
undéveloppement
deTaylor
enpuissances
de03B203BC
n’est paspossible
près
de la transition.Néanmoins,
on peutséparer
le comportementpour k
~ 0 et réécrirel’intégrale
(B1-1)
de la manièresuivante:
où il a été nécessaire d’introduire une coupure A afin de contrôler les
di-vergences ultraviolettes ainsi créées. Dans cette nouvelle
expression,
seule ladernière
intégrale
estdivergente
pour03B203BC
~0,
les autresintégrales
permettentun
développement
enpuissances
de|03B203BC|.
Prenons l’ordre zéro en|03B203BC|
de cesdeux
premières
intégrales,
nous obtenonsNous regroupons alors le premier terme de la
première intégrale
avec ladeuxième
intégrale,
cequi
donne la contributionPour
le second terme, il estregroupé
avec la dernièreintégrale,
et fournit : Cetteintégrale
est finie pour ~ ~ ~ et vaut-03BB
-3
403C0(-03B203BC).
Notons que ladépendance
en racine carrée dupotentiel chimique
peut aussi être obtenue par unsimple
changement
de variable(ou
un argumentdimensionnel).
Regroupons
les termes
obtenus,
nous pouvons alors écrire:Pour aller
plus
loin,
il fautregarder
les ordres suivants dans ledéveloppement
deTaylor
en|03B203BC|,
suivi d’une limite A ~ ~.Ce petit calcul montre dans le cas
simple
du gazparfait
que dessingularités
infrarouges,
liées à une transition dephase,
nécessitent engénéral
unregrou-pement des termes dans
l’expression
exacte pour obtenir unedépendance
FIG 1 3 - Le nombre moyen de
particules
k<m
k
>
N
dans uncycle
delongueur
k au voisinage de la temperature critique
T
0
pour N = 1000particules
dansl’ensemble canonique.
On peut la
justifier grâce
auchangement
de variables mk - 1 ~ mk. On faitainsi
apparaître
la fonction departition canonique
relative à N 2014 kparticules.
D’où
l’expression
de<m
k
>
N
ou, de manièreequivalente,
celle du nombre moyende
particules
dans uncycle
delongueur
k donné:k<m
k
>
N
La relation de conservation du nombre de
particules
03A3
k
k<m
k
>
N
=N,
permetde calculer par récurrence
Z
N
:
Cette formule est bien utile : elle permet de calculer par récurrence dans
l’en-semble
canonique
la fonction departition
pour toute valeur de N finie[25,
26,
27,
28]
Une nouvelleinterprétation
de cette formule est à la base de notrealgorithme
deMonte-Carlo, présenté
dans[III].
La
figure
1.3représente
le nombre moyen departicules
parcycle
delongueur
k au
voisinage
de latempérature
critiqueT
0
.
Commeattendu,
au-dessus de latempérature
critique, T >T
0
,
N
k
>
k<m
decroîtrapidement
avec lalongueur
decycle.
Enrevanche,
en dessous deT
0
,
on peutdistinguer
deuxrégimes:
unedécroissance
rapide
pour les petitscycles k,
k «N
2/3
,
et unplateau
pourk >
N
2/3
,
oùk<m
k
>
N
reste pratiquement constantNous avons réussi à relier le nombre
d’occupation
descycles
avec le nombred’occupation
moyen d’un état vd’énergie
03B503BD. Ce dernier est donné par<n
03BD
>
N
=-~logZ
N
/~(03B203B5
03BD
)
et peut être calculégrâce
àl’équation
(1.11).
On obtientOr,
e
-03BA03B203B5
03BD/s
03BA
est la moyennethermique classique
du nombred’occupation
de l’état v pour unetempérature
1/(k03B2).
Ainsi,
lesparticules
d’uncycle
delongueur
ment au nombre de
particules
condensées(n
03BD=0
).
Dans la limitethermodyna-mique,
la fraction condensée sera donnée par la valeur maximalek
max
/N
descycles
occupés.
Dans lechapitre
4,
page77,
je compare cettefaçon
d’obtenir la fraction condensée dans un simulation de Monte-Carlo avec un résultat obtenupar calcul des éléments
non-diagonaux
de la matrice densité dans le cas d’ungaz en interaction.
La fonction de distribution
P(n
03BD
~
k)
2014correspondant
au cas où au moinsk
particules
sont dans l’état v 2014s’exprime
sous la forme :Cette relation fait
apparaître
la fonction departition
à N-kparticules
Z
N-k
;
lacontrainte d’avoir au moins k
particules
dans l’état v estimposée
par le facteure
-03BA03B203B5
03BD.
Par sommation sur les états v, lesprobabilités
P(n
03BD
~
k)
peuvent êtrereliées au nombre moyen
k<m
k
>
N
departicules
dans uncycle
delongueur
k:La fonction de distribution
correspondant
à kparticules
exactement dans l’état v s’obtient par soustraction :P(n
03BD
=k)
=P(n
03BD
~
k) 2014 P(n
03BD
~
k +1).
On voit que la derivée discrète de
k<m
k
>
N
par rapport à k s’écrit.et
correspond
donc à laprobabilité
d’avoir exactement kparticules
dans unmême état. Cette formule
(1.28),
que nous avons obtenue dans[III],
présente
une relation surprenante entre les
longueurs
descycles
(membre
degauche
del’équation)
et laprobabilité d’occupation
des états(membre
dedroite).
Pour T >To,
k<m
k
>
N
est une fonction convexe, donc laprobabilité
d’avoir exactement kparticules
dans le même état est strictement décroissante enfonc-tion de k. En
revanche,
en dessous de latempérature
critique
T
0
(T ~ T
0
),
laprobabihté
d’avoir exactement k bosons dans le même état croît de manièresignificative
pour k
» 1. Cet effet est mis en évidence sur lafigure
1.4 par laprésence
d’unpic
deplus
enplus marqué
au fur et à mesure que latempérature
descend en dessous de la
température
critique Cepic
décrit la distribution dunombre de
particules
condensées n0. Dans l’ensemblecanonique,
lalargeur
decette distribution
(0394n
0
)
2
~
<n
2
0
-
>
N
0
2
>
<n
resteproportionnelle
à<n
0
>
N
pourT < T
0
[29],
d’où:Ce résultat reflète le fait
qu’un
cycle
delongueur
macroscopique
(k
~N)
ne peut pas êtreoccupé
macroscopiquement dans l’ensemble canonique. A cause deFIG. 1.4 - Fonction de distribution
correspondant
à kparticules
exactementdans le même état
k+1
.
N
>
-(k+1)<m
N
>
k
k<m
Calcul réalisé pour N = 1000par-ticules. En dessous de
T
0
,
le pic décrit la statistique desparticules
condensées. la contrainte d’un nombre fixe departicules,
les fluctuations dek<m
k
>
N
restentintensives
(sauf
auvoisinage
de latempérature
critique).
Jusqu’ici,
lastatistique
decycles
a été obtenue dans l’ensemblecanonique,
c’est-à-dire avec un nombre fixé de
particules.
Dans le formalismegrand-canonique
la valeur moyenne
<A>
GC
d’une observable A est reliée à sa valeur moyenne(A)N
dans lesystème
canonique
de la manière suivante :Par
exemple,
la formule pour le nombre moyen departicules
dans uncycle
delongueur
k,
équation
(1.22),
conduit dans l’ensemble
grand-canonique
à :De
même,
les autres formules établiesprécédemment
peuvent se calculersim-plement
en substituant le rapportZ
N-03BA
/Z
N
parz
k
.
L’équation
(1.35)
permet de calculer le nombre total departicules
dans lesystème.
A la limitethermodynamique
on retrouve facilement la formulepour la densité du gaz
parfait : équation
(1.16).
Notons que l’ensemblegrand-canonique
ne permet pas de décrire lesystème
au-dessus de la densitécritique
de la transition de Bose-Emstein à la limitethermodynamique.
Néanmoins,
dansun
système
fini de Nparticules,
laphase
condenséecorrespond
à unpotentiel
Pour montrer que cette
description
dusystème
condensé sedistingue
qualita-tivement de la
description
dans l’ensemblecanonique,
on peut s’intéresser auxfluctuations du nombre de
particules
Pour un
système
de taillefinie,
les fluctuations dans laphase
condensée(|03B203BC| ~
N
-1
)
prennent un caractèrepoissonien :
En
conséquence,
ladescription
d’unsystème
de la taille finie dans l’ensemblegrand-canonique
n’estplus équivalente
à l’ensemblecanonique
en dessous de latempérature
critique,
T <T
0
.
Ces fluctuations du nombre des
particules
reflètent dans unedescription
entermes de
cycles
le fait que,
GC
>
k
k<m
équation
(1.35),
reste une fonction convexe,même en dessous de la
température
critique et que la nombre departicules
dansun
cycle
macroscopique
a des fluctuationspoissoniennes
pour T <T
0
.
Les différences entre les ensembles statistique pour les bosons libres ont été
très étudiées dans une
optique
de gazparfait.
Dans nos travaux[III,IV,V],
elles ont été à la base des calculs portant sur le gaz en interaction.Notre
approche
pour relierquantitativement
lastatistique
decycles
à lacondensation de
Bose,
peutégalement
êtregénéralisée
au cas d’un gazpiégé
parun
potentiel
exténeur. Dans ce cas, seulel’expression
de sk est modifiée(voir
page 75 pour le cas d’un
potentiel
harmonique).
Dans lechapitre
4,
j’exposerai
le résultat d’un calcul Monte-Carlo quantique pour un gaz en interaction dans un
piège
harmonique.
Je calcule aussi les élémentsnon-diagonaux
de la matriceà un corps pour
regarder numériquement
les relations entre lastatistique
decycles
et celle du nombre departicules
condensées pour un gaz réel de faibleChapitre
2
Gaz
en
interaction : calculs
analytiques
La condensation de Bose-Einstein du gaz
parfait
est un de ces rares modèlesmicroscopiques
possédant
une transition dephase,
dont la solution estanaly-tiquement connue. La
première
observationexpérimentale
de cephénomène
a été la transitionsuperfluide
de
4
He
à 2.18 K. Même si les interactions dans celiquide
sont loin d’êtrenégligeables,
la transition dephase
ressembleremar-quablement
à celle d’un gazparfait
ayant la masse de4
He,
attendue à 3.3 K.L’abaissement de la
température critique
dans cesystème
dense a montré quele point de transition du gaz
parfait,
n03BB3 =03B6(3/2),
est engénéral
modifié parl’interaction.
La réalisation
expérimentale
de la condensation de Bose dans des vapeursatomiques
[14,
15,
16]
a déclenché de nouvelles études de la transition deBose-Emstein dans un gaz
dilué,
où les interactions entre des atomes sont décritespar un seul
paramètre,
à savoir lalongueur
de diffusion a[30].
Dans ce
chapitre je
présente
nos calculsanalytiques
pour obtenir lamodi-fication de la
température
critique
par rapport au résultat du gazparfait
dansun gaz
homogène
et dilué(na
3
«1)
[I,II].
Je montrequ’un
développement
perturbatif
en a conduit à unparamètre
dedéveloppement
de la structure :Dans la limite a ~
0,
lapotentiel chimique
(effectif)
au point de transitionc
s’approche
de la valeur du gazparfait
03BCc
~0,
et leparamètre
dedéveloppement
(2.1)
a une valeurfinie
1
.
Enconséquence
un calculperturbatif
n’estplus
pos-sible,
c’est-à-dire ne devientplus
exact dans la limitean
1/3
~ 0.Néanmoins,
nous avons réussi à montrer dans(II)
que la modification de latempérature
critique
est linéaire enan
1/3
,
où
T
0
est latempérature
critique
du gazparfait.
Dans[I]
et[II],
nous avonsdes bosons en
interaction,
par contre, est basée sur undéveloppement
en puis-sances dupotentiel
inter-atomique
v(r)
[32]
Dans la section 2.3
je
calculeexplicitement
la fonction departition
Z audeuxième ordre en
03B1/03BB
en utihsant les deux méthodes. Eneffet,
l’expression
den03BB
3
en fonctionde 03BC
contient la combinaison03B1/(03BB03B203BC.).
Même dans la limite03B1/03BB
~0,
ledéveloppement
n’estplus
valable pour03B203BC ~
a/03BB
et ne permet pas des’approcher
de latempérature
critique.
Néanmoins,
lareprésentation graphique
dudéveloppement
perturbatif
dansl’approche
d’Ursell et dans la théorie deschamps permet
de resommer tous cestermes
proportionnels
à unepuissance
duparamètre
adimensionnela/(03BB03B203BC).
On obtient de nouveau le résultat de
l’approximation
duchamp
moyen(section
2.2),
qui contientdéjà
toutes les corrections linéaires ena/03BB
à 03BCc. Notons quel’approximation
duchamp
moyen nechange
ni la forme du spectred’énergie
ni latempérature
critique
par rapport au cas du gazparfait. Cependant,
ces calculs illustrentl’avantage
des méthodesdiagrammatiques
qui
permettent d’étudier facilement la structure des corrections aux ordresélevés,
et ils montrent la nécessité de resommer desdiagrammes
avec le même comportementsi 03BC
~ 0.Dans
l’approche
d’Ursell,
il est commode de passer d’un calculperturbatif
deIog Z
à un calcul del’opérateur
densité à un corps03C1
(1)
.
Ledéveloppement
diagrammatique
de03C1
(1)
permetplus
facilement de resommer desdiagrammes
avec une structuresimilaire, grâce
à deséquations
non-linéaires(section 2.4).
Au-delà del’approximation
duchamp
moyen, les effets des corrélations donnenten
général
unchangement
du spectre del’énergie
et de latempérature
critique.
Les détails de ces calculs sont donnés dans l’article
[I].
Le passage à
l’opérateur
densité à un corps dansl’approche
d’Ursell estsimi-laire au passage à la fonction de Green
(à
uncorps)
dans la théorie deschamps.
Les
développements
perturbatifs
de ces deuxapproches
seressemblent
3
,
les contributions dominantes d’un calcul au pointcritique
deviennentidentiques
dans la limite
a/03BB
~ 0. Le formalisme desfréquences
de Matsubara dans le calcul de la fonction de Green permet d’étudier la structuregénérale
descorrec-tions au spectre, les
énergies
propres(section 2.5).
Ledéveloppement perturbatif
pour calculer les corrections par rapport au
champ
moyen indroduit aussi unparamètre
de la structure(2.1),
soitoù
c
03B2
=4a03BB
2
n - 03B203BC
tend vers zero comme2
.
a
/03BB
2
En nous fondant sur cesconsidérations,
nous avonsprouvé
la linéarité ena/03BB
de0394T
c
/T
c
dans la limitea/03BB
~ 0[II].
2 Pour tous nos calculs de Tc, nous avons utilisé la hberté de s’approcher de Tc par une
température plus haute, T ~ Tc+ 0 En conséquence la fraction condensée reste toujours
négligeable á la limite thermodynamique, ce qui simplifie les calculs analytiques.
3 Puisque le traitement des interactions est différent dans les deux approches, les
une preuve de la linéarité en a, formule
(2.2),
complètement indépendante
decelle
présentée
ici. La méthode de Monte-Carlo permet aussi un calcul exact dupréfacteur.
2.1
Hamiltonien
du
modèle
Pour étudier les
caractéristiques
de la condensation de Bose dans un gazréel,
il est nécessaire de tenir compte des interactions entre atomes. On se restreint au cas le
plus simple
oùl’énergie
d’interaction V s’écritEn deuxième
quantification,
l’hamiltonien total est donné par :où
03A8
~
(r)
(03A8(r))
estl’opérateur
champ
qui
crée(détruit)
uneparticule
en r.Pour un
système
homogène,
on peutexprimer
l’opérateur
03A8
~
sous la forme:03A8
~
(r)
=1 V
03A3
k
e
ik
.
k
~
a
r
Cettereprésentation
enimpulsion
diagonalise
lapartie
sans interactionsH’
0
de l’hamiltonien :où k = 03B5
2
/2m
k
2
0127
estl’énergie
cinétique
d’uneparticule
d’impulsion
k.L’opérateur
d’interaction conservel’impulsion
totale,
d’où.où
(q)
= d
3
re
iq
r
v(r)
est la transformée de Fourier dupotentiel
v(r).
Normalement,
lepotentiel
inter-atomique n’est pas connu avecprécision,
mais seule la connaissance des
propnétés
de diffusion binaires est nécessaire pour rendre compte de laphysique
du gaz dilué. Cespropriétés
de diffusionsont caractérisées par les
déphasages
03B4
l
(k)
ou de manièreéquivalente
parl’am-phtude
de diffusionf(k, k’).
Dansl’approche
d’Ursell,
la fonction departition
sedéveloppe
enagrégats
(" cluster expansion"),
cequi
autorise unedescription
des colhsions directement en termes desdéphasages
[33,
34, 35,
36].
Enrevanche,
dans uneapproche
de type théorie deschamps,
la fonction departition
estdéveloppée
en puissances dupotentiel,
le hen avec lespropriétés
de diffusion seavec K =
(p -
k)/2.
Pour des atomes
ultrafroids,
la diffusion entre bosons s’effectue dans lerégime
des ondes s. A unetempérature
suffisammentbasse, l’amplitude
dedif-fusion est dans la
majeure
partie des casindépendante
del’impulsion relative,
f(K, K’) ~ f(0,0)
= a ; lespropriétés
de diffusion sont alors bien décrites parun seul
paramètre
microscopique,
lalongueur
de diffusion a.En
général,
on ne connait pasl’expression
exacte de v, maisl’amplitude
de diffusionf
peut fairel’objet
de mesures. Il est donc commode deremplacer
lesdépendances
en v parf
vial’équation
deLippmann-Schwinger
(2.9).
A l’ordre leplus
bas,
(q)
peut êtreremplacé
par la constante decouplage g
=403C0
2
f/m
=403C00127
2
a/m.
Nous aurons l’occasion de revenir sur ce passage entre v etf
lors dudéveloppement
perturbatif
dulogarithme
de la fonction departition.
A l’ordre le
plus
bas,
la contribution des interactions dans l’hamiltonien s’écrit :Pour g = 0 on retrouve le cas du gaz
parfait,
où la densité moyenne departicules
avec
impulsion
k est donnée par la distribution deBose-Emstein,
Au
point
de la transition de Bose-Einstein(03BC
=03B5
0
),
la fonction de Bosediverge.
En
conséquence,
la densitécritique
dépend
defaçon non-analytique
dupotentiel
chimique
Auvoisinage
de la transition dephase,
la densité dansl’espace
dephases
est donnée par(voir
encadré1,
page16) :
A densité
fixée,
latempérature
critique du gazparfait
T
0
est donnée parComment la
transition,
et enparticulier
latempérature
critique
sera-t-elleaf-fectée par les interactions entre atomes?
2.2
Approximation
du
champ
moyen
En
première
approximation, les effets d’interaction peuvent êtrepris
encompte