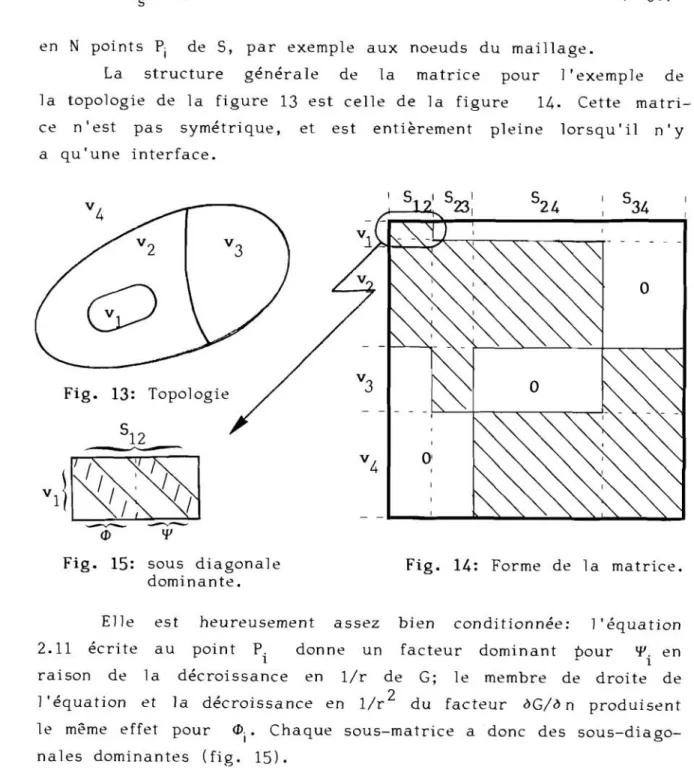
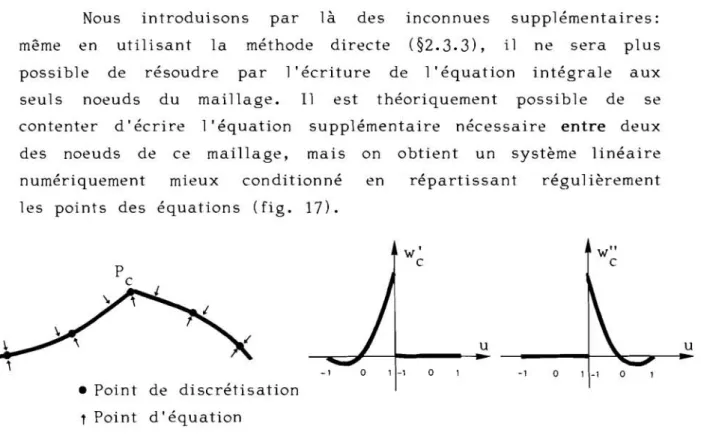
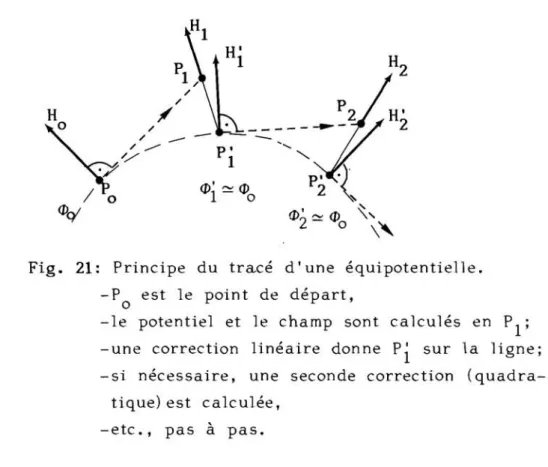
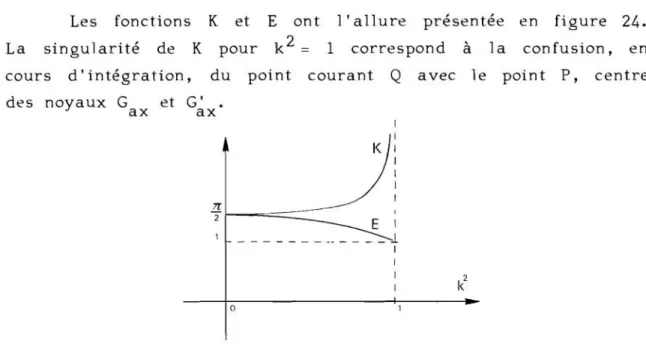
HAL Id: tel-00012060
https://tel.archives-ouvertes.fr/tel-00012060
Submitted on 30 Mar 2006HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
La méthode des équations intégrales de frontière pour la
résolution des problèmes de potentiel en
électrotechnique, et sa formulation axisymétrique
Laurent Krähenbühl
To cite this version:
Laurent Krähenbühl. La méthode des équations intégrales de frontière pour la résolution des problèmes de potentiel en électrotechnique, et sa formulation axisymétrique. Modélisation et simulation. Ecole Centrale de Lyon, 1983. Français. �tel-00012060�
N o d ' o r d r e : E.C.L. 83-13
présentée devant
L'ECOLE CENTRALE
DE
LYONpour obtenir
le t i t r e de DOCTEUR-INGENIEUR
Spécialité : Génie électrique.
p a r M. Laurent Krahenbühl ingénieur E.P.F.L.
La méthode des équations intégrales de frontière pour l a résolution des problèmes de potentiel en électrotechnique, et s a formulation axisymétrique.
soutenue l e 16 décembre 1983 devant l a commission d 'examen
J u r y : M. J .C. Sabonnadière, Président Année 1983 et MM. B. Ancelle, A. Foggia, M. J u f e r , M. Lajoie-Mazenc e t A . Nicolas.
ECOLE CENTRALE DE LYON
DIRECTEUR
A. MOIROUX
DIRECTEUR ADJOINT
R. RICHE
DEPARTEMENTS D'ENSEIGNEMENT ET DE RECHERCHE
MATHEMATIQUES-INFORMATIQUE-SYSTEMES
PHYSICOCHIMIE DES MATERIAUX
METALLURGIE ET PHYSIQUE DES MATERIAUX
ELECTRONIQUE
ELEC'TROTECHNIQUE
MECANIQUE DES SOLIDES MECANIQUE DES SURFACES
MECANIQUE DES FLUIDES ET ACOUSTIQUE
MACHIINES THERMIQUES
CONCEPTION ET DEVELOPPEMENT DE PRODUITS INDUSTRIELS
C.M. BRAUNER
J.F. MAITRE
P. CLECHET
J. CURRAN
P. GUIRNDENQ
D. TREHEUX
3.3. URGELL
P. VIKTOROVITCH
S. KRAWCZYK
R. BLANCHET
Ph. AURIOL
A. FOGGIA
F. SIDOROFF
J.M. GEORGES
J. SABOT
J. MATHIEU
G. COMTE-BELLOT (Mlle)
D. JEANDEL
X. LYS
M. BRUN
R. RUSSIER
P. CLOZEL
Sont
aussi habilitées
à
dirigerdes thèses
à
1'E.C.L.les personnes
dont les noms
suivent :MM. E. ALCARAZ H. ARBEY J. BATAILLE J. BOREL (LET]) Cl. CAMBON B. CAMBOU J.P. CHANTE G. CHARNAY B. COQUELET
J.
DIMNET A. HAUPAIS 3. JOSEPH Ph. KAPSA Cl. MARTELET J.M. MARTIN J.R. MARTIN T. MATHIA H. MONTES R. MOREL NGUYEN DU R. OLIER R. PHILIPPE G. ROJAT J.P. SCHON M. SUNYACH CI. SURRY A. TAILLAND G. THOMAS L. VINCENTJ e remercie Monsieur Moiroux, Directeur, e t Philippe Auriol, Directeur d u Département d ' Electrotechnique pour l e u r a c c e u i l à 1'Ecole Centrale de Lyon.
Jean-Claude Sabonnadière, Président d u j u r y d'examination e t Albert Foggia, Directeur de t h è s e , m'ont conseillé tout a u long d e ce t r a v a i l . Marcel J u f e r , Professeur dont j ' a i été l ' é l è v e à 1'Ecole Polytechnique F é d é r a l e de L a u s a n n e , Monsieur M. Lajoie- Mazenc, Professeur a u LEE1 à Toulouse e t Bernard Ancelle dont j ' a i p o u r s u i v i l e t r a v a i l de thèse d ' é t a t , ont accepté de p a r t i c i p e r à ce j u r y : je l e s en remercie tous.
J e remercie particulièrement Alain Nicolas, Maitre-assistant à 1'Ecole Centrale de Lyon pour s e s encouragements c o n s t a n t s et amicaux e t pour l e s précieux conseils dont i l m ' a f a i t béné- ficier.
J e remercie a u s s i chaleureusement mes c a m a r a d e s c h e r c h e u r s et e n s e i g n a n t s e t tout l e personnel d u l a b o r a t o i r e pour l ' a m b i a n c e a g r é a b l e q u ' i l s ont s u c r é e r e t l ' a i d e que j ' a i , a u besoin, trouvée chez chacun ( e l .
Ma profonde g r a t i t u d e v a enfin à l'ex-DGRST pour l ' i n e s t i - mable soutient f i n a n c i e r q u ' e l l e m'a prodigué.
?'liESL;S
LIE
L'ACADEMIE DE
LYOh'
:
ECOLL C E S T U L E
111:
LYON
-
L
r o M r K R A H E N B U H L
! r * ~ t o r b t i i f i . n a u mer d a Jeunr t t n l . , 8 . ra. & c h i a n t ) I r i m o r r I Laurent François h BATE 6. 6 o v r t w ~ w c t
16.12.83
1 1 1 I R t rLa méthode des équations intégrales de frontière pour l a résolution des problèmes de potentiel en électrotechnique
,
e t s a formulation axisyrnétrique. NATURE x 6-;va d ' o r d r e g #>m. D O S E U R - bOe+ORAT #)CTORlT d e 4 ' U N ~ Y . ZW;~YZLUI O * E ~ A T 3,c f C ~
s p i c i a 1 a t b sO
D
O
O
Génie électrique Coi* B . 1 . U . - L y a m:
T W / Z ~ O / ~ ) / r t bi CLASSE :Le chapitre se termine par un paragraphe consacrl A R E S U M E l'exploitation des r4sultats: calcul des prandeurs en dehors des f r m t i l r e s et des grandeurs globales. trac4 de llpnes iquipoten- tielles.
Sur le plan international. deux formulations des probllmcs h trolxlkme chapitre concerne la formulation axisym4trique de champs par les 4quations intigrales de fronttbres sur un poten- de la mithode de l'identit4 de Green: lorsqu'un systlme posslde tic1 scalaire se sont imposles. Au premier chapitre. nous Cta - une symdirie de r4volution. i l n'a en fait que deux dimensions bliswns cer deux formulations: "globale" et #'de I'identitl de et 11 est possible d'exprimer dlmtement l e s dquations Intlgralel Green" A partir des 4quations physiques fondamentales et nous dans ces deux dimensions.
dCgageons I'intlr@t et les limiter de chacune. Aprls avoir dtabli les expressions analytiques nécessaires Le domaine d'application privillgii de la premilre est et montr4 la dimarche faite pour les traiter numiriquement. -s I'llectroststique en rais0.n de la Hnlaritl des milieux giniralement prieentons des r l r u l t a t s de validation obtenus avec le progr.-•
rencontrls et des conditions aux Hmites qui lui sont propres. d'ordinateur PHlAX que nous avons d(velop#. La seconde est une g4n4ralisation de la premilre et permet de
rlroudre le probllme de Laplace associl A n'importe quelles condi- tions aux limites: on peut de ce fait envisager dans l'avenir un couplage avec une m4thode variationnelle pour la r4eolutlon des probllmes non lin4aires.
Le second chapitre est consacrl A la mlthode de I'identlt4 de Green en glnlral.
Dans un premier paragraphe. nous ltablissons de ficon originale Ies conditions d'4quivalence entre les 4quations physi- pues et les lquationr int4grales de fronttlres. ce qui nous conduit en particulier A une condition a priori d'4quivalence pour les systlmes plan.
Le traitement num4rlque et en parttculler la discrdti8atim des (quations introduit der erreurs que nous cherchons carac- tlriser au second paragraphe.
Le troixilme paragraphe est consacr4 plus s#cialement aux probllmes aswwils A la discrCtisation p a r des Cllments finis
I.oparaml1riques: critlres de choix des ensembles de points 0 Ù 1 -nt lcrites les lquationr. de l a mlthode de rlsolution
-
directew projective -: traitement particulier des points anguleux. rôle et utilisation du facteur angulaire de I'lquation inclgrale.
MOTS-CUI r
Electrotechnique
-
Equations intégrales de frontière-
Potentiel s c a l a i r e-
Axisyrnétrieb l , o r a t o i r r ( m ) d e r e e h e r c h r o a
Département d'électrotechnique
D l r r c t e u r 4 * recherche. 8 Prof. A.
FOGGIA
Ibr;.oi.rnt j v y : Prof.
J.
C. SabonnadièreC o * n ~ o r " ' o n lu j"m B. h c e l k
,
A .Foggia, M. J u f e r , M. Lajoie-Mazenc,A. Nicclas.
d e r n i è r e p a g e d e l a t h è s e
AUTORISATION D E SOUTENANCE
Vu les dispositions d e l'article 3 d e l'arrêté du 1 6 a v r i l 1974,
Vu l e rapport d e présentation d e Messieurs J.C. SABONNADIERE B. ANCELLE A. FOGGIA M. J U F E R M. LAJOIE-MAZENC A. NICOLAS M. KRAHENBUHL L a u r e n t
est autorisé
à
présenter une s o u t e n a n c e d e t h è s e pour l'obtention du t i t r e d e DOCTEUR INGENIEUR, Spécialité G é n i e Electrique.€COLE CENTRALE
DE
LYON
-
DEPARTEMENT
DTLECTROTECHNIQUE
U n i t é
Associée au
C.N.R.S.
n0829
La
méthode des équati ons
i
ntégral
es
de
f
ronti
ère
pour
l a
résolution
des
problèmes
de
p o t e n t i e l
en
électrotechnique,
e t
sa
formulation
axisymétrique.
Laurent
Krahenbühl
T A B L E D E S M A T I E R E S
RESUME 1
INTRODUCTION 3
CHAPITRE 1 Formulation en équation i n t é g r a l e d e frontière s u r un potentiel s c a l a i r e des problèmes d e champs électro- ou magnétostatiques
5
1.1 Les champs 6 1.2 Les potentiels s c a l a i r e s 9 1.3 Formulation i n t é g r a l e globale 10 1.4 Méthode i n t é g r a l e t i r é e de l ' i d e n t i t é de Green 16
1.5
Conclusion 22CHAPITRE 2 Méthode d e s équations i n t é g r a l e s de frontière t i r é e de l ' i d e n t i t é de Green 23 2.1 Equivalence avec l ' é q u a t i o n de Laplace 23 2.2 Généralités s u r l a discrétisation des
équations i n t é g r a l e s de frontière 3 1 2.3 Choix de l a discrétisation et résolution 37 2.4 Exploitation des r é s u l t a t s 49
2.5 Conclusion 54
CHAPITRE 3 Formulation en axisymétrie de l a méthode d'équations i n t é g r a l e s d e frontière t i r é e
de l ' i d e n t i t é de Green
55
3.1 Méthode
55
3.2 Détermination des noyaux et intégration 57
3.3 Résultats de validation 63
3.4 Conclusion 75
CONCLUSION
BIBLIOGRAPHIE
Sur l e p l a n i n t e r n a t i o n a l , d e u x formulations d e s problèmes d e champs p a r l e s é q u a t i o n s i n t é g r a l e s d e f r o n t i è r e s s u r un poten- t i e l s c a l a i r e se sont imposées. Au premier c h a p i t r e , nous é t a -
blissons ces deux formulations: "globale" e t ' "de l ' i d e n t i t é d e Green" à p a r t i r des é q u a t i o n s p h y s i q u e s fondamentales et nous dégageons l ' i n t é r ê t e t les limites d e c h a c u n e .
Le domaine d ' a p p l i c a t i o n p r i v i l é g i é d e l a première e s t l ' é l e c t r o s t a t i q u e en raison d e l a l i n é a r i t é des milieux généralement rencontrés et des conditions a u x limites q u i l u i sont p r o p r e s . La seconde e s t une g é n é r a l i s a t i o n d e l a première e t permet d e résoudre l e problème de Laplace associé à n ' i m p o r t e q u e l l e s condi- tions a u x limites: on peut d e ce f a i t e n v i s a g e r d a n s l ' a v e n i r un couplage avec une méthode v a r i a t i o n n e l l e pour l a résolution d e s problèmes non l i n é a i r e s .
Le second c h a p i t r e e s t consacré à l a méthode d e l ' i d e n t i t é de Green en g é n é r a l .
Dans un premier p a r a g r a p h e , nous é t a b l i s s o n s d e façon o r i 2 i n a l e l e s conditions d ' é q u i v a l e n c e e n t r e l e s é q u a t i o n s physi- q u e s et l e s é q u a t i o n s i n t é g r a l e s d e f r o n t i è r e s , c e q u i nous conduit en p a r t i c u l i e r à une condition a p r i o r i d ' é q u i v a l e n c e pour l e s systèmes p l a n s .
Le traitement numérique et en p a r t i c u l i e r l a d i s c r é t i s a t i o n d e s é q u a t i o n s i n t r o d u i t d e s e r r e u r s que nous cherchons à c a r a c - t é r i s e r a u second p a r a g r a p h e .
Le troisième p a r a g r a p h e est c o n s a c r é p l u s spécialement a u x problèmes associés à l a d i s c r é t i s a t i o n p a r d e s éléments f i n i s isoparamétriques: c r i t è r e s de choix des ensembles d e points où sont é c r i t e s l e s é q u a t i o n s , d e l a méthode d e résolution - d i r e c t e ou projective -; traitement p a r t i c u l i e r des points a n g u l e u x , rôle e t u t i l i s a t i o n d u f a c t e u r a n g u l a i r e d e l ' é q u a t i o n i n t é g r a l e .
Le c h a p i t r e s e termine p a r un p a r a g r a p h e c o n s a c r é à l ' e x p l o i t a t i o n des r é s u l t a t s : c a l c u l d e s g r a n d e u r s en dehors d e s f r o n t i è r e s e t d e s g r a n d e u r s g l o b a l e s , t r a c é d e l i g n e s équipoten- t i e l l e s .
Le troisième c h a p i t r e concerne l a formulation a x i s y m é t r i q u e de l a méthode de l ' i d e n t i t é d e Green: l o r s q u ' u n système possède une symétrie de révolution, i l n ' a en f a i t que d e u x dimensions e t i l e s t possible d ' e x p r i m e r directement l e s é q u a t i o n s i n t é g r a l e s d a n s c e s deux dimensions.
Après a v o i r é t a b l i l e s expressions a n a l y t i q u e s n é c e s s a i r e s et montré l a démarche f a i t e pour l e s t r a i t e r numériquement, nous présentons d e s r é s u l t a t s d e v a l i d a t i o n obtenus a v e c l e programme d ' o r d i n a t e u r PHIAX q u e nous a v o n s développé.
I N T R O D U C T I O N
Le modèle macroscopique de Maxwell conduit à d e s é q u a t i o n s différentielles simples pour l e s champs s t a t i q u e s ou q u a s i - s t a t i q u e s : l e s champs magnétique e t é l e c t r i q u e sont découplés et on o b t i e n t deux t y p e s d e problèmes i n d é p e n d a n t s : é l e c t r o s t a t i q u e ou magnéto- s t a t i q u e .
Si l e s é q u a t i o n s sont simples, l e u r solution a n a l y t i q u e ne peut ê t r e obtenue que d a n s d e r a r e s c o n f i g u r a t i o n s . Dans l a p l u p a r t d e s c a s p r a t i q u e s , l'emploi d e méthodes numériques de résolution s 'imposera donc.
Deux catégories d e méthodes ont é t é successivement déve- loppées: les méthodes de différences f i n i e s , p u i s l e s méthodes v a r i a t i o n n e l l e s associées a u x éléments f i n i s . Dans l a première, on approche l ' o p é r a t e u r différentiel lui-même et on cherche l a solution d ' u n système simplifié; pour l a seconde, c ' e s t l a solution ( l e potentiel p a r exemple) q u i e s t approchée a u d é p a r t e t l a méthode consiste à t r o u v e r l a meilleure approximation possible tout en c o n s e r v a n t l ' o p é r a t e u r d i f f é r e n t i e l t e l q u e l . Dans l e s d e u x c a s , l a solution approchée e s t obtenue s p a t i a l e m e n t et c e s méthodes peuvent ê t r e a p p l i q u é e s a u x problèmes non l i n é a i r e s .
Une troisième c a t é g o r i e de méthodes f a i t l ' o b j e t d ' é t u d e s e t de recherches, et a d é j à débouché s u r quelques logiciels mais n ' a p a s a t t e i n t l e degré de développement d e s précédentes. Dans c e t t e c a t é g o r i e , on trouve l a méthode d e s é q u a t i o n s i n t é g r a l e s d e f r o n t i è r e , l a méthode d e s multiples multipôles développée à Zürich
1
21 ,
l e s méthodes de développements limités1
61 ,
e t c . ; d a n s toutes c e s méthodes, l a solution cherchée e s t approchée Dar une somme d e solutions élémentaires d e l ' é q u a t i o n : on a p p l i q u e donc l e théorème de superposition et l ' h y p o t h è s e d e b a s e e s t l a l i n é a r i t é . Ces méthodes sont semi-analytiques.
En électrotechnique, l e s d i s p o s i t i f s rencontrés sont l e p l u s souvent formés d e régions parfaitement l i n é a i r e s d ' u n e p a r t ( p a r exemple l ' a i r d a n s l e s e n t r e f e r s e t à l ' e x t é r i e u r ) et de régions fortement non l i n é a i r e s d ' a u t r e p a r t ( f e r s a t u r a b l e ) . A terme, i l nous semble s é d u i s a n t de d é c r i r e l e s milieux non l i n é a i r e s à l ' a i d e d e s méthodes v a r i a t i o n n e l l e s e t l e u r i n t é r a c t i o n à d i s t a n c e , à t r a v e r s l e s milieux l i n é a i r e s , p a r l e s méthodes i n t é g r a l e s .
Ce t r a v a i l e s t consacré a u x s e u l e s méthodes i n t é g r a l e s d e f r o n t i è r e , mais i l a été pensé d a n s l ' o p t i q u e d e ce couplage e n t r e méthodes: deux c h a p i t r e s s u r t r o i s concernent l a formulation d i t e "de 1 ' i d e n t i t é de Green" q u i p a r a i t inutilement compliquée si on ne l a considère que d u point de vue d e s méthodes i n t é g r a l e s . Ceci d i t , l a p l u p a r t d e s r é s u l t a t s t h é o r i q u e s e t techniques obtenus d a n s l e c a d r e de l a méthode de l ' i d e n t i t é de Green s ' a p p l i q u e directement a u x a u t r e s formulations.
Nous ne prétendons p a s tout d i r e s u r l a méthode d e s é q u a t i o n s i n t é g r a l e s a p p l i q u é e s à 1 'électrotechnique: i l e x i s t e d é j à d a n s ce domaine des é t u d e s t r è s complètes q u ' i l é t a i t i n u t i l e de r é p é t e r , en p a r t i c u l i e r l a thèse d ' é t a t d e M . B. Ancelle Il
1
et celle de M . A. Nicolas (151.
Nous i n v i t o n s l e l e c t e u r à s ' y r e p o r t e r .Notre exposé e s t c e n t r é s u r ce que nous a v o n s a p p o r t é d ' o r i g i n a l à l a méthode et s u r l e s p o i n t s q u i ne font p a s l ' u n a n i m i t é d a n s l e s p u b l i c a t i o n s . Nous a v o n s r é d u i t l e s considé- r a t i o n s b a n a l e s a u s t r i c t minimum n é c e s s a i r e pour o b t e n i r un exposé s u i v i .
C H A P I T R E 1
FORMULATION EN EQUATION INTEGRALE DE FRONTIERE
SUR UN POTENTIEL SCALAIRE DES PROBLEMES DE
CHAMPS ELECTRO- OU MAGNETOSTATIQUES
Le modéle d e Maxwell des champs électromagnétiques s e
trouve d a n s l ' e s p r i t d e beaucoup de s c i e n t i f i q u e s e t , à d é f a u t , d a n s d e nombreux o u v r a g e s . Nous l e r a p p e l l e r o n s c e p e n d a n t t r è s brièvement pour f a m i l i a r i s e r l e l e c t e u r a u x notations e t terminologies que nous u t i l i s o n s .
Après a v o i r i n t r o d u i t l e s potentiels s c a l a i r e s , nous montrons q u ' u n e première formulation i n t é g r a l e s ' o b t i e n t simplement en e x p r i m a n t l e potentiel i n d u i t comme l a somme ( i n t é g r a l e ) d e s potentiels d e s dipôles i n d u i t s .
Cette formulation considère globalement tout 1 'e s p a c e ; on p e u t également exprimer d a n s c h a q u e région l ' é q u a t i o n diffé- r e n t i e l l e d u p o t e n t i e l , l ' i n t é g r e r e t l i e r l e s solutions r é g i o n a l e s e n t r e e l l e s p a r l e s conditions d ' i n t e r f a c e s : l ' i n t é g r a t i o n d e l ' é q u a - tion d i f f é r e n t i e l l e peut ê t r e éventuellement menée d a n s c h a q u e région p a r une méthode d i f f é r e n t e e t c ' e s t l à l ' i n t é r s t d e c e t t e démarche.
Pour l e s régions l i n é a i r e s e t homogènes, l a méthode i n t é - g r a l e d e f r o n t i è r e t i r é e de l ' i d e n t i t é d e Green p r é s e n t e d e s a v a n - t a g e s c e r t a i n s p a r r a p p o r t a u x méthodes v a r i a t i o n n e l l e s p a r exemple. Nous 1 'i n t r o d u i s o n s , de façon a s s e z b r è v e p u i s q u ' e l l e f a i t l ' o b j e t d e s d e u x a u t r e s c h a p i t r e s .
1.1 LES CHAMPS
1.1.1 Equations d e Maxwell e n s t a t i q u e , a i m a n t a t i o n , p o l a r i s a t i o n .
Les r e l a t i o n s fondamentales qui définissent l e s g r a n d e u r s électriques et magnétiques s t a t i q u e s sont l e s é q u a t i o n s de Maxwell s t a t i q u e s :
VxE =
O
champ é l e c t r i q u eVxH = j champ magnétique
V.D = p déplacement
V.B = O induction
a u x q u e l l e s i l f a u t ajouter les r e l a t i o n s q u i décrivent l a réaction des m a t é r i a u x :
qui définit l ' a i m a n t a t i o n M: une densité de moments magnétiques d i p o l a i r e s a p p a r a i t d a n s l e s milieux magnétiques sous 1 ' action du champ. Ces milieux sont p l u s ou moins susceptibles et on note:
M
= XH ( 1 . 6 )OU encore:
B = poprH ( 1 . 7 )
où X e s t l a susceptibilité magnétique et p r = l+X e s t l a permé- a b i l i t é r e l a t i v e ; X et ,ur dépendent éventuellement de H.
On a de même:
q u i définit l a polarisation P: une d e n s i t é de dipôles é l e c t r i q u e s a p p a r a i t d a n s les milieux diélectriques sous l ' a c t i o n du champ. Ces milieux sont. p l u s ou moins susceptibles et on note:
où .X est l a susceptibilité diélectrique relative et cf= l + X est l a permittivité r e l a t i v e ; X e t dépendent éventuellement de E.
M et P représentent l a réaction des matériaux face a u x
champs H et E. La difficulté du calcul des champs vient de
ce que cette réaction a g i t s u r l a cause; on peut s é p a r e r p a r l ' e s p r i t cause et conséquence en s é p a r a n t les g r a n d e u r s en g r a n - deurs inductrices et induites.
1.1.2 Champs inducteurs e t champs induits.
Les sources du champ magnétique sont les c o u r a n t s ; l a loi de Biot et Savart donne le champ dû à ces courants d a n s le vide:
Les mêmes courants en présence de matériaux magnétiques
donnent un champ H différent de Ho qui permet de définir l e
champ H i induit p a r les courants et l a matière:
H = H + H i
O ( 1 . 1 2 )
E n électrostatique, le champ inducteur est le champ coulom- bien E ; le champ induit Ei est définit p a r :
E = E + E .
O 1 ( 1 . 1 3 )
Pour ces g r a n d e u r s induites, les équations de Maxwell se simplifient; on a :
1.1.3
Conditions d ' i n t e r f a c e e t conditions a u x limites.Les conditions de continuité des d i v e r s champs a u x i n t e r - faces e n t r e régions de p r o p r i é t é s différentes s e déduisent des équations 1.1 à 1.7: pour l e s composantes t a n g e n t i e l l e s d e s champs on a :
n x ( H 1 - H 2 ) = A densité de c o u r a n t (1.19)
s u r f a c i q u e
e t pour l e s composantes normales d e l ' i n d u c t i o n e t d u déplacement:
n . ( D 1 - D a ) = ps d e n s i t é de c h a r g e (1.21) s u r f a c i q u e Pour l e s g r a n d e u r s i n d u i t e s , on obtient d e s r e l a t i o n s légèrement différentes: = n . ( 2 'ri ) Eo en absence de c h a r g e (1.26) de s u r f a c e
On peut a u s s i i n t r o d u i r e des conditions a u x limites ( a b r é - gées CAL d a n s l a s u i t e ) q u i excluent une p a r t i e de l ' e s p a c e du domaine de résolution. P a r exemple en é l e c t r o s t a t i q u e , un conducteur s e r a souvent considéré comme p a r f a i t : l e champ e s t n u l a l ' i n t é r i e u r e t on a u r a :
s u r l a face e x t é r i e u r e . On a l ' é q u i v a l e n t en magnétostatique lorsque p, e s t t r è s élevé: s u r l a face e x t é r i e u r e on posera:
D a n s l e s deux c a s , l e s l i g n e s de champ a r r i v e n t perpen- diculairement s u r l e conducteur.
1.2
LES POTENTIELS SCALAIRES
De l'équation 1.1 et de l ' i d e n t i t é Vx( V U ) = O on déduit que le champ électrique dérive d ' u n potentiel:
E
= - T V (1.29)E
= - G VO O (1.30)
i l en est de même des champs électrique et magnétique i n d u i t s :
On peut également définir un potentiel magnétique total
d a n s un domaine q u i ne contient p a s de courant:
H = - V V (1.33)
H = - V V
O O (1.34)
Ces potentiels s c a l a i r e s sont définis à une constante près qu 'on choisit généralement nulle à 1 'i n f i n i . Pour des problèmes i n t é r i e u r s , on l a fixe arbitrairement en un point.
L
'expression en potentiel s c a l a i r e est intéressante c a r elle permet de passer d ' u n champ vectoriel inconnu ( 3 inconnues p a r point) à un champ s c a l a i r e inconnu ( u n e inconnue p a r p o i n t ) . La t a i l l e des problèmes à résoudre est réduite d ' a u t a n t .1 . 3
FORMULATION INTEGRALE GLOBALELe potentiel d ' u n dipôle ponctuel v a u t :
La p o l a r i s a t i o n , q u i e s t une densité volumique de dipôles, c r é e donc l e potentiel i n d u i t 16 Vol. 3, 111, 100 e t s u i v a n t e s J :
ce q u i explicite l a relation 0 = 0 ( V ) . On v a donc pouvoir é c r i r e
1 'équation :
e t nous a l l o n s montrer q u e , sous l e s hypothèses d ' homogénéité, d ' i s o t r o p i e et de l i n é a r i t é d u d i é l e c t r i q u e , 0 ne dépend que du potentiel total s u r l a frontière d u d i é l e c t r i q u e .
( * ) Si p = - Xf0V V implique bien le p a s s a g e de 1.36 à 1.37, l a réciproque utilisée pour résoudre le problème n ' e s t é t a b l i e que s i les deux équations sont é c r i t e s s u r c e r t a i n s ensembles i n f i n i s de points. Un c a s s i m i l a i r e s e r a d i s c u t é en d é t a i l s a u 52.2
1.3.1 L'équation intégrale de frontière.
Avec l e s hypothèses ci-dessus,
X
est constant d a n s tout l e volume diélectrique: on peut i n t é g r e r 1 'expression 1.37 p a r p a r t i e s :où R t u ) e s t l ' a n g l e solide sous lequel le point P voit l e volume
P'
u ( 6 Vol. 1 , 1 , 0 L'équation 1.38 prend a i n s i l a forme explicite ( v o i r fig. 2 ) :
avec
Sources
S ' i l y a N régions d i é l e c t r i q u e s de p r o p r i é t é s d i f f é r e n t e s , on obtient ( v o i r f i g .
3 ) :
Le terme d e d r o i t e contient d a n s tous l e s c a s N i n t é g r a l e s de s u r f a c e s u r l e s s u r f a c e s des N régions. Le terme d e g a u c h e s ' é c r i t p a r exemple : s i P e s t à l ' i n t é r i e u r d e u
,
V ( P ' ) s i P ' e s t en dehors de tous l e s d i é l e c t r i q u e s , s i P" e s t s u r l ' i n t e r f a c e d e s d i é l e c t r i q u e s 1 e t 2, e t c .w
Diélectrique 1 Diélectrique3
Fig.3:
I l l u s t r a t i o n de l ' é q u a t i o n 1.41En magnétostatique et avec l e s hypothèses d'homogénéité, d ' isotropie et d e l i n é a r i t é d e s milieux magnétiques, l e s équations 1.39 et 1 . 1 sont v a l a b l e s à condition d ' a v o i r VxH=O c ' est-à- d i r e aucun c o u r a n t d a n s un domaine contenant toutes l e s régions magnétiques. Le potentiel de source est a l o r s défini à p a r t i r d ' u n point Po :
Cette formulation ne permet p a s d ' i n t r o d u i r e directement des CAL. Son domaine d ' a p p l i c a t i o n est r é d u i t mais, d a n s son domaine, c ' e s t de loin l a meilleure.
1.3.2 Distribution d e dipôles é q u i v a l e n t e à la polarisation.
L ' in t é g r a l e :
représente l e potentiel d ' u n e distribution s u r f a c i q u e de dipôles normaux
1
6 Vol. 1, VI,581
de densité T,.
L'équation 1.39 montre q u ' o n peut remplacer l e s volumes diélectriques p a r des densitésde dipôles normaux s u r l e u r s s u r f a c e s . Le potentiel t o t a l en un point se calcule comme l a somme du potentiel Vo des sources e t du potentiel 1.43 des d i s t r i b u t i o n s 1.44 é q u i v a l e n t e s à l a polari- sation.
1.3.3
Introduction d ' u n conducteur.Dans cette formulation, un conducteur ne peut ê t r e intro- d u i t que p a r l ' i n t e r m é d i a i r e du terme V c'est-à-dire sous forme
O '
de source: i l f a u d r a donc déterminer l a densité d e c h a r g e s à
s a s u r f a c e , autrement d i t l e déplacement ou le champ normal. On pose a i n s i :
V ( P I =
2
G p ( Q l d sO
'con d
q u i représente le potentiel coulombien de l a densité s u r f a c i q u e de c h a r g e s fo - dV
.
On obtient l ' é q u a t i o n 16 Vol.3,
111, 206-2071:dn
l a g r a n d e u r connue q u i permet de résoudre é t a n t l e potentiel total s u r l e conducteur ( f i g .
4 ) .
Diélectrique
'diel
Fig.
4:
Influence d ' u n conducteur s u r un diélectrique (équation 1.45).d V
On voit a p p a r a i t r e deux types d ' i n c o n n u e s : et
V,
dG
associées respectivement a u x noyaux G e t
.
Nous allons l e s retrouver d a n s le c a d r e de l a méthode de l ' i d e n t i t é de Green a u 91.4.1
. 3 . 4
DiscussionLa méthode que nous venons de développer e s t p a r t i c u - 1 ièrement a d a p t é e à 1 'é l e c t r o s t a t i q u e . Elle permet 1 ' introduction d e CAL sous l a forme de s u r f a c e s équipotentielles c o r r e s p o n d a n t a u x conducteurs. Pour l e s problèmes multirégions, l e s i n t é g r a l e s de s u r f a c e deviennent nombreuses pour l ' é c r i t u r e d e c h a q u e é q u a - t i o n , mais soulignons q u ' i l n ' y a q u ' u n e inconnue s c a l a i r e p a r point de s u r f a c e .
L ' é q u i v a l e n t magnétostatique a été largement p u b l i é p a r Trowbridge 118 ,19
1
.
L ' i n t é r ê t p r a t i q u e en e s t limité a u x milieuxl i n é a i r e s ( c e q u i e s t une importante limite en m a g n é t o s t a t i q u e ) : en effet, l ' i n t r o d u c t i o n d ' u n milieu non l i n é a i r e en
1.37
impose de compléter1.39
p a r 1 'i n t é g r a l e de volume1
181
:q u i e s t beaucoup p l u s lourde à c a l c u l e r q u e l ' i n t é g r a l e d e volume correspondante en méthode v a r i a t i o n n e l l e c a r l ' i n t é g r a n t e s t non nul d a n s tout l e volume.
On p o u r r a i t a u s s i c h e r c h e r à g é n é r a l i s e r l e s CAL i n t r o - d u i t e s à l a section
1 . 3 . 3
afin de t r a i t e r l a région non l i n é a i r e p a r méthode v a r i a t i o n n e l l e : on r e t o m b e r a i t , p a r une démarche p l u s compliquée, s u r l a méthode d e 1 ' i d e n t i t é d e Green.1.4 METHODE INTEGRALE TIREE DE L'IDENTITE DE GREEN
1.4.1 Equation de Poisson d a n s une région.
L'équation V.D = p ( 1 . 3 ) combinée avec (1.10) s ' é c r i t :
Comme E dérive du potentiel V (1.29) on a :
Si c, est constant d a n s l a région considérée, on obtient l ' é q u a t i o n de Poisson:
e t , en absence de c h a r g e s , l ' é q u a t i o n de Laplace:
De même en magnétostatique on obtient:
' I V = - - l TV. vp
r r
s a n s courant d a n s l a région, et une équation semblable s u r le potentiel induit s ' i l y a des courants:
e t , d a n s les deux c a s , l'équation de Laplace s i p est constant: r A V = O ( p = cste, s a n s c o u r a n t ) r OU A@ = O ( p = cste, avec c o u r a n t ) r
1.4.2 Discussion.
Dans c h a q u e région ( d i é l e c t r i q u e , magnétique, à s u r f a c e conductrice ou non, e n t r e f e r , milieu i n f i n i ) l e problème e s t d é f i n i p a r l ' u n e des é q u a t i o n s d i f f é r e n t i e l l e s c i - d e s s u s ; l a solution dépend d e s v a l e u r s limites d u potentiel ( t o t a l ou i n d u i t ) e t d e s a d é r i v é e normale. Comme nous 1 'é c r i v i o n s d è s 1 'i n t r o d u c t i o n d e c e c h a p i t r e , on peut r é s o u d r e d a n s c h a q u e région en fonction d e s v a l e u r s a u x limites a v e c l a méthode l a mieux a d a p t é e a u t y p e d ' é q u a t i o n d i f f é r e n t i e l l e , l a solution g l o b a l e é t a n t obtenue en l i a n t ces solu- tions e n t r e e l l e s à l ' a i d e des conditions d ' i n t e r f a c e e t en e x p r i - mant l e s éventuelles conditions a u x limites.
P a r exemple, l e s deux é q u a t i o n s 1.51 e t
1.53
sont d ' u n e complexité bien d i f f é r e n t e .Dans l a première, pr = f (
1
V V I ) : i l e s t n é c e s s a i r e d ' e x p r i - mer V e tPr en c h a q u e point d u domaine; l e s méthodes v a r i a t i o n - nelles associées a u x éléments f i n i s ont démontré l e u r e f f i c a c i t é pour r é s o u d r e ce problème.
La seconde e s t 1 ' é q u a t i o n de Laplace: c ' e s t un c a s p a r t i - c u l i e r de l a première, e t l e s méthodes v a r i a t i o n n e l l e s conduisent a u s s i à l a solution. Mais on montre facilement 1 . 4 que l ' e x - pression des v a l e u r s i n t é r i e u r e s d u potentiel n ' e s t p a s n é c e s s a i r e en c o u r s d e résolution (on p e u t s i besoin e s t l e s déterminer a p r è s - coup à p a r t i r des s e u l e s v a l e u r s a u x limites d e l a r é g i o n ) : l e s méthodes i n t é g r a l e s que nous a l l o n s p r é s e n t e r sont a d a p t é e s à ce c a s . Elles é v i t e n t l e t r a v a i l de m a i l l a g e en éléments f i n i s des r é g i o n s l i n é a i r e s e t r é d u i s e n t l e nombre d e s inconnues. Ce double g a i n s e r a spécialement a p p r é c i é pour l a résolution d e s problèmes tridimensionnel S .
De p l u s , l e s méthodes v a r i a t i o n n e l l e s ne permettent p a s directement l a modélisation e x a c t e d ' u n milieu e x t é r i e u r i n f i n i et sont peu a d a p t é e s à l a description d e l ' e s p a c e e n t r e d e u x pièces mobiles, en r a i s o n d e l a présence d u m a i l l a g e : ces d e u x inconvénients n ' e x i s t e n t p l u s a v e c l e s méthodes i n t é g r a l e s .
1.4.3
Autres problèmes conduisant a u x mêmes équations.D ' a u t r e s phénomènes physiques obéissent à l ' é q u a t i o n de Laplace associée à des conditions a u x limites: l a méthode des équations i n t é g r a l e s de frontière permet évidemment de l e s t r a i t e r tous. En r e s t a n t d a n s l e domaine de 1 'électrotechnique, citons p a r exemple:
- Les problèmes de conduction, pour l e s q u e l s l ' é q u a t i o n de conser-
vation de l a c h a r g e r.j = O et l a loi d'Ohm j = - a V V condui- sent à l ' é q u a t i o n de Laplace 1.50 à l a q u e l l e on peut a s s o c i e r des CAL a n a l y t i q u e s pour t e n i r compte d ' u n e conductivité de surface a, ( f i g .
5 ) .
Fig.
5:
Exemple de problème de conduction.- Les problèmes d'électromagnétisme s a n s p r o p a g a t i o n , d a n s un milieu l i n é a i r e non conducteur ( e n t r e f e r , milieu e x t é r i e u r ) . Lorsque l e s champs v a r i e n t "lentement" d a n s l e temps, c ' e s t - à - d i r e t a n t que l a longueur d ' o n d e reste g r a n d e p a r r a p p o r t a u x dimensions du système é t u d i é , seule l ' é q u a t i o n 1.1 e s t modifiée et d e v i e n t :
Le potentiel magnétique total ou i n d u i t obéit toujours à l ' é q u a t i o n de Laplace.
Dans ce c a s , qui e s t 1 ' approximation électrotechnique habituelle des é q u a t i o n s de Maxwell, l a méthode i n t é g r a l e p o u r r a ê t r e utilisée pour d é c r i r e l e s e n t r e f e r s et le milieu e x t é r i e u r des d i s p o s i t i f s . Le couplage avec une méthode v a r i a t i o n n e l l e envi- sagé dès l ' i n t r o d u c t i o n de cette thèse ne concernera donc p a s seulement l e s problèmes s t a t i q u e s , ce q u i donne un i n t é r ê t supplé- mentaire a u x méthodes i n t é g r a l e s .
- Problèmes d e c o u r a n t s d e F o u c a u l t à f r é q u e n c e é l e v é e
11s
1 .
A p a r t i r d ' u n e c e r t a i n e f r é q u e n c e d u c h a m p d ' e x c i t a t i o n , l a pro- f o n d e u r d e p é n é t r a t i o n d e s c h a m p s d e v i e n t f a i b l e p a r r a p p o r t a u x d i m e n s i o n s d e l a p i è c e é t u d i é e . Les c o u r a n t s d e F o u c a u l t n e s e d é v e l o p p e n t p l u s q u ' e n s u r f a c e . S u r c e t t e s u r f a c e , l e c h a m p i n d u i t q u ' i l s c r é e n t s ' o p p o s e e x a c t e m e n t a u c h a m p i n d u c t e u r . On a donc simplement l a c o n d i t i o n : s u r l a s u r f a c e , a s s o c i é e à l ' é q u a t i o n d e L a p l a c e à l ' e x t é r i e u r d e l a p i è c e m é t a l l i q u e . La r é s o l u t i o n permet d e d é t e r m i n e r l a d e n s i t é d e c o u r a n t s u r f a c i q u e e n fonction d e l ' i n d u c t e u r . Un t e l d i s p o s i t i f p e u t ê t r e u t i l i s é p o u r l a t r e m p e s u p e r f i c i e l l e ( e n g r e n a g e s p a r e x e m p l e ) , e t l a méthode i n t é g r a l e p e r m e t l e dimensionnement d e l ' i n d u c t e u r .1.4.4
Méthode "de l ' i d e n t i t é d e Green".Nous c h e r c h o n s à r é s o u d r e l e s é q u a t i o n s
1.49
ou1.50:
AV = - P ou AV = O d a n s w 'O 'r c ' e s t - à - d i r e à e x p r i m e r V d a n s w en fonction d e s v a l e u r s d e V e t d e s a d é r i v é e n o r m a l e s u r l a f r o n t i è r e S d e W . L a s e c o n d e i d e n t i t é d e Green p o u r u n s c a l a i r e s ' & r i t :S
(V3G - GAV) d v =S
(VVG - GVV).ds s En c h o i s i s s a n t p o u r G l a "fonction d e Green"1.40:
on obtient:
n,
( v )avec c = --
4~
L'équation de Poisson 1 . 4 portée d a n s 1.55 donne l ' é q u a t i o n i n t é g r a l e de f r o n t i è r e pour l ' é l e c t r o s t a t i q u e a v e c c h a r g e s : tv c . V ( P ) = V ( P )
-
- G -) d s ( * ) O bn e t l ' é q u a t i o n de L a p l a c e 1.50 conduit à 1 ' e x p r e s s i o n : a d a p t é e à 1 ' é l e c t r o s t a t i q u e s a n s c h a r g e e t à l a magnétostatique s a n s c o u r a n t . S ' i l y a l i e u , i l f a u t exprimer l e s c o n d i t i o n s d ' i n t e r f a c e 1.18 à 1.21 en fonction d u potentiel. La c o n t i n u i t é d e l a compo- s a n t e t a n g e n t e d u champ en absence d e c o u r a n t de s u r f a c e e s t a s s u r é e p a r l a définition unique d u potentiel s u r l a s u r f a c e . Pour l a composante normale de l ' i n d u c t i o n , on doit a v o i r :e t , pour l e déplacement normal:
Le choix de Y comme inconnue à l a p l a c e d e s d é r i v é e s normales d u potentiel d a n s l e s d e u x r é g i o n s
1
11
a s s u r e l a seconde condi- tion d ' i n t e r f a c e . L ' é q u a t i o n i n t é g r a l e 1.58 s ' é c r i t a l o r s :s
on a une expression semblable en é l e c t r o s t a t i q u e .
Pour l e s problèmes d e magnétostatique a v e c c o u r a n t , l a formulation en potentiel i n d u i t s ' impose. L ' é q u a t i o n i n t é g r a l e de d é p a r t e s t l a même q u e 1.58 mais l ' e x p r e s s i o n de Y e s t diffé- r e n t e ( v o i r équation 1.24) :
e t on obtient pour c h a q u e région l e s é q u a t i o n s i n t é g r a l e s :
E n posant Ho, = O on retrouve l e c a s p r é c é d e n t ; cette formulation e s t donc l a p l u s g é n é r a l e e t nous l ' a d o p t e r o n s d a n s l a s u i t e . Notons q u ' e l l e e s t p l u s complexe que l a méthode g l o b a l e d u
91.3:
nous a v o n s s u r l e s i n t e r f a c e s d e u x inconnues s c a l a i r e s p a r p o i n t ; p a r c o n t r e , c h a q u e équation s ' é c r i t p a r i n t é g r a t i o n s u r l a fron- t i è r e d ' u n e seule région.
1.4.5 Distributions de sources s u r f a c i q u e s é q u i v a l e n t e s .
Pour l a méthode g l o b a l e , nous avions remarqué a u $1.3.2 que le potentiel s ' e x p r i m a i t comme celui d ' u n e d i s t r i b u t i o n de dipôles normaux s u r l e s s u r f a c e s , auquel i l convenait d ' ajouter celui des sources, c'est-à-dire celui d ' u n e d i s t r i b u t i o n s u r f a c i q u e de monopôles d a n s le c a s des conducteurs
($1.3.3).
I l f a l l a i t , pour c a l c u l e r le potentiel en un p o i n t , t e n i r compte de toutes ces d i s t r i b u t i o n s , c'est-à-dire i n t é g r e r s u r toutes l e s i n t e r f a c e s .11 y a en f a i t pour c h a q u e région une i n f i n i t é de couples de d i s t r i b u t i o n s s u r f a c i q u e s de dipôles normaux e t de monopôles
( r ,
,
p ) q u i conduisent a u x conditions a u x limites V et.
Un deon
ces couples s ' i d e n t i f i e à (V, ) , nous venons de l e montrer à
dn
l ' a i d e de l ' i d e n t i t é d e Green. C ' e s t c e l u i q u i permet d ' e x p r i m e r le p l u s simplement l e s conditions d ' i n t e r f a c e , p u i s q u ' i l coincide avec e l l e s .
1.5
CONCLUSIONNous avons présenté l e s formulations "globale" p u i s "de l ' i d e n t i t é de Green" des équations i n t é g r a l e s de frontière. On a u r a i t a u s s i pu d é d u i r e l a première de l a seconde, q u i e s t l a plus g é n é r a l e e t que nous u t i l i s o n s d a n s l a s u i t e .
On peut imaginer des v a r i a n t e s de ces formulations. P a r exemple pour l a méthode de Green, l ' u t i l i s a t i o n simultanée du potentiel total d a n s l e s régions s a n s c o u r a n t et d u potentiel induit a i l l e u r s conduit à des équations bien a d a p t é e s à l a magnétostatique l i n é a i r e . Notre propos n ' e s t p a s l ' é n u m é r a t i o n de ces v a r i a n t e s , mais le développement de l a théorie et l'amélio- ration des techniques d ' é q u a t i o n s i n t é g r a l e s en g é n é r a l , q u e ce soit en vue d ' u n e u t i l i s a t i o n indépendante ou d ' u n couplage avec une a u t r e méthode.
C H A P I T R E 2
METHODE DES EQUATIONS INTEGRALES DE FRONTIERE
TIREE DE L'IDENTITE DE GREEN
Notre t r a v a i l a porté p l u s particulièrement s u r l a formu- lation axisymétrique de l a méthode des é q u a t i o n s i n t é g r a l e s de frontière t i r é e de l ' i d e n t i t é de Green. Cependant, c e r t a i n e s des réflexions et des remarques que nous avons à p r é s e n t e r s ' a p p l i - quent a u s s i a u x formulations tridimensionnelle ou bidimensionnelle plane: nous l e s avons regroupées d a n s ce c h a p i t r e .
2.1 EQUIVALENCE AVEC L'EQUATION DE LAPLACE
La méthode des équations i n t é g r a l e s de frontière
(4.
i . f . )e s t le p l u s souvent présentée comme nous l ' a v o n s f a i t a u c h a p i t r e 1: en p o r t a n t d a n s l ' i d e n t i t é de Green 1.55 l ' é q u a t i o n p h y s i q u e de Laplace 1.50, on obtient 1 ' é . i . f . 1.58:
Généralement, les a u t e u r s ne justifient p a s l ' é q u i v a l e n c e de cette équation avec 1 'équation physique de d é p a r t , ou a l o r s seulement a posteriori en c o n s t a t a n t l ' u n i c i t é de l a solution.
Pour l e s problèmes bidimensionnels p l a n s , Jawson 1 1 0
1
a démontré q u e , pour c h a q u e contour L, il e x i s t e u n contour homothétique Lm q u i conduit à un système s i n g u l i e r : i l proposed a n s un tel c a s de recommencer l a résolution a p r è s avoir changé l'échelle du contour. E n p r a t i q u e , on ne peut se contenter de ce remède: les contours approchant Lm donneront lieu à des sys- tèmes numériques mal conditionnés: les r é s u l t a t s pourront être faux s a n s qu'on en soit a v e r t i .
Nous allons directement rechercher les conditions d ' é q u i -
valence de l ' i f 1.58 et de l'équation de Laplace pour les
systèmes tridimensionnels e t nous en déduirons une condition d ' é q u i - valence pour les systèmes bidimensionnels p l a n s .
2.1.1 Signification de 1'é.i.f. écrite en un point P.
E n toute logique, l ' i f . 1.58 écrite en un point P. n ' e s t 1
pas équivalente à l'équation de Laplace écrite a u même point: l a comparaison avec l ' i d e n t i t é de Green 1.55 montre qu'on a seule- ment 1 ' équivalence:
Physiquement, m = AV représente l a densité de sources mono-
polaires d a n s v et
son potentiel en P . . L'équivalence 2.1 peut donc s'énoncer: 1
e . i . f . en P H l a distribution de monopôles m
i
annule son potentiel en P .
2.1.2 Equivalence a v e c 1 'é q u a t i o n d e Laplace, c a s tridimensionnel.
Parmi les méthodes permettant d ' a n n u l e r une g r a n d e u r R d a n s un volume v , celle q u i consiste à a n n u l e r l e s i n t é g r a l e s :
e s t appelée méthode projective. On n ' a u r a 1 ' é q u i v a l e n c e :
1. = O , f i € F H R = O d a n s v 1
que pour c e r t a i n s ensembles F de fonctions. L ' é q u i v a l e n c e 2 . 1 montre que l a méthode des é . i . f . e s t une méthode p r o j e c t i v e , les fonctions de projection é t a n t :
Ces fonctions présentent l ' i n t é r ê t de r é d u i r e l e s i n t é g r a l e s de volume 2 . 3 à des i n t é g r a l e s de s u r f a c e . Le choix de l ' e n s e m b l e F des fonctions f . revient a u choix de 1 'ensemble des points
1
Pi où seront é c r i t e s les é q u a t i o n s i n t é g r a l e s . Nous a l l o n s montrer q u ' u n e s u r f a c e S ' e n t o u r a n t v est s u f f i s a n t e .
Lorsque les conditions a u x limites sont posées correctement (problème de Dirichlet p a r exemple), le système:
J A V = O PE v
1
CALa une solution unique V
.
Nous nous plaçons d a n s ce c a s pour solNous cherchons donc un potentiel - sol - q u i n ' a p a s de source d a n s v. Si on é c r i t l ' i f en tous l e s p o i n t s d ' u n e s u r f a c e S' e n t o u r a n t v on obtient une condition apparemment moins forte: on n'impose p a s l a n u l l i t é d e l a d i s t r i b u t i o n A V
d a n s v mais seulement l a n u l l i t é d e s a contribution a u potentiel s u r S v .
P a r exemple, toute d i s t r i b u t i o n à "charge" t o t a l e n u l l e et symétrie s p h é r i q u e a n n u l e son potentiel à 1 ' e x t é r i e u r d ' elle- même ( f i g . 6 ) : i l y a donc d a n s l e volume v une i n f i n i t é d e solutions Vsol + V m à 1 ' é . i . f . é c r i t e s u r S ' .
Fig.
6
Mais Vm = O s u r S' et à l ' i n f i n i : i l e s t donc identique- ment nul d a n s tout l ' e s p a c e sauf peut-être d a n s v où sont s i t u é e s l e s sources m q u i i n t e r d i s e n t d ' a p p l i q u e r l e théorème d u maximum. On en d é d u i t q u e :
c ' e s t - à - d i r e q u e toutes l e s solutions données p a r l e s é . i . f . ont l e s mêmes v a l e u r s a u x limites s u r S q u e l a solution cherchée.
La solution V ( P l en un point P i n t é r i e u r à v e s t obtenue sol
en é c r i v a n t :
Ainsi l ' é q u a t i o n de Laplace é c r i t e en tout point de
v
est- e l l e équivalente à 1 ' é . i . f . é c r i t e en tout point de S ' ( 1 ' i n t é g r a t i o n s e f a i s a n t s u r S et S ' pouvant ê t r e confondue avec S ) e t en tout point dev ;
c e p e n d a n t , le problème physique e s t résolu l o r s q u e les v a l e u r s limites de Vsol s u r S sont déterminées, donc p a r l ' é c r i t u r e de 1 ' é . i . f . s u r S ' seule. La q u a d r a t u r e qui conduit à l a solution d a n sv
peut ê t r e considérée implicitement.2.1.3. Cas d e l a région e x t é r i e u r e .
Nous cherchons maintenant à résoudre l ' é q u a t i o n d e Laplace d a n s le volume
v
e x t é r i e u r à l a s u r f a c e S e t s ' é t e n d a n t j u s q u ' à l ' i n f i n i ( f i g .7 ) .
Fig.
7
Le raisonnement du p a r a g r a p h e précédent s ' a p p l i q u e à nouveau en c h o i s i s s a n t S' d a n s le volume
v'
limité p a r l a s u r f a c e S. Les é . i . f . é c r i t e s s u r tout S ' permettent d ' a f f i r m e r que l e s éventuelles sources m s i t u é e s d a n sv
a n n u l e n t l e u r potentiel s u r tout S ' , donc d a n sv'
tout e n t i e r : on en d é d u i t encore que l e potentiel V e t s a dérivée normale s ' a n n u l e n t s u r S ( 2 . 5 ) .m
Pour cette région e x t é r i e u r e , i l e s t encore n é c e s s a i r e de préciser l a v a l e u r d u coefficient a n g u l a i r e c défini en 1.56.
La région e x t é r i e u r e à S peut ê t r e considérée comme une région i n t é r i e u r e à l a sphère de s u r f a c e Y: dont on f a i t t e n d r e
l e rayon R v e r s l ' i n f i n i . Le potentiel décroissant a u moins comme 1/R et s a dérivée normale comme I / R ~ , l ' i n t é g r a l e de s u r f a c e 1.58 s u r S* tend v e r s 0. 11 f a u t p a r contre t e n i r compte d e :
.ds = lim J d n = i
R+m R+m
4n
s
*
s
*
d a n s l e calcul d u coefficient c. Remarquons que l a normale exté- r i e u r e à v e s t i c i tournée v e r s l ' i n t é r i e u r de S: 1 ' i n t é g r a l e 2.7 calculée s u r S prend l e s v a l e u r s :
O s i P e s t à l ' i n t é r i e u r de v
1
-? s i P e s t un point r é g u l i e r de S
-1 s i P est d a n s l e volume limité p a r S.
La somme des i n t é g r a l e s 2.7 s u r S* et s u r S donne bien a u coeffi- cient c l e s v a l e u r s h a b i t u e l l e s : 1 s i PEv Q , ( v ) c = --- -
4n
3 s i PES ( P r é g u l i e r )s
O s i PBVUS ( 2 . 8Concluons en s o u l i g n a n t que l e s é . i . f . p r e n d r o n t exactement en compte l a région e x t é r i e u r e i n f i n i e p a r l a seule i n t é g r a t i o n s u r S.
2.1.4 Cas des systèmes c y l i n d r i q u e s i n f i n i s .
Le raisonnement d u 52.1.2 q u i montre l ' é q u i v a l e n c e des é . i . f . avec l ' é q u a t i o n de Laplace e s t mis en défaut d a n s l e c a s des systèmes c y l i n d r i q u e s i n f i n i s (autrement d i t : problèmes bidi- mensionnels p l a n s ) . En e f f e t , l e potentiel d ' u n e d i s t r i b u t i o n uni- forme de monopôles s u r une d r o i t e i n f i n i e e s t donné p a r ( f i g . 8 ) :
d r o i t e c h a r g é e
Il s ' a n n u l e s u r l e cercle d e rayon r, s a n s q u e s a d é r i v é e normale ne s ' a n n u l e ( c e potentiel ne peut ê t r e posé n u l à l ' i n f i n i ) : I ' é q u a - tion 2.5 ne s e r a p a s vérifiée d a n s tous l e s c a s ; p a r exemple, les é . i . f . ne conduiront p a s à l a solution s i l a géométrie é t u d i é e est un c y l i n d r e c i r c u l a i r e i n f i n i d e r a y o n r,.
C ' e s t 1 à 1 'o r i g i n e des systèmes s i n g u l i e r s s i g n a l é s p a r Jawson d a n s l e c a d r e d e l a théorie du potentiel bidimensionnel et qui reçoivent i c i une explication simple e t concrète.
E n r é a l i t é , l e s systèmes c y l i n d r i q u e s i n f i n i s n ' e x i s t e n t p a s et i l est toujours possible de c o n s i d é r e r q u e l e potentiel s ' a n n u l e à 1 ' i n f i n i . Le potentiel logarithmique est c e p e n d a n t une bonne approximation du potentiel coulombien d a n s un domaine proche du milieu d ' o b j e t s t r è s longs: l e potentiel d ' u n segment de droite c h a r g é uniformément, d e longueur r,, e s t donné p a r :
d a n s l e plan médian e t pour r<< r,. Si c e t t e i n é g a l i t é est respectée c ' e s t - à - d i r e en c h o i s i s s a n t r, s u p é r i e u r * à l a p l u s g r a n d e dimen- sion de l a coupe d e l ' o b j e t c y l i n d r i q u e é t u d i é , on ne r i s q u e p a s d ' o b t e n i r un système i n t é g r a l s i n g u l i e r .
( * ) En p a r t a n t de l ' é t u d e formellement p l u s r i g o u r e u s e d e Jawson
110 1, on montre que l ' i n é g a l i t é s t r i c t e e s t mathématiquement
s u f f i s a n t e . Numériquement, i l f a u t p r e n d r e r, t r è s s u p é r i e u r à l a p l u s g r a n d e coupe pour é v i t e r les systèmes quasi-singu- 1 i e r s .
Cette condition de r é g u l a r i t é a p r i o r i d u système d t é . i . f . e s t p l u s e f f i c a c e q u ' u n e correction a posteriori c o n s i s t a n t à c h a n - g e r l ' é c h e l l e du domaine s i on a eu l a malchance d ' o b t e n i r un système s i n g u l i e r ou q u a s i - s i n g u l i e r .
2.1.5 Récapitulation.
Nous pouvons nous résumer de l a façon s u i v a n t e :
- Le problème de Laplace e s t résolu l o r s q u e l e s v a l e u r s a u x limites (potentiel et d é r i v é e normale s u r l a s u r f a c e S de v ) sont connues.
- Pour o b t e n i r ces v a l e u r s a u x limites, i l f a u t é c r i r e l e s é . i . f . s u r toute une s u r f a c e S ' e x t é r i e u r e à v , éventuellement confondue avec S. Pour l e s problèmes à p l u s i e u r s régions Ri
,
on a u r a a u t a n t de s u r f a c e s S ' que de régions R . e t on a p p l i q u e r a
i 1
l e s équations 1.61 ou 1.63.
- Pour l e s problèmes bidimensionnels p l a n s , i l f a u t c h o i s i r 1 a constante r, d u potentiel logarithmique 2.9 t r è s s u p é r i e u r e à l a p l u s g r a n d e dimension de l a coupe de l ' o b j e t étudié.
D'un point de vue p r a t i q u e , i l e s t exclu d ' é c r i r e l e s é . i . f . de façon continue s u r toute une s u r f a c e : nous a l l o n s é t u d i e r l e s conséquences de cette impossibilité à l a section 2.2.
2.2 GENERALITES SUR LA DISCRETISATION DES E.I.F.
Nous venons de montrer q u ' i l e s t é q u i v a l e n t d ' é c r i r e l ' é q u a - tion de Laplace d a n s un volume v ou l ' é q u a t i o n i n t é g r a l e de frontière s u r une s u r f a c e S' e n t o u r a n t v. A d e r a r e s exceptions p r è s pour des géométries t r è s p a r t i c u l i è r e s , i l e s t impossible de déterminer l e s fonctions 0 e t Y s u r S q u i v é r i f i e r a i e n t exac- tement l ' i f .
1.63
en c h a q u e point de S ' : on a donc r e c o u r s à des procédés d ' approximation numériques de c e s fonctions.Nous tentons d a n s cette section d ' a n a l y s e r l e comportement d a n s l ' e s p a c e de l ' e r r e u r associée à cette approximation numé- r i q u e e t nous cherchons un moyen de l ' e s t i m e r .
2.2.1 Démarche pour la résolution numérique e t s o u r c e s d ' e r r e u r .
Les g r a n d e u r s 0 e t Y sont a p p r o c h é e s s u r l a s u r f a c e S p a r des combinaisons l i n é a i r e s de fonctions de b a s e Ai e t Bi
.
On a u r a a i n s i en un point Q de l a s u r f a c e S:Les fonctions Ai e t Bi s o n t , p a r exemple, l e s fonctions p o i d s d e s éléments f i n i s ; l e t y p e p r é c i s de développement u t i l i s é ne joue aucun rôle d a n s notre raisonnement.
C e r t a i n s des coefficients a . ou bi peuvent ê t r e c o n n u s
1
a p r i o r i (CAL f i x é e s ) ; c e r t a i n s sont i n c o n n u s : pour l e s d é t e r m i n e r , nous écrivons d a n s c h a q u e région un système l i n é a i r e d u t y p e :
G(Q)
A- (-
+
H o n ( Q ) ) . G d s = c.@(Pi)Q
'rS (2.11)
avec Pi€S' ( c = O s i S'
#
S)Nous considérons ici que 1 'e r r e u r due à 1 ' approximation numérique de l ' i n t é g r a t i o n est négligeable et i l f a u d r a u t i l i s e r des tech- niques suffisamment performantes pour que ce soit l e c a s ( s a n s quoi les r é s u l t a t s finaux ne peuvent ê t r e c o r r e c t s ) . P a r contre nous admettons deux sources d ' e r r e u r :
A A
- Les développements et Y sont forcément limités: p a r
exemple, un développement en éléments finis du second o r d r e
ne pourra p a s se superposer exactement à une solution sinuso- ïdale: c ' e s t 1 ' e r r e u r de discrétisation
.
- La résolution du système l i n é a i r e 2.11 ne peut ê t r e numé- riquement exacte. C'est en face de cette e r r e u r numérique que l ' e r r e u r commise s u r une intégration doit ê t r e rendue négligeable. Une conséquence de cette e r r e u r de résolution est que les dévelop-
A A
pements et Y finalement obtenus ne vérifieront p a s rigoureu-
sement le système 2.11.
L ' e r r e u r due à l'approximation de l a géométrie est plus difficile à a n a l y s e r rigoureusement et nous ne l a prenons p a s en compte. A une c e r t a i n e distance des f r o n t i è r e s , elle se comporte comme les précédentes.
2.2.2 Valeur approchée d a n s 1 'espace d u potentiel et e r r e u r réelle maximale.
A
Le développement que nous avons noté est une v a l e u r approchée du potentiel, mais il n ' e s t défini que s u r l a frontière.
Dans le volume, nous notons a * l'approximation du potentiel
A A
obtenue à p a r t i r de et de Y p a r l a q u a d r a t u r e :
avec :
Le potentiel @* a i n s i d é f i n i e s t , d a n s v , l e potentiel d e s d i s t r i - butions s u r f a c i q u e s :
11 obéit donc à l ' é q u a t i o n de Laplace tout comme l a solution e x a c t e @
.
La différence ( @ - @ ? ) obéit p a r conséquent a u s s i à l ' é q u a t i o n de Laplace et on peut l u i a p p l i q u e r l e théorème d u maximum:"Les extréma de l ' e r r e u r sont s u r S" (2.14)
Cela peut sembler p a r a d o x a l d a n s l e c a s d ' u n problème de Dirichlet: l ' e r r e u r s u r l a g r a n d e u r cherchée est maximale justement l à où cette g r a n d e u r e s t connue!
Dans ce c a s d u problème de Dirichlet, l a v a l e u r e x a c t e
@ du potentiel est connue s u r l a s u r f a c e
..
S et e s t u t i l i s é e pour c o n s t r u i r e l e développement..
@ q u i peut ê t r e e x a c t . La résolution d e s é . i . f . nous donne Y q u i e s t l i é à l a d é r i v é e normale d u poten- t i e l : on p o u r r a i t penser q u e l ' e r r e u r s u r l e potentiel s e r a i t n u l l e s u r l a frontière e t non n u l l e en dehors.*
En r é a l i t é , s u r l a f r o n t i è r e , @ et @* ne sont p a s confondus. Pour a p p l i q u e r 2.14, on doit en effet poser ( f i g . 9 ) :
@*(P ) = lim I ( P )
P + P
s
s
ce qui n ' e s t p a s t r i v i a l puisque 1 n ' e s t p a s continue
..
à t r a v e r s S. Cette limite est liée a u x valeurs de 1 et de @ s u r S: en définis- s a n t @;:s
p a r analogie à 2.11:on obtient 1 'expression :
a*
-a
= c . ( @ * - 0 ) s u r S (2.18)s
Exemple :
Déterminons l ' e r r e u r commise pour le problème de Dirichlet. Le potentiel imposé s u r S est @ et le développement @ choisi de façon qu 'on a i t exactement:
..
@ = @ s u r S
L ' é c r i t u r e des é. i . f . permet de déterminer un développement
@
et le potentiel est approché en tout point de v p a r@*.
L ' e r - r e u r maximale s u r ce potentiel se trouve en un point de l a fron- tière: elle peut donc être déterminée; on a u r a :1
= F . ( @ - @ * )
s
pour un point réguli.er.@ est une donnée du problème, @" peut ê t r e calculé en tout point de S p a r 2.16 et 2.13. Une application numérique est présentée au $3.3.1.