Livre H PRÉPA TOUT EN UN MATH PDF - Web Education

H PRÉPA TOUT EN UN

1

ANNÉE

RE

• Le cours : connaissances et méthodes

• De nombreux exercices corrigés

• Des extraits de concours

TOUT LE PROGRAMME EN UN SEUL VOLUME !

MATHS

Crédits photographiques

Couverture : Getty Images/AKIRA INOUE Page 187 : Bettmann/CORBIS

Toutes les photographies de cet ouvrage proviennent de la photothèque HACHETTELIVRE.

Composition, mise en page et schémas : Publilog Maquette intérieure : Véronique Lefèbvre Maquette de couverture : Guylaine MOI

 HACHETTE LIVRE 2008, 43 quai de Grenelle 75905 Paris Cedex 15

Tous droits de traduction, de reproduction et d’adaptation réservés pour tous pays.

Le Code de la propriété intellectuelle n’autorisant, aux termes des articles L.122-4 et L.122-5, d’une part, que les « copies ou reproductions strictement réservées à l’usage privé du copiste et non destinées à une utilisation collective », et, d’autre part, que « les analyses et les courtes citations » dans un but d’exemple et d’illustration, « toute représentation ou reproduction intégrale ou partielle, faite sans le consentement de l’auteur ou de ses ayants droit ou ayants cause, est illicite ».

Cette représentation ou reproduction, par quelque procédé que ce soit, sans autorisation de l’éditeur ou du Centre français de l’exploitation du droit de copie (20, rue des Grands-Augustins, 75006 Paris), constituerait donc une contrefaçon sanctionnée par les articles 425 et suivants du Code pénal.

Avant-propos

En proposant ici réuni en un seul ouvrage le programme de la première année MPSI des Classes Préparatoires aux Grandes Ecoles, nous avons voulu privilégier la simplicité et la concision. Nous avons cherché pour chaque nouvelle notion l’introduction la plus économique et les démonstrations les plus compréhensibles pour le débutant. Ce livre ne se sub-stitue pas au cours oral d’un professeur, mais nous espérons qu’il consub-stituera pour l’étudiant un outil de travail et de référence. Quelques repères typographiques doivent aider le lecteur :

• tous les mots nouveaux, définis au fil du texte, sont repérés par un fond coloré et sont répertoriés dans l’index.

• les résultats essentiels et les énoncés des théorèmes sont encadrés ; les démonstrations sont clairement identifiées par un

filet marginal.

• des applications proposent, au fur et à mesure, des situations où sont mises en oeuvre les notions étudiées.

• une fiche-méthode résume, en fin de chapitre, les principaux savoir-faire indispensables pour les exercices.

• chaque chapitre comporte un exercice résolu qui propose une solution rédigée et commentée d’un exercice classique.

• les exercices de chaque chapitre sont accompagnés à la fin du livre d’indications et réponses qui peuvent aller, suivant la

difficulté, d’une simple réponse numérique à une solution détaillée en passant par le "coup de pouce" souvent nécessaire. Ces éléments de réponse n’ont évidemment d’intérêt que pour le lecteur qui a effectivement cherché l’exercice et qui veut vérifier ses résultats. Ils doivent être lus de façon active, le crayon à la main, et ne sont jamais définitifs : c’est au lecteur de conclure et, s’il le désire, de rédiger complètement sa solution.

• nous avons choisi des exercices posés aux oraux des concours lorsque ceux-ci ne portent que sur le programme de

Première Année, ce qui est tout de même assez fréquent.

Les nouveaux programmes préconisant l’introduction du calcul formel, nous avons choisi de présenter tout au long de l’ouvrage l’utilisation d’une calculatrice, en repèrant toutes les fonctions relatives aux notions étudiées et les complétant éventuellement par de petits programmes.

Nous remercions tous ceux qui ont bien voulu nous faire bénéficier de leurs remarques et de leurs conseils.

Les auteurs  Ha ch et te Li vr e– HP répa /M ath –L ap hotocopie non autorisée est un délit

Sommaire

Avant-propos

3

Partie I :

Programme de début d’année

1

Nombres complexes

7

2

Fonctions usuelles

30

3

Équations différentielles linéaires

52

4

Géométrie élémentaire du plan

73

5

Courbes paramétrées

94

6

Coniques

110

7

Géométrie élémentaire de l’espace

127

Partie II :

Nombres et structures algébriques usuelles

8

Vocabulaire relatif aux ensembles, aux applications et aux relations

148

9

Nombres entiers naturels – Combinatoire

166

10 Nombres entiers relatifs – Arithmétique

184

11 Structures algébriques usuelles

197

12 Espaces vectoriels

214

13 Polynômes

235

Sommaire

Partie III :

Nombres réels, suites et fonctions

15 Nombres réels

268

16 Suites réelles et complexes

280

17 Fonctions d’une variable réelle

304

Partie IV :

Calcul différentiel et intégral

18 Dérivation des fonctions d’une variable réelle

329

19 Intégration sur un segment

352

20 Intégrales et primitives d’une fonction continue

372

21 Formules de Taylor. Développements limités

387

22 Approximations

407

Partie V :

Algèbre linéaire

23 Dimension des espaces vectoriels

423

24 Matrices

441

25 Rang d’une matrice et systèmes linéaires

462

26 Groupe symétrique

476

27 Déterminants

486

Partie VI :

Espaces vectoriels euclidiens et géométrie euclidienne

28 Produit scalaire, espaces vectoriels euclidiens

507

29 Automorphismes orthogonaux

521

30 Transformations du plan et de l’espace

535

Partie VII :

Espace R

_{et géométrie différentielle}

31 Fonctions de deux variables réelles

549

32 Calcul intégral et champs de vecteurs

567

33 Étude métrique des courbes planes

581

Solutions

594

Index

665

1

Nombres

complexes

OBJECTIFS

OBJECTIFS

• Réviser et enrichir les notions

vues en Terminale.

• Préparer le cours d’algèbre en

donnant des premiers exemples de structures.

• Préparer le cours d’analyse, où

les fonctions pourront être aussi bien à valeurs complexes que réelles.

• Utiliser les nombres complexes

pour la trigonométrie.

INTRODUCTION

N

és de la résolution générale de l’équation du

troisième degré par Bombelli (1572) – voir

Exercice résolu – les nombres complexes sont

long-temps considérés comme de commodes intermédiaires

de calcul n’ayant pas d’existence propre. C’est

Ha-milton en 1837 qui donne pour la première fois une

construction satisfaisante des nombres complexes à

partir des couples de nombres réels.

L’intérêt majeur du corps des complexes réside dans le

théorème de d’Alembert que nous évoquerons dans le

chapitre Polynômes (chapitre 13) : tout polynôme

non constant à coefficients complexes possède des

ra-cines ! Par ailleurs, les nombres complexes constituent

un outil commode en géométrie plane et en

trigono-métrie.

COURS

₁

1

Corps des complexes

1

.

1

•

Définition des nombres complexes

On appelleensemble des nombres complexeset on note C l’ensemble R2 _que

l’on munit des lois de composition interne :

• addition :

∀(x, y) ∈ C ∀(x , y ) ∈ C (x, y) + (x , y ) = (x + x , y + y )

• multiplication :

∀(x, y) ∈ C ∀(x , y ) ∈ C (x, y)×(x , y ) = (xx − yy , xy + x y)

On peut identifier le complexe (x, 0) au réel x, ce qui revient à considérer R comme une partie de C ; nous constatons que ces deux lois prolongent à C l’addition et la multiplication définies sur R :

∀(x, x ) ∈ R2 _{(x, 0) + (x , 0) = (x + x , 0)}

(x, 0)×(x , 0) = (xx , 0)

Le complexe (0, 1) est tel que (0, 1)2_{= (−1, 0), nous le notons i.}

L’écriture du complexe z = (x, y) devient alors :

z = x + iy, (x, y) ∈ R2 _{où i}2 _{= −1}

ATTENTION

La partie imaginaire d’un complexe est un réel.

Par définition, (x, y) est l’unique couple de réels tel que z = x + iy :

x est appelépartie réellede z, y est appelépartie imaginairede z. Notations x = Re (z) y = Im (z).

La TI-92/Voyage 200 sait bien sûr calculer avec les nombres complexes.

Un complexe z est réel si et seulement si sa partie imaginaire

est nulle. Un complexe z est ditimaginairesi sa partie réelle

est nulle. L’ensemble des imaginaires est noté iR.

1

.

2

•

Structure de corps de C

La loi + définie sur C possède les propriétés suivantes :

• elle estassociative:

∀(z, z , z ) ∈ C3 _{(z + z ) + z = z + (z + z )}

• 0 estélément neutrede C pour + :

∀z ∈ C z + 0 = 0 + z = z

• tout élément de C possède unsymétriquepour + :

∀z ∈ C ∃z ∈ C z + z = z + z = 0 : si z = x + iy, z = −x + i(−y) = −z

Ces propriétés confèrent à (C, +) une structure degroupe, de plus l’addition est

commutativesur C.

Nombres complexes

_COURS

1

La loi × définie sur C possède les propriétés suivantes :

• elle estassociative:

∀(z, z , z ) ∈ C3 _{(z×z )×z = z×(z×z )}

• 1 estélément neutrede C pour × :

∀z ∈ C z×1 = 1×z = z

• tout élément non nul de C possède unsymétriquepour × :

∀z ∈ C∗ _{∃z ∈ C}∗ _{z×z = z×z = 1 :}

si z = x + iy, z = _xx − iy_{2+ y2} =1_z

(C∗_{,×) est donc ungroupe abélien, puisque × estcommutativesur C.}

Enfin, × estdistributivepar rapport à + :

∀(z, z , z ) ∈ C3 _{(z + z )×z = z×z + z×z}

Ces propriétés confèrent à (C, +,×) une structure decorps commutatif.

Ces notions seront étudiées de façon plus approfondie dans le chapitre 11

Structures algébriques usuelles.

1

.

3

•

Conjugué d’un nombre complexe

Le conjugué de z est noté conj(z).

On appelle conjugué du nombre complexe z = x + iy où

(x, y) ∈ R2_{, le complexe :}

z = x − iy

Cette application estinvolutive: ∀z ∈ C (z) = z, elle est

donc bijective. De plus : ∀(z, z ) ∈ C2 _{z + z = z + z , z · z = z · z} On en déduit : ∀(z, z ) ∈ C2 _{z − z = z − z} et ∀(z, z ) ∈ C×C∗ z z = z z ∀z ∈ C∗ _{∀n ∈ Z nz = nz ; z}n _{= z}n

Le conjugué permet d’exprimer facilement la partie réelle et la partie imaginaire d’un complexe, et donc de caractériser les réels et les imaginaires :

∀z ∈ C Re (z) = z + z₂ ; Im (z) = z − z_2i ∀z ∈ C z ∈ R ⇐⇒ z = z ; z ∈ iR ⇐⇒ z = −z  Hachette Li vre –H Pr épa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

1

.

4

•

Interprétation géométrique

Doc. 1 Image d’un nombre complexe.

On appelleplan complexeun plan P rapporté à un repère orthonormé (O, u, v).

On peut représenter le nombre complexe z = x + iy par le point M de coor-données (x, y) (Doc. 1).

Le point M est appeléimagede z, et réciproquement z est appeléaffixede

M.

Si M et M sont deux points d’affixes z et z , on appelle aussi affixe du vecteur −−−→

MM le complexe z − z.

Les axes (O, u) et (O, v) sont appelés respectivementaxe des réelsetaxe des

imaginaires. x y O y – y x M(z) M’(z)

Doc. 2 Image du conjugué.

L’image de z est symétrique de l’image de z par rapport à l’axe des réels, en accord avec le caractère involutif de la conjugaison (Doc. 2).

2

Module d’un nombre complexe

2

.

1

•

Module d’un nombre complexe

Soit z = x + iy ∈ C, où (x, y) ∈ R2 _:

zz = (x + iy)(x − iy) = x2_{+ y}2 _{: zz ∈ R} +

On appellemodulede z le réel positif : |z| =√zz.

Le module de z est noté abs(z).

Si z est réel, son module est aussi sa valeur absolue, c’est pour-quoi on emploie la même notation.

Mais attention ! pour un réel x : |x|2_{= x}2_{, tandis que pour un}

complexe quelconque z, |z|2_{= zz.}

Théorème 1

Pour tous complexes z et z : |zz | = |z| |z | Démonstration ∀(z, z ) ∈ C2 _{|zz |}2_{= (zz )(zz ) = (zz)(z z ) = |z|}2_{|z |}2 On en déduit : ∀(z, z ) ∈ C×C∗ z z = |z| |z | ∀z ∈ C∗ _{∀n ∈ Z |z}n_{| = |z|}n

2

.

2

•

Inégalité triangulaire

Pour tous complexes z et z :

|z + z | |z| + |z |

Nombres complexes

_COURS

1

Les deux membres de l’inégalité à démontrer étant des réels positifs, comparons leurs carrés. ⎧ ⎨ ⎩ |z + z |2 _{= (z + z )(z + z ) = z z + z z + z z + z z = |z|}2_{+ 2Re (z z ) + |z |}2 (|z| + |z |)2 _{= |z|}2_{+ 2|z||z | + |z |}2 _{= |z|}2_{+ 2|z z | + |z |}2

Or Re (z z ) |z z |. D’où l’inégalité demandée. L’égalité est vérifiée si et

seulement si Re (z z ) = |z z |, c’est-à-dire z z ∈ R+. Cette condition est

satisfaite si z = 0, ou (en divisant par z z ) si _zz ∈ R+.

x y

O

M(z) ⏐z⏐

Doc. 3 Module d’un nombre

complexe.

Dans le plan complexe, le module de z représente la distance de l’origine au point

M d’affixe z (Doc. 3).

Le réel |z − z | représente la distance entre les points M et M d’affixes z et

z . x z’ z z’’ y O ⏐z – z’⏐ ⏐z – z’’⏐ ⏐z’ – z’’⏐

Doc. 4 Inegalité triangulaire.

Comme dans le cas réel, on déduit de l’inégalité triangulaire que :

∀(z, z ) ∈ C2 _{|z| − |z | |z − z | |z| + |z |}

et :

∀(z, z , z ) ∈ C3 _{|z − z | |z − z | + |z − z |}

(Cette dernière inégalité représente l’inégalité triangulaire dans le plan complexe (Doc. 4).)

La notion de distance nous permet de définir dans le plan complexe :

• ledisque ferméde centre a et de rayon R : {M ∈ P, |z − a| R} où R ∈ R+;

• ledisque ouvertde centre a et de rayon R : {M ∈ P, |z − a| < R} où

R ∈ R∗ +;

• lecerclede centre a et de rayon R : {M ∈ P, |z −a| = R} où R ∈ R∗ +.

Pour s’entraîner : ex. 2 à 7

3

Représentation des nombres

complexes de module 1

3

.

1

•

Groupe

U

des nombres complexes de module 1

L’ensemble U des nombres complexes de module 1, muni du produit défini sur

C est un groupe, on dit que c’est un sous-groupe de (C∗_{,×) (voir chapitre 11) :}

• ∀(z, z ) ∈ U2 _{|zz | = |z|.|z | = 1, la loi multiplicative est bien une loi de}

composition interne sur U .

• Elle est associative sur C, donc en particulier sur U .

• Elle possède un élément neutre : le réel 1, qui appartient à U .

• Enfin, tout élément z de U est non nul, donc possède un inverse dans

C∗ _{: z =}1

z tel que |z | =

1

|z| = 1, ce qui prouve que z ∈ U .

x z 1 −1 i −i y

Doc. 5 Cercle trigonométrique.

|z| = 1 ⇐⇒ OM = 1 : l’ensemble des points M du plan d’affixe z ∈ U

est le cercle de centre O de rayon 1, appelécercle trigonométrique(Doc. 5).

 Hachette Li vre –H Pr épa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

3

.

2

•

Définition de e

Théorème 3

Un complexe z est élément de U si et seulement s’il peut s’écrire :

z = cosθ+ i sinθ, θ∈ R

Attention, cette écriture n’est pas unique.

Démonstration

Pour tout réel θ, | cosθ+i sinθ| =√cos2_{θ+ sin}2_{θ= 1 : cosθ+i sinθ∈ U .}

Réciproquement, soit z = x + iy un élément de U .

Comme x2_{+ y}2 _{= 1, il existe θ∈ R tel que x = cosθ et y = sinθ, on peut}

donc écrire z = cosθ+ i sinθ.

Attention, θ n’est pas unique : cosθ+ i sinθ = cosθ + i sinθ équivaut à

cosθ= cosθ et sinθ= sinθ, c’est-à-dire à θ−θ ∈ 2πZ.

x ei 1 −1 i −i y

Doc. 6 Représentation d’un nombre

complexe de module 1

Désignons par ϕ la fonction de R dans C définie par ϕ(θ) = cosθ+ i sinθ.

Les fonctions cos et sin sont dérivables, ce qui entraîne que ϕ l’est aussi et :

∀θ∈ R ϕ(θ) = (cosθ+ i sinθ) = − sinθ+ i cosθ= i(cosθ+ i sinθ)

soit :

∀θ∈ R ϕ(θ) = iϕ(θ)

Par analogie avec les fonctions réelles d’une variable réelle t → eλt_{, on note, pour}

tout θ∈ R, ϕ(θ) = eiθ, soit (Doc. 6) :

cosθ+ i sinθ= eiθ

Ainsi :

|u| = 1 ⇐⇒ ∃θ∈ R u = eiθ

3

.

3

•

Formules d’Euler

Pour tout θ∈ R, cosθ et sinθ sont respectivement la partie réelle et la partie

imaginaire de eiθ_{, d’où :}

∀θ∈ R cosθ=eiθ+ e₂−iθ et sinθ= eiθ− e_2i−iθ

3

.

4

•

Propriété de l’application

→ e

•cos(a + b)=cos a cos b − sin a sin b

•cos(a − b)=cos a cos b + sin a sin b

•sin(a + b)=sin a cos b + cos a sin b

•sin(a − b)=sin a cos b − cos a sin b

Théorème 4

Nombres complexes

_COURS

1

∀(θ,θ) ∈ R2

eiθ_eiθ _{= (cosθ+ i sinθ)(cosθ + i sinθ)}

= cosθcosθ − sinθsinθ + i(cosθsinθ + sinθcosθ)

= cos(θ+θ) + i sin(θ+θ)

= ei(θ+θ)

De même :

∀(θ,θ) ∈ R2 eiθ

eiθ = ei(θ−θ)

Par récurrence : ∀n ∈ N (eiθ₎n_{= e}inθ _{et (e}iθ₎−n_{= e}−inθ_{, d’où :}

∀n ∈ Z (eiθ₎n_{= e}inθ

c’est-à-dire :

(cosθ+ i sinθ)n_{= cos nθ+ i sin nθ}

ATTENTION

La formule de Moivre n’a de sens que si n est entier. Pour θ∈ 2πZ, l’égalité (e2iπ₎θ/2π_{= e}iθ _{est un} non-sens : elle conduirait à eiθ_{= 1.}

C’est laformule de Moivre.

3

.

5

•

Exponentielle complexe

Plus généralement, on peut étendre à C la fonction exponentielle : on appelle

exponentielle complexe l’application définie sur C à valeurs dans C qui à

z = x + iy, avec (x, y) ∈ R2_{, associe :}

ez_{= e}x_eiy_{= e}x_{(cos y + i sin y)}

On remarque que le module de ez _{est e}x _{: ∀z ∈ C |e}z_{| = e}Re (z)_.

Théorème 5

∀(z, z ) ∈ C2 _ez+z _{= e}z_ez Démonstration

Si z = x + iy et z = x + iy :

ez+z _{= e}x+x _ei(y+y )_{= e}x_ex _eiy_eiy _{= e}z_ez

On montre de même que :

∀(z, z ) ∈ C2 _ez−z ₌ ez

ez

et :

∀z ∈ C ∀n ∈ Z (ez₎n_{= e}nz

Attention : Tout complexe non nul peut s’écrire ez_{, mais un tel z n’est pas}

unique : il n’existe pas d’application réciproque de z → ez _{définie sur C}∗ _:

ez_=ρeiα _{⇐⇒ z = lnρ+ iα+ 2ikπ k ∈ Z}  Hachette Li vre –H Pr épa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

4

Applications à la trigonométrie

4

.

1

•

Linéarisation et factorisation d’expressions

trigonométriques

Unpolynôme trigonométriqueest une combinaison linéaire d’expressions de la

forme cosm_{x sin}n_{x, où (m, n) ∈ N}2_.

Les formules d’Euler permettent de le transformer en un polynôme des variables

eix _{et e}−ix_{. Après développement, en regroupant les termes conjugués, on obtient}

une combinaison linaire de cos px et sin qx.

Exemple : Linéariser cos x sin2_x.

cos x sin2_{x =} eix+ e−ix

2

eix_{− e}−ix

2i

2

= −1₈(eix_{+ e}−ix_)(e2ix_{− 2 + e}−2ix₎

= −1₈(e3ix_{− e}ix_{− e}−ix_{+ e}−3ix₎

= −1₄(cos 3x − cos x)

4

.

2

•

Transformations de produits en sommes

et vice versa

Des formules d’addition on peut déduire les formules suivantes :

• cos a cos b = 1₂(cos(a + b) + cos(a − b))

• sin a sin b = −1

2(cos(a + b) − cos(a − b))

• sin a cos b =1₂(sin(a + b) + sin(a − b))

En posant a + b = p, a − b = q, on obtient les formules inverses :

• cos p + cos q = 2 cosp + q₂ cosp − q₂

• cos p − cos q = −2 sinp + q₂ sinp − q₂

• sin p + sin q = 2 sinp + q₂ cosp − q₂

• sin p − sin q = 2 cosp + q₂ sinp − q₂

4

.

3

•

Calcul de cos

nx

et sin

nx

en fonction

de cos

x

et sin

x

D’après la formule de Moivre, nous avons, pour tout n ∈ N :

cos nx + i sin nx = (cos x + i sin x)n

En développant le premier membre de cette égalité par la formule du binôme, et en séparant partie réelle et partie imaginaire, on obtient cos nx et sin nx.

Nombres complexes

_COURS

1

Exemple : Calcul de cos 5x et sin 5x.

e5ix _{= (cos x + i sin x)}5

= cos5_{x + 5i cos}4_{x sin x − 10 cos}3_{x sin}2_x

− 10i cos2_{x sin}3_{x + 5 cos x sin}4_{x + i sin}5_x

D’où :

cos 5x = cos5_{x − 10 cos}3_{x sin}2_{x + 5 cos x sin}4_x

sin 5x = 5 cos4_{x sin x − 10 cos}2_{x sin}3_{x + sin}5_x

Remarque : Pour tout n ∈ N, cos nx est un polynôme en cos x.

Si n est impair, sin nx est un polynôme en sin x, si n est pair, sin nx est le produit de cos x par un polynôme en sin x.

Exemple :

cos 5x = cos5_{x − 10 cos}3_{x(1 − cos}2_{x) + 5 cos x(1 − cos}2_x)2

sin 5x = 5(1 − sin2_x)4_{sin x − 10(1 − sin}2_{x) sin}3_{x + sin}5_x

cos 2x = 2 cos2_{x − 1}

sin 2x = 2 sin x cos x

4

.

4

•

Calcul de

cos(

a

+

kb

) et de

sin(

a

+

kb

)

Ce sont la partie réelle et la partie imaginaire de la somme complexe :

S = n

k=0

ei(a+kb)

On reconnaît la somme de (n + 1) termes d’une suite géométrique de premier

terme eia _{et de raison e}ib_.

• Si b ∈ 2πZ , eib_{= 1 et S = (n + 1)e}ia_;

• si b /∈ 2πZ , S = eia1 − ei(n+1)b

1 − eib .

Dans ce cas, mettons ei(n+1

2 )b en facteur au numérateur et eib2 en facteur au

dénominateur : S = eiaei( n+1 2 )b(e−i(n+12)b− ei(n+12 )b) eib 2(e−ib2 − eib2) = e i(a+nb 2)sin (n+1)b 2 sinb 2 D’où : _n k=0 cos(a + kb) = cos a +nb 2 sin(n+1)b 2 sinb 2 et : _n k=0 sin(a + kb) = sin a +nb 2 sin(n+1)b 2 sinb 2

Pour s’entraîner : ex. 8

 Hac het te Li vre –H Pr épa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

5

Forme trigonométrique

d’un nombre complexe non nul

5

.

1

•

Forme trigonométrique d’un nombre complexe

non nul

Soit z ∈ C∗_{; le complexe} z

|z| appartient à U . Il existe donc

θ∈ R tel que _|z|z = eiθ_{, c’est-à-dire :}

z = |z|eiθ

Cette écriture est appeléeforme trigonométriquede z ; le réel

θ est unargumentde z noté arg(z).

L’ensemble des arguments de z est {θ+ 2kπ, k ∈ Z}.

5

.

2

•

Propriétés des arguments

u x

y

O

M(z)

arg z

Doc. 7 Argument d’un nombre

complexe.

Dans le plan complexe orienté, un argument de z est une mesure de l’angle

orienté (u,−−→OM), où M est l’image de z (Doc. 7).

On déduit de ∀(θ,θ) ∈ R2 _eiθ_eiθ _{= e}i(θ+θ) _:

∀(z, z ) ∈ C2 _{arg(zz ) = arg(z) + arg(z ) [2π]}

∀(z, z ) ∈ C×C∗ arg(z

z ) = arg(z) − arg(z ) [2π]

∀z ∈ C ∀n ∈ Z arg(zn_{) = n arg(z) [2π]}

APPLICATION 1

Distances et angles dans le plan complexe

1) Soit z un complexe tel que |1 + z| < 1₂. Montrer

que |1 + z2_{| > 1.}

2) Soit z un complexe de module 1 tel que

|1 + z| < 1 . Montrer que |1 + z2_{| > 1 .}

3) Soit z1 et z2 deux complexes de même module

supérieur à 1. Montrer que |z1 + z2| 1 ou

|z2

1+ z22| 1 .

1) Soit I le point d’affixe −1, M et M les points

d’affixes respectives z et z2_{. M appartient au disque}

ouvert de centre I de rayon 1₂. Soit K et K les

points de contact des tangentes issues de O au cercle

de centre I de rayon 1₂ (Doc. 8).

Le triangle (OIK ) est un demi-triangle équilatéral,

donc IOK =π 6. x y π 3 π 6 I _O K' K Doc. 8

On en déduit que arg z ∈ 5π

6 , 7π 6 [2π] , d’où arg z2_∈ 5π 3 , 7π 3 [2π]. Le point M appartient

donc à un secteur angulaire inclus dans le demi-plan

x > 0. La distance IM reste donc strictement

supé-rieure à 1 : |1 + z2_{| > 1.}

2) Ici, les points M et M appartiennent au cercle

Nombres complexes

_COURS

1

M appartient au petit arc de cercle AB inclus dans

le disque ouvert de centre I de rayon 1 (Doc. 9).

On en déduit arg z ∈ 2π 3 , 4π 3 [2π], d’où arg z2_∈ 4π 3 , 8π 3 [2π].

Le point M appartient au grand arc de cercle AB. La distance IM reste donc strictement supérieure à

1 : |1 + z2_{| > 1.}

3) On pose u = z_z1

2, on a donc |u| = 1. En

appli-quant à u le résultat de la question 2), on sait que :

|1 + u| 1 ou |1 + u2_{| 1} c’est-à-dire : 1 + z1 z2 1 ou 1 + z2 1 z2 2 1 d’où : |z2+ z1| |z2| 1 ou |z22+ z12| |z22| 1

5.3

•

Réduction de

a

cos

x

+

b

sin

x

où (

a

,

b

,

x

) ∈ R

Posons : z = a + ib.

z eix _{= (a − ib)(cos x + i sin x)}

= a cos x + b sin x + i(a sin x − b cos x) donc :

a cos x + b sin x = Re (z eix₎

Écrivons z sous forme trigonométrique :

z = r eiϕ

zeix _{= re}i(x−ϕ)

d’où :

a cos x + b sin x = r cos(x −ϕ) où reiϕ_{= a + ib}

Exemple :

Résolvons l’équation : cos x +√3 sin x =√2.

Ici : z = 1 + i√3 = 2 eiπ

3.

Donc : cos x +√3 sin x = 2 cos(x −π₃).

L’équation devient : cos(x −π₃) =

√ 2 2 = cos π 4. D’où : ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ x −π₃ = π₄ + 2kπ ou x −π 3 = − π 4 + 2kπ avec k ∈ Z S = {₁₂π + 2kπ, 7₁₂π+ 2kπ, k ∈ Z}

Pour s’entraîner : ex. 9 et 10

 Hachette Li vre –H Pr épa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

6

Racines

n-ièmes d’un nombre

complexe

6

.

1

•

Racines

n

- ièmes de l’unité

Soit n ∈ N∗_{. Résolvons l’équation z}n _{= 1. Cherchons une solution sous la}

forme trigonométrique z = |z|eiθ_.

zn_{= 1 ⇐⇒ |z|}n_einθ_{= 1 ⇐⇒} |z|n= 1 nθ= 2kπ ⇐⇒ ⎧ ⎨ ⎩ |z| = 1 θ=2k_nπ (k ∈ Z)

L’ensemble des solutions est donc :

Un= e2i kπn , k ∈ Z

Notons que (Un, ×) est un sous-groupe de (U, ×) (voir chapitre 11). On obtient

tous ses éléments en donnant à k , n valeurs consécutives (par exemple, k ∈ [[0, n − 1]]). x y 4iπ 5 e 2iπ 5 e 6iπ 5 e 8iπ 5 e 1 0

Doc. 10 Racines 5-ième de l’unité.

Dans le plan complexe, les images des éléments de Un forment un polygone

régulier à n côtés (si n 3) (Doc. 10).

La somme des éléments de Un est nulle (somme des termes d’une suite

géomé-trique) : n−1 k=0 e2i kπn = 1 − e 2inπ n 1 − e2iπn = 0

Exemple : Racines cubiques de l’unité. Posons j = e2iπ3 .

U3= {1, j, j2} et 1 + j + j2= 0.

6

.

2

•

Racines

n

-ièmes d’un nombre complexe quelconque

Soit Z un nombre complexe quelconque et n ∈ N∗_.

Résolvons l’équation zn _{= Z.}

Si Z = 0, il y a une solution unique : z = 0.

Si Z = 0, cherchons les solutions sous la forme trigonométrique z = |z|eiθ_.

Posons Z = |z| eiα zn_{= Z ⇐⇒ |z|}n_einθ_{= |Z|e}iα _⇐⇒ |z|n= |Z| nθ=α+ 2kπ ⇐⇒ ⎧ ⎪ ⎨ ⎪ ⎩ |z| = n _|Z| θ=α_n + 2k_nπ (k ∈ Z) zn_{= Z ⇐⇒ z =} n _{|Z| e}iα n_×e2i kπn (k ∈ Z)

Nombres complexes

_COURS

1

Tout nombre complexe non nul a donc n racines n-ièmes distinctes, qui se déduisent de l’une d’entre elles en la multipliant par un élément quelconque du

groupe Un. Leur somme est nulle.

x i 1 0 y z1 z3 z2

Doc. 11 Racines cubiques de 8i.

Exemple : z3_{= 8i ⇐⇒} ⎧ ⎨ ⎩ |z| = 2 θ= π 6+ 2kπ 3 z1= 2ei π

6 =√3 + i , z₂= 2e5iπ6 = −√3 + i et z₃= 2e3iπ2 = −2i (Doc. 11).

6.3

•

Cas des racines carrées

Tout nombre complexe non nul Z possède donc deux racines carrées opposées. Leur calcul effectif à l’aide de la méthode précédente n’est possible que si l’on peut écrire facilement Z sous la forme trigonométrique, ce qui est rare. La méthode suivante a l’avantage d’être plus systématique.

Posons Z = X + i Y , avec (X , Y ) ∈ R2_{, et cherchons z = x + i y, avec}

(x, y) ∈ R2 _{tel que z}2_{= Z.}

z2_{= Z ⇐⇒ x}2_{− y}2_{+ 2ixy = X + i Y ⇐⇒} x2− y2= X (1)

2xy = Y (2)

De plus : |z|2_{= |Z| ⇐⇒ x}2_{+ y}2 ₌√_X2_{+ Y}2 ₍₃₎

Les relations (1) et (3) donnent x et y au signe près. La relation (2) permet d’apparier les signes de x et de y.

Attention : la fonction racine carrée de la calculatrice ne donne qu’une solution. On peut utiliser cSolve pour ob-tenir les deux racines.

Exemple : Calculons les racines carrées de Z = 3 − 4i :

⎧ ⎪ ⎨ ⎪ ⎩ x2_{+ y}2_{= 5} x2_{− y}2_{= 3} 2xy = −4 ⇐⇒ ⎧ ⎪ ⎨ ⎪ ⎩ x = ±2 y = ±1 xy < 0 ⇐⇒ ⎧ ⎪ ⎨ ⎪ ⎩ x = 2 et y = −1 ou x = −2 et y = 1 Les racines carrées cherchées sont donc :

z1= 2 − i et z2= −2 + i

6

.

4

•

Équation du second degré

Considérons l’équation az2_{+ bz + c = 0, où (a, b, c) ∈ C}3 _et

a = 0. On peut écrire le trinôme sous la forme canonique :

az2_{+ bz + c = a z +} b

2a

2

−_4ab2 + c

L’équation équivaut donc à :

z + _2ab 2= b2_4a− 4ac₂

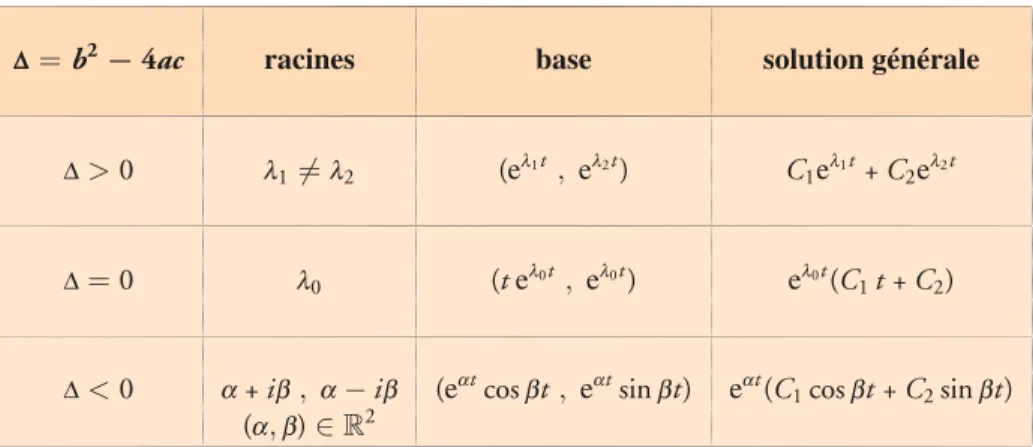
Posons Δ= b2− 4ac.

• Si Δ= 0, l’équation a une seule solution : z = −b

2a.

• Si Δ= 0, le nombre complexe Δ a deux racines carrées δ et −δ; l’équation

a deux solutions : z1= −b +_2a δ ; z2= −b −_2a δ  Ha ch et te Li vr e– HP répa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

Les formules sont les mêmes que celles qui donnent les solutions d’une équation du second degré à coefficients réels ; mais le calcul des racines carrées du discriminant constitue une étape supplémentaire.

Exemple : Résolvons l’équation 2z2_{− (1 + 5i)z − 2(1 − i) = 0.}

Δ= (1 + 5i)2+ 16(1 − i) = −8 − 6i

Cherchons δ= x + iy tel que δ2=Δ

(x + iy)2 _{= −8 − 6i ⇐⇒} ⎧ ⎨ ⎩ x2_{+ y}2_{= 10} x2_{− y}2 _{= −8} 2xy = −6 ⇐⇒ ⎧ ⎨ ⎩ x = ±1 y = ±3 xy < 0 D’où δ= 1 − 3i ou δ= −1 + 3i.

Les solutions de l’équation sont donc :

z1=1 + 5i + (1 − 3i)₄ = 1 + i₂ z2= 1 + 5i − (1 − 3i)₄ = 2i

Comme dans le cas réel, on peut exprimer la somme et le produit

des racines du polynôme az2_{+bz+c en fonction des coefficients :}

z1+ z2= −b_a ; z1z2= c_a

Réciproquement, deux nombres complexes dont la somme est S

et le produit P sont les racines, distinctes ou non, du polynôme z2_{− Sz + P.}

Pour s’entraîner : ex. 11 à 18

7

Nombres complexes et géométrie

plane

7

.

1

•

Configuration de trois points

Soit A, B et M trois points du plan complexe, distincts deux à deux, d’affixes

respectives a, b et z. Considérons le complexe Z = z − a_{z − b} :

⎧ ⎨ ⎩

|Z| = |z − a|_{|z − b|} =AM_BM

arg(Z) = arg(z − a) − arg(z − b) = (−−→BM,−−→AM) [2π]

Ainsi, le nombre z − a

z − b caractérise la position de M par rapport à A et B. Par

exemple :

• ABM est un triangle équilatéral ⇐⇒ z − a_{z − b} = e±iπ 3 ;

• ABM est un triangle isocèle rectangle en M ⇐⇒ z − a_{z − b} = ±i ;

Nombres complexes

_COURS

1

7

.

2

•

Transformations du plan complexe

Soit z → z = f (z) une application de C dans C ; nous pouvons lui associer une application f du plan complexe P qui au point M d’affixe z fait cor-respondre M d’affixe z . Nous allons interpréter géométriquement f , dans quelques cas particuliers :

• z → z

L’application f est la symétrie orthogonale s par rapport à l’axe réel. Rappe-lons que cette application est involutive.

• z → az, a ∈ C∗

Si a = 1, f = IdP, sinon l’origine est le seul point invariant par f .

Notons a =ρeiα_{, alors si z = 0, z = |z|e}iθ_{⇒ z =ρ|z|e}i(θ+α)_{, c’est-à-dire :}

OM =ρOM et (−−→OM,−−→OM ) =α [2π]

L’application f est donc la composée commutative de la rotation de centre

O et d’angle α et de l’homothétie de centre O et de rapport ρ; c’est une similitude directe.

f est bijective ; sa réciproque est la composée commutative de la rotation de

centre O et d’angle −α et de l’homothétie de centre O et de rapport 1

ρ.

• z → az + b, (a, b) ∈ C∗×C

Cherchons tout d’abord si cette application possède des points fixes :

z = az + b ⇐⇒ z(1 − a) = b

– si a = 1, f ne possède pas d’invariant, l’application f associée à

z → z + b est la translation de vecteur −→V , d’affixe b, dont la réciproque

est la translation de vecteur −−→V ;

– si a = 1, f possède un unique invariant, z0= _{1 − a}b , alors

z = az + b ⇐⇒ z − z0 = a(z − z0)

Soit Ω d’affixe z0; nous sommes ramenés à l’exemple précédent : f est

la composée commutative de la rotation de centre Ω et d’angle α et de

l’homothétie de centre Ω et de rapport ρ. Sa réciproque est la composée

commutative de la rotation de centre Ω et d’angle −α et de l’homothétie

de centre Ω et de rapport 1

ρ.

Dans tous les cas, f est une similitude directe. Réciproquement, toute simili-tude directe, translation ou composée rotation-homothétie, est associée à une application de C dans C de la forme z → az + b.

• z → 1_z f est définie sur C∗_{, à valeurs dans C}∗_{, il est immédiat que cette}

application est involutive.

Notons z = |z|eiθ_{; alors : z =} 1

|z|e−iθ, c’est-à-dire :

OM = _OM1 et _OM1 −−→OM = s _OM1 −−→OM

où s est la symétrie par rapport à l’axe des réels.

 Ha ch et te Li vr e– HP répa /M ath –L ap hotocopie non autorisée est un délit

COURS

₁

APPLICATION 2

Étude de l’inversion

Soit I l’application de C∗ _{dans C}∗ _{définie par}

I(z) = _z1. On note encore I l’application

correspon-dante du plan complexe, appeléeinversion.

1) Vérifier que l’inversion est une involution du plan P

privé de O dans lui-même.

2) Déterminer l’image par I :

• d’une droite passant par O, privée de O ;

• d’une droite ne passant pas par O ;

• d’un cercle passant par O, privé de O ;

• d’un cercle ne passant pas par O.

3) Soit M = I(M) et N = I(N), montrer que :

M N = _OM.ONMN

4) Soit A, B, C, D quatre points cocycliques distincts.

En considérant une inversion de pôle A, montrer que l’une des égalités suivantes est vérifiée :

⎧ ⎨ ⎩

BC.AD + CD.AB = BD.AC ou BC.AD + BD.AC = CD.AB ou CD.AB + BD.AC = BC.AD Étudier la réciproque.

1) Pour tout M = O, I(M) = M tel que :

O, M et M sont sur la même demi-droite issue de O et OM.OM = 1.

Ce qui prouve immédiatement que l’image par I de

M est M : l’inversion est une involution du plan P privé de O dans lui-même.

2) Image par I :

• D’une droite D passant par O, privée de O

D’après la remarque précédente, l’image de D est

D , incluse dans D, si D était strictement

in-cluse dans D, on aurait I(D ) strictement inin-cluse dans D, ce qui est absurde puisque I ◦ I(D) = D.

• D’une droite ne passant pas par O

Soit D une telle droite, considérons H projection orthogonale de O sur D et H image de H par I. Soit alors M un point de D et M son image (Doc. 12). Nous avons :

1 = OH.OH = OM.OM ⇐⇒ OM

OH = OH OM

et par alignement des points O, H, H d’une part, O, M, M d’autre part, (OH, OM) = (OM , OH ), les triangles OHM et OM H sont donc semblables, ce qui prouve que l’angle

OM H est droit : l’image de D est incluse dans

le cercle C de diamètre [OH ], privé de l’origine. O H H0 M0 M Doc. 12

Réciproquement, soit N un point de ce cercle autre que O, la droite (ON) coupe D en N . Les deux triangles rectangles ONH et OHN ont en commun l’angle O , ils sont donc semblables, ce qui prouve que :

ON OH = OH ON ⇐⇒ 1 = OH.OH = ON.ON N = I(N) ⇐⇒ N = I(N ).

L’image de D \ {O} est donc C \ {O}.

• D’un cercle passant par O, privé de O

D’après l’étude précédente l’image de C \ {O}, où C est un cercle passant par O, dont un dia-mètre est OH , est la droite perpendiculaire en

H = I(H ) à ce diamètre.

• D’un cercle ne passant pas par O

Soit un tel cercle C, d’équation cartésienne :

(E) x2_{+ y}2_{− 2ax − 2by + c = 0 c = 0}

Soit M un point de ce cercle et M = I(M) , donc M = I(M ), nous avons donc :

Nombres complexes

M ∈ C si et seulement si ses composantes x, y

vérifient (E), c’est-à-dire si et seulement si :

x2_{+ y}2_{− 2ax (x}2_{+ y}2_{) − 2ay (x}2_{+ y}2₎

+ c(x2_{+ y}2₎2_{= 0}

Soit, en simplifiant par c(x2_{+ y}2_{), qui n’est pas}

nul : x2_{+ y}2_{− 2}a cx − 2 b cy + 1 c = 0 M décrit donc un cercle C , ne passant pas

par O.

Remarquons que le centre du cercle image

C n’est pas en général l’image du centre du

cercle C.

3) Soit M = I(M) et N = I(N), montrons que :

M N = MN OM.ON

Pour ce calcul, choisissons un repère orthonormal

(O, i, j) tel que −−→OM = ai, a > 0, d’où

OM = 1_ai. N = (x, y), d’où : N = _x2x_{+ y2},_x2y_{+ y2} Alors : (M N )2 ₌ x x2_{+ y}2 − 1 a 2 + _x2y_{+ y2} 2 = _a2(x21_{+ y2)2}(a2_x2_{− 2ax(x}2_{+ y}2₎ +(x2_{+ y}2₎2_{+ a}2_y2₎ = a2− 2ax + x_{a2(x2+ y2}2₎+ y2 = (x − a)_{a2(x2+ y}2+ y₂₎2 = _OMMN_2.ON2 ₂

4) Soit A, B, C, D quatre points cocycliques distincts.

Supposons que C est entre les points B et D ; et notons B , C et D les images par I, inversion de pôle A, de ces points : B , C et D sont alignés et

C est entre B et D (Doc. 13), nous avons donc : B D = B C + C D , ce qui se traduit à l’aide de la

question 3) par : BD AB.AD = BC AC.AB + CD AC.AD A B C B0 D0 D O C0 I A( )0 Doc. 13

Soit, en réduisant au même dénominateur :

BC.AD + CD.AB = BD.AC

Les deux autres égalités proposées correspondent aux autres dispositions relatives des points B,

C et D.

Réciproquement, si l’une des trois égalités est vérifiée, les points B , C et D sont alignés.

Considérons alors leurs images B, C et D, directes ou réciproques par une inversion de pôle A.

• si A n’est pas un point de la droite (B , C ),

l’image de cette droite est un cercle passant par

A, ce qui signifie que A, B, C et D sont

co-cycliques ;

• Si A ∈ (B , C ), cette droite est invariante par I,

A, B, C et D sont alignés.

Quatre points du plan sont donc alignés ou co-cycliques si et seulement s’ils vérifient l’une des trois conditions proposées, c’est le théorème de

Ptolémée.  Hachette Li vre –H Pr épa /M ath –L ap hotocopie non autorisée est un délit

Nombres complexes

...

_MÉTHODE

Pour montrer qu’un nombre complexe est réel, on peut :

• montrer que sa partie imaginaire est nulle ;

• montrer qu’il est égal à son conjugué ;

• montrer qu’il est nul ou que son argument est 0 modulo π.

Pour montrer qu’un nombre complexe est imaginaire pur, on peut :

• montrer que sa partie réelle est nulle ;

• montrer qu’il est égal à l’opposé de son conjugué ;

• montrer qu’il est nul ou que son argument est π

2 modulo π.

Pour calculerune puissance d’un nombre complexe:

le mettre sous la forme trigonométrique.

Pourcalculer une somme de cosinus, respectivement une somme de sinus:

reconnaître la partie réelle, respectivement la partie imaginaire, de la somme des termes d’une suite géométrique complexe.

Pour écrire 1 + eiθ _{et 1 − e}iθ _{(θ∈ R) sous la forme r e}iα_{, avec (r,α) ∈ R}2_{, on peut}

factoriser par eiθ 2 : 1 + eiθ_{= e}iθ 2 e−iθ2 + ei2θ = 2 cosθ 2ei θ 2 1 − eiθ_{= e}iθ 2 e−iθ2 − eiθ2 = 2 sinθ 2ei( θ 2−π2) ...

Exercice résolu

ÉQUATION DU TROISIÈME DEGRÉ, MÉTHODE DE TARTAGLIA

On considère l’équation dans C : (1) z3_{+ pz + q = 0, où (p, q) ∈ R}2

1 Si z est solution de (1), on cherche deux complexes u et v tels que u + v = z et uv = −p

3.

Montrer que u3 _{et v}3 _{sont les solutions d’une équation du second degré (2).}

2 En déduire la résolution de l’équation (1) dans C.

3 Discuter selon les valeurs de p et q le nombre de solutions réelles de l’équation (1).

4 Exemples : Résoudre dans C et dans R les équations :

Nombres complexes

Conseils

Solution

1) Soit u et v deux complexes tels que uv = −p₃ . Le complexe u + v est solution de (1) si et seulement si :

(u + v)3_{+ p(u + v) + q = 0}

c’est-à-dire u3_{+ v}3_{+ (u + v)(3uv + p) + q = 0, d’où :}

u3_{+ v}3_{= −q et u}3_v3_{= −}p3

27

Deux nombres complexes de somme S et de produit P sont les racines du po-lynôme X2_{− SX + P.}

u3 _{et v}3 _{sont donc les solutions de l’équation du second degré :}

(2) X2_{+ qX −} p3

27 = 0

dont le discriminant est réel :

Δ=₂₇1 (4p3+ 27q2)

Si u est une racine cubique de U , les deux autres racines cubiques de U sont

u e2i3π et u e−2i3π.

2) Si Δ> 0, l’équation (2) a deux solutions réelles distinctes (U , V ).

⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ u3 _{= U} v3_{= V} uv = −₃p ⇐⇒ ⎧ ⎪ ⎨ ⎪ ⎩ u ∈ {√3_U,√3_{U j,}√3_{U j}} v ∈ {√3_{V ,}√3_{V j,}√3_{V j}} uv ∈ R

Apparier les solutions en u et v de sorte

que uv soit réel. D’où : (u, v) ∈ {(

3 √

U ,√3_{V ), (}√3_{U j,}√3_{V j), (}√3_{U j,}√3_{V j)}}

L’équation (1) a donc une solution réelle z0=√3U +3

√ V et deux solutions complexes conjuguées : z1= 3 √ U j +√3_{V j et z} 1 = 3 √ U j +√3_{V j}

Si Δ= 0, l’équation (2) a une racine double réelle U = −q₂

⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ u3_{= U} v3_{= V} uv = −p₃ ⇐⇒ ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ u ∈ √3_U,√3_{U j,}√3_{U j} v ∈ √3_{U ,}√3_{U j,}√3_{U j} uv ∈ R

D’où : (u, v) ∈ {(√3U,√3U), (√3U j,√3U j), (√3U j,√3U j)}

L’équation (2) a donc deux solutions réelles : z0= 23

√

U et z1= −3

√

U

Les racines cubiques de U sont u0, u0j

et u0j.

Si Δ < 0, l’équation (2) a deux solutions complexes conjuguées

(U, U ). Soit u0, u0j et u0j les trois racines cubiques de U .

(u, v) ∈ {(u0, u0), (u0j, u0j), (u0j, u0j)}

L’équation (1) a trois solutions réelles : z0 = 2Re (u0), z1 = 2Re (u0j)

et z2= 2Re(u0j).  Ha ch et te Li vr e– HP répa /M ath –L ap hotocopie non autorisée est un délit

Nombres complexes

3) En résumé, l’équation (1) a une solution réelle simple, deux solutions

réelles dont une double (voire triple) ou trois solutions réelles distinctes

suivant que 4p3_{+ 27q}2 _{est strictement positif, nul ou strictement négatif.}

On peut retrouver ces résultats par l’étude des variations de la fonction

f : x → x3_{+ px + q. L’équation f (x) = 0 a au moins une solution réelle,}

car f est continue et lim

x→−∞f (x) = −∞, limx→+∞f (x) = +∞.

f est dérivable sur R et f (x) = 3x2_{+ p. Si p 0, f est strictement}

croissante sur R , il y a une seule solution réelle (simple ou triple). Si p < 0, les variations de f sont les suivantes :

x −∞ − −p₃ −₃p +∞ α +∞ f −∞ β avec α= q − −4p₂₇3 et β= q + −4p₂₇3 d’où αβ=4p3+ 27q₂₇ 2. Appliquer le théorème :

« Toute fonction continue strictement monotone sur un intervalle I est une bijection de I dans f (I) »

successivement aux intervalles : −∞, − −p₃ , − −p₃, −₃p

et −p₃, +∞ .

Il y a trois solutions réelles si et seulement si αβ < 0, c’est-à-dire

4p3_{+ 27q}2_{< 0 ;}

Il y a deux solutions réelles dont une double si et seulement si αβ > 0,

c’est-à-dire 4p3_{+ 27q}2_{= 0 ;}

Il y a une solution réelle simple si et seulement si αβ > 0, c’est-à-dire

4p3_{+ 27q}2_{> 0.}

4) Exemples :

z3_{− 12z − 65 = 0}

u3_v3_{= 64 , u}3_{+ v}3_{= 65 ; d’où u}3_{= 1, v}3_{= 64}

u ∈ {1, j, j} v ∈ {4, 4 j, 4 j} uv ∈ R

L’équation a une solution réelle et deux solutions complexes conjuguées :

S = 5,−5 − 3 √ 3 i 2 , −5 + 3√3 i 2 z3_{− 12z − 16 = 0} u3_v3 _{= 64 , u}3_{+ v}3 _{= 16 ; d’où u}3_{= v}3_{= 8} (u, v) ∈ {2, 2j, 2j}2 _{uv ∈ R}

L’équation a deux solutions réelles : S = {4, −2}.

z3_{− 6z + 4 = 0}

u3_v3 _{= 8, u}3_{+ v}3_{= −4 d’où u}3_{= −2 + 2i = 2}√_{2 e}i3π

4, v3= u3

u ∈ √2 eiπ

4,√2 ei11π12,√2 ei19π12 v ∈ √2 e−iπ4,√2 e−i11π12,√2 e−i19π12

uv ∈ R

Nombres complexes

Complément : Pour résoudre une équation du troisième degré

quel-conque z3_{+ az}2_{+ bz + c = 0, on peut toujours se ramener à la forme}

Z3_{+ pZ + q = 0 en posant Z = z +}a

3 afin d’éliminer les termes en z2.

Exemple : Résoudre l’équation : z3_{+ 12z}2_{+ 42z + 44 = 0.}

Cette équation équivaut à (z + 4)3_{− 6(z + 4) + 4 = 0. On est ramené au}

troisième exemple ci-dessus. D’où S = {−2, −5 −√3, −5 +√3}.

Note historique

Nicolo Tartaglia (1500-1557) découvrit, vers 1540, une merveilleuse méthode de résolution algébrique d’équations du troisième degré. Lors d’un défi l’opposant à Antonio Maria Fior, qui l’accusait de l’avoir plagié, Tartaglia résolut trente équations proposées par Fior, alors que ce dernier ne put en résoudre une seule de Tartaglia. Invité par Jérôme Cardan qui lui proposait de financer ses recherches, Tartaglia commit l’imprudence de lui confier son secret. Cardan s’empressa de le publier sous son nom et il s’ensuivit une querelle de plusieurs années jusqu’à ce que des menaces de mort fassent renoncer Tartaglia à défendre ses droits...

La méthode de Tartaglia laissait cependant quelques zones d’ombre : on se ramenait à une équation du second degré qui, lorsqu’elle possédait deux racines réelles, fournissait une unique racine réelle de l’équation du troisième degré. Mais lorsque l’équation du second degré n’avait pas de racine réelle, la méthode semblait impuissante à fournir les racines réelles évidentes de l’équation du troisième degré ; pour comble de malchance, c’est justement dans ce cas qu’il y en avait le plus grand nombre... (au maximum trois, les racines négatives étant à l’époque écartées).

Quelques années plus tard, Raffaele Bombelli n’hésita pas, non seulement à considérer des nombres négatifs, mais aussi à leur attribuer une racine carrée... Il compléta ainsi la méthode de Tartaglia, trouvant systématiquement toutes les solutions réelles de l’équation du troisième degré après élimination des racines carrées de négatifs.

Exercices

1

Vrai ou faux ?

a. Deux complexes dont la somme et le produit sont réels,

sont des réels.

b. Pour tout complexe z, |z|2_{= z}2_.

c. Pour tous complexes a et b,

a + ib = 0 ⇒ a = b = 0

d. Deux complexes de même module dont les arguments

diffèrent de 2π sont égaux.

e. ∀z ∈ C ez_{= −1 ⇒ z = iπ}

f. L’application z → ez _{est bijective.}

g. L’ensemble des nombres complexes de module 1 est un

groupe multiplicatif.

h. Tout nombre complexe non nul possède n racines

n-ièmes distinctes.

i. Pour tout entier n 2, la somme des racines n-ièmes d’un nombre complexe est nulle.

j. Une équation du second degré dans C a toujours des

solutions.

Forme algébrique – module

2

réel. On note :

Z = z + z + azz + 1 et Z = z + z + zz + a

1) Montrer que Z = zz Z et que |Z| = |Z |.

2) On suppose que 1 + zz = 0. Montrer que le nombre

u = _{1 + zz}z + z est réel.

3

S1= 1 − 3 + 5 − 7 + · · · + (−1)p(2p + 1)

et

S2= 2 − 4 + 6 − 8 + · · · + (−1)p+12p

4

même module.

5

|u| + |v| |u + v| + |u − v|

|u + v|2_{+ |u − v|}2_{= 2(|u|}2_{+ |v|}2₎

(formule du parallélogramme)

6

(a, b) ∈ N2 _{tel que n = a}2_{+ b}2_{. Montrer qu’un produit}

fini de tels entiers est encore somme de deux carrés.

7

z = a − b 1 − ab. Montrer que : |z| = 1 ⇐⇒ |a| = 1 ou |b| = 1 Caractériser de même |z| < 1.

Applications à la trigonométrie –

forme trigonométrique

8

S1= n k=0 cos kx ; S2= n k=0 sin kx ; S3= n k=0 cos2_{kx ; S} 4= n k=0 sin2_{kx ;} S5= n k=0 cos kx cosk_x ; S6= n k=0 sin kx cosk_x ; S7= n k=0 n k cos kx ; S8= n k=0 n k sin kx.

9

√ 3 1 − i

20

10

1 + cosα+ i sinα en discutant suivant la valeur du réel α.

2) Soit z = 1 − i

1 + cosα+ i sinα où α∈ ]−π,π[. Calculer