Identification Algébrique et Déterministe de Signaux et Systèmes à Temps Continu : Application à des Problèmes de Communication Numérique

HAL Id: tel-00084799

https://tel.archives-ouvertes.fr/tel-00084799

Submitted on 10 Jul 2006

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Systèmes à Temps Continu : Application à des

Problèmes de Communication Numérique

Aline Neves

To cite this version:

Aline Neves. Identification Algébrique et Déterministe de Signaux et Systèmes à Temps Continu : Application à des Problèmes de Communication Numérique. domain_stic.theo. Université René Descartes - Paris V, 2005. Français. �tel-00084799�

Centre Universitaire des Saints-P`

eres

U.F.R. DE MATHEMATIQUES ET INFORMATIQUE

Th`ese pr´esent´ee en vue de l’obtention du grade de Docteur de

l’Universit´e Ren´e Descartes-Paris5

Discipline : Sciences de la Vie et de la Mati`ere

Sp´ecialit´e : Traitement du Signal

par

Aline DE OLIVEIRA NEVES

Identification Alg´

ebrique et D´

eterministe de Signaux et Syst`

emes

`

a Temps Continu : Application `

a des Probl`

emes de

Communication Num´

erique

Soutenue le 20 Mai 2005 devant la Commission d’Examen:

M. Michel FLIESS Pr´esident

M. Fran¸cois DESBOUVRIES Rapporteur

M. Eric MOREAU Rapporteur

M. Mamadou MBOUP Directeur

M. Jo˜ao C´esar MOTA Examinateur

Je tiens tout d’abord `a remercier Mamadou Mboup pour m’avoir encadr´e si brillamment et avec tellement de motivation, me permettant d’apprendre beaucoup sur des sujets peu connus dans notre domaine. Pour son enthousiasme, ses comp´etences et sa patience, un grand, grand merci.

Je remercie ´egalement Madeleine Bonnet, qui m’a si bien accueilli au sein de l’´equipe SPIR au laboratoire CRIP5 et qui a ´et´e mon ange gardien pendant ces 3 ans. Un grand merci!

Merci `a Jo˜ao Marcos Romano, qui m’accompagne d`es mes premiers pas dans la recherche, pour m’avoir, avant tout, mis en contact avec Paris 5. Je tiens `a le remercier pour avoir ´et´e examinateur de ce travail et pour ces propositions, toujours tr`es enrichissantes.

Je remercie M. Michel Fliess, pour m’avoir fait l’honneur de pr´esider le jury et pour le grand int´erˆet qu’il a apport´e `a ce travail.

Merci `a M. Fran¸cois Desbouvries et M. Eric Moreau, pour avoir accept´e d’ˆetre rapporteurs et pour les pr´ecieuses suggestions qui ont aid´e `a enrichir ce travail.

Merci `a Jo˜ao C´esar Mota, pour m’avoir permis de participer au projet CAPES-COFECUB, pour avoir ´et´e examinateur de ce travail et pour ses remarques tr`es pertinantes.

Je tiens aussi `a remercier Ga¨el Mah´e, pour toutes nos discussions et sa grande motivation. Je ne remercierais jamais assez Cristiano, qui, en plus des discussions techniques en-richissantes, ´etait toujours l`a, `a mes cˆot´es, pendant toutes ces ann´ees. Merci pour son soutien, son attention, sa patience, qui m’ont ´et´e plus qu’indispensables pour mener `a bien ce travail.

Mes sinc`eres remerciements `a tous mes amis de labo, qui m’ont accompagn´e et qui m’ont soutenu pendant toutes ces ann´ees. Merci `a Issam, Valentina, Nicolas, Jacques, Rim, Djamel et, plus r´ecemment, Hela. Merci aussi `a Rodrigo, Danilo, Romis et Ricardo, pour leur aide et leur soutien.

Je remercie aussi, tr`es fortement, mes parents, Aloisio et Lourdiney et mes soeurs, Larissa et Leticia. Malgr´e la distance, je n’aurais pas pu r´eussir sans leur soutien constant.

Enfin je remercie Nellie, Christophe, Mme Voeuni Keng et M. Jacques Buttel, dont l’aide 5

m’a ´et´e indispensable et tous les membres de l’UFR de Math´ematiques et Informatique qui ont contribu´e `a rendre mon s´ejour ici tr`es agr´eable.

Ce travail aborde le probl`eme de l’identification de signaux et syst`emes, appliqu´e `a

des probl`emes de communications num´eriques. Contrairement aux m´ethodes classiques

d’optimisation stochastiques, nous proposons une approche alg´ebrique et d´eterministe. De plus, nous consid´erons les signaux et syst`emes sous leur forme temps-continu, ce qui nous permet d’exploiter certaines propri´et´es qui peuvent ˆetre cach´ees ou oubli´ees apr`es un pro-cessus d’´echantillonnage. Enfin, avec les m´ethodes alg´ebriques propos´ees, on abouti `a des techniques simples et rapides, qui permettent une impl´ementation en temps r´eel.

Dans un premier temps, nous abordons le probl`eme de correction des distorsions dans un syst`eme de communication par courant porteur, en utilisant la platitude du syst`eme repr´esent´e par la ligne ´electrique. Le syst`eme inverse de la ligne obtenu est, par la suite, utilis´e dans un autre contexte, notamment celui de la correction du timbre de la voix dans un r´eseau t´el´ephonique.

Dans un deuxi`eme temps, le probl`eme de l’identification est abord´e dans le cadre d’une nouvelle th´eorie d´eterministe de l’estimation reposant sur l’alg`ebre diff´erentielle et le calcul op´erationnel. Partant de cette th´eorie, nous avons d´evelopp´e un algorithme g´en´eral d’identifi-cation entr´ee-sortie d’un syst`eme rationnel. De plus, la rapidit´e des estimations nous permet-tent d’introduire une notion de filtrage local. Ce filtrage rend possible la repr´esentation d’un syst`eme de grande dimension par un mod`ele de dimension tr`es r´eduite (ordre un ou deux), variable par morceaux dans le temps. Cette mod´elisation est tr`es int´eressante car elle permet une d´emodulation directe des symboles transmis, sans n´ecessiter d’identifier/´egaliser explicitement le canal.

Finalement, le probl`eme de d´emodulation des signaux modul´es en fr´equence `a phase con-tinue, re¸cus `a travers un canal `a bruit additif, a aussi ´et´e abord´e `a la lumi`ere de ces techniques alg´ebriques. Notre d´emarche consiste `a d´ecrire le signal re¸cu, dans chaque intervalle symbole, par une ´equation diff´erentielle lin´eaire bruit´ee (en g´en´eral `a coefficients variables), dont les coefficients sont des fonctions du symbole courant. La d´emodulation symbole par symbole devient alors imm´ediate et particuli`erement robuste aux perturbations.

This thesis is concerned with the problem of signals and systems identification applied to digital communication. While the majority of the existing methods are stochastic, we propose an algebraic and deterministic approach. Moreover, we will treat signals and systems directly in continuous time, which enables us to explore the knowledge of their shape, that may be hidden or forgotten by the sampling operation. Furthermore, the proposed techniques are simple and rapid, what allows their on-line implementation.

Firstly, we consider the problem of correcting distortions in a power-line communication system, exploring its flatness property. The inverse system obtained is then applied to another context, more specifically to the restoration of the voice timbre in telephone networks.

Afterwards, the system identification problem is considered in the context of a new de-terministic theory, based on differential algebra and operational calculus. This theory gives rise to a new general algorithm for the input-output identification of a rational system. The rapidness of estimation also allows the presentation of the local filtering notion, which consists in representing a high dimension system by a time-varying low dimension model. This ap-proach is interesting since it permits the direct demodulation of the received signal, without the need of explicitly identifying or equalizing the channel.

Finally, the demodulation of a continuous phase modulation signal is addressed in the light of the algebraic techniques proposed. The solution consists in describing the received signal, at each symbol period, as a linear differential equation (generally with time-varying coefficients), with coefficients that are functions of the current symbol. Therefore, the symbol by symbol demodulation becomes immediate and particularly robust to noise.

1 Introduction 15

2 Pr´ecompensation des Distorsions dans un Syst`eme de Communication par

Courant Porteur 19

2.1 Introduction . . . 19

2.2 Pr´ecompensation d’une Ligne de Transmission . . . 21

2.2.1 Mod`ele du Syst`eme . . . 21

2.2.2 Obtention du Filtre de Pr´ecompensation . . . 22

2.2.3 R´esultats des Simulations . . . 23

2.3 Pr´ecompensation de 2 Lignes en Parall`ele . . . 26

2.3.1 Obtention du Filtre de Pr´ecompensation pour 2 Lignes . . . 27

2.3.2 R´esultats des Simulations . . . 32

2.4 Analyse de la Robustesse du Syst`eme . . . 33

2.5 Application: Restauration du Timbre de la Voix dans un R´eseau T´el´ephonique 35 2.5.1 Mod`ele du Syst`eme . . . 36

2.5.2 Egaliseur Spectrale Aveugle . . . .´ 37

2.5.3 Nouvelle M´ethode Propos´ee . . . 39

2.5.4 Comparaison des Deux M´ethodes . . . 41

2.5.5 Analyse du R´esultat . . . 44

2.6 Conclusion . . . 45

3 M´ethode Alg´ebrique d’Identification de Syst`eme 47 3.1 Introduction . . . 47

3.2 Etat-de-l’Art . . . .´ 49

3.2.1 M´ethodes Stochastiques . . . 50

3.2.2 M´ethodes D´eterministes . . . 51 11

3.3 Nouvelle M´ethode: Un Exemple Simple

d’Identification de Syst`eme . . . 52

3.4 G´en´eralisation de la M´ethode d’Identification de Syst`eme . . . 56

3.5 La M´ethode dans le Domaine Temporel . . . 58

3.6 Base Alg´ebrique pour l’Identification Lin´eaire . . . 60

3.6.1 D´efinitions de Base, Alg`ebre . . . 60

3.6.2 D´efinitions de Base, Alg`ebre Diff´erentielle . . . 61

3.6.3 Op´erateurs Diff´erentiels Lin´eaires . . . 62

3.6.4 Corps Diff´erentiel d’Op´erateurs de Mikusi´nski . . . 63

3.6.5 Identifiabilit´e . . . 65

3.6.6 Perturbations Structur´ees et Estimateurs Lin´eaires . . . 67

3.6.7 Perturbations Non-Structur´ees . . . 69

3.7 Mod`ele Utilis´e dans les Simulations . . . 72

3.8 Analyse de la M´ethode . . . 74

3.8.1 Excitation Persistante . . . 74

3.8.2 _{Le Conditionnement de la Matrice P . . . .} 76

3.8.3 Mod´elisation Exacte et Sur-Mod´elisation . . . 79

3.8.4 Sous-Mod´elisation . . . 80

3.8.5 Addition de Bruit . . . 82

3.9 Mod´elisation Locale du Syst`eme . . . 84

3.10 Interpr´etation de la M´ethode, Cas Sous-Mod´elis´e . . . 89

3.11 Identification Autodidacte d’un Syst`eme SIMO . . . 91

3.12 Conclusion . . . 94 4 M´ethodes d’´Egalisation 97 4.1 Introduction . . . 97 4.2 Le Probl`eme de l’´Egalisation . . . 98 4.2.1 La Chaˆıne de Communication . . . 98 4.2.2 Etat-de-l’Art . . . .´ 99

4.3 Validit´e du Mod`ele de Canal par Fonction de Transfert Rationnelle . . . 100

4.4 D´emodulation en Utilisant l’Estimation de la Fonction de Transfert du Canal 104 4.4.1 Domaine Fr´equentiel . . . 105

4.4.2 Domaine Temporel . . . 105

4.4.3 R´esultats des Simulations et Discussion . . . 107

4.5 D´emodulation avec Mod´elisation Locale du Canal . . . 114

4.5.2 D´efinition de u(t) . . . 116

4.5.3 Mod`ele Simul´e . . . 117

4.5.4 R´esultats des Simulations . . . 119

4.6 Conclusion . . . 122

5 D´emodulation des Signaux CPM 123 5.1 La Modulation en Fr´equence `a Phase Continue . . . 123

5.2 Le Spectre d’un Signal CPM . . . 126

5.3 Le R´ecepteur de Maximum Vraisemblance . . . 126

5.4 Performance du R´ecepteur de Maximum Vraisemblance . . . 130

5.5 Etat-de-l’Art . . . .´ 131

5.6 Modulation CPFSK . . . 132

5.6.1 D´emodulation Indirecte du Signal Re¸cu . . . 132

5.6.2 D´emodulation Directe du Signal Re¸cu . . . 138

5.6.3 R´esultats des Simulations . . . 140

5.7 Modulation LRC . . . 144

5.7.1 M´ethode DDS . . . 144

5.7.2 R´esultats des Simulations . . . 148

5.8 Conclusion . . . 150

6 Conclusion 153

Introduction

Le probl`eme de l’identification de syst`emes est important dans plusieurs disciplines. Il intervient par exemple dans la mod´elisation des ph´enom`enes naturels, dans les probl`emes de contrˆole d’un syst`eme ou, dans le cas des communications num´eriques, dans la r´ecup´eration de l’information transmise. Pour cette raison, beaucoup a ´et´e d´ej`a fait dans la litt´erature pour essayer de r´esoudre ce probl`eme. Dans le contexte des communications num´eriques, dans lequel nous nous pla¸cons dans ce travail, les m´ethodes existantes sont d´evelopp´ees dans le cadre th´eorique de l’optimisation stochastique et traitent les signaux et syst`emes en temps discret. Or, avec la demande croissante pour les services de communication `a des d´ebits de transmission de plus en plus ´elev´es, les retards de traitement inh´erents aux m´ethodes d’optimisation stochastiques peuvent repr´esenter un inconv´enient important. Dans ce contexte, une approche alg´ebrique et d´eterministe d´evient int´eressante. Mˆeme si le cadre d´eterministe a toujours ´et´e d´econsid´er´e essentiellement en raison de la sensibilit´e des m´ethodes aux bruits, une telle approche peut se r´ev´eler efficace lorsqu’elle est abord´ee dans un cadre th´eorique appropri´e. De plus, elle pr´esente l’avantage de s’affranchir des hypoth`eses classiques de connaissance a priori d’informations statistiques du bruit ou des signaux trait´es.

Dans ce sens, notre d´emarche s’inspire de certains outils et d´eveloppements courants en automatique mais tr`es peu usuels en traitement du signal. L’objectif vis´e est la correction de distorsions introduites dans un canal de communication. Nous ´etudions deux probl`emes dis-tincts, mais li´es par un objectif commun d’identifier un syst`eme et/ou d’estimer les param`etres d’un signal.

Nous commencerons, dans le chapitre 2, par aborder le probl`eme de correction des distor-sions dans un syst`eme par courant porteur. Ce syst`eme est int´eressant, vu qu’il repr´esente une des solutions possibles pour l’acc`es des derniers m`etres au r´eseau internet et, pour cette rai-son, ils ont ´et´e beaucoup ´etudi´es ces derni`eres ann´ees. Notre d´emarche s’inspire du syst`eme soliton en optique, dont le principe est de pr´ecompenser les distorsions introduites par le

canal. L’objectif est donc, le d´eveloppement d’un filtre, d´evant ˆetre plac´e dans l’´emetteur, pour pr´e-corriger les distorsions qui seront introduites par le syst`eme. Pour cela nous uti-lisons la platitude du syst`eme repr´esent´e par la ligne ´electrique. Le concept de platitude a ´et´e d´evelopp´e dans le domaine de l’automatique et il fait r´ef´erence aux syst`emes dont toutes les variables, le signal d’entr´ee inclus, peuvent ˆetre ´ecrites uniquement en fonction de la sortie du syst`eme et de ses d´eriv´ees.

Ainsi, d’apr`es ce qui a ´et´e fait en [FMPR98], le filtre, donn´e par la r´eponse en fr´equence inverse de la ligne ´electrique, sera obtenu en appliquant le calcul op´erationnel directement aux ´equations de mod`ele du syst`eme. Nous reprenons, donc, le d´eveloppement r´ealis´e dans

[FMPR98], o`u le syst`eme est donn´e par une seule ligne, et nous l’´etendrons pour le cas o`u

il est donn´e par deux lignes en parall`ele. De plus, la solution trouv´ee sera appliqu´ee dans un autre contexte, notamment celui de la restauration du timbre de la voix dans un r´eseaux t´el´ephonique, puisque ce dernier peut aussi ˆetre mod´elis´e comme une ligne ´electrique [MG01]. Dans un deuxi`eme temps, le probl`eme de l’identification entr´ee-sortie d’un syst`eme ra-tionnel sera abord´e dans le cadre d’une nouvelle th´eorie d´eterministe de l’estimation,

re-posant sur l’alg`ebre diff´erentielle et le calcul op´erationnel. Propos´ee premi`erement par

[FMMSR03, FSR03], nous partons de l’´etude de cette th´eorie pour pr´esenter une nouvelle m´ethode alg´ebrique et d´eterministe qui abouti aux faits suivants:

• Aucune information statistique du bruit n’est n´ecessaire

• Nous consid´erons les signaux sous leur forme temps continu, ce qui nous permet d’exploi-ter certaines propri´et´es

• Il n’y a aucune distinction de traitement entre les signaux stationnaires et non station-naires

• Les calculs peuvent ˆetre faits en temps r´eel

Le fait de consid´erer les signaux directement en temps continu, ce qui est tr`es peu usuel en traitement du signal, nous permet d’exploiter leur forme connue pour d´evelopper des m´ethodes tr`es rapides.

Le chapitre 3 sera d´edi´e `a la pr´esentation de cette th´eorie et au d´eveloppement d’une nou-velle m´ethode d’estimation/identification de syst`eme, obtenue `a partir de son application. Le syst`eme sera toujours mod´elis´e par une fonction de transfert rationnelle. Nous montrerons qu’il existe deux fa¸cons d’approcher le probl`eme. La premi`ere consiste `a trouver une approxi-mation du syst`eme complet, sous un angle global, bas´ee sur ses signaux d’entr´ee et de sortie. Dans ce cas, la connaissance, au moins approximative, de son ordre est importante pour avoir une bonne performance. D’autre part, la rapidit´e des estimations nous permet de pr´esenter

une deuxi`eme m´ethode d’identification, o`u le syst`eme est mod´elis´e localement. Dans ce cas, il est possible de repr´esenter un syst`eme de grande dimension par un mod`ele de dimension tr`es r´eduite (ordre un ou deux) variable par morceaux dans le temps. Ainsi, la connaissance de l’ordre du syst`eme n’est plus n´ecessaire. Cette mod´elisation est tr`es int´eressante pour le probl`eme de l’´egalisation. En effet, contrairement `a la d´emarche classique, elle permet une d´emodulation directe des symboles transmis, sans n´ecessiter d’identifier/´egaliser explicite-ment le canal. Enfin, les m´ethodes seront analys´ees en d´etail, ce qui inclut l’´etude de l’effet du bruit.

Ensuite, ces m´ethodes seront appliqu´ees `a l’estimation des canaux de communication et, l’information ainsi obtenue, sera utilis´ee pour d´emoduler le signal re¸cu. Cela sera ´etudi´e dans le chapitre 4. Nous allons d´evelopper deux m´ethodes de d´emodulation diff´erentes: une

premi`ere o`u le r´ecepteur a besoin d’une bonne estimation de la fonction de transfert du canal

et, par cons´equent, son ordre doit ˆetre connu, information qui n’est pas souvent disponible,

et une deuxi`eme o`u les symboles sont r´ecup´er´es directement. Dans ce cas, la m´ethode est

bas´ee sur une mod´elisation locale du canal et, ainsi, la connaissance de son ordre n’est plus n´ecessaire.

Le chapitre 5 abordera le probl`eme de d´emodulation de signaux modul´es en fr´equence `a phase continue (CPM-Continuous Phase Modulation), transmis `a travers un canal `a bruit ad-ditif, `a la lumi`ere de ces techniques alg´ebriques. Ces signaux sont particuli`erement int´eressants puisque leur modulation est non-lin´eaire et introduit de la m´emoire, ce qui rend difficile un traitement par les m´ethodes classiques. Le r´ecepteur optimal dans le sens des moindres carr´es est le r´ecepteur `a maximum de vraisemblance, dont la grande complexit´e, qui peut mˆeme devenir prohibitive, est un inconv´enient d´ej`a bien connu [Pro95]. Jusqu’`a aujourd’hui, l’utilisation des signaux CPM pour des alphabets A-aire avec des valeurs de A ´elev´ees, est rest´ee restreint `a cause de la complexit´e du r´ecepteur. Notre d´emarche consiste `a d´ecrire le signal re¸cu, dans chaque intervalle symbole, par une ´equation diff´erentielle lin´eaire bruit´ee (en g´en´eral `a coefficients variables), dont les coefficients sont des fonctions du symbole courant. La d´emodulation symbole par symbole devient alors imm´ediate et particuli`erement robuste aux perturbations.

Pr´

ecompensation des Distorsions dans

un Syst`

eme de Communication par

Courant Porteur

2.1

Introduction

Les syst`emes plats sont des syst`emes dont les variables, le signal d’entr´ee inclus, peuvent ˆetre ´ecrites uniquement en fonction de la sortie du syst`eme et de ses d´eriv´ees. Dans ce cas, nous disons que le syst`eme a une sortie plate [RFLM93]. Ce concept est couramment utilis´e dans le domaine d’automatique. Cette structure particuli`ere facilite la description du syst`eme et son traitement, permettant ainsi le d´eveloppement d’algorithmes et de solutions simples.

Supposons par exemple, un syst`eme lin´eaire d’´equations avec n + m param`etres inconnus

ξ = (x1, ..., xn, xn+1, ..., xn+m) = (x, xn+1, ..., xn+m) = (x, f ) qui s’´ecrit comme:

Ax + Bf = 0, B 6= 0, rang[A, B] = n

Si A est inversible et B est `a rang plein m, toutes les solutions pour x peuvent s’´ecrire comme fonction du vecteur inconnu f :

x_{= −A}−1Bf

c’est-`a-dire, toutes les solutions sont param´etr´ees en termes de f . Par ailleurs, comme la matrice B est `a rang plein, la variable f peut aussi s’exprimer en fonction des composantes de x, comme:

f _{= −(B}TB)−1BTAx

Ainsi, ce syst`eme lin´eaire a un ensemble privil´egi´e de variables f = (xn+1, ..., xn+m). Cet

ensemble de variables internes au syst`eme d’´equations peut ˆetre choisi de sorte que x prenne une valeur d´esir´ee quelconque, fix´ee `a l’avance. Si on regarde le syst`eme d’un point de vue entr´ee-sortie, avec une entr´ee x et une sortie f , on dira que le syst`eme est plat et, ainsi, f est une sortie plate. Par contre, si la matrice A n’est pas inversible, f sera ´egal `a z´ero pour quelque soit x appartenant au noyau de A. Comme cons´equence, il n’est plus vrai que les composantes de x peuvent ˆetre compl`etement param´etr´ees en termes de f . Nous voyons, donc, comment la propri´et´e de platitude, pr´esente quand A est inversible, facilite l’obtention des solutions recherch´ees.

En ramenant ce concept au domaine du traitement du signal, les syst`emes plats sont tr`es int´eressants vu qu’ils permettent l’´egalisation autodidacte. Celle-ci consiste `a r´ecup´erer les symboles transmis par un syst`eme de communication en n’observant que la sortie du syst`eme et en connaissant quelques caract´eristiques statistiques du signal d’entr´ee. Si toutes les variables du syst`eme peuvent ˆetre ´ecrites en fonction de sa sortie, il est clair que le syst`eme pourra ˆetre ´egalis´e de fa¸con aveugle. Il faut observer, cependant, que, en traitement du signal, en g´en´eral le syst`eme est trait´e en temps discret et le concept de platitude est d´efinie seulement pour les syst`emes en temps continu. L’´equivalent discret serait d’avoir un syst`eme

o`u les variables (param`etres du canal et signal d’entr´ee) peuvent ˆetre ´ecrites en fonction de

la sortie du canal `a l’instant actuel et de ses ´echantillons pass´es.

Dans ce chapitre nous allons ´etudier un exemple de syst`eme plat `a param`etre distribu´es, donn´e par la transmission d’information sur une ligne ´electrique. Notre but sera de pr´ecompen-ser le signal `a transmettre, en utilisant un filtre `a l’´emetteur, pour que la r´eception soit plus simple. L’id´eal serait que, `a la sortie de la ligne, nous ayons le signal originalement transmis.

Cet exemple est aussi int´eressant dans la mesure o`u les syst`emes de communication par

courant porteur ont ´et´e l’objet de nombreuses ´etudes ces derni`eres ann´ees, en essayant de r´epondre `a un nouveau d´efi : quelle serait la meilleure technique pour les derniers m`etres du r´eseau internet (last miles), en incluant la facilit´e d’impl´ementation, prix, d´ebit et mobilit´e, parmi d’autres. Plusieurs solutions ont ´et´e propos´ees comme les r´eseaux personnels sans fils du type Bluetooth et Wi-Fi. Dans ce contexte, le r´eseau ´electrique de basse tension repr´esente

aussi une solution int´eressante, principalement dˆu `a son faible coˆut d’impl´ementation, vu que

les cˆables sont d´ej`a install´es et disponibles. De plus, presque toutes les pi`eces d’une maison ou d’un bureau ont au moins une prise ´electrique, ce qui facilite l’acc`es.

Ainsi, il est int´eressant d’´etudier des m´ethodes pour permettre une communication fiable en utilisant ce r´eseau. Nous allons, donc, essayer de corriger les distorsions introduites par une ligne ´electrique, tels que l’att´enuation et les r´eflexions dues `a la non homog´en´eit´e des diff´erentes portions de la ligne. Il faut observer qu’il existe aussi d’autres perturbations

comme le bruit de nature impulsionnelle [GD02] et l’effet de peau [WGS02] qui ne seront pas trait´ees ici. La mod´elisation du canal, donn´e par la ligne de transmission, prend en compte le ph´enom`ene physique de la propagation. Nous obtenons un syst`eme `a param`etres r´epartis, r´egi par une ´equation aux d´eriv´es partielles. Cette mod´elisation est int´eressante en raison de sa parcimonie (un nombre tr`es limit´e de param`etres) d’une part et en ce qu’elle est proche de la r´ealit´e physique du ph´enom`ene ´etudi´e. Le syst`eme sera toujours trait´e en temps continu. La m´ethode a premi`erement ´et´e propos´ee par [FMPR98] pour le cas de la transmission d’un signal t´el´egraphique par une ligne de transmission. Nous avons ´etendu ses r´esultats pour la transmission d’autres types de signaux et aussi pour un cas simple de trajet multiple,

o`u le signal est re¸cu par deux morceaux de ligne avec des param`etres diff´erents. L’analyse

de la m´ethode nous a montr´e qu’elle a aussi une bonne robustesse `a des erreurs d’estimation des param`etres de la ligne, ce qui est important vu que le canal n’est normalement pas connu `a l’´emetteur.

De plus, la m´ethode de pr´ecompensation propos´ee peut aussi avoir d’autres applications. Un exemple donn´e ici est la restauration du timbre de la voix dans un r´eseau t´el´ephonique, mod´elis´e comme une ligne de transmission. La m´ethode a ´et´e utilis´ee avec l’´egaliseur spectrale aveugle propos´e par [MG01, Mah02]. Nous allons montrer comment la nouvelle technique [NMM04] apporte un gain de performance significatif par rapport `a l’´egaliseur de [MG01, Mah02].

2.2

Pr´

ecompensation d’une Ligne de Transmission

2.2.1

Mod`

ele du Syst`

eme

Le syst`eme de pr´ecompensation ´etudi´e est montr´e dans la figure 2.1. o`u u(t) est le signal

Figure 2.1: Syst`eme de pr´ecompensation

transmis, z(t) est le signal pr´ecompens´e et y(t) est le signal re¸cu. Le but est d’avoir une sortie y(t) sans distorsion par rapport `a u(t), `a l’aide du filtre de pr´ecompensation. Autrement dit, le filtre de pr´ecompensation id´eal serait l’inverse exacte du canal. Il peut ˆetre vu comme un ´egaliseur plac´e `a l’´emetteur.

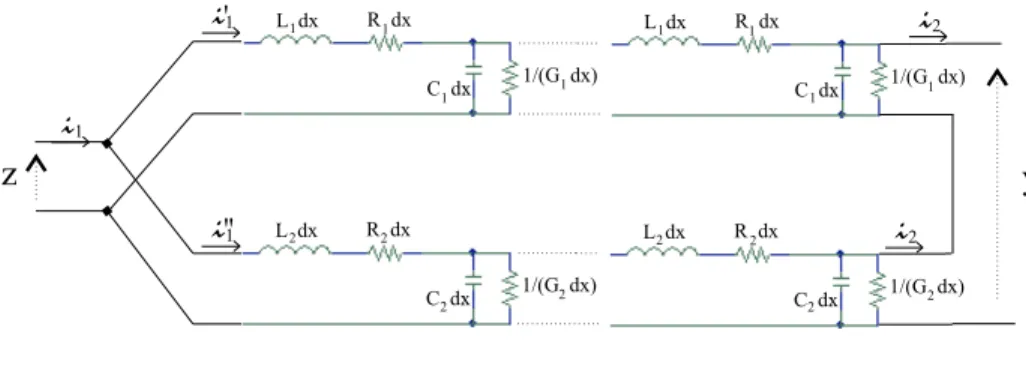
Le canal est mod´elis´e comme une ligne de transmission, montr´e dans la figure 2.2. Elle consiste en une cascade de cellules, chacune compos´ee d’une inductance Ldx, une

Figure 2.2: Mod`ele de ligne ´electrique

r´esistance Rdx, une capacit´e Cdx et une perditance Gdx. La valeur des param`etres R, L, C et G est donn´ee en unit´e S.I., par unit´e de longueur.

Ce mod`ele peut aussi ˆetre d´ecrit selon le syst`eme d’´equations aux d´eriv´ees partielles ci-dessous: L∂i ∂t = −Ri − ∂v ∂x C∂v ∂t = − ∂i ∂x − Gv (2.1)

o`u v(x, t) et i(x, t) sont respectivement la tension et le courant `a une distance x de l’origine

de la ligne et au temps t. Le signal d’entr´ee du canal, z(t), est la tension en d´ebut de ligne,

i.e. z(t) = v(0, t) et la sortie, y(t), est la tension en bout de ligne, i.e. y(t) = v(ℓ, t) o`u ℓ

d´esigne la longueur de la ligne.

2.2.2

Obtention du Filtre de Pr´

ecompensation

Le filtre de pr´ecompensation pour une ligne de transmission a ´et´e propos´e premi`erement par [FMPR98]. Dans cette section, nous reprenons ce qui a ´et´e fait.

A partir du syst`eme d’´equations (2.1), avec quelques manipulations, nous pouvons obtenir l’´equation des t´el´egraphistes :

∂2_{v(x, t)} ∂x2 = µ R + L∂ ∂t ¶ µ G + C ∂ ∂t ¶ v(x, t) (2.2)

avec, comme conditions au bords,

v(0, t) = z(t) v(ℓ, t) = Zi(ℓ, t)

o`u Z est l’imp´edance au bout de la ligne, et avec des conditions initiales nulles, c’est-`a-dire,

v(x, 0) = (∂v/∂t)(x, 0) = 0

En utilisant le calcul op´erationnel [Mik83] (transform´ee de Laplace) pour transformer (2.2) en une ´equation diff´erentielle ordinaire, avec, comme variable ind´ependante, la longueur x,

transform´ees de Laplace de z(t), y(t) et v(x, t) respectivement: ˆ z =  ch³ℓpβ(s)´+R + Ls Z sh³ℓpβ(s)´ p β(s)   ˆy (2.3) o`u β(s) = LCs2_{+ (RC + LG)s + RG.}

La solution dans le domaine temporel peut ˆetre trouv´ee grˆace `a l’application de la trans-form´ee inverse de Laplace `a (2.3). En consid´erant G = 0 pour simplifier les calculs, nous avons: z(t) = 1 2e −αλ Ã 1 − _Z1 r L C ! y(t − λ) + 1₂eαλ Ã 1 + 1 Z r L C ! y(t + λ) + Z +λ −λ · R 4Z√LCe −ατ_J 0 ³ iα√τ2_{− λ}2´ + e−ατiα 2√τ2_{− λ}2 Ã λ − 1 Z r L Cτ ! J1 ³ iα√τ2_{− λ}2´ # y(t − τ)dτ (2.4)

o`u α = R/(2L), λ = ℓ√LC, J0 et J1 sont les fonctions de Bessel de premi`eres esp`eces d’ordre

0 et 1 et τ ∈ [t − λ, t + λ].

Ainsi, comme nous voulons que la sortie y(t) soit la plus proche possible du signal ori-ginalement transmis, u(t), il suffit de calculer le signal d’entr´ee pr´ecompens´e, z(t), par (2.4) en rempla¸cant y(t) par u(t) (voir figure 2.1). Autrement dit, (2.3) repr´esente l’inverse de la fonction de transfert du canal, mod´elis´e comme une ligne de transmission. Il faut observer que, comme nous sommes plac´es dans l’´emetteur, le fait de connaˆıtre u(t) ne pose pas de probl`eme.

2.2.3

R´

esultats des Simulations

Les simulations ci-dessous illustrent la performance du syst`eme et aident aussi `a la compr´ehension de la m´ethode. La figure 2.3 montre comment la ligne de transmission d´eforme le signal d’entr´ee u(t) (sans pr´ecompensation). Les valeurs des param`etres de la ligne sont

R = 2.16 × 10−3_{, L = 18.42 × 10}−7_{, C = 1.8 × 10}−11_{, Z = 100 et ℓ = 10}6_{, en unit´es S.I}

[FMPR98]. Cette simulation a ´et´e r´ealis´ee avec le logiciel PSpice, en utilisant 4 cellules en

cascade, chacune de longueur ℓ = 2.5 × 105_.

Pour avoir, `a la sortie, un signal sans distorsion et le plus proche possible du signal transmis u(t), nous utilisons le filtre de pr´ecompensation. Le nouveau signal d’entr´ee du canal, z(t), donn´e par (2.4) en rempla¸cant y(t) par u(t), est montr´e `a la figure 2.4 (a). Dans

0 0.02 0.04 0.06 0.08 0.1 0.12 0 0.2 0.4 0.6 0.8 1 Temps u(t) 0 0.02 0.04 0.06 0.08 0.1 0.12 0 0.02 0.04 Temps y(t)

Figure 2.3: Transmission par une ligne ´electrique, sans pr´ecompensation

ce cas, la sortie de la ligne est montr´ee `a la figure 2.4 (b). Nous pouvons observer que, `a un facteur d’´echelle pr`es, le signal y(t) obtenu est tr`es proche du signal initialement transmis, u(t) (montr´e `a la figure 2.3).

0 0.02 0.04 0.06 0.08 0.1 0.12 −1 −0.5 0 0.5 1 1.5 2 Temps (a) z (t) 0 0.02 0.04 0.06 0.08 0.1 0.12 −0.01 0 0.01 0.02 0.03 Temps (b) y(t)

Figure 2.4: (a) Entr´ee avec pr´ecompensation z(t); (b) Sortie du syst`eme, y(t), ayant z(t) comme entr´ee

dans les syst`emes de communication. Ce signal est g´en´er´e par le filtrage d’une s´equence de

symboles 2-PAM (Pulse Amplitude Modulation), o`<sub>u chaque symbole appartient `a {−1, +1},</sub>

par un filtre en cosinus sur-´elev´e. Math´ematiquement nous avons: u(t) =

n

X

k=0

νkg(t − kT ) (2.5)

o`u νksont les symboles transmis et g(t) est l’impulsion de mise-en-forme du signal donn´e par

le cosinus sur-´elev´e:

g(t) = sinc(t)cos(παt)

1 − 4α2_t2

o`u sinc(t) est la fonction sinus cardinale et α est le facteur de roll-off. Pour les simulations

qui suivent, α a ´et´e pris ´egal `a 0.33.

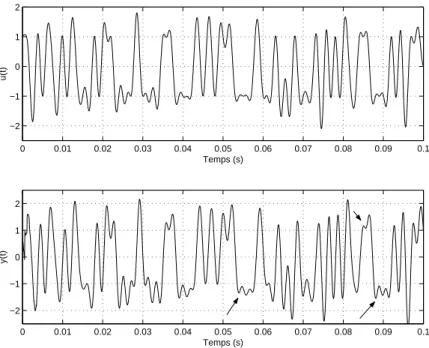
La figure 2.5 montre le cas o`u u(t) n’a pas ´et´e pr´ecompens´e. La d´eformation de y(t)

caus´ee par la ligne de transmission est clair. Les fl`eches indiquent un exemple d’instant o`u

la diff´erence entre le signal original, u(t), et la sortie, y(t), est importante.

Il faut aussi noter que, comme dans le cas pr´ec´edent (figure 2.3), la ligne de transmission introduit un retard. Le signal y(t) dans la figure 2.5 a ´et´e d´ecal´e pour faciliter la comparaison avec u(t). 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −2 −1 0 1 2 Temps (s) u(t) 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −0.05 0 0.05 Temps (s) y(t)

Figure 2.5: Transmission sans pr´ecompensation, u(t) 2-PAM

Le signal d’entr´ee du canal pr´ecompens´e, z(t), obtenu par (2.4), est montr´e dans la figure 2.6. La figure 2.7, montre le signal de sortie de la ligne ayant comme signal d’entr´ee z(t). Le signal d’entr´ee original, u(t), est montr´e dans la mˆeme figure pour faciliter la

comparai-Figure 2.6: Le signal pr´ecompens´e obtenu par (2.4)

son. Nous pouvons observer que, malgr´e la grande diff´erence d’amplitude, les deux signaux sont presque pareils, au contraire de la situation montr´ee dans la figure 2.5. Quelques pe-tites diff´erences peuvent encore ˆetre trouv´ees, comme montr´e par les fl`eches, mais elles ne compromettent pas la bonne performance du syst`eme. Si on calcule l’erreur quadratique

moyenne relative ky(t) − u(t)k2/ku(t)k2 pour le cas sans pr´ecompensation (figure 2.5) et avec

pr´ecompensation (figure 2.7), nous obtenons 0.2685 dans le premier et 1.2 × 10−4 _{dans le}

deuxi`eme. Le gain de performance est donc clair. Il faut observer aussi qu’au d´ebut du

signal de sortie `a la figure 2.7, jusqu’`a `a-peu-pr`es 0.007s, il y a une p´eriode de transition o`u

le signal de sortie y(t) est constant. Cet intervalle peut paraˆıtre un peu long mais il est dˆu

aussi au retard introduit par la ligne de transmission.

2.3

Pr´

ecompensation de 2 Lignes en Parall`

ele

D’apr`es la bonne performance de la m´ethode propos´ee par [FMPR98], montr´ee `a la section

2.2, nous traiterons un cas simple de trajet multiple o`u le canal sera mod´elis´e par deux lignes

de transmission en parall`ele. Ainsi, le mˆeme signal arrivera par deux chemins diff´erents, parcourant deux lignes avec des param`etres et des longueurs diff´erents. Le signal re¸cu sera donn´e par la somme de la sortie de ces deux lignes. Dans ce cas, la distorsion de y(t) sera plus importante que dans le cas d’une seule ligne, puisqu’il sera donn´e par la somme de deux

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −2 −1 0 1 2 Temps (s) u(t)

Signal d’entrée original

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −0.05 0 0.05 0.1 Temps (s) y(t)

Signal de sortie avec précompensation

Figure 2.7: Sortie de la ligne ayant, comme entr´ee, le signal pr´ecompens´e z(t)

signaux qui ont souffert des distorsions (att´enuation et l’effet des r´eflexions) diff´erentes et qui ont des retards distincts.

2.3.1

Obtention du Filtre de Pr´

ecompensation pour 2 Lignes

Le canal a ´et´e mod´elis´e par deux lignes de transmission diff´erentes en parall`ele, comme montr´e `a la figure 2.8. Les deux ont le mˆeme signal d’entr´ee pr´ecompens´e, z(t), et le signal de sortie y(t) est donn´e par la somme de la sortie de chaque ligne. Il est clair que chaque ligne satisfait le syst`eme d’´equations (2.1).

Figure 2.8: Le syst`eme en ´etude

Le filtre de pr´ecompensation sera, donc, donn´e par l’inverse du syst`eme ´equivalent com-pos´e par les deux lignes en parall`ele. Ainsi, nous devrons, premi`erement, obtenir ce syst`eme

´equivalent. Pour cela, nous pouvons voir chaque ligne comme ´etant un quadripole, c’est-`a-dire, une boite ferm´ee avec deux entr´ees et deux sorties, comme montr´e dans la figure 2.9.

La matrice de transfert 1 _{de ce quadripole, not´ee Q, est d´efinie par}

Figure 2.9: Quadripole à ˆ z ˆı1 ! = " q11 q12 q21 q22 # | {z } Q à ˆ y ˆı2 ! (2.6)

o`u i1 est le courant `a l’entr´ee du syst`eme et i2 est le courant `a la sortie. Notez que l’´equation

est ´ecrite dans le domaine fr´equentiel.

Ainsi, en utilisant des quadripoles, le syst`eme montr´e dans la figure 2.8 peut ˆetre vu comme celui montr´e dans la figure 2.10.

Figure 2.10: Deux quadripoles en parall`ele

Nous voulons, alors, trouver le quadripole ´equivalent, d´enot´e QT, qui nous permettra

d’obtenir directement z(t) en fonction de y(t) pour le syst`eme montr´e `a la figure 2.10. Cepen-dant, pour d´eterminer ses param`etres, il est plus commode d’utiliser une repr´esentation mixte. La repr´esentation mixte d’un quadripole, par exemple celui de la figure 2.9, est donn´ee `a l’aide

1_{Notons que dans la terminologie du traitement du signal, cette matrice Q repr´esente l’inverse de la}

d’une matrice M , d´efinie par à ˆ z ˆı2 ! = " m11 m12 m21 m22 # | {z } M à ˆı1 ˆ y ! (2.7)

Avec cette repr´esentation, la matrice MT du quadripole ´equivalent correspondant au syst`eme

de la figure 2.10 peut ˆetre facilement obtenue en faisant

M_T−1 = M₁−1+ M₂−1 (2.8)

o`u M1 est la matrice du premier quadripole et M2 celle du deuxi`eme. Comme ce que nous

voulons est le rapport entre z(t) et y(t), apr`es avoir trouv´e MT, nous utiliserons cette

infor-mation pour revenir `a la repr´esentation par matrice de transfert et trouver QT. Cela peut

ˆetre fait en utilisant la relation entre Q et M donn´ee par:

q11 = m12− m11_m21m22 q12 = m11 m21 q21 = −m_m2122 q22 = 1 m21 (2.9) Pour faciliter les calculs, dans le d´eveloppement qui suit, G a ´et´e prise ´egale `a z´ero.

Repr´esentation Mixte du Quadripole ´Equivalent

Pour d´eterminer MT, premi`erement nous avons besoin de trouver la matrice M , donn´ee

par (2.7), pour chaque ligne de transmission du syst`eme. Cela signifie trouver la tension d’entr´ee en fonction du courant d’entr´ee et de la tension de sortie de chaque ligne `a l’aide de

(2.1). En utilisant le calcul op´erationnel et en posant ˆv(ℓ, s) = Zˆı(ℓ, s), x = 0 et ˆz = ˆv(0, s),

(2.1) nous donne: ˆ v(0, s) = ˆz = ˆv(ℓ, s)ch(ℓpβ(s)) + (R + Ls)ˆı(ℓ, s)p β(s) sh(ℓ p β(s)) (2.10)

De la mˆeme fa¸con, nous pouvons aussi trouver le courant au d´ebut de la ligne, ˆı(0, s) comme fonction du courant et de la tension `a sa sortie. En faisant x = 0, nous trouvons:

ˆı(0, s) = ˆı(ℓ, s)ch(ℓpβ(s)) + v(ℓ, s)ˆ p β(s) (Ls + R) sh(ℓ p β(s)) (2.11)

donc: M = 1 ch(ℓpβ(s))   Ls+R √ β(s)sh(ℓ p β(s)) 1 1 − √ β(s) Ls+R sh(ℓ p β(s))   (2.12)

Ainsi, avec (2.8), nous trouvons la repr´esentation mixte du quadripole ´equivalent. L’inverse de la matrice M ci-dessus est :

M−1 = 1 ch(ℓpβ(s))   √ β(s) Ls+Rsh(ℓ p β(s)) 1 1 −(Ls+R)√ β(s) sh(ℓ p β(s))   (2.13)

L’inverse de l’addition des deux matrices, M₁−1 et M₂−1, o`u les sous-indices correspondent

`a la ligne en question, nous donne la matrice recherch´ee, MT :

MT = 1 D   L√1s+R1 β1(s)sh1ch2+ L√2s+R2 β2(s)sh2ch1 ch1+ ch2 ch1+ ch2 − √ β1(s) L1s+R1 sh1ch2− √ β2(s) L2s+R2sh2ch1   (2.14) o`u ch1 = cosh(ℓ1 p β1(s)); ch2 = cosh(ℓ2 p β2(s)) (2.15) sh1 = sinh(ℓ1 p β1(s)); sh2 = sinh(ℓ2 p β2(s)) et D = 2 + 2ch1ch2+ sh1sh2 " (L2s + R2) p β1(s) (L1s + R1) p β2(s) +(L1s + R1) p β2(s) (L2s + R2) p β1(s) #

La Matrice de Transfert du Quadripole ´Equivalent

Une fois que nous avons MT, la matrice de transfert du quadripole ´equivalent, QT, peut

ˆetre trouv´ee facilement en utilisant (2.9) :

QT = 1 ch1+ ch2   ch1ch2 L√1s+R1 β1(s)sh1ch2+ L√2s+R2 β2(s)sh2ch1 −√β1(s) L1s+R1 sh1ch2− √ β2(s) L2s+R2sh2ch1 D   (2.16)

Avec (2.16) et en consid´erant que ˆy = Zˆı2, o`u Z est l’imp´edance `a la sortie du syst`eme

´equivalent, le rapport qui nous int´eresse, entre ˆz et ˆy est donn´e par:

ˆ z = · ch1ch2+ (L1s + R1) Z√β1 sh1ch2+ (L2s + R2) Z√β2 sh2ch1 ¸ ˆ y ch1+ ch2 (2.17)

Pour simplifier ce r´esultat, nous pouvons consid´erer deux cas diff´erents:

• Les deux lignes de transmission ont les mˆemes param`etres R, L et C (en rappelant que

G = 0) mais ont des longueurs diff´erentes, c’est-`a-dire, β1 = β2 = β et ℓ1 6= ℓ2. Dans

ce cas, (2.17) peut ˆetre simplifi´e:

ˆ z= yˆ ch(ℓ1√β)+ch(ℓ2√β) h ch¡√β(ℓ1+ ℓ2)¢+(R+Ls)_Z√_β sh¡√β(ℓ1+ ℓ2)¢− sh¡ℓ1√β¢sh¡ℓ2√β¢i (2.18) • Les deux lignes ont la mˆeme longueur mais les param`etres sont diff´erents, c’est-`a-dire,

ℓ1 = ℓ2 = ℓ et β1 6= β2. Le r´esultat sera alors:

ˆ z = yˆ ch¡ℓ√β1 ¢ + ch¡ℓ√β2 ¢ h ch¡ℓ¡√β1+√β2 ¢¢ +³(R1+L1s) Z√β1 + (R2+L2s) Z√β2 ´ sh¡ℓ¡√β1+√β2 ¢¢ +³(R1+L1s) Z√β1 − (R2+L2s) Z√β2 ´ sh¡ℓ¡√β1−√β2 ¢¢ − sh¡ℓ√β1 ¢ sh¡ℓ√β2 ¢i (2.19)

Nous avons, ainsi, la r´eponse en fr´equence du filtre de pr´ecompensation recherch´e. En utilisant le calcul op´erationnel [Yos84, Mik83], il est possible de trouver la r´eponse de ce filtre

dans le domaine temporel, au moins pour le cas le plus simple, o`u les deux lignes ont les

mˆemes param`etres et des longueurs diff´erentes. La transform´ee inverse de Laplace de (2.18) est donc : z(t) = e−αλ 2 µ 0.5 − Z1 q L C ¶ y<sub>(t − λ) +</sub>eαλ<sub>2</sub> µ 0.5 + <sub>Z</sub>1q<sub>C</sub>L ¶ y(t + λ) +e−αλ ′ 4 y(t − λ ′ ) +eαλ′<sub>4</sub> y(t + λ′<sub>)</sub> + Z +λ −λ h R 4Z√LCe −ατ<sub>J</sub> 0 ¡ iα√τ2<sub>− λ</sub>2¢<sub>+</sub> e−ατiα 2√τ2 −λ2 ³ λ 2− 1 Z q L Cτ ´ J1 ¡ iα√τ2<sub>− λ</sub>2¢i<sub>y(t − τ)</sub> + λ′( λ0 λ−1) 4 q τ2<sub>(</sub>λ0 λ−1) 2 −(λ′<sub>)</sub>2e −ατ(λ0λ−1)iαJ 1 µ iα q τ2¡λ0 λ − 1 ¢2 − (λ′<sub>)</sub>2 ¶ y¡t− τ¡λ0 λ − 1 ¢¢ dτ (2.20) o`u α = R/(2L), λ = (ℓ1 + ℓ2) √ LC, λ′ _{= (ℓ} 1 − ℓ2) √ LC, λ0 = 2ℓ1 √ LC, J0 et J1 sont les

fonctions de Bessel de premi`eres esp`eces d’ordre 0 et 1 et, enfin, τ ∈ [t − λ, t + λ].

Nous avons, donc trait´e le cas o`u il y a deux lignes en parall`ele. La g´en´eralisation pour

un nombre quelconque de lignes est directe. La d´emarche `a suivre est la mˆeme, mˆeme si la complexit´e de calcul pour l’obtention du quadripole ´equivalent augmentera.

2.3.2

R´

esultats des Simulations

Nous allons, maintenant, refaire les simulations montr´ees dans la section 2.2.3, pour le cas des deux lignes de transmission en parall`ele. Dans ce cas, les simulations ont ´et´e faites avec Matlab au lieu de PSpice.

La figure 2.11 montre la d´eformation caus´ee au signal transmis, u(t) par les deux lignes

en parall`ele, dans le cas o`u elles ont les mˆemes param`etres et des longueurs diff´erentes. Les

valeurs des param`etres utilis´ees sont celles de la section 2.2.3. La longueur de la premi`ere

ligne est ℓ1 = 2 × 104 et de la deuxi`eme, ℓ2 = 104. Le signal u(t) a ´et´e obtenu par (2.5).

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −2 −1 0 1 2 u(t) Temps (s) 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −2 −1 0 1 2 Temps (s) y(t)

Figure 2.11: Transmission par deux lignes ´electriques en parall`ele, sans pr´ecompensation

La d´eformation caus´ee par le canal est claire. Les fl`eches indiquent des instants o`u la

diff´erence entre le signal original, u(t), et la sortie, y(t), est importante.

Nous voulons, alors, pr´ecompenser les distorsions introduites par le canal, en modifiant le signal d’entr´ee. Cela peut ˆetre fait en utilisant l’´equation (2.20) avec la substitution de y(t) par u(t), qui est la sortie d´esir´ee. La figure 2.12 montre la sortie du syst`eme, y(t), ayant comme entr´ee le signal pr´ecompens´e, z(t). Le signal d’entr´ee original, u(t), est montr´e dans la mˆeme figure afin de faciliter la comparaison. Nous pouvons voir que les deux signaux sont presque pareils, `a un facteur d’´echelle pr`es.

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −0.4 −0.2 0 0.2 0.4 0.6 Temps (s) y(t)

Signal de sortie avec précompensation

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 −2 −1 0 1 2 u(t)

Signal d’entrée original

Figure 2.12: Sortie du canal ayant, comme entr´ee, le signal pr´ecompens´e

2.4

Analyse de la Robustesse du Syst`

eme

Dans toutes les simulations pr´ec´edentes, les param`etres des lignes ´etaient consid´er´es comme parfaitement connus. Cependant, normalement le canal n’est pas connu `a l’´emetteur. Mˆeme si les lignes de transmission satisfont certaines normes et ont des param`etres, en moyenne, connus, leurs valeurs exactes peuvent varier. Pour cette raison, il est int´eressant d’analyser l’effet des erreurs dans l’estimation de ces param`etres dans la performance du syst`eme.

Ensuite nous avons utilis´e deux m´ethodes diff´erentes pour mesurer cet effet. La premi`ere consiste `a calculer l’erreur quadratique (EQ) entre le signal d’entr´ee du syst`eme, u(t), et le signal de sortie, y(t), rapport´e `a la puissance de u(t), ce qui nous permet de quantifier la diff´erence entre les deux. En effet, cette erreur sera ´equivalent `a l’erreur relative (ky(t) −

u(t)k2/ku(t)k2) puisque ku(t)k2 est `a peu pr`es ´egale `a 1 (u(t) a une modulation 2-PAM).

Pour la simulation qui suit, les lignes de transmission ont les mˆemes param`etres que celle de

la section 2.2.3. Pour le cas o`u le canal est donn´e par une seule ligne, la longueur utilis´ee

´etait de ℓ = 106 _{et, pour le cas des deux lignes en parall`ele, nous avons, une fois de plus,}

consid´er´e le cas o`u elles ont les mˆemes param`etres mais des longueurs diff´erentes, donn´ees

par ℓ1 = 2 × 104 et ℓ2 = 104. Le signal u(t) a ´et´e obtenu par (2.5). La variation de la valeur

des param`etres ´etaient de 10% et de 20% autour de la valeur correcte. La table 2.1 montre les r´esultats obtenus. Chacune des trois derni`eres lignes de la table repr´esente l’EQ suite `a

une erreur d’estimation sur le param`etre indiqu´e.

Nous pouvons observer que, tant pour le cas d’une seule ligne que pour le cas de deux lignes, l’EQ a la mˆeme ordre de grandeur pour tous les param`etres. L’EQ minimum a ´et´e

obtenue avec des variations sur la valeur de la capacit´e, ce qui est aussi dˆu `a sa faible valeur

originale. Le plus important, toutefois, est que l’EQ ´etait toujours suffisamment faible pour

garantir la r´ecup´eration du signal envoy´e `a la sortie du canal. `A titre de comparaison, l’EQ

entre le signal d’entr´ee u(t) et le signal de sortie y(t) sans aucune erreur d’estimation est de

7.78 × 10−4 _{pour le cas d’une seule ligne et de 1.7 × 10}−3 _{pour les deux lignes en parall`ele.}

Canal: 1 ligne Canal: 2 lignes

Param`etres

10 % 20 % 10 % 20 %

R 0.0070 0.0271 0.0033 0.0037

L 0.0042 0.0136 0.0055 0.0091

C 0.0043 0.0085 0.0027 0.0031

Table 2.1: EQ pour des erreurs dans l’estimation des param`etres

La deuxi`eme m´ethode consiste `a calculer l’interf´erence entre symboles (IES) `a la sortie de la ligne. L’interf´erence entre symboles apparaˆıt `a cause de l’´etalement de l’impulsion

transmise dˆu `a la nature dispersive du canal, ce qui r´esulte en une superposition des symboles

adjacents. En d´enotant c le vecteur de la r´eponse impulsionnelle du syst`eme ´equivalent ´echantillonn´ee `a la cadence de symbole, l’IES peut ˆetre calcul´ee de la fa¸con suivante:

IES = P

ic2i − (max{c})

2

(max{c})2 (2.21)

La r´eponse impulsionnelle du syst`eme ´equivalent est donn´ee par la convolution de la r´eponse du filtre de pr´ecompensation avec celle du canal.

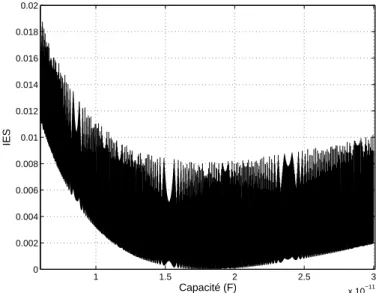
Les figures 2.13, 2.14 et 2.15 montrent l’IES r´esiduelle obtenue pour une certaine plage des valeurs possibles autour de la valeur exacte pour la r´esistance, l’inductance et la ca-pacit´e respectivement. Les param`etres du canal ´etaient les mˆemes utilis´es dans la simulation

pr´ec´edente. Seulement le cas d’une seule ligne a ´et´e consid´er´e. `A titre de comparaison, l’IES

r´esultante pour le cas de la pr´ecompensation avec des param`etres exacts est ´egale `a 5.7×10−5_.

Nous pouvons, ainsi, confirmer les r´esultats obtenus dans les simulations pr´ec´edentes. Pour des variations jusqu’`a 30% autour de la valeur exacte des param`etres, l’IES reste suf-fisamment faible pour permettre une bonne r´ecup´eration des symboles transmis.

0.5 1 1.5 2 2.5 3 3.5 4 x 10−3 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 Resistance (Ω) IES

Figure 2.13: IES pour l’erreur dans l’estimation de la r´esistance

0.5 1 1.5 2 2.5 3 3.5 4 x 10−6 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 Inductance (H) IES

Figure 2.14: IES pour l’erreur dans l’estimation de l’inductance

2.5

Application: Restauration du Timbre de la Voix

dans un R´

eseau T´

el´

ephonique

Nous allons, maintenant, appliquer la technique d´evelopp´ee dans un probl`eme de restau-ration du timbre de la voix dans un r´eseau t´el´ephonique. Les lignes analogiques de ce r´eseau peuvent ˆetre mod´elis´ees comme des lignes de transmission qui satisfont (2.1). Dans ce con-texte, nous avons utilis´e la m´ethode de pr´ecompensation coupl´ee avec l’´egaliseur spectrale aveugle d´evelopp´e par Mah´e en [MG01, Mah02] pour am´eliorer sa performance.

1 1.5 2 2.5 3 x 10−11 0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02 Capacité (F) IES

Figure 2.15: IES pour l’erreur dans l’estimation de la capacit´e

Figure 2.16: Liaison t´el´ephonique avec l’´egaliseur

2.5.1

Mod`

ele du Syst`

eme

La figure 2.16 pr´esente une liaison R´eseau T´el´ephonique Commut´e (RTC): chaque utilisa-teur est reli´e par une ligne analogique au central t´el´ephonique le plus proche, et la liaison entre les centraux emprunte un r´eseau enti`erement num´erique. Nous consid´erons que la transmis-sion num´erique est sans erreur et que les distortransmis-sions spectrales subies par le signal de parole proviennent uniquement des ´el´ements de transmission analogiques. Dans ces conditions, le spectre de la voix est affect´e par deux types de distorsions.

Le premier est le filtrage passe-bande des terminaux et des points d’acc`es `a la partie num´erique du r´eseau. Les caract´eristiques typiques de ce filtrage sont d´ecrites par l’UIT-T sous le nom de syst`eme de r´ef´erence interm´ediaire modifi´e (SRI). Les r´eponses en fr´equence de ces filtres sont d´efinies par [P.896].

Le deuxi`eme est le r´esultat du filtrage par les lignes analogiques, qui sont ´equivalentes `a de filtres passe-bas. L’att´enuation introduite d´epend de la longueur de la ligne et de la

fr´equence du signal transmis.

Notre but est, alors, de restaurer le timbre de la voix `a la r´eception. Ici, le terme “timbre” signifie les caract´eristiques spectrales `a long terme de la voix. Ainsi, il s’agira essentiellement de corriger les modifications de l’enveloppe spectrale du signal de mani`ere `a am´eliorer le naturel et la pr´esence de la voix.

Premi`erement, nous nous sommes bas´e sur l’´egaliseur spectrale aveugle (ESA) d´evelopp´e par Mah´e [MG01, Mah02]. Nous nous sommes aper¸cu qu’il serait possible d’avoir des gains de performance en utilisant cet ´egaliseur ensemble avec la m´ethode de pr´ecompensation.

En observant la figure 2.16, il faut noter que l’´egaliseur est plac´e dans la partie num´erique du r´eseau. Cela est int´eressant au niveau de l’impl´ementation vu que, dans cette partie du r´eseau, il y a d´ej`a d’autres dispositifs de rehaussement de la parole et les annuleurs d’´echo, ce qui limite les besoins mat´eriels de l’impl´ementation. De plus, cette position permet une allocation dynamique des ressources de calcul aux communications et facilite la maˆıtrise de la qualit´e du service fourni par un op´erateur `a un abonn´e.

Nous commencerons par la pr´esentation de la m´ethode d´evelopp´ee par Mah´e [MG01, Mah02] et, juste apr`es, nous proposerons un nouveau ´egaliseur spectrale aveugle qui utilisera les deux m´ethodes ensemble.

2.5.2

Egaliseur Spectrale Aveugle

´

L’´egaliseur propos´e par [MG01, Mah02] a pour objectif de rapprocher le spectre de la parole trait´ee d’un spectre de r´ef´erence, dans la bande de fr´equence [200Hz − 3150Hz]. Au dehors de cette bande l’att´enuation des composantes du signal par le syst`eme d’´emission et de r´eception est telle que le rapport signal `a bruit de quantification est faible. Ainsi, le rehaussement par l’´egaliseur conduirait `a une amplification du bruit haute et basse fr´equence. L’´egaliseur propos´e utilise deux filtres en cascade. Le premier, appel´e pr´e-´egaliseur, est un filtre fixe dont la r´eponse en fr´equence est l’inverse de la r´eponse globale de la par-tie analogique du canal moyen, c’est-`a-dire, nous consid´erons les r´eponses en fr´equences moyennes des syst`emes d’´emission, r´eception et des lignes analogiques, tous d´efinis par le SRI modifi´e [P.896]. Dans le domaine temporel, ce filtre est impl´ement´e comme un filtre RII (r´eponse impulsionnelle infinie) d’ordre 20 par la m´ethode de Yule-Walker.

Le deuxi`eme est un filtre adapt´e qui corrige le d´esajustement entre le pr´e-´egaliseur fixe et les conditions r´eelles de transmission. Pour obtenir sa r´eponse en fr´equence, nous partons de la r´eponse fr´equentielle globale du syst`eme, G(f ) qui peut ˆetre estim´ee par:

o`<sub>u |Y (f)|</sub>2 <sub>et |U(f)|</sub>2 <sub>sont les densit´es spectrales de puissance `a court terme du signal de</sub>

r´eception y(t) et du signal original envoy´e u(t) respectivement. G(f ) inclut les syst`emes d’´emission et r´eception et les deux lignes analogiques.

Comme le canal est invariant dans le temps, les moyennes temporelles de |Y (f)|2_{et |U(f)|}2

satisfont:

|Y (f)|2 _{= |G(f)|}2

|U(f)|2 _(2.23)

La r´eponse fr´equentielle du filtre adapt´e sera donc donn´ee par:

|EQ(f)| = 1 |G(f)| = s γu(f ) γy(f ) (2.24)

o`u γ est le spectre `a long terme du signal, d´efini comme ´etant la moyenne temporelle du

spectre `a court terme.

N´eanmoins, les spectres `a long terme ne sont pas connus. Rappelons que l’´egaliseur est plac´e dans la partie num´erique du r´eseau, n’ayant pas acc`es au signal original transmis ni

au signal `a la r´eception. Pour le signal original transmis, γu a ´et´e remplac´e par un spectre

de r´ef´erence, γref, d´efini par l’UIT [P.593]. Ce spectre est un spectre moyen, calcul´e `a partir

de mesures sur un grand nombre d’´echantillons de parole prononc´ee par diff´erents locuteurs dans 20 langues.

Pour le signal `a la r´eception, le spectre `a long terme peut ˆetre estim´e `a partir du signal connu d’entr´ee de l’´egaliseur, que nous allons appeler v(t):

γy(f ) = |L RX(f)|2|S RX(f)|2γv(f ) (2.25)

o`u L RX(f ) est la r´eponse en fr´equence moyenne de la ligne analogique de r´eception et

S RX(f ) est la r´eponse en fr´equence moyenne du terminal de r´eception, les deux d´efinis par l’UIT-T [P.896].

Enfin, la r´eponse en fr´equence de l’´egaliseur sera donn´ee par:

|EQ(f)| = 1 |L RX(f)||S RX(f)| s γref(f ) γv(f ) (2.26)

Il est vrai que l’allure g´en´erale du spectre `a long terme d’un signal de parole pour un locuteur quelconque est proche de celle du spectre de r´ef´erence, mais elle est beaucoup moins

lisse. A cause de l’approximation γu ≈ γref, seulement le format global de la r´eponse en

fr´equence est important. De plus, avec la pr´esence du terme γv, la r´eponse EQ(f ) oscille

dans le domaine temporel, le filtre adapt´e est obtenu par une transform´ee inverse de Fourier de |EQ| suivi d’une sym´etrisation (pour obtenir un filtre causal `a phase lin´eaire) et de la multiplication par une fenˆetre de Hamming de longueur 15 centr´ee sur le pic de la r´eponse impulsionnelle.

Cette m´ethode sera appel´ee ´egaliseur spectrale aveugle liss´e par une fenˆetre de la r´eponse impulsionnelle (ESA-F).

2.5.3

Nouvelle M´

ethode Propos´

ee

Pour continuer dans le mˆeme cadre de la technique propos´ee par [MG01, Mah02], l’ESA-F, nous consid´ererons aussi un ´egaliseur form´e par deux filtres. Le premier, appel´e pr´e-´egaliseur, sera aussi un filtre fixe et aura, comme r´eponse en fr´equence, l’inverse de la r´eponse moyenne du syst`eme d’´emission et de r´eception et de la ligne analogique de r´eception. Notez que, dans l’ESA-F, ce filtre incluait aussi la ligne analogique de transmission, ce qui ne sera pas le cas ici. Ainsi, seul le filtre adapt´e ira compenser les distorsions introduites par la ligne analogique de transmission et la d´esadaptation entre le pr´e-´egaliseur fixe et les conditions r´eelles de transmission.

De plus, nous allons mod´eliser les lignes analogiques comme des lignes de transmission qui satisfont (2.1). Nous savons, donc, de (2.3), que la r´eponse fr´equentielle du filtre adapt´e sera donn´ee par:

H(f ) = cosh³ℓpβ´+ R + iωL

Z

sinh¡ℓ√β¢

√

β (2.27)

qui est l’inverse de la r´eponse du canal. Ici, la variable s a ´et´e remplac´ee par ω, satisfaisant la relation s = jω, avec ω = 2πf . Il est important d’observer qu’ici le filtre donn´e par H(f ) sera utilis´e comme ´egaliseur et non comme pr´ecompensateur, comme nous avions vu au d´ebut de ce chapitre. En effet, la position du filtre dans le syst`eme (`a l’´emetteur dans un cas et au milieu du r´eseau dans l’autre) ne change pas sa r´eponse en fr´equence ni les calculs pour son obtention.

Pour calculer H(f ), donn´e par (2.27), nous avons besoin des param`etres de la ligne. Les param`etres R, L, C et G (ici, G ne sera pas nulle) peuvent ˆetre mesur´es ou nous pouvons utiliser des valeurs moyennes d´efinies par l’UIT [Q.501]. Nous avons d´ej`a vu dans la section 2.4 que le syst`eme est robuste `a des erreurs d’estimation des ces param`etres. L’imp´edance Z, dans un r´eseau t´el´ephonique, sera donn´ee par l’imp´edance d’entr´ee du convertisseur 2 fils/4 fils, d´efinie aussi par [Q.501]. Il manque, donc, juste la longueur ℓ. En principe, sa valeur n’est pas connue et peut changer `a chaque nouvelle liaison. Ainsi, nous avons besoin de l’estimer de fa¸con aveugle.

la m´ethode ESA-F, c’est-`a-dire, EQ, donn´e par (2.26). Ainsi, la valeur correcte de ℓ sera celle qui approchera le plus, H(f ) de EQ, dans la plage de fr´equence d’int´erˆet [200Hz − 3150Hz]. Toutefois, cette comparaison sera faite dans le domaine cepstral et non directement dans le domaine spectral. Le cepstre d’un filtre avec r´eponse fr´equentielle H est donn´e par:

CH _{= IDF T (ln(|H|))} (2.28)

La fonction coˆut devant ˆetre minimis´ee sera donc la distance entre H et EQ dans l’espace

des dix premiers coefficients cepstraux :

J(ℓ) = 10 X k=1 ³ C_kEQ_{− Ck}H´2 (2.29)

o`u C<sub>k</sub>EQ est le k-i`eme coefficient cepstral de EQ et CH

k est le k-i`eme coefficient cepstral de H.

L’int´erˆet de faire cette comparaison dans ce domaine au lieu du domaine spectral est multiple:

• la comparaison peut ˆetre faite sans le besoin de faire attention au niveau des deux r´eponses fr´equentielles, simplement en excluant le coefficient cepstral d’ordre z´ero. • nous pouvons contrˆoler la r´esolution spectrale de la comparaison, vu qu’elle d´epend

du nombre de coefficients cepstraux consid´er´es. Dans (2.29) nous avons utilis´e 10 coefficients, ce qui s’est montr´e suffisant.

Le minimum de J sera trouv´e de fa¸con it´erative, en utilisant un algorithme du gradient descendant:

ℓn+1 = ℓn− µ∇ℓJ(n) (2.30)

o`u µ est le pas d’adaptation et

∇ℓJ(n) = − 10 X k=1 ³ C_kEQ_{− Ck}H(ℓn) ´ ∂CH k ∂ℓ (ℓn) (2.31)

La d´eriv´ee de CH _{par rapport `a ℓ nous donne:}

∂CH ∂ℓ = IDF T Ã 1 p |H| µ H∗∂H ∂ℓ + H ∂H∗ ∂ℓ ¶! (2.32) o`u ∂H ∂ℓ = p βsh³ℓpβ´+R + iωL Z ch ³ ℓpβ´ (2.33)

0 5000 10000 15000 −17 −16 −15 −14 −13 −12 −11 Longueur (m) J(l) (dB)

Figure 2.17: Fonction coˆut J(ℓ)

La figure 2.17 pr´esente un exemple de la fonction coˆut J par rapport `a la longueur de

la ligne, ℓ. Dans cette simulation nous avons utilis´e une ligne d’abonn´e de 10 km. Nous pouvons, donc, voir qu’il y a un seul minimum, `a ℓ = 10 km. Par contre, nous ne pouvons pas garantir que J sera toujours unimodale, `a cause de la nature al´eatoire de EQ. De toute fa¸con, pour toutes les simulations faites et qui seront pr´esent´ees dans la prochaine section, J n’a jamais ´et´e multimodale.

Il est important de souligner que H est naturellement lisse. Ainsi, comme on cherche la longueur qui approche, le plus possible, H de EQ, cette nouvelle m´ethode peut ˆetre vue comme une fa¸con diff´erente de lissage, rempla¸cant l’utilisation de la fenˆetre de Hamming. Comme nous allons le montrer dans la section suivante, cela apporte un gain de performance pour la plupart des locuteurs test´es.

De plus, pour les simulations, nous n’allons pas utiliser la r´eponse dans le domaine tem-porel de H, donn´ee par (2.4) puisque G n’est plus nulle, ce qui complique beaucoup les calculs. D’autre part, ici nous sommes dans la partie num´erique du r´eseau, ce qui exige un filtre discret. Ainsi, pour que la comparaison avec la performance d’ESA-F soit juste, le filtre dans le domaine temporel sera obtenu `a partir de la transform´ee inverse de Fourier de H et aura 15 coefficients, comme celui obtenu `a partir de EQ dans ESA-F.

Cette m´ethode sera appel´ee ´egaliseur spectral aveugle bas´ee sur les param`etres physiques de la ligne (ESA-P).

2.5.4

Comparaison des Deux M´

ethodes

Pour comparer la nouvelle m´ethode propos´ee, l’ESA-P, avec la m´ethode ESA-F, nous avons utilis´e une liaison comme celle montr´ee `a la figure 2.16, compos´ee d’une ligne analogique

de transmission longue, une ligne de r´eception moyenne et des syst`emes d’´emission et de r´eception avec des r´eponses fr´equentielles d´efinis par le SRI modifi´e. Une ligne t´el´ephonique typique a, comme param`etres [Q.501]: R = 168 mΩ/m, L = 0.7 µH/m, C = 50 pF/m et G = 1 pS/m. L’imp´edance Z, qui est l’imp´edance d’entr´ee des convertisseurs 2 fils/4 fils, peut ˆetre une r´esistance de 600 Ω ou une r´esistance de 270 Ω en parall`ele avec une capacit´e de 150 nF (nouveaux appareils).

Les simulations ont ´et´e faites en utilisant le mˆeme corpus que [Mah02], c’est-`a-dire, 34 locuteurs diff´erents (hommes et femmes), pronon¸cant le mˆeme texte, repr´esentant une ving-taine de secondes d’activit´e vocale. Ce signal a ´et´e analys´e par trames de 32 ms, avec un recouvrement inter-trames de 50%. Les valeurs des param`etres des lignes, R, L, C et G sont celles donn´ees par [Q.501], cit´ees ci-dessus, et Z a ´et´e consid´er´ee complexe. La ligne de transmission avait une longueur de 10 km tandis que celle de r´eception avait 2 km.

De plus, le filtre adapt´e dans le domaine temporel, obtenu `a partir de EQ, a 15 coeffi-cients (section 2.5.2) tout comme celui obtenu `a partir de H (m´ethode ESA-P), pour que la comparaison soit juste. L’algorithme donn´e par (2.30) a ´et´e initialis´e avec ℓ = 2 km, qui est

la longueur moyenne d’une ligne d’abonn´e. Le pas d’adaptation a ´et´e pris ´egal `a 5 × 103_.

La performance des m´ethodes `a ´et´e mesur´ee par l’erreur cepstrale moyenne. Pour chaque trame du signal, l’erreur cepstrale (EC) est d´efini comme [Mah02]:

ECm= v u u t 20 X k=1 (Ci k(m) − Cke(m)) 2 (2.34) o`u Ci

k est le k-i`eme coefficient cepstral de l’´egaliseur id´eal et Cke est le k-i`eme coefficient

cepstral de l’´egaliseur test´e, pour la m-i`eme trame du signal. L’´egaliseur id´eal est celui qui inverse parfaitement la r´eponse en fr´equence du canal, en consid´erant les deux lignes analogiques et les syst`emes d’´emission et de r´eception. La figure 2.18 montre la comparaison de l’erreur cesptrale moyenne (ECM) des deux ´egaliseurs, calcul´ee comme la moyenne tem-porelle des erreurs cepstrales (EC) apr`es la convergence des ´egaliseurs, pour chaque locuteur. La convergence de l’algorithme est atteinte apr`es environ 4 secondes d’activit´e vocale ce qui varie un peu selon le locuteur. Il est clair que, comme la comparaison est faite par rapport `a l’´egaliseur id´eal, plus faible sera la valeur d’ECM, mieux sera la performance de l’´egaliseur test´e. Dans la figure, les r´esultats des deux m´ethodes, pour chaque locuteur, sont li´es pour faciliter la visualisation de la diff´erence de performance entre les deux.

La figure 2.18 nous montre, donc, que, pour la plupart des 34 locuteurs test´es, la m´ethode ESA-P a une meilleure performance que la m´ethode ESA-F. Toutefois, pour certains locu-teurs, comme le 4 et le 20, la performance de la nouvelle m´ethode est pire, tandis que pour

0 5 10 15 20 25 30 35 0 0.05 0.1 0.15 0.2 0.25 Locuteurs ECM ESA−F ESA−P

Figure 2.18: Comparaison de l’ECM des deux m´ethodes

le locuteur 6, les performances des deux m´ethodes sont ´equivalentes.

En effet, l’estimation de la longueur par la comparaison entre H et EQ d´epend fortement de ce dernier. Ainsi, si EQ ne repr´esente pas une bonne inversion du canal d´es le d´ebut du processus, il peut ˆetre difficile de trouver une longueur qui rapprochera H de EQ. Dans ce

cas, la nouvelle m´ethode n’a pas une bonne performance parce que la fonction coˆut J n’aura

pas de minimum et, ´etrangement, sa valeur diminue lorsque la longueur augmente. Ainsi, la longueur finale estim´ee sera beaucoup plus ´elev´ee que la correcte. De toute fa¸con, nous pouvons voir que cela n’arrive que pour 2 locuteurs.

Comme notre but est de restaurer le timbre de la voix, l’int´erˆet de cette r´eduction dans l’erreur cepstrale est, en effet, dans son impact subjectif. Les relations entre l’erreur cepstrale et la restauration du timbre ont ´et´e ´etablies dans [Mah02], bas´ees sur des tests subjectifs. Comme ces relations ont ´et´e ´etablies dans le mˆeme contexte et pour des distorsions cepstrales et spectrales similaires aux simulations r´ealis´ees ici, nous pouvons les utiliser pour ´evaluer la signification des r´esultats obtenus. Ainsi, bas´e sur [Mah02], nous pouvons dire que la m´ethode ESA-P apporte une am´elioration significative de la restauration du timbre de la voix, principalement pour les locuteurs 9, 11 et 29.

Nous pouvons aussi comparer la performance des deux m´ethodes par rapport `a leur r´eponse en fr´equence. La figure 2.19 montre la r´eponse en fr´equence du syst`eme complet pour le locuteur 13. Nous pouvons observer que celle obtenue par la m´ethode ESA-P est beaucoup plus proche de la r´eponse de l’´egaliseur id´eal que celle obtenue par ESA-F.

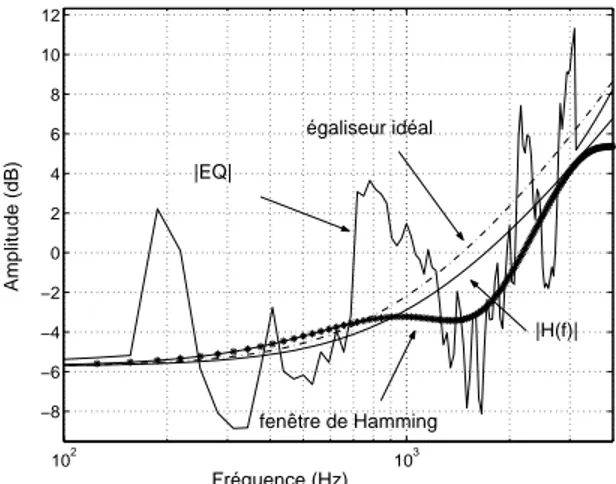
De plus, la figure 2.20 montre les r´eponses en fr´equence des ´egaliseurs obtenus `a partir des diff´erentes m´ethodes. Nous pouvons, donc, voir comme le r´esultat obtenu par la m´ethode ESA-F oscille beaucoup et que le lissage par la fenˆetre de Hamming de sa r´eponse impul-sionnelle ne donne pas un r´esultat si proche de l’id´eal comme celui de H (m´ethode ESA-P).

103 −5 −4 −3 −2 −1 0 1 2 3 4 Fréquence (Hz) Amplitude (dB) ESA−P ESA−F égaliseur idéal

Figure 2.19: R´eponse en fr´equence du syst`eme ´equivalent

102 103 −8 −6 −4 −2 0 2 4 6 8 10 12 Fréquence (Hz) Amplitude (dB) |EQ| égaliseur idéal |H(f)| fenêtre de Hamming

Figure 2.20: Comparaison de la r´eponse en fr´equence des ´egaliseurs ´

Evidemment, H, avec la valeur correcte de ℓ, est l’inverse exacte du canal. Nous pouvons voir que, avec la longueur estim´ee, sa r´eponse est tr`es proche de la r´eponse de l’´egaliseur id´eal.

2.5.5

Analyse du R´

esultat

Il peut sembler que, pour l’impl´ementation de l’´egaliseur propos´e, un nombre important d’´el´ements du syst`eme doivent ˆetre connus: les syst`emes d’´emission et de r´eception et les param`etres de la ligne de r´eception. En fait, ces suppositions ont ´et´e faites pour ˆetre dans le mˆeme cadre que [Mah02], et pouvoir comparer les r´esultats. En pratique, tr`es peu d’´el´ements doivent ˆetre connus pour caract´eriser une liaison entre deux abonn´es. Les deux m´ethodes, ESA-F et ESA-P, utilis´ees alternativement, nous permettent de caract´eriser toute une liaison en ne connaissant que les syst`emes d’´emission et de r´eception de l’abonn´e en question.