présentée en vue de l’obtention du
Doctorat de l’Université de Toulouse
Spécialité : Mathématiques Fondamentales
Déformations de
structures hyperboliques
coniques
par
Alexandre Paiva Barreto
Soutenance le 4 décembre 2009 devant le jury composé de :
Michel Boileau Université Paul Sabatier Directeur
Michael Heusener Université Blaise Pascal Rapporteur
Joan Porti Universitat Autònoma de Barcelona Rapporteur
Richard Cannary University of Michigan Examinateur
Jean-Pierre Otal Université Paul Sabatier Examinateur
Juan Soto University of Michigan Examinateur
Institut de Mathématiques de Toulouse
Résumé
L’objet de cette thèse est l’étude des déformations de structures hyperboliques co-niques de type topologique constant, sous l’hypothèse que la longueur de la singularité reste uniformément majorée pendant la déformation. Etant donnée une suite pointée (Mi; pi) de variétés hyperboliques coniques de type topologique (M; ), où M est une
variété di¤érentiable de dimension 3 fermée, orientable et irréductible, et un entre-lacs plongé dans M , on demontre le resultat suivant : soit la suite s’e¤ondre et dans ce cas là M est …brée de Seifert ou Sol, soit la suite sous-converge vers un espace d’Alexandrov de dimension 3, complet et dont la métrique est hyperbolique de volume …nie en de hors d’une famille …nie de quasi-géodésiques. On applique ce résultat au cas où est un entrelacs petit, pour obtenir des constantes uniformes pour le volume et le diamètre des variétés hyperboliques coniques de type topologique (M; ).
mots-clés : variétés de dimension 3, variétés hyperboliques coniques, déformation de structures géométriques, espaces d’Alexandrov, convergence au sens de Hausdor¤-Gromov, théorème de …bration.
en l’honneur du professeur Paulo Sabini (1972-2007)
Merci pour l’exemple de sa vie et de son dévouenement. Sa disparition soudaine m’a profondément a¤ecté et son souvenir restera à jamais gravé dans mon coeur.
"Il faut croire aux étudiants. Ils sont beaucoup plus intelligents et créatifs que les profs supposent." Paulo Sabini
Remerciements
Je voudrais avant tout remercier très vivement mon directeur de thèse le professeur Michel Boileau. Merci pour toute sa générosité, son dévouement, sa patience et son soutien indéfectible. Merci d’avoir été bien plus qu’un directeur.
Je tiens à remercier chaleureusement le professeur Joan Porti pour de nombreuses et précieuses discussions qui ont aidé à l’élaboration de cette thèse.
Je suis sincèrement reconnaissant aux professeurs Michael Heusener et Joan Porti d’avoir accepté d’être mes rapporteurs. J’exprime aussi ma gratitude envers Richard Canary, Jean-Pierre Otal et Juan Souto de m’avoir fait l’honneur d’accepter de parti-ciper à mon jury.
Je tiens aussi à remercier ...
... le professeur Sebastião Marcos Firmo pour avoir dirigé mes premiers pas dans la recherche et m’avoir guidé vers Toulouse.
... les professeurs qui ont marqué ma formation mathématique. Mes remerciements vont en particulier à Nilson Bernardes da Costa, Francisco Xavier Fontenele Neto, Luis Adrian Florit, Maria Luiza Correa e Paulo Sabini, dont le soutien est allé bien au-delà des obligations professionnelles.
... le professeur Julio Cesar Rebelo pour son amitié et pour tant de conversations mathématiques, politiques, sportives etc. Merci d’être l’ange gardien de mon innocence. ... les professeurs Jean-Marc Schlenker et Jean-Pierre Otal pour les enrichissantes discussions mathématiques.
... l’Equipe Emile Picard pour son hospitalité et son agréable ambiance de travail. En particulier, je voudrais remercier Agnès Requis et Jocelyne Picard pour l’aide qu’elles ont su m’apporter en toute occasion (toujours avec une énorme patience).
... les collègues doctorants qui ont rendu mon séjour en France beaucoup plus facile et agréable. Merci à Frédéric Protin et Landry Salle pour leur amitié. Merci à Anne Granier et Cécile Poirier pour avoir été toujours prêtes à m’aider. Merci Alexandre Dezzotti pour sa sympathie et pour avoir ri de mes mauvaises plaisanteries et blagues
très moyennes. Merci à ma "petite soeur" Claire Renard pour son amitié, pour sa sincerité, pour toutes les conversations (mathématiques ou non) et sourtout pour tous les sourires qui ont rapidement captivé tout le department. Merci à Kuntal, Benjamin, Iman, Guitta, Tony, Boubbacar, Thomas, Yohann, Julien, Mathieu, Florient pour leur compagnie pendant toutes ces années.
... les collègues Alexandre Dezzoti, Thomas Gauthier, Claire Renard et le professeur Julio Cesar Rebelo qui ont eu la patience de lire et de corriger les versions prélimi-naires de ce texte. Je vous remercie au nom de tous les "denotons par", "notons que", "on a que", "pouisse", "outiles" ... et sourtout les accents (leur absence ou présence inopinées).
... mes amis de l’université au Brésil qui m’ont accompagné tout au long de ce voyage. Merci à mon frère spirituel Rodrigo Salomão et mes amis João Domingos et Renato Alencar pour la chaleur de leur amitié.
... mes amis d’enfance Eduardo Barbosa Lima, Alexandre Villela, Fabio Moita et Robson Bertolossi pour leur amitié sans frontières, en dehors du temps et de l’espace, mais qui savent être présents lorsque c’est nécessaire.
... les amis brésiliens que j’ai rencontrés ici à Toulouse. Merci à Michely, Alessan-dra et Valentin, Lucieth, Daniel et Poliana, Eliane et Leonardo, qui ont rendu mon adaptation à la vie toulousaine beaucoup plus facile.
... ma petite Pudding au Lait (bien sûr à la sauce caramel !) Cynthia Ferreira de m’avoir accompagné dans cette grande aventure. Merci pour tout son soutien, son amour, sa "amizade" et sa présence indéfectible à mes côtés au cours de ces sept dernières années. Cette thèse aura été notre premier enfant ...
... ma famille : Mon Papa Alberto, ma Maman Celia et mes frères Cão, Loba (tu a été promue !) et Beto pour tout leur amour et leur soutien. Sans eux je n’aurais pu mener ce travail à son terme.
Et …nalement, je voudrais exprimer ma gratitude à la Coordenaçãao de Pessoal de Nivel Superior (CAPES) qui a …nancé mes études en France.
Table des matières
Table des matières v
1 Introduction 1 2 Rappels 7 2.1 Topologie de Dimension 3 . . . 7 2.1.1 Notions élémentaires . . . 7 2.1.2 Variétés de Seifert . . . 8 2.2 Espaces d’Alexandrov . . . 10 2.2.1 Notions élémentaires . . . 10 2.2.2 Convergence de Hausdor¤-Gromov . . . 15 2.3 Structures Géométriques . . . 18
2.3.1 Géométries Modèles et Variétés Géométriques . . . 18
2.3.2 Variétés Hyperboliques Coniques . . . 22
2.3.3 Déformation de structures hyperboliques coniques . . . 26
3 Partie mince d’une variété conique 31 3.1 Introduction . . . 31
3.2 Feuilletage canonique de la partie mince . . . 32
4 Théorème de Fibration 37 4.1 Introduction . . . 37
4.2 Esquisse de la preuve du théorème 4.1.3 . . . 40
5 Suites de Variétés Coniques 47 5.1 Introduction . . . 47
5.2 Preliminaires . . . 49
5.3 La suite Mi ne s’e¤ondre pas . . . 54
5.4 La suite Mi s’e¤ondre . . . 66
5.4.1 Cas où la limite a dimension 2 . . . 68
5.4.2 Cas où la limite a dimension 1 . . . 78
5.4.3 Cas où la limite a dimension 0 . . . 80
5.4.4 Démonstration du théorème (5.4.2) . . . 80
6 Applications 83
6.1 Entrelacs petits . . . 83
6.2 Résultats de Compacité . . . 84
6.3 Application à une conjecture de Thurston . . . 85
6.4 Volume de Représentation . . . 87
A Complements sur les volumes de représentations 91 A.1 Démonstration de la proposition 6.4.3 . . . 91
A.2 Démonstration de la proposition 6.4.4 . . . 93
Introduction
Ce texte s’intéresse aux structures hyperboliques coniques sur les variétés de di-mension 3. Une variété di¤érentiable M fermée et de didi-mension 3 admet une structure hyperbolique conique singulière le long d’un entrelacs plongé dans M si elle ad-met une métrique complète telle que tout point non-singulier (c’est-à-dire un point de M ) possède un voisinage isométrique à un ouvert de H3, l’espace hyperbolique de dimension 3, et tout point singulier (c’est-à-dire un point de ) admet un voisinage isométrique à un ouvert de l’espace obtenu en identi…ant par rotation les côtés d’un dièdre de H3 d’angle 2 (0; 2 ]. Les angles sont appellés angles coniques et sont, par dé…nition, constants sur chaque composante de .
Contrairement aux structures hyperboliques non-singulières, qui sont rigides d’après le théorème de Mostow ([Rat]), les structures hyperboliques coniques peuvent être dé-formées. Hodgson et Kercko¤ ont démontré ([HK2]) à la …n des années quatre-vingt dix que toute structure hyperbolique conique admet une petite déformation continue paramétrée par ses angles coniques. La stratégie utilisée remonte aux techniques en-treprises par Thurston pour démontrer son Théorème de Chirurgie Hyperbolique. En fait, si l’on voit la structure hyperbolique complète sur M comme une structure hyperbolique conique d’angle zéro, Thurston a démontré que cette métrique complète peut être deformée en des métriques non-complètes dont les completions donnent des structures hyperboliques coniques d’angles coniques positives proches de zéro.
La di¢ culté pour déformer une structure hyperbolique conique est la possibilité que la structure s’e¤ondre ou que l’entrelacs singulier s’auto-intersecte. En fait, les travaux de Kojima, Hodgson-Kerckho¤ et Fuji montrent ([Koj], [HK] et [Fuj]) que le seul phénomène à éviter est l’auto-intersection de la singularité. Sans cela la structure hyperbolique conique peut être déformée librement sans e¤ondrement.
L’objet de cette thèse est l’étude des déformations de structures hyperboliques coniques sous l’hypothèse que la longueur de la singularité reste uniformément ma-jorée pendant la déformation. Cette hypothèse permet d’éviter en particulier le cas indésirable où la singularité devient dense dans l’espace de longueur limite. Cette hypothèse est toujours véri…ée lorsque les holonomies des structures hyperboliques co-niques convergent, ce qui est le cas, par exemple, si est un entrelacs petit dans M (voir dé…nition 6.1.2 et [CS]).
Etant donné un couple (M; = 1t : : : t l), où M est une variété di¤érentiable
de dimension 3 fermée, orientable et irréductible, et un entrelacs plongé dans M , on considère une suite pointée (Mi; pi) de structures hyperboliques coniques sur M
singulières le long de . Quitte à extraire une sous-suite (voir section 1:2 et 1:3), on peut supposer que la suite pointée (Mi; pi) converge au sens de Hausdor¤-Gromov
pointé vers un espace d’Alexandrov pointé (Z; z0) dont la dimension (de Hausdor¤)
est plus petite ou égale à 3. Notre but est de comprendre les propriétés métriques de Z et, à partir d’elles, d’obtenir des informations topologiques sur la variété M .
L’étude décrite dans le paragraphee précedent est faite au chapitre 5. Elle est divisée en deux partie selon que la suite Mi s’e¤ondre ou non. On dira que la suite Mi
s’e¤ondre si, pour toute suite de points pi 2 M , la suite de ses rayons d’injéctivité
riemannien rMi
inj (pi) dans Mi tend vers zéro. Cette dichotomie est très naturelle
et représente intuitivement le fait que le volume de la suite tende ou non vers zéro. En fait, ces deux a¢ rmations sont équivalentes lorsque le diamètre de la suite Mi reste
uniformément majoré. En général, l’hypothèse que le volume de la suite tende vers zéro est plus forte que l’hypothèse d’e¤ondrement.
Quand la suite Mine s’e¤ondre pas, on démontre que Z a dimension (de Hausdor¤)
3 et qu’il admet une structure hyperbolique, non complète et de volume …ni, en dehors d’une famille …nie Z (peut-être vide) de quasigéodésiques de Z (pas nécessairement
disjointes). Dans ce cas-là, on conjecture que Z admet une structure hyperbolique conique (singulière le long de Z) dans un sens plus général, où la singularité pourrait
être un graphe (voir la dé…nition de conifold dans [BLP]).
Quand la suite Mi s’e¤ondre, on démontre que l’entrelacs singulier
s’auto-intersecte nécessairement à la limite et que la dimension (de Hausdor¤) de Z est strictement plus petite que 3, ce qui implique (voir section 1:2) que Z est une variété topologique connexe de dimension 2, 1 ou zéro. En utilisant une version plus générale du théorème de …bration de Yamaguchi pour les espaces d’Alexandrov (voir chapitre 2), on démontre que la variété M est géométrique.
Théorème 1.0.1 Soient M une variété di¤ érentiable de dimension 3, fermée, orien-table, irréductible, et un entrelacs plongé dans M . On suppose qu’il existe sur M une suite Mi de structures hyperboliques coniques singulières le long de telle que
sup fLMi( j) ; i 2 N et j 2 f1; : : : ; lgg < 1 .
Alors une des deux a¢ rmation ci-dessous est vraie :
i: la suite Mi s’e¤ ondre et M est …brée de Seifert ou Sol,
ii: la suite Mi ne s’e¤ ondre pas et, il existe une suite de points pik 2 M
telle que la suite (Mik; pik) converge au sens de Hausdor¤ -Gromov pointé vers
un espace d’Alexandrov Z de dimension 3 qui admet une structure hyperbolique non complète et de volume …ni sur le complémentaire d’une réunion …nie Z
de quasigéodésiques et dont les bouts sont des cusps paraboliques. De plus, Z est homéomorphe à M (en particulier, Z est compact) s’il existe " 2 ]0; [ tel que les angles coniques ij appartiennent tous à ]"; 2 "[.
Si l’on suppose que est connexe on a le corollaire suivant :
Corollaire 1.0.2 Soient M une variété di¤ érentiable de dimension 3, fermée, orien-table, irréductible, et un noeud plongé dans M . On suppose qu’il existe une suite Mi de variétés hyperboliques coniques de type topologique (M; ), d’angles coniques
i 2 (0; 2 ]. Alors la suite i converge vers zéro si et seulement si :
i: sup fLMi( ) ; i 2 N g < 1,
ii: lim
i!1diam (Mi) = 1,
iii: la suite Mi ne s’e¤ ondre pas.
Remarque 1.0.3 Sous les hypothèses du corollaire précédent et dans le cas où i
converge vers zéro, il existe une suite de points pik 2 M telle que la suite (Mik; pik)
converge au sens de Hausdor¤ -Gromov pointé vers M muni de la structure hyper-bolique complète.
Quand M est une variété hyperbolique et est une réunion …nie de géodésiques simples de M , M admet une structure hyperbolique complète et la question de l’existence d’une déformation entre ces deux structures par un chemin continu de structures hyperboliques coniques de type topologique (M; ) se pose naturellement. Plus précisément Thurston a conjecturé :
Conjecture 1.0.4 Etant données une variété hyperbolique conique fermée, orientable et une réunion …nie de géodésiques simples et disjointes, il existe une famille M de structures hyperboliques coniques de type topologique (M; ) et d’angle conique (le même pour tous les composantes) telle que varie de 0 à 2 .
Comme application du théorème 1.0.1, on obtient le résultat suivant qui donne des informations sur cette conjecture.
Corollaire 1.0.5 Supposons que M est une variété hyperbolique et que est une réunion …nie de géodésiques simples de M . Soit M une déformation de cette structure le long d’un chemin continu de structures hyperboliques coniques de type topologique (M; ) et d’angles coniques 2 (L; 2 ] [0; 2 ] (le même pour toutes les composantes de ). Si
sup fLM ( j) ; 2 (L; 2 ] et j 2 f1; : : : ; lgg < 1,
alors L = 0 si et seulement si lim
!Ldiam (M ) = 1. Dans ce cas là, le chemin s’étend
continûment à [0; 2 ].
Remarque 1.0.6 Si la déformation M donnée dans le corollaire ci-dessus est maxi-male, alors les résultats de Kojima dans [Koj] permettent d’assurer que L = 0 si et
seulement si L .
Une autre question intéréssante concernant les suites convergentes de variétés hy-perboliques coniques (de même type topologique) est la compacité de la limite. Le critère de compacité suivant est aussi une application du théorème 1.0.1 :
Corollaire 1.0.7 Soient M une variété di¤ érentiable de dimension 3, fermée, orien-table, irréductible qui n’est pas …brée de Seifert ou Sol et = 1t : : : t l un entrelacs
plongé dans M . Supposons qu’il existe une suite Mi de variétés hyperboliques coniques
de type topologique (M; ) et d’angles coniques ji2 ]"; 2 "[, où " 2 ]0; [. Si
sup fLMi( j) ; i 2 N et j 2 f1; : : : ; lgg < 1,
alors sup fdiam (Mi) ; i 2 Ng < 1.
Quand l’entrelacs est un noeud petit dans M (voir section 4.1), on obtient le corollaire ci-dessous :
Corollaire 1.0.8 Supposons que est un noeud petit dans une variété di¤ érentiable M de dimension 3 qui n’est pas …brée de Seifert ou Sol. Pour tout " 2 ]0; 2 [, il existe une constante K = K (M; ") > 0 tel que
diam (M) < K,
pour toute variété hyperbolique conique M de type topologique (M; ) et dont les angles coniques appartiennent à ]"; 2 ].
Sur le volume des variétés hyperboliques coniques, on a le résultat suivant : Corollaire 1.0.9 Soient M une variété di¤ érentiable de dimension 3, fermée, orien-table, irréductible qui n’est pas …brée de Seifert et un entrelacs petit dans M . Alors, il existe une constante V = V (M; ) > 0 telle que
V ol (M) > V ,
pour toute variété hyperbolique conique M de type topologique (M; ).
La dernière application utilise la notion de volume d’une représentation :
Corollaire 1.0.10 Soient M une variété di¤ érentiable de dimension 3, fermée, orien-table, irréductible et = 1t : : : t l un entrelacs plongé dans M . Supposons que la
variété M a un volume simplicial nul (ce qui arrive, par exemple, si M est graphée) et qu’il existe une suite Mi de variétés hyperboliques coniques de type topologique (M; ),
d’angles coniques ij convergeant vers 2 (pour tout j 2 f1; : : : ; lg). Si une suite de
re-présentations d’holonomie associées i2 R (M ) converge vers une représentation 12 R (M ), alors M est …brée de Seifert ou Sol.
Rappels
2.1
Topologie de Dimension 3
2.1.1 Notions élémentaires
Soit une variété topologique M de dimension n 2 f2; 3g. Etant donné une sous-variété S de M de codimension 1 et propremennt plongée (S \ @M = @S et T S est transverse à T @M ), notons par N (S) un petit voisinage tubulaire ouverte de S. La variété M N (S) est appelé le découpage de M le long de S et sera notée MjS. On dira que S sépare M quand M jS a au moins deux composantes connexes.
Dé…nition 2.1.1 On dira qu’une variété topologique M de dimension 3 est la somme connexe des variétés topologiques M1; : : : ; Mk (aussi de dimension 3) et on écrira
M = M1# : : : #Mk
s’il existe une sous-variété S de M telle que
i. les composantes connexes de S sont des sphères S2 et séparent M ,
ii. M jS s’écrit comme l’union disjointe M10 t : : : t Mk0 de variétés topologiques et
chaque Mi est obtenue à partir de la composante Mi0 en recollant des boules B3
sur ses composantes de bord provenant du découpage de M le long de S.
Notons que si une sphère S plongée dans M sépare et borde une boule d’un côté, on obtiendra que M = M #S3. Cette remarque motive les dé…nitions suivantes : Dé…nition 2.1.2 Soit une variété topologique M orientable et de dimension 3. La variété M est dite première si elle n’est pas homéomorphe à S3 et, pour toute de-composition en somme connexe M = M1#M2 , au moins une des variétés Mi est
homéomorphe à S3. La variété M est dite irréductible si toute sphère plongée dans
M borde une boule.
Un remarque important est que S1 S2 est l’unique variété topologique de dimen-sion 3 orientable qui est première et pas irréductible.
Dé…nition 2.1.3 Un arc proprement plongé dans une surface topologique S est
appelé essentiel s’il n’existe pas d’arc dans @S tel que [ borde un disque dans S. Un arc qui n’est pas essentiel est appelé inessentiel.
Dé…nition 2.1.4 Soit S une surface proprement plongée dans M , qui sépare et sans composantes connexes homéomorphes à S2 où D2. Un disque de compression pour S est un disque fermé D plongé dans M tel que S \ D = @D et @D ne borde pas de disque dans S. On dira que S est incompressible (compressible) si elle n’admet pas (admet) un disque de compression. Un disque de @-compression pour S est un disque fermé D, plongé dans M , dont le bord @D peut-être decomposé en deux arcs = D \ S et = D \ @M d’interieurs disjoints et tel qu’il n’existe pas de disque D0
contenu dans S avec @D0 et @D0 @M . On dira que S est @-incompressible
(@-compressible) si elle n’admet pas (admet) un disque de @-compréssion. On dira que S est essentielle lorsque elle est à la fois incompressible et @-incompressible.
On résume quelques propriétés des surfaces incompressibles dans la proposition suivante (voir [Hat]).
Proposition 2.1.5 Soient une variété topologique M orientable et de dimension 3, et une surface S qui sépare M , sans composante connexe homéomorphe à S2 où D2. Alors :
i. S est incompressible (@-incompressible) si et seulement si toutes ses composantes connexes sont incompressibles (@-incompressibles),
ii. une composante connexe Side S est incompressible (@-incompressible) si et
seule-ment si (si) l’application
i : 1(Si) ! 1M ( i : 1(Si; @Si) ! 1(M; @M ) )
induite par l’inclusion i : Si ,! M (i : (Si; @Si) ,! (M; @M)) est injective,
iii. supposons que S est homéomorphe à un tore T2 et que M est irréductible. Alors S est compressible si et seulement si elle borde un tore solide ou si elle est contenue dans une boule.
2.1.2 Variétés de Seifert
Etant donné un couple ( ; ) de nombres entiers premiers entre eux, on dé…nit T( ; ), le tore solide …bré de type ( ; ), comme le quotient du cylindre D2 R muni
de la …bration standard fdg R ; d 2 D2 par un vissage V d’axe f0g R, de pas 1 et d’angle de rotation 2 . On note V : D2 R !T( ; ) = D2 R =V la projection
quotient. L’entier est appelé l’indice de T( ; ). Notons que D = V D2 f0g est un disque méridien pour T( ; ) qui intersecte la …bre V(f0g R) une seule fois et les
…bres V(fdg R), où d 6= 0, exactement fois. Le tore T( ; ) est dite régulier si = 1, et exceptionnel si 6= 1.
Dé…nition 2.1.6 Une variété topologique M de dimension 3 (peut-être avec bord) est appelée variété (orientable) de Seifert (ou encore M admet une …bration de Seifert, ou M est …brée de Seifert) si M est orientable et admet un feuilletage en cercles tel que chaque …bre c admet un voisinage tubulaire Vc fermé et …bré (Vc est
une union de …bres) homéomorphe à un tore …bré T( ; ) par un homéomorphisme qui
preserve les …bres et qui envoie c sur la …bre V(f0g R). Les …bres c dont le voisi-nage Vc est homéomorphe à un tore exceptionnel (régulier) sont dites exceptionnelles
(régulières).
On remarque que la classi…cation des …bres donnée ci-dessus est exclusive, c’est-à-dire, une …bre ne peut pas avoir un voisinage homéomorphe à un tore exceptionnel et un autre homéomorphe à un tore régulier (voir [Jac]). Il découle de la dé…nition que les …bres singulières sont contenues dans l’intérieur de M et qu’elles sont en nombre …ni lorsque M est compacte.
Etant donnée une variété de Seifert M , soit B l’ensemble des …bres de M . On note p : M ! B la projection qui associe à chaque point de M la …bre qui le contient. Les voisinages modèles des …bres induisent une structure naturelle d’orbifold de dimension 2 (pas forcément orientable) sur B, dont l’ensemble singulier est discret et correspond à l’image des …bres singulières par la projection p.
Dé…nition 2.1.7 Soit M une variété (orientable) de Seifert. L’ensemble B des …bres de M muni de la structure d’orbifold de dimension 2 est appellé base de la …bration de Seifert de M et l’application p : M ! B est appelée la projection canonique sur la base.
On énonce quelques propriétés des variétés de Seifert :
Proposition 2.1.8 ([Jac]) Soit M une variété (orientable) de Seifert de base B. Alors :
i. @M 6= ; si et seulement @B 6= ;. Par conséquent, les composantes de @M sont des tores …brés,
ii. supposons que @M 6= ; et soit N la variété obtenue en recollant un tore solide V sur une composante de @M sans identi…er (à homotopie près) une …bre au méridien de V . Alors la …bration de Seifert sur M s’étend à une …bration de Seifert sur N ,
iii. si M n’est pas homéomorphe à S2 S1 ou P3#P3, alors M est irréductible. Pour …nir cette section, on distingue une importante famille de variétés de Seifert : Etan donné un tore solide fermée V , un lacet plongé sur le bord de V est appellé un méridien s’il existe un disque D V tel que D \ @V = @D et parametrise @D. Une longitude pour est un lacet l plongé sur le bord de V (basé sur le même point que ) qui intersect en un seule point et telle que les classes d’homotopie de et l engendrent le groupe fondamental du bord de V . Le couple ( ; l) est appéllé un couple méridien/longitudepour V .
Dé…nition 2.1.9 Etant donné un couple (p; q) d’entiers premiers entre eux (q > 0), on dé…nit l’espace lenticulaire Lp;q comme la variété topologique de dimension 3
obtenue en recollant deux tores solides fermés V et W de façon à ce qu’un méridien de W soit recollé sur le lacet plq du bord de V , où le couple ( ; l) dénote un couple méridién/longitude pour V .
On remarque que les ensembles Lp;q sont bien dé…nis, dans la mesure où
l’identi-…cation proposée des courbes sur les bords des tores détermine (à isotopie près) les homéomorphismes entre les bords des tores. On peut aussi obtenir les variétés lenti-culaires Lp;q comme le quotient de S3 C2 par l’action du groupe Zq de générateur
(z1; z2) 7 ! e 2 i q :z 1; e 2 ip q :z 2 .
2.2
Espaces d’Alexandrov
2.2.1 Notions élémentairesSoit Z un espace métrique. Par convention, la métrique de Z sera notée dZ( ; ).
Pour tout r 0 et pour tout sous-ensemble A Z, on désigne les r-voisinages
métriques(ouverts et fermés) de A dans Z par BZ(A; r) = S
a2Afz 2 Z ; d
Z(z; a) < rg et BZ[A; r] = S
a2Afz 2 Z ; d
Z(z; a) rg :
Dé…nition 2.2.1 Un espace métrique Z est appelé un espace de longueur si dZ(z1; z2) = inf fLZ( ) ; est une courbe recti…cable reliant z1 à z2g ,
pour tous z1; z2 2 Z, où LZ( ) représente la longueur d’une courbe dans Z. Dans
Une courbe dans un espace de longueur Z est une application : I ! Z, continue et paramétrée par longueur d’arc, où I est un intervalle de R. On dira qu’une courbe : I ! Z est une géodésique minimisante de Z (ou segment géodésique minimisant de Z lorsque I est compact) si elle réalise la distance entre deux points quelconques de son image. C’est-à-dire, pour tous t1; t2 2 I,
dZ( (t1) ; (t2)) = LZ j[t1;t2] = t2 t1 . (2.1)
Une géodésique de Z est une courbe : I ! Z qui réalise localement la distance entre les points de son image. Plus précisément, pour tout t02 I, il existe un intervalle
Jt0 I tel que t0 2 int (J) et satisfait (2.1), pour tous t1; t22 Jt0.
Quand tous les points d’un espace de longueur Z peuvent être reliés par un segment géodésique minimisant, on dira que Z est (géodésiquement) complet. Le théorème de Hopf-Rinow montre que cette notion de complétude coïncide avec la notion cano-nique de complétude pour les espaces métriques (Cauchy).
Etant données deux courbes ; : [0; "[ ! Z telles que z0= (0) = (0), l’angle
entre et est dé…ni par
] ( ; ) = lim (s;t)!(0;0)arccos dZ( (s) ; z0)2+ dZ(z0; (t))2 dZ( (s) ; (t))2 2:dZ( (s) ; z0)2:dZ(z0; (t))2 ! ,
lorsque cette limite existe. Notons que, d’après la loi des cosinus, si l’on prend un triangle euclidien de côtés de longueur dZ( (s) ; z0), dZ(z0; (t)) et dZ( (s) ; (t)),
alors l’expression entre parenthèses représente le cosinus de l’angle (t; s) 2 [0; ] opposé au côté de longueur dZ( (s) ; (t)) (…gure 2.1).
Fig. 2.1 –Interprétaton géométrique de ] ( ; )
Une charnière ( ; ) dans un point z0 d’un espace de longueur Z est le choix
de deux segments géodésiques minimisants : [0; a] ! Z et : [0; b] ! Z tels que z0 = (0) = (0). On dé…nit l’angle de la charnière ( ; ) par] ( ; ), lorsque cet
angle existe. La longueur d’une charnière ( ; ) est dé…nie par LZ( ; ) = min fLZ( ) ; LZ( )g .
Pour tout k 2 R, on note M2k la variété riemannienne complète, simplement
connexe, de dimension 2 et de courbure sectionelle constante égale à k. On remarque que comme toute paire de points distincts de M2k est reliée par un unique segment
géodésique, l’angle de toute charnières de M2k est bien dé…ni et que toutes charnières
de même angle et de segments de même longueur sont égales à isométrie prés.
Etant donne une charnière ( ; ) dans un espace de longueur Z, on appelle une
k-charnière de comparaison pour ( ; ) une charnière ; de M2k tel que
LZ( ) = LM2
k( ), LZ( ) = LM2k et dZ( (a) ; (b)) = dM2k (a) ; (b) . Notons
que les proprietés données dé…nissent une charnière de comparaison à isométrie près. De plus, si k 0, toute charnière ( ; ) admet une k-charnière de comparaison. Pour k > 0, la même a¢ rmation est véri…ée par les charnière ( ; ) avec LZ( ; ) < pk.
Dé…nition 2.2.2 On dit que un espace de longueur Z a courbure minorée par
k 2 R lorsqu’il satisfait l’une (et en fait le deux) des propriétés suivantes :
i. tout point z 2 Z admet un voisinage Uz tel que l’angle de toute charnière ( ; )
contenue dans Uz est bien dé…ni. De plus, si ( ; ) admet une k-charnière de
comparaison ; , alors ] ( ; ) ] ; ,
ii. tout point z 2 Z admet un voisinage Uz tel que, pour toute charnière ( ; )
contenue dans Uz, la fonction
(t; s) = arccos dZ( (s) ; z0) 2 + dZ(z0; (t))2 dZ( (s) ; (t))2 2:dZ( (s) ; z0)2:dZ(z0; (t))2 ! satisfait (t1; s1) (t2; s2), si t1 t2 et s1 s2.
On remarque que les propriétés (i) et (ii) sont equivalentes et qu’elles sont valables globalement, c’est-à-dire, pour n’importe quelles charnières de Z ([BBI] - 10.3.1). Dé…nition 2.2.3 Un espace d’Alexandrov est un espace de longueur, localement compact, dont la courbure est minorée et la dimension est …nie. On l’appellera k-espace d’Alexandrov si l’on veut préciser que la courbure est minorée par k 2 R. La dimension d’un espace de Alexandrov est sa dimension de Hausdor¤ .
Proposition 2.2.4 ([BBI]) La dimension d’un espace d’Alexandrov Z est un entier. De plus, tous les ouverts de Z ont la même dimension.
Proposition 2.2.5 ([BBI] et [SY]) Les espaces d’Alexandrov de dimension 1 (di-mension 2) sont des variétés topologiques, peut-être à bord non vide, de di(di-mension 1 (dimension 2).
Soient un k-espace d’Alexandrov Z et un point z 2 Z. Notons Tzl’ensemble de tous
les segments géodésiques issus de z. On dira que , 2 Tz sont équivalents ( tz )
si et seulement si] ( ; ) = 0. Cela dé…nit une relation d’équivalence sur Tz. De plus,
la fonction angle ( ; ) 7 ! ] ( ; ) est une métrique sur le quotient Tz= tz.
Dé…nition 2.2.6 Soient un espace d’Alexandrov Z et un point z 2 Z. Le complété métrique de Tz= tz sera appelé espace des directions de Z en z et sera noté DzZ.
Proposition 2.2.7 ([BBI]) Soient un espace d’Alexandrov Z de dimension n et un point z 2 Z. Alors diam (DzZ) et :
i. si n 2, alors DzZ est un 1-espace d’Alexandrov compact et de dimension n 1,
ii. si n = 1, alors DzZ est un ensemble à un ou deux éléments.
Dé…nition 2.2.8 L’intérieur et le bord d’un espace d’Alexandrov Z de dimension n, notés int (Z) et @Z, sont dé…nis (par recurrence) de la façon suivante :
i. si n 2, alors les notions coïncident avec celles des variétés topologiques, ii. si n 3, alors @Z est l’ensemble des points z 2 Z tels que DzZ est un espace
d’Alexandrov de dimension (n 1) avec bord et int (Z) = Z @Z.
Considérons l’espace topologique DzZ [0; 1) (avec la topologie produit) et la
relation d’équivalence : ( ; t) t ( ; s) si et seulement si t = s = 0.
Dé…nition 2.2.9 Soient un espace d’Alexandrov Z et un point z 2 Z. L’espace tan-gent de Z en z est l’espace topologique quotient TzZ = DzZ [0; 1) = t munie de la
structure d’espace de longueur induite par la métrique dTzZ ( ; t); ( ; s) =
p
t2+ s2 2:t:s: cos (d
DzZ( ; )) ,
où ( ; t) ; ( ; s) 2 DzZ [0; 1) et la barre dénote la classe de ces éléments dans TzZ.
Proposition 2.2.10 ([BBI]) Soient un espace d’Alexandrov Z de dimension n et un point z 2 Z. Alors TzZ est un 0-espace d’Alexandrov de dimension n.
Dé…nition 2.2.11 Soient un espace d’Alexandrov Z, un point z 2 Z et une direction 2 DzZ représentée par un segment géodésique t 7! expz(t ) issu de z. La dérivée
d’une fonction lipschitzienne f : Z ! R dans la direction de est dé…nie par dfz( ) = lim
t!0+
f (expz(t )) f (z)
Proposition 2.2.12 Soient un espace d’Alexandrov Z et un point z 2 Z. Il existe une unique application dfz : TzZ ! R telle que
dfz( ; s) = s:dfz( ) = s: lim t!0+
f (expz(t )) f (z)
t ,
pour tout s 2 [0; 1[ et pour toute direction 2 DzZ représentée par un segment
géodésique t 7! expz(t ) issu de z. L’application dfz est appellée la dérivée de f en z.
Soient un espace d’Alexandrov Z et une constante 2 R. Quand @Z = ;, une
application localement lipschitzienne f : Z ! R est dite -concave si, pour toute
courbe : I ! Z, l’application t 7 ! f (t) 2t2 est concave. Quand @Z 6= ;,
notons D (Z) le double de Z muni de la structure d’espace de longueur induite et soit p : D (Z) ! Z la projection canonique. Une application localement lipschitzienne f : Z ! R est dite -concave si l’application f p : D (Z) ! R est -concave.
Dé…nition 2.2.13 Une courbe dans un espace d’Alexandrov Z est appellée une
quasi-géodésique si, pour tout 2 R et pour toute application -concave f : Z ! R,
f est une application -concave.
Soient > 0, un espace d’Alexandrov Z de dimension n et un point z 2 Z. Un -strainer en z est une famille A = f ( i; i) ; i 2 f1; : : : ; ngg de charnières de Z
en z telle que, pour tous i; j 2 f1; : : : ; ng, ] ( i; i) > et ] ( i; j)
2 ; ] ( i; j) 2 ; ] ( i; j) 2 < . Notons que, comme toutes les charnières sont basées en z, les expressions ] ( i; j),
] ( i; j) et ] ( i; j) ont un sens. La longueur du -strainer A est dé…nie par
LZ(A) = min fLZ( i; i) ; i 2 f1; : : : ; ngg .
Dé…nition 2.2.14 Etant donnés > 0 et un espace d’Alexandrov Z de dimension n, l’ensemble R (Z) des points de Z pour lesquels il existe un -strainer sera appelé l’ensemble des points -réguliers de Z. Son complémentaire S (Z) sera appelé l’en-semble des points singuliers de Z. Le -rayon d’injectivité d’un point z 2 R (Z)
et le -rayon d’injectivité d’un sous-ensemble Y R (Z) sont dé…nis par
-rinjZ (z) = sup fLZ(A) ; A est un -strainer en zg
-rZinj(Y ) = inf -rZinj(z) ; z 2 Y :
On remarque que la dé…nition ci-dessus est, d’un certain point de vue, une géné-ralisation de la dé…nition de rayon d’injectivité d’une variété riemannienne.
Proposition 2.2.15 ([BBI], [SY] et [SY2]) Soient > 0 et un k-espace d’Alexandrov Z de dimension n. Alors
i. R (Z) est un ouvert dense de Z localement homéomorphe à des ouverts de Rn, ii. Si k = 1, alors -rZinj(Y ) > 0, pour tout compact Y R (Z),
iii. Si n = 2, alors S (Z) = fz 2 int (Z) ; L (TzZ) 2 g t @Z. De plus, les
ensembles fz 2 int (Z) ; L (TzZ) 2 g et fz 2 @Z ; L (TzZ) g sont
…nis.
2.2.2 Convergence de Hausdor¤-Gromov
Soit Z un espace métrique. Rappelons que la distance de Hausdor¤ entre deux sous-ensembles A et B de Z est dé…nie par
dH(A; B) = inf fr > 0 ; A BZ(B; r) et B BZ(A; r)g .
Lorsque il sera nécessaire d’expliciter l’espace Z et la métrique dZen question, on écrira
dH;(Z;dZ)(A; B) à la place de dH(A; B). On dira qu’une suite Ai de sous-ensembles de
Z converge au sens de Hausdor¤ vers un sous-ensembles A de Z si la suite de nombres réels dH(Ai; A) converge vers zéro.
Il est bien connu ([BBI] - section 7.3.1) que la distance dH dé…nit une métrique
sur l’ensembleF (Z) des sous-ensembles fermés de Z. La proposition ci-dessous énonce quelques autres proprietés classiques de la distance de Hausdor¤.
Proposition 2.2.16 Soient un espace métrique Z et une suite Ai 2 F (Z) convergeant
au sens de Hausdor¤ vers A 2 F (Z).
i. A est l’ensemble des limites de toutes les suites de points ai 2 Ai (i 2 N),
ii. si Z est complet (compact) alors F (Z) est complet (compact),
iii. si Z est un espace de longueur et les ensembles Ai sont convexes, alors A est
convexe.
Dé…nition 2.2.17 La distance de Hausdor¤ -Gromov entre deux espaces
mé-triques Z et Z0 est dé…nie par
dHG Z; Z0 = inf dH;(ZtZ0;d) Z; Z0 ; djZ = dZ et djZ0 = dZ0 .
On dira qu’une suite d’espaces métriques Zi converge au sens de Hausdor¤
-Gromov vers un espace métrique Z lorsque la suite de nombres réels dHG(Zi; Z)
C’est un fait remarquable que la classe C des espaces métriques compacts à isomé-trie près muni de la distance dHG est un espace métrique ([BBI]).
Remarque 2.2.18 La convergence de Hausdor¤ -Gromov peut-être vue comme une
convergence au sens de Hausdor¤ . Plus précisément, si une suite d’espaces métriques Zi converge au sens de Hausdor¤ -Gromov vers un espace métrique Z, alors il existe
une sous-suite Zik et une métrique sur l’union disjointe Z = Z t
F
Zik telle que Zik
converge vers Z au sens de Hausdor¤ . Cet observation nous permet d’écrire, sans perte de généralité, qu’une suite de points zi2 Zi converge au sens de Hausdor¤
-Gromov vers un point de Z.
Proposition 2.2.19 ([BBI]) Soit une suite d’espaces de longueur Zi qui converge au
sens de Hausdor¤ -Gromov vers un espace métrique Z. Alors le complété métrique de Z est un espace de longueur.
Notons que la distance de Hausdor¤-Gromov entre un espace métrique et son complété métrique est nulle. On peut ainsi supposer sans perte de généralité que les limites de Hausdor¤-Gromov de suites d’espaces métriques sont toujours complètes. Avec cette convention, la proposition ci-dessus a¢ rme que la limite de Hausdor¤-Gromov d’une suite d’espaces de longueur est toujours un espace de longueur.
Dé…nition 2.2.20 Soient deux suites d’espaces métriques Zi et Zi0 convergeants au
sens de Hausdor¤ -Gromov respectivement vers des espaces métriques Z et Z0. On dira qu’une suite d’applications fi: Zi! Zi0 converge au sens de Hausdor¤ -Gromov
vers une application f : Z ! Z0 si, pour toute suite zi2 Zi convergeant vers z 2 Z, la
suite fi(zi) converge vers f (z).
Proposition 2.2.21 Soit une suite équicontinue d’applications fi : Zi ! Zi0, où
Zi et Zi0 sont deux suites d’espaces métriques convergentes (au sens de Hausdor¤
-Gromov). Alors la suite fi admet une sous-suite fik : Zik ! Zi0k convergente (au sens
de Hausdor¤ -Gromov).
Etant donné " > 0, une "-isométrie entre deux espaces métriques Z et Z0 est une application (pas nécessairement continue) f : Z ! Z0 telle que BZ0(f (Z) ; ") = Z0 et
dis (f ) = sup fdZ0(f (z1) ; f (z2)) dZ(z1; z2) ; z1; z2 2 Zg < ".
Proposition 2.2.22 ([BBI]) Soient Z et Z0 deux espaces métriques . Alors :
i. si dHG(Z; Z0) < ", il existe une 2"-isométrie f : Z ! Z0,
Corollaire 2.2.23 ([BBI]) Une suite d’espaces métriques Zi converge au sens de
Hausdor¤ -Gromov vers un espace métrique Z si et seulement s’il existe une suite de nombres réels "i > 0 convergeant vers zéro et une suite de "i-isométries fi: Z ! Zi.
La convergence de Hausdor¤-Gromov telle qu’elle a été dé…nie, est un outil puissant pour étudier les suites d’espaces métriques compacts, mais elle devient très restrictive dans le cas général. Pour combler cette lacune on a la généralisation ci-dessous. Dé…nition 2.2.24 Un espace métrique pointé est un couple (Z; z0), où Z est un espace
métrique et z02 Z. Une suite d’espaces métriques pointés (Zi; zi) converge au sens
de Hausdor¤ -Gromov pointé vers un espace métrique pointé (Z; z0) si elle satisfait
la propriété suivante : Pour tout r > " > 0, il existe i02 N et une suite d’applications
(pas nécessairement continues) fi : BZi(zi; r) ! Z tels que, pour tout i i0,
i. fi(zi) = z0,
ii. dis (fi) < ",
iii. BZ(z0; r ") BZ(fi(BZi(zi; r)) ; "),
iv. fi(BZi(zi; r)) BZ(z0; r + ").
On remarque que, pour les espaces compacts, la convergence de Hausdor¤-Gromov pointée implique la convergence de Hausdor¤-Gromov. De plus, si une suite d’espaces métriques compacts Zi converge au sens de Hausdorf-Gromov vers un espace métrique
compact Z, alors pour tout point z0 2 Z, il existe une suite de points zi 2 Z telle que
la suite pointée (Zi; zi) converge au sens de Hausdor¤-Gromov pointé vers (Z; z0).
Une isométrie entre deux espaces métriques pointés (Z; z) et (Z0; z0) est une isomé-trie f : Z ! Z0 qui l’envoi z sur z0. Comme précédemment, on peut toujours supposer que la limite Hausdor¤-Gromov pointée d’une suite d’espaces métriques pointés est complète. Après ces considérations, on a la proposition suivante :
Proposition 2.2.25 ([PP], [BBI]) Soit une suite (Zi; zi) d’espaces de longueur
poin-tés qui converge au sens de Hausdor¤ -Gromov vers un espace métrique (Z; z0). Alors
i. (Z; z0) est un espace de longueur pointé et il est bien dé…nie à isométrie près,
ii. pour tout r > 0, la suite de boules BZi[zi; r] (avec la métrique induite) converge
au sens de Hausdor¤ -Gromov vers la boule BZ[z0; r].
iii. si Zi est une suite de k-espace d’Alexandrov de dimension n, alors Z est un
k-espaces d’Alexandrov de dimension plus petite ou égale à n,
iv. si i : I ! Zi est une suite de quasi-géodésiques qui converge (ponctuellement)
Le théorème suivant est appelé Théorème de Stabilité et il est dû à G.Perelman. Théorème 2.2.26 ([Kap]) Pour tout k-espace d’Alexandrov Z compact et de dimen-sion n, il existe " > 0 qui satisfait la propriété suivante : si Y est un k-espace d’Alexan-drov compact, de dimension n et dHG(Z; Y ) < ", alors Y est homéomorphe à Z.
Corollaire 2.2.27 Soit (Zi; zi) une suite de k-espaces de longueur pointés de
dimen-sion n qui converge au sens de Hausdor¤ -Gromov pointé vers un k-espace de longueur pointé (Z; z0). Alors, pour tout r > 0, il existe i02 N tel que les boules BZi[zi; r] sont
homéomorphes à la boule BZ[z0; r], pour tout i i0. En particulier, si Z est compact,
alors il existe i0 2 N tel que Zi est homéomorphe à Z, pour tout i > i0.
On termine la section avec un résultat sur les suites de variétés riemanniennes. Proposition 2.2.28 ([Gro]) Soit (Mi; pi) une suite pointée de variétés riemanniennes
de dimension n, completes et à courbure uniformement pincée. Si la suite (Mi; pi)
converge au sens de Hausdor¤ -Gromov pointé et la suite des rayons d’injectivité des point pi converge vers zéro, alors la limite a dimension plus petite que n.
2.3
Structures Géométriques
2.3.1 Géométries Modèles et Variétés Géométriques
Pour tous n; k 2 N, on note Mn
k l’unique (à isométrie près) variété riemannienne
complète, connexe, simplement connexe de dimension n et de courbure constante k. Pour k égal à 0, 1 et 1, on écrira aussi En, Sn et Hn à la place de Mn0, Mn1 et Mn1. On présente rapidement la variété Hn.
Un modèle pour Hn est donné par la variété di¤érentiable Rn+= f(x1; : : : ; xn) 2 Rn; xn> 0g muni de la métrique hu; viHn = p hu; vi (xn)2 ,
où x 2 Rn+, u; v 2 TxHn et h:; :i est la métique canonique de Rn. Les géodesiques de
Hnsont toutes les demi-droites et demi-cercles ortogonaux au plan xn= 0.
On dé…ni @Hn, le bord de Hn, comme le bord de Rn+ en tant que sous-espace
topo-logique du compacti…é d’Alexandrov de Rn. Notons Hn= Hn
t @Hn. Il est bien connu que les géodesiques de Hn sont les demi-droites et demi-cercles de Rn
+ orthogonaux à
Quand n = 2, le groupe Isom+(H2) des isométries positives de H2 peut-être iden-ti…é à P SL2(R). Premièrement, notons que R2+= fz 2 C ; Im (z) > 0g. Le groupe des
isométries de H2 est donné par les applications
A : z 2 H27 ! az + bcz + d 2 H2 , où A = a b
c d
!
2 SL2(R),
et A représente la classe de A dans P SL2(R). Une isométrie A 6= Id est dite :
ellipitiquesi tr2(A) < 4 et F ix A \ H2 = fxg H2
parabolique si tr2(A) = 4 et F ix A \ H2 = fxg @H2
hyperbolique si tr2(A) > 4 et F ix A \ H2 = fx; yg @H2.
Quand n = 3, le groupe Isom+(H3) des isométries positives de H3 peut-être iden-ti…é à P SL2(C). Premièrement, notons que R3+t f(z; t) 2 C R ; t > 0g. Le groupe
des isométries de H3 est donné par les applications A : (z; t) 2 H3 7! (az + b) :(cz + d) + act2; t jcz + dj2+ jcj2t2 2 H 3 , où A = a b c d ! 2 SL2(C)
et A représente la classe de A dans P SL2(C). Notons que les isométries A 2 Isom+(H3)
s’étendent à une application dé…nie sur C R. De plus, la restriction de cette extension à C t C f0g = @H3\ R3 satisfait
A (z) = A (z; 0) = (az + b) :(cz + d) jcz + dj2 ; 0
!
t az + bcz + d 2 C . Une isométrie Id 6= A 2 Isom+(H3) est dite :
ellipitique si tr2(A) < 4 et F ix A \ H3 est une géodésique de H3,
parabolique si tr2(A) = 4 et F ix A \ H3 = fxg @H3,
loxodromique si tr2(A) > 4 ou tr2(A) 2 C, et F ix A \ H3 = fx; yg @H3.
Les paires (En; Isom+(En)) ; (Sn; Isom+(Sn)) et (Hn; Isom+(Hn)) sont appelées respectivement géométrie euclidienne, géométrie sphérique et géométrie hy-perbolique, et sont connues comme étant les 3 géométries classiques. On dé…nit maintenant la notion plus générale de géométrie modèle.
Dé…nition 2.3.1 Une géométrie modèle de dimension n est un couple (X; G), où X est une variété riemannnienne de dimension n orientable, connexe, simplement connexe et G est un groupe de Lie d’isométries de X, maximal pour les propriétés :
ii. il existe H < G qui agit de façon discrète sur X et tel que X=H soit compact. Une (X; G)-structure sur une variété topologique M est la donnée d’un atlas A(X;G)= f'i : Ui ! X ; i 2 Ig maximal pour les propriétés :
i. fUigi2I est un recouvrement ouvert de M ,
ii. chaque 'i est un homéomorphisme sur les ouverts 'i(Ui) de X,
iii. si Ui\ Uj 6= ;, alors il existe gij 2 G tel que, pour tout q 2 Ui\ Uj,
gij 'i(q) = 'j(q) . (2.2)
Une (Hn; Isom+(Hn))-structure et aussi appelée une structure hyperbolique. De façon analogue on dé…nit les notions de structure euclidienne et sphérique. Dé…nition 2.3.2 On dira qu’une variété topologique M est géométrique quand elle admet une (X; G)-structure. Une (X; G)-variété est un couple M; A(X;G) , où M est
une variété topologique et A(X;G) une (X; G)-structure sur M . Quand il n’y aura pas
de risque de confusion, on dira simplement que M est une (X; G)-variété ou que M est modélé sur la géométrie (X; G). Les variétés modelés sur les géométries classiques seront aussi appelés variétés euclidiennes, sphériques et hyperboliques.
Notons que l’atlas A(X;G) induit une structure riemannienne sur M de façon à ce
que les applications 'i deviennent des isométries. De plus, si N est une autre variété
topologique et si f : N ! M est un homéomorphisme local, on peut utiliser f pour induire une (X; G)-structure sur N de façon à ce que f devienne une isométrie locale. La propriéte (2.2) permet de développer une courbe : [a; b] ! M dans X de la façon suivante : soient '1; : : : ; 'k 2 A et P = fa0 = a; a1; : : : ; ak 1; ak= bg une
subdivision de [a; b] telle que ([ai 1; ai]) Ui. Quitte a composer les applications 'i
avec un élément de G, on peut supposer qu’elles véri…ent :
'i( (ai)) = 'i+1( (ai)) et '0i( (ai)) = '0i+1( (ai)) ,
pour tout i = 1; : : : ; k 1. Alors, l’application : [a; b] ! X dé…ni par
j[ai 1;ai]= 'i j[ai 1;ai] , i = 1; : : : ; k
est appelée un développement de . Notons que ne dépend que de la première carte et que, pour tout g 2 G, la courbe g est aussi un développement de .
Soient M = M; A(X;G) une (X; G)-variété et : fM ! M son revêtement
uni-versel. Fixons des points p0 2 M et ep0 2 1(p0) et une carte ' : U ! X de A(X;G)
Pour toutq 2 fe M , on choisit un chemin qe: [0; 1] ! fM tel que eq(0) =pe0 et qe(1) =qe
et on pose d (eq) = qe (1), où eq représente le développment de qeen
utilisant ' comme première carte. L’application d (dite une développante de M ) est un di¤éomorphisme local qui ne dépend que de la carte ' (voir [Rat]). De plus, il existe un unique morphisme de groupes = d: 1(M ) ! G tel que
d ( :q) =e ( ) d (q) ,e (2.3)
pour tout dans 1(M ) et pour toutq 2 fe M . Ce morphisphe est appelé l’holonomie
de M associée à d et la propriété (2.3) est connue comme l’equivariance de d par . Notons que si l’on considére sur fM la structure riemannienne induite par la pro-jection , alors 1(M ) agit sur fM par isométries et l’application d est une isométrie
locale. Une autre remarque importante est que toutes les applications développantes pour M peuvent être obtenues à partir d’une telle application d. Plus précisément, si d est une appplication développante pour M , alors D = fg d ; g 2 Gg est l’ensemble de toutes les développantes de la (X; G)-variété M . De plus, pour tout g 2 G, l’holonomie
g associée à g d est dé…nit par g( ) = g ( ) g 1.
Le résultat suivant est connu comme le théorème de géométrisation de Thurston-Perelman :
Théorème 2.3.3 Il existe 8 géométries modèles en dimension 3 qui sont : les (six) géométries de Seifert (E3, S3, S2 E, H2 E, Nil et ^SL
2(R)), la géométrie
hyperbo-lique (H3) et la géométrie résoluble Sol. De plus, si M est une variété topologique de dimension 3 compacte, orientable et première, alors il existe une surface incompres-sible S dans M dont les composantes connexes sont homéomorphes à T2, et telle que chaque composante de M jS peut-être modélé sur une des huit géométries ci-dessus.
Les 6 géométries de Seifert sont appellées ainsi car une variété topologique de dimension 3 est une variété de Seifert si et seulement si elle peut-être modélée sur une de ces 6 géométries. Pour les dé…nitions et propriétés des géométries modèles, on renvoit le lecteur au papier de Peter Scott [Sco].
On termine la section avec quelques résultats sur les variétés hyperboliques : Proposition 2.3.4 Soient M et N deux variétés hyperboliques homéomorphes. Fixons des holonomies M et N pour M et N respectivement. Alors M et N sont conjugués
dans P SL2(C) si et seulement si M et N sont isométriques.
Théorème 2.3.5 (de Mostow) Soient M et N deux variétés hyperboliques
com-plètes, de volume …ni et de dimension n > 2. S’il existe une equivalence
d’homoto-pie f : M ! N, alors il existe aussi une isométrie : M ! N homotope à f. En
Proposition 2.3.6 Soient M une variété hyperbolique de dimension 3 et une géo-désique fermée de M . Alors, il existe sur M une métrique hyperbolique complète.
2.3.2 Variétés Hyperboliques Coniques
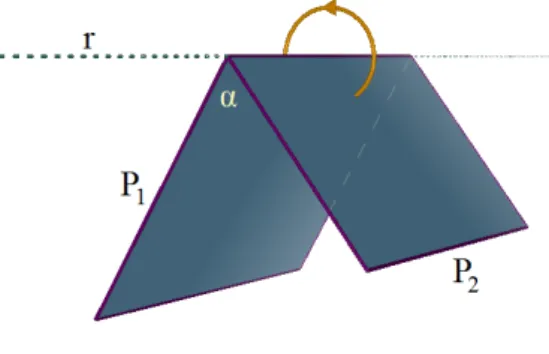
Fixons 2 (0; 2 ] et k 2 R arbitraires. On note M2k( ) l’espace obtenu en recollant par rotation les faces d’un secteur dihedral d’angle dans M2k. Plus précisément, soit R la région de M2k delimitée par deux demi-plans P1 et P2de M2ktels que @P1= @P2= r
et l’angle dihedral (du côté de R) est égale à (…gure 2.2). Alors, M2k( ) est l’espace obtenu en recollant P1 et P2 par une rotation autour de r. La géodésique r sera
appelée géodésique singulière de M2k( ) et les points de r seront dits singuliers. On
écrira H3( ), E3( ) et S3( ) à la place de M31( ), M30( ) et M31( ).
Fig. 2.2 –Dihèdre d’angle dans Mk3
Dé…nition 2.3.7 Soient une variété di¤ érentiable M orientable de dimension 3, un
entrelacs = 1 t : : : t k plongé dans M et = f 1; : : : ; kg (0; 2 ]. Une
structure hyperbolique conique d’angle sur le couple (M; ) est une structure hyperbolique A(H3;P SL
2(C)) (non-complète) sur M telle que :
i. il existe une (et une seule) métrique intrinsèque dM sur M telle que (M; dM) est
le complété métrique de M ,
ii. tout point p appartenant à une composante i de admet un voisinage
isomé-trique à un voisinage d’un point singulier de H3( i).
Une variété hyperbolique conique est un quadruplet M = M; ; ; A(H3;P SL 2(C)) ,
où M; et sont comme ci-dessus et A(H3;P SL
2(C)) est une structure hyperbolique
co-nique d’angle sur (M; ). Quand la précision de la structure n’est pas importante on dira simplement que M est une variété hyperbolique conique de type topologique (M; ) (et d’angle conique si l’on veut préciser les angles).
Remarque 2.3.8 Une variété hyperbolique telle que nous l’avons dé…nie, est un es-pace d’Alexandrov avec courbure minorée par 1.
Notons que si = ; ou = f2 ; : : : ; 2 g, alors M est une variété hyperbolique complète. On peut étendre la dé…nition de variété hyperbolique conique de façon à admettre l’angles zéro sur les composantes de . Pour cela il faut permetre que la structure hyperbolique soit complète autour des singularités, c’est-à-dire, qu’un com-posante i puisse avoir un voisinage Ui tel que Ui i soit isométrique à une cusp
parabolique (de rang 2). Dans ce cas-là, on dira que l’angle conique i sur la
compo-sante i est égal à zéro. Naturellement, le complété de M ne sera plus M , mais
M moins les composantes singulières dont les angles coniques sont nuls.
D’après le théorème d’hyperbolisation de Thurston, s’il existe une structure hyper-bolique conique sur une paire (M; ), alors M est hyperbolique, c’est-à-dire qu’il existe une structure hyperbolique complète sur M (voir [Koj]). Cette structure (unique par Mostow) est, avec les notations précédentes, la structure hyperbolique conique d’angle = f0; : : : ; 0g.
On dé…nit les développantes et les holonomies d’une variété hyperbolique conique de type topologique (M; ) comme celles de la structure hyperbolique sur M .
Les modèles locaux autour des points singuliers d’une variété hyperbolique M per-mettent d’obtenir plusieurs informations utiles sur la métrique autour de la singularité. Nous les avons rassemblée dans la proposition suivante :
Proposition 2.3.9 Soit M une variété hyperbolique conique de type topologique (M; ), d’angles coniques = f 1; : : : ; kg, d’holonomie : 1(M ) ! P SL2(C) et
d’ap-plication développante d : ^M ! H3 (associée à ), où : ^M ! M est le
revêtement universel de M . Alors
i. les composantes i de sont des géodésiques de M,
ii. si est un segment géodésique minimisant de M et int ( ) \ 6= ;, alors , iii. admet un voisinage ouvert maximal U = U1t : : : t Uk, où chaque Ui est un
voisinage de i homéomorphe à un tore solide et les ouverts Ui= Ui (appelés
cusps de M) admettent une structure produit du type T2 [0; 1) de façon à ce que
chaque courbe (fxg [0; 1))i soit une géodesique minimisante de M qui touche i orthogonalement et chaque feuille T2 ftg i soit une sous-surface
rieman-nienne de M à courbure zéro, orthogonales aux géodésiques (fxg [0; 1))i et
incompressibles dans M . Si l’angle i6= 0, alors les développés d 1(Ui)
sont des voisinages métriques disjoints des géodésiques gij distincts de H3,
c’est-à-dire qu’il existe "i > 0 tel que
d 1(Ui) =
[
De plus, les développés d 1 T2 ftg i des feuilles de Ui sont des
sur-faces equidistantes des géodésiques gij. Si l’angle i = 0, alors les développés
d 1(Ui) sont des horoboules centrées en pij distincts de @H3 et les
dévelop-pés d 1 T2 ftg i des feuilles de Ui sont des horosphères en pij,
iv. Soient i une composante de et un méridien de . Si i6= 0, alors ( ) est
une rotation d’angle i autour d’une des géodésiques gij. Si i = 0, alors ( )
est un élément parabolique qui …xe un des points pij,
v. Soient i une composante de et un couple ( ; ) méridién/longitude pour Ui.
Si i 6= 0, alors ( ) est un élément loxodromique de même axe que ( ) et dont
la longueur de translation coïncide avec la longueur de i. Si i = 0, alors ( )
est un élément parabolique qui …xe le même point à l’in…ni que ( ). La proposition ci-dessus motive la dé…nition suivante :
Dé…nition 2.3.10 Soit M une variété hyperbolique conique de type topologique (M; ) et d’angles coniques = f 1; : : : ; kg. Pour tout i 2 f1; : : : ; kg, la constante non nulle
RM( i) ( i6= 0) présenté dans le (iii) de la proposition précédent est appelée rayon
d’injectivité normal de la composante i. Pour les composantes i de d’angle
conique i = 0, on pose RM( i) = 1. Le rayon d’injectivite normal de sera
dé…ni par RM( ) = min fR ( i) ; i 2 f1; : : : ; kgg.
Soit i une composante de telle que i 6= 0. Une remarque importante est qu’il
existe une composante i0 de (avec peut-être i = i0) telle que, pour toute géodésique
gij, il existe au moins une géodésique gi0j0 telle que
RM( i) = RM( i0) et BH3[gij; RM( i)] \ BH3 gi0j0; RM( i0) 6= ; .
De plus, il existe un segment géodésique minimisant qui rélie i à i0
orthogonale-ment et tel que LM( ) = 2:RM( i) = 2:RM( i0) (= dM( i; i0), si i 6= i0).
La structure riemannienne sur le complementaire de la singularité permet de dé…nir la notion de rayon d’injectivité et de volume.
Dé…nition 2.3.11 Soient M une variété hyperbolique conique de type topologique (M; ) et g la métrique riemannienne induite par la structure hyperbolique sur M . Pour tout point p 2 M , le rayon d’injectivité rinjM (p) de p dans M est le rayon d’injectivité de p dans la variété riemannienne (M ; g). Le volume de M est le volume riemannien de la variété riemannienne (M ; g) et sera noté par V ol (M). La proposition suivante dé…nit le polyhèdre de Dirichlet d’une variété hyper-boliques coniques :
Proposition 2.3.12 Soit M une variété hyperbolique conique de type topologique (M; ), d’angles coniques = f 1; : : : ; kg, de développante d : ^M ! H3 et
d’holonomie : 1(M ) ! P SL2(C), où : ^M ! M est le revêtement
universel de M . Etant donné p 2 M et x 2 d 1(p) , il existe un polyhèdre
etoilé DM = DM(p) dans H3 tel que x 2 int (D
M) et M est isométrique au quotient
de DM par une identi…cation de ses faces. De plus :
i. pour chaque face F de DM, il existe un élément F 2 1(M ) tel que
F y 2 H3; dH3(x; y) = dH3( ( F) :x; y) ;
ii. DM est convexe si et seulement si les angles coniques i appartiennent à [0; ].
L’intérieur du polyhèdre DM = DM(p) est isométrique à l’ensemble des points non singuliers de M qui ont une seule géodésique minimisante d’extrémité p. Les points singuliers de M sont associés aux points des arètes de DM contenues dans les
géodésiques gij décrites ci-dessus.
Une notion très important pour l’étude de déformations de structures hyperbo-liques coniques est celle d’e¤ondrement dont la dé…nition est :
Dé…nition 2.3.13 On dit qu’une suite Mi de variétés hyperboliques coniques de type
topologique (M; ) s’e¤ ondre si, pour toute suite de points pi 2 M , la suite
rMi
inj (pi) converge vers zéro. Dans le cas contraire, on dira que la suite Mi ne
s’ef-fondre pas.
On termine cette section avec quelques résultats de base sur les variétés coniques. Proposition 2.3.14 ([Fuj]) Etant données des constantes D1; D2; I > 0, il existe une
constante U = U (D1; D2; I) > 0 qui satisfait la propriète suivante : Soient une variété
hyperbolique conique M de type topologique (M; ) et deux points p; q 2 M . Alors rinjM (q) U si et rMinj(p) I, dM(p; ) ; dM(q; ) D1 et dM(p; q) D2.
Proposition 2.3.15 ([Fuj]) Soit Mi une suite de variétés hyperboliques coniques de
type topologique (M; = 1t : : : t l) et d’angles coniques ( i1; : : : ; il) 2 (0; 2 )l.
Si inf fRMi( ) ; i 2 Ng > 0, alors il existe une suite de points pik 2 M tel que la
suite pointé (Mik; pik) converge au sens de Hausdor¤ -Gromov pointé vers une variété
hyperbolique conique M1de dimension 3 et d’angles coniques j = lim
k!1 ikj 2 [0; 2 ].
De plus, si j > 0, pour tout j 2 f0; : : : ; lg, alors le type topologique de M1 est aussi
2.3.3 Déformation de structures hyperboliques coniques
Dans ce paragraphe, M denotera une variété di¤érentiable, orientable, de dimension 3 et = 1 t : : : t k un entrelacs plongé dans M tel que le groupe fondamental
1(M ) de M soit …niment engendré. On considera sur SL2(C) la topologie
induite par la norme "
a11 a12
a21 a22
#
= max fjaijj ; i; j 2 f1; 2gg
et sur P SL2(C) = SL2(C) = f Idg la topologie quotient.
Dé…nition 2.3.16 L’espace de représentations de M dans P SL2(C) est
l’en-semble R (M ) de tous les homomorphismes de 1M dans P SL2(C). Les éléments de
R (M ) sont appelés représentations. Une représentation 2 R (M) sera appelée ré-ductible si le groupe ( 1M ) P SL2(C) …xe un point de @H3. Les représentations
qui ne sont pas réductibles sont appellées irréductibles.
Fixons une présentation h 1; : : : ; n; r1; : : : ; rli pour 1M . On considère sur R (M )
la topologie dont la base est donné par les éléments
B ( ; V1; : : : ; Vn) = f' 2 R (M) ; ' ( k) 2 Vk 8k = 1; : : : ; ng
où 2 R (M) et, pour tout k 2 f1; : : : ; ng, Vkest un voisinage de ( k) dans P SL2(C).
La notion de convergence pour cette topologie est la notion de convergence ponc-tuel, c’est-à-dire, une suite de représentations i 2 R (M) converge vers une
représen-tation 2 R (M) si et seulement si i( ) converge vers ( ), pour tout 2 1M .
Le groupe P SL2(C) agi sur R (M) par conjugaison. Plus précisément, pour tout
2 R (M), pour tout 2 1M et pour tout A 2 P SL2(C), on a A: ( ) = A ( ) A 1.
On considère sur R (M ) =P SL2(C) la topologie quotient.
On peut munir R (M ) d’une structure algébrique. Plus précisément, on peut voir R (M ) comme un sous ensemble algébrique fermé de C9n. Commençons pour rappeler qu’on peut plonger le groupe P SL2(C) dans C9 (voir [BMP]). Considérons
la présentation
1(M ) = h 1; : : : ; n; r1; : : : ; rli
et l’application injective
: 2 R (M ) 7! ( ( 1) ; : : : ; ( n)) 2 P SL2(C) C9n .
Comme l’image de est un sous-ensemble algebrique fermé de C9n qui ne depend pas (à isomorphisme algébrique près) de la présentation choisi ([BMP]), R (M ) a une structure de fermé algébrique bien dé…nie.
On remarque que toute holonomie d’une variété hyperbolique conique de type to-pologique (M; ) est irréductible ([Koj2]). De plus, les conjugués d’une représentation irréductible sont contenus dans la même composante irréductible de R (M ).
Le quotient R (M ) =P SL2(C) n’a pas une jolie structure comme R (M ).
Parcontre les représentations d’holonomie des variétés hyperboliques coniques de type topologique (M; ) ont des voisinages avec des bonnes propriétés. Commençons par dé…nir les coé…cients généralisés de remplissage de Dehn.
La longueur complexe d’un élément A non parabolique de P SL2(C) est le
nombre complexe LC(A) = lA+ i A, où lA et A sont respectivement la distance de
translation de A et l’angle de rotation de A. Il est connu (voir [CHK]) que l’application LC est invariante par conjugation et qu’elle satisfait
jtrAj = 2: cosh LC2(A) . En particulier, si A est elliptique on a
jtrAj = 2: cosh i2A = 2: cos A
2 ) LC(A) = 2i: arccos
jtrAj
2 .
Etant donnée une variété hyperbolique conique M de type topologique (M; ) et d’angle conique = ( 1; : : : ; k) 2 ]0; 2 ]k, soit Mune représentation d’holonomie de
M. Fixons des méridiens 1; : : : ; k et de longitudes 1; : : : ; k pour les composantes 1; : : : ; kde tels que les éléments M( i) et M( i) de P SL2(C) laissent invariant
la même géodésique de H3. Alors, on peut dé…nir les applications continues L : 2 R (M ) =P SL2(C) ! (L 1( ) ; : : : ;L k( )) C
k
L : 2 R (M ) =P SL2(C) ! (L 1( ) ; : : : ; L k( )) C
k
où L i( ) =LC( ( i)) et L i( ) = LC( ( i)), pour tout i 2 f1; : : : ; kg.
Comme, pour tout i 2 f1; : : : ; kg, M( i) est un imaginaire pure et M( i) non, on
a un voisinage U M de M dans R (M ) =P SL2(C) et deux application continues
p : 2 U M! (p1( ) ; : : : ; pk( )) 2 Rk et q : 2 U M ! (q1( ) ; : : : ; qk( )) 2 Rk
qui sont les seules solutions sur U M du système
pi:L i+ qi:L i = 2 i i 2 f1; : : : ; kg .
Les applications p et q sont appellés les coe…cients généralisés de remplissage de Dehn. Notons que pi( M) = 2
i et qi( M) = 0, pour tout i 2 f1; : : : ; kg. Quitte à réduire
Rappelons le concept de chirurgie de Dehn. Soit M une variété topologique de dimension 3 avec bord composé d’une union disjointe de tores @M = @M1t : : : t @Mk.
Etant données des courbes fermées i non triviales sur @Mi (i = 1; : : : ; k), on dé…nit
M 1;:::; k une variété tridimensionelle compacte obtenue à partir de M en recollant des
tores solides T1; : : : ; Tk sur les composantes de son bord par des homéomorphismes i: @Mi! @Ti tels que i( i) borde un disque dans Ti. On remarque que, à isotopie
près, la variété M 1;:::; k ainsi obtenue ne depend pas des homéomorphismes choisis.
Supposons maintenant M est une variété hyperbolique conique de type topologique (M; ) et d’angle conique = ( 1; : : : ; k) 2 [0; 2 ]k (c’est-à-dire on admet les cusps
paraboliques de rang 2). Considérons l’application F : 2 V M ! (F1( ) ; : : : ; F1( )) 2 R
2
[ f1g : : : R2[ f1g , où, pour tout i 2 f1; : : : ; kg,
Fi( ) =
(
(pi( ) ; qi( )) si i 6= 0
1 si i = 0
.
Fixons des voisinages tubulaires ouvertes N ( i) de i homéomorphes à des tores
solides et supposons que les éléments i et i peuvent être écrits comme i = i i i 1 et i = i i i 1;
où i est un chemin reliant le point base de M à @N ( i) et le couple i; i est
une couple méridien/longitude pour les tores N ( i).
Comme conséquence du théorème ci-dessous, les points de R (M ) =P SL2(C)
associés aux représentations d’holonomie de structures hyperboliques coniques de type topologique (M; ) ont des voisinages lisses. Il combine le théorème de chirurgie hy-perbolique de Thurston (voir [BoP] - appendice) et le théorème de dé¤ormation de Hodgson-Kerckho¤ (voir [Koj2])
Théorème 2.3.17 Soit M une représentation d’holonomie d’une variété hyperbo-lique conique M de type topologique (M; ), alors il existe un voisinage V M U M
de M dans le quotient R (M ) =P SL2(C) tel que la restriction
FjV
M : V M ! F (V M) C
k
est un di¤ éomorphisme. De plus, si 2 V M et, pour tout i 2 f1; : : : ; kg,
Fi( ) = 1 ou Fi( ) 6= 1 et
qi( )
pi( ) 2 Q,
alors est une représentation d’holonomie d’une variété hyperbolique coniques de type topologique (N; ) dé…nie de la façon suivant :