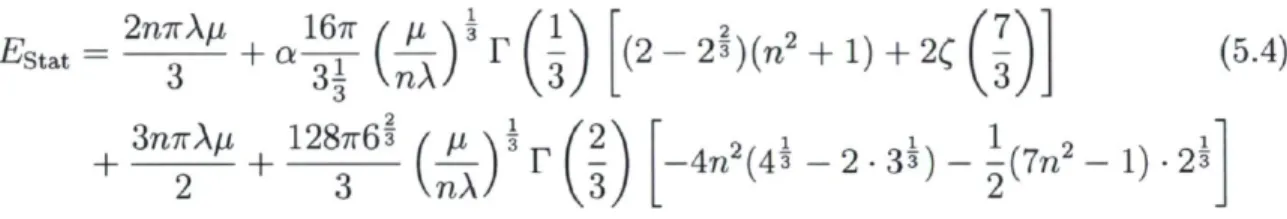Multi-skyrmions quasi-BPS et noyaux atomiques : énergie de Coulomb et configurations pleines

Multi-skyrmions q u a s i - B P S et noyaux a t o m i q u e s

Énergie de Coulomb et configurations pleines

Mémoire présenté

à la Faculté des études supérieures et postdoctorales de l'Université Laval dans le cadre du programme de maîtrise en physique

pour l'obtention du grade de Maître es sciences (M.Sc.)

FACULTÉ DES SCIENCES ET DE GÉNIE UNIVERSITÉ LAVAL

QUÉBEC

2012

Le modèle de Skyrme est une théorie des champs classique non-linéaire qui possède des solitons topologiques comme solutions. De façon innovatrice, ces solutions sont uti-lisées par Skyrme pour décrire les baryons. Ceci est justifié puisque le modèle est une théorie efficace de la chromodynamique quantique à basse énergie et puisque les solu-tions possèdent un nombre topologique conservé qu'on associe au nombre baryonique. Le modèle original permet de décrire les propriétés des nucléons avec une précision de 30% ou mieux, mais a de la difficulté à reproduire les caractéristiques des baryons de masse élevé. En effet, l'énergie de liaison des multi-skyrmions est très grande et les den-sités baryonique possèdent des structures spatiales complexes et de type coquille ce qui s'éloignent des observations expérimentales. On propose alors une extension du modèle afin d'améliorer précisément les deux problèmes précédents.

Ce travail introduit le modèle de Skyrme quasi-BPS dont les solutions analytiques saturent presque la borne de Bogomol'nyi améliorant les prédictions de l'énergie de liaison des multi-skyrmions. Le choix d'un potentiel permettant d'obtenir des densités baryonique de configurations pleines et l'ajout de l'énergie de Coulomb et de brisure de symétrie d'isospin à la masse du skyrmion sont les contributions originales de ce travail. Ceci permet d'obtenir des meilleurs prédictions physiques pour les multi-skyrmions de nombre baryonique très élevé que dans le modèle original et l'analyticité des solutions en simplifie le traitement. Pour ces raisons, le modèle de Skyrme quasi-BPS s'avère une bonne théorie efficace pour la descriptions des noyaux atomiques.

Résumé ii

Table des matières iii Liste des tableaux v Table des figures vi

1 Introduction 1 2 Solitons topologiques et modèle de Skyrme 6

2.1 Topologie et solitons 6 2.1.1 Classe d'homotopie 7 2.1.2 Solitons topologiques 7 2.1.3 Stabilité et théorème de Derrick 9

2.2 Modèle de Skyrme original 10 2.2.1 Symétrie chirale 11 2.2.2 Paramétrisation des champs de pions 12

2.2.3 Lagrangien du modèle du Skyrme 13 2.2.4 Masse du skyrmion et borne de Bogomol'ny 14

2.2.5 Configuration de l'hérisson 15

3 Multi-skyrmions et multi-baryons 18

3.1 Propriétés des multi-skyrmions 18 3.1.1 Skyrmion de charge supérieure 18

3.1.2 Validité du modèle à la description des multibaryons 19

3.2 Phénoménologie des multi-baryons 20 3.2.1 Structure des nucléons 20 3.2.2 Énergie de liaison et formule de Weizacker 22

4 Extension du modèle de Skyrme 25

4.1 Modèle de Skyrme BPS 26 4.2 Modèle de Skyrme quasi-BPS 29

4.2.1 Stratégie du modèle 29 4.2.2 Lagrangien du modèle 29 4.2.3 Énergie statique et stabilité de Derrick 30

4.2.4 Moments d'inertie et énergie de rotation 31 4.2.5 Densité de charge électrostatique du skyrmion 34

4.2.6 Énergie de Coulomb 36 4.2.7 Énergie de brisure de symétrie d'isospin 37

4.2.8 Masse totale du skyrmion quasi-BPS 38

5 Prédictions du modèle quasi-BPS 39

5.1 Skyrmions quasi-BPS coquilles 39 5.2 Skyrmions quasi-BPS pleins 42

5.2.1 Potentiel et angle chiral 42

5.2.2 Énergie statique 44 5.2.3 Moments d'inertie et énergie de rotation 44

5.2.4 Densité baryonique et densité de charge 45 5.3 Prédictions physiques du modèle quasi-BPS 46

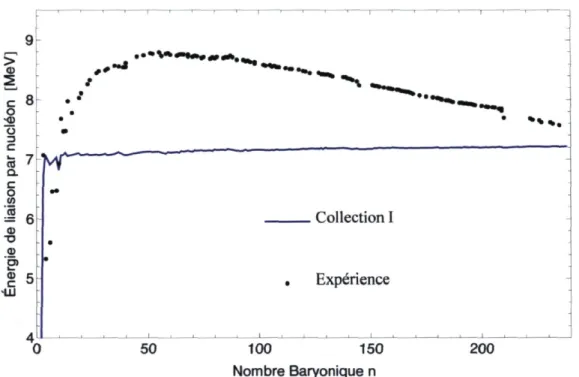
5.3.1 Collection de paramètres I 46 5.3.2 Collection de paramètres II et III 49

5.4 Discussion des résultats 52 5.4.1 Validité du modèle quasi-BPS 52

5.4.2 Angle chiral et densité de charge électrique 54 5.4.3 Contribution de l'énergie de Coulomb 56

6 Conclusion 60 Annexe A

Calcul du courant vecteur 63

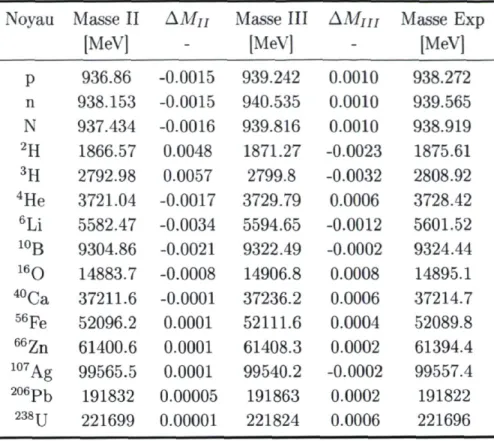
5.1 Valeurs des paramètres du modèle de Bonenfant et Marleau 40 5.2 Valeurs des paramètres de la collection I du modèle quasi-BPS 47 5.3 Masses des multi-skyrmions de la collection I du modèle quasi-BPS . . 47

5.4 Valeurs des paramètres des collections II et III du modèle quasi-BPS . 49 5.5 Masse des multi-skyrmions des collection II et III du modèle quasi-BPS 50 5.6 Écarts type de l'énergie de lisaison prédite par le modèle quasi-BPS . . 51 5.7 Contribution de chacun des termes du lagrangien à l'énergie statique . 53 5.8 Valeurs des paramètres du modèles de Skyrme dans le modèle quasi-BPS 53 5.9 Contribution de chacun des types d'énergie à la masse des skyrmions . 57

1.1 Densityé baryonique dans le modèle de Skyrme originial 3 2.1 Configuration de l'hérisson dans le modèle de Skyrme 16 2.2 Profil radial de l'angle chiral £(r) dans le modèle de Skyrme 16 3.1 Exemples de densités baryoniques des multi-skyrmions 19 3.2 Densité de charge dans le modèle de Fermi à 3 paramètres 22 3.3 Énergie de liaison par nucléon de la formule de Weizacker 24 4.1 Profil radial de l'angle chiral £(r) dans le modèle d'ASW 28 5.1 Énergie de liaison par nucléon dans le modèle de BM 41 5.2 Exemples de densité baryonique dans le modèle de BM 41

5.3 Énergie de liaison par nucléon de la collection I 48 5.4 Énergie de liaison par nucléon de la collection II et III 50

5.5 Comparaison entre l'énergie de liaison des collections I, II et III . . . . 52 5.6 Exemples de profil radial du modèle quasi-BPS pour différents n . . . . 54 5.7 Densité de charge du proton et du neutron dans le modèle quasi-BPS . 55

5.8 Exemples de densité de charge dans le modèle quasi-BPS 55 5.9 Contributions différentes à l'énergie de liaison du modèle quasi-BPS . . 57

5.10 Comparaison de l'énergie de Coulomb du modèle quasi-BPS et de la

Introduction

On associe souvent le début de la physique nucléaire à la découverte de la radioac-tivité en 1896 par Becquerel [1]. À cette époque, uniquement les interactions gravita-tionnelles et électromagnétiques sont connues et il est impossible de décrire pourquoi les propriétés chimiques de certains matériaux radioactifs sont modifiées au cours du temps. En 1911, en effectuant de la diffusion d'électrons sur certains matériaux, Ruther-ford propose que les atomes possèdent une petite région centrale dont Chadwick parvint à mesurer le rayon. En effet, en 1920, en effectuant de la diffusion de particules a sur des noyaux lourds, il détermine que les rayons sont de l'ordre de 10~14 m ce qui s'éloigne

grandement du rayon des atomes qui sont plutôt de l'ordre de 10"10 m. À ce moment,

uniquement les protons sont découvert puisque les expériences de diffusion impliquent uniquement l'interaction électromagnétique et il faut attendre jusqu'en 1932 pour la confirmation de l'existence du neutron, par Chadwick, Curie et Joliot [2, 3]. Les noyaux constitués uniquement de protons et de neutrons doivent être instables s'il n'existe pas une autre force attractive pour combattre la répulsion électromagnétique entre les protons. C'est cette observation qui nécessite l'introduction d'un nouveau type d'inter-action qui doit posséder certaines propriétés importantes. En effet, cette nouvelle force possède une attraction très forte uniquement à très courte distance contrairement aux interactions gravitationnelles et électromagnétiques, qui possèdent une portée infinie et dont la force diminue comme le carré de la distance entre les objets.

Au début des années 40, la théorie quantique des champs décrit l'interaction élec-tromagnétique en terme d'échange de photons, qui sont les particules messagères de cette force. Yukawa [4] propose alors de décrire l'interaction entre les nucléons comme l'échange d'un autre type de particules, soit les mésons. Il explique alors la courte dis-tance d'interaction par la masse non-nulle des mésons messagers contrairement aux pho-tons sans masse. Cependant, la chromodynamique quantique (QCD), qui est le premier

exemple d'une théorie de jauge exacte asymptotiquement libre, formulée par H. David Politzer, Frank Wilczek et David Gross en 1973, s'avère être un cadre théorique plus adéquat pour décrire l'interaction forte. Les particules fondamentales de cette théorie sont les quarks, qui interagissent entre eux via l'échange de gluons [5]. Les protons et les neutrons ne sont alors plus considérés comme des particules élémentaires, mais plutôt comme des états liées de trois quarks tandis que les mésons sont composés d'une paire de quarks et d'antiquarks. Par contre, les nucléons sont des baryons de basse énergie et des calculs perturbatifs en QCD sont difficiles car la constante de couplage entre les quarks et les gluons est trop grande. Des méthodes non-perturbatives, telles que la théorie de jauge sur réseaux [6], permettent d'obtenir plusieurs résultats intéressants, mais de-mandent des calculs numériques très compliqués nécessitant des super-ordinateurs. Une alternative est alors d'utiliser une théorie efficace afin d'obtenir une idée générale des propriétés du modèle exact. Pendant les années 70, c'est dans cette axe de pensée que t'Hooft [7] cherche à faire un développement en série de QCD selon l'inverse du nombre de couleurs des quarks ^ - en espérant simplifier la théorie pour un grand nombre de couleurs. Ces travaux sont de grande importance puisque dans cette limite, QCD est l'équivalent d'une théorie efficace de mésons. Par la suite, en 1979, Witten [8, 9] propose alors de décrire les baryons comme une solution solitonique de cette théorie efficace en négligeant totalement la structure en quarks.

C'est précisément ce que Skyrme [10, 11, 12, 13, 14] avait déjà proposé, pendant les années 1960, dans une série d'articles remarquables parue bien avant l'existence de QCD. En effet, suivant l'idée proposée par Yukawa, Skyrme tente de décrire la dynamique des baryons à l'aide d'une théorie de champs de pions. A cette époque, les nucléons et les pions sont considérés approximativement comme un doublet et un triplet de la symétrie d'isospin introduite par Heiseinberg [15] pour décrire l'interaction forte. Par contre, peu après, les expérimentateurs en physique des particules découvrent que la physique des pions ne respecte pas la symétrie de parité. Pour expliquer ce nouveau phénomène, il faut introduire une nouvelle symétrie approximative : la symétrie chirale. Afin d'inclure cette propriété dans son modèle efficace, Skyrme impose une contrainte non-linéaire entre les champs et suggère alors un lagrangien invariant sous la symétrie chirale afin de décrire la physique des pions et du même coup, la physique des baryons. Une particularité importante de ce modèle est qu'il existe des solitons topologiques stables comme solutions d'énergie minimale provenant de la nature non-linéaire de la théorie. Ceux-ci sont caractérisés par un nombre entier conservé n que Skyrme propose d'associer au nombre baryonique B ou au nombre de masse A d'un noyau atomique. Les champs du modèle peuvent être parametrises de façon matricielle et Skyrme propose une configuraton sphérique d'énergie minimale dites de l'hérisson pour n = 1. Le modèle permet de décrire les propriétés du nucléon avec une erreur maximale d'approximativement 30% ce qui est un très bon résultat pour un modèle à

deux paramètres [16, 17].

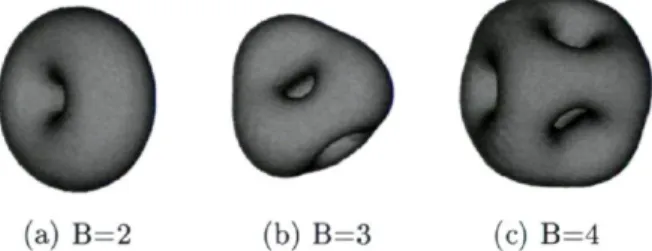
Puisqu'on désire étendre le modèle à la description de noyaux plus lourd, il est nécessaire que les solitons respectent les lois statistiques des différents types de parti-cules. Les travaux de Finkelstein et al [18] ainsi que ceux de Balachandran et al [19] démontrent que les solitons de charge topologique impaire sont des fermions tandis que ceux de charge paire sont des bosons. Cette identification des multi-skyrmions aux deux différents types de particules est une autre raison favorable à l'utilisation du modèle de Skyrme à la description des baryons. Cependant, la non-linéarité des équations associées au lagrangien ne permet pas d'obtenir facilement les solutions pour les skyrmions de charge n > 2. En effet, en étendant la configuration hérisson à des charges topologiques supérieurs, les masses et les énergies de liaisons des solutions sont bien supérieures à l'expérience et les multi-skyrmions sont alors instables sous désintégrations en plusieurs skyrmions. Les premiers avancements notables à la descriptions de multi-skyrmions pro-viennent de Braaten et Carlson [22] qui décrivent le deutéron comme un skyrmion de charge topologique n = 2. Cependant, la densité d'énergie de cette solution présente une configuration toroïdale s'éloignant des mesures expérimentales. Pour déterminer les solutions pour de plus grandes charges topologiques, des méthodes numériques, tels le recuit stimulé et la relaxation, ont été appliquées et ont permis de calculer les densités d'énergie des multi-skyrmions (voir figure 1.1).

# ©

(a) B=2 (b) B=3 (c) B=4

FIGURE 1.1 - Densityé baryonique dans le modèle de Skyrme originial.

La complexité des densités baryoniques et le temps d'exécution élevé des calculs nu-mériques suggèrent alors de modifier le modèle de Skyrme original. La forme du lagran-gien proposé par Skyrme n'est pas unique et plusieurs généralisations d'un lagranlagran-gien efficace de QCD sont proposées. Par exemple, l'ajout de termes d'ordre supérieur en dérivée du champ de pions [24, 25], l'ajout de mésons vectoriels supplémentaires à la théorie [26, 27] ainsi que la modification du terme de masse des pions responsable de la brisure de symétrie chirale [28, 29, 30, 31].

Récemment, une nouvelle approche intéressante, proposée par Adams, Sanchez-Guillen et Weresczynski [32] (ASW), se base sur un lagrangien contenant uniquement

un terme d'ordre six en dérivée du champ et un potentiel. En utilisant une paramétrisa-tion à symétrie axiale pour les champs, ils obtiennent une soluparamétrisa-tion analytique saturant la borne de Bogomol'nyi. Cette borne limite la masse minimale du skyrmion et la satu-rer diminue l'énergie de liaison des multi-skyrmions. Par contre, le lagrangien proposé par ASW ne permet pas de faire le lien avec la physique des particules puisqu'il ne contient pas de terme d'ordre 2 en dérivée du champs responsable de la propagation des pions. La faible énergie de liaison des noyaux suggère alors la recherche d'un modèle dont les solutions saturent presque la borne BPS afin d'obtenir une description viable de la physique nucléaire.

Dans cette perspective, nous proposons d'étudier un modèle de Skyrme quasi-BPS. Celui-ci se base sur un lagrangien proposé par Jackson et al. [33] contenant les termes du modèle de Skyrme original ainsi que ceux du modèle d'ASW. Pour diminuer l'énergie de liaison des multi-skyrmions, on étudie le régime où les contributions du modèle de Skyrme original peuvent être considérées comme des perturbations relativement aux termes d'ordre 6 et au potentiel. D'autre part, puisqu'on tente d'associer les skyrmions à des états nucléaires, il est possible d'améliorer les prédictions de l'énergie de liaison des multi-skyrmions en introduisant explicitement d'autres contributions à leurs masses. Premièrement, les nucléons sont des états de spin et d'isospin bien définis qu'on peut incorporer aux modèles de Skyrme en effectuant une quantification semi-classique du skyrmion. L'obtention d'un hamiltonien de rotation permet alors d'inclure l'énergie de rotation et d'iso-rotation à la masse du skyrmion. Deuxièmement, puisque les nucléons sont constitués de particules chargés électromagnétiquement, il est nécessaire d'inclure l'énergie de Coulomb. Les densités de charge électrique très complexes des solutions du modèle de Skyrme original posent problème pour calculer le potentiel électromagnétique ainsi que l'énergie de Coulomb. La symétrie axiale des solutions du modèle quasi-BPS permet un calcul relativement facile et presque totalement analytique de l'énergie de Coulomb. De plus, les deux contributions d'énergie précédentes ne sont pas suffisantes pour expliquer la différence de masse entre le proton et le neutron dans le modèle quasi-BPS. On introduit alors un terme d'énergie proportionnel à la troisième composante d'isospin qu'on parametrise à l'aide de la différence de masse expérimentale des neutrons et des protons. L'ajout de toutes ces contributions permet alors une meilleure prédiction de l'énergie de liaison par nucléon des multi-skyrmions quasi-BPS.

L'objectif de ce travail est d'obtenir une théorie des champs efficace permettant de décrire les propriétés des noyaux atomiques tout en gardant le lien avec la physique des particules. On désire, plus précisément, améliorer l'énergie de liaison ainsi que la structure des densités d'énergie et des densités de charge électrique pour mieux re-produire les mesures expérimentales. Dans le chapitre 2, on présente les éléments de topologie nécessaires à la classification et à l'existence de solutions de type solitonique

dans une théorie des champs. On présente aussi la construction du modèle de Skyrme original où on parametrise les champs de pions par une matrice SU(2) et où on obtient la configuration d'énergie minimale pour n = 1. Le chapitre 3 présente brièvement la construction de multi-skyrmions dans le modèle original et ses difficultés à décrire les propriétés nucléaires. De plus, on présente les caractéristiques des noyaux qu'on désire plus particulièrement reproduire à l'aide du modèle quasi-BPS, c'est-à-dire, l'énergie de liaison par nucléon et la structure du noyaux. Par la suite, le chapitre 4 présente le modèle BPS proposé par ASW dont les solutions saturent la borne de Bogomol'nyi ainsi que le modèle quasi-BPS que nous proposons d'utiliser pour décrire les noyaux atomiques. Par la suite, on présente le traitement de chacune des contributions d'éner-gie aux multi-skyrmions quasi-BPS. Le choix d'un potentiel adéquat à l'obtention d'un angle chiral analytique ainsi que la présentation des prédictions physiques du modèle quasi-BPS sont discutés dans le chapitre 5.

Solitons topologiques et modèle de

Skyrme

Tel que mentionné dans l'introduction, les travaux de Witten, pendant les années 70, ont permis d'associer la chromodynamique quantique à basse énergie à une théorie de mésons. Il n'est pas clair quelle doit être la forme exacte du lagrangien décrivant celle-ci, mais on sait que ce dernier doit posséder la symétrie chirale SU(2)L <g) SU(2)R

caractérisant la dynamique à basse énergie de QCD, c'est-à-dire la dynamique des pions. Dès le début des années 60, Skyrme avait déjà introduit un modèle de pions possédant des solutions non-perturbatives d'énergie finie et de volume non-nul. Ces solutions sont nommées solitons et leur stabilité provient de la structure topologique non-triviale de l'espace dans lequel elles sont inscrites. Dans un premier temps, on introduit les proprié-tés des solitons grâce aux outils mathématiques de la topologie pour ensuite présenter le modèle de Skyrme original et sa capacité à décrire le nucléon efficacement.

2.1 Topologie et solitons

En théorie quantique des champs, les particules élémentaires habituelles sont consi-dérées comme des excitations quantiques du vide et sont traitées comme une défor-mation lisse du champ. Contrairement à celles-ci, les solitons sont des solutions devant leurs stabilités à leurs structures topologiques non-triviales. L'étude de ceux-ci nécessite alors des considérations topologiques qu'on présente dans les sous-sections suivantes.

2.1.1 Classe d'homotopie

Soit A et B deux variétés différentielles sans bord et soit l'application continue 0o : A —T B avec les points de base an G A et b0 G B tels que 0o(an) = b0. L'application

0o est dite homotopique à l'application 0i s'il est possible de déterminer une application continue

0 : X x [0,1] -► Y (2.1) où le paramètre t de l'intervalle [0,1] s'assure que l'application 0 satisfasse

<P = 00 0

t=0 t = l

= 0i­ (2­2) La relation d'homotopie 0O ~ 0i forme une classe d'équivalence qu'on note [0o] . En

effet, la relation est symétrique 0o ~ 0i et 0i ~ 0O puisqu'il est possible d'inverser le

flot de t. De plus, la relation est transitive (0O ~ 0i ; 0i ~ 02 —► 0o ~ 02) puisqu'il est

toujours possible d'associer d'autres paramètres U et de renormaliser.

On dénote par irn(Y) l'ensemble des classes d'homotopie lorsque la variété initiale

est une sphère 0 : Sn —» Y. Il est possible de démontrer que pour n > 1, les classes

d'homotopie forme un groupe [35]. Le calcul des groupes d'homotopie 7rn(F) est une

tâches très ardue de la topologie algébrique et on présente un résultat fondamental à la classification des solitons

7r„(Sn) = Z Vra > 1. (2.3)

Par exemple, on démontre brièvement que TT^S1) = Z en définissant l'application / :

S1 ­> S1 telle que

f(9) = eie 0 € [ O , 2 4 (2.4)

En posant /(O) = 1, la continuité de la fonction nécessite /(27r) = et 2 m pour n 6 Z. Ce

nombre est le degré de l'application et ne peut pas être transformé par une homotopie. La composition des applications /0 et / i de degré n0 et ni respectivement forme ainsi

une application de degré n = no + ni et le groupe fondamental d'homotopie de la 1­sphère est bel et bien Z avec l'addition habituelle.

2.1.2 Solitons topologiques

Le but de cette section est de comprendre certains aspects topologiques [36] élémen­ taires de la théorie des champs sur un espace plat M.d. En absence de contraintes sur les

champs, ils représentent l'application

Ceux­ci sont considérés comme topologiquement triviaux puisqu'il est toujours possible de remplacer une configuration 0(x) par (1 — t)<p(x). En effet, la définition de l'ho­ motopie contraint le paramètre t à varier entre 0 et 1 ramenant ainsi n'importe quelle configuration des champs à celle triviale 0 = 0. Il est possible d'obtenir plus d'infor­ mation sur la classification topologique des champs lorsqu'on impose une diminution rapide de leurs densités d'énergie quand la distance à l'origine tend vers l'infini. La nécessité que la densité d'énergie soit nulle à l'infini impose des conditions frontières modifiant de façon significative la structure topologique qu'on démontre dans ce qui suit.

D'une part, on considère l'ensemble de k champs scalaire linéaire 0 = (0i, • • • ,<t>k) indépendant du temps dont la fonctionnelle d'énergie prend la forme simple

E =

J Qô

M

0,^0, + • ■ ■ + V(0x, ■ • • , 0

fc

)J d

d

x, (2.6)

où la dépendance en dérivée des champs peut être d'ordre supérieur en général. En

supposant que le potentiel prend ses valeurs minimales Vmin = 0 sur la sous­variété du

vide V G M.d, il est nécessaire que les champs 0 prennent leurs valeurs à l'infini dans

V afin de s'assurer que la densité d'énergie soit nulle. La valeur du champ à l'infini 0oo peut être différente selon la direction d'approche et on peut alors considérer qu'une configuration du champ définit l'application

0oe : S ^1 ­> V (2.7)

où S^1 est la sphère à l'infini de Rd. La charge topologique de la configuration 0(x)

est alors déterminée par la classe d'homotopie de l'application 0oo qui est un élément du groupe d'homotopie 7Td­i(V).

D'autre part, les champs scalaires non­linéaires représentent une application du type

0 : Rd ­» Y (2.8)

avec Y une variété fermée représentant la contrainte et avec la dimension d > 2. Il peut y avoir un potentiel V(0) dont les minina appartiennent à une sous­variété non­triviale V G Y. Dans le cas linéaire, on considère les configurations de champs dont les densités d'énergie diminuent suffisament rapidement à l'infini, mais ceci n'oblige pas la solution à avoir une énergie finie. Pour que les champs possèdent cette caractéristique, il est nécessaire qu'ils tendent vers une valeur constante, indépendamment de la direction, afin d'éviter un gradient d'énergie divergent. La configuration représente ainsi une ap­ plication constante 0oo : S ^1 —> Y avec la valeur yo G Y (en présence de potentiel

yo G V) qui doit être le point de base de Y. Cette condition frontière permet d'utiliser la projection stéréographique afin de compactifier l'espace Rd en Sd en ajoutant un

point xo à l'infini et en l'utilisant comme point de base de Sd. Finalement, les champs

représentent alors l'application

0 : Sd -> Y (2.9)

dont la charge topologique est un élément du groupe d'homotopie 7rd(Y).

2.1.3 Stabilité et théorème de Derrick

Tel que présenté dans la section précédente, les configurations du champ 0 d'énergie minimale sont classées selon leurs classes d'homotopie, mais cela n'assure pas nécessai-rement la stabilité de la solution. En effet, un théorème de non-existence, obtenu par Derrick [37], permet de déterminer si la fonctionnelle d'énergie d'une théorie est inva-riante sous un changement d'échelle. Dans le cas contraire, puisqu'une configuration statique du champ d'énergie minimal doit être stationnaire sous variation, incluant le changement d'échelle, il s'avère qu'il ne peut exister de solution d'énergie finie dans une telle théorie excepté la solution triviale du vide. Selon la structure du terme dyna-mique et la dimension de la théorie, il est possible de déterminer si des solutions stables existent.

Soit le champ scalaire 0(x) qui, sous changement d'échelle, prend la forme 0(Ax) et dont le gradient extrait un facteur A tel que

V(0(Ax)) = AV0(Ax). (2.10) De façon générale, l'énergie cinétique d'une théorie de champs scalaires dépend du

gradient à une puissance 7 G T qu'on dénote T7(0(x)) où T est l'ensemble des puissances

en dérivée du champ pour chacun des termes cinétiques. L'énergie statique prend la forme

£(0(x)) = J f £ T7( 0 ( x ) ) + V(0(x)) J ddx (2.11)

= J 2 E J + EO (2-12)

En effectuant le changement de variable x —>• Ax, l'énergie prend alors la forme

E(A) = £(0(Ax)) = J ( £ r7( 0 ( A x ) ) + V(0(Ax)) J * * (2-13)

= Y^ A7"d£7 + A~dE0, (2.14)

qui doit posséder un minimum lorsque A —> 1. Cette condition s'exprime ainsi comme

dE{\)

dA = 0 d2E(A) A = l dA2 > 0 , (2.15) A = l

qui dépend explicitement de la dimension de l'espace d.

Par exemple, dans le modèle sigma, où le terme cinétique dépend quadratiquement (7 = 2) de la dérivée du champ, on obtient l'énergie

E{A)d = A2~dE2 + A~dE0. (2.16)

Lorsque d = 1, les conditions pour un minimum d'énergie s'expriment comme

dE(A)d=1 dA d2E(A)d=l = E2 — EQ = 0 —> Ei — EQ A = l dA2 = E 0>0 (2.17) (2.18) A = l

ce qui permet l'existence de solutions stables par rapport à une variation d'échelle. Par contre, lorsque d = 3, on obtient les conditions

dE(A) d=2 dA d?E(A)d=2 dA2 A = l -£/2 — 3-EQ = 0 —r E2 = —3£/Q = 2E2 + 12£0 > 0 (2.19) (2.20) A = l

qui sont manifestement impossibles puisque E2 et E0 doivent être positifs. Il n'existe

donc pas de solutions stables au modèle sigma en 3 dimensions. Il est alors très important de vérifier cette propriété afin de confirmer l'existence de solitons stables dans la théorie.

2.2 Modèle de Skyrme original

Skyrme est souvent considéré comme un pionnier de la théorie des solitons topolo-gique puisqu'il fut le permier à associer ce type de solutions à des particules physiques réelles. Dans cette section, on présente les étapes et considérations scientifiques qui ont permis à Skyrme de construire son modèle original décrivant le nucléon comme un soliton.

2.2.1 Symétrie chirale

Suite à la découverte du neutron, Werner Heisenberg [15] introduisit, en 1932, le concept d'isospin afin d'expliquer l'indépendance de l'interaction forte sur la charge électrique ainsi que la faible différence entre la masse du neutron et du proton. De fa-çon équivalente à une particule de spin s = 1/2 qui peut être dans un état s3 = ±1/2,

le proton et le neutron sont considéré comme un doublet tpN = (p,n)i/2 d'une même

particule d'isospin total / = 1/2 avec la troisième composante d'isospin 1$ = ±1/2. De façon identique, après la découverte des pions en 1947, ces derniers ipn = (n~ ,w°,n+)i

furent décrit comme un triplet d'isospin 1 = 1 avec I3 = +1,0,1. Cependant, à la

même époque, les expérimentateurs en physique des particules découvrent que l'in-teraction mésons-mésons ne conserve pas la parité des particules. Il fallu introduire l'interaction faible afin de tenir compte des transformations permettant la violation de la conservation de la parité.

Pour ce faire, il est nécessaire d'étendre le concept de symétrie d'isospin en ajoutant au trois générateurs d'isorotation Ij les trois générateurs axiaux Aj [17]. Les générateurs li ne modifient jamais la parité des états tandis que les générateurs A* mélangent des états de parité différente. De façon similaire à l'extension du groupe de rotation de l'espace £0(3) au groupe de Lorentz où, en plus des générateurs de rotations autours des trois axes spatiaux, il y a l'introduction des générateurs de "boost" de Lorentz. Dans l'extension de l'algèbre SU(2), les six générateurs doivent alors satisfaire les relations de commutations

[Ij, I,-] = ieijkIk [h, Aj] = iei j kAk [A,, Aj] = ieijkIk, (2-21)

ainsi que la transformation sous l'opérateur de parité P

P l i P -1 = h P A i P -1 = - Ah (2.22)

De façon similaire au groupe de Lorentz, il est nécessaire d'introduire une quatrième composante 0o au vecteur n = (01,02,03) afin de former le quadri-vecteur 0 = (0o, 0») de telle sorte que

[li,0j] = ieijk(j)k [Ij,0o] = 0 (2.23)

[Ai, 0j] = -iSijtpo [Ai, 0O] = i<f>i. (2.24)

Finalement, en introduisant les opérateurs de "gauche" et de "droite"

Li = ^ ( Ii- Ai) Ri = ^(Ii + Ai), (2.25)

on obtient la structure de deux groupes SU(2) indépendants formant le groupe chiral SU(2)L x SU(2)R défini par les relations de commutation

C'est dans cet axe de pensée qu'un lagrangien tentant de décrire la physique des hadrons doit posséder la symétrie chirale afin que le modèle puisse décrire les interactions ne préservant pas la parité telles qu'obtenues expérimentalement.

2.2.2 Paramétrisation des champs de pions

Cette nouvelle symétrie des champs de pions 0j pousse Skyrme à introduire un nouveau champ mésonique 0o en incluant explicitement la dépendance non-linéaire avec les pions par la relation

00 + ^ + ^ + ^ = 1- (2.27) Il est possible de réécrire cette contrainte entre les champs mésoniques en introduisant

la matrice

U = I(/>0 + iTi<f>i G S U ( 2 ) , (2.28)

où Tj sont les matrices de Pauli et / la matrice identité de dimension 2. Il s'avère que la non-linéarité entre les champs de mésons décris par la matrice U impose une caractéristique topologique importante.

En effet, la contrainte (2.27) limite le nombre de degrés de liberté de la solution à trois et implique l'application U : M3 —t S3. Pour s'assurer que les solutions soient

dotées d'une énergie finie, il est nécessaire que la matrice de champs tende vers une valeur constante à l'infini qu'on choisit être U(r —>• oo) = /. Cette condition implique alors une compactification de l'espace Euclidien M3 en une hypersphère S3 = M3 U {oo}

(grâce à la projection stéréographique). Finalement, la matrice U admet un ensemble de configurations de champs statiques (solitons) considérés comme des applications de U : S3 —>• S3 dont la charge topologique est un élément du groupe d'homotopie

n3(53) = Z, (2.29)

où on utilise le résultat (2.3). Du point de vue de la section précédente, les champs représentent l'application 0 : S3 —» Y où la variété différentielle du groupe SU(2) est

isomorphe au groupe de Lie de S3, ce qui confirme le résultat précédent (2.29).

Cet entier du groupe Z est le degré de l'application U et Skyrme introduit alors le courant topologique conservé

où L^ = U^dfjU est le courant de chiralité gauche. Il fut le premier à proposer l'idée d'associer le nombre baryonique à la charge topologique conservée

n = f d3xB° = i ^ / v ^ f d3xTv [LvLaLp). (2.31)

Il est à noter qu'on utilise le symbole B en physique des particules ainsi que le symbole A en physique nucléaire pour décrire le nombre baryonique (2.31), mais qu'on utilisera le symbole n dans ce travail.

2.2.3 Lagrangien du modèle du Skyrme

Skyrme entame alors la construction d'un lagrangien à symétrie chirale décrivant la dynamique de la matrice de champs U. Il débute en utilisant le lagrangien chiral le plus simple, soit le modèle non-linéaire o. En terme de la matrice, celui-ci prend la forme simple

£

ff

= - S T r [ V / ] , (2.32)

où F„ est la constante de désintégration du pion mesurée expérimentalement à 93 MeV. Par contre, ce lagrangien n'est pas adéquat puisqu'il ne mène pas à des solitons stable selon le théorème de Derrick. En effet, le terme non-linéaire o est d'ordre 7 = 2 en dérivées des champs et l'énergie statique en trois dimensions d = 3 varie comme

K(A)d=3 = A - %

dA A = l = - E2 = 0 -> E2 = 0, (2.33)

ce qui ne permet pas de solutions non-triviales. Les solutions de (2.32) sont alors in-stables et se contractent pour atteindre une énergie et une dimension spatiale nulle.

Il est possible de remédier à cette contraction en ajoutant un terme répulsif d'ordre 4 en dérivées des champs. Il existe trois invariants chiraux linéairement indépendants d'ordre 4 , satisfaisant aussi l'invariance de Lorentz, à partir desquels on pourrait construire le terme à ajouter

aiTr [(L^)(LUL»)} a2Tx [L»UL»LV\ a3Tr [dllLv&ÀLv]. (2.34)

Pour réellement stabiliser les solitons, le terme doit dépendre au plus de dérivées tem-porelles d'ordre 2 et Skyrme proposa le terme

où e est un paramètre sans dimension. Finalement, le lagrangien introduit par Skyrme prend la forme

C>s = Ar + £-s

= ­ § T r [ L ^ ] + ^ T r [ [ L

; i

, L , ]

2

] ,

qui possède bel et bien la stabilité requise puisque l'énergie

ES(A) = A~1E2 + A£4

respecte les conditions de stabilité

dEs dA d2E, = —E2 + E\ = 0 —r E2 = E±, A = l dA2 = 2E2 > 0 ­¥ E2 > 0. (2.36) (2.37) (2.38) (2.39) A = l

Afin de briser la symétrie chirale, il est possible d'introduire un terme de masse dont la forme la plus simple s'écrit

C

m

= \mlF^r[I­U}.

o

(2.40)

En considérant de faibles fluctuations du champ de pions autour du vide, la matrice de champs prend la forme

U ~ / + iTjitj + ■■■ (2.41) et le potentiel redonne le terme de masse habituel dans le modèle de Klein­Gordon

1

Crr, « ­ ­ m ^ , . _{ir J '} (2.42)

2.2.4 Masse du skyrmion et borne de Bogomol'ny

À partir du lagrangien de Skyrme, on calcule l'énergie statique du skyrmion

E = ­ Id

3

r C

s

= ­ f d

3

',

En réorganisant l'énergie statique s'écrit

§^[^L

i

]+^r[[L

l

,L

]

}

2

}

32e2 (2.43)

et il est possible d'obtenir une borne inférieure sur la masse du skyrmion. En effet, en utilisant l'inégalité vectorielle de Cauchy-Schwarz a2 -l- b2 > 2|a • b|, on obtient le

résultat

E

-

2

^ïéhe~

2

S

dh

'

Tr

^

kL

^

L

^ i

(2

-

45)

En comparant l'intégrale du côté droit de l'inégalité avec (2.31), on identifie la charge topologique

Tr [eijkLi[Lj, Lk\] = -48ir2B°. (2.46)

Finalement, la borne de Bogomol'ny du skyrmion impose une limite inférieure à la masse de celui-ci en fonction de sa charge topologique et des paramètres du modèle

E>^LlJL\n\. (2.47) e

Il est maintenant nécessaire de déterminer la configuration de la matrice U qui minimise l'énergie statique (2.43).

2.2.5 Configuration de l'hérisson

Il a été démontré numériquement que le skyrmion de charge n = 1 minimisant l'énergie statique doit posséder la symétrie sphérique. Une solution sphérique proposé par Skyrme, dites configuration de l'hérison, s'écrit sous la forme

U = é n r ? ( r ) = / cos i(r) + i n • r sin f (r) (2.48)

avec le vecteur unitaire

n = [ s i n # c o s 0 , sin#sin0, cos# ] (2.49) où (r, 9,0) sont les coordonnées sphériques. L'angle chiral £(r) dépend uniquement de la

distance radiale et possède les conditions frontières £(0) = n et £(oo) = 0 afin d'assurer la conservation de la charge topologique.

Les champs mésoniques prennent alors la forme

0^ = ( cos£, sin £ sin 6 cos 0, sin £ sin 9 sin 0, sin£cos0), (2.50) où il est toujours nécessaire de déterminer l'angle chiral £(r) qui minimisent l'énergie

statique du skyrmion. En substituant la configuration de l'hérison (2.48) dans l'énergie statique (2.43), on obtient une équation différentielle pour l'angle chiral permettant de minimiser l'énergie

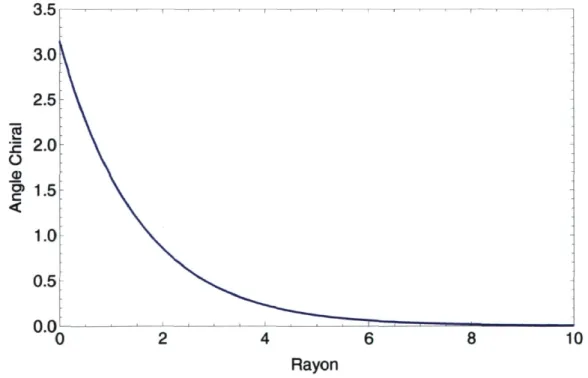
En solutionnant numériquement cette équation, on obtient l'angle chiral présenté à la figure 2.2.

FIGURE 2.1 - Configuration de l'hérisson dans le modèle de Skyrme original. Les flèches représentent la direction du vecteur des champs pionniques n = (0i, 02, 03).

FIGURE 2.2 - Profil radial de l'angle chiral £(r) dans le modèle de Skyrme original pour la charge topologie n = 1.

En effectuant le changement de variable

V2

r.

la masse du skyrmion et la densité baryonique s'écrivent alors E = 4TT

W

dr r' 1

_r+2-

-12 s i n2A lsin

₊

2£ 2 r2 2£' 2 + sin2^

#(r) = 4^ J

_m

_**ffle

(2.52) (2.53) (2.54) où £' = - ^ - Finalement, grâce à la solution numérique pour l'angle chiral, l'énergie statique du skyrmion de charge topologique n = 1 est calculée en unités de Fn/4e à

Multi-skyrmions et multi-baryons

3.1 Propriétés des multi-skyrmions

3.1.1 Skyrmion de charge supérieure

L'utilisation du modèle de Skyrme en physique nucléaire nécessite la description de skyrmions de charge topologique élevée . Pour ce faire, il est tentant d'utiliser la configuration hérisson, pour la matrice des champs U, en modifiant la condition initiale telle que £(0) = nzr avec n G Z. Cependant, on constate rapidement que ces solutions ne représentent pas l'énergie minimale du skyrmion de charge n et sont donc instables. En effet, la masse du skyrmion pour n = 2, toujours en unités de Fw/4e, est supérieure

au double de celle dans le cas n = 1 ce qui rend possible, en principe, une désintégration en |n| skyrmions de charge n = 1

En = 2 = 3.67 > 2 x 1.232 = 2 x En = l. (3.1)

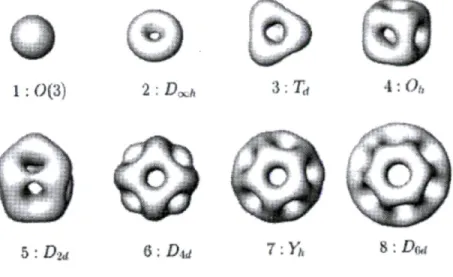
Il est possible de démontrer que le skyrmion de charge topologique n = 2 ne possède pas une symétrie sphérique, mais plutôt une symétrie axiale [20, 21]. Ces travaux permirent à Braaten et Carson [22] de décrire le deutéron comme un multi-skyrmion et d'en prédire des propriétés physiques très acceptable. Cependant, dépourvu d'hypothèses et de symétries particulières pour les configurations de charge n > 3, des méthodes numériques, tel le "recuit stimulé", sont utilisées afin de trouver le minimum global de l'énergie. Ces méthodes permettent d'obtenir des solutions exactes minimisant l'énergie totale, mais demandent des ressources informatiques très importantes. Les densités baryoniques de ces solutions possèdent des symétries discrètes particulières telles que la symétrie tétrahédrale Td et cubique Oh pour n = 3 et n = 4 respectivement. On

présente les surfaces de densité baryonique constante pour 1 < n < 8 à la figure 3.1 telles que présentées dans [36].

1 : 0(3) b:D-2:D ni U Ù.D u 3:Trf 7:Y„ 4 : Ou S'.DM

FIGURE 3.1 - Exemples de densités baryoniques de multi-skyrmions et leurs symétries contre-intuitives

Houghton, Manton et Sutcliffe [39] firent alors le lien entre la symétrie de ces solu-tions et celles d'un monopôle de même charge topologique d'une théorie de Yang-Mills-Higgs. Ces observations permirent la construction approximée de skyrmions à partir de monopôle en utilisant la correspondance entre un monopôle de charge N et une appli-cation rationnelle R d'ordre N. En utilisant un ansatz pour la matrice U en fonction de l'application R, il s'avère que cette dernière représente approximativement les symé-tries discrètes déterminées précédement de façon numérique pour minimiser l'énergie. Cette méthode permet d'obtenir une très bonne approximation de la solution exacte du lagrangien et fut utilisée pour décrire les solutions de charge topologique maximale n > 2 2 .

3.1.2 Validité du modèle à la description des multibaryons

À l'aide de ces méthodes de calculs, le modèle de Skyrme original prédit les pro-priétés physiques des nucléons et des pions avec une précision de 30% ou mieux. Par contre, certaines lacunes persistent et les énergies de liaison sont vraiment plus élevées que les valeurs expérimentales mesurées en physique nucléaire. Une raison permettant d'expliquer la différence dans l'énergie de liaison serait le grand écart entre l'énergie du skyrmion et la borne de Bogomol'ny. En effet, la solution de l'angle chiral présenté à

la figure (2.2) permet d'obtenir la masse du skyrmion E = 1.232 dépassant d'approxi-mativement 23% la borne. Suivant (2.47), plus la masse du skyrmion s'approche de la borne de Bogomol'nyi, plus l'énergie de liaison est faible. Une solution permettant de se rapprocher de la borne serait ainsi un bon point de départ à la description de la physique des multibaryons.

D'autre part, le modèle de Skyrme original n'est pas en mesure de différentier la masse du proton et du neutron. En effet, l'énergie statique (2.43) n'inclut pas cer-taines propriétés fondamentales de ceux-ci telles que la charge électrique et la troisième composante d'isospin i3. Afin d'améliorer les prédictions du modèle, il est impératif de

pouvoir distinguer l'énergie associée à des états nucléaires de spin et d'isospin définis. Une méthode de quantification semi-classique est utilisée pour faciliter ce traitement puisque les skyrmions sont des états possédant un volume non-nul. Ceci permet d'inclure une énergie de rotation explicite aux skyrmions, mais n'est pas suffissante pour décrire l'écart de masse entre les deux nucléons. On propose d'inclure l'énergie de Coulomb au modèle afin d'améliorer cette prédiction. Par contre, les configurations complexes des densités de charge électrique des skyrmions du modèle original ne permettent pas de calculer facilement l'énergie électrostatique de ceux-ci. On désire donc modifier le modèle afin d'obtenir des configurations de densités ressemblant plus à celles observées expérimentalement qu'on présente dans la section suivante.

3.2 Phénoménologie des multi-baryons

De façon générale, les expériences réalisées en physique nucléaire peuvent être di-visées en quatre grandes catégories importantes, soit l'énergie, les moments statiques, les amplitudes de transition ainsi que les taux de réaction. Cependant, les différentes contributions à l'énergie du nucléons ainsi que les propriétés structurales de celui-ci sont ce qu'on désire améliorer à l'aide d'un modèle efficace. Les propriétés de la physique nucléaire présentées dans ce travail proviennent principalement de [1].

3.2.1 Structure des nucléons

La distribution des protons à l'intérieur des nucléons est mesurée expérimentalement en effectuant de la diffusion sur ceux-ci. Ces expériences utilisent essentiellement des électrons puisque ceux-ci facilitent grandement les mesures et le traitement des résul-tats car ils sont des particules ponctuelles et intéragissent principalement via la force

électromagnétique. Cependant, on ne mesure pas directement la densité de charge, mais plutôt le module au carré du facteur de forme de celle-ci (transformée de Fourier)

F(q) = / p ( r ) e ^ ' d V (3.2) puisque la section efficace, en diffusion élastique, d'un électron avec un nucléon de spin

J = 0 est donnée par

De façon générale, puisqu'on s'intéresse principalement à la dépendance radiale de la distribution de densité de charge électrique p(r), il est fréquent d'effectuer une moyenne sur la contribution angulaire et considérer uniquement

F(q2) = — p(r)sin(qr)rdr p(r) = —— / F(q2)sin(qr)qdq. (3.4)

q J 27r2r Jo

De plus, on mesure fréquemment la valeur efficace du rayon (r2) des nucléons puisqu'à

bas transfert d'impulsion, il est possible d'effectuer le développement en q2

Ait f

F(q2) = — / p(r) sm(qr)rdr (3.5)

= j J P(r) (qr - ^(qr3) + - - - \ r d r (3.6)

= 47T / p(r)r2dr —— / r2p(r)r2dr + • • • (3.7)

= Z( l - ^ ( r2) + . . . ^ (3.8)

où Z est la charge électrique du noyau. Les mesures de sections efficaces permirent de déterminer que la densité de charge possède une région centrale constante avec un bord diffus plus ou moins exponentiel. Il est possible de modéliser ce type de distribution par les fonctions

( \ P° n fr.\ 1 + w(r/c)2

p2F(r) = — r, ry-r p3F{r) = pQ— r, r j ^ (3.9)

1 + exp[(r — c)/z\ 1 + exp[(r — c)/z\

où P2F{I') e t/93ir(r) sont les distributions de Fermi à deux et à trois paramètres

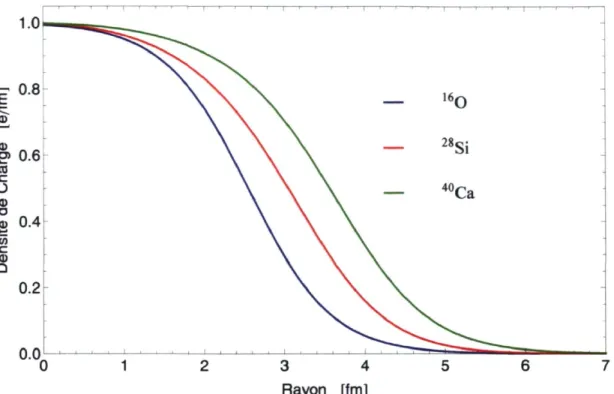
res-pectivement. Les paramètres c, z et w sont ensuite fixés en effectuant un lissage avec l'expérience. Des exemples sont présentés à la figure 3.2 pour différents noyaux ato-miques.

3 4 Rayon [fm]

FIGURE 3.2 - Profil radial de la densité de charge pour 1 60, 28Si et 40Ca dans le modèle

de Fermi à trois paramètres (c,z,w) avec (2.608,0.513, -0.051), (3.340,0.580,-0.233) et (3.766,0.586,-0.161) respectivement.

Grâce aux expériences de diffusion à bas transfert de momentum, on remarque que le rapport (r2)1'2/'B1'3 en fonction du nombre baryonique est pratiquement constant

avec la valeur 0.97 ± 0.004 [fm]. Ce résultat suggère l'idée que le noyau atomique se-rait un "liquide nucléaire incompressible" puisque le volume augmente linéairement en fonction du nombre baryonique n. On rencontre alors souvent la relation suivante dans la littérature

r = r0n1 / 3 (3.10)

où r est le rayon nucléaire et où r0 varie autour de 1.4 [fm].

3.2.2 Énergie de liaison et formule de Weizacker

Les noyaux sont des états très complexes et des modèles empiriques sont utilisés afin d'expliquer plusieurs résultats expérimentaux [1]. De ceux-ci, l'énergie de liaison EB est

un résultat très important puisqu'il permet de comparer les noyaux entre eux. Soit A le nombre total de nucléons, Z le nombre de protons et N le nombre de neutrons, la

masse d'un noyau atomique est donnée par

EB

m = Zmv + Nmn — (3.11)

c2

où mp est la masse du proton et mn celle du neutron. Le modèle de la goutte considère le

nucléon comme un liquide nucléaire imcompressible et permet d'obtenir une expression empirique pour l'énergie de liaison en fonction de différentes types d'énergie

EB = avA - asA2'3 - a C ^ ~ ^ ~ aA { A~ ^Z f + Ô(A, Z). (3.12)

Le terme ayA est le terme volumique et est introduit pour décrire l'interaction forte entre chacun des nucléons du noyau atomique. L'interaction forte possède un rayon d'action très court limitant les nucléons à interagir uniquement avec leurs plus proches voisins ce qui est proportionnel au nombre de nucléons A.

Le terme asA2/3 est le terme de surface et il est introduit pour tenir compte des

nucléons à la surface du noyau qui sont en contact avec moins de voisins. Ce terme est l'équivalent de la tension de surface pour les liquides et est proportionnel aux nombre de nucléons à la surface A2/3.

Le terme de ac est un estimé de l'énergie de Coulomb que l'on calcule en supposant que le noyau est une sphère de rayon R et uniformément chargée de Z proton

5 \Ane0) R 5 \ r0 J A1/3 A1/3 v '

où on a utilisé la propriété 3.10 pour le rayon du nucléon et où Z2 —> Z(Z — 1)

afin de ne pas inclure l'énergie d'interaction d'un proton avec lui-même. Cependant, la forme exacte de la densité de charge possède plutôt des bords diffus, tel qu'expliqué auparavant, et on laisse alors un paramètre libre ac afin de s'ajuster à la forme non-sphérique des nucléons.

Les deux termes restant proviennent de considérations quantiques où le premier est le terme de symétrie et le deuxième est le terme de pairage. Le terme d'énergie symétrique permet de prendre en compte le fait que les nucléons stables obéissent grossièrement à la relation N w Z qui peut être pris en compte en incluant une dépendance quadratique sur (N — Z)2 = (A — 2Z)2. D'autre part, le terme de pairage est introduit pour tenir

compte de la propriété des nucléons à être plus fortement liés lorsqu'il y a un nombre pair de proton Z et de neutron N. Le terme de pairage prend la forme

S(A, Z)

25 MeV pour A pair, Z et N pair

0 pour A impair (3.14) —~ MeV pour A pair, Z et N impair

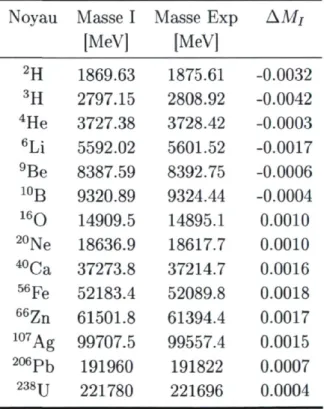
Finalement, en effectuant un fit avec les données expérimentales, on obtient les résultats suivant pour les coefficients dans l'énergie de liaison (3.12) [23]

av = 15.8 MeV as = 18.3 MeV ac = 0.714 MeV aA = 23.2 MeV. (3.15)

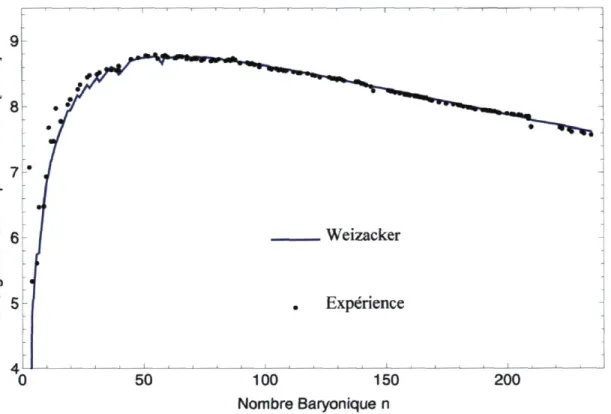
Ceci permet d'obtenir les résultats de l'énergie de liaison des nucléons qui est présenté à la figure 3.3 Weizacker . Expérience 50 100 150 Nombre Baryonique n 200

FIGURE 3.3 - Énergie de liaison par nucléon pour les valeurs expérimentales et les prédiction de la formule semi-empirique de Weizacker.

Le but de cet ouvrage est d'introduire un modèle de soliton quasi-BPS qui puisse reproduire sensiblement les mêmes résultats pour l'énergie de liaison que le modèle de la goutte nucléaire. Le terme surfacique et volumique sont causés uniquement par la force nucléaire forte et devraient être inclus dans l'énergie statique du soliton. L'énergie de Coulomb doit cependant être calculé implicitement de façon indépendante et être ajoutée à la masse du soliton. De plus, pour prendre en compte le spin et l'isospin des nucléons, on effectue une quantification semi-classique afin d'inclure l'énergie de rotation et d'isorotation du multi-skyrmion.

Extension du modèle de Skyrme

À priori, la forme exacte du lagrangien efficace de QCD n'est pas connue et peut contenir des termes d'ordres supérieurs en dérivée du champ et un terme de masse différent. Une étude de ces posibilités fut effectuée par Marleau [28] mais les solutions de lagrangien incluant plusieurs ordres différents deviennent rapidement compliquées. D'autre part, un modèle proposé par Suttcliffe [26] propose d'inclure un méson vectoriel dans le lagrangien du modèle o afin de stabiliser le soliton tel que requis par le théorème de Derrick au lieu d'introduire le terme de Skyrme. Cependant, la construction de multi-skyrmions dans cette théorie nécessite l'utilisation de la solution construite à partir d'applications rationnelles telle que mentionnée dans le chapitre 3 et se limite à la description des baryons de charge n > 22.

Par contre, un modèle se basant uniquement sur un terme d'ordre 6 en dérivée et d'un potentiel, proposé par Adam, Sanchez-Guillen et Weresczynski (ASW) [32], possède des propriétés très intéressantes. En utilisant une configuration des champs possédant une symétrie axiale, ils obtiennent des solutions analytiques saturant la borne de Bogo-mol'ny (solution BPS) pour toutes charges topologiques. Cependant, ce modèle perd la correspondance avec une théorie de pions étant donné l'absence du terme quadratique en dérivées dans le lagrangien. On propose alors d'introduire, comme perturbation, les termes du lagrangien de Skyrme original à celui proposé par ASW pour obtenir des solutions saturant presque la borne (solution quasi-BPS). Ce lagrangien n'est pas nouveau et fut proposé par Jackson [33] , mais notre innovation est de traiter celui-ci dans le régime quasi-BPS, c'est-à-dire dans la limite où Ca et Ca sont traités comme

des perturbations. Le but de cette proposition est de réduire l'énergie de liaison des multi-skyrmions tout en utilisant une solution analytique. Par la suite, on présente les propriétés physiques du skyrmion quasi-BPS telles que sa quantification semi-classique, sa densité de charge électrique et son énergie de Coulomb.

4.1 Modèle de Skyrme BPS

ASW proposent de construire un lagrangien uniquement à partir de quantités to-pologiques et utilisent le terme introduit par Jackson [33] construit à partir du courant baryonique (2.30)

Cj = \ 2 ^ B ^ = - f ^ R l [L„,LV][L\L"\[L„,LA ]. (4.1)

Cependant, le théroème de Derrick ne permet pas de soliton stable si le modèle consiste uniquement en C j puisque l'énergie statique ne possède pas de minimum non trivial sous un changement d'échelle

Ej(A)d =, = A3E6 ^ = 3£6 = 0 -> E6 = 0. (4.2) A = l

L'ajout d'un potentiel suffit à stabiliser le soliton et ils proposent alors d'étudier le lagrangien de la forme

CASW = - ^ T r t iL^ L^L" > L1 [ A . , L,} ] - p2V(U). (4.3)

Sous un changement d'échelle x —> Ax, l'énergie statique se modifie telle que

EA S W = A3E6 + A-3£0 (4-4)

et possède bien un minimum

= 3E6 - 3 Eo = 0 ^ E6 = Eo, (4.5) A = l = 6E6 + 12E0 > 0 -> £0 > 0. (4.6) d2E dA ASW dA2 _{A = l}

Ils proposent d'utiliser une configuration à symétrie axiale

[/(x) = ei n'r ? ( r ) = / cos f (r) H- i n • r sin £(r) (4.7)

où n = [ sin 9 cos n<\>, sin 9 sin nef), cos9 ], où n £ Z et où £(0) = n et £(oo) = 0. Celle-ci permet d'obtenir des solutions saturant la borne de Bogomol'nyi et dont l'énergie de liaison est nulle.

En utilisant cette forme, l'énergie statique est donnée par roo / r w , 2 \ 2 • 4

E ASW f°° , /9n2A2sin4£(r) M. ,2 2 l„r r N\

et la minimisation de celle­ci fournit une équation différentielle pour l'angle chiral

^ ^ | ( ^ r « ) - ^ = o . ,4,,

Le changement de variable z = i ^ f r3 permet de réécrire l'équation différentielle plus

simplement

, J ­ n ' € M | (an*«z) £ & ) ­ „ ' ^ | > = 0. (4.10)

En intégrant la dernière expression, on obtient un résultat d'équipartition de l'énergie

totale entre le terme d'ordre 6 et le potentiel

^ i n ^ ( z ) ^ ) 2 = V ( 0 . (4.11)

ASW ont démontré qu'une solution respectant la relation (4.11) sature la borne de Bogomol'nyi

EB P S = 2À/i7T2|n| C(V) (4.12)

où C(V) est une constante qui dépend du potentiel, mais non de la forme de la solution. Finalement, il est possible d'intégrer l'équation separable (4.11) afin d'obtenir la relation importante entre l'angle chiral et le potentiel

^■/«^Sfe-=*-*>

<4

-

13)

avec ZQ une constante d'intégration. Cette relation permet ainsi de déterminer l'angle chiral en fonction du rayon lorsque le potentiel est connu et lorsque la fonction G(£) est invertible.

Par exemple, l'utilisation du terme de masse habituel

V(Ç) = ­ T r [ U + U* ­ 2 ] = l ­ c o s £ (4.14) permet d'obtenir C(V) = 32\/2/157r. De plus, en solutionnant l'intégrale 4.13, on ob­

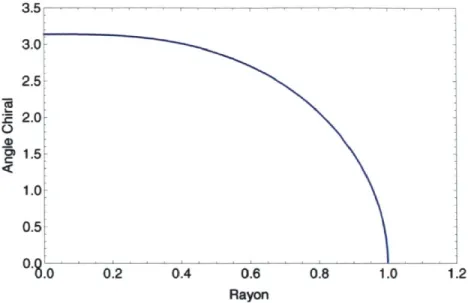
tient l'angle chiral analytique (voir figure 4.1)

2arccos (ur3) pour r€ 0, v~*

£(r) = \ L_x J (4.15)

0 pour r > v $

qui correspond à un compacton puisque la distribution d'énergie sera localisée dans un intervalle fini de l'espace.

1.0 1.2

FIGURE 4.1 - Profil radial de l'angle chiral £(r) dans le modèle d'ASW pour n = 1.

Ce modèle possède des caractéristiques très intéressantes pour la description des noyaux. L'énergie est proportionnelle au nombre baryonique n et le rayon RMS baryo-nique est proportionel à n1/3 tel que discuté dans la section 3.2.1.

. o . 1 1

E A S W C* n (r )2 oc n3. (4.16)

De plus, la possiblité d'obtenir une solution analytique pour l'angle chiral £(r) qui sa-ture la borne de Bogomol'nyi pour toute charge topologique n est intéressante puisqu'on désire décrire des multi-skyrmions de l'ordre de l'uramium avec n = 238. Les paramé-trisations de la matrice de champs U en terme d'applications rationnelles [39] dans le modèle de Skyrme original sont déterminées pour n < 22. Le modèle de Skyrme BPS est alors très avantageux si on désire décire les propriétés des noyaux atomiques. Il sera donc la base du modèle quasi-BPS qu'on propose d'utiliser afin de décrire l'énergie de liaison par nucléon ainsi que les densités de charge électrique.

Dans un article subséquent [34], ASW incluent l'énergie de rotation aux multi-skyrmions mais n'incluent pas les contributions provenant de l'énergie de Coulomb et de l'énergie de brisure de symétrie d'isospin. Ces solutions saturent complètement la borne de Bogomol'nyi et possèdent une énergie de liaison faible provenant uniquement de l'énergie de rotation. Dans l'optique d'améliorer la prédiction de EB, le modèle

quasi-BPS utilise un lagrangien contenant des termes additionnels et inclut des contributions d'énergie supplémentaires.

4.2 Modèle de Skyrme quasi­BPS

4.2.1 Stratégie du modèle

On désire utiliser l'angle chiral analytique qui sature la borne de Bogomol'nyi pro­ posé par ASW puisqu'il permet de décire facilement les multi­skyrmions de charge topo­ logique élevée. Cependant, l'absence d'un terme d'ordre 2 en dérivé du champ ne permet pas de décrire la dynamique des pions et perd le lien avec la physique des particules du modèle de Skyrme original. Pour rétablir ce lien, on suggère d'étudier un modèle consti­ tué du terme non­linéaire sigma Cc = C2 du terme de Skyrme Cs = £4, du terme de

Jackson C j = C§ et d'un potentiel V = C0. Pour pouvoir utiliser la solution analytique

pour £(r), on propose d'étudier le régime où les termes C2 et £4 peuvent être considé­

rées comme des perturbations par rapport deux autres termes. Le choix du potentiel est important puisqu'il permet d'obtenir la solution de l'angle chiral par la relation (4.13). De plus, on désire que dans la limite des champs faibles de pions, le potentiel brise la symétrie chirale sous la forme d'un terme de masse. L'utilisation du terme de masse le plus simple (2.40) permet d'obtenir la solution proposée par ASW (4.15). Par contre, celle­ci cause des divergences dans l'énergie statique lorsque les contributions C2 et £4

sont ajoutées. En effet, l'énergie statique provenant du lagrangien de Skyrme dépend de £'(r) et diverge lorsque r —>■ i/­ 1/3 pour la solution compacton.

Dans le chapitre suivant, on propose donc de déterminer un potentiel permettant d'obtenir une solution pour l'angle chiral compatible avec le lagrangien original de Skyrme. De plus, celui­ci prendra la forme d'un potentiel de masse généralisée étudié par Marleau [28, 29]. L'ajout des deux termes perturbatifs au lagrangien d'ASW mo­ difie légèrement la borne de Bogomol'nyi et c'est pour cette raison qu'on nomme les solutions de notre modèle "skyrmions quasi­BPS". Ceci permet d'autant plus d'obtenir une énergie statique possédant une énergie de liaison non nulle à laquelle on ajoute l'énergie de (iso)­rotation, l'énergie de Coulomb ainsi que l'énergie de brisure d'isospin dont les dérivations sont présentées dans les sections suivantes.

4.2.2 Lagrangien du modèle

Nous proposons alors d'étudier le modèle basé sur la densité lagrangienne incluant les termes originaux de SKyrme ainsi que le terme d'ordre 6

avec

Co = -p2V(U) (4.18)

C2 = - a Tr[LML"] (4.19)

C4 = 0 T r [ [L^LJ2] (4.20)

où p, cx,p et \ sont les paramètres libres du modèle. La solution saturant la borne de Bogomol'nyi du modèle de ASW dépend explicitement du potentiel choisi et l'expression d'un terme de masse généralisé introduit par Marleau [29, 41]

oo

V = - J 2

c

^ [U

k

+

u

*

k

-

2

] (

4

-

22

)

j t = i

= -4TT J 2 H dr r2 8Ck sin2 ( ~ ^ - ) (4-23)

possède plusieurs avantages. En effet, le potentiel peut facilement être écrit en fonction des champs de pions et il permet de retrouver, dans la limite de faibles fluctuations du champ, le terme de masse des pions — ^m27r • it brisant la symétrie chirale à condition

que

oo / r? \ 2

£fc

2

C

fc

= - ( ^ p ) . (4.24)

fe=i ^ '

On désire ainsi déterminer un potentiel sous la forme d'un terme de masse généralisé qui permet d'intégrer analytiquement la relation G(£) et qui est invertible afin d'obtenir une solution analytique pour l'angle chiral £(r).

Puisqu'on désire utiliser le modèle de Skyrme quasi-BPS afin de modéliser les noyaux, il est nécessaire d'inclure les propriétés fondamentales de ceux-ci décrites dans la sections 3.2. Les sections suivantes consistent alors en une vérification du théorème de Derrick, une description de la quantification semi-classique ainsi qu'au calcul de la densité de charge et de l'énergie de Coulomb du skyrmion quasi-BPS.

4.2.3 Énergie statique et stabilité de Derrick

L'énergie statique du modèle prend alors la forme

E ^ t = f d3r (aTt[Lil}} - /Hrf [Lu Lj}2} + p2V (4.25)

+\^v[[L

l

,L

]

][U,L

k

][L

k

,L

l

]]\

qui sous changement d'échelle se modifie tel que

E(A) = A-1E2 + AEi + A3E6 + A~3E0 (4.26)

où Ei est l'énergie statique associée au terme du lagrangien Ci d'ordre i. L'énergie possède un minimum pour un A dans la région 0 < A < oo. En effet, E(A) est une fonction continue bornée inférieurement par zéro et tend vers l'infini lorsque A —» 0 (le terme E0) et lorsque A —» oo (le terme E6) ce qui s'assure que E(A) possède un

minimum lorsque Ei > 0. En terme de la solution axiale (4.7), la masse du skyrmion quasi-BPS s'exprime alors comme

E _stat

= 4 * / ^ [2a (r(rf + (n« + 1 ) ^ ) + ^ Ç ' M

2

^ (4.27)

4.2.4 Moments d'inertie et énergie de rotation

Les noyaux atomiques sont des états quantiques de spin et d'isospin bien définis. Les skyrmions, comme les noyaux, ne sont pas des particules ponctuelles ce qui rend beaucoup plus compliquées les procédures de quantification habituelles. On utilise plutôt une quantification semi-classique qui consiste à ajouter une dépendance temporelle aux modes d'ordre 0 du skyrmion en appliquant des rotations et isorotations sur les champs par les matrices B(t) et A(t) G SU(2) respectivement. Par souci de simplification, on suppose que les skyrmions sont rigides car ceci empêche toute déformation sous rotation. La matrice des champs U(r) se transforme alors comme suit

Û(r, t) = Aj(t)U(R(B(t))r)A(t), (4.28)

où R(B(t)) e 50(3) est la matrice de rotation associée. Il est alors possible d'obtenir la composante temporelle du courant de chiralité

L0 = U % U = Tbab + e6yb x5Lybb (4.29)

où

Th = iU] ~ , u ] a i = -iTvA^A bi = i T v È B l (4.30)

Dans le langage de la mécanique classique, les Oi et bi représentent des vitesses angu-laires. En insérant ce résultat dans la partie temporelle du lagrangien total, on obtient un lagrangien de (iso)-rotation

où on identifie alors les densités de moments d'inertie du soliton Uij = - 2aTr (T{Tj) + 4/3Tr ([Lk, Tt] [Lk, Tf\) + — Tr ([T9A2 u Lk] [Lk, Ln) [Ln, Tj\) Wy = ejklxk 162 9A2 2aTr (T^) + 4/3Tr ([Lp, T,} [Lp, L{\) + — Tr (pi, Lm] [Lm, Ln) [Ln, L{\)

Vij = -ei k lej m nxkxm [2aTr (LtLn) + A/3Tr ([Lp, L{\ [Lp, Ln]) +

9A2

+

₁₆2 Tr{[lnjLp][LptLq][LqtLn))

De plus, puisqu'on travaille avec une solution à symétrie axiale (4.7), les moments d'inertie sont tous diagonaux et, suivant les travaux de Houghton et Magee [42], on écrit l'hamiltonnien de rotation du soliton

Hrot — 1 i^ + Wn^)2 , (L2 + W22^)2 (L3 + W3^)2 K\ K2 K2

V i i - _Un

+

^ " S

+

_{V33 u33} Un U22 Uzz

Les Ki etLi sont les moments canoniques conjugués d'isorotation et de rotation de a, et bi respectivement et sont exprimés comme suit

Ki = UijOj - Wijbj, Li = -W?aj + Vybj. (4.32)

Dans le cas n = 1, la solution possède une symétrie sphérique et l'énergie de rotation est donnée par

(4.33)

1711=1 _

rot " 8UU

ou

U^ = / d3r Uij similaire pour Vy, Wy

Pour n > 2, les solutions, ayant une symétrie axiale (autour de l'axe 3), permettent d'effectuer plusieurs simplifications sur l'hamiltonien de rotation. En effet, en utilisant les relations entre les moments d'inertie et les moments conjugués canoniques

1 — ^11 = U22 =£ C/33 similaire pour V^, W%i 2 - n2[/33 = nW33 = V33 3 _ Wn = W22 = 0 pour n > 2 4 - L3 + nK3 = 0, (4-34) (4.35) (4.36) (4-37)

l'hamiltonien de rotation se simplifie finalement à

Hrnt — 1

V_ K

2

^ (J_ J_ n_

Vn + Un + U33 Uu Vu

Les moments L et K dans le repère du centre de masse sont liés au spin J et à l'isospin I dans le repère du laboratoire par les transformations orthogonales

Ji = -R(A2%Lj li = -R(Ax)ijKj (4.39)

et on remarque alors que les deux opérateurs de Casimir donnent les valeurs propres

L2 = J2 = J ( J + 1) K2 = I2 = i(i + 1). (4.40)

On suppose que l'isotope le plus stable correspond à la valeur propre minimale de l'opérateur HTOt agissant sur un état \i,i3,k3)\j,j3,l3), qui coïncide avec l'état de plus

petite valeur propre A;3 de l'opérateur K3, . Puisque les nucléons sont constitués de B

fermions, on obtient nécessairement j < B/2 et puisqu'on utilise une solution à symétrie axiale, on obtient k3 = —l3/n. On obtient alors la partie entière de |/3/n| dans le cas de

B pair,

0 < \k3\ = < < B

2n = 0

et dans le cas B impair, où |A;3| doit être un demi-entier

1 <\k\-2 - lhl ~ < < B 2n 1 2' (4-41) (4.42)

Pour simplifier le modèle, on prendra donc les valeurs suivantes pour la valeur propre de k3

. . . 0 pour B pair

K = max \k3\ = < 1

5 pour B impair Finalement, l'énergie de rotation du skyrmion prend la forme

E r n t — 1 j(j + l) , i(i + l)

Vn Un

+

1 1 _n"

Vn

K

Par exemple, l'énergie de rotation du deutéron (n = 2, i = 0, j = 1 K simplement et se lit de (4.44)

F

D

J

-TOt~Vn

En utilisant la solution axiale (4.7), il est possible de calculer les densités de moment d'inertie Un, Vu et U33, nécessaires au calcul de l'énergie de rotation

(4.43)

(4.44) 0) s'obtient

(4.45)

Un(r, 9,4>) = Aa sin2 f (sin2 9 sin2 ntf) + cos2 9)

H r-^ (cos2 9 cos2 n4> + n2 sin2 ntj)) £n

8 rl

+ 32/3^-^ (sin2 £(cos2 9 cos2 ntj) + n2 sin2 n<p)

+(1+ cos2 n<j> sin2 9)r2£,'),

V n ( r , 9, <f>) = Act sin2 £ ( n2 cos2 9 cos2 <f> + sin2 <f>) (4.47)

+ ^ ^ (cos2 0 cos2 0 + sin2 fi?

8 r2

+ 32/3^ (n2 sin2 £(1 - cos2 0sin2 9)

+(n2 cos2 0 cos2 cj) + sin2 0 ) r2^ ) ,

,sin2g /sin2£ 2\ 9A2sin4$,

U33(r, 9, tj>) -- ( Aa sin2 £(r) + 3 2 / 3 ^ ^ + ^ + ^ f ^ ' 2 sin2 0. (4.48)

4.2.5 Densité de charge électrostatique du skyrmion

Puisque les noyaux atomiques contiennent plusieurs protons liés entre eux par la force nucléaire forte, on s'attend, de façon générale, à une contribution de l'énergie coulombienne de répulsion associée à la densité de charge électrique. Pour calculer celle-ci dans le modèle de Skyrme quasi-BPS à symétrie axiale, on définit le courant électromagnétique

JJBM = \B" + JV (4-49)

où B** est la densité baryonique et Jv est la densité du courant vectoriel. La charge

électrique conservée est alors

Q = f d3xJ%M = f d3x ( ± B ° + Jy3) (4.50)

où il est possible de définir la densité de charge électrique

Pc = \ B ° + J y . (4.51)

La partie cinétique du lagrangien quasi-BPS est invariante sous le groupe de transfor-mation SU(2)L ® SU(2)R

U -> LUR] (4.52)

où L, R G 5(7(2) et la densité du courant vectoriel est alors la somme des densité du courant de gauche et de droite

Jv a = J f + j £ \ (4.53)

Afin de calculer les densités de courant vectoriel, on applique les transformations infi-nitésimales de S U ( 2 ) L , R de façon indépendante sur la matrice de champs

U ^ LU = ( l + i ea( x ) ^ ) U U] ^ U]L* = U* ( l - i ea( x ) ^ j (4.54)