DM n°4: Écoulement parallèle de fluide - PCSI-PSI AUX ULIS

Chapitres PT4 DM n◦₄

DM n

4 : Ecoulement parallèle de fluide

L’énoncé comporte deux problèmes indépendants, seul le premier est obligatoire : Problème A : L’entropie dans le système respiratoire, d’après CCP PSI 2008 (partie I). Problème B (facultatif) : Trajectoire d’un volant de badminton, d’après X/ENS PC 2015





_________________________________________________________________________

Les calculatrices sont autorisées.

***

N.B. Le candidat attachera la plus grande importance à la clarté , à la précision et à la concision

de la rédaction. Si un candidat est amené à repère ce qui peut lui semble une erreur d’énoncé, il le

signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives

qu’il a été amené à prendre.

Les candidats doivent respecter les notations des énoncés et préciser, dans chaque cas la

numérotation de la question traitée.

***

PROBLEME

B : L’ENTROPIE DANS LE SYSTEME

RESPIRATOIRE

E

TUDE D

’

UN ÉCOULEMENT DANS UN TUYAU CYLINDRIQUE

ETUDE

LOCALE

On s’intéresse à l’écoulement d’un fluide incompressible et homogène de viscosité et de masse

volumique dans un tuyau cylindrique horizontal d’axe Oz, de longueur

et de rayon . Cet

écoulement unidirectionnel est caractérisé dans un repère cylindrique





par un champ

de vitesse







.

O

R

z

=

L

z

r

M

,



,



r

z



e

v

,



,

Figure 1

Problème A

Tournez la page SVP

Les expressions des opérateurs en coordonnées cylindriques sont données à la fin du sujet.

On note

P z





0





P

et

P z





L





P

.

On néglige les phénomènes de pesanteur.

A.1. Justifier que le champ de vitesse est indépendant de



.

A.2. Rappeler dans le cas général, l’équation locale de conservation de la matière.

Que devient cette relation dans le cas d’un

écoulement incompressible et homogène ?

En déduire que le champ de vitesse ne dépend pas de z.

A.3. Quelle propriété présente le champ de vitesse dans le cas d’un écoulement stationnaire

?

On étudie maintenant un écoulement stationnaire.

A.4. Représenter l’allure des lignes de courant et justifier que l’accélération d’une particule de

fluide est nulle. En projetant le principe fondamental de la dynamique, en déduire que

la pression P ne dépend que de z.

On ne demande pas d'expliciter ici la force de viscosité.

A.5.

Etablir l’expression de

P z en fonction de

 

P ,

P , z et L.

E

COULEMENT STATIONNAIRE

E

TUDE GLOBALE

On s’intéresse toujours à l’écoulement d’un fluide incompressible de viscosité



et de masse

volumique



dans un tuyau cylindrique horizontal d’axe Oz de longueur

et de rayon

. On

désire déterminer l’expression du champ de vitesse.

On s'intéresse à une portion de liquide (représentée en grisé sur la figure 2 ci-dessous) contenue

dans un cylindre de rayon r



r



R



, compris entre les plans

et

. On rappelle que sur la

surface latérale de ce cylindre de rayon

s'exerce une force de viscosité parallèle à Oz et dont la

norme est

F

S

v r

 

r









, où S est la surface latérale du cylindre et

v la vitesse du liquide. On

note

P z





0





P

et

P z





L





P

. On néglige les phénomènes de pesanteur.

O

R

z

=

L

A.7. Faire l’inventaire des forces s'exerçant sur le cylindre de rayon

.

A.8. On rappelle que la vitesse ne dépend que de

. En appliquant le principe fondamental de la

dynamique au petit cylindre en régime permanent, déduire alors une équation de la forme

dv kr

dr 

où

s'exprime en fonction de

,

P ,

P et 

.

En déduire que le champ de vitesse s’écrit

 





4 L P P v r R r L



 

sachant que la vitesse

R

ÉSISTANCE HYDRAULIQUE

A.9. Calculer le débit volumique Q dans la conduite. On l’exprimera sous la forme





Q



K P



P

connue sous le nom loi de Poiseuille. Calculer la constante K.

En déduire la vitesse moyenne,

en fonction de

,

P ,

P , R

et



.

La comparer à la vitesse maximale,

.

A.10. On définit

, résistance hydraulique de longueur

et de surface

, par la relation

0 L Hy P P R Q

.

Exprimer

en fonction de

,

et



. Quelle est l’analogie avec la définition de la résistance

électrique ?

A.11. Comment varie la résistance hydraulique

avec le rayon

?

Comparer ce résultat avec la résistance électrique d’un barreau de longueur

de section

²

S 



et de conductivité électrique



. Justifier qualitativement la différence.

A.12. La loi de Poiseuille n’est valable que pour un écoulement laminaire.

Rappeler la signification du terme en gras.

En déduire une inégalité sur le rayon

pour que le calcul soit valable si on prend une

vitesse moyenne

, une viscosité dynamique



et une masse

volumique



.

en r = 0 est bornée.

Tracer le profil de la vitesse v(r) en fonction de r.

Préciser la valeur maximale v

de la vitesse.

Tournez la page SVP

A

SSOCIATION DE RÉSISTANCES HYDRAULIQUES

A.13. On associe deux cylindres

A et

A (figure 3) de résistances hydrauliques

R

et

R

de

même section

, l'un est compris entre

x



0

et

x



L

, le second est compris entre

x



L

et

2 1 2

x

 

L

L

. On note

P ,

P et

P les pressions pour

x



0

,

x



L

,

x

 

L

L

. On suppose

le raccordement parfait..

0 0

x = x1=L1 x2 =L1+L2

Figure 3

a) Établir l'expression de la résistance hydraulique

R (qu’on définit bien sûr par la relation :

0 L Hy

P P R Q

) de l'ensemble en fonction de

R

et

R

.

Indiquer, en la justifiant, une analogie avec un problème d’électrocinétique.

b) En déduire la pression

P en fonction de

P ,

P ,

R

et

R

.

0

0

x =

Figure 4

A.14. Les deux cylindres

A , de section

S et de longueur

L et

A de section

S et de longueur

2

L sont associés en « parallèle » (figure 4). On note

P , la pression sur les faces d'entrée pour

0

x



et

P , la pression sur les faces de sorties (

x



L

pour

A , et

x



L

pour

A ).

Etablir l’expression de la résistance hydraulique de cette association en raisonnant par

analogie avec l’électrocinétique.

En déduire le débit

Q dans le cylindre

A de section

S en fonction du débit total

,

R

et

R

.

A.15. Rappeler l’expression de la puissance électrique dissipée dans une résistance électrique,

traversée par un courant d’intensité

. Par analogie, déterminer la puissance dissipée par les

forces de viscosité en fonction de

et

.

L’

ARBRE BRONCHIQUE

ET L

’

ENTROPIE

Dans un arbre bronchique, les voies respiratoires se

divisent

par

dichotomie

avec

une

réduction

systématique de la longueur et du diamètre. Dans le

problème, nous allons supposer que la trachée se

divise en deux bronches. Chacune d’elles se divise à

son tour en deux autres, et ainsi de suite. Nous notons

générations les différentes subdivisions qui seront

indicées par les nombres successifs,

: la trachée est

la génération

, les bronches,

, et ainsi de

suite. Nous nous plaçons en régime permanent et l’air

est assimilé à un fluide de viscosité



.

Une bronchiole de génération

est assimilée à un

cylindre de rayon

et de longueur

. Nous

admettrons que la loi de Poiseuille établie

précédemment reste valable (en particulier entre

6

p

et

).

A chaque génération, chaque dimension (rayon comme longueur) est multiplié par une constante

que l’on supposera identique pour les deux dimensions.

1ère génération de résistance hydraulique, et volume 1

V

R

2ème génération : Les dimensions rayon et longueur) sont multipliées par h par rapport à la génération(1)

3ème génération : Les dimensions rayon et longueur) ont multipliées par h² par rapport à la génération(1)

A.16. Déterminer le nombre

N p de bronchioles à la p

 

génération en fonction de

.

A.17. Déterminer le rayon

et la longueur

de la bronchiole de génération

en fonction de

,

Tournez la page SVP

A.18. Calculer le volume

d’une bronchiole de génération

en fonction de

V ,

et

. En

déduire le volume total

V de la génération

. On posera

2 X  h

.

Montrer que le volume de l’arbre supposé contenir n générations est

1

1

X

V

V

X







.

A.19. Calculer la résistance hydraulique

d’une bronchiole de génération

en fonction de

R ,

résistance hydraulique pour

et

. En déduire la résistance hydraulique

totale de la

génération

.

Déterminer la résistance hydraulique

R de l’arbre supposé contenir

n générations.

A.20. Montrer que le volume total diverge quand n

 

lorsque

est supérieure à une valeur

critique

h dont on précisera la valeur numérique.

A quelle condition sur

, la résistance hydraulique diverge-elle ?

La puissance thermique cédée à l’environnement assimilé à un thermostat de température

, est

due à la puissance des forces de viscosité.

A.21. En utilisant la loi de Poiseuille, calculer la puissance thermique cédée par un arbre

bronchique ayant

n générations en fonction de

Q , débit à la génération 1,

R ,

et

n .

A.22. A partir d’un bilan d’entropie entre les instants t et t + dt , établir l’expression



de

l’entropie créée par unité de temps pour cet écoulement unidimensionnel en régime

permanent.

A.23. Exprimer l’entropie crée





par unité de temps et de volume dans un arbre

bronchique ayant

n générations en fonction de

,

Q ,

R ,

et

n . Montrer que ce terme

diverge quand

n

 

si

h



h

. Conclure pour l’homme où

.

Il est à remarquer que cette application au système pulmonaire n’est pas exacte puisque le flux

n’est pas stationnaire mais pulsé.

ANNEXE

Données pour les coordonnées cylindriques

r e  e z e M O  z e x e y e

 

 

 

 



 









1

, ,

f

f

f

grad f r

z

e

e

e

r

r

z























_{ }

_

_

FIN DU PROBLEME

A

´

ECOLE POLYTECHNIQUE – ´ECOLES NORMALES SUP´ERIEURES ´

ECOLE SUP´ERIEURE DE PHYSIQUE ET DE CHIMIE INDUSTRIELLES

CONCOURS D’ADMISSION 2015 FILI`ERE PC

COMPOSITION DE PHYSIQUE – B – (XEULC)

(Dur´ee : 4 heures)

? ? ?

L’utilisation des calculatrices n’est pas autoris´ee pour cette ´epreuve. On se contentera, pour les applications num´eriques, d’un seul chiffre significatif.

Les deux probl`emes sont ind´ependants.

I. Trajectoire d’un volant de badminton

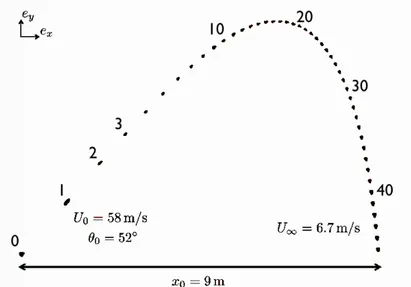
Le badminton est un sport dans lequel les joueurs frappent un projectile, appel´e volant, `a l’aide d’une raquette. Le but de ce probl`eme est de proposer une mod´elisation simplifi´ee de la trajectoire du volant sous l’effet conjugu´e de la pesanteur et de la r´esistance de l’air, et de confronter le mod`ele aux r´esultats d’une exp´erience. On n´egligera la pouss´ee d’Archim`ede dans tout le probl`eme.

On n´eglige dans un premier temps la force de freinage exerc´ee par l’air.

I.1 On lance depuis le sol le volant de masse m avec une vitesse initiale U0, dans une direction

faisant un angle θ0avec le plan du sol, suppos´e horizontal. Quelle est la nature de la trajectoire ?

Dessiner son allure. D´eterminer la port´ee L0 (distance horizontale `a laquelle le volant retombe

sur le sol) en fonction de U0, de θ0, et de l’acc´el´eration de la pesanteur g.

I.2 Validez dimensionnellement l’expression de L0 obtenue et v´erifiez-la sur des cas limites

simples que vous choisirez.

I.3 La vitesse initiale ´etant fix´ee, quel angle θ0 permet d’envoyer le volant le plus loin possible ?

On tient maintenant compte du freinage de l’air, mod´elis´e en assimilant le volant `a une sph`ere solide en mouvement dans un fluide newtonien. On ´ecrit la force de freinage sous la forme ~F = ₋1₂ρSCxU ~U , o`u ~U est la vitesse du volant et U sa norme, ρ la masse volumique de

l’air, S la surface de r´ef´erence du volant, et Cx le coefficient de traˆın´ee.

I.4 D´eterminer la dimension de Cx. Tracer l’allure de sa variation en fonction du nombre de

Reynolds, et indiquer les r´egimes o`u l’´ecoulement est laminaire ou turbulent.

I.5 La viscosit´e cin´ematique de l’air est ν = 1.5_{× 10}−5 m2_·s−1 _{et la taille caract´eristique d’un}

volant de badminton est L ' 6 × 10−2 _{m. Des valeurs de la vitesse sont indiqu´ees sur la}

chronophotographie de la figure 1. Estimer les valeurs correspondantes du nombre de Reynolds. `

A quel r´egime d’´ecoulement correspond-il ?

1

Problème B

I.6 ´Ecrire l’´equation du mouvement du volant. Montrer qu’elle admet une solution particuli`ere, correspondant `a un mouvement rectiligne uniforme dont on exprimera la vitesse, not´ee U_∞, en fonction des param`etres du probl`eme.

I.7 R´ecrire l’´equation du mouvement en faisant notamment apparaˆıtre le rapport ~U /U_∞. I.8 `A quelle condition sur U peut-on n´egliger la pesanteur ? On suppose dans toute la suite du probl`eme que cette condition est initialement v´erifi´ee. Dans ce cas, quelle est la nature de la trajectoire ? Int´egrer l’´equation du mouvement pour obtenir U en fonction du temps.

I.9 En utilisant cette expression, d´eterminer et calculer le temps t_1/2 pour lequel la vitesse est ´egale `a la moiti´e de la vitesse initiale. Rep´erer le point correspondant sur la chronophotographie de la figure 1. V´erifier, par une mesure que l’on expliquera, que la vitesse en ce point est bien approximativement la moiti´e de la vitesse initiale.

Figure 1: Positions successives d’un volant de badminton allant de la gauche vers la droite, enregistr´ees toutes les 50 ms. Le premier point, rep´er´e par le chiffre 0, correspond au lancer `a t = 0.

I.10 Toujours dans le cadre de l’approximation de la question I.8, d´eterminer l’expression don-nant la distance horizontale x(t) parcourue au temps t.

I.11 Obtenir x en fonction de U .

I.12 On suppose que l’approxi-mation de la question I.8 cesse d’ˆetre valable lorsque la com-posante verticale de la force de freinage est ´egale au poids. Quelle est l’expression de U `a cet instant ? En d´eduire la distance horizontale parcourue L.

On mod´elise la trajectoire du

volant en distinguant trois r´egimes successifs : (1) le r´egime que l’on vient d’´etudier, durant lequel l’acc´el´eration de la pesanteur est n´egligeable ; (2) un r´egime interm´ediaire ; (3) un r´egime limite durant lequel l’acc´el´eration du volant est n´egligeable.

I.13 Localiser sur la chronophotographie le r´egime limite ainsi d´efini, en justifiant pr´ecis´ement votre r´eponse.

I.14 Une approximation de la trajectoire consiste `a oublier la partie correspondant au r´egime interm´ediaire. Dessiner la trajectoire obtenue dans cette approximation.

I.15 Donner l’expression litt´erale de la port´ee du tir dans cette approximation. Comment se compare-t-elle `a la port´ee en l’absence de freinage, d´etermin´ee `a la question I.1 ?

I.16 Estimer num´eriquement la port´ee du tir. On donne ln 8 ' 2, cos θ0 ' 0, 6, sin θ0 ' 0, 8.

Comparer le r´esultat avec la valeur indiqu´ee sur la chronophotographie.

I.17 Durant le r´egime interm´ediaire, tous les termes de l’´equation du mouvement sont du mˆeme

ordre de grandeur. En d´eduire, par un argument dimensionnel, une expression litt´erale de l’ordre de grandeur de la distance parcourue lors du r´egime interm´ediaire. Dans quelle limite l’approximation faite `a la question I.14 est-elle justifi´ee ?

I.18 Comment faudrait-il modifier les param`etres de l’exp´erience pour que la trajectoire cor-responde plus pr´ecis´ement `a celle obtenue `a la question I.14 ? On discutera suivant la vitesse initiale et la nature du projectile. La convergence vers cette solution limite est-elle plutˆot rapide, ou lente ?

I.19 Donner les expressions litt´erales des temps de mont´ee et de descente du volant. Estimer, par un argument dimensionnel, l’ordre de grandeur litt´eral de la dur´ee du r´egime interm´ediaire. Comparer les dur´ees de ces trois r´egimes dans la limite ou` l’approximation de la question I.14 s’applique.

3