Focalisation extrême par des éléments optiques
non-paraxiaux
Thèse Denis Panneton Doctorat en Physique Philosophiæ doctor (Ph. D.) Québec, Canada © Denis Panneton, 2018Focalisation extrême par des éléments optiques
non-paraxiaux
Thèse
Denis Panneton
Sous la direction de :
Michel Piché, directeur de recherche Simon Thibault, codirecteur de recherche
Résumé
Ce projet s’inscrit comme un effort de modélisation et de développement d’outils analytiques décrivant la focalisation non-paraxiale de champs électromagnétiques. Des solutions vecto-rielles sont développées, suivant une généralisation du formalisme intégral de Richards-Wolf. La thèse se scinde en deux principales avenues. La première consiste à décrire, en langage mathématique moderne, le formalisme de Richards-Wolf qui permet de décrire les champs électromagnétiques vectoriels au foyer de systèmes focalisants. Le formalisme est exploré et plusieurs solutions analytiques aux équations intégrales de Richards-Wolf sont introduites. La deuxième avenue consiste en la généralisation du formalisme de Richards-Wolf pour des systèmes à foyer étendu (par exemple, distribué sur une ligne). Utilisant une méthode com-binée, basée sur le tracé de rayon et le traitement intégral de la diffraction, le modèle permet une amélioration en trois volets des descriptions classiques des champs au foyer. En premier lieu, l’analyse vectorielle de la diffraction permet de s’affranchir de toute hypothèse paraxiale. En second lieu, l’analyse exacte et l’analogie rayon/onde plane uniforme permet d’éviter la description de systèmes à foyer étendu par des termes de phases aberrés, qui réduisent la robustesse du modèle et la justesse des solutions trouvées. Finalement, l’élégance analytique de la méthode permet une compréhension physique plus instinctive des phénomènes d’inter-férence au foyer de systèmes complexes et encourage le développement de méthodes inverses, permettant de retracer les conditions nécessaires à l’obtention d’un profil d’intensité et de phase données, sans a priori sur le système focalisant.
Sur le plan concret, les outils mathématiques décrits et développés dans cette thèse permettent une avancée pour l’étude de phénomènes et le développement de technologies, notamment en microscopie à haute-résolution, mais également en stockage de données, en piégeage optique ou même en accélération de particules à l’échelle microscopique.
Il s’agit de la première méthode systématique proposée pour calculer le profil de faisceaux focalisés par des sections coniques (sphères, ellipses, etc.) par des moyens analytiques.
Abstract
This project is part of a global effort toward modelization and development of mathemat-ical tools describing non-paraxial focusing of electromagnetic fields. Vectorial solutions are proposed, according to a generalization of the Richards-Wolf formalism.
The objective of this thesis is two-fold. The first part covers the Richards-Wolf formalism with a modern mathematical formulation, which permits the formal description of focused vectorial electromagnetic fields. An in-depth exploration of the theory is exposed and multiple analytical solutions of the integrals are given.
The second part covers the generalization of the Richards-Wolf formalism to systems without a single-point focus, by combining geometrical optics and diffraction principles. The vectorial analysis agrees with the assumption of non-paraxial focusing while the development is free of constraints upon the existence of an optical focus. Finally, the analytical treatment helps forge a physical intuition of the electromagnetic solutions and the development of inverse methods, which would help find the necessary illumination upon a system to produce a given electromagnetic pattern near the focus.
The mathematical tools presented in this thesis may lead to advances in high-resolution microscopy, data encryption, optical tweezers and particle acceleration.
Table des matières
Résumé iii
Abstract iv
Table des matières v
Liste des figures vii
Remerciements ix
1 Introduction 1
1.1 La genèse et l’objectif de cette thèse . . . 2
1.2 Revue des théorèmes classiques . . . 3
1.3 Divisions de cette thèse . . . 13
2 Formalisme de Richards-Wolf 15 2.1 Préalable . . . 15
2.2 Formalisme général . . . 17
2.3 États de polarisation et simplifications . . . 26
2.4 Exemple : Focalisation d’un anneau radialement polarisé par un miroir pa-rabolique . . . 28
2.5 Sélection d’applications de pointe en optique . . . 31
3 Quelques solutions analytiques 35 3.1 Cas uniforme . . . 36 3.2 Profil cosinusoïdal . . . 39 3.3 Aiguille infinie . . . 42 3.4 Bulle optique . . . 44 3.5 Onde sphérique . . . 51 3.6 Discussion . . . 54
4 Généralisation du formalisme de Richards-Wolf 56 4.1 Contexte et pertinence . . . 56
4.2 Définition de la surface focalisante . . . 57
4.3 Terme de phase généralisé . . . 60
4.4 Facteur d’apodisation généralisé. . . 62
4.5 Influence d’un front de phase incident non-plan . . . 64
4.7 Focalisation par des sections coniques . . . 71
4.8 Résumé . . . 83
5 Aiguilles de lumière 85 5.1 Contexte. . . 85
5.2 Génération des aiguilles . . . 86
5.3 Caractéristiques des aiguilles . . . 88
5.4 Régime impulsionnel . . . 93
6 Conclusion 98 6.1 Retour sur la thèse . . . 98
6.2 Contributions originales et principales présentations . . . 99
6.3 Travaux connexes et pistes à explorer. . . 99
6.4 Épilogue . . . 101
A Méthode inverse 102 A.1 La problématique . . . 102
A.2 Transformée analytique - principes de base . . . 103
A.3 Champ solution donné sur l’axe . . . 105
A.4 Champ solution donné dans le plan focal. . . 111
A.5 Généralisation de l’inversion - sur l’axe . . . 112
B Microscopie différentielle 3D 114 B.1 Mise en contexte . . . 114
B.2 Microscopie et imagerie différentielle . . . 115
B.3 Analyse de l’illumination. . . 116
C Accélération directe d’électrons 119 C.1 L’accélération par laser. . . 119
C.2 Schéma d’accélération par onde quasi-stationnaire . . . 120
C.3 Résultats d’accélération . . . 123
C.4 Illumination modulée . . . 126
C.5 Hypothèse en régime impulsionnel . . . 128
Liste des figures
1.1 Principe de Huygens . . . 8
1.2 Principe de diffraction de Kirchhoff. . . 10
2.1 Visualisation du principe de focalisation. . . 19
2.2 Géométrie et définition des vecteurs de polarisation des champs incidents et focalisés.. . . 21
2.3 Différence fondamentale entre le traitement vectoriel exact et par aberrations. . 25
2.4 Faisceau incident sur le miroir parabolique. . . 30
2.5 Profil d’intensité au foyer d’un miroir parabolique. . . 30
3.1 Profil en intensité, selon la méthode par fonction hypergéométrique. . . 38
3.2 Écart (en pourcentage) entre l’intensité calculée par quadrature numérique et par la fonction hypergéométrique, pour un champ incident uniforme sur une parabole. . . 39
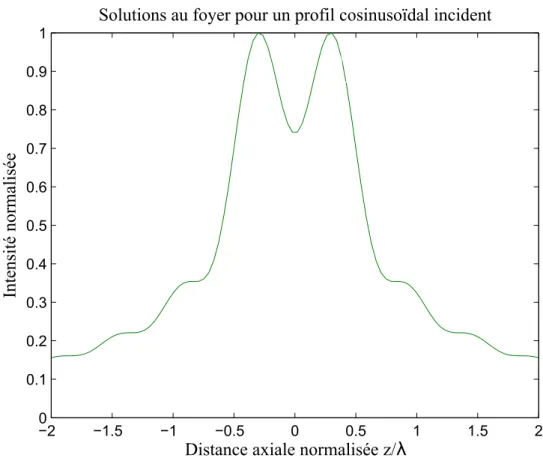
3.3 Profil axial du champ focalisé pour le profil incident cosinusoïdal par rapport au profil incident uniforme. . . 41
3.4 Amplitude et phase du champ électrique sur l’axe optique, près du foyer de la parabole. . . 42
3.5 Profils modulés et solutions numériques pour un champ à deux foyers. . . 43
3.6 Profil incident pour la création d’une bulle optique.. . . 45
3.7 Résultats au foyer pour la forme analytique. . . 47
3.8 Solution au foyer de l’intensité du champ. . . 50
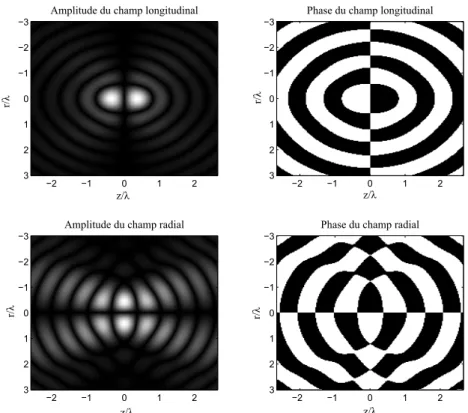
3.9 Amplitude et phase des composantes radiales et longitudinales du champ solu-tion au foyer. . . 51
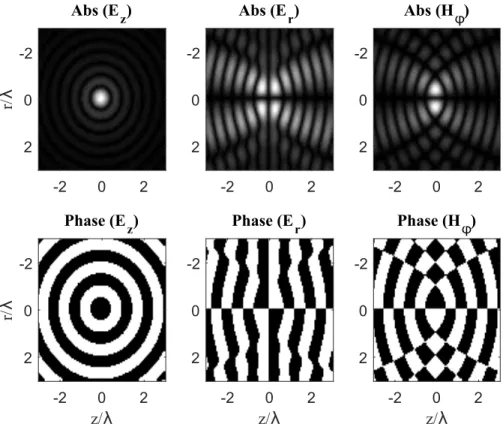
3.10 Champs au foyer avec le modèle de focalisation prescrit pour l’onde sphérique au foyer. . . 54
4.1 Géométrie utilisée pour le développement du formalisme ERWT. . . 58
4.2 Principe de superposition. . . 59
4.3 Correction à la phase pour l’onde plane de vecteur d’onde ⃗𝑘. . . 61
4.4 Faisceau annulaire envoyé sur une parabole. . . 65
4.5 Approche par propagation paraxiale. . . 66
4.6 Définition de l’angle Γ pour une onde conique. . . 68
4.7 Section conique. . . 72
4.8 Profils incidents utilisés pour les calculs de l’ERWT. . . 73
4.9 Carte d’intensité et profils produits par un miroir parabolique. . . 75
4.10 Carte d’intensité et profils produits par un miroir sphérique.. . . 78
4.12 Carte d’intensité et profils produits par un miroir elliptique d’excentricité 𝜖 = 0, 5. 81 4.13 Carte d’intensité et profils produits par un miroir hyperbolique d’excentricité
𝜖 = 1, 25. . . . 82
4.14 Facteur d’apodisation pour différentes valeurs d’excentricité. . . 83
5.1 Anneau de lumière incident sur un miroir sphérique et non-paraxialement fo-calisé en une aiguille de lumière. . . 86
5.2 Longueur à mi-hauteur d’une aiguille de lumière sur l’axe optique. . . 90
5.3 Largeur à mi-hauteur de l’aiguille. . . 92
5.4 Profil d’intensité de l’aiguille de lumière. . . 93
5.5 Profil longitudinal de l’aiguille de lumière. . . 93
5.6 Évolution de la densité d’énergie d’une aiguille de lumière en régime impulsionnel. 96 5.7 Densité d’énergie d’une aiguille de lumière en régime impulsionnel. . . 96
A.1 Champ prescrit et transformée de Fourier. . . 108
A.2 Aiguille supergaussienne d’ordre 5 et spectre associé. . . 110
B.1 Schéma proposé d’illumination d’un spécimen. . . 115
B.2 Faisceau brillant proposé. . . 116
B.3 Comparaison des PSF axiales des faisceaux clair et sombre. . . 117
B.4 Comparaison des PSF radiales des faisceaux brillant et sombre. . . 118
C.1 Principe d’accélération proposé. . . 121
C.2 Gain en énergie normalisé d’un électron relativiste voyageant selon l’axe d’un champ focalisé optimal. . . 122
C.3 Gain d’énergie sur l’axe pour un électron relativiste se propageant dans un champ 𝑇 𝑀01.. . . 123
C.4 Énergie de l’électron le long de sa trajectoire sur l’axe (en considérant 𝜙0= 0). 124 C.5 Énergie finale d’un électron accéléré selon la phase 𝜙0du champ électromagné-tique. . . 125
C.6 Profils angulaires incidents sur le miroir parabolique pour l’accélération d’élec-trons. . . 127
C.7 Champ électromagnétique d’accélération réaliste au foyer. . . 128
C.8 Gain d’énergie sur l’axe pour un électron relativiste passant dans le champ semi-statique réaliste. . . 129
Remerciements
Pendant les années sous lesquelles se tisse graduellement une thèse, force est de constater que l’aide apportée par nos pairs prend une place non pas considérable, mais plutôt essentielle. Malgré les dizaines de pages, les résultats d’analyse, les outils développés et les conséquences scientifiques d’intérêt qui meublent cette thèse, je crois qu’un grand crédit doit revenir à cette fameuse section « Remerciements ». Section sans intérêt pour le lecteur pragmatique, elle symbolise pourtant la force des réseaux humains, la persévérance accumulée par mimétisme et le soutien sans borne qu’un geste aux apparences bénin peut nous apporter.
Pour moi, cette section, c’est la chance de dédier humblement ma réussite à mes amis, ma famille. Parfois trop avare de reconnaissance, je me repends aujourd’hui et redonne, si mai-grement, le mérite qui leur est dû.
À mes collègues, ceux qui m’ont tellement bien accueilli à mon arrivée. À ceux qui sont devenus des amis au-delà des enceintes professionnelles. À ceux que j’ai à mon tour accueilli et qu’il me fait du tort de quitter. À tous ces professeurs qui ont été mentors, source d’inspiration, complices. À ma famille, la meilleure qui soit. À mes amis, mes voisins, mes compagnons de scène, mes coéquipiers et mes amours.
Merci aux stagiaires qui m’ont assisté pendant plusieurs sessions et qui ont permis de faire avancer plusieurs sujets abordés ici. Merci à Guillaume, qui a entamé les premiers débrous-saillages avec un brio qui peut lui laisser miroiter le plus grand avenir en sciences. Merci à Katherine et Cédric, dont l’audace ont permis d’agrandir l’horizon du projet. Merci à Jeck de m’avoir rejoint dans cette nouvelle équipe et pour son dévouement à notre projet commun. Merci à Michel et Simon de m’avoir fait confiance pour un projet un peu différent et de m’avoir accompagné dans les échecs comme dans les succès. Merci à Nathalie d’être qui tu es et d’être restée si proche après ma maîtrise. Merci au CRSNG et au FRQNT d’avoir soutenu le projet et de croire en l’avenir des jeunes en science (et de nous permettre de ne pas systématiquement courir après le free food).
Chapitre 1
Introduction
La physique optique a historiquement engendré un grand intérêt puisque les phénomènes y étant reliés sont à la fois fascinants et facilement accessibles. Avec le développement de méthodes mathématiques au service de l’étude physique de notre environnement, plusieurs formalismes - en quelque sorte la grammaire et le vocabulaire associés à une réalité physique - se sont côtoyés. Une richesse encore grandissante a toujours défini ce domaine de la science. Autant les phénomènes lumineux ont développé la curiosité et l’admiration de nos ancêtres, autant ces mêmes phénomènes sont aujourd’hui la source d’inspiration des plus grandes avan-cées en technologie de pointe.
La recherche en optique permet de pousser de nouvelles technologies ou d’exploiter les techno-logies existantes pour de nouvelles applications. Les barrières à abattre sont souvent techniques et l’apport de l’ingénierie au progrès se trouve souvent à en être la réponse. D’autres freins à la créativité scientifique prennent racine dans le manque d’outils mathématiques, de visuali-sation ou de vulgarivisuali-sation. Le développement de formalismes simples et élégants permet à la communauté scientifique d’aller de l’avant plus facilement et de se rallier derrière une vision commune des phénomènes qu’elle étudie. C’est dans cette veine que la présente thèse s’inscrit. On y suggère un formalisme, basé sur les principes de base en optique ondulatoire et diffractive, pour décrire avec précision et simplicité la focalisation de faisceaux optiques par des éléments focalisants non-paraxiaux extrêmes et fortement aberrés. Le formalisme proposé, basé sur les principes introduits par Richards et Wolf en 1959, tient compte du caractère vectoriel des champs électromagnétiques et l’interaction complexe entre ceux-ci. Le formalisme, aussi, prend racine dans la compréhension empirique des champs et de leur interdépendance, comme édictée par Maxwell. Ces concepts depuis longtemps reconnus sont combinés dans un but concret pour former un ensemble de lois et d’équations permettant le calcul de l’influence d’un système focalisant sur les champs, en n’impliquant que les paramètres macrométriques dudit système.
Plusieurs formalismes mathématiques entourant le sujet de près seront présentés, sans être exhaustivement développés, afin de bien mettre la thèse en contexte dans l’échiquier complexe des outils mathématiques existants au moment d’écrire ces lignes. Finalement, l’organisation du reste du document sera étayée pour bien en saisir la structure.
1.1
La genèse et l’objectif de cette thèse
Un problème en apparence très simple et académique s’est déposé sur mon bureau il y a quelques années :
Problématique initiale
Quelle est la solution rigoureuse du champ électromagnétique vectoriel produit par la focalisation à très grand angle d’un faisceau polarisé de profil d’amplitude connu par un miroir sphérique.
Le questionnement, aux apparences naïves pour le chercheur aguerri, naît d’une expertise de notre groupe de recherche en modélisation de faisceaux non-paraxiaux et d’un outil glo-balement utilisé, soit le formalisme de Richards-Wolf. Ce formalisme, comme plusieurs, se base sur la prémisse d’un foyer optique défini et de fronts de phase sphériques de référence. En régime hautement non-paraxial, il est cependant rigoureusement impossible de définir un foyer optique à une sphère. Des traitements par aberration peuvent être implémentés, mais existerait-il une version exacte du formalisme de Richards-Wolf qui permettrait d’éviter une approximation par un ajustement scalaire1?
L’optique purement géométrique peut facilement traiter le miroir sphérique (comme toute autre forme de surface focalisante), mais ne peut considérer les procédés de diffraction qui importent grandement dans un cas de focalisation non-paraxiale d’un faisceau polarisé. La solution directe des équations de Maxwell avec conditions limites, à l’inverse, permet une solution absolument exacte, au coût de calculs vertigineux. L’exploration des formalismes en intégrales de diffraction à la Kirchhoff, Fraunhofer, Fresnel et Sommerfeld révélait que ces outils ne sont pas tout désignés pour le problème. Un formalisme basé sur une définition vectorielle sans restrictions angulaires, celui de Richards-Wolf, semblait avoir un meilleur potentiel pour être adapté à la situation.
Cette thèse est donc à la fois le rafraîchissement et l’extension du largement cité formalisme de Richards-Wolf, issu des principes fondamentaux de diffraction de Debye.
1. Une discussion sur la nature scalaire de l’introduction de termes d’aberration est proposée à la sec-tion2.2.5
Objectif de cette thèse
Fournir un formalisme adapté au calcul rigoureux des champs électromagnétiques vec-toriels produits par la focalisation non-paraxiale de faisceaux polarisés de profil d’ampli-tude connu par un élément focalisant extrême dont on ne peut définir un foyer ponctuel (i.e. à foyer distribué).
1.2 Revue des théorèmes classiques
Puisque cette thèse porte sur certains éléments fondamentaux de l’expression mathématique en optique, il est de mise d’exposer en premier lieu les principaux théorèmes à partir desquels le travail est fait. Cette section englobe les bases nécessaires de certaines théories et, surtout, les expose en contexte et de façon cohérente.
Un objectif constamment en filigrane des recherches fondamentales en optique est de mélanger et de confronter les différents formalismes mathématiques afin de les alléger, de les consoli-der ou de les harmoniser. Cependant, puisque tous les formalismes développés se basent sur les mêmes quantités fondamentales et les mêmes phénomènes physiques, ils se distinguent davantage les uns des autres par leur contexte d’utilisation, par la définition des conditions d’applicabilité et par les éléments requis pour faire les calculs concrets. Un formalisme est donc une collection de fonctions définies selon une quantité donnée d’informations connues. Les formalismes présentés ici servent à obtenir la forme du champ électromagnétique en tout point d’un volume donné à partir d’un champ et de son interaction avec lui-même (pro-pagation) ou avec un élément externe (diffraction et focalisation). Ceci étant un chapitre introductif, les formalismes ne sont pas développés formellement. Leurs résultats, hypothèses et interprétations majeures sont exposés. Des références sont données pour guider le lecteur afin d’en savoir davantage sur leur dérivation rigoureuse.
1.2.1 L’électromagnétisme
L’électromagnétisme consiste en l’analyse de la lumière sous la prémisse de sa description « ondulatoire ». Les bases du traitement mathématique de l’optique électromagnétique sont attribuées à James Clerk Maxwell, qui proposa, en 1865, 20 postulats de base régissant le comportement des 20 composantes électromagnétiques de la nature [1]. Ces postulats furent retravaillés pour éventuellement correspondre aux 4 équations vectorielles modernes dites « de Maxwell », mais qui furent, dans les faits, développées par Heaviside. Si l’on accepte la théorie dictant que l’on retrouve en tout point de l’espace un champ électrique ( ⃗𝐸) et magnétique ( ⃗𝐵) directionnels, lesdits champs seront alors en relation entre eux et avec leur environnement - spatialement et temporellement - selon
∇ × ⃗𝐸 = −𝜕 ⃗𝐵 𝜕𝑡; (1.1) ∇ × 𝐵⃗ 𝜇 =𝐽 +⃗ 𝜕𝜖 ⃗𝐸 𝜕𝑡 ; (1.2) ∇ ⋅𝜖𝐸 = 𝜌;⃗ (1.3) ∇ ⋅ ⃗𝐵 = 0, (1.4)
où 𝜇 est la perméabilité magnétique du milieu, 𝜖 est la permittivité diélectrique du milieu, 𝐽⃗ représente la densité de courant dans le milieu et 𝜌 représente la densité volumique de charge du milieu.
Au-delà des modèles analytiques, ces lois servent également à vérifier les modèles numé-riques puisqu’elles doivent systématiquement être respectées pour qu’un modèle soit considéré comme juste. Les équations de Maxwell peuvent par ailleurs être résolues de façon discrète en tout point de l’espace et du temps par force de calculs numériques. Cette méthode brute et sans approximation peut être utilisée pour vérifier des modèles analytiques ou pour traiter des problèmes pour lesquels aucun formalisme ne semble être adapté.
Note historique
Ces lois universelles du comportement ondulatoire de la lumière sont à la base de plusieurs théories et servent aujourd’hui à obtenir les solutions du champ sous diverses contraintes. On attribue historiquement ces lois à une approche empirique. Plusieurs traités ont été publiés afin de dériver les lois de Maxwell à partir de principes plus fondamentaux, dont les équations de champ d’Einstein. Cependant, puisqu’une grande partie des travaux d’Einstein, dont la relativité restreinte, sont des conséquences directes des équations de Maxwell, il reste encore controversé de retrouver un principe plus fondamental pour une dérivation exhaustive de ces formes analytiques. Une brève lettre de Hughes [2] fait mention d’une dérivation plutôt simple des équations de Maxwell à partir de simples principes de commutativité des lois de Newton et apporte une réflexion sur le caractère conflictuel du sujet inspiré par Richard Feynman.
L’équation d’onde
Une des conséquences les plus importantes des équations de Maxwell est l’équation d’onde électromagnétique. Cette équation (ou plutôt famille d’équations) est une version simplifiée, dans un système de conditions données, qui limite les formes possibles que peut prendre le champ électromagnétique dans l’espace comme dans le temps. La forme canonique de cette équation d’onde, pour le champ électrique, est donnée par
∇2𝐸 − 𝜇⃗ 0𝜖
𝜕2𝐸⃗
𝜕𝑡2 = 0. (1.5)
Cette équation, par exemple, décrit les solutions du champ électrique d’un milieu homogène. Elle peut être résolue en présence de conditions limites connues et, généralement, dans des cas paraxiaux où la constante de propagation selon l’axe optique est beaucoup plus importante que celle dans les axes transverses.
Une grande partie des efforts déployés par les pionniers des formalismes optiques est de ré-soudre ces équations selon différentes approximations pour servir à différents contextes. En effet, la résolution brute en tout point de l’espace des équations de Maxwell lorsque les sources sont connues, comme mentionné précédemment, n’est que très rarement la voie à privilégier.
L’onde plane vectorielle
Le champ électromagnétique le plus simple, solution des équations de Maxwell et de l’équation d’onde, est l’onde plane. En considérant le caractère vectoriel de la lumière, et en supposant une direction de propagation de l’onde dénotée par le vecteur ⃗𝑠, on peut retomber sur l’inter-dépendance des champs électriques et magnétiques
⃗ 𝐸 = −√𝜇 𝜖𝑠 ×⃗ 𝐻;⃗ (1.6) ⃗ 𝐻 = √𝜖 𝜇𝑠 × ⃗⃗ 𝐸, (1.7)
où on introduit la forme𝐻 pour le champ magnétique. Cette forme est telle que, dans un milieu⃗ non-magnétique, on peut écrire 𝐵 = 𝜇⃗ 0𝐻, où⃗ 𝐵 est appelée « induction magnétique ». Ces⃗ expressions impliquent simplement que les champs électriques et magnétiques se situent dans un plan perpendiculaire à la direction de propagation, qu’ils sont également perpendiculaires l’un par rapport à l’autre et dans un rapport d’amplitude
| ⃗𝐸| = √𝜇
𝜖| ⃗𝐻|. (1.8)
L’onde plane implique donc une onde sans composante de polarisation dans sa direction de propagation. Bien entendu, puisque toute onde de dimension finie diverge, l’onde plane ne peut être qu’une approximation macrométrique valable pour un faisceau hautement collimaté de taille nettement supérieure à sa longueur d’onde.
Les lois de réflexion, telles que dérivées par l’application de conditions limites aux équations de Maxwell, décrivent par ailleurs que l’onde plane incidente sur une interface se réfléchira
(en partie ou en totalité) au même angle pour lequel elle y était incidente. Ainsi, il a été généralement admis que l’onde plane, à une interface, pouvait être considérée localement comme un rayon perpendiculaire à son front de phase. Les lois simples régissant l’optique géométrique peuvent donc être appliquées à une onde plane incidente sur une interface plane. Bien entendu, les propriétés vectorielles restent les mêmes après la réflexion, c’est-à-dire que les composantes de champ doivent rester perpendiculaires à la direction de propagation de l’onde plane réfléchie.
L’onde sphérique
L’onde sphérique est également une solution de l’équation d’onde. On peut en écrire le champ sous forme scalaire simplifiée comme
𝑈 (𝑟) = 𝐴𝑒
𝑖𝑘𝑟
𝑟 , (1.9)
où 𝐴 est une constante réelle et 𝑟 représente la distance par rapport à son centre. On désigne le champ 𝑈 comme étant la solution, qui peut donc être le champ électrique 𝐸 ou le champ magnétique 𝐻.
Historiquement, l’onde sphérique fut un outil de premier plan dans le développement des théories de diffraction et c’est cette forme de champ qui mène aux premiers formalismes de la section 1.2.3.
1.2.2 Optique géométrique
L’optique géométrique consiste dans l’analyse de la lumière sous la prémisse du « rayon ». L’optique géométrique, dans son expression la plus fondamentale, considère donc la lumière comme une collection de traits directionnels, sans égard à son caractère ondulatoire ou parti-culaire. En fait, l’optique géométrique peut être vue comme une limite au champ ondulatoire dont la définition la plus simple est
𝜆 → 0. (1.10)
En conception optique, notamment, il est coutume d’utiliser cette approximation puisqu’elle s’applique, avec grande précision, aux systèmes macrométriques. On considère dans ce cas qu’un système est macrométrique si ses dimensions typiques sont nettement plus grandes que la longueur d’onde réelle du rayonnement incident. Dépendamment des sources et des applications, un facteur entre 10 et 100 entre la longueur d’onde et les dimensions typiques du système est suffisant pour se situer dans le régime de l’optique géométrique.
L’optique géométrique a pour principal fondement la propagation rectiligne de la lumière dans un milieu homogène [3]. En ce sens, une partie des hypothèses de cette approche sera récupérée dans cette thèse, qui se concentre sur la focalisation de faisceaux électromagnétiques dans le vide par des éléments réflectifs dans un milieu homogène. Bien que le formalisme qui sera développé soit fondé sur l’optique diffractive, les tracés de rayons seront utilisés comme outil de développement. Cet artifice mathématique peut être appliqué en considérant que chaque rayon peut être associé à une onde plane dont le front de phase lui est perpendiculaire. Le formalisme qui sera proposé et analysé dans cette thèse ne sera donc pas fondé sur les principes de l’optique géométrique, mais se servira de ses conséquences pour en simplifier la compréhension.
1.2.3 Optique ondulatoire
L’optique géométrique pure ne peut décrire adéquatement certaines conséquences du caractère ondulatoire de la lumière, dont les franges d’interférence dues à la recomposition des ondes selon leur phase. Une famille de formalismes s’est développée, depuis la fin du 19e siècle, pour décrire adéquatement les champs électromagnétiques selon les prémisses de Maxwell sous une forme intégrale. Cette vision des procédés optiques est appelée « optique ondulatoire », dont une des conséquences les plus importantes est la diffraction. Puisque l’objectif de cette thèse est de décrire les champs électromagnétiques produits par une recombinaison complexe de composantes vectorielles de champs focalisés, son fruit est conséquemment à classer sous cette même nomenclature.
De très grands scientifiques se sont successivement penchés sur la description mathématique des phénomènes et cette section permet de mettre en contexte les différents formalismes retrouvées dans la littérature. Un survol assez exhaustif et de grande qualité peut être retrouvé dans le livre « Principles of Optics » de Born et Wolf [4]. On retrouve également d’intéressants commentaires dans le livre « Lasers » de A.E. Siegman [5]. On s’en tient ici cependant aux grandes lignes afin de faire un portrait plus digeste du monde de l’optique ondulatoire et de situer le formalisme de Richards-Wolf par rapport à ses prédécesseurs.
Principe de Huygens
Le formalisme de Huygens est une forme d’intégrales de diffraction basée sur le principe selon lequel chaque point d’un front de phase peut être considéré comme une source ponctuelle secondaire. Les fronts de phase sphériques de chaque point se combinent pour décrire le front de phase plus loin dans l’espace. Par un traitement intégral, il est possible de décrire le champ en tout point de l’espace à partir d’une source ponctuelle donnée. L’intégrale de Huygens suppose une superposition d’ondes sphériques pondérées par l’angle duquel elles proviennent. En d’autres termes, on suppose une source ponctuelle et on construit le champ à un point 𝑃 en considérant que chaque point du front de phase envoie une onde secondaire sphérique,
dont on évalue l’amplitude et la phase au point 𝑃 . Chaque onde secondaire est pondérée par un facteur dépendant de l’angle dit « de diffraction », déterminé empiriquement. L’intégrale a donc la forme 𝑈 (𝑃 ) = 𝐴𝑒 𝑖𝑘𝑟0 𝑟0 ∬𝑆 𝑒𝑖𝑘𝑠 𝑠 𝐾(𝜒)𝑑𝑆, (1.11) où 𝐴𝑒𝑖𝑘𝑟0
𝑟0 représente le champ complexe provenant du point source initial sur la sphère de référence2, 𝑆 représente la surface de la sphère de référence, 𝑠 représente la distance entre le
point 𝑃 et un point de la sphère de référence, 𝐾(𝜒) est un facteur pondérant empirique et 𝜒 est l’angle entre un point de la surface et la ligne la liant au point 𝑃 . En d’autre termes, en intégrant sur la surface 𝑆, on combine une infinité d’ondelettes sphériques de même longueur d’onde que l’onde source, à différentes distances 𝑠 et à différents angles de diffraction 𝜒. La figure 1.1permet de visualiser ces définitions.
Source
P
s
S
Figure 1.1 – Principe de Huygens
Le principe de Huygens, cependant, est basé sur une hypothèse physique (celle des ondes secondaires créées en tout point de l’onde primaire) et sur des observations empiriques. Le formalisme de Huygens est une approximation scalaire pour des champs optiques propagés (dont la longueur d’onde est très petite par rapport aux dimensions des surfaces d’intégration). De plus, le facteur 𝐾(𝜒) n’est pas défini analytiquement, quoi qu’il puisse être associé à la dérivée de surface de l’onde sphérique considérée. Le formalisme de Huygens est considéré aujourd’hui comme une approximation des intégrales de Kirchhoff, ou plutôt une visualisation plus instinctive de ce qu’elles représentent. Dans les faits cependant, il leur est antérieur et se trouve à être une première ébauche des théories diffractives exhaustives.
Intégrales de Kirchhoff
Afin de donner une solution sous forme intégrale à partir des définitions de champs données par les équations de Maxwell, soit les champs électriques et magnétiques, Kirchhoff utilise, en 1883, les identités de Green qui relient les intégrales de surface à des intégrales de volume. Il essaie donc de retrouver le résultat empirique de Huygens de façon plus rigoureuse.
L’intégrale de diffraction de Kirchhoff est, cependant, un formalisme très abstrait et général. Il est un point de départ puissant pour le développement d’autres formalismes plus applicables puisqu’il est une solution des équations de Maxwell, sous forme intégrale. Le formalisme de Kirchhoff permet d’appliquer le principe de superposition pour générer le faisceau propagé à partir d’une solution initiale connue. L’intégrale de Kirchhoff s’écrit
𝑈 (𝑃 ) = 1 4𝜋∬𝑆[𝑈 𝜕 𝜕 ̂𝑎𝑛 ( 𝑒𝑖𝑘𝑠 𝑠 ) − 𝑒𝑖𝑘𝑠 𝑠 𝜕𝑈 𝜕 ̂𝑎𝑛] 𝑑𝑆, (1.12) où 𝑈 représente le champ solution à l’équation d’onde (électrique ou magnétique), 𝑃 représente la position à laquelle on évalue le champ, 𝑆 représente la surface sur laquelle une solution à l’équation d’onde est connue (et qui délimite un volume qui contient le point 𝑃 ), 𝑘 est le nombre d’onde, ̂𝑎𝑛 représente la normale à la surface 𝑆, pointant vers l’intérieur de celle-ci et 𝑠 représente la distance entre la surface et le point 𝑃 .
Diffraction de Kirchhoff
Le formalisme de diffraction de Kirchhoff peut être considéré comme une dérivation de celui de Huygens-Fresnel à partir du principe intégral de Kirchhoff. En considérant les mêmes hypothèses de petite longueur d’onde et en supposant une source ponctuelle, l’intégrale (1.12) peut se réduire à une forme plus simple si on impose une limite au front de phase effectif de la source (c’est-à-dire en ajoutant un masque opaque et d’ouverture dont la surface est appelée 𝒜) 𝑈 (𝑃 ) = −−𝑖𝐴𝑒 𝑖𝑘𝑟0 2𝜆𝑟0 ∬𝑊 𝑒𝑖𝑘𝑠 𝑠 (1 + 𝑐𝑜𝑠 𝜒)𝑑𝑆, (1.13)
où 𝑊 est la portion de 𝑆 (de la surface de l’onde sphérique source) contenue dans l’ouverture 𝒜 (voir Fig.1.2).
En comparant cette forme à celle du formalisme de Huygens, on constate que Kirchhoff, en se basant sur son principe intégral et les identités de Green, parvint à déterminer le facteur pondérant 𝐾(𝜒) comme étant
Source
P
W
Ouverture
Figure 1.2 – Principe de diffraction de Kirchhoff
𝐾(𝜒) = − 𝑖
2𝜆(1 + 𝑐𝑜𝑠 𝜒). (1.14)
Concrètement, on utilise le formalisme de Kirchhoff régulièrement dans un contexte où une onde est incidente sur des masques de forme donnée. Il est alors facile de décrire la source comme étant une sommation infinie de sources ponctuelles dans les zones où l’onde incidente est transmise au travers le masque. Selon les identités de Green, il est possible de se convaincre que l’intégrale sur 𝑆, dans le cas d’une ouverture donnée, peut être réduite à une intégrale sur 𝑊 , soit la portion du front de phase incident sous-tendue par ladite ouverture, le reste ayant une contribution nulle.
Diffraction de Fraunhofer et Fresnel
Les intégrales de diffraction de Fraunhofer et Fresnel se basent aussi sur les intégrales de Kirchhoff. Dans ce cas, toujours en supposant la prémisse d’onde sphérique obstruée par une ouverture et en ajoutant une contrainte de petite ouverture par rapport aux distances impliquées (soit une source et un point de calcul éloignés de l’ouverture), l’intégrale se réduit à 𝑈 (𝑃 ) = −𝐴𝑖𝑒 𝑖𝑘(𝑟′+𝑠′) 𝜆 𝑐𝑜𝑠 𝛿 𝑟′𝑠′ ∬ 𝒜 𝑒𝑖𝑘𝑓(𝜉,𝜂)𝑑𝜉𝑑𝜂, (1.15)
où 𝑟′ est la distance entre un point 𝑂 (situé sur 𝒜) et la source, 𝑠′ est la distance entre ce
même point 𝑂 et le point 𝑃 , 𝛿 est l’angle entre la normale à l’ouverture et la ligne reliant la source au point 𝑃 et, finalement 𝜉 et 𝜂 représentent les coordonnées des différents points 𝑂 sur lesquels on intègre. La fonction 𝑓, elle, est une fonction incluant les différentes coordonnées et qui influence la phase résultante de l’ondelette secondaire. Selon la troncation de cette fonction en série, on parle de l’intégrale de Fraunhofer ou de Fresnel. Cette série est définie par 𝑓(Fraunhofer)(𝜉, 𝜂) = −𝑥0𝜉 + 𝑦0𝜂 𝑟′ − 𝑥𝜉 + 𝑦𝜂 𝑠′ ; (1.16) 𝑓(Fresnel)(𝜉, 𝜂) = −𝑥0𝜉 + 𝑦0𝜂 𝑟′ − 𝑥𝜉 + 𝑦𝜂 𝑠′ + 𝜉2+ 𝜂2 2𝑟′ +𝜉 2+ 𝜂2 2𝑠′ − (𝑥0𝜉 + 𝑦0𝜂)2 2𝑟′3 − (𝑥𝜉 + 𝑦𝜂)2 2𝑠′3 . (1.17)
Il s’agit donc d’une approximation paraxiale de la diffraction au travers une ouverture. Encore ici, les définitions sont entièrement basées sur une ouverture plane et sur la reconstruction du front d’onde sphérique incident selon différentes conditions d’échelles.
Les formalismes de Fraunhofer et de Fresnel sont donc des outils pratiques extrêmement efficaces en analyse de l’influence de masques et de lentilles sur un front de phase sphérique qui lui est incident.
Diffraction de Rayleigh-Sommerfeld
Les intégrales de diffraction de Rayleigh-Sommerfeld sont, quand à elles, une extension du principe intégral de Kirchhoff sous les conditions respectives d’incidence à petit angle (source éloignée du masque) et de diffraction à petit angle (point d’observation éloigné du masque). On a alors les intégrales de Rayleigh-Sommerfeld de premier et de deuxième type,
𝑈(𝐼)(𝑥, 𝑦, 𝑧) = 1 2𝜋∬𝐴𝑈 (𝑖)(𝑥′, 𝑦′, 0) 𝜕 𝜕𝑧′( 𝑒𝑖𝑘𝑠 𝑠 ) 𝑑𝑥 ′𝑑𝑦′; (1.18) 𝑈(𝐼𝐼)(𝑥, 𝑦, 𝑧) = − 1 2𝜋∬𝐴 𝜕𝑈(𝑖)(𝑥′, 𝑦′, 𝑧′) 𝜕𝑧′ 𝑒𝑖𝑘𝑠 𝑠 𝑑𝑥 ′𝑑𝑦′. (1.19)
À partir de ces équations, on peut obtenir le champ en connaissant le champ incident sur l’ouverture ou en connaissant sa courbure. Par exemple, pour une onde sphérique comme source d’illumination, on a
𝑈(𝑖)= 𝐴𝑒𝑖𝑘𝑟 𝑟 ; (1.20) 𝜕𝑈(𝑖) 𝜕𝑧 = 𝐴𝑒𝑖𝑘𝑟 𝑟 (𝑖𝑘 − 1 𝑟) 𝑐𝑜𝑠(𝜃𝑖), (1.21)
où 𝜃𝑖 représente l’angle, en tout point dans l’ouverture, entre la ligne reliant ce point à la source et la normale à l’ouverture.
Formalisme de Richards-Wolf
On a parlé de formalismes tenant compte d’une ouverture et des limites sur les angles d’ou-verture numérique. Dans le cas du formalisme de Richards-Wolf, on oublie cette limitation et considère l’entièreté de l’angle solide comme étant une source de radiation. Ainsi, le for-malisme de Richards-Wolf est une forme de diffraction intégrale adaptée pour la focalisation hautement non-paraxiale. Elle se base sur la recombinaison d’ondelettes provenant d’un angle solide pouvant aller jusqu’à 4𝜋.
Contrairement aux formalismes présentés jusqu’ici, le formalisme de Richards-Wolf considère les différentes polarisations impliquées dans le champ incident (plutôt qu’une onde sphérique scalaire). Puisque, comme il a été dit plus haut, la direction de propagation d’une onde est perpendiculaire à son état de polarisation dans un milieu homogène, la focalisation et la diffusion d’ondes par une surface ou une ouverture ont une influence sur la polarisation du champ résultant. Le formalisme proposé par Richards et Wolf en 1959 s’inscrit dans cette veine [6]. Il propose une description du champ électromagnétique par spectre angulaire. Ce formalisme découle des équations de Maxwell et du principe de Green, tout en se visualisant simplement par des tracés de rayons, et sera discuté plus en détail dans le chapitre 2. Il se base sur l’exploitation des ondes planes et de leur principe de réflexion et de réfraction s’associant à celui de l’optique géométrique et diffractive en régime de grande échelle. Le for-malisme de Richards-Wolf est conséquemment extrêmement puissant et élégant pour décrire les champs électromagnétiques produits par la focalisation d’une onde de profil d’amplitude donné par un système connu. Au delà de l’interaction de la lumière avec elle-même, le forma-lisme de RW est donc un outil tout désigné pour déduire l’influence d’une focalisation forcée par des conditions physiques extérieures. Il est conçu pour être facilement applicable et les fonctions sont développées pour être directement associées à un élément concret du système analysé.
Ce formalisme, comme il sera développé au prochain chapitre, tient compte entièrement du caractère vectoriel de la lumière et ne se base pas sur l’approximation scalaire. Bien que le champ incident doive être considéré comme plan selon son utilisation classique, la focalisation engendrée par le miroir ou la lentille peut être grandement non-paraxiale. En d’autres termes, l’onde plane vectorielle, solution des équations de Maxwell décrite à la section précédente, en
est le point de départ et est transformée de façon non-paraxiale par un élément focalisant donné. Le formalisme considère que
— Le front de phase incident est plan et on en connaît la polarisation et le profil d’ampli-tude.
— Le système focalisant est parfait (ou peut être représenté par une correction par aber-ration).
— La focalisation peut faire en sorte qu’au point 𝑃 (où est évalué le champ), la contribution par le champ focalisé peut provenir d’un angle solide de 4𝜋 sr.
— Les dimensions du système focalisant sont beaucoup plus grandes que la longueur d’onde considérée.
La pleine exploitation de ce formalisme pour des systèmes concrets est le principal défi de cette thèse et la compréhension des bases de l’optique diffractionnelle en est la clé.
1.3
Divisions de cette thèse
La thèse est structurée afin de renforcer son côté pédagogique.
Le chapitre 2 décrit avec plus de précision le formalisme sur lequel se basent les travaux et les études des chapitres suivants, soit le formalisme de Richards-Wolf classique. Ce chapitre est une modernisation des articles de 1959 et 1960 de Richards et Wolf. De plus, une discussion sur l’approximation par aberrations est apportée et un exemple d’application du modèle est fourni. Cette application a été récemment appliquée avec la forme moderne du formalisme grâce à l’expertise de notre groupe de recherche. La portée du travail sera aussi justifiée par une sélection d’applications concrètes des méthodes mathématiques décrites dans cet ouvrage. Le chapitre 3 est une collection de solutions analytiques aux équations intégrales de Richards-Wolf. Quelques formes de champs incidents sont introduits dans les intégrales et le champ résultant au foyer est déduit par différentes propriétés analytiques. Ce chapitre sert de point de départ à plusieurs utilisations éventuelles du formalisme de Richards-Wolf grâce aux différents constats sur les propriétés des différentes solutions calculées.
Le chapitre 4 développe le formalisme décrit au chapitre 2 pour des conditions moins restric-tives afin d’en augmenter significativement la portée et l’adaptabilité. Il s’agit de la contri-bution originale principale de cette thèse. Le chapitre permet de revisiter les définitions des différentes fonctions impliquées dans le formalisme de Richards-Wolf sans présupposition de foyer ponctuel. L’influence réelle du front de phase non-plan incident sur le système focalisant est également étudiée et des exemples d’application sont apportés pour différentes formes de miroirs.
Le chapitre 5 expose plus en détail une forme de solution analytique au nouveau formalisme de Richards-Wolf étendu. Cette contribution originale a développé un intérêt certain et propose une exemple probant permettant de constater la pertinence des généralisations apportées au chapitre 4. Une étude en régime impulsionnel des solutions aux équations de Richards-Wolf généralisées y est aussi présentée.
Un dernier chapitre récapitulatif servira à la fois de rappel et d’aide mémoire pour une utili-sation judicieuse des formalismes décrits et développés dans ce manuscrit.
En annexe, on propose aussi une méthode d’inversion originale des intégrales de diffraction de Richards-Wolf. L’inversion des problèmes de diffraction est un défi important qui est abordé dans le contexte de la présente thèse. Des pistes de réflexion sont posées afin de propulser l’ingénierie de faisceau vers des applications plus vastes et faciles d’accès. Des pistes de ré-flexions sont aussi déposées sur une utilisation des solutions non paraxiales aux intégrales de diffraction en microscopie à haute résolution et en accélération d’électrons.
Chapitre 2
Formalisme de Richards-Wolf
Cette thèse et les publications qui y sont reliées ont un point de départ commun, soit le formalisme de Richards-Wolf. Ce paradigme mathématique fut introduit pour répondre à un besoin bien précis, celui de modéliser convenablement et le plus simplement possible la focalisation non-paraxiale de faisceaux dont le caractère vectoriel ne peut être négligé. La première itération de ce formalisme, de ses antécédents et de ses implications, fut publiée en 1959, par B. Richards et E. Wolf [6].
Dans ce chapitre, on développera plus en détail la théorie de Richards-Wolf (RWT). Puisque la publication de 1959 est très complète et instructive, ce chapitre sert à la fois à condenser le développement original, à moderniser les formulations intégrales et à redéfinir avec plus de recul les différents paramètres qui y avaient été introduits.
Dans la publication originale, on traitait de faisceaux uniformes et polarisés linéairement. Dans ce chapitre, cependant, on utilise une version plus générale en considérant une polarisation non-uniforme incidente ([7], chap. 3).
2.1
Préalable
Les travaux de modélisation de la focalisation par Richards et Wolf sont principalement scindés en une publication en deux volets. Le premier volet [6], canoniquement cité comme étant la contribution majeure, décrit la solution optique d’imagerie non-paraxiale de façon (relativement) synthétisée en apportant quelques solutions numériques grâce à l’apport de B. Richards du Computing Machine Laboratory de Manchester. Il se base, cependant, sur le principe plus fondamental apporté par Emil Wolf dans la première publication, au début de la même année [8], qui consiste en la généralisation vectorielle des intégrales de Debye et de la théorie diffractionnelle de Stratton-Chu [9]1.
1. La théorie diffractive de Stratton-Chu est reconnue pour son caractère exhaustif, prenant en compte le courant induit aux surfaces pour les conditions aux frontières des intégrales de Kirchhoff. Avec les années,
Au moment d’écrire ces articles majeurs, réconciliant par la même occasion l’électromagné-tisme et l’optique géométrique dans un contexte d’imagerie idéalisée, les formalismes étaient limités à une description scalaire des flux énergétiques ou encore à la description vectorielle de systèmes d’ouverture numérique correspondant à une focalisation ne dépassant pas 40∘
(limite généralement admise comme frontière entre le régime paraxial et non-paraxial). Ces descriptions consistent en la base des intégrales de diffraction décrites en introduction. À partir des mêmes principes fondamentaux et des identités de Green, le formalisme de Richards et Wolf devient une intégrale de diffraction vectorielle non-paraxiale, à partir de la théorie de Debye selon laquelle, contrairement aux formalismes basés sur le principe de Huygens, le champ peut être développé en une superposition d’ondes planes (plutôt qu’une superposition d’ondes sphériques) [10]. Ces postulats, dans les faits, sont équivalents lorsque les systèmes focalisants ou diffractifs analysés sont beaucoup plus grands que la longueur d’onde de la lumière [11].
2.1.1 Postulat de départ - Spectre d’ondes planes
Selon les équations de Maxwell, le champ électromagnétique doit respecter, en tout point, l’équation d’onde dépendante du temps. Une forme très complète de solutions peut résoudre cette équation. On sait que l’onde plane uniforme résout l’équation d’onde homogène libre (milieu uniforme infini) alors qu’une superposition linéaire d’ondes planes uniformes peut résoudre l’équation d’onde avec des conditions limites. Ce principe est appelé spectre
angu-laire d’ondes planes. La solution, en notation phaseur (c’est-à-dire sans tenir compte de la
composante temporelle 𝑒−𝑖𝜔𝑡), prend alors la forme
⃗ 𝐸(𝑥, 𝑦, 𝑧) = ∬ ∞ −∞ 𝑒𝑖(𝑘𝑥𝑥+𝑘𝑦𝑦)[ ⃗𝑈 (𝑘 𝑥, 𝑘𝑦)𝑒𝑖𝑘𝑧𝑧+ ⃗𝑉 (𝑘𝑥, 𝑘𝑦)𝑒−𝑖𝑘𝑧𝑧] 𝑑𝑘𝑥𝑑𝑘𝑦, (2.1)
où les composantes 𝑘𝑥, 𝑘𝑦et 𝑘𝑧représentent le nombre d’onde dans les trois axes indépendants de l’espace et les fonctions 𝑈 et 𝑉 représentent les composantes propageantes et contre-propageantes du champ dans l’espace des fréquences spatiales. On peut toujours choisir un axe principal (ici 𝑧), de telle sorte que le spectre d’ondes planes est une superposition des deux autres composantes indépendantes, puisque, pour une longueur d’onde donnée,
𝑘 = 2𝜋 𝜆 = √𝑘
2
𝑥+ 𝑘2𝑦+ 𝑘2𝑧, (2.2)
où 𝑘 = 2𝜋/𝜆. Cette formulation implique deux groupes de solutions pour 𝑘𝑧. Les composantes pour lesquelles 𝑘2
𝑥+ 𝑘2𝑦 < 𝑘2 sont appelées ondes planes propageantes alors que celles pour des formalismes simplifiés, comme celui de Richards-Wolf, ont été grandement préférés pour leur élégance analytique. Dans le contexte de cette thèse, principalement dirigé vers les systèmes à symétrie de révolution, les courants de surface deviennent indépendants de l’angle de révolution et leur apport devient négligeable.
lesquelles 𝑘2
𝑥+ 𝑘2𝑦 > 𝑘2 sont appelées ondes évanescentes. Cette distinction provient du fait
que le nombre d’onde 𝑘𝑧est respectivement réel et imaginaire, rendant le facteur 𝑒±𝑖𝑘𝑧𝑧 soit
complexe (propagation oscillante) ou réel (décroissance exponentielle). 2.1.2 Hypothèse d’échelle
Dans le cadre de cette thèse, il est admis que les échelles des systèmes focalisants sont grande-ment supérieures à la longueur d’onde afin de garder toute cohérence avec les hypothèses de Debye. Cette hypothèse considère comme négligeable la contribution évanescente du spectre angulaire décrit par l’équation (2.1). Elle écarte aussi de l’analyse les systèmes possédant des artéfacts de surface de l’ordre de la longueur d’onde.
En pratique, cette hypothèse est admise pour une majorité d’applications en technologies optiques. Les principales sphères d’application des outils mathématiques pour la focalisation à grande ouverture numérique sont la microscopie, l’accélération d’électrons, l’encodage de donnée et le piégeage optique (voir la section 2.5). Ces domaines impliquent tous des miroirs ou des lentilles dont la taille dépasse grandement la longueur d’onde utilisée. En d’autres termes, on suppose que
𝑘𝑓 >> 1. (2.3)
Bien que dans les prochains chapitres il soit question de s’attaquer au problème de sys-tèmes focalisants n’ayant pas une longueur focale 𝑓 bien définie, il sera question de « facteur d’échelle » s’apparentant à cette définition afin de maintenir une cohérence avec la théorie de Richards-Wolf.
Toujours en se référant à l’équation (2.1), cette hypothèse revient à limiter les bornes d’inté-gration pour des valeurs de 𝑘𝑥 et 𝑘𝑦 associées aux ondes planes.
2.2
Formalisme général
Le formalisme de Richards-Wolf est, dans les prochaines pages, développé dans le but de donner au lecteur une compréhension de l’intégrale de diffraction vectorielle. Il est développé en quatre étapes essentielles :
1. Définition d’un système focalisant par optique géométrique
2. Description du transfert de géométrie entre le faisceau incident et le faisceau focalisé 3. Définition d’un champ vectoriel focalisé à partir du champ incident
Ce développement permettra d’obtenir la forme canonique des intégrales de diffraction de Richards-Wolf ⃗ 𝐸(𝑟, 𝜃, 𝑧) = 1 4𝜋∫ 2𝜋 0 ∫ 𝛼𝑚𝑎𝑥 0 𝑞(𝛼, 𝛽) ⃗𝐸𝑠𝑝ℎ(𝛼, 𝛽)𝑒−𝑗𝑘Φ(𝛼,𝛽,𝑟,𝑧)𝑠𝑖𝑛 𝛼𝑑𝛼𝑑𝛽; (2.4) ⃗ 𝐻(𝑟, 𝜃, 𝑧) = 1 4𝜋∫ 2𝜋 0 ∫ 𝛼𝑚𝑎𝑥 0 𝑞(𝛼, 𝛽) ⃗𝐻𝑠𝑝ℎ(𝛼, 𝛽)𝑒−𝑗𝑘Φ(𝛼,𝛽,𝑟,𝑧)𝑠𝑖𝑛 𝛼𝑑𝛼𝑑𝛽, (2.5)
où chaque fonction et paramètre sera défini lors de leur introduction. 2.2.1 Le système focalisant
Puisqu’on considère les systèmes suffisamment grands pour se fier à l’approximation de De-bye, il est de mise de décrire les systèmes focalisants par le biais de l’optique géométrique. L’interaction des champs électromagnétiques au foyer se fait par le biais des intégrales de diffraction, mais l’interaction du champ incident avec le système focalisant, elle, peut être analysée par tracé de rayons. Comme mentionné au chapitre précédent, une onde plane peut être considérée comme un peigne de rayons perpendiculaires à son front de phase. Ainsi, dans l’approximation de Debye, on cherche à transformer un peigne de rayons parallèles en une collection de rayons convergents, lesquels seront utilisés pour décrire le spectre d’ondes planes polarisées fortement focalisées.
La RWT s’applique parfaitement aux cas focalisants idéaux, c’est-à-dire les systèmes pouvant être décrits par une sphère de référence (front de phase sphérique) centrée en un point focal unique. La figure 2.1 permet de visualiser l’élément focalisant et la sphère de référence qui décrit la combinaison des ondes planes créant le front de phase convergeant. Le schéma, simplifié, montre le chemin parcouru par un rayon incident sur la surface focalisante à une hauteur ℎ et focalisé à un angle 𝛼 vers le foyer du système. Aucune contre-indication, ici, n’empêche le système focalisant de renvoyer un rayon à partir de n’importe quel angle 𝛼. En d’autres termes, l’entièreté de la sphère de référence peut être couverte par des rayons focalisés.
À partir de ces définitions simples, le formalisme de Richards-Wolf utilise le principe selon lequel chaque onde plane est définie par un rayon étant perpendiculaire à son front de phase pour relier les champs𝐸⃗𝑖𝑛𝑐et𝐸⃗𝑠𝑝ℎ(toujours selon la figure 2.1).
2.2.2 Transfert de géométrie
Si on examine un rayon donné, incident à une hauteur ℎ d’un système parfaitement focalisant, il doit exister une fonction 𝑔(𝛼) telle que
ℎ = 𝑓𝑔(𝛼), (2.6)
h
α
Foyer
Front de phase
sphérique
Système
focalisant
Axe optique
Figure 2.1 – Visualisation du principe de focalisation.
Cette fonction est entièrement dépendante du système de focalisation et permet de relier la géométrie incidente à celle de focalisation. Concrètement, le but de ce transfert de géométrie est de décrire le champ focalisé 𝐸⃗𝑠𝑝ℎ en fonction du champ incident 𝐸⃗𝑖𝑛𝑐. Le principe per-mettant de relier ces deux champs est celui de la conservation d’énergie, selon lequel l’énergie contenue dans le peigne de faisceaux incidents doit être la même que sur la surface de la sphère de référence (après la focalisation).
En considérant un faisceau en trois dimensions et axisymétrique (dont un plan serait défini par la figure 2.1), on peut exprimer la condition de conservation d’énergie comme
∫ | ⃗𝐸𝑖𝑛𝑐|22𝜋ℎ𝑑ℎ = ∫ | ⃗𝐸
𝑠𝑝ℎ|22𝜋𝑓2𝑠𝑖𝑛 𝛼𝑑𝛼. (2.7)
Cette égalité implique que
| ⃗𝐸𝑖𝑛𝑐|22𝜋ℎ𝑑ℎ = | ⃗𝐸
𝑠𝑝ℎ|22𝜋𝑓2𝑠𝑖𝑛 𝛼𝑑𝛼, (2.8)
puisqu’elle doit être vérifiée pour tout domaine d’intégration, « aussi petit soit-il » [12]. En utilisant le changement de référence de l’équation (2.6), on obtient
| ⃗𝐸𝑖𝑛𝑐|2𝑔(𝛼)𝑔′(𝛼)𝑑𝛼 = | ⃗𝐸
où 𝑔′(𝛼) et la dérivée, par rapport à 𝛼, de la fonction 𝑔(𝛼).
Cette égalité sert à définir le « facteur d’apodisation » 𝑞(𝛼), un concept important en focali-sation, définit comme
| ⃗𝐸𝑠𝑝ℎ| = | ⃗𝐸𝑖𝑛𝑐|𝑞(𝛼). (2.10) Comme on peut le remarquer, ce facteur d’apodisation est en quelque sorte un facteur per-mettant de pondérer le spectre d’onde plane focalisé à partir de la description du système focalisant. En effet, on remarque que la fonction 𝑞(𝛼) est reliée à la relation 𝑔(𝛼) comme
𝑞(𝛼) = [𝑔(𝛼)𝑔
′(𝛼)
𝑠𝑖𝑛 𝛼 ]
1/2
. (2.11)
En connaissant le système focalisant et par analyse géométrique de l’angle de focalisation en fonction de la hauteur ℎ d’incidence d’un rayon donné, il est possible de définir cette fonction d’apodisation afin de relier l’amplitude du champ incident 𝐸⃗𝑖𝑛𝑐connu dans un plan à l’amplitude du champ focalisé 𝐸⃗𝑠𝑝ℎ sur la sphère de référence après la focalisation. Par exemple, un miroir parabolique respecte la condition
ℎ = 2𝑓 𝑡𝑎𝑛(𝛼/2), (2.12)
ce qui implique un facteur d’apodisation
𝑞(𝛼) = 𝑠𝑒𝑐2(𝛼/2). (2.13)
Note sur le facteur 𝐾(𝜒)
Il est intéressant de constater que le facteur d’apodisation 𝑞(𝛼) est en fait l’inverse du facteur 𝐾(𝜒) introduit par Kirchhoff dans son principe diffractionnel (voir la section 1.2.3).
On y voyait que 𝐾(𝜒) ∝ 12(1+𝑐𝑜𝑠 𝜒) = 𝑐𝑜𝑠2(𝜒/2) alors que 𝑞(𝛼) = 𝑠𝑒𝑐2(𝛼/2) pour un système
parfaitement convergent. On peut comprendre ici que, si l’on considère l’angle d’incidence 𝛼 comme étant l’angle de diffraction 𝜒 depuis un point source (en se référant à la figure 1.2), le formalisme de Richards-Wolf représente un principe inverse à celui de la diffraction. La pondération de chaque onde plane convergente est exactement reliée à la pondération de chaque ondelette provenant du point source confondu avec le point focal du procédé inverse.
2.2.3 Définition du champ vectoriel sur la sphère de référence
Pour connaître le champ au foyer du système de focalisation, il faut d’abord définir, à partir du champ incident connu, la forme du champ et du front de phase post-focalisation. Pour ce faire, on décompose les composantes vectorielles du champ incident et on observe l’effet du système, par l’entremise du facteur d’apodisation, sur lesdites composantes.
Supposons que l’on considère une onde plane incidente, selon un axe optique en 𝑧, sur notre surface focalisante. On peut décomposer la polarisation de cette onde comme une polarisation radiale (en 𝜌) et azimuthale (en 𝛽). Après la focalisation, dans le plan d’incidence, la com-posante azimuthale reste inchangée tandis que la polarisation radiale est transférée en une nouvelle composante ̂𝑎𝛼, perpendiculaire au rayon focalisé dans le plan de focalisation (voir Fig. 2.2).
α
Foyer
Système
focalisant
Axe optique
Figure 2.2 – Géométrie et définition des vecteurs de polarisation des champs incidents et focalisés.
En utilisant la définition du facteur d’apodisation de la section précédente, permettant de relier l’influence du système focalisant sur les différentes composantes angulaires du champ focalisé, on peut déterminer vectoriellement le champ sur la sphère de référence comme
⃗
𝐸𝑠𝑝ℎ= 𝑞(𝛼)[ ̂𝑎𝛼( ̂𝑎𝜌⋅ ⃗𝐸𝑖𝑛𝑐) + ̂𝑎𝛽( ̂𝑎𝛽⋅ ⃗𝐸𝑖𝑛𝑐)]. (2.14) Cette équation considère donc une transition parfaite de la polarisation radiale du champ
incident en une polarisation selon ̂𝑎𝛼 alors que la polarisation azimuthale reste dans la même direction.
À ce moment, on a donc décrit vectorielement la forme du champ sur la sphère de référence, à partir de la définition du système focalisant et du champ vectoriel incident sur ledit système. 2.2.4 Intégrales de Richards-Wolf
Pour obtenir les intégrales de diffraction de Richards-Wolf, il faut considérer que le champ sur la sphère de référence 𝐸⃗𝑠𝑝ℎest le champ lointain qui se propagera jusqu’au foyer du système. En reprenant la définition du spectre d’ondes planes tel que donné plus haut, on voit que l’on peut réécrire le champ2 en tout point comme étant
⃗ 𝐸(𝑥, 𝑦, 𝑧) = 1 4𝜋2∫ ∞ −∞ ∫ ∞ −∞ ⃗ 𝐸(𝑘𝑥, 𝑘𝑦)𝑒−𝑗(𝑘𝑥𝑥+𝑘𝑦𝑦+𝑘𝑧𝑧)𝑑𝑘𝑥𝑑𝑘𝑦; (2.15) ⃗ 𝐻(𝑥, 𝑦, 𝑧) = 1 4𝜋2∫ ∞ −∞ ∫ ∞ −∞ ⃗ 𝐻(𝑘𝑥, 𝑘𝑦)𝑒−𝑗(𝑘𝑥𝑥+𝑘𝑦𝑦+𝑘𝑧𝑧)𝑑𝑘𝑥𝑑𝑘𝑦, (2.16)
où on élimine les composantes évanescentes du spectre, puisque leur comportement en dé-croissance exponentielle les rend négligeables près du foyer du système.
Sous la géométrie analysée (soit en considérant les angles 𝛼 et 𝛽 décrits plus haut), on peut écrire
𝑘𝑧= 𝑘 𝑐𝑜𝑠 𝛼; (2.17)
𝑘𝑥= −𝑘 𝑠𝑖𝑛 𝛼 𝑐𝑜𝑠 𝛽; (2.18)
𝑘𝑦= −𝑘 𝑠𝑖𝑛 𝛼 𝑠𝑖𝑛 𝛽. (2.19)
De plus, puisqu’on considère un système focalisant axisymétrique (condition nécessaire pour obtenir un foyer unique), il est judicieux d’utiliser un système de coordonnées cylindriques près du foyer, pour lequel
𝑥 = 𝑟 𝑐𝑜𝑠 𝜃; (2.20)
𝑦 = 𝑟 𝑠𝑖𝑛 𝜃, (2.21)
où 𝜃 est l’angle azimuthal du plan de la figure 2.2.
2. Il est important de noter que le spectre angulaire 𝐸(𝑘⃗ 𝑥, 𝑘𝑦) a des unités de Vm alors que le champ
⃗
Ces définitions mènent à la forme en spectre d’ondes planes en géométrie cylindrique ⃗ 𝐸(𝑟, 𝜃, 𝑧) = 1 4𝜋2∫ 2𝜋 0 ∫ 𝜋 0 ⃗ 𝐸(𝛼, 𝛽)𝑒−𝑗𝑘Φ(𝛼,𝛽,𝑟,𝑧)𝑠𝑖𝑛 𝛼𝑑𝛼𝑑𝛽; (2.22) ⃗ 𝐻(𝑟, 𝜃, 𝑧) = 1 4𝜋2∫ 2𝜋 0 ∫ 𝜋 0 ⃗ 𝐻(𝛼, 𝛽)𝑒−𝑗𝑘Φ(𝛼,𝛽,𝑟,𝑧)𝑠𝑖𝑛 𝛼𝑑𝛼𝑑𝛽, (2.23) avec Φ(𝛼, 𝛽, 𝑟, 𝑧) ≡ 𝑧 𝑐𝑜𝑠 𝛼 − 𝑟 𝑠𝑖𝑛 𝛼 𝑐𝑜𝑠(𝜃 − 𝛽). (2.24)
Ce formalisme est en tout point conforme pour un système à grande ouverture numérique. On peut finalement introduire 𝛼𝑚𝑎𝑥 tel qu’il permette de délimiter les bornes physiques du système focalisant. Pour une lentille, par exemple, on peut relier l’ouverture numérique 𝑁 𝐴 à cet angle maximal par
𝑁 𝐴 = 𝑛 𝑠𝑖𝑛 𝛼𝑚𝑎𝑥, (2.25)
où 𝑛 représente l’indice du milieu entre la lentille et le foyer du système.
Cependant, rien ne limite l’étendue d’intégration pour un 𝛼𝑚𝑎𝑥 de 𝜋. En effet, un système focalisant comme un miroir parabolique à courte focale, par exemple, permettrait une focali-sation avec des composantes contre-propageantes pour lesquelles 𝑘𝑧 est négatif.
Finalement, considérant l’hypothèse d’échelle, on considère que le champ sur la sphère de référence est le champ lointain à partir duquel on définit le spectre d’ondes planes, ce qui permet d’écrire, en terme des fonctions définies ici,
⃗ 𝐸(𝑟, 𝜃, 𝑧) = 1 4𝜋2∫ 2𝜋 0 ∫ 𝛼𝑚𝑎𝑥 0 ⃗ 𝐸𝑠𝑝ℎ(𝛼, 𝛽)𝑒−𝑗𝑘Φ(𝛼,𝛽,𝑟,𝑧)𝑠𝑖𝑛 𝛼𝑑𝛼𝑑𝛽; (2.26) ⃗ 𝐻(𝑟, 𝜃, 𝑧) = 1 4𝜋2∫ 2𝜋 0 ∫ 𝛼𝑚𝑎𝑥 0 ⃗ 𝐻𝑠𝑝ℎ(𝛼, 𝛽)𝑒−𝑗𝑘Φ(𝛼,𝛽,𝑟,𝑧)𝑠𝑖𝑛 𝛼𝑑𝛼𝑑𝛽. (2.27)
En connaissant le champ vectoriel incident𝐸⃗𝑖𝑛𝑐et le système focalisant défini par 𝑔(𝛼), il est possible de retrouver le champ vectoriel total au voisinage du foyer du système. Ces dernières intégrales sont la version moderne des intégrales de Richards-Wolf, valides pour un système à grande échelle et pour toute forme de polarisation incidente.
Ondes évanescentes et transformée de Fourier
On pourrait associer les ondes décrites par un angle 𝛼 au-delà de 𝛼𝑚𝑎𝑥 comme étant les contributions évanescentes du spectre. Auquel cas, la définition du champ incident 𝐸⃗𝑖𝑛𝑐 devrait contenir une certaine quantité d’énergie non-négligeable dans sa description angulaire au-delà des limites d’intégration. Il s’agit alors d’un artifice mathématique pour décrire une situation non couverte pas le présent formalisme. Il n’en sera donc pas question dans les prochains développements.
On constate également que la forme en spectre d’ondes planes possède une certaine appar-tenance aux fonctions dites « Transformées de Fourier ». Cette apparappar-tenance laisse miroiter l’inversion potentielle des équations (2.26) et (2.27) afin de déduire le champ incident requis pour obtenir un champ au foyer donné. Cette avenue est explorée davantage à l’annexe A.
2.2.5 Traitement par aberrations
Dans le formalisme de Richards-Wolf, on a mentionné que l’on suppose un point focal commun pour tous les rayons incidents. Si la surface focalisante n’est pas parfaite, il est toujours possible d’ajouter un terme de phase corrigé 𝑝(𝛼, 𝛽) tel que
Φ(𝛼, 𝛽, 𝑟, 𝑧) → Φ(𝛼, 𝛽, 𝑟, 𝑧) − 𝑝(𝛼, 𝛽). (2.28) On retrouve les termes de phase associés aux différentes aberrations primaires dans le ta-bleau 2.1.
Table 2.1 – Facteurs d’aberration Aberration primaire Facteur de phase 𝑝(𝛼, 𝛽)
Distorsion 𝐶1,1𝑠𝑖𝑛 𝛼 𝑐𝑜𝑠 𝛽 Courbure de champ 𝐶2,0𝑠𝑖𝑛2𝛼
Coma 𝐶3,1𝑠𝑖𝑛3𝛼 𝑐𝑜𝑠 𝛽 Astigmatisme 𝐶2,2𝑠𝑖𝑛2𝛼 𝑐𝑜𝑠(2𝛽) Aberration sphérique 𝐶4,0𝑠𝑖𝑛4𝛼
Ces facteurs sont associés aux coefficients de Seidel [13,14,15]. Il est à noter que les facteurs d’aberration peuvent être utilisés aussi bien dans des systèmes à géométrie sans axisymétrie. 2.2.6 Analyse physique du formalisme et limitations
Comme il a été mentionné précédemment, les intégrales de Richards-Wolf supposent un front de phase sphérique convergent vers un point focal global. La méthode par aberration qui sert habituellement à corriger le modèle pour des systèmes focalisants imparfaits considère, quant à elle, une modification locale de la phase du front d’onde convergent.
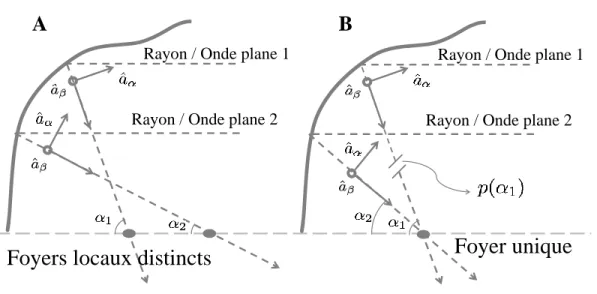
Physiquement, l’introduction d’un facteur d’aberration dans la fonction de phase de la RWT représente une correction scalaire dans un modèle autrement vectoriel [13, 14, 16]. Cette approche fonctionne donc très bien pour les systèmes hautement non-paraxiaux mais dont la déviation par rapport au front de phase parfaitement sphérique est faible. Cette approche peut également fonctionner pour une grande déviation par rapport au front sphérique, mais dans un régime paraxial. Cependant, le traitement par aberration n’est pas adapté pour calculer l’effet de focalisation d’un front de phase à la fois hautement non-paraxial et non-sphérique (voir Fig. 2.3).
A
Foyers locaux distincts
Rayon / Onde plane 1
Rayon / Onde plane 2
B
Rayon / Onde plane 1
Rayon / Onde plane 2
Foyer unique
Figure 2.3 – Différence fondamentale entre le traitement A vectoriel exact (développé au chapitre 4) et B par aberrations.
Dans la figure2.3, il est possible de remarquer que le traitement par aberrations considère un système parfaitement focalisant avec une correction locale du chemin optique des rayons en ajustant leur phase relative. En approximation scalaire, les deux méthodes sont équivalentes mais en considérant une approche vectorielle non-paraxiale extrême, l’aberration ne permet pas de considérer les effets d’interaction des polarisations des différentes ondes individuelles à la recombinaison. Mathématiquement, le terme de phase 𝑝(𝛼, 𝛽) dans le traitement intégral ne s’applique alors pas à la bonne composante de polarisation.
De plus, l’approche par aberration ne considère pas l’influence de la surface focalisante sur le facteur d’apodisation. Cette influence sera également soulignée au chapitre 4.