HAL Id: jpa-00206533
https://hal.archives-ouvertes.fr/jpa-00206533
Submitted on 1 Jan 1967
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of
sci-entific research documents, whether they are
pub-lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diffusion de documents
scientifiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Étude théorique de la relaxation d’atomes alcalins par
collisions sur une paroi et sur un gaz
Françoise Masnou-Seeuws, Marie-Anne Bouchiat
To cite this version:
Françoise Masnou-Seeuws, Marie-Anne Bouchiat.
Étude théorique de la relaxation d’atomes
al-calins par collisions sur une paroi et sur un gaz. Journal de Physique, 1967, 28 (5-6), pp.406-420.
�10.1051/jphys:01967002805-6040600�. �jpa-00206533�
ÉTUDE
THÉORIQUE
DE LA RELAXATIOND’ATOMES ALCALINS
PAR
COLLISIONS
SUR UNE PAROI ET SUR UN GAZPar
FRANÇOISE MASNOU-SEEUWS,
MARIE-ANNE BOUCHIAT.Résumé. 2014 L’étude
théorique présentée
a pour but de calculer l’évolution dans letemps
de la valeur moyenne d’une observable
Q
relative à un ensemble d’atomes alcalins dans l’étatfondamental,
lorsque
la relaxation a pour cause les deux processus suivants : d’unepart
les collisions contre laparoi après
diffusion dans le gaz, d’autrepart
les collisions des atomesalcalins contre les atomes du gaz. Le calcul utilise le formalisme de la matrice densité, ce
qui
permet
de calculer l’évolution de différentes observables et de tenircompte
de ce que desobservables différentes
peuvent
relaxer sur laparoi
ou sur le gaz avec des constantes detemps
différentes. La mise enéquation
est valable pour uneparoi
recouverte d’un enduit(collisions
faibles de
type
magnétique)
et pour uneparoi
très désorientante(verre
nu ou recouvert d’unmiroir
alcalin).
Cette étude doit
permettre
d’interpréter
les résultatsexpérimentaux
et d’en déduire le coefficient de diffusion de l’alcalin dans le gazétranger
et les sections efficaces de désorientation(alcalin-gaz étranger)
relatives à diverses observables. Lesrapports
entre ces derniersparamètres
apportent
desrenseignements quant
à la nature de l’interaction désorientatrice enphase
gazeuse et au caractère du
spectre
de ses fluctuations. Abstract. 2014 The timedependence
of the mean value of an observableQ
(measured
over an ensemble of alkali atoms in theground state)
istheoretically
studied when two relaxation processes aresimultaneously present :
collisionsagainst
the walls of the cell, after diffusionthrough
aforeign
gas and collisions with the molecules of the gas. The use of thedensity
matrix formalism makes it
possible
to calculate the time evolution of différent observablestaking
into account the fact that their relaxation in the gas
phase
and on the walls can exhibit differenttime constants. The
present theory
is valid for a coated wall(weak
collisions of themagnetic
type)
or for an uncoated wall(strong collisions).
It should lead to aninterpretation
ofexperi-mental results and allow a determination of the diffusion constant of alkali atoms in a buffer
gas and of the deorientation cross sections for different observables. The ratios between these cross sections
give
information on thephysical
nature of thedisorientating
interaction inthe gas
phase
and on its fluctuationspectrum.
I. Introduction. -
L’expérience
a montre[1]
quetoute collision d’un atome alcalin dans 1’6tat fonda-mental sur une
paroi
de verre nueproduit
lad6sorien-tation de son
spin
S. Auxpressions
de vapeurauxquel-les on
produit
l’orientation par pompageoptique,
lelibre parcours moyen est
grand
devant les dimensions de lacellule,
par suite le temps de relaxation est letemps
qui
s6pare
deux collisions successives sur laparoi,
soit de l’ordre de 10-4 s. 11 existe deux m6thodes
permettant
d’allonger
lestemps
de relaxation. Lapremiere
consiste a recouvrir laparoi
de la cellule d’un enduit deparafhne
satur6e. On trouve que 1 000a 10 000 collisions sur un enduit de ce
type
sontn6cessaires pour
produire
la desorientation duspin
Set du
spin
nucleaire I d’un atome alcalincouples
statiquement
par interactionhyperfine.
L’6tudeth6o-rique
etexp6rimentale
de la relaxation du Rb sur untel enduit
[2], [3]
a montre que la desorientation estdue a une interaction aliatoire
faible
et detype
magni-tique
YsS.H(t) (H (t)
6tant lechamp
magn6tique
al6atoire vu par 1’atome au cours des collisions sur la
paroi
et satisfaisant a la condition de moyennage parle mouvement
[4]).
L’origine
de l’interaction est enpartie
la suivante. Lesspins
nucl6aires K desprotons
de laparafhne
cr6ent auvoisinage
de laparoi
unchamp
magn6tique.
Du fait de son mouvement, unatome de
spin
S est soumis a uneperturbation
y sS . H (t)
fonction al6atoire dutemps.
Si dans lespectre
de Fourier de cetteperturbation
se trouvel’une de ses
fréquences
propres, une transitionpeut
etre
induite,
entrainant la desorientation de S et parsuite de I. Le deuton
ayant
un momentmagn6tique
nucl6aire
plus
faible que celui duproton,
la valeurquadratique
moyenne deH(t)
est considérablement reduite si l’on substitue a uneparaffine
usuelle uneparafhne
deut6r6e ;
on observe bien dans ce cas unerelaxation
plus
lente[3].
La seconde m6thode utilis6e pour
prot6ger
S de 1’action désorientatrice desparois
consiste aoperer
enpresence
d’un gazetranger
ou « gaztampon
». Si lelibre parcours moyen de 1’atome alcalin est
petit
devant les dimensions de lacellule,
l’influence désorientatrice de laparoi
est nettement reduite pour les atomes de Rb situ6s en son centre et diffusant lentement vers lesbords.
Cependant,
les collisions de l’alcalin sur lesatomes de gaz
tampon
sont elles-memes une cause derelaxation. Pour les divers gaz rares, la section efficace de desorientation est tres
faible ;
il a 6t6 montre[5]
qu’il
faut 104 a 108 collisions pour d6sorienter unatome de Rb. Une etude
th6orique
[6], [7]
aboutit ala conclusion
qu’il
existe desperturbations
al6atoires faibles detype
magnitique
dont l’ordre degrandeur
permettrait
d’expliquer
lestemps
de relaxationobser-vés en
phase
gazeuse. Pour les gaz raresqui
n’ont pasde
spin
nucl6aire,
ils’agit
de l’interaction «spin-orbite » S. N ou N
repr6sente
le momentcin6tique
orbital relatif des atomes
alcalin-gaz
rare entrant encollision
[6].
Dans le cas ou le gaz rarepossede
unspin
nucl6aireK,
la th6orie d’Herman[7] pr6voit
que l’interactionmagn6tique
entre S et K estn6gligeable
devant l’interaction
S. N,
sauf dans le cas de 3He et 21Ne.Il nous a paru int6ressant de
reprendre
1’6tudeth6orique
de la relaxation sousl’effet
simultani descollisions sur la
paroi
et sur le gazmalgr6
le nombre detravaux ant6rieurs
d6jh
relatifs a cesujet.
Les raisons en sont les suivantes :- Jusqu’ici
les calculsth6oriques publi6s [8]
ontseulement
envisage
le cas d’uneparoi
totalementd6so-rientante. Celui que nous exposons ici est aussi valable si les
parois
de la cellule sont recouvertes d’un enduit de bonnequalite.
- Les calculs ant6rieurs
supposent
6galement
que la relaxation sur le gazpeut
etre caract6ris6e par uneseule constante de
temps.
Or il a ete montre[2]
que, sous 1’effet d’une interaction faible al6atoire detype
magn6tique,
la relaxation des diverses observables d’un alcalin despin
nucleaire I fait intervenir ungrand
nombre de constantes de
temps :
il existe parexemple
(41 + 1)
constantes detemps
longitudinales
dont lesrapports
mutuels sontcompris
entre 1 et(21
+ 1)2.
Lepresent
calcul est fait dans le formalisme de la matrice densite et tientcompte
de cet effet a la fois pour les collisions sur le gaz et sur laparoi.
L’interprétation
des résultatsexp6rimentaux
dans le cadre de lapr6sente
th6orie devraitpermettre
d’6viter 1’enormedispersion
que l’on note actuellementdans la litterature entre les valeurs des sections
effl-caces de desorientation
alcalin-gaz
rare d6termin6espar des
experimentateurs
differents ;
eneffet,
cettedispersion
tient tresprobablement
enpartie
al’ambi-guit6 qui regne
quant
a l’observable 6tudi6e par chacun d’entre eux.II. Mise en
dquation
duprobl6me.
-Etant
donneeune
grandeur physique
alaquelle
est associe unope-rateur
Q,
nous nous proposons d’etudier l’évolution dansle
temps
de Q),
valeur moyenne de l’observableQ
prise
sur 1’ensemble des atomes alcalins(dans
1’6tatfondamental)
etoccupant
un certain volumeVd (le
volume de vapeur
analyse
par leproc6d6
dedetec-tion).
Nous supposons que cette evolution estproduite
par les
quatre
causes suivantes :1)
Hamiltonienstatique
Ho : couplage hyperfin
aS. I et interaction
Zeeman;
2)
Diffusion dans le gazetranger;
3)
Relaxation par collisions sur laparoi;
4)
Relaxation par collisions sur le gaz.Nous ne tenons
compte
ni de 1’effet du faisceau lumineux ni de 1’effet des collisionsd’6change
desatomes alcalins entre eux.
(Les
valeursexpérimentales
des
temps
de relaxationqui
nous int6ressent sontdeduites de mesures effectuées « dans le noir »
apres
extrapolation
a la valeur nulle de la tension de vapeurd’alcalin.)
Nous allons considerer
s6par6ment
1’effet de chacun de ces processuspuis
1’effetglobal.
1.
EVOLUTION
SOUS L’EFFET DE.0’0.
-Nous
suppo-sons que
Ho
est le mime en tous lespoints
du volume VCM sont
confinis
les atomes : nousnigligeons
leseffets
Iiis a
l’inhomogénéité
duchamp
Ho.
Dans cescondi-tions,
une observable 6volue d’unepart
sous 1’effetde
Ho,
et, d’autrepart,
sous l’effet du mouvement desatomes ; ces deux évolutions sont
ind6pendantes (1).
Nous pouvons passer en
representation
d’interactionde mani6re a éliminer revolution
rapide (li6e
aYPo)
des elements de la matrice densite de 1’ensemble de
tous les atomes
a(t).
Le passage de cetterepresentation,
a*,
a celle dulaboratoire,
a, se fait au moyen des formules :On montre que 1’evolution de a* se calcule
simple-ment en omettant
a£
parmi
lesquatre
causesd’évolu-tion cit6es ci-dessus.
2. DIFFUSION DANS LE GAZ ETRANGER
(en
l’absence de relaxation sur cedernier).
- La densite d’atomesalcalins en un
point
est une fonction de r etde t,
n ( r, t )
dont 1’evolution dans letemps
ob6it a1’6quation
de diffusion :
Nous nous int6resserons
plus g6n6ralement
a l’effetdu mouvement sur 1’evolution d’une
grandeur
phy-(1)
Lecouplage
entre les évolutions dues au hamiltonienstatique
et au mouvement de diffusion est essentiel aucontraire dans le cas d’une assembl6e de
spins
soumis àdes
pulses
deradiof requence,
tandisqu’ils
diffusent dansun
champ statique inhomogene.
La th6orie faite enajoutant
dans1’6quation
de Bloch un terme décrivant la diffusion montre que les 6chos despin peuvent permettre
de mesurer le coefficient de diffusion[9].
sique quelconque.
Consid6rons unpetit
element de volume d v centre aupoint
r et 1’ensemble desp
ato-mes
(p = n d V >> 1)
de cet element ayant pour matrices densités individuelles al, a2, ..., , ap(a
al ,
...,a,
enrepresentation d’interaction).
Nouspouvons définir une matrice densite relative a cet
ensemble d’atomes :
et introduire la valeur moyenne locale de l’observa-ble
Q:
aupoint
r,qui repr6sente
la valeur moyennede l’observable
Q*
calcul6e a un instant t sur 1’ensembledes
p
atomesqui
occupent
1’element de volume d v àcet instant :
Supposons
1’616ment de volume d v centre aupoint
rdelimite par deux surfaces
planes
dsparall6les
(d’abs-cisses x et x +dx)
et consid6rons 1’evolution dea* (x,
t )
qu’entraine
le seul effet de diffusion des atomesalcalins dans le gaz
etranger
suivant la direction Ox. Nous connaissons a l’instant t le flux d’atomes traver-sant lesplans
d’abscisses x et x + dx et entrant dans 1’616ment de volume considéré :La nouvelle valeur
prise
par la matrice densite al’instant t + dt s’6value en consid6rant le nouvel
ensemble d’atomes
occupant
1’element de volume dVa cet instant. Le calcul se fait
simplement,
car dans leshypotheses
ou nous nousplaçons
la contribution dechaque
atome nedépend
que de sa matrice densité a l’instant t,elle est
ind6pendante
de l’histoirequi
lui est advenuea des instants ant6rieurs : d’une part,
l’hypothèse
d’unchamp Ho
homog6ne
nous apermis
de nousplacer
enrepresentation
d’interaction,
d’autrepart,
les collisionssur le gaz sont des collisions faibles. Ceci nous
permet
d’ecrire :
qui
segeneralise
facilement au cas où l’on s’intéresse à la diffusion dans les 3 directions deFespace :
On
peut
obtenir de maniereanalogue 1’equation
d’6volution,
sous le seul effet de ladiffusion,
pour lavaleur moyenne locale de l’observable
Q* :
D est le coefficient de diffusion de l’alcalin dans le gaz
etranger.
Si la masse mol6culaire du gazM2
estvoisine de celle de I’alcalin
M1,
D est donn6 par1’ex-pression
classique :
X libre parcours moyen de 1’alcalin dans le gaz; v vitesse moyenne de I’alcalin.
Dans le cas
contraire,
lagrande
difference de masseentre les
particules
diffusantes et celles du milieu diffuseur rend le processusanisotrope :
onpeut
montrer
[10]
que la valeur moyenne du cosinus deI’angle
0 entre les directions de latrajectoire
de laparticule
avant etapres
la collision n’est pas nulle. Si on suppose la diffusionisotrope
dans lesyst6me
ducentre de masse,
l’anisotropie apparait
lorsqu’on
passe de cesyst6me
a celui du laboratoire et elle est d’autantplus grande
que lerapport m
=M2/M1
estpetit
devant 1. Fermi a montre que le mouvement des
particules
diffusantespeut
etre dans ce cas encoredecrit par une
equation
de diffusion avec un coefficientde diffusion :
Ceci revient a dire
qu’au
bout de1 / (1 -
cos0)
colli-sions on peut considerer que le processus de diffusion
devient
isotrope. 1/(1 2013
cos0)
repr6sente
le nombrede collisions que doit subir l’atome alcalin pour etre
d6vi6 dans une direction non corr6l6e avec sa direction
initiale.
L’équation
(3)
définit le libreparcours
moyen detransport Xi
== ÀI (1 -
cos0)
qui
s’interprete
comme ladistance moyenne que doit
parcourir
un atome pouretre d6vi6 de sa
trajectoire
d’unangle
arbitraire.Le calcul de cos 0 a 6t6 fait par
Cohen-Tannoudji
dans le cas ou les
particules
diffusantes et celles du milieu diffuseur sont anim6es de vitesse ob6issant a la distribution maxwellienne de la th6oriecin6tique
desgaz
[11].
Nousrappelons
ici le resultat : pour m >> 1pour
m
1pour m = 1
On voit en
particulier
que pourm
1,
Xt
differebeaucoup
de À.Notons que, pour que
1’equation
de diffusion ait unsens, il faut que
Àt
soitpetit
devant les dimensions du volume V.3. RELAXATION PAR COLLISIONS SUR LA PAROI. - Il est utile de
rappeler
tout d’abordquelques
résultats ant6rieurs obtenus au cours de 1’etudeth6orique
etexp6rimentale
de la relaxation par collisions sur uneparoi
recouverte d’un enduitparaffin6,
en 1’absencede gaz.
3. a. Relaxation
par
collisions sur laparoi
en l’absence degaz. - Pour
un enduit
paraffin6
noncontaminé,
l’interac-tion désorientatrice est une interaction al6atoire faible
de
type
magn6tique [3].
La th6orie[2]
fournitl’équa-tion d’evolul’équa-tion de
a* ;
elle estcomplexe
quand
ontient
compte
duspin
nucl6aire I de 1’alcalin. Parcontre, nous ferons usage du r6sultat
simple
suivant :certaines observables
Qi
ont leur evolution caract6ris6epar une constante de
temps
Ti
unique,
quel
que soit 1’6tat initial apartir duquel
s’effectue la relaxation :( Qi
>B*
valeur moyenne deQi
al’équilibre
deBoltzmann;
par lasuite,
nous supposons lesobser-vables
Qi
définies defaçon
telleque Qi
>*B
=0).
C’est par
exemple
le cas des observables S. I(6cart
par
rapport
a1’equilibre
de Boltzmann de ladiffé-rence de
populations
entre niveauxhyperfins),
Iz
pola-risation nucl6aire
longitudinale
etNotons
qu’il
y a en tout(41
+1)
observablesQi
sion se limite aux
grandeurs
longitudinales
et quen’importe quelle grandeur longitudinale représentée
par uneobservable Q
peut
se mettre de manièreunique
sous laforme d’une combinaison lin6aire des observables
Qi
Par
exemple Sz
n’est pas une observableQi :
c’est unecombinaison lin6aire de
Qe
et deIz.
Pour les observables
Qi
ob6issant a1’equation
d’6volution
[4],
nous pouvons définir uneprobabilite
de « desorientation » par collision sur la
paroi :
ai
repr6sente
l’inverse du nombre de collisionsn6ces-saires pour que 1’ecart a
1’equilibre
de BoltzmannQ,a
>*
-
Qi
)i
soit divise par e. a2depend
engene-ral de l’observable
Q;.
Remarquons
que le fait de définir uneprobabilité a
de desorientation par collision suppose
que les propriétés
de laparoi
sontuniformes :
parexemple,
pour une cellulerecouverte d’un enduit localement
contaminé,
cepro-cede
perd
son sens, mais il est encore valable si unefaible densite d’atomes
paramagnétiques
(alcalins)
ser6partit
sur toute laparoi.
Dans le cas d’une cellule de verre nue ou recouverte
d’un enduit volontairement contamini par un miroir
m6tallique
del’alcalin,
les atomesqui
heurtent laparoi
ont uneprobabilite
a ~ 1 dedisparaitre
de laphase
vapeur, soit par reactionchimique
sur le verre,soit par condensation sur le miroir : ils sont
remplac6s
en
phase
vapeur par d’autres atomes dont lesspins
ont en moyenne des directions
correspondant
al’équi-libre de Boltzmann. Nous sommes alors dans un cas
particulier
de collisionsfortes
où toutes les observa-blesQ,
ont la memeprobabilite
de desorientation parcollision a =
ai N 1 et
Ti
=Ty. Nous verrons que
formellement la mise en
equation
s’effectue exactementcomme dans le cas cxi 1.
3. b. Relaxation
par
collision sur laparoi
enprésence
degaz. - Par
rapport
au casprecedent,
seul lemouve-ment de l’atome entre deux collisions sur la
paroi
change,
mais noussupposons
que tous les caractères de l’interaction lors d’une collision restent les mimes. L’atomefrappe
laparoi apres
avoir diffus6 dans le gaz : lesprocessus de diffusion et de relaxation sur la
paroi
sontcorr6l6s. L’effet des collisions sur la
paroi
se traduitpar une condition aux limites de
L’equation
dediffusion
que nous allons écrire dans le cas d’une cellulesph6rique
de rayon
R,
l’origine
des coordonnées 6tant au centrede la cellule.
Par unite de
temps,
un certain nombre d’atomesalcalins
frappent
laparoi,
restent adsorb6spendant
letemps moyen Tg,
puis
retournent enphase
vapeur. Onexprime
cecialgébriquement
a 1’aide du flux sortantJ+
(nombre
departicules
sortant de lacellule,
par unite desurface)
et du flux entrantJ_.
L’expression
de ces flux est bien connue en th6orieclassique
de la diffusion. Nous utiliserons1’expression
g6n6ralis6e
au cas ou lesparticules
diffusantes et celles du milieu diffuseur ont une masse tresdifferente,
tellequ’on
peut
la d6duire parexemple
de[10] :
a’ (r,
t )
etQ: (r,
t )
ob6issent a1’equation
dediffu-sion ;
nous pouvons donc paranalogie
avec(7)
definirun flux sortant et un flux entrant
J+*
(R, t),
Ji*
(R, t)
pour cr* (r,
t ) ;
JQ* (R,
t),
JQ*
(R, t )
pourQ,*
( r, t ) .
Si on effectue a l’instant t une mesure de la
grandeur
physique G
sur les atomesqui
vontfrapper
laparoi
et sur ceux
qui, apres
untemps
deséjour
Tg sur laparoi,
retournent en
phase
vapeur, le r6sultat estNous avons vu
qu’une
connaissanceprecise
de lanature de l’interaction entre 1’atome et la
paroi
fournitune
prevision statistique
de la maniere dont a*(ou
Q*)
est affectee par une collision 616mentaire. L’effet sur la
matrice densite
(ou
sur uneobservable)
descolli-sions sur la
paroi
peut
donc etre decrit par unerela-tion entre
J3* (R, t + r,,)
etJ"* (R, t)
(ou
entreJQ* (R, t + r,)
etJ’Q* (R, t)).
Dans le cas d’un enduit
paraffin6
noncontaminé,
une collision
produit
uncouplage
entre les divers elements de la matrice densité : pour la matrice densiteou une observable
Q
quelconque,
la relation cherch6eest en
general
trescomplexe.
Par contre, elleprend
uneforme simple
pour
les observablesQi
que les collisions sur laparoi
necouplent
a aucune autre :Le temps
d’adsorption
-c,, est inferieur a 10-9 s, parconsequent
tres court devant les diverses constantes detemps d’evolution de 6*. Ceci nous
permet
desimplifier
1’equation pr6c6dente (2)
et d’obtenir la conditionaux limites :
avec
Le
paramètre
y; joue
dans la suite un rôleimportant.
Il a les dimensions de l’inverse d’une
longueur :
I jy;
estde l’ordre de
Xt/oci
ets’interprète
comme la distanceminimum que doit
parcourir
un atomeorient6,
confin6pres
de laparoi
avant de se d6sorienter sur laparoi
(cf, fig. 1).
FIG. 1. -
Le
plus
courttrajet
quepeut parcourir
unatome alcalin confine
pres
de laparoi
avant d’avoir subi les1/oci
collisions n6cessaires pour lui faireperdre
son
orientation
Qi
>,
est de l’ordre deÀd r:xi.
4. RELAXATION PAR COLLISIONS SUR LE GAZ. - NOUS
faisons l’ hypothèse
que lors d’une collision entre un atomealcalin et un atome de gaz rare l’interaction désorientatrice
est
aléatoire faible
et detype
magnitique.
(2) Dans
le casparticulier
ouQi
repr6sente
une «cohé-rence
hyperfine
)), si on s’int6resse audéplacement
defréquence produit
par les collisions sur laparoi,
il y a lieu d’introduire devant 1- ai(eq. 8)
un facteurimaginaire
dutype
eiaw’cs : il traduit le fait quependant
la durée del’adsorption
1’atome est soumis, enplus
de laperturbation
magn6tique,
au hamiltonien al6atoireAa (t) S I (a
6tant la constante de structurehyperfine)
qui
nepeut
pas induirede transitions entre niveaux F, mF différents mais cause un
déplacement
def requence,
cequi
a 6t6 mis en6vi-dence
expérimentalement
[12].
L’6tude
th6orique
de la relaxationprovoqu6e
parune ou
plusieurs
interactions dutype
precedent
apermis
de d6montrer le r6sultat suivant : si lechamp
Ho
est faible
(6cart
Zeeman wFpetit
devant 1’6carthyperfin
Aw)
quelle
que soit la valeur destemps
de corri-lation ’t’c, ce sonttoujours
les mêmes observablesQi
qui
relaxent avec une constante de
temps
unique [2].
Ces observables sont donc les mêmes dansl’hypothèse
précé-dente pour la relaxation sur le gaz seul et pour la relaxation sur une
paroi
enduite deparafhne
(colli-sions faibles de type
magn6tique)
(3).
Pour les observables
Qi, 1’6quation d’évolution,
sousle seul effet des collisions sur le gaz, est la suivante :
avec
No
nombre d’atomes de gaz par unite de volume a lapression
po;
vrel
vitesse relative des atomes d’alcalin et de gaz rare.a section efficace de desorientation
alcalin-gaz
rare.La th6orie fournit le rapport des diverses constantes
de
temps
Ti.
Nous posonsTis
6tant letemps
de relaxationlongitudinale
pourun
spin
S isol6(c’est-a-dire
pour unisotope
de l’atomealcalin
consid6r6,
qui
n’aurait pas despin
nucleaire).
En
particulier,
les observablesS. I,
Iz, Qe
relaxentavec les constantes de temps
uniques T’H, Tn, T’ :
avec
j(w)
=1/(1
+úJ2’t"),
C =1/Tis,
Aw = 6carthyperfin.
En
phase
gazeuse, on s’attend a ce que la duree dela collision
(de
l’ordre de lO-12s)
soit untemps
de(3)
Si l’interaction désorientatricealcalin-gaz
rare n’estpas une interaction faible de
type magn6tique,
la situationest la suivante : il existe bien encore un ensemble
d’obser-vables caractérisées par une constante de
temps unique
pour la relaxation sur le gaz, mais ces observables different engeneral
desQ;,
saufpeut-etre
unpetit
nombre d’entreelles
Qj .
Pour uneparoi
de verre nue ou recouverte d’unmiroir alcalin
a = 1quelle
que soit l’observableenvi-sag6e,
et la suite du calculs’adapte
directement a toutes les observables de ce nouvel ensemble. Si laparoi
est recouverte d’un enduit non contaminé, la suite du calculest seulement valable pour les observables
Q
ou l’unecorrelation. S’il n’en existe pas d’autres
(4),
puisque
Tc est tres court, nous
avons i(AW)
= j (wF)
= 1. Lesformules
(14)
sesimplifient
pour donner :Nous avons donc
T n T e
=(21
+1)2/2
etT
=
T’H.
Notons que,
d’apres
sadefinition,
arepresente
lasection efficace de desorientation pour un
isotope
alca-lin
qui
n’aurait pas despin
nucl6aire etqui
serait donc caractérisé par une constante detemps
unique Tis.
Ainsid6finie,
la sectionefficace
estindipendante
de lamultiplicité
de l’étatfondamental
et est la même pour diversisotopes.
C’est ceparamètre qui
a faitl’objet
des 6tudes
th6oriques,
enparticulier
celles de Her-man[6], [7].
Par contre, lesparametres
fournis
par
l’ expérience
sontp;a
=ai. On voit
l’importance qu’il
y a a bien
pr6ciser
la nature de l’observableQi
mesur6eainsi
qu’a
v6rifier danschaque
cas la validite deshypotheses
utilis6es pourévaluer j(ûJF)
et j(Aw)
lors-qu’on
veut d6duire a de la valeur ai mesur6e.5.
EQ,UATION
D’ÉVOLUTION GLOBALE D’UNEOBSER-VABLE. - L’evolution
globale
a la forme suivante :Le
premier
terme traduit 1’evolutionde Q >
sous1’effet du hamiltonien
statique
--1’0.
Il s’6crit :Nous avons vu
qu’on
1’61imine enpassant
enrepre-sentation d’interaction
Le deuxi6me terme traduit 1’effet de la relaxation par
collisions sur la
paroi apres
diffusion dans le gaz(processus
2 et 3corr6l6s),
le troisieme terme traduit 1’effet de la relaxation par collisions sur le gaz (pro-cessus4).
Les processus 2 et 3 d’unepart,
4 d’autre.part ne sont pas corr6l6s. Leur etude men6e de maniere
ind6pendante
a abouti a un r6sultatparti-culi6rement
simple
en cequi
concerne lesobser-vables
Qi*,
on a :avec la condition aux limites :
(4)
Des mesures de relaxation r6centes effectuées sur Rben
presence
dekrypton
[13]
ont montre que l’interactiondésorientatrice en
phase
gazeuse 6tait dans ce cascarac-t6ris6e par l’existence d’un second
temps
de corr6lation de l’ordre de 10-8 s.En
particulier
dans le cas d’unegrandeur
longitu-dinale,
le terme d(1)Q/dt
est nul( Q >
=
Q >*)
etl’op6rateur Q s’exprimant
de maniereunique
enfonction des
Q;,
1’evolutionglobale de Q >
peut
secalculer
compl6tement
et de maniere exacte apartir
des41 + 1
equations analogues
a(16)
et(17).
6. CHOIX DES CONDITIONS INITIALES. - Pour d6crire
totalement revolution du
syst6me,
il faut en outreconnaitre son état à l’instant initial à
partir duquel
onitudie la relaxation. En
pratique,
c’est l’étatd’equilibre
que lepompage
optique
permet
d’atteindre enprésence
des diff6rents processus de relaxationanalyses
ci-dessus :Q; (r, t
=0) )
est donc la solution stationnaire desequations (16)
et(17) lorsqu’on ajoute
dans le secondd(5)
membre de
(16)
Ie termed(5)
(
Q* (r,
t
qui
decritdt
Qi
( r,t )
>
qui1’evolution de
Q*
sous le seul effet du pompageoptique.
Dans les cas de pompage
usuels,
d(5)
Q >Idt
agene-ralement une forme tres
complexe
pour lesobser-vables
Q*,
que lesabsorptions
et r66missionssucces-sives de
photons couplent
entre elles. Dans un butde
simplification,
nousenvisagerons
ici seulement unproc6d6
de pompage tel que pour une ouplusieurs
observables
Q,2 (r,
t)
onpuisse
écrire1’equation
devo-lution sous la forme
simple
suivante :Notons que ce
type
d’6quation
est celui que l’onobtient
rigoureusement
parexemple
dans le cas deSz >
et d’un alcalin sansspin
nucléaire. q?
est la valeur maximum que letype
de pompage utilisepermet
d’obtenir pour la valeur moyenne locale del’observable
Q;. ki
est un coefficientnum6rique qui
secalcule
explicitement,
connaissant lescaractéristiques
du pompage.Tp(r)
est letemps
moyenqui s6parerait
I’absorption
successive de 2photons
par un atomesuppose fig6
aupoint
r. Ce facteur fait intervenir lar6partition
g6om6trique
de l’intensit6 lumineusepom-pante
dans le volume V :Tp(r)
est inversementproportionnel
aIp ( r) .
Nous ne traiterons
explicitement
le calcul que dansle cas ou
Ip (r)
est une fonction uniforme dans levolume
V ;
nous supposons6galement
queq*O
et ki
nedependent
pas de r, c’est-a-dire que l’intensit6pom-pante
a memepolarisation
et meme formespectrale
en tous les
points
du volume V. Ceshypotheses
sontraisonnables
lorsque
I’absorption
par la vapeur alcalineest tres faible.
Qi(r,
t =0) >
satisfait alors lesCes
equations
sontind6pendantes
de 0 et de cp et parconsequent
Q,*(r, t
=0)
estisotrope.
Nous discutons maintenant la validité de
1’6qua-tion
(18).
Lorsque
le pompageoptique
peut
etre consid6r6comme
apportant
unepetite
perturbation
aux effetsdus a la
relaxation,
on obtient avec une tr6s bonneapproximation
1’evolutionglobale
des observablesQ*
en utilisant
(18)
pour d6crire 1’effet du pompage(la
demonstration est
analogue
a celle que l’on trouvedans la référence
([15], § III . D).
Au
contraire,
lorsque
le pompage en lumi6re intense cree a1’6quilibre
un 6tat tr6s différent de celui deBoltzmann,
etdependant
tr6s peu des effets de larelaxation,
d(5) Q)/dt
est le seul termeimportant
pour d6crire 1’evolution
globale
dusysteme
et son6tat
d’6quilibre.
Onpeut
montrerqu’il
existe unensemble
Qp
d’observables pourlesquelles
il est exactd’6crire ce terme sous la forme
(18),
mais engeneral
les observables
Qi
sont diff6rentes desQp,
ets’expri-ment de mani6re
unique
comme une combinaisonlin6aire de
plusieurs
d’entre elles. A1’equilibre,
onobtient :
Ceci
signifie
que lar6partition
dans le volume V de la valeur moyenne locale des observablesQ*,,
et parsuite
Q*, ne
dépend
pas
de r.Remarquons
que le mêmer6sultat aurait ete obtenu si nous avions 6crit que
Q*
satisfaisait
(18).
En
conclusion,
lesequations (19)
et(20)
ne sontqu’exceptionnellement
valables(proc6d6
de pompageparticulier,
observablesparticulières),
mais ellesdon-nent des résultats corrects sur la distribution dans le
volume obtenue pour toutes les observables
Q,i
auxtrès
faibles
et aux trèsfortes
intensitispompantes.
C’est enfait dans ces cas
qu’il
est int6ressant de connaitre les résultats du calcul.Remarquons
que noshypotheses
different de cellesadopt6es
par P.Minguzzi et
al.[14]
en deuxpoints.
Ces auteurs
adoptent
pourd(5) Q>/dt 1’expression
suivante :
Ils
envisagent
le cas ou la tension de vapeur d’alcalindans la cellule est assez forte pour
produire
uneabsorption
considerable du faisceaupompant
Fp
entrela face d’entr6e et la face de
sortie,
et par suite unebaisse
exponentielle
deIp
suivant 1’axe du faisceaupompant.
Nous ne nous int6ressons pas ici a un effetde ce
type,
car les mesures que nous avons effectuéessont faites a une faible tension de vapeur.
D’autre
part,
puisque
le second membre de(21)
nedepend
pasde Q; (r, t),
ilsadmettent,
implici-tement,
qu’en
tous lespoints
du volumeV,
Q* (r, t)
esttr6s
éloigné
de la valeur maximumq,*O.
III.Principales dtapes
du calcul. -Au §
II,
noussommes arriv6es a la conclusion que la valeur moyenne
locale de l’observable
Q*
6tait une solution de :satisfaisant a la condition aux limites :
et a une condition initiale que nous supposons
isotrope.
La resolution d’un
probl6me
de cetype
estclassique
(voir
parexemple [16]),
aussi nous n’enindiquons
que les
6tapes
essentielles,
pour une discussionplus
détaillée nous renvoyons a
[17].
1. SOLUTIONS PARTICULIHRES ET SOLUTION GiNiRALE.
- La recherche des solutions du
type
ayant
un sensphysique
conduit au r6sultat :On est ramene a r6soudre
1’6quation
(25)
avec lacondition aux limites
(23).
Ceproblème
admet pour solutions les fonctionsou
Ylm
(6, cp)
sont lesharmoniques sph6riques
d’ordre Iet de rang m,
Jz + 1/2
(x)
les fonctions de Bessel d’ordre I+
1/2
et ou w =Cù’i’z
l faitpartie
de la suite discretedes racines de
1’6quation
aux valeurs propres constitu6epar
1’6quation
aux limites(équation 23).
Nous posons :On
peut
d6montrer que lesfonctions yvm e- I I’ll"
sontdeux a deux
orthogonales ;
en outre, elles forment unsystème
complet
dans 1’ensemble des fonctions r6elles continues définies sur le segment[0, R],
solutions denotre
probl6me.
La solutiong6n6rale
est donc de la forme :Les coefficients
Ai’ z. m
se d6duisent de la connaissancede la condition initiale
2.
CONSEQUENCE
DE L’ISOTROPIE DE LA CONDITION INITIALE. - Si a l’instant t= 0 nous supposons une
r6partition spatiale
isotrope
pour la valeur moyenne locale de l’observableQ,z
a l’int6rieur de lacellule,
ilen r6sulte que
Donc,
par lasuite,
n’interviendront que les solutionsde
1’6quation
aux valeurs propres 6crite pour l =0,
soit
Ü)i’o
=Ü)lv),
et lapartie
radiale de la solution serade la forme sin
Ü)lV) rlÜ)lV)
r.L’équation (28)
sesim-plifie :
avec
3. RESOLUTION DE
L’ÉQUATION
AUX VALEURS PRO-PRES. - Pour l=
0,
1’6quation
aux limites s’ecrit : :Cette
equation
a une infinite d6nombrable desolu-tions
positives hv
=wzv
R > 0.hv
(v
entier)
estl’abscisse du vième
point
d’intersection des courbesrepr6sentant
les fonctions :La
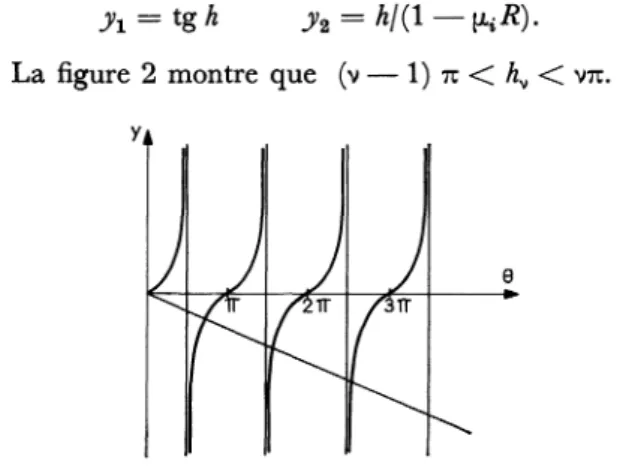
figure
2 montre que(v - 1) 7c
g
v7c.FIG. 2. -
Les valeurs propres hv =
c.>1V)
R sont les abscissesdes
points
d’intersection de la courberepr6sentant
y =
tg
6 et de la droite y =0/(l -
[Li R)
-La valeur de la constante de
temps
’"t"lV)
se deduitde hv
en utilisant1’equation (30).
Nous posons :Chacune des constantes de
temps
T1V)
est associ6e à un mode v de diffusion vers laparoi.
La resolution de
1’6quation
aux valeurs propres est int6ressante dans les cas limites(.LiR
1 et(.LiR
1.a)
Limite auxpressions fortes.
-Lorsque
la condition[ti R >>
1 estsatisfaite,
les solutions de1’equation
auxvaleurs propres tendent vers v7r. Un
d6veloppement
limit6 en1 /ti R
auvoisinage
de cette valeurpermet
d’obtenir :Aux tres fortes
pressions,
lestemps
de relaxation deviennentindependants
de laqualite
de laparoi;
ce fait est
interprete
physiquement
au §
I V.A.I.b)
Limite auxfaibles
pressions
pour
un bon enduit.-Nous cherchons la limite de
wwa
R dans le cas d’unepression
faible(ti R
1)
mais suffisammentgrande
pour que
1’6quation
de diffusion ait encore un sensXt
R.(On
verifie ais6ment que lacompatibilité
deces deux conditions
exige
un bon enduit oci1.)
En ce
qui
concerne lepremier
mode,
und6velop-pement
limit6 de1’equation
aux valeurs propres auvoisinage
de h = 0 et de(LiR
= 0permet
d’obte-nir :
(hl)2
=3(Li
R.La valeur
limiter9
verslaquelle
tend" T,(1)
se calculedonc en utilisant les relations
(32), (10)
et(3) :
Il est int6ressant de comparer
T°
autemps
derelaxa-tion caract6risant
Q" en
l’absence de gaz :Ti
=v/fXi’
Un calcul
simple (5)
permet
d’6valuer r, =4R/3v
etmontre donc que
T°
=T;.
Pour les modes d’ordre
sup6rieur,
on v6rifiequ’aux
faibles
pressions hv
vautpratiquement (v -1 )
1t, et parconsequent
les constantes detemps
Ti(v)
proportion-nellesh p
deviennent tres courtes, d’autantplus
que le mode v estplus
élevé,
mais nous verrons(§ III.4)
que simultan6ment leurpoids
tend vers z6ro.c)
Dans toute la zone despressions
où1’6quation
de diffusion estvalable,
les valeursde hv
sont donn6esen fonction de
lJ.iR
dans le tableau I pour v = 1et v = 2. Dans le m6me tableau
figure
enfonc-tion de
fl’t R
lepouvoir
tampon
du gazetranger
(")
Les atomes sont confinés dans le volume V d6limit6 par laparoi
de surface S. Le nombre d’atomesfrappant
N
v-la
paroi
par cm2 et par seconde estN
4 .
Le nombre total de collisions par unite detemps
sur laparoi
estN s
V4
qui,
pour une cellulesph6rique,
donne N3v/4R
=N/’f;v.
TABLEAU I
Les valeurs tabul6es permettent d’6valuer
et
4.
Importance
relative desdiffirents
modes. - Lacondi-tion initiale à satisfaire
(19)
est :mais nous savons que,
quel
que soit t :Tenant
compte
de(29)
et(35),
, onpeut
r66crire lacondition initiale :
Nous avons vu que le
syst6me
des fonctionsforme un
systeme orthogonal complet
dans1’espace
des solutions du
probl6me
physique.
Onpeut
montrer(cf. [16], § VI. 3)
que, bien que le second membrede
(36)
ne satisfasse pas nécessairement a la condition aux limites(23),
il admetcependant
und6veloppement
convergent en tout
point
a l’int6rieur dusegment
[0, R[,
de la forme :avec :
on obtient alors :
La mesure
physique
porte
non pas sur la valeurmoyenne locale de l’observable
Q*
mais sur sa valeurmoyenne mesurie sur la totalité du volume
Va
de la celluleque traverse le faisceau d6tecteur :
Nous définissons les
poids
yiV)
des constantes detemps
"t"V)
caract6risant 1’evolutionde
Q* >
apartir
de sa valeur
initiale
Q*
>0
par1’6quation :
Lorsque
la détectionporte
sur la totalité du volumeV,
oncalcule aisément que
ylV}
se déduit deA1V}
par larelation suivante :
ou, tenant
compte
de(37)
et(38) :
Cette
expression
conduit a des résultatssimples
dans les cas extremes[ii R >
1 etlLi R
1.Cas
[Li R >
1 :hv N
vTc et 1’on deduit de(40) :
On trouvera
au §
IV. A une discussion d6taill6e de cer6sultat.
Cas fliR
1 : Pour lepremier
mode(h1
--*0),
lavaleur limite de
yi1>
est calcul6e apartir
de1’6qua-tion
(40) :
Pour les modes v >
1,
hv ~ (v -1 )
7r,l’équation (40)
montre queDonc,
enpratique,
seul lepremier
modesubsiste,
dans ce cas.IV.
RÉSULTATS
DU CALCULTHÉORIQUE
ET
INTERPRETATION
Nous r6sumons
ci-apr6s
lesprincipaux
résultats relatifs a 1’evolution dans le temps de la valeurmoyenne d’une observable
Q, lorsque
la relaxation apour cause les deux processus
envisages :
a)
Collisions sur laparoi apres
diffusion dans legaz;
b)
Collisions sur les atomes du gaz tampon. L’évolution deQ, se
deduit de celle des observablesQi
que nous avons choisies pour base(cf. §
II. 3. a,
equation (5)).
Une observable
Qi
relaxe avec une infinitédenom-brable de constantes de
temps
’Ti’J),
chacune 6tant associ6e a un mode de diffusion v vers laparoi.
Lepoids
y")
dechaque
modedepend
de lar6partition
g6om6trique
de lagrandeur physique
associ6e àl’observable
Qi
a l’instant initial apartir
duquel
onétudie la relaxation :
avec
1 / T,")
traduit 1’effet de la relaxation sur laparoi
pour l’observable
Qi, apres
diffusion a traversle gaz selon le vi6me mode.
1IT’
traduit 1’effet de la relaxation sur le gaz pourl’observable
Qi.
Dans les
expressions
deTJV)
etyV)
intervient leparamètre lLi
sous la forme duproduit
sansdimen-sion
i R.
Nousrappelons
que1/ui
repr6sente
la distance minimum que doitparcourir
un atome orient6 confinepres
de laparoi
avant de se d6sorienter surelle. On remarque que les résultats
prennent
uneforme totalement diff6rente suivant que
pi R
estpetit
ou
grand
devant 1. La raison en est la suivante : si laparoi
est peu d6sorientante et lapression
de gaz faibleiR
1,
un atomepeut
traverserplusieurs
fois la cellule avant de se d6sorienter par le processus a.
Par contre, si la
paroi
est tres d6sorientante ou si lapression
du gaz est tresforte,
un atome orient6qui
diffuse du centre au bord de la celluleperd
sonorien-tation avant d’avoir une chance de
s’61oigner
denouveau de la
paroi
(1 j,z
R).
Dans lepremier
cas, on s’attend a ce que le mouvement des atomes
rende
uniforme
Qi(r, t) >
dans tout le volumeoccupe
par la vapeur, et cela meme si les conditions de pompage sont différentes d’unpoint
a un autre.Dans le second cas au contraire on s’attend a ce que
l’orientation soit faible
pres
de laparoi,
et resteplus
ou moins confinée dans la zone ou elle est
produite.
Par la
suite,
nous ferons encore souvent allusion a cesdeux cas extremes :
I/[.Li
>> R orientation « non confinée »I/[.Li
R orientation « confinée ».On
peut
remarquer que 1’effet de « confinement »de l’observable
Qi
estaggrav6
par la relaxation surle gaz.
Comme nous 1’avons vu, la th6orie de la diffusion
n’6tant valable que
pour Xt R,
il en r6sulte que lacondition
[.Li R
1(orientation
« non confinée»)
n’est realisable
qu’avec
de bons enduits.Nous
analysons
maintenant lesexpressions
de’t’1v)
et
yv)
obtenueslorsque
le processus a est seulpresent.
La meme etude est faite ensuite dans le cas ou les
processus a et b
agissent
simultanément.A. Rdsultats concernant la relaxation sous 1’effet
du processus a seul.
2tude
deTw
et1’1’1).
- Enfonction de
[.Li R,
du coefficients de diffusionDo
de 1’alcalin dans le gaz a lapression
po
et du rayon R de lacellule,
nous avons obtenu queTw
a lapres-sion p est
donne parl’expression:
ou
h,,
solution de1’equation (31) comprise
entre(v - 1)
7r et v7r, est donne dans le tableau I pourv = 1 et v = 2.
Interpr6tons
les résultatsauxquels
cette
expression
conduit dans les cas limites :1. CAS D’UNE « ORIENTATION CONFINEE »
fJ-i R
1.Alors hv
= v7r. On a :On remarque que
T1v)
estindépendant
de i(on
obtient la meme constante detemps
pour toutes les obser-vablesQi)
etindependant
de laqualite
de 1’enduit. Ce r6sultats’explique
de la maniere suivante : unatome au centre de la cellule doit diffuser du centre
au bord avant de subir une
premiere
collision sur laparoi.
Ensuite,
ilpeut
diffuser parexemple
dans unedirection normale a celle-ci sur une distance de l’ordre
de R et
échapper
a son influence. Ilpeut
aussi diffuserdans une direction
parall6le, auquel
cas, desqu’il
aparcouru une distance
sup6rieure
ou6gale
aI/fJ-ü
il a une chanceappreciable
d’effectuer les11 (Xi
collisionscontre la
paroi qui
lui fontperdre
son orientation.Puisque
nous sommes dans des circonstances ouIllLi
estpetit
devant R,
le second processus estbeaucoup plus
probable
que lepremier :
I’atome estemprisonn6
pres
de laparoi
assezlongtemps
pourperdre
sonorientation. Le
temps
de relaxation est alorsprati-quement
le temps que met un atome initialement aucentre de la cellule pour diffuser