en fr

HAL Id: tel-02582031

https://hal.inrae.fr/tel-02582031

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

de rupture de barrage

André Paquier

To cite this version:

André Paquier. Modélisation et simulation de la propagation de l’onde de rupture de barrage. Sci-ences de l’environnement. Doctorat Analyse numérique, Université Jean Monnet Saint-Etienne, 1995. Français. �tel-02582031�

95/0220

LA RECHERCHE POUR L'INGENIERIE DE L'AGRICULTURE ET DE L'ENVIRONNEMENT

Département gestion des milieux aquatiques

Division Hydrologie - Hydraulique

THESE

présentée par André PAQUIER

pour obtenir le titre de Docteur de l'Université Jean MONNET Spécialité : analyse numérique

MODELISATION ET SIMULATION DE LA PROPAGATION

DE L'ONDE DE RUPTURE DE BARRAGE

Soutenue le : 9 octobre 1995

devant le jury composé de :

A. BACHOC, A. BOURGEAT, B. CHASTAN, C. CARASSO, J. JAFFRE (rapporteur), A. LARGILLIER,

A. PETITJEAN, J. P. VILA (rapporteur)

Groupement de Lyon

3 bis, quai Chauveau, CP 220 69336 LYON Cedex 09

REMERCIEMENTS

Mes premiers remerciements vont à Alain BOURGEAT qui a soutenu l'ensemble de ce travail et m'a apporté de précieux conseils tout au long de ces années.

Je suis très reconnaissant à Bernard CHASTAN qui m'a accueilli à la division Hydrologie -Hydraulique du Cemagref et a rendu possible la réalisation effective de cette thèse.

De chaleureux remerciements à Jean - Paul VILA qui est à l'origine de ce travail par les méthodes de résolution des équations de Saint-Venant qu'il a développé et qui a bien voulu en être le rapporteur.

J'adresse aussi mes remerciements aux autres membres du jury, C. CARASSO qui m'a initié à l'hyperbolique, A. BACHOC, A. LARGILLIER et A. PETTTJEAN, et plus encore à J. JAFFRE qui a accepté la lourde tâche de rapporteur.

Merci aussi à tous ceux qui au sein de la division Hydrologie - Hydraulique m'ont aidé : P. FARISSIER, H. FAURANT, J.B. FAURE, N. GENDREAU, P. GIVONE, E. HEROUIN, P. RAMEZ,... et pardon à ceux que j'ai oubliés.

Enfin, tout ce travail n'aurait pu venir à terme sans le soutien et la patience sans limite de mon épouse Dominique à qui j'adresse beaucoup plus que ma reconnaissance.

Introduction page 3

Introduction

Les équations de Saint-Venant établies pour la première fois au X I Xe m e siècle [BARRE DE

SAINT-VENANT, 1848] sont actuellement les équations les plus utilisées pour modéliser l'écoulement de l'eau dans les rivières en régime transitoire. Ce sont des équations hyperboliques pour la résolution desquelles subsistent encore des difficultés théoriques et pratiques malgré les nombreux logiciels qui existent de par le monde pour résoudre ce type de problème. La méthode numérique la plus utilisée est sans doute le schéma de Preismann (méthode implicite aux différences finies à 4 points) dans lequel l'algorithme du double balayage (les débits sont d'abord calculés de l'amont à l'aval puis les hauteurs d'eau en sens inverse) permet d'effectuer l'inversion de matrices de manière simple. Cette méthode est très performante lorsque l'écoulement est relativement lent : en particulier, le nombre de Froude (rapport de la vitesse à la célérité des ondes) doit rester strictement inférieur à 1 (voire inférieur à 0,5).

En pratique, cette méthode (et celles basées sur des considérations équivalentes) n'est donc pas utilisable lorsque l'écoulement est torrentiel (nombre de Froude supérieur à 1, équivalent de "supersonique" pour l'hydraulique), lorsqu'il y assèchement ou remplissage d'un bief, lorsqu'il y a une discontinuité dans la ligne d'eau (ressaut hydraulique par exemple), etc. Les logiciels les plus courants utilisent alors des approximations plus ou moins adaptées pour résoudre ces types de problèmes.

Le cas que j'étudierai plus particulièrement est celui de la propagation d'une onde de rupture de barrage. Les ouvrages retenant de l'eau peuvent se rompre sous la pression de l'eau ou du fait de leur submersion lors d'une crue. Ce phénomène peut être très brutal (de l'ordre de la seconde) lorsqu'il s'agit, par exemple, d'un barrage voûte en béton : on parle alors de rupture instantanée ; il peut être plus lent, par exemple, lorsqu'un renard se développe à l'intérieur d'un ouvrage en remblai (quelques heures voire quelques jours). En cas de rupture instantanée sur un barrage important, un front d'eau se déplace vers l'aval balayant l'ensemble des zones avec une forte érosion et des destructions importantes ; la propagation à l'aval est moins brutale et moins dévastatrice pour une rupture progressive où l'hydrogramme s'apparente plus à celui d'une crue naturelle. Pour élaborer les plans d'alerte qui prévoient les dispositions d'évacuation de la population si une telle catastrophe arrivait ou menaçait, il est nécessaire de simuler les conséquences d'une telle rupture, en particulier, en matière de zones inondées.

Ces simulations sont généralement numériques, les modèles physiques étant réservés à des cas particulièrement difficiles. Le plus souvent, malgré la présence d'une forte charge en matériaux solides, on ne simule que l'écoulement de l'eau. En outre, on utilise presque toujours des modèles monodimensionnels et malgré une zone de front très turbulente qui implique à l'évidence que les équations de Saint-Venant ne s'appliquent pas, celles-ci ou des modèles encore plus simplifiés sont le plus souvent utilisés pour résoudre ce problème (voir [WURBS, 1987], [PAQUIER, 1993, (1)] pour la description de ces méthodes et leur comparaison). La zone de front est alors modélisée comme une discontinuité ponctuelle. Certains ([BASCO, 1989], [GHARANGIK et CHAUDHRY, 1991]) ont cherché à utiliser les équations de Boussinesq (qui ajoutent, aux équations de Saint-Venant, un terme d'accélération relativement important dans la zone du front) pour obtenir des résultats plus précis ; en pratique, les différences semblent négligeables.

Si, pour ce problème de propagation d'onde de rupture de barrage, on modélise par les équations de Saint-Venant et si on utilise les logiciels courants, on se trouve alors face à des

problèmes numériques du même type que ceux cités précédemment. Pour résoudre convenablement les équations, il est, en général, nécessaire de faire appel à des méthodes numériques différentes. Une des méthodes les plus anciennement utilisées a été de traiter de manière différente la zone de front et le reste de l'écoulement, l'avancée du front impliquait alors qu'à une zone géographique déterminée, des traitements numériques différents étaient successivement appliqués.

De nouvelles méthodes ont été développées à partir de 1980 : la solution était recherchée dans un ensemble de distributions ce qui permettait de prendre en compte des discontinuités. Le front (discontinuité) étant alors traité comme un point courant, il n'était plus nécessaire de le suivre pendant le calcul et d'effectuer des traitements spécifiques. Les premières applications faisaient appel à des schémas de type Glimm ([MARSHALL et MENENDEZ, 1981], [JEFFREY et MVUNGI, 1982]). VILA [1984, (1), (2)] a ensuite utilisés des schémas explicites de type GODUNOV. Depuis, d'autres schémas numériques (explicites ou implicites) fondés, de manière similaire, sur la forme conservative des équations de Saint-Venant ont été utilisés. Les plus mentionnés semblent être les schémas (explicites) de type Mac Cormack ([BELLOS et SAKKAS, 1987], [GHARANGIK et CHAUDHRY, 1991], [GARCIA-NAVARRÒ et al., 1992, (1), (3)]). L'emploi de méthodes numériques similaires a ensuite été étendu aux équations de Saint-Venant bidimensionnelles : schémas explicites, par exemple, de type Mac Cormack ([JIMENEZ et CHAUDHRY, 1988], [DAMULLER et al., 1989], [FENNEMA et CHAUDHRY, 1990], [BHALLAMUDI et CHAUDHRY, 1992], [ALCRUDO, 1994]) ou implicites, par exemple, de type Beam et Warming [FENNEMA et CHAUDHRY, 1989].

Les travaux décrits ici utilisent un schéma numérique de type Godunov d'ordre 2 présenté dans [VILA, 1986]. Ils visent principalement à améliorer le traitement du second membre des équations afin d'obtenir une précision satisfaisante dans les cas d'application pratique où, en particulier, le relief est tourmenté. La mise en oeuvre de conditions aux limites variées sera aussi examinée. Enfin, un des objectifs a été d'étendre ce traitement à un ensemble de situations plus vastes. Parmi celles-ci, on pourra citer :

- le cas des ouvrages hydrauliques (vannes, déversoirs, etc.) où localement les équations de Saint-Venant ne sont pas vérifiées. Plus généralement, on essaiera de traiter les singularités hydrauliques où localement des pertes de charge viennent modifier la ligne d'eau (relations particulières entre les grandeurs hydrauliques);

- le passage du calcul sur un seul bief à celui sur plusieurs biefs (réseau ramifié ou maillé) ; le problème supplémentaire est ici le traitement des points de jonction entre biefs où l'écoulement ne peut plus être considéré comme monodimensionnel ;

- la prise en compte de plusieurs lits d'écoulement fonctionnant avec des vitesses différentes ; la représentation classique est de distinguer un lit mineur qui coule en permanence du lit majeur qui ne reçoit de l'eau qu'en période de crue ; dans ce dernier lit, la présence de végétation (par exemple) a tendance à ralentir l'écoulement ;

- le transport solide qui se traduit par l'addition de une ou plusieurs équations pour le mouvement des sédiments ; dans le cas général où il y a soit dépôt soit érosion, le niveau du fond de la rivière est modifié, ce qui implique que les équations supplémentaires sont couplées avec les équations de Saint-Venant ;

- le passage de la représentation monodimensionnelle où les vitesses transversales sont négligées à une modélisation bidimensionnelle (horizontale) où les vitesses normales au sens principal d'écoulement sont calculées. On traitera des équations de Saint-Venant bidimensionnelles établies à partir d'hypothèses similaires à celles utilisées pour les équations de Saint-Venant (monodimensionnelles) ; une équation supplémentaire permet bien

Introduction page 5

évidemment de calculer l'évolution de la vitesse transversale. Certains des problèmes complémentaires traités en écoulement monodimensionnel se retrouvent en bidimensionnel (ouvrages hydrauliques par exemple) et seront donc examinés.

Dans le premier chapitre, je commencerai par montrer comment les équations de Saint-Venant (monodimensionnelles et bidimensionnelles) peuvent être établies à partir des équations de Navier - Stokes et quelles hypothèses sont alors effectuées ; de manière générale, je préciserai quelles équations seront étudiées par la suite. Les 2 chapitres suivants traiteront de la résolution des équations de base (successivement monodimensionnelles et bidimensionnelles) en détaillant les résultats théoriques et les différentes options possibles ; des tests numériques et des exemples d'application compléteront l'exposé des méthodes. Enfin le dernier chapitre présentera les premiers résultats et des exemples d'application pour les problèmes complémentaires mentionnés ci-dessus.

1 Les équations

Je commencerai par indiquer comment, à partir des équations de Navier - Stokes, sont obtenues les équations bidimensionnelles puis je détaillerai le passage de ces dernières équations aux équations monodimensionnelles.

1.1 Etablissement des équations bidimensionnelles

Dans toute l'étude, je considérerai que le seul fluide modélisé est de l'eau pure, c'est-à-dire que les matières ou matériaux contenus dans l'eau n'ont aucune influence sur l'écoulement. Dans ce cadre, les équations de base sont les équations de Navier - Stokes pour un fluide newtonien incompressible :

fdiv(u) = 0

I —- + div(u) ® u +—grad(P) = vAu + f [dt p

où u est le vecteur vitesse, p est la masse volumique de l'eau, P la pression, v la viscosité et f la somme des forces extérieures(volumiques) qui, dans le cadre qui nous intéresse, d'un référentiel lié à la Terre, peuvent être réduites à la force de pesanteur et la force de Coriolis. Compte tenu des relativement faibles vitesses du fluide (au maximum quelques m/s), nous négligerons aussi la force de Coriolis devant la pesanteur.

Le système d'équations (1.1) peut aussi s'écrire scalairement sous la forme suivante :

(1.2) 1 ^ = 0

j=idxj

(1.3) - T ^ + Z ' J +-rr— = VZ—-r-r + fi pour i = 1,2,3

dt j=i dxj pdxi j=idxj

Lorsqu'on ne s'intéresse pas aux phénomènes de turbulence, on intègre les équations précédentes sur une échelle de temps microscopique correspondant aux fluctuations turbulentes afin de se ramener aux équations sur des valeurs moyennes. On peut se ramener à des équations de même type que les précédentes. Toutefois, il y a lieu d'introduire l'apport d'énergie turbulente à l'écoulement moyen ; on remplacera le terme vgrad(u) par vgrad(u) + Ub®Ub où u représente maintenant la valeur moyenne de la vitesse, ub la

fluctuation de vitesse turbulente par rapport à la moyenne et le signe " " la moyenne obtenue par intégration sur l'échelle de la turbulence (on a donc ub = 0) ; cette somme peut être écrite sous la forme d'un tenseur de contraintes de termes T¡j d'où la nouvelle expression de (1.3) :

at j=i dxj pdxi pj=i oxj

Les équations de base sont donc maintenant (1.2) et (1.4) où les variables sont des valeurs moyennes qui ne prennent plus en compte la turbulence, cette dernière apparaissant au second membre.

Les mouvements que nous cherchons à modéliser sont, en général, dans les problèmes d'hydraulique fluviale, horizontaux ce qui amène à simplifier la troisième équation (1.4)

Chapitre1 Les équations page 7

portant sur la verticale. La simplification la plus couramment utilisée est l'hypothèse de pression hydrostatique qui consiste à négliger dans cette équation, l'ensemble des termes sauf la pression et la force (la gravité). On obtient donc l'équation :

1 3P

= - g ce qui donne en intégrant : P = P o - p g ( x 3 - z ) où Po est la pression

POX3

atmosphérique, g l'accélération de la pesanteur et z la cote de la surface libre. Cette hypothèse de pression hydrostatique impose [HEROUIN, 1991]:

- des accélérations verticales faibles devant la pesanteur

- des rayons de courbure verticaux des lignes de courant importants ce qui impose, en particulier, des rayons de courbures de l'écoulement dans un plan horizontal (méandres d'une rivière) importants et des hauteurs d'eau grandes devant les aspérités du fond

- une faible pente de la surface libre.

Les termes ——— dans les 2 équations (1.4) restantes s'écrivent alors g O Xi

L'intégration des équations ainsi obtenues sur la verticale (entre le fond de cote Z et la surface libre) permet d'éliminer la vitesse verticale qui ne nous intéresse pas. Pour une variable

()

quelconque A, on posera A = —ÍAdx3 et on aura J dx3 = l-Af As

h „ V3xi 3xi 3xi 3xi

(même type d'expression en remplaçant Xj par t) où Af et As sont les valeurs de A

respectivement au fond et à la surface libre. On remarque, en outre, que, en l'absence

r)7 2 ( 7Y7 \

d'apports, la vitesse verticale au fond est égale à — + £ u ¡ - — (même type d'expression à 3t ,=iv 3xijf

la surface libre) et que la hauteur d'eau h égale z - Z. (1.2) devient alors : (1.5) ^ - 4 3t i=i dxi et (1.4) devient (pour i = 1 ou 2) : z

_

_ 3

h

^

í

u

|

¿

gh

dt j=i dxj j=i dxj 3xi p 2 3(hTJi)

où Tj est l'expression suivante : I J

3

( 2 9Z A ( 2 dz

+ Ti 3- l T i j ^ - Ti3-lTij^—

^ j i 3 x J ^ j 3

Dans l'équation (1.6), 4 termes sont à expliciter :

tl) le terme lié à la dispersion des vitesses sur la verticale

j(ui-Ui)(uji-Uj)dX3

Z J

qui est habituellement modélisé sous la forme de la somme de 2

termes : — et Di £—^r où t¡ et D¡ sont des coefficients constants dans le temps. dx j i 3 x

- t2) le terme lié aux contraintes à l'intérieur du fluide (viscosité, turbulence)

i 2 a(hTij) . 2 I aX j I

— X—^ remplacé par un terme D¡ E — ^ où D'¡ constante dans le temps. pj=i 3xj j=i 3xj

- t3) le terme de frottement au fond — T Í 3 - ¿ T Í ¡ - — qui est classiquement

PI J=i d x J

remplacé par une formule de type Chézy : - g u ¡ ; — o u ^ e s t u n e c o n s t a n t e dans Ie

temps (ou est égale à K h ^ avec K coefficient de Strickler constant dans le temps pour la formule de Manning - Strickler).

- t4) le terme de frottement à la surface — Ti3-XTirr— qui, lorsqu'il s'agit de P{ j-i d x js

l'action du vent, peut être estimé par différentes formules ([RASPOPIN et al., 1989],...). J'utiliserai la formule suivante proposée par [FALCONER et al., 1991] :

p r^ 2

twi = -Cd —(WioX JX(Wio)¡ où W,o est la vitesse du vent à 10 mètres au - dessus de la

P V j=i J

surface du sol (donnée météorologique classique), pa la masse volumique de l'air et cd une

constante.

En écartant les cas où h est nul (car alors il n'y a pas d'écoulement), on effectue le changement de variables suivant U = hui et V = hu2 * et les coordonnées horizontales sont renommées x et y. L'équation (1.5) s'écrit alors :

dh dU 3V n

dt dx 3y et les équations (1.6) deviennent :

(1.8)

_a_

a

3y

dx | ' a

+v

)

ax

_a

_a

a

a

U et V sont les produits de la hauteur d'eau par une vitesse. Ils seront appelés débits et s'expriment habituellement en m2/s.

Chapitre 1 Les équations page 9

qui s'écriront, en ajoutant (1.7) multiplié par U/h (respectivement par V/h), en écrivant Di + D'i = D2 + D2 = D et en négligeant le coefficient t¡ :

(1.9)

ay_

Le second membre des équations (1.9) et (1.10) peut se trouver sous des expressions légèrement différentes en fonction des problèmes posés ; outre les variantes concernant le terme de frottement au fond et l'action du vent, variantes vues ci-dessus, je signale aussi que le terme en facteur de D peut être remplacé par un laplacien (le terme de (1.9) étant alors écrit DAU ) mais ceci ne change pas la méthode numérique pour traiter ce terme.

Les équations (1.7), (1.9) et (1.10) constituent la formulation la plus classique des équations de Saint - Venant bidimensionnelles (en concurrence avec une formulation équivalente faisant intervenir la hauteur et les vitesses). C'est la résolution de ce système d'équations qui sera étudiée au chapitre 3.

1.2 Etablissement des équations monodimensionnelles

On suppose (pour simplifier les expressions) D = 0 et Twi = 0 et on s'intéresse à un écoulement

monodimensionnel selon l'axe Ox.

Axe

vertical

V

Z cote du fond Axe des abcisses

longitudinale^/ Axe des abscisses transversales y ou axe d'écoulement

x /

Si on intègre (1.7) entre y, et y2, on obtient :

9 9 a_{+ h i n 2 ^ + T + U}

ä

3t 3t dt dx dx dx

où S est la section mouillée (aire de la partie de la section en travers située au-dessous de la surface libre et au-dessus du fond) et Q le débit (selon l'axe d'écoulement Ox) entre les abscisses transversales y, et y2 où les hauteurs d'eau sont respectivement hx et h2.

Si on néglige V, et V2 perpendiculaires à l'écoulement et si on considère en y! des apports

extérieurs de vitesse v , (de même en y2), on peut écrire à la limite : — + ui—— =

-dt dx

+ u i v a i

d t d x

(signe opposé au second membre en y2 si v^ positif signifie apport) d'où :

as 9Q

avec q débit d'apport latéral égal à hi vai + b.2 va

2-Si on intègre (1.9) entre y,et y2, on obtient de même :

y, C2h2 a v

où on a introduit la différence entre le carré de la vitesse moyenne sur la verticale u et le carré de la vitesse moyenne sur la section u (égale à % et notée V par la suite]. Cette différence, de la même façon qu'avait été traitée la dispersion des vitesses sur une verticale (terme tl de l'équation (1.6) au paragraphe 1.1), est habituellement modélisée par la somme de 2 termes :

- un terme comprenant des dérivées secondes que nous négligerons et

- un terme exprimé sous la forme — (ß - 1 ) — avec ß un coefficient supérieur à 1. ox y^ J

De même, on écrit, en général, le terme d'apports sous la forme kq — où k est un coefficient qui tient compte de l'apport en quantité de mouvement *, les vitesses u, et u2 n'étant pas

obligatoirement égales à u.

Le terme de frottement est réécrit sous la forme - g -2 Pe où Pe est le périmètre mouillé

(longueur du périmètre du fond de la section mouillée S), le coefficient C n'étant strictement égal à C que pour une largeur infinie ; en général, en 1 dimension, on préfère remplacer cette expression de type Chézy par une expression de type Strickler avec C = K R% en utilisant R le rayon hydraulique égal à S/Pe et K coefficient de Strickler constant dans le temps.

L'équation obtenue est alors :

En ce qui concerne le terme d'apports, il y a lieu de noter que les équations bidimensionnelles pouvaient le faire apparaître en considérant des apports au fond ou à la surface libre. Dans les équations (1.7), (1.9) et (1.10), on aurait alors eu au second membre, les termes va, kvaU et

k'vaV. L'intégration perpendiculairement à l'axe de l'écoulement faisait alors apparaître les

Chapitre 1 Les équations page 11

termes d'apports au fond et en surface dans l'équation monodimensionnelle y compris dans le cas où on supposait h, = h2 = 0.

Le système d'équations (1.11) et (1.12) constituent une formulation des équations de Saint-Venant monodimensionnelles, moins généralisée toutefois que les formulations équivalentes en hauteur d'eau et vitesse ou en section et vitesse. La résolution des équations (1.11) et (1.12) dans le cas particulier oà ß = 1 etk = 0 sera étudiée au chapitre 2.

Dans le cas général, ß est variable (entre 1 et 1,2 le plus souvent) en fonction de la hauteur d'eau et de la vitesse. Au paragraphe 4.4, on examinera le cas particulier (très utilisé dans la pratique) où cette variation provient de la représentation de la rivière en lit composé (distinction entre un lit mineur et un lit majeur où les coefficients de Strickler et les vitesses moyennes sont différents).

Dans le cas d'un confluent de rivières, chaque branche peut être considérée comme modélisable par les équations monodimensionnelles, seule la zone de confluence ressort des équations bidimensionnelles. En première approximation, cette zone de confluence pourra également être traitée de manière monodimensionnelle si l'angle d'incidence entre les 2 vallées confluentes est faible ; en effet, dans ce cas, on peut définir perpendiculairement à la vitesse moyenne une section où la cote de la surface libre sera constante, ce qui rend possible l'intégration précédente de passage des équations bidimensionnelles aux équations monodimensionnelles. Ce point particulier de traitement d'un confluent par une modélisation monodimensionnelle sera examiné au paragraphe 4.3.

1.3 Intégration de lois d'ouvrages

Dans les applications pratiques, il est souvent impossible d'utiliser les équations de Saint-Venant pour modéliser de manière convenable l'écoulement sur la totalité du linéaire d'un canal ou d'une rivière. En particulier, le problème d'un autre type de modélisation se pose en présence d'ouvrages (seuils, vannes). Classiquement, la modélisation de l'écoulement au droit d'ouvrages repose sur un ensemble de formules essentiellement empiriques qui ont été établies en régime permanent et sont extrapolées en régime transitoire. La plupart de ces formules ou lois d'ouvrages correspondent à une représentation monodimensionnelle de l'écoulement. L'écoulement de l'eau dans un tronçon de rivière sur lequel un ouvrage est installé ne peut être modélisé par les équations de Saint-Venant du fait, par exemple, de la forte pente locale, du resserrement prononcé qui implique des vitesses transversales et verticales qui ne peuvent plus être négligées, etc. Dans une loi d'ouvrage, on ne tente plus de décrire la hauteur d'eau et le débit en chaque point du tronçon mais on cherche seulement à déterminer un débit défini comme le débit de l'ouvrage. Expérimentalement, on peut obtenir une relation donnant le débit en fonction de la charge hydraulique * en amont de l'ouvrage, de la charge hydraulique en aval de l'ouvrage et des caractéristiques de l'ouvrage. Dans la plupart des cas, la section mouillée S, située à l'amont immédiat de l'ouvrage et la section mouillée S2 située

* La charge hydraulique est la variable z + VXg où z est la cote de la surface libre, V est la vitesse moyenne dans la section et g est l'accélération de la pesanteur.

immédiatement à l'aval de l'ouvrage sont proches, si bien que la relation peut être simplifiée en ne faisant intervenir que la cote amont z, et la cote aval z2.

A titre d'exemple, je présente ci-dessous les formulations que j'ai utilisé (dans les logiciels développés) pour le cas d'un déversoir - orifice de forme rectangulaire. Habituellement, on distingue 4 cas selon que l'ouvrage est en charge ou à surface libre et selon que le régime est noyé ou dénoyé. Je prendrai ainsi :

- en écoulement dénoyé à surface libre :

/ ^ z i +j^Zd et z i ^ pour z 2 < / ^ z i

- en écoulement dénoyé et en charge :

pour z 2 < / ^ z i + j^3Zd et zi >Zd + % k i w et Z2^ - en écoulement noyé et en charge :

pour z 2 < / ^ z i + j^Zd et ou pour z 2 ^ / ^ z i + j^Zd et - en écoulement noyé et à surface libre :

et z2^Zd + k2W

où Q est le débit à travers l'ouvrage, z, la cote amont, z2 la cote aval, zd la cote du seuil

(supposé horizontal), 1 la longueur de la crête du seuil, w l'ouverture (ou hauteur) de l'orifice, \i le coefficient de débit du déversoir dénoyé, \L' le coefficient du déversoir noyé, cd le

coefficient de débit de l'orifice dénoyé, cn le coefficient de débit de l'orifice noyé, k, et k2

deux autres constantes.

Pour que ceci soit cohérent (et réaliste), des relations doivent exister entre les coefficients ; je prendrai ki = 0,75 , k2 = 0.58 , cn = Cd = 1,51p. = k2|x' ce qui ramène la caractérisation de

l'ouvrage aux seules grandeurs géométriques et au coefficient de débit du seuil dénoyé \L. L'intégration de ces lois d'ouvrage dans le calcul par les équations de Saint-Venant monodimensionnelles et bidimensionnelles est examinée au paragraphe 4.1.

Chapitre 1 Les équations page 13

1.4 Intégration du transport solide

Tout ce qui a été écrit précédemment et, en particulier, les équations bidimensionnelles (1.7), (1.9) et (1.10) et les équations monodimensionnelles (1.11) et (1.12) restent vraies lorsque le fond est mobile si on néglige (ce que je ferai) la variation du volume d'eau contenu dans les sédiments * . En fond fixe, la relation z = Z + h permet de fermer les équations, la fonction Z(x,y) (représentant la topographie bidimensionnelle) ou les fonctions Z(x) et S(h,x) (représentant la cote du fond et la description de la section en travers en monodimensionnel) étant a priori connues. En fond mobile, il y a lieu de considérer en outre les équations donnant l'évolution de la topographie.

En 2 dimensions, une modélisation simple est possible. On définit un débit solide (exprimé en m2/s) dont nous noterons Us et Vs les composantes selon chaque direction, ce qui amène à

l'équation de continuité de la masse solide :

(1.13)

_ p ) M

^

^ = 0

at dx dy

où p est la porosité du matériau, 1 - p représentant donc le rapport du volume de matériau solide au volume total à l'intérieur du terrain en place.

Ces débits Us et Vs sont définis ensuite (par des formules empiriques) comme fonction des

variables h, U et V ainsi que de différents paramètres qu'il est possible de ramener, en général, à des fonctions des seules variables x et y (et éventuellement Z en cas d'évolution du matériau solide en fonction de la profondeur). La formulation la plus simple est de supposer que vitesse solide et vitesse liquide ont la même direction et d'utiliser alors une formule monodimensionnelle (par exemple formule de Meyer-Peter-Muller ci-après) pour déterminer le débit solide par unité de largeur. Cette modélisation est la plus utilisée (voir par exemple [LATTEUX et PELTIER, 1993], [VALIANI, 1992]).

En 1 dimension, la modélisation devient plus complexe ; par analogie avec le liquide, on est conduit à définir une section solide Ss (schématisée sur la figure ci-après avec une limite

arbitraire fixe) et à écrire l'équation définissant son évolution.

Section solide

Figure 1.2 Représentation schématique d'une section solide.

* Si on ne néglige pas ce volume d'eau, un terme supplémentaire est ajouté. Par exemple, l'équation (1.7) devient

az 3h au 3v . , . t, . az

P-T-+——1-——i-r— = 0 ou le terme supplémentaire est p — .

Nous considérons alors le seul débit solide Qs selon l'axe de l'écoulement et des apports

solides latéraux qs. L'équation de continuité de la masse solide devient alors :

Le système constitué des équations (1.11), (1.12) et (1.14) est le système couplant hydraulique et transport solide le plus simple. Il demeure encore largement utilisé et étudié (voir, par exemple, [ZHANG et al., 1988], [KO, 1990]).

Dans le cas du transport des sédiments par charriage (entraînement sur le fond par roulement et saltation) qui sera le seul que je prendrai en compte, Qs est classiquement exprimé comme

une fonction de la hauteur d'eau, de la largeur et de la vitesse ainsi que d'autres paramètres qui généralement peuvent être considérés comme uniquement fonction de x. La complexité provient en particulier de la difficulté d'exprimer hauteur et largeur en fonction des variables S et Ss. En effet, dans le cas le plus général, la section se déforme de manière irréversible et,

pour 2 temps différents, des valeurs de Q, S et Ss identiques peuvent correspondre à des

sections de forme différente d'où des débits solides différents. Si on considère qu'il y a réversibilité du phénomène de transformation des sections, à chaque valeur de Ss, va

correspondre une seule forme de section, c'est-à-dire la définition de la cote du fond en fonction de l'abscisse transversale (à x donné). Les hauteurs d'eau, largeurs et rayons hydrauliques ne sont plus alors fonction que de x, S et Ss sans qu'il soit besoin de faire

intervenir l'historique. C'est ce dernier cas qui sera traité au paragraphe 4.6 ; la connaissance de la seule fonction Qs permet alors d'obtenir un système hyperbolique de 3 équations

différentielles pour les 3 variables S, Ss et Q.

Les formules empiriques donnant le débit solide sont très nombreuses. Je ne cite ci-dessous que celles qui ont été utilisées dans le cadre de la modélisation décrite au chapitre 4. Ces formules sont globales ; en particulier, elles ne tiennent compte que du diamètre médian du matériau sans prendre en compte le comportement éventuellement différent de plusieurs classes granulométriques. En outre, la plupart des formules donnent le débit solide par unité de largeur car elles ont été établies dans le cas de canaux à section rectangulaire. L'extension au cas de section quelconque pose problème ; je me suis contenté de considérer une simple multiplication par la largeur et de remplacer la hauteur d'eau par le rayon hydraulique qui intervient dans le calcul des frottements au fond par la formule de Strickler.

[MEYER - PETER et MÜLLER, 1948] ont établi une formule qui est valide pour des hauteurs d'eau de 1 cm à 1,2 m, pour une pente comprise entre 0,04 % et 2 % et pour un matériau de diamètre médian compris entre 0,4 mm et 3 cm. Avec les considérations mentionnées ci-dessus, cette formule s'écrit :

(1.15) Qs = ( p 8 ^ ^ - (pJR-O,O47D5o(ps-p)f2

où La est la largeur sur laquelle le transport solide est actif, largeur à la cote de la surface libre

le plus souvent, ps est la masse volumique du matériau solide, p la masse volumique de l'eau,

D50 le diamètre médian des grains du matériau, J la perte de charge par frottement au fond

exprimée par un coefficient de Strickler mais modifiée pour tenir compte du seul frottement sur les grains du matériau. On écrira :

(1.16) JR = 2 f K

Chapitre 1 Les équations page 15

où le coefficient de Strickler K est celui intervenant dans l'équation (1.12) et K' correspond au seul frottement sur les grains (ou plus généralement sur le fond, frottement de peau). D existe des formules empiriques qui permettent de calculer K' en fonction du diamètre des grains ; par exemple 2 1 / ., ou 2 6 /

/D

</

Certaines formules de transport solide ne donnent pas uniquement le débit correspondant au charriage mais celui correspondant au total charriage + suspension. Parmi celles-ci, je citerai la formule de [ENGELUND et HANSEN, 1967] valide pour un diamètre médian du matériau compris entre 0,2 mm et 1 cm. Comme pour la formule de Meyer - Peter - Müller, pour se placer hors du cadre initial de validité constitué par un canal rectangulaire en régime uniforme, le produit hi est remplacé par le produit JR dans les applications pratiques. Cette formule peut alors s'écrire:

(1.17)

OÙ tf.PizP. e = ^ - . h- = R ° ^

e

Pour la présentation effectuée au paragraphe 4.6, le système constitué des équations (1.11), (1.12) et (1.14) complété par les formules (1.15) et (1.16) sera utilisé.

2 Le logiciel monodimensionnel RUBAR 3 2.1 Description générale du logiciel

La première version du logiciel RUBAR 3 a été développée au groupement de Grenoble du Cemagref à partir des travaux de J. P. VILA pour la simulation monodimensionnelle de problèmes de choc (avalanches, ondes de rupture de barrage, glissements de terrain dans une retenue,...)- A partir de 1990, j'ai modifié cette version afin de spécifiquement l'adapter au but principal de modélisation de la propagation des ondes de rupture de barrage. Outre les problèmes d'interfaçage, l'adaptation a consisté à modifier le traitement originel (et, plus particulièrement, le traitement du second membre) afin d'obtenir des solutions plus précises en cas de second membre important. Dans toute la suite du rapport, l'expression "logiciel RUBAR 3" correspondra à la dernière version du logiciel; les variantes indiquées seront décrites par référence à cette version.

Le logiciel se compose de 4 programmes informatiques : - un module de saisie des données

- un module de calcul

- un module de visualisation des résultats sous forme de courbes

- un module d'exploitation des résultats sous forme de tableaux conformes aux demandes du CTPB (Comité Technique Permanent des Barrages)* en matière de calcul de propagation d'onde de rupture de barrage.

En annexe, est indiqué l'enchaînement des programmes et la liste des fichiers.

Les 4 programmes sont écrits en Fortran 77 et les graphiques (courbes ou visualisation tridimensionnelle) font appel à la bibliothèque de programmes UNIRAS. La portabilité a été vérifiée sous 3 environnements différents (systèmes d'exploitation VMS, UNIX et CMS) ; les programmes hors graphique peuvent également être utilisés sur PC.

Le module de saisie génère l'ensemble des fichiers contenant les données nécessaires au module de calcul. Chaque type de donnée (hors conditions aux limites et paramètres propres à une simulation) est défini en certains points de la vallée simulée puis interpolé en chaque point où le calcul est effectué **. Dans la version de base, une seule vallée sans affluent peut être modélisée et chaque point est donc repéré par son abscisse longitudinale dans l'axe de la vallée. La topographie est alors décrite par un ensemble de sections en travers (voir figure 1.1) qui, classiquement, sont déterminées par un ensemble de couples abscisses (transversales) -cotes (y, z) ; en fait, à l'exception du calcul des frottements au fond, le calcul ne fait intervenir que la description des sections en couples largeurs - cotes (L, z). Compte tenu de la difficulté d'interpolation entre des sections en travers décrites en abscisses - cotes, le choix a été fait dans RUBAR 3 de n'utiliser pour le calcul qu'une description en largeurs - cotes. En outre, il existe une option qui permet de simplifier encore cette description d'une section en travers qui est alors assimilée à une parabole (la section mouillée S étant alors égale à K ha où K et a ne

sont fonctions que de l'abscisse longitudinale x, h étant la hauteur d'eau).

* Le CTPB est réglementairement chargé d'examiner tous les dossiers concernant les grands barrages français y compris le calcul de propagation de l'onde de rupture.

" On notera que le logiciel permet d'utiliser un pas d'espace variable d'une maille à la suivante (mais fixe dans le temps). Toutefois, dans la suite de ce chapitre 2, je ne présenterai, sauf mention explicite, que des résultats en pas d'espace fixe.

Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 17 \

Le module de calcul permet une visualisation en temps réel de la ligne d'eau (c'est-à-dire hauteur d'eau et vitesse en chaque point de la vallée) et engendre différents fichiers de résultats contenant des hydrogrammes (c'est-à-dire courbes donnant le débit Q en fonction du temps), des limnigrammes (courbes donnant la hauteur d'eau h ou la cote de la surface libre z en fonction du temps), des lignes d'eau à des temps fixés, des enveloppes (c'est-à-dire valeurs maximales sur la durée de la simulation des variables : vitesse, débit, hauteur d'eau,...), etc. La résolution des équations de Saint-Venant est effectuée selon un schéma numérique explicite qui est décrit ci-dessous. Je présenterai en premier lieu les résultats théoriques concernant l'existence de solutions et la convergence des schémas numériques. Ensuite, je traiterai des grandes lignes du schéma numérique retenu puis je détaillerai certaines étapes de ce schéma afin de présenter les différents aspects de mon travail.

2.2 Rappel des résultats théoriques généraux disponibles

Le système d'équations à résoudre est constitué des équations (1.11) et (1.12) avec ß = 1 et k = 0. On peut réécrire l'équation (1.12) afin de mettre les 2 équations sous forme conservative. Le système devient alors :

- équation de conservation de la masse

(2.1,

f

+

f

dt dx

- équation de conservation de la quantité de mouvement

(2

.

^

A

Í

Q

!

i

^

dt d{ S

^ + + p g S g

dt dx{ S ) B dx K2

avec* t le temps, x l'abscisse longitudinale, S la section mouillée, Q le débit, q le débit d'apport latéral, g l'accélération de la pesanteur, Z la cote du fond, K le coefficient de Strickler (frottement), R le rayon hydraulique, h la hauteur d'eau, L la largeur, la pression P = Í g(h - y)L(x,y)dy et la pression latérale B = [ g(h - y ) — d y .

Jo Jo 9x

En posant U = (S,Q)T, le système constitué de ces équations (2.1) et (2.2) apparaît alors sous

la forme générale : (2.3)

8t 9x

qui est celle d'un système hyperbolique non linéaire sous forme conservative pour la résolution duquel un grand nombre de schémas numériques a été développé. La recherche de solutions faibles de ce système permet de trouver des solutions présentant des discontinuités vérifiant les relations de Rankine - Hugoniot suivantes :

fc[S]

= |

(2.4)

où a représente la vitesse du choc (ou de déplacement de la discontinuité) et [ ] une discontinuité.

Ces relations sont également les équations dites du ressaut qui sont classiquement utilisées en hydraulique pour la détermination de l'amplitude d'un ressaut hydraulique (phénomène * Voir paragraphe 1.2 pour la définition plus détaillée de ces variables.

hydraulique ne relevant pas des équations de Saint - Venant, se produisant lors du passage d'un régime hydraulique torrentiel (supersonique) à un régime hydraulique fluvial (subsonique) et se traduisant par une rapide modification de la hauteur d'eau accompagnée d'une perte d'énergie importante).

2.2.1 Résultats d'existence en présence d'un second membre

La plupart des résultats rappelés ci-dessous sont extraits de la thèse de J.P. VILA [1986] à laquelle nous renvoyons pour les démonstrations.

[VILA, 1986] a établi une grande partie des résultats indiqués ci-dessous sur le système de la dynamique des gaz isentropiques qui est analogue aux équations de Saint-Venant, la densité du gaz remplaçant la section mouillée et la quantité de mouvement le débit. Le second membre est habituellement nul mais [VILA, 1986] a également traité le cas où, au second membre de la seconde équation, apparaissaient un terme de frottement et un terme de pente. Ceci revient à traiter des équations (écrites avec les variables S et Q) :

(2.S, f

;

où I(x) = - g — et J(V) = g—-—77 avec K2R% considéré comme une constante ce qui n'est

dx K2R/3

pas l'approximation effectuée en hydraulique habituellement. Ces équations (2.5) et (2.6) supposent en outre l'absence d'apports (q = 0) et une section en travers constante (la largeur est uniquement fonction du tirant d'eau d'où B = 0 et P indépendante de x). On recherche une solution faible pour le problème (pi) constitué de (2.5) + (2.6) pour ( x , t ) e R x R+ et d'une

condition initiale où S0(x) et Q0(x)) appartiennent à L°°(R)nBV(R). En outre, la solution

doit vérifier la condition d'entropie :

J - (E(U)) + - | - (F(U)) - E (U). G(U) < 0 où E(U) = <p(S) + ^ - est l'entropie et dt ox 2S

F(U) = Qcp' (S) + - ^ 7 le flux associé avec (p"(S) = - ^ - ^ pour que E'(U). f'(U) = F'(U). Dans l'hypothèse où la célérité est constante c'est-à-dire que P(S) = c2S, [VILA, 1986, (1)] a

établi le résultat suivant : Sous les hypothèses que :

I(x) e B V ( R ) D L ~ ( R ) , I(X) = I» constante pour |x| > M constante strictement positive, In So (x) et Vo(x)eBV(R)riL~(R), S0(x) = Soo constante et V0(x) = 0 pour | x | > M

le problème (pi) admet une solution faible entropique qui possède les propriétés suivantes : V T > 0 UeLip(0,T;Lio c(R))

V t < T ¡U(.,t)L < C(T) , |U(.,t)|BV < C(T)

Ce résultat d'existence d'une solution est fondamental mais il demande à être étendu à d'autres cas pour pouvoir être appliqué aux problèmes physiques qui nous intéressent. En effet, le cas d'une célérité constante (qui revient pour nous à une hauteur d'eau constante) n'est jamais rencontré en pratique. La démonstration qui s'appuie dans sa première partie sur ce point ne peut être aisément étendue.

Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 19 \

On notera que l'introduction d'un second membre comportant un terme de pente qui, le plus souvent, accroît l'énergie (contrairement aux frottements qui tendent à réduire les fluctuations) limite très fortement les résultats existants et leur généralité. Ceci explique que l'ensemble des résultats concernant la convergence des schémas numériques ne porte que sur les équations homogènes (sans second membre).

2.2.2. Schémas numériques pour les systèmes homogènes

Si on ne s'intéresse qu'au système homogène dans le cas d'une section en travers constante, le problème s'écrit :

(p2) 7 T + "|-(f(U)) = 0 avec U(x,O) = U0(x).

dt dx

On retrouve un problème très largement étudié où certains résultats existent en particulier dans le cas 2 x 2 qui nous intéresse ici. Toutefois, l'existence et l'unicité d'une solution faible entropique n'est pas démontrée de manière générale (saufen dimension 1). En revanche, dans certains cas, on sait construire des schémas numériques convergeant vers une solution faible entropique.

Un pas d'espace h et un pas de temps k constants sont utilisés avec les notations suivantes Xj = j h, tn = n k et r = k/h. On rappelle les définitions suivantes :

Définition 1 :

On appelle schéma explicite sous forme conservative à p + q + 1 points un schéma aux différences finies qui peut s'écrire

Uy+1 = Uy-r(gJ+^-gJ_^) où gJ_^ = g(uy.p,...,U?+q_1) est une fonction localement lipschitzienne par rapport à ses p + q arguments.

Définition 2 :

Un schéma sous forme conservative est dit consistant avec la forme conservative du problème (p2) si g(U,...,U) = f(U).

Définition 3 :

Un schéma explicite sous forme conservative est dit consistant avec la condition 8E d¥

d'entropie associée au problème (p2) soit — + — < 0 s'il existe une fonction H appelée dt dx

flux numérique d'entropie telle que HJ_y = H(uj%,...,UJ4.q_1) soit localement

lipschitzien par rapport à ses arguments et telle que :

On dira que le schéma est entropique si pour toute entropie convexe E associée au problème (p2), il existe un flux numérique d'entropie satisfaisant les 2 conditions précédentes.

Théorème 1 (Lax-Wendroffl :

Soit Un une solution approchée définie par :

Uh (X, t) = U? Si (X, t) G \\]-y2, Xj+^[ X [tn, tn+l[

où U" est la suite des valeurs calculée à partir d'un schéma sous forme conservative consistant avec la forme conservative du problème (p2).

On suppose que Un tend vers U (quand h tend vers 0 avec r = k / h fixé) presque partout

en restant borné dans

L~(R)-Alors U est solution faible du problème (p2). Et si de plus, le schéma est consistant avec une condition d'entropie associé au problème (p2), U est solution faible entropique du problème (p2) pour le même choix de l'entropie.

Théorème 2 :

Soit Un une solution approchée définie par :

Un (x, t) = Ujn si (x, t) € ]xj_j£, xj+j¿[ x [tn, tn+i[

où U" est la suite des valeurs calculée à partir d'un schéma sous forme conservative consistant avec la forme conservative du problème (p2).

On suppose qu'il existe K^ > 0 et K2 > 0 telles que : pour t < T |Uh(..t)|BV < Ki et |uh(.,t)|L * K2.

Alors il existe une sous-suite Uhm de Un qui tend vers U solution faible du problème

(p2) quand h tend vers 0 dans L~(0,T;L¡oc(R)).

Si, de plus, le schéma est consistant avec une condition d'entropie, U est solution faible entropique du problème (p2) pour la même entropie.

Schémas à variation totale décroissante (TVDÌ

Dans le cas scalaire, une classe de schémas importante est celle des schémas à variation totale décroissante (TVD). Ces schémas vérifient :

+— + ~ . .

X

j=— J=-~

Les schémas TVD possèdent la propriété de conserver la monotonie (si la suite ( up) pour j

dans Z est monotone, (u"+1) l'est aussi). Ceci évite donc la création d'oscillations à proximité

des zones de fort gradient ou des discontinuités. Un résultat fondamental est qu'un schéma TVD à 3 points est au plus du premier ordre, c'est-à-dire que U(x,tn + 1)-Ü(x,tn + 1) = AtO(Atp) où Ü est la solution approchée par le schéma calculée à

partir de U(x,t„) et p un entier égal à 1 pour le premier ordre (2 pour le second ordre, etc.). Sous certaines hypothèses complémentaires, on peut démontrer que ces schémas convergent vers une solution faible entropique.

Dans le cas d'un système de 2 équations scalaires qui nous intéresse ici, aucun résultat théorique semblable n'existe. Je m'inspirerai toutefois des résultats du cas scalaire pour définir les schémas et, en particulier, je chercherai à maintenir un caractère de variation totale décroissante sur chacune des 2 variables scalaires.

2.2.3 Schémas de GODUNOV d'ordre 2

Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 21

Définition :

On suppose la solution connue au temps tn et qu'elle appartient à V}, où V}, est

l'ensemble des fonctions de L^R) telles que la restriction de chaque fonction à ]xj-J^,Xj+}J soit un polynôme de degré 1.

On calcule les valeurs moyennes par :

^ ^ ^ ' f t ) ^ où U

est la

solution exacte en Xj+1/2 d'un problème similaire à (p2) mais posé en Xj+1/2 et tn.

On calcule les pentes pour chaque composante i :

ôj = max(o,min(aôii,a8J2, aôjs)) où a est le signe de Sji,

Un+l,i _ Tin+l.i TTn+l,i T T Í I + U TTII+1,Í Tjn+l.i

x. _ H UJ - i Xi _ Uj + i ~ UJ Xi _ U j - U j - i

Ojl - >Oj2— .Oj3 —

Xj+i - Xj-l Xj+l - Xj Xj - Xj-1

Le résultat suivant a été établi par [VILA, 1986] : Théorème :

Soit Uh une solution approchée définie à l'aide d'un schéma de Godunov d'ordre 2. On

suppose que Uh tend vers U (quand h tend vers 0 avec r restant borné) presque partout

en restant bornée dans L°°, alors U est solution faible du problème homogène (p2). Si le schéma utilise le limiteur de pente :

ôj = max(o,min(aoji,aoÍ2>aoJ3,Cha)) où C est une constante e t a e ] 0 , l [ ,

et si Uh est bornée uniformément dans BV, alors U est solution faible entropique de

(p2).

Dans le cas scalaire, des résultats en terme de stabilité et de convergence peuvent être établis aussi bien dans le cas où g " ^2 e s t calculé exactement que de manière approchée ; en

revanche, rien de tel dans le cas général et même en dimension 2 où nous sommes.

L'utilisation dans le logiciel de schémas numériques apparentés à ces types de schéma ne permet pas d'affirmer de quelconques résultats de convergence ou de stabilité même dans des conditions restrictives. Toutefois, les résultats obtenus pour les problèmes scalaires seront utilisés afin d'améliorer la stabilité, la prise en compte des problèmes composante par composante rendant la transposition aisée. Les conditions d'emploi ne seront justifiées qu'à partir des résultats sur les cas tests qui sont décrits au paragraphe 2.10. Ces mêmes cas tests seront également utilisés dans l'ensemble du chapitre 2 pour illustrer les comparaisons entre variantes.

2.3 Description générale du schéma numérique mis en oeuvre dans RUBAR 3 J'ai présenté au paragraphe précédent les principaux résultats théoriques actuellement disponibles pour la résolution des équations de Saint-Venant mises sous forme conservative (2.1) + (2.2). Je détaille ci-dessous la construction d'une méthode de résolution efficace. Les notations utilisées feront référence à l'écriture condensée (2.3) de ces équations.

Dans le logiciel RUBAR 3, est utilisé un schéma explicite aux différences finies à 5 points. Pour le problème homogène, un tel schéma mis sous forme conservative s'écrit (voir annexe pour notations) :

Uï

= Uj

- r f g ^ - g]_y) où g]_y

= g(u*_

, Uj

.,, UJ, U j J

avec g fonction localement lipschitzienne par rapport à ses 4 arguments, g est dénommée flux numérique. En fait, le schéma utilisé est proche du schéma de Godunov d'ordre 2 décrit précédemment ; les modifications (si on excepte le problème du second membre) résident dans le calcul approché (et non exact) du flux à X; 1/2 et éventuellement (voir paragraphe

suivant) dans le calcul des pentes. Je propose ci-dessous une description complète incluant la prise en compte du second membre.

On peut pratiquement diviser le schéma en 4 étapes : - étape 1 :

On estime indépendamment sur chaque variable scalaire et sur chaque maille, les pentes à partir de la valeur (moyenne) sur la maille en question et les 2 mailles de part et d'autre ; pour chaque variable scalaire A*, la pente ôj sur la maille j est définie ainsi :

ôj = amax(o,min(aaôj,CTÔj?,ocaôj)) où a est un coefficient compris entre 1 et 2,

a est le signe de ôf et 8j,ô2,8j respectivement les pentes calculées à partir des 2 mailles de

gauche, des 2 mailles de part et d'autre et des 2 mailles de droite. - étape 2 :

On calcule de façon approchée au temps t„+1/2 = t,, + 0,5 At et à chaque interface d'abscisse

Xj-y2 = 0,5(xj-i + Xj), les valeurs U " ^2 des variables en fonction des valeurs en Xj., (ou Xj) à

tn et des pentes correspondantes. Le passage du temps tn au temps tn+1/2 s'effectue à l'intérieur

d'une maille par la formule de type centré :

Vplï = Uj".va - 0,5r[f (x

, UJ

) - f (xj-,/2, Uy_

)] + 0,5 Ato(x j , U])

On obtient ainsi pour chaque variable, 2 valeurs : U J I ^ L obtenue à partir de la maille j - 1 et

obtenue à partir de la maille j . - étape 3 :

On résout le problème de Riemann constitué du système homogène (sans second membre), posé en chaque Xj.1/2 et tn+1/2, soit :

(p3)

9t dx'

u(x,t

)=u5

_

,y

Ce problème est résolu grâce à un solveur approché qui donne la valeur de H U " . ^2) . Le solveur retenu est une linéarisation de Roe qui est présentée et discutée au paragraphe 2.4.

- étape 4 :

On calcule la solution au temps tn+1 par :

Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 23

In + l _

où G"+1/2 est une valeur approchée de G ( X J , U "+ 1 / 2) calculée de manière différente pour chacun des termes du second membre (voir paragraphe 2.7).

L'architecture de la méthode de résolution (la séparation en 4 étapes) est classique. Les problèmes qui se produisaient dans un certain nombre d'applications pratiques (impossibilité de maintenir une surface horizontale au repos,...) ont conduit à réexaminer en détail la manière de traiter chacune des étapes, c'est ce qui est exposé dans les paragraphes ci-après.

Le schéma défini par les 4 étapes telles qu'elles sont décrites ci-dessus est précis à l'ordre 2 (là où la solution est régulière) pour un choix convenable du pas de temps et du pas d'espace. En annexe 2.2, on détaille l'obtention de ce résultat.

Par analogie avec le cas des systèmes homogènes, on impose la condition de Courant -A #• i O Friedrichs - Levy (CFL) : (Ivi + c ) — < 0,5 où v est la vitesse et c la célérité (avec c = ,/g—).

Ax V L Ceci correspond, en fait, à une condition de CFL ou de non-interaction des ondes pour le problème de Riemann (p3) (voir détails au paragraphe 2.4). Chaque maille j donne donc une condition différente ; le pas de temps choisi devra toutes les vérifier.

Sur la figure ci-dessous, on observe que, pour le test TE2 (problème de Riemann avec valeur nulle, voir description en paragraphe 2.10.2.2), c'est cette valeur de 0,5 qui donne le meilleur résultat. Pour une valeur de 1, un petit défaut apparaît en pied de détente ; pour une valeur de 0,2, la diffusion est augmentée (la solution restant valide).

4.2 y 4.0 3.8 3.6 3.4 3.2 3.0 2.8 g* 2.6 *~* 2.4 + 2.2 2.0 1.8 1.6 1.4 1.2 1.0 0.8 0.6 0.4 0.2 0.0 I - CFL = 0,2 - CFL = 1 : — CFL = 0,5 ! - - SOL. ANALYTIQUE

Abscisse (m)

Figure 2.1 Test TE2 - Hauteurs d'eau pour différents nombres de Courant.

Ce résultat obtenu sur le test TE2 est largement généralisable : pour un nombre de Courant maximal de 1, de petits défauts apparaissent (une valeur supérieure donnant des résultats

totalement faux) ; pour un nombre de Courant maximal inférieur à 0,5, la diffusion augmente (en même temps que le temps de calcul) ; ainsi, il apparaît que, pratiquement, l'utilisation d'un nombre de Courant maximal de 0,5 semble optimale. Sauf indication contraire, c'est cette valeur de 0,5 que nous avons également retenu pour l'ensemble des résultats numériques que nous montrons dans la suite de ce chapitre.

2.4 Résolution du problème de Riemann

On rappellera tout d'abord que le problème homogène constitué des équations (2.1) et (2.2) avec second membre nul admet comme Jacobien :

( °

Ì Q (T Í , ,

2 2 a v e c v = —. c = Jg— = J-r— • Les valeurs propres sont donc v - c et v + c.

Pour S > 0 (ce qui est toujours le cas sauf s'il n'y pas d'eau (le vide)), c est non nul ; le système est donc strictement hyperbolique et les vecteurs propres sont : et . Les

\v-c) l v + c j invariants de Riemann associés respectivement aux premier et deuxième champs sont v + H(S) et v - H(S) avec H(Si) = J dS avec So donnée quelle que soit S, (les invariants de

So S

Riemann étant définis à une constante près).

Pour la résolution du problème de Riemann (p3) correspondant, 2 types de solutions ont été testées :

- la solution classique qui consiste à linéariser le problème : il s'agit du solveur de Roe (voir paragraphe 2.4.1).

- la résolution directe du problème non linéarisé en conservant le type des ondes (choc ou détente) mais en calculant une solution approchée dans le cas le plus complexe, celui des chocs (voir paragraphe 2.4.2). Cette dernière méthode proposée pour ce problème par [VILA,

1986] utilise les concepts développés par [OSHER, 1984].

2.4.1. Solveur de Roe

Le solveur de Roe revient à chercher la solution exacte du problème de Riemann linéarisé (p4) qui peut être défini ainsi :

i f •A(U

.U.)fi-0

(p4) < dt dx

[u(x,O) =

avec A qui doit répondre aux 3 propriétés ci-dessous : 1) A(UL,UR).(UL-UR) = f(UL) - f(UR)

2) A strictement hyperbolique (c'est-à-dire qui a ses valeurs propres réelles distinctes)

3) A(U,U) = f(U)

Dans notre cas, où on utilise le problème de Riemann pour calculer le flux d'un schéma de type Godunov, il est bon de savoir que le flux numérique a 3 expressions :

Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 25

où A+ est la matrice de valeurs propres Xt = — L dans la base des vecteurs propres r¡ de

A, A' de même pour X7 = ———-, |A| de même pour

\X¡\-Une telle matrice a été construite par [ROE, 1981] pour la dynamique des gaz isentropiques à partir d'un vecteur paramètre. Les équations étant formellement identiques à notre système homogène, nous indiquons ci-dessous cette méthode.

Dans notre cas, le vecteur paramètre est | ' | = | /_ | où v est la vitesse soit Q/S. On

désigne par le signe " ", la demi-somme des valeurs à gauche et à droite. On définit : 2wi W2

o"

a

3

R L

Alors A = CB1 vérifie les 3 propriétés ci-dessus. Ses valeurs propres sont va - ca et va + ca,

ses vecteurs propres f * ) et f

) avec v

= -Ü = ^JsL + v*^

f c T

^

J ^ + y

+

\ 2

Si on appelle T la matrice de passage à la base de vecteurs propres, on a alors, par exemple, dans la base initiale |A| = TDT"1 avec T =

Va- C a Va +

et D = |va-Ca| 0 0 |va + Ca

On obtient ainsi grâce à une des 3 formes du flux indiquées ci-dessus une méthode pratique pour calculer une valeur approchée du flux. Toutefois, dans le cas scalaire, il est bien connu que ce type de solveur ne respecte pas la condition d'entropie ; ceci pose, en particulier, problème dans le cas de "détente sonique" où f ( U J < 0 < f' (UR) ; différentes méthodes

existent pour modifier le flux de manière à obtenir une solution entropique. Dans notre cas (variable bidimensionnelle et non scalaire), ces méthodes peuvent se traduire par le remplacement dans l'expression de la solution d'une valeur propre trop proche de 0 par une autre valeur. Dans l'expression du flux

où Xi et r¡ sont les valeurs et vecteurs propres de A, avec UR - UL = E a ¡ r¡, nous avons testé les remplacements de Xt par les valeurs suivantes (l'indice i n'est pas mentionné étant toujours le même) dans les cas où XL < 0 < XR :

- d'après [LEVEQUE, 1990],

- d'après [HARTEN, 1983], ^ + ' si \X\ < Ô avec Ô = 0,1 ou, d'après [LEVY et al.,

45 1989], 5 =

- d'après [HARTEN et HYMAN,1983], - ^ ^ avec Ô = max(0, X-XL.

*--- d'après [ROE, 1992], *--- + *--- si \k\ < Ô avec Ô = XR - XL

8 2 - d'après [DUBOIS et al.], X - g¡,

avec g ^ a w ^ b w ^ X L W , w = , L a =

Selon les auteurs, pour la première valeur propre (i = 1), ^,R est pris en UR ou UA ; de même,

pour le second champ, XL est pris en UL ou UA, UA étant l'état intermédiaire dans le solveur

de Roe, c'est-à-dire UA = UL + a i n- J'ai testé les 2 possibilités.

Les tests de ces différentes variantes sur plusieurs des exemples décrits au paragraphe 2.10 n'ont pas montré de différence significative (voire aucune sur de nombreux tests) dans les résultats même si la correction (en vue de l'obtention d'une solution entropique) s'applique effectivement. Le choix s'est donc orienté vers une méthode aisée à mettre en oeuvre du point de vue numérique et demandant un faible temps de calcul ; pour le logiciel, nous avons utilisé la méthode préconisée par [LEVEQUE, 1990].

2.4.2 Détermination approchée de la solution stationnaire

Le second type de résolution du problème de Riemann testé correspond à la détermination approchée de la solution dans l'ensemble du plan (x,t) puis d'utiliser la valeur stationnaire Us

obtenue pour x = 0 afin de déterminer le flux par f(Us). Cette idée peut être illustrée par les 2

figures 2.2 et 2.3 ci-après dans le cas particulier où la 1-onde est une détente et la 2-onde un choc.

Le type d'onde (choc ou détente) est conservée dans la solution approchée mais le choc est remplacé par un choc approché dont la vitesse (pente de la droite dans le graphique (x,t)) est calculée comme la demi-somme des deuxièmes valeurs propres des états UA et UR. L'état UA

se distingue lui-même de l'état Uc par le fait qu'il est calculé comme l'intersection de la

1-détente en provenance de UL et de la 2-détente en direction de UR au lieu d'être déterminé

comme l'intersection de la 1-détente en provenance de UL et du 2-choc en direction de UR.

L'avantage par rapport à une résolution exacte réside dans la résolution plus facile de l'intersection de 2 détentes qui, dans notre cas, peuvent être caractérisées par un invariant de Riemann (w, = v + H et w2 = v - H), que celle d'un choc et d'une détente qui implique, de

toute façon une inconnue de plus (la vitesse du choc). Dans le cas où la solution exacte comporte 2 détentes, la solution approchée est confondue avec la solution exacte.

Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 27

2-choc

vitesse du choc d'après Rankine-Hugomot

Figure 2.2 Problème de Riemann - Solution exacte.

2 - choc oché

pente: l/2(v+c)deUA I/2(v+c)deUR

Figure 2.3 Problème de Riemann - Solution approchée.

L'algorithme pour obtenir la solution stationnaire approchée est alors le suivant : Us = UL si SA< SLe t X i ( UL) > 0 o u s i SA> SLe t

US = UR si S A < S R et ^2( UR) < 0 o u s i SA> SR et

US = UI si X,(UL)<0<Xi(UA), Ui définie par Xi(Ui) = O et W l(Ui) = wi(UL)

Us = U2 si X2( UA) < 0 < X2( UR) , U2 définie par >.2(U2) = O et w2(U2) = W2( U R ) Us = UA dans les autres cas.

Les tests effectués montrent que cette solution donne des résultats plutôt moins bons que la résolution par le solveur de Roe. Les figures 2.4 et 2.5 ci-dessous illustrent cette comparaison sur le test TE2 (problème de Riemann avec valeur nulle, voir description en paragraphe 2.10.2.2). *-* co X — SOLVEUR D'OSHER — SOLVEUR DE ROE — SOL. ANALYTIQUE Abscisse (m)

Figure 2.4 Test TE2 - Hauteurs d'eau - Comparaison des solveurs.

o V) V) o 15 14 13 12 11 10 9 8 7 6 5 4 3 2 • 1 SOLVEUR D'OSHER SOLVEUR DE ROE SOL. ANALYTIQUE "b (» <o Figure Abscisse (m)

2.5 Test TE2 - Vitesses - Comparaison des solveurs.

Par ailleurs, du fait du calcul assez complexe des invariants de Riemann, cette solution est plus coûteuse en temps de calcul (de l'ordre de 20 %). Le seul avantage, à première vue, est la

I Chapitre 2 Le logiciel monodimensionnel RUBAR 3 page 29 connaissance d'une valeur approchée de la solution stationnaire. Toutefois, l'utilisation de cette valeur approchée dans le calcul du second membre (voir paragraphe 2.7.1.1) ne semble pas apporter d'amélioration. En conséquence, cette résolution ne sera pas utilisée dans le logiciel.

2.5 Calcul des pentes sur les variables

2.5.1 Description générale de la méthode

D s'agit de l'étape la plus importante qui conditionne la qualité des résultats. On s'inspire ici des travaux de VAN LEER [1977, 1979].

On estime indépendamment sur chaque variable scalaire et sur chaque maille, les pentes à partir de la valeur (moyenne) sur la maille en question et les 2 mailles de part et d'autre ; pour chaque variable scalaire A, la pente 8: sur la maille j est définie ainsi :

ôj = o max(o, min(aaôj, CJôf, a o 5])) où a est un coefficient compris entre 1 et 2, a est le signe de 5? et ò] = ^ZAti^ =

XX

Xj-Xj-l Xj+l-Xj-l Xj-Xj+l

La pente ôj est donc nulle si les 3 pentes ne sont pas de même signe et les valeurs Aj.1/2

(respectivement Aj+1/2) sont obligatoirement comprises entre A¡ et ^ A j - i + ^ l - ^ J A j

(respectivement % Aj+i + ( l - % J A j ) pour un pas d'espace constant, ce qui a été supposé dans tout ce chapitre.

Dans la pratique, le logiciel permet un pas d'espace variable et le coefficient a est alors

, a ( x j x j - i ) . a ( x j x j + i ) . , . , . .

remplace par —? r (respectivement —-,— —r) pour garder la même limitation sur

2Uj-Xj-|/2J 2(Xj-Xj+l/2J

les valeurs en extrémités de maille.

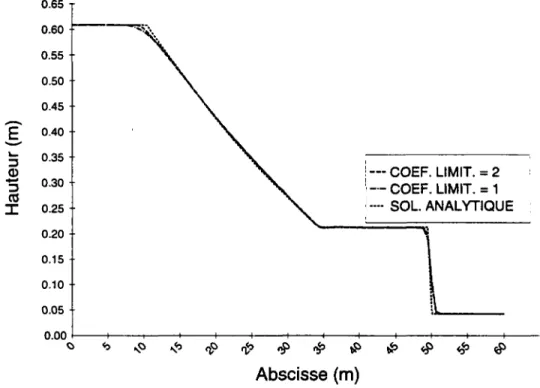
Avec a = 2, on s'assure que les valeurs en extrémité de mailles sont comprises entre les valeurs au centre de maille de part et d'autre; des valeurs de a plus faibles limitent plus fortement les pentes ce qui assure une plus grande stabilité des calculs mais augmente la diffusion comme cela apparaît en haut de la détente sur la figure 2.6 ci-dessous pour le test TEI (problème de Riemann, voir description en paragraphe 2.10.2.1).

o T — COEF. LIMIT. = 2 — COEF. LIMIT. = 1 •-• SOL. ANALYTIQUE 0.00 <$> Abscisse (m)

Figure 2.6 Test TEI - Hauteurs d'eau - Comparaison des coefficients de pente.

Pour nos calculs, nous avons retenu, le plus souvent, des valeurs de 1,5, ce coefficient n'ayant, dans la plupart des cas, aucune influence notable sur les résultats. La figure 2.7 ci-dessous montre un cas extrême (test TE2 - problème de Riemann avec valeur nulle) où ce coefficient a une influence sur la position du front et la vitesse dans cette zone ; toutefois, la même figure tracée pour les hauteurs d'eau donnerait 3 courbes confondues à l'épaisseur du trait près, les hauteurs d'eau étant de toute manière très faibles dans la zone concernée par les différences.

17 T 16 1 5 • 1 4 •• 13 12 "7n 11

E

°

<x>