Résonance magnétique en champ de radiofréquence inhomogène. 1 re partie : Étude théorique

HAL Id: jpa-00208198

https://hal.archives-ouvertes.fr/jpa-00208198

Submitted on 1 Jan 1974

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Résonance magnétique en champ de radiofréquence

inhomogène. 1 re partie : Étude théorique

R. Barbé, M. Leduc, F. Laloë

To cite this version:

R. Barbé, M. Leduc, F. Laloë. Résonance magnétique en champ de radiofréquence inho-mogène. 1 re partie : Étude théorique. Journal de Physique, 1974, 35 (10), pp.699-725. �10.1051/jphys:019740035010069900�. �jpa-00208198�

RÉSONANCE

_MAGNÉTIQUE

EN CHAMP

DE

_{RADIOFRÉQUENCE}

INHOMOGÈNE.

1re

_{partie : ÉTUDE}

_THÉORIQUE

R.

_BARBÉ,

M. LEDUC et F. LALOË

Laboratoire de _{Spectroscopie} Hertzienne de l’E. N. S., 24, rue _Lhomond, 75231 Paris Cedex 05 (Reçu le 26 mars 1974)

Résumé. 2014 On étudie dans cet article l’effet d’un

champ de _{radiofréquence} très inhomogène

sur un ensemble de _spins en mouvement. _Lorsque le _champ magnétique statique est _balayé au

voi-sinage de la résonance, les variations de l’aimantation _{longitudinale} globale des _spins donnent des courbes de résonance nettement différentes des courbes habituelles ; elles sont en _général la

super-position de deux courbes de largeurs très différentes, la courbe _large et la _{courbe fine.} La forme de la _{première dépend} essentiellement des _{caractéristiques} du mouvement des atomes dans le _champ de _{radiofréquence inhomogène.} On étudie en détail le cas où ce mouvement est _{régi par} un _processus

de diffusion : l’étude de la _largeur à mi-hauteur de la courbe large donne alors le temps de diffusion des atomes dans la cellule, ce _qui fournit un _procédé commode de mesure des coefficients de diffusion dans les gaz. La courbe fine _peut avoir, suivant les variations _spatiales des _{inhomogénéités statique}

et de _{radiofréquence (et} notamment suivant les corrélations entre les différentes composantes de

ces _{inhomogénéités)} des formes variées : elle _peut être constituée d’une courbe _{d’absorption positive}

ou _{négative (aimantation} minimale ou maximale à _résonance), ou de la superposition d’une courbe

d’absorption et d’une courbe de _dispersion. De _plus, des _{déplacements importants} de la _position de la résonance fine sont _possibles, notamment sous l’effet de termes croisés entre _{inhomogénéités}

statiques et de _{radiofréquence.} Abstract. 2014 The effect of

a very inhomogeneous radiofrequency field on an ensemble of _moving

atoms is _{investigated theoretically.} When _sweeping the static _magnetic field and _measuring the

longitudinal magnetization, one observes a resonance curve of unusual _shape. In most cases it is

the _{superposition} of two curves _{differing substantially} in width. The _shape of the broad curve _depends

primarily on the atomic motion in the _{inhomogeneous radiofrequency} field. The case in which the

motion follows a diffusion process is _investigated in detail and the half-width of the broad curve

is then _simply related to the diffusion time of the atoms _through the cell. This _yields a sensitive

method for _measuring diffusion coefficients in gases without _requiring determination of the magni-tude of the field _gradient. The narrow curve may have various shapes according to the _spatial varia-tions of the static and _{radiofrequency} field _{inhomogeneities (and mainly} to the correlations between the different _components of such _{inhomogeneities).} The curve _may have an _{absorption shape,}

with a _positive or a _{negative sign (the magnetization being} minimum or maximum at _resonance)

and may also be a _{superposition} of an _absorption and a _dispersion curve. Furthermore, under certain

conditions, the narrow curve _{undergoes large shifts,} in particular due to crossed terms between the static and _{radiofrequency} field _{inhomogeneities.}

Classification

Physics Abstracts 8.610-6.140

Le _{principe général} des _expériences de résonance

magnétique est bien connu _{[1] :} on considère un

ensemble _d’atomes, dont chacun _possède un moment

cinétique S et un moment _magnétique m = yS

(y : rapport gyromagnétique des _{atomes) qu’un} processus _{quelconque (relaxation thermique,} pom-page optique, etc.) tend à orienter dans une

direc-tion _{Oz ;} ces atomes sont _plongés dans un _champ

statique Bo parallèle à Oz et soumis à l’action d’un second _{champ magnétique B,(t) (champ} de radio-fréquence), tournant autour de Oz avec la vitesse angulaire co ; _{lorsque B, --- - co/y,} il se _produit un

phénomène de résonance (résonance magnétique) :

le _champ de _{radiofréquence,} même faible, peut

détruire l’orientation des atomes. Les variations en

fonction de _Bo de la _{composante Mz} sur Oz de M (aimantation globale de l’ensemble des _atomes) sont

données par une courbe d’absorption de Lorentz,

centrée en _Bo = - wlr, _et dont la largeur dépend

de _{Bl ainsi que des temps} de relaxation _{longitudinale}

et transversale du _système.

En _pratique, les _{champs Bo} et _BI ne sont

évidem-ment _{jamais parfaitement homogènes,} et il se _pose

le _problème de tenir _compte de cette _{inhomogénéité.}

Si _chaque atome est _{parfaitement immobile,} on _peut

simplement calculer l’évolution de son moment

magnétique à _partir du _champ local _Bo(r) et _{B,(r, t)}

qu’il voit, quitte à sommer ensuite sur les _différents

atomes _pour obtenir l’aimantation _globale M. En

fait, dans un _grand nombre d’expériences, les atomes

se déplacent sous l’effet de _{l’agitation thermique et,}

par l’intermédiaire de leur position r, les valeurs des champs Bo et _{B, auxquels} ils sont soumis sont des

fonctions aléatoires du _temps. C’est d’ailleurs

sur-tout l’effet des _{inhomogénéités} du _{champ Bo qui} est

susceptible de se manifester _car, le _champ statique

étant _{généralement} bien _plus intense _{que le champ} de _{radiofréquence,} ses variations sur l’échantillon

étudié _peuvent être _{beaucoup plus grandes.} Ainsi l’effet des _{inhomogénéités} de _Bo a-t-il été

fréquem-ment _{étudié ; par exemple,} dans le cas où le

mou-vement des atomes est suffisamment _rapide

(condi-tion de rétrécissement _{par le} mouvement _[1]

_[2]),

ces

inhomogénéités se traduisent _simplement par un

raccourcissement des _temps de relaxation

exponen-tielle de M _{[3] [4] [5] [6]} et, par suite, par un

élar-gissement de la courbe de Lorentz donnant la

réso-nance. Des _{déplacements} de la _fréquence de

réso-nance sont _{également possibles mais,} sauf dans certains cas _particuliers

_(voir

_{par exemple}

_[7]),

ils

restent faibles devant la _largeur de raie. Toutefois,

bien que souvent _faible, l’effet des _{inhomogénéités} de _{B1 n’est pas toujours négligeable,} surtout dans les _expériences où, pour obtenir une _puissance

importante de _{radiofréquence,} on utilise des bobines

de _{petite taille pour créer B, ;} il existe d’ailleurs

des types d’expériences où, précisément pour

éli-miner les effets des _{inhomogénéités} de _Bo, on utilise

un _{champ B1} très intense _{[1] [8]}

_[9l’

_(B, doit être supérieur aux _{inhomogénéités} de _Bo sur la _cellule). Ce sont alors les _{inhomogénéités} de _{B1 qui} deviennent

gênantes et, pour s’en affranchir, on utilise

quel-quefois la _technique des _{rotary echoes [10]} ou échos

de _spin dans le _{référentiel} tournant.

Les _{inhomogénéités} du _champ de _{radiofréquence} dans une _expérience de résonance _{magnétique peuvent}

donc dans certains cas _jouer un rôle _{important ;}

c’est ce rôle que nous allons étudier ici. Nous allons

d’emblée considérer un cas _extrême, celui où la

radiofréquence est _{complètement inhomogène (à} tout

instant, la valeur _moyenne de _B1 sur la cellule

ren-fermant les atomes est _{nulle) ;} le cas où _{B, comprend}

également une _{partie homogène} sera examiné ensuite.

Nous nous limiterons _{cependant toujours} au cas où le _{champ Dl} est suffisamment faible _(ou le

mouve-ment des atomes dans la cellule suffisamment _rapide)

pour que son action soit soumise au « rétrécissement

par le mouvement », comme c’est très _fréquemment le cas en _{pratique (au} moins dans les _expériences de

résonance _magnétique sur des échantillons gazeux).

L’hypothèse du rétrécissement par le mouvement

permet de mener les calculs _jusqu’au bout en

carac-térisant l’orientation des atomes _par une aimantation

globale M, sans avoir besoin d’introduire une

aiman-tation _{M(r) dépendant} de r _{[ 11 ].} Nous verrons alors

que l’effet des inhomogénéités de la radiofréquence

peut être _plus radical _{qu’un simple changement} des caractéristiques (largeur, hauteur) de la courbe de résonance. De _fait, cette courbe _apparaîtra comme

la _{superposition} d’une courbe _{d’absorption large} (souvent beaucoup plus large que celle de résonance magnétique habituelle) et d’une courbe fine _(de largeur comparable à la _{largeur habituelle)} dont la forme peut, suivant les conditions _{expérimentales,}

être _plus ou moins compliquée : elle _peut se

pré-senter comme une courbe _{d’absorption, positive} ou

négative (Mz est minimal ou maximal à _résonance),

ou encore comme une _{superposition} d’une courbe

d’absorption et d’une courbe de _dispersion. De _plus, des _{déplacements} notables _(comparables à la _largeur) de la courbe fine sont _possibles. D’un _point de vue

pratique, de tels _{déplacements peuvent} être _importants

pour certaines expériences de haute résolution : si le champ de _{radiofréquence} n’est pas parfaitement

homogène, la faible _{composante inhomogène peut}

produire une courbe large _peu visible dans

l’expé-.

rience _{(elle apparaîtra} comme une _légère remontée

du fond _{continu) ; cependant,} lors du _pointé de la résonance _fine, le fait _qu’elle soit _déplacée et, de

plus, comprenne une courbe de _{dispersion (courbe}

asymétrique) peut conduire à des erreurs. Une

autre _{application pratique} de notre étude _provient de ce _que les _paramètres associés à la courbe _large

(forme et _{largeur) dépendent} de façon critique du

mouvement des atomes dans .la cellule ; dans le cas

où ce mouvement obéit à _{l’équation} de la _diffusion,

l’étude _{expérimentale} de ces caractéristiques _peut

conduire à des mesures de coefficients de diffusion.

Dans ce _{premier article,} nous étudierons

théori-quement l’effet des _{inhomogénéités} du _champ de radiofréquence sur l’aimantation M de l’ensemble des

atomes. Un _premier modèle _{simple (§ A)} montrera

que l’effet de la partie inhomogène se traduit par

l’existence d’un _processus de relaxation résonnante

agissant sur les atomes. Les variations en fonction

de _Bo du _temps de relaxation _{longitudinale}

corres-pondant permettent de _comprendre l’existence de la courbe _large. Nous _reprendrons ensuite _{(§ B)} le

problème de _{façon plus précise} et calculerons en

détail les _équations d’évolution des _composantes

de M, compte tenu de l’existence de _plusieurs modes de diffusion dans la cellule _sphérique, du fait que la

carte du _{champ inhomogène} sur cette cellule _peut

être _plus ou moins _complexe, etc. Pour traiter le cas

le _{plus fréquent} en _pratique, nous _envisagerons celui

où les _{champs statique} et oscillant sont tous deux

inhomogènes. Enfin _{(§ C),} nous calculerons la forme

de la courbe de résonance donnant les variations

de _M, en fonction de _{Bo ;} en particulier, dans le cas

où _Bo et _B, sont tous deux _{inhomogènes,} nous

étudierons l’influence de la relaxation résonnante

anisotrope correspondante sur la forme _plus ou

moins _complexe de la courbe fine.

compte des vérifications détaillées de ces _calculs,

effectuées au _moyen d’une _expérience d’orientation nucléaire de 3 He _gazeux obtenue _{par pompage}

optique. Signalons qu’un bref résumé des résultats

théoriques et _{expérimentaux} de ces deux articles est

donné dans les références _[12] et _[13]. Par ailleurs,

des _{expériences de pompage optique} sur

201 Hg

_[14]

et 87Rb _[15] ont _permis d’observer des effets

ana-logues sur des atomes autres que l’hélium. A. Modèle _simple. - A. 1 CHAMP

DE

RADIOFRÉ-QUENCE PARFAITEMENT _{INHOMOGÈNE ;} COURBE

LARGE.-Nous supposons ici que la cellule contenant les

atomes est _plongée dans un _{champ statique Bo,}

parallèle à l’axe Oz, d’intensité

Les atomes sont _également soumis à l’action d’un champ inhomogène oscillant _{Dl (r, t) que} nous

appel-lerons _champ de _{radiofréquence :}

où _û,(r) est une fonction vectorielle donnée variant

d’un _point r à un autre dans la cellule. La valeur moyenne sur la cellule, de volume _V, s’écrit :

Nous allons commencer _{par supposer dans} cet

article

que fl,(r) > = 0 (champ de radiofréquence

parfaitement inhomogène) ; ’par contre, bien

évi-demment :

Du fait de son mouvement _{d’agitation thermique,}

chaque atome du _{gaz voit} un _{champ qui dépend} du

temps à la fois _{explicitement} et _{implicitement,} la

dépendance implicite venant des variations aléatoires

de sa position r. Pour comprendre l’effet sur les

atomes du _champ de _{radiofréquence,} il est utile d’utiliser le référentiel tournant _{(référentiel} tournant autour de Oz à la vitesse _{angulaire m)}

_(1).

Le _champ de _{radiofréquence} devient alors un _{champ statique,}

à condition de _négliger en chaque point r de la cellule

la _composante tournante antirésonnante de _{B, (r, t)}

ainsi que sa _partie oscillante _parallèle à _{Oz ;} cette

approximation est valable _lorsque l’intensité du champ Bo n’est pas trop faible

_(il

faut notamment

que co, >

Q,(r»,

ce qui est le cas en _pratique dans

la _plupart des _{expériences.} Nous sommes alors (’) On _prend en fait en _{chaque point} r un référentiel tournant, dont l’origine reste au _point fixe r, et animé d’une rotation de vitesse angulaire w. En d’autres termes, on effectue en chaque point une transformation sur les _composantes de M et de _BI, mais pas de r.

ramenés à un _problème bien connu : celui de l’effet

d’un _{champ statique inhomogène} sur une collection

d’atomes en mouvement _{thermique ;} on sait

([3]

à

_[6])

que l’existence d’un tel champ se traduit _pour

les atomes _par une relaxation supplémentaire de

leur aimantation _globale. Nous allons _supposer ici

que la pression dans la cellule est telle que le

mouve-ment des atomes _peut être traité _{classiquement} et

qu’il obéit à _{l’équation} de diffusion

_(2).

_Désignons

par rd le temps de diffusion des atomes dans la

cel-lule _(la définition _précise de _rd sera donnée dans le

§ B. 2 _{suivant) ;} id est le _temps de corrélation de la

perturbation magnétique aléatoire _agissant sur les

atomes. _{Lorsque :}

(condition

de rétrécissement par le mouvement _[1]

[2]

[16]),

le _temps de relaxation _Ti de la composante

longitudinale Mz de l’aimantation _globale M des

1 atomes est donné par

(’) :

où :

et où :

est la valeur _moyenne sur la cellule du carré de la

projection transversale du _champ de _{radiofréquence} inhomogène

(physiquement,

il est évident _que la

composante longitudinale Ql,,(r) n’agit pas sur

_Mj.

La formule _{(A. 6)} est _{classique ;} on notera seulement

que c’est Jo qui apparaît à son dénominateur, et

non _w. comme _{habituellement ;} ceci tient tout

simplement au fait que nous raisonnons ici dans le

référentiel tournant où l’intensité du _champ

sta-tique efficace le _long de Oz est _{proportionnelle} à _{d o} (et non à _coo). La _probabilité de relaxation _1/T* a

donc un _comportement résonnant dans la _région 40 = 0, et devient _beaucoup moins _importante dès que d o > 11’rd ; physiquement, ceci tient au fait

que la perturbation aléatoire _magnétique dans le

référentiel tournant _possède une densité _spectrale

notable dans une bande de fréquence centrée en zéro

et de _{largeur comparable} à _’/Td’ la _{fréquence propre} du _spin dans ce référentiel _{étant J(J/2} n.

L’effet d’un _champ de _{radiofréquence}

parfaite-ment _inhomogène est donc très notablement

diffé-rent de celui d’un _{champ homogène ;} au lieu de coupler entre elles les _{composantes longitudinale M,,}

(2) Aux faibles _pressions où le libre _{parcours moyen des} atomes

serait comparable ou _supérieur aux dimensions de la cellule, cette

hypothèse ne serait pas valable.

(3) Dans l’expression (A. 6), le facteur _{1/4 provient} de ce que

seule une des deux composantes tournantes du champ de

radio-fréquence intervient. Il faut d’ailleurs noter _que cette expression

n’est qu’approchée ; la valeur _précise de _Ti sera calculée au

et transversale _M+ =

Mx +

_iM,,,

il ne _{couple M’,}

qu’à Mz, dont l’évolution _globale s’écrit :

Dans cette _équation, le terme en

_{1 / Tp}

traduit l’action

d’un processus d’orientation _{longitudinale} des atomes (pompage optique par exemple), le terme en

IIT, + _IIT,* l’effet des autres _{processus de} relaxa-tion _{(Tr désigne} le _temps de relaxation de _Mz en

l’absence _{d’inhomogénéités} de _{radiofréquence} et du processus d’orientation des atomes). L’orientation M,

évolue donc avec une constante de _{temps globale 7B} donnée _{par :}

où :

désigne la _probabilité de relaxation de _Mz en l’absence

de _champ de _{radiofréquence inhomogène. Quant} à la valeur stationnaire limite _Mi de _Mz, on l’obtient

facilement à _partir de _{(A. 6), (A. 9)} et _{(A. 10) :}

Comme en résonance _{magnétique ordinaire,} les

variations de _Ms sont donc _{données par} une courbe

de Lorentz, centrée en _{d o} = 0, _et dont la largeur _et

la hauteur sont des fonctions croissantes de l’inten-sité du _champ de _{radiofréquence appliqué.} Des

différences _{importantes apparaissent toutefois ; par}

exemple, le _temps de relaxation transversale

_Tfl

ne

figure pas dans (A. 11), ce qui se _comprend bien

puisque Mz n’est pas couplé à _M+. La différence la

plus importante tient _cependant à la valeur de la

largeur L de la courbe _prévue par (A. 11) qui vaut,

exprimée en unités de _{pulsations (dans} tout cet

article nous _{appelons simplement largeur} des courbes

leur _demi-largeur à _{mi-hauteur) :}

Cette _{largeur, extrapolée} à intensité de _{radiofréquence}

nulle, donne _1/,r,, et non

IITO

comme en résonance magnétique ordinaire

_{(T,’ :}

_temps de relaxation transversale en l’absence de _champ R. F. inhomo-gène). Nous allons _{supposer ici que :}

La courbe _{de résonance donnée par (A. 1 1)} est alors

beaucoup plus large que celle que donnerait la

réso-nance avec un _champ de radiofréquence homogène ;

c’est _pourquoi nous _{l’appellerons} « courbe _{large ».}

Remarques :

(i) La formule _{(A. 9) prévoit} exactement la même forme de courbe que les formes habituelles de

réso-nance _{magnétique pour} un _système dont les _temps

de relaxation _{longitudinale} et transversale seraient

_Tf

et _zd.

(ii) Les courbes centrées en _úJo = _{+ co ne se}

recouvrent _{pas si :}

Dans toute la suite, nous _{supposerons que :}

L’effet de la _composante antirésonnante est alors négligeable.

A. 2 CHAMP DE _{RADIOFRÉQUENCE} COMPORTANT UNE PARTIE HOMOGÈNE ; ; COURBE FINE. -

Que se _passe-t-il

maintenant si le _champ de _{radiofréquence} n’est _pas parfaitement inhomogène, c’est-à-dire _{si ( Q,(r) >} n’est pas nul (ou parallèle à _{Oz) ?} Il est clair _que, contrairement à ce _qui se _{produisait au §} 1 _précédent,

les évolutions de _M, et de _M+ ne sont _plus

décou-plées ; on s’attend donc à une modification de la

forme de courbe de résonance.

On _{peut décomposer} tout _champ de _{radiofréquence} inhomogène en deux _{parties :} la _première

est _{purement inhomogène ;} la seconde

est au contraire _parfaitement homogène et _dépend

uniquement de la _{valeur moyenne du champ} de radiofréquence, notée _{pour simplifier :}

Le _problème est maintenant de savoir dans _quelle

mesure on _peut simplement ajouter l’effet de la

partie inhomogène du _{champ (relaxation résonnante)}

et celui de sa partie homogène. Dans tout cet _article,

nous _{supposerons que :}

Cette condition, réalisée en _pratique dans la plupart

des _expériences du fait de la _petite valeur du _temps de diffusion _(rd est couramment de l’ordre de 10-3 _s),

exprime que la partie homogène du champ de radio-fréquence n’a pas le temps d’agir pendant le _temps de

corrélation de la _{perturbation magnétique} aléatoire

à _laquelle est soumis _chaque atome. Dans ce _cas, on sait _{[1] [16]} que la relaxation associée à cette

perturbation aléatoire n’est pas modifiée par la

pré-sence du _champ de _{radiofréquence homogène}

(4).

Par suite, tous les résultats _{du §} 1 _précédent

concer-nant l’effet de la _{partie inhomogène} sur l’évolution

de l’aimantation M restent valables. _{L’équation} d’évolution _globale de M s’obtient donc _simplement

en _ajoutant au second membre les termes _provenant

de la _présence du _champ de _{radiofréquence} homo-gène.

Nous sommes donc ramenés à un problème

clas-sique de résonance _{magnétique :} calculer l’effet d’un champ de _{radiofréquence} oscillant _homogène sur

l’aimantation M d’un ensemble _{d’atomes, compte}

tenu bien sûr du fait _que la _{partie inhomogène} du champ oscillant _produit une relaxation

supplémen-taire pour M. Au § 1 _précédent, nous avons vu _que

la modification de la relaxation _{longitudinale} conduit à _remplacer

_T°

par Tl

T? (cf.

(A.

1 Oa» ;

il faut évidemment _{envisager également} les modifications de la relaxation _{transversale,} et _remplacer le _temps

transversal

_T2

en l’absence de _{radiofréquence} par un

temps T2 plus court

_{(5) :}

( T2 :

temps de relaxation transversale associé au

champ de _{radiofréquence inhomogène}

_(6)).

Ces modifications une fois _faites, on _{peut appliquer} les classiques formules de Bloch _pour obtenir l’effet sur

la valeur stationnaire de M du _champ de

radiofré-quence homogène ; on trouve _pour la valeur

sta-tionnaire _Ms de _{M,, l’expression} habituelle

_(voir

par exemple, réf. _[1], formule ₍₃₎ du _Chap. III, p.

44) :

où _{mii désigne} le module de la _projection de _wl sur

le _{plan x0y perpendiculaire} à Oz. Si _Tl et _T2 étaient des constantes, cette formule donnerait _{pour Mi} une

courbe de Lorentz de _{largeur :}

(4) La condition (A. 18) est discutée dans la référence [17]

(Chap. VII) en termes d’atomes habillés _par le _champ de

radio-fréquence (elle exprime que les modifications des fréquences de

Bohr sont faibles devant la _{largeur spectrale} de la perturbation aléatoire).

(5) La relaxation produit également un _{déplacement àoeg} de la

fréquence propre de M+ ; ce _déplacement sera étudié au § B. _3a.

suivant.

(6) La valeur exacte de Ti sera _{précisée plus} bas (§ B. 3 . a . _{P) ;}

signalons dès ici que Ti est _comparable à Ti .

En _{fait, Tl} et _{T2 dépendent} de _A, par l’intermédiaire de _T* et _T2

_(voir

_{par exemple (A. 6)} et _(A.

_10)).

Cependant leurs variations ne sont notables _que

si _Jo varie d’une _quantité de l’ordre de _{1 /-r, ;} nous

allons supposer ici que :

hypothèse qui, sauf pour les très grandes valeurs du champ de _{radiofréquence homogène (résonance}

_très,

fortement saturée) revient à :

Dans ces conditions, les variations de T, et T2 sur

la _largeur 1 sont _{complètement négligeables} et on

peut les _remplacer dans (A. 20) par leurs valeurs pour Jo = 0 ; cette formule _prévoit alors pour la

valeur stationnaire _Mi de l’orientation _{longitudinale}

une variation lorentziénne dans la région 1 A 0 1.

Globalement, la courbe de résonance est donc la

somme de deux courbes _{d’absorption} lorentziennes

(cf. Fig. 1). Loin de la résonance

_(j

_{do > l),}

l’effet

du _champ de _{radiofréquence homogène} est

négli-geable, et la courbe de résonance est confondue avec

la courbe _{large donnée par (A. 11).} L’effet du _champ

de _{radiofréquence homogène} n’est sensible (comme habituellement en résonance magnétique) _{que si}

1 A 0 1 ;$ 1; lorsque cette condition est _réalisée, la partie homogène du _champ de _{radiofréquence} peut, suivant son _intensité, détruire une _{proportion plus} ou moins _grande de l’orientation

_{M.. T, (,J,, = 0)/ Tp}

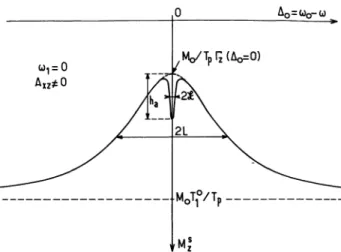
FIG. 1. - Forme de la courbe de résonance obtenue

avec un

champ de radiofréquence partiellement inhomogène ; on _porte en fonction de _do =

coo - co les variations de la valeur

station-naire _M.’ de l’aimantation longitudinale des atomes. _{Mo Tf /Tp} est l’orientation des atomes en l’absence de radiofréquence (on

suppose ici Mo > _0). La partie inhomogène de ce _champ donne des variations résonnantes du temps Tl de relaxation longitudinale

des atomes, ce _qui entraîne l’existence d’une courbe _large de

lar-geur L (l’extrapolation de L à radiofréqueace nulle donne l’inverse

du temps de diffusion des atomes). La partie homogène donne une courbe fine, située au sommet de la courbe _large, et de largeur 1 ;

cette courbe fine peut se décrire comme une résonance _magnétique

habituelle, au cours de _laquelle est détruite une _partie de l’orien-tation Md = _{Mo T,(Ao} =

O)ITP qui aurait subsisté au sommet

qui aurait subsisté au sommet de la courbe _{large ;} il en résulte une courbe de résonance _{fine, superposée}

à la _{précédente (’).}

A. 3 DISCUSSION : DANS QUELLES CONDITIONS

EXPÉ-RIMENTALES LA COURBE LARGE APPARAÎT-ELLE ?

-Dans une _expérience où le _champ de _{radiofréquence}

est _homogène il faut, pour produire la résonance fine, un _champ d’intensité telle que :

Par contre, si le _champ de _{radiofréquence} est

par-faitement _inhomogène, la résonance _{large apparaît} lorsque :

Comme

_{TZ >}

id, l’intensité du champ oscillant nécessaire pour observer une résonance est _plus

faible

_(d’un

facteur

_",/rd/T2)

_lorsque ce _champ est

homogène que lorsqu’il est _inhomogène. On _peut

alors se poser la question suivante : dans les expé-riences réalisées en _pratique où le _champ n’est, ni parfaitement homogène, ni _parfaitement inhomo-gène, l’effet de la composante homogène du _champ de _{radiofréquence} ne suffira-t-il pas dans la plupart des cas _{à masquer} celui de la _composante inhomo-gène ? En d’autres termes, si l’on désire observer la

résonance _large, avec _{quelle précision} faut-il annuler la valeur moyenne du champ oscillant sur la cellule ?

Désignons par k un coefficient caractérisant

l’in-homogénéité du _champ de _{radiofréquence :}

k varie entre 0 _{(champ parfaitement homogène)} et

l’infini _(champ de _{radiofréquence} nul en valeur

moyenne sur la _cellule). Pour que l’on puisse

dis-tinguer la courbe _large de la courbe fine il faut _que,

lorsque l’intensité du _champ de _{radiofréquence} est

assez _{grande pour qu’apparaisse} la courbe _large, la courbe fine soit encore suffisamment _{peu élargie}

pour rester nettement _plus étroite que la courbe

large. Or la courbe _{large apparaît lorsque :}

(’) On _peut se demander si la condition (A. 22b) est réellement essentielle et s’il ne _{suffit pas, pour} s’en affranchir, de remplacer

dans _{(A. 20) Tl} et T2 par leurs expressions complètes sans _négliger leur dépendance en _{d o.} En fait, cette manière de faire ne serait

pas correcte : pour écrire (A. 6), nous avons _{supposé implicitement}

que, parmi les _processus d’évolution des atomes, seule l’évolution due au _{champ magnétique statique} est _capable d’agir notablement sur les atomes en un _{temps id.} De même que la condition (A. 18)

est nécessaire _pour assurer _que l’action du champ de radiofréquence homogène est négligeable pendant le _temps Zd, de même il faut

pour que (A. 6) reste valable _{qu’aucun processus} de relaxation

n’agisse efficacement sur l’atome _pendant le même temps, ce _qui

implique nécessairement _{(A. 22b).}

Pour cette intensité de _{radiofréquence,} la _largeur de la courbe étroite est, d’après (A.21) :

Compte tenu de (A. 13), on montre facilement _que

cette _largeur est très inférieure à

_{rd ’}

1

si

Donc, pour observer nettement l’effet des

inhomo-généités du _champ de _{radiofréquence} et obtenir une

courbe ayant l’allure de celle de la _{figure 1,} il faut

que l’inhomogénéité du _champ de _{radiofréquence,} repérée par le paramètre k, soit supérieure à une

quantité qui ne _{dépend que de id} et du _temps de

relaxation transversale

_T2.

_{D’après (A.22b),} cette

condition n’est pas très sévère ; si l’on pousse

suffi-samment l’intensité du _champ de _{radiofréquence,} la courbe _large doit _apparaître en fait dans la _plupart

des _{expériences.}

Remarque. -

Compte tenu de _{(A . 26), l’inégalité} (A .18) devient

condition _qui est, en _général, satisfaite si (A. 28) l’est.

B. Calcul complet : effets du _{champ inhomogène}

sur l’orientation. - Etudions

plus en détail l’effet du

champ de _{radiofréquence inhomogène} sur

l’aiman-tation des atomes _(dans tout ce _{paragraphe B,} nous

n’étudierons que le rôle de la partie inhomogène du champ de _{radiofréquence,} dont nous _supposerons

que la valeur moyenne sur la cellule est _nulle). Les

calculs que nous avons menés jusqu’ici ne sont

valables que dans le cadre d’un modèle simple, où

l’effet du _champ de _{radiofréquence peut} être

carac-térisé _par un _temps de relaxation T* dont

l’expres-sion est donnée en (A. 6). En fait, la valeur exacte

du _temps de relaxation _{longitudinale} est _plus

complexe ; elle fait intervenir _{plusieurs temps} de

corrélation _id associés aux différents modes de

diffusion dans la cellule, avec des _{poids qui dépendent} des variations _spatiales du _champ de _{radiofréquence.}

De _{plus, il n’est pas} suffisant de _{décrire le processus}

de relaxation résonnante étudié par un _temps de

relaxation _{longitudinale T*,} même en lui _adjoignant un second _temps Ti _{pour décrire la relaxation}

trans-versale : d’une _part, la relaxation _{peut également} introduire des _{déplacements} de la _fréquence de précession de l’aimantation ; d’autre _part, elle _peut

présenter un caractère _anisotrope et _coupler entre

elles différentes _composantes de l’aimantation, de

sorte _que sa _{description complète} nécessite

l’intro-duction d’une matrice 3 x 3 de relaxation _(R). Nous

que ces _{propriétés complexes} de la relaxation (ani-sotropie, déplacements de _{fréquence) peuvent} conduire à des effets _importants et facilement observables.

C’est _pourquoi nous allons _reprendre les calculs du

§ A de façon plus détaillée et _complète.

B .1 EVOLUTION DES COMPOSANTES DE

L’AIMANTA-TION DANS L’HYPOTHÈSE DU RÉTRÉCISSEMENT PAR LE MOUVEMENT. - Calculons l’effet sur la matrice densité

de l’ensemble des atomes de la _perturbation magné-tique aléatoire _{que subit chacun d’entre} eux, du fait

de son mouvement _{d’agitation thermique} dans le

gradient de _{champ magnétique (contrairement} au

§ A _précédent, nous allons ici raisonner dans le

référentiel du _{laboratoire). Nous supposons que les}

atomes étudiés ont un

spin t

et _{désignons par 6x, 6y} et _Uz les _opérateurs dans _l’espace des états d’un

spin 2

associé aux trois matrices de Pauli. L’hamil-tonien _X(t) de _couplage entre un _atome, de

posi-tion _r(t) à l’instant t, et le _champ de _{radiofréquence}

inhomogène s’écrit alors :

où _{Q,:,: = Q lx} ±

_{iQ ly}

et _SlIZ sont les _composantes

du vecteur _{01 (r) caractérisant, d’après (A.2),} le champ Bi(r, t) ; on a _{posé u, = Qx ± iQy.} Nous allons supposer ici satisfaite _{l’hypothèse} selon _laquelle

l’action de _Je(t) est soumise au « rétrécissement _par

le mouvement » _{[1] ] [2] [16] :}

(cette condition étant vérifiée en tout _point r intérieur

à la _{cellule) ; te désigne} le _{(ou les) temps} de corréla-tion de la _{perturbation JC(t),} dont la valeur exacte

sera discutée en détail dans _{le §} 2 suivant. La condi-tion _{(B.2) exprime} que, avant d’avoir eu le _temps

d’agir de façon importante sur un atome _donné, la perturbation à _laquelle il est soumis a _perdu toute

« mémoire » de sa valeur initiale. Dans ce _cas,

l’évo-lution de la matrice densité _p(t) de l’ensemble des

atomes sous l’effet du _{champ inhomogène} est donnée par [1] [16] :

Dans _{(B. 3),} la barre _{qui apparaît} au-dessus d’une partie du second membre _{signifie qu’il} faut _prendre la valeur moyenne sur l’ensemble des atomes étudiés

de _{l’expression qui} y figure ; Uo(t, t -

r) désigne l’opérateur d’évolution libre entre les instants t et

t - L _{qui, pour} des atomes _plongés dans un _champ

magnétique parallèle à Oz d’intensité - _w.1y, s’écrit :

D’autre _{part, l’expression} de la matrice densité _p(t)

en fonction des composantes M,,,

My

et _Mz de l’ai-mantation M du niveau fondamental est :

(on a posé Mt =

Mx ±

_iMy).

En reportant (B .1 )

et _(B.5) dans _{(B. 3),} on voit _apparaître un certain

nombre de doubles commutateurs des _opérateurs a,,

Q_ _{et a,,} dont le calcul ne _présente pas de difficulté ;

et, comme :

on obtient, tous calculs faits :

Dans ces _égalités, les coefficients de relaxation R

(les coefficients R dont le deuxième indice est +

ont eiroot dans _{l’intégrale} sur r, ceux dont le deuxième

indice est - ont _{e-"00", l’exponentielle} étant absente pour ceux dont le deuxième indice est _z).

Nous avons donc calculé la matrice de

relaxa-tion _{(R) qui permet} d’écrire l’évolution de M due

au champ de radiofréquence inhomogène sous la forme :

,

Les éléments de matrice de (R) dans la base _M+, Mz, M_ apparaissent explicitement dans _(B.7). Cependant, pour la suite, il nous sera commode

d’utiliser _{l’expression} de _(R) dans la base _M,,,

_My,

M,,, expression qui est, bien sûr, réelle. Dans _(R), les termes _{indépendants} du _{champ Bo s’expriment} en

fonction des coefficients réels :

où _{x,, xj} =

x, y ou z ; les K, qui dépendent de co

mais pas de co., seront _appelés coefficients non

résonnants. Pour les coefficients de la relaxation

dépendant de co(,, nous introduisons les _quantités

réelles C et S définies paru :

(l’expression de S étant _simplement obtenue en

remplaçant cos _{mo i par sin coo i) que} nous

appel-lerons « coefficients résonnants » _(ils deviennent importants si mo = co). On montre _{aisément que :}

d’où l’on déduit _{l’expression} suivante de la matrice _(R), dans la base Ox, Oy, Oz :

Lorsque la condition de rétrécissement par le

mouvement est satisfaite, les _{équations que} nous avons obtenues sont _générales et donnent l’évolution de l’aimantation _{M, quelle que} soit la loi _{qui régit}

le mouvement aléatoire des atomes dans la cellule ;

cette loi n’interviendra _que dans le calcul des valeurs

moyennes sur tous les atomes, qui sont _symbolisées

par des barres horizontales dans l’expression des

coefficients R. En _{effet, désignons par F(r, t ; r’, t’)} d’r

la _{probabilité pour} que, sachant qu’un atome se

trouve en r’ à l’instant _t’, il soit à un instant t ultérieur dans un volume d’r centré en _{r ;} un raisonnement

simple montre alors que :

où _{f (r, t)} est la densité

_{relative I}

des atomes à l’instant t

_(des

formules semblables à (B. 13) peuvent immédiatement être écrites _{pour les}

autres _composantes de

_{01 (r)).}

Si nous connaissons la

fonction _{F(r, t ; r’, t’),} nous _pouvons calculer

l’in-tégrale figurant dans _{(B. 13), puis} les coefficients R

grâce à _{(B. 8),} et le _problème est en principe résolu.

Dans le _paragraphe suivant, nous allons effectuer

ces calculs dans le cas _particulier où le mouvement

des atomes est _{régi par l’équation} de diffusion. B. 2 APPLICATION A LA DIFFUSION D’ATOMES DANS UN CHAMP INHOMOGÈNE OSCILLANT. - Pour

un

ensem-ble d’atomes diffusant dans une cellule _sphérique de rayon Ro, dont les _parois sont _supposées

parfaite-ment réfléchissantes (elles ne _produisent aucune

ne _dépend que de r = t - t’ et vaut _{(voir appendice,}

formule

_{(18)) :}

où V = 4

nR’13

est le volume de la cellule,

qJn,l,m(r)

la fonction _spatiale associée au mode _{repéré par les}

indices n, 1, m, de temps de diffusion _zn,l. Les

expres-sions _précises de _qJn,l,m et de _1’n,1 sont

_{(8) :}

D étant le coefficient de diffusion des atomes dans la _{cellule, Ym(O, lfJ) l’harmonique sphérique} d’ordres 1

et _{m, j1} la fonction de Bessel _sphérique d’ordre 1 et

fin’

le n-ième zéro de sa dérivée :

(an,l

i est un coefficient de normalisation défini dans

l’appendice ; cf.

_(10)).

_Compte tenu de _(B.13) et en

supposant que :

(densité uniforme des atomes), il _apparaît dans les

coefficients de relaxation R des _intégrales de la forme :

qui s’écrivent _{Q, ,}

_{1 (p.@l@. >}

_(p.@l@.

_{1 Q, , >} en

uti-lisant la notation _{simplifiée :}

(l’intégrale étant étendue à toute la _cellule). Nous

supposons ici que la valeur moyenne ( 121(r) > est

nulle _(champ de _{radiofréquence purement} inhomo-gène) ; c’est la raison _{pour laquelle} le terme en _{1 / V}

dans _{(B. 14) disparaît lorsqu’on} le _reporte dans (B. 13)

(9).

(8) Au lieu des fonctions _{Pn.l.m(r) qui} sont complexes (sauf

si m = 0), on _{peut prendre} des fonctions réelles n _.(r) propor-tionnelles à _{Pn.l.m(r):I: Pn.l. -m(r).}

(9) Si le _champ de radiofréquence comportait une _partie

homo-gène, il ne serait évidemment pas suffisant d’en tenir compte dans le cadre du _présent calcul en gardant simplement la contribution

du terme en _{1 / V :} la _{partie homogène} du _{champ agit} sur les atomes

non _pas comme une _{perturbation aléatoire,} mais certaine, et ne donne pas une relaxation de M (en d’autres termes, pour cette

partie homogène, le temps de corrélation serait infini, ce _qui exclut

qu’elle puisse satisfaire la condition de rétrécissement par le

mou-Les _{valeurs moyennes} sur l’ensemble des atomes

ayant ainsi été calculées dans les _{expressions (B. 8)} des coefficients R, il reste à effectuer _{l’intégration}

sur i des _{quantités obtenues, multipliées par} cos

_{[CO(t - 1’)].}

Un calcul élémentaire donne alors :

R+z ayant la même _{expression, après remplacement}

de .

921. 1

_{(p.,,,. >’par}

Q, - 1 (p.,,,. >. De _même, il vient :

[les

notations id _{(- mo) signifient qu’il} faut dans chacun des crochets _ajouter, ou _retrancher, la même expression où le _{signe de coo} a été

changé].

Les

expres-sions _complètes de _R,,, et _{R+ +} sont semblables à celle de _{R - ,} la seule différence étant que Q, , 1

{Jn,l,m >

est _{remplacé par D1z 1}

_{{Jn,l,m >}

dans

le _{premier cas, ( Q, - 1}

_{(p.,,,. >}

dans le second cas.

Les _égalités ainsi _{obtenues, reportées} dans _{(B. 7),} permettent donc de connaître exactement l’effet du champ de _{radiofréquence inhomogène. Nous pouvons} d’ailleurs à ce stade _préciser la condition de

rétré-cissement _{par le} mouvement _qui fournit une limite

de leur validité. La _{perturbation subie par} les atomes

possède en fait une infinité de _temps de corrélation

’qui sont les _temps de _{diffusion in,l,} de sorte _que la

condition de rétrécissement par le mouvement devient :

Les modes de diffusion de _{temps ’en,l} les _{plus longs}

sont les 3 modes _{dégénérés n = l =1, m = 1, 0, -} 1 vement). La façon correcte de tenir _compte de la _{partie homogène} du _champ de _{radiofréquence} est de la traiter à part de la

partie inhomogène, et d’écrire directement sous la forme

dM/dt = _yM x _B(t) l’évolution _{correspondante} de M (c’est bien ce _qui a été fait au § A. 2 où, de plus, ont été discutées les conditions dans lesquelles la _{partie homogène} ne modifie pas la relaxation

(cf. Appendice) ; par suite, (B. 23a) se réduit à :

comme :

(et des _égalités semblables _{pour les} autres compo-santes de _Qi), on voit que tous les _{coefficients R}

satisfont :

L’hypothèse du rétrécissement _par le mouvement

entraîne donc que les probabilités de relaxation sont

faibles devant

_I/’rl,l’

B.3 DISCUSSION : PROPRIÉTÉS DE LA RELAXATION

RÉSONNANTE ANISOTROPE PRODUITE PAR UN CHAMP R. F.

INHOMOGÈNE. - Dans

(B.7), on _peut distinguer,

parmi les coefficients R, deux _types de coefficients de _{couplage :} ceux _qui donnent des termes

diago-naux de la matrice _(R), reliant _M+ à _{M+, Mz} à _MZ ou M- à _M-, et ceux _qui donnent des termes non

diagonaux couplant entre elles des _composantes différentes de M. Dans un _{champ magnétique}

sta-tique Bo, les _{fréquences propres} d’évolution de _M+, Mz et M- sont _{différentes ;} les termes non _diagonaux

sont non séculaires et leur effet est donc _{négligeable,}

sauf pour certaines valeurs de Bo (résonances) qui

seront discutées _plus bas _{(§ 3. b. f3).} Par _contre, les

termes _{diagonaux correspondent toujours (au} moins pour leur partie indépendante du temps) à des termes

séculaires ; c’est _pourquoi nous allons commencer

par les étudier.

B. 3 . a Termes diagonaux de la relaxation. -

Consi-dérons tout d’abord le terme de _couplage de _Mz avec

lui-même _{(relaxation longitudinale) ;} le terme

dia-gonal concernant _{M+ (relaxation transversale)} sera

étudié ensuite.

B . 3 . a . a Relaxation _{longitudinale.} - On voit

sur

la deuxième _{égalité (B.7) que} le coefficient du terme

de _couplage de _Mz avec lui-même est :

D’après (B. 22), ce terme _comprend deux _parties,

l’une _constante, l’autre oscillant à la _pulsation 2 m.

Seule la _première de ces deux _parties est en fait

importante, puisque les termes oscillants sont non

séculaires _lorsque m » R, condition _qui est

effecti-vement satisfaite _puisque co »

_{1 /i 1,1}

1

[cf.

(A.

1 5a)]

et

_{» R}

_{[cf. (B.25)].}

L’effet du terme _diagonal

(B.26) est donc de créer une relaxation

supplémen-taire, caractérisée par un _{temps T*} tel que :

avec :

On montre _{d’ailleurs,} en utilisant des modes de

diffusion réels

_[cf.

note

_{(8)] d.)ue :}

les _composantes sur Ox et _Oy de _{l’inhomogénéité} fl,(r) jouent donc un rôle _symétrique dans _Ti.

Les formules (B.27) et _(B.28) sont _{à comparer}

avec _{l’expression approchée (A. 6)} de _IITt. On remarque tout d’abord que, dans les deux cas, IIT,*

présente un _comportement résonnant au _voisinage

de _Wo = co ; la formule _{(B. 27) prévoit} d’ailleurs

également une résonance en _Wo = - w _(terme

anti-résonnant), ce qui n’est pas étonnant puisque nous avons _pris un _champ linéaire _{oscillant ; cependant,}

si _wo est _positif comme co, et si _{co, >}

_{lit 1) [cf.}

(A.

.15)],

on _{peut négliger} le terme antirésonnant dans le

cro-chet de _{(B. 27). L’expression} exacte de _{1 / Tl} ressemble alors nettement à _{l’expression approchée (A. 6).} En

effet, remplaçons dans _{(B. 27)} tous les _{temps par}

un seul _{temps de diffusion rd (rd} est _{par exemple} le temps tn,l associé aux modes n, 1, m dont les _poids

sont les _{plus grands) ;} il _apparaît alors _{l’expression :}

(l’intégrale étant étendue à toute la _cellule) et _{(B. 27)}

se réduit à _{(A. 6). Cependant,} l’intérêt de la formule

(B . 27) est de faire intervenir de façon exacte les différents _temps de corrélation de la _{perturbation (et}

nous verrons dans la _{partie expérimentale} que plu-sieurs d’entre eux _peuvent être nettement _visibles) en

donnant leurs _{poids, qui dépendent} de la carte du champ de _{radiofréquence} comme le montre _{(B. 28).}

Examinons de _{façon plus précise} comment les

variations _spatiales de _{Q, , (r)} affectent le _temps de

relaxation _Ti. La fonction _{Q 1 , (r) étant, d’après} les

équations de Maxwell, harmonique

(10) :

elle peut être _développée sous la forme :

(10) Nous supposons ici _qu’aucun des fils _{parcourus par} des

[nous

excluons ici le terme 1 = 0 qui correspondrait

à une partie homogène du _champ de _{radiofréquence ;}

cf. note

_(9)].

Il vient _{alors, d’après (B. 15) :}

L’intégrale de normalisation

_Qn"

est définie dans l’appendice

[éq. (II)].

Posons d’autre _{part :}

Pour _finir, il vient :

Notons que, si la carte du _{champ (c’est-à-dire} les

coefficients

_c"m)

est _modifiée, on _change bien sûr les

poids des modes associés à des valeurs différentes

de 1 ou de m, mais pas le poids relatif de tous les

modes ne différant _{que par} les valeurs de n. De plus,

les formules _{(B. 34) permettent} de savoir comment

varie _Ti en fonction du rayon Ro de la cellule, lorsque les _{coefficients c"m} sont fixés _{(c’est-à-dire pour} une

configuration donnée des fils créant le _champ RF inhomogène, et des intensités données _les

parcou-rant). A résonance _{(coo = co),} la contribution

_{(1 / T*),,@l@.}

de _chaque mode _{{ n, 1, m;} à la _probabilité de relaxa-tion est telle _{que :}

Par contre, loin de la résonance

_[j

_{W - Wo 1}

_{» 1],}

on a :

Si seul le mode le _plus bas ₍₁ = 1) _est pratiquement

présent, on a une _probabilité de relaxation

propor-tionnelle à

_Rô

à résonance, loin de la résonance

une relaxation _{indépendante} de _Ro. Dans le cas

opposé où la carte du _champ de _{radiofréquence} est

suffisamment _{complexe pour qu’apparaissent} des modes de diffusion de 1 élevés, la _probabilité de

relaxation varie très vite avec _Ro

[rappelons

_que

toute cette discussion _{suppose que Ro} ne _dépasse

pas le domaine où la condition (B. 23b) reste

satis-faite].

B. 3. a. _f3 Relaxation _{transversale ; déplacement} de

la _fréquence de résonance. - On voit

sur _{(B. 7)} que

le terme de

_couplage

de _M+ avec lui-même a _pour

coefficient :

RzZ est un coefficient réel, mais _{R + -} est en _général

complexe ; par suite, ce terme _correspond non

seulement _(pour sa _{partie réelle)} à une probabilité de

relaxation transversale _IIT2*, mais _{également (pour}

sa _{partie imaginaire)} à un déplacement de la

fré-quenee propr d’oscillation de M +’. Commençons

par l’étude de T2 ; nous avons :

où

_{RO ,}

est donné _{par les} termes constants de _(B.2I) [comme dans le § a _précédent, nous _négligeons

l’effet des termes oscillants dans la _{relaxation, qui}

sont non séculaires]. On remarque tout d’abord que seul le terme en IIT,* a un _comportement résonnant

lorsque coo - w, alors que

R,

est _{indépendant de (00 ;}

en _fait,

RI

reste _négligeable tant _{que co » 1 co - coo 1,}

1

et : .

ce qui signifie que la relaxation transversale est

deux fois _plus lente que la relaxation longitudinale.

Physiquement, ceci _peut se _{comprendre par} un

passage dans le référentiel tournant, où seules les deux _composantes transversales du _champ de

radio-fréquence deviennent _statiques, la _composante lon-gitudinale restant oscillante _{(ce qui permet} de _négliger

son _{effet) ;} les deux _{composantes statiques} contribuent

alors à la relaxation de _Mz, alors _qu’une seule d’entre elles _peut contribuer à la relaxation _{de la}

compo-sante _{Mx par exemple (OX} étant un axe du référentiel

tournant _{perpendiculaire} à _{OZ) :} la _{composante Qi} y

sur l’axe OY _{perpendiculaire} à OX. Par _suite, il

n’est pas étonnant que M., relaxe deux fois _plus vite que Mx.

Le terme en

R’

_correspond à ce que l’on nomme

souvent le terme _adiabatique dans la relaxation de la cohérence du _système. Pour un _{champ inhomogène}

statique, ce terme _adiabatique serait de l’ordre de (

DfJ.. > ’rd

[comme

le montre _{(B.21) lorsqu’on y}

porte w =

0],

tandis _que 1 /Tl* serait de l’ordre

de (

1 -L

rd/[’

1 + _(mo

_{’rd)2] ;}

_{pour un champ} inho-mogène statique, le terme _adiabatique est donc presque toujours le terme dominant dans la _relaxation transversale (ce n’est _{qu’en champ} très faible, lorsque mo ’rd ;5 l, que le terme en _IIT* devient _comparable au terme _{adiabatique).} Par contre, pour un _champ

de _{radiofréquence inhomogène} comme celui étudié

ici, il en va autrement : le fait que la composante 5212

soit modulée réduit le terme _adiabatique dans un

facteur

_{(1 /(Ord) ’,}

alors que 1/Tl prend toujours une

valeur maximale de l’ordre _de

_{Q’ >}

_{ia ; par}

suite, c’est le terme _{adiabatique qui} est _{généralement}

pour un _{champ inhomogène statique,} le terme

adiabatique redevient dominant).

La _{partie imaginaire} de _R,- donne un

déplace-ment _ôco*/2 n de la fréquence d’évolution de _{M + :}

D’après (B. 22), on a _{(comme plus haut,} nous ne

gardons dans R que la partie constante des termes

résonnants pour mo ri m) :

Dans _{l’approximation} où tous les _temps de diffusion

sont _{remplacés par} un _{temps unique id,} cette

expres-sion devient _{simplement :}

La relaxation _produite par le champ de radiofré-quence inhomogène entraîne donc l’existence d’un

déplacement de la _fréquence de résonance de M. Ce

déplacement, nul pour Wo = _co,

peut devenir notable

lorsque coo e m ; dès que 1 Wo - (0 1 ’rd » 1, il est en

fait _{beaucoup plus important que l’élargissement} de la résonance lié au raccourcissement de _T2*; c’est

pourquoi il est aisément observable _{expérimentalement}

(ce qui n’est _pas le cas _{lorsque l’inhomogénéité} est statique, l’élargissement de la résonance _provenant du

terme _adiabatique de la relaxation transversale étant

toujours comparable, ou _supérieur, au _{déplacement).}

Contrairement à la _probabilité de relaxation _IIT*,

qui est due aux transitions réelles subies _par les

atomes sous l’effet du _{champ magnétique aléatoire,}

le _{déplacement bco* provient} des transitions vir-tuelles induites _par ce même _{champ [16] :} ces

tran-sitions virtuelles font apparaître un _couplage entre

-les deux niveaux non _perturbés des _{spins, d’énergies} ± _{hco012, couplage} qui change leurs _énergies.

Remarques. -

(i) Nous avons _négligé le terme

antirésonnant dans Im _{{ R + 1 pour} obtenir _{bwô .}

D’après (B.22), lorsque mo ri m et m »

_l/Ln",

ce

terme vaut :

ômg’ est _analogue au _déplacement de _{Bloch-Siegert [18]}

qui, pour un ensemble de _spins soumis à l’action d’un champ linéaire _homogène oscillant _{d’intensité - co, /y,}

vaut

_co’/4

_{coo. Cependant} la formule (B. 40) montre

que, pour un ensemble de _spins se déplaçant

rapide-ment dans un _champ oscillant _{inhomogène, àmg’} n’est pas simplement la moyenne sur la cellule des

dépla-cements de _{Bloch-Siegert} en _{chaque point r,} mais sa

moitié seulement.

ii) L’expression (B. 14) de la fonction F que nous

avons _prise n’est certainement pas valable _{pour les}

temps r très courts. Cette _{expression ayant} été obtenue à _partir de _{l’équation} de _{diffusion, elle suppose}

implicitement que i est _grand devant le _{temps Ait}

qui sépare deux collisions _cinétiques successives subies _par un atome donné

_(par

_exemple, pour un

gaz d’hélium à 1 torr, Ar,,, - 10-’ s

_[4]).

En effet, le

mouvement très _rapide des atomes entre deux

colli-sions n’obéit évidemment pas à l’équation de diffu-sion : ce n’est que sur des temps longs (r > ArJ

que ces mouvements _rapides se _{moyennent pour}

donner un _processus de diffusion. Tant que les

intégrales sur i _{qui figurent} dans les coefficients R

sont _peu sensibles aux valeurs de F _pour 1 5 !e’

les calculs que nous avons _{développés jusqu’ici} sont

valables ; c’est effectivement le cas _{lorsque OJo} Ai « 1.

Par contre, si _{OJo ;:}

_(Aïg)’

la relaxation devient sensible au mouvement _rapide des atomes et ses

caractéristiques peuvent être très différentes

_(Ar,,,

_joue le rôle d’un temps de corrélation court _{de la}

per-turbation). C’est ce _{qui explique pourquoi} les réfé-rences _[4] et _[5] donnent des _expressions de _T*,

valables en _champ très fort seulement, très différentes des nôtres _{(elles dépendent de Ar,,,,} mais pas de Ro). Bien _sûr, les deux théories doivent donner le même résultat dans le domaine intermédiaire

c’est bien ce _{que l’on constate,} du moins si on ne

retient de _{l’expression (B. 34)} de _IIT* que la

contri-bution du mode 1 = 1 (dont _{nous avons}

effective-ment noté _plus haut _qu’elle est _{indépendante} de _Ro

en _{champ fort).}

B. 3. b Termes non diagonaux. - Comme le

montre _{(B. 7),} l’effet de la relaxation _{produite par} le, champ de _{radiofréquence inhomogène} n’est pas simplement de modifier les _{caractéristiques} de l’évo-lution _{propre de chacune des composantes M+,}

M, et M- _prise isolément ; la relaxation introduit

également un couplage entre les différentes

compo-santes de M. _Jusqu’ici, nous n’avons étudié _que les

éléments _diagonaux de la matrice _{(R) qui, d’après}

(B . 9), caractérise l’effet de la relaxation sur M. Mais,

nous le verrons _{plus bas,} les éléments non _diagonaux

de _(R) peuvent avoir un effet important sur la

pola-risation M _lorsque le _{champ Bo passe par certaines}

valeurs _(coo = 0, _{co ou} 2 co). C’est pourquoi _nous

allons étudier de _{façon plus} détaillée la matrice _(R),

ce _qui nous _permettra de mieux _dégager les