HAL Id: hal-01717112
https://hal.archives-ouvertes.fr/hal-01717112
Submitted on 25 Feb 2018HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Public Domain
Extension non-linéaire des méthodes FFT accélérées par
gradient conjugué
Lionel Gelebart
To cite this version:
Lionel Gelebart. Extension non-linéaire des méthodes FFT accélérées par gradient conjugué. 11e colloque national en calcul des structures, CSMA, May 2013, Giens, France. �hal-01717112�
CSMA 2013
11e Colloque National en Calcul des Structures 13-17 Mai 2013
Extension non-linéaire des méthodes FFT accélérées par gradient
conjugué
Lionel GELEBART 1
1 CEA Saclay, DEN, DMN, SRMA, lionel.gelebart@cea fr
Résumé — Les méthodes de résolution par Transformée de Fourier Rapide permettent de résoudre
des problèmes mécaniques (ou thermiques, ou autre...) sur des cellules hétérogènes, discrétisées sous forme de grilles régulières 2D ou 3D, soumises à des conditions aux limites périodiques. Ces méthodes, hautement parallélisables, constituent une alternative performante à la méthode des éléments finis. Proposées dans les années 90, elles sont en plein essor tant du point de vue de leur application que de leur développement. Parmi les développements récents, on note la proposition d’accélérer la résolution itérative de problèmes linéaires par l’utilisation de solveurs itératifs type gradient conjugué (ou « solveurs itératifs de Krylov »). On propose ici d’étendre cette proposition à la résolution de problèmes non- linéaires [1].
Mots clés — matériaux hétérogènes, FFT, gradient conjugué, non-linéaire
1. Cas linéaire : méthode de base et accélération par gradient conjugué
Les méthodes FFT s’appuient sur une réécriture du problème mécanique linéaire à résoudre sur la cellule hétérogène (où est la déformation moyenne imposée), via l’introduction d’un milieu de référence homogène (de rigidité ) et la définition d’un champ de polarisation périodique , sous la forme suivante:
Avec l’opérateur de Green périodique associé au milieu de référence et * le produit de convolution. Ce système d’équations peut alors s’écrire (de manière plus formelle) sous la forme de l’équation dite de Lippmann-Schwinger dont la recherche de la solution peut être envisagée par un algorithme itératif de type « point fixe » (équation 1) (méthode de base proposée initialement par Moulinec en 1994[2]).
(1)
L’évaluation du terme de droite peut être réalisée par passage dans l’espace de Fourier dans lequel l’opérateur de Green est connu analytiquement et le produit de convolution transformé en un simple produit tensoriel. Cette méthode présente cependant deux inconvénients (figure 1). La vitesse de convergence dépend fortement du choix du milieu de référence (même si un choix optimal existe dans le cas très particulier où tous les constituants ont un comportement isotrope). La vitesse de convergence décroit fortement lorsque le contraste élastique entre les constituants augmente (la convergence n’étant plus assurée pour des contrastes infinis). Différentes méthodes ont alors été proposées (et certaines étendues au cadre non-linéaire) afin d’améliorer ce second point (notamment par Eyre en 1999[3], Michel en 2001 [4], Zeman [5] ainsi que Brisard en 2010 [6] et Monchiet en 2012 [7]). Parmi ces méthodes, la méthode accélérée par gradient conjugué (proposée simultanément
par Brisard et Zeman en 2010) consiste à considérer l’équation 1 comme un système linéaire (cette équation devant être vérifiée en tout point de la grille, on obtient un système linéaire à 6N inconnues, où N est le nombre de points de la grille). L’utilisation des solveurs de type gradient conjugué ne nécessitent toutefois pas de connaitre la matrice associée à ce système mais simplement de pouvoir évaluer la fonction en tout point. Ceci peut être réalisé comme précédemment par un passage dans l’espace de Fourier avec un coût numérique similaire à l’évaluation de utilisée dans la méthode de base (équation 1). Comparativement aux autres méthodes, on observe une moins grande sensibilité de la vitesse de convergence au choix du milieu de référence, ce qui semble plutôt favorable pour son utilisation lors de la résolution de problèmes non-linéaires.
Fig. 1. Comparaison des nombres d’itération à convergence de la méthode de base et de la méthode accélérée, en fonction du contraste élastique (matrice/inclusion sphérique), et en fonction du milieu de référence ( est un
paramètre multiplicatif du milieu de référence optimal de la méthode de base).
2. Extension aux problèmes non-linéaires
Pour simplifier la présentation on s’intéresse ici à des comportements élastiques non linéaires définis par (ou pour alléger l’écriture), l’algorithme proposé a toutefois été étendu à des comportements plus complexes (modèle de plasticité cristalline basé sur l’évolution des densités de dislocations, voir figure 6). De la même manière que précédemment le problème à résoudre s’écrit sous la forme où est ici une fonction non-linéaire de :
La résolution de ce problème non-linéaire peut donc être réalisée par l’algorithme de Newton-Raphson suivant :
(2- a)
(2-b)
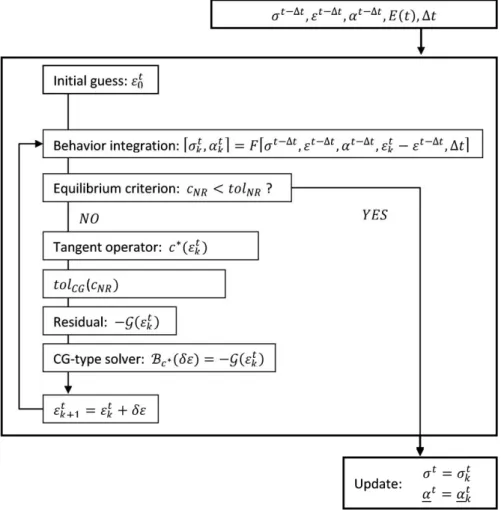
L’équation 2-a revient à résoudre le système linéaire avec , où est le comportement linéaire tangent ( ). Ce système linéaire peut donc être résolu par une méthode de gradient conjugué, avec une fonction équivalente à la fonction introduite précédemment, en remplaçant les propriétés élastiques du problème linéaire par les propriétés élastiques du matériau « tangent ». En pratique, le chargement appliqué (la déformation macroscopique) est discrétisé et l’algorithme proposé est relancé à chaque pas de temps avec une initialisation évaluée à partir des déformations obtenues aux pas de temps précédents. La figure 2
présente l’algorithme mis en place dans le code AMITEX_FFT décrit au paragraphe suivant. On remarquera ici qu’une dépendance de la tolérance du solveur linéaire itératif (bicgstab dans matlab) est ici proposée en fonction de la valeur du critère évaluée dans la boucle de Newton-Raphson. L’algorithme est également présenté avec une loi de comportement quelconque à variables internes .
Fig. 2. Description schématique de l’algorithme implémenté dans AMITEX_FFT.
3. AMITEX_FFT
Les développements réalisés autour des méthodes FFT au fil des applications sont capitalisés au sein du code AMITEX_FFT (Analyse de Microstructures Théoriques et eXpérimentales par FFT) comportant classiquement 3 grands blocs : le pré-traitement lié notamment à la génération de microstructures, le post-traitement et le bloc calcul lui-même. Les objectifs de ce code sont :
- D’avoir une base de développement permettant de tester simplement er rapidement différentes propositions d’évolution des méthodes FFT (comme dans ce papier),
- D’avoir un code suffisamment efficace pour traiter des problèmes réels : microstructures et lois de comportements complexes,
- De pouvoir tester et comparer l’efficacité de différents algorithmes sur un problème donné,
Pour ces différentes raisons, le code a été développé sous matlab (simplicité de programmation) et les fonctions les plus coûteuses (application du tenseur de Green, évaluation du comportement, évaluation
de critères de convergence) ont été programmées en fortran et parallélisées en mémoire partagée à l’aide d’openMP.
Actuellement, AMITEX_FFT peut prendre en charge des microstructures quelconques, avec des propriétés « matériau » constantes par domaine mais aussi continument variables, ainsi qu’une grande variété de chargements (contrainte imposée sur certaines composantes, déformation imposée sur les autres, en monotone ou en cyclique).
On notera que le code est interfacé avec les procédures utilisateurs umat utilisées dans ABAQUS (et CAST3M) pour l’intégration de la loi de comportement. Ainsi, tout type de comportement peut être pris en compte, dans la limite actuelle du cadre des petites déformations.
Concernant, les algorithmes, AMITEX_FFT propose actuellement en non-linéaire la méthode de base et la méthode accélérée par gradient conjugué (proposée ici). Il est prévu d’implémenter la méthode du Lagrangien Augmenté.
On notera enfin, que l’opérateur de Green filtré proposé par Brisard en 2012 a également été implémenté : il permet une diminution drastique des oscillations parasites associées aux méthodes FFT ainsi qu’une meilleure convergence des algorithmes, en revanche, la solution obtenue est alors sensible au choix du milieu de référence.
4. Application
4.1. Cas test : matrice élastique non-linéaire, inclusion sphérique linéaire
Le motif périodique élémentaire étudié est décrit par une inclusion sphérique élastique linéaire noyée dans une matrice élastique non-linéaire. Le comportement élastique non-linéaire n’est pas détaillé ici mais on retiendra que le module de compressibilité reste linéaire et que la non-linéarité porte sur le module de cisaillement de la matrice (la figure 3 représente le comportement de la matrice pour un chargement en traction axiale isochore, ainsi qu’un exemple de résultat de calcul). Les coefficients élastiques de l’inclusion sont associés aux coefficients élastiques initiaux de la matrice par le paramètre :
Les coefficients élastiques du milieu de référence sont choisis proportionnels aux coefficients optimums de la méthode de base du problème linéaire initial :
(3)
Les paramètres et permettront d’étudier la sensibilité de la convergence de l’algorithme au choix du milieu de référence et à la raideur de l’inclusion.
Le chargement imposé est une traction isochore
monotone avec une discrétisation en 10 pas.
Fig. 3. Comportement des deux phases (contrainte axiale en fonction de la déformation axiale) pour une sollicitation de traction isochore, à gauche. A droite, exemple de résultat obtenue sur la cellule matrice/inclusion
sphérique (contrainte axiale en Pa).
4.2. Sensibilité au milieu de référence (avec
=1)
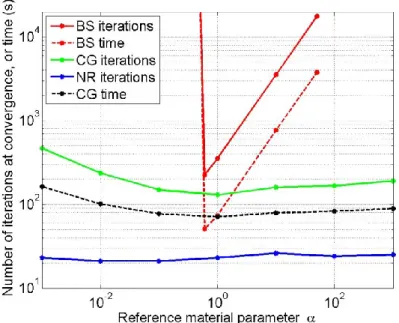
La figure 4 montre que, conformément au cas linéaire, la convergence de la méthode de base (BS, en rouge) est très fortement sensible au choix du milieu de référence pour supérieur à ~0.5 et ne converge pas pour des valeurs inférieures à ~0.5. Au contraire, la méthode accélérée par gradient conjugué présente un comportement très stable vis-à-vis du choix du milieu de référence pour une gamme de variant entre 0.1 et 1000. On remarquera que le nombre d’itérations de l’algorithme de Newton-Raphson est stable et que c’est bien le nombre total d’itérations dans les résolutions par gradient conjugué qui est sensible au choix du milieu de référence.
Fig. 4. Convergence des deux méthodes en fonction du choix du milieu de référence (équation 3). BS iterations et BS time : nombre total d’itération et temps de calcul pour le schéma de base. CG itérations, le nombre total d’évaluation de la fonction par l’algorithme itératif de gradient conjugué ; NR itérations, le nombre total
D’autres simulations [1], réalisées pour des valeurs de de 0.01 et 100 montrent qu’il existe dans ces trois cas une gamme variant entre 0.1 et 10 pour laquelle la convergence est très stable. Par ailleurs, dans ces trois cas, =1 correspond toujours à une valeur optimale.
4.3. Sensibilité au comportement de l’inclusion (avec
=1)
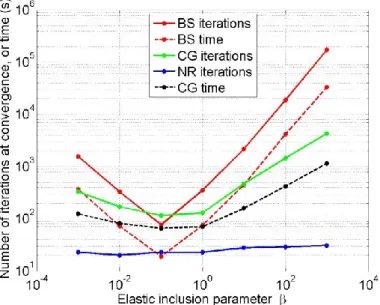
La figure 5 compare la convergence des deux méthodes en fonction de la raideur de l’inclusion. On peut constater que la sensibilité à la raideur de l’inclusion est bien mois grande pour la méthode accélérée par gradient conjuguée, le gain pouvant être très importants pour les forts contrastes. On remarquera cependant que pour les valeurs de autour de 0.1 la méthode de base semble plus efficace. En réalité, cette observation est probablement due à l’algorithme utilisée pour la résolution du problème linéaire : le gradient conjugué (« bicgstab » dans matlab) est introduit dans une boucle au sein de laquelle sa tolérance est diminuée si la solution obtenue ne vérifie pas le critère d’équilibre, ainsi, le nombre d’itération est toujours sur évalué.
Fig. 5. Convergence des deux méthodes en fonction du contraste élastique initial. On se reportera à la figure 4 pour le détail de la légende.
5. Conclusion et perspectives
La méthode accélérée par gradient conjuguée, récemment proposée en élasticité linéaire et pour un chargement en déformation imposée [5] [6], a été étendue au cas non-linéaire et à des chargements quelconques (non présenté dans ce papier, on se reportera à la présentation orale ou à [1], si accepté). L’application au cas matrice inclusion sphérique en élasticité non-linéaire montre les avantages de cette méthode par rapport au schéma de base : une moins grande sensibilité de la convergence au choix du milieu de référence ainsi qu’au contraste mécanique entre les phases. Des comparaisons plus poussées avec les différentes méthodes de la littérature sont envisagées sur des calculs plus réalistes (composites SiC/SiC [8], polycristaux, bétons…).
On insiste également sur la différence essentielle entre cette méthode et les méthodes itératives proposées jusqu’ici (schéma de base, accéléré de Eyre et Milton, Lagrangien Augmenté, accéléré de Monchiet et Bonnet) : le comportement n’est ici évalué que lors des itérations de newton Raphson et donc un nombre de fois bien moins important que dans les autres méthodes (surtout si le contraste mécanique est élevé). Ainsi, pour des lois de comportement numériquement lourdes, il est fort probable que cette méthode soit d’un intérêt majeur. Ce point sera discuté ultérieurement sur le cas de
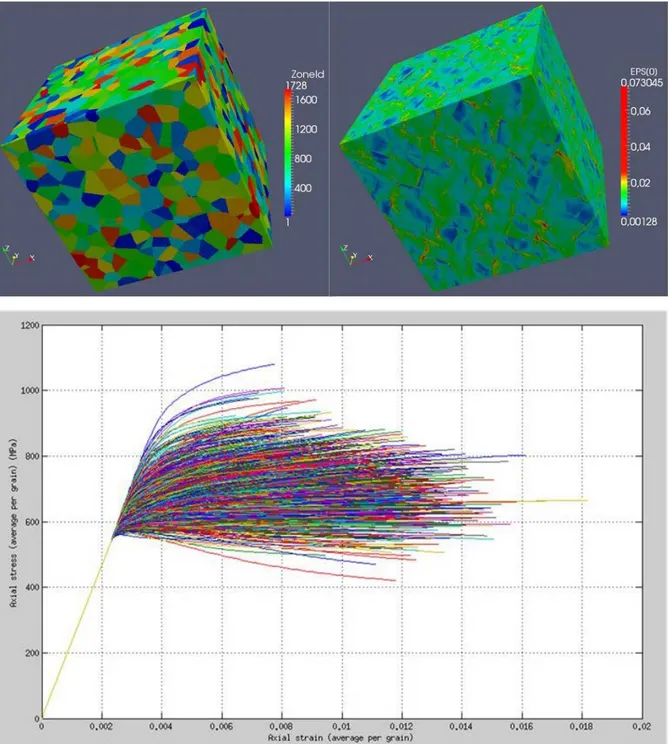
polycristaux pour lesquels la loi de comportement de plasticité cristallines (~50 variables internes) fondée sur les mécanismes physique de la déformation plastique [9] est très lourde à évaluer (figure 7).
Fig. 6. Exemple d’application pour un polycrystal constitué de 1728grains avec une résolution de 256x256x256 soumis à un chargement de traction uniaxiale (déformation axiale imposée). La loi de comportement prend en
compte ici la plasticité cristalline par le biais de 24 systèmes de glissement et de leurs densités de dislocations[9].
6. Références bibliographiques
[1] L. Gélébart and R. Mondon-Cancel, “Non-linear extension of fft-based methods accelerated by conjugate gradients to evaluate the mechanical behavior of composite materials,” Computational Material
Science, (accepté).
[2] H. Moulinec and P. Suquet, “A fast numerical-method for computing the linear and nonlinear mechanical-properties of composites,” Comptes Rendus De L Academie Des Sciences Serie Ii, vol. 318, no. 11, pp. 1417–1423, Jun. 1994.
[3] D. J. Eyre and G. W. Milton, “A fast numerical scheme for computing the response of composites using grid refinement,” European Physical Journal-applied Physics, vol. 6, no. 1, pp. 41–47, Apr. 1999.
[4] J. C. Michel, H. Moulinec, and P. Suquet, “A computational scheme for linear and non-linear composites with arbitrary phase contrast,” International Journal For Numerical Methods In Engineering, vol. 52, no. 1-2, pp. 139–158, Sep. 2001.
[5] J. Zeman, J. Vondrejc, J. Novak, and I. Marek, “Accelerating a fft-based solver for numerical homogenization of periodic media by conjugate gradients,” Journal of Computational Physics, vol. 229, no. 21, pp. 8065–8071, Oct. 2010.
[6] S. Brisard and L. Dormieux, “Fft-based methods for the mechanics of composites: A general variational framework,” Computational Materials Science, vol. 49, no. 3, pp. 663–671, Sep. 2010.
[7] V. Monchiet and G. Bonnet, “A polarization-based fft iterative scheme for computing the effective properties of elastic composites with arbitrary contrast,” International Journal For Numerical Methods In
Engineering, vol. 89, no. 11, pp. 1419–1436, Mar. 2012.
[8] L. Gélébart and C. Lestringant, “Estimation du comportement élastique de composites sic/sic par transformée de fourier rapide : calculs sur microstructures réelles (tomographie x) et simulées,” in 1ères
Journées Matériaux Numériques, Loches, france, 2013.
[9] L. Vincent, L. Gélébart, R. Dakhlaoui, and B. Marini, “Stress localization in bcc polycrystals and its implications on the probability of brittle fracture,” Materials Science and Engineering A-structural Materials