La Commande prédictive généralisée robustifiée par la paramétrisation de Youla

Université Mentouri, Constantine Département d’Electronique

MEMOIRE

Présenté pour l’obtention du diplôme de magister

en Electronique

THEME

La Commande Prédictive Généralisée robustifiée par

la paramétrisation de Youla

OPTION

Contrôle

Présenté Par

M

r

: FAS Mohamed Lamine

SOUTENU LE : Mercredi 30 / 11 / 2005

Devant le jury :

Président : Mr Belarbi Khaled Professeur Univ. CONSTANTINE Rapporteur: Mr Filali Salim M.C Univ. CONSTANTINE Examinateurs : Mr Charef Abdelfatah Professeur Univ. CONSTANTINE Mr Chaabi Abdelhafid M.C Univ. CONSTANTINE

Je dédie ce mémoire

A mes très chers parents qui ont tellement fait de sacrifices pour moi

A ma grande mère

A mes sœurs et mon frère Lotfi

A tous mes amis et tous qui me connaît

A tous mes collègues de l'option Contrôle des systèmes

Remerciements

Avant tous je voudrai remercier allah qui ma permis d'arriver la ou je suis, et de conclure ce modeste travail, et de remercier mes parents pour leur sacrifice, durant toute ma scolarité et soucieux de mon avenir.

Je voudrai témoigner de ma grande gratitude envers le Docteur S.Filali, qui m’a apporté toute l'aide dont j'avais besoin, et pour toutes les connaissances que j'ai pu acquérir sous sa direction, je voudrai tout spécialement le remercier pour sa patience.

Mes vifs remerciements vont au Professeur K.Belarbi pour ses précieux conseils.

Mes vifs remerciements vont aussi aux membres du jury qui ont accepté de juger ce modeste travail.

Que toutes les personnes, qui ont contribué de près ou de loin, directement ou indirectement à ce travail, trouvent ici le témoignage de ma profonde reconnaissance.

Enfin je ne pourrais terminer ces remerciement sans une pensée à l'ensemble des mes enseignants qui sont à l'origine de tout mon savoir.

Introduction générale

Généralités 01

But du projet 02

Organisation de la thèse 03

Chapitre 1 Synthèse et robustification du correcteur initial RST - GPC 1.1. Introduction 04

1.2. Modèle de base et le critère 04

1.3. Structure du prédicteur optimal 05

1.4. Loi de commande et le régulateur polynomial RST équivalent 07

1.4.1. Expression du critère sous forme matricielle 07

1.4.2. Loi de commande 08

1.4.3. Régulateur polynomial équivalent 08

1.5. Choix des paramètres du GPC 09

1.5.1. Choix de l'Horizon minimal N1 09

1.5.2. Choix de l'Horizon maximal N2 09

1.5.3. Choix de l'Horizon de commande Nu 09

1.5.4. Choix du coefficient de pondération λ 09

1.6. Fonction de transfert en boucle fermée 10

1.7. Relation entre le correcteur RST et les paramètres de GPC pour C = 1 et C ≠ 1 11

1.8. Rôle du polynôme C 13

1.8.1. Rôle de filtrage 14

1.8.2. Exemple 1 15

1.8.3. Rôle de robustification de la loi de commande 20

1.9. Méthodes de robustification 22

1.9.1. Paramétrisation de tous les régulateurs stabilisants amenant au même transfert entrée/sortie 23

1.9.2. Approche SGPC 25

1.9.3. Approche C – design 26

1.9.4. Approche Q – design 26

1.9.5. Exemple 2 27

1.10. Conclusion 30

Chapitre 2 Paramétrisation de Youla 2.1. Contexte 31

2.2. Historique 32

2.3. Définition 32

2.4. Propriétés 34

2.5. Interprétations pour un système stable 39

2.5.1. Correcteur à un degré de liberté 39

2.5.2. Correcteur à deux degrés de liberté 40

2.6. Spécifications en boucle fermée 43

2.6.1. Contrainte d’enveloppe temporelle 43

2.6.2. Critère sur la norme d’un transfert ou d’une matrice de transferts 43

2.6.3. Problème d’optimisation avec le paramètre de Youla 44

3.3. Spécifications de robustesse et performance nominale 50

3.3.1. Robustesse en stabilité - Spécifications fréquentielles 51

3.3.2. Performance nominale - Spécifications temporelles 54

3.4. Problème d’optimisation convexe 55

3.5 Résolution par programmation linéaire 57

3.5.1. Utilisation de la norme H∞ pour les spécifications fréquentielles 58

3.5.2. Respect d’un gabarit temporel 61

3.6. Approche d’un polynôme par un transfert 63

3.7. Conclusion 65

Chapitre 4 Application de la stratégie de robustification sur deux processus 4.1. Introduction 66

4.2. Paramètres de réglage utilisés par la méthode de robustification 66

4.2.1. Paramètres de l’optimisation utilisés 67

4.3. Exemple 1 : Application à la commande d'un moteur asynchrone 67

4.4. Exemple 2 : Application sur un système de pilotage automatique de l’angle d’assioette d’un avion de combat 73

4.5. Conclusion 80

Conclusion Générale 81

Annexe 82

Généralités

La commande prédictive a commencé à donner ses premiers résultats théoriques et pratiques à la fin des années 1970. Dans les années 1980, plusieurs méthodes basées sur les mêmes concepts prédictifs ont été développées. Parmi ces méthodes, on peut citer la commande prédictive généralisée (GPC), développée par David Clarke et son équipe, qui a été la technique la plus largement utilisée par la suite. Ces commandes prédictives possèdent toutes la même philosophie, à savoir créer un effet anticipatif, fondée sur les idées suivantes:

• Utilisation d’un modèle du système pour prédire la sortie du système dans le futur.

• Calcul de la suite de commandes à appliquer au système de façon à minimiser un critère à horizon fini portant sur l’écart entre la sortie prédite et la sortie future désirée.

• Application du premier élément de la suite de commandes calculées.

• Répétition du processus à la période d’échantillonnage suivante, selon le principe de l’horizon fuyant (receding control horizon).

En regardant de plus près les points communs de la commande prédictive, la Figure 1 présente un diagramme temporel illustrant le critère minimisé dans ce type de commande. La suite des commandes futures est calculée par minimisation d’un critère portant classiquement sur l’erreur entre la trajectoire de référence et la sortie prédite, et l’énergie utilisée pour y parvenir. On voit donc l’intérêt de ce type de commande quand la trajectoire à suivre par le système est connue à l’avance, comme par exemple, dans le cas des robots, des machines outils ou des processus chimiques.

Figure 1: Diagramme temporel du critère à minimiser

Le régulateur obtenu avec une commande prédictive peut être représenté comme indiqué Figure 2. On constate effectivement que la sortie prédite par le modèle du système est utilisée pour l’obtention de la commande. t t + j Passé Futur Sortie y Sortie prédite Commandes futures Consigne w

Figure 1.2 : Schéma bloc de la structure prédictive

Tous les développements des chapitres à venir se basent sur une approche discrète de la commande prédictive. Par ailleurs, même si les résultats méthodologiques obtenus s’avèrent généraux, on se focalisera essentiellement sur l’application à la Commande Prédictive Généralisée (GPC).

But du projet

Le but de notre travail est axé sur l'utilisation de la paramétrisation de Youla pour la robustification de la commande prédictive généralisée GPC.

La robustification d’une loi prédictive présentée dans ce travail a pour objectif la synthèse d’un correcteur invariant, permettant d’assurer la stabilité et la performance de la loi de commande face à des perturbations extérieures agissant sur le système.

La méthodologie est développée pour un système mono-entrée/mono-sortie. Son application à des systèmes multivariables est possible et donne une perspective pour la suite des travaux. Par ailleurs, on travaille avec des systèmes LTI (linéaires et invariants dans le temps) et discrets.

Organisation du mémoire

Ce travail est divisé en quatre chapitres. Le premier chapitre comporte quelques définitions et notions de base de la commande prédictive généralisée, et le correcteur RST polynomial résultant. Le deuxième chapitre développe la paramétrisation de Youla d’un point de vue général et conceptuel. Les deux chapitres précédents pour but de préciser les bases théoriques nécessaires pour la suite de ce mémoire. Le troisième chapitre est consacré à la méthodologie de robustification développée, utilisant

⊗

Processus Modèle Régulateur yˆ y w u + - Perturbations Calculateur

la paramétrisation de Youla. Le quatrième chapitre présente une application de la méthode de robustification sur deux processus. Voici, plus en détail, un résumé des aspects examinés dans chaque chapitre.

Chapitre 1

Ce chapitre présente la commande GPC. On introduit la structure du correcteur RST polynomial obtenu et les méthodes utilisées dans la littérature pour améliorer la robustesse de ce type de correcteur. L’influence du polynôme C modélisant le bruit au sein de la structure CARIMA est tout particulièrement analysée, afin de préciser la nécessité d’une robustification performante.

Chapitre 2

Ce chapitre présente la paramétrisation de Youla, ainsi que ses principes et propriétés. Chapitre 3

Ce chapitre développe la méthode proposée dans [1] pour la robustification d’une commande GPC. Le chapitre commence avec la paramétrisation de Youla d’un correcteur GPC. Ensuite, on définit les spécifications formulées pour robustifier un correcteur initial puis la transformation du problème en un problème d’optimisation convexe. L’étape suivante consiste à élaborer la méthode de résolution par programmation linéaire. Un correcteur satisfaisant les contraintes et minimisant le critère est obtenu. Enfin.

Chapitre 4

La méthodologie originale de robustification de la structure GPC proposée dans [1] est appliquée ici en simulation sur deux processus, La première concerne la commande de vitesse d’un moteur asynchrone, la deuxième est la commande de pilotage automatique de l’angle d’assiette d’un avion de combat. On a démontré comment utiliser les paramètres de Youla (Q1 et Q2) pour robustifié un correcteur on

s'appuyant sur les caractéristiques de robustesse désirés à partir des spécifications fréquentielles et temporelles de la boucle fermée.

1.1. Introduction

La commande prédictive généralisée (GPC) a été développée par David Clarke et al dans les années 80. C'est en 1985 que D.Clarke et al présente la première version de la Commande Prédictive Généralisée (GPC). Il faut attendre 1987, pour voir publier les premiers résultats obtenus par J.Richalet et al. Sur des systèmes électro-mécaniques rapides, tels que des commande de d'axes d'un robot.

La GPC est capable de contrôler des systèmes simples (du premier et deuxième ordre) elle peut même contrôler des systèmes complexes (processus avec retard assez long) à phase non minimale et instable, système linéaires et non linéaires, mono ou multivariables.

1.2.

Modèle de base et le critère

Toute commande prédictive nécessite la connaissance d'un modèle afin de prédire le comportement futur du système. Dans la commande GPC, le modèle classiquement utilisé est le modèle CARIMA

(Controlled AutoRegressive Integrated Moving Average), de la forme: [1]

( )

( ) ) ( ) ( ) 1 ( ) ( ) ( ₁ 1 1 1 _t q q C t u q B t y q A ₋ ξ − − − ∆ + − = ……….………...….……..…….. (1.1) ) (t

u , y

( )

t et ξ(t) sont respectivement l'entrée, la sortie et le signal de perturbation du système. )

(t

ξ est considéré aléatoire et de moyenne nulle. Le polynôme C modélise l'influence du bruit sur le système. L'introduction de ∆ (q-1_{) = 1 – q} -1 _{dans le modèle de bruit assure une action intégrale dans le}

correcteur et permet, donc, d'annuler toute erreur statique vis-à-vis d'une entrée ou d'une perturbation en échelon. L'utilisation de ce modèle de perturbation est en fait une conséquence da la présence de perturbations de charge en échelon dans de nombreux processus industriels, celui-ci garantissant donc un comportement avec une erreur statique nulle face aux perturbations considérées. Ceci est une conséquence directe du principe du modèle interne. Ce principe dit que pour contrôler un système avec des perturbations instables, la dynamique de la perturbation doit apparaître dans la dynamique du régulateur. Ce modèle CARIMA est représenté Figure 1.1.

) ( 1 1 − q A u(t) ) ( 1 1 − − _{B q} q y(t) d(t) + + ) ( ) ( 1 1 − − ∆ q q C

)

(t

ξ

⊗

A (q-1_{) , B (q}-1_{) et C (q}-1_{) sont des polynômes dans l'opérateur retard q}-1_{, définis par :} ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ + + + = + + + = + + + = − − − − − − − − − c c b b a a n n n n n n q c q c q C q b q b b q B q a q a q A ... ... 1 ) ( .. ... ) ( .... ... 1 ) ( 1 1 1 1 1 0 1 1 1 1 ……….……….…………..……….(1.2)

Où les degrés des polynômes A, B, et C sont respectivement na , nb , nc. La loi de commande GPC

est obtenue par minimisation d'un critère quadratique portant sur les erreurs futures avec un terme de pondération sur les incréments de commande :

∑

[

(

)

(

)

]

∑

(

)

= = − + ∆ + + − + = 2 1 1 2 2 1 ˆ N N j N j u j t u j t w j t y J λ ………...…….…………...(1.3) avec ∆u

(

t+ j

)

=0 pour j ≥ N_u

N1 et N2 définissent les horizons de prédiction sur la sortie et Nu l'horizon de prédiction sur la

commande. λ est un coefficient de pondération sur la commande, w représente la consigne à suivre, yˆ la prédiction de la sortie, obtenue à partir d'un prédicteur polynomial optimal, et u la commande.

1.3. Structure du prédicteur optimal

On s'intéresse ici à prédire la sortie du modèle à l'instant j , en fonction des données connues, c'est à dire, la sortie jusqu' à l'instant t et la commande jusqu'à l'instant t – 1. [9]

La valeur de la sortie à l'instant t + j est compte tenu de (1.1)

( ) ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( _{1 1} 1 1 1 j t q q A q C j t u q A q B j t y + ∆ + − + = + ₋− ₋ − ₋ ξ ………..…...……….(1.4) Le terme ( ) ) ( ) ( ) ( 1 1 1 j t q q A q C ₊ ∆ − − −

ξ peut être décomposé en une partie dépendante des valeurs futures de ξ et en une deuxième partie dépendante des valeurs passées de ξ , d'où la relation :

( ) ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( _{1 1} 1 1 1 1 t q q A q F j t q E j t u q A q B j t y j j ξ − − ξ − − − − ∆ + + + − + = + ………..………..(1.5)

Ej et Fj sont donnés par la résolution de l'équation diophantienne suivante :

_C(_q−1)_{= E} (_q−1)_A(_q−1)_∆(_q−1)_+q− _F (_q−1)

j j

j ……….………..……….(1.6)

Remarque :

De façon pratique, Ej et Fj peuvent être trouvés par division polynomiale, sous la forme :

degré de Ej (q) = j – 1 ) ( ) ( ) ( ) ( q A q q C q q E a c n j n j = _∆ − +

degré de Fj (q) = na

Les polynômes sont exprimés alors en puissances positives de q . Pour un polynôme P (q) de degré np ,

on notera donc :

_P(q−1₎ = _P(q)q−np

Ainsi, pour le polynôme Fj , il faut prendre en compte que si nc – j > na , Fj (q) a des coefficients avec

puissances négatives de q. On a : na j j q F q q F ( −1) = ( ) − _{degré de}

F

(

q

1

)

max(

n

,

n

j

)

c a j

=

−

−

Les valeurs passées de ξ(t) peuvent être déduites des valeurs passées connues à l’instant t : les mesures y jusqu'à l’instant t et les commandes u jusqu’à l’instant t –1 . A partir du modèle (1.1), on obtient : ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ₁ 1 1 1 1 − − − − − _{∆ − ∆ −} = q C t u q q B t y q q A t ξ ………..……….…..(1.7)

Soit en remplaçant dans (1.5) :

( 1) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( _{1 1} 1 1 1 1 1 1 1 − − + + + − + = + _{− −} − − − − − − − t u q C q A q B q F t y q C q F j t q E j t u q A q B j t y _j ξ j j ...(1.8)

En développant et avec (1.6) on obtient :

( 1) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ₁ 1 1 1 1 1 − + ∆ + + + = + ₋ − − − − − j t u q C q E q B j t q E t y q C q F j t y j j j ξ ……….…….(1.9)

Le terme qui multiplie la commande peut être divisé en deux parties ; de cette façon, on fait apparaître les commandes passées et futures. On a :

( 1) ( ) ( ) ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 1 j t q E t u q C q H j t u q G t y q C q F j t y + = j + _j ∆ + − + j ∆ − + _j − + − − − − − ξ …(1.10)

Gj et Hj sont donnés par la résolution de l’équation Diophantienne suivante :

_E (_q−1)_B(_q−1)_=G (_q−1)_C(_q−1)_+q− _H (_q−1) j j j j ………..……….…...(1.11) Remarque :

De façon pratique, Gj et Hj peuvent être trouvés par division polynomiale, sous la forme :

degré de Gj (q) = j – 1 degré de Hj (q) = nc – 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∆ = + − ) ( ) ( ) ( ) ( q A q q C q reste q F a c n j n j ) ( ) ( ) ( ) ( q C q B q E q q G j n n j b c− = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ = − ) ( ) ( ) ( ) ( q C q B q E q reste q H j n n j b c

Pour le polynôme Hj , il faut prendre en compte que si nb – 1 > nc – 1 , Hj (q) possède des coefficients

avec puissances négatives de q . On a : ₍ −1_{)= ( )} −nc+1

j

j q H q q

H degré de Hj (q-1) = max (nc –1 , nb –1 )

Le prédicteur optimal est enfin défini en considérant que la meilleure prédiction du bruit dans le futur est sa moyenne ( supposée nulle ici ), soit :

( 1) ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) / ( ˆ ₁ 1 1 1 1 − ∆ + − + ∆ + = + ₋ − − − − t u q C q H j t u q G t y q C q F t j t y j _j j …………...…...(1.12) Si C (q-1) = 1. On a : _yˆ(_{t+ j}/_t)_{= F} (_q−1)_y(_t)_+G (_q−1)_∆u(_{t+ j−}1)_+H (_q−1)_∆u(_t−1) j j j ………...……...(1.13)

1.4. Loi de commande et le régulateur polynomial RST équivalent

1. 4. 1. Expression du critère sous forme matricielle

La minimisation du critère nécessite la mise sous forme matricielle de l’équation de prédiction (1.12) et de la fonction de coût (1.3), soit respectivement : [3]

ŷ = G ũ + ) ( 1 1 − q C if y(t) + ( ) 1 1 − q C ih ∆ u(t - 1) et : J =[G ũ + ) ( 1 1 − q C if y(t) + ( ) 1 1 − q C ih ∆ u(t-1) – w ] T _{[G ũ +} ) ( 1 1 − q C if y(t) + ( ) 1 1 − q C ih ∆ u(t-1) – w ] + λ ũ T _ũ Avec : if = [

F

N₁

(

q

−1

)

⋅

⋅

⋅

F

N₂

(

q

−1

)

] T w = [w(t+N₁) ⋅ ⋅⋅ w(t+N₂)] T ih = [ ( 1) ( 1) 2 1 − − _{⋅ ⋅⋅ H q} q H_{N N} ] T ŷ = [ yˆ(t+N₁) ⋅ ⋅⋅ yˆ(t+N₂)] T _{ũ = [∆ ( ) ⋅ ⋅⋅ ∆ ( + −1)} u N t u t u ] T G = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ ⋅⋅ + − − + + + − 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 N N N N N N N N N N N N N N N u g g g g g g g = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + − − + − 1 1 1 1 2 2 2 1 1 1 1 u N N N N N N N N g g g g g g g

1.4.2. Loi de commande

La minimisation analytique du critère conduit à la séquence optimale de commandes futures [3], elle est obtenue par minimisation classique du critère précédent ∂J/∂u~ =0 :

ũ opt = - N [ ) ( 1 1 − q C if y(t) + ( ) 1 1 − q C ih ∆ u(t - 1) – w ] ……….….…...(1.14) avec : N = [ GT G + λ I ] _Nu –1 GT = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ T N T 1 u n n M

ũ opt = [ ∆u (t) opt . . . ∆u (t + Nu -1) opt ] T

De façon classique en commande prédictive, seule la première valeur de la séquence (1.14) est appliqué sur le système, selon le principe de l’horizon fuyant (receding horizon control) : uopt (t) = uopt (t - 1) - n₁T [ ) ( 1 1 − q C if y(t) + ( ) 1 1 − q C ih ∆ u (t - 1) – w ] ……….…(1.15)

1.4.3. Régulateur polynomial équivalent [1 , 3]

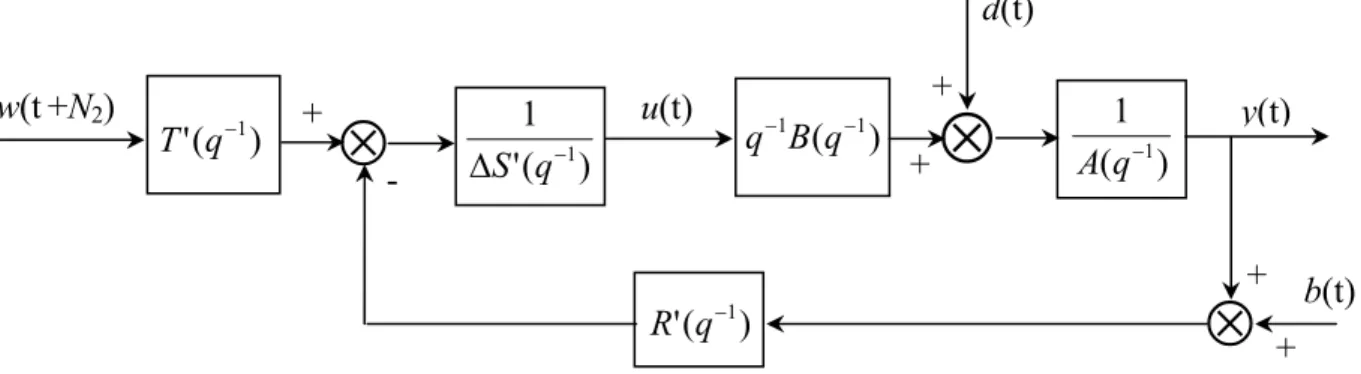
La structure polynomiale est introduite ici afin d’obtenir une relation entre la sortie y(t), la commande u(t) et la consigne w(t), et représentée sur le schéma de la Figure (1. 2 ) .

Reprenons l’équation fournissant la loi de commande optimale : ∆ uopt (t) = uopt (t) - uopt ( t -1) = - n₁T [

) ( 1 1 − q C if y(t) + ( ) 1 1 − q C ih ∆ u(t - 1) – w ] ⇒ ∆ u (t) [ C (q-1_{) +} T 1 n ih q-1 ] = - T 1 n if y(t) + C (q-1) T 1 n w ……….…...…..(1.16) Cette relation doit correspondre d’après la Figure (1. 2) à l’équation :

S (q-1) ∆ u (t) = - R (q-1) y (t) + T (q-1) w ( t + N2) ………..(1.17)

Ce qui fournit par identification les trois polynômes R , S et T constituant le régulateur linéaire équivalent : S (q-1) = C (q-1) + T 1 n ih q-1 degré de S (q-1) = max (nc , nb) R (q-1) = T 1 n if degré de R (q-1) = max (na , nc - N1) T (q-1) = C (q-1) T 1 n [ 2 1 2 1 1 1 L + + − + −N N _q N N q ] T degré de T (q-1) = nc + N2 – N1

Figure 1.2 : Structure du régulateur polynomial équivalent

Notons que T est volontairement choisi ici causal ( puissance de q-1 ), en considérant que le signal de consigne est w(t + N2) et non w(t).

1.5. Choix des paramètres du GPC

Ce paragraphe donne maintenant quelques règles pratiques pour guider le choix des quatre paramètres de l’algorithme GPC. [3]

1.5.1. Choix de l'Horizon minimal N1 :

Généralement N1 = 1, cependant si le retard K est connu avec exactitude, alors il sera mieux que

N1 ≥ K car sinon il y aura des calculs supplémentaires ou les sorties correspondantes ne peuvent être

affectées par la première commande u(t) . 1.5.2. Choix de l'Horizon maximal N2 :

En général N2 doit être plus grand que le degré du polynôme B (q-1) pour inclure toute réponse affectée

par la commande courante, cependant on suggère une valeur de N2 égale au temps de montée du

système.

1.5.3. Choix de l'Horizon de commande Nu :

Pour des systèmes simple (stables en boucle ouverte même avec retard et phase non minimale)

Nu =1 donne généralement une commande acceptable. Pour des systèmes complexes une valeur plus

élevée de Nu est mieux appropriée, Nu dans ce cas est au moins égale au nombre de pôles instable ou

mal amortis.

1.5.4. Choix du coefficient de pondération λ:

En général, le coefficient de pondération doit être augmenté si plus d'amortissement est jugé nécessaire et vice versa.

Donc, globalement, les paramètres peuvent être pris par défaut comme suit :

Régulateur polynomial équivalent

d(t) ) ( 1 1 − −_{B q} q ) (_q−1 R ) ( 1 1 − q A u(t) + + y(t) ) (_q−1 T +

⊗

- w(t +N2) ) ( 1 1 − ∆ qS

⊗

N1 = 1

N2 = temps de montée du système.

Nu = 1, ce qui pourrait donner des performances acceptables. Pour des applications aux

performances élevées, il est recommandable d'augmenter Nu .

1.6. Fonction de transfert en boucle fermée

[9]

Cette structure Figure 1.2 permet de déduire les fonctions de transfert entrée/sortie et perturbation/sortie, de façon à examiner l’influence du polynôme C sur les transferts en boucle fermée. A partir de (1.1) et (1.17), la boucle fermée est donnée par :

_A(_q−1)_∆(_q−1)_y

( )

_{t = B}(_q−1)_∆u(_{t −} 1) _{+ C} (_q−1)_ξ (_t) S (q-1) ∆ u ( t - 1) = T (q-1) w ( t + N2 –1 ) - R (q-1) y ( t - 1 ) On a arrive à : [ ( ) ( ) ( ) ( ) ( ) ]

( )

( ) ( ) ( 1) ( 1) ( 1) ( ) 2 1 1 1 1 1 1 1 1 _{S q q B q R q q yt B q T q wt N S q C q t} q A − − ∆ − + − − − = − − + − + − − ξ ...… (1.18)

On note que le polynôme caractéristique de la boucle fermée est : _{P (q}−1_{) = A(q}−1_)S(q−1_)∆(q−1_{)+ B(q}−1_)R(q−1_)q−1

c ………..………....(1.19)

En remplaçant R et S par les expressions trouvées en (1.16), on a : S (q-1) = C (q-1) + T 1 n ih q-1 =

∑

= − − − ₊ 2 1 1 1 1_{) ( )} ( N N i i i q q H q C α R (q-1) = T 1 n if =

∑

= − 2 1 ) ( 1 N N i i iF q α Avec : n = [ 1T

α

N1

α

N1+1 L

α

N2 ] AS∆+ BRq −1 = A₍

∑

= − + 2 1 1 N N i i iH q C α ) ∆ + B

∑

= 2 1 N N i i iF α q-1 = AC ∆ +

∑

= − + ∆ 2 1 1 ) ( N N i i i i q BF H A α = C _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ∆ + ∆

∑

= − 2 1 1 ) ( N N i i i i q C BF C H A A α A partir de (1.6) et (1.11), on trouve : i i i i i _{A Gq} C B F Bq C H A∆ _{= − − ∆}

Il vient en substituant dans la relation précédente :

⎪⎩ ⎪ ⎨ ⎧

_c N N i i i i B A G q CA A C BRq AS _⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ ∆ − + ∆ = + ∆

∑

= − − 2 1 1 1 _{α ( ) ………...……….………..(1.20)}

Où Ac dépend des paramètres de réglage N1 , N2 , Nu et λ .

La polynôme C se retrouve donc en facteur du polynôme caractéristique. En revenant sur le transfert en boucle fermée (1.18) et en décomposant T (q -1 ) en deux parties, on a :

_T(_q−1)_=C(_q−1) T 1 n 1 ( ) ( 1) 1 1 1 1 2 1 2+ − + − − − − ₌ ⎥⎦ ⎤ ⎢⎣ ⎡_q N N _q N N _{C q T q} L et la boucle fermée : ( ) ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ₁ 1 2 1 1 1 1 t q A q S N t w q A q T q B t y c c ξ − − − − − + − + = ………..………..(1.21)

On constate alors avec cette dernière expression que le transfert en boucle fermé entre l’entrée et la sortie n’est pas modifiée par le polynôme C. Il faut remarque que ce n’est vrai toutefois que dans le cas où le modèle est parfait.

D’autre part, C a une influence sur le transfert entre la perturbation et la sortie. Dans le cas de simulations, on utilise plutôt le transfert entre le signal de perturbation d(t) (indiqué Figure 1.2) et la sortie, la relation (1.21) devient :

( ) ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( _{1 1} 1 1 2 1 1 1 1 t d q A q C q S q N t w q A q T q B t y c c − − − − − − − _∆ + − + = ……….………...(1.22)

On remarque clairement ici le rôle d’observateur que joue le polynôme C. En fait, le polynôme caractéristique Pc , est décomposé en un polynôme de commande Ac et en un polynôme observateur

correspondant C.

1.7. Relation entre le correcteur RST et les paramètres de GPC pour C = 1 et C ≠ 1

A partir des équations Diophantiennes (1.6) et (1.11) pour C =1 et C ≠1, on déduit les résultats suivants : (On note " X' " les résultats pour C =1 et " X "les résultats pour C ≠1). [1]

Pour (1.6), on a respectivement : ⎪⎩ ⎪ ⎨ ⎧ + ∆ = + ∆ = − − − − − − − − − − − ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 1 1 ' 1 1 1 ' q F q q q A q E q C q F q q q A q E j j j j j j

En multipliant la deuxième par la première, il vient :

j _j j j j jA q F E A q F E C( ' ∆ + − ') = ∆ + − _{………...………(1.23)} d'où :

' ( ' ) j j j j j CF A q CE E F = + ∆ −

La substitution de cette dernière expression dans la relation définissant R fournit :

[

]

M A C R E CE q A CF E CE q A CF F R N N i N N i i i i i i i i i i i N N i i N N i i i ∆ + = − ∆ + = − ∆ + = =

∑

∑

∑

∑

= = = = ' ' ' ' ' 2 1 2 1 2 1 2 1 ) ( ) ( α α α α avec :

∑

= − ₌ 2 ₋ 1 ) ( ) ( 1 N ' N i i i i iq CE E q M α degré de ( −1)_{= −}1 c n q M ………..…...(1.24) L'équation (1.11) procure les expressions respectives :

⎪⎩ ⎪ ⎨ ⎧ + = + = − − − − − − − − − − − ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 1 ' 1 1 1 ' q H q q C q G q B q E q H q q G q B q E j j j j j j j j

En isolant Gj dans la première et en remplaçant dans la deuxième, il vient :

j _j j j j jB E B q H C q H E =( ' − − ') + − d'où : ' ( ' ) j j j j j H C Bq CE E H = − −

On remplace cette dernière expression dans la relation donnant S :

BM q CS E CE q B q q H C C q E CE Bq C H C q H C S N N i N N i i i i i i i i i i i N N i i N N i i 1 ' ' 1 1 ' 1 ' ' 1 2 1 2 1 2 1 2 1 ) ( )) ( ( − = = − − − = = − − = − − + = − − + = + =

∑

∑

∑

∑

α α α α Pour le polynôme T on a : _{T =CT}'

Le régulateur RST lorsque C ≠1 s'exprime donc en fonction de celui pour C =1 à l'aide des trois relations suivantes: C T T M A C R R BM q C S S ' ' 1 ' = ∆ + = − = − ………...……….…….(1.25)

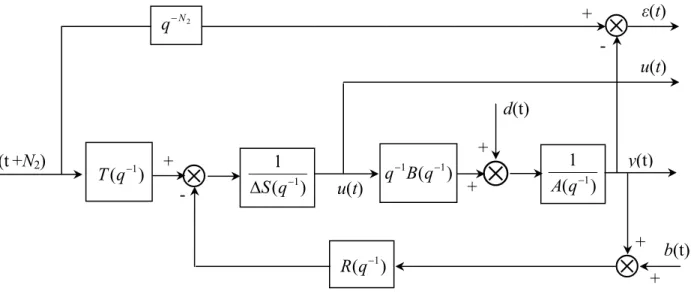
Avec ces expressions, on peut représenter le correcteur comme indiqué Figure 1.3 :

Figure 1.3 : Régulateur polynomial équivalent pour C ≠1, En fonction de celui obtenu avec C =1

La relation (1.25) permet de déduire la boucle fermée et de constater que le transfert entrée/sortie n’est pas modifié par C. En effet, en remplaçant R , S , T dans (1.18 ) , il vient :

[_A(_S'_C−q−1_BM)_∆+B(_R'_{C +∆AM})_q−1]_y(_t)_{= BT}'_Cw(_{t+N2 −}1)_+SCξ(_t) _C(_AS'_∆+BR'_q−1)_y(_t)_=BT'_Cw(_t+N2−1)_+SCξ(_t)

On obtient la fonction de transfert en boucle fermée :

( ) ) ( ) ( ) 1 ( ) ( ) ( ' ) ( ) ( ₁ 1 2 1 1 1 t q A q S N t w q A q T q B t y c c ξ − − − − − + − + =

On arrive à l’équation (1.21) de la boucle fermée.

1.8. Rôle du polynôme C

On peut analyser le rôle du polynôme C de deux façons. Dans le cas où l’on connaît le polynôme C du système ou une estimation du bruit agissant sur le système, le polynôme C sert à réaliser une prédiction optimale de la sortie dans le sens de la minimisation de la variance. Dans ce cas, on peut voir C comme un filtrage, permettant d’atténuer l’erreur de prédiction. D’autre part, on peut se servir

w(t+N2) T’ ' 1 S ∆ R' u(t) y(t) + + -+ A B q−1 + -A B q−1

⊗

⊗

⊗

C M∆

de C comme un paramètre du système servant à robustifier la commande. C peut être vu, alors, comme un observateur ou un préfiltrage du système. Dans ce cas, on perd l’optimalité dans la prédiction, mais on augmente la robustesse. [1]

1.8.1. Rôle de filtrage

L’expression de la prédiction à j pas (1.12) peut s’écrire : ) ( ) 1 ( ) ( ) 1 ( ) ( ) ( ) ( ) / ( ˆ 1 ₁ 1 1 − − − − _{+ ∆ + − +} ∆ − = + q C t u q H j t u G q C t y q F t j t y _{j j j}

C a un effet de filtrage sur " y " et " u ". On peut dire que la prédiction effectuée avec la méthode de GPC est réalisée à partir des données filtrées de " y " et " u ". De cette façon, on donne plus ou moins d’importance à une certaine bande du spectre des données. Si, par exemple, on sait que l’on a un bruit en haute fréquence ou que le modèle ne représente pas bien les dynamiques à haute fréquence, on accordera moins de confiance aux données mesurées à haute fréquence et, dans ce cas, on les fera intervenir dans la structure avec un poids moindre.

Considérons à titre d’exemple un système avec un bruit de mesure à haute fréquence v (t). On peut le représenter par le schéma de la Figure 1.4 :

Figure 1.4 : Système avec bruit à haute fréquence en sortie Ce système ce traduit par le modèle CARIMA de la Figure 1.5.

Figure 1.5 : Modèle CARIMA du Système avec bruit de mesure

⊗

E (q-1) ) ( ) ( 1 1 1 − − − q A q B q u(t) y(t) ym(t) v(t) vf(t) + + u(t)

⊗

q-1B(q-1) ) ( ) ( ) ( 1 1 1 − − − ∆ q q A q E ym(t) ξ(t) d(t) + + ( ) 1 1 − q A

1.8.2. Exemple 1

Dans cet exemple, on verra comment utilisé le polynôme C du modèle CARIMA pour robustifié un régulateur polynomial RST – GPC. On considère un système de premier ordre suivant :

s 1 1 G(s) + = ( s variable de Laplace) .

et un filtre pour le bruit blanc ξ (t) de fonction de transfert :

s 0 2 20 ) ( + = s F .

La discrétisation du système G(s) avec une période d’échantillonnage de 0,1 secondes, fournit la fonction de transfert discrète :

9048 , 0 1 0952 , 0 ) ( ) ( ) G( -1 1 ₁1 1 ₁ − − − − − − = = q q q A q B q q On obtient : A (q-1) = 1 – 0,9048 q-1 B (q-1) = 0,0952 E (q-1) = 1 – 0,1353 q-1

Un correcteur RST polynomial basé sur GPC est synthétisé avec C (q-1) = 1 et C (q-1) ≠ 1 , et les paramètres de réglage ci-dessous :

N1 = 1 , N2 = 5 , Nu = 1 et λ = 1 .

Ces paramètres de réglage de la structure CPC, ont été cherchés pour un comportement stable bien amorti.

• Les deux résultats obtenus pour les deux régulateurs sont : Pour C = 1, on obtient le régulateur polynomial R0S0T0 suivant :

R0 (q-1) = 3,4984 – 2,5812 q-1

S0 (q-1) = 1

T0 (q-1) = 0,2867 + 0,2402 q -1 + 0,1889 q -2 + 0,1321 q -3 + 0,0693 q -4

Pour C = A * E on obtient le régulateur polynomial R1S1T1 suivant :

R1(q-1) = 0,793 – 0,7175 q -1

S1 (q-1) = 1 – 0,7828 q -1 + 0,089 q –2

T1 (q-1) = 0,2867 – 0,0580 q -1 – 0,0259 q -2 – 0,0349 q –3 - 0,0449 q -4 – 0,0560 q -5 + 0,0085 q -6

• La fonction de transfert en boucle ouverte corrigée pour les deux cas donnés par les deux équations suivantes : 9048 , 0 905 , 1 1 0,2457 -0,333 ) (q S ) ( A ) ( R ) ( B ) ( G _{1 2} 2 1 1 -0 1 --1 0 -1 -1 1 -BO − − − − 1 − ₎ = _{− +} ( ∆ = q q q q q q q q q q

08053 , 0 8778 , 0 485 , 2 688 , 2 1 06831 , 0 0,07549 ) ( S ) ( A ) ( R ) ( B ) ( G _{1 2 3 4} 2 1 1 -1 1 --1 1 -1 -1 1 -BO ' − − − − − − 1 − _{− + − +} − = ) ( ∆ = q q q q q q q q q q q q q

• La fonction de transfert en boucle fermée corrigée pour les deux cas :

6591 , 0 1,572 -006597 , 0 01258 , 0 01798 , 0 02287 , 0 0,02729 ) ( R ) ( B ) ( S ) ( A ) ( T ) ( B ) ( H 5 4 3 8 7 6 5 4 1 -0 1 -1 -1 -0 1 --1 0 -1 -1 1 -BF − − − − − − − − 1 − + + + + + = + ) ( ∆ = q q q q q q q q q q q q q q q q q q 6591 , 0 1,572 -2420 , 0 4608 , 0 6586 , 0 8378 , 0 ) ( R ) ( B ) ( S ) ( A ) ( T ) ( B ) ( H' 5 4 3 8 7 6 5 4 1 -1 1 -1 -1 -1 1 --1 1 -1 -1 1 -BF − − − − − − − − 1 − + + + + + = + ) ( ∆ = q q q q q q q q q q q q q q q q q q

Les pôles de la boucle ouverte corrigée et la boucle fermée sont donnés par le Tableau 1.1 :

Boucle ouverte Boucle fermée C = 1 q1 = 1 q2 = 0,9048 q1 = 0 (triple) q2 = 0,7859 + 0,2037j q3 = 0,7859 – 0,2037j C = A * E q1 = 1 q2 = 0,9048 q3 = 0,6448 q4 = 0,1380 q1 = 0 (triple) q2 = 0,7859 + 0,2037j q3 = 0,7859 – 0,2037j

Tableau 1.1 : Les pôles de la boucle ouverte et fermée corrigées

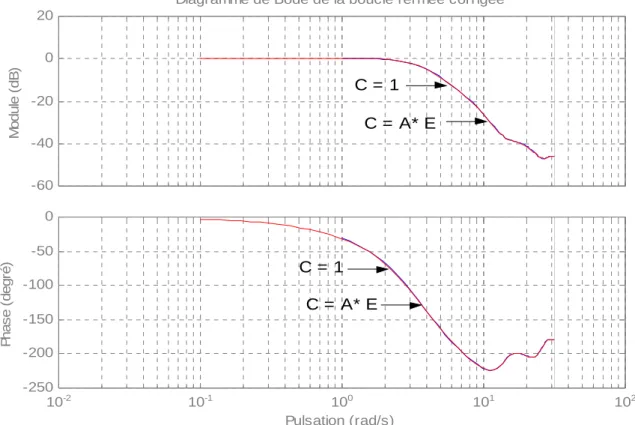
Les pôles de la boucle fermée sont les mêmes pour les deux cas, car la boucle fermée, dans le transfert ym / w, n’est pas modifiée par C. Comme indiqué le diagramme de Bode de la Figure 1.6.

Le diagramme de Bode de la boucle fermée ci-dessous montre que le transfert entrée/sortie n’est pas modifié par C.

-40 -20 0 20 40 60

Diagramme de Bode de la boucle ouverte corrigée

10-2 ₁₀-1 ₁₀0 ₁₀1 ₁₀2 -200 -150 -100 -50 Pulsation (rad/s) P has e ( degr é ) C = 1 C = A * E C = A * E C = 1 M o dul e ( d B ) -60 -40 -20 0 20

Diagramme de Bode de la boucle f ermée corrigée

M o dule ( d B ) 10-2 ₁₀-1 ₁₀0 ₁₀1 ₁₀2 -250 -200 -150 -100 -50 0 Pulsation (rad/s) P has e ( d egr é ) C = 1 C = A* E C = 1 C = A* E

Figure 1.6 : représentation fréquentielle de la boucle fermée pour C (q-1) = 1 et C (q-1) = A * E La représentation fréquentielle de la boucle ouverte corrigée représentée par le plan de Bode, Figure (1.7).

A partir du diagramme de Bode de la fonction de transfert en boucle ouverte corrigée, on constate que les marges de Gain et de Phase on été augmentées par le choix C = A * E par apport a C = 1. Ce que indique dans le Tableau 1.2.

Tableau 1.2 : Marge de Gain et de Phase de système corrigée

• La sensibilité directe et complémentaire

Soit un système contrôlé par un correcteur RST, représenter par la Figure ci-dessous :

Figure 1.8 : Système contrôler par RST avec C dans la boucle

La fonction de sensibilité direct et complémentaire du système représenté par la Figure 1.8, contrôlé par un correcteur RST, données par les deux fonctions de transferts suivantes : [20]

) ( ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 − − − − − _∆ = = q C q A q S q q A t v t y c f m d σ ………..……...………..(1.26) ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 − − − − − = = q C q A q R q B q t v t y c f c σ ………....(1.27) Avec :

y (t) : la sortie avant d'ajouter le bruit de mesure. ym (t) : la sortie après avoir ajouté le bruit de mesure .

vf (t) : bruit de mesure.

Marge de phase Marge de gain C =1 55,6 ° 16,3 dB C = A * E 61 ° 32,2 dB ) ( ) ( 1 1 − − q C q R w(t+N2)

⊗

⊗

⊗

T ' (q-1) ) ( ) ( 1 1 − − ∆ qS q C q-1 B (q-1) y(t) E (q-1) ) ( 1 1 − q A v(t) u(t) d(t) vf (t) ym(t) + + + + +

-- 3 5 - 3 0 - 2 5 - 2 0 - 1 5 - 1 0 - 5 0 5 F o n c t i o n d e s e n s i b i l i t é c o m p l é m e n t a i r e P u l s a t i o n ( r a d / s ) M odul e (d B ) 0 . 0 1 0 . 1 1 1 0 1 0 0 C = 1 C = A * E - 5 0 - 4 0 - 3 0 - 2 0 - 1 0 0 1 0 F o n c t i o n d e s e n s i b i l i t é d i r e c t e P u l s a t i o n ( r a d / s ) mo d u le ( d B ) 0 . 0 1 0 . 1 1 1 0 1 0 0 C = 1 C = A * E

Les représentations fréquentielles des transferts bruit vf / sortie ym (sensibilité direct) et bruit vf / sortie

y (sensibilité complémentaire) sont données dans les deux Figures 1.9 et 1.10.

Figure 1.9: Transfert bruit vf / sortie ym (fonction de sensibilité directe )

Figure 1.10: Transfert bruit vf / sortie y (fonction de sensibilité complémentaire)

A partir de Figure 1.9 on remarque que l'effet du bruit sur la sortie est plus important pour C ≠ 1 par apport à C = 1, notamment en basses fréquences. En hautes fréquences, l'effet du bruit sur la sortie et un peu plus faible pour les deux cas.

Les évolutions de la fonction de sensibilité complémentaire traduit avec C = A * E une augmentation de la robustesse face à des incertitudes en haute fréquence.

-20 0 20 40 60

Diagramme de Bode du correcteur

Mo du le ( d B ) 10-2 ₁₀-1 ₁₀0 ₁₀1 ₁₀2 -400 -300 -200 -100 0 Pulsation (rad/s) P h as e ( d e g ré ) C = 1 C = A * E C = 1 C = A * E

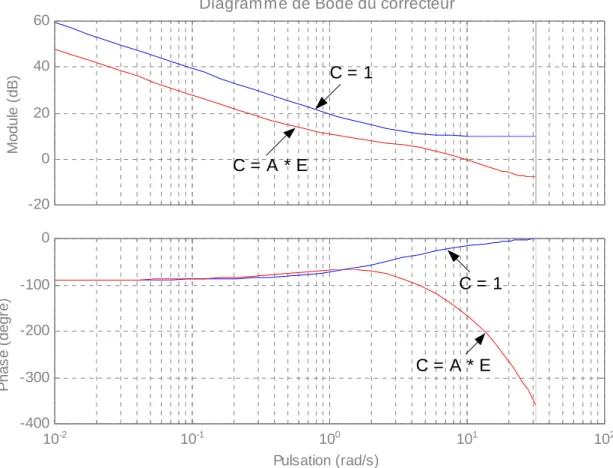
Considérons pour conclure l'allure fréquentielle du correcteur, traduite Figure 1.11 par le diagramme de Bode du rapport R / ∆ S :

Figure 1.11: Diagramme de Bode du correcteur

On constate que le caractère intégrateur du correcteur est conservé, on remarque également l'effet de filtrage à haute fréquence.

1.8.3. Rôle de robustification de la loi de commande 1.8.3.1 Robustesse en stabilité

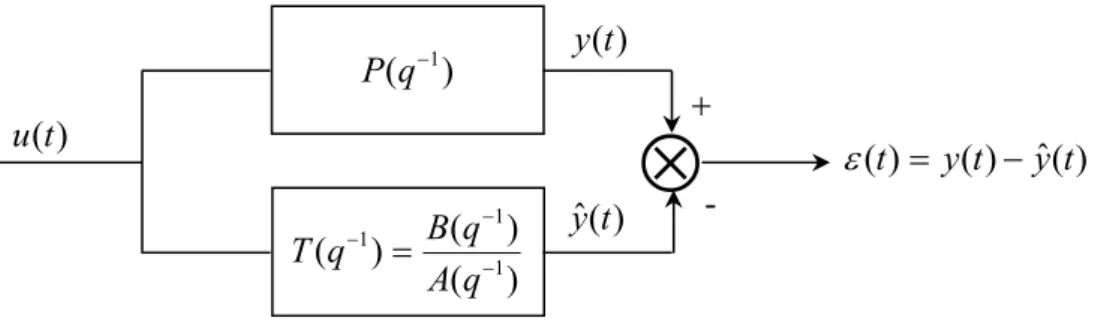
Considérons le système de la Figure 1.12.

Figure 1.12: Système bouclé pour analyse de la robustesse

On notera G(q-1) la transmittance modélisant le système et G0(q-1) le système réel. Le théorème 1.1

basé sur le critère de stabilité de Nyquist, donne les conditions de stabilité du système bouclé.

⊗

y(t) w(t) u(t) G0 (q-1) K (q-1₎ + -

Théorème 1.1

Le système de la Figure 1.12 est stable si : • Le système bouclé avec G(q -1_{) est stable.}

• G(q -1_{) et G}

0(q -1) ont le même nombre de pôles à l’extérieur du cercle unité.

• Si G0(q -1) a des pôles sur le cercle unité, ceux-ci sont aussi pôles de G(q -1).

• La condition suivante est satisfaite pour ∀ω∈[0,π].

| G(e-jω) K(e-jω) – G0(e-jω ) K(e-jω) | < | 1+ G(e-jω) K(e-jω) |……….…..……..……..(1.28)

Cette condition peut s’interpréter graphiquement sur le diagramme de Nyquist, comme montré Figure 1.13

Figure 1.13: Interprétation de la condition de robustesse en stabilité

La stabilité est garantie si, pour tout point du lieu de Nyquist nominal G(e-jω) K(e-jω), le cercle de centre GK et de rayon | GK – G0K| ne contient pas le point (-1).

1.8.3.2. Condition de stabilité dans le cas du correcteur GPC

Appliquons la condition précédente relation (1.28) au système de la Figure 1.2. On a : ) ( ) ( ) ( ) ( ) ( 1 ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 − − − − − − − − − − − − − − − − − − ∆ + < ∆ − ∆ A q q S q q R q B q q S q q A q R q B q q S q q A q R q B q En considérant (1.19), il vient : c _Br q R q A q P q A q B q A q B = < − ₋− ₋ − ₋ − − ) ( ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 0 1 0 1 1 ………...…………...………...(1.29) plus la partie droite de l’inégalité sera grande, plus notre système sera robuste face aux incertitudes de modèle. Ce transfert est donc une marge de robustesse du système, que l’on va nommer Br .

En considérant la relation (1.20), Pc (q-1) = C (q-1) Ac (q-1) on obtient :

) ( ) ( ) ( ) ( ) ( ) ( ) ( 1 1 1 1 1 1 1 − − − − − − − = = q R q C q A q A q R q A q P B c c r ………..………...…..………....(1.30)

A et Ac sont fixés respectivement par le modèle et les paramètres de réglage de GPC ( N1 , N2 , Nu , λ) .

Il nous reste C pour augmenter la robustesse.

GK Re Im |GK-G0K| |1+GK| -1 •

-15 -10 -5 0 5 10 Marge de robustesse Br |( A c /A )( C /R )| = |B r| 0.1 0.01 1 10 100 C =1 C = A * E Pulsation (rad/s) Remarque :

En basses fréquences, cette quantité Br est égale au gain du modèle. En effet :

) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( ₁ A B R A T B R A C T B R A P_c = = =

Reprenons le système de l’exemple précédent et comparons maintenant les marges de robustesse Br

pour les deux cas C = 1 et C = A* E. Dans le deuxième cas, la marge de robustesse est plus grande, notamment à haute fréquence, comme illustré en Figure 1.14.

Figure 1.14 : Marges de robustesse Br pour C = 1 et C = A * E

Donc on peut conclure :

Le polynôme C peut être utilisé pour robustifier le régulateur, par exemple pour faire augmenter la taille de la plus grande incertitude additive admise sans perte de sensibilité. Cette robustification est en plus effectuée sans modification du transfert entrée / sortie de la boucle fermée.

1.9. Méthodes de robustification

Dans ce paragraphe, sont examinées trois approches développées dans la littérature, pour la robustification d’une commande GPC. Ces méthodes, ainsi que la méthode développée dans ce travail, sont des méthodes à deux étapes : dans une première étape, on cherche les paramètres GPC ( N1 , N2 ,

Nu et λ) conférant au système le comportement entrée/sortie désiré, et dans une deuxième étape, on

cherche à robustifier ce correcteur initial sans changement du comportement entrée/sortie fixé par l’étape initiale. On a vu, dans le paragraphe précédent, que le polynôme C permet de robustifier le correcteur initial sans changement du comportement entrée/sortie de la boucle fermée.

Ce comportement peut être généralisé à une classe de contrôleurs stabilisant le système. Avant d’aborder les différentes approches de robustification, la paramétrisation permettant de paramétrer cette classe de contrôleurs stabilisant le système est préalablement développée.

1.9.1 paramétrisation de tous les régulateurs stabilisants amenant au même transfert entrée/sortie

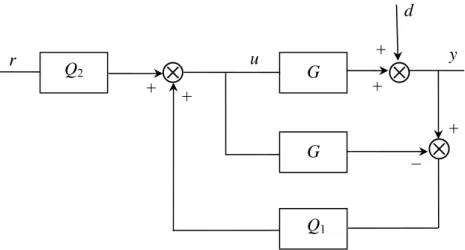
A partir d’un régulateur polynomial RST initial, stabilisant le système, représenté Figure 1.2, et que l’on notera R ' – S ' – T' , on paramètre la classe des régulateurs stabilisants, conférant au système bouclé le même transfert entrée/sortie que celui du régulateur initial, de la façon suivante : [19]

S = S َ' – q-1 B Q

R = Rَ' + ∆ A Q ………..……….(1.31) T = T َ'

Où Q peut être n’ importe quel transfert stable.

Cette paramétrisation (1.31) est représentée dans le Figure 1.15.

Figure 1.15 : Régulateur polynomial équivalent avec paramétrisation de tous les régulateurs stabilisants amenant au même transfert entrée/sortie

La démarche adoptée considère comme préalable un régulateur GPC initialement synthétisé ave C = 1. Si l’on note R ' – S’ – T’ ce régulateur obtenu lorsque C = 1 , le régulateur RST correspondant à C ≠ 1 est déduit par la paramétrisation précédente avec le paramètre

C M Q = .

Ainsi, à tout régulateur obtenu avec un polynôme C ≠ 1 , correspond un paramètre Q , mais l’inverse n’est pas vrai , car M dépend de C . On constate que si Q est stable, alors son numérateur et son dénominateur sont libres, de sorte que ce paramètre Q apporte un degré de liberté supplémentaire par rapport au polynôme C . T' ' 1 S ∆ u(t) y(t) + + -+ 0 0 1 A B q− w(t+N2) + -A B q−1 ∆ Q R'

⊗

⊗

⊗

Remarque :

La dénomination R – S – T des expressions (1.25) et (1.31) ne traduit pas en fait exactement le même concept. Dans (1.25), en effet, les grandeurs mentionnées traduisent des expressions polynomiales, alors que dans (1.31) interviennent des transferts, car Q est un transfert stable. Pour retrouver des expressions polynomiales, il est nécessaire de décomposer Q en numérateur et dénominateur, sous la forme : ' ' 1 ' T T Q R Q AQ Q R R Q S Q BQ q Q S S Q Q Q den den num den den den num den den num = = ∆ + = = − = = −

Ces expressions correspondent au schéma de la Figure 1.16

Figure 1.16 : Correcteur RST après paramétrisation Elles peuvent être représentées aussi comme indiqué Figure 1.17

Figure 1.17: Correcteur RST polynomial après paramétrisation On a donc : den num den num den Q T T AQ Q R R BQ q Q S S ' ' 1 ' = ∆ + = − = −

⊗

Q_denS ∆ T’ den Q R ) ( ) ( 1 1 1 − − − q A q B q -+ w(t+N2) u(t) y(t)

⊗

_∆1_S T'' Qden R -+ w(t+N2) u(t) y(t) ) ( ) ( 1 1 1 − − − q A q B q

Les degrés des polynômes R – S – T après la paramètrisation sont :

ƒ Degré de R (q-1) : max (n_R' +nQ_den,na +1+nQ_num) = na + max (nQ_den,1+nQ_num)

ƒ Degré de S (q-1) : max (n_S' +n_Qden,n_b+1+n_Qnum)= n_b+ max (n_Qden,1+n_Qnum) ƒ Degré de T (q-1) : nc +N2− N1+nQ_num

On utilisera par la suite la relation (1.31) . Bien que l’expression donnant un correcteur RST soit basée sur des transferts, le passage à un correcteur polynomial est trivial comme il vient d’être montré. 1.9.2 Approche SGPC

Cette approche est appelée Stable Generalized Predictive Control ( SGPC ) [19], car elle présente une méthode basée sur la GPC pour des systèmes instables et difficilement stabilisables avec GPC. La dernière phase de cette méthode réalise une robustification de la commande obtenue à partir du paramètre Q . Il s’agit de trouver le paramètre Q qui apporte le maximum de robustesse au régulateur, en minimisant une norme pondérée.

La relation (1.29), soit la marge de robustesse Br , peut ici s’exprimer en fonction du régulateur

R ' – S’ – T’ obtenu pour C = 1, et du paramètre Q compte tenu de (1.31) . Pour le régulateur R ' – S’ – T’ et à partir (1.20), on a : Ac = A ∆ S’ + q-1 B R’………..………..…....(1.32) La relation (1.24) devient : AQ R A AQ R B q BQ q S A AR BR q S A AR P B c r _+∆ ∆ + + − ∆ = + ∆ = = −1 ( ' −1 ) −1 ( ' ) _' 1 ...……...(1.33) U AQ R A A_c 1 1 ' _+∆ = =

Pour augmenter la robustesse, on doit trouver Q tel que 1/U soit maximisé. En introduisant une pondération W , cette relation devient :

min ( 1) ( 1) minsup ( ω) ( ω)

ω j j Q Q W q U q W e U e − − ∞ − − ₌ ………...…....(1.34) On doit alors trouver Q tel que la norme H∞ soit minimisée. W permet de pondérer de façon plus

importante les fréquences où les incertitudes du modèle sont les plus grandes. Pour A (q-1) est stable, une expression pour Qoptest donnée par :

₂ ' ' ) 1 ( ) 1 ( ) 1 ( ) 1 ( WA A A R A W WAR Qd Qn Q c c opt opt opt ∆ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = = ………....………....(1.35)

1.9.3 Approche C - design

Cette approche [1] propose un choix simple de C pour les cas où le système est stable. Ce choix procure une robustesse équivalente à celle obtenue par l’approche précédente.

Le polynôme C proposé est :

C(q−1) = A(q−1)(1−

β

q−1)N1−δ(P) ………...(1.36)

avec les paramètres GPC recommandés suivants :

i u n N N n N N 2 1 2 1 1 − = − + = ≥ = α λ pour : n = ordre du système ) ( ) ( ) ( 1 1 1 1 − − − − ∆ q q A q B q et où :

• β doit être approximativement de l’ordre du pôle dominant de A .

• δ(P)représente le degré du polynôme P. Ce polynôme correspond à la définition d’une trajectoire de référence issue de la consigne. Dans notre cas, il n’est pas utilisé, et donc δ(P)= 0 .

la relation (1.36) devient :

C(q−1)= A(q−1)(1−βq−1)N1………..……….……..…....(1.37)

Cette approche montre que l’on peut trouver des marges de robustesse égales ou supérieures à celles obtenues par la méthode SGPC.

1. 9. 4 Approche Q – design

Cette approche [2]vise à trouver un polynôme Q simple qui permette de robustifier la commande sans trop dégrader les performances du système. En effet, l’objectif des deux méthodes précédentes était de maximiser la robustesse, sans trop s’inquiéter de la perte de performances que cette robustification peut engendrer : AQ R R AR A AQ R A A R C A A B c c c r = = _+∆ = '_+∆ ' ' ' 1 Dans l’expression R C A A_c

, Ac et A sont fixés par les paramètres GPC choisis et le modèle. Il serait

possible de robustifier le système en modifiant C / R , mais le problème qui se pose est de ne pas pouvoir choisir librement la forme de C / R , car R dépend de C . Pour éviter ce problème, l’idée

consiste à choisir un paramètre Q permettant de découpler les deux parties, sous la forme : * * ' C M A R Q = ………...……….………..………..…....(1.38) On obtient alors : * * 1 1 * * ' ' ' ' ' ' ' ' C M AR A C M A R A R R AR A AQ R R AR A B c c c r _∆ + = ∆ + = ∆ + =

Dans cette expression, la première partie est donnée par les paramètres GPC choisis, et la deuxième partie est libre, car on peut fixer librement les valeurs de ∆ M * et C * .

Le choix proposé par la méthode considère

* * 1 1 C M ∆ +

sous la structure d’un filtre passe-haut, afin que le

système devienne ainsi moins sensible aux incertitudes à haute fréquence. La structure classiquement définie est la suivante :

₁ 1 2 2 1 1 ) ( ) 1 ( 1 * * 1 1 − − − + − − = ∆ + q q C M _{µ µ µ} µ avec : µ_{1 p}1 et 0 _p µ₂ ≤ µ₁ Cela implique : ⎩ ⎨ ⎧ − = − = ⇒ − − − = ∆ − − − 1 1 2 1 1 1 2 1 * * 1 ) 1 ( * * q C M q q C M µ µ µ µ _{………..………..…....(1.39)}

on replacer dans (1.33) on obtient :

₁ 1 2 2 1 1 ' _{(1 ) ( )} 1 − − − + − − = q q AR A B c r _{µ µ µ} µ

Pour régler les paramètres

µ

₁ et

µ

₂, on commence par

µ

₁=

µ

₂ et 0,6 ≤

µ

₁≤ 0,9 de façon à assurer largement la stabilité du système. Une fois la valeur de

µ

₁fixée, on diminue

µ

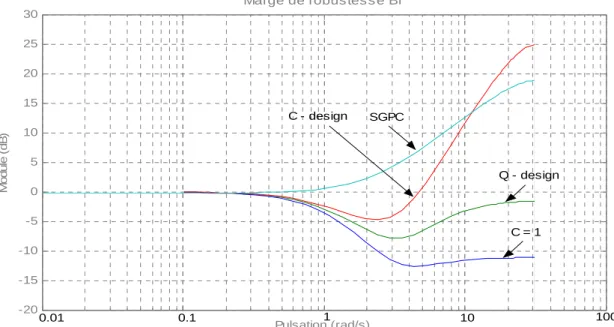
₂. Cela a pour résultat de diminuer l’effet passe-haut, sans toucher à la bande passante. On joue donc avec les dynamiques négligées autorisées à haute fréquence et la performance.

1.9.5 Exemple 2

Dans cet exemple, un premier régulateur RST- GPC est calculé avec C = 1 pour les paramètres N 1, N 2,

N u et λ conférant de bonnes propriétés, puis la commande est robustifiée, soit en modifiant le

polynôme C, soit à partir du transfert Q. Les trois méthodes présentées précédemment sont comparées, on prendre le système de l' exemple 1.