Description de la dynamique de la fission dans le formalisme de la méthode de la coordonnée génératrice dépendante du temps

HAL Id: tel-01559158

https://tel.archives-ouvertes.fr/tel-01559158

Submitted on 10 Jul 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires

Description de la dynamique de la fission dans le

formalisme de la méthode de la coordonnée génératrice

dépendante du temps

Marc Verrière

To cite this version:

Marc Verrière. Description de la dynamique de la fission dans le formalisme de la méthode de la coordonnée génératrice dépendante du temps. Physique Numérique [physics.comp-ph]. Université Paris-Saclay, 2017. Français. �NNT : 2017SACLS113�. �tel-01559158�

NNT : 2017SACLS113

Thèse de doctorat

de l’Université Paris-Saclay

préparée à l’Université Paris-Sud

Ecole doctorale n

₅₇₆

Particules, hadrons, énergie et noyau : instrumentation, imagerie,

cosmos et simulation (PHENIICS)

Spécialité de doctorat : Structure et réactions nucléaires

par

M. Marc Verrière

Description de la dynamique de la fission dans le formalisme de la

méthode de la coordonnée génératrice dépendante du temps

Thèse présentée et soutenue à l’IPN d’Orsay, le 16 mai 2017. Composition du Jury :

M. _{Peter Schuck} Directeur de recherche (Président du jury) Institut de Physique Nucléaire d’Orsay

M. _{Denis Lacroix} Directeur de recherche (Rapporteur) Institut de Physique Nucléaire d’Orsay

M. _{Luis Robledo} Professeur (Rapporteur) Universidad Autónoma de Madrid

M. _{Walid Younes} Directeur de recherche (Rapporteur) Lawrence Livermore National Laboratory

M. _{Michael Bender} Directeur de recherche (Examinateur) Institut de Physique Nucléaire de Lyon

Mme _{Beatriz Jurado} Chargée de recherche (Examinatrice) Centre d’Études Nucléaires de Bordeaux-Gradignan

Remerciements

Ces trois années ont été pour moi l’occasion de découvrir un nouveau do-maine : la physique nucléaire. Quelle a été ma déception quand je me suis rendu compte qu’en réalité, un physicien nucléaire n’est pas (dans le cas général, je ne souhaite pas trop m’avancer là-dessus) capable de désamorcer une bombe à anti-matière dans l’espace... Malgré cela, j’ai eu la chance d’avoir des collègues, amis et collègues-amis de grande qualité. Comme le titre de cette partie l’indique, je profite ici de quelques pages de ce manuscrit pour remercier les personnes qui ont, de manière directe ou indirecte, contribuées à son écriture (en espérant n’oublier personne ! !).

En tout premier lieu, je tiens à remercier Noël Dubray pour m’avoir encadré pendant mon stage et surtout tout au long de ces trois années avec un optimisme inébranlable. Tu as été pour moi bien plus qu’un encadrant : tu as réussi à me supporter et à répondre judicieusement aux nombreuses questions fondamentales que je me posais de logique, de mathématique, d’informatique, de philosophie, de musique et de linguistique (sauf pour albatros atroce qui ne fonctionne pas) ... ah, et de physique, aussi !

Je remercie aussi Pierre Dossantos-Uzarralde pour le soutien qu’il m’a apporté ces trois années de thèse et les trois précédentes à l’ENSIIE. Je te suis extrême-ment reconnaissant de m’avoir proposé cette thèse et m’avoir accompagné tout du long, bien que ce doctorat se soit transformé en doctorat en physique, t’empê-chant par la même occasion de contribuer à la hauteur de ce que tu aurais souhaité.

Bien évidemment, je souhaite aussi remercier David Regnier, mon voisin de bureau, pour m’avoir aidé, guidé, soutenu et conseillé depuis que je le connais. Je le remercie aussi pour les nombreuses discussions toutes plus intéressantes les unes que les autres.

Je remercie aussi mon jury pour avoir lu mon manuscrit et pour l’intérêt qu’ils y ont porté. Je tiens à remercier particulièrement Denis Lacroix, Luis Robledo et Walid Younes, qui ont acceptés d’être rapporteurs.

Je remercie Nathalie Pillet pour avoir accepté d’être la directrice officielle de cette thèse, et plus généralement le Service de Physique Nucléaire pour m’avoir accueilli à bras ouverts pendant ces trois ans. Je remercie en particulier Jean-Paul E. pour ses explications avisées, Sylvain, Julie-Fiona et mon dual Marc D. pour

avoir égayé les pauses, la Banda pour m’avoir fait découvrir la trompette et pour l’ensemble des sorties, François pour m’avoir supporté, Alix pour nos nombreuses discussions sur une vieille série anglaise. Je remercie Daniel pour m’avoir donné la vrai recette de la Tortilla (dédicacée, en plus). Merci aussi à Julien T. pour m’avoir appris à enlever le frein à main, à Paula pour son soutien anti-cigarettes et Gilbert B. pour ses blagues. Merci aussi à Guillaume H., Noël M. et Rémi pour leurs conseils de postdocs aguerris et leur bonnes idées. Je remercie aussi Amine pour avoir sifflé avec moi dans les rues de Bruxelles et Julien R. pour sa gen-tillesse et son soutien quand j’étais bloqué dans mon bureau entre midi et deux. Je remercie aussi Stéphane, Jean-Paul D., Pierre C., Pascal M. & R., Benjamin M., Jean-Michel, Olivier R., Véronique, Laurent, Gilbert G., Adeline E., Marta, Sophie, Benoît, Lucie, Caroline et Thomas. Je tiens à conclure ce paragraphe en remerciant Audrey pour ses concerts de qualités et Guillaume B. pour ces rendez-vous avortés passés minuit et pour m’avoir fait découvrir des coins perdus de Paris.

Merci à Nicolas Schunck et Patrick Talou pour m’avoir accueilli au LLNL et au LANL, et pour me permettre d’y retourner en tant que post-doctorant.

Merci à mes amis de longue date qui m’ont été d’un grand soutien même si je n’étais que très peu disponible, et aussi aux amis rencontrés pendant ces trois ans. Merci à ma famille pour m’avoir soutenu pendant mes études, de m’avoir permis d’en arriver là où j’en suis maintenant.

Pour conclure, je tiens à utiliser ce dernier paragraphe pour remercier Anastasia qui a toujours été présente pour moi dans les moments les plus difficiles de cette thèse.

Table des matières

Table des matières v

Table des figures ix

I Introduction 1

II Description microscopique du processus de fission à l’approxi-mation des recouvrements gaussiens 7

II.1 Présentation des méthodes utilisées . . . 8

II.1.1 Méthode de Hartree-Fock-Bogoliubov . . . 9

II.1.1.1 Approximation BCS . . . 10

II.1.1.2 Transformation de Bogoliubov . . . 12

II.1.1.3 Définition de l’état HFB . . . 14

II.1.1.4 Résolution de l’équation HFB . . . 18

II.1.1.5 Interaction nucléaire effective de Gogny . . . 23

II.1.2 Méthode de la coordonnée génératrice dépendante du temps à l’approximation des recouvrements gaussiens . . . 25

II.1.2.1 Approximation des recouvrements gaussiens . . . . 26

II.1.2.2 Dérivation du hamiltonien collectif . . . 28

II.2 Enchaînement des méthodes . . . 31

II.2.1 Calcul des surfaces d’énergie potentielle . . . 31

II.2.1.1 Base de particules à deux centres . . . 32

II.2.1.2 Calcul de surfaces d’énergie potentielle par propa-gation . . . 33

II.2.2 Description de la dynamique de la fission . . . 38

II.2.2.1 Discrétisation de l’espace des configurations . . . . 39

II.2.2.2 Détermination de l’évolution temporelle . . . 40

II.2.2.3 Extraction des fragmentations . . . 42

II.2.2.4 Flux et calcul des rendements . . . 45

II.2.3 Application à la description de la réaction239_{Pupn, fq . . . . 46}

II.2.3.2 Description de la dynamique . . . 48

II.2.3.3 Rendements en charge et en masse des fragments . 50 III Méthode de la coordonnée génératrice dépendante du temps 55 III.1 Description du système fissionnant en TDGCM . . . 56

III.1.1 État TDGCM . . . 57

III.1.1.1 Définition de l’état TDGCM . . . 57

III.1.1.2 Opérateurs collectifs . . . 59

III.1.1.3 Choix des coordonnées génératrices . . . 60

III.1.2 Espace collectif . . . 60

III.1.2.1 Signature de discontinuités par le semi-déphasage entre états HFB . . . 61

III.1.2.2 Nouvel algorithme de calcul de surfaces d’énergie potentielle . . . 63

III.1.3 Équation de Hill-Wheeler dépendante du temps . . . 70

III.2 Calcul des noyaux des recouvrements et du hamiltonien collectif . . 70

III.2.1 Calcul du noyau des recouvrements . . . 71

III.2.1.1 Méthode de Q. Haider et D. Gogny . . . 71

III.2.1.2 Cas de deux bases de particules différentes . . . 74

III.2.2 Calcul du noyau du hamiltonien collectif . . . 78

III.2.3 Calcul des termes centraux de l’interaction de Gogny dans une base d’oscillateur harmonique à deux centres . . . 82

III.2.3.1 Calcul du terme central de portée finie de l’inter-action . . . 88

III.2.3.2 Calcul du terme dépendant de la densité . . . 89

III.3 Résolution de l’équation de la TDGCM . . . 89

III.3.1 Expression dans une base d’états propres de la parité . . . . 90

III.3.2 Résolution par le calcul du propagateur . . . 92

III.3.3 Résolution par discrétisation en temps . . . 94

III.3.4 Absorption . . . 95

III.3.5 Calcul des observables . . . 97

IV Résultats 101 IV.1 Description 1D du système fissionnant 236_{U . . . 102}

IV.1.1 Surface d’énergie potentielle . . . 102

IV.1.2 Description de la dynamique . . . 109

IV.2 Description 1D du système fissionnant 240Pu . . . 112

IV.2.1 Surface d’énergie potentielle . . . 112

IV.2.2 Description de la dynamique . . . 120

IV.3 Description 2D du système fissionnant 240_{Pu . . . 124}

IV.3.2 Étude de l’appariement . . . 129

IV.3.3 Vers une description 2D de la dynamique de la fission avec la TDGCM . . . 132

V Conclusion 133 A Propriétés des fonctions de l’oscillateur harmonique 137 A.1 Solutions de l’oscillateur harmonique axial . . . 137

A.2 Fonctions de la base à deux centres . . . 138

A.3 Décomposition du produit de deux fonctions de la base à deux centres138 Cas de deux fonctions évaluées au même point de l’espace . . . 138

Cas de deux fonctions évaluées en des points différents de l’espace . 141 A.4 Action des opérateurs de symétrie sur les fonctions de la base à deux centres . . . 141

Opérateur parité ˆP . . . 142

Opérateur de renversement du sens du temps ˆT . . . 142

Opérateury-signature ˆRy . . . 143

Opérateury-simplexe ˆSy . . . 143

B Expression de l’énergie totale de liaison dans la base d’oscilla-teur à deux centres 145 B.1 Expression du hamiltonien nucléaire en seconde quantification . . . 145

B.2 Base biorthogonale . . . 147

B.3 Expression de la valeur moyenne du hamiltonien nucléaire dans la base à deux centres . . . 149

C Calcul des densités généralisées Sqq1 , Tqq1 et Yqq1 151 C.1 Calcul de Sqq1 . . . 151 C.2 Calcul de Yqq1 . . . 153 C.3 Calcul de Tqq1 . . . 154

D Expression du champ d’appariement généralisé 155 D.1 Cas λ “ 0 . . . 157

D.2 Cas λ “ 1 . . . 157

D.3 Cas λ “ ´1 . . . 158

Table des figures

I.1 Représentation du processus de fission en une succession d’étapes. . . . 2 I.2 Rendements en charge de la photofission du système fissionnant 234_U

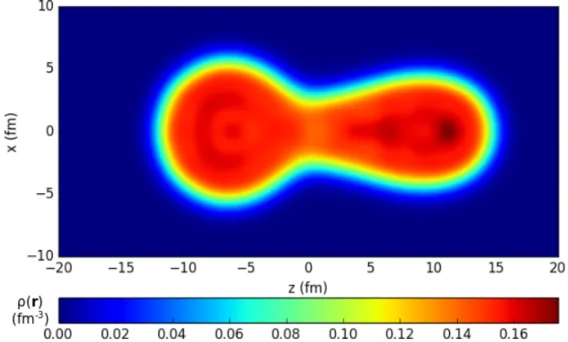
obtenus par une approche macroscopique-microscopique, P. Möller et al. [1]. . . 4 I.3 Charte des méthodes de description de la structure des noyaux [2]. . . . 5 II.1 Densité locale à un corps d’un état HFB obtenu avec une contrainte en

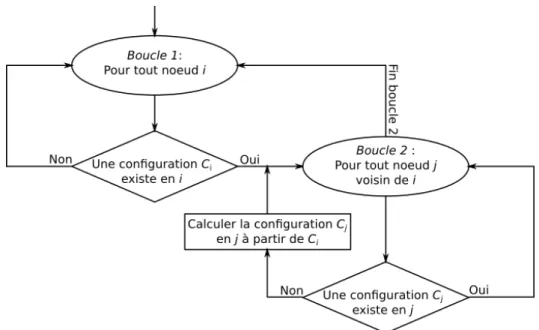
élongationq20 “252b. Le système décrit est 240Pu. . . 32 II.2 Algorithme “idéal” de propagation de proche en proche. . . 34 II.3 Algorithme de propagation de proche en proche tenant compte des

configurations non convergées. Le mécanisme de propagation est effec-tué en boucle continue. La validation d’un résultat est effeceffec-tuée parallè-lement pour chaque état calculé. Le calcul d’une configuration pour un jeu de contraintes donné et commençant par une configuration donnée n’est jamais répété. . . 35 II.4 Illustration de discontinuité en énergie obtenue dans le cas d’un calcul

contraint en élongation uniquement. L’abscisse correspond à la valeur moyenne de l’élongationq20, l’ordonnée à une observable non contrainte xQxxy et le niveau de rouge représente l’énergie, N. Dubray et al. [3]. . 36 II.5 Algorithme de propagation-rétropropagation (PR). Le mécanisme de

propagation-rétropropagation est effectué en boucle continue. La vali-dation d’un résultat est effectuée parallèlement pour chaque état cal-culé. Les parties rouges correspondent aux modifications apportées à II.3. 37 II.6 Exemple de discontinuité en densité entre deux états, obtenus pour du

240_{Pu, contraints en élongation avec q20 “ 269.375b (figure du haut)} etq1

20 “269.438b (figure du bas). Les valeurs moyennes de ˆQ30 et ˆQ40 associées sont respectivement q30 “ 41.904b3{2 et q301 “ 15.257b3{2, et q40 “105.387b2 etq1

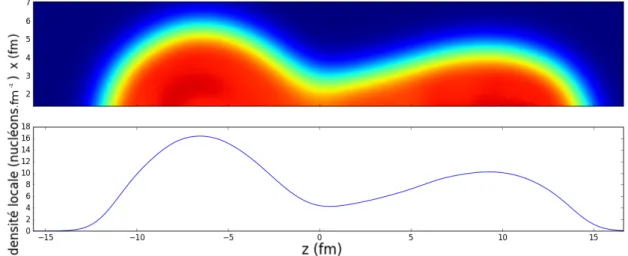
40“68.435b2. . . 39 II.7 Densité locale selon l’axe z (figure du bas) de l’état HFB présenté sur

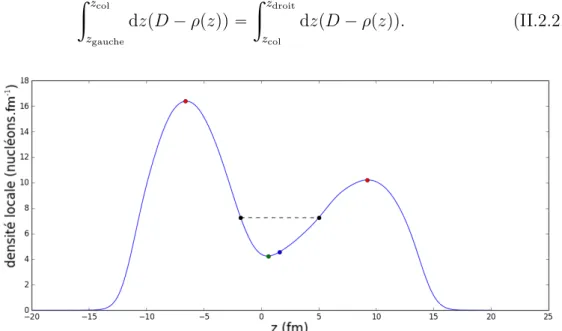
II.8 Calcul de la position du col de l’état HFB présenté dans les figures II.1 et II.7. . . 44 II.9 Surfaces d’énergie potentielle obtenues avec les interactions SkM* (a)

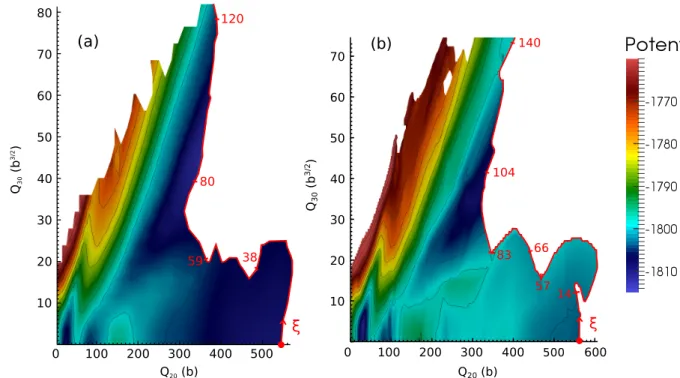
et D1S (b) en symétrie axiale. La ligne rouge sépare les configurations associées à une densité dans le col Qcol ą4 des autres. L’abscisse cur-viligne de cette ligne, ξ, démarre dans la vallée symétrique et longe la frontière. Les valeurs le long de cette ligne sont les masses des fragments. D. Regnier et al.[4] . . . 48 II.10 Propriétés statiques du système le long de la ligne de scission définie par

x ˆQcoly “4. La position sur cette frontière est représentée par l’abscisse curviligneξ en partant de la configuration associée à q30“0. L’abscisse de SkM* est décalée de 20 unités arbitraires pour que les principales structures coincident. L’énergie HFB est représentée en MeV et les va-leurs des moments multipolaires en puissances de barn. D. Regnier et al. [4]. . . 49 II.11 État TDGCM+GOA à t “ 0s (figure du haut) et à t “ 2.8.10´21_s

(figure du bas). L’échelle de couleur représente la densité de probabilité associée à l’état TDGCM+GOA. D. Regnier et al. [4]. . . 51 II.12 État TDGCM+GOA àt “ 5.5.10´21_{s (figure du haut) et àt “ 9.1.10}´21_s

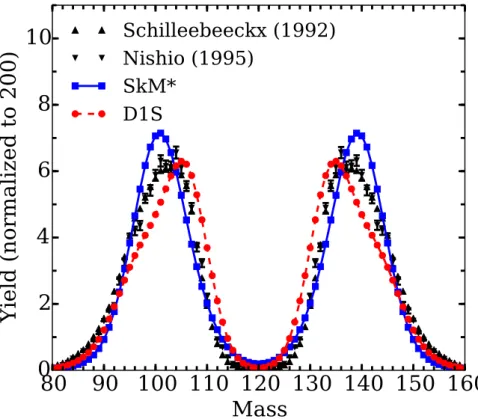
(figure du bas). L’échelle de couleur représente la densité de probabilité associée à l’état TDGCM+GOA. D. Regnier et al. [4]. . . 52 II.13 Rendements en masse avant émission neutron pour la réaction239_{Pupn, fq.}

Les calculs avec les interactions SkM* et D1S sont comparés à deux en-sembles de données expérimentales [5, 6]. Les incertitudes des données de Nishio et al. sont de plus affichées. D. Regnier et al. [4]. . . 53 II.14 Rendements en charge obtenus pour la réaction 239_{Pupn, fq. Les}

résul-tats obtenus avec les interactions SkM* (ligne bleue) et D1S (tirets rouges) sont comparés avec l’évaluation européenne JEFF-3.1 (tirets noirs). . . 54

III.1 Représentation du semi-déphasage entre |Φy et |Ψ1y d’une part et entre |Φy et |Ψ2y d’autre part sur le cercle trigonométrique. . . 64 III.2 Exemple dans l’espace des déformations pq20, q30q des voisinages entre

les points. Les arcs entre les points sont obtenus avec la triangulation de Delaunay. Les deux arcs rouges correspondent aux arcs éliminés car distM

Dpq, q1q ą dmaxD etdist M

Dpq1, q2q ą dmaxD . Les points voisins sont ceux reliés par un arc gris. . . 65

III.3 Illustration du raffinement de l’espace des déformations. L’échelle de couleurs correspond au semi-déphasage entre les voisins de Dpiq_,SDmax est la valeur maximum du semi-déphasage et les 9 disques noirs repré-sentent les points ajoutés à l’espace des déformations par l’algorithme PRN. Le trait noir représente une discontinuité. . . 65 III.4 Une triangulation de Delaunay est à nouveau effectuée à partir des

points de Dpi`1q _{pour déterminer les voisins de cet ensemble. . . . 66} III.5 Illustration de l’ajout d’une configuration associée aux déformations

¯

q “ q`q<sub>2</sub> 1 lorsque q et q1 <sub>sont de part et d’autre d’une discontinuité. Le</sub> semi-déphasage entre q et q1 <sub>est supposé être très élevé et est donc</sub> raf-finé. Un pointq est donc ajouté à D¯ pk`1q_{. Cependant, le semi-déphasage} entreq et q¯ 1 _{est très faible. . . . . 67} III.6 Illustration de l’ajout d’une configuration associée aux déformations

¯

q “ q`q₂ 1 lorsque q et q1 _{sont de part et d’autre d’une discontinuité.} Les points q, q1 _{et q correspondent à ceux de la figure III.5. L’abs-¯} cisse correspond aux contraintes en déformation et qxx correspond à une variable non contrainte qui signe la discontinuité. La ligne verte représente le chemin qui contient, pour chaque vecteur de l’espace des déformations, la configuration associée au minimum d’énergie. . . 67 III.7 Mécanisme de propagation-rétropropagation de proche en proche de

l’algorithme PRN. . . 68 III.8 Mécanisme de sélection et de lancement des calculs HFB de l’algorithme

PRN. . . 69 III.9 Mécanisme de validation d’un résultat HFB de l’algorithme PRN. . . . 69 III.10Illustration du mécanisme d’absorption présenté en [7,8] appliqué dans

une base de configurations non orthonormée. L’état TDGCM est repré-senté en rouge avant (figure du haut) et après absorption (figure du bas). 96 IV.1 Surface d’énergie potentielle du système composé 236_{U selon q20. . . 103} IV.2 Évolution de x ˆQ30y en fonction de q20 pour la surface d’énergie

poten-tielle de la figure IV.1. . . 104 IV.3 Évolution de x ˆQcoly en fonction de q20 pour la surface d’énergie

poten-tielle de la figure IV.1. . . 104 IV.4 Matrice des recouvrements N pq20, q1

20q du système composé 236U. . . 105 IV.5 Erreur relative εp¯q20q (IV.1.1.4) en fonction de q20¯ . . . 106 IV.6 Hamiltonien réduithpq20, q1

20q de236U. Les zones blanches correspondent à des couplages non calculés car les recouvrements correspondants sont inférieurs à 10´8_{. . . 107} IV.7 Hamiltonien collectif Hpq20, q1

IV.8 Probabilité Pt“0spqiq pour chaque i de l’état initial de la propagation en temps. L’abscisse correspond aux indices des configurations triés parq20 croissant, la courbe en gris représente la surface d’énergie potentielle de l’236_{U et la courbe en noir la probabilité Ppqiq d’être dans l’état}

|ΦHFBpqiqy. . . 109

IV.9 Comme figure IV.8 en t “ 3.10´21_{s. . . 111}

IV.10Comme figure IV.8 en t “ 1.10´20_{s. . . 111}

IV.11Surface d’énergie potentielle du240Pu. . . 113

IV.12Premiers moments multipolaires non contraints. . . 114

IV.13Semi-déphasage entre points voisins en fonction deq20. . . 115

IV.14Matrice des recouvrements N pq20, q1 20q du 240Pu. . . 116

IV.15Matrice des recouvrements NPpq20, q120q du 240Pu entre les états de l’en-semble des configurations (indicé par q20) et les états renversés par parité (indicé par q1 20). . . 117

IV.16Hamiltonien réduit hpq20, q1 20q du 240Pu. . . 118

IV.17Hamiltonien collectif Hpq20, q1 20q du 240Pu. . . 119

IV.18Surface d’énergie potentielle extrapolée à partir de la première barrière de potentiel, pour q20ă100b. . . 121

IV.19Norme au carré de f ptq en fonction des itérations en temps. . . 121

IV.20Probabilité pour chaque q20 de l’état |ΦHFBpq20qy dans |GCMpt “ 0qy. . 122

IV.21Probabilité pour chaque q20 de l’état |ΦHFBpq20qy dans |GCMpt “ tfinalqy. 122 IV.22Probabilité pour chaqueq20de l’état |ΦHFBpq20qy dans |GCMpt “ tfinalqy, agrandissement. . . 123

IV.23Présentation de l’ensemble de configurations 2D du système composé 240_{Pu. . . 125}

IV.24Matrice des recouvrements autour du fondamental HFB de l’ensemble de configurations 2D du système composé 240Pu . . . 126

IV.25Hamiltonien collectif autour du fondamental HFB de l’ensemble de configurations 2D du système composé 240Pu . . . 127

IV.26Matrice des recouvrements autour d’une discontinuité de l’ensemble de configurations 2D du système composé 240_{Pu . . . 128}

IV.27Énergie d’appariement en fonction des variables collectives pour le sys-tème 240Pu. . . 129

IV.28Gap énergétique autour du niveau de Fermi en fonction de la déforma-tion pour le système 240Pu. . . 130

IV.29Diagramme de corrélation entre l’énergie d’appariement et le gap pour les neutrons. . . 131

Chapitre I

Introduction

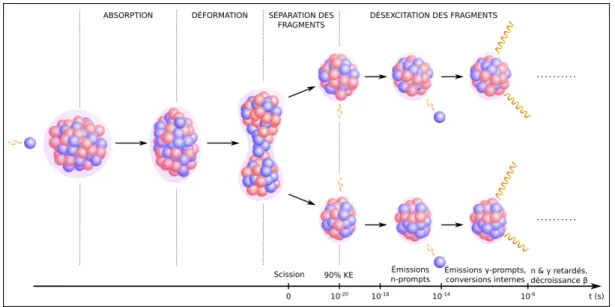
La fission est l’un des phénomènes les plus spectaculaires de la physique nu-cléaire au cours duquel, notamment, le noyau se sépare en deux fragments (voire davantage). Le processus de fission est particulièrement complexe car il fait interve-nir un nombre important de degrés de liberté non triviaux. Il résulte de différentes étapes qui sont schématisées sur la figure I.1 dans le cas d’une fission induite par neutron. On distingue quatre étapes majeures dans le cas d’une fission induite :

1. Le noyau est excité par une source extérieure. Dans le cas présent, un neu-tron est absorbé par le noyau pour former un système composé. La fission peut également être induite, par exemple, par l’absorption d’un photon vir-tuel. L’absorption de ce dernier conduit à une excitation de résonnances multipolaires, principalement la résonnance dipolaire géante. Il s’agit alors de photofission. Il est à noter que la photofission peut aussi être induite par le rayonnement Bremsstrahlung lors d’expériences avec des électrons.

2. Le système ainsi excité se déforme en s’allongeant jusqu’à des déformations extrêmes, ce qui conduit à la formation des pré-fragments.

3. Le système se sépare en plusieurs fragments primaires excités (en général deux). Cette étape est provoquée par l’interaction coulombienne qui domine complètement la partie nucléaire.

4. Les fragments se désexcitent, principalement en émettant des neutrons et des photons.

Il existe des modèles très élaborés pour décrire la plupart de ces différentes étapes, par exemple pour décrire la capture de la particule incidente par le noyau cible et l’émission des neutrons et des photons de radiation à partir du noyau excité (composé ou non). Cependant, la modélisation de la réorganisation des nucléons du système excité en deux (voire plus) fragments est encore un défi pour la théorie nucléaire. L’estimation des propriétés des fragments de fission avec la

Figure I.1 – Représentation du processus de fission en une succession d’étapes.

qualité requise pour les applications civiles et militaires repose toujours sur des modèles empiriques.

La composition des fragments en masse et en charge détermine les points de départ des chaînes de décroissance radioactives et leur énergie d’excitation déter-mine les caractéristiques de l’émission des neutrons-prompts et desγ-prompts. La principale difficulté est qu’un noyau fissionnant est un système ouvert qui évolue d’une configuration quasi-liée vers un continuum de configurations possibles sur le chemin de la fission, formant finalement des centaines de fragments différents avec de larges distributions en énergie cinétique, en énergie d’excitation et en moment angulaire [9, 10,11, 12].

Une des approches les plus avancées pour la modélisation de la fission nucléaire de basse énergie décrit le processus de fission via la résolution numérique des équa-tions de Langevin [13, 14]. Un sous-espace de variables collectives, restreint par la puissance de calcul disponible, est explicitement considéré. Le couplage aux de-grés de liberté internes est remplacé par un bain thermique. Une partie des effets d’origine quantique ne sont pas pris en compte dans cette approche. Une autre ap-proche propose de suivre l’évolution du système fissionnant en utilisant justement les outils de la mécanique quantique : il s’agit des approches microscopiques qui ont pour objectif de décrire le processus de fission à partir de la seule donnée de l’interaction entre nucléons. Ces méthodes nécessitent cependant une grande puis-sance de calcul. Il est à noter que des efforts sont faits pour inclure les processus dissipatifs même s’il reste encore beaucoup de progrès à faire.

après sa découverte, de nombreux développements expérimentaux et théoriques sont encore nécessaires pour comprendre son mécanisme. Les principales obser-vables qui permettent d’extraire des informations pertinentes sont, par exemple :

— les sections efficaces de réaction,

— les énergies et les multiplicités des neutrons prompts et des émissions γ, — les rendements des fragments de fission en masse et en charge ainsi que leurs

énergies cinétiques.

L’objectif de ce travail de thèse est de construire une approche microscopique pour décrire le chemin de fission jusqu’à la scission et donc l’évolution temporelle des déformations qui interviennent lors du processus de fission (deuxième étape sur la figure I.1), nous donnant accès a priori à une description microscopique des rendements de fission en masse, en charge, en énergie cinétique, et des multiplicités d’émissions de neutrons prompts.

La compréhension du phénomène de la fission nucléaire a énormément évo-lué depuis sa découverte, et la suite de cette introduction en présente un bref historique. Il a été découvert en 1938 par O. Hahn et F. Strassmann, lors d’une expérience consistant à bombarder un noyau d’uranium avec des neutrons. Cette expérience est interprétée la même année par L. Meitner et O. Frisch : le noyau d’uranium s’est séparé en deux fragments de tailles approximativement égales au cours de l’expérience, libérant une grande quantité d’énergie. Il s’agit de la pre-mière expérience de fission documentée [15,16]. Plus précisément, cette expérience a permis la découverte de la fission induite par neutron.

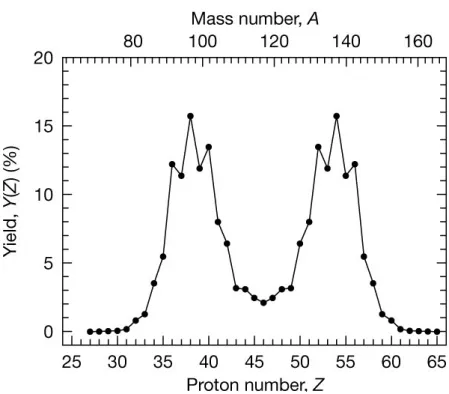
L’un des premiers modèles utilisés pour décrire la fission a été celui de la goutte liquide (Liquid Drop Model ou encore LDM), appliqué à la fission par A.N. Bohr et J.A. Wheeler [17]. Le LDM a été initialement développé par G. Gamow en 1934 [18] et a permis une des premières estimations de l’énergie totale de liaison en fonction du nombre de constituants dans le noyau. Ce modèle macroscopique représente le noyau par une goutte d’un liquide chargé (l’interaction de Van der Waals entre les molécules est remplacée par l’interaction nucléaire). Il approxime l’énergie totale de liaison des systèmes de nucléons par une formule qui dépend du nombre de pro-tons et de neutrons (Semi-Empirical Mass Formula) [19, 20]. Cependant, certains effets d’origine quantique ne sont pas pris en compte comme, par exemple, les fer-metures de couches ou encore l’appariement. En 1967, V. Strutinsky propose une méthode permettant d’ajouter ces effets microscopiques au modèle de la goutte liquide [21]. La dynamique de la fission peut ensuite être obtenue, par exemple, en résolvant l’équation de Langevin [13]. La figure I.2 présente un exemple de résultat de rendements en charge obtenus avec une approche de type LDM avec correction de Strutinsky.

À partir de 1970, une description microscopique du processus de fission com-mence à être envisagée. La description du processus de fission pour un noyau avec

Figure I.2 – Rendements en charge de la photofission du système fissionnant234U obtenus par une approche macroscopique-microscopique, P. Möller et al. [1].

A nucléons consiste alors à résoudre un problème à A corps quantique incluant sa dynamique qui contient de nombreux degrés de liberté non triviaux. La puis-sance de calcul nécessaire à l’obtention d’une telle description impose le recours à des approximations et notamment l’approximation de champ moyen, à l’origine développée pour la physique atomique. En effet, en 1928, D.R. Hartree propose une méthode de résolution approchée de l’équation de Schrödinger àA-corps [22], appelée alors méthode des champs autocohérents [23], plus connue aujourd’hui sous le nom de méthode de Hartree [24]. J.C. Slater et V.A. Fock [25] ajoutent en 1930 l’antisymétrisation de l’état quantique et élaborent ainsi la méthode de Hartree-Fock (HF). Cette méthode, appliquée à la description du noyau, consiste à remplacer les interactions entre les nucléons par un champ moyen et permet de transformer le problème à A-corps quantique en un ensemble de problèmes à une particule dans un champ moyen produit par les nucléons eux-mêmes. Elle est adaptée à la description de noyaux doublement magiques. Dans le cas de noyaux non doublement magiques, des corrélations d’appariement apparaissent : des paires de nucléons se forment de manière analogue aux paires de Cooper expliquant la supraconductivité dans les systèmes électroniques. La théorie BCS, qui a été in-troduite par J. Bardeen, L.N. Cooper et J.R. Schrieffer en 1957 pour décrire la supraconductivité [26], est appliquée à la description du noyau dès l’année

sui-vante par A.N. Bohr, B.R. Mottelson et D. Pines [27]. Une méthode plus générale permettant de prendre en compte les corrélations d’appariement au niveau du champ moyen est ensuite développée indépendamment par N.N. Bogoliubov et J.G. Valatin (méthode Hartree-Fock-Bogoliubov ou encore HFB) [28]. Cependant, ces méthodes ne permettent pas de décrire certaines corrélations de longue por-tée qui ont un rôle important dans le processus de fission, comme par exemple les corrélations collectives liées aux déformations du noyau. Des méthodes au-delà du champ moyen sont donc utilisées pour ajouter ces corrélations. La méthode de la coordonnée génératrice (GCM) est l’une de ces méthodes [29, 30] et permet l’inclusion explicite de corrélations collectives (déformations, rotations ou encore vibrations du noyau) [31]. Sa version dépendante du temps, la TDGCM, peut être utilisée pour décrire l’évolution temporelle des déformations du noyau au cours du processus de fission. L’équation principale de cette méthode, l’équation de Hill-Wheeler dépendante du temps (TD-HW), est une équation non-locale en espace. Le coût numérique élevé de sa résolution dans le cas de la description de la fission a conduit à recourir à l’approximation des recouvrements gaussiens (GOA) [32] dès les années 80. Elle permet de transformer TD-HW en une équation de type Schrö-dinger locale. Cependant, la GOA induit une erreur [33, 34] sur les prédictions d’observables telles que les rendements de fission, qui n’a, à notre connaissance, jamais été évaluée jusqu’à aujourd’hui.

Figure I.3 – Charte des méthodes de description de la structure des noyaux [2]. Le deuxième chapitre de ce manuscrit présente l’approche microscopique qui se

base sur la TDGCM+GOA utilisée jusqu’à présent pour déterminer les rendements de réactions de fission induite par neutrons. J’ai conçu la première implémentation du code utilisé pour résoudre l’équation de la TDGCM+GOA. Des extensions ont ensuite été ajoutées par D. Regnier. Dans la dernière partie du deuxième chapitre sont présentés les résultats obtenus avec la TDGCM+GOA. Le troisième chapitre introduit les développements effectués au cours de ce travail de thèse, consistant à décrire le processus de fission avec la TDGCM sans recourir à la GOA. Enfin, le quatrième chapitre expose les résultats obtenus avec cette méthode.

Chapitre II

Description microscopique du

processus de fission à

l’approximation des recouvrements

gaussiens

Pour décrire le processus de fission, nous utilisons une approche microscopique qui se décompose en deux étapes. La première consiste à déterminer un ensemble d’états nucléaires statiques qui représentent l’état du système fissionnant sous l’ac-tion de différentes contraintes en déformal’ac-tion. Ces dernières sont utilisées pour imposer à chaque état une forme spécifique, par exemple contrôlée par son élonga-tion et son asymétrie. La seconde étape consiste à modéliser l’évoluélonga-tion temporelle du système fissionnant en mélangeant les configurations, les poids de ce mélange étant dépendants du temps. Les observables sont ensuite calculées à partir des propriétés des configurations et des poids du mélange.

Ce chapitre se décompose en deux sections. La première présente la méthode de Hartree-Fock-Bogoliubov qui permet de déterminer les états nucléaires statiques, les configurations, ainsi que la méthode de la coordonnée génératrice dépendant du temps à l’approximation des recouvrements gaussiens (TDGCM+GOA).

La seconde section décrit l’ensemble des étapes permettant d’aboutir à une évaluation des observables associées au processus de fission, via le traitement de la dynamique. Les résultats obtenus lors de l’application de la TDGCM+GOA à la description de la fission induite par neutron de basse énergie sont ensuite discutés.

Sommaire du chapitre

II.1 Présentation des méthodes utilisées . . . 8

II.1.1 Méthode de Hartree-Fock-Bogoliubov . . . 9

II.1.1.1 Approximation BCS . . . 10

II.1.1.2 Transformation de Bogoliubov . . . 12

II.1.1.3 Définition de l’état HFB . . . 14

II.1.1.4 Résolution de l’équation HFB . . . 18

II.1.1.5 Interaction nucléaire effective de Gogny . . . 23

II.1.2 Méthode de la coordonnée génératrice dépendante du temps à l’approximation des recouvrements gaussiens . . . 25

II.1.2.1 Approximation des recouvrements gaussiens . . . . 26

II.1.2.2 Dérivation du hamiltonien collectif . . . 28

II.2 Enchaînement des méthodes . . . 31

II.2.1 Calcul des surfaces d’énergie potentielle . . . 31

II.2.1.1 Base de particules à deux centres . . . 32

II.2.1.2 Calcul de surfaces d’énergie potentielle par propa-gation . . . 33

II.2.2 Description de la dynamique de la fission . . . 38

II.2.2.1 Discrétisation de l’espace des configurations . . . . 39

II.2.2.2 Détermination de l’évolution temporelle . . . 40

II.2.2.3 Extraction des fragmentations . . . 42

II.2.2.4 Flux et calcul des rendements . . . 45

II.2.3 Application à la description de la réaction 239Pupn, fq . . . . 46

II.2.3.1 Surface d’énergie potentielle . . . 46

II.2.3.2 Description de la dynamique . . . 48 II.2.3.3 Rendements en charge et en masse des fragments . 50

II.1

Présentation des méthodes utilisées

Dans ce travail, nous nous intéressons principalement à la description de la fission des actinides, tels que le Pu, U, Th, Fm... Il s’agit de noyaux lourds qui comportent plus de 200 nucléons. La description microscopique de ce processus est donc un problème quantique à A particules en interaction pour A ą 200. Les méthodes de type ab-initio [35, 36] (en rouge sur la figure I.3) ou encore Configu-ration Interaction [37] (en vert sur la figure I.3) ne sont pas applicables à l’heure actuelle dans ce cas. Les méthodes de type fonctionnelle de la densité pour l’éner-gie (EDF) semblent être les plus adaptées et sont donc utilisées pour décrire le processus de fission. Son premier niveau d’implémentation est une approximation

de type champ moyen qui permet d’approcher la description d’un système nu-cléaire composé de A particules en interaction par un problème à A particules ou quasi-particules indépendantes dans un potentiel effectif, le champ moyen, qui représente en moyenne l’ensemble des interactions effectives entre les nucléons. Il existe plusieurs façons de mettre en œuvre cette approximation. Par exemple, le potentiel de Woods-Saxon correspond à une paramétrisation directe de ce champ moyen par une fonction [38]. Dans notre travail, nous utilisons une méthode dite auto-cohérente qui permet d’obtenir le champ moyen et l’état du système à partir de la seule donnée de l’interaction nucléon-nucléon, via un principe de minimisa-tion de l’énergie. La méthode de Hartree-Fock-Bogoliubov (HFB), qui est utilisée dans notre travail, est exposée dans la première partie de cette section.

La description de l’état nucléaire à l’approximation de champ moyen n’est en général pas suffisante. En effet, la prise en compte des corrélations de longue portée est capitale pour obtenir une description précise des états du noyau. On distingue essentiellement trois types de corrélations de longue portée :

— les corrélations d’appariement, qui se manifestent dans tous les noyaux, en dehors des noyaux doublement magiques, qui correspondent à une partie attractive de l’interaction nucléaire et s’exercent entre deux nucléons dans des états renversés du temps l’un de l’autre ;

— les corrélations collectives rotationnelles et vibrationnelles, qui peuvent être de petite ou de grande amplitude ;

— les corrélations particule-vibration qui décrivent le couplage entre les degrés de liberté collectifs et individuels.

Dans notre approche, les corrélations d’appariement sont déterminées directement par la méthode HFB. La méthode de la coordonnée génératrice (GCM), une mé-thode au-delà du champ moyen qui prend pour point de départ un ensemble d’états HFB, permet de décrire, par exemple, des oscillations collectives de grande am-plitude. Sa version dépendante du temps, la TDGCM, est utilisée dans ce travail pour décrire l’évolution temporelle du système fissionnant. La seconde partie de cette section présente cette méthode à l’approximation des recouvrements gaus-siens (TDGCM+GOA).

II.1.1

Méthode de Hartree-Fock-Bogoliubov

L’une des premières méthodes de champ moyen auto-cohérent a avoir été pro-posée est la méthode de Hartree-Fock [24]. Il s’agit d’une méthode variationnelle qui consiste à minimiser l’énergie totale de liaison d’un système de nucléons indé-pendants les uns des autres, décrit par un déterminant de Slater. Cela conduit à la résolution de l’équation [39] :

rhHF

oùhHF_{rρs désigne le hamiltonien à un corps de Hartree-Fock. Il décrit un système} de particules indépendantes soumises au champ moyen. ρ représente la densité à un corps de l’état de ce système. Cependant, dans ce formalisme, les corrélations d’appariement ne sont pas prises en compte. Ces corrélations correspondent à une partie attractive de l’interaction nucléaire et proviennent principalement du canal singulet-pair (S “ 0, T “ 1) qui agit entre deux nucléons dans des états renversés du temps et qui tend à les corréler par paires [40]. Dans le cas de noyaux dou-blement magiques, les effets liés à l’appariement sont inexistants. En revanche, ils contribuent de façon importante à la structure nucléaire lorsque le niveau de Fermi est situé en milieu de couche. C’est pourquoi la méthode Hartree-Fock est généra-lement utilisée avec l’approximation BCS, proposée par J. Bardeen, L.N. Cooper et J.R. Schrieffer en 1957 [26] qui permet de décrire des corrélations similaires dans la matière condensée supraconductrice.

II.1.1.1 Approximation BCS

On s’intéresse ici à des noyaux pair-pair invariants par renversement du sens du temps. Dans ce cas, la fonction d’onde de paire exacte, notée |Ψy, d’un noyau ayant N “ A{2 paires de nucléons a pour expression, en seconde quantification :

|Ψy “ ÿ i0ăi1㨨¨ăiN ´1 Ci0¨¨¨iN ´1ˆa : i0ˆa : s i0¨ ¨ ¨ˆa : iN ´1ˆa : Ğ iN ´1|0y. (II.1.1.2)

Dans cette expression, les opérateursˆa:

i sont des opérateurs de création de fermion dans l’état i, obtenus par exemple avec la méthode de Hartree-Fock. Ils vérifient les relations d’anticommutation de fermions :

tˆa: i, ˆa

:

ju “ tˆai, ˆaju “0 (II.1.1.3) tˆa:

i, ˆaju “ tˆai, ˆa :

ju “ δij, (II.1.1.4) avec ˆai l’opérateur d’annihilation de fermion dans l’état i et t ˆA, ˆBu ” ˆA ˆB ` ˆB ˆA l’anticommutateur de ˆA et ˆB. L’indice ¯i désigne l’état renversé du temps de i, |0y correspond au vide de particules et les Ci0¨¨¨iN ´1 sont des réels, ce qui peut être

démontré en utilisant l’invariance par renversement du sens du temps de |Ψy. Pour déterminer la fonction d’onde de paire approchée de la méthode BCS (état BCS, noté |BCSy), on suppose que les coefficients Ci0¨¨¨iN ´1 s’écrivent comme un produit :

Ci0¨¨¨iN ´1 « N pi0¨ ¨ ¨ piN ´1, (II.1.1.5)

où N est un facteur de normalisation et les pi sont des nombres réels. Ainsi, la fonction d’onde corrélée se réécrit de manière condensée sous la forme :

où l’opérateur ˆA: _{est un opérateur de création de paire de nucléons invariant par} renversement du temps : ˆ A: ” ÿ ią0 piˆa:iˆa : ¯_i. (II.1.1.7)

Le calcul des commutateurs entre les opérateurs ˆA et ˆA: _{permet de montrer qu’ils} vérifient en moyenne les relations de commutation entre bosons lorsqueř_ią0|pi|2 “ 1 :

x0|r ˆA, ˆA:_{s|0y “ 1 (II.1.1.8)} x0|r ˆA, ˆAs|0y “ x0|r ˆA:

, ˆA:

s|0y “ 0. (II.1.1.9)

On les appelle des opérateurs de quasi-bosons. On peut donc approcher l’état |Ψy par un état cohérent, qui est l’état BCS [41] :

|Ψy « |BCSy ” N eAˆ:

|0y. (II.1.1.10)

Comme les opérateurs ˆa:iˆa :

¯_i qui apparaissent dans ˆA: commutent entre eux, l’ex-ponentielle eAˆ:

qui apparait dans (II.1.1.10) se réécrit :

eAˆ: “exp ˜ ÿ ią0 piˆa: iˆa : ¯_i ¸ (II.1.1.11) “ź ią0 exp ´ piˆa: iˆa : ¯_i ¯ , (II.1.1.12)

et le développement en série entière de chaque exponentielle dans (II.1.1.12) donne :

eAˆ: “ ź ią0 p1 ` piˆa: iˆa : ¯_iq. (II.1.1.13)

L’état BCS peut donc s’écrire :

|BCSy “ Nź ią0 ´ 1 ` piˆa: iˆa : ¯<sub>i</sub> ¯ |0y, (II.1.1.14) ou encore : |BCSy “ź ią0 ´ ui` viˆa: iˆa : ¯_i ¯ |0y, (II.1.1.15)

où ui et vi sont des nombres réels entre 0 et 1, tels que pi “ vi

ui. Comme l’état

BCS est normé, la relation u2

i ` vi2 “ 1 est vérifiée. Les v2i sont appelés nombres d’occupation des orbitales.

Pour obtenir une description de l’appariement, la symétrie de conservation du nombre de particules a été brisée : l’état BCS n’a pas un nombre de particules défini. Sa dispersion en nombre de particules∆ ˆN2 _{est définie comme :}

∆ ˆN2 _{” xBCS| ˆN}2_{|BCSy ´ A, (II.1.1.16)} où ˆN désigne l’opérateur de nombre de particules dont l’expression est :

ˆ

N ” 2ÿ ią0

ˆa:

iˆai. (II.1.1.17) Cette dispersion s’exprime en fonction des nombres d’occupation de la manière suivante : ∆ ˆN2 “4 ÿ ią0 u2iv 2 i. (II.1.1.18) Remarquons par ailleurs que la dispersion en nombre de particules est nulle seule-ment dans le cas où les nombres d’occupation sont 0 ou 1. Ce cas limite est équi-valent à ne pas utiliser l’approximation BCS.

II.1.1.2 Transformation de Bogoliubov

La transformation de Bogoliubov permet de représenter un état BCS sous la forme d’un déterminant de Slater d’états de quasi-particules, et de générali-ser la méthode HF+BCS pour arriver à la méthode de Hartree-Fock-Bogoliubov (HFB) [39]. Cette transformation agit sur l’espace de Fock (antisymétrisé pour tenir compte du caractère fermionique des nucléons).

L’espace de Hilbert à une particule est muni d’une base orthonormale tˆa: i|0yu, où |0y représente le vide de particules et ˆa:

i est un opérateur de création de particule dans l’état i. Le conjugué hermitique ˆai de ˆa

:

i est un opérateur d’annihilation de particule qui vérifie ˆa_i|0y “ 0. Les opérateurs ˆa:

i et les ˆai vérifient les relations d’anticommutation (II.1.1.3) et (II.1.1.4).

L’ensemble des états de la forme ˆa:i0¨ ¨ ¨ˆa

:

iN|0y, pour tout N et tout i0 ă i1 ă

¨ ¨ ¨ ă iN, forme une base orthonormale de l’espace de Fock (ce qui se montre en utilisant les relations d’anticommutation (II.1.1.3) et (II.1.1.4)).

La transformation de Bogoliubov mélange les opérateursˆa:_{etˆa pour construire} de nouveaux opérateurs de création/annihilation, notés ˆβ: _{et ˆβ, qui ne} corres-pondent pas à des états de particule mais de quasi-particule :

Transformation de Bogoliubov : # ˆβk ” ř lVlk‹ˆa : l ` Ulk‹ˆal ˆ β: k “ ř lUlkˆa : l ` Vlkˆal . (II.1.1.19)

Les coefficients Ulk et Vlk sont des nombres a priori complexes qui définissent la transformation.

La transformation de Bogoliubov peut être écrite sous forme matricielle : ˆˆ β ˆ β: ˙ “ˆ U : _V: VJ _UJ ˙ ˆ ˆa ˆa: ˙ ”W:ˆ ˆa ˆa: ˙ , (II.1.1.20)

où W est la matrice des coefficients Ulk et Vlk. Elle est appelée matrice de Bogo-liubov.

La transformation de Bogoliubov préserve les relations d’anticommutation. Le calcul des anticommutateurs entre les opérateurs de création ˆβ:

i et d’annihilation ˆ

βj de quasi-particules permet de montrer que la matrice W est unitaire : WW:

“W:W “1, (II.1.1.21) ce qui permet d’inverser la relation (II.1.1.20) :

ˆ ˆa ˆa: ˙ “W ˆ_ˆ β ˆ β: ˙ . (II.1.1.22)

Le théorème de Bloch-Messiah permet de décomposer la transformation de Bo-goliubov en trois transformations unitaires successives TD, TU,V et TC. La première transformation mélange les opérateurs de création (respectivement annihilation) de particule entre eux pour construire de nouveaux opérateurs de création ˆb:

i (respec-tivement annihilation ˆbi) de fermion dont l’ensemble est appelé la base canonique de particules : TD : $ ’ ’ & ’ ’ % ˆ b_i ” ÿ j D‹ jiˆaj ˆ b: i ” ÿ j Djiˆa: j , (II.1.1.23)

où D est une matrice unitaire. La deuxième transformation TU,V, appelée trans-formation spéciale de Bogoliubov, mélange chaque opérateur d’annihilation de la particule i dans la base canonique avec l’opérateur de création de l’état renversé du temps ¯i : TU,V : # ˆ γi “ uibˆi´ vibˆ : ¯i ˆ γ¯_i:“ uibˆ : ¯_i ` vibˆi . (II.1.1.24)

Les ui etvi sont des réels compris entre 0 et 1 qui vérifient u2

i ` vi2 “1. De façon similaire aux v2

i de l’approximation BCS (II.1.1.15) les v2i sont appelés nombres d’occupation. Les opérateurs γˆ:

i et ˆγi sont des opérateurs de création/annihilation de fermion. Enfin, la troisième transformation TC mélange séparément les γˆ_i et les ˆ

γ:

i pour obtenir les ˆβi et les ˆβ : i : TC : $ ’ ’ & ’ ’ % ˆ β_i “ÿ j C‹ jiγˆj ˆ β: i “ ÿ j Cjiγˆ: j. (II.1.1.25)

L’enchaînement de ces transformations est résumé ci-dessous : TC TU,V TD # ˆ βi “ ř jC ‹ jiγˆj ˆ β: i “ ř jCjiγˆ : j Ð $ ’ ’ ’ & ’ ’ ’ % ˆ γ_i “ uiˆb_i´ viˆb¯:_i ˆ γ: i “ uiˆb : i ´ vib¯ˆi ˆ γ¯_i “ uiˆb¯_i` viˆb : i ˆ γ: ¯<sub>i</sub> “ uiˆb : ¯<sub>i</sub> ` vibˆi Ð # ˆ bi “ ř jD ‹ jiˆaj ˆ b: i “ ř jDjiˆa : j . (II.1.1.26) La matrice de Bogoliubov introduite en (II.1.1.20) peut donc s’écrire :

W “ˆD 0 0 D‹ ˙ ˆ_¯ U ¯V ¯ V ¯U ˙ ˆC 0 0 C‹ ˙ , (II.1.1.27)

où 0 désigne la matrice nulle. Les éléments de la matrice D sont les coefficients de la transformation TD, les éléments de la matrice C sont les coefficients de la transformation TC, et les matrices ¯U et ¯V sont de la forme :

¯ U ” ¨ ˚ ˚ ˚ ˝ ¯ U0 0 ¨ ¨ ¨ 0 0 U1¯ . .. ... .. . . .. ... 0 0 ¨ ¨ ¨ 0 UM ´1¯ ˛ ‹ ‹ ‹ ‚ ¯ V ” ¨ ˚ ˚ ˚ ˝ ¯ V0 0 ¨ ¨ ¨ 0 0 V1¯ . .. ... .. . . .. ... 0 0 ¨ ¨ ¨ 0 VM ´1¯ ˛ ‹ ‹ ‹ ‚ , (II.1.1.28)

oùM est le nombre d’indices i ą 0. Ces matrices sont unitaires : D:_{D “ DD}:

“1 (II.1.1.29) C:_{C “ CC}:

“1. (II.1.1.30) Les ¯Ui et ¯Vi sont des matrices carrées de dimension deux de la forme :

¯ Ui”ˆui 0 0 ui ˙ ¯ Vi ” ˆ 0 vi ´vi 0 ˙ . (II.1.1.31)

II.1.1.3 Définition de l’état HFB

La transformation de Bogoliubov est maintenant utilisée pour définir l’état HFB. Ce dernier, noté |Φy, est défini comme le vide associé aux opérateurs d’an-nihilation de quasi-particules ˆβ_i. Il vérifie donc, pour touti :

ˆ

β_i|Φy “ 0. (II.1.1.32) On impose de plus à cet état d’être normé :

La transformation TC des γˆi en ˆβi ne mélange que les opérateurs d’annihilation entre eux. Par conséquent, l’état |Φy est également un vide associé aux ˆγi. Le produit |Ψy de l’ensemble des opérateurs ˆγ_i et γˆ¯i sur le vide de particules |0y :

|Ψy ”ź ią0

ˆ

γiγ¯ˆi|0y, (II.1.1.34)

s’annule sous l’action des opérateurs d’annihilation ˆγ. Il suffit pour le montrer d’utiliser les règles d’anticommutation des γ. Comme la transformation TCˆ agit séparément sur les opérateurs de création γˆ:

i et d’annihilation ˆγi, |Ψy s’annule aussi sous l’action des ˆβ_i. En utilisant les relations d’anticommutation des ˆb et des ˆ

b:_{, et ˆb|0y “ 0, |Ψy se réécrit :}

|Ψy “ ˜ ź ką0 vk ¸ ź ią0 ´ ui` vibˆ_iˆb¯_i ¯ |0y. (II.1.1.35)

Étant donné queś_ią0 ´

ui` viˆbib¯ˆi ¯

|0y est normé, |Ψy ne s’annule que lorsque l’un au moins des vi est nul. De plus, l’action d’un opérateur γˆ_i ou ˆγ¯i associé à un vi nul sur |0y est nulle. Par conséquent, le vide de quasi-particule, défini à une phase eiθ _{près, peut se réécrire :}

|Φy “ eiθ ź ią0 vi‰0 1 viγˆiγ¯ˆi|0y, (II.1.1.36) ou encore : |Φy “ eiθź ią0 ´ ui` viˆb_iˆb¯_i ¯ |0y, (II.1.1.37)

où eiθ _{est une phase arbitraire.}

Lorsque ˆO ” ˆOp1q _{est une observable à un corps, son expression en seconde} quantification dans la base des ˆa:

i est : ˆ

Op1q “ÿ

ij

xi| ˆOp1q|jyˆa:_iˆaj. (II.1.1.38)

La valeur moyenne de cette observable par rapport à |Φy s’écrit donc : xΦ| ˆOp1q_{|Φy “}ÿ

ij

xi| ˆOp1q|jyxΦ|ˆa:iˆaj|Φy. (II.1.1.39)

Elle ne dépend que des éléments de matrice de l’opérateur ˆOp1q _{dans la base des} |iy ”ˆa:_i|0y ainsi que de la matrice densité à un corps ρp1q définie par :

ρp1q_ji ” xΦ|ˆa:

qui est hermitienne :

ρp1q_ji “ xΦ|ˆa:

iˆaj|Φy “ pxΦ|ˆa : jˆai|Φyq

‹

“ ρp1q‹ij . (II.1.1.41)

Si ˆO ” ˆOp2q _{est une observable à deux corps, son expression dans la base des ˆa}: i est : ˆ Op2q “ 1 4 ÿ ijkl

xij| ˆOp2q|klyˆa:_iˆa:_jˆalˆak. (II.1.1.42)

La valeur moyenne de ˆOp2q _{dans la base des ˆa}:

i s’exprime donc comme :

xΦ| ˆOp2q_{|Φy “} 1 4

ÿ ijkl

xij| ˆOp2q|klyxΦ|ˆa:_iˆa:_jˆalˆak|Φy, (II.1.1.43)

et ne dépend cette fois que des éléments de matrice de ˆOp2q _{dans la base des états} à deux corps |ijy ” |iy b |jy et de la matrice densité à deux corps ρp2q _{définie par :}

ρp2q_klij ” xΦ|ˆa: iˆa

:

jˆalˆak|Φy. (II.1.1.44) Le théorème de Wick (appendice C4 de [39]) permet de décomposer ρp2q _{sous la} forme :

ρp2q_klij “ ρp1q_ki ρp1q_lj ´ ρp1q_li ρp1q_kj ` κ‹ijκkl, (II.1.1.45) oùκ désigne le tenseur d’appariement défini par :

κji ” xΦ|ˆa_iˆa_j|Φy, (II.1.1.46)

qui est antisymétrique :

κji “ xΦ|ˆa_iˆa_j|Φy “ ´xΦ|ˆa_jˆa_i|Φy “ ´κij. (II.1.1.47)

Par conséquent, la densité à un corps, qui est maintenant notée ρ, et le tenseur d’appariement κ suffisent pour exprimer les valeurs moyennes d’opérateurs à un et deux corps.

En utilisant la transformation de Bogoliubov inverse (II.1.1.22), la matrice ρ et le tenseurκ se réécrivent : ρji “ÿ kl VikV‹ jlxΦ| ˆβkβˆ : l|Φy (II.1.1.48) κji “ÿ kl UikV‹ jlxΦ| ˆβkβˆ : l|Φy, (II.1.1.49)

puis les relations d’anticommutation entre les ˆβ: _{et les ˆβ permettent d’obtenir :} ρji “ÿ k VikV‹ jk “ pV‹VJqji (II.1.1.50) κji “ÿ k UikV‹ jk “ pV‹UJqji. (II.1.1.51) En calculant le produit matriciel par bloc du membre droit de l’équation (II.1.1.27), on obtient :

U “ D ¯UC (II.1.1.52) V “ D‹_VC.¯ _(II.1.1.53) En introduisant ce résultat dans l’équation (II.1.1.50), on obtient :

ρ “ D ¯V ¯VJ_D:_{“ ´D ¯V}2_D: _(II.1.1.54) κ “ D ¯V ¯UDJ_,

(II.1.1.55) et les équations suivantes sont donc vérifiées :

ρ2´ ρ “ κκ‹, (II.1.1.56) ρκ “ κρ‹_{, (II.1.1.57)} ρ: “ ρ, (II.1.1.58) κJ “ ´κ. (II.1.1.59) La base canonique de particules définie par la transformation D est donc celle qui diagonalise la matrice densité et met la matrice d’appariement dans sa forme canonique : ¯ V ¯U “ ¨ ˚ ˚ ˚ ˝ ¯ V0U0¯ 0 ¨ ¨ ¨ 0 0 V1¯ U1¯ . .. ... .. . . .. . .. 0 0 ¨ ¨ ¨ 0 VM ´1¯ UM ´1¯ ˛ ‹ ‹ ‹ ‚ , (II.1.1.60) avec : ¯ ViUi¯ “ ˆ 0 uivi ´uivi 0 ˙ , (II.1.1.61) où M est le nombre d’indices i ą 0. La matrice densité généralisée, notée R, permet de regrouper la matrice densité à un corps et le tenseur d’appariement en une seule matrice. Elle est définie comme :

R ” ˆ

xΦ|ˆa:_{ˆa|Φy xΦ|ˆaˆa|Φy} xΦ|ˆa:_ˆa:_{|Φy xΦ|ˆaˆa}:_|Φy

˙ (II.1.1.62) R “ ˆ ρ κ ´κ‹ 1 ´ ρ‹ ˙ , (II.1.1.63)

et est diagonale dans la base de Bogoliubov :

W:_{RW “}ˆ0 0 0 1

˙

. (II.1.1.64)

On en déduit que R est un projecteur hermitien (R2

“ R et R: “ R).

II.1.1.4 Résolution de l’équation HFB

Le hamiltonien nucléaire ˆH qui décrit le système de A “ N ` Z nucléons contient un terme cinétique ˆT à un corps et une série de termes ˆVpnq _{qui décrivent} les interactions simultanées den nucléons entre eux :

ˆ

H “ ˆT ` ˆVp2q

` ˆVp3q` ¨ ¨ ¨ ` ˆVpAq. (II.1.1.65) Le terme cinétique ˆT décrit un système de A particules libres et a pour expression, en supposant l’égalité des masses des protons et des neutrons :

ˆ T ” A ÿ i“1 ˆti. (II.1.1.66) L’opérateur ˆti est défini comme :

ˆti ” ˆp 2 i 2M `vˆ 1 cdmi, (II.1.1.67) oùpiˆ est l’opérateur d’impulsion etˆv1

cdmiest l’opérateur de correction à un corps du centre de masse associés à la particulei. Le terme à deux corps décrit l’interaction entre chaque paire de particules :

ˆ Vp2q ” 1 2 A ÿ i‰j“1 ˆ vij, (II.1.1.68)

où l’opérateurvijˆ décrit l’interaction à deux corps entre la particulei et la particule j. Les termes décrivant les interactions à trois corps ou plus sont négligés dans ce travail. Le hamiltonien nucléaire ˆH se réécrit :

ˆ H “ A ÿ i“1 ˆti`1 2 A ÿ i‰j“1 ˆ vij, (II.1.1.69) et en seconde quantification : ˆ H ”ÿ ij

xi|ˆt|jyˆa:iˆaj` 1 4 ÿ ijkl xik|ˆvpaq |jlyˆa:iˆa :

où ˆt ” ˆt1. L’opérateur à deux corps vpaq _{représente l’interaction antisymétrisée} entre deux nucléons :

ˆ vpaq

”v12p1 ´ ˆˆ PrPσˆ Pτˆ q, (II.1.1.71) où ˆPr, ˆPσ et ˆPτ sont respectivement les opérateurs d’échange d’espace, de spin et d’isospin. L’énergie totale associée à un état HFB |ΦHFBy, notée E pΦHFBq, est définie par :

EpΦHFBq ” xΦHFB| ˆH|ΦHFBy. (II.1.1.72) Par conséquent, en utilisant les relations (II.1.1.39), (II.1.1.40) et (II.1.1.43)– (II.1.1.45), puis en utilisant l’antisymétrie de ˆvpaq_{, l’expression de l’énergie} to-tale (II.1.1.72) devient :

EpΦHFBq “ ÿ ij xi|ˆt|jyρji`1 2 ÿ ijkl

xik|ˆvpaq_|jlyρjiρlk `1

4 ÿ ijkl

xik|ˆvpaq_{|jlyκkiκjl. (II.1.1.73)}

On cherche à déterminer l’état HFB qui minimise E pΦHFBq. Pour cela, une ap-proche variationnelle est utilisée, qui consiste à résoudre :

δEpΦHFBq “0 et δ2_{EpΦHFBq ą0. (II.1.1.74)}

Dans la pratique, seule la première équation est résolue (voir par exemple [42] pour une discussion sur la condition δ2_{EpΦHFBq ą 0). La minimisation s’effectue} par rapport aux éléments de la matrice densité généralisée R définie en (II.1.1.62). Afin de préserver ou d’imposer certaines propriétés, la minimisation se fait en pratique sous contraintes par la méthode des multiplicateurs de Lagrange [43]. Voici les principales contraintes utilisées dans ce travail.

— L’état HFB n’a pas des nombres de protons ou de neutrons définis et leurs nombres moyens, N et Z, sont imposés :

trpρnq “ N (II.1.1.75) trpρpq “ Z, (II.1.1.76)

oùρn (ρp) est la matrice densité à un corps associée aux neutrons (protons). Ces contraintes permettent seulement de contraindre la valeur moyenne du nombre de protons et de neutrons. Pour aller plus loin, une projection sur le bon nombre de particules pourrait être envisagée, ce qui n’est pas fait dans ce travail.

— La transformation de Bogoliubov doit être unitaire pour que les opérateurs de création et d’annihilation de quasi-particule vérifient les relations d’an-ticommutation de fermions. Dans ce cas, R est un projecteur hermitien. L’hermicité de R est directement imposée dans son expression en fonction

deρ et κ. La matrice densité généralisée R doit cependant être une projec-tion hermitienne, ce qui correspond à la contrainte :

R2 “ R. (II.1.1.77)

— On peut vouloir imposer au système nucléaire de se déformer de façon à pré-senter des valeurs arbitraires pour certaines valeurs moyennes d’opérateurs multipolaires ˆQk. Les contraintes correspondantes sont alors :

xΦHFB| ˆQk|ΦHFBy “ qk. (II.1.1.78)

Par exemple, l’opérateur de centre de masse noté ˆQ10 est contraint dans tous les calculs à 0fm pour imposer au centre de masse du système d’être en moyenne situé à l’origine :

xΦHFB| ˆQ10|ΦHFBy “0fm, (II.1.1.79)

car l’état HFB est exprimé dans le repère intrinsèque et brise l’invariance par translation.

La fonctionnelle F pΦHFBq qui est finalement minimisée est :

F pΦHFBq ” E pΦHFBq ´ λnptrpρnq ´ N q ´ λpptrpρpq ´ Zq ´

ÿ k

µk´xΦHFB| ˆQk|ΦHFBy ´ qk¯´tr`ΛpR2 ´ Rq˘ , (II.1.1.80) oùλnetλpsont les paramètres de Lagrange associés respectivement aux contraintes sur les nombres de neutrons et de protons et s’interprètent comme les potentiels chimiques des neutrons et des protons ;Λ est une matrice carrée de paramètres de Lagrange associés à la contrainte d’unitarité de la transformation de Bogoliubov ; µ0 est le paramètre de Lagrange associé à la contrainte sur le centre de masse et les µk pour k ą 0 sont les paramètres de Lagrange associés aux contraintes additionnelles, en déformation dans notre cas.

L’équation de minimisation de F pΦHFBq s’écrit :

BF

BRpΦHFBq “0. (II.1.1.81) Le calcul de la dérivée de F pΦHFBq par rapport à la matrice densité ρ et au tenseur d’appariementκ permet d’exprimer (II.1.1.81) sous la forme :

BF

La matrice H est appelée le hamiltonien HFB. Elle est définie comme : H ”ˆh ´ λ ∆ ´∆‹ _´h‹ ` λ ˙ ´ÿ k µkˆQk 0 0 ´Q‹k ˙ . (II.1.1.83)

La matrice h représente le hamiltonien à un corps HF et s’écrit :

hij ” BE

Bρji “ pt ` Γ ` Γ rea

qij. (II.1.1.84)

La matricet de l’équation (II.1.1.84) correspond à la matrice de l’opérateur ˆt dans la base des ˆa:

i, Γ est la matrice de champ moyen et a pour expression : Γij ”ÿ

kl

xik|ˆvpaq_{|jlyρlk, (II.1.1.85)}

et Γrea _{est un terme qui apparaît lorsque l’interaction entre les nucléons dépend} explicitement de la densité du milieu :

Γrea ij ” 1 2 ÿ klmn Bxkl|ˆvpaq_|mny Bρji ˆ ρmkρnl` 1 2κklκmn ˙ . (II.1.1.86)

La matrice ∆ correspond au champ d’appariement :

∆ij ” BE Bκji “ 1 2 ÿ kl

xij|ˆvpaq_{|klyκlk, (II.1.1.87)}

et λ est une matrice diagonale :

λ ”ˆλn1 0 0 λp1

˙

, (II.1.1.88)

oùλnetλpsont déterminés de manière à ce que |ΦHFBy vérifie (II.1.1.75) et (II.1.1.76). Enfin, Qk est la matrice associée à l’opérateur ˆQk dans la représentation desˆa:i :

rQksij ” xi| ˆQk|jy. (II.1.1.89) Les équations (II.1.1.81) et (II.1.1.82) conduisent à la relation suivante :

H ´ ΛR ´ RΛ ` Λ “ 0. (II.1.1.90) Afin d’éliminer Λ, on multiplie chaque membre de cette équation à gauche puis à droite par R pour obtenir :

HR ´ ΛR2_{´ RΛR ` ΛR “ 0}

(II.1.1.91) RH ´ RΛR ´ R2Λ ` RΛ “ 0. (II.1.1.92)

Si R est solution de l’équation (II.1.1.90), elle vérifie R2 _{“ R étant donné qu’il} s’agit d’une contrainte. En soustrayant chaque membre de (II.1.1.91) à (II.1.1.92), on obtient l’équation HFB :

HR ´ RH “ 0, (II.1.1.93) qui se réécrit :

rH, Rs “0. (II.1.1.94) Le hamiltonien HFB H commute par conséquent avec la matrice densité généralisée R lorsque l’équation HFB est vérifiée.

Il existe plusieurs méthodes pour résoudre l’équation (II.1.1.94), qui sont toutes itératives [31]. Cela est dû à la dépendence entre H et R.

Par exemple, une méthode permettant de résoudre l’équation (II.1.1.94) consiste à suivre l’algorithme suivant :

1. une densité généralisée initiale Rp0q _{est construite en supposant que les états} de l’oscillateur harmonique de plus basse énergie sont complètement occupés et les autres états sont complètement vides ;

2. on détermine le hamiltonien HFB Hp0q _{associé à R}p0q _{en utilisant (II.1.1.83)} et en ajustant les multiplicateurs de Lagrange λn, λp et µi de sorte que les contraintes associées soient vérifiées ;

3. le hamiltonien HFB Hp0q _{est diagonalisé pour obtenir la matrice de} Bogoliu-bovWp0q _{qui est définie en (II.1.1.20) ;}

4. la matrice densité à un corps ρp0q _{et le tenseur d’appariement κ}p0q _sont dé-terminés à partir des relations (II.1.1.50) et (II.1.1.51) ;

5. la matrice densité généralisée Rp1q _{est construite à partir de ρ}p0q _{et κ}p0q _en utilisant (II.1.1.62) ;

6. on revient en 2 jusqu’à ce que le critère de convergence suivant soit vérifié :

max |Rpn`1q

´ Rpnq| ă εHFB, (II.1.1.95)

où εHFB _{est un paramètre du calcul qui correspond à la précision requise.} Dans notre travail, εHFB_{P t10}´4_{, 10}´6

u.

L’algorithme qui vient d’être présenté est directement utilisable dans le cas d’une base de particules orthonormale. Dans notre cas, la base d’oscillateur har-monique à deux centres utilisée n’est pas orthonormée. Une méthode de résolution modifiée, fondée sur l’algorithme qui vient d’être présenté, est adoptée [42]. Les bases d’oscillateur harmonique à deux centres sont présentées en II.2.1.1.

II.1.1.5 Interaction nucléaire effective de Gogny

Les interactions nues entre les nucléons ne peuvent pas être utilisées direc-tement dans une méthode HFB. En effet, les corrélations de courte portée qui interviennent dans l’interaction nucléaire nue, caractérisée par un cœur très répul-sif, sont incompatibles avec une description de type champ moyen. Une première possibilité pour pallier cette difficulté consiste à renormaliser l’interaction nue, par exemple avec la théorie de Brueckner [44]. Cependant, cette renormalisation est numériquement coûteuse. Une seconde possibilité consiste à utiliser une interac-tion effective phénoménologique dont les paramètres sont ajustés sur des données expérimentales.

Deux interactions nucléaires effectives phénoménologiques sont principalement utilisées au sein des approches de type champ moyen et au-delà :

— l’interaction de Skyrme [45, 31, 46], qui est de portée nulle,

— l’interaction de Gogny [7, 47, 48], dont le terme central indépendant de la densité est de portée finie, permettant de traiter sur un pied d’égalité champ moyen et appariement dans l’approche auto-cohérente HFB.

L’interaction qui est utilisée dans ce travail est celle de Gogny dans sa paramétri-sation D1S. Son expression est [7] :

ˆ vGognypr1, r2q ” 2 ÿ j“1 e´pr1´r2q2{µ2jpWj <sub>`</sub>BjPσ<sub>´</sub>HjPτ <sub>´</sub>MjPσPτ<sub>q (central)</sub> ` t0p1 ` x0Pσqδpr1´ r2qρα ´r 1` r2 2 ¯ (dép. de la densité) ` iWLSÐ∇Ý12δpr1´ r2q ˆÝÑ∇12¨ p~σ1` ~σ2q. (spin-orbite) (II.1.1.96) On distingue le terme central de portée finie qui contient une première gaus-sienne attractive et une seconde répulsive, le terme dépendant de la densité qui simule les effets à trois et N -corps, et le terme spin-orbite. Les 14 paramètres de cette interaction sont Wi, Bi, Hi, Mi et µi pour chaque portée i “ 1, 2 et les t0, x0, WLS et α. Les valeurs de ces paramètres pour la force D1S sont données dans les tableaux II.1 et II.2.

j µi(fm) Wi(MeV) Bi(MeV) Hi(MeV) Mi(MeV) 1 0.7 -1720.30 1300.00 -1815.53 1397.60 2 1.2 103.639 -163.483 162.812 -223.933

Table II.1 – Valeur des paramètres de la partie centrale de l’interaction de Gogny D1S.

t0(MeV.fm3_{) x0 α(MeV) WLS(MeV)} 1390.60 1.0 1/3 -130.00

Table II.2 – Valeur des paramètres des termes densité et spin-orbite de l’interac-tion de Gogny D1S.

II.1.2

Méthode de la coordonnée génératrice dépendante

du temps à l’approximation des recouvrements

gaussiens

La méthode de la coordonnée génératrice dépendante du temps (TDGCM) permet de prendre en compte les corrélations associées aux oscillations collectives du noyau. [29].

L’expression de la fonction d’onde à A-corps associée à l’état TDGCM est :

|GCMptqy ” ż

dq|ΦHFBpqqyf pq, tq. (II.1.2.1)

Le vecteur q ” pq0, ¨ ¨ ¨ , qNc´1q représente les valeurs moyennes des Nc opérateurs

de contrainte associées à la configuration |ΦHFBpqqy, appelées dans la suite les coordonnées collectives :

qi ” xΦHFBpqq| ˆQi|ΦHFBpqqy, (II.1.2.2) f pq, tq est une fonction de poids à valeurs complexes qui détermine entièrement l’état TDGCM (II.1.2.1). La fonction de poids est déterminée par le principe de moindre action :

δSt1

t0 “0, (II.1.2.3)

où St1

t0 est l’action du système décrit par l’état |GCMptqy entre un instant initial

t0 et un instant final t1. Elle est définie par :

St1 t0 ” żt1 t0 dt xGCMptq|´i¯hB Bt ´ ˆH ¯ |GCMptqy xGCMptq|GCMptqy . (II.1.2.4) La minimisation de cette action par rapport à la fonction de poids f pq, tq conduit à l’équation de Hill-Wheeler dépendante du temps, qui est une équation intégro-différentielle non locale en q dont la résolution exacte est présentée dans le cha-pitre III. Elle a pour expression :

i¯h ż dq1_{N pq, q}1 qB Btf pq 1_{, tq “} ż dq1_{Hpq, q}1 qf pq1, tq. (II.1.2.5) où : Hpq, q1_{q ” xΦHFBpqq| ˆH|ΦHFBpq}1

qy le noyau du hamiltonien collectif, (II.1.2.6) N pq, q1_{q ” xΦHFBpqq|ΦHFBpq}1

qy le noyau des recouvrements. (II.1.2.7) Dans cette partie, nous nous intéressons à sa résolution dans le cadre de l’ap-proximation des recouvrements gaussiens (GOA). Cette apl’ap-proximation permet de

transformer l’équation de Hill-Wheeler dépendante du temps en une équation aux dérivées partielles du second ordre. La fonctionnelle d’énergie E pGCMptqq est dé-finie comme : EpGCMptqq ” xGCMptq| ˆH|GCMptqy “ ż dq ż dq1_f‹ pq, tqHpq, q1qf pq1, tq “ ż dq ż dq1_f‹ pq, tqhpq, q1qN pq, q1qf pq1, tq, (II.1.2.8) où : hpq, q1 q ” Hpq, q 1 q

N pq, q1_q le hamiltonien collectif réduit. (II.1.2.9) À l’approximation GOA, l’expression (II.1.2.8) se réduit à :

EpGCMptqq « ż dqaγpqqg‹ pq, tqHGOApq, B Bqqgpq 1_{, tq.} (II.1.2.10)

Dans l’équation (II.1.2.10), HGOApq, B

Bqq représente le hamiltonien collectif à l’ap-proximation GOA etgpq, tq est une fonction qui décrit entièrement l’état |GCMptqy. Le passage de l’expression (II.1.2.8) à (II.1.2.10) se fait au travers de deux approximations :

1. le recouvrement entre deux configurations est supposé gaussien ;

2. un développement limité à l’ordre deux du hamiltonien collectif réduithpq, q1_q est effectué.

L’évolution temporelle de gpq, tq est alors déterminée par une équation diffé-rentielle du second ordre de type équation de Schrödinger locale en espace de la forme :

i¯hB

Btgpq, tq “ HGOApq, B

Bqqgpq, tq. (II.1.2.11) II.1.2.1 Approximation des recouvrements gaussiens

La GOA a été initialement introduite pour des descriptions comprenant une seule variable collective q [29]. Dans ce cas, le noyau des recouvrements N pq, q1_q est approché par une expression gaussienne en q ´ q1 _:

N pq, q1 q «exp ˆ ´1 2γ0p¯qqpq ´ q 1 q2 ˙ , (II.1.2.12)

oùq correspond à la moyenne arithmétique de q et q¯ 1_{etγ0p¯qq est un réel strictement} positif.