HAL Id: hal-00589307
https://hal.archives-ouvertes.fr/hal-00589307
Submitted on 28 Apr 2011HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
A BGK-type model for inelastic Boltzmann equations
with internal energy.
Aude Champmartin, Laurent Desvillettes, Julien Mathiaud
To cite this version:
Aude Champmartin, Laurent Desvillettes, Julien Mathiaud. A BGK-type model for inelastic Boltz-mann equations with internal energy.. Rivista di Matematica della Università di Parma, Istituto di Matematica, 2010, 1 (2), pp.271-305. �hal-00589307�
A BGK-TYPE MODEL FOR INELASTIC BOLTZMANN EQUATIONS WITH INTERNAL ENERGY
AUDE CHAMPMARTIN, LAURENT DESVILLETTES, AND JULIEN MATHIAUD
Abstract. We introduce a model of inelastic collisions for droplets in a spray, leading to a specific Boltzmann kernel. Then, we build caricatures of this kernel of BGK type, in which the behavior of the first moments of the solution of the Boltzmann equation (that is, mass, momentum, directional temperatures, variance of the internal energy) are mimicked. The quality of these caricatures is tested numerically at the end of the paper.
1. Introduction
Sprays are flows in which a dispersed phase (e.g. droplets) is surrounded by a gas. Such flows can be found in natural phenomena, like for example clouds. They also appear in many industrial devices, like diesel engines, fluidized beds, etc. We refer to [Wil85, AOB89, O’R81] for an intro-duction to the study of this kind of flows. When the dispersed phase occupies a significant part of the total volume, one must take into account the collision phenomena (like in [AOB89]), that is, droplets can meet, remain in contact for some time, and then separate again.
Those droplets are characterized by their radius r > 0, their position x∈ Ω (domain of computa-tion), their velocity v∈ R3, and their internal energy (by unit of mass) e > 0 [some other parameters are sometimes taken into account, like the distortion of the droplets, Cf. [AOB89, O’R81], etc.]. We restrict ourselves in this paper to so-called monodisperse sprays, where all droplets have the same radius r > 0.
During a collision, two droplets are in contact and therefore exchange some internal energy. Moreover, the droplets being macroscopic objects, part of the kinetic energy (in the center of mass reference frame) is transformed in internal energy (that is, the collisions are inelastic).
A standard model for inelastic collisions (Cf. [BCG00, BGP04, Vil06] for example in the context of granular gases) consists in writing
v′ = v + v ∗ 2 + 1− γ 4 (v− v ∗) +1 + γ 4 |v − v ∗|σ, (1) v′∗ = v + v ∗ 2 − 1− γ 4 (v− v ∗)−1 + γ 4 |v − v ∗|σ, (2)
where v, v∗ ∈ R3 are precollisional velocities, v′, v′∗ ∈ R3 are postcollisional velocities, γ ∈ [0, 1] is the inelasticity parameter, and σ is parametrizing the sphere S2.
The kinetic energy lost (by unit of mass) in (1), (2) is given by ∆Ec′ = (1− γ2)|v − v ∗|2 8 − 1− γ2 8 |v − v ∗| < σ, v − v∗ >, (3)
where <, > is the scalar product in 3D : < x, y >:=∑3i=1xiyi.
The exchange of internal energy is then simply modelled by the equations e′ = 2− a 2 e + a 2e ∗+ 1 2∆E ′ c, (4) e′∗ = a 2e + 2− a 2 e ∗+1 2∆E ′ c, (5)
where e, e∗ > 0 are precollisional internal energies, e′, e′∗ > 0 are postcollisional internal energies,
and a∈ [0, 1] is the parameter which characterizes the typical time scale of the exchange.
Note that the kinetic energy lost in (1), (2) is equally distributed between the energies e′ and
e′∗.
In all generality, both γ and a are functions of |v − v∗| which sometimes can be assessed (Cf. [Mat06], [DM10]).
The corresponding Boltzmann operator Q can be written in weak form according to the following formula (for all function ψ for which the integrals make sense)
∫ v ∫ eQ(f, f )(v, e) ψ(v, e)dvde (6) =∫v∫e∫v∗ ∫ e∗ ∫ σf (v, e)f (v∗, e∗) [ψ(v ′ , e′)− ψ(v, e)]r2S(|v − v˜ ∗|)dvdedv∗de∗dσ, (7) where (8) S(w) = w˜
corresponds to the cross section of hard spheres, and r > 0 is the radius of the droplets.
Note that by taking ψ(v, e) = 1; vi;|v|22 + e, we obtain the conservation of mass, (ith component of the) momentum, and total (kinetic + internal) energy:
(9) ∫ v ∫ e Q(f, f ) (vi)i=1,2,31 |v|2 2 + e dvde = 0.
We also briefly indicate here the strong formulation of Q [in the case of hard spheres], which makes explicit the Jacobian of the transformation (v, v∗, e, e∗) 7→ (v′, v′∗, e′, e′∗), but which is not used in the sequel (cf. [Vil06] for more on the Jacobian):
Q(f, f )(v, e) = ∫ v ∫ e ∫ σ ( J(v,v∗,e,e∗)→(′v,′v∗,′e,′e∗) | ′v−′v∗| |v−v∗| f (′v∗,′e∗) f (′v,′e) −f(v∗, e∗) f (v, e))r2|v − v∗|dσdvde =∫v∫e∫σ ( 1 γ21−a1 f (′v∗,′e∗) f (′v,′e)− f(v∗, e∗) f (v, e) ) r2|v − v∗|dσdvde. (10)
The Jacobian J is composed of a part (γ12 |v−v
∗|
|′v−′v∗|) which is typical of the inelastic collision kernels
([GPV04, Vil02]), and of another part (1−a1 ) which comes from the exchanges of internal energies. In (10) is used the following shorthand (related to precollisional velocities, Cf. [Mat06], [DM10])
′v = v + v∗ 2 − 1− γ 4γ (v− v ∗) + 1 + γ 4γ |v − v ∗|σ, (11) ′v∗ = v + v∗ 2 + 1− γ 4γ (v− v ∗)− 1 + γ 4γ |v − v ∗|σ, (12) 2
′e = 2− a 2− 2ae− a 2− 2ae ∗+1 2∆ ′E c, (13) ′e∗ =− a 2− 2ae + 2− a 2− 2ae ∗+1 2∆ ′Ec, (14) ∆′Ec= 1− γ2 8γ2 |v − v∗| 2−1− γ2 8γ2 |v − v∗| < σ, v − v∗ > . (15)
In many instances, the Knudsen number related to the droplets in a spray is small (Cf. [Mat06], [DM10]), so that the number of collisions to perform in a computation is quite high, and the treatment of Q sometimes requires a large part of the time spent in the computation (up to an increase of more than 100%).
As a consequence, one needs simplified models of collision, which lead to less expensive compu-tations, but keep some of the main features of the original model (10) – (15).
This problem has already been studied by many authors in the case of the elastic Boltzmann operator for rarefied gases, and has led to various models, among which the BGK model (Cf. [BGK54]) and the ESS model (Cf. [LHH66]). These models have been adapted to the case of inelastic Boltzmann kernels for granular media (Cf. [AS04], [MA00], [San03]), and to the case of Boltzmann kernels taking into account chemical reactions (Cf. [CGS07], [GK02], [GS99]).
The simplified model that we propose writes (16) ∂tf +∇v·
(
c1f (v− vavr)
)
+ ∂e(c2f ) + ∂e(c3(e− eavr)f )
+ ∂e(c4|v − vavr|4∂ef ) =−ν(f − f0),
where vavr is the mean velocity
(17) vavr= ∫ v ∫ ef (t, v, e)vdvde ∫ v ∫ ef (t, v, e)dvde , eavris the mean internal energy
(18) eavr= ∫ v ∫ ef (t, v, e)ededv ∫ v ∫ ef (t, v, e)dedv , f0 is the Maxwellian function of v with the same parameters as f
(19) f0(t, v, e) = ( 1 2πT (t) )3/2 e−|v−vavr|22T (t) ∫ w f (t, w, e)dw,
and T is the statistical temperature:
(20) T (t) = 1 3 ∫ v ∫ ef (t, v, e)|v − vavr| 2dvde ∫ v ∫ ef (t, v, e)dvde . It combines:
• a drift towards the mean velocity ∇v·
(
f (v− vavr)
)
, which enables to model the inelasticity (loss of kinetic energy) coupled with a term which ensures the conservation of total energy (∂ef ),
• a relaxation towards a Maxwellian distribution −ν(f − f0),
• a drift towards the mean internal energy ∂e((e− eavr)f ), which models the exchange of
internal energies during collisions,
• a diffusive term ∂e(|v − vavr|4∂ef ) coming from the fact that some diffusion w.r.t. internal
energy appears when part of the kinetic energy is transformed into internal energy. Note that the term |v − vavr|4 naturally appears by homogeneity if we want c4 to be the inverse
of a time.
The parameters c1, c2, c3, c4, ν are defined by (21) c1= 3S1(t) 8r [ − 1 +γ 2 + γ 2](1− α), (22) c2 =− 9S1(t) 8r [ − 1 +γ 2 + γ 2](1− α)T (t), (23) c3=− 3S2(t) 4r a(2− a)(1 − α), c4 =− S3(t) 32r (1− γ 2)2(1− α), (24) (25) ν = 3S1(t) 8r (1 + γ) 2(1− α),
where S1, S3, S3 depend on the type of collision kernel:
• In the case of Maxwell molecules that is, when ˜S(|v − v∗|) = S is a constant in (7), we take
S1(t) = S2(t) = S3(t) = S;
• In the case of hard spheres (that is, when ˜S(|v − v∗|) = |v − v∗|), we take
(26) S1= √ 3( ˜T2 11+ ˜T222+ ˜T332)+2( ˜T11T˜22+ ˜T22T˜33+ ˜T11T˜33) 9T2 √ 6T , S2= 4√T √ π , (27) S3= 32√T 5√π . (28)
Here, the ˜Tii are the eigenvalues of the matrix made out of the Tij, which are the directional temperatures:
(29) Tij(t) =
∫ v
∫
ef (vi− v∫ iavr)(vj− vjavr)dvde
v ∫
ef dvde
; i, j = 1, 2, 3
and α is the volume fraction of gas in the spray:
(30) 1− α(t) = ∫ v ∫ e f (t, v, e)4 3πr 3dvde.
Those coefficients are chosen in such a way that the main properties of the kernel Q (conservation of mass, momentum, total energy) are satisfied, and that some typical quantities (kinetic energy, directional temperatures, variance of the internal energy) have a behavior which is as close as possible to the original kernel Q.
Their choice can be made in an almost completely rational way when one wishes to mimic a kernel with a cross section of Maxwell molecules type (that is, when one chooses ˜S as a constant
function instead of (8)). Unfortunately, in the (much more realistic) case of hard spheres (that is, when ˜S is given by (8)), this choice is made after some approximations which are not always valid,
and other choices of coefficients are possible (we shall discuss this point in subsection 2.3).
This paper is built as follows: first, in Section 2, we consider a solution f of the Boltzmann equation ∂tf = Q(f, f ), and we compute the value of various moments (like Tij (29)). This computation is exact (except for the variance of internal energy) when hard spheres are replaced
by Maxwell molecules, but can only be an approximation in the realistic case of hard spheres. The difficulties related to the treatment of hard spheres [that is, the link between S1, S2, S3 and ˜S] are
discussed in subsection 2.3.
Then, the same computation is repeated in section 3 for the simplified model (16) – (19), with arbitrary coefficients c1, ., c4, ν. This enables the identification of the coefficients (formulas (21) to
(25)).
Section 4 is devoted to the numerical simulations and comparisons between the simplified and original model. In subsection 4.1 is presented the numerical (particle Monte Carlo) scheme used to solve (16) – (19). Then, comparisons when ˜S is constant (case of Maxwell molecules) are shown in
subsection 4.2, while the case of hard spheres is treated in subsection 4.3. Finally, we provide in subsection 4.4 some results when a and γ depend on |v − v∗|.
2. Evolution of some moments of the solution of Boltzmann equation We consider in this section a solution f of the spatially homogeneous Boltzmann equation
(31) ∂tf = Q(f, f ),
where Q is the kernel defined in (1) – (7) [or (10) – (15)].
We want to track the following moments in order to build our simplified model:
• The directional temperatures Tij defined by (29),
• The variance of the internal energy
(32) g(t) := ∫ v ∫ ef (e∫ − eavr)2dvde v ∫ ef dvde .
2.1. Computation of some moments of the collision kernel in the case of Maxwell
molecules.
In next proposition, we denote by
(33) M0 = ∫ v ∫ e m f dvde
the total mass of the spray (where m is the mass of a droplet).
Proposition 2.1. We consider Q defined in (1) – (7), in the case when ˜S(|v − v∗|) := S is a constant function of the relative velocity (case of Maxwell molecules). The following identities hold (provided that f is a smooth enough nonnegative function of v)
• For i, j = 1, 2, 3, i ̸= j, (34) ∫ v ∫ e
Q(f, f )m(vi− viavr)(vj− vjavr)dvde =
3S r [ −3 8+ γ 4( γ 2 − 1) ] (1− α)M0Tij, • For i = 1, 2, 3, ∫ v ∫ e Q(f, f )m(vi− viavr) 2dvde = 3S r [ −3 8 + γ 4( γ 2 − 1) ] (1− α)M0Tii (35) + 3S 8r(1 + γ) 2(1− α)M 0T, 5
•
∫ v
∫ e
Q(f, f )m(e− eavr)2dvde =
(36) − 3S 2ra(2− a)(1 − α)M0g + πr2(1− γ 2)S 4 ∫∫∫∫ v,e,v∗,e∗
f f∗m(e + e∗− 2eavr)|v − v∗|2dvdedv∗de∗ + πr2(1− γ 2)2S 48 ∫∫∫∫ v,e,v∗,e∗ f f∗m|v − v∗|4dvdedv∗de∗.
Eq. (36) can be simplified if f is a tensor product (as a function of v and e) in the following way:
∫ v
∫ e
Q(f, f )m(e− eavr)2dvde =
(37) − 3S 2ra(2− a)(1 − α)M0g + πr2(1− γ 2)2S 48 ∫∫∫∫ v,e,v∗,e∗ f f∗m|v − v∗|4dvdedv∗de∗.
It can even be further simplified when moreover f is an (isotropic) Gaussian function of v:
(38) f (v, e) = (∫ w f (w, e) dw ) 1 (2πT )3/2exp(− |v − vavr|2 2T ).
In that case, we end up with
∫ v
∫ e
Q(f, f )m(e− eavr)2dvde =
(39) − 3S 2ra(2− a)(1 − α)M0g + 15S 16r(1− γ 2)2(1− α)M 0T2. Proof of Proposition 2.1:
We use formula (7) for ψ = m(vi− viavr)(vj − vjavr). Remembering that v′ = v+v2 ∗ +1−γ4 (v− v∗) +1+γ4 |v − v∗|σ, (40)
we see that for i̸= j,
ψ′ = m ( vi+v∗i 2 − viavr+ 1−γ 4 (vi− v∗i) + 1+γ 4 |v − v∗|σi ) ×(vj+vj∗ 2 − vjavr + 1−γ 4 (vj− v∗j) + 1+γ 4 |v − v∗|σj ) . (41)
Using the symmetry relations
∀i ̸= j, ∫ σ∈S2 σidσ = 0, ∫ σ∈S2 σiσjdσ = 0, (42) we end up with 1 4π ∫ σ∈S2 ψ′dσ = m[(vi+ v ∗ i 2 − viavr )(vj+ vj∗ 2 − vjavr ) +(vi+ v ∗ i 2 − viavr )1 − γ 4 (vj− v ∗ j) +1− γ 4 (vi− v ∗ i)( vj + v∗j 2 − vjavr) + (1 − γ 4 )2 (vi− vi∗)(vj − v∗j) ] , (43) 6
and 1 4π ∫ σ∈S2 (ψ′ − ψ)dσ = m[−7 16 − 3γ 8 + γ2 16 ]
(vi− viavr)(vj− vjavr)
+m [1 16 + γ 8 + γ2 16 ] (v∗i − viavr)(v∗j − vjavr)
+A⊥(v,v∗)(vi− viavr)(v∗j − vjavr) + B⊥(v,v∗)(vj− vjavr)(vi∗− viavr),
(44)
for some quantities A⊥(v,v∗) and B⊥(v,v∗) that will disappear when the integration over dvdv∗ is
performed.
Using the weak formulation (7), (45)
∫ v
∫ e
Q(f, f )m(vi− viavr)(vj− vjavr)dvde
= 4πS[−3 8 − γ 4 + γ2 8 ] ∫∫∫∫ v,e,v∗,e∗ f f∗m(vi− viavr)(vj − vjavr)r 2dvdedv∗de∗ = 4πS[−3 8 − γ 4 + γ2 8 ]( ∫ v ∫ e
f m(vi− viavr)(vj− vjavr)dvde
| {z } TijM0 )( ∫ v∗ ∫ e∗ f∗r2dv∗de∗ | {z } 3 4πr(1−α) ) = 3S r [−3 8 + γ 4( γ 2 − 1) ] (1− α)M0Tij. We obtain therefore formula (34).
We now turn to the case when i = j, and take consequently ψ = m(vi−viavr)
2. The computation runs thus: (46) 1 4π ∫ σ∈S2 (ψ′− ψ)dσ = m(vi− viavr) 2[−7 16 − 3γ 8 + γ2 16] + m(v∗i − viavr) 2[1 16 + γ 8 + γ2 16] + m (1 + γ)2 16 |v − v ∗|21 3 + C⊥(v,v∗)(vi− viavr)(vi∗− viavr),
where the last term will vanish after integration over dvdv∗. Then, ∫∫∫∫ v,e,v∗,e∗ f f∗m(1 + γ) 2 16 |v − v ∗|24π 3 r 2S(˜ |v − v∗|)dvdedv∗de∗ (47) = 3S 8r(1 + γ) 2M 0(1− α)T.
Recalling the computation leading to formula (34), we end up with formula (35). Next computation is related to the moment g defined in (32). We observe that
1 4π ∫ σ [(e′∗)2+ (e′)2− (e∗)2− e2] dσ (48) = −a(2− a) 2 (e− e ∗)2+ (1− γ2)|v − v∗|2 8 (e + e ∗) + 1 128(1− γ 2)2|v − v∗|4+ 1 128(1− γ 2)2|v − v∗|2 1 4π ∫ σ ( < σ| v − v∗ >)2dσ, 7
so that (49)
J : =
∫∫ v,e
Q(f, f )m(e− eavr)2dvde
= 1 2 ∫∫∫∫ v,e,v∗,e∗ ∫ σ f f∗m [ −a(2− a) 2 (e− e ∗)2 | {z } A + (1− γ2)|v − v ∗|2 8 (e + e ∗) | {z } B + 1 128(1− γ 2)2|v − v∗|4 | {z } C + 1 128(1− γ 2)2|v − v∗|2(< σ| v − v∗>)2 | {z } D −eavr(1− γ2)|v − v ∗|2 4 | {z } E ] r2S(˜ |v − v∗|)dvdedv∗de∗dσ.
Some of the terms appearing in this formula can be computed:
• For A: (50) ∫∫∫∫ v,e,v∗,e∗ ∫ σf f∗mAr2S(|v − v˜ ∗|)dvdedv∗de∗dσ =− 3S r a(2− a)(1 − α)M0g.
• We deal with the terms B and E together, since they both lead to the appearance of a
”cross moment”. ∫∫∫∫ v,e,v∗,e∗ ∫ σ f f∗m(B + E)r2S(˜ |v − v∗|)dvdedv∗de∗dσ (51) = πr2S1− γ 2 2 ∫∫∫∫ v,e,v∗,e∗
f f∗m(e + e∗− 2eavr)|v − v∗|2dvdedv∗de∗.
In the case when the distribution w.r.t. energy is independent of the distribution w.r.t. velocity (i.e. when f is a tensor product), we see that
∫∫∫∫ v,e,v∗,e∗ ∫ σf f∗m(B + E)r 2S(˜ |v − v∗|)dvdedv∗de∗dσ = 0. (52)
• We now focus on the terms C and D. After integration w.r.t. σ, we obtain
(53) J2 := ∫∫∫∫ v,e,v∗,e∗ ∫ σ f f∗m(C + D)r2S(˜ |v − v∗|)dvdedv∗de∗dσ = (1− γ 2)2 24 r 2Sπm ∫∫∫∫ v,e,v∗,e∗ f f∗|v − v∗|4dvdedv∗de∗.
Then, if f is an (isotropic) gaussian function of v (that is, (38) holds), one gets (54) ∫∫∫∫ v,e,v∗,e∗ f f∗|v − v∗|4dvdv∗dede∗= 60T2( ∫ v ∫ e f dvde)2.
All in all, we end up with (36), (37) and (39).
2.2. Evolution of the moments of the Boltzmann equation in the case of Maxwell
molecules. We now consider a (smooth) solution of eq. (31).
Using (34) and (35), we get an equation satisfied by the directional temperature Tij, for i, j = 1, 2, 3, i̸= j: d dtTij(t) = 3S r [−3 8 + γ 4 (γ 2 − 1 )] (1− α)Tij(t), (55)
and by the directional temperature Tii, for i = 1, .., 3: d dtTii(t) = 3S r [ −3 8 + γ 4 (γ 2 − 1 )] (1− α)Tii(t) + 3S 8r(1 + γ) 2(1− α)T (t). (56)
Note that the evolution of the temperature T (t) can be recovered by adding (56) for i = 1, 2, 3:
d dtT (t) = 3S 4r(γ 2− 1)(1 − α)T (t). (57)
It is not possible to obtain a closed equation for g without using some approximation. We shall use formula (39), which in principle only holds for functions which are tensor products, and which moreover are Gaussian functions of v.
We end up with the following approximate equation:
(58) d dtg(t)≈ − 3S 2ra(2− a)(1 − α)g(t) + 15 16r(1− γ 2)2(1− α)ST2.
The quality of the approximation leading to (58) will be tested at the numerical level in subsec-tion 4.2 (Fig. 6).
2.3. Evolution of the moments of the Boltzmann equation in the case of hard spheres. In the case of hard spheres (that is, when ˜S satisfies (8)), no closed equations can be written down
for the directional temperature Tij. We use therefore approximate equations. Our choice is the following: we write
(59) d dtTij(t)≈ 3S1(t) r [ −3 8 + γ 4 (γ 2 − 1 )] (1− α)Tij(t), ı, j = 1, 2, 3, i̸= j, (60) d dtTii(t)≈ 3S1(t) r [ −3 8 + γ 4 (γ 2 − 1 )] (1− α)Tii(t) + 3S1(t) 8r (1 + γ) 2(1− α)T (t), i = 1, 2, 3,
that is, a set of equations identical to those which are written in the case of Maxwell molecules, except that the constant S is replaced by a function S1(t) of the time t, which approximates|v −v∗|
at time t.
Many different choices are possible for S1, our proposition is formula (26). This corresponds to
taking for f an anisotropic gaussian function of v, that is, in a diagonal basis for the matrix of directional temperatures (where v = (˜v1, ˜v2, ˜v3) and vavr= (˜v1avr, ˜v2avr, ˜v3avr):)
(61) f =( ∫wf dw ) 1 (2π)3/2√T˜11T˜22T˜33e −(˜v1−˜2 ˜v1avr )T11 2 e− (˜v2−˜v2avr )2 2 ˜T22 e− (˜v3−˜v3avr )2 2 ˜T33 , 9
in the formula (∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗| 4dvdv∗dede∗ ∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗|2dvdv∗dede∗ )1/2 , (62) considered as an approximation of ∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗| 3dvdv∗dede∗ ∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗|2dvdv∗dede∗ . (63)
We now discuss the relevance of our approximation: we compare the results obtained with the original Boltzmann equation (with hard spheres) and different approximate models of the cross section with the simplified BGK type model. We try three differents approximations of the cross section, the first one consists in computing|v − v∗| as a quadratic mean, that is:
(64) |v − v∗| ≈ √∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗|2dvdedv∗de∗ ∫ v ∫ e ∫ v∗ ∫ e∗f f∗dvdedv∗de∗ ,
which amounts to replace|v−v∗| by√6T (t). The second choice consists in replacing the anisotropic gaussian function by an isotropic one. This leads to the formula |v − v∗| ≈
√
15 9
√
6T (t). The last one corresponds to formula (26).
The numerical results are presented in Fig. 1 and show that formula (64) is much less efficient than the other ones. The gain obtained by using an anisotropic gaussian function instead of an isotropic one is slight (and does not necessarily justify the use of a complex formula like (26)).
We now propose an approximate equation for the variance g of the internal energy. We write
(65) d dtg(t)≈ − 3 2ra(2− a)(1 − α)S2(t) g(t) + 15 16r(1− γ 2)2(1− α)S 3(t) T2,
that is, an equation identical to the one written in the case of Maxwell molecules, except that the constant S is replaced by functions S2(t) and S3(t) of the time t, which approximate |v − v∗| at
time t.
Here, we propose the simplest formula for S2, that is, we consider (27), which corresponds to
taking S2 as the quantity
|v − v∗| ≈ ∫∫∫∫ v,e,v∗,e∗f f∗|v − v∗|dvdv∗dede∗ ∫∫∫∫ v,e,v∗,e∗f f∗dvdv∗dede∗ , (66)
when f is an (isotropic) Gaussian function of v (that is, formula (38) holds).
We now discuss the quality of this approximation. We compare in Fig. 2 the results obtained with the original Boltzmann equation and the results with our simplified kinetic model with two different approximations for S2(t) : the one given by (27), and the other using|v −v∗| ≈
√
6T (that is, (64)). We use a numerical simulation of the elastic case (γ = 1) since in that case, the positive term in (65) disappears, so that only the approximation involving S2(t) counts.
Fig. 2 shows that the approximation using (27) is much more efficient than the one using (64). We take for S3 the formula S3 = 32 T
1/2
5√π . This corresponds to computing S3(t) as the value of the following ratio:
S3(t)≈ ∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗|5dvdv∗dede∗ ∫ v ∫ e ∫ v∗ ∫ e∗f f∗|v − v∗|4dvdv∗dede∗ , (67) 10
when f is given by (38). The formula S3 = 32 T 1/2 5√π is a consequence of (68) ∫∫∫∫ v,e,v∗,e∗f f∗m|v − v∗| 5dvdv∗dede∗ = 384T5/2 √π m( ∫v∫ef dvde )2 ,
and (54) [with f given by (38)].
This yields for J2 in eq. (53) (replacing S3(t) by its value) the following formula:
J2 = 12 r√π(1− γ 2)2(1− α)M 0T5/2, (69) and so, d dtg(t)≈ − 3 2ra(2− a)(1 − α)S2g(t) + 6 r√π(1− γ 2)2(1− α)T5/2. (70)
The interest of using formula (28) instead of √6T (that is, (64)) can be seen on the numerical simulation yielding Fig. 3. There, we have set the internal energy exchange parameter at 0, so that the negative part of (70) vanishes, and only the quality of the approximation of S3 is tested.
3. Establishment of the simplified model
3.1. Evolution of the moments of the simplified model with arbitrary coefficients. We introduce here the simplified model [which hopefully mimics the behavior of (10) – (11)], with arbitrary coefficients c1, .., c4, ν: ∂tf +∇v· ( c1f (v− vavr) ) + ∂e(c2f + c3(e− eavr)f + c4|v − vavr|4∂ef ) (71) = −ν(f − f0)
where vavr, eavr, and f0 are defined by (17), (18) and (19).
It is possible to compute explicitly the evolution of some moments of the solution of eq. (71). Those computations are summarized in the following
Proposition 3.1. We assume that c1, .., c4, ν ≥ 0 do not depend on v, e (they can depend on T and t). Then the (smooth) solutions of eq. (71) satisfy the following properties:
• Conservation of mass and momentum:
(72) ∂t ∫ v ∫ e f ( 1 v ) dvde = 0, • Evolution of the total energy:
(73) ∂t ∫ v ∫ e m f ( |v|2 2 + e ) dvde = [3c1T + c2] M0, • Evolution of the directional temperatures:
(74) ∀i, j = 1, 2, 3, i ̸= j, ∂tTij = (2c1− ν) Tij,
(75) ∀i = 1, 2, 3, ∂tTii= (2c1− ν) Tii+ ν T,
• Evolution of the variance of the internal energy:
(76) ∂tg = 2c3g− 2c4 M0 ∫ v ∫ e f m|v − vavr|4dvde. 11
Proof of Proposition 3.1: The property of conservation
(72) is directly obtained due to the definition of vavr.
We then compute the evolution of the kinetic energy. The terms in ∂eobviously do not contribute to its evolution. Moreover,
∫ v ∫ e∇v· ( c1f (v− vavr) ) m|v|22dvde =−3c1M0T, (77) (78) ∫ v e−|v−vavr|22T m|v| 2 2 dv = 3 2m (2π) 3/2T5/2+1 2m (2πT ) 3/2|v avr|2, and thus : ∫ v ∫ ef0(t, v, e)m |v|2 2 dvde = M0 [ 3 2T + 1 2|vavr|2 ] =∫v∫ef m|v|22dvde := Ec. (79)
The evolution of the internal energy can easily be computed since the only term giving a non-zero contribution is ∂e(c2f ). We get (80) ∫ v ∫ e
me∂e(c2f )dedv =−c2M0.
Collecting all those terms, we end up with eq. (73).
Next, we examine the evolution of directional temperatures for solutions of (71). As in the computation of the evolution of the total energy, the terms in ∂e obviously give no contributions at this level.
For the contributions related to c1f (v− vavr), we get the following formulas:
For k̸= l, ∫∫ v,e∇v· ( c1f (v− vavr) )
m(vk− vkavr)(vl− vlavr)dvde
=−c1 ∑ i=1,2,3 ∫∫ v,ef m [ (vi− viavr)∂vi ( (vk− vkavr)(vl− vlavr) )] dvde =−c1 ∑ i=1,2,3 ∫∫ v,ef m(vi− viavr) [
δi=k(vl− vlavr) + δi=l(vk− vkavr)
]
dvde
=−2c1
∫∫
v,ef m(vl− vlavr)(vk− vkavr)dvde
=−2c1M0Tkl(t); (81) For k = l, (82) ∫ v ∫ e ∇v· ( c1f (v− vavr) ) m(vk− vkavr) 2dvde =−2c 1M0Tkk(t). Finally, for the contribution related to−ν(f − f0), we get when k̸= l:
(83)
∫ v
∫ e
−ν(f − f0) m(vk− vkavr)(vl− vlavr)dvde =−νM0Tkl(t),
and when k = l, ∫ v ∫ e −ν(f − f0) m(vk− vkavr) 2dvde =−νM 0Tkk(t) + νM0T (t). (84)
Collecting all the terms, we obtain eq. (74) and eq. (75).
We finally examine the contributions of the various terms on the evolution of g. Obviously, the terms in ∇v do not contribute to the evolution of g, and the same holds for ∂e(c2f ).
Then,
∫ v
∫ e
∂e(c3(e− eavr)f )m(e− eavr)2dvde =−2c3M0g(t),
(85) (86)
∫ v
∫
e∂e(c4|v − vavr|4∂ef )m(e− eavr)2dvde = 2c4 ∫∫
v,ef m|v − vavr|4dvde, and −ν ∫ v ∫ e
f m(e− eavr)2dvde =−νM0g(t),
(87) ν ∫ v ∫ e
f0m(e− eavr)2dvde = νM0g(t).
(88)
Finally, the evolution of g is given by eq. (76). This ends the proof of Prop. 3.1.
3.2. Computation of the coefficients; case of Maxwell molecules. We now write down the constraints on the parameters which enable to identify the behavior of the moments (total energy,
g and Tij) for the simplified model and for the original model, in the case of Maxwell molecules
(that is, when ˜S(|v − v∗|) = S).
In order to recover the conservation of total energy which held in the original model, one needs to ensure (according to (73)) that
(89) c2=−3c1T.
In order to mimic the behavior of the directional temperatures when f satisfies the original model, we write the following constraints (corresponding to the cases i̸= j and i = j respectively):
(90) 2c1− ν = 3S r [− 3 8 + γ 4( γ 2 − 1)](1 − α), (91) ν = 3S 8r(1 + γ) 2(1− α).
Finally, we wish to mimic the behavior of g. This first leads to
(92) c3=−
3
4ra(2− a)(1 − α)S.
It remains to perform the computation of ∫∫v,ef m|v − vavr|4dvde. This is not possible in general,
and we retain as an approximate result what is obtained when f is assumed to be an (isotropic) Gaussian w.r.t. v (that is, f is given by formula (38)). In this situation, one is led to
∫∫ v,e
f m|v − vavr|4dvde = 15M0T2.
(93)
Then, the identification with the (approximate) o.d.e. (58) satisfied by g(t) when f is solution of the Boltzmann equation with Maxwell molecules leads to:
c4=−
1
32r(1− γ
2)2(1− α)S.
(94)
Collecting all those identities, we get the equations (21) – (25) for the parameters of the model described in the introduction (with S1(t) = S2(t) = S3(t) = S).
3.3. Computation of the coefficients; case of hard spheres. In this subsection, we write down the constraints on the parameters which enable to identify the behavior of the moments (total energy, g and Tij) for the simplified model and for the original model, in the case of hard spheres (that is, ˜S(|v − v∗|) = |v − v∗|).
The conservation of total energy still leads to eq. (89). Then, it is easy to see that (90) – (92), (94) become (95) 2c1− ν = 3S1 r [− 3 8 + γ 4( γ 2 − 1)](1 − α), (96) ν = 3S1 8r (1 + γ) 2(1− α), (97) c3 =− 3 4ra(2− a)(1 − α)S2, (98) c4 =− 1 32r(1− γ 2)2(1− α)S 3,
where S1, S2 and S3 are given by (26), (27) and (28). In the last equation, the same assumptions
on ∫v∫ef m|v − vavr|4dvde have been performed as in the case of Maxwell molecules. We end up
again with the equations (21) – (25) for the parameters of the model described in the introduction.
We have thus obtained our simplified model in the case of Maxwell molecules as well as in the case of hard spheres.
3.4. Extension of the model when a, γ depend on |v − v∗|. We now briefly explain how to extend our analysis when the kernel Q (with hard spheres cross section) defined in (10) – (15) includes inelasticity and energy exchange parameters a and γ which depend on|v − v∗| instead of being absolute constants, that is, a := ˜a(|v − v∗|), γ := ˜γ(|v − v∗|) (Cf. [Mat06] and [DM10]).
Our proposition consists in introducing the simplified model (16) – (30), where a and γ (appearing in formulas (21) – (25)) are replaced by ˜a(√6T ) and ˜γ(√6T ) respectively [that is,|v−v∗| is replaced by its mean quadratic value, as in formula (64)].
4. Numerical simulations
4.1. Numerical method. In order to solve (16) – (30), we use a particle method ([LPS98]) (with constant weight w): the density f is discretized as
f (n∆t, v, e)∼
N ∑
i=1
w δvi(n∆t),ei(n∆t),
where δvi(n∆t),ei(n∆t)is the Dirac mass at velocity vi(n∆t) and internal energy ei(n∆t) and N is the
number of particles. The ”Vlasov-Fokker-Planck” part of eq.(16) [that is, the l.h.s. of the equation] is solved by discretizing (at the first order) the characteristic o.d.e.s for vi and ei. Moreover, a realization of the Brownian motion is used for the term proportional to ∂e2f . The exact conservation
of the momentum and total energy is enforced at the end of this procedure. The ”BGK” part of eq. (16) [that is, the r.h.s. of the equation] is treated by modifying the velocities of a randomly chosen set of particles (Monte-Carlo method). Once again, the conservation of momentum and kinetic energy (which implies total energy too since the internal energy remains unchanged in that step) is enforced at the end of the time step.
Note also that the numerical results obtained with this discretization of eq. (16) – (30) are compared with simulations of the original equation (31) obtained by a DSMC scheme (the code is a modified version of the code used in [Bar04, DM10])
4.2. Numerical experiments; Maxwell molecules. This subsection is dedicated to the study of the behavior of solutions of eq. (16) – (30) in the case of Maxwell molecules. Since the evolution of some moments of the original eq. (31) is explicitly known for this cross section (in particular the evolution of Tij), it is possible to make comparisons with this explicit formula. When no such explicit formula exists, we use instead a comparison with solutions of eq. (31) obtained numerically.
We start with the study of the evolution of the directional temperatures Tij for an anisotropic initial distribution. We provide Fig. 4 for T12 when γ = 0.3. We compare in this figure the values
of T12 obtained by the discretization of the original Boltzmann eq. (31) and those obtained by
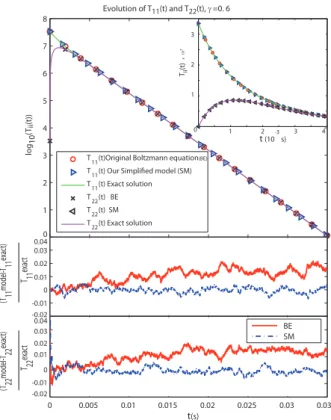
the discretization of our simplified eq. (16) – (30). The same is performed in Fig. 5 for T11, T22
when γ = 0.6. The trend to equilibrium of directional temperatures can be observed during a short transient phase.
As expected, the curves are extremely close, since the Tij satisfy in both models the same o.d.e. [the coefficients in eq. (16) have been built for that purpose]. This test in fact shows that the error of dicretization for eq. (16) as well as eq. (31) is negligeable. We have added on the figures the curve corresponding to the exact solution of the o.d.e. satisfied by T12, T11, T22.
We then turn to the evolution of the parameter g. We provide figures (Cf. Fig. 6) which show a comparison of the case when f is the (discretized) solution of the Boltzmann equation (31) with the case when f is the (discretized) solution of the simplified model (16). The different figures correspond to different choices of parameters (of inelasticity) γ and (of exchange of energy) a.
As can be seen on the figures, the curves for the two models are very close, except in the special (and non-physical) case when a = 0 (that is, when internal energy is not exchanged at all during the collisions). The fact that g behaves in the same way for the two models is no surprise since the parameters of the simplified model are built for that purpose. It was however not completely obvious that this behavior would be so close (still except when a = 0), since g does not exactly satisfy any o.d.e. (as Tij did): remember that the computations leading to the parameters in the simplified model were only approximations.
Next curves concern moments which have not been used for specifying the parameters of the simplified model (16), namely|e − eavr| (Cf. Fig. 7), and √ |v2|
T (t)+|v1|
(Cf. Fig. 8).
As could be guessed, the curve coming out of eq. (31) and those coming out of the simplified model (16) do not fit as well as the curves for Tij or even g. The gap between them however remains reasonable.
4.3. Numerical experiments; hard spheres. We provide in this subsection computations for the same quantities as in the previous subsection, but in the case when the cross section is that of hard spheres (which is much more physically relevant). In this situation, even quantities like Tij are not exactly solutions of an o.d.e., so that it is only possible to compare the numerical experiments for the two models.
As in the previous subsection, we start with the evolution of the directional temperatures Tij, for an anisotropic initial distribution. The fit between the curves for models (31) and (16) is of course not as perfect as in the case of Maxwell molecules, but it still remains quite satisfactory (Cf. Fig. 9).
The same experiment is done for the directional temperature Tii when γ = 0.6 (Fig. 10)
The same can be said of the evolution of g (Cf. Fig. 11), notice that the case when a = 0 still remains the worst.
We use a logarithmic scale in order to check that the slope of the decay of g (when the time is large) is respected in the simplified model. This can be seen in Fig. 12 (we consider the elastic case γ = 1 so that an exponential behaviour is expected for g(t), as can be guessed from (65)).
We conclude this subsection by presenting curves for the moments |e − eavr| (Cf. Fig. 13), and
|v1| √
T (t)+|v2|
(Cf. Fig. 14).
We observe (as expected) a slight degradation of the results w.r.t. the case of Maxwell molecules. 4.4. Numerical experiments; velocity-depending parameters.
This subsection is devoted to the presentation of results when both γ and a are functions of
|v − v∗| in eq. (31), as described in subsection 3.4.
More precisely, we consider the following formulas for the parameters γ and a (Cf. [Mat06] and [DM10]):
(99) γ(˜ |v − v∗|) = exp(− γ1
|v − v∗|),
(100) ˜a(|v − v∗|) = 1 − exp(− a1
|v − v∗|).
We compare the results obtained on one hand by using the original Boltzmann equation (with
a := ˜a(|v − v∗|) and γ := ˜γ(|v − v∗|) given by (99), (100); and with hard spheres), and on the other
hand by using our simplified model with a := ˜a(√6T ), γ := ˜γ(√6T ), as proposed in subsection 3.4.
We first compare the evolution of the directional temperatures T12(t), T11(t), T22(t), in order to
observe the trend to equilibrium of those temperatures (Fig. 15 and 16). We take two different values for the parameter γ1 in ˜γ.
On a longer time scale, we also present results in LogLog scale (Fig. 17) for the evolution of the temperature T (that is, we check Haff’s law numerically).
We end up this series of simulation by one example of evolution of the variance of internal energy
g(t) (Fig. 18).
In our simulations, no sensible degradation was observed w.r.t. the case of hard spheres (with given a, γ).
5. Conclusion
We introduced in this paper a model of BGK type for the description of the effect of collisions which are inelastic and in which the internal energy of the particles (droplets) is tracked (and can be exchanged during collisions).
This model can be obtained almost entirely in a rational way when the collisions occur with a cross section of Maxwell molecules type.
In the more realistic case of hard spheres (and even more when the inelasticity and internal energy exchange parameters can depend on the relative velocity of incoming droplets), approximations must be performed.
The quality of these approximations was tested at the numerical level.
References
[AOB89] A.A. Amsden, P.J. O’Rourke, and T.D. Butler. Kiva II, a computer program for chemical reactive flows with spray. Technical report, Los Alamos National Laboratory, 1989.
[AS04] A. Astillero and A. Santos. A granular fluid modeled as a driven system of elastic hard spheres. Mallamace, F. (ed.) et al., La fisica dei sistemi complessi. (Nuovi sviluppi e prospettive). Rendiconti della Scuola Internazionale di Fisica “Enrico Fermi”, CLV Corso, Varenna, Italia, 1–11 Luglio 2003. Bologna: Societ`a Italiana di Fisica; Amsterdam: IOS Press. Proceedings of the International School of Physics “Enrico Fermi” 155, 475-480 (2004)., 2004.
[Bar04] C. Baranger. Modelling of oscillations, breakup and collisions for droplets: the establishment of kernels for the T.A.B. model. Math. Models Methods Appl. Sci., 14(5):775–794, 2004.
[BCG00] A. V. Bobylev, J. A. Carrillo, and I. M. Gamba. On some properties of kinetic and hydrodynamic equations for inelastic interactions. J. Statist. Phys., 98(3-4):743–773, 2000.
[BGK54] P.L. Bhatnagar, E.P. Gross, and M. Krook. A model for collision processes in gases. I: Small amplitude processes in charged and neutral one-component systems. Phys. Rev., II. Ser., 94:511–525, 1954.
[BGP04] A. V. Bobylev, I. M. Gamba, and V. Panferov. Moment inequalities and high-energy tails for the boltzmann equations with inelastic interactions. J. Statist. Phys., 116(5-6):1651–1682, 2004.
[CGS07] G.L. Caraffini, M. Groppi, and G. Spiga. On BGK approximation for reactive and nonreactive flows. Transp.
Theory Stat. Phys., 36(4-6):475–494, 2007.
[DM10] L. Desvillettes and J. Mathiaud. Some aspects of the asymptotics leading from gas-particles equations towards multiphase flows equations. J. Statist. Phys., 141:120–141, 2010. 10.1007/s10955-010-0044-3. [GK02] M. Groppi and W. Koller. Kinetic calculations for chemical reactions and inelastic transitions in a gas
mixture. Zeitschrift f¨ur Angewandte Mathematik und Physik (ZAMP), 5:855–876, 2002.
[GPV04] I. M. Gamba, V. Panferov, and C. Villani. On the Boltzmann equation for diffusively excited granular media. Comm. Math. Phys., 246(3):503–541, 2004.
[GS99] M. Groppi and G. Spiga. Kinetic approach to chemical reactions and inelastic transitions in a rarefied gas.
Journal of Mathematical Chemistry, 26:197–219, 1999. 10.1023/A:1019194113816.
[LHH66] Jr. Lowell H. Holway. New statistical models for kinetic theory: Methods of construction. Physics of Fluids, 9(9):1658–1673, 1966.
[LPS98] B. Lapeyre, E. Pardoux, and R. Sentis. M´ethodes de Monte-Carlo pour les ´equations de transport et de diffusion, volume 29 of Math´ematiques & Applications (Berlin) [Mathematics & Applications].
Springer-Verlag, Berlin, 1998.
[MA00] J.M. Montanero and A.Santos. Computer simulation of uniformly heated granular fluids. Granular Matter, 2:53–64, 2000. 10.1007/s100350050035.
[Mat06] J. Mathiaud. Etude de syst`emes de type gaz-particules. PhD thesis, CMLA, Ecole normale sup´erieure de Cachan, 2006.
[O’R81] P. O’Rourke. Collective drop effects on vaporizing liquid sprays. PhD thesis, Princeton University, 1981. [San03] A. Santos. Transport coefficients of d-dimensional inelastic maxwell models. Physica A: Statistical Mechanics
and its Applications, 321(3-4):442 – 466, 2003. Appendix C.
[Vil02] C. Villani. A review of mathematical topics in collisional kinetic theory. Elsevier Science, 2002.
[Vil06] C. Villani. Mathematics of granular materials. J. Statist. Phys., 124:781–822, 2006. 10.1007/s10955-006-9038-6.
[Wil85] F. A. Williams. Combustion Theory. The Fundamental Theory of Chemically Reacting Flow Systems. Benjamin-Cummings Publishing Company, 1985.
CEA,DAM,DIF, F-91297 Arpajon, France, e-mail aude.champmartin@cea.fr
CMLA, Ecole Normale Sup´erieure de Cachan, IUF & CNRS, PRES UniverSud, 61, Av. du Pr´esident Wilson, 94235 Cachan Cedex, FRANCE. e-mail desville@cmla.ens-cachan.fr
CEA,DAM,DIF, F-91297 Arpajon, France, e-mail julien.mathiaud@cea.fr
0 1 2 3 4 5 6 7 8 x 10−8 2 4 6 8 10 12 14x 10 7 t T11 (t), T 33 (t)
Evolution of T11(t) and T33(t) with different approximations of cross section T11 Our simplified model (SM) S1(t)= T33 Our simplified model (SM) S1(t)=
T11 SM with S1(t) given by (26) T33 SM with S1(t) given by (26) T11 SM model with S1(t)=
T33 SM model with S1(t)=
T11 Original Boltzmann equation T33 Original Boltzmann equation
15 / 9 6T
15 / 9 6T
6T 6T
(a) Evolution of T11(t) and T33(t). The upper curve corresponds to T33(t). The simulation is performed on the typical time of equilibrium of directional temperatures (which is much shorter than the time of decay due to the inelastic behavior). The approximation with the anisotropic Gaussian (26) fits best with the evolution of the solution of the Boltzmann equation.
0 0.2 0.4 0.6 0.8 1 1.2 x 10−5 4.5 5 5.5 6 6.5 7 7.5 8 t lo g10 (T(t))
Evolution of T(t) with different approximations of cross section Our simplified model(SM), with S(t) given by (26)
SM model with S1(t)=
SM model with S1(t)=
Original Botlzmann equation
15 / 9 6T
6T
(b) Evolution of the temperature T (t) in the same conditions, but on a longer time scale. We see that on this time scale, the isotropic ap-proximation
√ 15
9 √
6T works as well as formula (26).
Figure 1. Initial datum corresponding to T33 = 4 T11. Hard spheres. The
in-elasticity parameter is γ = 0.6, different approximations of the cross section are performed.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 x 10−7 0 1 2 3 4 5 6 7 8 9x 10 14 t g(t)
Evolution of g(t) with different approximations of cross section,γ =1,a=0. 5
Our simplified model with S2(t)= SM with S2(t)=
Original Boltzmann equation6T 4T/ π
Figure 2. Evolution of g(t) with γ = 1, a = 0.5. Hard Spheres. The formula (27) fits best with the original Boltzmann model.
0 0.5 1 1.5 x 10−6 0.8 0.9 1 1.1 1.2 1.3 1.4x 10 15 t g(t)
Evolution of g(t) with different approximations of cross section
Original Boltzmann equation Our Simplified model with S3= SM with S3= 6T
32 T/ (5 π)
Figure 3. Evolution of g(t) with a = 0, γ = 0.6. Hard Spheres. In that case (a = 0), only the growing part of g(t) is represented (65). We tested our simplified model versus the original Boltzmann one with two different approximations of the cross section. The formula (28) fits the best with the original Boltzmann model.
0.5 1 1.5 2 2.5 3 3.5 4 x 10−3 0 0.5 1 1.5 2 2.5 3 3.5x 10 7 t Evolution of T12(t), γ=0.3 Exact solution of T12(t)
Our simplified model Original Boltzmann equation
T12
(t)
Original Boltzmann equation Our simplified model 0 0 -0.04 0.04 (T12 model-T12 e xac t) T1 2 e xac t
Figure 4. Evolution of T12(t) with γ = 0.3. Maxwell molecules. In that case, (55)
has an exact solution which allows to observe the discrepancies between the two models and the exact solution.
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0 1 2 3 4 5 6 7 8 t(s) Evolution of T11(t) and T22(t), γ=0. 6 T
11(t)Original Boltzmann equation(BE)
T
11(t) Our Simplified model (SM)
T 11(t) Exact solution T 22(t) BE T 22(t) SM T 22(t) Exact solution 0 1 2 3 4 t (10-3 s) 1 2 3 Tii (t) x 10 7 log 10 (Tii (t)) (T 22 model-T 22 exac t) T 22 exac t BE SM (T 11 model-T 11 exac t) T 11 exac t 0 0.01 0.02 -0.01 -0.02 0.03 0.04 -0.01 0.01 0.02 0 0.03 0.04 -0.02
Figure 5. Evolution of T11(t), T12(t) with γ = 0.6. Maxwell molecules. In that
case (56) has an exact solution. We observe on the top the transient part : first a trend to equilibrium of the temperature between the different directions, and then a decay of the Tii. At the bottom, the discrepancies between the two models and the exact solution are computed for T11 and T22.
0 0.002 0.004 0.006 0.008 0.01 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3x 10 15 t g(t) Evolution of g(t), a=0, =0.6
Our simplified model Original Botzmann equation γ 0 0.002 0.004 0.006 0.008 0.01 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25 1.3x 10 15 t g(t) Evolution of g(t), a=0, =0.6
Our simplified model Original Botzmann equation γ 0 1 2 3 4 5 6 7 8 x 10−3 0 1 2 3 4 5 6 7 8 9x 10 14 t g(t) Evolution of g(t), a=1, =0.6
Our simplified model Original Boltzmann equation
0 1 2 3 4 5 x 10−3 0 1 2 3 4 5 6 7 8 9x 10 14 t g(t) Evolution of g(t), a=0.5, =1
Our simplified model Original Botzmann equation γ 0 1 2 3 4 5 x 10−3 0 1 2 3 4 5 6 7 8 9x 10 14 t g(t) Evolution of g(t), a=0.5, =1
Our simplified model Original Botzmann equation γ
γ
Figure 6. Evolution of g(t) with different values of the two parameters a and γ. Maxwell molecules.
0 0.005 0.01 0.015 0.02 0 1 2 3 4 5 6 7 8 9 10x 10 6 t Evolution of q1(t), a=0.5, =0.6
Original Boltzmann equation Our simplified model
γ
q1
(t)
Figure 7. Evolution of q1(t) = ∫
f (t)|e−e∫ avr|dvde
f (t)dvde with a = 1, γ = 0.6. Maxwell molecules.
0 0.02 0.04 0.06 0.08 0.1 0.12 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 t Evolution of q2(t), γ=0.3
Original Botzmann equation Our simplified model
q2 (t) Figure 8. Evolution of q2(t) = ∫ v ∫ ef (t) |v2| √ T (t)+|v1|
dvde with γ = 0.3. Maxwell molecules.
0 1 2 3 4 5 x 10−7 0 0.5 1 1.5 2 2.5 3 3.5x 10 7 t T12 (t) Evolution of T12(t), γ=0.3
Our simplified model Original Boltzmann equation
Figure 9. Evolution of T12(t) with γ = 0.3. Hard spheres.
0 0.2 0.4 0.6 0.8 1 x 10−3 0 1 2 3 4 5 6 7 8 t Evolution of T11(t) and T22(t),γ=0.6 T
11(t) Original Boltzmann equation
T
11(t) Our simplified model
T
22(t) Original Boltzmann equation
T
22(t) Our simplified model
log 10 (Tii (t)) (x 10 7) Tii (t) t( 10-7 s) 0 2 4 1 2 3
Figure 10. Evolution of T11(t), T22(t) with γ = 0.6. Hard Spheres. On the top
right is shown the trend to equilibrium of the different directional temperatures. The decays of the Tii(t) are also in fair agreement.
0 0.5 1 1.5 2 2.5 3 x 10−6 0 1 2 3 4 5 6x 10 14 t g(t) Evolution of g(t), a=0, =0.6
Our simplified model Original Boltzmann equation γ 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 x 10−6 0 0.5 1 1.5 2 2.5x 10 14 t g(t) Evolution of g(t), a=0.5, =0.6
Our simplified model Original Boltzmann equation γ 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 x 10−6 0 2 4 6 8 10 12 14 16 18x 10 13 t g(t) Evolution of g(t), a=1, γ=0.6
Our simplified model Original Boltzmann equation
0 0.5 1 1.5 2 2.5 3 3.5 4 x 10−7 0 1 2 3 4 5 6 7 8 9x 10 4 t g(t) Evolution of g(t), a=0.5, γ=1
Our simplified model Original Boltzmann equation
0 0.5 1 1.5 2 2.5 3 3.5 4 x 10−7 0 1 2 3 4 5 6 7 8 9x 10 4 t g(t) Evolution of g(t), a=1, γ=1
Our simplified model Original Boltzmann equation
Figure 11. Evolution of g(t) with different values of the parameters a and γ. Hard spheres.
0 0.2 0.4 0.6 0.8 1 x 10−6 −2 −1 0 1 2 3 4 5 t lo g10 (g(t)) Evolution of g(t), a=0.5, γ=1
Our simplified model Original Boltzmann equation
(a) a = 0.5, γ = 1. 0 0.2 0.4 0.6 0.8 1 x 10−6 −4 −3 −2 −1 0 1 2 3 4 5 t lo g10 (g(t)) Evolution of g(t), a=1, γ=1
Our simplified model Original Boltzmann equation
(b) a = 1, γ = 1.
Figure 12. Evolution of g(t). Hard spheres. Semilog scale.
0 0.5 1 1.5 2 2.5 3 3.5 x 10−6 0 1 2 3 4 5 6 7 8 9 10x 10 6 t Evolution of q1(t),γ=0.6, a=1
Original Boltzmann equation Our simplified model
q1 (t) Figure 13. Evolution of q1(t) = ∫ v ∫
e∫f (t)|e−eavr|dvde v ∫ ef (t)dvde , a = 1, γ = 0.6. Hard spheres. 0 1 2 3 4 5 6 7 8 x 10−3 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 t Evolution of q3(t), γ=0.6
Our simplified model Original Boltzmann equation
q3 (t) Figure 14. Evolution of q3(t) = ∫ f (t)√ |v1| T (t)+|v2|
dvde, γ = 0.6. Hard spheres.
0 0.5 1 1.5 2 2.5 x 10−7 0 0.5 1 1.5 2 2.5 3 3.5x 10 7 t T12 (t) Evolution of T12(t), γ1=160
Original Boltzmann equation
Our simplified model
(a) γ1= 160. 0 0.5 1 1.5 2 2.5 x 10−7 0 0.5 1 1.5 2 2.5 3 3.5x 10 7 t T12 (t) Evolution of T12(t), γ1=1600
Original Boltzmann equation
Our simplified model
(b) γ1= 1600.
Figure 15. Evolution of T12(t). γ depending on |v − v∗|.
0 0.5 1 1.5 2 x 10−6 0 0.5 1 1.5 2 2.5 3 3.5x 10 7 t Tii (t) Evolution of T11(t) and T22(t), γ1=160
T11(t) Original Boltzmann equ.
T11(t) Our simplified model T22(t) Original Boltzmann equ.
T22(t) Our simplified model
(a) γ1= 160. 0 0.5 1 1.5 2 x 10−6 0 0.5 1 1.5 2 2.5 3 3.5x 10 7 t Tii (t) Evolution of T11(t) and T22(t), γ1=1600 T11(t) Original Boltzmann equ.
T11(t)
T22 (t) Original Boltzmann equ.
T22(t) Our simplified model Our simplified model
(b) γ1= 1600.
Figure 16. Evolution of T11(t), T22(t). γ depending on|v − v∗|.
−10 −9 −8 −7 −6 −5 −4 −3 −1 0 1 2 3 4 5 6 7 8 log10(t) lo g10 (T(t)) Evolution of T(t), γ1=160
Original Boltzmann equ. Our simplified model
(a) γ1= 160. −100 −9 −8 −7 −6 −5 −4 −3 1 2 3 4 5 6 7 8 log10(t) lo g10 (T(t)) Evolution of T(t),
Original Boltzmann equ. Our simplified model
γ1=1600
(b) γ1= 1600.
Figure 17. Evolution of T (t). γ depending on |v − v∗|. Log-log scale.
0 1 2 3 4 5 6 x 10−7 0 1 2 3 4 5 6 7 8 9x 10 14 t g(t) Evolution of g(t), γ1=160, a1=6000
Original Boltzmann equ. Our simplified model
Figure 18. Evolution of g(t) for γ1= 160, a1= 6000. γ, a depending on |v − v∗|.