HAL Id: dumas-01768908
https://dumas.ccsd.cnrs.fr/dumas-01768908
Submitted on 17 Apr 2018HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Création d’une brochure d’information et de prévention
sur le trouble spécifique des apprentissages en
mathématiques à destination des professeurs des écoles
Clémence Landais
To cite this version:
Clémence Landais. Création d’une brochure d’information et de prévention sur le trouble spécifique des apprentissages en mathématiques à destination des professeurs des écoles. Neurosciences [q-bio.NC]. 2016. �dumas-01768908�
1
Université de Bordeaux
Département d’orthophonie
Année universitaire 2015-2016
Mémoire présenté en vue de l’obtention
du Certificat de Capacité d’Orthophoniste
par Clémence LANDAIS,
née le 3/12/1993 à Lannion (22)
Création d’une brochure d’information et
de prévention sur le trouble spécifique des
apprentissages en mathématiques à
destination des professeurs des écoles
2
Remerciements
Je souhaite remercier les nombreuses personnes qui m’ont soutenue dans ce projet de mémoire.
Je remercie, tout d’abord, ma directrice de mémoire, Anne FRANCOIS-SAINT-CYR, qui m’a guidée et encouragée tout au long de l’élaboration de ce mémoire.
Je remercie Patrick URRUTY et Sarah DUBOUIL qui ont accepté de faire partie du jury de ma soutenance.
Je remercie tous les professeurs des écoles qui ont accepté de répondre aux questionnaires. Leurs avis ont été précieux pour la mise en œuvre de ce projet.
Je remercie également mes maîtres de stage, Anne-Céline ASSELIN et Pascale CELERIER, qui m’ont encouragée dans l’orthophonie au quotidien pendant toute cette année.
Un immense merci à ma sœur, Lucile, pour son aide dans la réalisation infographique de la brochure. Sans elle, la brochure n’aurait jamais été aussi belle !
Merci aussi à mes proches pour leur présence et leur soutien.
Je remercie tout particulièrement Céline, ma colocataire, collègue et amie, qui a partagé mes passades de doute et m’a redonné de la motivation à plusieurs
reprises.
Je remercie finalement ma famille, mes parents et mes frère et sœurs, Amandine, Emilien et Lucile, de leur intérêt pour mon projet, de leur soutien et de leurs encouragements.
3
Sommaire
Introduction ... 7
Partie théorique ... 9
I- L’acquisition des mathématiques ... 9
A) Un peu d’histoire ... 9
B) Les modèles ... 10
1) Le modèle du triple code (Dehaene & Cohen, 1995) ... 11
2) Le modèle de Von Aster et Shalev (2007) ... 12
3) La ligne numérique mentale ... 13
C) Les données anatomiques ... 14
D) Le développement des compétences en mathématiques chez l’enfant ... 15
1) Les capacités en mathématiques du bébé ... 15
2) L’acquisition progressive des différentes compétences en mathématiques ... 15
3) Les difficultés pouvant être rencontrées ... 18
4) Les repères ... 21
II- Le trouble spécifique des apprentissages en mathématiques (TSAM)
... 22
A) Définition ... 22
B) Différenciation TSAM / Trouble du raisonnement logico-mathématique ... 26
C) Prévalence ... 27
4
E) Causes ... 29
F) Comorbidités ... 32
G) Signes d’alerte ... 34
H) Remédiations ... 35
I) Accompagnement des parents ... 38
J) Aménagements pédagogiques ... 39
III- Les brochures d’information à propos de ce trouble ... 42
A) Diverses brochures d’information ... 42
B) Une brochure d’information pour les enseignants ... 45
Partie pratique ... 47
I- Le questionnaire préalable ... 47
A) Une première approche du TSAM ... 47
B) Le TSAM dans la pratique enseignante ... 48
C) La définition du TSAM ... 49
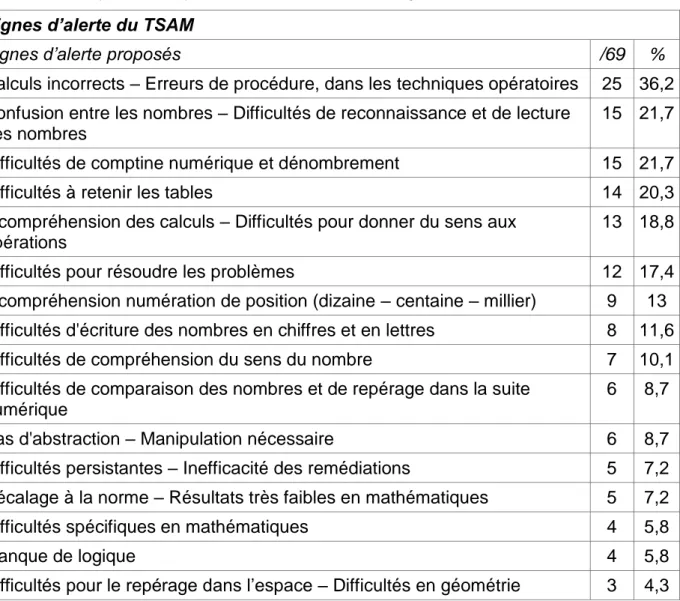
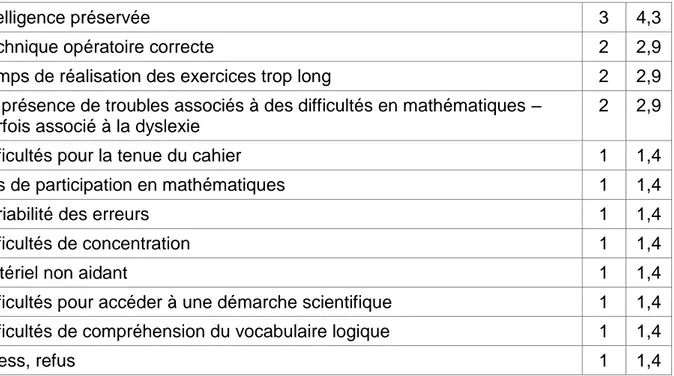
D) Les signes d’alerte du TSAM ... 51
E) Les aménagements scolaires en cas de TSAM ... 52
F) Les souhaits d’information sur le TSAM ... 54
II- La création de la brochure d’information ... 55
A) La présentation visuelle ... 55
B) Définition, p. 2 ... 57
C) Troubles associés, p. 3 ... 57
D) A ne pas confondre, p. 3 ... 58
5
F) Parcours et aménagements, p. 6 et 7 ... 65
G) Pour aller plus loin, p. 8 ... 66
Discussion ... 68
I- La mise à l’épreuve de la brochure ... 68
A) Questionnaire de satisfaction ... 68
B) Finalisation de la brochure ... 71
II- Les implications ... 72
A) Difficultés rencontrées et réflexions associées ... 72
B) Limites ... 75
C) Ouvertures ... 76
Conclusion ... 79
6
Table des annexes
Annexe 1 : Le questionnaire préalable ... 89
Annexe 2 : La première version de la brochure ... 92
Annexe 3 : Le questionnaire de satisfaction ... 97
7
Introduction
L'apprentissage des mathématiques est un des apprentissages fondamentaux de l'école élémentaire. Grâce aux bases acquises dans ce domaine, la vie de chacun d'entre nous se construit et toutes sortes de projets s'ouvrent à nous. Selon le PISA 2012 (Programme International pour le Suivi des Acquis des élèves) (Keskpaik & Salles, 2014), chez les jeunes adultes, le niveau de compétences en mathématiques est intimement lié à la possibilité de réaliser des études après le secondaire et aux revenus financiers une fois la vie active débutée.
Cependant, bien que cet apprentissage soit un tremplin pour l'épanouissement durant toute la vie, il pose des difficultés pour certains d'entre nous. En France, cette problématique nous concerne particulièrement. Le PISA 2012 a présenté des tests en mathématiques à des adolescents de 15 ans dans 65 pays. Cette étude place la France en 25ème position avec un score obtenu correspondant tout juste à la moyenne des scores de tous les pays. De plus, 22,4% des élèves testés présentent des résultats en-dessous du niveau 2, correspondant au seuil de compétences.
Parmi ces élèves en difficultés en mathématiques, certains présentent un trouble spécifique des apprentissages en mathématiques. Dans ce cas, les difficultés sont persistantes et la rééducation orthophonique est un moyen essentiel pour agir sur ces difficultés.
Il est donc primordial de prendre en considération les difficultés en mathématiques. En effet, lorsque celles-ci sont repérées, une investigation peut débuter et des aides peuvent être apportées. La famille peut faire appel à des professionnels tels que les orthophonistes afin de réaliser un bilan. Un diagnostic peut ensuite être posé, notamment le diagnostic de trouble spécifique des apprentissages en mathématiques si des indices suffisants sont réunis. Et ainsi, la prise en charge proposée permet à l'enfant de réaliser le maximum de progrès possibles dans le domaine atteint et d'apprendre à pallier ses difficultés.
Toutefois, ce processus n'est pas systématiquement mis en marche. En réalité, les orthophonistes rencontrent régulièrement de jeunes adolescents n'ayant jamais
8 réalisé de bilan orthophonique et pour lesquels les mathématiques ne prennent pas sens.
En effet, le trouble spécifique des apprentissages en mathématiques reste peu connu du grand public, et également peu connu des médecins et des professeurs (Habib, 2014). C'est également un domaine qui a bénéficié de moins de recherches que le trouble spécifique du langage écrit. Entre 2000 et 2011, la NIH (National Institutes of Health) qui est un des plus grands centres de recherche médicale au monde a dépensé 107,2 millions de dollars pour la recherche sur le trouble spécifique des apprentissages en lecture contre 2,3 millions pour la recherche sur le trouble spécifique des apprentissages en mathématiques (Butterworth, Varma, & Laurillard, 2011).
L'objectif de ce mémoire est ainsi de faire connaître le trouble spécifique des apprentissages en mathématiques aux professeurs des écoles qui sont en première ligne pour le détecter et pour accompagner l'apprentissage des mathématiques chez les enfants présentant ce trouble. Nous avons donc réalisé une brochure d'information concernant le trouble spécifique des apprentissages en mathématiques à destination des professeurs des écoles.
Après une partie théorique exposant les connaissances récentes sur l'apprentissage des mathématiques et les difficultés pouvant l'entraver, nous décrirons notre démarche de création et discuterons de la pertinence de notre outil.
9
Partie théorique
I- L'acquisition des mathématiques
A) Un peu d'histoire
Les recherches les plus récentes sur l’acquisition des mathématiques ont remis en cause des théories précédemment élaborées. Ce paragraphe présente brièvement l'évolution de la recherche afin de mieux comprendre les théories actuelles et de resituer le contexte.
Dans les années 60, la conception piagétienne a largement influencé les connaissances dans le domaine des mathématiques. Cette conception se fonde alors sur la prédominance de la logique. Pour Piaget, l'accès au nombre dépend des opérations logiques telles que, par exemple, la classification et la sériation. Cette théorie a été appliquée d'un point de vue pédagogique ; et ainsi, la classification et la sériation ont été particulièrement entraînées lors des activités proposées à l'école, notamment en maternelle (Fayol, 2013). Dans le programme scolaire de 1995, un paragraphe est consacré aux classifications et aux sériations pour l’école maternelle.
Désormais, plusieurs controverses ont remis en question la vision piagétienne. Tout d'abord, la diversité des difficultés dans le domaine des mathématiques (difficultés d'apprentissage des faits numériques, incapacité de transposition du code verbal à la numération arabe...) ne semble pas correspondre à une atteinte unique de la logique. De plus, l'acquisition tardive des compétences de classification et de sériation (à partir de 6 ans) ne permet pas d'expliquer l'apparition des capacités de comptage et de calcul élémentaire avant l’âge de 6 ans.
En outre, Piaget considère que les capacités logiques sont à la base de l'acquisition du nombre, et que ce dernier émerge spontanément au fur et à mesure du développement (Fayol, 2013).
10 d'un entraînement numérique à la fois sur les compétences en logique et en numération alors qu'un entraînement aux sériations et aux classifications n'a d'impact aussi significatif que sur les compétences en logique, tandis que l’amélioration des capacités numériques est moindre (Clements, 1984).
Les apports piagétiens ne répondent donc pas parfaitement aux problématiques concernant l'acquisition du nombre (Fayol, 2013).
Les recherches en neuropsychologie, à partir des années 80, ont envisagé les capacités mathématiques sous un autre angle. En effet, grâce à l'étude des déficits en mathématiques chez des patients cérébro-lésés, différentes atteintes modulaires sont mises en évidence. Les mathématiques ne sont plus considérées comme un seul élément, soit bon, soit mauvais, mais comme un ensemble complexe de multiples acquisitions. On peut, par exemple, observer une atteinte du calcul sans difficulté de raisonnement, ou une atteinte du calcul exact alors que le calcul approximatif est préservé (Fayol, 2013).
L'évolution des techniques d'imagerie cérébrale a ensuite permis de conforter le modèle du « triple code » élaboré par Stanislas Dehaene et Laurent Cohen (Dehaene & Cohen, 1995). Celui-ci associe les différents codes numériques (code analogique, code verbal et code arabe) à des localisations cérébrales différentes. Chacun des 3 codes possède son propre réseau de neurones et ils sont reliés deux par deux indépendamment, sans accès sémantique obligatoire. Cette théorie sera développée dans la partie suivante.
Ainsi, le développement des mathématiques est constitué de multiples facettes que les recherches actuelles visent à décrire le plus précisément possible.
B) Les modèles
Plusieurs modèles tentent d'expliquer l'acquisition des mathématiques. Le premier appelé « modèle du triple code » a été élaboré par S. Dehaene. Le second est proposé par Von Aster et Shalev. Puis nous détaillerons les connaissances sur la ligne numérique mentale qui est à la base de la compréhension actuelle des acquisitions en mathématiques.
11 1) Le modèle du triple code (Dehaene & Cohen, 1995)
D'après ce modèle, les aptitudes arithmétiques reposent sur trois systèmes de représentation mentale des nombres : le code analogique, le code verbal et le code arabe. Chacun de ces codes est lié à une région cérébrale.
La représentation analogique est une représentation non symbolique du nombre, permettant l'acquisition du sens du nombre et une possibilité de calcul approximatif. Ce code est également impliqué dans les tâches d'estimation et de comparaison de quantités. Les aires cérébrales correspondantes sont les zones pariétales bilatérales, et en particulier le sillon intrapariétal.
La représentation verbale joue son rôle dans la manipulation des concepts liés au nom des nombres et des opérations. Au fil du développement, l'enfant pourra associer une quantité donnée au mot-nombre correspondant. La maîtrise des faits arithmétiques, le comptage et le calcul exact mettent tous en jeu le code verbal. Les zones cérébrales associées au code verbal sont situées dans les aires du langage de l'hémisphère gauche.
La représentation visuelle-arabe est acquise par l'enfant grâce à un entraînement spécifique basé sur la notation positionnelle (notation en base 10, notion de rang). Grâce à cet apprentissage, les enfants accèdent aux jugements de parité et à l'arithmétique écrite. Ils peuvent alors réaliser des opérations complexes. Ce code est lié au traitement visuo-spatial et ne dépend pas du langage. Sa localisation cérébrale se situe dans les régions occipito-temporales des deux hémisphères.
Schéma n°1 : Localisation cérébrale des codes de représentation mentale des nombres Code verbal Code analogique Code visuel
12 Ce modèle permet ainsi de catégoriser les différentes représentations du matériel mathématique et leur localisation cérébrale. Par ailleurs, d'autres auteurs examinent les mathématiques d'un point de vue développemental afin de préciser la progression dans l'apprentissage des mathématiques chez l'enfant.
2) Le modèle de Von Aster et Shalev (2007)
Plusieurs auteurs estiment qu'il existe un sens du nombre génétiquement déterminé, permettant au bébé de discriminer précisément de petites quantités ; et approximativement, de plus grands ensembles d'objets (Habib, 2014). Butterworth (Butterworth, 2010) appelle « système du nombre approximatif » le module en jeu dans ce sens du nombre. Quant à Von Aster et Shalev, ils parlent de « système central
de représentation cardinale des nombres et de la magnitude » (quantité concrète à
laquelle réfère le nombre). Ce système permet le développement des capacités numériques en 4 étapes, au fur et à mesure de l'augmentation des capacités en mémoire de travail (M. G. Von Aster & Shalev, 2007).
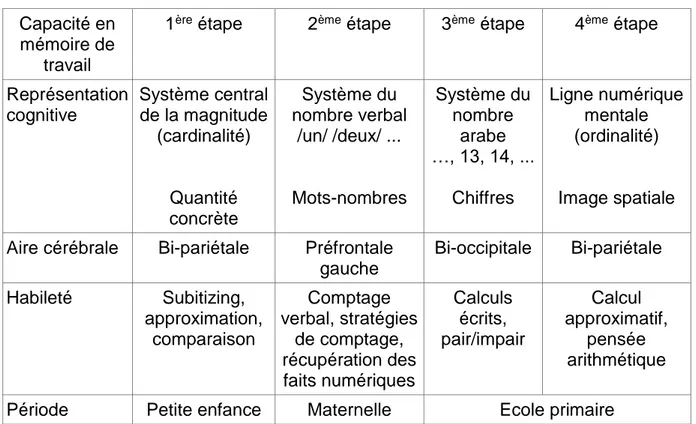
Tableau n°1 : Les quatre étapes du modèle de Von Aster et Shalev (2007)
Capacité en mémoire de
travail
1ère étape 2ème étape 3ème étape 4ème étape
Représentation cognitive Système central de la magnitude (cardinalité) Quantité concrète Système du nombre verbal /un/ /deux/ ... Mots-nombres Système du nombre arabe …, 13, 14, ... Chiffres Ligne numérique mentale (ordinalité) Image spatiale Aire cérébrale Bi-pariétale Préfrontale
gauche Bi-occipitale Bi-pariétale Habileté Subitizing, approximation, comparaison Comptage verbal, stratégies de comptage, récupération des faits numériques Calculs écrits, pair/impair Calcul approximatif, pensée arithmétique
13 La 1ère étape du modèle de Von Aster et Shalev est basée sur les capacités
innées de représentation numérique. Les petites collections d'objets sont reconnues grâce au subitizing et les collections plus grandes peuvent être comparées par un système d'approximation. Ce 1er système est un pré-requis permettant ensuite
l'acquisition des différents codes et la construction de liens entre eux.
La 2ème et la 3ème sont caractérisées par la mise en place de la symbolisation
linguistique et arabe du nombre. Ces 2 étapes sont nécessaires à l'élaboration de la 4ème, c'est-à-dire l'utilisation de la ligne numérique mentale.
L'élaboration de la ligne numérique mentale débute dès l'apparition des premiers mots-nombres et se développe progressivement. Entre 7 et 11 ans, les nombres de 0 à 100 sont d'abord représentés de manière logarithmique, c'est-à-dire que la distance entre deux nombres sur la ligne numérique mentale est de plus en plus petite lorsque les nombres sont plus grands ; puis une représentation linéaire se met en place pour atteindre une représentation d'adulte (Habib, 2014).
Le paragraphe suivant s'attachera à présenter les caractéristiques de cette ligne numérique mentale.
3) La ligne numérique mentale
La ligne numérique mentale permet donc à l'Homme d'avoir des capacités d'estimation approximative. En effet, cette ligne comprend les quantités dans l'ordre croissant de gauche à droite et est à l'origine des capacités de comparaison et de compréhension des additions et des soustractions. Elle serait inconsciente, automatique et non symbolique ; et ne serait déterminée ni par le langage, ni par l'éducation. Les caractéristiques de cette ligne numérique mentale engendrent plusieurs effets :
L'effet de distance : deux nombres proches sont plus difficiles à comparer que deux nombres plus éloignés.
L'effet de taille : deux grands nombres sont plus difficiles à comparer que deux nombres plus petits (Fayol, 2013).
L'effet SNARC (Spatial Numerical Association of Response Code) : en tâche de jugement de parité, les sujets doivent répondre en cliquant avec la main droite ou gauche. Suivant les items, les côtés de réponse sont intervertis entre nombre pair et impair. Les résultats montrent que la réponse est plus rapide avec la
14 main gauche pour les petits nombres et avec la main droite pour les nombres plus grands (M. G. Von Aster & Shalev, 2007).
C) Les données anatomiques
D'après une première étude, les activités numériques sollicitent différentes zones du cerveau lors de leur apprentissage et de leur exécution (Butterworth et al., 2011) :
Les aires frontales qui sont associées aux fonctions exécutives et à la mémoire de travail.
Les aires temporales médianes, associées à la mémoire déclarative.
Les aires pariétales, liées à la magnitude et à la rétention des faits arithmétiques.
Les aires occipito-temporales, associées aux traitements des formes symboliques.
M. Habib donne des informations plus précises, notamment sur le segment horizontal du sillon intrapariétal qui est une zone spécifiquement en jeu dans la réalisation des calculs. Il est activé lors de comparaisons de quantités ou lors de calculs en code arabe ou verbal. Selon les études, plusieurs rôles lui sont attribués. Il permet un traitement approximatif des nombres selon l'effet de distance. Il est aussi facilitateur du jugement de numérosité. De plus, le sillon intrapariétal est à la fois activé pour les soustractions et pour les multiplications, dont les mécanismes sont très différents. Le sillon intrapariétal serait alors un vérificateur de plausibilité du résultat.
Un autre élément constaté par les recherches concerne l'évolution de l'activation des zones cérébrales dans des tâches numériques entre l'enfance et l'âge adulte. Il se trouve que ce sont principalement les mêmes zones qui sont activées, notamment les régions temporo-occipitales médianes et les régions pariétales. On observe toutefois l'implication spécifique des régions pariétales supérieures chez l'adulte alors que chez l’enfant, les régions frontales sont aussi activées. Ainsi, on peut penser que le système de base est bien présent déjà chez l'enfant, et qu'il se spécialise au cours des acquisitions.
15 hémisphères sont impliqués avec une dominance à gauche (Habib, 2014).
Une autre étude visant à déterminer la localisation cérébrale des activités de calcul met en évidence l'implication de nombreuses zones cérébrales. Cependant, on remarque que le segment horizontal du sillon intrapariétal gauche est la seule zone spécifiquement activée pour les tâches de calcul (Simon, Mangin, Cohen, Le Bihan, & Dehaene, 2002).
D) Le développement des compétences en mathématiques chez l'enfant
1) Les capacités en mathématiques du bébé
Dès les premiers mois de vie, les bébés sont capables d'effectuer des calculs simples et de discriminer de petites quantités, ou de plus grandes mais plus éloignées (Habib, 2014). Plus précisément, on envisage l'existence de deux systèmes numériques chez le bébé. Le premier permet la représentation approximative des grandes quantités, et le second la représentation très précise des petites quantités, collections allant jusqu'à 3-4 objets (Hauser & Spelke, 2004).
La représentation approximative des grandes quantités est déterminée par un ratio. En effet, les bébés de 6 mois peuvent discriminer 8 de 16 mais pas 8 de 12 (Xu & Spelke, 2000). L'importance de ce ratio diminue en grandissant. Dès 9 mois, les enfants sont capables de discriminer 8 de 12 mais pas encore 8 de 10 (Lipton & Spelke, 2004).
Les bébés présentent également une capacité d'appariement de collections de même taille, par exemple présentées sous forme visuelle et auditive (Kobayashi, Hiraki, & Hasegawa, 2005).
2) L'acquisition progressive des différentes compétences en mathématiques
A partir des capacités innées que présentent les bébés, les compétences en mathématiques s'acquièrent petit à petit.
Le système de représentation exacte des petites quantités (inférieures à 4) chez les bébés pourrait se transformer ensuite en subitizing.
16 Quant à la capacité d'estimation des quantités plus grandes, il n'est pas sûr qu'elle évolue directement en dénombrement. Au contraire, l'acquisition d'un système symbolique tel que le langage, la constitution des classes, leur emboîtement et la sériation serait à l'origine des capacités de dénombrement. Lors d'une première phase, cela permettrait progressivement le traitement des quantités de 1 à 4. Puis la compréhension de la correspondance entre le mot-nombre suivant et l'ajout de un se mettraient en place (Fayol, 2013).
Toutefois, cet autre versant des possibilités numériques du nourrisson pourrait permettre de réaliser des estimations de plus en plus précises au fur et à mesure que l'acuité numérique se développe (Halberda & Feigenson, 2008).
De ce fait, certains pensent que la représentation approximative pré-verbale pourrait être à la base des apprentissages mathématiques verbaux (Gallistel & Gelman, 1992) ; alors qu'une autre hypothèse met en avant le rôle du système de représentation exacte des petites quantités, puisqu'il permet la compréhension du sens des mots-nombres grâce à son exactitude. Le système de représentation approximative serait alors mis en lien avec cette représentation exacte plus tardivement et ne serait donc pas véritablement à l'origine de l'acquisition de la cardinalité (Le Corre & Carey, 2007).
De manière plus précise et chronologique, voici comment le développement des capacités de dénombrement puis de résolution des opérations se déroule.
A 2 ans et demi, les enfants peuvent différencier un de plusieurs. Mais ce n'est qu'au moins un an plus tard qu'ils peuvent associer un nombre tel que 3 ou 4 à sa cardinalité. La comptine numérique se développe mais ce n'est pas pour autant que l'enfant est en mesure de dénombrer. En effet, le parallèle entre les représentations des quantités mentales et préverbales et le comptage verbal demande beaucoup de temps avant de pouvoir être réalisé (Fayol, 2013).
Lorsque les premières difficultés sont dépassées et que le dénombrement simple est bien mis en place, les techniques de dénombrement continuent d'évoluer avec l'utilisation de stratégies telles que le regroupement ou le calcul.
En ce qui concerne l'apprentissage des codes, il se réalise tout d'abord de manière implicite puisque les codes sont utilisés par l'entourage. L'enfant va observer et imiter ce qui se passe autour de lui.
17 Par ailleurs, les capacités opératoires commencent à se développer de concert. Néanmoins, même si les enfants ont une perception très précoce des transformations appliquées aux quantités, ils ne comprennent pas immédiatement les opérations. A 3 ans, l'enfant est capable de rassembler physiquement deux collections et de compter l'ensemble obtenu pour effectuer une petite addition. Puis à 4-5 ans sont davantage utilisés le comptage verbal ou le comptage sur les doigts pour répondre à ce type de problématique. A l'étape suivante, la récupération des petites additions en mémoire devient possible. C'est grâce à cette élaboration progressive des manipulations que les opérations verraient le jour.
Ainsi, dès 5 ans, différentes stratégies sont mises en place, et l'une ou l'autre est choisie en fonction de la situation. Suivant la personnalité de l'enfant, telle ou telle stratégie sera davantage utilisée. Par exemple, les perfectionnistes tâcheront de calculer l'opération même s'ils ont accès à la récupération directe en mémoire, afin de s'assurer de la réponse (R. S. Siegler, 1988). De plus, le choix de la stratégie sera déterminé par plusieurs facteurs : la vitesse de résolution mais aussi l'histoire de la stratégie pour l'enfant et le coût de mise en œuvre de la procédure (Fayol, 2013).
La soustraction se développe ensuite de la même manière que l'addition. Toutefois, la récupération en mémoire d'une soustraction est beaucoup moins fréquente. C'est souvent l'addition correspondante qui est récupérée.
Ainsi, les stratégies utilisées sont plus ou moins efficaces et leur élaboration progressive permet une maîtrise croissante des opérations. Cependant, celles-ci ne sont pas le seul facteur de réussite des opérations. Lors de la résolution de problèmes notamment, on remarque que la réalisation des opérations est plus aisée lorsqu'elles sont visualisables. En effet, grâce à la représentation mentale, une image de la situation se crée et permet d'accéder à la résolution.
On s'aperçoit aussi que les enfants mettent en place les différentes procédures sans nécessairement connaître les connaissances conceptuelles associées (Fayol, 2013).
Quant à la division, jusqu'à présent elle a été très peu étudiée. Correspondant à une situation partitive (chercher le nombre d'éléments dans chaque partie) ou quotitive (chercher le nombre de parties), la division peut être résolue à l'aide de trois stratégies : l'addition réitérée avec dénombrement du nombre d'itérations, la récupération en mémoire et l'utilisation de la multiplication correspondante (Fayol, 2013).
18 L'estimation est une des compétences mathématiques les plus difficiles à acquérir. Elle reste très longtemps médiocre. Son amélioration se poursuit même à l'âge adulte. Seules trois techniques d'estimation sont utilisées. Elles sont universelles bien qu’elles ne soient pas systématiquement enseignées :
Arrondir et ainsi faciliter le calcul
Reformuler à l'aide d'une autre opération
Compenser pour réajuster un calcul arrondi ou reformulé (Fayol, 2013)
3) Les difficultés pouvant être rencontrées lors du développement des compétences en mathématiques
En réalité, plusieurs difficultés doivent être surmontées pour parvenir à la maîtrise du dénombrement. Le dénombrement se met d’abord en place grâce à l’utilisation de quantités manipulables, telles que des jetons. Cependant, dès que le matériel à dénombrer n’est plus palpable, des difficultés apparaissent. Le dénombrement d’un nuage de points, par exemple, nécessite l’utilisation d’un pointage oculaire ou manuel. Le risque de compter deux fois le même élément ou d’en oublier un est alors augmenté.
Ensuite, la connaissance de la chaîne numérique ne permet pas tout de suite un dénombrement efficace. Même si les enfants comprennent qu'un mot-nombre est associé à une seule quantité, l’association entre chacune des quantités et l’élément de la chaîne numérique correspondant est plus longue à acquérir. D’un point de vue phonologique, les mots-nombres ne possèdent pas de signes distinctifs qui traduisent la quantité exprimée. Seule la place dans la chaîne numérique permet de faire un parallèle entre le mot-nombre et la quantité associée. Ainsi, les mots-nombres doivent être associés individuellement à chacune des quantités qu’ils désignent. Les correspondances doivent être automatisées et cela nécessite davantage de temps que le simple apprentissage de la chaîne numérique.
L’obstacle suivant consiste en la reconnaissance de la cardinalité, sans considération des autres facteurs. Les enfants plus jeunes reconnaissent le changement de numérosité seulement lorsque les collections à comparer sont constituées d’éléments identiques. Puis, au fur et à mesure de l’apprentissage, la comparaison d’éléments de plus en plus hétérogènes devient efficiente.
19 habiletés : la chaîne numérique qui doit être correctement récitée, les objets à dénombrer qui doivent être correctement pointés. Cela engendre une grande variabilité des performances en dénombrement chez les jeunes enfants bien que la mémoire et l'attention puissent être impliquées également dans cette variabilité (Fayol, 2013).
Une considération du nombre sous l'angle des codes symboliques permet de mettre en évidence d'autres difficultés considérables que devront franchir les apprenants en mathématiques.
De manière générale, l'apprentissage des codes, tout d'abord réalisé implicitement, présente plusieurs obstacles tels que le tracé des chiffres ou la longueur phonologique des suites de mots. Toutefois, ces difficultés ne vont généralement pas empêcher l'apprentissage et vont simplement le retarder (Fayol, 2013).
Parmi les codes symboliques existe le code verbal. Ce code est caractérisé par l'utilisation de mots dont la phonétique n'a aucune similitude avec la quantité correspondante. Seule la place dans la chaîne verbale se réfère à la quantité dénommée. L'aspect abstrait du code verbal est le premier obstacle à son apprentissage.
Le second élément à acquérir afin de maîtriser le code verbal est la syntaxe ou combinatoire de la dénomination verbale des quantités. En effet, un terme lexical n'a pu être attribué à chaque quantité à cause de son caractère infini. La prise en compte de l'ordre des éléments en l'associant à des relations additives ou multiplicatives a ainsi permis d'obtenir un code numérique verbal fonctionnel pour un grand nombre de quantités. Ce système nécessite alors un apprentissage pour que l'enfant puisse l'acquérir. De plus, ce système est particulièrement difficile à acquérir dans les langues occidentales qui comportent de nombreuses irrégularités (treize, soixante, quatre-vingts...).
Le code indo-arabe est lui aussi source de difficultés. En effet, il est élaboré à partir de l'utilisation de 10 symboles, les chiffres, combinés ensuite à l'aide d'une notation positionnelle. Or, cette notation positionnelle peut poser problème. Dès le passage à la dizaine, la position des chiffres est à prendre en compte pour savoir de quel nombre il s'agit. Ensuite, cette numération indo-arabe doit être mise en relation avec le code verbal, à l'oral et à l'écrit, et comme nos langues occidentales présentent des irrégularités, la base 10 est moins perceptible à l'oral, et il est donc plus difficile de
20 la retranscrire dans le code indo-arabe. Le positionnement des 0 dans l’utilisation de ce code est tout particulièrement complexe à acquérir (Fayol, 2013).
Quant aux opérations, elles suscitent diverses difficultés. Tout d'abord, leur utilisation n'a d'intérêt qu'en contexte et il est alors nécessaire de savoir dans quelle situation utiliser quel type d'opération.
Les multiplications sont très régulièrement sources d'erreurs et ce sont des interférences qui empêchent généralement d'obtenir le résultat escompté. En effet, on remarque que de nombreuses erreurs de ce type sont produites, même à l'âge adulte. Très souvent, ce sont des résultats proches dans les tables activées qui sont substitués au résultat correct. Cela pourrait être dû à un mauvais apprentissage des tables ; des erreurs produites au moment de l'apprentissage resteraient stockées à la place des réponses correctes. D'ailleurs, les produits appris le plus tardivement (tels que 8*7 ou 8*9) restent parmi ceux qui posent le plus de difficultés.
L'organisation des connaissances des opérations en mémoire pourrait également être à l'origine de ce type d'erreurs. En effet, les résultats seraient reliés sous forme de réseaux d'associations entre les facteurs et leur résultat. Lorsque l'on voit les deux facteurs d'une multiplication, le réseau d'association s'active à l'endroit correspondant et n'active pas seulement la multiplication en question mais également des facteurs et des produits voisins. Cela engendre les interférences. Ainsi, les produits les plus lents à être résolus sont ceux qui génèrent un maximum d'interférences.
L'interférence entre addition et multiplication est elle-aussi remarquée.
L'analyse des opérations écrites permet de mettre elle-aussi en lumière plusieurs difficultés, notamment deux types d'erreurs : des erreurs banales mais également des erreurs récurrentes, par exemple, soustraire le plus petit nombre du plus grand, même si c’est le premier terme. Ce type d'erreur de procédure indique une mauvaise compréhension du sens de l'opération et ces erreurs dépendent des procédures enseignées (Fayol, 2013).
La compréhension des signes mathématiques est à prendre en compte. Une atteinte spécifique des signes mathématiques a été constatée chez certains patients (Fayol, 2013).
21 mathématiques. La possibilité de garder en mémoire plusieurs informations et de pouvoir opérer un traitement sur elles impacte tout particulièrement la réalisation des opérations et la mémorisation des faits arithmétiques (Fayol, 2013).
Pour conclure, l'apprentissage des mathématiques consiste en l'association de deux types de connaissances : les connaissances conceptuelles et les connaissances procédurales. L'ordre d'acquisition de ces deux types de connaissances est très variable suivant l'activité mathématique et d'un enfant à l'autre ; excepté pour le dénombrement pour lequel les connaissances procédurales sont systématiquement acquises avant les connaissances conceptuelles. On remarque, en effet, que certains enfants sont capables de dénombrer une collection de 5 objets en récitant la comptine numérique, pointant les 5 objets les uns après les autres, et répétant le dernier nombre prononcé. La procédure est donc acquise. Pour autant, ils n’ont pas nécessairement compris que la collection d’objets est associée au nombre 5. Si on leur demande une seconde fois le nombre d’objets présents, ils répéteront le comptage à partir de un, car ils n’ont pas acquis le principe de la cardinalité. Dans ce cas, la connaissance procédurale précède la connaissance conceptuelle. Ainsi, de nombreuses difficultés en mathématiques s'expliquent par l'absence de relation entre ces deux types de connaissances.
4) Les repères
Synthétisons les principaux repères concernant le développement des habiletés mathématiques, dans un ordre chronologique.
Chez le bébé, on observe déjà une capacité de différenciation et de représentation des petites quantités.
Lorsque l'enfant commence à parler, il commence à apprendre la chaîne numérique verbale même s'il ne lui attribue pas encore de sens mathématique.
Avant 4 ans, les enfants peuvent manipuler des objets pour répondre à de petites questions additives.
Vers 4-5 ans, la quantification par l'intermédiaire du dénombrement débute. De petites additions et soustractions à partir de petites collections sont possibles. L'association des nombres, de 0 à 9, à une quantité d'objets est acquise.
22 types de comptage se développent : comptage exact, comptage à rebours, comptage « à partir de » et « jusqu'à ».
Au cours de l'école primaire, les enfants développent de nombreuses stratégies permettant de calculer les additions et les soustractions. A 9 ans, l'enfant peut calculer la soustraction « 8 – 3 » en enlevant 3 à 8 ou en comptant le nombre de pas entre 3 et 8. Quelques soustractions simples seulement sont alors connues par cœur.
A l'entrée au collège, les multiplications simples (de nombres à un chiffre) sont correctement réalisées par les trois quarts des élèves, mais les divisions simples ne le sont que pour un tiers. La règle de trois simple est maîtrisée par un tiers des élèves et la moitié calcule correctement un produit entre un nombre à un chiffre et un nombre à deux chiffres (Ménissier, 2015).
Nous avons ainsi étudié la mise en place des acquisitions en mathématiques et les difficultés susceptibles d’être rencontrées au cours de ces acquisitions. A la suite de ces éclairages, nous allons désormais nous focaliser sur le trouble spécifique des apprentissages en mathématiques, qui s’avère être présent lorsque les difficultés rencontrées persistent de manière significative.
II- Le trouble spécifique des apprentissages en
mathématiques (TSAM)
A) Définition
La définition la plus complète est celle du DSM 5. Dans ce manuel est proposée une définition du trouble spécifique des apprentissages, avec plusieurs points concernant en particulier les mathématiques. Nous avons donc sélectionné les éléments relatifs au trouble spécifique des apprentissages en mathématiques.
Les troubles spécifiques des apprentissages sont classés parmi les troubles neurodéveloppementaux. Ces troubles neurodéveloppementaux débutent précocement durant le développement, souvent avant l'entrée au primaire. Ils ont un
23 retentissement sur le fonctionnement personnel, social, scolaire ou professionnel. (American Psychiatric Association, 2015)
Les critères diagnostiques du trouble spécifique des apprentissages et notamment les items correspondant aux mathématiques sont les suivants :
« A. Difficultés à apprendre et à utiliser des compétences scolaires ou universitaires, comme en témoigne la présence d'au moins un des symptômes suivants ayant persisté pendant au moins 6 mois, malgré la mise en place de mesures ciblant ces difficultés :
[…]
5. Difficultés à maîtriser le sens des nombres, les données chiffrées ou le calcul (p. ex. a une compréhension médiocre des nombres, de leur ordre de grandeur et de leurs relations ; compte sur ses doigts pour additionner des nombres à un seul chiffre au lieu de se souvenir des tables d'addition comme le font ses camarades ; se perd au milieu des calculs arithmétiques et peut être amené à changer de méthode).
6. Difficultés avec le raisonnement mathématique (p. ex. a de grandes difficultés à appliquer des concepts, des données ou des méthodes mathématiques pour résoudre les problèmes).
B. Les compétences scolaires ou universitaires perturbées sont nettement au-dessous du niveau escompté pour l'âge chronologique du sujet, et ce de manière quantifiable. Cela interfère de façon significative avec les performances scolaires, universitaires ou professionnelles, ou avec les activités de la vie courante, comme le confirment des tests de niveau standardisés administrés individuellement ainsi qu'une évaluation clinique complète. Pour les individus âgés de 17 ans et plus, des antécédents avérés de difficultés d'apprentissages perturbantes peuvent se substituer à une évaluation standardisée.
C. Les difficultés d'apprentissage débutent au cours de la scolarité mais peuvent ne pas se manifester entièrement tant que les demandes concernant ces compétences scolaires ou universitaires altérées ne dépassent pas les capacités limitées du sujet (p. ex. lors d'examens chronométrés, de la lecture ou de la rédaction de rapports longs et complexes dans un bref délai, d'une charge de travail intellectuel excessivement lourde).
24
handicap intellectuel, des troubles non corrigés de l'acuité visuelle ou auditive, d'autres troubles neurologiques ou mentaux, une adversité psychosociale ou universitaire ou un enseignement pédagogique inadéquat. »
Le DSM 5 précise également de spécifier les modules atteints en cas de déficit du calcul parmi le sens des nombres, la mémorisation de faits arithmétiques, le calcul exact ou fluide et le raisonnement mathématique.
Quant au terme « dyscalculie », il peut être utilisé pour désigner un ensemble de problèmes caractérisés par des difficultés à traiter des données numériques, à apprendre des faits arithmétiques et à réaliser des calculs exacts et fluides. Il est alors nécessaire de préciser si d'autres difficultés sont présentes telles que des difficultés de raisonnement mathématique ou de raisonnement verbal.
Nous utiliserons donc le terme « trouble spécifique des apprentissages en mathématiques » et le sigle « TSAM » pour désigner le trouble étudié dans ce mémoire, bien que de nombreux auteurs choisissent le terme « dyscalculie » dans leurs ouvrages et articles.
D'autres définitions plus simples ont été proposées. A. Ménissier, orthophoniste et praticien-chercheur, propose ainsi les deux définitions suivantes qui se complètent (Ménissier, 2015):
« La dyscalculie définit un trouble des acquisitions numériques et arithmétiques et décrit une insuffisance du « sens du nombre » chez l'enfant. » « La dyscalculie qualifie les troubles sévères et persistants des apprentissages numériques sans atteinte organique ou déficience mentale identifiée. »
Plus concrètement, un enfant avec un TSAM présente des défaillances dans certains éléments de l'arithmétique. Les difficultés rencontrées vont alors concerner les acquisitions suivantes :
- Comprendre la cardinalité, c'est-à-dire savoir que, lorsque l'on compte, le dernier mot-nombre représente ce qu'il y a en tout.
- Retenir les mots-nombres irréguliers tels que onze, douze, ou soixante-dix, quatre-vingts.
- Respecter la correspondance terme à terme.
25 - Tenir compte de la position du chiffre dans le nombre pour savoir si c'est une
unité, une dizaine...
- Différencier les chiffres proches comme 6 et 9. - Estimer le résultat d'un calcul.
- Réaliser un calcul exact.
- Placer un nombre sur une ligne numérique. - Comparer deux nombres en numération arabe. - Acquérir les techniques opératoires.
- Donner du sens aux techniques opératoires. - Retenir les faits numériques.
- Comprendre les problèmes.
Les difficultés de mémoire de travail souvent présentes dans le TSAM impactent l'apprentissage des tables d'addition et de multiplication. Des difficultés d'inhibition sont également repérées.
La classification et la sériation sont nécessaires à la résolution des problèmes et sont souvent atteintes chez l'enfant présentant un TSAM. La réversibilité de la pensée est elle-aussi un pré-requis à la bonne résolution des problèmes et fait souvent défaut chez les enfants avec un TSAM (Ménissier, 2015).
Quant à une classification des TSAM, plusieurs ont été proposées mais aucune n'est véritablement acceptée aujourd'hui. On différencie toutefois les TSAM associés à d'autres difficultés, du TSAM pur, c'est-à-dire isolé. Les difficultés associées concernent très fréquemment le langage écrit mais peuvent également toucher les domaines du langage oral, de l'attention, de la mémoire de travail ou le domaine visuo-spatial (Fayol, 2013).
Le diagnostic de TSAM est rarement posé avant l'âge de 8 ans. Toutefois, de nombreux signes sont repérables plus précocement et notamment dès la maternelle. Il est important de les déceler. Ces signes peuvent être des difficultés de comptage, de dénombrement et de calcul élémentaire (Ménissier, 2015).
26
B) Différenciation TSAM / Trouble du raisonnement logico-mathématique
Le trouble du calcul et le trouble du raisonnement logico-mathématique sont distincts (Legeay, 2013). En effet, les difficultés de raisonnement logico-mathématique sont en lien avec des difficultés de compréhension globales n’atteignant pas seulement les mathématiques ; alors que des difficultés de calcul peuvent être présentes sans impact sur la compréhension en général.
Le trouble du calcul évoqué par M-P. Legeay peut être élargi au TSAM. De fait, le TSAM est défini par la spécificité des difficultés dans les compétences numériques alors que dans le cadre du trouble du raisonnement logico-mathématique, des difficultés sont retrouvées dans d’autres domaines que le champ des compétences numériques. Ces difficultés plus globales peuvent être, par exemple, des difficultés de langage oral ou une déficience intellectuelle.
L’exploration du raisonnement logico-mathématique vise à comprendre où en est l’enfant dans sa construction de sens, dans son fonctionnement de pensée. Ainsi, les appuis théoriques de ce trouble s’appuient davantage sur la théorie piagétienne.
Les notions piagétiennes de classification, conservation, sériation, inclusion et combinatoire sont prises en compte, et le raisonnement logico-mathématique consiste en leur utilisation. Voici les définitions de ces opérations logiques (Brin, Courrier, Lederlé, Masy, & Kremer, 2006) :
La classification consiste en la réunion d’objets en fonction de propriétés communes selon un ou plusieurs angles de vue. Ainsi, on classe les chats avec les baleines parmi les mammifères.
La conservation est la capacité à reconnaître qu’une propriété d’un objet n’a pas été modifiée bien qu’une action ait été réalisée sur cet objet. Lorsqu’on verse un verre d’eau dans une casserole, il y a autant d’eau dans la casserole qu’il y en avait dans le verre bien que le niveau d’eau soit plus bas puisque la casserole est plus large. La sériation équivaut à mettre dans l’ordre un ensemble d’objets, à les ranger, par exemple, du plus petit au plus grand.
On parle d’inclusion lorsqu’un ensemble d’éléments est compris dans un autre. C’est le cas, par exemple, des tulipes qui sont incluses dans le groupe des fleurs.
27 T-shirts, 4 pantalons et 5 paires de chaussures différentes, il est possible de réaliser 60 tenues.
Ainsi, l’exploration du raisonnement logico-mathématique est réalisée par le biais de toutes ces opérations logiques qui ne portent pas nécessairement sur des nombres.
Un trouble du raisonnement logico-mathématique est donc un déficit dans l’acquisition de ces opérations logiques, qui ne sont pas directement corrélées aux capacités en mathématiques. De ce fait, le TSAM se différencie bien du trouble du raisonnement logico-mathématique par sa définition et ses critères diagnostiques, qui ne font pas appel aux notions logiques.
Ainsi, certaines personnes présentent des difficultés en mathématiques alors que les opérations logiques sont bien mises en place. C’est le cas, par exemple, de Charles, étudiant décrit par Butterworth (Butterworth, 2000). Il présente en effet des difficultés massives du traitement des quantités numériques, alors que ses capacités de raisonnement sont tout à fait correctes.
Dans le cadre de ce mémoire, nous avons choisi de nous focaliser sur le TSAM, et non sur le trouble du raisonnement logico-mathématique.
C) Prévalence
Il n'existe pas de données précises sur la prévalence du TSAM. D'après M. Habib (Habib, 2014), l'incidence du trouble est d'environ 3 à 5% dans la population générale, et les filles comme les garçons sont touchés.
Dans le DSM 5 n'est précisée la prévalence que pour l'ensemble des troubles spécifiques des apprentissages incluant les déficits en lecture, en expression écrite et en calcul. Elle est de 5 à 15% pour l'ensemble de ces pathologies à l'âge scolaire, et de 4% environ à l'âge adulte (American Psychiatric Association, 2015).
Quant à M. Fayol, il indique que la prévalence du TSAM est comprise entre 3 et 8 % (Fayol, 2013).
28
D) Données anatomiques
A l'heure actuelle, peu d'études sur le TSAM ont été menées en imagerie cérébrale. Les deux premières études réalisées à ce propos ont étudié les cerveaux de patients présentant un syndrome de Turner (Molko et al., 2003), et de patients prématurés avec un très faible poids de naissance (Isaacs, Edmonds, Lucas, & Gadian, 2001). Ces deux études ont convergé vers une anomalie du cortex du sillon intrapariétal.
Une étude a, par la suite, permis de comparer le cerveau d'enfants avec un TSAM sans troubles associés à celui d'enfants contrôles (Karin Kucian et al., 2006). De nouveau, des différences ont été repérées au niveau du cortex du sillon intrapariétal, à droite, mais les régions frontales et les régions parahippocampiques, régions impliquées dans la mémoire, et notamment la mémoire de travail, ont également montré un volume moins important de matière cérébrale.
La tâche de comparaison permet tout particulièrement de mettre en évidence une faiblesse d'activation de certaines zones chez les enfants présentant un TSAM. Le sillon intrapariétal droit est impliqué lorsque les éléments à comparer sont des collections (Price, Holloway, Räsänen, Vesterinen, & Ansari, 2007) et les deux sillons intrapariétaux le sont pour les chiffres arabes (Mussolin, De Volder, et al., 2010). L'effet de distance module l'activation du sillon intrapariétal chez les sujets contrôles, ce qui n'est pas le cas chez les enfants présentant un TSAM.
L'implication d'une faiblesse de mémoire de travail visuo-spatiale dans le TSAM a également été investiguée lors d'une étude (Rotzer et al., 2009). Et celle-ci confirme son implication, puisque dans une tâche de mémorisation immédiate de points sur un écran, l'activation du sillon intrapariétal est nettement diminuée chez les personnes avec un TSAM et ce résultat est corrélé à la performance en mémoire de travail verbale et non-verbale.
Grâce à la tractographie, on présume qu'une réduction de la connexion des régions inféro-temporales de la région pariétale, ou des régions temporo-pariétales droite et gauche entre elles pourraient être à l'origine du TSAM (Rykhlevskaia, Uddin, Kondos, & Menon, 2009). Ces dysconnexions empêcheraient une bonne liaison entre les systèmes de traitement verbal des nombres et ceux du système analogique, et également la connexion entre la représentation spatiale des magnitudes et l'utilisation
29 de la représentation symbolique des nombres et du calcul (Habib, 2014).
Plusieurs chercheurs envisagent de réaliser une classification des TSAM en fonction de la localisation de l'atteinte cérébrale. Toutefois, cette hypothèse n'est pas vérifiée pour le moment (A. J. Wilson & Dehaene, 2007).
E) Causes
Plusieurs études ont été menées afin de déterminer les causes du TSAM. Actuellement, l’hypothèse majoritaire concernant le TSAM pur réside dans un déficit du sens du nombre.
Toutefois, d'autres déficits sont fréquemment mis en lien avec le TSAM, on parle alors de TSAM secondaire, influencé par des facteurs cognitifs généraux.
Selon le modèle de Von Aster et Shalev, plusieurs causes ont été déterminées. Le TSAM pur pourrait être dû à un déficit de la 1ère étape du modèle
(représentation innée du nombre), permettant le subitizing et l'approximation.
Quant au déficit de la 2nde étape (symbolisation linguistique du nombre), il
pourrait également occasionner des troubles du calcul, mais plus précisément dans les stratégies de dénombrement, de calcul et en récupération de faits numériques. Ainsi, ce type de TSAM serait secondaire et en lien avec un trouble du langage oral ou écrit.
Des difficultés dans la 3ème étape (symbolisation arabe du nombre) peuvent
également conduire à un trouble. C'est alors l'acquisition du principe de position du système numérique arabe qui est difficile à mettre en place, ce qui engendre des troubles du calcul.
Une atteinte de la 4ème étape (acquisition de la représentation mentale de la
ligne numérique) peut aussi être la source d'un déficit durable en raisonnement arithmétique.
Ainsi, la mauvaise réalisation d'une des étapes peut engendrer des troubles du calcul mais le véritable TSAM correspondrait à l'atteinte de la 1ère étape. Les troubles du calcul en lien avec les autres étapes seraient, au moins en partie, provoqués par les conditions environnementales (Habib, 2014).
30 Selon les diverses études, les 5 compétences qui ont été principalement étudiées afin de déterminer leur implication dans le TSAM sont les suivantes : la mémoire de travail, la mémoire à long terme verbale, le traitement phonologique, l'inhibition et les gnosies digitales (Habib et al., 2011).
La mémoire de travail a un rôle indéniable dans la réalisation des calculs, surtout au début de leur acquisition (Adams & Hitch, 1997).
Il a d'ailleurs été prouvé que les capacités en mémoire de travail, chez des enfants de CP, sont un bon prédicteur de leurs performances en mathématiques un an plus tard (De Smedt et al., 2009).
L'étude suivante (Geary et al., 2007) a également permis de mettre en évidence une faiblesse significative de la mémoire de travail chez les personnes présentant un TSAM, comparées aux enfants avec de légères difficultés en mathématiques ou sans difficultés.
Cette faiblesse de la mémoire de travail contribue à un mauvais développement de la chaîne numérique verbale, des stratégies de calcul par comptage et à des difficultés de constitution du réseau des faits arithmétiques en mémoire à long terme (Habib et al., 2011).
L'hypothèse d'un déficit global en mémoire à long terme a également été envisagée. En effet, les enfants avec un TSAM présentent des difficultés pour retenir les faits arithmétiques. Toutefois, ces difficultés en mémoire à long terme n'ont pas été retrouvées dans d'autres exercices réalisés à partir de matériel verbal. Les difficultés mnésiques à long terme chez les enfants présentant un TSAM sont donc spécifiques au matériel arithmétique (Mussolin, De Volder, et al., 2010).
Une autre cause proposée concerne la conscience phonologique. Une faible conscience phonologique empêcherait une bonne acquisition de la chaîne numérique verbale et expliquerait les comorbidités fréquentes entre TSAM et trouble spécifique des apprentissages en langage écrit (TSALE). Les résultats en conscience phonologique sont en effet liés aux capacités de résolution de petits calculs, mais ceci n'est pas valable pour les grands calculs tels 7 ᵡ 8 (De Smedt, Taylor, Archibald, & Ansari, 2010). De plus, on retrouve une différence de capacités en traitement phonologique entre les enfants avec un TSAM et des enfants sans difficultés en mathématiques (Vanbinst, Ghesquière, & De Smedt, 2014).
31 L'hypothèse d'un déficit en inhibition lié au TSAM a été envisagée. L'inhibition comporte plusieurs fonctions :
La suppression d'informations non pertinentes de la mémoire de travail. L'inhibition de réponses automatiques.
Le contrôle des interférences.
Ces trois fonctions ont pu être évaluées chez des enfants portant un TSAM, et une étude récente a finalement révélé que l'inhibition, dans sa spécificité, n'est pas significativement atteinte chez ces enfants en comparaison des enfants contrôles (Censabella & Noël, 2008).
Les gnosies digitales permettent de « reconnaître, identifier, différencier,
dénommer, sélectionner chacun des doigts de chaque main » (Noël, 2005). Elles ont
été reliées aux capacités numériques, puisque les doigts sont très utilisés pour le comptage et les zones cérébrales impliquant les gnosies digitales et les compétences arithmétiques sont très proches. Ainsi, il a été prouvé que les capacités en gnosies digitales sont un bon prédicteur des compétences numériques futures (un an plus tard), alors qu'elles ne prédisent pas les capacités en lecture. Un entraînement des gnosies digitales est d'ailleurs possible et permet une amélioration de certaines tâches numériques, comme la tâche de subitizing (Gracia-Bafalluy & Noël, 2008).
Ainsi, plusieurs théories existent concernant les causes du TSAM. Les difficultés d'apprentissage en mathématiques proviendraient d'une atteinte de la mémoire de travail, de la conscience phonologique et/ou des gnosies digitales. Toutefois, l'inhibition et la mémoire à long terme ne seraient pas spécifiquement impliquées.
L'autre théorie envisagée qui serait la plus susceptible d'expliquer le TSAM pur évoque un déficit numérique de base. Certains auteurs précisent le caractère de ce déficit. M. Habib parle de déficit du « module de représentation approximative des
quantités », siégeant au niveau du sillon intrapariétal (Habib et al., 2011).
M. Fayol, quant à lui, envisage deux explications possibles du TSAM pur. La première considère le TSAM comme un trouble du sens du nombre. Ce trouble atteint la représentation analogique non symbolique des quantités qui traite de manière approximative la magnitude et constitue le socle sémantique de l'apprentissage des
32 mathématiques.
Par ailleurs, la seconde théorie envisage une déconnexion entre la représentation analogique et le traitement des codes symboliques. Sans lien entre ces deux éléments, les techniques opératoires peuvent être apprises mais sans qu'aucun sens ne soit donné aux opérations (Fayol, 2013).
Afin d'étudier l'hypothèse d'un déficit numérique de base, une série de tâches numériques de base a été proposée à des enfants présentant un TSAM qui ont eu besoin d'un temps plus important pour les réaliser. Cependant, dans toutes ces épreuves, la numération arabe ou verbale orale était utilisée. Ainsi, on peut penser que les enfants avec un TSAM présentent des difficultés de représentation de la magnitude, ou de traitement des nombres symboliques, ou des difficultés de représentation de la magnitude avec un matériel symbolique (Landerl, Bevan, & Butterworth, 2004).
L'importance de l'impact du matériel symbolique a ensuite été confirmée. C'est la représentation sémantique du nombre à partir de codes symboliques qui est déficitaire chez les jeunes enfants avec un TSAM (Rousselle & Noël, 2007). En effet, ces enfants présentent davantage de difficultés pour comparer des nombres écrits en code indo-arabe que pour comparer des quantités manipulables.
Ce déficit pourrait ensuite avoir des répercussions sur le traitement approximatif de la magnitude des collections à partir de 10-11 ans. En effet, la représentation exacte et la représentation approximative se développeraient, dans un premier temps, en parallèle. Puis elles se connecteraient pour un perfectionnement des deux représentations. Mais dans le cas d'un déficit de la représentation exacte des nombres, via le code symbolique, la connexion entre les deux représentations ne se réaliserait pas correctement et empêcherait le perfectionnement du traitement approximatif de la magnitude des collections (Mussolin, Mejias, & Noël, 2010)
Le déficit en représentation exacte des nombres symboliques serait peut-être le résultat de mauvaises capacités de subitizing (Schleifer & Landerl, 2011).
F) Comorbidités
33 fréquente concerne le langage écrit. Lorsque le TSAM est associé au TSALE, les difficultés en mathématiques sont généralement plus marquées que dans le cas d'un TSAM isolé.
Le second trouble particulièrement souvent associé au TSAM est le TDAH (Trouble Déficit de l'Attention avec ou sans Hyperactivité). Dans ce cas, les symptômes attentionnels majorent la persistance du TSAM. Les enfants atteints des deux troubles présentent un déficit plus important en mémorisation des faits arithmétiques qu'en résolution de problèmes. Ces difficultés précises pourraient être liées à l'impact des interférences verbales, empêchant une bonne rétention des faits arithmétiques.
L'association à un trouble des habiletés visuo-spatiales est également décrite. En effet, ce type de trouble peut perturber le transcodage et en particulier l'écriture positionnelle, ainsi que la résolution des opérations, notamment quand il est nécessaire de les poser. M. Mazeau relate ce type de difficultés (Mazeau, 2000). En ce sens, le trouble des habiletés visuo-spatiales impacterait simplement le traitement des codes. Cependant, d'autres estiment que les troubles de l'espace empêchent également le bon développement de la ligne numérique mentale. Ceci a été montré grâce à l’exemple du syndrome de Williams. Dans ce syndrome, les difficultés visuo-spatiales sont associées à des difficultés en mathématiques, concernant, à la base, la représentation de la magnitude du nombre, mais pouvant ensuite avoir des répercussions sur l’ensemble des compétences numériques (O’Hearn & Luna, 2009). Quant au trouble du langage oral, il a inévitablement un impact sur l'apprentissage des mathématiques. De fait, le dénombrement, par exemple, nécessite un recours au langage. Cependant, le développement de connaissances conceptuelles en mathématiques repose majoritairement sur des compétences non-verbales et des enfants présentant un trouble spécifique du langage oral montrent de meilleures connaissances numériques que des enfants plus jeunes appariés sur le plan des compétences orales (Fayol, 2013).
L’association du TSAM à la dyspraxie est clairement constatée (Pouhet, 2011). Toutefois, peu de chercheurs ont mené d’investigations à ce propos pour le moment. La dyspraxie engendre des difficultés en mathématiques puisque les difficultés praxiques entraînent une variabilité des résultats en tâche de dénombrement. Les capacités numériques et la compréhension du vocabulaire mathématique se développent ainsi plus difficilement. De plus, les enfants avec une dyspraxie
34 présentent souvent une faiblesse en mémoire auditive qui complexifie l’apprentissage des tables de multiplication. L’utilisation des instruments de mesure (compas, équerre…) pose également davantage de difficultés et ceci impacte les copies de figures (Kirby & Peters, 2013).
G) Signes d'alerte
Divers signes peuvent permettre de suspecter un TSAM. Voici une synthèse des signes d’alerte proposés par A. Ménissier (Ménissier, 2015) et par l’INS HEA (Institut d’enseignement supérieur et de recherche - Handicaps et besoins éducatifs particuliers) :
- Des difficultés pour estimer les quantités.
- Des difficultés d’apprentissage et de maîtrise de la comptine numérique. - Des difficultés de comptage ou de dénombrement caractérisées par des
difficultés à propos des principes de cardinalité et de non pertinence de l’ordre. - Une lenteur et des difficultés dans la réalisation des calculs.
- Un comptage sur les doigts en fin de primaire pour une addition facile. - Des difficultés pour donner du sens aux soustractions et pour les calculer. - Des difficultés d’acquisition et de maîtrise du système numérique écrit. - Des difficultés de transcodage (passage d’un code à un autre).
- Des difficultés de mémorisation concernant particulièrement les tables de multiplication.
- Des difficultés de compréhension de la numération en base 10.
- L'absence de lien entre ce qui est appris en mathématiques à l'école et la vie quotidienne.
- Une difficulté à établir des relations entre les choses.
- Des difficultés d'acquisition du langage dans la petite enfance. - Des difficultés attentionnelles et une agitation motrice.
- Des difficultés d'orientation et une confusion droite/gauche. - Des antécédents de TSAM chez les parents.
35
H) Remédiations
Actuellement, la remédiation du TSAM est mise en place sous forme d'interventions pédagogiques ou de rééducation orthophonique. Ces prises en charge sont souvent inspirées du modèle piagétien et visent à rétablir des mécanismes globaux tels que la conservation ou l'inclusion par exemple, bien que les avancées théoriques actuelles ne soient pas en faveur d'un lien direct entre ces mécanismes de base et les capacités dans les activités numériques.
En effet, en ce qui concerne les orthophonistes, la présentation du TSAM est très brève au cours de la formation initiale. A Bordeaux par exemple, dans le programme de la formation en 4 ans, seules douze heures sur le TSAM et les troubles logico-mathématiques sont dispensées. Désormais, la formation a été élargie à 5 ans, et le nouveau programme donne une plus large part à la formation sur la cognition mathématique dans son ensemble (140 heures). Toutefois, les orthophonistes formées à Bordeaux jusqu’à présent ont été très peu renseignées sur le TSAM.
Par la suite, les formations continues proposées s’inspirent, pour la majorité, des théories piagétiennes. Il s’agit notamment des formations Cogi’Act, Gepalm et Evoludys.
Néanmoins, il existe de plus en plus de formations continues prenant en compte les considérations récentes. L’organisme Dystingo propose des formations sur le bilan et la rééducation du TSAM, adressées aux orthophonistes. Ces formations distinguent clairement le TSAM du trouble du raisonnement logique. Ainsi, les deux types de troubles sont considérés et présentés différemment. Alain Ménissier anime également ce type de formations, selon l’approche neuro-constructiviste. Au Québec, le Cénop (Centre d’évaluation neuropsychologique et d’orientation pédagogique) propose des formations sur le développement du calcul, le TSAM et les rééducations des difficultés en mathématiques pour les enfants en primaire, dont les bases théoriques prennent aussi en compte les avancées récentes de la recherche.
En outre, certaines remédiations concernent directement les activités numériques mais consistent en la poursuite de l'entraînement d'activités déjà exercées au cours de l'apprentissage scolaire et notamment dès la maternelle. L'efficacité de ce