Estimation des préférences face au risque à l'aide d'une approche flexible

ESTIMATION DES PREFERENCES FACE AU RISQUE

À L'AIDE D'UNE APPROCHE FLEXIBLE

Mémoire présenté

à la Faculté des études supérieures de l'Université Laval dans le cadre du programme de maîtrise en économique

pour l'obtention du grade de Maître es Arts (M.A.)

DEPARTEMENT D'ECONOMIQUE FACULTÉ DES SCIENCES SOCIALES

UNIVERSITÉ LAVAL QUÉBEC

2011

Résumé

Ce mémoire présente une méthode flexible utilisant les splines cubiques d'estimer le coefficient d'aversion au risque absolue ou relative d'individus en contexte d'utilité espérée. Cette méthode est développée de manière à être utilisée conjointement avec la méthode expérimentale de l'arbitrage de Wakker et Deneffe (1996) permettant de trouver des points sur la courbe d'utilité d'une personne répondant à des questions au sujet de loteries. À l'aide de simulations de type Monte Carlo, nous montrons qu'il est possible d'utiliser ces points afin d'estimer les paramètres de segments cubiques de splines et ensuite d'utiliser ces paramètres pour estimer l'aversion au risque sans imposer d'hypothèse forte quant à la forme de la fonction d'utilité de l'individu. Cela a pour but d'éviter les biais dus aux erreurs de spécification et nous montrons que lorsque la fonction d'utilité réelle est inconnue, les splines s'avèrent un instrument utile générant des erreurs plus faibles qu'une approche paramétrique classique utilisant une forme fonctionnelle non flexible. Cette conclusion tient même lorsque nous introduisons des erreurs sous forme d'arrondissement des réponses obtenues lors de l'application de la méthode de l'arbitrage malgré le fait que les estimations tendent à être de moins en moins précises au fur et à mesure que le niveau d'arrondissement augmente.

IV

Avant-propos

Je me permets de retarder votre lecture quelques instants afin de remercier ceux et celles qui ont contribué à la réalisation de ce mémoire. Bien que mon nom apparaisse seul en page couverture, je ne peux nullement prétendre être le seul responsable de sa parution. J'ai eu beaucoup d'aide et cette aide se doit d'être mentionnée.

Tout d'abord, je tiens à remercier Mme Sabine Kroger, ma directrice de recherche, dont les

conseils inestimables ont guidé mon travail depuis le début et dont la patience face à mes nombreux dépassements de délais fut fort appréciée. Elle est la motivation derrière ce mémoire et mérite sa juste part des honneurs.

Ensuite, je ne peux passer sous silence la contribution de Luc Bissonnette. Une part non négligeable de mon travail s'appuie sur des simulations effectuées à l'aide d'un programme informatique qu'il a bien gentiment voulu adapter à mes besoins et pour lequel il m'a fournit beaucoup de soutien technique. Son aide m'a permis d'économiser de nombreuses heures de travail à tâtons.

Je me dois également de remercier le CRSH et le CIRPÉE qui, grâce à leurs contributions financières, m'ont permis de me concentrer sur mes études et d'investir le temps requis à la rédaction de ce document. Il n'y a pas plus grande aide pour un étudiant de maîtrise que celle qui lui offre un peu plus de temps libre.

Finalement, je remercie tous ceux et celles qui m'entourent et qui m'ont soutenu dans cette aventure. Merci à ma famille qui m'a écouté parler de l'estimation des préférences face au risque sans comprendre la moitié de ce que je disais. Merci à ma conjointe, Chloé, qui a partagé mon quotidien et qui m'a poussé à travailler lorsque l'envie s'en faisait moins sentir. Merci à mes amis qui ne m'en voulaient pas lorsque je quittais les soirées qu'ils avaient organisées pour aller continuer ma rédaction. C'est grâce à vous tous que je suis passé à travers.

Merci à tous et à toutes et bonne lecture! Bruno Trottier-Pérusse

Résumé iii

Avant-propos iv

Table des matières v

Liste des tableaux vii

Liste des figures viii

Chapitre 1 : Introduction 1

Chapitre 2 : Revue de la littérature 4

2.1 Le risque en contexte d'utilité espérée 4 2.2 Les mesures d'aversion au risque 6

2.3 La méthode expérimentale de l'arbitrage de Wakker et Deneffe 8

2.4 Les estimations paramétriques 10

2.5 Les splines cubiques 11

Chapitre 3 : Méthodologie 14

3.1 Identification des valeurs théoriques initiales 14 3.2 Obtention des points sur les courbes d'utilité par la méthode de l'arbitrage 18

3.3 Arrondissement 19 3.4 Calcul des paramètres des splines et de l'aversion au risque 21

3.5 Estimations paramétriques 25 3.6 Identification ex post de la tendance suivie par l'aversion au risque 27

3.7 Préparation des données 29

Chapitre 4 : Analyse des résultats 30

4.1 Résultats généraux 30 4.2 Filtre de Hyman et valeurs extrêmes 32

4.3 Arrondissement lorsque la fonction d'utilité est connue 34 4.4 Nombre de points optimal lorsque la fonction d'utilité est connue 37

4.5 Comparaison entre les estimations à l'aide des splines et les estimations

paramétriques en absence d'erreur de spécification 40 4.6 Implications de l'incertitude au sujet de la fonction d'utilité 41

VI

Chapitre 5 : Discussion 46 5.1 Propagation des erreurs en chaîne 46

5.2 Hypothèses concernant les splines 48 5.3 Identification de la tendance suivie par l'aversion au risque (extension) 48

5.4 Utilisation d'autres approches flexibles 50

Chapitre 6 : Conclusion 51

Bibliographie 53

Annexe A 56 Annexe B 58

Liste des tableaux

3.1 : Règles d'arrondissement proportionnel aux montants enjeu 20

3.2 : Environnement de simulation 21 3.3 : Environnement de simulation lors de l'identification de la tendance suivie par l'aversion

au risque à l'aide des splines cubiques 29 4.1 : Exemple d'estimations de l'aversion au risque obtenues à l'aide des splines cubiques 31

4.2 : Comparaison des écarts en pourcentage entre les estimations et la valeur d'aversion au

risque postulée 31 4.3 : Effet du filtre de Hyman sur les données 32

4.4 : Progression des écarts entre les estimations et les véritables valeurs d'aversion au

risque selon le niveau d'arrondissement 35 4.5 : Écarts en pourcentage entre les estimations et les vraies valeurs d'aversion selon le

niveau d'arrondissement et le nombre de points sur la courbe lorsque la fonction d'utilité

est connue 38 4.6 : Écarts en pourcentage entre les estimations et les vraies valeurs d'aversion selon le

niveau d'arrondissement et le nombre de points sur la courbe lorsque la courbe d'utilité

est connue (extension) 39 4.7 : Écarts en pourcentage entre les estimations de l'aversion relative et les vrais

coefficients dans les cas utilisant les splines et dans les cas spécifiant une fonction non

flexible lorsque la fonction d'utilité est connue 40 4.8 : Écarts en pourcentage entre les estimations et les vraies valeurs d'aversion selon le

niveau d'arrondissement et le nombre de points sur la courbe d'utilité lorsque la

fonction d'utilité est inconnue 41 4.9 : Écarts en pourcentage entre les estimations et les vraies valeurs d'aversion au risque

en présence d'erreurs de spécification 42 5.1 : Estimations linéaires des fonctions d'aversion au risque résultant de l'utilisation des

splines cubiques 49 A.l : Écarts en pourcentage moyens entre les estimations et les vraies valeurs de l'aversion

Vlll

Liste des figures

2.1 : Courbe d'utilité obtenue par la méthode de l'arbitrage 9 2.2 : Exemple de spline cubique estimant une fonction d'utilité 11 2.3 : Spline cubique avant et après imposition du filtre de Hyman 13 4.1 : Exemple graphique de l'application du filtre de Hyman à une spline cubique estimant

une courbe d'utilité 33 4.2 : Progression de l'aversion au risque et de ses estimations selon les enjeux 44

5.1 : Exemple d'impact de l'arrondissement sur la propagation des erreurs absolues et

Introduction

Les préférences face au risque prennent une place importante dans toutes les discussions concernant les choix des ménages et des entreprises. Traditionnellement, on identifie ces préférences à l'aide des décisions des individus et on s'en sert ensuite pour rationaliser ces décisions. Ultimement, le but à atteindre est de parvenir à les utiliser pour expliquer le comportement des agents, prédire leurs choix et fournir un support au processus décisionnel. Afin de mesurer ces préférences, plusieurs méthodes ont été proposées. Par exemple, il est possible de classer les individus en fonction du niveau d'assurances qu'ils se procurent (Halek et Eisenhauer, 2001). Logiquement, une personne préférant une protection complète devrait être considérée plus averse au risque que quelqu'un qui ne choisit qu'une protection partielle. De même, plusieurs auteurs, dont Guiso et Paiella (2002) établissent une mesure des préférences en se basant sur la proportion d'actifs risqués dans les portfolios d'investissement des individus. L'inconvénient de telles mesures est qu'elles sont souvent influencées par des considérations autres que les seules préférences. Par exemple, quelqu'un qui assure son loyer peut le faire simplement parce qu'il est obligé en vertu de son contrat de location. Quelqu'un qui achète l'action d'une compagnie peut le faire simplement parce qu'elle connaît quelqu'un qui y travaille. Dissocier les préférences pures de ces éléments extérieurs peut s'avérer complexe, voire impossible.

Cependant, dans la littérature économique, il existe également plusieurs méthodes pour faire ressortir les préférences indépendamment d'un processus décisionnel courant. À l'aide de tâches expérimentales, il est d'ailleurs possible de les quantifier ou de les représenter sous forme graphique. Les différentes méthodes proposées sont toutefois souvent sources de biais. Par exemple, la méthode de l'équivalent certain, consistant à obtenir la valeur équivalente que des individus attribuent à une loterie, existe depuis longtemps et continue d'être employée de nos jours (Abdellaoui et al., 2008). Selon la manière dont elle est utilisée, elle peut nécessiter l'imposition d'hypothèses fortes ou ne fournir que des valeurs seuils pour caractériser les préférences des individus. Or, des méthodes plus récentes ont attiré beaucoup d'attention en proposant de corriger certains de ces biais. Celles-ci ne sont toutefois pas sans failles. La méthode de l'arbitrage de Wakker et Deneffe (1996) en est un bon exemple. Cette méthode se distingue des autres en utilisant un procédé non paramétrique afin d'obtenir des points sur les courbes d'utilité des individus dont on peut ensuite se servir pour estimer les préférences face au risque de ces mêmes individus (Wakker et Deneffe, 1996, Abdellaoui, 2000).

Or, l'estimation d'un coefficient permettant de quantifier les préférences n'est pas possible à l'aide uniquement de la méthode de l'arbitrage. Dans la littérature, une approche paramétrique est généralement employée pour compléter l'analyse et obtenir les résultats désirés. Booij et al. (2009) utilisent d'ailleurs des maximums de vraisemblance à information limitée en raisonnant que la méthode de l'arbitrage est soumise à des biais et que même si des hypothèses doivent être faites concernant la forme de la fonction d'utilité, une approche paramétrique permet d'atténuer l'impact de ces biais sur les estimations. En combinant les deux procédés, ils parviennent à quantifier les préférences face au risque de la population néerlandaise. Toutefois, un biais engendré par une erreur de spécification de la fonction d'utilité au cours d'un procédé d'estimation paramétrique peut s'avérer problématique et l'importance de ce biais peut difficilement être mesurée ex post tant que la véritable fonction d'utilité reste inconnue. Il est donc pratiquement impossible de savoir si l'approche paramétrique résout plus de problèmes qu'elle n'en cause.

Il existe cependant des approches employant des formes fonctionnelles plus flexibles dont l'utilisation pourrait théoriquement engendrer un biais moindre qu'avec une approche paramétrique. Parmi elles, les splines cubiques ont déjà donné des résultats concluants dans l'estimation des anticipations subjectives quant à la réalisation de variables aléatoires continues (Bissonnette, 2007 et Bellemare, Bissonnete et Kroger, 2010). L'utilisation des splines n'a, à notre connaissance, toutefois pas encore été testée dans le contexte de l'estimation des préférences face au risque. Pourtant, si ce procédé s'avérait viable, il permettrait d'obtenir des coefficients reflétant les comportements de la population en étant moindrement soumis aux problèmes généralement associés aux approches paramétriques. Nos travaux ont donc pour but de tester les performances d'une méthode d'estimation flexible des préférences face au risque utilisant des splines cubiques. De plus, nous comparerons la précision des estimations obtenues à l'aide de cette approche à la précision des estimations résultant d'un procédé paramétrique utilisant des fonctions plus communes dans la littérature.

Notre problématique se divise en quatre questions auxquelles nous devrons répondre dans ce mémoire. Premièrement, comment les splines peuvent-elles être combinées à la méthode de l'arbitrage pour permettre d'estimer des coefficients d'aversion au risque? Deuxièmement, cette approche fonctionne-t-elle en présence d'erreurs causées par l'arrondissement des réponses fournies par les individus participant aux expériences? Troisièmement, existe-t-il un nombre de points optimal à obtenir sur les courbes d'utilité de manière à ce que les splines génèrent les estimations les plus précises possibles? Et quatrièmement, le procédé basé sur les splines cubiques permet-il d'éviter l'introduction d'erreurs de spécification pouvant résulter de l'adoption d'un procédé d'estimation paramétrique classique? Afin de répondre à ces questions, nous proposons une méthodologie s'appuyant sur des simulations informatiques de type Monte Carlo. De fait, ce n'est qu'en comparant les estimations avec les vrais coefficients à estimer que nous pouvons commenter les performances des approches étudiées. En postulant des individus fictifs dont les préférences sont connues et en utilisant l'approche flexible et l'approche

sommes en mesure d'observer laquelle des méthodes fournit les estimations les plus proches des véritables valeurs. Notons toutefois que notre objectif n'est pas de développer au maximum de ses capacités le procédé employant les splines cubiques et de fournir une comparaison exhaustive avec la méthode paramétrique. Nous désirons simplement commencer les travaux concernant l'utilisation des splines en tant qu'outil d'estimation des préférences face au risque et tester leurs performances dans un contexte général. Dans cette optique, plusieurs choix concernant l'environnement de simulation utilisé ont été faits de manière à simplifier la démarche et les calculs.

Ce document est divisé selon la logique suivante. Dans le deuxième chapitre, nous présentons une revue de la littérature et des concepts théoriques importants à la compréhension de nos travaux. Dans le troisième, nous détaillons la méthodologie suivie pour répondre aux questions de la problématique. Nous incluons dans ce chapitre les équations importantes et des exemples de calculs afin de faciliter la lecture. Le quatrième chapitre présente l'analyse des résultats obtenus à l'aide de notre méthodologie. C'est dans ce chapitre que nous répondons aux questions de la problématique. Ensuite, dans le cinquième chapitre, nous discutons brièvement de questions supplémentaires soulevées par nos travaux. Finalement, le chapitre 6 conclue ce mémoire.

Chapitre 2

Revue de la littérature

Dans l'introduction, nous avons mentionné que nous nous intéressons à l'estimation de l'aversion au risque en contexte d'utilité espérée. Dans le présent chapitre, nous rappelons les concepts de base tels que l'utilité espérée, le risque et l'aversion au risque qui sont nécessaires à la compréhension de nos travaux. Nous présentons également la méthode de l'arbitrage et les splines cubiques qui sont au cœur de notre méthodologie et discutons brièvement de la littérature concernant les estimations paramétriques des préférences face au risque.

2.1 Le risque en contexte d'utilité espérée

Théorie classique étudiée depuis la parution des travaux de Daniel Bernouilli (1738, traduit en 1954), la théorie de l'utilité espérée propose que les individus attribuent une valeur à un élément en se basant sur l'utilité que cet élément leur procure. Les préférences des gens peuvent ensuite être modélisées en représentant graphiquement l'évolution du niveau d'utilité selon la quantité disponible de l'élément en question. La courbe en résultant est nommée « courbe d'utilité ». Les économistes croient que cette courbe peut être représentée par une fonction U(x) permettant de prédire mathématiquement le niveau d'utilité associé à une quantité précise de l'élément JC considéré. En 1947, von Neumann et Morgenstern ont axiomatisé cette théorie pour définir le comportement d'un individu rationnel. Il en ressort que pour satisfaire la théorie, les préférences représentées par une fonction d'utilité doivent être complètes, transitives, continues et indépendantes.

Nous utilisons le terme « utilité espérée » lorsque nous étudions un événement risqué présentant plusieurs résultats possibles. L'utilité espérée de l'événement est alors calculée en faisant la somme des utilités des différents résultats possibles pondérées par la probabilité de réalisation de ces mêmes résultats. Soit un événement A pouvant fournir le résultat xo avec probabilité/» ou le résultat x\ avec probabilité (1 - p). Si un individu attribue une utilité U(xo) au résultat JCO et une utilité U(x\) au résultat x\, alors l'utilité espérée de l'événement A sera représenté par l'équation suivante :

EU(A) = pU(x0) + (1 - p)U(X l) (2.1)

rapport à un état initial dont la connaissance n'est pas nécessaire. En présence d'enjeux financiers, on parle alors d'utilité espérée de la richesse et d'utilité espérée du revenu. Le premier cas a été l'objet de critiques suggérant une remise en question de la théorie de l'utilité espérée (Rabin, 2000). Toutefois, ces critiques ne tiennent souvent plus lorsque nous utilisons un modèle basée sur l'utilité espérée du revenu (Cox, 2002). Ce mémoire présente une méthodologie s'appuyant sur des simulations d'individus fictifs ayant tous un état de richesse initiale nulle. Les résultats des situations risquées présentées peuvent donc être vus autant comme des états finaux que comme des variations de l'état initial de l'agent considéré.

Dans le présent contexte, la notion de risque implique une connaissance des résultats possibles et des probabilités, mais pas du résultat final. Toute situation pouvant résulter avec une probabilité non nulle en plusieurs éléments différents est donc risquée. Mathématiquement, on peut exprimer une augmentation du risque associé à un événement par une augmentation de la

■y

variance des résultats pondérée par les probabilités de réalisation . Par exemple, un événement permettant de gagner 25$ ou 75$ avec probabilité de 50% est moins risqué qu'un événement permettant de gagner 0$ ou 100$ avec probabilité de 50%, mais est plus risqué qu'un événement permettant de gagner 55.56$ avec probabilité de 90% et 0$ avec probabilité de 10%. Pourtant, la valeur espérée est de 50$ dans les trois cas.

Aussi, une courbe d'utilité concave présentant une utilité marginale décroissante sera associée à un comportement d'aversion envers le risque alors qu'une courbe convexe exhibant une utilité marginale croissante traduira un comportement de goût pour le risque . La logique derrière ce fait est que, dans le cas d'aversion au risque, un individu associera une utilité moindre à un événement risqué qu'à un événement fournissant avec certitude la même valeur espérée4.

Inversement, pour un individu aimant le risque, l'utilité espérée d'un événement risqué sera supérieure à l'utilité découlant de l'obtention certaine de la valeur espérée. L'égalité entre les deux implique la neutralité face au risque. Si on reprend l'exemple présenté par l'équation 2.1, nous obtenons les équations 2.2 à 2.4 :

Aversion au risque ■ EU(A) < U(px0 + (1 — p)*i) (2.2)

2 Notons qu'une variance des utilités de chaque résultat pondérées par les probabilités de réalisation constituerait une

définition plus subjective du risque. De fait, dans ce contexte, un événement pourrait être très risqué pour un individu ayant une certaine fonction d'utilité, mais peu pour un autre ayant une fonction différente.

3 Nous n'employons au cours de ce mémoire que le terme « aversion au risque » pour traiter des préférences des

individus.

4 Le résultat espéré d'un événement risqué est la moyenne pondérée par les probabilités de réalisation de tous les

Goût pour le risque ■ EU(A) > U(px0 + (1 - p)xx) (2.3)

Neutralité au risque ■ EU (A) = U(px0 + (1 - p)x^) (2.4)

Bien que plusieurs auteurs étudient la volonté à payer des agents (Guiso et Paiella, 2008) ou leur comportement lors d'enchères (Isaac et James, 2000), l'outil privilégié lors de l'estimation des préférences face au risque en contexte d'utilité espérée demeure les loteries. Il y a plus de vingt-cinq ans, Farquhar (1984) résumait une littérature déjà importante à ce sujet en présentant une analyse des différentes manières d'utiliser les loteries en contexte expérimental. De nos jours, elles sont encore fréquemment utilisées (Holt et Laury, 2002, Andersen et al., 2005, etc.)

malgré certaines critiques remettant en question la pertinence d'estimer les préférences face au risque (Isaac et James, 2000, Rabin, 2000). Leur grande simplicité d'utilisation et leur adaptabilité a toutefois permis aux analystes d'étudier les préférences des agents dans différentes situations. Le concept de base des loteries est simple. Il s'agit de résumer une situation risquée par les résultats qu'elle peut engendrer et par les probabilités associées à ces résultats. Ainsi, un grand nombre de situations de la vie courante peut être exprimé sous la forme :

[x0, x^, x2, ■■■ , xn; p0, p1, p2, ...,pn\ (2-5)

Les différents x, représentent chacun des n+l résultats possibles associés aux probabilités de réalisation p,5. En demandant aux agents de comparer des loteries ou d'identifier des valeurs

(résultats certains ou probabilités) les rendant indifférents entre elles, il devient possible aux chercheurs d'utiliser la théorie de l'utilité espérée pour estimer des paramètres de fonctions d'utilité, tracer des courbes d'utilité ou estimer un coefficient d'aversion au risque représentant les préférences des individus. Dans le prochain sous-chapitre, nous présentons justement les mesures d'aversion au risque les plus couramment utilisées en contexte d'utilité espérée.

2.2 Les mesures d'aversion au risque

À la recherche d'un indice pouvant caractériser les préférences des agents face à une situation risquée, Arrow et Pratt, dans les années 60 et 70, proposèrent des mesures utilisant le ratio suivant pour évaluer les préférences d'un agent :

™

w

—ôès

(26)

Ici, x représente l'élément dont on mesure l'utilité alors que Lr(x,) et C/"(x,) sont respectivement les dérivées première et seconde de la fonction d'utilité évaluées au point x,

Pi-risque et permet de modéliser le comportement des individus lorsque leur richesse initiale varie, mais que le choix risqué s'offrant à eux reste le même (Binswanger, 1981) ou lorsque leur richesse initiale reste la même, mais que les montants en jeu varient de manière absolue. Notons qu'une fonction d'utilité concave génère un coefficient ARA(x) positif et une fonction convexe génère un coefficient négatif. Ainsi, plus ARA(x) est élevé, plus l'individu est considéré averse au risque. La prédiction initiale d'Arrow (1971) était que l'aversion absolue au risque des individus devait en général être décroissante avec la richesse finale. Des expériences subséquentes confirmèrent cette prédiction (Binswanger, 1981) et celle-ci devint un fait presque inébranlable dans la littérature économique6.

Arrow et Pratt ne se limitèrent cependant pas à l'aversion absolue et proposèrent également une autre mesure qui prit le nom de coefficient d'aversion relative au risque. Cette dernière est le produit de l'aversion absolue et de la valeur de JC, enjeu :

U"(Xi)

RRA(Xi) = - j j r r i x i = ARAixd ' xt (2.7)

U {Xi)

Cette équation nous donne une mesure des préférences d'un agent dans un cas où sa richesse initiale et la taille des enjeux varient proportionnellement (Binswanger, 1981). Par exemple, elle peut servir à décrire les comportements d'individus ayant une richesse initiale nulle, mais faisant face à une situation risquée dont les résultats possibles sont multipliés par une constante k. Il était initialement de l'avis d'Arrow que l'aversion relative au risque devait être croissante avec la richesse finale, mais les résultats des études expérimentales menées depuis ce temps fournissent des conclusions partagées. Binswanger (1981) trouve que l'aversion relative au risque tend à être décroissante alors que Holt et Laury (2002) identifient plutôt une aversion qui serait croissante tel que prédit par Arrow. Harrison et al. (2004) quant à eux trouvent, en utilisant la même méthode expérimentale qu'Holt et Laury, que l'aversion relative est négative pour des petits enjeux, mais croît pour devenir positive et presque constante pour des enjeux plus élevés. Ils ne rejettent d'ailleurs pas l'hypothèse qu'elle soit constante sur la majorité de la courbe d'utilité.

Tout au long de ce mémoire, nous traitons à plusieurs reprises du caractère constant ou variable de l'aversion relative et absolue des individus étudiés. Afin d'alléger le texte, nous utilisons donc parfois la notation courante dans la littérature. Ainsi, une fonction d'utilité engendrant un coefficient d'aversion absolue au risque constant est dite de type CARA. Les fonctions présentant des coefficients d'aversion décroissants ou croissants sont respectivement dites de type DARA ou LARA. De même, les fonctions générant des coefficients d'aversion relative au risque constants, décroissants et croissants sont respectivement dites de type CRRA, DRRA et IRRA.

2.3 La méthode expérimentale de l'arbitrage de Wakker et Deneffe

La méthode de l'arbitrage7 de Wakker et Deneffe (1996) est une méthode non paramétrique

permettant d'obtenir des courbes d'utilité normalisées en identifiant des égalités de différences d'utilité. La logique est la suivante. Soient x, (i = 0, 1, 2, 3, ... , n), S et R des quantités d'un élément x dont on mesure l'utilité. Si un individu est indifférent entre les loteries [x\, S; p] et [xç,, R; p] et qu'il est aussi indifférent entre les loteries [x2, S; p] et [x\, R; p], alors on peut poser les

égalités suivantes :

pU(X l) + (1 - p)U(S) = pU(x0) + (1 - p)U(R)

pU(x2) + (1 - p)U(S) = pU(X l) + (1 - p)U(R)

D'où:

p(U(xt) - U(x0)) = (1 - p)(U(R) - U(S))

p(U(x2) - U(xx)) = (1 - p)(U(R) - U(S))

Donc :

p(U(X l) - U(x0)) = p(U(x2) - U(X l))

U(Xl) - U(x0) = U(x2) - U(Xl) (2.8)

En contexte expérimental, en posant des valeurs arbitraires pour p, S, R et xo, en demandant aux répondants d'identifier quelle valeur de xi satisfait l'indifférence entre [x\, S; p] et [xo, R; p], en utilisant ensuite cette valeur pour demander d'identifier la valeur de x2 satisfaisant

l'indifférence entre [x2, S; p] et [x\, R; p] et en répétant ce processus plusieurs fois, nous pouvons

obtenir n+l valeurs de xt. Puisque les préférences représentées par une fonction d'utilité peuvent

être aussi représentées par une transformation linéaire positive de cette même fonction, nous pouvons normaliser sans perdre d'information en posant u(x,) = (U(x,) - U(XQ)) I (U(x„) - U(XQ))

où U(XJ) représente l'utilité normalisée de x„ u(xo) = 0 et u(x„) = 1. Selon l'équation 2.8, nous savons que l'expression U(xi+\) - U(x,) sera toujours constante. La normalisation n'affecte pas ce

résultat et la différence «(*,+/) - u(x,) sera également toujours constante. Nous obtenons donc n+l points sur une courbe d'utilité normalisée représentés par les coordonnées (JC„ u(x,) = Un) et que nous pouvons situer sur un graphique semblable au suivant :

«00 = 1

u(x2) = 2/n

u(xj) = l / n uixo) = 0

XQXJ X2

Notons que XQ n'est pas nécessairement nul et que si nous nous intéressons autant au domaine des gains qu'au domaine des pertes, il est possible d'appliquer la méthode sur tout le spectre de valeurs pour obtenir une courbe d'utilité sur les deux domaines. De plus, la courbe obtenue n'est pas influencée par les distorsions des probabilités. En effet, selon la littérature, les agents tendent à donner trop de poids aux résultats qu'ils considèrent certains. Ce phénomène porte le nom d'« effet de certitude » et peut engendrer des violations des axiomes de von Neumann et Morgenstern de la théorie de l'utilité espérée tel que le prouve le fameux paradoxe d'Allais (1953). Kahneman et Tversky (1979) l'ont même utilisé comme argument lors de l'élaboration de la théorie des perspectives8, une alternative à la théorie de l'utilité espérée. Or,

l'équation 2.8 montre que les différences d'utilité entre les points sur la courbe résultent d'un processus qui élimine les probabilités des calculs et qui évite que la méthode de l'arbitrage soit soumise aux problèmes de distorsion. Notons toutefois que le fait de procéder en chaîne peut causer la propagation des erreurs. Si un individu commet une erreur en répondant à une question, puisque sa réponse sera utilisée dans la question suivante, son erreur se répercutera sur sa réponse suivante et ainsi de suite. Ce phénomène est d'ailleurs la source de la critique principale du procédé de Wakker et Deneffe. Nous en discutons plus longuement au sous-chapitre 5.1 et utilisons notre méthodologie afin de tester la gravité de cette critique lorsque de l'arrondissement vient biaiser les réponses des individus.

Après avoir obtenu la courbe d'utilité d'un individu, nous pouvons continuer l'analyse afin de récupérer ses coefficients d'aversion au risque absolue ou relative. Pour ce faire, deux possibilités s'offrent à nous. Soit nous procédons de manière paramétrique, éliminant ainsi l'un

10

des principaux avantages de la méthode de l'arbitrage, soit nous trouvons une autre manière d'estimer les coefficients désirés. Le prochain sous-chapitre aborde le premier cas qui est le plus courant dans la littérature.

2.4 Les estimations paramétriques

La majorité des économistes optent pour une approche paramétrique lorsque vient le temps d'estimer l'aversion au risque et ce, peu importe la méthode expérimentale utilisée ou le contexte théorique (théorie de l'utilité espérée ou autre). Cette approche consiste généralement à spécifier une forme fonctionnelle pour l'utilité et à estimer les paramètres inconnus à l'aide de la méthode des moindres carrés, du maximum de vraisemblance ou autrement. Par exemple, Booij et al. (2009), ont utilisé la méthode de l'arbitrage avec estimation paramétrique pour étudier les préférences de la population néerlandaise. En spécifiant une fonction puissance pour l'utilité, ils ont pu estimer les paramètres inconnus par maximum de vraisemblance. Dans le cadre de la théorie de l'utilité espérée, ces paramètres peuvent être utilisés pour calculer les coefficients d'aversion absolue et relative au risque.

Le problème avec l'approche paramétrique est qu'elle force généralement l'analyste à poser des hypothèses fortes concernant la forme de la courbe d'utilité. Or, nous avons vu dans le sous-chapitre 2.2 qu'il n'y a pas toujours consensus quant à la forme des fonctions d'utilité des agents. Si, lors des estimations, la fonction spécifiée ne s'accorde pas avec le comportement d'un individu, nous obtiendrons des résultats erronés. Nous avons d'ailleurs déjà mentionné dans l'introduction que les approches paramétriques génèrent des résultats difficilement vérifiables compliquant ainsi l'évaluation de l'ampleur du biais. Il serait donc souhaitable de développer un procédé d'estimation qui ne serait pas soumis à cette source de biais. C'est ce que nous tentons de faire en spécifiant une forme fonctionnelle flexible pour l'utilité. Dans la littérature, ce procédé est déjà présent. Holt et Laury (2002) et Harrison et al. (2004) adoptent une approche expérimentale basée sur des choix entre des loteries et spécifient ensuite une fonction hybride flexible appelée « puissance-expo9 » pour estimer, à l'aide des maximums de vraisemblance, les

coefficients d'aversion absolue et relative d'individus. Dans nos travaux, nous nous concentrons toutefois sur l'utilisation des splines cubiques dont le fonctionnement est détaillé dans le prochain sous-chapitre.

2.5 Les splines cubiques

Dans les sous-chapitres précédents, nous avons mentionné que la méthode de l'arbitrage nous permet d'obtenir des « courbes d'utilité », mais ce que nous obtenons en fait, ce sont les coordonnées de points se trouvant sur les courbes en question. Ces dernières ne sont complètes que lorsque nous relions tous les points. Cela peut être fait grossièrement en traçant des segments de droites entre chacun d'eux ou un peu plus précisément en spécifiant une forme fonctionnelle de manière paramétrique. Dans ce dernier cas, nous avons vu que nous nous exposons aux erreurs de spécification, mais dans le premier il nous est impossible de calculer les coefficients d'aversion au risque. De fait, des segments linéaires entraînent des dérivées secondes nulles et, par extension, des coefficients d'aversion au risque nuls également (voir les équations 2.6 et 2.7).

Or, en plus d'obtenir une courbe complète, nous aimerions obtenir une estimation de l'aversion au risque qui nous permettrait de prédire le comportement d'un individu et ce, sans poser d'hypothèse forte au sujet de la forme que devrait avoir la courbe d'utilité. Ce problème pourrait être résolu en utilisant les splines cubiques10. Ce procédé a d'ailleurs déjà été utilisé de

manière concluante afin d'estimer les anticipations subjectives d'individus quant à la réalisation de variables aléatoires (Bissonnette, 2007 et Bellemare, Bissonnette et Kroger, 2010). Dans le présent mémoire, nous souhaitons voir si les splines cubiques peuvent fournir le même genre de résultats dans le cas de l'estimation d'une fonction d'utilité et de l'aversion au risque. Avant toute chose, nous devons étudier la logique derrière cette approche. La figure 2.2 montre un exemple de spline cubique.

Figure 2.2 : Exemple de spline cubique estimant une fonction d'utilité

«00

«00 = V2

u(Xo) = 0

12

Tout comme dans les sous-chapitres précédents, xt (i = 0,1,2, ... ,n) représente une certaine

quantité d'un élément x dont on mesure l'utilité. La véritable fonction d'utilité normalisée u(x) est toutefois inconnue et c'est cette dernière que nous estimons à l'aide d'une spline. Pour ce faire, nous cherchons à identifier les paramètres at, 6„ c, et di de chacun des segments. Cela peut

être fait en utilisant 4« équations où n représente le nombre de segments de notre problème (par exemple, trois points sur la courbe génèrent deux segments). On obtient tout d'abord 2« équations en posant :

at + biXi + c(x\ + d(x\ = u(x;) pour i < n (2.9)

at + btxi + 1 + Cixf+l + dtxf+1 — u(xi + 1) pour i < n (2.10)

De fait, rappelons que nous normalisons les utilités entre 0 et 1 dans le cadre de la méthode de l'arbitrage. Les valeurs de u(x,) et u(xi+]) sont donc connues et sont égales à :

r A ' , ^ t + 1

u(Xi) = — et u(xi + 1) = pour i < n

n n

L'hypothèse faible que la fonction doit être continue et différentiable en tout point nous permet d'obtenir 2 n - 2 équations supplémentaires en posant les contraintes :

/i'Oi+i) = /i'+iOi+i) Pour i < n - l (2.11) fi"(.xl+1) = ft'it(xi + 1) pour i < n - 1 (2.12)

Ici, fi(x) représente la fonction cubique du segment /' de la spline. Afin d'identifier complètement les paramètres, il manque encore deux contraintes. Nous les obtenons en imposant que les splines soient naturelles, c'est-à-dire que les dérivées secondes aux extrémités de la courbe d'utilité soient nulles.

/o"Oo)=/n-xOn) = 0 (2.13) Il s'agit d'une hypothèse faible comparativement aux hypothèses paramétriques classiques, mais il serait quand même préférable de trouver des contraintes plus intuitives. Nous abordons le sujet plus en détail dans le sous-chapitre 5.2.

En bout de ligne, nous obtenons donc bel et bien 4« équations nous permettant d'identifier les 4« paramètres des segments cubiques de notre spline. Le résultat est une fonction continûment différentiable sur tout le spectre de valeurs qu'elle couvre. Or, c'est exactement ce que nous recherchons pour approximer les fonctions d'utilité. Notons cependant que les splines ne sont pas contraintes par la monotonicité de la croissance, mais que lorsque nous étudions des cas où x est un bien normal (qui représente la majorité des cas), l'utilité doit être monotone croissante. En utilisant les splines cubiques, nous risquons donc d'obtenir des courbes dont l'interprétation économique est contraire au contexte dans lequel elles sont utilisées. Le problème

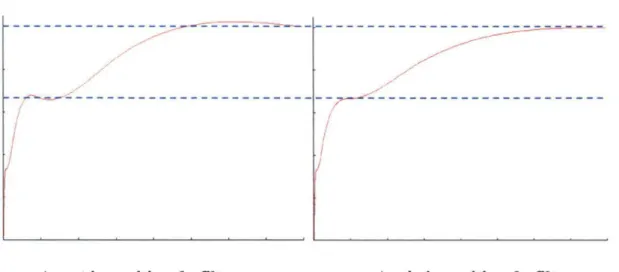
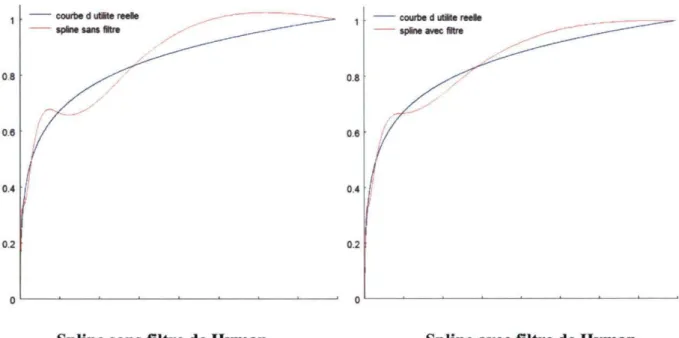
peut toutefois être évité grâce au filtre de Hyman (Hyman, 1983). Ce dernier est un critère qui fait en sorte que les segments où l'utilité est décroissante sont aplanis de manière à conserver la croissance de la fonction. La figure 2.3 en montre un exemple.

Figure 2.3 : Spline cubique avant et après imposition du filtre de Hyman

Avant imposition du filtre Après imposition du filtre

Le problème de l'imposition du filtre de Hyman est qu'il change les contraintes d'identification des paramètres des splines et qu'il devient alors possible que les splines ne soient plus continûment différentiables en tous points. Or, ce dernier critère est essentiel pour l'estimation de l'aversion au risque. Nous devrons donc en tenir compte dans nos travaux et voir dans quelle mesure la présence ou l'absence du filtre de Hyman s'avère nécessaire. Notons toutefois que puisque nous nous intéressons d'abord et avant tout à l'estimation des coefficients d'aversion au risque, si la présence du filtre de Hyman s'avérait source de problème, nous pourrions nous en passer. Le scénario idéal serait quand même d'obtenir des splines fournissant des estimations acceptables des coefficients tout en respectant la monotonicité de la croissance de l'utilité. Dans le prochain chapitre, nous présentons la méthodologie suivie pour obtenir ces splines et pour répondre aux questions de la problématique.

Chapitre 3

Méthodologie

Afin de répondre aux questions de la problématique, nous développons dans ce chapitre un procédé pour évaluer les performances des splines cubiques comme outil d'estimation des préférences face au risque, pour comparer ces performances à celles d'approches paramétriques standards, pour tester l'impact de l'arrondissement et des erreurs de spécification dans les deux cas et pour déterminer le nombre de points optimal à obtenir sur les courbes d'utilité lors d'expériences basées sur la méthode de l'arbitrage.

Pour atteindre tous ces objectifs, nous procédons à des simulations informatiques de type Monte Carlo. Plus précisément, nous simulons le comportement d'un certain nombre d'individus fictifs ayant tous des coefficients d'aversion au risque différents et une richesse initiale nulle. Nous utilisons ensuite la théorie de l'utilité espérée pour déterminer quelles réponses ces individus fictifs devraient fournir à des questions basées sur la méthode de l'arbitrage. Ces résultats sont par la suite utilisés pour estimer l'aversion au risque des individus à l'aide de l'approche paramétrique ou de l'approche flexible s'appuyant sur les splines cubiques et finalement, ces estimations sont comparées aux valeurs réelles d'aversion au risque ayant servi pour les calculs. En répétant ce processus en variant le nombre de points sur les courbes d'utilité, le niveau d'arrondissement et le type d'aversion au risque à calculer, nous sommes en mesure de répondre à nos questions. Nous pouvons également utiliser les résultats pour mener l'analyse au-delà du cadre défini par nos travaux.

Le présent chapitre décrit donc en détail la méthodologie employée. Tout d'abord, nous devons déterminer l'environnement des simulations et, plus précisément, choisir les fonctions d'utilité à utiliser, les valeurs d'aversion au risque théoriques, le niveau d'arrondissement, le nombre de points, etc. Les procédures de sélection des détails de l'environnement des simulations et leur utilisation sont décrites dans le prochain sous-chapitre.

3.1 Identification des valeurs théoriques initiales

Nous avons vu au sous-chapitre 2.2 que la littérature n'arrive pas à un consensus concernant l'évolution de l'aversion relative au risque des individus le long des courbes d'utilité, mais qu'un comportement de type DARA est généralement admis pour l'aversion absolue. Toutefois, Harrison et al. (2004) affirment qu'on ne peut rejeter l'hypothèse d'un comportement suggérant

une aversion relative constante et cette dernière implique justement une aversion absolue décroissante (puisque RRA(x) -e- x = ARA(x)). De plus, dans les études menées en dehors du contexte de la théorie de l'utilité espérée, nous trouvons qu'une fonction de forme puissance (U(x) = xa) approxime mieux les préférences des gens que bien d'autres formes (Stott, 2006,

Booij et al., 2009). Or, en contexte d'utilité espérée, cette fonction retourne un coefficient d'aversion relative au risque constant. Un avantage non négligeable de cette forme fonctionnelle est également qu'elle ne présente qu'un seul paramètre inconnu à estimer. Nous utilisons donc une fonction de ce genre pour nos simulations en n'apportant qu'un petit changement. En effet, en appliquant la formule de calcul de l'aversion relative (équation 2.7), nous obtenons, pour une fonction puissance standard, l'équation suivante :

U"(x)

RRA(x) = - — ^ x = l - a (3.1) il (x)

En posant l'égalité RRA(x) = 1 - a = r, nous pouvons réécrire la fonction puissance ainsi : Fonction puissance ■ U(x) = x1 _ r (3.2)

En estimant le paramètre inconnu r, nous nous trouvons donc à estimer directement l'aversion au risque relative des individus. Certains économistes dont Holt et Laury (2002) utilisent une fonction puissance de forme :

U(x) = xx~r 1 - r

Or, cette fonction retourne également un coefficient d'aversion au risque constant égal à r. Elle présente de plus l'avantage d'être croissante lorsque r > 1. Or, il s'agit d'une propriété désirable puisque nous supposons que l'utilité croît avec x pour tous les individus, peu importe leur aversion au risque r. Toutefois, comme nous l'expliquons un peu plus loin, nous nous limitons aux cas où r < 1. Nous avons donc opté pour la forme la plus simple. Le fait que r soit constant tout au long de la courbe facilite également les calculs contrairement à des cas IRRA ou DRRA où l'aversion relative est variable.

Nous étudions également des cas où des agents ont une courbe d'utilité de type exponentielle représentée par l'équation suivante :

Fonction exponentielle •• U(x) = —e_rx (3.3)

Bien que cette fonction génère un coefficient d'aversion absolue au risque constant (ARA(x) = r) alors que la littérature empirique tend à observer un comportement d'aversion absolue au risque décroissante dans la population, elle peut toujours nous être utile pour vérifier si les résultats obtenus dépendent de la fonction d'utilité utilisée. Comme dans le cas de la

16

fonction puissance, il n'y a qu'un seul paramètre inconnu et, lors de son estimation, nous nous trouvons à estimer directement l'aversion au risque, facilitant ainsi les calculs.

Après avoir identifié les fonctions à utiliser, nous devons déterminer des intervalles pour les valeurs d'aversion au risque absolues et relatives théoriques. Ces intervalles doivent couvrir un ensemble suffisamment grand de valeurs généralement admises dans la littérature et doivent nous permettre d'étudier autant le cas de l'aversion au risque que le cas du goût pour le risque. Les études expérimentales estimant la distribution de l'aversion au risque au sein d'une population, dont une majorité a été effectuée auprès d'étudiants, nous indiquent qu'environ 90% de la population possède une aversion relative inférieure à 0.9 (Ivanova-Stenzel et Kroger, 2008). Les individus fictifs postulés pour nos simulations auront donc des coefficients d'aversion au risque relative répartis de manière équidistante sur l'intervalle [-1, l]1 1.

En ce qui concerne l'aversion absolue, nous n'avons pas de point de départ pour établir un intervalle de coefficients pour nos simulations puisque la littérature tend à infirmer un coefficient constant (voir sous-chapitre 2.2). Le problème peut cependant être résolu en adaptant l'intervalle d'aversion relative au cas absolu. De fait, l'aversion relative est égale à l'aversion absolue multipliée par le montant en jeu (équation 2.7). Ainsi, en divisant les bornes de l'intervalle d'aversion relative par une estimation de la valeur moyenne des montants enjeu lors de l'application de la méthode de l'arbitrage (moyenne des valeurs de x,), nous pouvons obtenir un intervalle comparable et réaliste pour nos simulations. Par exemple, si nous croyons que les valeurs en abscisse sur les courbes d'utilité obtenues avec la méthode de l'arbitrage tournent en moyenne autour de 1000, alors nous posons un intervalle d'aversion absolue au risque de [-0.001, 0.001]. Cependant, afin d'approximer la moyenne des montants enjeu (les valeurs de xt

en abscisse sur les courbes d'utilité) il nous faut d'abord déterminer les loteries à utiliser lors de l'application de la méthode de l'arbitrage.

Nous nous sommes encore une fois tournés vers la littérature afin de choisir des loteries déjà utilisées dans des expériences et nous permettant de placer nos résultats dans un contexte existant. Wakker et Deneffe (1996) suggèrent d'utiliser des valeurs suffisamment élevées et éloignées les unes des autres afin de pouvoir couvrir une plus grande partie de la courbe d'utilité et d'éviter que la courbure soit minime. Cette idée est d'ailleurs reprise par Abdellaoui (2000). De plus, comme notre but est de tester une nouvelle méthode d'estimation de l'aversion au risque, nous aimerions savoir si celle-ci est influencée par la magnitude des valeurs utilisées. Nous avons donc opté pour les valeurs de Booij et al. (2009). Ces derniers utilisent d'abord les

11 Dans une population plus générale, il se peut qu'un plus grand nombre d'individus aient une aversion au risque

relative supérieure à 1. Des études expérimentales telles que celle de Harrison et al. (2004) montrent que c'est le cas pour une portion non négligeable de la population danoise. D'autres études, de nature empirique, telles que celle de Chiappori et Paiella (2008) menée auprès de la population italienne concluent même qu'un quart de la population aurait en fait une aversion relative supérieure à 3.

loteries [xo = 100, 64; 0.5] et [JCI, 12; 0.5] qui présentent des valeurs plutôt faibles et cherchent la valeur de x\ entraînant l'indifférence entre les deux. Ils utilisent également les loteries [xo =

1000, 640; 0.5] et [xi, 120; 0.5] afin d'étudier le comportement des individus confrontés à des montants plus élevés. La répartition des valeurs utilisées entre 12 et 100 dans le cas des loteries à valeurs basses et entre 120 et 1000 dans le cas à valeurs élevées assure que les résultats obtenus permettent de couvrir une portion importante des courbes d'utilité tout en évitant les problèmes de changement de préférences pour de très petits enjeux identifiés par Harrison et al. (2004). Notons que dans le cas de Booij et al. (2009), les montants utilisés représentent des sommes d'argent exprimés en Euros et que leur expérience s'appuie sur des informations recueillies auprès d'environ 2000 personnes. Nous pouvons donc présumer qu'en utilisant leurs valeurs pour nos simulations nous nous trouvons en milieu commun et reconnu par la littérature. Dans nos travaux, nous considérons que les enjeux sont bel et bien des sommes monétaires, mais la devise utilisée n'a pas d'importance puisque nous procédons à des simulations informatiques.

Nous sommes maintenant en mesure de déterminer l'intervalle d'aversion absolue au risque à utiliser pour les simulations. En effet, selon les loteries spécifiées, puisque nous simulons des individus rationnels appuyant leurs choix sur la théorie de l'utilité espérée, nous savons que les montants en abscisse sur les courbes d'utilité seront plus grands que 100 (la valeur de xo dans le cas des loteries à valeurs basses) et augmenteront en importance selon le nombre de points sur les courbes, la magnitude des valeurs de référence des loteries et le coefficient d'aversion au risque de l'individu fictif postulé. Toutefois, si nous divisons les bornes de l'intervalle d'aversion relative au risque par un nombre trop élevé, nous obtenons un intervalle d'aversion absolue au risque trop petit. Il est donc préférable d'être conservateur dans nos démarches. Ainsi, nous avons choisi une distribution uniforme des coefficients d'aversion absolue au risque sur l'intervalle [-0.002, 0.002] dont les bornes sont le cinq-centième des bornes de l'intervalle de l'aversion relative.

Pour chacune des formes fonctionnelles spécifiées et des loteries choisies, nous postulons 100 individus fictifs ayant chacun un coefficient d'aversion au risque absolu ou relatif unique. Ainsi nous obtenons 50 individus averses au risque et 50 individus aimant le risque dans chacun des cas. Notons qu'il n'est pas nécessaire de postuler un individu ayant une aversion au risque relative ou absolue exactement égale à zéro et ayant un comportement de parfaite neutralité envers le risque. Si des conclusions spécifiques concernant la neutralité au risque doivent être tirées, elles peuvent l'être à partir des données obtenues pour les agents dont le coefficient d'aversion au risque est proche de zéro. Notons aussi qu'à chaque fois que nous changeons une variable dans les prochains sous-chapitres (nombre de points sur les courbes, arrondissement, etc.), nous postulons 100 nouveaux individus fictifs de façon à obtenir un nombre suffisamment grand de données pour faire nos calculs.

18

3.2 Obtention des points sur les courbes d'utilité par la méthode de

l'arbitrage

Nous sommes maintenant en mesure d'obtenir les points sur les courbes d'utilité de nos individus fictifs à l'aide de la méthode de l'arbitrage. Dans un contexte d'utilité espérée, si un individu est indifférent entre deux loteries [x,+i, S ; p] et [x„ R; p], nous obtenons la relation :

P

Or, rappelons que nous étudions les formes fonctionnelles puissance et exponentielle données par les équations 3.2 et 3.3 pour U(x). Dans les deux cas, l'aversion au risque est donnée par le paramètre r et est connue pour un individu fictif donné. De plus, R et S sont également connus et, pour la simulation de la première question de la méthode de l'arbitrage, x, = xo est aussi donné. Nous pouvons donc poser l'égalité entre l'équation 3.4 et l'une ou l'autre des équations 3.2 ou 3.3 évaluées à x,+i et isoler x,+i. En remplaçant x, par la valeur obtenue, nous pouvons recommencer l'opération aussi souvent que nous le souhaitons afin d'obtenir n+l valeurs de x,. Nous associons ensuite ces valeurs à des utilités également espacées et normalisées entre 0 et 1 et trouvons ainsi «+1 points (x„ w(x,)) sur une courbe d'utilité normalisée qui peuvent être utilisés pour estimer l'aversion au risque d'un individu fictif. Tous les calculs ont été effectués par ordinateur à l'aide d'un programme développé expressément pour nos travaux avec le logiciel Oxmetrics.

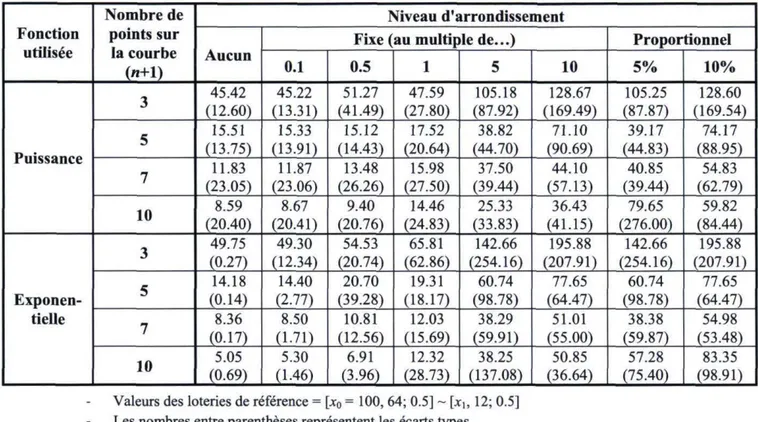
Enfin, nous devons décider combien de points (n+l) nous désirons sur nos courbes d'utilité. Un nombre élevé de points permet aux courbes de couvrir un plus grand éventail de valeurs, mais ouvre la porte à des biais tels que la propagation des erreurs en chaîne. Un plus grand nombre de points impliquent également une expérience plus longue et plus cognitivement exigeante pour les participants. L'identification du nombre de points minimum fournissant des résultats acceptables devient donc importante. Encore une fois, la littérature nous fournit des repères pour nous guider dans notre démarche. De fait, Wakker et Deneffe (1996) utilisent quatre questions afin d'obtenir cinq points sur leurs courbes. Abdellaoui (2000) en fait autant. Booij et al. (2009), ainsi que Fennema et Van Assen (1999) utilisent quant à eux six questions afin d'obtenir sept points dans un même domaine (gains ou pertes). Nos simulations incluent donc des cas à cinq et sept points. De plus, nous étudions un cas où ce nombre est moindre (trois points) et un cas où il est supérieur (dix points) afin de voir l'effet de la variation de ce nombre de points sur les estimations finales et ainsi de déterminer le nombre optimal. Le scénario engendrant les estimations de l'aversion au risque les plus proches des véritables valeurs sera identifié comme scénario optimal lors de l'application du procédé d'estimation flexible présenté dans ce mémoire.

3.3 Arrondissement

Dans les étapes précédentes, nous avons considéré que les individus fictifs postulés connaissaient parfaitement leur aversion au risque et répondaient aux questions de la méthode de l'arbitrage sans se tromper et de manière très précise. Or, il est probable que cela ne soit pas représentatif de la réalité où des erreurs peuvent survenir. Un type d'erreur qui reçoit beaucoup d'attention dans la littérature est l'arrondissement des réponses fournies par les gens (Manski et Molinari, 2010). Afin que nos simulations se situent en contexte plus réaliste, nous introduisons donc de l'arrondissement sur les valeurs rapportées (x,) par les individus fictifs en répondant aux questions de la méthode de l'arbitrage. Pour bien comprendre où s'applique l'arrondissement, regardons l'exemple suivant :

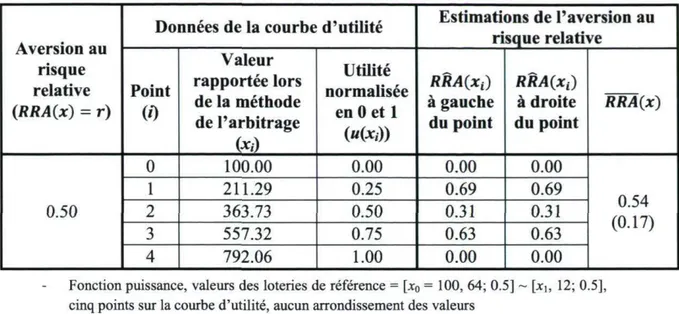
Un individu fictif ayant une fonction d'utilité de type puissance et un coefficient d'aversion relative au risque de 0.5 participe à une expérience basée sur la méthode de l'arbitrage. À la première question, on lui demande de donner la valeur de xi satisfaisant l'indifférence [xo = 100, 64; 0.5] ~ [xi, 36; 0.5]. Si l'individu n'arrondit pas et ne commet pas d'erreur en donnant sa réponse, il répondra que :

* i =

(0.5 x 64(1-°-5> + 0.5 x ÎOO^1-0-s> - 0.5 x 3 6 ^ - ° ^ y2

0.5 = 144

Le nombre 144 sera alors utilisé à la question suivante et l'individu devra rapporter la valeur de x2 satisfaisant l'indifférence [144, 64; 0.5] ~ [x2, 36; 0.5]. Toutefois, si l'individu

arrondit ses réponses au multiple de 10 le plus proche, au lieu de rapporter la véritable valeur de 144, il répondra que x\ vaut 140. On lui demandera ensuite de donner la valeur de x2 satisfaisant

[140, 64; 0.5] ~ [x2, 36; 0.5], propageant ainsi l'erreur de question en question.

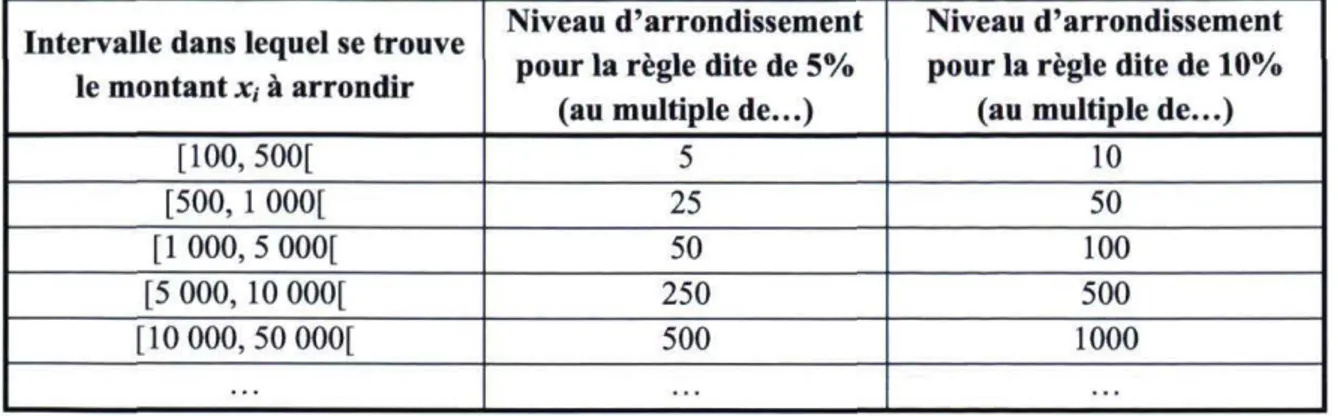
À notre connaissance, peu d'auteurs se sont intéressé aux attitudes d'arrondissement dans le contexte qui nous intéresse. Cela a pour conséquence que nous devons donc choisir de façon arbitraire les niveaux d'arrondissement à utiliser lors des simulations. Initialement, nous voulions simplement étudier les cas où les gens arrondissent à l'entier, au multiple de cinq et au multiple de dix le plus proche. Toutefois, il nous a semblé que ces paliers d'arrondissement étaient peut-être un peu trop faibles pour des cas où les montants en jeu peuvent atteindre les milliers. Ainsi, en s'appuyant sur les travaux de Manski et Molinari (2010), nous avons ajouté deux règles d'arrondissement variables. Ces dernières établissent un niveau d'arrondissement qui augmente lorsque les valeurs de x, à arrondir atteignent certains paliers. Le tableau 3.1 présente la progression de ces deux règles.

20

Tableau 3.1 : Règles d'arrondissement proportionnel aux montants en jeu

Intervalle dans lequel se trouve le montant x, à arrondir

Niveau d'arrondissement pour la règle dite de 5%

(au multiple de...)

Niveau d'arrondissement pour la règle dite de 10%

(au multiple de...)

[100, 500[ 5 10

[500, 1 000[ 25 50

[1000, 5 000[ 50 100

[5 000, 10 000[ 250 500

[10 000, 50 000[ 500 1000

Ces deux règles portent les noms de règles d'arrondissement proportionnel à 5% et 10% puisque, pour chaque intervalle de montants à arrondir, les niveaux d'arrondissement correspondent respectivement à 5% et 10% de la borne inférieure.

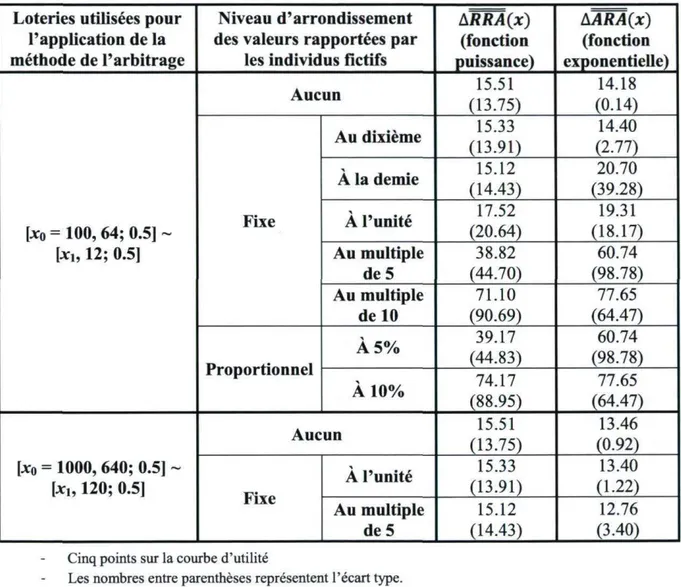
Ensuite, nous avons ajouté les niveaux d'arrondissement fixes au dixième (0.1) et à la demie (0.5) pour avoir une idée de ce qui se passe lorsqu'en situation d'arrondissement fixe, la magnitude des enjeux et le niveau d'arrondissement sont multipliés par le même facteur. Par exemple, en comparant le cas utilisant les loteries [xo = 100, 64; 0.5] et [xi, 12; 0.5] et un arrondissement au dixième avec le cas utilisant les loteries [xo = 1000, 640; 0.5] et [xi, 120; 0.5] et un arrondissement à l'unité, nous pouvons voir l'impact sur la précision des estimations de l'aversion au risque d'une multiplication par dix de toutes les valeurs impliquées (montants en jeu et niveaux d'arrondissement). Finalement, notons que nous n'utilisons tous les niveaux d'arrondissement précédemment mentionnés que dans les cas où les loteries de référence pour la méthode de l'arbitrage ont des montants faibles. Dans les cas avec des montants plus élevés, nous n'utilisons que l'arrondissement à l'entier et au multiple de cinq.

Rappelons aussi que pour obtenir suffisamment de données pour nos calculs, 100 individus fictifs sont postulés pour chaque combinaison possible de forme fonctionnelle, de nombre de points sur la courbe d'utilité, de loteries et de niveau d'arrondissement. Par exemple, 100 individus ayant des aversions relatives distribuées de manière équidistante sur l'intervalle [-1, 1] sont postulés pour le cas où la fonction d'utilité a la forme puissance, les loteries utilisées pour la méthode de l'arbitrage sont [xo = 100, 64; 0.5] et [xi, 12; 0.5], il y a trois points sur les courbes d'utilité et les individus arrondissent au multiple de cinq. Changer l'un où l'autre de ces éléments implique de simuler 100 nouveaux individus. Nous obtenons donc un environnement pour nos simulations qui est résumé par le tableau 3.2.

Tableau 3.2 : Environnement de simulation

Forme fonctionnelle

utilisée pour l'utilité Puissance (type CRRA) et Exponentielle (type CARA) Nombre d'individus

fictifs postulés 100 dans chaque cas

Distribution des coefficients d'aversion

Aversion relative (fonction puissance) : équidistante sur [-1, 1] Aversion absolue (fonction exponentielle) : équidistante sur [-0.002, 0.002] Loteries pour la méthode de l'arbitrage Valeurs basses : [x0 = 100, 64; 0.5] ~ [xh 12; 0.5] et Valeurs élevées : [x0 = 1000, 640; 0.5] ~ [x,, 120; 0.5] Niveaux d'arrondissement

Valeurs de référence basses : - Aucun arrondissement - Arrondissement fixe aux multiples de 0.1, 0.5, 1, 5 et 10 - Arrondissement proportionnel à 5% et 10%

Valeurs de référence élevées : - Aucun arrondissement;

- Arrondissement fixe aux multiples de let 5

Nombre de points sur

les courbes d'utilité 3, 5, 7 et 10

3.4 Calcul des paramètres des splines et de l'aversion au risque

Lorsque nous avons obtenus les points sur les courbes d'utilité pour chacun des individus fictifs postulés dans chacun des cas décrits précédemment, nous pouvons relier ces points par des segments de splines cubiques en employant le procédé décrit dans le sous-chapitre 2.5. Tous les calculs nécessaires à cette fin ont été effectués à l'aide du programme SplineSim (Bellemare, Bissonnette et Kroger, 2010) développé à l'aide du logiciel Oxmetrics.

Lorsque les paramètres des splines sont estimés, nous pouvons utiliser les formules d'aversion relative et absolue afin de calculer les coefficients à gauche et à droite de chaque point intérieur sur les courbes d'utilité normalisées. Le fait de normaliser les valeurs d'utilité n'a pas d'impact sur l'estimation des coefficients d'aversion au risque puisqu'il s'agit d'une transformation linéaire positive qui génère une fonction d'utilité caractérisant les mêmes préférences que la fonction initiale. Les coefficients d'aversion au risque absolue et relative en un point (x,,_/(x,)) sur un segment cubique de spline s'écrivent donc:

/"(*<) ARA(Xi) =

n*ù

rt*ù

n*d

~

22

La notation ARA(xt) et RRA(Xi) signifie qu'il s'agit des estimations et non des véritables

valeurs d'aversion au risque. Les coefficients b, c et d sont des paramètres de la fonction cubique sur laquelle se trouve le point auquel nous estimons l'aversion au risque. Dans le cas de splines cubiques reliant des points obtenus par la méthode de l'arbitrage, nous devons trouver, pour chacun des points intérieurs, les équations :

2ci_1 + 6di^1xi 2C[ + 6diXi bi-i + 2c/_1Xi + 3di^1xf bi + 2c(x{ + 3d(xf

iiftifa)—

T

:r: _.,:'

3

— . *,'T;^ W

x--Ici, x, est toujours une valeur de x obtenue par la méthode de l'arbitrage, bt.\, ct.\ et du\ sont

les paramètres du segment de spline à gauche de x, et 6„ c, et dt sont les paramètres du segment

de spline à droite de x,. Les équations 3.7 et 3.8 impliquent donc que l'estimation de l'aversion au risque en un point séparant deux segments doit être la même en utilisant les paramètres de gauche qu'en utilisant les paramètres de droite. Cela est une conséquence directe de l'imposition de l'égalité entre les dérivées premières ainsi que de l'égalité entre les dérivées secondes à chaque point (voir les équations 2.11 et 2.12) comme contraintes dans les calculs des paramètres des splines. Il n'y a que lors de l'utilisation du filtre de Hyman que ces égalités peuvent être violées. Si cette situation venait à se présenter trop souvent, nous devrions peut-être remettre en question la possibilité d'utiliser les splines pour tracer les courbes d'utilité. Si l'absence du filtre permet toutefois des estimations acceptables des coefficients d'aversion au risque, alors nos objectifs seront quand même atteints.

Ensuite, notons que les segments cubiques, bien que plus flexibles que des segments linéaires, ne sont pas exempts de défauts. Par exemple, pour que l'aversion relative soit constante, il faut que la dérivée de l'équation 3.6 soit nulle. En calculant cette dérivée pour le côté droit de l'égalité, nous trouvons qu'elle est bel et bien nulle lorsque 3cdx,2 + bc + 6bdxt = 0.

Cette égalité ne tient que si deux des paramètres prennent la valeur zéro (nous excluons le cas où x, est nul puisque nous cherchons les situations où l'aversion relative reste constante peu importe la valeur de x). Or, si Z? et c sont nuls, l'équation 3.8 retourne, pour toutes les valeurs de x„ une aversion relative de -2. Si b et d sont nuls, l'aversion relative est de -1. Si c et c/sont nuls, l'aversion relative est égale à 0. Les splines s'accordent donc peu avec les résultats expérimentaux et empiriques qui tendent à identifier des coefficients d'aversion relative au risque positive pour la majorité de la population.

Les défauts des splines ne sont cependant pas suffisamment importants pour que nous mettions cet outil potentiel de côté sans l'étudier. Peut-être pourraient-ils d'ailleurs être évités en utilisant des splines de degrés supérieurs. Nous discutons de cette possibilité au sous-chapitre 5.2. Aussi, nous avons vu que l'approche paramétrique utilisant une forme fonctionnelle moins

flexible possède également ses failles. Le but de nos travaux n'est donc pas de prouver que les splines sont un outil parfait, mais plutôt de comparer leurs performances lors de l'estimation de l'aversion au risque avec les performances de l'approche paramétrique. En ce sens, même si les splines ont des défauts, si les estimations qu'elles fournissent sont plus proches des véritables valeurs que les autres estimations paramétriques, leur utilisation sera justifiée d'autant plus que ces estimations auront été obtenues dans un contexte suboptimal. Des travaux futurs, s'appuyant sur les nôtres, pourront peut-être mener à un raffinement de la méthodologie présentée dans ce mémoire.

Pour l'instant, rappelons que les équations 3.7 et 3.8 fournissent des estimations pour l'aversion au risque uniquement aux points intérieurs des courbes d'utilité normalisées. De fait, nous avons imposé comme contraintes que les dérivées secondes devaient être nulles aux extrémités (équation 2.13). Les coefficients d'aversion au risque ne peuvent donc qu'être nuls également à ces points. Une question se pose cependant à savoir quelle estimation utiliser comme estimation « officielle » de l'aversion au risque. Prenons l'exemple suivant :

Supposons que nous avons obtenu à l'aide de la méthode de l'arbitrage une courbe d'utilité normalisée à cinq points pour un individu A ayant une fonction d'utilité de forme exponentielle et une aversion au risque de type CARA égal à 0.001. À l'aide des splines cubiques, nous estimons que les coefficients d'aversion absolue au risque de cet individu aux trois points intérieurs de la courbe d'utilité sont respectivement 0.0008, 0.0012 et 0.0011. Bien que ces résultats nous donnent déjà une idée des préférences de l'individu, pour poursuivre notre analyse, nous devons choisir l'un de deux scénarios possibles. Premièrement, nous pouvons spécifier une forme fonctionnelle retournant un coefficient d'aversion absolue constant pour l'utilité de l'individu A. Cela implique toutefois de poser une hypothèse forte ou de connaître au préalable la forme de sa fonction d'utilité. Deuxièmement, nous pouvons poursuivre notre analyse sans imposer de forme fonctionnelle pour l'utilité.

Dans le premier scénario, si nous savons que l'individu A a une fonction d'utilité exponentielle fournissant une aversion au risque absolue constante ou si nous en faisons l'hypothèse, nous pouvons utiliser individuellement les trois estimations ponctuelles obtenues (ARA(x1), ARA(x2) et ARA(x3)) pour décrire ses préférences ou nous pouvons les agréger

sous forme d'une moyenne1 notée ARA(x). Afin de voir quel cas est le plus adéquat, après nos

simulations nous calculons donc, autant pour l'aversion absolue que pour l'aversion relative, les moyennes des estimations aux points intérieurs et comparons les écarts en pourcentage entre ces moyennes et les véritables valeurs d'aversion au risque avec les écarts en pourcentage entre

12 II est de notre avis que la moyenne doit ici être privilégiée à la médiane et au mode. Notons aussi que s'il n'y a

que trois points sur la courbe d'utilité, il n'y a donc qu'un seul point intérieur et le calcul d'une moyenne est superflu.

24

chacune des estimations ponctuelles et les véritables coefficients d'aversion au risque à l'aide des équations suivantes :

, x ARA(x) - ARA(x) M R A M ARAQO X W ° ( 3 9 ) ARA(xt) - ARA(xt) AARA(Xi) = p " x l O O ; i = 1,2,... , n - l (3.10) RRA(x) - RRA(x) " " W = RRAQO X 1 0° ( 3 U ) ARÊA(xi) = ***<**>-***<**> x 100 ; i = l,2 n - 1 (3.12) A,4/M(Xi) <, > ou = A4/M(x) (3.13) Ai?Ki4(Xj) <, > ou = Afl/?,4(x) (3.14) Les écarts en pourcentage ont été choisis comme mesure des erreurs d'estimation de

l'aversion au risque parce qu'ils sont indépendants des valeurs d'aversion au risque. L'estimation (moyenne ou à un point intérieur précis) engendrant les écarts les plus faibles est choisie comme meilleure estimation des préférences des individus résultant de l'application de la méthode des splines cubiques lorsque la fonction d'utilité est connue ou spécifiée par hypothèse. Dans ce contexte, c'est cette estimation que nous utilisons pour analyser tout d'abord l'impact de l'arrondissement et ensuite le choix du nombre de points sur les courbes d'utilité. Nous nous en servons aussi pour comparer l'approche paramétrique standard et l'approche utilisant une forme flexible en absence d'erreurs de spécification. Notons que cette analyse ne s'applique que si l'aversion au risque est constante. Si elle est croissante ou décroissante le long de la courbe d'utilité, alors l'agrégation des estimations sous forme de moyenne est déconseillée et les préférences peuvent mieux être décrites par un ensemble d'estimations ponctuelles.

Dans le deuxième scénario où nous n'avons pas d'information concernant la forme de la fonction d'utilité et où nous ne spécifions donc pas de forme fonctionnelle précise, nous devons utiliser individuellement les estimations ponctuelles de l'aversion au risque. Dans ce contexte, seuls les écarts en pourcentage entre ARA(Xi) et ARA(x) ainsi qu'entre RRA(xt) et RRA(x)

peuvent nous fournir une idée de la précision des estimations et ce sont donc eux que nous utilisons également pour analyser l'impact de l'arrondissement, choisir un nombre de points optimal pour les courbes d'utilité et comparer les différentes approches. Le sous-chapitre suivant traite plus en profondeur de la démarche paramétrique utilisée pour accomplir ce dernier objectif.