Géométrie vectorielle et analytique de l'espace / 3e  / 20-21

GÉOMÉTRIE VECTORIELLE

ET ANALYTIQUE DE L’ESPACE

3

e

_année

2.1 Vecteurs de l’espace

1

2.1.1 Introduction

1

2.1.2 L’ensemble



3

2

2.1.3 Composantes et norme d’un vecteur

3

2.1.4 Opérations élémentaires sur les vecteurs

6

2.1.5 Produit scalaire

17

2.1.6 Déterminant d’ordre 3

23

2.1.7 * Produit vectoriel *

28

2.1.8 Ce qu’il faut absolument savoir

35

2.2 Droites dans l’espace

36

2.2.1 Équations paramétriques d’une droite

36

2.2.2 Équations cartésiennes d’une droite

39

2.2.3 Positions relatives de deux droites et intersections

41

2.2.4 Angles entre deux droites

42

2.3 Plans dans l’espace

46

2.3.1 Équations paramétriques d’un plan

46

2.3.2 Équations cartésiennes d’un plan

47

2.3.3 Positions relatives d’une droite et d’un plan

et intersections

52

2.3.4 Angles entre une droite et un plan

53

2.3.5 Positions relatives de deux plans et intersections

55

2.3.6 Angles entre deux plans

56

2.3.7 Distances entre points, droites et plans

57

2.3.8 Ce qu’il faut absolument savoir

60

2.4 Sphères dans l’espace *

61

2.4.1 * Équations cartésiennes d’une sphère *

61

2.4.2 * Équations paramétriques d’une sphère *

62

2.4.3 * Équations d’un plan tangent à une sphère *

63

2.4.4 * Ce qu’il faut absolument savoir *

65

AVANT-PROPOS

• Ce document a été conçu pour l’enseignement des mathématiques dispensé au Collège de

Genève en troisième année ; il traite de la géométrie vectorielle et analytique de l’espace.

Cela dit, il peut servir de support de cours pour d’autres filières d’enseignement.

• Vous trouverez dans ce chapitre de la théorie (définitions, théorèmes, démonstrations, etc.) et des exercices qui vous permettront progressivement de vous familiariser et de maîtriser les diverses notations et concepts mathématiques. À la fin du chapitre se trouvent les solutions des exercices.

• Les exercices accompagnés d’un astérisque (*), sont des exercices supplémentaires de

développement destinés, par exemple, aux élèves ayant choisi l’option, niveau avancé (MA2). • Pour mieux repérer les points importants de la théorie, les définitions sont dans un encadré

blanc et les théorèmes dans un encadré grisé.

• Pour vérifier votre niveau de compréhension à la fin de l’étude d’un sous chapitre, vous pouvez vous référer à la section : « Ce qu’il faut absolument savoir ».

• Des QR CODES apparaissent à certains endroits du cours. Une fois scannés avec vos smartphones, ils donnent (aux personnes ayant un compte EDUGE) accès à la lecture de vidéos dont le contenu est en lien avec certains sujets du cours.

• Vous pouvez télécharger ce document au format PDF à l’adresse suivante :

http://www.sismondi.ch/disciplines/mathematiques/espace-perso-profs/serge-picchione

• Pour finir, un grand merci aux collègues de divers établissements scolaires qui ont partagé leurs cours : Nicolas Chabal, Yves Drevous, Bernard Gisin, Alain Klopfenstein, Maurizio Lalicata, Bernard Lenggenhager, Romanita Nagy Gauxachs, Adrien Schleining et Serge Zoutter.

A B C D E F G H I J • _• • • •

2.1 Vecteurs de l’espace

2.1.1 Introduction

Dans ce cours de Mathématiques, nous allons reprendre le concept de vecteur étudié en Physique. Nous nous intéresserons à généraliser et à modéliser ce concept afin de l'utiliser dans l'étude de la Géométrie.

Pour rappel, certaines grandeurs physiques peuvent être modélisées à l'aide d'un seul nombre. Par exemple, la température, la masse, une distance, un angle d'inclinaison, etc.

Ces grandeurs sont appelées grandeurs scalaires. D'autres grandeurs comme une force, une position, une vitesse, un champ électrique ne peuvent pas être modélisées qu'à l'aide d'un seul nombre. On a besoin de connaître leur direction, leur sens et leur intensité (un nombre).

Ces grandeurs sont alors appelées grandeurs vectorielles. t

v =vecteur position du"point" au temps t.



Définitions

Un vecteur vest un objet entièrement déterminé par la donnée d'une direction, d'un sens et d'une intensité (un nombre).

Si on considère deux points quelconques A et B du plan, on peut tracer une flèche de A à B. Cette flèche définit un vecteur car on a une direction (une droite), un sens (pointe) et une intensité (longueur de la flèche).

• On note ce vecteur v=AB et v = AB son intensité (on dit aussi norme de v). Le point A est l’origine du vecteur et le point B son extrémité.

• On appelle vecteur nul, noté 0, le vecteur dont le point d'application et l’extrémité coïncident :   AA=BB=0. Le vecteur nul 0 à une intensité nulle, sa direction est indéterminée.

• Le vecteur opposé de v=AB est le vecteur dont l’origine est B et l’extrémité A. Il est noté − = −v  AB=BA.

Deux vecteurs sont égaux si et seulement s’ils ont même direction, même sens et même intensité (longueur).

Exemples Les vecteurs AB et CD sont égaux (même norme, direction et sens). Les vecteurs AB et EF ne sont pas égaux car ils n’ont pas la même norme. Les vecteurs GH et JI ne sont pas égaux car ils n’ont pas le même sens.

O

•

•

•

A B A • B

2.1.2 L’ensemble

3



Définitions

• Dans l'espace, un repère cartésien (orthonormé) est constitué d’un point O, nommé origine et de trois axes orientés Ox, Oy et Oz, perpendiculaires deux à deux, (muni d’une même échelle). • Un point P de l’espace, peut alors être représenté par trois nombres réels : x, y et z.

On notera : P x; y; z

(

)

.

•

₍

x; y; z

₎

est un triple de nombre réel et x, y, z sont les coordonnées cartésiennes de P.

• Autrement dit, un point P de l'espace est identifié à un triple de nombre: P • ←→

₍

x; y; z

₎

Illustration

L'ensemble de tous les triples de nombres

{

(

x ; y ; z

)

x, y et z∈ se note :

}

   × × = 3 Notre espace usuel est donc identifié à 3.

Exemple

Déterminons les coordonnées des points A, B, C, D, E, F et G de l’espace muni d’un repère orthonormé. O y z x x y z 0

•

A

•

B 1 1 1

•

_E

•

C

•

D

•

F

•

G

(

)

(

)

(

)

(

)

(

)

(

)

(

)

A 3;4 ;0 B 1;2 ; 1 C 2; 3 ;2 D 1; 1 ; 4 E 1;0 ; 4 F 0; 3 ;2 G 1;2 ;0 − − − − − − − − −

•

•

2.1.3 Composantes et norme d’un vecteur

Soient A a ;a ;a et

(

_{1 2 3}

)

B b ;b ;b sont deux points de l’espace et

(

_{1 2 3}

)

AB est un vecteur de l’espace.

Illustration

1 2 3

a , a et a sont les coordonnées du point A , origine du vecteur AB.

1 2 3

b , b et b sont les coordonnées du point B , extrémité du vecteur AB.

Pour « aller » du point A (origine) au point B (extrémité) nous devons, suivant : - l’axe Ox, effectuer un déplacement de b₁−a₁unités.

- l’axe Oy, effectuer un déplacement de b2−a2unités.

- l’axe Oz, effectuer un déplacement de b₃−a₃unités. Définition

Soient A a ;a ;a et

(

_{1 2 3}

)

B b ;b ;b deux points de l’espace et

(

_{1 2 3}

)

AB un vecteur de l’espace. Le nombre b₁−a₁ est la 1ère _{composante du vecteur AB} _{(différence des coordonnées en x).}

Le nombre b₂−a₂ est la 2e _{composante du vecteur} _{AB (différence des coordonnées en y).}

Le nombre b₃−a₃ est la 3e _{composante du vecteur} _{AB (différence des coordonnées en z).}

On note alors AB=

(

b₁−a ;b_{1 2} −a ;b_{2 3}−a₃

)

Exemples

Considérons les quatre points A 5; 1;0 , B 1; 4;5 , C 2; 2;4 et D 6;1; 1

(

−

)

(

−

)

(

−

)

(

−

)

de l’espace. On peut considérer les trois vecteurs :

( ) ( )

(

)

(

)

( ) ( )

(

)

(

)

( )

( )

(

)

(

)

AB 1 5; 4 1 ;5 0 4; 3;5 BA 5 1; 1 4 ;0 5 4;3; 5 DC 2 6; 2 1;4 1 4; 3;5 = − − − − − = − − = − − − − − = − = − − − − − = − −   

• Le vecteur opposé de AB est le vecteur BA.

• Les vecteurs AB et DC sont équivalents (même direction, sens et intensité). • Les composantes d’un vecteur peuvent être négatives.

Proposition

Soient A a ;a ;a et

(

_{1 2 3}

)

B b ;b ;b deux points de l’espace et

(

_{1 2 3}

)

AB un vecteur de l’espace.

La norme du vecteur (intensité) AB est donné par : AB =

(

b₁−a₁

) (

2+ b₂−a₂

)

2 +

(

b₃−a₃

)

2 Démonstration

On utilise le théorème de Pythagore.

On a deux triangles rectangles : r2 =

(

b₁−a₁

) (

2+ b₂−a₂

)

2 et AB 2 = +r2

(

b₃−a₃

)

2

donc AB 2 =

(

b₁−a₁

) (

2+ b₂−a₂

) (

2 + b₃−a₃

)

2

⇔ AB =

(

b₁−a₁

) (

2+ b₂−a₂

) (

2+ b₃−a₃

)

2

Exemple

Considérons les points A 5; 1;0

(

−

)

et B 1; 4;5

(

−

)

de l’espace. On a : AB= −

(

1 5;

( ) ( )

− − −4 1 ;5 0−

)

= − −

(

4; 3;5

)

AB =

(

1 5−

)

2+ − − −

(

( ) ( )

4 1

)

2+ −

(

5 0

)

2 =

( ) ( )

−4 2+ −3 2+52 = 50 =5 2 ≅7.07 BA=

(

5 1;−

( ) ( )

− − −1 4 ;0 5−

)

=

(

4;3; 5−

)

BA =

(

5 1−

)

2+ − − −

(

( ) ( )

1 4

)

2+ −

(

0 5

)

2 = 42 +32+ −

( )

5 2 = 50 =5 2 ≅7.07 A • • r

Remarques

a) Chaque vecteur de l’espace est associé à un unique triple de nombre. Ces nombres sont les composantes du vecteur qui définissent sa direction, son sens et son intensité.

b) Deux vecteurs sont égaux si et seulement s’ils ont les mêmes composantes.

c) Il ne faut pas confondre le pointP

(

− −4; 3;5

)

dont les coordonnées sont − −4, 3 et 5 avec le vecteur AB= − −

(

4; 3;5

)

dont les composantes sont − −4, 3 et 5.

Dans les deux cas nous utilisons le même triple de nombres ; cependant les coordonnées de P représentent la « position » du point P relativement aux axes Ox, Oy et Oz alors que les composantes de ABreprésentent un « déplacement », une « translation ».

d) Pour chaque point P x; y; z

(

)

de l’espace on peut construire un vecteur OP d’origine O 0;0;0

(

)

et d’extrémité P x; y; z

(

)

:

Les composantes de OP=

(

x 0; y 0; z− − −0

) (

= x; y; z

)

.

Dans ce cas, les coordonnées de P et les composantes de OP ont mêmes valeurs.

Illustration

Un peu d'histoire

L’Irlandais Sir William Hamilton (1805-1865) fut l’un des premiers à utiliser les vecteurs et il est probablement l’inventeur du mot (mot venant du latin vehere, qui signifie « porter »). L’Allemand Hermann Grassman (1809-1877) introduisit la notation vectorielle à l’occasion de problèmes de physique. L’Américain Gibbs (1839-1903) et l’Anglais Heaviside (1850-1925), disciples de Hamilton, donnent au calcul vectoriel sa forme quasi définitive, mais ce type de « calcul » met assez de temps à

s’introduire en France. Michel Chasles (1793-1880), avait déjà pressenti l’importance du sens sur un axe sans aller jusqu’à la notion de vecteur.

•

2.1.4 Opérations élémentaires sur les vecteurs

Il y a deux opérations élémentaires qu’on peut définir sur les vecteurs. Définition

Additionner deux vecteurs a et b  c’est obtenir le vecteur a +b en faisant coïncider les origines des vecteurs a et b et en dessinant un parallélogramme. Le vecteur a +b est la flèche sur une diagonale du parallélogramme.

On peut aussi faire coïncider l’extrémité de a avec l’origine de b et tracer une flèche de l’origine de a avec l’extrémité de b , on obtient a +b :

Définition

Multiplier un vecteur apar un scalaire λ (un nombre), c’est obtenir le vecteur λ⋅a en considérant qu’il a : • la même direction que a.

• une norme égale à λ ⋅ a .

• le même sens que a si λ > 0 et il est de sens opposé à a si λ < 0.

Remarques

a) En Physique le vecteur a +b est la « résultante » du vecteur a et b .

b) On constate que l’addition de deux vecteurs est un vecteur et que la multiplication d’un vecteur par un scalaire est aussi un vecteur.

c) Ces deux opérations sont essentielles pour modéliser les phénomènes physiques ainsi que pour obtenir certains résultats en géométrie.

Définition

Considérons a=

(

a ;a ;a_{1 2 3}

)

et b=

(

b ;b ;b_{1 2 3}

)

deux vecteurs de l’espace et λ∈ un scalaire.

(

1 2 3

) (

1 2 3

) (

1 1 2 2 3 3

)

a + =b a ;a ;a + b ;b ;b = a +b ;a +b ;a +b (addition entre deux vecteurs)

(

1 2 3

) (

1 2 3

)

a a ;a ;a a ; a ; a

λ⋅ = ⋅ λ = λ⋅ λ⋅ λ⋅ (multiplication d’un vecteur par un scalaire)

Illustration

Exemple

Considérons v₁=

(

3;1; 7−

)

et v₂ =

(

10 ;0; 2−

)

deux vecteurs de l'espace.

Calculons : a=2v1+2v2 = ⋅2 3;1; 7

(

− + ⋅

)

2 10 ;0; 2

(

− =

) (

6;2; 14−

) (

+ 20 ;0; 4− =

) (

26;2; 18−

)

  

b =3v ₁+v₂ = ⋅3 3;1; 7

(

−

) (

+ 10 ;0; 2− =

) (

9;3; 21−

) (

+ 10 ;0; 2− =

) (

19;3; 23−

)

Remarque

Les vecteurs sont devenus des triples nombres (composantes du vecteur).

Les opérations entre les vecteurs sont devenues des opérations entre des triples de nombres. On peut alors s'affranchir de la représentation géométriquement des vecteurs pour effectuer des opérations entre vecteurs. C'est plus facile et plus rapide.

Définition

La soustraction de deux vecteurs est définie, grâce à l’addition, par : a b  − = + − = + − ⋅a

( )

b a

( )

1 b

Exemple

(

) (

) (

) ( ) (

) (

) (

) (

)

a − =b 3;1; 2− − 6; 2; 4− − = 3;1; 2− + − ⋅1 6; 2; 4− − = 3;1; 2− + −6;2;4 = −3;3;2 Remarque

Les vecteurs a +b et a −b donnent les directions des diagonales du parallélogramme construit sur a et b.

O z x y A B

Définition

Soit n scalaires λ λ₁, ₂,...,λ et n vecteurs _n v ,v ,...,v _{1 2} _n .

Le vecteur défini de la manière suivante : λ_{1 1}v+λ₂v₂ +...+λ_nv_n est appelé combinaison linéaire des vecteurs v ,v ,...,v _{1 2} _n .

Exemples

a) Le vecteur d= ⋅λ₁ v₁ est combinaison linéaire du vecteur v₁. b) Le vecteur c= ⋅ +λ₁ v₁ λ₂⋅v₂ est combinaison linéaire

des vecteurs v et v₁ ₂.

c) Le vecteur v₁ n’est pas combinaison linéaire du vecteur v₂ car il n’existe pas de scalaire λ tel que : v₁= ⋅λ v₂ .

Définition

Deux vecteurs a et b de l’espace sont colinéaires ⇔ ∃ ∈λ  tel que b= ⋅λ a.

Trois vecteurs a,b et c de l’espace sont coplanaires ⇔ ∃λ µ, ∈ tel que c=λa+µb Illustration

Exemples

a) a = − −

(

9; 9;12

)

et b =

(

3;3; 4−

)

sont colinéaires car a = − ⋅

( )

3 b ou b 1 a 3

 

= −_{ }⋅

 

 

b) a =

(

3;3; 4 , b−

)

=

(

2;1;3 et c

)

= − −

(

5; 7;18

)

sont coplanaires car c= − ⋅ + ⋅

( )

3 a 2 b Remarques

a) Deux vecteurs a et b colinéaires non nuls ont la même direction mais pas forcément le même sens ou intensité.

Si λ> alors a0  et b ont le même sens. Si λ< alors a0  et b sont de sens contraires.

b) Si deux vecteurs non nuls sont colinéaires alors un est combinaison linéaire de l'autre et réciproquement.

c) Si trois vecteurs non nuls sont coplanaires alors chaque vecteur est combinaison linéaire des deux autres.

Proposition (propriétés de l'addition vectorielle et de la multiplication par un scalaire) Soient a , b et c   trois vecteurs de l’espace ainsi que λ µ, ∈ deux scalaires.

a   + = +b b a commutativité de l'addition

P1)

( )

a b     + + = + +c a

( )

b c associativité de l'addition

P2)

0  + =a a 0 est l' élément neutre pour l' addition

P3)

( )

a+ − =a 0 tout vecteur a possède un vecteur opposé a −

P4)

1 a⋅ = a 1 est l'élément neutre pour la multiplication

P5)

( )

a b a b distributivité λ⋅ +  = ⋅ + ⋅λ  λ  P6)

(

λ µ+

)

⋅ = ⋅ + ⋅a λ a µ a P7)

( )

a

(

)

a associativité λ µ⋅ ⋅ = λ µ⋅ ⋅ P8) Exemples P1) a + =b ( 3;1;2 ) ( 0; 2;1 ) ( 3+ − = +0;1−2;2+1 )=( 3; 1;3 )− b + =a ( 0; 2;1 ) ( 3;1;2 )− + =( 0+ − +3; 2 1;1+2 )=( 3; 1;3 )− P4) Si a =( 0; 2;1 )− alors − =a ( 0;2; 1 )− car a+ − =

( )

a

(

0;0;0

)

=0 P6) 2⋅

( )

a +b = ⋅2 ( 3;1;2 ) ( 0; 2;1 )

(

+ −

)

= ⋅2 ( 3; 1;3 ) ( 6; 2;6 )− = − 2 a⋅ + ⋅ = ⋅ 2 b 2 ( 3;1;2 )+ ⋅2 ( 0; 2;1 ) ( 6;2;4 ) ( 0; 4;2 )− = + − =( 6; 2;6 )− Démonstration P1) a b ( a ;a ;a ) ( b ;b ;b ) ( a + = _{1 2 3} + _{1 2 3} = ₁+b ;a_{1 2} +b ;a_{2 3}+b )₃ b a + =( b ;b ;b ) ( a ;a ;a )_{1 2 3} + _{1 2 3} + =( b₁+ +a ;b_{1 2}+ +a₂ ;b₃+a )₃ P3) 0 + =a ( 0;0;0 ) ( a ;a ;a ) ( 0+ _{1 2 3} = +a ;0₁ +a ;0₂ +a ) ( a ;a ;a )₃ = _{1 2 3} =a P4) a ( a )+ − =

(

a ;a ;a_{1 2 3}

) (

+ −a ; a ; a₁ − ₂ − ₃

) (

= a₁−a ;a_{1 2}−a ;a_{2 3}−a₃

)

=( 0;0;0 )=0 P6) λ⋅

( )

a +v = ⋅λ

(

( a ;a ;a ) ( b ;b ;b )_{1 2 3} + _{1 2 3}

)

= ⋅λ ( a₁+b ;a_{1 2} +b ;a_{2 3}+b )₃ =

(

λ⋅

(

a₁+b ;₁

) (

λ⋅ a₂+b ;₂

) (

λ⋅ a₃ +b₃

)

)

=

(

λa₁+λ λb ; a_{1 2}+λ λb ; a_{2 3}+λb₃

)

λ⋅ + ⋅ = ⋅a λ b λ ( a ;a ;a )_{1 2 3} + ⋅λ ( b ;b ;b ) ( a ; a ; a ) ( b ; b ; b )_{1 2 3} = λ λ_{1 2} λ ₃ + λ λ λ_{1 2 3} =

(

λa₁+λ λb ; a_{1 2} +λ λb ; a_{2 3}+λb₃

)

Les autres démonstrations sont à la discrétion du lecteur.

• C

A •

• B

O •

Proposition (propriétés de la norme d’un vecteur)

Soient a et b  deux vecteurs de l’espace ainsi que λ∈ un scalaire. P9) a ≥0 P10) a =0 ⇔ =a 0

P11) λ⋅a = λ ⋅ a P12) a b + ≤ a + b ( inégalité du triangle )

Les démonstrations sont à la discrétion du lecteur. Exemple P11) a =

(

3;4;5

)

et 5 a⋅ =

(

15;20;25

)

2 2 2 2 2 2 5 a 15 20 25 1250 625 2 25 2 5 a 5 3 4 5 5 50 5 25 2 5 25 2 25 2 ⋅ = + + = = ⋅ = ⋅ ⋅ = ⋅ + + = ⋅ = ⋅ ⋅ = ⋅ ⋅ = ⋅  

Proposition (Relations de Chasles)

Quels que soient les points A, B, C et O de l’espace, on a les trois relations suivantes :

P13)   AB+BC= AC P14) − AB=BA P15)   AB=OB−OA Exemple Points : O 0;0;0

(

)

; A 1;2 : 3

(

−

)

; B 5; 1;4 ; C

(

−

)

(

−5;2;4

)

Relations de Chasles : •   AB=OB−OA=

(

5; 1;4−

) (

− 1;2; 3− =

) (

4; 3;7−

)

• BC  =OC−OB= −

(

5;2;4

) (

− 5; 1;4−

) (

= −10;3;0

)

•   AC=AB+BC=

(

4; 3;7−

) (

+ −10;3;0

) (

= −6;0;7

)

• BA= −AB= − ⋅

( ) (

1 4; 3;7−

) (

= −4;3; 7−

)

Remarques

a) La première relation de Chasles se généralise par exemple :    AB+BC+CD=AD

b)   AB≠OA OB+ Démonstration

P13) En mettant les deux vecteurs AB et BC de sorte que l'extrémité de



AB

coïncide avec le point d’origine de BC on obtient :  AB BC+ qui est égal au vecteur AC.

P14) On pose C=A et on considère   AC= AB BC+

On obtient :   AA=AB BA+ ⇔ =0  AB BA+ ⇔ + −0

( )

AB = + AB BA+ + −

( )

AB ⇔ − AB=BA

Définition

Un vecteur u est unitaire ⇔ u =1 Proposition

P16) Si v ≠0, alors le vecteur u 1 v v

= ⋅

 

 est un vecteur unitaire, de même direction et de même sens que v.

Remarque Cette opération, est appelée normalisation d’un vecteur. Exemple

• On considère le vecteur v=

(

1;1;1

)

qui n’est pas unitaire car v = 12+ +12 12 = 3

• On normalise le vecteur v :

(

)

2 2 2 1 1 1 1 1 u v 1;1;1 ; ; 3 3 3 3 v 1 1 1 1 1 1 et u 1 1 3 3 3 3 3 3   = ⋅ = ⋅ _{=  }         = _{ } +_{ } +_{ } = + + = =          

Le vecteur u est unitaire et à la même direction el le même sens que v.

• On cherche un vecteur w de norme 3 et qui à la même direction et même sens que v : w 3 u 3 1 v 3 1 ; 1 3 ; 3 2 2 2 2 v     = ⋅ = ⋅ ⋅ = ⋅_{  }= _         et w =3 . Démonstration

Considérons le vecteur v=

(

a;b;c

)

de norme v = a2 +b2 +c2 et le vecteur :

(

)

2 2 2 2 2 2 2 2 2 2 2 2 1 1 a b c u v a;b;c ; ; v a b c a b c a b c a b c   = ⋅ = ⋅ _{=  } + +  + + + + + +     • Calculons sa norme : 2 2 2 2 2 2 2 2 2 2 2 2 a b c u a b c a b c a b c       = _{ } +_{ } +_{ } + + + + + +        2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 a b c a b c 1 1 a b c a b c a b c a b c + + = + + = = = + + + + + + + +

Le vecteur u est unitaire.

• Les vecteurs uet v sont colinéaires car il existe 1 0 v

λ= _ > tel que u= ⋅λ v Ils ont donc la même direction et le même sens.

Exercice 1

Considérons v



₁=

(

3;1; 7−

)

et v



₂ =

(

10 ;0; 2−

)

deux vecteurs de l’espace. Calculer les composantes et la norme des vecteurs suivants :

1 2 a=3v +2v    b  = −v₁ v₂   c=v₂−v₁ d 1v₁ 2v₂ 2 3 = −    e= ⋅5 a  

Exercice 2 Réponse sur l’énoncé

Les vecteurs OA, OB et OCon une origine commune mais ne sont pas dans le même plan. a) Dessiner les vecteurs suivants qui sont combinaisons linéaires des vecteurs OA, OB et OC : 1) OA OB − 2) 2OA OC + 3) OB+2OC

3) OA OB + 4) OB OA − 5) −2OC −OB b) Parmi les vecteurs ci-dessus lesquels sont colinéaires ?

Exercice 3

On considère le parallélépipède représenté ci-contre. Compléter les égalités afin qu’elles soient vraies : a)   AB+FG=A.... b)   AG+CD=....H c)   H .... CA+ =HA d)    EH+DC+GA=....A e)   AH+EB= A.... f)     AB+CC+BH +GF =....E Exercice 4

Soit la pyramide de sommet S dont la base ABCD est un parallélogramme. On pose u     =SA , v=SB , w=SC

Exprimer chacun des vecteurs     AB , BC , AD , AC , SD et BD comme combinaison linéaire de u , v et w   . A B C O

•

•

•

•

D • C • G • • B • A H • • E • F

Exercice 5

On considère, dans un repère orthonormé d’origine O 0 ;0 ;0

(

)

, les points A 0 ; 3 ;2

(

−

)

,

(

)

B − −2 ; 3;2 et C

(

−1;2 ;0

)

de l’espace.

a) Dessiner, dans le repère ci-dessous, les vecteurs OA, OB, OC,   AB, BC et AC. (Réponse sur l’énoncé)

b) Exprimer   AB, BC et AC comme combinaison linéaire de OA , OB et OC   (relations de Chasles) et calculer algébriquement les composantes de ces vecteurs : AB=

BC= AC=

c) Complétez les phrases suivantes :

1) Les composantes de



AB=

(

... ; ... ; ...

)

indiquent que, pour aller du point A au point B, il faut se déplacer de ………unités dans la direction x, de ……….unités dans la direction y, et enfin de ………unités dans la direction z.

2) Les composantes de BC



=

(

... ; ... ; ...

)

indiquent que, pour aller du point B au point C, il faut se déplacer de ………unités dans la direction x, de ……….unités dans la direction y, et enfin de ………unités dans la direction z.

3) Les composantes de



AC =

(

... ; ... ; ...

)

indiquent que, pour aller du point A au point C, il faut se déplacer de ………unités dans la direction x, de ……….unités dans la direction y, et enfin de ………unités dans la direction z.

d) Calculer la norme des vecteurs   AB, BC et AC. e) Calculer le périmètre du triangle ABC.

x y z O 1 1 1

•

B

•

A

•

C

•

Marche à suivre pour résoudre les problèmes

1) Représenter la situation à l’aide d’un dessin schématique (points, droites, triangles, etc.) et déterminer les inconnues. Il n’est pas nécessaire de dessiner le problème à l’échelle. 2) Dessiner les vecteurs utiles à votre problème sur le schéma et écrire les égalités vectorielles. Utiliser, si nécessaire, les règles de Chasles.

3) Écrire les vecteurs à l’aide des composantes (couples de nombres). 4) Résoudre algébriquement.

Exercice 6

Considérons les 4 points A 3; 3; 2 , B

(

− −

) (

− −1; 6;3 , C 0; 4;2 et D 4; 1; 3

) (

−

)

(

− − .

)

a) Déterminer les composantes des vecteurs      AB, AC , AD, BC , BD , BA et CD en utilisant les relations de Chasles .

b) Parmi ces vecteurs, lesquels sont égaux ?

c) Que peut-on conclure à propos du quadrilatère ABCD ? Exercice 7

Soit le pointA 1;1;1

(

)

. En utilisant les relations de Chasles déterminer : a) les coordonnées du point B tel que AB=

(

4; 3; 1− −

)

.

b) les coordonnées du point C tel que BC=

(

4; 3;8−

)

. c) les composantes du vecteur CA.

d) les coordonnées des points E et F si EF=

(

2;3;3

)

. Exercice 8

On donne le points A

(

−1;8;3

)

et B 9; 7; 2

(

− − .

)

Calculer les coordonnées des points C, D, E et F qui divisent le segment [AB] en 5 parties égales. Exercice 9

a) On considère le point M, milieu du segment [AB]. 1) Monter que OM 1

(

OA OB

)

2

= ⋅ +

   .

2) Déterminer les coordonnées du pointM si A a ;a ;a

(

_{1 2 3}

)

et B b ;b ;b

(

_{1 2 3}

)

. b) Si A 2; 3;5 et B 4;4;4

(

−

)

(

)

, déterminer les coordonnées du point M. c) Considérons les trois points distincts A, B et C du plan.

Soit M le milieu de

[ ]

AC et N le milieu de

[ ]

BC . Montrer que MN 1AB 2 =   . B A C D A B M O

Rappel Convention d’écriture

• On dessinera un triangle défini par les lettres ABC en plaçant les sommets en tournant dans le sens trigonométrique (anti-horaire). • On dessinera un quadrilatère défini par les lettres ABCD en plaçant les sommets en tournant dans le sens trigonométrique (anti-horaire). Exercice 10 *

Le centre de gravité G d'un objet est une notion physique qui est liée, entre autres choses, à la répartition de la masse à l'intérieur de cet objet. C'est en ce point qu'une force égale au poids de l'objet doit être appliquée pour que celui-ci soit en équilibre. Dans le cas d'une masse homogène et d'un champ de gravitation uniforme, le centre de gravité est en rapport

direct avec la géométrie de l'objet et ses axes de symétrie : le centre de gravité d'un triangle se trouve à l'intersection de ses médianes et celui d'un rectangle à l'intersection de ses diagonales. Soit A a ;a ;a , B b ;b ;b

(

_{1 2 3}

) (

_{1 2 3}

)

et C c ;c ;c

(

_{1 2 3}

)

les sommets

du triangle ABC dans le plan. Par définition, le point G g ; g ; g

(

_{1 2 3}

)

est le centre de gravité du triangle ABC s’il satisfait vectoriellement

GA GB GC+ + =0     . a) Montrer que OG 1

(

OA OB OC

)

3 = ⋅ + +     . b) Déterminer les coordonnées du point G. Exercice 11

Soit A, B, C et D, quatre points distincts. On a l’équivalence suivante :

AD BC ( vecteurs égaux ABCD est un parall

) ou DC AB ( vecteurs égaux élogram ) me  =  ⇔   ₌     

Soit les 4 points A 5; 1;0 , B 1; 4;5 , C 2; 2;4 et D 6;1; 1

(

−

) (

−

) (

−

)

(

−

)

. a) Déterminer les composantes des vecteurs AB et DC .

b) Que peut-on conclure à propos du quadrilatère ABCD ?

c) Déterminer les coordonnées du point M milieu du segment

[ ]

AC et les coordonnées du point N milieu du segment

[ ]

BD . Que constate-t-on ? Quelle conjecture peut-on énoncer ?

Exercice 12

Soit les 3 points A 2; 5;2 , B

(

−

) (

−2;3;4 et C 6;4;10

)

(

)

.

a) Déterminer, à l’aide du calcul vectoriel, les coordonnées du point D tel que ABCD soit un parallélogramme.

b) Déterminer, à l’aide du calcul vectoriel, les coordonnées du point M intersection des 2 diagonales de ce parallélogramme.

A D B C B A C B A C D G • G B A C O

•

•

•

•

Exercice 13

a) Soit A, B et C trois points distincts.

On a l’équivalence suivante :

(

)

(

)

A, B et C sont alignés

se trouvent sur la même droite ⇔ ∃ ∈λ tel que BC= ⋅λ AB AC et AB sont colinéaires    



En utilisant l’équivalence ci-dessus, déterminer dans chaque cas si les points A, B et C sont alignés. 1) A 6;4; 3 , B 14; 12;3 et C 2;12; 6

(

−

) (

−

)

(

−

)

2) A 6;4; 3 , B 14; 12;3 et C 4;14; 4

(

−

) (

−

)

(

−

)

b) Soit A, B, P et Q, quatre points distincts.

On a l’équivalence suivante :

(

)

AB PQ

d d

tel que AB PQ AB et PQ sont colinéaires ( les droites sont parallèles ) ⇔ ∃ ∈λ = ⋅λ

   

 _

En utilisant l’équivalence ci-dessus, déterminer dans chaque cas si la droite passant par le point P et Q est parallèle à la droite passant par A et B.

1)P 1; 1;1 , Q 4;3;2 , A

(

−

) (

) (

−1;5;1 et B 5;2;2

)

(

)

2) P 1; 1;1 , Q 4;3;2 , A 3; 3;3 et B 12;9;6

(

−

) (

) (

−

)

(

)

Exercice 14

Déterminer par calcul, un vecteur u de l’espace :

a) unitaire du plan ayant la même direction et même sens que v=

(

4; 3;1−

)

.

b) de l'espace de longueur 5 ayant la même direction et même sens que w =

(

7 ;3; 4−

)

. c) unitaire de l'espace ayant la même direction que x = − − −

(

3 ; 3; 3

)

.

Exercice 15

Soit les trois points A 1;2;3 , B 2;5;8 et C

(

)

(

)

(

−2;7;4

)

. a) Le triangle ABC est-il isocèle ou équilatéral ? Justifier. b) Calculer le périmètre et l’aire du triangle.

A B C

•

•

•

P Q A B

•

•

•

•

2.1.5 Produit scalaire

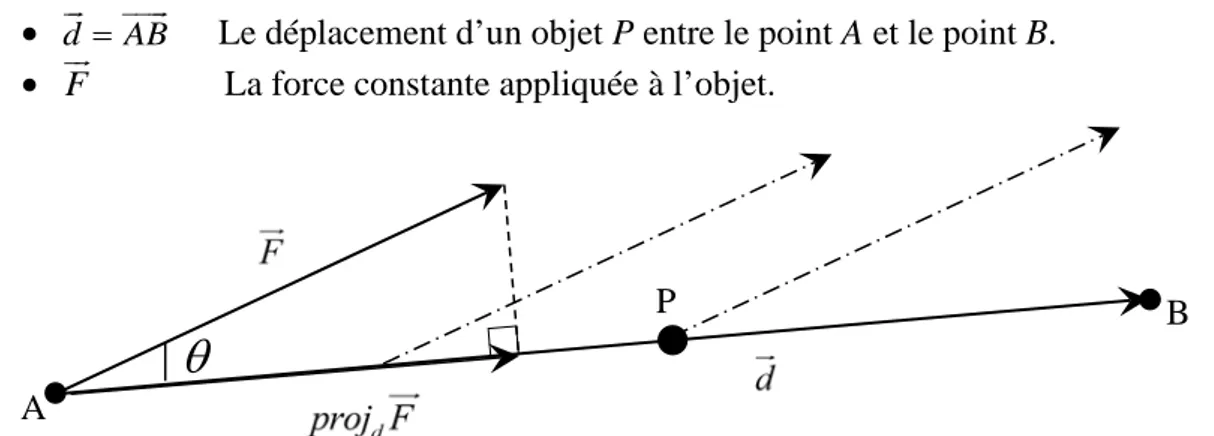
Considérons les deux vecteurs :

• d = AB Le déplacement d’un objet P entre le point A et le point B. • F La force constante appliquée à l’objet.

En Physique, on définit le travail W d’une force F constante appliquée à un objet P se déplaçant d’un point A à un point B ( d = AB) par : W = proj F_d ⋅ d

Donc :

( )

( )

(

)

d

notation

W = proj F ⋅ d = F ⋅cos θ ⋅ d = d ⋅ F ⋅cos θ = F d  produit scalaire de F et d 

Remarque Si F est perpendiculaire à d = AB alors laproj F_dest nulle et le travail W est nul. Définition (Mathématique)

Le produit scalaire de deux vecteurs a et b  noté a b  , est le nombre réel (scalaire) défini par

a b= a ⋅ b cos( )⋅ θ    

 avec 0≤ ≤θ 180 qui est la mesure de l’angle formé par les vecteurs

a 

et b lorsqu’on les rapporte à une même origine.

Illustration Exemples a) Si a =

(

1;1;0 et b

)

=

(

0;0;3

)

alors a b  = 2 3 cos 90⋅ ⋅

( )

 = 2 3 0⋅ ⋅ =0 b) Si a =

(

1;1; 2 et b−

)

= − −

(

2; 2;4

)

alors a b  = 6⋅ 24 cos 180⋅

( )

 = 6⋅ 24⋅ − = −

( )

1 12

θ

A B P θ

Théorème (Expression du produit scalaire de deux vecteurs a et b  de l’espace à l’aide des composantes)

(

1 2 3

)

(

1 2 3

)

Si a = a ;a ;a et b= b ;b ;b alors on peut calculer le produit scalaire a b  de la manière suivante : a b  = ⋅ +a b_{1 1} a b₂⋅ + ⋅₂ a b_{3 3}

Exemples

a) Si a=

(

1;1;0 et b

)

 =

(

0;0;3

)

alors a b  = ⋅ + ⋅ + ⋅ =1 0 1 0 0 3 0

b) Si a=

(

1;1; 2 et b−

)

= − −

(

2; 2;4

)

alors a b  = ⋅ − + ⋅ − + − ⋅ = −1

( )

2 1

( ) ( )

2 2 4 12

Démonstration

Appliquons le théorème du cosinus :

(

)

2 2 2 2 2 2 a b a b a b 2 a b cos( ) 1 a b cos( ) a b a b 2 θ θ = − = + − ⋅ ⋅ ⇔ ⋅ ⋅ = ⋅ + − −                 Avec les composantes :

(

) (

) (

)

(

)

(

)

(

) (

) (

)

(

)

(

) (

) (

)

(

)

2 2 2 2 2 2 2 2 2 1 2 3 1 2 3 1 1 2 2 3 3 2 2 2 2 2 2 2 2 2 1 2 3 1 2 3 1 1 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 1 2 3 1 2 3 1 1 1 1 2 2 2 2 3 3 3 3 2 2 2 2 2 2 1 2 3 1 2 3 1 a b a a a b b b a b a b a b 2 1 a a a b b b a b a b a b 2 1 a a a b b b a 2a b b a 2a b b a 2a b b 2 1 a a a b b b a 2 ⇔ = ⋅ + + + + + − − + − + − = ⋅ + + + + + − − − − − − = ⋅ + + + + + − − + − − + − − + = ⋅ + + + + + −   

(

2 2 2 2 2 2

)

1 +2a b1 1−b1 −a2 +2a b2 2−b2 −a3 +2a b3 3−b3

(

1 1 2 2 3 3

)

1 1 2 2 3 3 1 2a b 2a b 2a b a b a b a b 2 = ⋅ + + = + + Proposition

Soit a , b et c   trois vecteurs de l’espace ainsi que λ∈ un scalaire.

P1) a b  =b a Le produit scalaire est commutatif.

P2) a b c  

( )

+ =a b    +a c Le produit scalaire est distributif par rapport à l'addition. P3)

( )

λa b   =a

( ) ( )

λb =λ a b 

P4) b b   = b 2 Le produit scalaire d'un vecteur avec lui-meme donnele carré de sa norme.ˆ

Démonstration

P1)  a b =

(

a ;a ;a_{1 2 3}

) (

 b ;b ;b_{1 2 3}

)

=a b_{1 1}+a b_{2 2}+a b_{3 3} b a  =

(

b ;b ;b_{1 2 3}

) (

 a ;a ;a_{1 2 3}

)

=b a_{1 1}+b a_{2 2} +b a_{3 3}

Les autres démonstrations sont à la discrétion du lecteur. θ

Proposition

La mesure de l’angle formé par deux vecteurs a et b  est donné par : arccos a b avec 0 180

a b θ =   ≤ ≤θ  _⋅          Remarque : 1 arccos=cos− Exemple

Considérons les deux points A 1;1;1 et B 1;1;0 .

(

)

(

)

Calculons la mesure de l’angle θ =AOB à l’aide du

produit scalaire : arccos OA OB arccos 1 1 1 1 1 0 arccos 2 35,26

3 2 6 OA OB θ =  = _ ⋅ + ⋅ + ⋅ _= _ _≅ °  ⋅   ⋅          

Démonstration a b a b cos( ) cos( ) a b arcos a b

a b a b θ θ θ   = ⋅ ⋅ ⇔ = ⇔ =   ⋅ _ ⋅ _         _{ }      Remarques

De la définition du produit scalaire a b    = a ⋅ ⋅b cos( )θ , il ressort que le signe du produit scalaire dépend uniquement de l’angle θ entre les deux vecteurs

(

0≤ ≤θ 180

)

:

cosθ 0 ⇔ > ⇔  _ θ aigu a b > 0. cosθ 0 ⇔ = ⇔   _ θ = 90 a b = 0. cosθ 0 ⇔ < ⇔  _ θ obtus a b < 0. Définition

Deux vecteurs non nuls a et b  sont orthogonaux ⇔a b 0  =

Autrement dit : a et b  sont orthogonaux si et seulement si l’angle formé par les vecteurs a et b  est un angle droit.

Exemple a =

(

1;1;0 et b

)

=

(

0;0;3 sont orthogonaux car a b

)

  = ⋅ + ⋅ + ⋅ =1 0 1 0 0 3 0

θ θ -1

•

0 ₁

•

θ

•

cos(θ) θ = 90° θ θ

Projection orthogonale d’un vecteur sur un autre vecteur

Proposition Illustration

Soit aet b ≠0 deux vecteurs de l’espace. Si p est le vecteur résultant de la projection orthogonale de asur b alors p a b₂ b

b = ⋅    _   . Exemple

Soit deux vecteurs a = −

(

2;1;3 et b

)

=

(

2; 1;1−

)

. La projection orthogonalep de a sur b est donnée par :

(

)

(

)

2 2 2 2 a b 2 2 1 ( 1 ) 3 1 1 2 1 1 p b 2; 1;1 2; 1;1 ; ; 2 ( 1 ) 1 3 3 3 3 b − ⋅ + ⋅ − + ⋅   = ⋅ = ⋅ − = − ⋅ − = −_ − _ + − +      _   Démonstration

Par construction p et b



sont colinéaires, c’est-à-dire qu’il existe un nombre réel

λ

tel que p =λ b⋅.

Déterminons le réel

λ

qui est l’inconnue :

(

  p−a b

)

 =0  p−a et b sont orthogonaux par construction. p b a b 0

⇔    _ − _ = propriété du produit scalaire : distributivité

( )

λb b a b 0

⇔     −  = p et b



sont colinéaires : p =λ b⋅

( )

b b a b 0 λ

⇔    _ − _ = propriété du produit scalaire : associativité

a b b b λ ⇔ =     

 algèbre : on isole le nombre

λ

2 a b b λ ⇔ =   

 propriété du produit scalaire :norme

Conclusion : p =λ b a b₂ b b ⋅ = ⋅     _   Remarques

a) p et b sont colinéaires donc

p à la même direction que b mais pas forcément le même sens. b) La projection orthogonale de a sur b notée a' n’est en général pas égale à la projection orthogonale de b sur a notée b'.

•

Exercice 16

À partir de la définition du produit scalaire remplir le tableau suivant :

(réponse en valeur exacte et il s'agit de vecteurs de l’espace)

  i j k i + j  i− j i  j  k i+ j   Exercice 17

Soit les cinq vecteurs a = −

(

3;3;1 , b

)

 = −

(

1;2; 1 , i−

)

=

(

1;0;0

)

, j=

(

0;1;0 et k

)

 =

(

0;0;1

)

. Calculer les expressions suivantes en utilisant uniquement les composantes des vecteurs :

1)  i j 2) −a  

( )

b−i 3) a   

( )

i b 4) a i    +b j +

(

a  −b

)

 k Exercice 18

a) Soit les deux vecteurs a =

(

3;2; 1 et b−

)

=

(

1;1;0

)

.

Calculer la mesure de l'angle θ formé par les vecteurs a et b . b) Soit les trois points A

(

−1;2 ; 3 , B 2;1; 4 et C−

) (

−

)

(

−1;0;5

)

. Calculer la mesure de l’angle BAC.

Exercice 19

Soit les deux vecteurs a =

(

2;0;1 et b

)

=

(

1;2;3

)

. a) Déterminer un vecteur n=

(

n ;n ;n_{1 2 3}

)

, orthogonal à a.

b) Combien y a-t-il de vecteurs c, orthogonaux à a et à b ? Justifier votre réponse. c) Déterminer un vecteur c=

(

c ;c ;c_{1 2 3}

)

, orthogonal à a et à b.

d) Déterminer un vecteur u=

(

u ;u ;u_{1 2 3}

)

, orthogonal à a et à b et unitaire. Exercice 20

Soit deux vecteurs a=

(

1;2; 3 et b−

)

 =

(

1;1;2

)

.

a) Déterminer la projection orthogonale de a sur b notée a'. b) Déterminer la projection orthogonale de b sur a notée b'. c) Que constate-t-on ? 0 z 1 1 1 y x

A C D B O • • • • •

Marche à suivre pour résoudre les problèmes

1) Représenter la situation à l’aide d’un dessin schématique (points, droites, triangles, etc.) et déterminer les inconnues. Il n’est pas nécessaire de dessiner le problème à l’échelle. 2) Dessiner les vecteurs utiles à votre problème sur le schéma et écrire les égalités vectorielles. Utiliser, si nécessaire, les règles de Chasles.

3) Écrire les vecteurs à l’aide des composantes (couples de nombres). 4) Résoudre algébriquement.

Exercice 21

Considérons les trois points A 3;1; 3 , B 5;2; 7

(

−

) (

−

)

et C 6;5; 8

(

−

)

.

a) Déterminer les coordonnées d’un point D tel que ABCD soit un parallélogramme. b) Déterminer la projection orthogonale p du vecteur AD sur le vecteur AB.

c) Déterminer les coordonnées d’un point P situé sur le segment

[ ]

AB tel que le triangle ADP soit rectangle en P.

d) Calculer l’aire du parallélogramme ABCD.

Exercice 22

Considérons A 1;2;3 , B 4;8; 3 et C 6;3;2

(

) (

−

)

(

)

, les trois sommets du triangle ABC.

a) Déterminer la projection orthogonale du vecteur AC sur le vecteur AB.

b) Déterminer les coordonnées du point D, pied de la perpendiculaire abaissée du point C sur le segment [AB]. c) Calculer l’aire du triangle ABC.

Exercice 23 *

Dans le minerai de sphalérite, chaque atome de zinc est entouré de quatre atomes de soufre qui forment un tétraèdre régulier dont l'atome de zinc occupe le centre.

L'angle de liaison θ est l'angle formé par la combinaison S-Zn-S.

Démontrer que la valeur en degré de l'angle de liaison vaut : θ ≅109,47°.

Remarque : un tétraèdre régulier (toutes ces faces sont des triangles équilatéraux) peut toujours s'inscrire dans un cube : les arêtes du tétraèdre coïncident alors avec les diagonales des faces du cube.

2.1.6 Déterminant d’ordre 3

Définition

Soient trois vecteurs a =

(

a ;a ;a , b_{1 2 3}

)

 =

(

b ;b ;b_{1 2 3}

)

et c=

(

c ;c ;c_{1 2 3}

)

de l’espace. Le déterminant d'ordre 3 de a ,b et c   (pris dans cet ordre), noté Det a;b;c

(

  

)

, est le nombre réel (scalaire) défini par :

(

)

(

)

(

)

(

)

1 1 1 2 2 1 1 1 1 2 2 2 1 2 3 3 3 3 3 2 2 3 3 3 1 2 3 3 2 2 1 3 3 1 3 1 2 2 1 a b c b c b c b c Det a;b;c a b c a a a b c b c b c a b c a b c b c a b c b c a b c b c = = ⋅ − ⋅ + = − − − + −   

Autrement dit, pour calculer un déterminant d’ordre 3, il faut multiplier chaque terme de la 1ère colonne par les déterminants d’ordre 2 obtenus en traçant la ligne et la colonne passant par ce terme. Exemple

(

)

(

)

(

)

Si a = 2;0;1 , b = −1;3; 2 et c− = 0;2; 3−

(

)

2 1 0 3 2 1 0 1 0

alors Det a;b;c 0 3 2 2 0 1 10 2 12

2 3 2 3 3 2 1 2 3 − − − = = ⋅ − ⋅ + ⋅ = − − = − − − − − − −    Remarque

(

)

(

)

(

)

(

)

Det a;b;c   = −Det b;a;c   = −Det a;c;b   = −Det c;b;a  

L'ordre dans lequel sont pris les vecteurs a ,b et c  , influence le signe du déterminant. Proposition

Soient trois vecteurs a =

(

a ;a ;a , b_{1 2 3}

)

 =

(

b ;b ;b_{1 2 3}

)

et c=

(

c ;c ;c_{1 2 3}

)

de l’espace. Le volume V du parallélépipède engendré par a ,b et c   est égale, au signe près, à la valeur du déterminant d'ordre 3 de a ,b et c   c’est-à-dire : V = Det a;b;c

(

  

)

Illustration

O

z

x

Exemple

Soit trois vecteurs a =

(

2;0;0 , b

)

=

(

0;2;0 et c

)

=

(

0;0;2

)

.

2 0 0 2 0 Det( a;b;c ) 0 2 0 2 2 ( 2 2 ) 8 0 2 0 0 2 0 2 0 2 0 Det( b;a;c ) 2 0 0 2 2 ( 2 2 ) 8 0 2 0 0 2 = = ⋅ = ⋅ ⋅ = = = − ⋅ = − ⋅ ⋅ = −      

Le volume V du parallélépipède engendré par a ,b et c   (cube de côté 2) est égal à Det( a;b;c )   =8

.

Démonstration * En exercice.

Rappels

• Deux vecteurs a et b de l’espace sont colinéaires ⇔ ∃ ∈λ  tel que b= ⋅λ a.

• Trois vecteurs a,b et c de l’espace sont coplanaires ⇔ ∃λ µ, ∈ tel que c=λa+µb

Exemples

a) a=

(

1;2;3 et b

)

=

(

2;4;6

)

sont colinéaires car b=2a. b) i=

(

1;0;0 et j

)

=

(

0;1;0

)

ne sont pas colinéaires car i≠λj c) Dans l'espace a =

(

1;2;0 , b

)

 =

(

2;1;0 et c

)

=

(

4;4;0

)

sont coplanaires car c 4a 4b

3 3

= +

  

.

d) Dans l'espace i=

(

1;0;0 , j

)

 =

(

0 ;1;0 et k

)

=

(

0;0;1

)

ne sont pas coplanaires car i≠λj+µk.

0 z 2 2 2 y x