Effet d'un champ magnétique uniforme sur les instabilités de Rayleigh–Bénard avec effet Soret. Influence of a magnetic field on the stability of a binary fluid with Soret effect

O

pen

A

rchive

T

OULOUSE

A

rchive

O

uverte (

OATAO

)

OATAO is an open access repository that collects the work of Toulouse researchers and

makes it freely available over the web where possible.

This is an author-deposited version published in:

http://oatao.univ-toulouse.fr/

Eprints ID : 15919

To link to this article :

DOI:10.1016/j.crme.2015.09.006

URL :

http://dx.doi.org/10.1016/j.crme.2015.09.006

To cite this version :

Ben Sassi, Mokhtar and Kaddech, Slim and Abdennadher, Ali and

Henry, Daniel and Ben Hadid, Hamda and Mojtabi, Abdelkader

Effet d'un champ magnétique uniforme sur les instabilités de

Rayleigh–Bénard avec effet Soret. Influence of a magnetic field on

the stability of a binary fluid with Soret effect.

(2016) Comptes

Rendus Mécanique, vol. 344 (n° 1). pp. 1-11. ISSN 1631-0721

Any correspondence concerning this service should be sent to the repository

administrator:

staff-oatao@listes-diff.inp-toulouse.fr

Effet

d’un

champ

magnétique

uniforme

sur

les

instabilités

de Rayleigh–Bénard

avec

effet

Soret

Influence

of

a

magnetic

field

on

the

stability

of

a

binary

fluid

with

Soret

effect

Mokhtar

Ben

Sassi

a

,

Slim

Kaddeche

a,_∗

_,

_Ali

_Abdennadher

b

_,

_Daniel

_Henry

c

_,

Hamda

Ben

Hadid

c

,

Abdelkader

Mojtabi

d

a_{UniversitédeCarthage,Institutnationaldessciencesappliquéesetdetechnologie,Laboratoirederecherchematériaux,mesures}

et applications,LR11ES25,INSAT,B.P.676,1080Tuniscedex,Tunisie

b_{UniversitédeCarthage,Institutnationaldessciencesappliquéesetdetechnologie,Laboratoired’ingénieriemathématique,EPT,LaMarsa,}

Tunisie

c_{Laboratoiredemécaniquedesfluidesetd’acoustique,CNRS/UniversitédeLyon,UniversitéClaude-BernardLyon-1/Écolecentrale}

de Lyon/INSAdeLyon,ECL,36,avenueGuy-de-Collongue,69134Écullycedex,France

d_{IMFT,UMRCNRS/INP/UPS5502,UFRMIG,UniversitéPaul-Sabatier,118,routedeNarbonne,31062Toulousecedex,France}

r é s u m é Mots-clés : Magnétohydrodynamique Stabilité Soret Keywords: Magnetohydrodynamics Stability Soret

L’effetdel’intensitéetdel’orientationd’unchampmagnétique uniformesurlatransition critique au sein d’une couche fluide binaire, électriquement conductrice, stratifiée en température et en concentration, en prenant en considération l’effet Soret, est étudié numériquement. Pour une telle configuration, les résultatsont misen évidence que les seuilscritiques correspondant àun champ magnétique de directionquelconque peuvent se déduire de ceux obtenus pour un champ magnétique vertical et que les axes des rouleaux marginaux des modes instables sont désormais alignés avec la composante horizontale du champ magnétique. Par ailleurs, une étude analytique est menée pour étudierl’impactduchampmagnétiquesurlesinstabilitésmonocellulaires.L’effetduchamp magnétique sur de tellesinstabilités a misen évidence un phénomèneinédit consistant à modifier profondément la nature des modes instables, qui perdent leur caractère monocellulairepourretrouverleuraspectàplusieursrouleauxquilescaractérisaientsans champmagnétiquepourψ < ψℓ0=131Le/(34−131Le).Pourunfluidebinairecaractérisé

par un nombre de Lewis Le et un facteur de séparation ψ > ψℓ0, lavaleur du nombre

de Hartmann Haℓ(ψ,Le)correspondantà cettetransition responsabled’une modification

significative des transferts de masse et de chaleur peut être déterminée à partir des relationsanalytiquesétabliesdanslecadredecetravail.

*

Auteur correspondant.

Adressese-mail :slimkaddeche@yahoo.fr, slim.kaddeche@insat.rnu.tn(S. Kaddeche), ali_abdennadher@yahoo.fr, ali.abdennadher@insat.rnu.tn

(A. Abdennadher).

a b s t r a c t

The effect of both magnitude and orientation of a uniform magnetic field on the critical transitionoccurringwithin an electrically conductingbinaryfluid layer,stratified in temperature and concentration, taking into account the Soret effect, is investigated numerically. For such a configuration, the results show that the critical thresholds correspondingtoanarbitraryorientatedmagneticfieldcanbederivedfromthoseobtained fora verticalmagnetic fieldandthat theaxesofthemarginalcellsare alignedwiththe horizontal componentof the magnetic field. Moreover, an analytical study isconducted toinvestigatetheimpactofthemagneticfieldonlong-wavelengthinstabilities.Theeffect ofthemagneticfieldonsuchinstabilitiesrevealsanewphenomenonconsistinginmajor changesoftheunstablemodesthatlosetheirunicellularnaturetoregaintheirmulti-roll characteristic,as itisthecasewithoutmagnetic fieldforψ < ψℓ0=131Le/(34−131Le).

For a binaryfluid characterizedby a Lewis numberLe and a separationfactor ψ > ψℓ0,

thevalueoftheHartmannnumberHaℓ(ψ,Le)correspondingtothattransitionresponsible

fora significantchangeinmass andheattransfer canbedeterminedfrom theanalytical relationsderivedinthiswork.

2015Académiedessciences.PubliéparElsevierMassonSAS.Cetarticleestpubliéen

OpenAccesssouslicenceCCBY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/4.0/).

AbridgedEnglishversion

Theheatand masstransferoccurringintheRayleigh–Bénard configurationisinvolvedinmanyindustrialprocesses.The non-intrusive control of such heat and mass transfer by an external magnetic field [1,2], an acoustic wave [3] or high-frequency vibrations [4] is a crucial problem that allows the optimization of devices incorporating a fluidlayer confined betweentwo solidwallsmaintainedatdifferenttemperatures.Forelectricallyconductingfluids, applyinganexternal mag-neticfieldiscommonlyusedtodelaycriticaltransition,andconsequentlytheappearanceofnaturalconvection,toachievea purelyconductivetransfermode[5,6].Forbinaryfluids,itisnolongerrealistictoneglecttheexistingcouplingbetweenheat and masstransfer, and thestabilityoftheRayleigh–Bénard configurationwith Soreteffectwas particularlyinvestigated to determine theeffectofthiscouplingonthecritical thresholdfortheonsetofthermosolutalconvection[7].Butdespitethe importanceofsuchanissuefrombothafundamentalandanappliedpointofview,toourknowledge,studiesonthecontrol ofthecriticaltransitionbyamagneticfieldinthepresenceofSoreteffectarerelativelyrare.Theaimofourinvestigationis toextendthestudytotheimpactofamagneticfieldofvariableorientationandmagnitudeon theRayleigh–Bénardcritical transitionbytakingintoaccounttheSoreteffect.Thepresentstudyismainlybasedonanumericalapproach.Nevertheless, ananalyticalapproachisalsoperformedtocharacterize thetransitionforthelong-wavelength instabilitiesandtostudyits evolutionundertheinfluenceofamagneticfield.Themainresultscanbesummarizedasfollows:

– for thecase ψ < ψℓ0,the unstablemodes aremultiple finitewavelengthcellsand they keepsuchastructurewhen a

magneticfieldisapplied.The mostefficientstabilizing effectisobtainedwhen themagneticfieldisperfectly vertical, corresponding to the case _{β =}0◦_{. Any change in the polar angle is responsible for an attenuation of the stabilizing}

effect,which correspondstoreplacingthestrength ofthemagneticfieldHa byaneffectivestrength Hacosβ.Through

thistransformation,all theresults related to anarbitrary orientated magneticfield withan azimuthalangle

α

and a polar angleβ are derived fromthose obtained for aperfectly verticalmagnetic field(_{β =}0◦)with unstable marginal

cellscharacterized by their axes, which are parallelto the horizontal component of themagnetic field.Moreover, for thecaseofahorizontalmagneticfield (_{β =}90◦_{), thecriticalthresholds remainthesameasfor Ha=0 corresponding}

tothesituationwithoutmagneticfield(Rac=Rac(Ha=0)=1707.76 andk→−kck =hc(Ha=0)=3.11).Thechange ofthe

azimuthalangle

α

affectsonlytheorientationofthemarginalcellswhoseaxiswillbealignedwiththedirectionofthe magneticfield;

– for the case_{ψ ≥ ψ}ℓ0, thestabilization process changes significantly. Indeed, for Ha=0, theinstability corresponds to

asingle-cell mode (infinite wavelength instability), which isnot favorable to heat and masstransfer. As observedfor

ψ < ψℓ0,themagneticfieldmaintainsitsstabilizingeffect.However,theevolutionoftheunstablemodesissignificantly

different. Indeed, theinitially single-cell modes for Ha₌0 remain so until a Hartmann number Ha_ℓ(ψ,Le) for which

a major change affecting the critical wave number hc occurs. Indeed, for Ha=Haℓ(ψ,Le), the critical wave number

hc sharplyincreases fromzerotowardsfinitevalues,with,asadirectconsequence, thedisappearanceofthesingle-cell

instabilityandtheemergenceofthemoreusualmultiplefinitewavelengthcells.Thischangehaspracticalconsequences ofprimaryimportance sincethismultiple-finite-wavelength-cellmode contributestoenhanceheat and masstransfer. Moreover, thevalue of theHartmann number Haℓ(ψ,Le) that ensures this optimization oftransfers could bederived

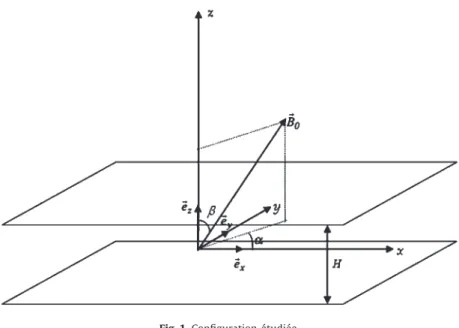
Fig. 1.Configuration étudiée.

Fig. 1.Studied configuration. 1. Introduction

Les transferts de masse et de chaleur spécifiques à la configuration de Rayleigh–Bénard se retrouvent dans plusieurs processus industriels. Le contrôle non intrusif detels transferts thermiqueset massiques par application d’unchamp ma-gnétique[1,2],d’uneondeacoustique[3]oudevibrationsàhautesfréquences[4]estundéficrucialquipermetd’optimiser les rendements des dispositifs intégrant unecouche fluideconfinée entre deux parois solidesportées à des températures différentes.Pourlesfluidesélectriquementconducteurs,l’applicationd’unchampmagnétiqueestcourammentutiliséepour contrôler la convectionnaturelle sedéveloppantau-delà duseuil critique et retarderainsi son apparitionpour assurerun modedetransfertpurementconductif[5,6].Pourlesfluidesbinairesoùiln’estplusréalistedenégligerlecouplageexistant entreletransfert dechaleuretdemasse, lastabilitédelaconfigurationdeRayleigh–Bénardavec effetSoret aété particu-lièrementétudiéepourcernerl’impactdececouplagesurleseuilcritiqued’apparition delaconvectionthermosolutale[7]. Mais, en dépit de l’importance de cette problématique, aussi bien d’un pointde vue fondamental qu’appliqué, les études portant surlecontrôleparchampmagnétiquedelatransitioncritique enprésencedel’effet Soretsontrelativementrares. L’objectifdenosinvestigationsestd’étendrel’étudedel’impactd’unchampmagnétiqued’orientationvariablesurla transi-tion critique enconfigurationdeRayleigh–Bénard avec effetSoret paruneapproche numérique,maisaussi decaractériser cette transitionpourdesinstabilitésmonocellulairesàlongueurd’ondeinfinieparuneapprocheanalytiqueetd’étudierson évolutionsousl’effetd’unchampmagnétique.

2. Formulationduproblème

Soit une couche d’un fluide binaire, newtonien et électriquement conducteur, de conductivité électrique

σ

e, de

vis-cosité cinématique

ν

et obéissant à la loi de Boussinesq :

ρ

=

ρ

0[1− βT(T−T0) − βC(C−C0)] où βT et βC désignent

respectivement les coefficients d’expansion thermique et solutale. Les flux de masse et de chaleur, incluant l’effet Soret, s’écrivent :→−JC = −

ρ

DC →∇−C−

ρ

DS→−∇T et→−JT = −λ→−∇T, où DC, DS et λ sont, respectivement, le coefficient de

diffu-sion de masse, le coefficient de diffusion deSoret et la conductivité thermique. Cette couche, confinée entre deux plans horizontaux distants de H et différentiellement chauffés, est le siège d’une stratification linéaire de température et de concentration,etestsoumiseàunchampmagnétiqueuniformepouvantêtreorientédanstouteslesdirectionsdel’espace :

− →_B

0=B0 ¡sinβcos

α

→−e_x+sinβsin

α

→−e_y+cosβ→−ez¢ (Fig. 1).Enprenant commegrandeursderéférence H pourleslongueurs,

κ

/H pour lavitesse, H2/

κ

pour letemps et

ρ

0

κ

2/H2 pour lapression(

κ

désigne ladiffusivitéthermique),1T=T1−T2

pour la température et 1C=C1−C2= −(DS/DC)1T pour la concentration, les équations d’évolution linéarisées d’une

perturbationinfinitésimale(→−v,p, θ,

η

_{(= θ −}c_{), φ) = (}→−_{v(z),p(z), θ (z),}

_η

_{(z), φ (z)) e}i(hx+ky)+ωt _{peuvents’écrire :}

Pr

h

D2

₋

³

h2

₊

k2

´i

u

₋

ih p

+

Pr Ha2Fm,x

=

ω

u (1) Pr

h

D2

₋

³

h2

₊

k2

´i

v

₋

ik p

₊

Pr Ha2Fm,y

=

ω

v (2) Pr

h

D2

₋

³

h2

₊

k2

´i

w

₋

Dp

₊

Pr Ha2Fm,z

+

Ra Pr [

(

1

+ ψ)θ − ψ

η

]

=

ω

w (3) ihu

+

ikv

+

D w

=

0 (4)

h

D2

₋

³

h2

₊

k2

´i

_{θ −}

w

₌

ω

θ

(5)

Le

h

D2

₋

³

h2

₊

k2

´i

η

+

h

D2

−

³

h2

+

k2

´i

θ =

ω η

(6)

h

D2

₋

³

h2

₊

k2

´i

_{φ = (−}

ik cos

_{β +}

sin

β

sin

α

D

)

u

+ (

ih cos

β −

sin

β

cos

α

D

)

v

+

i sin

β (

cos

α

k

₋

sin

α

h

)

w (7)

où D₌ ∂

∂z, D2= ∂ 2

∂z2 etoù Fm,x, Fm,y et Fm,z sontlescomposantesdelaforce magnétiqueselonlestroisaxes (Ox),(O y)

et(O z),quis’écriventcommesuit :

Fm,x

= −

³

cos2

_{β +}

sin2

β

sin2

α

´

u

₊

sin2

β

cos

α

sin

α

v

₊

cos

β

sin

β

cos

α

w

+

sin

β

sin

α

D

_{φ −}

ik cos

β φ

(8)

Fm,y

=

sin2

β

cos

α

sin

α

u

−

³

cos2

_{β +}

sin2

β

cos2

α

´

v

₊

sin

β

cos

β

sin

α

w

−

sin

β

cos

α

D

_{φ +}

ih cos

β φ

(9)

Fm,z

=

sin

β

cos

β

cos

α

u

₊

sin

β

cos

β

sin

α

v

₋

sin2

β

w

−

isin

β (

sin

α

h

₋

cos

α

k

) φ

(10)

Les nombres sans dimension figurant dans les équations (1)–(10) sont le nombre de Rayleigh : Ra₌gβT1T H3/

νκ

, le

nombre dePrandtl :Pr₌

ν

/

κ

, lenombredeHartmann : Ha₌B0H√

σ

e/

ρ

0

ν

,lefacteurdeséparation : ψ = −βCDS/βTDC

etlenombredeLewis :Le₌D_C/

κ

.Parailleurs,nousprécisonsquelecoefficientdethermodiffusiondépendnonseulement delatempératuremoyennedelasolutionbinaire,maiségalementdelafractionmassiquedesdeuxconstituantsdumélange binaire étudié. Àtitred’exemple,unesolutionaqueuse deNaCl (0.5 mol/L)présenteuncomportementinhabituelpuisque, pour une température inférieure à 12◦_{C, le coefficient de Soret DS/DC est négatif, alors qu’il devient positif pour une}

températuresupérieure à12◦_{C[8].Dansnotreétude,enformulationadimensionnelle,lecoefficientdethermodiffusionest}

remplacé par le facteur de séparation ψ. Nous avons conduit une étude de stabilité linéaire en considérant des valeurs

positivesetnégativesdufacteurdeséparationψ.

Leséquationslinéarisées(1)–(10) développéesci-dessuspeuventdoncs’écrire commeunproblèmeauxvaleurs propres généralisé du type : £ X=

ω

5 X, où X désigne le vecteur (→−v(z),p(z), θ (z),

η

(z), φ (z)), £ est unopérateur linéaire

dé-pendant de h, k, Ra, Pr, Le, Ha,

α

et β et 5 est un opérateur linéaire creux contenant des zéros et des uns. Ce système

auxvaleurs propresgénéralisé estrésolu paruneméthodenumériquebaséesurlacollocationspectrale deTau–Chebyshev et utilisant des développements en polynômes de Chebyshev (N inconnues pour l’ensemble des variables du problème

u,v,w,p,θ,

η

et φ). La méthode de Tau–Chebyshev permet d’éviter l’apparitionde valeurs propres parasites en mettant

des conditions auxlimites àla findechaque sous-matrice constituantla matriceprincipale£. Le nombredeRayleigh cri-tique Rac est déterminé à partir des minimums de la fonction à deux variables h et k correspondant au seuil marginal Ra0(Ha,Pr,Le,α,β)(h,k)obtenupour unjeudeparamètres Ha,Pr,Le,

α

etβ fixé.CeseuilmarginalRa0(Ha,Pr,Le,α,β)(h,k)

corres-pond à unevaleur propre

ω

n admettantunepartie réellenulle, alors que toutes lesautres valeurs propres (

ω

m)1_≤m6=n≤N

sontàpartiesréellesnégatives.LenombredeRayleigh critiqueRacpeut doncs’écrire :

Rac

=

Min(h,k_)∈R2Ra₀(Ha,Pr,Le,α,β)

(

h

,

k

)

(11)

3. InstabilitésdeRayleigh–BénardaveceffetSoretetchampmagnétiquededirectionquelconque

Sanschampmagnétique,lesinstabilitésdeRayleigh–Bénardencavitéinfiniesedéclenchentau-dessusd’unseuilcritique

Rac0=Rac(Ha=0)=1707.76 et correspondentàdes structuresthermo-convectives stationnaires denombred’onde hc0=

hc(Ha=0)=3.11. Pourunfluidebinaireavec unfacteurdeséparation ψ positif,lesseuilscritiquesainsi quelesnombres

d’onde correspondants (ne dépendant que de Le et pas de Pr) décroissent fortement lorsque ψ augmente. Ce nombre

d’ondedevientnulpourunevaleurdeψ supérieureàψℓ0=131Le/(34−131Le) etparconséquentdescellulesconvectives

detailleinfinieapparaissent.Pourψ négatif,leseuilstationnaireaugmente,maisilestviteprécédéparunseuiloscillatoire

(dépendant deLe et dePr) qui évolue peuavec ψ. Nous allonsétudier successivementl’influence du champmagnétique

dans lescasoùψ < ψℓ0 puisψ > ψℓ0.

3.1. Influenceduchampmagnétiquepourψ < ψℓ0

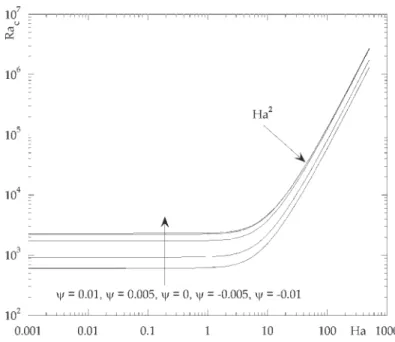
La Fig. 2 illustrant la variation de Rac en fonction de Ha pour un champ magnétique vertical et Le=0.01 montre

clairementquelechampverticalretardel’apparitiondelaconvectionthermosolutale,etce,pourlesdifférentesvaleursdeψ

considérées.Les nombresd’ondeassociésaugmententaussiavec Ha,indiquantquelatailledes cellulesmarginalesdevient deplusenplusréduitequandlechampmagnétiquedevientplusintense(Fig. 3).Nousnotonscescourbescritiquesobtenues souschampmagnétiqueverticalrespectivementRav(Ha)ethv(Ha).ÀfortHa,desloisasymptotiquessontobtenues,etelles

s’avèrent similairesàcellesobtenuessans effetSoret.Par ailleurs,elles semontrententrèsbonneconcordanceavec celles établies parJulienet al. [9],à savoir :Ra_c∼10 Ha2 _eth

c∼1.9Ha

1

3, ou encoreRa_c∼10 Q eth_c∼1.9 Q16 (où Q ₌Ha2

est le nombre de Chandrasekhar). Pour _{ψ ≥}0, le champ magnétique préserve le caractère bi-dimensionnel stationnaire des modesinstables. Parailleurs, pour lesvaleursnégativesdeψ considérées,lecaractère bi-dimensionneloscillatoire des

Fig. 2.Variation de Racavec Ha pour Pr=0.01, Le=0.01 et différentes valeurs deψ. Fig. 2.Variation of Racwith Ha for Pr=0.01, Le=0.01 and different values ofψ.

Fig. 3.Variation de hcavec Ha pour Pr=0.01, Le=0.01 et différentes valeurs deψ. Fig. 3.Variation of hcwith Ha for Pr=0.01, Le=0.01 and different values ofψ.

modes instables est aussi conservé, avec une célérité critique qui augmente avec Ha, comme illustré sur la Fig. 4. Nous proposons à présent de déterminer l’effet de la variation de ladirection d’un champ magnétique ayant une composante horizontale non nulle (_{β 6=}0◦_{) surl’apparition dela convection.Les investigationsnumériques mettent en évidencedeux}

résultats importants : toutd’abord, le nombre deRayleigh critique Rac reste exactement lemême que celui obtenu pour

un champ magnétique parfaitement vertical si on remplace la valeur de Ha par Hacosβ (Rac=Rav(Hacosβ)) ; ensuite,

le vecteur d’onde devient :→−kc= (hv(Hacosβ)sin

α

,−hv(Hacosβ)cos

α

,0), indiquant que le champ magnétique, en plus

de stabiliser, aligne les cellules marginales sur sapropre direction ; enfin, k→−kck =hv(Hacosβ), indiquant que la longueur

d’ondedescellulesmarginalesλc=2

π

/k→−kck =2

π

/hv(Hacosβ)resteconstantequellequesoitlavaleurdel’angleazimutal

α

que fait le champ magnétique avec la direction de l’axe Ox. Pour parachever l’étude de l’impact de la direction d’un champ magnétiquesurlatransitioncritique, on considèreàprésentle casd’unchampmagnétiquecoplanairepar rapport à la couche de fluide (_{β =}90◦_{). Les résultats des simulations numériques montrent que le champ magnétique n’a plus}

aucun effet stabilisant : Rac(Ha,

α

)=Rac0=Rac(Ha=0)=1707.76, mais uniquement uneffet d’orientation où, à l’instar

du cas _{β 6=}0◦_{, les cellules marginales s’alignent avec la direction du champ magnétique avec un vecteur d’onde :}→−_kc= (hc(Ha=0)sin

α

,−hc(Ha=0)cos

α

,0) de norme constante k→−kck =hc0=hc(Ha=0)=3.11, qui indique que la longueur

Fig. 4.Variation de ccavec Ha pour Pr=0.01, Le=0.01 et deux valeurs négatives deψ.

Fig. 4.Variation of ccwith Ha for Pr=0.01, Le=0.01 and two negative values ofψ.

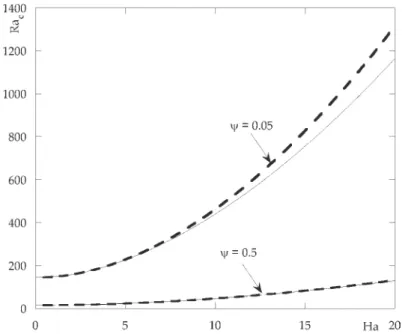
Fig. 5.Variation de Racen fonction de Ha pourψ =0.05,ψ =0.5 et Le=0.01 (traits continus : numérique, traits discontinus : analytique).

Fig. 5.Variation of Racas a function of Ha forψ =0.05 and Le=0.01 (solid lines: numerical results, heavy dashed lines: analytical results).

le seuil d’apparition de laconvection est une conséquence directe del’alignement des cellules marginales avec le champ magnétique.Eneffet,sil’onconsidèrelerotationneldutermemagnétique→−j_×→−_e

B0,onobtient : −−→ rot

¡

→−j

_×

→−_e B0

¢

=

→−j

¡

→−

∇ ·

→−eB0

¢

− (

→−j

.

→−

∇)

→−eB0

−

→−eB0

(

− →

∇ ·

→−j

) +

¡

→−eB0

.

− →

∇

¢

→−j

=

i

¡

→−eB0

.

− → k

¢

→−j

₌

→−0 (12)

ce qui impliquequ’il existe unpotentiel U telque→−j_×→−_e

B0= −

− →

∇U qui, une fois intégré à la pression,fait disparaître le

termemagnétiquedusystèmed’équationsauxperturbations(1)–(10).

3.2. Influenceduchampmagnétiquepour_{ψ ≥ ψℓ0}

Nous choisissons maintenant des fluides dont le nombre deLewis est toujours Le₌0.01, mais dont le facteur de

sé-paration ψ est supérieurà ψℓ0(Le=0.01)=0.0400734 (ψ =0.05 et ψ =0.5),correspondant donc à des modes instables

monocellulaires. LaFig. 5nousmontrequelechampmagnétiqueconservesoneffetstabilisantcorrespondant àunehausse dunombredeRayleighcritique Ra_c avecHa.Mais,enobservant laFig. 6,nousconstatonsqueceteffetstabilisant s’accom-pagne d’unchangement majeur par rapport auxcas ψ < ψℓ0. En effet, il existe unevaleur limite de Ha dépendant deψ

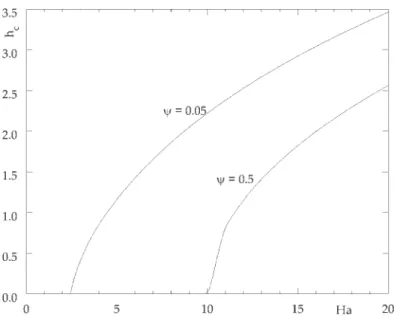
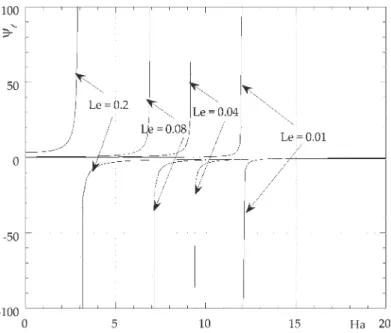
Fig. 6.Variation de hcen fonction de Ha pourψ =0.05,ψ =0.5 et Le=0.01.

Fig. 6.Variation of hcas a function of Ha forψ =0.05,ψ =0.5 and Le=0.01.

Fig. 7.Variation de hcavecψpour Le=0.01 et différentes valeurs de Ha. Fig. 7.Variation of hcwithψfor Le=0.01 and different values of Ha.

etnotéeHaℓ(ψ )(avec, parexemple, Haℓ(0.05)≈2.6 etHaℓ(0.5)≈10) telleque, pourHa<Haℓ(ψ ), lemodeinstable reste

monocellulaire (hc∼0) et, dès que Ha≥Haℓ(ψ ), le nombre d’ondecritique hc se met à croîtretrès significativement de

zéro versdes valeurs finies.Notonsqu’uneprocéduredecalcul plusprécise deHaℓ(ψ ) etdonnantHaℓ(0.05)=2.64937 et

Ha_ℓ(0.5)=10.01908 pouruneprécisionde10−4estdétailléeauniveaudelapartie4.Nousconstatonsd’aprèslaFig. 5que

l’écart entre les valeurs numériques etanalytiques du nombre deRayleigh critique Ra_c augmente avec Ha. Pour Ha_≤20, cetécartcommenceàêtresignificatifàpartir d’unnombredeHartmannpluspetit pourlecas_{ψ =}0.05 quepour celuioù ψ =0.5.Cerésultatest dûau faitquel’expressionanalytiquedeRacn’est valablequepourdes instabilitésmonocellulaires

et par conséquent pour Ha<Haℓ(ψ ), ce qui correspond à Ha<2.64937 pour ψ =0.05 et Ha<10.01908 pour ψ =0.5.

Par ailleurs, lechoixqui aété faitdelimiter l’intervallede variationà Ha_≤20 montre qu’ilest possible d’êtreen dehors delalimite devaliditédudomainedeprévalence des modesmonocellulaires etconserverpour autantunebonne concor-dance entrelesrésultats numériqueset analytiques,notamment pour lecas _{ψ =}0.5. Par conséquent,les résultatsrelatifs

au nombredeRayleigh critique nesontpas enmesureàeuxseuls denous renseignersurlavaleurprécisedunombrede Hartmann au-delà duquellatransition entreinstabilités monocellulaireset multicellulairess’opère. Si on souhaite obtenir ces valeurs Ha_ℓ(ψ ) avec unebonne précision enprocédant parune approchepurementnumérique, la connaissancedela

variation du nombre d’onde critique hc en fonction de Ha à l’instar de ce qui est illustré sur la Fig. 6 s’impose. De ces

Fig. 8.Variation deψℓen fonction de Ha pour différentes valeurs de Le.

Fig. 8.Variation ofψℓas a function of Ha for different values of Le.

En effet, quand uneinstabilité initialementmonocellulaire change destructure pour devenir unmode critique àplusieurs rouleaux, ils’ensuituneintensification destransfertsthermiquesetmassiquesquipeut êtrerecherchéepourl’optimisation d’unprocessusimpliquantundispositifdutypeconfigurationdeRayleigh–Bénard.

3.3. Influenceduchampmagnétiquesurlatransitionentremodesmulticellulairesetmonocellulaires

Latransitionentrelesmodesmulticellulairesetmonocellulairescorrespondauxvaleursdeψ pourlesquelleslenombre

d’onde h tend vers zéro. Nousdonnons sur laFig. 7 la variationde ce nombre d’ondecritique hc en fonctionde ψ pour

un fluideavec Le₌0.01 et différentesvaleurs dunombre deHartmann Ha. Nousobservonsque ladécroissancevers zéro de hc alieu d’autant plus loin que la valeur de Ha est grande.Afin de mieux appréhender la transition entreles modes

monocellulairesetmulticellulaires,nousreprésentonssurlaFig. 8lavariationdeψℓ (obtenuanalytiquement,voirpartie4)

enfonctiondeHa pourdifférentesvaleurs dunombredeLewis. Cettefigureillustreclairementqu’aprèsuneaugmentation assez modéréeavec le nombredeHartmann,ψℓ semet àcroîtretrès significativementavec Ha etàatteindre des valeurs

quasimentinfiniesquandHatendversHa_n(lesvaleursdeHa_nsontconsignéesdansleTableau 2)pourbasculerdanslazone

ψℓ<0 quandHa>Han.Cerésultat indiqueclairementquelechampmagnétiquecontrôlelatransitionentremodes

mono-cellulairesetmodesmulticellulairesenrepoussantdeplusenplusloinlavaleurdufacteurdeséparationcritiqueψℓ au-delà

duquel lesmodes monocellulaires sontsusceptibles d’apparaître. D’un point devue pratique,en considérantun fluide bi-nairecaractériséparunnombredeLewisLe etunfacteurdeséparationψ telqueψ > ψℓ0,avecψℓ0=131Le/(34−131Le),

il est alors manifeste que lespremières instabilitésqui apparaissent seront monocellulaires. En appliquantun champ ma-gnétiquecorrespondantàunevaleurdeHa>Haℓ(ψ,Le) quiferaitcroîtrelavaleurdufacteurdeséparationcritique deψℓ0

à ψℓ afin que la relationψ < ψℓ soit vérifiée (ce qui est toujours possible d’après lesrésultats illustrés sur la Fig. 8),les

premiersmodesinstablesserontdésormaismulticellulairesetnonplusmonocellulaires,permettantainsiuneintensification des transfertsthermiquesetmassiques.

4. Influenceduchampmagnétiquesurlesmodesinstablesmonocellulaires

D’après l’étude de stabilité réalisée plus haut, nous constatonsqu’un champ magnétique, dontl’orientation est définie par son angle azimutal

α

et son anglepolaire β, préservait lecaractère bi-dimensionnel des modes critiques àcondition

de se placer dans le repère (OXY Z) obtenu par une rotation d’angle

α

autour de l’axe vertical (Oz) durepère initial de

travail(Oxyz).Ceconstatnouspermetd’introduireunefonctiondecourantφ dansleplan(XOZ).Leséquationsd’évolution

du problème perturbé(1)–(10) peuvent donc s’écrire dans ce plan (XOZ). Nous lesécrivons pour un champmagnétique

parfaitementvertical,sachantquepourunchampnonvertical,nousavonsmontréquelesseuilscritiquesrestentinchangés enremplaçant HaparHacosβ :

i

λ(

d 2 dz2

−

k2

)φ +

Pr

·

(

d 2 dz2

−

k2

)

2

−

Ha2 d2 dz2

¸

φ −

i kRa Pr [

(

1

+ ψ)θ − ψ

η

]

=

0 (13) i

_{λθ + (}

d2 dz2

−

k2

)θ −

ik

φ =

0 (14)

i

λ(

η

− θ) +

Le

(

d

2

dz2

−

k2

)

η

+

ik

φ =

0 (15)

avec lesconditionsauxlimitessuivantes :

φ =

d_dz

φ

=

0

,

_{θ =}

0 et d

η

dz

=

0 pour z

= ±

1 (16)

Notonsque, dans ces équations,nous avons conservé lanotation z à laplace de Z dès lorsque lesaxes (OZ) et(Oz)

sontconfondus.Pourétudierlesinstabilitésmonocellulaires(surlesquelleslechampmagnétiqueauneinfluenced’aprèsce quenousavonsvudansleparagrapheprécédent),nousutilisonsledéveloppementensérieenpuissancesdekauvoisinage dek₌0 desperturbations delafonctiondecourant,delatempératureetdelafonction

η

,etnousfaisonsdemêmepour

le tauxd’amplification λ. Nouspouvons ainsi déterminer analytiquement pour ces instabilitésmonocellulaires les

expres-sions du nombre de Rayleigh critique Rac en fonction du facteur de séparation ψ. Par ailleurs, nous sommes en mesure

de déterminerle facteur deséparation limite ψℓ qui donne lavaleurde ψ en deçàde laquelle l’approximation

monocel-lulaire n’est plus valable,c’est-à-dire qu’ellenedonneplus lemode dominant.Notonsquel’obtentionde Rac nécessiteun

développement enk àl’ordre 2,alors que l’ordre 4est nécessairepour obtenir ψℓ. Les expressionsobtenues àla suitede

développementsanalytiquescomplexesréalisésaveclelogicielMAPLEsontprésentéesci-dessous(notonsqu’ilestjudicieux dedéfinirunfacteurdeséparationgénéralisé eψ) :

Rac

=

12 Le Ha 4

ψ

¡

12

₊

Ha2

₋

6 Ha cothHa₂

¢

(17)

e

ψ

ℓ

=

1 Le

ψ

ℓ 1

+ ψ

ℓ

=

N

(

Ha

)

D

(

Ha

)

(18) avec : N

(

Ha

_{) = −}

3 2

(−

40 320

+

40 320 exp

(

3Ha

) −

420 Ha 4

+

1680 Ha3

−

120 960 exp

(

2Ha

_{) −}

17 Ha6

+

10 080 Ha2

+

120 960 exp

(

Ha

)

−

168 Ha5

−

10 080 exp

(

3Ha

)

Ha2

−

20 160 exp

(

2Ha

)

Ha2

+

17 Ha6 exp

(

3Ha

_{) +}

420 Ha4 exp

(

3Ha

_{) +}

420 Ha4 exp

(

2Ha

)

+

5040 Ha exp

(

3Ha

_{) −}

51 Ha6 exp

(

2Ha

_{) +}

1680 Ha3 exp

(

3Ha

)

−

168 Ha5 exp

(

3Ha

_{) −}

1680 Ha3 exp

(

2Ha

_{) −}

5040 exp

(

2Ha

)

Ha

+

168 Ha5 exp

(

2Ha

_{) +}

20 160 Ha2 exp

(

Ha

_{) +}

168 Ha5 exp

(

Ha

)

−

1680 Ha3 exp

(

Ha

_{) −}

5040 Ha exp

(

Ha

_{) +}

5040 Ha

−

420 Ha4 exp

(

Ha

_{) +}

51 Ha6 exp

(

Ha

))

(19)

D

(

Ha

_{) =}

Ha

(

504 Ha3

+

6300 Ha2

−

Ha5

+

30 240 Ha

−

21 420 Ha2 exp

(

Ha

_{) −}

52 920 exp

(

Ha

_{) −}

30 240 Ha exp

(

3Ha

)

+

15 120 exp

(

2Ha

)

Ha

+

Ha5 exp

(

3Ha

_{) −}

504 Ha3 exp

(

3Ha

)

+

4032 Ha3 exp

(

2Ha

_{) −}

4032 Ha3 exp

(

Ha

_{) +}

52 920 exp

(

3Ha

)

+

3 Ha5 exp

(

Ha

_{) −}

3 Ha5 exp

(

2Ha

_{) +}

6300 exp

(

3Ha

)

Ha2

−

21 420 exp

(

2Ha

)

Ha2

−

15 120 Ha exp

(

Ha

_{) +}

52 920

(

1

−

exp

(

2Ha

)))

(20)

Parundéveloppementlimitédecesexpressionsàl’ordre4enHa,nouspouvonsretrouver,àl’ordrezéro,lesexpressions classiques deRa_c etψℓ pour lesinstabilitésmonocellulairesenl’absencedechampmagnétique(Ha=0) :

Rac

=

720 Le

ψ

+

120 Le 7

ψ

Ha 2

−

₄₉Le

ψ

Ha 4

+

O

(

Ha6

)

(21)

e

ψ

ℓ

=

131 34

+

196 867 1 577 940Ha 2

+

_{73 232 195 400}58 185 319 Ha4

+

O

(

Ha6

)

(22) etdonc :

ψ

ℓ

(

Ha

=

0

) = ψ

ℓ0

=

131 Le 34

₋

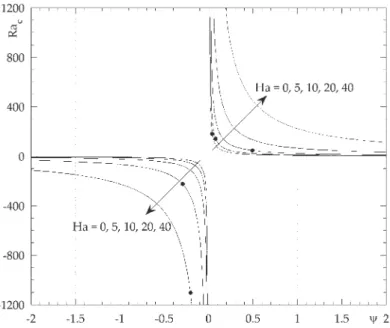
131 Le (23)

Sur la Fig. 9, nous présentons les courbes donnant les seuils critiques Ra_c pour l’instabilité monocellulaire pour dif-férentes valeurs du nombre de Hartmann Ha et Le₌0.01. Ces courbes s’étendent sur le domaine (ψ >0,Ra>0), mais

Fig. 9.Variation de Racavecψpour Le=0.01 et différentes valeurs de Ha.

Fig. 9.Variation of Racwithψfor Le=0.01 and different values of Ha.

Tableau 1

Variation en fonction de Hade ψeℓ, puis, pour Le=0.01, variation

de ψℓet du nombre de Rayleigh critique Raccorrespondant.

Table 1

Variation of eψℓas a function of Ha, and then, for Le=0.01,

varia-tion of ψℓand of the corresponding critical Rayleigh number Rac.

Ha eψℓ Le=0.01 Le=0.01 ψℓ Rac 0 3.853 0.0401 179.67 5 7.536 0.0815 139.57 10 33.080 0.494 46.69 20 −41.401 −0.293 −224.58 40 −25.419 −0.203 −1104.76

aussi sur le domaine(ψ <0,Ra<0).Pour chacunede cescourbes, nous donnons aussi, sousla formed’un pointnoir, la

limite au-delàde laquelle lemode monocellulaire est lemode dominant.Les valeurs de ψℓ correspondantes ainsi queles

valeurs deRac associées sontdonnées dans leTableau 1. Nousconstatons toutd’abord queles seuils critiques |Rac| pour

l’instabilité monocellulaire croissentavec l’augmentationdeHa.Le facteurdeséparation limite ψℓ dépendaussi fortement

de Ha : ψℓ croît d’abord quand Ha augmente dans le domaine (ψ >0,Ra>0), puis décroît en valeur absolue dans le

domaine (ψ <0,Ra<0).Cesvariationsindiquent queledomained’apparition des modes monocellulairesserestreint

for-tement quandHa augmente. À titred’exemple, ce domaineévolue des intervalles (ψ >0.0401,Ra>0)et (ψ <0,Ra<0)

pour Ha₌0,à(ψ >0.494,Ra>0)et(ψ <0,Ra<0)pour Ha=10 etàseulement (−0.293< ψ <0,Ra<0)pour Ha=20.

L’ensembledecesrésultatsconfirmedefaçonplusprécisecequiaétéobservédanslapartie3.D’unpointdevuepratique, cerésultatestd’uneimportancemajeuredèslorsqu’ilestdésormaispossiblepourtoutfluidecaractériséparunnombrede LewisLeetunfacteurdeséparationψ (permettantd’obtenirlavaleurdeψecorrespondante)d’éviterl’apparitiondes

instabi-litésmonocellulairespréjudiciablesàl’intensificationdestransfertsthermiquesetmassiquesenajustantl’intensitéduchamp magnétiquede façonàce que Ha_≥Haℓ. Haℓ estla valeurde Ha vérifiantlacondition :ψeℓ(Haℓ)= eψ = ψ/[Le(1+ ψ)], où e

ψℓ est explicitement déterminé parles relations analytiques (18)–(20). Quelques valeurs de Haℓ peuvent être obtenues à

partir du Tableau 1.Par exemple, pour Le₌0.01, Haℓ=5 pour ψ =0.0815 et Haℓ=10 pour ψ =0.494. Nousmontrons

aussi, dans leTableau 2, lesvaleurs de Ha (notées Han)qui correspondent àl’intensité duchamp magnétiqueau-delà de

laquelle l’instabilité monocellulaire n’apparaîtque pour des facteurs deséparation ψ négatifs etun chauffagepar le haut

(Ra<0).Unedesconséquences est qu’au-delàdecette valeur,l’instabilité monocellulairen’apparaîtplus pour des ψ

posi-tifs.Le nombredeHartmannHan atteintunevaleurlimite prochede13.5 lorsquelenombredeLewisLe tendverszéroet

décroît lorsquelavaleurdeLeaugmente.

5. Conclusion

Cetteétude consacréeàl’effetd’unchampmagnétiquesur lastabilité deRayleigh–Bénardavec effetSoret a principale-mentmisenévidencelespointssuivants :

Tableau 2

Valeurs de Han au-delà desquelles l’instabilité monocellulaire n’apparaît que pour ψ <0 et Ra<0.

Table 2

Values of Hanabove which the mono-cellular instability only appears for

ψ <0 and Ra<0. Le Han 0.0001 13.44249647 0.001 13.29867806 0.01 12.04102372 0.02 10.92902561 0.04 9.251004523 0.06 8.001913693 0.08 7.003098866 0.1 6.163030711 0.15 4.449488979 0.2 2.948319760

– Pour lecas ψ < ψℓ0, lesmodes instables sontde longueur d’ondefinie etledemeurent quandils sontsoumis à

l’ac-tiond’unchampmagnétique.L’effetstabilisantdûau champmagnétiqueest optimalquandcedernierestparfaitement vertical,correspondant aucas _{β =}0◦_{.Toute variationdel’anglepolaireβ està l’origined’une atténuationdecet effet}

stabilisant,ce qui revient à remplacerl’intensité réelle duchamp magnétiqueHa parune intensité effective Hacosβ.

Aprèsavoirréalisécettetransformation,touslesrésultatsrelatifsàunchampmagnétiqued’angleazimutal

α

etd’angle polaire β se déduisentde ceux obtenus pour un champmagnétique parfaitement vertical (_{β =}0◦) avec les axes des

cellulesmarginales alignés sur lacomposante horizontaleduchamp magnétique.Par ailleurs, pour unchamp magné-tique horizontal (_{β =}90◦_{), aucun effet de stabilisation, ni de modification du nombre d’onde critique, n’est constaté}

(Rac=Rac(Ha=0)=1707.76 etk→−kck =hc(Ha=0)=3.11), etlavariation del’angleazimutal

α

agit uniquementsur l’orientationdescellulesmarginales dontlesaxess’alignentavec ladirectionduchampmagnétique.

– Pour le cas _{ψ ≥ ψ}ℓ0, le processus destabilisation change radicalement. En effet, pour Ha=0, l’instabilité correspond

à un mode monocellulaire qui est peu favorable au transfert de masse et de chaleur. À l’instar de ce qui a été ob-servé pour ψ < ψℓ0, le champ magnétique conserve son effet stabilisant. Cependant, l’évolution des instabilités est

différente.En effet,lesinstabilités,initialementmonocellulairespourHa₌0,ledemeurentjusqu’àunnombrede Hart-mann Ha_ℓ(ψ,Le) pour lequel une variation marquée du nombre d’onde critique hc a lieu. Pour Ha=Haℓ(ψ,Le), ce

derniervoitsavaleurpasser subitement dezéroàdes valeurs finies,avec pour conséquencedirecteladisparitiondes instabilitésmonocellulairesetl’apparitiondenouveaux modesinstables àplusieursrouleaux. Cettemodificationades conséquencespratiques depremièreimportancedès lorsquelesmodesàplusieursrouleauxcontribuentà l’intensifica-tiondestransfertsthermiquesetmassiques.Parailleurs, lavaleurdunombredeHartmannHaℓ(ψ,Le) quiassurecette

optimisationdes transfertsapuêtrecalculéeanalytiquementetestdonnéeparlesrelations(18)–(20),commeindiqué danslapartie4del’article.

Pourconclure,onpeutaffirmerquelesaspectsdel’actiond’unchampmagnétiquesurlesinstabilitésdeRayleigh–Bénard avec effet Soret sontmultiples etqueson impactpratiquele plussignificatif reste lecontrôlesélectif des phénomènesde transfertdemasseetdechaleurquisedéveloppentau seindelacouche fluide.

Références

[1]U.Burr,U.Müller, Rayleigh–Bénardconvection inliquid metallayer underthe influence ofa horizontal magnetic field,J.Fluid Mech.453(2002) 345–369.

[2]M.Takashima,M.Hirasawa,H.Nozaki,Buoyancydriveninstabilityinahorizontal layerofelectricallyconductingfluidin thepresenceofavertical magneticfield,Int.J.HeatMassTransf.42(1999)1689–1706.

[3]M.K.Achour,S.Kaddeche,A.Gharbi,H.BenHadid,D.Henry,OnthestabilityoftheHadleyflowundertheactionofanacousticwave,FluidDyn.Mater. Proc.1 (4)(2005)277–283.

[4]C.Benzid,S.Kaddeche,A.Abdennadher,D.Henry,H.BenHadid,InstabilitésdeRayleigh–Bénardsousvibrationshautesfréquencesetchampmagnétique, C.R.,Méc.337 (5)(2009)291–296.

[5]S.Kaddeche,D.Henry,T.Putelat,H.BenHadid,Instabilitiesinliquidmetalscontrolledbyconstantmagneticfield,Part I:verticalmagneticfield,J. Cryst. Growth242(2002)491–500.

[6]S.Kaddeche,H.BenHadid,T.Putelat,D.Henry,Instabilitiesinliquidmetalscontrolledbyconstantmagneticfield,Part II:horizontalmagneticfield, J. Cryst.Growth242(2002)501–510.

[7]J.Hu, H.BenHadid,D.Henry,LinearstabilityanalysisofPoiseuille–Rayleigh–Bénardflowsin binaryfluidswithSoreteffect,Phys. Fluids19(2007) 034101.

[8]A.Mojtabi,J.K. Platten,M.-C. Charrier-Mojtabi,Onsetof freeconvectionin solutionswithvariable Soretcoefficients,J.Non-Equilib.Thermodyn.27 (2002)25–44.