Méthodes intéractives pour la synthèse des systèmes combinatoires à l'aide du système graphique CDC 1700-274.

GRAPHIQUE

cnc

1700 - 274 •

j?ar

Abde1ali 11EZZOUR

Department of Electrical Engineering

GRAPHIQUE CDC 1700 - 274 •

par

Abdelali MEZZOUR , Ingénieur ÉlectroniquE'!

INSA de LYON , FRANCE

,

Mémoire présenté à la Faculté des Etudes Graduées en vue de l'obtention du grade de :·~îtrise en génie •

A thesis submitted to the Faculty of Graduate Studies and Research in partial fulfillment of the requirements for the degree of Master of Engineering •

Department of Electrical Engineering McGill University,

Montreal, Quebec

SOI-ft1AlRE

Le but de ce travail , est de développer un ensemble de programmes intéractifs , afin de mettre en place dans le système graphique

cne

1700, une méthode générale pour la synthèse des cir~uits combinatoires •

On a mis au point deux programmes appelés MINIMA et SBE, qui corres-pondent aux deux méthodes suivantes :

1) Une méthode de minimisation classique,permettant d'obtenir la réunion minimale d'urie fonction booléenne •

2) Une méthode générale indépendante du développement de la techno-logie , permettant la synthèse des circuits combinatoires avec un inventaire

fixe des modules de circuits intégrés • L'algorithme de cette méthode permet de décrire tout systèw~ digital combinatoire à réaliser , par un Système d'Equations Booléennes Simultanées (SEBS) •

Le problème revient donc à résoudre un SEBS en génaral , celui-ci posséde plusieurs solutions ; on propose une base pour les coder et les ordonner •

Une notion de catalogue des équations de contraintes a été L~troduite, pour sélectionner une solution L~téressante parmi toutes les solutions du SEES. Il ya une intéraction entre l'ordinateur "et l'utilisateur. Il incombe à ce dernier d'accepter l'équation de contrainte choisie par le programme SBE,ou de lui substituer une autre , suivant ses propres critères d'optimisation.

REMERCIEMENTS

Qu'il me soit permis d'exprimer ma profonde gratitude à tous ceux qui m'ont aidé dans mon travail à savoir:

- Monsieur Miguel MARIN , mon directeur de thèse, qui m'a orienté et m'a p~odigué ses conseils et ses encouragements •

- r·fonsieur Syed HEER, qui s'est vivement intéressé à mon travail en me donnant des conseils et en me permettant l'accès au Centre de Calcul de l'Université de Montréal •

- Messieurs SCHNEEGANS , MALŒoJ'ANY et BORRISSOV qui ·m' ont aidé dans la réalisation de ce travail •

- La Coopération Technique Franco-Québecoise qui m'a accordé la bourse France-Québec •

- Et enfin .' mon épouse qui m'a aidé dans la correction et la dacty~

TABLE DES MATIERES

SmlMAIRE REMERCIEMENTS TABLE DES MATIERES TABLE DES FIGURES

INTRODUCTION •••••••••••••••••••••••••••••••••••••••••••••••••

CHAPITRE I: CONCEPI'S GENERAUX ET DEFINITIONS ••••••••••••••••

1.1 Introduction ••••••••••••••••••••••••••••••••••••••••

1.2 Description du Système 1700 •••••••••••••••••••••••••

1.2.A Outils Technologiques ••••••••••••••••••••••••• 1.2.A.1 Configuration du Système •••••••••••••••• 1.2.A.2 Console Graphique ••••••••••••••••••••••• 1.2.A.3 Le Contreleur 1744

...

1.2.B Outils de Programmation •••••••••••••••••••••••

1.2.B.1 Outils de Génération •••••••••••••••••••• 1.2.B.2 Outils de Transmission ••••••••••••••••••

1.2.B.3 Outils de Communication

...

1.3 E1éments Log:iques de Base ••••••••••••••••••••••••••• 1.3.A Système de Variables Booléennes •••••••••••••••

Page i i iii iv xi i 1

4

4

4

4

5

5

6 7 7 8 8 9 9

1.3.B Minterme , Vecteur Minterme •••••••••••••••••••• 1.3.C Terme •••••••••••••••••••••••••••••••••••••••••• 1.3.D Forme Canonique d'une Fonction Booléenne ••••••• 1.3.E Matrice des Combinaisons ou Diagramme Logique

Binaire •••••••••••••••••••••••••••••••••••••••• 1.3.E.l Définition •••••••••••••••••••••••••••••••

1.3 .B.2 Diagramme de Marquand •••••••••••••••••••• 1.4 Réalisation du Diagramme de MARQUAND dans le système

Graphique •••••• 0 • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

1.4.A La

Grille ••••••••••••••••••••••••••••••••••••••

1.4.B Position Logique ••••••••••••••••••••••••••••••• 1.4.c Transmettre la Forme Canonique dans la Table _••• 1.4.D Reconnaissance dl une Position Logique •• ' •••••••• 1.4.E Avantages de la Représentation Graphique ' •••••••

CHAPITRE II:RESOLUTION DES SYSTEMES DIEQUATIONS BCOLEENNF...S.

SIMULTANEES ••••••••••••••••••••••••••••••••••••••

2.1 Système,.,dl'Equations Booléennes Simultanées (SEBS) ••••

2.1.A Définition •••••••••••••••••••••••••••••••••••••

2.1.B Réduction d'un SEBS en une Seule Equation ••••••

2.2 Discriminant ••••••••••••••••••••••••••••••••••••••••• 2.2.A Définition •••••••••••••••••••••••••••••••••••••

2.2.B Réduction du SEES, par les Diagra~s Logiques ••

Binaires ••••••••••••••••••••••••••••••••••••••• 9 10 10 l i l i 12 14 14 14

15

15

16

17

17

17

17

19

19

20

2.3 Représentation Matricielle ••••••••••••••••••••••••••

2.3.A Forme Canonique Minterme •••••••••••••••••••••• 2.3.B Equation Vectorielle Minterme •••••••••••••••••

2.4 Singularité •••••••••••••••••••••••••••••••••••••••••

2.5 Nombre des Solutions du SEES •••••••••••••••••••••••• 2.6 Décomposition du Discriminant ••••••••••••••••••••••• 2.6.A Règles de Décomposition ••••••••••••••••••••••• 2.6.B Méthode de Décomposition •••••••••••••••••••••• 2.6.c Codage des Composants du Discriminant ••••••••• 2.6.D Base proposée pour la Décomposition du

Discri-minant ••••••••••••••••••••••••••••••••••••••••

2.7 Solution d'un Composant du Discriminant ••••••••••••• 2.7.A Equation Vectorielle Minterme d'un Composant du

Discriminant ••••••••••••••••••••••••••••••••••

2.7.B Transformation Inverse entre les Variables et le Vecteur Minterme •••••••••••••••••••••••••••••• 2.7.C Recherche de la Solution Yj(x) à partir d'un

Composant du Discriminant •••••••••••••••••••••

CHAPITRE III : OPTIMISATION

...•.

3.1 Introduction ••••••••••••••••••••••••••••••••••••••••

3.2 Minimisation Classique des Fonctions Booléennes ••••• 3.2.1 Caractéristiques de la Méthode Proposée •••••••

21 21 22 22

24

24

24

25 26 26

29

29

29

30 32 32 34 34

"3.2.2 Représentation Cubique ••••••••••• ~ ••••••••••••• 3.2.2.A Représentation Géomètrique d'un Minterme •• 3.2.2.B Représentation Géomètrique d'un Terme ••••

3.2.3 Adjacence •••••••••••••••••••••••••••••••••••••• 3.2.3.A Définition •••••••••••••••••••••••••••••••

3.2.3.B Relations d'adjacence sur le Diagramme de

MARQUAND

...•...•...

Propriété 1 _{•••••••••••••••••••••••••••••••••}

Propriété 2 •••••••••••••••••••••••••••••••••

3.2.4 Les Termes Nécessaires de la Réunion Minimale. 3.2.u.A Poids Associés aux l-points

3.2.4.B Théorème dlUrbano - Mueller

...•..

...

3.2.5 Cellule Maximale

...

3.2.5.A Définition

...

3.2.5.B Expression Algébrique ••••••••••••••••••••

3.2.5.c

Remarque ••••••••••••••••• : •••••••••••••••

3.2.6 Les Termes Suffisants de la Réunion Hinirna1e

...

3.2.6.A Réunion Minimale Partielle •••••••••••••••

3.2.6.B

Sommet Critique •••••••••••••••••••••••••• 3.2.6.c Théorème dlExtension ••••••••••••••••••••• 3.2.7 Cellules Ninimale et Optimale •••••••••••••••••• 3.2.7.A Définition de la Cellule Minimale ••••••••

3.2.7.B Remarque •••••••••••••••••••••••••••••••••

3.2.7.C Définition de la Cellule Optimale ••••••••

3.2.J.D

Recherche de la Cellule Optimale •••••••••

35 35 36 36 36

31

31

38

39

40

40

40

40

hl

hl

42

42

42

42

44

44

45 45 45

3.2.8 Choix du Sommet Critique ••••••••••••••••••••••• 3.2.9 Chaîne Logique •••••••••••••••••••••••••••••••••

3.2.9.A Définition •••••••••••••••••••••••••••••••

3.2.9.B Propriété d'une Chaîne Logique ••••••••••• 3.2.9.C Brlser une Chaîne Logique ••••••••••••••••

3 .2 .10 Remarque •••••••••••••••••••• ' ••••••••••••••••••

3.3 Méthode Générale pour la Synthèse des Systèmes

Combi-natoires •••••••••••••••••••••••••••••••••••••••••••••

3.3.1 Description d'un Système Combinatoire par un

SERS •••••••••••••••••••••••••••••••••••••••••••

3.3.I.A Introduction •••••••••••••••••••••••••••••

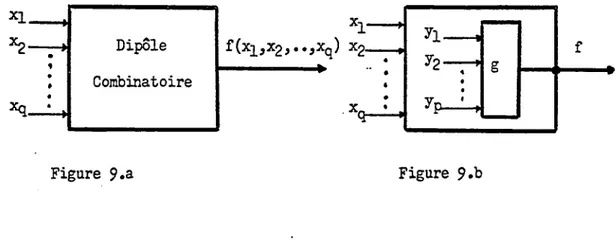
3.3.l.B Cas d'un Dipôle Combinatoire ••••••••••••• 3.3.l.C Cas Général d'un Multipôle Combinatoire ••

3.3.l.D Remarque •• 0 • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •

3.3.2 Réduction du Nombre de Solutions d' tm SEES par une Equation de Contrainte ••••••••••••••••••••• 3.3.2.A Définition d'tme Equation de Contrainte •• 3.3.2.B Réduction du tJombre de Solutions dl un SEBS 3.3.3 Catalogue des Equations de ContraL~tes •••••••••

3.3.3.A

Compatibilité d'une Equation de Contrainte

avec le SEES •••••••••••••••••••••••••••••

3.3.3.B Sensibilité d'un SEBS pour une Equation de Contrainte

...

3.3.3.C Déterminer les Equations de Contraintes •• 3.3.3.D Formation du Catalogue des Equations de

Contraintes ••••••••••••.••••••••.•••.••••

47

48

48

49

49

50

51

51

51

54

54

55

55

55

57

57

57

57

58

...

3.3.tl.A Procédure Graphique

...

3.3.4.B Caractéristiques de la Procédure Graphique. 3.3.4.c Procédure Numérique

...

3.3.4.D Codage des Equations de Contraintes

...

3.3.4.E Choix automatique de l'Equation de contrainte

3.3.4.F Remarque ••••••••••••••••••••••••••••••••••

CHAPITRE V PROGRAMME MINIMA

4.1 Introduction

...

4.2 L'Algorithme de Minimisation

...

4.3 Organisation de MINIMA

...

U.3.A Le Menu ••••••••••••••••.•••••••••••••••••••••••• 4.3.B Schéma Simplifié

...

4.3.C Remarque

...

4.4 Commande ERASE

...

4.5 Commande ENDOFJOB 4.6 Commande I/o-:,.DATA

...

...

...

4.6.1 Acquisition des données

4.6.2 Imprimer les données

...

4.7 Com~de TABLES

...

4.8 Co~ande WEIGHTS

...

u.9

CO~4nde AUTO ••••..••••.•••••.•...••••••...••••••.••••

4.10 Commande POH!TEST

...

L. .11 Commande LO. CHA TIr ••••••••••••••••••••••••••••••••••••

4.12 Com.:-nande ENDOFMIN

...

60 61 62 62 63 65 66 66 67 67 68 70 70 70 71 71 73 73 76

79

79

84

84

u.lu Conclusion

...

CHAPITRE V PROGRAMME SBE

5.1 Introduction

...

5.2 Algorithme de la Synthèse

...

.

"

... .

5.3 Organisation de SBE

...

5.3.A Le Menu •••••••••••••••••.•••••••••••••.•••••••• 5.3.B Schéma Simplifié

...

5.4 Commande ERASE

...

5.5 Commande ENDOFJOB 5.6 Commande I/~~DATA

· ... .

· ... .

5.6.1 Acquisition des Données

...

...

5.6.2 Organisation de I/~~DATA 5.6.3 Sous-programme DISCRI

...

5 •

.7

Commande TABLES

...

5.8 Cor:1.:i1ande DISCRIHINANT •••••••••••••••••••••••••••••••• 5.9 Com.rnande POINTE;ST

·

... .

5.9.1 Décomposition graphique du discrL~inant

5.9.2 Codage des impliquants du composant

n

S du discri-minant "

....

"

...

"

...

"

... .

5.10 Comma13.de SOLlYrIOE

...

5.11 Commande COHSTRAUITS

...

"

... ..

5.12 Commande AUTO

.

"

....

"

...

"

... ..

5.13 Comma~de CATALOG

...

"

... ..

'.lu Résultats Expérimentaux

...

5.15 Conclusions

...

"

... ..

87 92 92 94 94 94 96 96 96 96 98 100 102 103

106

106

106

107 107 109 112 11u 121

CHAPITrrG VI: LIiUTATIONS ET RECOI'lJ'1fl.lIDATIONS FOUR lnΠRECHERCHE FUTURE

6.1 Introduction .••••.••••••••••••••••••••••••••••.••••••• 128

6.2 Limitations actuelles •••••••••••••• ~... 128 6.3 Problème du Codage des Fonctions Booléennes ••••••••••• 129 6.3.A Nécessité d'identifier les fonctions booléennes • 129 6.3.B Solution Existante •••••••••• " ••

!...

129 6.3.C Possibilité d'établir le Catalogue à l'avance ••• 130 6.3.D Chercher une autre Solution ••••••••••••••••••••• 131 6.)-1 Codage Proposé pour les portes NI et ON ... 131 6.h.A Caractéristiques du catalogue dans le cas général 131 6.u.B Contourner le problème pour les portes NI et ON • 131 6.u.c Influence du nombre des entrées du module ••••••• 133 6.u.D" Nombre total des équations du catalogue... 133 6.5 ETAPE l:Vers un catalogue complet des équations de

con-traintes •••••••••••••••.••••••••••••.•.••.•••• 135

6.5.A Construction du catalogue des fonctions

directe-ment réalisables ••••••••••••••••••••• ,... 135

6.5.B Complément sur le codage des fonctions booléennes 135 6.5.C Assembler les programmes SBE et MINIr~ .••••••••• 137 6.5.D Cas particulier des portes NI et ON

...

138 6.5.E Codage des équations de contraintes compatibles

avec le SEBS .•.••...••..••••...• ... . . . .• • 139

6.6 ETAPE 2 :Permettre une Sélection Optimale de l'Equation

de Contrainte

...

18

TABLE DES FIGURES

page Figure 1 : Diagrammes logiques binaires pour n =h ••••••••••••• 11 Figure 2 : Représentat ion du diagramme de l'f.ARQUA!.JD sur l'écran

cathodique •••••••••••••••••.••••••••••••••.•••••••• 13

Figure 3 Décomposition du discriminant d'un SEBS •••••••••••• 28 Figure

h

Représentation cubique d'une fonction booléenne ••••

35

Figure

5

Représentation graphique d'une fonction booléenne ••

37

Figure 6 Voisins d'un point du diagrame de MARQUAND ••••••• 39 Figure 7 : Diagramme de MARQUAHD et table des poids ••••••••••• 39 Figure 8 : Exemple d'une chalne logique ••••••••••••••••••••••• 49 Figure 9 Dipôle Combinatoire •••••••••••••••••••••••••••••••• 51 Figure 10: Organigramme simplifié de HINIHA •••••••••••••••••••

69

Figure 11: Format de l'acquisition des données pour mNIl'f.A •••• 71 Figure 12: Position de deux grilles sur l'écran •••••••••••••••

75

Figure 13: Organigramme simplifié de SBE ••••••••••••••••••••••

95

Figure 14: Format de l'acquisition des données pour SBE ••••••• 97 Figure 15: Position des grilles sur l'écran cathodique •••••••• 105

INTRODUCTION

Les méthodes classiques pour la synthèse des systèmes combina-toires sont basées sur la logique combinatoire utilisant des éléments de commutation tel les circuits à relais ou transistors avec lesquels on peut produire un répertoire d' opérations logiques : ET , OU , NON, qui constituent un groupe comPlet d'opérations •

L'objectif de ces méthodes est de réaliser la synthèse avec un nombre minimum d'éléments de commutation, vu la correspondance entre chaque porte ET , OU , NON, et chaque opération logique ET , OU ,NON.

Le problème de minimisation a été tout d'abord formolé et résolu par QUINE [ 19,20 ] ' en termes de formes minimales normales conduisant à des circuits à deux étages •

Par la suite , Plusieurs méthodes de minimisation des circuits logiques, ET , OU , NON, à deux étages ont été élaborées [ 17,21, 22,25,26,15 ] •

Le problème classique de la minimisation des formes booléennes normales . a été généralisé dans Plusieurs directions ; par exemple , la minimisation des fonctions simultanées [ 8,9,6] ,expression minimale absolue [ 8 ] ' minimisation pour la synthèse des réseaux à plusieurs étages [ 6,8 ] •

Des progrès très importants , effectués depuis Plusieurs années, dans les techniques d'intégration des éléments discrets, permettent de réaliser des circuits comPlexes connus sous le nom de

circuits' intégrés • Des recherches ont été orientées , vers une augmen-tation du degré d'intégration et ont abouti aux techniques nouvelles de L.S.I. (Large Scale Integration ) qui permettent de réaliser avec un module plusieurs fonctions logiques complexes •

Ce développement de la technologie a conduit à l'abandon progres-sif des méthodes classiques ,utilisant des composants discrets , en faveur d'autres méthodes tenant compte de cet impo~~t facteur.

Il n'existe pas une méthode qui résoud entièrement le problème de la synthèse des réseaux logiques • On peut approcher le problème par des méthodes heuristiques [ 2 ] ' combinées avec des techniques de programmation linéaire pour l'optimisation du coût du système •

Une méthode algorithmique a été initialement proposée par ASHENHURST [ l ] ' puis développée par CURTIS [

5 ]

et récemment par MARIN [ I l ] • Cette méthode est basée sur la théorie de la décomposi-tion.

Quand le nombre des solutions possibles est élevé , on ajoute des contraintes pour le réduire; on procéde ainsi, d'une manière itérative , jusqu'à ce que le nombre des solutions converge vers une valeur raisonnable •

Cette méthode itérative a l'avantage d'être indépendante du développement de la technologie , mais la sélection des équations de contraintes est parfois difficile et dépend de l'expérience du logicien ou de son intuition • On peut surmonter ces difficultés , en utilisant un système graphique intéractif afin de permettre une sélection rapide et adéquate des équations de contraintes •

Dans ce sens , uneméthode intéractive est proposée , pour la synthèse des circuits combinatoires utilisant le système graphique

cne

1700 - 274 •

L'utilisateur peut ajouter, au système combinatoire à réaliser, n'importe quelle équation ou système d'équations de contraintes.

Le choix de certaines contraintes particulières (quand elles sont compatibles avec le système combinatoire à réaliser ) est auto-matisé au cours de la décomposition •

L'utilisateur a la possibilité d'accepter ces contraintes ou de les refuser • La décision que l'homme devrait prendre dépend de la technologie utilisée et du critère d'optimisation adopté.

CHAPITRE l

1 1 1

CONCEPTS GENERAUX ET DEFINITIONS

1.1 Introduction

Il est nécessaire de définir uneterminologie cohérente pour que d'une part on sache de quoi on parle, et d'autre part on évite les con-fusions dûes à la traduction de l'américain •

L'utilisation du système graphique offre des facilités nouvelles, par exemple tracer des diagrammes logiques binaires sur l'écran à l'aide de droites , de points et de symboles alphanumériques •

Ces possibilités nouvelles doivent être exploitées le plus utile-ment possible et créent ainsi un état d'esprit nouveau pour la mise en oeuvre des méthodes de synthèse dans l'ordinateur.

Tout d'abord, on fournira unedescription du système ( DIGIGRAPHIC 1700 - 274 ) afin d'expliquer le pourquoi de certaines décisions;

ensuite ,on profitera de cette description pour définir les éléments de base du point de' vue logique air.si que les outils graphiques utilisés pour les réaliser •

1.2 Description du Système 1700

1.2.A.l Configuration du Système-CONSOLE 274 ORDINATEUR CONTROLEUR _X ~ Y 1700 1744 poineur opti e

-0

1.2.A.2 Console Graphique

La console graphique ou terminal graphique posséde un tube à rayons cathodiques. L'écran est la face de ce tube et présente une surface plane de 20 pouces de diamètre • On peut adresser tout point P(X,y) de cette surface grâce à la déviation du faisceau d'électrons par un convertisseur digital-analogique .Les coordonnées (X,Y) sont exprimées en unité digi-graphique ( DGU , DigiGraphic Unit) et sont comprises entre -2048 DGU et +2048 DGU •

1.2.A.3

Le Contrôleur

17uu

Le contrôleur sert d'interface entre le terminal graphique (274 )

et

11

ordinateur (

1700 ) •

Ses fonctions principales sont :

- traitement des opérations d'entrée-sortie avec l'ordinateur

1700 •

- transfert à l'ordinateur des signaux d'interruption. - entretien de l'image.(refreshing).

Le

1744

entretient l'image, c'est à dire la régénère toutes les

25

millisecondes • les ordres de génération sont placés dans une mémoire d'entretien de

4

K • Les instructions dtaf-fichage sont des multiplets de

12

bits et constituent ce qU'on appelle la liste d'affichage.

Dans le bloc - diagranur.e du contrôleur

1744""*

on peut voir les éléments suivants :

- l'horloge a une période de

1.67

micro-secondes.

- le registre Z sert de transfert des données entre l'ordina-teur et le contrôleur •

- la mémoire d'entretien qui pourrait servir de mémoire auxi-liaire •

- le registre S contient l'adresse du mot de la mémoire d'ent-retien • Pendant le cycle d'affichage i l est autorratiquement augmenté de l toutes les

1.67

micro-secondes.

-H Le bloc-diagramme du contrôleur 1744 est une courtoisie de la

cnc

Voir ANNEXE E

- Les circuits' de traitement des multiplets qui sont composés de décodeurs X et Y , des additionneurs d'incréments ~ X et â Y et les registres pour les coordonnées X et Y •

1.2.B Outils de Programmation 1.2.B.1 Outils de génération

Les outils de gén~ration servent à constituer la liste d'affichage. Dans le système .( Digigraphic 1700 ) il existe des sous-prograrnmes qui

permettent de constituer des points , des vecteurs , des segments , des arcs et des cercles ; on les appelle ( Increment programs ) car les mul-tiplets graphiques ont le format suivant :

11 10 8 7

4 3

1

~

1

ECHEILE

+

âY

+

â X et  Y sont respectivement les incréments en X et Y •

- ECHELLE correspond au facteur d,échelle •

o

- Le bit Il spécifie si le faisceau d'électrons doit être allumé ou éteint •

De même on peut générer les caractères alphanumériques qui sont définis dans la zone macro •

Si un object pourrait être généré Plusieurs fois dans l'image, on peut alors le définir une seule fois dans la zone macro en lui asso-ciant un code macro • On peut générer tout objet ainsi défini, en faisant appel à son code macro dans la liste d'affichage •

1.2.B.2 Outils de Transmission

Ce sont des facilités pour

- transmettre ~a liste d'affichage d'un objet au contrôleur

l74~ , par exemPle le sousprogramme DEDIT.

- modifier la liste d'affichage de la mémoire d'entretien , par exemple les sous-programmes MODIF ,. RETRV et DELETE • - arrêter la régénération ou la relancer à uneadresse de la

mémoire d'entretien • 1.2.B.3 Outils d~ communication

Il existe une ligne interrupt* qui permet la conversation entre l'ordinateur et le terminal graphique •

Le terminal peut envoyer soit une information graphique sous forme de coordonnées

(X,Y)

,soit une information logiqu~ en montrant un objet affiché • Cette dernière méthode est possible grâce à un pointeur opti-que ( Light Pen ) ; c'est une cellule photoélectriopti-que capable d'envoyer un signal quand elle détecte de la lumière •

Il existe un sou&programme IDINT qui permet d'identifier l'objet choisi et on peut s'en servir pour toutes sortes d'applications ; par exemple, l'objet peut être un texte alphanumérique qui permet le bran-chement à un point du prograrnIl":e et l'exécution d'une commande spéciale. La

liste de ces commandes est appelée le menu •

1.3 Eléments Logigues de Base

1.3.A Système de Variables Booléennes

Considérons un système X ayant n variables booléennes xi ~

i=1,2,3, ••••• ,n ; l'identificateur

n

X

l~}iX2i-l

( 1.1 )

est une valeur entière comprise entre 0 et 2 -1 • t==l n

Il existe une relation de correspondance l à l entre 1l

identifica-teur x et chaque point (XJ.,x2," .. ,xn) de l'espace logique

~

X!

lequel contient 2n points •

1.3.B Hinterme • Vecteur lwlinterme

Le mintenne

ma

== llla (x) est une fonction booléenne des variables xi qui est égale

à

1 quand x=a et zéro pour tout x=t=a j

n

a== LaiX2i-l i==l

( 1.2 )

Le vecteur minterme m(x) contient les 2n mintermes comme le montre la relation ( 1.3 ) •

m(x)

(f )

~n-l

1.3.C Terme

Le terme tn th (x) est une fonction booléenne définie par l'inter-section th = XlXx2 ••••••••• Xxn

" "

"

( 1.4 )

,

"

,

-ou Xj correspond a l,xj -ou x_j inclusivement •.

"

I l existe une relation biunivoque entre Xj et les digits ternaires hj E { 0,1,2 } comme suit :

"

xj=l , Xj , Xj hj=O , 1 , 2

On peut définir le code h comme suit : n

h=

L

( 1., )

i=l

n

h est donc compris entre

°

et 3 -1 •

Remarque: un minterme est un terme particulier , i l peut être codé , soit en digits binaires aj , soit en digits ternaires hj ; la relation entre ces digits est :

h.=2-a.

J J ( 1.6 )

1.3.D Forme Canonique d'une Fonction Booléenne

La forme canonique d'une fonction booléenne F est obtenue par la SO!l'-Ine booléenne des mintermes mj impliquanfs F .

( 1..7a )

mJ' implique F

1.3.E Matrice des Co~binaisons ou Diagramr.~ Logieue Binaire 1.3.E.l Définition

C'est une représentation graphique pour contenir l'information' logique • La matrice d'cne fonction booléenne de n variables contient 2n cases organisées en 2P lignes et 2q colonnes tel que :

( 1.8 ) En général on choisit p=q , si n est pair; et q=p+l , si n est impair.

Il existe une correspondance 1 à l entre chaque case du diagramme logique binaire et un point de l'espace logique •

Le nombre d1affectations possibles est égal au produit fac~oriel p=" ( 2n )

1

Parmi ces ( 2n), diagrammes , deux sont généralement utilisés ( 1.9 ) - diagramme de MARQUAND (1881) - diagr~~ de KARNAUG (1953)

x2x

l _ X2Xl~ x

_xhx3

00 01 11 10

~

00 0 1 3

2

h

X

3

00 01 10 11

~

1

00 0 l 2

₃

Cl

_h

₅ 6 7 01

h

5 7 6 10 8 9 10 11 11 12 13 15

lh

11 12 13

Ih

15 10 8 ₉ 11 10

DiagraIllIl"~ de V.ARQUAND D iagrarnIT'.e de KARNA UG Figure l - diagrammes pour n=4

1.3.E.2 Diagraz1".r.:e de MARQUAND

Bien que le diagramme de KARNAUG est Plus utilisé dans les ouvra-ges de logique combinatoire , celui de MARQUAND est préférable pour Plusieurs raisons :

• La description du diagramme de MARQUAND dans un programme est très simple, elle correspond à l'ordre naturel des entiers: 0,1,2, ••• •••• ,2n -1 • Il suffit d'une seule liste de 2n mots, contenant chacun l'information logique 0 ou 1 •

- L'ordre naturel des entiers est valable pour les lignes ainsi que pour les colonnes •

Voir figure

Z

page 13 •

Soit , un point d du diagramme de MARQUAND

n d

-

2:

Xkx2k- l d'après ( 1.1 ) k==l q n d -

2:

Xk X2k-l +

L:

Xk X2k-l k==l k==q+l q p d

_-

2:

Xk X2k- l + 2q

x2:

_Xq+kX2 k-l k==l k==l d == j i ( 1.10 )

L'élément d est équivalent à _{dij , i et j vérifiant la relation ( 1.10 ) •}

La _{notation matricielle dij est celle qU'on utilise habituellement}

dans les relations mathématiques , elle permet de bénéficier des calculs matriciels _•

- Les points adjacents à un point x du diagra~2 de r~RQUAND se trouvent sur la même ligne , ou sur la même colonne que le point x et à

une distance arithmétique de 2j , ( j

=0~1,2,....

) .

Cette règle arithmétique est eJ..-trêmement simple, elle est parfois plus' pratique que la règle de symétrie du diagramme de KARNAUG.

D'ailleurs, le diagr.amme de KARNAUG n'est plus lisible quand le nombre de variables booléennes dépasse

6

ou

1 •

y en Yo YL-DGU - - - 0 1 2 3 _ _ i Diagramme de MARQUAND 0 1 2 3 j _-r-...,~--r---r..

..

.

f • •

· .

·

.

·

.

_{élément d ou dij}

···CO····h1

8 ,.

--+---"----'--...

1 •••• ..

W

DGU Xo 1

x·

"

X en DGU

X et Y sont les coordonnées en DGU sur l'écran cathodique.

i et j sont les coordor~ées matricielles • n étant le nombre de variables , p +q =n •

l.u Réalisation du Diagrariune de MARQUAND dans le Système Graphique Voir figure 2 .page 13 •

1.h.A La Grille

La gr~e est faite de lignes horizontales et verticales • Les longueurs de ces lignes dépendent, du nombre n de variables booléen-.· nes , ainsi que du côté de la case, comme le montre la relation ( 1.11 )

- Longueur de la ligne horizontale = 2q X L\ ( l.lla ) - Longueur de la .ligne verticale = 2P X L\ ( l.llb )

J). étatlt le côté d'une case exprimé en DGU ( DigiGraphic Unit ). Ces lignes sont générées plusieurs fois dans la grille , elles doivent donc être définies d'une manière paramétrique dans la zone macro.

Ceci est ainsi réalisé par le sous-prograrnrne LINES •

Pour constituer l'objet qU'est la grille, il fau~ faire appel au macro correspondant à la ligne horizontale 2P-rl fois, de même il faut 2q -rI lignes verticales •

Ce travail de génération est fait par le sousprogra.'Tll11e MAroPY

( MAP DISPLAY ). Ainsi , grâce à ces deux outils , on peut tracer une grille d'une manière modulaire et très économique en mots de la mémoire d'entretien. Ainsi ,on peut tracer les grilles à n'importe quelle place de l'écran et pour toute valeur de la variable n •

1.h.B Position Logique

Chaque centre d'~e case de la grille est une position logique. Les coordonnées ( X_{j 'Yi ) sur l'écran d'un point dij du diagramme de}

les relations suivantes :

-X_j

=.x

_o

+

j X 8

Yi

=

Yo - i X b.

( 1.12a ) ( 1.12b )

On peut garder en mémoire les valeurs Xj et Yi , dans deux listes qui nécessitent respectivement 2q et 2P mots de mémoire • Ce travail est fait grâce au sousprograrnme TABXY •

1.h.C Transmettre la Forme Canonisue dans la Table

La forme canonique renseigne sur les identificateurs pour lesquels la fonction booléenne vaut l •

t

partir des identificateurs, on peut calculer les coordonnées matricielles par la relation ( 1.10 ) , et

obtenir les coordonnées sur l'écran de ces points par la relation ( 1.12 ); on peut donc dessiner , dans les positions logiques correspondantes ,_

n'importe quel s~bo1e pour contenir l'information logique. Le sou&programme TABDPY génére les s~~boles suivants :

- +

si la fonction booléenne vaut l pour le point considéré •

*

si la fonction booléenne est indifférente •

un symbole numérique en coàe hexadécimal pour informer sur

..

::-:(-le poids des points critiques •

1.h.8 Reconnaissance d'une Position Logique

Pour reconnattre une position logique , i l suffit de comparer ses coordonnées avec les deux listesX_j et Yi , et en déduire ainsi les coor-données ~4tricielles i et j , à partir desquelles , on peut calculer

l'dentificateur correspondant par la relation ( 1.10 ) • Ceci est possible par l'intermédiaire du pointeur optique et du sousprogramme !DENT ( identificateur ) •

1.u.E Avantages de la Représentation Graphique

La représentation graphique de la fonction booléenne , ainsi réalisée, offre les avantages suivants:

- On peut faire manuellement le choix des points critiques* et des commandes du menu • De cette manière, on utilise les capacités : intelligence et reconnaissance des formes de l'homme , en laissant à la machine le soin d'exécuter les calculs •

- La partie prograllll'nation se trouve allégée et simplifiée •

- Il Y a un avantage du point de vue pédagogique , car les étudiants peuvent apprendre plusieurs aspects du problème de la synthèse des circuits combinatoires à travers des exemples bien choisis • Ils ont à choisir les commandes du menu qui correspondent à chaque application particulière • Quand la décision de l'homne n'est pas nécessaire, uneoption automatique

pé~et de synchroniser les opérations à la place de l'homme pour éviter les retards dûs aux choix manuels •

CHAPITRE II

RÉSOLUTION DES SYSTÈMES D'ÉQUATIONS BOOLÉENNES

SIMULTP~ÉES

2.1 Système d'Équations Booléennes Simultanées ( SEBS ) 2.1.A Définition

On peut représenter un SEBS par la formule suivante

où i==1,2,3, •••••• ,k

( 2.1 )

~Xl'X2'

••••• ,Xq! l'ensemble des variables connues ou variables

l

,

indépendantes •

jn, ...

,ypfl'ensemble des variables inconnues ou variables dépendantes qU'on représente par :

( 2.2 ) Notant qu'un système de la forme ( 2.2 ) satisfait le système

( 2.1 ) , si l'ensemble des fonctions.( 2.2 ) implique le système ( 2.1 ); dans ce cas le système ( 2.2 ) est une solution de ( 2.1 ) •

2.1.B Réduction dl~~ SEBS en une Seule Eauation

_.

Le système ( 2.1 ) est équivalent ( équivalent veut dire:il a les mêmes solutions) à l'unique équation:

k

f

=

TI

(Eix

gi

+

fiX gi ) = l i=l

Démonstration : Soit e_i la fonction équivalence qui est vraie quand fi

=

gi , à partir de la table de vérité de ei on peut écrire fi gi e· _l.

0 0 1

( 2.4 )

0 1 0

1 0 0

1 1 1

Comme la relation (

2.4 )

doit être vérifiée pour toutes les valeurs de i , i l faut et i l suffit , que le produit de toutes les fonctions ei soit égal à 1 • Clest à dire :

k

~IT

i=l k

-e--,

IT

fiXgi+fiXgi i = l

<

_>

f 1 1

On peut aussi utiliser la négation de f

k

f -

L

i=l

ExemPle 2.1 Considérons le SEES sui~~t :

fl= xl

+

x2 f₂

=

Y2

+

xlY1 a) e1=fIX~

+

flX~ c) f= el x e2

( 2.5 )

( 2.6) ( 2.7 ) (2.8 )

=XJ. x2Yl+XJ. + x2Y.J..

2.2 Discriminant 2.2.A Définition

On appelle discriminant D dl un SEES , le diagramme logique binaire, contenant llinformation logique de la fonction f définie par (

2.3 )

.Le diagramme logique binaire est un diagramme de l1ARQUAND particulier ,

. , 2q l 2P 1

organ~se en co onnes et ignes , ...

ou q nombre de variables connues et p no~bre de variables inconnues • Exemple 2.2 SEES f2

=

Y2+xl

Y

l =~Y2

=

g2 f

=

~YlY2+x2YlY2+ ~x2Y2+~~Yi

DISCRIMINANT D x2 Xl

-

-1 YI

1

1 1 1 1 1 y ₂

1

1

2.2.B Réduction du SEES

par

les Diagrammes Logiaues BinaireE

Toutes les transformations permettant de réduire le SEES en une seule équation 3 peuvent être exécutées facilement sur les diagrammes logiques binaires. L'équation de récurrence 3 pour obtenir le dis cri-minant D du SEES défini par ( 2.1 ) est :

DO=l

Di=Di-1 X ( _{figi +figi )}

D =Dk

( 2.9a ) ( 2.9b ) ( 2.9c )

Remarque: La multiplication booléenne et la somme booléenne agissent uniquement sur des éléments correspondants à une même ligne et une même colonne •

Exemple 2.3

fI =xI+

x

₂ = xl +Y1 =gl f₂=Y2+

Y

Ixl = ~Y2=g2

( Comparer les résultats avec ceux de 11exemple 2.2 )

~ 9. 1 1 1 1 1 1 1 1 1 1 1 1 1 ₁ 1 1 1 1 1 1 1 1 1 1 1 1 1 1

!

1 1 1 1 1 1 1 1 1 1 1 ₁ Do 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ₁ 1 1 1 1 1 1 1 1 1

1

Soit le vecteur (z)

=

( 2.10 )

t

p

Considérons un des 2P+q mintermes

me(z)=mc (

x , y) ;

me

(z)

est l'intersection des n variables: mc(z)=xlx2 .. Xj .. Xqhy2 ••••

Yk •••

Yp (2~1l) Xj

=

Xj ou Xj

aj = l ou 0

.

-, Yk=Yk ou Yk , bk=l ou 0

D'après la relation ( 1.1 ) on peut écrire

c = al +a2 X 21 _{+ •••• aq X2q-l+bl X2}q+b2 X2Q+l ••••

+b

_{p X2}n

c

₊

c a

₊

Le minterme mc(z) est donc le produit de ffia(x) et ~(y) ;

mc(z)

=

Ilk(x)X~(Y) ( 2.12a )

( 2.12b )

Soit dij un élément du discriminant ; l'élément booléen d_ij peut valoir l ou 0 suivant que f(x,y) est vrai ou faux ~espectivement •

Le minterme correspond~~t à _{dij est l'intersection mi(y)xmj(x)}

vu que d=j +2q xi •

La forme canonique de la fonction f , peut être obtenue du dis cri-mina.ît D , par l'équation suiva.:1te: 2P-l

f(x,y)

=L

i=O

2.3.B Equation Vectorielle Minterme

En

combinant les relations ( 2.3 ) et ( 2.13 ) on obtient la représentation matricielle suivante

( 2.14 )

2.h Singularité

La matrice[nJpeut être divisée en 2q colonnes , c'est à dire

[n

J=

[dO

1

dl

1···1

~q

-1 ] ( 2.15 ) Soit ~, l'ensemble défini

à

partir de n comme suit:

( 2.16 )

La condition nécessaire et suffisante pour que ( 2.14 ) ait une solution est que :

L:

m-(x) =0

jE~ J

( 2.17 ) Si ~=J= ~ (ensemble vide) ,le SEBS est dit singulier; dans ce cas les variables connues sont reliées entre elles par la relation

( 2.17 ) • Toutes les colonnes définissant ~sont considérées co~~e indifférentes. On peut ajouter , à chaque fonction Yj(xl,~, ••• ,Xq) , nI importe quo: minterme mk(x)

1

k E~, pour simplifier Yj (x) ;

Pour le développement des mintermes nécessaires

à

Yj(x) , i l suf-fit de travailler à partir du discriminant réduit Dr défini comme suit :

Dr=l

dk

1

k

$

r

f

(

2.18 )

Exemple

2.4

SEBS Yl.

+

Y2

=

x1Y2

x.3Y1=~

+

Y2 Discriminant D

°

1 2 3 4 1 1

5

6

1 1 Discriminant réduit Dr

0 1 2 3 4 5 6

r=

lk

1

d

k

=

°

f

r=lo,1,u,7f

7

2.5

Nombre de Solutions du SEES

Soit U_{j ,} le nombre d'éléments non nuls de la colonne d_j de la matrice[D

]-Le nombre total S des solutions du SEES , est égal au produit des entiers U_{j ,} 'dont l'indice j n'appartient pas à ~ •

S

=

il

Uj ; j = 0,1,2, ••• ,2Q -1

j~r ( 2.19 )

Notant Qll~ j

$

r~ U_j ~ 1 ; le nombre S est donc supérieur ou égal

à

1 compte tenu de la relation ( 2.11 ) •

Exemple

2.5

Discriminant D

o

1 2 3 1 1 1 1 1 ₁ 1 S

=

UO)(. Ul x U2 x U3 S 1 xlX2 X _{3 ==6} 2.6 Décomposition du DiscrimL~ant 2.6.~ Règles de Décomposition

Les solutions du SEBS de la forme Yj=Yj (x) , j =1,2, •••• ,p , peuvent être obtenues soit d'~~e manière paramétrique par la méthode de BROM'J

[3 ] ;

soit, en décomposant le discriminant par la méthode de

SVOBODA

[24] .

Cette dernière méthode manipule plus les diagrammes logiques binaires • Elle est plus adaptée pour le présent travail •

Le discriminant D , peut être décomposé en S composants booléens D

o

, Dl , ••••••• , , •••••• , . DS D5-1 ; S'tant d'f" e e ~1 par ( 2 l •

9

)

•

Les trois règles de décomposition sont :

l _ D -_ DO + Dl •••••••• +D s ••••• +D S -1 ( somme booleenne ' ) (2.20) 2 - DS

=#: Dt pour tout s:#:t

3 -

U~=l

pour s

=

0,1,2, •••• ,5-1 ; j$

r ,

j = 0,1,2, •••• ,2q -1

2.6.3 Méthode de Décomposition

Pour éviter d'attribuer aux S composants DS les codes s =.0,1, •• •••• S -1 , d'une manière arbitraire on propose l'algorithme suivant pour les déterminer :

- La solution DO est celle qui contient le premier élément non nul rencontré dans chaque colonne d_j du discriminant D , j

f

r .

Pour développer DO,nl, •••• ,DS -1 , on prend l'élément non nul suivant de la colonne d_j , après avoir fait toutes les combL~aisons pos-sibles pour les colonnes dk tel que :

• • • • • • •

k = O , l , _{• •}

.

,

j-l j

~

r

et k$

r

2.6.c

Codage des Composants du Discriminant

DS _{peut être déterminé à partir du discriminant D , par une} séquence

as.

_{(ao, a} l' •••••• a

J ••• ~q -1 ) , où aj , correspond au rang de l'élément non nul , parmi les U_j éléments non nuls de la colonne d_{j ;} donc

( 2.21 ) Exemple

2.6

a3

=

( 1 , 1 , 2 , 2 ) Voir figure 3 page

28

Remaraue : i l serait souhaitable de trouver une base

/J;( /JO,

/J1J ••••

:fkq -1) , permettant de déterminer la séquence

aS

à partir de s .On peut en déduire directement de l'algorithme de décomposition du paragraphe

2.6.B

les deux relations suivantes :

o

a

==(1,1,1, • • • c • • • • • , l )

• • • • • • • •

2.6~D Base Proposée pour la décomposition du discriminant

Le nombre de combinaisons, que l'on peut faire avec les colonnes

fJ .

+

l =

II

_{Uk ,k}

$

r

et k < j

J k

( 2.22a )

Comme, Uk ~ l pour k

$ r

_{on peut en déduire: P k}

+

_l ~ Pk • D'après la méthode de décomposition du paragraphe 2.6.B ,(Jk augmente de l , après toutes les Pk combinaisons possibles pour les colonnes da,dl, ••••••• ,dk-l ; la relation liant (Jb Pk et s est la suivante s

=

L

(ak - l ) x Pk

k$r

kE

1

a,1,2, ••• ,2q -lI ( 2.23a ) ( 2.23b )

La relation 2.2) permet de déterminer la séquence (aa' al' a2' •••

••• • , Cl 2q -1 ) sans ambiguité • La méthode de récurrence pour trouver

cette séquence est la suivante :

P

2q

=

S , S2q -1= s ( 2.2ha ) Pk +1 pour k E

r

Pk

=

P k

+

l -:- Uk pour k

ef:

r

( 2.2hb ) ( 2.2hc ) ( 2.2hd ) Exemple 2.7 . )

Déterminer la séquence ( {la, al' a2, a) ) pour le composant D du discriminant D • Voir figure )

P

h = S

=

6 , S) = s = )

,p

3

=

Il

h -: TJ) =-6 -:-) = 2 ,

S)

=

3

=

(a 3 -1 )

Il

3 + S2

= (

2 - 1 ) 2

+

1 ,

P

2

=

2 -:- 2 = 1 , S2

=

l

= (

2 - l ) 1 + a , SI = a

3

o

1 2 3 1

1

1

₁

1

1

1

S = UO>CUI )( U2 >CU) S

=

l)rl )(2)(3 1 1 1 ₁

,

1 1 1

o

~ =( l , 1 , l , 1) 1

cr=(

l , l , 2, 1 ) 1 1 1 1 1 1 1 ₁ 2 CI. =( l , l , l , 2)

cr

3

= (

l , 1·, 2, 2 ) 1 1 1 1

1

1 1 1 1

U .

)

a

=t

l , l , l ,

3

Ct

5

=( l , l , 2, 3 )

2.7 Solution dl~~ Composant du Discriminant

2.7.A Equation Vectorielle Minterme dlun Composant du Discriminant

À partir dl !ID composant DS du discriminant D , s

=

0,1, ••• ,S-1 ,

i l existe une solution unique satisfaisant ( 2.14 ) • Les vecteurs mintermes m(x) el m(y) sont liés par la relation suivante

( 2.25 )

2.7.B Transformation Inverse entre les Variables et le Vecteur Minterme on a défini le vecteur minterme m(y) pour Yi , i=l,2, ••• ,p , comme suit

m(Y)=C~~~l

)

m_{2P -1 (y)}

La transformation inverse permettant dl obtenir le vecteur (y)

à partir du vecteur minterme m(y) est exprimée par le produit matriciel

( 2.26 )

La matrice Kp contient px 2P éléments, contenant 0 ou l , définis par la rel~tion de récurrence suivante :

,

( 2.27a )

K. + l

= [

Kj

1

Kj ]

J 0000 ••••• 0

Illll. ...

1

( 2.27b )

2.7.C Recherche de la Solution Yj(x) à partir d'un Comoosant du Discriminant Notant que chaque ligne j de la matrice Kp , j

=

1,2, •••• ,p , est une succession de 2j- l zéros ,

~uivis

de 2j- l 1 et ainsi de suite •

Pour former la solution Yj:Yj(x) satisfaisant l'équation vectorielle ( 2.25 ) , i l suffit de cons.idérer la moitié des éléments non nuls de cette ligne j •

Les mintermes mb(Y) correspondants ~ ces éléments non nuls sont déterminés par la relation suivante

Yi = Yi ou Yi b_i

=

1 ou 0

,

i = 1,2, •••••• ,p b - 2j-l

+

L

bi2i- l i~j ( 2.28 ) S'il existe un élément d~~ non nul , tel que, b vérifie la rela-tion ( 2.28 ) , le minterme mk(x) appartient nécessairement à la forme canonique de Yj ==Yj(X) ; on obtient ainsi, Yj =Yj(x) d'une manière unique car chaque colonne du composant DS contient un seul élément non nul •

Exemple 2.8

Trouver la solution Yj =Yj (x) du SEBS dont le discriminant est le

suivant : Discriminant D

1 1

Le SEaS est singulier

;r=~O,1,ù,7l;

les colonnes correspondantes sont indifférentes.

1

~

Discriminant réduit Dr

o

1 2 3

4 5

6 7

o

1 2 3 S

=

S

=

1 q=3,p=2,n=p+q=5 1) YI

=

YI (x) : 1 ~ 1 b

=

21- 1 + 0 '<22-1 = 1 b

=

21- 1

+

1 )(22-1

=

3 "1 xl Yi

=

Yi ou Yi b_i

=

1 ou 0

- b =1 : i l _{existe 2 éléments non nuls qui sont diJ et d15 ; les}

mintermes m3(x) et mS(x) sont donc nécessaires. - b = 3 : i l nI existe aucun élément non nul •

En combinant aux mintermes nécessaires les deux mintermes

indiffé-2) Y2 = Y2 (x) :

b = 2 et b = 3

Les lignes 2 et 3 sont toutes les deux nulles; donc Y2(x)= 0 • La solution du SEES est donc:

CHAPITRE III

OPTIMISATION

3.1 Introduction

Les systèmes combinatoires sont utilisés dans plusieurs domaines et deviennent de plus en plus complexes • Il est très avantageux , de minimiser le coût de la réalisation de ces systèmes du point de vue économique.

La fonction coût dépend de certains facteurs dont les principaux sont

l - Nombre dréléments de co~~utation : le coût du'cicuit est fonc-tion croissante du nombre dréléments utilisés ; avant, il lui était prati-quement proportionnel • Par exemple , quand les diodes nécessaires pour

.

les portes ET , OU étaient les plus coûteuses , il fallait minimiser le nombre de celles-ci , en négligeant les prix des résistances et des autres composants , ainsi que le coût du montage du circuit. Après lrapparition du transistor , il fallait plutôt axer la minimisation sur cet élément qui était relativement le plus cher de tous • Le développement de la tech- _ nologie , a permis une baisse significative du prix de revient des compo-sants électroniques ; par conséquent, la minimisation du nombre dréléments prend de moins en moins d r importance •

2 - Sytèmes rapides : on cherche à réduire le temps de délai td entre les entrées et les réponses du système combinatoire • Après avoir

déterminé la technologie à _{utiliser , la minimisation de t d est obtenue ,} en minimisant le nombre des étages du réseau logique • La minimisation classique des fonctions booléennes permet d'avoir un réseau logique à deux étages; elle peut s'imposer, si on est très exigent du point de

vue rapidité du système • Le coût du système est fonction croissante de sa rapidité •

3 - Nombre d'interconnections pour certaines applications , il faut plutôt minimiser le nombre d'interconnections des éléments afin de réaliser des circuits compacts ; comme pour les avions ,satel-lites ,modules lunaires •••• etc , où le circuit doit occuper le minimum d'espace possible •

4 -

Nombre de soudures de connections le coût pour faire les soudures afin de connecter les portes et les monter sur des supports , peut égaler ou dé~sser le coût de la porte elle même • LI utilisation des circuits L.S. I. (Large Scale Integration ) permet d'optimiser ce facteur •

Pour être complet, un critère d'optimisation de la fonction coût doit englober tous ces quatre facteurs , ainsi que d'autres non cités ici.

Toutefois , on se limite aux deux premiers facteurs , en pré-sentant les deux méthodes de minimisation décrites ci-dessous •

3.2

Minimisation Classique des Fonctions Boléennes •

3.~1 Caractéristiques de la Méthode Proposée :

La méthode décrite ci-dessous permet d'obtenir la réunion minimale (ou intersection minimale ) , conduisant

à

un réseau à deux étages logiques avec des éléments ET-OU • Cependant , cette méthode est aussi valable pour les circuits utilisant les éléments universels ON ( complément du ET ) et NI ( complément du OU ) par une transformation • Dans la référence [13 ] il est démontré, que la minimalité ( nombre minimum d'éléments) est sauvegardée par la transforœ4tion •

La méthode est basée sur la théorie développée par SVOBODA

[23J

utilisant le fait, que l'ensemble des composants premiers , est un ense~ ble ordonné. Les composants premiers constituent ce qU'on appelle la base première dorit les éléments sont sélectionnés à partir de l'ensemble des

3n termes, en apPliquant deux règles arithmétiques • Cette sélection n'est

.

faite ni par comparaisons , ni par itérations , co~~e dans les méthodes basées sur les théories de QUINE [17,21 ] ,d'URBANo-MUELLER [26 ] ou

PRATHER [ 18 ] •

De ce fait , la recherche des composants premiers est facilitée ainsi que le processus de minimisation • L'algorithme de SVOBODA a l'avan-tage sui~t : il n'est pas nécessaire de travailler dans tout l'ensemble des 3n termes • La méthode est fondamentalement basée sur le théorème dl extension de SVOBODA

[22 ] '

mais elle combine les avantages du théorème

La formulation de ces théorèmes fait appel à une terminologie utili-sant en harmonie entre elles , les représentations cubique et graphique d'une fonction booléenne.

Pour pouvoir énoncer ces théorèmes sans confusions , certaines définitions et notions s'imposent.

3.2.2Représentation Cubique

3.2.2.A Représentation Géomètrique d'un Minterme

Si on considère les variables booléennes Xl , X2 •••• , Xn comme les coordonnées rectangulaires dans un espace à n dimensions, l'état de ces n variables correspond alors à un sommet de l'hypercube à n dimensions, dont les arêtes sont égales à l'unité.

Chaque minteme défini par ( 1.2 ) correspond donc d'une manière unique à llun des 2n sommets de l'hypercube à n dimensions.

Exemple 3.1 n =3 , F

=~IIIa(X),

aE

1

2

,4,5,6,7

i

X3 5 7 4 ....

--t-r

2

-

o

l 0 (en binaire) ]J'i+--~ 0 1 1

₄

_{- l 0 0}

5

-

1 0 l 6

-

1 1 0 7

-

111 ~----~~---.X2 000 2

3.2.2.B Reorésentation Géomètrigue d'~~ Terme

La représentation géomètrique d'un terme défini par (

1.4 )

est une cellule appartenant à l'hypercube à n dimensions •

Désignons par lettre toute variable booléenne barrée ou non barrée •

, l ' n-m .

Un terme de m lettres represente a somme booleenne de 2 mlIlter-mes • De même la cellule correspondante à ce terme est incidente aux 2n-m

sommets de la cellule en question dont la dL'Ilension est ( n - m ) •

Exemple 3.2 : Voir figure 4 page 35 •

Considérons le terme x3 - - :

x) - -

=

0(xl ,

aEl

h,5,6,71

La représentation géomètrique du terme x3 est une cellule à ( 3 - l ) dimensions •

n

s1_{agit de la face du cube qui engendre les 2}2=

4

_sonunets

4,5,6

et 1 • Sur la figure

4

cette face est l'intersection du cube avec le plan x₃ =1 •

3.2.3 Adjacence 3.2.3.A Définition

Deux états adjacents , c'est à dire différents d'une seule des n variables xl'x2 ••••

'xn

,correspondent à deux so~~ts voisins, reliés par une arête parallèle à l'axe des coordonnées, correspondant à la variable en question •

Un sommet posséde n voisins, du fait, qu'il est le point àe

Exemple 3.3 Voir figure

4

page

35 .

Le sommet 6 posséde les 3 voisins 2,4 et 7 •

3.2.3.B Relations d'Adjacence sur le Diagr~~e de MARQUAIID

Notons qU'une position logique, (définie dans le paragraphe 1.4.B ) est la représentation graphique d'un des 2n sommets dans le diagramme de MARQUAND •

Exemple 3.4

Les 2

3

= 8 sommets du cube de la figure

4

correspondent aux 8 positions logiques du diagramme de MARQUAND ci-dessous •

o 1 DJAGRAMME DE MARQUAND 0 1 2 3 0 1

_j

3 1 4 5 \6 7 c:

...

....

_!.,.;8

---n =3 q =2 p =1 n =p+q

Les courbes représentent les arêtes reliant les voisins •

Figure

5 :

Représentation graphique d'une fonction booléé n·ne

Propriété l : Les voisins d'un sommet x doivent être sur la même ligne ou colonne que le point x sur le diagramme de ~.ARQUAND •

Preuve: Comme les voisins différent d'une seule des variables x_k ' k

==

1,2, ••• ,n , on peut déduire une des deux conclusions suivantes

a) k ~ q

==>

le voisin appartient nécessairement à la même ligne

i définie par x=j

+

2q

x

i tel que j < 2q • ( voir la relation 1.10) page 12) b) k > q

===>

le voisin appartient nécessairement à la même colonne

j définie par x= j

+

2q Xi tel que j < 2q •

Exemple 3.5 : voir figure 5 page ~ 7

Sur la figure 5,le point 6 est repéré par ses coordonnées matricielles l et 2 ,car 6= 2

+

22 X l

a) Les voisins

4

et 5 qui diffèrent respectivement de

X2

et xl se trouvent sur la ligne l •

b) Le voisin 2 qui diffère de x3 se trouve sur la colonne 2 •

Propriété 2 : Dans chaque bande verticale ou horizontale contenant 2j cases ,

( j =1,2, •••••• ) , contenant le point x , i l existe un voisin de x , situé

. l

à l'intérieur de la bande et à une distance égale

à.

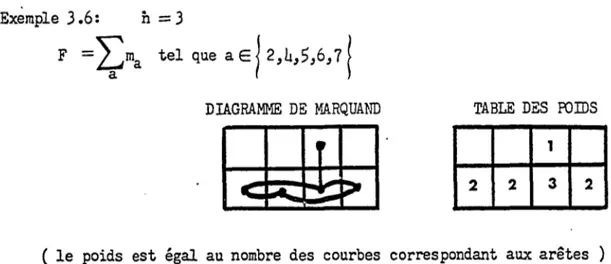
2J- carreaux.

Exemple 3.6

Pour n = 3 considérons les voisins de 6. Voir figure 6 •

. l .. 1-1

a) Bande vert~cale de 2 cases, le voisin 2 est a une distance 2 • b) Bande horizontale de 21 cases, le voisin 7 est· à une distance 21-1 c) Bande horizontale de 22cases, le voisin

4

est à une distance 22-1

Voisins du point 6 pour n:::3 • "2

T

~

' - -

I{~

~)

Il

4 6

l

fig. 6.a fig. 6.b fig. 6.c

Fig.6 Voisins dl un point dans un diagramme de MARQUAND

3.2,4 Les Termes Nécessaires de la Réunion Minimale 3.2.ù.A Poids Associés aux l-points

Soit mx un impliquant de F Cl est à dire

rnx-

l ~F = l

Le sommet x est dit couvert par la fonction booléenne F • Le poids associé au sommet x. est égal au nombre de ses voisins couverts par F •

Exemple 3.6:

n :::

3

F :::

~ma

tel que a E 12,u,S,6, 7

!

DIAGRAMME DE MARQUAND TABLE DES FOIDS

1 1

--

....

•

~ - : -I.;iil' 2 2 3 2

( le poids est égal au nombre des courbes correspondant aux arêtes )

3.2.u.B Théorème dlURBANo-MUELLER

Soit m , le poids associé à un sommet x , couvert par une fonction booléenne donnée F •

SI i l existe une cellule C~ ; 1- de dimension m ; 2- incidente à x ; 3- ne contenant aucun sommet pour lequel la fonction F est nulle ; alors la cellule Cm appartient nécessairement à toute forme minimale de la fonction

x

booléenne donnée F ".

Exemple 3.7 Voir figure

7

page 39 .

Le poids associé au sommet 2 est 1 ; ce sommet est incident à une

1

arête C

2 qui le relie à son voisin 6 • Le terme équivalent

à

cette cellule t

l

=

x2xl appartient donc nécessairement à la réunion minimale de F ; ce terme recouvre les points 2 et 6 •

De même le poids associé au sommet u est 2 ; ce sommet est incident

2

à la face Cu contenant les sommets u,5,6 et

7 •

Le terme éqUivalent t

2 = x3 appartient donc nécessairement à la réunion minimale de F • Les termes \ et t

2 sont les composants premiers de F • LI expression f 2 = t l

+

t 2 recouvre tous les impliquants de F •

3.2.5 Cellule Maximale

m 3.2.5.A Définition: Une cellule C

x

vérifie les trois conditions suivantes 1- De dimension m •

m est dite cellule maximale C