Le col circulaire comme articulation flexible

Texte intégral

(1)6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. 1. Le col circulaire comme articulation flexible P. Merken1, J.F. Debongnie1 Université de Liège, Dept. ASMA – Méthodes de fabrication Chemin des Chevreuils 1 Bât. 52/3, 4000 Liège email: P.Merken@ulg.ac.be, JF.debongnie@ulg.ac.be. 1. Résumé: Nous présentons un modèle permettant de déterminer les dimensions du col, R et h0, en fonction du matériau, de l’angle de rotation désiré et du nombre de cycles envisagé. Dans le cas du col circulaire, les équations de base de la résistance des matériaux appliquées aux poutres à section variable admettent une solution analytique grâce à un changement de variable judicieux inspiré de la théorie de la lubrification. Pour un rapport entre l’épaisseur de col et son rayon tendant vers zéro, nous pouvons également dériver des formes asymptotiques des équations obtenues. Dans le cas de rapports h0/R moyens, ces résultats doivent être affectés de coefficients correcteurs qui dépendent eux-mêmes du rapport h0/R et que l’on détermine à partir des résultats numériques obtenus par la théorie complète. Ainsi, toutes les propriétés du col peuvent déduites grâce aux équations aux limites et à ces coefficients simples.. II. FORMES ASYMPTOTIQUES A. Variables géométriques Afin d’étudier le col, nous fixerons des axes de référence : l’axe x correspond à l’axe de symétrie du col et l’axe y relie les centres des arcs de cercle définissant le col. En plus des deux variables définies précédemment, nous en introduirons 2 autres : l’angle de balancement j et l’épaisseur du col b, perpendiculairement au plan xy.. Mots clefs: col circulaire, articulation élastique, modèle. I. INTRODUCTION Dans un environnement technologique où les machines remplissent de plus en plus de fonctions dans un espace de plus en plus réduit, où le besoin de miniaturisation se fait sentir sans cesse davantage, où les contraintes imposées sont de plus en plus sévères, il devient essentiel de concentrer les fonctions et de leur donner un plus large champ d’application. En micromécanique en particulier, la recherche d’une articulation sans frottement, d’un encombrement faible, incluant le moins de pièces possible, pour des rotations limitées et travaillant dans un milieu non-lubrifié, amène à écarter les solutions classiques telles que roulements, paliers lisses et autres pivots qui ne possèdent pas toutes ces qualités. Un système particulier déjà connu [1] et travaillant par déformation, présente ces différentes caractéristiques : il s’agit du col circulaire. La figure 1 montre la géométrie générale de ce type d’articulation. Le col est défini par son rayon , R, et par l’épaisseur minimale de matière, h0.. 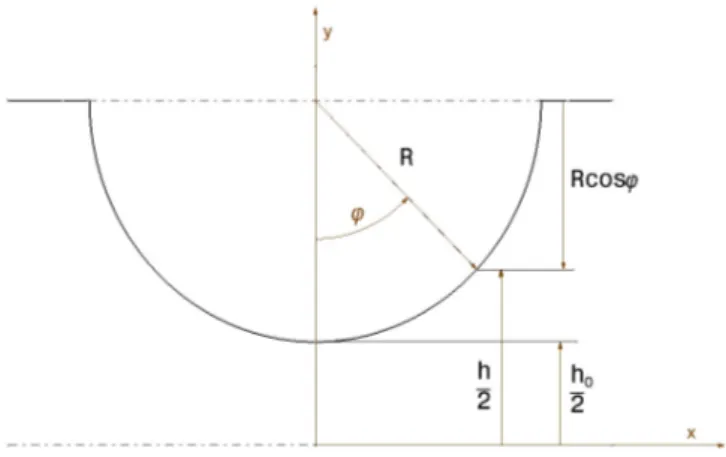Fig. 1. Géométrie du col circulaire. Fig. 2. Variables géométriques B. Rigidité en flexion L’angle de flexion total se calcule par la formule classique, R. α=. ∫. 12 M 12M dx = 3 Eb Ebh −R. R. ∫h. dx 3. (1). −R. On considère que seule la zone du col (qui s’étend de –R à R) est soumise à l’action du moment de flexion et que le reste de la poutre est infiniment rigide. Calculons cette dernière intégrale. La géométrie du col nous donne,   h  h = h0 + 2 R (1− cosϕ )= 2 R 1 + 0  − cosϕ  2 R   .  h  = 2 R 1+ 0  (1− ε cosϕ )  2R  2R = (1 − ε cosϕ ) ε en posant,. (2).

(2) 6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. ε=. 1 h 1+ 0 2R. 2. • ε ≈1. (3). • 1− ε 2 ≈ • α ∗ ≈π. Sachant que,. x = R sin ϕ , dx = R cos ϕdϕ on transforme l’intégrale (1) sous la forme, R. π 2. ε R cosϕdϕ ε = 2 3 3 (1− ε cosϕ ) 4 R. ∫ h = ∫π 8R dx 3. −R. −. 3. 3. π 2. cosϕdϕ. ∫ (1− ε cosϕ ). 3. =. 0. ε Ι (5) 4R 2 3. 2. L’intégrale à évaluer ne diffère des intégrales apparaissant en théorie de la lubrification [2] que par le signe de la variable e et peut donc être résolue par le célèbre changement de variables de Sommerfeld [3] qui devient ici, cosα + ε cos ϕ = (6) 1+ ε cosα On en déduit successivement, 1− ε 2 • 1− ε cosϕ = 1+ ε cosα. • sin 2 ϕ =. (1− ε )sin 2. 2. 1− ε 2 dα (8) (1+ ε cosα ) En ce qui concerne les bornes d’intégration, ϕ = 0, cos ϕ =1 ⇔ cosα =1 α = 0  (9)  π ∗ ϕ = 2 , cos ϕ = 0 ⇔ cosα = − ε α = ar cos(− ε ) L’intégrale I se ramène ainsi à dϕ =. α∗. ε   (1+ ε )cosα + 2 (1+ cos 2α )+ ε  dα ∫  (1− ε )  ε 1 3ε   = (1+ ε )sin α + α + sin 2α  2 4   (1− ε ) 2. 2 52. 0. ∗. ∗. (10). ∗. 2 52. Tenant compte de la valeur ci-dessus de la limite a* (9), on a,. sin α ∗ = 1− cos 2 α ∗ = 1− ε 2 sin 2α ∗ = 2 sin α ∗ cosα ∗ = − 2ε 1− ε 2 ce qui ramène finalement l’équation cherchée à 1. (1− ε ). 2 52. (.  2  1+ ε . ). (11).  3ε ε2 1 − ε + ar cos (− ε )− 1 − ε 2  (12) 2 2  2. Nous nous limiterons au cas où obtenons alors,. 52. (14). 52. dx ε 3 3  R  3 R = 2 π   ≈ π 5 2 3 8 h0 h 4 R 2  h0  −R L’angle de flexion s’écrit finalement,. ∫. ∫ Ebh. 12 M 3. dx =. −R. 9π R M 52 2 Eb h0. (15). (16). Ce qui revient à dire, 52. ce qui donne,. 2. 3  h0  3  R   π + Ο  ≈ π    R  2  h0  2. h M 2 = Eb 0 α 9π R. (1+ ε cosα )2. Ι=. 52. R. 2. 1. (13). et. 2. (1−ε )sin α dα d (cosϕ ) = − sin ϕ dϕ = −. •. Ι=. R Ι =    h0 . R. (7). h0 R. 3ε 3 ar cos(− ε )≈ π 2 2 2 h ε • 1− ε 2 = 0 2 R En remplaçant les différents termes dans l’intégrale, nous obtenons,. α=. 1− ε 2 sin α • sin ϕ = 1+ ε cosα. ). •. α. (1+ ε cosα ). (. 1− ε 2 1+ ε 2 ≈ 2. •. (4). h0 R. h0 est petit devant 1. Nous R. (17). Cette expression mesure la raideur en flexion. En ce qui concerne la contrainte maximum au niveau du col, 52 h 6M 6 2 Eb h0 4 σ= 2= 2 α = Eα 0 (18) 3π R bh0 bh0 9π R soit,. α=. 3π σ 4 E. R h0. (19). C. Rigidité en torsion L’angle de torsion varie avec la coordonnée x car la section n’est pas constante, nous avons alors, Mt Mt 3M t dα = = = (20) 3 3 dx G c1bh bh Gbh 3 G 3 Le coefficient c1 est donné dans des tables, il dépend du rapport b/h. Lorsque ce rapport est supérieur à 4, le coefficient tend vers 1/3. Ce rapport est, dans notre cas, toujours beaucoup plus grand que 4. Calculons l’angle de torsion total, en considérant que la partie de la poutre non entamée est toujours infiniment rigide,. 3M t α= Gb. R. ∫h. dx 9 M t R = π 3 8 Gb h05 2 −R. (21). La raideur en torsion vaut, quant à elle, 52. h Mt 8 = Gb 0 α 9π R. (22).

(3) 6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. 3. D. Rigidité en extension Le déplacement d’une section infinitésimale de la poutre soumise à un effort de traction vaut,. du N = dx Ebh. N ⇔ u= Eb. R. ∫h. dx. (23). −R. Remplaçons h par sa valeur calculée dans la partie flexion, R. ∫. −R. dx ε = h 2. On a,. π 2. ∫π. −. cos ϕ dϕ = ε (1− ε cosϕ ). π 2. cos ϕ. ∫ (1− ε cosϕ ) dϕ = Ι 0. 2. ε cos ϕ 1 = − 1+ 1− ε cos ϕ 1− ε cos ϕ. Fig. 3. Application de la charge. (24). (25). et. 1) Contribution de la flexion Le moment vaut P.x, la rotation vérifiant, dα 12 M 12 Px − = = dx Ebh 3 Ebh 3 le déplacement vaut, R. ∫. π 2. w = αdx. π dϕ π Ι=− + =− +Γ 2 1− ε cos ϕ 2. ∫. (26). 0. En utilisant encore le même changement de variable, α∗. Γ=. ∫. 1 + ε cos α 1− ε 2. 0. 1− ε 2. (1+ ε cosα ). dα =. 1 1− ε 2. α. ∗. (27). π α∗ π R R + ≈ − +π ≈π 2 2 2 h h 0 0 1− ε Il vient ainsi, N R u= π Eb h0 et la rigidité en extension est représentée par h N 1 = Eb 0 u π R Ι=−. Intégrons par parties, u =α dv = dx   dα du = dx dx v = x R. w = [xα ]−RR − x. ∫. (28). 12 M Eb 3. ∫h=. −R. dx. 12 M Eb 3. π. R h0. (29). (30). w=. =. 12 P Eb. 3 Pε Eb. R. ∫ Ebh. 12 Px 3. dx = 0. (38). R. ∫h x. 2 3. dx =. −R. π 3 2. 12 P Eb. π 2. ∫π 8R. −. sin 2 ϕ cos ϕ. ∫ (1− ε cosϕ ). 3. 0. 2. R 2 sin 2 ϕ 3. ε3. dϕ =. R cos ϕ dϕ. (1− ε cos ϕ ). 3. (39). 3 Pε 3 Ι Eb. En utilisant toujours le même changement de variable, nous obtenons α∗. ∫ 0. F. Rigidité en translation ou cisaillement technologique Par translation, on entend la translation de l’un des côtés de la poutre par rapport à l’autre côté, le col circulaire délimitant les côtés. Afin de pouvoir effectuer une translation, on doit appliquer une charge au droit du col. Cela sera réalisé grâce à l’artifice montré sur la figure 3.. (37). car l’intégrand est impair. Donc α (0) = 0 . Reste donc à calculer. Ι=. (33). dα dx dx. −R. (32). La raideur angulaire transverse vaut,. h M 1 = Eb 3 0 α 12π R. −R. (36). Il est clair que,. − α (R ) =. E. Rigidité en flexion transverse Voyons ce qu’il se passe lorsque le col est soumis à un moment de flexion transverse, dα 12 M = (31) dx Ehb 3. α=. (35). −R. On a donc,. R. (34). (1−ε )sin. 1− ε 2 α cosα + ε (1+ ε cosα )3 dα 2 3 (1+ ε cosα ) 1+ ε cosα 1− ε 2 (1+ ε cosα ) 2. 2. (. ). (40) sin 2 α (cosα + ε ) 1 = dα = Γ 32 32 1+ ε cosα 1− ε 2 1− ε 2 0 Transformons ce dernier intégrand. On a successivement. (. 1. α. ∗. ) ∫. (. ). •. sin 2 α (cosα + ε ) 1 2 1  sin 2 α  = sin α +  ε −  1+ ε cosα ε ε  1+ ε cosα . •. sin 2 α 1− cos 2 α ε + cosα = =1− cosα 1+ ε cosα 1+ ε cosα 1+ ε cosα. •. cosα (ε + cosα ) 1 1  cosα  = cosα +  ε −  1+ ε cosα ε ε  1+ ε cosα . (41).

(4) 6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. 4. La flexion est largement prépondérante. Nous négligerons l’effet de l’effort tranchant. La rigidité en cisaillement technologique se ramène à. 1 1   cosα +  −  cosα 1 ε  ε 1 1   • = = −  1+ ε cosα 1+ ε cosα ε ε  1+ ε cosα . P 2 h  ≈ Eb  0  w 3π R. Intégrons chacun des termes ; nous obtenons, α∗. ∫ ε sin 1. 2. α dα =. 0. α. 1 2ε.  ∗ sin 2α α −  2 . ∗.    . ∗. ∫ ε cosα dα = ε sin α 1. 1. (42). ∗. 0. Pour calculer la dernière intégrale, effectuons le changement de variable de Sommerfeld classique, cos β − ε cosα = 1− ε cos β. dα =. 1− ε 2 dβ 1− ε cos β. 1+ ε cosα =. (43). α. ∫. ∫. −R. dα dx =α (R )⋅ R − dx. α (R )⋅ R = (44). R. dα. ∫ x dx dx. (53). −R. ∫. −R. α∗. Ι=. ).  h0  h0  π   +  1+ −π   R  R  2     . ∫. (45). Rassemblons chacun des termes, nous obtenons,  1 1  π  π Γ =  π + ε 1− ε 2  + 2 1− ε 2  1− ε 2 1+  −   ε 2ε   2ε  ε  . ∫ 0. (46). 9π R3 2 M 52 2 Eb h0. (54). Calculons, R. (. R. ∫. π 2. 1− ε 2 π dα 1− ε cos β dβ = = 2 1+ ε cosα 1 − ε cos β ε 1 − 2 1− ε 2 0 0. h 1 = π + 0 2  R π ≈ 2 Finalement,. R. w = α dx = [αx]−RR − x. Résolvons cette équation. On connaît (16),. α = 0, cosα =1 ⇔ cos β =1 β = 0   ∗ π α = ar cos(− ε ) ⇔ cos β = 0 β = 2 ∗. (51). G. Déplacement de l’extrémité du col On se propose, ici, de calculer le déplacement de l’extrémité du col sous l’influence d’un moment de flexion. Ceci permettra d’obtenir des informations sur la position du centre de rotation du col. On a le gradient de l’angle de rotation dans la direction x, dα 12 M = (52) dx Ebh 3 et le déplacement global,. −R. 1− ε 2 1− ε cos β. 32. dα 3Mε 3 x dx = dx EbR. π 2. sin ϕ cos ϕ. ∫ (1− ε cosϕ ). 3. 0. dϕ =. 3Mε 3 ⋅Ι EbR. 1− ε 2 sin α cosα + ε (1+ ε cosα )3 1− ε 2 dα 1+ ε cosα 1+ ε cosα 1− ε 2 3 (1+ ε cosα ). (. α. ). ∗. sin α (cosα + ε )dα (1− ε ) ∫  sin α  1 = + ε (1− cosα )  (1− ε )  2  1 1  =  2 (1+ ε )+ ε   (1− ε )  =. (55). 1. 2 2. 0. 2. ∗. ∗. 2 2. (56). 2. πR Ι ≈   2  h0 . 32. (47). 32. 3π P  R    w≈ (48) 2 Eb  h0  Cette dernière expression mesure la contribution de la flexion. 2) Contribution de l’effort tranchant Le déplacement localisé vaut, dw P 6P = = (49) dx 5 5Ebh Ebh 6 Le déplacement, 6P 5Eb. R. ∫. −R. R2 h02 On a donc, ≈2. et. w=. 2 2. dx 6π P = h 5 Eb. R h0. Ce déplacement est équivalent à la contribution de l’effort tranchant.. (50). R. ∫. α. −R. dα 6Mε 3 R 2 6 M R dx = ≈ dx EbR h02 Eb h02. (57). Au total,. h  M R 3 2  9π −6 0  (58) 52  Eb h0  2 R  On constate que le grand terme est a(R).R dans l’expression  h  (53), c’est-à-dire que la rotation se fait à Ο 0  près autour  R    du centre du col. w=.

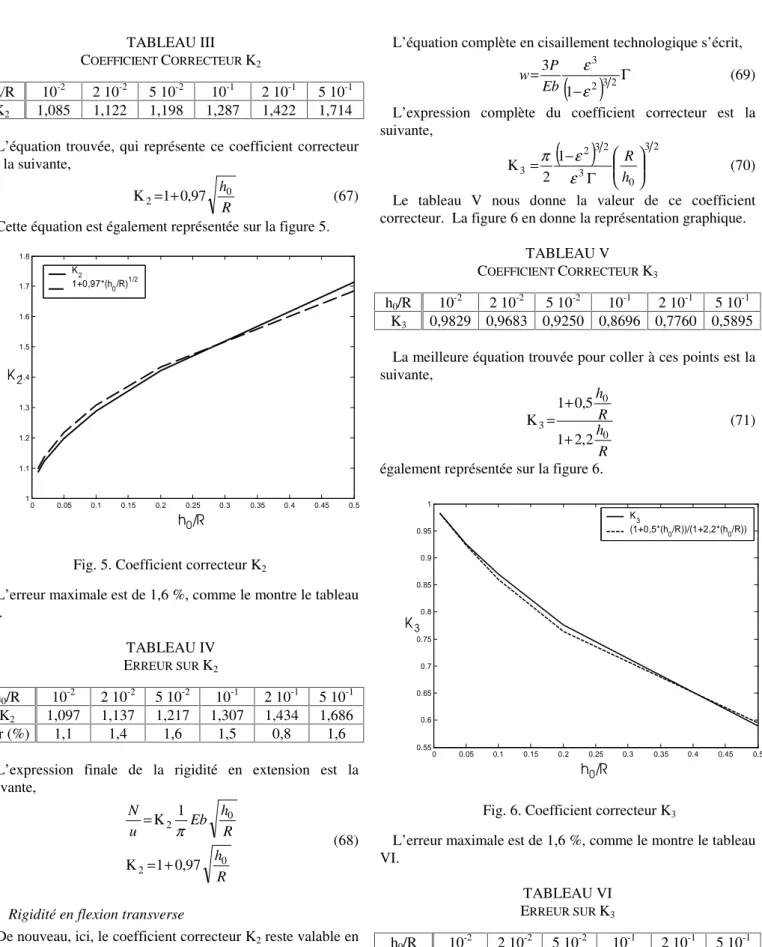
(5) 6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. III. COEFFICIENTS CORRECTEURS. 1.08. Les équations obtenues précédemment sont valables tant que le rapport h0/R reste proche de zéro. Ce qui signifie que, soit l’épaisseur h0 doit être très petite, soit le rayon R doit être très grand. En pratique, cependant, l’épaisseur h0 peut atteindre des valeurs significatives par rapport au rayon. Ceci peut arriver pour des questions de fabrication (h0 sera alors limité inférieurement) ou d’encombrement (R sera, lui, limité supérieurement), lorsque la fonction du col le permet. Ainsi, le rapport h0/R pourrait atteindre des valeurs telles que 0,5. Nous sommes alors devant un cas pour lequel les équations asymptotiques ne sont plus valables rigoureusement. Nous allons montrer que nous pouvons aisément les conserver, par l’application de coefficients correcteurs uniquement fonctions du rapport h0/R. Ces coefficient correcteurs seront déduits des équations de la théorie complète, avant leurs simplifications pour obtenir les formes asymptotiques. Il est bien entendu que ces coefficients doivent tendre vers un lorsque le rapport h0/R tend vers zéro. A. Rigidité en flexion Rappelons l’équation complète en flexion,. 12 M ε 3 Ι α= Eb 4 R 2. (59). M Eb R 2 = (60) 3 ε 3Ι α Le coefficient correcteur se mesure alors par le rapport entre les raideurs complète et asymptotique, 52. 3π 1  R    (61) 2 ε 3Ι  h0  Evaluons numériquement chacun des termes intervenant dans l’expression I, pour obtenir la valeur du coefficient correcteur. Κ1 =. 2 10-2 1,0025. 5 10-2 1,0064. 10-1 2 10-1 1,0129 1,0264. 1.06. 1.05. K 11.04 1.03. 1.02. 1.01. 1. 0. 0.05. 0.1. 0.15. 0.2. 0.25. 0.3. 0.35. 0.4. 0.45. h0/R Fig. 4. Coefficient correcteur K1 L’approximation nous donne une erreur maximale de 0,1%, comme le montre le tableau suivant. TABLEAU II ERREUR SUR K1. Nous obtenons finalement l’équation corrigée suivante, 52. h M 2 = Κ1 Eb 0 α 9π R 1 h0 Κ 1 =1 − 8 R De même, pour calculer un angle limite,. α=. 1 3π σ Κ1 4 E. R h0. (63). (64). B. Rigidité en torsion Il est clair que le coefficient correcteur K1 est également valable dans le cas de la torsion.. TABLEAU I COEFFICIENT CORRECTEUR K1 10-2 1,0013. K1 0,137*(h0 /R)+1. 1.07. h0/R 10-2 2 10-2 5 10-2 10-1 2 10-1 5 10-1 K1 1,0014 1,0027 1,0069 1,0137 1,0274 1,0685 Err (%) 0,01 0,02 0,05 0,08 0,1 0,02. h  avec Ι = f  0  , donnée par l’équation (10). R La raideur en flexion est alors mesurée par. h0/R K1. 5. 5 10-1 1,0683. Il reste à trouver une expression simple, faisant apparaître le rapport h0/R uniquement. La figure 4 nous montre que l’évolution du coefficient est sensiblement linéaire. La recherche d’une droite de coefficient de corrélation le meilleur possible nous amène à l’expression simple suivante, h Κ 1 = 0,137 0 +1 (62) R La figure 4 nous montre également cette droite.. C. Rigidité en extension Nous avons obtenu L’équation complète suivante, en extension,  N  α∗ π  u= − (65) Eb  1− ε 2 2    Le coefficient correcteur s’exprime par,  1 h0  α ∗ π  Κ −21 = − (66) π R  1− ε 2 2    Le tableau III nous donne la valeur de ce coefficient correcteur. La figure 5 en donne la représentation graphique.. 0.5.

(6) 6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. L’équation complète en cisaillement technologique s’écrit,. TABLEAU III COEFFICIENT CORRECTEUR K2 10-2 1,085. h0/R K2. 2 10-2 1,122. 5 10-2 1,198. 10-1 1,287. 2 10-1 1,422. 5 10-1 1,714. L’équation trouvée, qui représente ce coefficient correcteur est la suivante,. h0 (67) R Cette équation est également représentée sur la figure 5. Κ 2 =1+ 0,97. ε3 3P Γ (69) Eb 1− ε 2 3 2 L’expression complète du coefficient correcteur est la suivante, w=. ). 32. 32. TABLEAU V COEFFICIENT CORRECTEUR K3 10-2 0,9829. h0/R K3. 1.5. 2 10-2 0,9683. 5 10-2 0,9250. 10-1 2 10-1 0,8696 0,7760. 5 10-1 0,5895. La meilleure équation trouvée pour coller à ces points est la suivante, h 1+ 0,5 0 R (71) Κ3 = h0 1+ 2,2 R également représentée sur la figure 6.. K 21.4 1.3. 1.2. 1.1. 0. 0.05. 0.1. 0.15. 0.2. 0.25. 0.3. 0.35. 0.4. 0.45. 1. 0.5. h0/R. 0.9. L’erreur maximale est de 1,6 %, comme le montre le tableau IV.. 2 10-2 1,137 1,4. 5 10-2 1,217 1,6. 10-1 1,307 1,5. 0.85. 0.8. K3 0.75. TABLEAU IV ERREUR SUR K2 10-2 1,097 1,1. K3 (1+0,5*(h0 /R))/(1+2,2*(h0 /R)). 0.95. Fig. 5. Coefficient correcteur K2. h0/R K2 Err (%). ). (. K2 1/2 1+0,97*(h0 /R). 1.6. 1. (. R π 1− ε 2   Κ3 = (70) 3 2 ε Γ  h0  Le tableau V nous donne la valeur de ce coefficient correcteur. La figure 6 en donne la représentation graphique.. 1.8. 1.7. 6. 0.7. 2 10-1 1,434 0,8. 5 10-1 1,686 1,6. 0.65. 0.6. 0.55. 0. 0.05. 0.1. L’expression finale de la rigidité en extension est la suivante,. N 1 h = Κ 2 Eb 0 u π R. 0.15. 0.2. 0.25. 0.3. 0.35. 0.4. 0.45. 0.5. h0/R. Fig. 6. Coefficient correcteur K3 (68). h Κ 2 = 1 + 0,97 0 R D. Rigidité en flexion transverse De nouveau, ici, le coefficient correcteur K2 reste valable en flexion transverse. E. Rigidité en cisaillement technologique Il a été démontré que la flexion est largement prépondérante. Nous négligerons encore la contribution de l’effort tranchant.. L’erreur maximale est de 1,6 %, comme le montre le tableau VI. TABLEAU VI ERREUR SUR K3 h0/R 10-2 2 10-2 5 10-2 10-1 2 10-1 5 10-1 K3 0,9834 0,9674 0,9234 0,8607 0,7639 0,5952 Err (%) 0,05 0,09 0,17 1,03 1,56 0,97 L’équation est donc,.

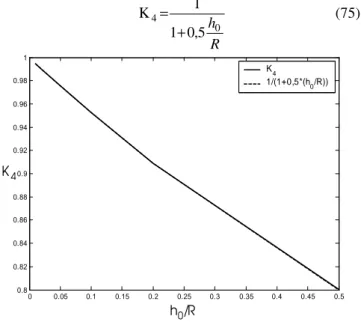
(7) 6th National Congress on Theoretical and Applied Mechanics, Ghent, May 26-27, 2003. NCTAM-2003-077. P 2 h  =Κ3 Eb  0  w 3π R h 1+ 0,5 0 R Κ3 = h0 1+ 2,2 R. L’erreur maximale est de l’ordre de 10-11%, comme le montre le tableau VIII.. 32. h0/R 10-2 2 10-2 5 10-2 10-1 2 10-1 K4 0,9950 0.9901 0,9756 0,9524 0,9091 Err (%) 0,00 0,00 0,00 0,00 0,00.  h  Nous avons vu qu’à Ο 0  près, la rotation du système se  R    fait autour du col. Ici, nous ne pouvons plus négliger le second terme de l’équation (58). Celui-ci représente, lorsque le rapport h0/R atteint des valeurs telles que 0,5, jusqu’à 25% du premier terme, ce qui n’est plus négligeable. Nous devons par conséquent, calculer un coefficient correcteur pour chaque termes de la relation (58). Nous connaissons le premier coefficient grâce aux relations (16) et (63). Le second terme de l’expression nous a donné,. 3Mε 3 ⋅Ι EbR où I est donné par l’expression (56). Le second coefficient se calcule donc par, w2 =. (73). 2. ε 3  h0  (74)   Ι 2 R Le tableau VII nous donne la valeur de ce coefficient correcteur. La figure 7 en donne la représentation graphique. Κ4 =. TABLEAU VII COEFFICIENT CORRECTEUR K4 10-2 0,9950. 2 10-2 0,9901. 5 10-2 0,9756. TABLEAU VIII ERREUR SUR K4. (72). F. Déplacement de l’extrémité du col. h0/R K4. 10-1 2 10-1 0,9524 0,9091. 5 10-1 0,8000. La meilleure équation trouvée pour coller à ces points est la suivante, 1 (75) Κ4 = h0 1+ 0,5 R.  1 9π h  −Κ 4 6 0   R   Κ 1 2 1 h0 1 Κ 1 =1 − , Κ4 = h 8 R 1+ 0,5 0 R w=. 0.94 0.92. K 4 0.9 0.88 0.86 0.84 0.82. 0. 0.05. 0.1. 0.15. 0.2. 0.25. 0.3. 0.35. 0.4. h0 /R. Fig. 7. Coefficient correcteur K4. 0.45. 0.5. (76). Nous avons montré qu’il était possible d’obtenir, dans le cas du col circulaire, des expressions analytiques décrivant leur comportement en tant que système élastique. Ceci grâce au célèbre changement de variable de Sommerfeld. Ces expressions analytiques ne sont cependant pas commodes pour une étude de mécanisme comportant un certain nombre de ces cols. Nous avons donc dérivé des expressions asymptotiques simples permettant ce genre d’étude. Les expressions asymptotiques obtenues ne sont pas encore suffisantes dans certains cas. Nous les avons corrigées pour tenir compte de leurs imperfections. Nous avons montré que les expressions déduites pour les coefficients correcteurs approchent de façon précise la correction idéale à apporter. Ainsi, dans tout le domaine de variation du rapport épaisseur sur rayon, nous disposons maintenant d’un modèle simple du col circulaire, déduit analytiquement. Nous pensons, par toutes ces considérations, que nous avons apporté une contribution intéressante à l’étude des cols circulaires employés comme articulation flexible. RÉFÉRENCES [1]. [3]. 0.96. M R3 2 Eb h05 2. IV. CONCLUSION. [2]. K4 1/(1+0,5*(h0 /R)). 0.98. 5 10-1 0,800 0,00. L’équation est donc,. 1. 0.8. 7. Simon Henein, Conception des guidages flexibles, Presses Polytechniques et Universitaires Romandes, Collection META, 2001. L. Leloup, Etude de la lubrification et calcul des paliers, 2ème édition, Sciences et Lettres, Liège, 1961 A. Sommerfeld, Zur hydrodynamische Theorie des Schmiermittelreibung, Zeitschrift für Math. und Physik, vol. 50, 1904.

(8)