Analyse et tolérancement de systèmes
ayant une lentille frontale à forme libre
Mémoire
Xavier Dallaire
Maîtrise en physique
Maître ès Sciences (M.Sc.)
Québec, Canada
© Xavier Dallaire, 2013
iii
Résumé
Suite au développement récent des méthodes de production, les lentilles à forme libre sont de plus en plus utilisées dans les designs optiques. Néanmoins, leurs définitions mathématiques et leurs formes particulières rendent leur tolérancement et leurs réactions aux perturbations d’alignement difficilement prévisibles. Par conséquent, les outils à la portée des concepteurs optiques, tels que les logiciels de conception optique, ne sont pas toujours en mesure de fournir l’aide nécessaire. Dans ce mémoire, nous présentons d’abord les concepts théoriques et les récents développements relatifs à ces notions. Par la suite, l’analyse d’une lentille panomorphe dont la première surface est une lentille à forme libre nous révèle nombres de comportements particuliers mettant en évidence des relations entre l’empreinte du faisceau et la courbure de champ. Finalement, une nouvelle technique de tolérancement est présentée. Via une analyse en perturbative nécessitant peu de temps de calcul, il est possible de réduire les marges d’erreur allouées sur certaines variables, tout en maximisant l’effet sur la qualité d’image. Cette technique s’est avérée particulièrement efficace dans le cas où l’ajustement de la mise au point (mise au foyer) est limité spatialement.
v
Abstract
In light of the new development of the production methods, free-form lens are used more frequently in optical design. However, their mathematical definitions as well as their specific shapes tend to make their tolerancing and reactions to perturbations hardly predictable. In consequence, the tools used by optical designers, like optical design programs, are not always able to help as they should. First, this document presents the recent developments and the theoretical concepts concerning these subjects. Thereafter, the analysis of a panomorph lens which has a free-form lens as a first surface reveals numbers of particular behavior showing relations between the field curvature and the footprint. Finally, a new tolerancing technique is presented. Using a perturbative analysis requiring a minimum of computing power, it is possible to reduce the allowed margins of error of certain variables while maximising the gain in image quality. This technique was particularly efficient in cases where the adjustment of the focus was spatially limited.
vii
Table des matières
Résumé ... iii
Abstract... v
Table des matières ... vii
Liste des Tableaux ... ix
Table des figures ... xi
Remerciements ... xv
Chapitre 1 Introduction ... 1
Chapitre 2 Conception optique... 5
2.1 Concepts de bases en optique ... 5
2.1.1 Diaphragme d’ouverture, pupilles et champ de vue ... 5
2.1.2 Rayon chef et rayon marginal ... 7
2.1.3 Logiciels de conception optique ... 9
2.2 Aberrations optiques... 10
2.2.1 Les aberrations de Seidel ... 11
2.3 Les surfaces en optique ... 17
2.3.1 La constante conique... 18
2.3.2 Lentille à forme libre... 20
2.4 Tolérancement ... 27
2.4.1 Les méthodes communes ... 28
2.4.2 Nouvelles méthodes ... 33
2.4.3 Tolérancement de surfaces asphériques ... 39
Chapitre 3 Analyse de la lentille frontale d’un système optique panomorphe ... 43
3.1 Lentille panomorphe ... 45
3.2 Empreinte du faisceau... 48
viii
3.3.1 Décentrement... 53
3.3.2 Tilt... 58
Chapitre 4 Exploration d’une méthode de tolérancement intuitive ...63
4.1 Démarche et méthode ... 63
4.2 Résultats et analyses... 68
Chapitre 5 Conclusion...75
ix
Liste des Tableaux
Tableau 1 – Correspondance entre les coefficients de Seidel et les coefficients de déformation du front d’onde ... 16
Tableau 2 – Taille RMS de la tache pour différentes surfaces ... 22 Tableau 3 – Les cinq premiers polynômes de Forbes et cinq polynômes de Zernike ... 25
Tableau 4 – Coefficients de Seidel du système panomorphe ... 53 Tableau 5 – Exemple de tolérances utilisées dans le grade commercial de précision. ... 67
xi
Table des figures
Figure 1.1 – Visualisation d’une lentille sphérique et asphérique... 2
Figure 2.1 – Schéma des pupilles et des rayons principaux ... 8
Figure 2.2 – Fenêtre de travail typique dans Zemax ... 10
Figure 2.3 – Schéma d’un miroir parabolique ... 11
Figure 2.4 – Démonstration de la convergence vers l’approximation paraxiale. 14 Figure 2.5 – La constante conique et ses surfaces ... 18
Figure 2.6 – Exemple de variation des coefficients de polynômes ... 22
Figure 2.7 – Représentation des six premiers polynômes orthogonaux de Forbes ... 23
Figure 2.8 – Construction d’une surface par des courbes gaussiennes ... 26
Figure 2.9 – Exemple d’une charte de précision/coûts d’un commerçant ... 30
Figure 2.10 – Organigramme représentant l’analyse statistique Monte-Carlo. .. 31
Figure 2.11 – Représentation graphique des quatre principales distributions utilisées lors du tolérancement. ... 32
Figure 2.12 – Organigramme pointant la différence entre les deux méthodes de conception optique. ... 36
Figure 2.13 – Équivalence entre le décentrement et le tilt pour une surface sphérique ... 40
Figure 3.1 – Lentille panomorphe ... 44
Figure 3.2 – Lentille téléphoto ... 45
Figure 3.3 – Distorsion en coussinet et en barillet ... 46
Figure 3.4 – Exemple de grandissement local d’une lentille panomorphe ... 47
Figure 3.5 – Zones privilégiées de la lentille panomorphe analysée ... 47
Figure 3.6 – Comparaison entre l’empreinte du faisceau et la variation de la position des rayons chefs par rapport à l’angle d’arrivée du champ de vue ... 49
Figure 3.7 – Courbure de la lentille frontale panomorphe ... 50
Figure 3.8 – Caractéristiques supplémentaires de la lentille panomorphe ... 51
Figure 3.9 – Variation de la position du meilleur foyer en fonction du champ de vue pour différents décentrements ... 54
Figure 3.10 – Empreinte du faisceau et différence de courbure de champ pour un décentrement de la frontale de 0.25mm ... 56
Figure 3.11 – Variation de la courbure de la première surface et variation de la courbure de champ pour un décentrement ... 57
xii
Figure 3.12 – Variation de la position du meilleur foyer en fonction du champ de
vue pour différents tilts... 59
Figure 3.13 – Empreinte du faisceau et différence de courbure de champ pour un tilt de la frontale de 10’ ... 60
Figure 3.14 – Variation de la courbure de la première surface et variation de la courbure de champ pour un tilt... 61
Figure 4.1 – Points d’intérêts pour le tolérancement ... 64
Figure 4.2 – Exemple d’informations issues d’une analyse de tolérance dans Zemax... 65
Figure 4.3 – Exemple de variation de la qualité selon les tolérances ... 69
Figure 4.4 – Analyse Monte-Carlo des tolérances ... 70
xiii
xv
Remerciements
J’aimerais tout d’abord remercier mon directeur de recherche, Simon Thibault, pour ses conseils et sa patience tout au long de ce projet qui a su prendre maintes formes au cours des mois.
J’aimerais aussi remercier Pierre Deslauniers, Martin Larivière Bastien et Denis Brousseau pour leur aide précieuse, tout particulièrement lors de la période d’apprentissage nécessaire à l’utilisation des logiciels de conception optique.
Finalement, je désire remercier le reste du LRIO, le café, mes collègues physiciens et tous ceux qui m’ont supporté durant ces dernières sessions.
1
Chapitre 1
Introduction
Mise en contexte
Au cours des vingt dernières années, la présence de systèmes optiques dans la vie de la population en générale a grandement augmenté. D’une génération où certains possédaient des appareils photos, nous sommes passés à une génération où pratiquement tout le monde a un téléphone intelligent ou une webcam. Il n’est bien sûr question ici que des applications visibles à première vue. Pourtant, lorsque l’on sait que l’art de la conception optique est vieux de plus de cent ans [1], il est pertinent de se demander quels furent les changements majeurs permettant ce développement. Plusieurs diront que la solution est double. D'une part, la constante croissance du pouvoir computationnel des ordinateurs a permis aux concepteurs optiques de créer de plus en plus rapidement des systèmes beaucoup plus complexes et ce, en se basant sur de l’information qui auparavant n’était pas ou difficilement accessible. Avec ces nouveaux outils de plus en plus puissants, les calculs qui prenaient des jours à effectuer prennent aujourd’hui quelques secondes. Cependant, cette avancée n’aurait eu qu’un impact limité sans le développement, en parallèle, de l’industrie et de sa capacité de fabrication. L’ingéniosité présente dans tout
2
design doit encore s’accommoder des limites sur la précision des composantes et de leur positionnement.
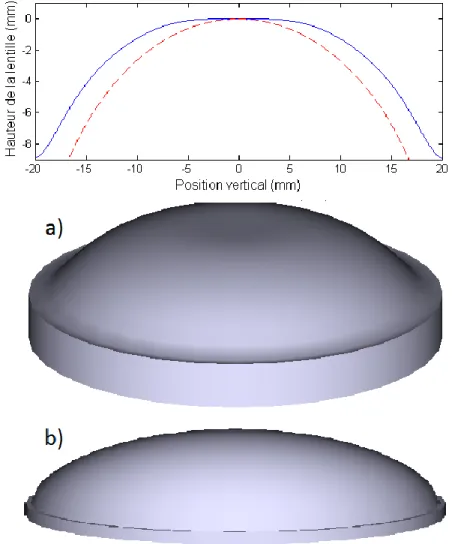
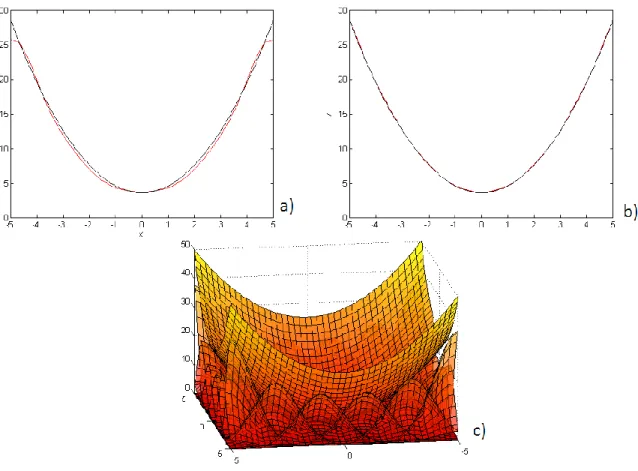
Figure 1.1 – Visualisation d’une lentille sphérique et asphérique
On peut voir en a) et sur le graphique en bleu continu, la lentille asphérique utilisée comme frontale dans un système optique couvrant un champ de vue de 170°. La lentille en b) et la courbe en rouge segmentée représentent une lentille sphérique standard.
Au-delà de cette constante course vers la précision, le développement de l’industrie a aussi réussi à amener au niveau commercial un type de lentille
3 jusqu’ici réservé aux appareils les plus spécialisés : les surfaces à forme libre. On peut voir un exemple de ce genre de lentille à la figure 1.1. Celles-ci seront décrites en détail à la section 2.2.3. Les possibilités offertes par ce nouvel apport à la conception optique sont grandes, mais les défis sont tout aussi nombreux.
Problématique et but
L’émergence des surfaces à formes libres dans le milieu commercial soulève plusieurs questions, notamment au niveau du tolérancement. De grands développements ont vus le jour dans les dernières années, mais leurs applications sont majoritairement réservées aux lentilles sphériques. À cause de leur définition mathématique particulière, les logiciels optiques n’apportent qu’une aide limitée lors de cette étape et le concepteur n’a que peu d’outils pour parvenir à un compromis permettant la mise en production. Le but du projet présenté dans ce mémoire est de dégager des pistes et des méthodes intuitives facilitant le tolérancement de lentilles à forme libre en étudiant notamment des lentilles panomorphes dont la lentille frontale est une surface à forme libre. Ces travaux s’inscrivent dans la continuité des recherches du groupe [2] sur le tolérancement de systèmes optiques complexes et sur le développement de méthodes de caractérisation de ce type de surface en laboratoire.
Corps du mémoire
Le présent mémoire est divisé en cinq chapitres, le premier étant l’introduction.
Le deuxième chapitre, quant à lui, est un survol sommaire de l’ensemble des notions de théorie nécessaires à la compréhension de la conception optique. De
4
plus, on y présente les principales avancées récentes dans les domaines relatifs à ce projet, c’est-à-dire les surfaces à forme libre et le tolérancement.
Le troisième chapitre constitue une analyse de certains paramètres relatifs à la lentille frontale asphérique d’un système à grand champ panomorphe. Certains comportements sont dégagés via l’observation des effets des perturbations d’alignement tels que le décentrement de la surface ou le tilt. Une emphase particulière est mise sur l’empreinte du faisceau sur la frontale et la courbure de champ.
Le quatrième chapitre présente une méthode intuitive de tolérancement applicable à des systèmes utilisant des compensateurs dont l’ajustement de la mise au point est limité dans l’espace. Via une analyse faible en coût de calcul, il est démontré qu’il est possible de resserrer les tolérances à des points particuliers pour maximiser le ratio entre la coupure et le gain en qualité d’image. Finalement, le dernier chapitre conclut ce travail en faisant un rappel général des éléments présentés dans ce mémoire et propose certaines pistes permettant de pousser plus loin la réflexion.
5
Chapitre 2
Conception optique
2.1 Concepts de bases en optique
Étant donné qu’il s’agit ici du domaine de ce mémoire, il est important que le lecteur soit familier avec certaines notions de base de la conception optique. Ces notations, concepts et appellations sont largement utilisés dans la littérature et leur explication ici permettra de s’assurer qu’il ne subsiste aucune ambiguïté quant à la désignation des termes. Ceux-ci sont essentiels pour quiconque désire décrire sommairement un système optique. De plus ample informations sont disponibles dans des ouvrages de références dédiés au sujet [3] [4].
2.1.1 Diaphragme d’ouverture, pupilles et champ de
vue
Le diaphragme d’ouverture, aussi appelé le ‘’stop’’ dans la plupart des cas, est probablement l’élément le plus important d’un système optique. Par soucis de simplicité, l’appellation stop sera utilisée dans le reste de ce document. Son rôle est de définir la quantité de lumière qui va être captée par le système. Il peut
6
s’agir d’une ouverture dans le système ou alors d’un élément optique spécifique. Dans tous les cas, il s’agit de l’élément limitant la grandeur acceptée par le système du cône de lumière (rayons) provenant d’un point source sur l’axe optique.
Chacune des images du stop porte le nom de pupille. Cependant, deux d’entre-elles sont principalement utilisées comme référence. La première, la pupille d’entrée, est l’image du stop dans l’espace objet. Les définitions courantes d’illumination du système y réfèrent explicitement. On parle entre autre de l’ouverture numérique dans l’espace objet :
(2.1)
Ici, n représente l’indice de réfraction du milieu dans lequel se trouve l’objet et θ le demi-angle entre l’axe optique et l’extrémité du cône d’illumination entrant dans la pupille d’entrée. L’autre définition largement utilisée est le nombre f
(f-number) :
⁄ (2.2)
Dans cette équation, D représente le diamètre de la pupille d’entrée et f la longueur focale effective.
La deuxième pupille d’intérêt est la pupille de sortie. Elle constitue l’image du stop dans l’espace image. En général, les systèmes ayant comme détecteur l’œil humain cherchent à ce que la position et la taille de l’iris correspondent plus ou
7 moins à cette ouverture. De cette façon, l’ensemble de la lumière est conservé. Par exemple, lorsque nous utilisons un microscope, pour bien voir, l’iris de l’œil (pupille d’entrée de l’œil) doit s’aligner sur la pupille de sortie de l’oculaire.
Le diaphragme de champ joue aussi un rôle important dans un système optique. Celui-ci a pour rôle la limitation du champ de vue du système optique. Les rayons hors axes, produisant souvent des images de moins bonne qualité, peuvent alors être contrôlés et rejetés. Habituelleme nt, le détecteur rempli ce rôle de par sa dimension, mais parfois un diaphragme est mis en place dans le système. Généralement, celui-ci est positionné à un plan image intermédiaire pour limiter la taille de l’image finale.
Si pour une raison quelconque, par exemple des lentilles de dimensions trop petites, le système bloquait certains rayons qui ont passé ou qui passeraient par le stop, ce système souffrirait de vignettage. Par conséquent, les champs de vue en question, typiquement les champs les plus loin de l’axe optique, souffriraient d’une perte de luminosité à leur arrivée au détecteur. Visuellement, cet effet se traduit par une obscuration progressive du centre vers les bords de l’image.
2.1.2 Rayon chef et rayon marginal
Avant d’expliquer ce que sont le rayon chef et le rayon marginal, il est important que lecteur comprenne l’importance du tracé de rayon en conception optique. Il s’agit ni plus ni moins du procédé par lequel la grande majorité de l’information sur un système optique est extraite. Étant do nné que le système doit pouvoir performer face à un continuum de rayons, il est raisonnable de tester et analyser ses performances via le comportement de quelques rayons simulés. Dans certains cas, une grille ou des cercles concentriques de rayons plus ou moins fins seront envoyés dans notre système pour l’analyser. Dans d’autres situations, seulement deux rayons précis suffisent à obtenir l’information voulue,
8
le rayon chef et le rayon marginal. Les rayons seront ‘’lancés’’ contre la première surface, réfractés, frapperont la deuxième et ainsi de suite jusqu’au plan image. De nos jours, des calculs par ordinateur ont intégré les équations analytiques qui étaient autrefois utilisées à la main mais la technique reste semblable.
Le rayon chef est le rayon qui traverse l’axe optique au niveau du stop. Étant donné la définition de la pupille de sortie et de la pupille d’entrée, il traverse aussi l’axe optique à ces endroits. De tous les rayons émis à partir d’un point dans l’espace objet et qui entrent dans un système sans vignettage, il est le rayon central. Certains auteurs ajoutent à la définition du rayon chef qu’il doit partir de l’extrémité de l’objet ou du champ de vue le plus élevé. La définition qui sera adoptée dans ce mémoire ne sera pas aussi restricti ve et chaque point source de l’espace image qui traverse notre système optique possèdera un rayon chef.
Les rayons marginaux, quant à eux, sont les rayons frappant les rebords du stop et de ses images. Un système souffrant de vignettage bloquera tout d’abord ces rayons. Dans un système où l’approximation paraxiale est valide, le trajet de l’ensemble des rayons peut être déterminé à l’aide de seulement deux rayons : le rayon chef issu de l’extrémité du champ de vue et le rayon marginal issu d’un point sur l’axe optique dans l’espace objet. Un schéma de système optique présentant ces notions est visible à la figure 2.1.
Figure 2.1 – Schéma des pupilles et des rayons principaux
Schéma présentant les éléments de base servant à décrire un système optique. Les flèches représentent ici un objet et ses images.
9
2.1.3 Logiciels de conception optique
Le logiciel de conception optique est probablement l’outil le plus important à la disposition du concepteur. Celui-ci permet, via le tracé de rayons, de calculer une grande variété d’informations essentielles à la conception, l’analyse et au tolérancement de tout système optique. De plus, il incorpore des algorithmes d’optimisation permettant d’assister à la création de s ystèmes optiques. Cependant, la recherche du meilleur design à travers l’espace des solutions est encore loin d’être parfaite pour plusieurs raisons. Tout d’abord, les fonctions d’erreurs utilisées pour minimiser les défauts d’images ne prennent presque jamais en compte la sensibilité du système aux variations. Un concepteur optique désireux d’intégrer cet aspect doit créer lui-même des sous-sections du programme. Il est aussi important de noter qu’en aucun cas il est possible de s’assurer qu’un minimum global a été obtenu et que le point de départ influencera grandement l’endroit où convergera la solution. Les choix faits en ce qui attrait aux paramètres de départ sont donc extrêmement importants. De plus, un bon concepteur optique doit pouvoir savoir quand et comment sortir d’un minimum local pour améliorer son design, et quand est-ce qu’il faut reculer d’un pas et recommencer une étape. Il s’agit donc d’un outil devant être utilisé par quelqu’un d’expérimenté et en aucun cas une optimisation aveugle ne sera à même d’égaler un design éclairé.
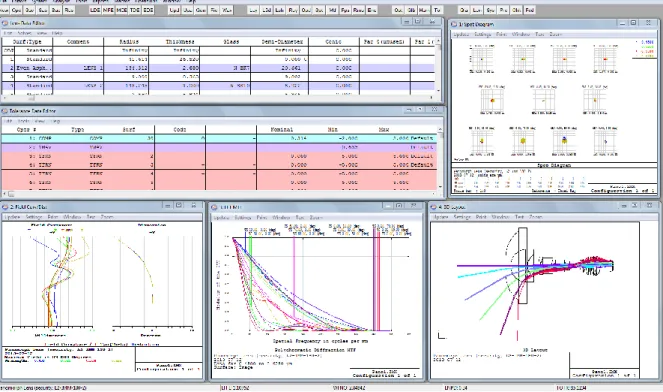
Dans le cadre de ce mémoire, le logiciel Zemax et un élément de sa banque d’exemple [5] furent utilisés lors des analyses. La figure 2.2 présente une fenêtre de travail typique que l’on peut retrouver lors de l’utilisation de ce logiciel.
10
Figure 2.2 – Fenêtre de travail typique dans Zemax
On présente ici les données nominales du design, les tolérances, la taille de la tache RMS, la courbure de champ, la distorsion, la MTF et le schéma du système.
2.2 Aberrations optiques
Il existe plusieurs critères permettant de juger de la qualité d’un système optique. Lorsque que l’on cherche à examiner la qualité d’image produite, l’étude des aberrations optiques présentes dans notre système peut s’avérer un choix judicieux. Ces aberrations sont les coefficients d’une série en puissance représentant la déformation du front d’onde par rapport à un front d’onde parfait convergent en un seul point. Il existe plusieurs définitions ainsi que représentations de ces aberrations optiques. Cette section est dédiée à leur présentation.
11
2.2.1 Les aberrations de Seidel
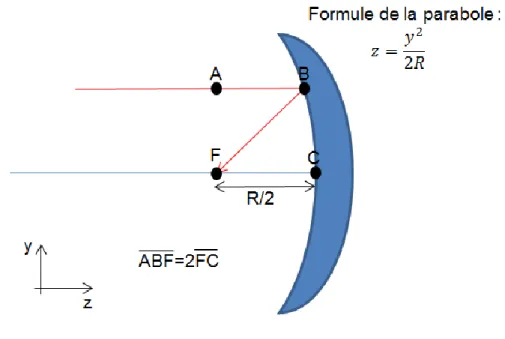
Nous savons, via l’optique paraxiale, l’endroit exact sur le plan image où devrait se retrouver tous les rayons issus d’un point source dans notre espace objet. Or, un système optique réel ne focalisera pas les rayons en questions avec exactitude à cet endroit. Un bon exemple de cette réalité est l’approximation faite sur un front d’onde plan reflété par un miroir sphérique de rayon de courbure R. Si l’on ne considère que deux dimensions, soit z l’axe de propagation et y l’axe perpendiculaire à celui-ci, nous savons que la surface permettant de focaliser une onde plane en un seul point est la parabole. Deux rayons auront toujours le même parcours optique tel que démontré à la figure 2.3 et aux équations 2.3 à 2.8.
Figure 2.3 – Schéma d’un miroir parabolique
Pour un miroir parabolique de rayon R, les rayons provenant de l’infini seront focalisé au point focal F. La différence de parcours optique sera nulle pour les différents rayons.
12 ̅̅̅̅ (2.3) ̅̅̅̅ √ ( ) (2.4) ̅̅̅̅ (2.5) ̅̅̅̅̅̅ ̅̅̅̅ √ ( ) (2.6) ( ) ( ) (2.7) (2.8)
Les termes à l’équation 2.8 s’annulent et démontrent que le chemin optique des différents rayons n‘est pas dépendent du point d’arrivée de ceux-ci, les différents rayons ont un parcours optique égal. Un miroir parabolique fait donc converger parfaitement les rayons en un seul point. Lorsqu’il s’agit d’un miroir sphérique, celui-ci est plutôt décrit par l’équation suivante [6] :
13
( ) (2.9)
(2.10)
À partir de l’équation 2.10, il est possible de retrouver le régime paraxiale si l’on admet une simplification. S’il s’avère que z est petit et que y2 est petit par rapport à R, alors on peut négliger le terme quadratique en z. Cela nous donne un miroir de la forme suivante:
(2.11)
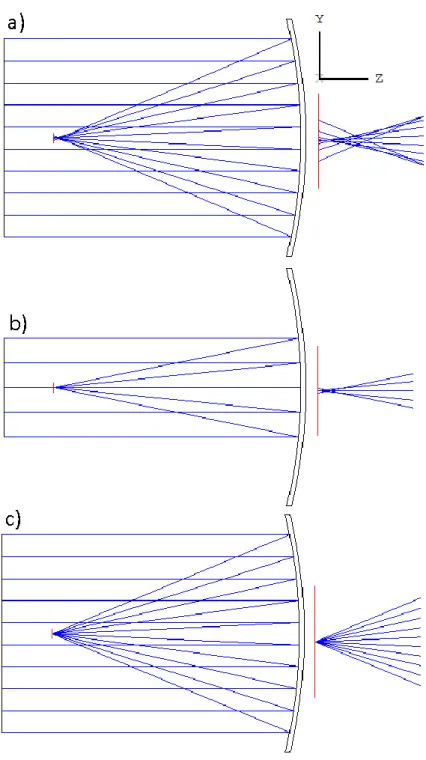
L’approximation paraxiale a donc pour effet ici d’approximer un miroir sphérique à un miroir parabolique. Il est possible de s’en convaincre visuellement à la figure 2.4. En diminuant progressivement l’ouverture du système, la convergence relative des rayons se rapproche progressivement de celle atteinte avec une surface parabolique.
14
Figure 2.4 – Démonstration de la convergence vers l’approximation paraxiale
a)Un miroir sphérique recevant des rayons éloignés de l’axe. Les rayons convergent en différents endroits. b)Encore le même miroir, mais cette fois les rayons sont limités à une région plus proche de l’axe. La convergence est nettement améliorée. c)Un miroir parabolique recevant des rayons éloignés de l’axe. La convergence est parfaite.
15 Pour représenter un front d’onde imparfait, ou encore aberré, il est possible d’exprimer celui-ci en une série de puissance autours des coordonnées du point source (x,y) et des coordonnées de l’image paraxiale (x0,y0). La symétrie de révolution du système nous permet de redéfinir les axes pour que y0 soit toujours égal à zéro, ce qui permet de simplifier les choses. Nous pouvons alors exprimer le front d’onde comme [6] :
( ) ( ) ( ) ( ) ( )
(2.12)
Le premier terme de cette série représente une translation longitudinale, donc le long de l’axe optique, du centre de référence de la sphère et est appelé défocus. Le deuxième terme est une translation transverse et représente un tilt. Le troisième représente une translation de la phase, mais n’affecte pas la qualité d’image en lumière monochromatique. Les termes d’ordre quatre, soit les coefficients B, sont reconnus dans la littérature comme les aberrations de troisième ordre car leur représentation sous forme de rayons transverse est d’ordre trois. Ils sont directement reliés aux aberrations de Seidel. On réfère à cette autre notation car elle est largement utilisée dans la littérature et les programmes de conception optique. Contrairement à une série en puissance basé sur la déformation du front d’onde, les aberrations de Seidel se basent sur l’erreur transverse du point d’arrivée des rayons. Celle-ci est directement proportionnelle à la dérivée première du front d’onde [7].
Finalement, il est possible d’utiliser une représentation polaire où x= r cos θ et où r et x0 sont normalisés de zéro à un. Nous obtenons alors cette représentation très pratique [6] :
16
( ) ∑ ( ) ( )( )
(2.13)
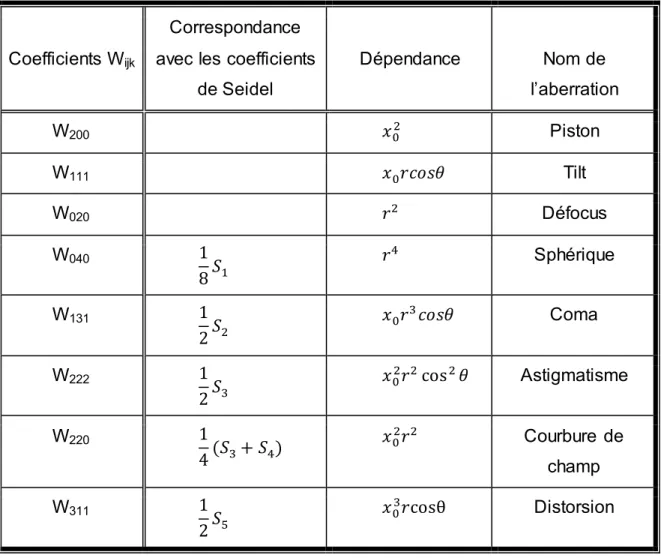
Chacun des termes est relié à une aberration et la correspondance avec les coefficients de Seidel est simple, tel que montré au tableau 1.
Tableau 1 – Correspondance entre les coefficients de Seidel et les coefficients de déformation du front d’onde
Coefficients Wijk
Correspondance avec les coefficients
de Seidel Dépendance Nom de l’aberration W200 Piston W111 Tilt W020 Défocus W040 Sphérique W131 Coma W222 Astigmatisme W220 ( ) Courbure de champ W311 Distorsion
17 Il est à noter que le piston, le tilt et le défocus ne sont pas considéré comme des aberrations, mais plutôt comme des conséquences d’un mauvais positionnement de notre système optique.
2.3 Les surfaces en optique
La majorité des systèmes optiques utilisent principalement des surfaces sphériques. Elles ont l’avantage d’avoir une définition mathématique plutôt simple, ce qui est non négligeable. Cette simplicité a permis, par exemple, une compréhension avancée du comportement de ces surfaces vis-à-vis les aberrations présentes dans un système ou encore de leur tolérancement. Il faut aussi noter que l’ensemble de l’industrie de production optique s’est raffiné autour de la production de ces surfaces et que par conséque nt, leur coût en est d’autant plus faible. Ceci étant dit, il arrive parfois un point lors d’un design optique où l’ajout ou la substitution par une surface d’un autre type comporte bien des avantages. Elle peut permettre d’améliorer la qualité d’image, de relâcher les tolérances et même de réduire le nombre d’éléments optiques. Une alternative possible à la surface sphérique est la surface toroïdale décrite par l’équation suivante [8] :
( )
* ( ) ⁄( )+ (2.14)
Dans l’équation précédente, cx et cy sont les courbures pour l’axe x et y respectivement. Il existe plusieurs autres alternatives tel que les surfaces coniques, asphériques et à forme libre.
18
2.3.1 La constante conique
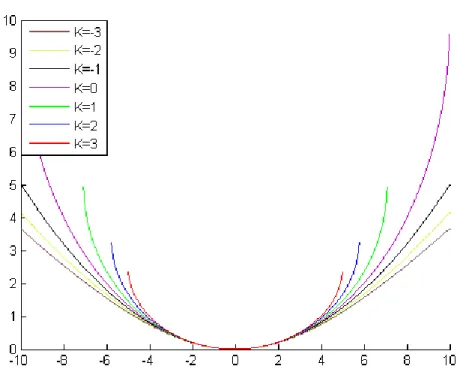
L’ajustement de la constante conique est probablement la plus simple forme d’asphérisme. Celle-ci représente le négatif de l’excentricité de la surface élevée au carré [3]. Elle est largement utilisée, notamment dans certains types de télescope. Le degré de liberté supplémentaire qu’elle fournit permet de compenser parfaitement certaines aberrations telles que l’aberration sphérique. Différentes valeurs donneront différents type de surface tel que montré à la figure 2.5.
Figure 2.5 – La constante conique et ses surfaces
On peut voir ici différents types de surface ayant toutes un rayon de 10 unités. Le cercle corresponde à K=0. À K=-1, on obtient un paraboloïde. Pour des valeurs inférieures à K=-1, les courbes sont des hyperboloïdes. Les autres valeurs de K constituent des rotations d’ellipses par rapport à un de leurs axes.
19 Une forme conique est définie comme l’intersection d’un plan à un certain angle avec un cône selon la formule suivante :
( ) (2.15)
Dans le cadre d’une lentille, z représente l’axe de propagation et la distance radiale r est perpendiculaire à celui-ci. R est le rayon de courbure et k la constante conique. Contrairement à un cas paraxial, le terme en z2 n’est pas négligeable et impliquera une déformation de la surface z de la lentille de rayon R de la forme :
( )
( √ ( ) ) (2.16)
Une constante conique de zéro impliquera une surface sphérique alors qu’une constante de valeur -1 nous donnera la même équation parabolique qu’en 2.11. Une constante conique située entre 0 et -1 donnera une ellipse alors que si elle descend en dessous de -1, nous aurons une hyperbole. Par le passé, beaucoup d’analyses et de recherches ont été effectuées sur les systèmes intégrant ce genre de surface et aujourd’hui encore , il s’agit d’un sujet d’actualité [9]. La relative simplicité de l’équation mathématique a permis de travailler analytiquement et l’intégration de la famille des coniques à l’ensemble des notations pour les sphériques existe déjà [3].
20
2.3.2 Lentille à forme libre
Le grand développement des méthodes de production au cours des dernières années a permis une utilisation croissante des lentilles à forme libre dans les designs. Dans le cadre de ce mémoire, l’appellation lentille à forme libre inclura aussi les lentilles asphériques à symétrie de révolution nécessitant une description plus complexe que la modification de la constante conique. Dans la plupart des logiciels optiques, elles sont définies par une suite de polynômes comme suit où le premier terme représente le terme sphérique et la constante conique:
( )
( √ ( ) )
(2.17)
Il est théoriquement possible de décrire n’importe quelle surface symétrique pourvu que n soit assez grand. Cependant, il est nuisible d’utiliser des polynômes au-delà de l’ordre douze. Des variations reliées à des polynômes plus élevés peuvent créer des angles d’incidence exagérément élevés et des effets de bords comme des redressements, ce qui rend le système extrêmement sensible aux perturbations. De plus, les logiciels de conception optique échouent bien souvent à bien choisir les coefficients appropriés si le nombre de terme est trop élevé [10]. Par exemple, l’ajout de terme supplémentaire peut parfois mener l’algorithme d’optimisation à faire en sorte que l’un compense les effets d’un autre sans pour autant améliorer le système. De plus, lorsqu’il est question de créer physiquement la lentille, la fonction la décrivant sera bien souvent utilisée pour créer une lentille plus grande que requis pour laisser une marge de
21 manœuvre au fabricant. Une fonction capricieuse avec un fort rebroussement en dehors de la zone précise d’intérêt peut grandement compliquer sa fabrication.
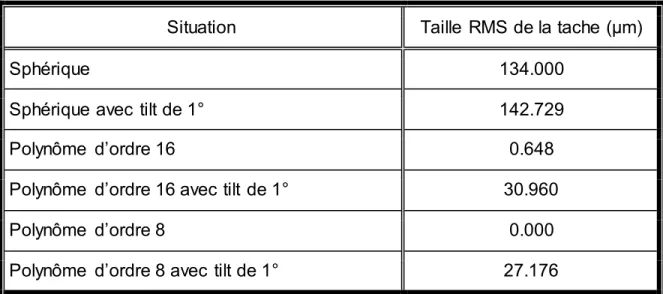
La figure 2.6 présente un exemple simple d’optimisation utilisant des polynômes. L’optimisation avait pour but de minimiser la taille RMS de la tache d’un front d’onde plan reflété par un miroir ayant un foyer paraxial au plan image. L’expérience fut d’abord tenté avec les polynômes d’ordre 4,6 et 8 et après, avec ceux allant jusqu’à 16. Par la suite, l’optimisation fut répétée pour un tilt de 1° du miroir. Le graphique à barres présente le ratio entre les coefficients pour chaque situation. On peut voir que les variations pour les deux premiers ordres sont plutôt similaires dans les deux cas. Dans le cas du polynôme à trois termes, la variation du troisième terme est presque nulle alors qu’on peut observer, pour le cas allant jusqu’à l’ordre 16, une variation des termes élevés. Au niveau de la performance, on peut voir que dans les deux cas, avec ou sans tilt, l’optimisation n’utilisant que trois polynômes est nettement meilleure. Dans le cas sans tilt, la solution converge vers l’équivalent d’une parabole alors que son homologue à 16 ordres n’y arrive pas. Lorsqu’un tilt est présent, la tendance se maintient et on observe de meilleures performances de la part du polynôme allant jusqu’à l’ordre 8. De plus, sa convergence est beaucoup plus rapide. Cela montre la difficulté rencontrée par le logiciel pour optimiser un nombre élevé de coefficients.
22
Tableau 2 – Taille RMS de la tache pour différentes surfaces
Situation Taille RMS de la tache (μm)
Sphérique 134.000
Sphérique avec tilt de 1° 142.729
Polynôme d’ordre 16 0.648
Polynôme d’ordre 16 avec tilt de 1° 30.960
Polynôme d’ordre 8 0.000
Polynôme d’ordre 8 avec tilt de 1° 27.176
Figure 2.6 – Exemple de variation des coefficients de polynômes
En bleu, le rapport entre les coefficients des polynômes de 16e ordre. En rouge, le rapport pour les coefficients des polynômes de 8e ordre.
Seul des termes pairs sont utilisés en vertu de la symétrie de révolution présente dans la grande majorité des cas. Bien qu’intuitive en apparence, cette définition mathématique de surface est bien loin d’être idéale et ne permet pas
23 une analyse ou une compréhension profonde des différents effets sur le système optique. Ces surfaces sont habituellement générées via un processus d’optimisation progressif où l’on débloque terme à terme des coefficients d’ordre croissant. Il n’existe pas encore de processus intuitif ou analytique général permettant d’intégrer une lentille à forme libre avec des paramètres prédéfinis dans un système.
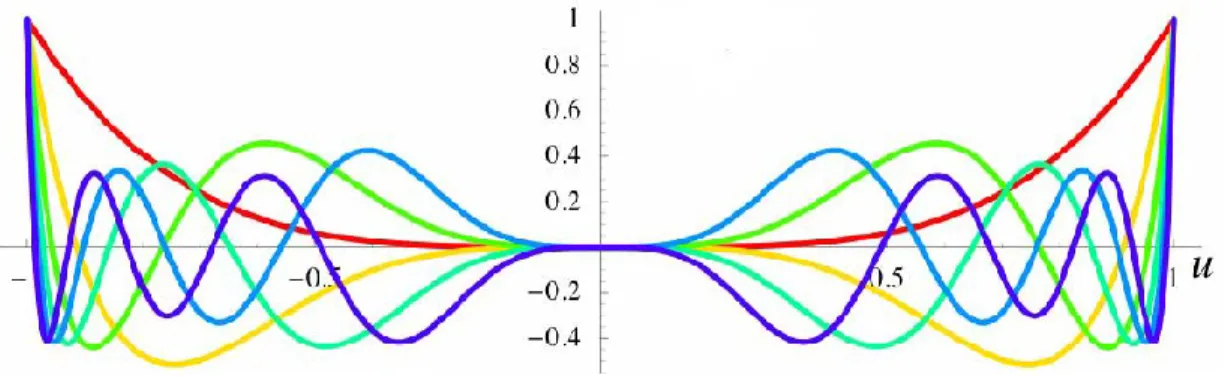
Néanmoins, une nouvelle définition mathématique comportant de nombreux avantages a été présentée dans les dernières années. Il s’agit de la représentation des asphères via les polynômes orthogonaux de Forbes [11] tel que présenté à la figure 2.7 et au tableau 3.
Figure 2.7 – Représentation des six premiers polynômes orthogonaux de Forbes
. Les polynômes d’ordre plus élevés ont plus de maximum locaux, tels que présentés au tableau 3. Source [10]
Ceux-ci furent développés notamment en réponse à l’instabilité des solutions polynomiales ayant un nombre de termes élevé. L’un des aspects les plus importants reliés à l’orthogonalité de la base est une grande réduction du nombre de chiffres significatifs nécessaires à la description d’une surface pour un même nombre de polynômes. Cette réduction peut atteindre un facteur trois pour six ordres de polynômes. De plus, les résultats issus des méthodes existantes de
24
recherche des meilleurs coefficients lors de l’optimisation sont beaucoup plus stables et intuitifs que ceux se basant sur les polynômes en puissance habituels. Avec ceux-ci, une légère variation de la fonction cible peut entraîner de grands changements sur tous les coefficients alors que pour une base orthogonalisée et normalisée sur l’ouverture, tels que les polynômes de Forbes, on peut noter que de petits changements n’aurons de conséquences que sur les derniers coefficients, le dernier étant le plus affecté. Cela revient donc à dire que l’ajout de coefficients n’influence que les variations d’ordre élevé sans modifier la forme de base. Cette propriété peut s’avérer très utile pour le tolérancement et l’optimisation.
Dans certains cas où la symétrie rotationnelle du système ne peut pas être respectée, par exemple dans un système désaxé, il est essentiel d’utiliser une définition prenant en compte cette asymétrie. Les polynômes en puissance sont peu recommandables étant donné que l’augmentation de termes rend l’optimisation instable. Déjà fortement utilisés lors de l’analyse de surfaces optiques, les polynômes de Zernike présentent une option intéressante pour cette application [12]. La surface est alors décrite comme suit :
( √ ( ) )
∑ ( )
(2.18)
Le premier terme représente le terme sphérique et la constante conique. Les Cj sont les coefficients devant chacun des polynômes de Zernike Zj tel que présentés au tableau 3. Comme dans la plupart des cas, il est avantageux de se limiter à un certain ordre de polynôme, habituellement seize. La présence de termes non symétriques et l’orthogonalité de cette base normalisée permettent, tout comme les polynômes de Forbes, d’obtenir des résultats plus fiables.
25
Tableau 3 – Les cinq premiers polynômes de Forbes et cinq polynômes de Zernike
Ordre Zernike Forbes
0
1 ( )
2 √ ( ) ( )
3 √ ( ) ( ( ( ))) 4 √ ( ) ( ( ( )))
Contrairement aux polynômes de Zernike [12], les polynômes de Forbes sont à symétrie de révolution et une seule variable suffit à les décrire. La variable u représente (
) où r est la coordonnée radiale.
Une autre approche peut être effectuée en utilisant une sommation de courbes gaussiennes décrivant une surface comme suit [13] :
( ) ∑ ( ) ( ) (2.19)
Ici, les termes wi représente les poids alors que M est la matrice de la covariance. En sélectionnant, un nombre adéquat de courbe gaussienne, il est possible d’optimiser les poids pour obtenir une surface répondant aux critères sélectionnés. Un exemple est présenté à la figure 2.8.
26
Figure 2.8 – Construction d’une surface par des courbes gaussiennes On a ici tenté de reconstruire une surface sphérique avec une somme de courbes gaussienne. En a), la courbe rouge montre la somme de six gaussiennes. La courbe noir est la référence sphérique. En b), onze courbes furent utilisées. En c), une représentation en 3D d’une surface sphérique créée avec une grille 6x6 de courbes gaussiennes. Source [13].
Étonnamment, cette technique a présenté de meilleurs résultats , c’est-à-dire un gain de 18.5% sur la MTF moyenne du système, que les polynômes de Zernike ou les polynômes en puissance dans un cas particulier de design d’asphère anamorphique présenté dans l’article. Ceci montre l’importance que peut avoir la définition de la surface sur la qualité de la solution finale obtenue.
27 Même si les représentations de surfaces à forme libre présentées précédemment sont les plus populaires actuellement, plusieurs autres avenues sont actuellement explorées par des groupes de recherches à tra vers le monde. On fait ici référence à des surfaces définies par des sommes de fonctions différentes de celles présentées tels que des superconiques [14] ou encore à des procédés géodésiques gaussiens utilisant des éléments statistiques dans leur design [15]. Malgré tout, dans la majorité des cas, l’implémentation de ces techniques s’avère compliquée et les bénéfices à en retirer sont maigres ou inexistant face aux autres techniques.
2.4 Tolérancement
Il pourrait être facile de croire que la conception optique se limite au design de système sur papier et que le processus qui consiste à allouer des marges d’erreurs aux composantes en est complètement dissocié. Ce serait une grave erreur. Le processus de tolérancement est un aspect de la conception optique qui doit toujours être gardé en tête lors du design. Il est évident qu’un système optique remplissant parfaitement les critères demandés, mais qui cesse de fonctionner correctement si une surface nécessite une précision de fabrication plus grande que ce qui est possible d’atteindre ne sera pas considéré adéquat. Cependant, tolérancer un système optique peut rapidement s’avérer incroyablement difficile si l’on cherche à prendre en compte tous les facteurs en question.
Concrètement, il s’agit de choisir les marges permises sur la précision des épaisseurs de verre, des rayons de courbure, de l’alignement, de la fiabilité de l’index de réfraction, des irrégularités de surface, etc., pour que leur s effets accumulés ne dégradent pas la qualité de notre système de façon trop importante. La quantité de variable impliquée rend une analyse complète
28
coûteuse en calcul, mais la complexité des interactions rend le développement d’alternative non trivial.
Avant l’arrivée des ordinateurs vers les années soixante, les concepteurs optiques devaient se baser sur des tracés de rayons exécutés à la main et une démarche d’essai erreur qui pouvait parfois s’avérer coûteuse pour produire des lentilles. Depuis l’automatisation des calculs, certaines méthodes on fait leur apparition et sont encore fortement utilisées aujourd’hui [16]. Néanmoins, la capacité grandissante de calcul des ordinateurs et la poursuite de la recherche dans ce domaine permet aujourd’hui l’élaboration de nouvelles techniques qui pourraient être largement utilisées dans un futur proche. Ces méthodes seront présentées dans cette section.
2.4.1 Les méthodes communes
Bien qu’il ne s’agisse pas à proprement parler d’une variable à tolérancer, l’utilisation d’un compensateur, qui se révèle dans bien des cas un bon choix, se classe dans cette catégorie. Un compensateur est une variable déterminée d’avance, tel que la position de notre capteur ou encore le décentrement d’une composante, qui sera ajustée et optimisée une fois l’ensemble du système optique produit. L’idée est de se donner un dernier levier pour obtenir la meilleure qualité d’image possible malgré les erreurs de fabrication et d’alignement. Naturellement, on essaie habituellement de limiter le nombre de compensateurs à un ou deux éléments pour limiter la complexité de ces derniers ajustements. Le gain en qualité d’image, de même que l’augmentation du budget de tolérance peut être substantiel, mais nécessite dans la plupart des cas une intervention humaine pour les réglages. Cependant, il ne faut surtout pas croire que l’utilisation d’un compensateur peut remplacer à lui seul l’étape du tolérancement. Dans bien des cas, notamment celui de l’appareil photo commercial, l’ajustement du meilleur focus, aussi appelé la mise au point, sera
29 laissé libre via la position du détecteur et l’utilisateur aura à corriger l’image lui -même.
Lorsque que le système optique que l’on cherche à tolérancer est assez simple et permissif, aucune raison ne nous empêche d’utiliser la technique de tolérancement la plus simple et la plus largement répandue. Présente dans la plupart des logiciels de conception optique, elle consiste à analyser l’effet qu’une imprécision particulière, par exemple une erreur sur le rayon de courbure de la première surface, aura sur la qualité de l’image si toutes les autres variables sont à leur valeur nominale. Le critère de qualité en question est laissé à la discrétion du concepteur optique, mais à moins de créer ses propres définitions, les logiciels de conception optique ne proposent qu’une sélection restreinte de critères tels que l’erreur RMS du front d’onde et la MTF [17]. Habituellement, des valeurs par défaut de tolérance sont sélectionnées pour représenter un certain grade de précision et de coût (commercial, précision, haute précision et maximal) offert chez certain manufacturier, tel que présenté à la figure 2.9.
30
Figure 2.9 – Exemple d’une charte de précision/coûts d’un commerçant
Source [18]
De cette façon, il est possible de déterminer quelles variables sont les plus sensibles et quels éléments sont les plus nuisibles, appelé en anglais les worst
offenders. Avec cette information en main, le concepteur optique peut resserrer
les tolérances de ces éléments en particulier. Il est aussi possible, via la technique de la sensibilité inverse, de poser une limite supérieure de dégradation pour une variable et automatiquement trouver la tolérance nécessaire. L’avantage de cette méthode est la faible quantité de calcul nécessaire. Chaque variable perturbée nécessite peu de tracés de rayons. Cependant, il est impossible ici d’analyser et de comprendre les effets combinés de plusieurs variables n’étant pas à leur valeur nominale. Il s’agit là d’un manquement
31 important qui peut réserver bien des surprises à celui que ne se limite qu’à ce genre d’analyse. C’est pourquoi celle-ci est souvent combinée à une deuxième analyse utilisant un procédé statistique Monte-Carlo.
L’analyse Monte-Carlo complète adéquatement l’analyse décrite précédemment car ses forces et faiblesses en sont principalement l’opposé. En choisissant une distribution représentant la possibilité que la variable s’éloigne de sa valeur nominale, l’ensemble du système est perturbé aléatoirement et la qualité d’image simulée. De cette façon, nous pouvons constater l’effet cumulatif des perturbations dans notre système via une analyse statistique des résultats, au détriment d’une compréhension individuelle de la sensibilité des variables. Un schéma du processus Monte-Carlo est présenté à la figure 2.10.
Figure 2.10 – Organigramme représentant l’analyse statistique Monte-Carlo.
Habituellement, une distribution normale ou uniforme de l’amplitude des perturbations de chaque variable est sélectionnée pour représenter les
Design nominal Perturbation aléatoire Optimisation des compensateurs Évaluation par rapport au critère de qualité Quantité suffisante ? Analyse statistique Non Oui
32
variations. Cependant, il est à noter qu’une connaissance plus approfondie des procédés de fabrication peut grandement améliorer la fiabilité d’une telle analyse. Par exemple, une variable comme l’épaisseur d’un élément optique avec une tolérance de ±0.1mm autours de 10mm ne possède la plupart du temps pas une distribution normale, mais plutôt une qui ressemble à une fonction χ2, tel que présenté à la figure 2.11. La raison pour cela est que le manufacturier, désirant en cas d’erreur avoir une chance de corriger la surface, va interpréter la tolérance comme +0/-0.2mm autours de 10.1mm dans le but de laisser le plus épais possible de matériel pour pouvoir travailler avec sans devoir jeter la pièce. Les distributions constantes, paraboliques et limites sont aussi parfois représentatives de la réalité [19].
Figure 2.11 – Représentation graphique des quatre principales distributions utilisées lors du tolérancement.
33 Ce type d’analyse comporte plusieurs avantages. Tout d’abord, le profil de dégradation de notre critère n’est pas forcé d’être quadratique. Étant donné la nature statistique de notre analyse, ce profil sera pris en compte même s’il est inconnu. Cette propriété nous permet par ailleurs de choisir virtuellement n’importe quel critère de qualité. Deuxièmement, les effets des différentes perturbations entre-elles sont pris en compte car c’est un ensemble de système perturbé qui est analysé. Troisièmement, il est possible de choisir la distribution de probabilité pour chacune des variables présentes, augmentant la fiabilité de l’analyse. Finalement, l’information issu de notre échantillon statistique nous permet de voir dans quel mesure certaines erreurs peuvent se compenser entre-elles et produire un design moyen étonnamment meilleur que ce qu’une prédiction issue d’une analyse séparée des variables pourrait suggérer. Cependant, le temps de calcul nécessaire pour obtenir un échantillon statistique de taille raisonnable peut s’avérer nettement plus long qu’une méthode comme la sensibilité inverse et représente un énorme désavantage.
2.4.2 Nouvelles méthodes
Au cours des dernières années, un développement notable des procédés de tolérancement a pu être observé. De vieux concepts furent déterrés pour être réétudiés et certaines innovations ont vu le jour. Ces méthodes sont entre autre la réponse à la compétitivité croissante du marché de l’optique qui demande toujours des coûts de production minimaux.
L’une des nombreuses techniques proposées par la communauté est la désensibilisation du design. Il ne s’agit pas de tolérancement dans le sens classique du terme, mais plutôt de la prise en compte de cette étape lors du design. Cette technique fut toujours plus ou moins utilisée par les concepteurs optiques via le balancement des aberrations optiques ou encore un certain contrôle de la puissance des éléments. Cependant, les logiciels de conceptions
34
optiques permettent maintenant de porter cette prévoyance à un niveau plus élevé. Il est notamment possible, grâce à l’introduction de certains paramètres et contraintes dans la fonction de mérite lors du design, de grandement réduire la sensibilité en choisissant par exemple un angle maximal d’incidence et de réfraction sur les surfaces [20] [21].
Une autre possibilité est le remplacement d’une surface sphérique par une surface asphérique. Il peut s’agir d’une constante conique ou alors d’une lentille à forme libre. Dans certains cas, bien souvent impliquant un système avec un nombre élevé de lentille, cette conversion permet, avec des performances nominales semblables, de relâcher les tolérances sur bien des éléments [22].
Certains concepteurs optiques ont aussi mis de l’avant dans certains articles des méthodes se basant sur l’information issue de quelques systèmes perturbés, notamment à l’aide d’analyse Monte-Carlo [23], à partir de leur design nominal. En investiguant une faible quantité de systèmes, leurs performances et leur robustesse face à ces perturbations, il est possible de dégager des éléments clés permettant d’améliorer le design nominal. Dans certain cas, ces designs modifiés deviendront alors de nouveaux designs nominaux qui seront optimisés et perturbés dans plusieurs directions différentes jusqu’à satisfaction [24]. Cependant, certaines techniques impliquent l’investigation partiellement manuelle de ces designs [25], ce qui peut ralentir le processus de conception. C’est pourquoi certains auteurs ont poussé plus loin cette idée.
Traditionnellement, la conception et l’optimisation d’un système étaient une étape séparée du tolérancement. Or, les méthodes suggérant l’analyse des modèles perturbés pour revenir modifier la valeur nominale ouvrent la porte à quelque chose de relativement nouveau dans le domaine : une optimisation maximisant directement le nombre de design remplissant les critères de production, tel que présenté à la figure 2.12 [26].
35 Les techniques proposées utilisent majoritairement des analyses Monte-Carlo qui sont introduites dans le parcours d’optimisation [27]. Chaque système perturbé produit ainsi sera un point dans l’hyperespace des possibilités. Pour chacun d’entre eux, il est possible de savoir quel serait sa performance par rapport à un critère sélectionné. Pour une limite donnée, il est possible de trouver le centre de gravité des solutions remplissant le critère, et le centre de gravité pour les solutions ne le remplissant pas. Une fois ces informations en main, les valeurs nominales sont modifiées selon l’équation suivante :
( )
(2.20)
Ici, x est un point représentant notre design nominal. G représente un centre de gravité et ε la grandeur des pas de correction. Les valeurs nominales sont donc ajustées en suivant un vecteur dans l’hyperespace des variables à tolérancer qui relie les deux centres de gravité. Il est ainsi possible de trouver une zone qui maximise (localement du moins) notre production en recentrant le design sur le centre de la zone remplissant les critères. Bien sûr, cette technique est assez couteuse en termes de calculs. De plus, il est important de s’assurer à chaque itération qu’il y a un nombre suffisant de point dans les deux catégories car sinon le calcul du centre de gravité ne sera pas représentatif.
36
Les méthodes présentées précédemment avaient pour but de sélectionner des valeurs nominales ou des limites acceptables de tolérance pour que le système optique soit produit avec la meilleure qualité possible et des tolérances permissives. Il ne faut cependant pas oublier une motivation très importante derrière ce procédé : une production à moindre coût. Les méthodes utilisées vont habituellement tenter de diminuer ce coût car règle générale, moins les
Non Spécifications Design Nominal et Optimisation Tolérancement Analyse Finale Adéquat ? Analyse Intermédiaire Adéquat ? Production Non Oui Oui Spécifications Design Nominal, Optimisation et Tolérancement Analyse Finale Adéquat ? Production Non Oui
Figure 2.12 – Organigramme pointant la différence entre les deux méthodes de conception optique.
37 tolérances sont serrées, moins grand sera le coût de production. Certains auteurs tels que Youngworth [28] [29] et Kehoe [30] ont proposé des méthodes incluant des arguments de coûts dans des fonctions de mérite pour le tolérancement. Cet ajout nécessite une bonne connaissance des procédés de fabrications, connaissance n’étant malheureusement pas assez souvent utilisée dans ce genre de processus. On peut, par exemple, imaginer que de resserrer les tolérances d’un élément dispendieux par un facteur 1.5 modifierait le coût par un facteur 1.2 alors que de resserrer 3 éléments plus abordable par un facteur 3 modifierait le coût seulement par un facteur 1.1. En l’absence de connaissance sur le coût, le choix intuitif sera de choisir la première option, ce qui serait ici une erreur. Un autre exemple intéressant concerne la fonction de coût d’une tolérance. En l’absence d’information, on peut considérer que plus les tolérances sont serrées, plus le coût est élevé. Cependant, la plupart des fonctions de coût de production sont sous la forme d’un escalier et non d’une droite. Chaque palier représente un grade et tant que l’on ne change pas de palier, le coût reste le même malgré un changement sur les tolérances. Il est donc possible d’utiliser cette marge ``gratuite`` pourvu que l’on connaisse les spécifications du fabricant.
La dernière méthode qui sera présenté dans cette section n’est pas nouvelle, mais est d’autant plus intéressante que le pouvoir de calcul des ordinateurs augmente. Il s’agit des méthodes utilisant la dérivée première, le gradient, et la dérivée seconde, le Hessian, de la fonction de mérite [16] [28]. Il est possible d’inclure les perturbations, donc le tolérancement, dans une fonction de mérite M:
( )
38 ( ) (2.22) ( ) (2.23)
Dans les équations précédentes, x représente le vecteur contenant les limites accordées aux variables de tolérancement alors que x0 représente les valeurs
nominales et M est la fonction de mérite perturbée. De cette façon, il est possible de déterminer l’ensemble des interactions au deuxième ordre entre les différentes variables que l’on cherche à tolérancer. L’argument utilisé pour se limiter à une approximation de deuxième ordre est que l’on considère de petites perturbations. Cette hypothèse est plutôt raisonnable pour le minimum local autour de la valeur nominale. Par le passé, le Hessian a été utilisé pour effectuer des analyses sur des systèmes optiques car il caractérise entièrement celui-ci dans le cadre de l’approximation. Cependant, le temps de calculs nécessaire est énorme et il est actuellement impensable de l’utilisateur dans le cadre de l’optimisation. Malgré tout, la détermination des limites lors du tolérancement n’implique habituellement pas une modification des valeurs nominales et une recherche complète de tolérance peut être effectuée avec un seul calcul de Hessian.
39
2.4.3 Tolérancement de surfaces asphériques
Le tolérancement des surfaces asphériques peut s’avérer une tâche très compliquée, et ce pour plusieurs raisons. Tout d’abord, le manque de convention universelle quant à leur description mathématique peut nettement compliquer les échanges entre le manufacturier et le concepteur optique. Vient ensuite le problème du tolérancement lui-même. Il a été démontré qu’il était impossible d’appliquer des tolérances aux coefficients d’une série en puissance représentant une surface asphérique car leur variation par rapport à la valeur nominale n’était pas directement reliée à la dégradation de l’image [31]. Pire encore, les erreurs de surface sont couplées avec les erreurs de positionnement comme le tilt et le décentrement [32]. De plus, plusieurs simplifications sont désormais impossibles et les effets des différentes erreurs d’alignement sont nettement plus imprévisibles. Par exemple, lorsque l’on analyse l’effet d’un tilt sur une surface sphérique, on observe qu’il produit le même effet qu’un décentrement, tel que montré à la figure 2.13. La raison en est bien simple : étant donné la nature sphérique de la surface, la variation de la pente est la même en tout point. Ainsi, un ensemble de rayons frappant une surface décentrée subira le même effet que ceux frappant une surface possédant un certain tilt. La seule différence sera au niveau de la zone couverte par les rayons. Cependant, ce genre de raisonnement est impossible avec les lentilles asphériques car presqu’aucune assomption ne peut être faite quant à la nature de leur surface.
40
Figure 2.13 – Équivalence entre le décentrement et le tilt pour une surface sphérique
On peut voir que la nature sphérique de la lentille implique qu’un tilt d’angle θ équivaut à un décentrement de Δy verticalement et de Δz le long de l’axe optique.
Malgré tout, de nombreuses méthodes peuvent être utilisées pour anticiper la qualité d’une composante asphérique et allouer des marges d’erreurs en vue de sa production : contrôle de l’erreur RMS sur la surface, la pente, la valeur RMS de la pente, l’utilisation de polynômes de Zernike, etc. [33]. Cette grande variété d’analyse est symptomatique non seulement d’une représentation mathématique inadéquate, mais aussi d’une grande diversité des procédés de fabrication, laissant chacun leur marque sur la qualité du système. Un bon exemple représentant la complexité du tolérancement de ces surfaces est l’erreur allouée sur les irrégularités de surface. Par exemple, si on regarde la surface frontale d’une lentille grand angle, la taille du faisceau sur la surface sera grandement influencée par l’angle d’arrivée : on note habituellement une empreinte de faisceau plus petite pour les champs élevés que pour les champs faibles. Ce
41 phénomène est illustré à la section suivante, à la figure 3.6. De plus, l’empreinte de ce faisceau est relativement petite face à la taille de la lentille. Par conséquent, différentes régions de la lentille auront une réponse différente face aux irrégularités de surface [2]. Il s’en suit qu’une tolérance allouée sur l’irrégularité de cette surface est dépendante de la position sur la lentille , ce qui complique les choses.
Le tolérancement de surfaces asphériques est un processus qui est encore extrêmement dépendant des méthodes de fabrication. Il existe une variété de solutions permettant la production, mais aucune n’intègre avec efficacité la description mathématique utilisée lors de la conception du système. Les polynômes de Forbes décrits précédemment pourraient s’avérer prometteurs. Il fut en effet démontré une certaine corrélation entre la variation des coefficients et la qualité d’image pour une lentille près du stop [34], mais cette corrélation disparait lorsque l’on s’en éloigne.
Face à ces problèmes, il est intéressant d’étudier plus en détail certains aspects des lentilles grand angle. De cette façon, il serait peut-être possible de dégager certains comportements utiles dans ces situations. Avec cette idée en tête, le chapitre suivant se consacre à l’étude d’une lentille panomorphe.
43
Chapitre 3
Analyse de la lentille frontale d’un
système optique panomorphe
Il existe de nombreux designs de système optique panoramique , notamment plusieurs lentilles panomorphes, intégrant une lentille frontale asphérique ou même à forme libre. Il s’agit d’une composante critique du système car cette lentille va devoir rediriger, entre autre, des rayons provenant d’un angle de 90 degrés ou plus pour les faire passer dans le reste des lentilles. Hors, l’utilisation d’une composante sur mesure comme une lentille à forme libre amène son lot de complexité. Plusieurs questions doivent être posées dans le but de vérifier si les définitions conventionnelles permettant de caractériser notre système s’appliquent encore, ou alors dans quelle mesure des perturbations de cette lentille influenceront notre système. De plus, les balises existantes pour l’implémentation de ce genre d’optique sont assez vagues et se basent énormément sur l’utilisation partiellement aveugle de logiciels d’optimisation. Finalement, dans le cas assez répandu où la première lentille du système est asphérique, il est intéressant de se demander à quel genre de comportement est-ce que l’on peut s’attendre tant au niveau des perturbations que des éléments caractéristiques. Ce chapitre sera consacré à l’étude des relations
44
entre différents paramètres d’une lentille frontale à forme libre. Cependant, une courte section présentera ce qu’est une lentille panomorphe. Le système panomorphe utilisé est présenté à la figure 3.1. Dans le but de pouvoir faire certaines comparaisons, un système sphérique commun, un téléphoto, sera aussi utilisé lors de certaines analyses et est présenté à la figure 3.2. Nous reviendront plus en détail sur celui-ci au chapitre 4.
Figure 3.1 – Lentille panomorphe
Ce design comporte des lentilles à forme libre. La longueur focale à 0° est de 1.176mm et le diamètre de la lentille frontale est de 39.42mm. Elle possède un champ de vue de 170°. L’image produite par ce système est une ellipse, permettant ainsi de maximiser l’utilisation du détecteur. Cela est possible via l’utilisation de quelques lentilles cylindriques. On peut observer, sur la première surface, le phénomène de rebroussement discuté au chapitre deux.
45
Figure 3.2 – Lentille téléphoto
Ce système ne comporte pas de surface asphérique. La longueur focale à 0° est de 100mm pour la lentille frontale de diamètre 11.34mm. Il possède un champ de vue de 4.1°.
3.1 Lentille panomorphe
Ce qui différencie la lentille panomorphe de la lentille habituelle est l’utilisation de la distorsion. En général, les systèmes optiques tendent à vouloir réduire la distorsion à un minimum car elle modifie localement le grandissement de l’image. Celle-ci est habituellement présente dans tous les systèmes et ce, sous différentes formes, tel que présenté à la figure 3.3.
46
Figure 3.3 – Distorsion en coussinet et en barillet
De gauche à droite on peut voir une grille sans distorsion, avec de la distorsion coussinet et, finalement, avec de la distorsion en barillet [35].
Cependant, contrairement aux autres aberrations, la distorsion n’a pas comme conséquence directe la perte d’information de l’image. L’approche des lentilles panomorphe est l’utilisation de la distorsion pour permettre un grandissement des zones d’intérêt de l’image, tel que montré dans la figure 3.4.
Le principal avantage de ce type de lentille est l’immense quantité d’information qu’il est possible d’emmagasiner en une seule image. Un seul système peut couvrir un hémisphère complet en tout temps et facilement raffiner l’image sur une section en particulier via un contrôle de la distorsion. Dans le cas de la lentille présentée à la figure 3.5 [36], le système est créé pour favoriser des zones du champ de vue hors axe. C’est en effet dans ces régions qu’il est important d’avoir une bonne résolution, compte tenu des applications possibles en vidéosurveillance et en vidéoconférence.