Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions : a survey of recent results

(1)

J

OURNAL DE

T

HÉORIE DES

N

OMBRES DE

B

ORDEAUX

A. M. O

DLYZKO

Bounds for discriminants and related estimates

for class numbers, regulators and zeros of zeta

functions : a survey of recent results

Journal de Théorie des Nombres de Bordeaux, tome

2, n

o

_{1 (1990),}

p. 119-141

<http://www.numdam.org/item?id=JTNB_1990__2_1_119_0>

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

(2)

Bounds for

discriminants

and

related estimates for

class

_numbers,

_regulators

and

zeros

of

zeta

functions :

a

_survey

of

_presents

a

guide

to the recent literature on lower bounds for

discriminants of number fields and on several related

topics,

and discusses some _open

_problems

in these areas. Let Ii be an

algebraic

number field of

degree

n = _overthe

rationals Q

with _r,real and

2r2

complex

conjugate

fields,

so that n = _ri₊

2r2.

Let D =

DK

denote the absolute value of

the discriminant of A.

_(Recall

that the

_sign

of the discriminant is

_(-1)r~,

so little information is lost

by

considering

_just

D.)

The root-discrimina.nt

rd =

rdK

of K is defined

_by

The Dedekind zeta function of Il is denoted

_by

_(¡«(s).

The Generalized R,iemann

_Hypothesis

for Il is the

_conjecture

that all the zeros of

the zeta function

_(1«S)

that lie within the critical

_strip

0

_Re(s)

1

actually

lie on the critical line

Re(s)

=

1/2.

For Il =

Q,

D =

1,

and one of Minkowski’s fundamental results was the

proof

that D > 1 for n > 1. He la.ter obtained a lower bound for D that was

exponential

in n. MinkoNvski’s bound was

subsequently improved

_by

many authors. Most of the papers on this

subject

before

1970,

including

all those with the

_{strongest estimates,}

used

_geometry

of numbers methods.

Manuscrit reçu le 25 aout 1989, r4vis6 le 26 f4vrier 1990

(3)

H. Stark

_[Bl,B2]

introduced a new

analytic

method for

proving

lower

bounds for discriminants

_by

_showing

that _{for every complex}s

(other

than

0,1,

or a zero of

~’If(s)),

where _pruns over the zeros of in the critical

strip,

and

2:’

means

that the _p

_{and p}

terms are to be taken

together,

and

This

_identity

is a variant of the classical

_identity

_[12;

Satz

180]

that comes

from the Hadamard factoriza.tion of

_~’j~(.s),

and Stark noticed that two of the constants that occur in that

identity

a.nd which are hard to estimate

can be eliminated.

(It

is ironic that Landau did not notice

_this,

since he

proved

the

_{corresponding}

result for Dirichlet L-functions

_[Il].

Ila,d he seen

the extension to Dedekind zeta

_functions,

a

large

_part

of the recent research

might

have been done 70 years

earlier.)

Since

for Re

_(s)

>

_{1, where q3}

runs over the

_prime

ideals of one finds that for

sreal,s>

1,

By

taking s

= 1 ₊

n-~~2,

say, one obtains from

(1..5)

the estimates

where C = 0.5772156... denotes Euler’s

_constants,

and

These estimates are

substantially

better tha.n

Minkowski’s,

although

not as

(4)

The Stark bound

_(1.5)

was

_{improved by}

the a,uthor in a series of _pa.pers

[B3,B4,B5].

Those _papersused the fundamental

_identity

_(1.2)

and

com-binations of identities derived from it

_by

differentiation with

_respect

to s.

This led to substantial

_improvements

on

GRH,

a,nd others are unconditional.

Serre

_[B7]

introduced the use of the

_explicit

formulas of Guina,nd

[15,16]

and Weil

_[17,110]

to discriminant bounds. This enabled him to

_improve

the author’s GRH bounds. What’s

_perhaps

most

_important,

the

_resulting

for-mulas

_provided

a much more

elegant approa,ch

to

bounding

discriminants,

which made it clear what the

_requirements

and limitations of the method

are. Serre’s

_approach

was extended to

_provide

unconditional bounds

by

the

_author,

and further

_improvements

were made

by

Poitou and the author

The latest results in this area are summarized in Section 2. Discriminant bounds have numerous

_{a.pplications,}

and there has been

very substantial work in recent years on this and related

topics.

The

pur-pose of this note is to

_present

a

guide

to the recent litera,ture and sta,te some

of the

_outstanding

_{open problems.}The references tha.t are listed _appear

to be

_{fairly complete regarding}

the main

_topic,

but cover

only

some of the

applications.

The comments in this and the

_succeeding

sections are much

less

_complete,

due to the extensive litera.ture in this area.. Several

_topics,

such as determination of fields of small discriminants

(see

Section F for

references),

the _{very interesting}recent work on relative conductors

[E13,

E14,

E15],

a,nd Mestre’s work on conductors of

elliptic

curves are not

dealt with in the text at all.

2. Lovver bounds for discriminants.

In this section we state the latest bounds for discrimina.nts obtained

by

use of

explicit

formulas of

_prime

number

theory,

as well as some of their

applications.

We also discuss how close these bounds are to

_{being optimal.}

Consider a differentiable function F : R -

R,

with

.F(-x)

=

F(x),

F(O) =

1,

and such tha,t

(5)

Then the

_explicit

formula for the discriminant states tha,t

For a derivation of this

formula,

see

[B9, B 10~ .

The G ui n a.n d

[15, 16]

and

Weil

_[17,110]

formulas are more

general, although

less

explicit

as to some

terms. See Besenfelder

_[111]

for even more

_general

kernels.

_Many

of the

published

formulas,

including

those of

_Guinand,

are derived

_only

for the

Riemann zeta

_function,

but there is no

difficulty

in

extending

them to Dedekind zeta functions.

In the absence of _any

_{special knowledge}

about zeros and

_prime

ideals

(see

sections 4 and 6 and later _partsof this section for a discussion of

their

_influence),

in order to obtain a lower bound for D from

(2.3)

one

selects

_{F(x) >}

0 for and

_{Re(~(s)) >}

0 for all s in the critical

_strip,

so that the contributions of the

_prime

ideals a.nd zeros are

_nonnegative.

The above

_{nonnegativity}

conditions on

_F(.x)

a,nd

4l(s)

are

equivalent

to

the

_requirement

that

where

_{f (x)}

> 0 and

_{f (x)}

has

_nonnegative

Fourier transform. The best

currently

known unconditional bounds are obtained

by selecting

f (x) _

g(x/b)

for some

_parameter

b

_(depending

on ri and

;2),

where

g(x)

is a

certain function constructed

_by

L. Tartar

_[BIO,B11].

With this choice one

finds that

No other choice of

_f(x)

can

_give

a lower bound for rd tha.t has a

_la.rger

(6)

the same estimates as

Eq.

(2.5),

but with

larger

constants in the remainder

term

O( n-2/3).

The

_question

of how small the remainder term can be made

is still _open.Tartar showed that his

_g(x)

was

optimal

in a certain

class,

but

it

_is

_possible

that better choices exist that do not

_satisfy

his

_assumptions.

Furthermore,

it is not known whether the

_optimal

functions a,re of the

form

_g(x/b)

for a fixed function

_g(x).

Open

Problem 2.1. What functions

_satisfying

_{f (x) >}

0 and

having nonnegative

Fourier transforms

_give

the best unconditional lower bounds for discriminants ?

The bound

_(2.5)

was stated above

_only

in a _very

_{rough asymptotic}

form.

There are much more

_explicit

versions with

_precise

estimates of the remain-der term in

_Also,

there are extensive tables of bounds for all

_degrees

n 100

_(and

for some fields of

_higher

_degrees)

in

_[Bll].

Some of these tables are

reprinted

in

[B12].

When one assumes the GRH for

(1«8),

much better results are

possible.

In this case one

only

reeds

_{F(x) >}

0 such that the Fourier transform of

F(x)

is

_nonnegative.

Open

Problem 2.2. What functions

_F(x)

_give

the best GRH bounds for discriminants ?

There are _manychoices of

G(x)

such that

_F(x)

=

G(xjb)

for a _proper

choice of the

_scaling

_parameter

b

_gives

the bound

Just as in the unconditional _case,no choice of

F(x)

can

give

a better

main term. As was noted in

[115],

it is

possible

to

_{show, using}

some results

of Boas and Kac

_[14],

that the choice of

_G(x)

_{proposed by}

the author

_(see

[B10])

is

_{asymptotically optimal among}

all

_possible

functions in terms of

minimizing

the remainder term

_O((log

_{n )-2 ).}

_IIowever,

it is not known whether the

_optimal

_F(x)

have to be of the form

_F(x)

= for a fixed

function

_G(x).

As in the case of unconditional

bounds,

there are estimates that a.re much

more

_precise

than

_(2.6).

_Fairly

extensive tables of bounds for modera.te

degrees

have been

_prepared

_[B8],

and some of them have been

reprinted

in

(B12~.

Explicit

formula bounds can also be obtained for conductors of Artin

(7)

it is _necessaryto assume Artin’s

conjecture,

as otherwise the

poles

of the

L-functions

_might

_give

a contribution that seems hard to control.

A

_point

of view advocated

_by

J.-P. Serre is to ask for lower bounds for discriminants of

_global

fields Il whose

completions

at some

places

give

a

prescribed

collection of local fields

_I(j.

If the

_I(j

are the reals taken r1 times and the

_complex

numbers taken

2r2

times,

we are in the standard

_setting

described above. If the

_Ki

are a certain number of

copies

of a function

field over

_Fq,

and one

_replaces

the discriminant

_by

the genus, one is led

to estimate the minimal _genusof a curve over

_Fq

that has at least a

_given

number of

_points

_[114].

One of the main

_applications

of discriminant bounds is to estimate class numbers. Some of the results

_give

lower bounds for class numbers of

_totally

complex

extensions of

_totally

real

_fields,

for

_example

_[B2,B3,D4],

that grow very fast. This is in contrast to the

_{typical situation,}

where it is

_expected

on heuristic

_grounds

that class numbers will

_equal

_{1 very}often

[113,117].

So

_{far, though,}

we do not even know whether there exist

_infinitely

_many

number fields of class number one.

Discriminant bounds are often used to show that class numbers of par-ticular fields are small. The basic tool that is used is the Hilbert class field.

If a field Il has class number

h,

then there is an extension L of Il with

[L : ~~~

= 1~ such that

_rdL

=

rdK-

If lower bounds for discriminants

imply

that

_rdL

> for all fields L with

_{[L :}

_{li ~ >}

2,

then we can conclude

that L = Il and h = 1. Most

applications

(see

Section D of

References)

are more

sophisticated,

and use discriminant bounds to

_get

_upperbounds

for class

_numbers,

which a,re then lowered

by

algebraic

methods.

For some other

_{a.pplications}

of discriminant

_bounds,

see

[112,116].

For a

long

time it was

conjectured

that if

_dn

denotes the minimal

root-discriminant of a number field of

degree

n, then dn -+ oo as n -- oo.

(This

is known to be true for abelian

_fields.)

If

_true,

this would have shown that

all Hilbert class field towers

_terminate,

and so all number fields could be

embedded in fields of class number one.

_Ilowever,

Golod a.nd Shafarevich

showed that infinite Hilbert class field towers do exist. The best current

results are due to Martinet

_[Bl2,C2]

who showed that there is a.n infinite

sequence of

totally

real number fiels

(with

degrees equal

to _powersof

₂₎

with

(8)

degrees

5 times _powersof

₂₎

with

It is

_{thought likely}

that the field

_{Q((-3-5.7-13)1/’)}

with

also has an infinite class field _tower,but this has not been

_proved.

Open problem

2.3. What are the minimal discriniiiiants of number

fields of various

_degrees?

Tables

1-4

_present

some data on this

problem.

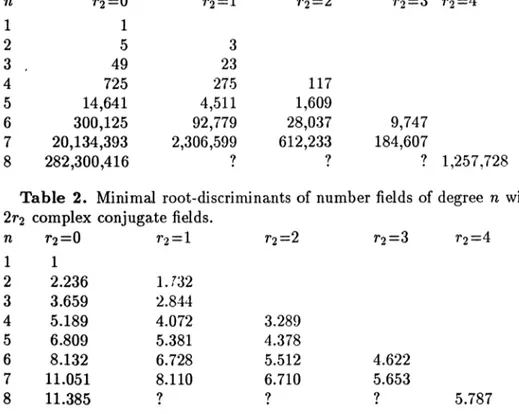
It is

interesting

that the

lower bounds

_(especially

those tha,t assume the

GRH)

are _veryclose to the smallest values of root-discriminants that are known for

_{totally complex}

fields. Even for

_totally

real

_fields,

the

_discrepancy

is not

_large,

_except

for

n = 7. The anomalous results for n = 7

suggest

strongly

that the minimal,

root discriminants

_probably

do not increase

_{monotonically}

with the

_degree,

especially

if one restricts attention to

_totally

real fields.

The GRH bounds

_presented

in Tables 3 and 4 ca.n be

_improved

somewhat.

For

_example,

as was noted in

_[B8],

from which these bounds are

ta,ken,

one can show that all fields of

_degree

8

satisfy

_5.743,

and not

_just

rd > 5.734.

The

_entry

for n = 9 in Table 4 _comesfrom the field

generated by

_a_rootof

the

_polynomial

_{~-2~-7~~+14~+15~~-30~-10~+19~~+2~-1,}

which

was discovered

_{recently by}

Leutbecher

(unpublished).

The discriminant of

the

_polynomial

_(and

thus of the

_field)

is

_{9,685,993,193,}

a

prime,

but it is

not known

_yet

whether it is minimal.

Known constructions for infinite Hilbert class field towers

_rely

on

_x5,orking

with the

_2-part

or

_3-part

of the class _group,a,nd so

produce

fields with

degrees

that are _powersof a small number of

primes. Essentia,lly

_nothing

is

known about fields of

_prime

_degree,

which lea.ds to the

_{following problem.}

Open

Problem 2.4. Is

_dp

bounded as p 2013~ oo

ivith » prime?

Sor far we have been

_discussing

discriminants of number fields.

IIow-ever, another relevant

question,

asked

_by

J.-P. Serre a.nd

_others,

concerns

discriminants of

_polynomials.

Let denote the smallest absolute value of the discriminant of an irreducible monic

polynomial

with

_integral

coeffi-cients and

_degree

n.

Open

Problem 2.5. Is there an infinite subset S of

_positive

_integers

(9)

Nothing

is known on this

topic.

The

analytic

methods discussed in this

paper do not

apply

to this situation. When one examines known fields with

minimal

_{discriminants, they}

tend to have

_algebraic

_integers

a that

_generate

them over

Q

and such that the discriminant of the minimal

polynomial

of a

_equals

the discriminant of the field.

(This

means that if n is the

degree

of _a,then

_1,

a,

c~2, ...,

an-l

forms a basis of the

a1gebraic

_integers

of the

field over the rational

_integers,

or what is called a _power

basis.)

However,

it is

_{generally thought}

that this

_phenomenon

does not

_persist

for

_higher

degree

fields.

_Already

in the case of the field with

(n, r2)

=

(8, 2)

that has

the smallest known discriminant for all such

fields,

no _powerbasis has been

found so far.

3. Elkies’ GRH bound for discriminants

Noam Elkies has observed that a form of the GRH bound

(2.6)

can be

obtained without

_invoking

the Guinand-Weil

_{explicit formulas, by}

_relying

on the Landau-Stark formula

_(1.2)

_along

the lines of the estimates of

_[B3,

B4,

B5].

The remainder term in _{Elkies’ estimate appears}to be much worse

than in the

_explicit

formula

_estimates,

so it is not of

_practical

_{significance,}

but it is

_interesting

that tlus can be done at all. With Elkies’

_permission,

we _presenta sketch of the

proof

here.

From

_(1.1),

we see that and its delivatives of even order

with

_respect

to s are

_positive

for s >

_1,

and the deriva.tives of odd order

negative;

thus

_{by differentiating}

_(1.1)

m times

_{(m =0,1,2,...)}

we find

_(with

p =

1/2

₊

i-y

for

real

under the

assumption

of the

GRH)

Elkies’’ idea is that for fixed s > 1 and

_large

m the term in

_{(s -}

is

_negligible,

and so

by

dividing

the rest of

_(3.1)

_by

and

_summing

over m we obtain

_(1.2)

with s

replaced by s -

1/2 (Taylor

_expansion

about

s);

since 1 --

_iy))

is still

_positive,

we then find

by

bringing s

(10)

and thus obtain the bound from the known

_special

values

To make this

_rigorous,

we _argueas follows: for _anysmall E >

_0,

take so =

_1-f-E,

and

pick

_an

_integer

M _so

large

that

(i)

the values _at_s=

so -1/2

of the M-th

_partial

sums of the

_Taylor

_expansions

of

_0(s)

and

v(s /2)

about s = _soare

within

E of

_{v(so - 1/2)}

and

_1/4)

respectively

(this

is

possible

because both functions are

analytic

in a circle of radius 1 >

_1/2

about

_{so); (ii)}

the value at s = _{so -}

1/2

of the A1-th

pa.rtial

sum of the

Taylor

expansion

of

_{1/2 - i7))}

about s = _sois

positive

for all

y > 0

_(note

that since

_{Re(1/(s -}

1 -

_iy))

=

E/(E’

₊

¡2),

and the value of

the M-th

_partial

sum of the

_{Taylor expansion}

differs from this

_by

it’s clear that the

_positive

value

_{E/(E2 + ,2)}

dominates the error

(1

+

C2

+

-y2)-~t~2

for

_{all -y}

once Al is

sufficiently

large).

Now divide

(3.1)

by

2’nm!,

sum from m = 0 to

1,

and set s = _{so to}obtain

since c was

arbitrarily

small and so

arbitrarily

close to

_1,

,ve’re don. N 4. Prime ideals of small norms

It is not known how much of a contribution is ma.de

by prime

ideals of

small norm to the minimal discriminants when one

applies

the

identy

(2.3).

(See

Section 6 for further discussion and numerical evidence on this

point.)

In some situations

some prime

ideals of small norm are

known,

a.nd tllis can be

_{exploited by computing}

their contributions to the

_explicit

formula. The kernels

_F(x)

that are used to obtain the best known discriminant bounds in the absence of any

knowledge

a.bout

prime

ideals ha.ve the

prop-erty that

_F(x)

decreases _very

_rapidly

as z --+ oo, and in some cases

they

do

(11)

Ll

to take

_advantage

of

_prime

ideals whose norms are not too small. In such cases, the author’s older bounds

[B3,B4,B5]

have

occasionally

been used.

However,

in most cases one can obtain

_stronger

a.nd more

elegant

bounds

by using explicit

formulas. For

_example

_{(see [118]}

for an

application),

if one

takes 1

_{c~ 2,}

then one finds that 0 for 0

Re(s)

_1,

and that

On the other

_hand,

by

a

term-by-term

comparison

of the

series,

and so one

finds,

for

exa.mple,

that

’

for all w e

_{( 1,1}

+

_{6 )}

for some b > 0 and n > no . With more effort one

can obtain more

_precise

estimates.

_Further,

if there are no

_prime

ideals of norm

_2,

for

_example,

the

_8/3

in

_(4.4)

can be

replaced by

_3,

and so on. One can also devise other kernels

_F(x~

tha.t will

_emphasize

the contributions of

particular

ideals.

5. Minkowski constants and

_regulators

The

_analytic

bounds for discriminants that were discussed a.bove are

substantially

better than earlier ones that came from

_geometry

of numbers.

(12)

apply only

to discriminants.

_Geometry

of numbers bounds are derived

from results that _{say, typically,}that if

_L,

_{(x),~ ~ ~ ,}

_L~

_(x)

are linear forms

in xl, ... , xn with x=

(x1, ~ ~ ~ ,

then there are

integer

values of the

xi, not all of them _zero,such that the

_{product rj Lj(x)}

is small. These bounds

_{imply Minkowski-type}

estimates for norms of

ideals; typically they

state that each ideal class of Ii contains an ideal 2t of small _{norm, say}with

where

_CI

and

_C2

are some constants

_independent

of K.

_(BVe

will refer to

C‘1

and

_C2

as Afinkowski

_constants.)

Since N2t

_1,

_Eq.

_(.5.1)

_immediately

implies

a discriminant bound

Bounds of the form

_(5.1)

contain more information than

_(5.2),

_though,

and are useful in other

_problems.

Zimmert

_[E4]

has discovered a.n

_{ingenious analytical}

method that uses

zeta functions of ideal classes to obtain

_improved

h4inkowski constants.

(See

Oesterl6’s _paper

_[E6]

for an

elegant

reformulation of the

method.)

In

particular,

he showed that

_(5.1)

holds with

which is

_considerably

better than the known

_geometry

of numbers bounds.

_Furthermore,

Zimmert showed tha,t for _everycla,ss

_T~,

there is

always

an ideal 2l either in TZ or in

VR-1

(where

D denotes the different

of

_K)

for which

_(5.1)

holds with

This last estimate

_implies

the unconditional bound

_(2.5)

for

discrimi-nants,

although

with a worse error term.

Open

Problem 5.1.What are the best

possible

AIinkowski consta.nts ?

It would be

_interesting

to find out whether one can obtain estimates such

as those of

_(5.4)

that would hold for _everyideal class. It would be _very

(13)

C2 z 44,

since these would

_give

bounds for discriminants that

_currently

can be obtained

only

under the

assumption

of the GRH. There does not seem to be any clear way to

bring

the GRH into Zimmert’s

method,

since

he works with zeta functions of ideal

_classes,

which do not have an Euler

product,

and for which the GRH is in

_general

false.

Open

Problem 5.2.Obtain

_improved

bounds for minima of

_products

of several linear forms

_by

_analytic

methods.

The Zimmert bounds

_{apply only}

to

_products

of li near forms

_{comi ng}

from

an

integral

basis of a number field. It is not known whether these linear forms are extremal in the sense that their minimal nonzero values at

_integet

points

are the

largest

_{among all linear forms.}

Zimmert has also found an

analytic

method for

proving

lower bounds for

regulators

of number fields

_[E4].

His methods show that the

_regulator

R of ~1 satisfies

which

_{significantly improves}

on the results of Remak

[13,18,19].

_(Inequality

(5.5)

is

_stronger

than the

_asymptotic

result stated

_by

Zimmert in

_[E4],

but E. Friedman has

_pointed

out that it follows

_easily

from Satz 3 of

_[E4].)

Friedman

_[E10]

has found

_another,

related method for

_{obtaining analytic}

bounds for

_regulators

that is very effective for small

degrees,

and has

proved,

for

_example,

that the smallest

_regulator

of any number field is 0.2052.

Very

recently,

Friedman and

_Skoruppa

_[E16]

have found a

generaliza.tion

and

a much clearer formulation of Zimmert’s method for

obtaining regulator

bounds,

which will

_hopefully

lead to substa.ntial

_improvements

on

_(5.5).

Open

Problem 5.3. What are the best

_possible

lomer bounds for the

regulator

R of a number field a.s functions

of r1

a.nd

r2 ?

are the best

bounds in terms and D?

E. Friedman has

_suggested

that the

_{following regulator}

bound

_might

be vali d:

(14)

6. Low zeros of Dedekind zeta functions

The Landau-Stark formula

_(1.2)

as well as the Guinand-Weil

explicit

formula

_(2.6)

are

_identities,

and so when D is

_larger

than the bound we

obtain for it

_by

the method sketched

_earlier,

this must be due either to the contribution of

_prime

ideals or of zeros of

_(I(s).

The kernels used in the

explicit

formula

bounds

are such that the contribution of

prime

ideals of

large

norm is

neglipble,

as is the contribution of zeros of

_{(j (s)}

that are far

from the real axis. Therefore it is

_primarily

the

_prime

ideals of small norms

and the low zeros that determine the sizes of the minimal discriminants.

If we fix the

_degree

and let the discriminant _grow,then we can select a

kernel

_F(x)

with bounded

_support,

so that the contribution of the

_prime

ideals will be

_bounded,

and so it will be the zeros that will dominate. The

interesting

question

is to ask what

_happens

when we choose the

_optimal

kernel

_F(x)

without _any

_knowledge

of zeros or

_{prime ideals,}

and then ask

which contribution is

_larger

for the small discriminants.

Currently

no methods are known for

efficiently computing

_high

zeros of

Dedekind zeta functions of

_general

nonabelian fields. For low zeros there is

a _{very nice}method of Friedman

_[H3].

_However,

this method has not been

implemented

yet,

and _{in any}case it

requires

one to

_compute

small norms

of ideals. Therefore it seemed much easier to

_compute

the small norms of

prime

ideals

_(by

_factoring

the minimal

_polynomial

of a

_generator

modulo

rational

_primes),

evaluate their contribution to the

_explicit

formula

_(2.3),

and obtain the contribution of the zeros

by

subtraction.

Table 5

_presents

the results of the

_computation

that wa.s carried out for six

_fields,

those with the smallest discriminants for

_{(71, r2)}

=

(7,0), (8, 0),

(8,4),

and the next smallest for

_{(n, r2)}

=

(8, 0)

a,nd

(8,4)

a.nd the _one

with the smallest known discriminant for

_{(n, r2)}

=

(9, 0).

In ea.ch _case

the kernel

_F(x)

that

_gives

the GRH bounds of Tables 3 and 4 was

_used,

so that in the notation of

[B8],

b = 1.9 for

(n, r2)

=

(?, 0),

b - 1.6 for

(n, r2 ) = (8, 4),

b = 2.05 for

_{(n, r2 ) = (8, 0),}

and b = 2.2 for

_{(n, r2 ) = (9,0).}

The column labelled

_"deficiency"

denotes the difference between

n-1

_{log rd}

for each field and the GRH lower bound. The "ideals" column denotes the value of the sum over

prime

ideals in

(2.3),

and the "zeros" column

the value of the sum over the zeros

(obtained

by

subtracting

the "ideals"

column from the

_"deficiency"

_column).

_Finally,

the "norms" collimn

_gives

the norms of

_prime

ideals that contributed to the sum.

Open

Problem 6.1. What are the relative contributions

of prime

ideals

and zeros to the

_explicit

formula for minimal discriminants?

(15)

but it would be nice to obtain data for

_{higher degree}

fields.

_(This

should

not be too

_difficult,

SlIlCe the fields of small discriminant found

by

Martinet in

_[C3]

are

_{given quite explicitly}

as _rayclass

fields.)

It is worth

noting

that

if we use the kernel that

gives

the best unconditional

bound,

then the

contribution of zeros becomes

considerably

larger

relative to that of the

prime

ideals.

Open

Problem 6.2. Do the zeros

_of(¡«s)

in the critical

_strip

approach

the real axis as n -~ _oo,and if

they do,

how fast do

they

do _so,and how

many of them are there?

There does not seem to be _{any hope}of

_proving

_{algebraically}

that fields with small discriminant must have

_prime

ideals of small norm. If we fix the

degree

n, then we can find fields of that

degree

in which the smallest norm

of a

_prime

ideal will be

_2n,

_although

this

_usually

seems to

_require

a

_large

discriminant. On the other

_hand,

if we let D --~ oo while

_keeping

n

fixed,

then one can show that there will be zeros of

(J«8)

arbitrarily

close to the real axis

_(roughly

_{c(b) log D}

zeros in 0

Im(s)

6 for some

c(b)

>

_0).

One

might

hope

that one could _provethat there are _manyzeros near the real

axis even for minimal discriminants. If one could obtain

enough

such _zeros, one could _prove

improved

discriminant bounds.

Unfortunately

the known

bounds are far too weak for this. The best results _appearto be due

_to,the

author

_[G5],

and show that on the

GRII,

~’~,~ (s)

has a zero on the critical

line at

_height

_O((log

_{n)-1 )}

as n ---1- oo.

Unconditionally,

it has

only

been

shown

_[G5]

that there is a zero at

_height

0.54 +

_{o( 1 )}

as n --~ _oo,a.nd that

for _everyIl with n >

_2,

there is a zero at

_height

14.

_(The

first zero of

the Riemann zeta function is at

_height

_14.1347...,

so this result shows that

the zeta function is extremal in terms of

_having

its lowest zero a.s

high

aas

possible.)

Open

Problem 6.3. Are the GRH bounds for discrimina,nts valid even

without the

_assumption

of the GRH ?

The unconditional bounds are weaker than the GRH ones beca.use of the

requirement

that 0

_throughout

the critical

_strip.

_Ilowei,er,

if we

consider _{any one}of the kernels used in

_obtaining

the GRII bounds

_(which

are

_{required only}

to

_satisfy

0 on the critical line Re s =

1/2),

they

will

_usually

have Re 0 in

_large

sectors of the critica.l

_strip.

In

particular,

all these kernels are > 0 for s

_real,

so if the

_only

viola.tions of

the GRH were on the real

_a.xis,

the GRH bounds for discriminants would be valid ! t As an

_{illustration,}

consider the kernel

_(s)

=

2(rb)1

exp(b(s

(16)

real,

as well as for _manyother

_regions

of the critical

strip.

In

IIm( s)1

>

_{.Re(s -}

_1/2)1,

is very

small,

(b

is taken

large

for

large

n),

so

by taking

a linear combination

(1 - 6)4J(s)

+

_6111*(s),

where is a

carefully

chosen kernel of the

_type

used for the unconditional

bounds,

and 6 > 0 is

_small,

we can ensure that Re > 0 in

IIn1( s)1

>

1/2)1

+

_1/100

for

_{large b,}

_say.The discriminant bound

_{given by}

4li (s)

would be

_only

_slightly

inferior to that of It would take a _very

unusual

combination of zeros

_violating

the GRII to make the sum over the

zeros be _{very negative}for all

possible

choices of b.

Unfortunately,

as far as we

_know,

such unusual distributions

_might

occur.

Acknowledgements.

The author tha.nks A.-M.

_Bergé,

E.

_Triedman,

J.

Martinet,

and J.-P. Serre for their detailed comments on an earlier version

of this

_manuscript.

Table 1. Minimal absolute values of discriminants of number fields of

degree n

with

2r2

complex conjugate

fields.

Table 2. Minimal root-discriminants of number fields of

_{degree n}

with

(17)

Table 3. Small root-discriminants of

_{totally complex}

fields and the best known lower bounds.

_(For

n

_8,

the root-discriminants are known to be minimal for each

_degree.)

Table 4. Small root-discriminants of

_totally

real fields and the best known lower bounds.

_8,

the root-discriminants are known to be minimal for each

_degree.)

Table 5. Contributions of

_prime

ideals a.nd zeros to discriminant bounds for some fields.

_(See

Section 6 for detailed

_{explanation.)}

(18)

REFERENCES

References are _{grouped by topic,}and are _{arranged approximately chronologically}

within each group. For most areas _only_papers_publishedafter 1970 are listed. References to earlier ones can be found in the publications listed _{here, especially}in the book of Narkiewicz

_[A1].

A - Books and surveys

1. W. NARKIEWICZ, Elementary and _{Analytic Theory of Algebraic Numbers,} PWN-Polish Scientific Publishers Warsaw _(1974).MR _50#268. _(Very_completereferences for work before

_1973.)

2. L. C. WASHINGTON, Introduction to _{Cyclotomic Fields, Springer.}1982. MR _{85g :} 11001.

3. J. _MARTINET,Méthodes géométriques dans la recherche des petits discriminants. pp. 147-179, Séminaire Théorie des Nombres, Paris, 1983-84, C. Goldstein éd.,

Birkhäuser Boston, 1985. MR 88h:11083.

B - _Analyticlower bounds for discriminants

1. H.M. STARK, Some _effectivecases _ofthe Brauer-Siegel theorem, Invent. math. 23

(1974),

135-152. MR 49 _#7218.

2. H.M. STARK, The analytic theory of algebraic numbers, Bull. Am. Math. Soc. 81

(1975),

961-972. MR _{56 #}2961.

3. A.M. ODLYZKO, Some _analyticestimates _ofclass numbers and discriminants,

Invent. math. 29 _(1975),275-286. MR 51 # 12788.

4. A.M. _ODLYZKO,Lower bounds. _fordiscriminants _ofnumber _fields,Acta Arith. 29 _(1976),275-297. MR 53 _#5531.

5. A.M. _ODLYZKO,Lower bounds _fordiscriminants _ofnumber _fields.II. MR _{56 #} 309.

6. A.M. ODLYZKO, On conductors and discriminants. _pp._377-407,_Algebraic Num-ber Fields, (Proc. 1975 Durham _Symp.),A. _Fröhlich,_ed.,Academic Press 1977. MR 56 _#11961.

7. J.-P. SERRE, Minorations de discriminants. note of October 1975, published on

pp. 240-243 in vol. 3 of Jean-Pierre SERRE, Collected _{Papers, Springer}1986. 8. A.M. _ODLYZKO,Discriminant bounds. tables dated Nov. 29, 1976 (unpublished).

Some of these bounds are included in Ref. B12.

9. G. _POITOU,Minorations de discriminants _(d’aprèsA.M. _Odlyzko),Séminaire Bourbaki. Vol. _1975/7628ème _{année, Exp.}No. 479, pp. 136-153, Lecture Notes in Math. _#567,_Springer1977. MR 55 _#7995.

10. G. _POITOU,Sur les _petitsdiscriminants, Séminaire Delange-Pisot-Poitou. 18e

(19)

Math., Paris, 1977. MR 81i:12007.

11. F. DIAZ Y DIAZ, Tables minorant la racine n-ième du discriminant d’un corps de _degrén. Publications _{Mathématiques}_d’Orsay80.06. Université de Paris-Sud, Département de _{Mathématique, Orsay,}

_(1980).

59 _{pp. MR 82i:12007.}_(Someof these bounds are included in Ref.

B12.)

12. J. MARTINET, Petits discriminants des corps de nombres. pp. 151-193, Jour-nées _{Arithmétiques}1980, J.V. _{Armitage, ed.,}_CambridgeUniv. Press 1982. MR 84g:12009.

_(1986),

209-220. MR 88a:11121.

_(1982),

693-707. MR 84e:12005.

(20)

8. A. LEUTBECHER and J. _MARTINET,Lenstra’s constant and Euclidean number fields, Astérisque 94 _(1982),87-131. MR 85b:11090.

9. A. _LEUTBECHER,Euclidean fields having a _largeLenstra constant, Ann. Inst.

Fourier _(Grenoble)35. no.2 _(1985),83-106. MR _86j:11107.

10. J. HOFFSTEIN and N. JOCHNOWITZ, On Artin’s _conjectureand the class

num-ber _ofcertain _{CM fields,}Duke Math. J. 59 _(1989),553-563.

11. J. HOFFSTEIN and N. _JOCHNOWITZ,On Artin’s _conjectureand the class

num-ber _ofcertain CM _fields-II,Duke Math. J. 59 _(1989),565-584. See also _Bl,B2,B5.

E. Bounds for _regulatorsand norms of ideals in ideal classes

1. M. _{POHST, Regulatorabschätzungen für}total reelle _{algebraische Zahlkörper,}J. Number Theory 9 _(1977),459-492. MR 57 _#268.

2. G. GRAS and M.-N. _GRAS,Calcul du nombre de classes et des unités des

exten-sions abéliennes réelles de Q, Bull. Sci. Math. 101 _{(2) (1977), 97-129.}MR 58 #

586.

3. M. _POHST,Eine _{Regulatorabschätzung,}Abh. Math. Sem. Univ. _Hamburg47

(1978),

95-106. MR 58 _#16596.

4. R. _ZIMMERT, Ideale kleiner Norm in Idealklassen und eine Regulatorabschätzung, Invent. math. 62 _(1981),367-380. MR _83g:12008.

5. G. _POITOU,Le théorème des classes _jumellesde R. Zimmert, Sém. de Théorie des Nombres de Bordeaux

_(1983-1984).

_{Exp. #}_5,4 pp., Univ. Bordeaux 1984,

(Listed

in MR _86b:11003.)

6. J.

OESTERLÉ,

Le théorème des classes jumelles de Zimmert et les formules

ex-plicites de Weil. pp. 1.81-197, Sém. Théorie des _Nombres,Paris 1983-84, C. Gold-stein _ed.,Birkhäuser _Boston,1985.

7. J. _SILVERMAN,An _{inequality connecting}the _regulatorand the discriminant _ofa

number _field,J. Number _Theory19 _(1984),437-442. MR 86c:11094.

8. T.W. CUSICK, Lower bounds _{for regulators.}pp. 63-73 in Number Theory,

Noord-wijkerhout 1983, H. _{Jager ed.,}Lecture Notes in Math. # 1068, Springer 1984. MR 85k:11052.

9. A.-M. BERGÉ and J. _MARTINET,Sur les minorations _{géométriques}des régu-lateurs. pp. 23-50, Séminaire Théorie des Nombres, Paris 1987-88, C. Goldstein ed., Birkhäuser _Boston,1990.

10. E. _{FRIEDMAN, Analytic formulas for regulators of}number fields, Invent. math. 98 _(1989),599-622.

11. M. POHST and H. ZASSENHAUS, Algorithmic Algebraic Number Theory,

Cam-bridge Univ. Press. _(1989).

12. R. SCHOOF and L.C. _{WASHINGTON, Quintic polynomials}and real cyclotomic fields with large class _numbers,Math. Comp. 50 _(1988),543-556.

(21)

Acta Arith. 54 _(1989),155-170.

14. A.-M. BERGÉ and J. MARTINET, Minorations de hauteurs et _{petits régulateurs}

relatifs, Sém. Théorie des Nombres Bordeaux _(1987-88)._Exp.#11,Univ. Bordeaux 1988.

15. A. COSTA and E. FRIEDMAN, Ratios of regulators in _totallyreal extensions of number _fields.to be _published.

16. E. FRIEDMAN and N.-P. _{SKORUPPA, Explicit formulas for regulators}and ratios of regulators of number _fields._manuscriptin preparation.

17. T. W. _{CUSICK, The : egulator spectrum of totally}real cubic fields. to appear.

F. Determination of minimal discriminants

1. P. CARTIER and Y. ROY, On the enumeration of quintic fields with small

dis-criminants, J. reine _angew.Math _268/269_(1974),213-215. MR 50 # 2119. 2. M. _{POHST, Berechnung}kleiner Diskriminanten total reeller _{algebraischer}

Zahlkörper, J. reine _angew.Math. _{278/279 (1975),}278-300. MR _{52 #}8085. 3. M. _POHST,The minimum discriminant _ofseventh _{degree totally}real _algebraic

number fields. pp. 235-240, Number theory and _algebra,H. Zassenhaus _ed., Aca-demic Press 1977. MR 57 _#5952.

4. J. LIANG and H. ZASSENHAUS, The minimum discriminant _ofsixth _degree

to-tally complex algebraic number field, J. Number Theory 9 _(1977),16-35. MR 55

# 305.

5. M. _POHST,On the computation of number fields of small discriminants _including the minimum discriminants _ofsixth _{degree fields,}J. Number Theory 14 _(1982), 99-117. MR _83g:12009.

6. M. _POHST,P. _WEILER,and H. ZASSENHAUS, On effective computation of fundamental units, Math. _Comp.38 _(1982),293-329. MR 83e:12005b.

7. D.G. RISH, On _algebraicnumber _fields_of_degree_five,Vestnik Moskov. Univ. Ser. I Mat. Mekh. no _2,_(1982),76-80. _Englishtranslation in Moscow Univ. Math. Bull. 37

_(1982),

no. 99-103. MR _83g:12006.

8.. F. DIAZ Y _DIAZ,Valeurs minima du discriminant des _corpsde _degré7 _ayantune

seule _{place réelle,}C.R. Acad. Sc. Paris 296 _(1983),137-139. MR 84i:12004. 9. F. DIAZ Y DIAZ, Valeurs minima du discriminant pour certains types de corps

de _degré_7,Ann. Inst. Fourier _(Grenoble)34, no 3 (1984), 29-38. MR 86d:11091.

10. K. _{TAKEUCHI, Totally}real algebraic number fields of degree 5 and 6 with small discriminant, Saitama Math. J. 2 _(1984),21-32. MR 86i:11060.

11. H.J. GODWIN, On _{quartic fields of signature}one with small discriminant. _II,

Math. _Comp.42 _(1984).707-711. _Corrigendum,Math. Comp. 43 _(1984),621. MR 85i:11092a, 11092b.

12. F. DIAZ Y _DIAZ,Petits discriminants des corps de nombres totalement imagi-naires de _degré_8,J. Number _Theory25 _(1987),34-52.

(22)

J. reine angew. Math. 375/376 (1987), 12-23. MR _88g:11080.

14. F. DIAZ Y _DIAZ,Discriminants minima et _petitsdiscriminants des corps de nombres de degré 7 avec _{cinq places réelles,}J. London Math. Soc. 38 _{(2) (1988),} 33-46..

15. J. BUCHMANN and D. _FORD,On the _{computation of totally}real _{quartic fields} of small discriminant, Math. Comp. 52 _(1989),161-174.

16. S.-H. KWON, Sur les discriminants minimaux des corps quaternioniens. preprint 1987.

17. P. LLORENTE and J. QUER, On _totallyreal cubic fields with discriminant D

107,

Math. Comp. 50 _(1988),581-594.

18. J. BUCHMANN, M. POHST and J. v. _SCHMETTOW,On the computation of unit groups and class groups of totally real quartic fields, Math. Comp. 53 _(1989), 387-397.

19. A.-M.

_BERGÉ,

J. MARTINET and M. _OLIVIER,The _{computation of}sextic _fields with a _{quadratic subfield.}in Math. _Comp.to appear.

20. F. DIAZ Y DIAZ, Table de corps quintiques totalement réels. Université de Paris-Sud, Département de _{Mathématiques, Orsay, Report}no. _{89-14, 35}_{pp., 1989.}

21. M. POHST, J. MARTINET and F. DIAZ Y _DIAZ,The minimum discriminant _of totally real octic fields, J. Number _Theory.to _appear.

G. Small zeros of Dedekind zeta functions

1. J. _HOFFSTEIN,Some results related to minimal discriminants. pp. 185-194, Num-ber _Theory,Carbondale 1979, Lecture Notes in Math. _#751,

Springer

1979, MR 81d:12005.

2. A. _NEUGEBAUER,On zeros _ofzeta _functionsin low _rectanglesin the critical strip. (in Polish), Ph.D. Thesis, A. Mickiewicz University, Poznan, Poland, 1985. 3. A. NEUGEBAUER, On the zeros _ofthe Dedekind _{zeta-function}near the real axis,

Funct. _Approx.Comment. Math. 16 _(1988),165-167.

4. A. NEUGEBAUER, Every Dedekind _{zeta-function}has a zero in the _rectangle

1/2 ~ 03C3 ~ 1, 0 t

60,, Discuss. Math.. to _appear.

5. A.M. ODLYZKO, Low zeros _ofDedekind zeta _{function. manuscript}in _preparation.

H. Other related _papers

1. J.-F. MESTRE, Formules _expliciteset minorations de conducteurs de variétés algébriques, Compositio Math. 58 _{(1986), 209-232.}MR _87j:11059.

2. E. _FRIEDMAN,The zero near 1 _{of an}ideal class zeta _function,J. London Math. Soc. 35 _{(2) (1987).}1-17. MR _88g:11087.

3. E. FRIEDMAN, Hecke’s integral formula, Sém. Théorie des Nombres de Bordeaux

(23)

I. Other papers cited in the text

1. E. _LANDAU,Zur Theorie der Heckeschen _{Zetafunktionen,}welche komplexen Charakteren _entsprechen,Math. Zeit. 4

_(1919),

152-162.. _Reprintedon _{pp. 176-186}

of vol. 7, Edmund Landau : Collected _Works,P.T. _Bateman,et _{al., eds.,}Thales

Verlag.

2. E. LANDAU, Einführung in die elementare und _analytischeTheorie der algebrais-chen Zahlen und der Ideale, 2nd _ed.,_{Göttingen (1927).} _{Reprinted by Chelsea,} 1949.

3. R. _REMAK,Über die _Abschätzungdes absoluten _Betragesdes _Regulatorseines algebraischen Zahlkörpers nach unten, J. reine angew. Math. 167. _{(1932), 360-378.} 4. R.P. BOAS and M. _{KAC, Inequalities for}Fourier transforms of positive functions,

Duke Math. J. 12 _(1945),189-206. MR 6-265.

5.. A.P. _{GUINAND, A}summation _formulain the _theoryof prime numbers, Proc. London Math. Soc. 50 ₍₂₎

_(1948),

107-119. MR 10, 104g.

6. A.P. GUINAND, Fourier reciprocities and the Riemann zeta- function, Proc. Lon-don Math. Soc. 51 _{(2) (1949),}401-414. MR 11, 162d.

7. A. _WEIL,Sur les _{"formules explicites"}de la théorie des nombres _premiers,Comm. Sem. Math. Univ. Lund, tome _{supplémentaire}_(1952),252-265. MR 14, 727e. 8. R. _{REMAK, Über Grössenbeziehungen}zwischen Diskriminante und _Regulatoreines

algebraischen Zahlkörpers, Compos. Math. 10 _(1952),245-285. MR 14, 952d. 9. R. REMAK, Über algebraische Zahlkörper mit schwachem _{Einheitsdefekt, Compos.}

Math. 12 _(1954),35-80. MR 16, 116a.

10. A. _WEIL,Sur les _{formules explicites}de la théorie des nombres, Izv. Akad. Nauk SSSR Ser. Mat. 36 _(1972).3-18. MR 52 # 345. _Reprintedin A. _Weil,Oeuvres Scientifiques, vol. 3, pp. 249-264, Springer 1979.

11. H.-J. BESENFELDER, Die Weilsche _"ExpliziteFormel" und _temperierte Distri-butionen, J. reine angew. Math. 293/294 (1977), 228-257. MR 57 _#254. 12. J.-P. SERRE. note on _p.710 in vol. 3 of Jean-Pierre SERRE, Collected Papers,

Springer 1986.

13. H. COHEN and H. W. LENSTRA Jr., Heuristics on class groups of number fields.

pp. 33-62 in Number Theory, Noordwijkerhout 1983, H. _Jagered., Lecture Notes in Math. # 1068, Springer 1984. MR 85j:11144.

14. J.-P. _SERRE,Sur le nombre des _pointsrationnels d’une courbe algébrique sur

un _corps_fini,C.R. Acad. Sci. Paris 296 _(1983).sér. _I,397-402. MR 85b:14027. Reprinted on _{pp. 658-663}in vol. 3 of Jean-Pierre Serre, Collected _{Papers, Springer} 1986.

15. A.M. ODLYZKO and H.J.J. te RIELE, Disproof of the Mertens _conjecture,J. reine angew. Math. 357 _(1985),138-160. MR 86m:11070.

16. J.-M. FONTAINE, Il _n’ya _{pas de}variété abélienne sur _Z,Invent. math. 81 _(1985), 515-538. MR _87g:11073.

17. H. COHEN and J. _MARTINET,Etude _heuristique_{des groupes de}classes des corps de nombres, J. reine angew. Math. 404 _(1990),39-76.

(24)

18. A. BOREL and G. PRASAD, Finiteness theorems _fordiscrete _{subgroups of} bounded covolume in _semi-simple_{groups, Publ:}Math. I.H.E.S. 69 _{(1989), 119-171.}

AT & T Bell Laboraties Murray Hill, New Jersey 07974 U.S.A.