Étude théorique de la structure de bandes des systèmes périodiques

RESEARCH OUTPUTS / RÉSULTATS DE RECHERCHE

Author(s) - Auteur(s) :

Publication date - Date de publication :

Permanent link - Permalien :

Rights / License - Licence de droit d’auteur :

Bibliothèque Universitaire Moretus Plantin

Institutional Repository - Research Portal

Dépôt Institutionnel - Portail de la Recherche

researchportal.unamur.be

University of Namur

Étude théorique de la structure de bandes des systèmes périodiques Andre, Jean-Marie

Publication date: 1968

Link to publication

Citation for pulished version (HARVARD):

Andre, J-M 1968, 'Étude théorique de la structure de bandes des systèmes périodiques', Ph.D., UCLouvain.

General rights

Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain

• You may freely distribute the URL identifying the publication in the public portal ? Take down policy

If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim.

"

.

UNIVERSITÉ CATHOLIQUE

FACULTÉ DES SCIEN

~ ~ ~ A ; " 1 'NIVER91TAIRIS DE NAMUR

ÉTUDE THÉORIQUE

LABORATOIRE DE

CHIMIE THÉORIQUE APPUQUIE RUE DE BRUXELLES 61 B-5000 NAMUR (BELGIQUE) T~L 081 / 22 90 61

DE LA

STRUCTURE DE BANDES

DES

SYSTÈMES PÉRIODIQUES

1968 Dissertation de Doctorat Jean-Marie ANDRÉ

Examinateurs MM. Les Professeurs A, BRUYLANTS J .C. JUNGERS A. VAN TIGGELEN M, VAN MEERSSCHE G, LEROY

Qu' i l me so.it permis à la f'n de ce travail d'exprimer mes remerciements les plus chaleureux

a

Monsieur le Professeur LEROY pour l'intérêt pro-fond qu'il a porté à mes recherches et pour le soutien qu' i l m'a toujours accordé.

Je tiens également à exprimer ma sincère re-connai ssance â tous les professeurs de la Faculté des Sciences qui ont contribué à ma formation scientifique; en particulier, j 'exprime ma vive gratitude à Monsieur le Professeur VAN MEERSSCHE qui m'a initié à la chimie physique.

Enfin, je remercie l 'Institut pour l'Encou ra-gement de la Recherche Scientifique dans l 1_Industrie et l'Agriculture pour les mandats successifs qu'i l m'a oct royé ainsi que l'Université Catholique de Louvain, le Ministère de l'Educat 'on Nationale et de

la Culture, la Chambre de Commerce Suédoi se en Belgi-que et au Luxembourg pour les subsi des qui m'ont per-mi s d'effectuer plusieurs séjours à l 'étranger.

RESUME ,

Nous proposons une méthode• théorique permettant une étude quantitative de la structure de bandes des systèmes périodiques conjugués.

Cette méthode, la méthode des orbitales cristallines, ré-duit, grâce à l 'utilisation du ·théorème de BLOCH, l'ordre élevé du déterminant séculaire des grands systèmes périodiques.

Reposant sur l 'approximati on monoélectronique, ce pr océ-dé exige la connaissance des éléments de matrice de l'opérateur du champ auto-cohérent du système considéré, Nous déduisons le formalisme complet de l a méthode lCAO-SCF-CO et son schéma de calcul. En par ticulier, les phénomènes de divergence qui apparais-sent si l'on sépare les termes d' interaction électronique et les termes de coeur de l 'opérateur monoélectronique sont examinés en détail.

1 Deux appli cations sont décrites. Dans l 'étude d 'une chaîne polyénique infini e, nous reproduisons l ' a lternance entre les lon -gueurs de liaison. Notre procédé est le seul à fourn1r ce résul-tat sans référence à 'expérience. La structure de bandes nous amène, de plus, a formuler une nouvelle théorie de l 1_{évolution du} spectre électronique des polyênes en fonction de la cai l le du sys-tème. Dans l 'étude dü graphi te, les caractér i.stiques électroniques sont reproduites correctement et notre procédé permet de di stinguer les propriétés d'un plan de graphite de celles du cristal réel.

SAMENVATTING.

Wij stellen een teoretische metode voor, om kwantitatief de bandenstruktuur van gekonjugeerde periodieke systemen te be -studeren.

Dank zij het gebruik van de stelling van BLOCH, verlaagt deze metode de hoge orde van de seculaire determinant in grote periodieke systemen.

Gesteund op de mono-elektronische benadering, vereist dit procédé de kennis van de matrixelementen van de self-consistent -field-operat or van het beschouwde systeem. Wij ontwikkelen volle-dig het formalisme van de LCAO-SCF-CO-metode, evenals haar reke n-schema. De divergentieproblemen, die optreden, indien men de

elektronen-wisselwerkingstermen en de core-termen scheidt, worden bijzonder nauwkeurig onderzocht.

rü j beschrijven twee toepassingen. In de studie van een oneindige polyeenketen, wordt de afwisseling tussen de bindings-lengten weergegeven. Ons procédé is het enige, dat dit resultaat bereikt zonder beroep te doen op het experiment. Bovendien leidt de bandenstruktuur ons tot de formulering van een nieuwe teorie over de evolutie van het elektronisch spektrum van de polyenen in funktie van hun lengte. In de studie van grafiet, worden de elek-tronische karakteristieken korrekt voorspeld, en ons procédé laat toe de eigenschappen van een grafiet-vlak te onderscheiden van die van het werkelijke kristal.

INTRODUCTIONo

Du point de vue théorique, un cri st al ou un système périodique infini est une molécule géante caractérisée par une symétrie de translation.

Dans l'approximation du modèle indépendant, chaque électron est décrit par une orbitale décrivant sa position et son énergie dans le champ moyen des noyaux et des autres élec-trons du systèmeo En passant d'un système moléculaire à un cristal, les niveaux monoélectroniques convergent l'un vers l'autre et donnent nai ssance à une série de bandes d'énergie caractéristiques du cristal infini.

La structure de ces bandes électroniques permet la détermination de toutes les caractéristiques énergétiques. En • particulier, le premier potentiel d'ioni sation et l 'é

lectro-affinité peuvent être assimilés respectivement aux énergies de la dernière orbi tale occupée de la bande de valence et de la première orbitale inoccupée de la bande de conduction et la dif-férence ·entre ces deux quantités est une mesure de la première énergie d'excitation du système. De plus, les populations élec-troniques et les largeurs de bandes interdites sont fondamenta-les dans l'interprétat ion des propriétés magnétiques et conduc-trices des solidesn

Le but du présent travail est de proposer une méthode permettant une étude quantitative de la structure de bandes des systèmes périodiques conjugués. Après une étude critique des différents procédés util i sés en physique de l 1

état solide, nous déduisons le formali sme de la méthode des orbitales cristallines que nous appliquons ensuite à l'étude des propriétés électroni-ques et des caractéristiques énergétiques d'une chaîne polyénique infinie et du cristal de graphi te.

.l.

CHAPITRE I __ E S P R PK I PAL c. S M ê. . HO D f. 5 1

·n

L 1 S E C S EN PH Y S I QUE DE

I . l. La th€orie des orblt ales dans le trait~~ent théorique des

systèmes pniyélectr--1üques.

- - -

- -

-

- -

--·---

-J _{usqu a} 1 ,. ·• _{_a ~~n} " • d _.u · _i~ · ème _si' _ec' _{_e}1 _{, on a}

a

_me·tat . _i . t _{genera e-}~ ~ 1 ment que la matière était constituée d ' at.ornes, insécables par définition. La dé~o~vsrte du rayonnement ca~hodique par THOM-ON en 1897 et les és~ltats de RUTHERFORD e~ 1911 sur la diffrac-tion des particules :x amenèrent à postuler l 'exist ence de

noyaux positifs e~ d êlectrons négatifs en ~~terac~ ·on électro-st atique.

La théo:c::..e at..Y.r..iq:.1e de BOhR co,:i ·.:n . .:. tu1:.• le p:cemJ.er essai sati sfaisant d'int erprètation d~ mouveme~c des électr n~ dans les atomes o Rerc a:cql;a.7J.t l lanalogie e1n.re le3 dimensions d un moment angul ai re et la constante de PLANCK, i i proposait un postulat de q:1a:'.'l-~i f i cation imposc1nt a.·.1.x ê:tcct:r.:)n3 d I _{u.n atome} de se mouvoir :sur él-2:s ,.::;ir conférenc2s r,empl.issan_ la condition:

(_p + _{., r} ... J -- n -h 2

-. "ff ( I-1)

Combin&nt cette der;:üère avec .les rblati.0:,12 de la M:écan.:'~que Classique

E.: -

e2

2m a ( I -2)

- 2

-E

=

~

-

e2

2m a (I-3)

BOHR expliquait remarquablement la structure du spectre de l'hydrogène atomiq· e, retrouvait la constante de RYDBERG et ouvrait le domaine de l'atomistique moderne.

La théor ie de BOHR a donné naissance à deux idées fé-condes le concept d'orbites électroniques définies et la relation étroite entre la répartition des électrons dans les atomes et la structure de la matière.

Malheureusement, cette théorie n'est vérifiée que pour les systèmes monoélectroniques : l'atome d'hydrogène et les ions hydrogénoides. Cette limitation est due essentiellement au fait que la théorie de BOHR est un mélange de notions clas-siques et quant queo. Bien vite, i l apparut nécessaire d'aban-donner les notions classiques en .généralisant les conceptions quantiques de BOHRo , •

Cette gPnéralisation fut accomplie indépendamment en 1925 par SCHRODINGER, HE ENBERG et DIRAC dont les théories étaient vérifiées expérimentalement dès 1926 par DAVISSON et GERMER. Un des résultats importants de la nouvell e t héorie quantique fut l'abandon de la notion d'orbite. Les relations d'incerti-tude d'HEISENBERG imposent, en effet, l'impossibilité de dé-terminer, a priori, la position et la vitesse d'un électron et i l nous est désormais impossible d'observer le mouvement individuel d'un électron. Tous les renseignements possibles sont contenus dans une fonction d'état du système, appelée fonction d'onde. Le carré de son module nous renseigne sur la probabilité de trouver le système dans une configuration donnée. La notion d'orbite ou de trajectoire est remplacée par celle de pr babi l ité d'existence de certaines configura-tions du système.

- 3

-La fonction d'onde du système est solution d'une équa-tion différenti elle appelée "équation de SCHRODINGER" :

(I -4) ,.,

Dans le cadre de l 'approximation de BORN et OPPENHEIMER et en ne considérant que les interactions coulombiennes entre

élec-,. t

trons et noyaux, l 1_{hamiltonien d'un système, dans un état} stationnaire, s'écri t

H

=

n

I

(-i=1 Z e2 \ _E_) + _21 ) ) L, r . ~ ~ p lp i i '

m désigne la masse de l'électron, Z _p le nombre de protons du noyau p, r . une distance noyau-électron,

lp

rii' une dist ance électron-électron et r une distance noyau-noyau.

pq

(I-5)

Les solutions exactes de l 'équation de SCHRODINGER indépendante du temps ne peuvent, à l'heure actuelle, être obtenues que dans le cas des systèmes monoélectroniques. Il est, dès lors, néce s-saire de recourir à des méthodes d'approximation pour détermi -ner les fonctions d'onde des €tats stationnaires d 'un système polyélectronique.

Le procédé qui s'est avéré le plus utile repose sur le théorème des variations. Il est, en effet, aisé de montrer que les énergies associ ées aux états stationnaires d'un système sont des limites inférieures pour les va eurs moyennes de l'é-nergie obtenues à partir d'une fonction approchée. Il est pos -sible, dès lors, d' introduire dans une fonction d'essai un ou

4

-plusieurs paramètres variationnels qui peuven~, par minimisation, faire converger l a s luti on approchée vers la solution réelle.

Une forme d'essai généralement ut.il -· sée pour la fonction d'onde est le produi c de fonctions monoélect r niques appelées orbitales par analogie avec les orbites de l 'atome de BOHR. Cette situation correspond, physiquement, à un modèle de particules in-dépendantes et se traduit par un hamiltonien rnonoélectronique de la forme: h 2

z

e 2 h .

₌

-

- -

,-v 2

-

\ _E__ -t- V. l 8··:2m i !., r . _l p l p ( I-6)

Vi peut s' interpréter comme l e potenti el électrique moyen que ressent l'électron i .

Ce procédé dû a HARTREE[l], ne t ient pas compte du prin-cipe de PAULI . SLATER[2] a amélioré l 'idée de HARTREE en appro-chant la fonction d 'onde par un déterminant. construit sur des spins-orbitales, produits de fonctions d'espace et de fonctions de spins:

\jl

=

A ~ ( 1 ) a ( 1 J ~

1 t 2 ) B ( 2 ) . . . . ~ n ( 2 n -1 } ·:t ( 2 n -1 ) ~ n ( 2 n ) B ( 2 n )

(I-7)

Il faut remarquer ici qu'une fonction du type (I-7) n'est fonc-tion propre de l'opérateur S2 _{que si l'on ut ilise deux fois la}

z

même orbitale associée à deux fonctions de spins difffrentes .

On peut obtenir les meilleures spins-orbitales de la fonction (I-7), en résolvant la pseudo-équation aux valeurs propres de HARTREE- FOCK[ 3

J

5 ..

-

-où h2

z

e2 q1 • (1) ...

-

- -

92 _{<JJ , (l)}

-

\ _E__ _{q, ' (1)} l 8 ,T 2m 1 l -~' r ]_ p lp (I- 9)

Si les orbitales sont doublement occupées, on a explicitement:

hHf (1) h2

z

e2 <b . 1) _--

-

1/ 2 <P , ( l)

-

\ _e__ q> . (1) 1 L, ·1 8n2m l _p rlp l .,. \{[2/·'<ti"'(2) t . (2) ~ J J J e2 - [fcp . (2) cp.(2) dv 2] ct,J. (l)}(I-10) . J i rl2

SLATER[4J a discuté en détail l'interprétation d l 'équation(I-10): le troisieme terme représente évidemment l ' énf';rgie potentielle électrostatique d'un électron dans un é at i soumis au champ moyen des autres é·ectrons; lE:! quatrième t.e:r-rne, le terme d'échan-ge, possède une origine quantique sans analogie classique. Ce terme rédui t l ' inte~action flectrostatique des électrons et re -flète le principe de PAULI qui interdit à deux électrons de

spins parall~les de se trouver dans le voisinage l'un de l 'autre. Enfin, les énergies d'orbitales peuvent être reliées à des po-tentiels d'ionisati n par le théorème de KOOPMANS[SJ _

Dans le déterminan~ de SLATER, la relation avec les orbites de BOHR est devenue assez vague. Il apparai t, en effet, que dans les produits antisymé risés, nous n'avons plus de correspondance biunivoque entre électrons et orbitales. Par contre, nous gar-dons la possibi lité de visualiser la stru_ture d'un atome ou d'une molécule en uti lisant des orbitales doublement occupées.

- 6

-On peut d'ailleurs décrire le syst ème périodique des éléments sur

cette base.

Signalons, enfin, qu'il n'existe pas de correspondance univoque

entre foncti on d'onde et orbitale. En effet, toute t ransformation

unitaire modifie lea orbitales sans transformer les fonct ions

d'onde. C'est ainsi que, dans .Les moléc11les , on peut ut.ili ser des

orbitales, soi t délocalisées s~r l'ensemble des noyaux, soit loc

a-lisées autour des coeurs, des liaisons et des paires l ibres des

atomes const it uants.

En concluslon, on peut di re que l'approximation du modè-le indépendant fournit un langage pour déc~ire le mouvement des

électrons dans les atomes, les molécules ou les solides. Si on

veut obt enir des données quantitatives, i l est nécessai re de r

é-soudre les équations de HARTREE-FOCK.

Celles-ci sont tres d~fficilement solubles dans le cas des sol i -des et i l est néces ~i::iire de simp Lifi.er la forme de l 'équation

monoélect ronique (I-10); nous montrons dans le paragraphe 2 les

procédés utilisés en physiq~e de l 'éta solide"

Par contre, même la t héorie élaborée de HAR,,..REE-FOCK ne calcule que 99,5% de la valeur expérimentale de l 'énergie de l 'ét at

fondamental. Si cet accord est satis.fa.i.sant., l 'erreur est du

même ordre de grandeur que les différences énergétiques que l 'on

peut mesurer. Ceci montre la n€cess1té de surpasser la théorie

originale de H/i.RT EE-FOC K en tenant compte de la corrélation

électronique. Nous décrirons dans le paragraphe 3 les procédés

- '7

--I.2. La thforie des bandes dans les systèmes périodiques infinis.

I.2.1. Le théorème de BLOCH et les zones de BRILLOUIN,

---

-

----

--

--Avant d'examiner les méthodes d'approximation utilisées

pour résoudre l'équat ion monoélt i l est nécessaire de

simplifier le problème en tenant compte de la périodicité carac-téristique des cristaux. Tout système pér iodique infini possède, en effet, une symétrie de translation que l'on peut caractériser

·~--- ·+ + par trois vecteurs a

1, a2 et a3 délimitant une mai lle primitive du cristal.

Le réseau cristallin est alors représenté par un ensemble de noeuds définis par i:-c:.ation

 n

=

(I-11)

avec n

1, n2, n3 entiers.

L'expression I-11) peut se mettre sous la forme matr.icielle:

alx a2x a3x nl

A n

=

_{aly a 2y} a _n2 (I-12)

3y

a.

.Z a2z a3z n3

De plus, i l est avant ageux de considérer un réseau réciproque construit sur trois vecteurs de base

b

1 ,

b

2,

b

3, remplissant les condit ions:

...,,. -~

(a . , b .) ··- 2..-, à. ,

i J i J (I-13)

Le réseau réciproque possède ainsi l'ensemble de noeuds:

- 8

-qui s'exprime en langage matriciel de façon analogue à (I-12):

blx bly blz m B = (ml' m2, m3) b2x b2y bLz

b3x b3y b3z

L' équation (I-13) se met plus simplement sous la forme:

A.B

=

2ii 1

(I-15)

(I-16)

Les vecteurs de base du réseau r~ciproque peuvent, dès lors, s'obtenir facilement a partir des vecteurs du réseau direct par une i nversion de matrice.

En effet,

A B

=

2'.r .1.

A -l A B -- A - l 2 rr 1 1 B

=

2 -,.- A - l 1

(I-17)

A partir de ces consi~érations,on défini t un opérateur de trans -lation T(An) tel qu'il agisse sur une fonction f (r) en fournis

-+ _.,_ sant la valeur de cett e fonction au point ,r + An):

T (An) f (~) == f

(f

+

An) (I-18)

➔- -,. Pour un système périodique, caractérisé par les vecteurs a

1, a2,

â

3, l'opérateur de translation T commute avec l'hamiltonien monoélectroniqueç

Soit:

T (An) {h (rj ç, (f) } = h (f + An) <P (r

+

An) (I-19)

si on admet l a périodicité du potentiel:

h (r

+

':J.:n) ·- h (r) (I-20)

(I-19) s'écrit maintenant:

T (An) { h (

r)

q, (f) }

=

h (f) T (An) <P ( ~) (I-21)

L'équation (I- 21) définit la condition de commutat ion des opér a-teurs Tet h.

Il faut remarquer que l a relation "cruciale" est l'équation(I-20). L'opérateur monoélectronique contient, en effet, des termes de répulsion électronique et dléchange. On voit immédiat ement que le potenti el de répulsion électronique est périodique grâce à la périodicité de la densité électronique; le potentiel d 'échange, par son caractère non local, nécessite un examen plus approfondi .

En effet, si l 1_{on associe l 'opérat eur de translation au}

déplacement d'une seule coordonnée (1), par exemple, on peut écrire: (I-22) T (An) . \ 1 -~ .+ ) ➔ 1 dv 2} ➔ (I-23)

=

tL_. •_/ <P_J , (r2

<Pi

(r 2) _{➔ +} <l>j (rl) j ' _{lr1-r2 f} ) r i<· ➔ ·+ 1 dv :r

:ï\

+An> (I-24)

=

{LJ<f>,(r 2) <J>.(r2) Q) • . J l , 1

r

1 +Ân-1\ 1 2 _J J

10

-En changeant l'origine de l 'intégration sur les coordonnées (2) de An, on ne modifie pas la valeur de l'intégrale, et on obt ient ainsi l ' équation (I-26):

-~ ,... ..,- ·+ .... l : _( <Pj (r 2+An) cp1 (r2+An) _dv 2 1 -► ➔ (I-22)

₌

"·.; (r 1 +An) j 1

r

1 +Ân-1\-An i J (I-25) t.- -+ + qi • _{r 2) cpi(r2)} T (A.n) </> • (t: . 'i' ( _{J dv} 2}

=

1. L. 1 j _{lr 12I} J .L (I- 26)

qui vérifie les propt iétés de commutation du potentiel d 'échange et de l'opérateur de translationo

Puisque l 'opérateur monoélectronique h et l 'opérateur de translation commutent, i.ls admettent le même système de fonctions propres, et i l est normal de choisir les orbi·tales parmi l es

fonctions propres de 'opérateur de translationo

BLOCH[6] a montré que ces fonctions propres pouvaient s'écrire :

➔ ·+

(+ ->- )

·r

.-A ... ) .-+) _ eikAn ".· r_...1:.··-.,

</> r + An -· l n qi t r w , - 1 (I- 27)

L'expression (I-27) peut encore se simplifier et l'on peut prendre pour fonctions propres de l'opôrateur de translation des fonctions de la forme:

-7 ➔

et· +, ik. r ;~ ...,.r)

qi(Jr, rJ == ê U(r .. ₁ (I-28)

'

si u(t ,

f)

possède la pfriodicitf du r{seau.

+ ➔ L'équation (I-28) montre que les orbitales cristallines qi (k ,r ) sont caractérisées par un vecteur d'onde

k;

défini dans l'espace réciproque . En chaque point de cet espace réciproque, on peut , dès lors, définir une orbitale cristalline satisfaisant le théo-rème de BLOCH (I-27)

a

laquelle est associée une énergie mono-électror.ique 2(k) . Nous verrons dans la sui te comment préciser les valeurs de r (f) .

-· 11

-Le raisonnement ci-dessus concerne un cristal parfai t, in-ini dans les trois directions de l'ë~~ace. L'ensemble des

_,..

opérat eurs de translation T(An) est d'ordre i nfini. En vue

dtétudier un cri stal réel de dimensions finies , i l est né

ces-saire d 'introduire des conditions aux l imites. Toutefois, vu

le faib:e nombre d'atomes en surface du cristal, i l est normal

de penser que ces condit ions aux limites ont peu d'influence sur

le comportement global du système et i l est ainsi li cite d 'uti

-liser les conditions les plus commodes au poi nt de vue mat

héma-t ique. On utilise universellement l es conditions périodiques de BORN-VON KARMAN[?]•

Leur interprétation physiq e se conçoit le plus facilement en

examinant une chaine de N atomes identiques. Si le nombre d'at o-mes N est très grand, le comportement dlune chaine ouverte ou

fermée est ident ique. Les effets des limi tes ne sté.tendent, en

effet, que sur quelques atomes. Ainsi , si l Lon considère une

chaine ouverte, on peut trai ter le problème t héorique comme une

chaî ne cyclique, en admet.tant que l 1_{orbitale reprend périodi}

-quement la même va e r après N atomes. Ceci permet d'uti liser

un ensemble d'opérateurs d'ordre fini. Dans l'étude des propri

-étés de cette chaîne ouverte, il est nécessaire de prendre un

nombre d'atomes N suffisamment grand pour que les résultats en

soient indépendantso Dans ces conditions, le problème sera

traitP correct ement, excepté en ce qui concerne les effets de surface, aspect important que nous négligerons au cours de ce travail.

Dans le cas tr idimensionnel, on définit par analogie

un domaine cyclique délimité par les arêtes N

1; 1, N2

i

2, N3

i

3

et contenant ainsi N ~ N

1.N2.N3 cel lules uni taires . Si ce

domai ne est suff' samrnent grand et possède dans chaque direction

des dimensions macroscopiques, plutôt qu'atomiques, nous

pou-vons êt re sfirs que les résul tats physiques obtenus seront

- 12

-Au point de vue formel, l'application des conditions aux limites de BORN-VON KARMAN revient à écrire:

. ·➔

=

cp(r) (I-29)

De ces conditions associées au théorème de BLOCH (I-27), dé-coule directement: ➔ _,. ikNa 1 e -- e si l'on précise

k:

-, ➔ ikNa 2

=

e . k,l- ➔ l Na 3

=

1

les conditions (I-30) ü,1p·.:,sent automatiquement:

K 1 Nl

=

ml ml ent ier K2N2

=

m2 m? - entier K'3,';3 ... _-~-Y1'" _. -.) ..J m3 ;:: er:t:i .. sr (I-30) ( I-:3 l)

et les seules valeurs possibles de

k

stobti ennent immédiatement:

k

₌

m

_"ff""

l .... _bl + m2

_b2

+ m3

E

1 N2 N3 3 -1 (mlbl ➔ =" (I-32)

=

N ;- _{m2b2 + m3b3)}

Les opérateurs de t ranslation T(An) sont des opérateurs cycli-ques d'ordre No

- L1 -En effet:

r

(NA) -P t

r) -

r~\

-- (!)

f

r ,-

NA) ' ' - l.cp(r·) (I-33) d'où _,. (TN - 1) ·- 0 (I-34)

Pn~r des ~r0upes finis, on peut dêfinir aisément les

opé~a-teurs de proJection correspondant aux translations par la

technique de LOWDIN[B] : -1 0 _k ~ N ,'. e -l·➔ ikAn T(-Anj (I~35J n

Il est aisé de mon~rer que les opérateurs de projection

satis-font les relations suivantes:

()~

-Ok () i. Ok ri

o

+

k

-0 k ... 00 )., f ' V K 0 ... ₀ (I-36) si k ~ 9v (I-37 J s i k -/: t (I-38) St est un opérateur quelconque (I-39)

Le forrnalism8 très ,,,:iirnple des cpérateu1:s de projection permet de démontrer plu.siPurs théorèmes nécessaires dan;:, les

- 14

-Une fonction de BLOCH s'écrit plus simplement sous la forme:

(I-40)

L'opérateur de projection (Ok) "sélectionne" dans la fonction

<P(;)

la composante qui obéit au théorème de BLOCH avec le

vec-teur d'onde

k.

Dès lors, les orbitales cristallines appartenant à deux

points différents de l 'espace k sont orthogonales. En effet:

( I-41)

De plus, dans ces conditions, elles n~interagissent pas:

➔ + 1 ➔

= '-<P (r) jOk h ok' <P (r ) >

( I-4 2)

Ce thforème présente des conséquences impo1·tantes pour préciser les probabilités de transition entre différents états ou pour

élaborer un procédé d'i nteraction de configuration.

Il est égale~ent intéressant de préci ser l tévolution des énergies monoélectroniques €(k) lorsque l 'on passe d'un point à un autre dans l'espace réciproque.

Les bandes d'énergie s (k) sont symétriques vis-à-vis du point

15 -En effet:

s

t-k)

:a, <<j>(-k,r)\ h \cp(-k.,t) >

=

, <j,(r) Juk h

o

;lcp(t)

>

(I-44) puisque s k)

=

é:(-k) (I-45) +

La courbe d'énergie s k) est périodique dans l 1_espace

réciproque.

Si

K

représente une translation du réseau réciproque,

~ -+ ➔ cp (k,r) -== ok

cp

(r) ( I -4 6) ~ ➔·

·l-r

>

cp k+K,r )

-

o.

cp .!<+ ( I -4 7) Ok+K - 1 _\ ik.Ân ii<An T(-An)

=

N _:.., e e n -1 _\ l _

"kA

n T(-An) _Ok

=

N _l e

₌

(I-48) n on voi t que ~ ➔- + + ➔ cp(k,r ) :: cp(k+K,r) (I-49) et s (k)

=

s (k+k) (I-50)

- 16

-Lléquation (I-5O) nous apprend que les bandes d' énergie e(') sont p0riodiques dans l 'espace réciproque et , dès lors, tout volume 6gal à celui de la mai lle réciproque contient tous les états monoélectroniques d'un électron évoluant dans un champ de potent iel périodique. Comme i l ressort de l'équation (I-32), ce volume contient N états correspondant à N extrémités pos-sibles du vecteur

k

o

BRILLOUIN a proposé de choisir ce polyèdre d'une façon bien particulière. Dans le langage de bandes d'éner-gie, l'équation (I-5O) montre que deux poi nts

k

et

k'

séparés par une translat ion du réseau réciproque sont équivalents.

➔ - ➔• • .l.

kl

=

k + k (I-51)

En imposant la condi t ion supplémentaire

j

k

'

12

=

lk

l

2_{, BRILLOUIN} obtient les équations des plans qui bissect ent normalement les lignes joignant l 'origine aux noeuds les plus proches du réseau. Le polyèdre compris entre ces plans est connu comme la première zone de BRILLOUIN et sert à représenter tous les états mono-électroniques possibles dans un systèmeo Les équations de ces plans sont:

l

k'

l

2

₌

_i~l

2 ₌

_!

_k

₊

_'

_Kl

2 _(I-52) :t· ou encore ➔ . .,, -l• -~ 2 (k,K) - K,K) (I-53)

Il est remarquable de constater que l 'équation (I-53) corres-pond au:: candi t i ons de diffraction de BRAGG. En effet, la représentation grapnique I-1) montre clairement que si

lk' 1

=

\

k

\

e t , ,

=,

+ ~

- 17

-Figure I-1.

+ K

0t, i l est bien connu que tout vecteur du réseau réciproque

est relié à la dist ance d entre plans paral lèles du réseau direct par la relat'on:

!KI

=

2~m (I-55)

en se rappelant que k·est un vecteur d'onde relié à la l on-gueur d'onde:

211 À

on obtient sans difficulté:

\KI

d'où

2d sine= m>-.

2 2n sin. e À

L'expression (I-58) est la condition de BRAGG.

(I-56)

(I-57)

- 18

-En rPsumé, la symétrie de translation du réseau direct

permet de choi si r les solutions de l'équation monoélectronique

parmi les fonctions propres des opérateurs de translation.

Les énergies associées à ces orbitales se groupent par bandes

d'énergie, périodiques dans lLespace réci proque. Si lton se

choisit une .:··-2...'.·1.:...=! <lCmentaire,la première zone de BRILLOUIN

par exemple, et si l'on fixe les conditions aux limites de

BORN-VON KARi'1AN, i l est facile d'énumérer tous les états

mono-électroniques d 1_{un électron Pvoluant dans un champ de forces}

➔

périodiques. Le problème est de déterminer la fonction E(k)

dans la première zone de BRILLOUIN. Dans les paragraphes

sui-vants, nous résumerons les pri ncipales mét hodes d'approximation

de l'équation monoélectronique de HARTREE-FOCK,

I.2.2. La_méthode_de_l1_{électron_libre_(Free_electron Model_:_FE)}

Le procédé le plus simple de résolution de l'équation monoélectronique ( -8) , consiste à étudier l 'ensemble des élec-trons comme un gaz d'électrons sans i nt eraction[9

J.

En effet, si

nous considérons, par exemple, un système infini constitué

d'ato-mes de carbone dans un état d'hybridation sp2 comme dans les

longs polyènes, l~s deux électrons de la couche (ls) du carbone

sont fortement local isés autour des noyaux, t rois autres

élec-trons sont utilisés dans les hybrides trigonales et, dès lors,

localisés entre les coeurs d'atomes. Le sixième électron ne

possède pas de place définie dans la chaîne et sera par consé-quent délocalisé sur tout l'ensemble du système. Ceci revient à considérer un potentiel peu variable et à la l imite constant.

- 19

-Dans ces conditions, l'équation de HARTREE-FOCK devient:

(I-59) avec V .,,_(lj 0 'l'l ,;f, V:{ ,".L) ( I-60)

Remarquons que, dtaprès l 'équation précédente, et, contrairement

à ce qui est généralement admis, le modèle de l 1

électron libre

ne néglige pas les effets de répulsion et d1

échange, mais les

considère implicitement dans un potentiel constant. On peut

ainsi admettre formellement qu'une partie de l'interaction

élec-tronique est introdui te dans l'expression (I-59).

Les solutions de BLOCH s'obti ennent aisément dans ce cas

et s'écrivent:

.

(k

.,.

)

_,_

cp~E (~,r ) l i +Kn r e ·-·

-Fi

(I-61) en posant: FE .=: . _- C ~ l l. 0 ~FE(

k

'

h2 _jk+i<ni2 :.. n I J

·

-8;, 2m (I-62)

Dans le cas général, la méthode de l'électron libre

présente un int érêt considérable car elle permet de définir

aisément diver ses notions intéressantes. Si nous considérons

un cristal de N mail les et de Z électrons l ibres par maille,

- 20 ·

-à ltintérieur de laquelle tous les ~tats rnonoêlectroniques sont

doublement occupés,

(I-67)

et la valeur de FERMI:

i::

=

F (I.-68)

Enfin, ce modêle permet dtobtenir une estimation des effets d'échange: le terme d 1

fchange peut, en effet, sl~crire :

' 7 ( 1) avec • ·,'>- ·• i l.K _rl q,.(1) _·- e _j J

iv

·+ ➔• q,.(2) 1 ik 1r2 -· e l _✓v

L'fquation (I-69) prend alors la forme suivante:

e 2

V j

(I-69)

(I- 70)

L'intégration est düe à DIRAC[lü] qui précise la constante Ak:

Ak

o.

306 e 2 [2 + 1 -

--

_{r o.} (I-71) s avec k a

-

_I~

i-4 JT 2 ₃ V/N

- y

r ,._ s

- 21

-Le terme de COU~OMB ~nrrespond à une rêpulsio~ d'une densité

électroninue uniforme et constante contrebalanc~e par l'ensemble

positif des coeu~s. On voit donc que les solutions du modêle de

l'électron liore, s.ont. fonctions propres de l 'opéra t.eur d léchange

et sont donc des solutions de HARTREE-FOt:K possédant l 'énergie:

FE -H

r

,

_

;,;

\

s , r1, K., -8" 2m + __ ,_ , 2 2 ,.,. ..,_ _l.-_a2 lo l+et

1

}

1k-kn; - e jkF

i

'._2 , o. g l-a (I-72)

De plus, i l est bie0 connu que la fornte des orbitales d~pend peu du potentiel élec-~-rique du système" On peut donc admettre que les orbitales de l ' é lectron libre sont une bonne approximation des orbitales de HART~EE- FO:K du système réel et l 1

on peut

ob-tenir une valeur de l 1_{fnergie d'€change totale égale, d'après}

l'équation (I-71), à la moitié de la valeur moyenne de Ak pour

tous les élect rona. D'après WIGNER[ll],

E, . echang-8

..,

e --- - 0. 458

~. · .. , i l faut noter que le modèle de l 'élec-ron libre d~veloppé

par

SOMMERFt LD et BfT~l pour l '~tude des cristaux mftalliques a ~té d'une i~portance particulière dans

la compréhension des propriétés des électrons de valence dans

les systèmes infiniso De plus , ce modèle fournit des expressions

analytiques s1.ITLple.s pour certaines grandewrs intéressantes comme le niveau de f-[:RMI,

Par contre, ce modèle n'est pas assez rigoureux pour

des études correctes mais, dans les théories plus élaborées,

i l est utile pour estimer les effets d'échange et de corrélation.

SLATER[121 a même proposé d'utiliser systématiquement ce

poten-tiel d'échange dans ies molécules. Signalons, enfin, que dans la théorie des systèmes moléculaires conjugués, ce modèle a été développé beaucoup plus tardivement par KUHN[ 3

J,

BAYLISS[l 4]

- 2L

-et qulun modèle ramifié(lSJ plus exact fournit de bons résultats

tant en ce qui concerne les Vdleurs éneLgétlques que les d

en-sités électroniques.

I.2.3. La_méthode_des_électrons_2resgue_libres.

(Nearly_Free_Electron_Model_:_NFE)

Dans la thé~rie des électrons libres, les spins-orbitales

présentent un spectre énergétique continu; la th6orie des

élec-trons presque ibres perm~:::?t de .cendre compte des rv.od.1.f icat ions

de ce spectre lorsque le cristal possède un potentiel périodique

non constant.

Ainsi, l 'équation de HARTREE-FOCK peut s'écrire:

heff. . _{-1' i} ,1. _{J -- "'-i} q, (1) - {

-1. ;,• ] l. + V ( 1 ) } cp 1 • ( 1 )

( I-7 3)

et, en t oute gAn~ralité, le potentiel pf~iudique se décompose en

série de FOJRJER. V(iJ 1 ::: 1 K

=

V 0 2 e2 1 __ E _ L r. p lp .-, 1 -lK.c, 1 uK e + 1 L _ui<. ·;.:.u (I-74)

-11<:r.

1 e (I-75)

- 23

-Si l'amplitude des composantes est suffisamment faible, l'équa··

tion (I-73) peut être rPsolue par la méthoèe des perturbat i ons

~ partir des fonctions non perturbées, solutions de l'équation

èes électrons libres:

.... H

q,

\k,n)

=

{-o fE -~

q,

(k,n FE ..,,. FE

-c1-=

c {k,n) $ k,nJ (I-76)

Les énergies du système perturbé sont, au premier ordre, i

denti-oues aux énergies de l'flectron libre.

+·+

sNFE (n,k)

=

<iFE(k,n) IH +

I

uK e-iKri<t>f'E (k ,n) >

o K (I-77) F-E c+ , , FE(..,.

•

-

,q,

(k,n) 1H 0 icp k,n) > FE .,.

I

FE ,,. + <q, lk,n) H' jcp k,n) ,, (I-78)

=

t/=-,k,n) -i- ~<t>FE(k,n) IH' jc/E(k,n) > (I-79)

L' élPmen _.-::1.e m2. t ..::· __ .:.;:,· i'.fi c'. la _r~ t'•'-'r ... _{~ 1 -}t· .,..D, at.1. _{on esc nu~ ~}

NFE .k+ ,

s t ,n, - (I-80)

Les orbitales de la rnfthode de l 'électron presque libre co rres-pondantes sont:

'i' ,<jJfE(k' ,n1 )

iH

'

l<t>FE(k ,n) :-+L.

(k, n) ' _(k,n)' + - r.(-+ k,n)

- 24

-Les éléments de la mat rice H' sont faciles à éval uer :

FE(-k' - , , 1I FE(,.,.k · <~ ,nJ

!

H

~ ,nJ ✓ - i e -+ -+ ➔ Kn L-Kn)r dr (I -8 2)

Si l'on t ient compte de la périodicité, l 'intégrale sur t out

l'espace peut être remplacée par une intégrale portant sur toute l a mai lle, en fai sant la substitution suivant e:

on obti ent ainsi : i(J<:' -~) N (+ a _.,.. ➔· 1,-a2-ra3) (I-82) _- 1. N N N

₂

\ \ \

v

<.., L L, e s _1--("\ _{, s :::.O s =O} 2 3

J

.

e -1 (

k

'

-

k

p

H , e -i ( '.n ' -

K

n) -;;· d P ,Vl L'intégrale est nulie si

k

'

f

k

.

(I-83) -+ -+

Lorsque k'= k, les él~ments de matrice prennent la forme:

FE FE 1 - i <~ (~,n• ) ;H' 1 ~ {k,n) ,, - V _[ H1 _e M M l- -+ + i<.n ' -Kn) p dp (I-84)

Il apparai t ainsi que seuls les états appartenant au J. ê~ne point

de la première zone de BRiLLOU N se combinent. nous l 1_avions

- ~5

-De plus, i l faut remarquer que lLéquation (I - 81) qui s Lécrit

maintenant: <j> N F E (

it

1 n ) __ FE+ cp (k,n) + \ l n';;tn _<-pH: (

k,

n L)

_

I

H L

I

cp FE (

t

,

n) > + + c (k,nL) - s (k,n) (I--85)

n'est plus valable aux points de la premiêre zone de BRlLLOUIN où:

( I -8 6)

Sous sa forme explicite cette expression devient:

_h:__

l~+~n1 : 2

=

h 2 jk+Knj2 8n2m 8~2m (I-87)

L'égalité (I-87) correspond

a

l'~quation de définition des plans délimitant la première zone de BRILLOUIN:

On constate que lLon est devant un cas doublement dégénéré oü

l'on doi t résoudre l'~auation du second ordre:

FE + · · FE ➔ N~E +

<cj> (k,n) jh jcj> (k ,n)~ - ë: ' (k,n) <cj> FE, ➔ tk,n') 1 h · l<P FE (k,n)+ ,,

FE + j j . FE + .

<;cj> (k,n) h cp (k,n'p cep FE (k+ ,nt) . , 1h l4> · FE _,_ (k,n' . P, - E NFE (+ k,n) ( I -8 8)

Grâce. au théorème 1.1-42), on peut voir sans difficulté que:

( I -8 9)

(I-90)

-

26

(I-91)

et les valeurs de : 'énergie se déduisent aisément:

+

V

.

FE (-+k .) FE k" nt) , 2 .,..

1 l. In - ,;: I ! ' Hl 1 2 1

1 k

,

n n

,

l ·

( I-9 2)

Cet te équation e t la formulation g~nérale dont l'expression(I -80) est un cas particulier pour & ,,n) - E(f,nL) P~ Hk' et l 'on

· nn

remarque qu'aux l im' tes de la première zono de BRiLLOUIN , on a

les relations:

NFE (➔k· • FE k·➔ ) , ,

s ,n, - ~· ,n + IH k , 1

- ,n,n ( I-9 3)

et i l survient une discontinuité dans les bandes d'énergie:

~ FE ,> . , N f E ~ 1 1 , l

62

=

s (k,nJ - s (k,n ) ~21H k . 1I

,n,n (I-94)

Ce domaine d'énergie où ne peuvent exister de niveaux

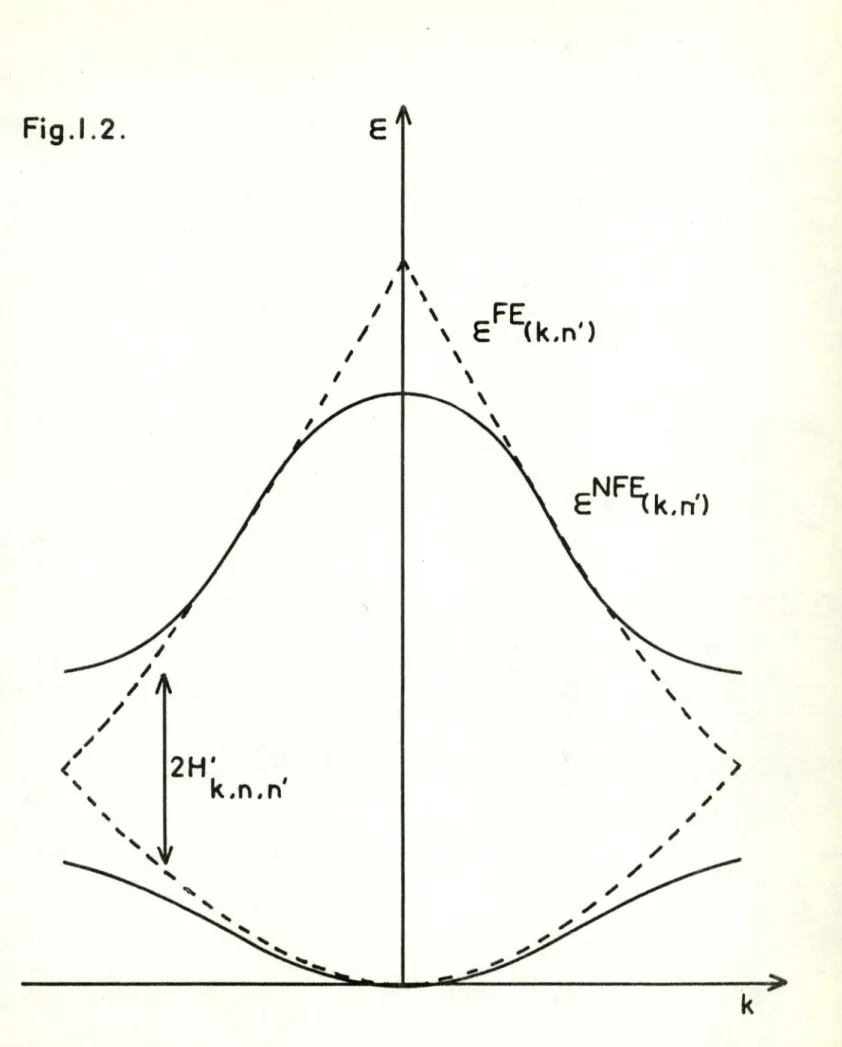
mono-électroniques est appelé "bande d'énergie .interdite" ou

"bande interdite" o Cette sit·üation est i i:ùst .rée dans la figure (I-2) dans laquelle les courbes en pointillé représ en-tent les courbes de l'~lectron libre.

En conclusion, si nous considérons le comportement des

courbes ~N FE

(k,

n) , elles ressemblent aux co1,r :es d lé.r1ergie des

électrons l ibres, mais présentent des disccntinuités aux l imi-tes de la première zone de BRI LOUIN. Il apparait ainsi que pour certaines valeurs énergétiques, le spect re présente des

bandes d1

énergie i nterdit es responsables des propriétés élec-troniqu~s des solides.

Fig

.1.

2.

<

/ ~

' '

I

/

'

_'

I

I

I

I

2H'

k

.n. n'

'

'

_'

I

E

I

I

/

\ \

', EFE(k.n')

'

\ \

\

~

'

' '

_'

'

_>

k

- 27

-Afin que la méthode des électrons presque libres pui sse

être appli cable, i l faut que les composantes de FOURIER du potentiel convergent rapidement. La présence des coeurs posi-t ifs d'atomes exclut cette possibilité; i l y correspond, en effet, des osci l ations rapides de courtes longueurs d'onde, qui sont reliées à des composantes de FOURIER d'ordre élevé.

Pour cette raison, la théorie originale des électrons presque libres n'a guère servi en pratique et ne présente qutun intérêt

didactique. Nous reviendrons sur ce sujet dans la suite de notre travailo

Signalons, ·enfin, que ce modèle a été appliqué en

chimie quantique moléculaire à l'étude·du spectre électronique

[16]

des polyènes o

I.2.4. Mé.thodes_loCoA,O. Tight_Binding_AEEroximation_:_TBA)

(Hückel_Crystalline_Orbitals_:_HCO)

Comme nous l 'avons vu au paragraphe précédent, la

méthode des élec~rons libres converge si lentement qulelle ne présente que peu d'intérêt pratique. Au voisinage des coeurs d'atomes, les orbit ales devraient présenter un comportement analogue a celui des orbitales atomiques. Ceci suggère un principe nouveau po ·r construire les orbitales cristallines en combinant les orbitales atomiques, chacune localisée sur un atome, en une orbitale délocalisée sur tout le système, Cette méthode a ét é historiquement, une des premières à être proposée. Flle porte généralement le nom que son auteur,

BLOCH, lui a donné: méthode L,C,A.O,[l7] ou ·"Tight Binding Approximation" dont la traduction française peut être

"Méthode aux bases atomiques" ou "Méthode des électrons

- 28

-Dans le cas où i l n'y a qu'une orbitale atomique

x

(r)

par maille, i l est aisé d'obtenir,d'après la technique des

opérateurs de projection[lBJ, une orbitale cristalline

satis-faisant le théorème de BLOCH:

</>LCAO (k)

_-

_-

,-X

r)

vk ( I-9 5) 1/2 ikÂ.

-I

1 T(-Ai) ·,)

-=

N e X ( r) i ( I-9 6)

+t..

1/2 ik . N

I

·

1 x (r-A.)

·-

e i 1 (I-97)

Les orbitales atomiques sont fonctions propres de l'opérateur

monoélectronique atomique:

ho = - (I-98)

Ainsi, pour les orbitales de SLATER (S.r.o.~slater Type Orbitals),

le potentiel u (~) prend la forme hydrogénoïde d'un électron

soumis à une charge positive:

-+ u(r)

=

;li, 2 Z e

lri

*

[

2]

SLATER a montré comment obtenir la valeur de Z

Pour les orbitales hydrogPnoïdes, on obtient :

+ -+ h0 x(r)

=

2 x (r) 0 ' ,t_f ," (I-99) (I-100)

Dans les systèmes périodiques, l'opérateur monoélectronique

s'écrit:

- 29

-où V(r) dési gne un potentiel effectif, par exemple,le potentiel

de HARTREE-FOCK V (i)

=

z

e2

,_

,

E_+ \

1., ~ r . p lp j \<jl~ (2) ., J jl -P12I <P • ( 2) dv 2 rl2 J

L'opérateur h peut ainsi se mettre sous la forme:

_,,_ ➔

h = ha + V(r) - u(r)

(I-102)

(I-103)

et llénergie associée aux orbitales cristallines s'obtiendra

par la relation:

avec

E:TBA(k) -- -,cpTB~

k)

lh i<PTBA(k) ;,

. <P TBA(k)

I

<P TBA(k) > -r ➔ ikR. ·· .. , . ' e J B t:. ·r l . J

-=-

---

---:., e j ,➔k ➔ . l R. J

s

.

J

s

.

=

-

x

(~-A.,) 1

x

(f) > J J (I-104) H-105} (I-106)

Si l'on admet que les orbitales atomiques sont orthonormalisées,

l'expres~ion(I-104) se simplifie et devient:

E: TBA (k) - E ,. + B 0 + \ l j~O e ➔ ... ikR . J _B. J (I-107)

Si nous considérons plusieurs orbitales atomiques par maille, l'orbitale cristal l ine sera une combinai son linéaire dtorbitales

de B~OCH (I-97) étendues sur chaque type d'orbitales atomiques.

q, (t,n)

= \

c ~n(~)

L 'knp -r

p

(I-108)

Les coefficients et les énergies associées peuvent être obtenues

en résolvant le système séculaire traditionnel de la théorie des variations comme le fait LADIK[l 9 , 2

oJ

.

(I-109)

OÙ

H _pq (1<) - "·c/>p ]() jhicpq(:it)~ (I-110)

s

(~)

=

< cp (l<)

i

<P (R)

:--pq p . q (I-111)

La méthode LCAO permet de visualiser un important

prin-cipe reliant les niveaux atomiques aux bandes cristallines.

Si nous avons N atomes infiniment loin l'un de l'autre, on ob

-serve des niveaux d'énergie atomiques N fois dégénérés.

Lorsque les atomes se rapprochent, la dégénérescence se lève

et les niveaux se séparent en donnant naissance à une série de

bandes électroniques. C,'t.te situation est représentée sur la

fig_ure (I-3) et permet de donner une justification simple à

l'origine des •:.c.trll .. '.L;S 0lec..:.rGniqu.es Jans ..1..t,S 2,,:,.1..,_~~-e>s.

Récemment, un procédé analogue a été proposé par ANDRE,

[21]

GOUVERNEUR et LEROY . En voulant conserver le formalisme de

la méthod~ LCAO-MO de la chimie quantique molécul aire, ces

au-teurs ont développé un procédé gPnéral (la méthode LCAO-HCO)

permettant l'étude thforique des systèmes périodiques et le

calçul de toutes les grandeurs définies en chimie quantique,

Fig.1

.

3: Origine des bandes d'énergie dans les soli

de

s

E

E3

Niveaux

des

Bandes

E2

atomes

libres

d'énergie

N fois

e,

dégénérés

r

- 31

-Si on considère la maille comme un ensemble, i l est

normal d 1

y centrer des orbitales délocalisées dans la maille:

,i, - 1 C

'l'n - np XP

p

(I-112)

La combinaison de BLOCH s'obtient aisément grâce aux opérateurs

de projection: .i-HCO ·k* . 'I' , nJ ·- N ~·l/ 2,;- ₁

=

l

~ ckn e j p p

i~A

.

J X

(°t:-A

.

)

p J (I-113)

Les coefficients sont calculés en résolvant le système

d'équa-tions séculaire:

(I-114)

où:

dont la condition de compatibilité s 1_écrit:

i

i

A

h

().oh

dét

iI

e µt t - € ot il ~

o

h

(I-115)

L _{es in egra} · t ' 1 _es · _{ptt, son} oh t ' _{eva uees} l ' d _ans l _{e ca} d _re d _{es approxima} . t ₁. _.ons

de HUCKEL. Nous ve+rons plus loin que le procédé LCAO-HCO peut

être justifié dans le cas des systèmes conjugués grâce à une

analyse des éléments de matrice de la méthode LCAO-SCF-CO.

On peut comparer les méthodes TBA et LCAO-HCO.

Considé-rons le cas où i l n'y a qu•un seul atome par maille, la forme de

la bande d1

énergie sera: ·

- 32

-avec

Les relations 1-10·/) et (I-116) sont formellement équivalentes

mais les parametr s qui. y interviennent nLont pas la même

signi-fication. En effet~ I-117) en fait: (I-118) D'autre part: ·J· • + .,. -)· + - , )( ( r. ;

!

h O

i

X ( r -Ah ) ,,

+

•,

X ( r ) J '✓ ( r ) ... x (r ) 1

x

i::-Â

,

,

-o h (I-119) (I-:-120) Il apparaît, dès l ~s, que: TBA ·➔· E_HCO(=t-k) E ( k ) -- (I-121)

La m~thodL LCAO-HCO est ainsi formel lement identique à la "Tight-Binding Appro irnation". Elle possede l'avantage de

reprêc~C~- en physique fc l Létat solide la dëfinition de

gran-deurs défini~s en chimie quantique, telles les charges et les

- 33

-les potenti els d'ionisation, les électroaffinités et les

éner-gies de transition, peuvent, en général, être exprimées

analy-tiquement en fonction des paramètres a et P , vu que ces

pro-priétés correspondent à des orbitales appartenant aux points

de haute symétrie de l a première zone de BRlLLOUIN,

En to1.'te rigueur, la méthode LCAO pose plusieurs

pro-blèmes importants dans son application aux sol ides:

principa-lement, le calcul des i ntégrales intervenant dans (I-114) et

(I-115). Pour le simplifier, on procède souvent à de grossières

approximations, Lelles la négligence des intégrales de

recouvre-ment et des élément s de matrice de l'opérateur monoélectronique

entre atomes non voisins. Pour ces raisons, la méthode LCAO est

généralement sujette à caution.

Signalons, enfin, qu[il est vain d'espérer améliorer

les résultats en étendant la base des c ··bi tales atomiques. Le

problème a, en effet, été étudié par PARMENTER[22] qui a

mon-tré que les orbitales de BLOCH formées à part i r d'orbitales

atomiques trop excitées devenaienf''identiques et ne modi fiaient

plus les résultat s. Ces orbitales s'étendent sur plusieurs dis

-tances internuc éaires et leur résultante est pratiquement nulle.

Par contre, à côté de ces limitations, la méthode LCAO

fournit d'excel ents résul tats dans les systèmes où les propri

-étés de certains électrons peuvent être représentées a partir

d'une base d'orbitales atomiques pas trop étendue comme dans les

4

-I.2.5. La_méthode_des_ondes_Elanes_orthogonali sées_et_le

ESeudo-Eotentiel. (Orthogonalized_Plane_Waves:_OPW)

Comme nous l 'avons vu dans le paragraphe précédent,

la m§thode TBA rencontre des difficultés pour reproduire des

orbitales correspondant aux états dlénergie élevée. Par contre,

la méthode des él ctrons presque libres ne peut reproduire

valablement la forme correcte des .~rbi ta~.es auprès des coeurs

dlatomes, sans :introduire un grand nombre d'ondes planes de

courtes longueurs d onde.

I 1 est normal d 'utiliser une base d'orbi tal es hyi-;:rid,e; pour les états dlénergie l es plus bas jusqulau pied de l a

bande de valence}, on utilisera des orbitales de B OCH LCAO et pour les état s plus élevés états qe valence et supérieurs) on

choisira des orbitales de l 'électron presque libre conv

enable-ment orthogonalisées aux orbi tales de BLOCH.

23]

Ce procédé a été proposé par HERR N en 1940

Dans l a fonction de départ, utilisant le procédé d lorthog onali-sation de SCHMIDT:

q,OPW(k,n) 1. ( , k+ --;---Kn )--;-r

-- e - 1_nn' .p TBA (k,n l) _(I-122)

La sommation sur

n'

est étendue jusqu'à la bande de valence.

Remarquons que, puisque les orbitales de BLOCH sont orthogonales,

, q,TBA(k,n) l<PTBA(k,n') >

=

6nn' (I-123)

la condition d'orthogonalisation:

OPW ... TBA -+

s

-revient à écrire: i O

=

,e - p 1 1.. Tnn" q,TBA(~,n") Î<P1BA(k,n' )> n"

et permet de déduire la valeur des coefficients T ,: nn _\. ,.,. ·+ T = ~ei(k+Kn)r ,~TBA

k

n') > nn1 _~ ' (I-125) (I-126)

De plus, si l 'on constate que les fonctions (I-122) forment une base complète, on peut développer les orbitales de la bande de valence en combinaisons linéai res:

(I-127)

les énergies associées aux états de la bande de valence et les coefficients de la combinaison linéaire s'obt iennent en résol-vant le système séculaire:

dét jH 1 - ~ A 1 j

=

0

nn nn (I-128)

la forme des élément s de matrice d'un opérateur

n

s'écrit en toute généralité:

<q,OPW k,n) i1ij q,OPW(k,n') >

•➔ -Y -~ -i (k+Kn)r

=

<e -➔ ·+ ➔

L

T

.,

q,

TBA(k,n") 1

n

I ei (k+Kn') r "nn n . - \" _{l "} T _, ~TBA(k➔ "') > ,11~ ,n n \•) . .t n n (I-129)

(I-l_{29 )} __ <e-i.(k+Kn)

t=

I

s-i lei (k+Kn')

i

\

• (+k -,. Il)+ _ , ₁. ,,. - i +Kn r

I ;_,

,

"TBA (;? ,: ) • , " , e iG 1 'i' K, n , ~" nn n _ 1 Î . -i(k+Kn'}r,,1,1,TBA(+k '" );, L . , " [ , e 1 :G ₁ 'i' , n Ill n n n + 1 'ï' T T < "T l3 A ( ~ n" ) , 1 ,., 1 " TB A ( ~ n ,, L ) .,. L , ' "' nn" 'i' , ~G 1 'Y , n"

n_

"L

n n (I-130)

Il en découle normalement les expressions de H L et A L:

nn nn ~ ➔ + + + -H

=

· e-i(k+Kn)r lhl ei(k+Kn')r~ - ) + nn, , 1 _·11 T _n , _n "T _nn "E (k, n") {, _nn

'

-

L

n" T n (I-131) nn" Tnn' (I-132)

La précision des résultats dépend du nombre de termes introduits

dans le développement (I-127) et l'on peut être certain, que

l'énergie d'un état convergera vers la valeur exacte à mesure

que l'on augmente le nombre de termes dans (I-127). Les

limi-tations de la méthode des ondes planes augmentées proviennent

du calcul des orbitales de coeur et du développement {I-127)

aux voisinages des limites de la première zone de BRILLOUIN.

Il faut, en effet, remarquer que le déterminant (I-128) doit

être résolu èri chaque point de la àellule réciproque.

L 1:~in, l 'examen des termes d'orthogonalisation d 'une

onde plane augmentée suggère un potentiel répulsif, idée qui

7

-En effet, si l'on regarde l'équation monoélectronique:

h c/> OPW (k) "" € (k) c/> OPW {k) _(I-133) en tenant compte de (I-122), c/> OPW (k) = -+ -+ -+ \ i(k+Kn)r \ 1 T c/>TBA(k,n!) L akn e . - L l ,akn nn' n n n (I-134)

Le premier terme représente les fonctions de l'électron presque

libre définies au paragraphe (I.2.3.) et on obti ent ai nsi:

,l,OPW k)

=

11\NFE (k) - ~ \ T ... .TBA '}➔ 1'

'f' .,, ~ L akn . nn ' 'f' . • . \ : ' n )

n n'

(I-135)

L'équation monoélectronique devient:

h{cj>NFE

_k

₎

_-

\ _{\ ak} T c/> TBA

(k

n, ) } L, _L n _{nn' '} n n ' + _c/>NFE -► \ \ T c/>TBA -+

=

e: (k) k)

-

_L. L, ak _nn' k, n') ' n n n (I-136) d'où (I-137) ou encore: NFE -+ _{1 \} -+ -+ TBA + h c/> (k) + l l akn T ,[ E(k)-s (k,n' )]qi (k,n') n n' nn

=

E: (k) c/>NFE (k) (I--:138)

/

- 38.

-puisque les énergies e(k,n') correspondent •~ux Atats~-de cue •r ,

la différence entre z(k) et e(k,n') est posit ive et représente

un potentiel répulsif qui permettra une convergence plus rapide

du développement en ondes planes.

Si on écrit:

(I-139)

on 2.ura une pse ... 1<·'._1.0 ·f.l~lEJ.tion mon·•-éle ·:l:rcvnique:

(I-140)

L'équation I-140) justifie l 'utilisation du modê e des électrons

presque libres. Le procédé. décrit est à la ti= .3e -c.·- l fa, mél. 10 e u

pseudo-potentiel pr posée par PHILIPS et KLEINMAN[24

J

,

Comme i l

est montré ci-dessus, cette méthode n'est qu'un cas particulier

de la méthode des·· ondes planes vr · hcgc,n~:d i-s,ie.i._ t'._, · '-~ "t ·- · • ,t l icite

clairement la filiation entre cette dernière et la méthode des

électrons presque l ibres.

I.2.6. Les_méthodes_cellulaires_et_la_méthode_des_ondes_Elan~s

augmentées.

Il est possible de classer les méthodes de résolution

de l'équation m noélectronique en 'deux groupes. En premier l ieu,

les méthodes satisfaisant rigoureusement, les, ,conditions-aux l i 1 '.tes

de l'équation de SCHRODINGER, mais utilisant un potentiel

cris-tallin approché. En second lieu, les procédés résolvant

exacte-ment l'équation monoélectronique mais utilisant des conditions

aux limites approchées.

_-

_-

La méthode cellu~aire de WIGNER et SEITZ[251

.

est un , :cemple de ce type de procédé, applicable essentiellement

aux métaux.

- 39

-On a Vü que le théorème de BLOCH pouvait s 1_écrire:

-.o;..- +-~ <P ( k .l .:i. kr _,. - e u, (r) K (I-141) ➔

oü uk(r) possède l a pér iodicit~ du réseau et satisfait l a

relation:

1.- {V2+2ikV)

(I-142)

Moyennant certaines hypothèses, il est possible de résoudre

l'équation (I-142~ dans ne cellule élémentaire. Il est licite

d'admettre que le pot entiel ressent i par l'électron a une

sy-métrie sphérique. En effet, en première approximation, la

den-sité électroniqu"'! au voisinage des atomes, possède la symétrie

sphérique. La cont ribution des atomes contenus dans les cellules

voisines est négligeable puisque, â ces di st ances, les atomes

sont neutres et le champ extérieur nul . La conséquence de la

périodicité implü. J1R: que:

(I-143)

'

et, dès lors, comme la fonction doit être continue et régulière:

(~ ) -)- _,,

a

r r

+

An

- - e

i

kAn

(I-144)

WIGNER et : SElTZ remplacent à ce moment la cellule par une sphère

de même volume en imposant qu'à la surface de cette sphère, la

dérivation première s 'annule, Vu la symétrie du potentiel,

l'équation (I-142) est soluble exactement. Dans l , L·2::.. · '": ···i.-·

>

- 40

-semi-empirique dé-ter.miné par PROKOF EW[2G] dans une étude des

orbitales de valence de l'atome de sodiumo Ces auteurs obtenaient

ainsi au point da ·~n~tri e

'

=

O~

les solutions de l 'équation:

h cp MC . tO,r . +) ·-· t: MC ( 0) ~ ~• C ( o,

r

)

(I-145)

avec la condition:

I -146)

Dans leurs premiers travaux·, ils obtena.ient. uniquement 1 'énergie du point zéro de la bande 3s du sodium métall ique. Ils utilisaient

pour les niveaux s~périeurs, l'énergie obtenue à partir du point zéro en ajoutant l 'énergi e cinétique d'un électron libre:

(I-147)

A partir de ces résultats, ils ~taient en mesure d1_estimer

l'éner-gie totale du crist~l en fonction du paramétre réticulaire et

de tirer des renseignements sur l '~nergie de cohésion.

La méthode cellulaire de WI NE~ et SEITZ a été

générali-, 1934 ,~LA-ER(27128 ] Pl t-t d ' ._ .. L. 1

see en · par ::i . , • u o que u·• .. 1.. iser es .sph~:.:es

de WIGNER et SEITZ, : 1 s 'efforce de c nsidérer la cellule élé-mentaire de l 'espace direct. Il importe, dès lors, que l'orbitale

soit continue en tout point de l'espace; en particulier, entre

deux plans paral è e. de la cellule de WIGNER et SEITZ,la valeur

de l'orbitale doit être multipliée p~r l'exponentielle de BLOCH

'

correspondant à une translation du réseau direct:

+·+

~ + + ikAn + +