Etude des Propriétés Optoélectroniques, Magnétiques et Thermodynamiques des Pérovskites et des Doubles Pérovskites

Recherche Scientifique

Université Abdelhamid Ibn Badis de Mostaganem

Faculté des Sciences et de la Technologie

Département de Génie Electrique

N° D’ORDRE: D.../2020

THÈSE

Présentée pour

DOCTORAT EN SCIENCES

Spécialité: Génie Electrique

Option: Génie Electrique

Présentée Par

Mme. BENOSMANE WIAME

Soutenue le : 01 / 07 / 2020 Devant le jury composé de :

Pr B. YAGOUBI PRESIDENT Université de Mostaganem Pr B. BOUHAFS EXAMINATEUR Université de Sidi-Bel-Abbès Pr B. ABBAR EXAMINATEUR Université de Sidi-Bel Abbes Pr S. BENTATA EXAMINATEUR Université de Mascara Dr W. BENSTAALI DIRECTEUR DE THESE Université de Mostaganem

DrA. ABBAD CO-DIRECTRICE DE THESE Université de Mostaganem ANNEE UNIVERSITAIRE: 2019/2020

Etude des Propriétés Optoélectroniques,

Magnétiques et Thermodynamiques

des Pérovskites et des Doubles Pérovskites

Ce travail est l’issue d’un long cheminement au cours duquel j’ai bénéficié de l’encadrement,

des encouragements et du soutien de plusieurs personnes, à qui je tiens à dire extrêmement

et sincèrement merci.

Tout d’abord, je remercie DIEU le tout puissant de m'avoir donné le courage, la patience et la

force durant toutes ces années d'étude.

La majeure partie de ce travail a été réalisée au Laboratoire de Technologie Et Des Propriétés

Du Solide à l’Université Abdelhamid Ibn-Badis, Faculté des Sciences et de la Technologie,

Mostaganem, sous la direction du Docteur BENSTAALI Wissam.

Je tiens en premier lieu à remercier le directeur du laboratoire respectif pour son accueil : Mr

A. CHOUIYAH, J’exprime toute ma reconnaissance à mes directeurs de thèses, Mr

W.BENSTAALI et Mme A. ABBAD pour le sujet passionnant qu’ils m’ont proposé, leur conseil

avisé, leur soutien permanent, leur disponibilité et leur gentillesse. Pendant ces années de

thèse, ils m’ont beaucoup appris sur la manière d’exercer le métier de chercheur. Merci, pour

le suivi de cette thèse, pour l’encadrement et pour les corrections apportées à ce manuscrit.

Merci de m’avoir fait confiance.

Je tiens à remercier vivement Messieurs ABBAR Boucif et BOUHAFS Bachir Professeurs à

l’Université de Sidi Belabbes, et Mr BENTATA Samir Professeur à l’Université de Mascara,

d’avoir accepté d’évaluer la qualité de ce travail en tant que rapporteurs.

Ma profonde gratitude à Monsieur le Professeur YAGOUBI Ben Abdallah, d’avoir accepté de

présider mon jury de thèse.

soutenu tout au long de ma vie, pour son encouragement, son fierté …, je ne serai jamais allée

si loin sans son amour.

Un grand MERCI à mon mari Mr MAHOUR Abdelkader, pour son aide précieuse et son

soutien inconditionnel tout au long de ces interminables études, ces 4 années de thèse et

surtout pour le marathon final de la rédaction. Toujours derrière moi, il m’a insufflé la force

d’écrire les derniers mots pour mettre un point final à ce manuscrit.

J’adresse mes profonds remerciements à Mr

T. LANTRI,

Mme R. BENTATA et chère amie S.

BENATMAN

p

our toutes leurs bonnes remarques et pour toutes les améliorations qu’ils m’ont

apportées à cette thèse, pour leurs aides à corriger ce manuscrit scientifiquement et

linguistiquement.

Mes sincères remerciements à toute l’équipe de notre laboratoire LTPS pour leur soutien,

solidarité et pour l’esprit d’équipe qui les anime.

À mes chers parents,

À

mon cher mari,

À

mes enfants, Med el Amin, Zaza

Ines & Malek.

À

mes frères et ma sœur.

À ma belle famille…

À toute ma famille…

Résumé

Remerciements

Dédicaces

Table des Matières

Liste des Tableaux

Liste des Figures

Introduction Générale

2

CHAPITRE I: Théorie de la Fonctionnelle de la Densité

I.2 Equation de Schrödinger………...9

I.3 Approximation de Born Oppenheimer...10

I.4 Approximation de Hartree………...12

I.5 Approximation d’Hartree-Fock………...13

I.6 Théorie de la fonctionnelle de la densité………..14

I.6.1 Théorèmes d’Hohenberg et Kohn……….……….…...16

a. Premier théorème………16

b. Deuxième théorème………....17

I.6.2 Approche de Kohn et Sham...18

I.6.3 Potentiel de Coulomb……….………...20

I.6.4 Potentiel d’échange-corrélation…….………..…....20

I.7 Différents types de la fonctionnelle d’échange et de corrélation………...16

I.7.1 Approximation de la Densité locale (LDA)……….20

I.7.2 Approximation du Gradient généralisé (GGA)………...…22

I.7.4 Potentiel de Becke et Johnson modifié mBJ...23

I.8 Méthodes des ondes planes linéarisées à Potentiel Total (FP-LAPW)………...25

I.8.1 Méthode des ondes planes (APW)...25

I.8.2 Méthode des ondes planes augmentées linéarisées (LAPW)……….…….…29

I.8.3 Principe de la méthode FP-LAPW……….….29

I.8.4 Rôles des énergies de linéarisation El……..………...30

I.9 Code de wien2k………...…32

I.10 Conclusion……….….36

Références Bibliographiques………...38

CHAPITRE II: Généralité sur les Pérovskites et les Doubles

pérovskites

II.2 Matériaux à Structure Pérovskites……….………...41

II.3 Structure Pérovskite………..……….….42

II.4 Structure de LaBO3 (B= Co, Fe, Mn)………...45

II.5 Intérêt des Pérovskites………....………....47

II.6 Structure Double Pérovskite……….….47

II.7 Intérêt des Doubles Pérovskites……….….51

II.8 Origine des Structures de Ca2XNbO6 (X= Co, Cr, Mn)…….………..……..51

II.9 Conclusion………..………..52

Chapitre III : Résultats et discussions

I.1 Introduction………...56

Propriétés structurales, électroniques et optiques des pérovskites LaBO

(B= Co, Mn, Fe)

III.3 Propriétés structurales………...59

a. Structure orthorhombique………...……...59

b. Structure pérovskite tétragonale……..……….…...60

III.4 Propriétés électroniques ………...65

III.4.1 Structure de bandes électroniques….……….………..……..65

III.4.2 Densité d’état……….………...72

III.5 Propriétés magnétiques ……….……….………...……77

III.6 Propriétés optique……….…….79

III.6. Fonction diélectrique………..………..79

III.6.2 Réflectivité………...82

III.6.3 Indice de réfraction………..………....……...83

Propriétés structurales, électroniques, optiques et thermodynamique des

doubles pérovskites Ca

XNbO

(X= Co, Mn, Cr)

III.8 Propriétés Structurales………...…....86

III.9 Propriétés Electroniques ………...………93

III.9.1 Structure de bande….…..……….………...93

III.9.2 Densité d’état……….…….……….…..99

III.11 Propriétés optiques……….107

III.11.1 Fonction diélectrique…….……….…..………..106

III.11.2 Réflectivité………...………..108

III.11.3 Indice de réfraction………..………...109

III.12 Propriétés thermodynamique…..………..110

III.12.1 Modèle quasi-harmonique……..………....110

III.12.2 Volume de la cellule unitaire sous l'effet de pression et température.………112

III.12.3 Module de compressibilité (BS)……….………..…...113

III.12.4 Température de Debye θD….….……….…….…………...114

III.12.4 Capacité Calorifique à volume constante (CV)……… ….………...115

III.13 Conclusion………...117

Références Bibliographiques………118

Conclusion Générales et Perspectives..………...122

Figure I.1 : Schéma décrivant le processus itératif de résolution des équations de

Kohn-Sham……… .19

Figure I.2 : Organigramme du code Wien2K………..34

Figure II.1 : Les différentes phases de déformation de la pérovskite CaTiO3………….……….……...37

Figure II.2 : Directions des déformations dues au déplacement de l’ion B dans

l’octaèdre………...40

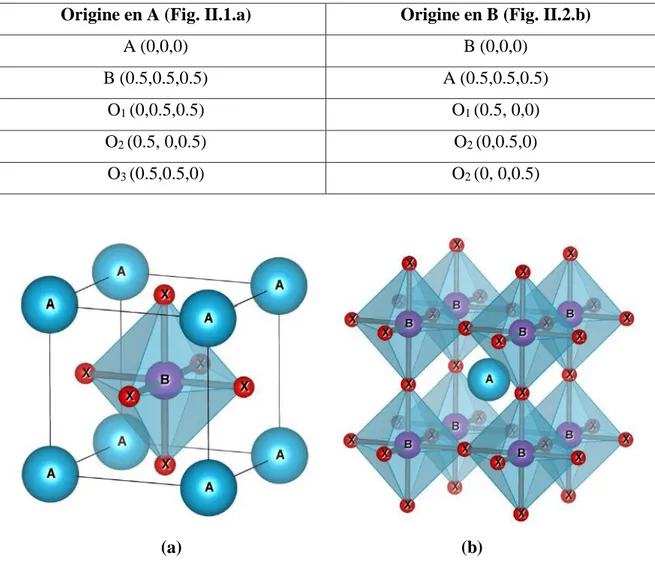
Figure II.3 : Maille élémentaire de la pérovskite simple cubique ABO3………...42

a. Origine en A. b. Origine en B.

Figure II.4 : Représentation de la structure de LaBO3 utilisée………...43

Figure II.5 : Structure de double pérovskite A2BB’O6………..………..47

a. Cubique (groupe d’espace Fm_m3 avec inclinaison a°a°a°),

b. Tetragonale (groupe d’espaceI 4/m inclinaison a°a°c-),

c. Monoclinique (groupe d’espace P21/n avec inclinaison a-a-c+).

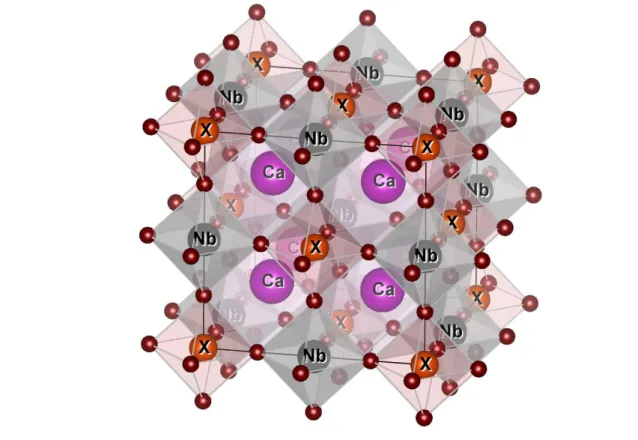
Figure II.7 : Représentation de la structure du Ca2XNbO6 utilisée (X= Co, Cr, Mn)………..49

Figure III.1 : Représentation des structures utilisées pour les pérovskites LaBO3 (B=Co, Fe,

Mn)………59

Figure III. 2 : Variation de l’énergie totale en fonction du volume de LaCoO3 dans différentes

structures………...62

Figure III.3 : Variation de l’énergie totale en fonction du volume de LaFeO3 dans différentes

structures………...63

Figure III.4 : Variation de l’énergie totale en fonction du volume de LaMnO3 dans différentes

structures………...63

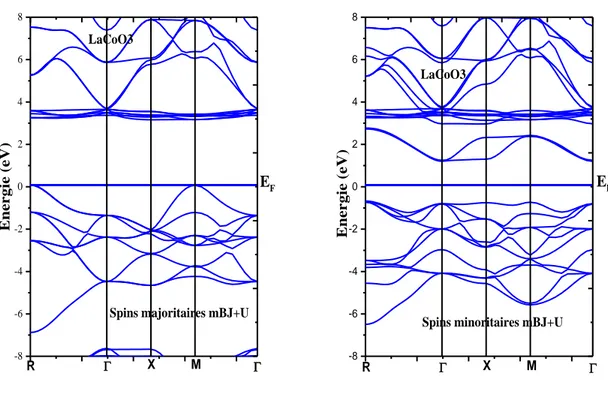
Figure III.5 : Structures de bandes du composé pérovskite LaCoO3 en utilisant l’approximation

GGA, GGA+U et mBJ………..……...69

Figure III.6 : Structures de bandes du composé pérovskite LaFeO3 en utilisant les

approximations GGA, GGA+U et mBJ. ………..70

Figure III.7 : Structures de bandes du composé pérovskite LaMnO3 en utilisant les

approximations GGA GGA+U et mBJ………….………72

Figure III.8 : Densité d’états totale et partielle des états de LaCoO3 calculées par GGA-PBE,

Figure III.9 : Densité d’états totale et partielle des états de LaFeO3 calculées par GGA-PBE,

GGA+U et mBJ………75

Figure III.10 : Densité d’états totale et partielle des états de LaMnO3 calculées par GGA-PBE,

GGA+U et mBJ……….76

Figure III.11: Fonction diélectrique de LaCoO3: La partie réelle ε1(ω) et la partie imaginaire

ε2(ω) avec spin polarisé……….82

Figure III.12: Variation la réflectivité en fonction du l’énergie du photon (eV) pour le composé

LaCoO3………..83

Figure III.13: Variation d’indice de réfraction en fonction du l’énergie du photon (eV) pour le

composé LaCoO3……….…..84

Figure III.14 : La configuration magnétique des trois phases. ………...……87 a. Ferromagnétique (FM),

b. Ferrimagnétique (FiM) c. Antiferromagnétique (AFM)

Figure. III.15: Variation de l’énergie totale en fonction du volume du composé Ca2CoNbO6,

avec spin polarisé (SP) en utilisant et GGA+U dans les différentes phases (FM, AFM et FIM)………..89

Figure. III.16: Variation de l’énergie totale en fonction du volume du composé Ca2CrNbO6

avec spin polarisé (SP) en utilisant GGA et GGA+U dans les différentes phases (FM, AFM et FIM)………..90

Figure. III.17: Variation de l’énergie totale en fonction du volume du composé Ca2MnNbO6

avec spin polarisé (SP) en utilisant GGA et GGA+U dans les différentes phases (FM, AFM et FIM)………..91

Figure. III.18: Structure de bande du Ca2CoO6 obtenue par GGA GGA+U et mBJ ….…...97

Figure. III.19: Structure de bande du Ca2CrO6 obtenue par GGA GGA+U et mBJ. …….….98

Figure. III.20: Structure de bande du Ca2MnNbO6 obtenue par GGA. GGA+U et mBJ ……99

Figure III.21: Densité d’état totale et partiel de composé Ca2CoNbO6 obtenues par GGA,

GGA+U et mBJ………..……….101

Figure III.22 : Densité d’état totale et partiel de composé Ca2CrNbO6 obtenues par GGA,

GGA+U et mBJ……….….…….102

Figure III.23 : Densité d’état totale et partiel de composé Ca2MnNbO6 obtenues par GGA,

Figure III.24: Fonction diélectrique du composé Ca2CrNbO6: ε1(ω) la partie réelle et ε2(ω) la

partie imaginaire………..………108

Figure III.25 : Variation de la réflectivité en fonction du l’énergie du photon (eV) pour le

composé Ca2CrNbO6………..……….109

Figure III.26 : Variation d’indice de réfraction du composé Ca2CrNbO6 …….………..…..110

Figure III.27 : Variation du volume en fonction de la température à différentes pressions de la

double pérovskite Ca2CoNbO6………..………..113

Figure III.28 : Le module en vrac de Ca2CoNbO6 est fonction de la température pour

différentes pressions Ca2CoNbO6………..……….114

Figure III.29 : Variation de la température de Debye en fonction de la température du composé

Ca2CoNbO6……….……….…….…..115

Figure III.30 : Variation de la capacité thermique CV en fonction de la température à

Tableau II.1: Position atomiques dans la phase cubique pérovskite Pm_3m………42 Tableau III.1: les paramètres cristallins utilisés dans le calcul des LaCoO3, LaFeO3 et LaMnO3

orthorhombiques………...…59

Tableau III.2: Paramètres cristallins utilisés dans le calcul des LaCoO3, LaFeO3 et LaMnO3

tétragonale……….60

Tableau III. 3: Paramètre du réseau a en (Ǻ), le module de compressibilité B en (GPa) et

l’énergie de cohésion Ecoh calculés par l’approximation GGA avec spin polarisé, pour les

composés LaCoO 3, LaFeO3 et LaMnO3, dans les structures : cubique, orthorhombique, et

tétragonale comparés à d’autres résultats expérimentaux ou théoriques disponibles dans la littérature….. ………64

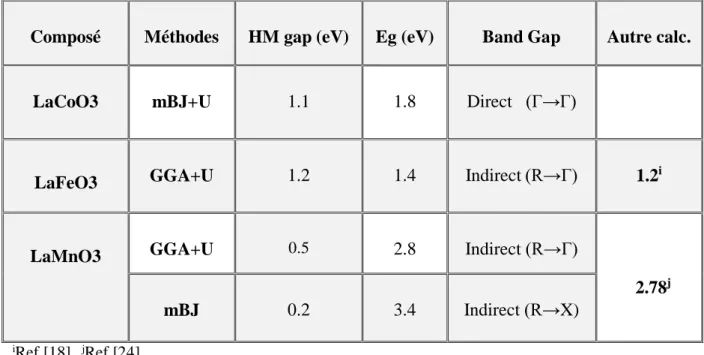
Tableau III.4: Les énergies des bandes interdites en eV et leurs natures (gap) des pérovskites

LaCoO3, LaFeO3 et LaMnO3………...……… 66

Tableau III.5 : Moments Magnétiques Partiels, Totaux et Interstitiels de LaBO3 (B = Co, Fe,

Mn)………78

Tableau III.6: Paramètre du réseau a en (Ǻ), le module de compressibilité B en (GPa) et

d’autres paramètres calculés par les approximations GGA et GGA+U, pour les composés Ca2CoNbO6, Ca2CrNbO6 et Ca2MnNbO6 comparés à d’autres résultats théoriques, ou

expérimentales………... ..92

Tableau III.7 : Les énergies des bandes interdites en eV et leurs natures (gap)……….94 Tableau III.8 Moments Magnétiques Totaux, Partiels et Interstitiels de CaXNbO6 (X= Co, Cr,

2

Introduction générale

Ce dernier siècle a été marqué par le développement scientifique et technologique, tel que la télévision HD, la téléphonie mobile, internet à haut débit, et d’autres applications dans l’industrie moderne comme la photovoltaïque, l’énergie renouvelable (panneaux solaires...), nanosciences, nanotechnologies, … et d’autre domaine des capteurs et de l’électronique, qui ont augmenté le besoin de stockage de la chaleur et la capacité de transfert de l'information. Il devient alors essentiel d'utiliser des dispositifs électromécaniques et électroniques.

Pour cela, il est nécessaire de connaitre la caractérisation des matériaux, qui sont la base de tout développement technologique, et qui feront la patte de tout dispositif électronique utilisé dans l’industrie moderne et technologique.

La classification des matériaux dépend de l’application souhaitée. En particulier, pour une application optoélectronique ou photovoltaïque on s’intéresse aux semi-conducteurs qui ont suscités un vif intérêt tant dans leur analyse expérimentale que dans leur développement théorique. Les semi-conducteurs ont permis une nouvelle alternative pour l’électronique moderne. C’est en fait la nature directe du gap d’énergie de la plupart de ces matériaux qui lui confère une place privilégiée dans le domaine de l’optoélectronique. De plus, la possibilité de réaliser des alliages binaires, ternaires ou encore quaternaires ou pérovskites a permis l’essor d’une multitude de choix pour réaliser de nouveaux dispositifs optoélectroniques pouvant couvrir une gamme de longueurs d’onde allant de l’infrarouge à l’ultraviolet avec des paramètres de maille assez variés.

Un intérêt tout à fait particulier a été porté depuis longtemps aux matériaux semi-métalliques pour une utilisation dans des dispositifs de spintronique, ou l’électronique de spin qui est toujours un sujet d’actualité et d’innovation permanente. Son potentiel industriel est important tels que les têtes de lecture de disques durs, les mémoires magnétiques non volatiles à accès aléatoire (MRAM) et les capteurs magnétiques. Les matériaux semi-métalliques présentent une forte polarisation en spin qui peut atteindre les 100%. Ces matériaux ont une grande valeur technologique dans plusieurs domaines d’application telle que les dispositifs de spintronique [1], ou l’électronique de spin, les réfrigérants magnétiques [2], [3] les capteurs magnétorésistifs [4], la réfrigération magnétique [5], les mémoires non volatiles, cellule voltaïques, condensateurs, sonars piézoélectriques, capteurs ultrasoniques, technologie de puissance, radiocommunication et médecine. A la lumière de ces explications, notre choix s'est fixé sur la famille des matériaux pérovskites (ABO3).

3

Bien que cette thèse, s’inscrit dans le domaine de la modélisation théorique à l’échelle atomique des propriétés des solides, une famille d’oxydes complexes présentant un intérêt important au niveau fondamental. Parmi ces oxydes complexes, Nous nous sommes intéressés plus particulièrement à deux familles de matériaux pérovskites de type ABO3, où A est un métal alcalin comme : Ca, Sr, Ba ou bien lanthanide comme : La et B est un métal de transition magnétique comme par exemple: Fe, Co, Ni, Mn ou Cr. Ces matériaux sont déjà utilisés dans le domaine des capteurs et de l’électronique. Bien qu’ils présentent tous à haute température la même structure cubique simple, l’intérêt pour ces composés réside en grande partie dans les distorsions structurales qu’ils peuvent développer à basse température. Et d’autre structure dérivée de la forme A2BB’O6 où B’ est un alcalin terreux généralement non magnétique comme : Mo, W, Nb. La structure est définie par un arrangement régulier d'octaèdres BO6 et B'O6 au site substitutionnels alternant le long des trois directions du cristal et dont le cation A occupe les sites interstitiels. Ces oxydes présentent une variété de structures cristallines, autour de la température ambiante, leurs structures pourrait être: cubique (Fm3m) comme par exemple Sr2CrNbO6 [6], tétragonale (I4/m) comme exemple Sr2CoWO6 [7] et monoclinique (P21/n) comme exemple Ca2CoNbO6 [8]. Comme ils présentent aussi des propriétés électriques et magnétiques qui comprennent; la métallicité, multiferroicité, piézoélectricité, ferro/ferri/antiferromagnétisme (FM, FIM, AFM), magnétorésistance colossale [9, 10,11] et la réponse magnétoélectrique, et d’autres propriétés physiques intéressantes comme la conduction ionique, transition isolant→métal et métal→isolant, changement de structure sous pression et température, … etc

Il est actuellement possible de définir les caractéristiques de plusieurs matériaux, en appliquant des méthodes de calculs théoriques bien spécifiées et adaptées selon les objectifs tracés, en allant de la mécanique classique vers la mécanique quantique.

Le but de notre travail de recherche est d’étudier certains matériaux basés sur les atomes de métaux de transition et terre rare.

Bien que ces composés ont été étudiés intensivement depuis plus de 50 ans, plusieurs questions fondamentales subissent concernant leurs comportements à l’échelle microscopique. Plusieurs études théoriques ab-initio ont mené à des études plus vastes sur les oxydes de métaux de transition à structure pérovskite, et qui ont permis d’acquérir une compréhension à l’échelle atomique, et donné une vue globale à des avancées réalisées.

L’étude de différentes propriétés des matériaux solides comme les propriétés structurales, électroniques, optiques, mécaniques et thermodynamiques du solide, est devenue possible à

4

l’aide de l’exécution des traitements basés sur la mécanique quantique. Notamment, les simulations quantiques de premiers principes « ab initio » utilisant le formalisme de la théorie de la fonctionnelle de la densité DFT et la méthode des ondes planes augmentées linéarisées FPLAPW [12] développée par l’équipe de Schwarz, basée sur la résolution auto-cohérente des équations de Kohn-Sham permette d’obtenir des résultats satisfaisantes pour des systèmes fortement corrélés, et déterminer avec précision une large gamme de propriétés physico-chimiques de la matière. Ce qui offre une importance technologique des matériaux. En effet la DFT (Théorie de la Fonctionnelle de la densité) est actuellement la théorie la plus utilisée dans les calculs ab-initio [13]. Elle permet d’obtenir une large gamme d’informations sur l’origine microscopique des propriétés des solides, et de bonnes prédictions structurales et énergétiques. L’objectif principal de notre travail de recherche est l'étude des propriétés structurales, optoélectronique et magnétiques des oxydes-pérovskites LaBO3 (B= Co, Fe, Mn) et double pérovskites Ca2XNbO6 (X=Co, Cr, Mn) basée sur la méthode des ondes planes augmentées linéarisées à potentiel total (FP-LAPW) implémentée dans le code Wien2k, avec les approximations du gradient généralisé (GGA-PBE) plus le potentiel de Becke-Johnson modifié (mBJ) comme potentiel d'échange-corrélation. Les propriétés thermodynamiques ont été explorées dans la gamme de température 0 -1200 K en utilisant le modèle quai-harmonique de Debye moyennant le programme GIBBS [14].

Notre travail est devisé en deux parties :

La première partie est contribuée à l’étude structurale, électronique et optique, des oxydes de pérovskite, LaBO3, avec B=Co, Fe, Mn.

La deuxième partie porte sur l’étude des propriétés structurales, électroniques, optiques et thermodynamiques des doubles pérovskites Ca2XNbO6, X=Co, Cr, Mn.

Ces matériaux ont été largement étudiés depuis les années cinquante, vu qu’ils présentent de nombreuses transitions de la phase structurales. Nos matériaux sans stables dans la phase cubique, autrement dit, ils ont tous à température ambiante la même structure cubique, qu’elle est relativement moins étudiée.

Mis à part l’introduction et la conclusion générales, cette thèse s’articule autour de trois chapitres sont :

 Le premier chapitre, donne un aperçu sur cadre théorique suivi par le code de calcul utilisé au cours de ce travail, particulièrement les fondements de la DFT, plusieurs approximations ont été utilisées pour l’énergie d’échange-corrélation, la méthode FP-LAPW et

5

une description de code de calcul Wien2k employé pour simuler les propriétés structurales, magnétiques, optoélectroniques et thermodynamiques de nos matériaux.

 Le second chapitre, présente des généralités sur les pérovskites ABO3 et les doubles pérovskites Ca2AA’O6, et particulièrement, les matériaux LaBO3, (B= Co, Fe, Mn), et CaXNbO6, (X= Co, Cr, Mn), et leurs caractéristiques selon leurs domaine d’application. Ces deux premiers chapitres permettent d’apporter les éléments nécessaires à la compréhension du sujet.

 Le chapitre trois regroupe tous les résultats de nos calculs avec une interprétation parallèle, suivi par une comparaison de ces derniers avec les résultats des autres travaux expérimentaux et théoriques disponibles dans la littérature.

6

Références Bibliographiques:

[1] Bader, S.D., Parkin, S.S.P.: Spintronics. Annu. Rev. Condens. MatterPhys. 1, 71–88 (2010).

[2] G.Sharma, T.S. Tripathi, J. Saha andS. Patnaik, Journal of Magnetism and Magnetic Materials. 368, 318-323 (2014).

[3] V. Franco, J.S. Blzquez, B. Ingale andA. Conde, Annu. Rev. Mater. Res. 42, 305 (2012),

[4] S. Jin, M. McCormack, T.H. Tiefel and R. Ramesh, J. Appl. Phys. 76 (1994) 6929-6933

[5] G.V. Brown, J. Appl. Phys. 47(1976) 3673,

[6] J . Chem. Soc., Faraday Trans., 1996, Vol. 92 1057

[7] R.P. Borges, R.M. Thomas, C. Cullinan, J.M.D. Ceoy, R. Suryanarayanan, L. Ben-Dor, L. P-Gaudart and A. Revcolevski, J. Phys. Condens. Matter 11, 445 (1999).

[8] R. Shaheen, J. Bashir / Solid State Sciences 12 (2010) 1496e1499

[9] K.I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature 395, 677

(1998).

[10] M.T. Anderson, K.B. Greenwood, G.A. Taylor and K.R. Poeppelmeier, Prog. Solid State Chem. 22, 197-233 (1993).

[11] M. Azuma, K. Takata, T. Saito, S. Ishiwata, Y. Shimakawa and M. Takano, J. Am. Chem. Soc. 127, 8889 (2005).

[12] Blaha P, Schwarz K, Madsen G K H, Kvasnicka D and LuitzJ 2001 Karlheinz Schwarz, Techn. Universitat (Wien, Austria).

[13] C. Pisani, R. Dovesi and C. Roetti, Hartree-Fock, ab-initio treatment of crystalline systems, springer-Verlag (1986)

[14] Bouadjemi, B., Bentata, S., Abbad, A., Benstaali,W., Bouhafs, B.: Solid State Commun. 168, 6 (2013).

Théorie de la Fonctionnelle

de la Densité

Ce chapitre présente les fondements théoriques de la théorie de la Fonctionnelle de la Densité sur laquelle repose le code FP-LAPW. Décrivant

les approximations quantiques fondamentales utilisées pour résoudre l’équation de Schrödinger pour un système complexe. Ensuite, nous proposons quelques approximations comme GGA, GGA+U et mBJ qui sont

implémentées dans le code wien2k, ainsi le modèle quasi harmonique de Debye dans le code GIBSS.

8

I.1 Introduction :

De nombreuses et différentes techniques de calcul au niveau atomique sont apparues au cours des dernières décennies, elles sont basées principalement sur une description empirique des interactions entre les électrons et les noyaux, que nous pouvons distinguer et classer en trois modèles selon la nécessité de chaque méthode, des résultats expérimentaux, ou des données fondamentales :

 Les méthodes empiriques nécessitent des résultats expérimentaux.

 Les méthodes semi-empiriques nécessitent des résultats expérimentaux, et les données fondamentales.

 Les méthodes ab-initio, basées uniquement sur les données fondamentales (densité électronique et l’énergie totale de l’état fondamental), elles différents par le choix des fonctions enveloppes, parmi elles, celles des méthodes linéarisées comme la méthode des ondes planes augmentées linéarisées (FL-LAPW)

Ce chapitre a pour but de présenter le cadre théorique de l’une des méthodes ab-initio qui semblent bien adaptées à l’étude des matériaux ioniques et le calcul des structures de bandes, et tout système ayant des états électroniques indépendant de l’arrangement local des atomes, qui a pour but fondamental le calcul des propriétés structurales, électroniques des systèmes complexes. Un simple modèle physique est limité pour résoudre les problèmes d’une vaste série des matériaux. Le traitement s’est fait en faisant appel tout d’abord à une série d'approximations quantiques introduites par Borh-Oppenheimer en 1927[1], et Hartree en 1928 et Hartree-Fock [2-3] en 1930, pour résoudre l’équation de Schrödinger [4-5] d’un système complexe. Par la suite nous définissons le concept de base de la théorie de la fonctionnelle de la densité, qui se base particulièrement sur les théories d’Hohenberg-Kohn [6] en 1964, et Kohn-Sham [7] en 1965. Ensuite, nous proposons quelques approximations comme l’approximation de la Densité Locale (LDA), l’approximation de gradient généralisé (GGA) et avec la correction d’Hubbard (GGA+U), plus le Potentiel de Becke et Johnson modifié (mBJ), et finalement, nous décrivons les divers choix possibles selon la base des fonctions d’onde et la forme du potentiel, particulièrement, les méthodes linéarisées comme la méthode des ondes planes linéarisées augmentée (LAPW) [8] couplées au potentiel total (FP) qui sont implémentées dans le code wien2k.

9

L’étude des propriétés structurales d’un matériau à N corps, ou les interactions entre les électrons et les noyaux sont fortement corrélés, se fait par la résolution de l’équation de Schrödinger, d’où est apparu la théorie de la fonctionnelle de la densité (DFT), fondée sur un principe explicite de la structure électronique, son concept de base est :l’énergie totale d’un système est en fonction de la densité électronique, c’est en fait le modèle de Thomas [9] et Fermi [10] exprimé en 1927, où les interactions électroniques sont traitées d’une manière classique, et l’énergie cinétique est calculée en considérant que la densité électronique est homogène, puisque la densité électronique n’est toujours pas homogène, il était indispensable d’introduire d’autre théories profondes suite au modèle de Thomas-Fermi.

Un tel système ayant un nombre important d’atomes et une forte interaction entre les atomes, nécessité une approche intermédiaire entre les calculs empirique et les calculs ab initio : la méthode quantique qui repose sur l’Hamiltonien explicitée dans les orbitales atomiques localisées minimales. Empirique, parce qu’elle introduit des paramètres ajustables dans lesquels la difficulté principale de la théorie réside.

I.2 Equation de Schrödinger :

Les méthodes ab-initio servent à prédire la structure électronique des matériaux, par la résolution des équations de la mécanique quantique à plusieurs corps, sans utiliser de variable ajustable. L’objectif est de modéliser un système quantique possédant Nn noyaux, de charge Zn et de masse mn et de Ne électrons en interaction coulombienne.

L’énergie E et la fonction d'onde Ψ d'un système quantique est décrite par l’équation de Schrödinger (1887-1961) suivante [4]:

(I.1)

Où :

Ψn la fonction d’onde associée au niveau d’énergie En, avec n est le nombre entier introduisant la quantification du système.

H est l'opérateur Hamiltonien du système (noyaux + électrons) s’écrit en générale comme :

(I.2)

𝑯𝜳_𝒏 = 𝑬_𝒏𝜳𝒏

10

Avec :

Vnn : représente l’interaction noyaux-noyaux,

Tn : l'énergie cinétique des noyaux,

Ven : est l'interaction électrons-noyaux,

Vee : d’interaction électrons-électrons

Te : est l'énergie cinétique des électrons.

Le développement de l’Hamiltonien d’un système s’écrit :

(I.3)

Ћ la constante de Plank, donnée par ћ =_𝟐𝝅𝒉

Mi : la masse du noyau i, Zi et Zj sont les nombres atomiques des noyaux i et j respectivement.

ri (i=1, …, n) définissent la position des électrons, n est le nombre d’électrons.

R (𝞪=1, …, N): présente la position des noyaux, et N est le nombre d’atomes dans le système. Les indices i et j corresponds aux électrons et aux noyaux.

Non seulement la résolution de l’équation (I.1) rejoint la résolution d’un problème à N corps, mais en plus l’existence du terme d’interaction électron-électron, rendent la résolution de l'équation de Schrödinger plus complexe, autrement dit, il est impossible d’obtenir les énergies fondamentales. Ce qui oblige de passer par une série d’approximations.

La masse des noyaux et des électrons nous permet de justifier l’approximation de Bohr-Oppenheimer.

I.3 Approximation de Born et Oppenheimer :

L’approximation de Born et Oppenheimer en 1927 [1] est basée sur la différence d’inertie entre les électrons et les noyaux, par conséquent les noyaux sont plus massifs que les électrons

mp=1836me, ce qui fait que leur mouvement est moins accéléré que ceux des électrons et leur énergie cinétique est faible, ainsi leur énergie potentielle est constante, et les électrons réagissent quasi instantanément. Ce fondement théorique conduit Born et Oppenheimer à proposer une simple résolution de l’équation de Schrödinger (I.1), en partageant la partie nucléaire de la partie électronique.

𝐻 = −ћ2 2 ∑ 𝛻2_(𝑅 𝛼) 𝑀_𝑖 − ћ2 2 ∑ 𝛻2_(𝑟 𝑖) 𝑚_𝑒 𝑖 + 1 8𝜋𝜀₀∑ 𝑒2 |𝑟𝑖− 𝑟𝑗| 𝑖,𝑖≠𝑗 𝛼 + 1 8𝜋𝜀₀∑ 𝑒2 _𝑍 𝛼𝑍𝛽 |𝑅𝛼− 𝑅𝛽| 𝛽<𝛼 − 1 4𝜋𝜀₀∑ 𝑍𝛼𝑒2 |𝑅_𝛼− 𝑟_𝑖| 𝛼,𝑖

11

L’hamiltonien d’un système donné par l’équation (I.3), s’écrit sous la forme de la somme des deux parties, comme suit :

(I.4)

Où :

He et Hn présentent les Hamiltoniens électronique et nucléaire respectivement. Ils sont donnés par les expressions suivantes :

(I.5)

(I.6)

Ainsi la fonction d’onde s’écrit comme le produit des deux fonctions :

(I.7)

L’énergie moléculaire totale est la somme des énergies, nucléaire et électronique, s’écrit comme suit :

(I.8)

L’équation de Schrödinger devient :

(I.9)

Le problème comporte la résolution de l’équation de Schrödinger électronique, même avec cette approximation, l’existence du terme associé à l’interaction électron-électron rend la solution analytique plus difficile.

𝐇𝐞 = − 𝟏 𝟐∑ 𝛁𝐢𝟐∑ ∑ 𝟏 |𝐫_𝐢− 𝐫_𝐣| 𝐍𝐞 𝐢>𝑗 − ∑ ∑ 𝐙𝐚 |𝐫𝐢− 𝐑𝛂| 𝐍𝐧 𝐚=𝟏 𝐍𝐞 𝐢=𝟏 𝐍𝐞 𝐢=𝟏 𝐍𝐞 𝐢 𝐇𝐧= − 𝟏 𝟐∑ 𝛁𝐚𝟐 + ∑ ∑ 𝐙_𝐚𝐙_𝐛 |𝐑𝐚− 𝐑𝐛| 𝐍𝐧 𝐛>𝑎 𝐍𝐧 𝐚=𝐛 𝐍𝐧 𝐚=𝟏 {−𝟏 𝟐∑ 𝜵𝒊𝟐 𝑵𝒆 𝒊=𝟎 − ∑ ∑ 𝒁𝒂 |𝒓𝒊− 𝒓𝒂|+ ∑ ∑ 𝟏 |𝒓_𝒊− 𝑹_𝒋| 𝑵𝒆 𝒋>𝑖 𝑵𝒆 𝒊=𝟏 𝑵𝒏 𝒂=𝟏 𝑵𝒆 𝒊=𝟏 } 𝜳 = 𝑬𝒆 𝜳 𝑯 = 𝑯_𝒆+ 𝑯_𝒏 𝜳 = 𝜳_𝒆𝜳_𝒏 𝑬 = 𝑬𝒆+ 𝑬𝒏

12

I.4 Approximation de Hartree (1928):

Hartree [2] a résolu l’équation de Schrödinger en supposant que chaque électron se comporte comme s’il était seul dans un potentiel moyen crée par tous les autres électrons, c’est-à-dire l’approximation des électrons libres. Dans ce cas la fonction d’onde à N électrons est le produit direct des fonctions d’onde mono-électronique

φ

(I.10)

L’Hamiltonien électronique donné par l’équation (I.5), s’écrit comme la somme des Hamiltoniens à un électron :

(I.11)

L’équation de Schrödinger mono électronique dans l’approche de Hartree est définie comme suit :

(I.12)

Le premier terme de cette équation, correspond à l’énergie cinétique Veff(r) le potentiel qui subit l’électron, nommé effectif, en outre ce potentiel doit prendre en considération l’interaction électron-noyau :

(I.13)

Où :

r et R expriment les positions spatiales de l’électron et du noyau respectivement.

𝚿 (𝐫) = ∏ 𝛗𝐢 (𝐫𝐢) 𝐍𝐞 𝐢=𝟏 𝑯_𝒆 = ∑ (−𝟏 𝟐𝛁𝐢𝟐+ ∑ 𝟏 |𝐫𝐢− 𝐑𝐣| − ∑ 𝐙𝐚 |𝐫_𝐢− 𝐫_𝐚| 𝐍𝐧 𝐚=𝟏 𝐍𝐞 𝐣>𝑖 ) 𝐍𝐞 𝐢=𝟏 − ћ 𝟐𝐦𝛁𝟐𝛗𝐢 (𝐫) + 𝐕𝐞𝐟𝐟(𝐫) = 𝛆𝐢𝛗𝐢 (𝐫) 𝑽_𝑵(𝒓) = −𝒁𝒆𝟐_∑ 𝟏 |𝒓 − 𝑹| 𝑹

13

Pour les autres électrons, selon l’approximation de Hartree, ces électrons forment une distribution de charge négative ρ(r'), où l’électron se déplace dans un potentiel électrostatique

moyen VH(r') (potentiel de Hartree), dérivant de l’ensemble des électrons voisins défini par :

(I.14)

La somme des contributions nous donne le potentiel effectif donné par :

(I.15)

Remarquons que dans l’équation (I.13) le terme à un seul centre tandis que l’équation (I.14) le terme à deux centre r et r’.

Les fonctions propres résultantes de la solution de l’équation (I.12) permettent un calcul d’une nouvelle densité électronique :

(I.16)

La fonction d’onde, la densité électronique et le potentiel de Hartree sont interdépendantes. Ce qui empêche le calcul simultanément avec une méthode directe. Dans ce cas il faut faire appel à une autre approche.

I.5 Approximation de Hartree-Fock :

Fock [3] en 1930 a rectifié le modèle de Hartree, dont il a montré qu’il a négligé le terme d’échange dû à la forme antisymétrie de la fonction d’onde. Fock a présenté la fonction d’onde sous la forme d’un déterminant de Slater [11], il a combiné linéairement les fonctions d’onde des électrons libres afin d’arriver au concept de Pauli [12] :

(I.17)

L’énergie peut s’écrire comme :

𝑽_𝑯(𝒓) = −𝒆 ∫ 𝒅 𝒓҆_𝝆(𝒓҆₎ 𝟏 |𝒓 − 𝒓′_| Veff (r) = VH (r)+ VN (r) 𝝆(𝒓) = ∑ 𝝋_𝒊∗_(𝒓)𝝋 𝒊(𝒓) 𝒊 𝚿é𝐥 (𝐫) = 𝟏 √𝐧! | | 𝛗_𝟏(𝐫_𝟏) . . 𝛗_𝐧(𝐫_𝐧) . . . . . . 𝛗_𝟏(𝐫𝐧) . . 𝛗𝐧(𝐫𝐧) | |

14

(I.18)

(I.19)

Le terme Ji est l’intégral de Coulomb, présent dans l’approximation de Hartree, mais Kij est le terme de Fock (intégral d’échange), qui résulte de la nécessité d’anti symétrie la fonction d’onde.

Afin de calculer les fonctions d’onde Ψi (r) par l’utilisation du concept de minimisation de

(I.20)

Rayleigh- Ritz l’équation (I.17) devient [13] :

(I.21)

En diagonalisant la matrice ci-dessus des multiplicateurs de Lagrange λi,j, en obtenant l’équation mono électronique de Fock :

Avec : (I.22)

I.6 Théorie de la Fonctionnelle de la Densité :

Le principe de la DFT exprime l’énergie totale d’un système électronique en fonction de sa densité électronique. C’est en fait un modèle ancien datant particulièrement des travaux de Lhewllyn Thomas et Enrico Fermi en 1920 [9-10], qui a été reformulé dans les années soixante

𝜹 (𝑬𝑯𝑭(𝒓) − ∑ 𝝀𝒊,𝒋(⟨𝜳𝒊|𝜳𝒊⟩ − 𝜹𝒊𝒋)) = 𝟎 𝒊,𝒋 [𝑻é𝒍+ 𝑽é𝒍−𝒏𝒖+ 𝑽𝑯𝒂𝒓𝒕é𝒆+ 𝑽𝑭𝒐𝒄𝒌 ({𝜳(𝒓)})]𝜳𝒊(𝒓) = 𝜺𝒊𝜳𝒊(𝒓) 𝑬𝑯𝑭(𝒓) = 〈𝝋é𝒍({𝒓})|𝑯|𝝋é𝒍({𝒓})〉 = ∑ 𝐇𝐢+ 𝟏 𝟐∑ (𝐉𝐢,𝐣 𝐢𝐣 − 𝐊𝐢𝐣) 𝐢 { 𝐇𝐢 = ∫ 𝐝𝐫𝛗𝐢(𝐫)∗[− 𝟏 𝟐𝛁𝟐+ 𝐕é𝐥−𝐧𝐮(𝐫) + 𝐕𝐞𝐱𝐭(𝐫)] 𝛗𝐢(𝐫) 𝐉_𝐢𝐣 = 𝟏 𝟐∬ 𝐝𝐫𝐝𝐫′𝛗𝐢(𝐫)𝛗𝐢∗(𝐫) 𝟏 |𝐫′_{− 𝐫|}𝛗𝐣∗(𝐫′)𝛗𝐣(𝐫′) 𝐊_𝐢𝐣 = 𝟏 𝟐∬ 𝐝𝐫𝐝𝐫′𝛗𝐢 ∗ (𝐫)𝛗_𝐢(𝐫) 𝟏 |𝐫′_{− 𝐫|}𝛗𝐢(𝐫′)𝛗𝐢∗(𝐫′)𝛅(𝛔𝐢− 𝛔𝐣 { 𝑽𝑯𝒂𝒓𝒕𝒓é𝒆= ∑ ∫ 𝒅𝒓 ′_𝝋 𝒋(𝒓)𝝋𝒋(𝒓∗) 𝟏 |𝒓′_{− 𝒓|} 𝒋 𝑽𝑭𝒐𝒄𝒌= [∑ 𝒅𝒓′𝝋𝒋(𝒓)𝝋𝒋(𝒓∗) 𝟏 |𝒓′_{− 𝒓|} 𝒊 ] 𝝋_𝒋(𝒓) 𝝋𝒊(𝒓) 𝜹(𝝈𝒊− 𝝈𝒋)

15

par Hohenberg et Kohn [6] et par Kohn et Sham [7]. La DFT [14-15] est devenue l’une des méthodes applicable dans la physique du solide et dans l’étude des propriétés structurales, électroniques, élastiques, optiques, et thermodynamiques. Cette théorie a été particulièrement évoluée dans le domaine de la mécanique quantique (application des équations de Schrödinger [4] et approximation de Born-Oppenheimer [1]) en raison de son utilisation possible dans le code de calcul numérique ab-initio et la fiabilité de ses résultats dans le calcul des paramètres physique dans un système complexe.

La DFT remplace les méthodes de calcul traditionnelle basées sur la fonction d’onde multiélectronique, elle dépend juste de 3N variables, c’est-à-dire la densité électronique est en fonction de seulement 3N inconnus où N est le nombre d'électrons considérés, tandis que la DFT permet de résoudre un problème à plusieurs corps, en outre elle permet de calculer l’énergie totale de l’état fondamental d’un système d’électrons en forte interaction entre eux. D’où le déplacement des électrons ne se fait pas indépendamment les uns des autres, ils ont un mouvement corrélé. Ce qui est remarquable dans cette théorie est qu’elle a un concept variationnel, autrement dit, elle considère la densité électronique d’un système à l’état fondamental variable et décrit tous les autres paramètres en fonction de cette variable ce qui conduit au théorème de Hohenberg et Kohn [6]. Ces auteurs ont prouvé que toutes les propriétés, et en particulier l’énergie de l’état fondamental non dégénéré d’un tel système, sont entièrement déterminées par la densité électronique. La corrélation de l’énergie par rapport à la densité n’est toujours pas connue, mais la valeur exacte de la densité électronique ρ(r), conduit à l’énergie minimale du système. Alors l’énergie E[ρ(r)], est une fonctionnelle de la densité

ρ(r).

I.6.1 Théorèmes d’Hohenberg et Kohn:

Hohenberg et Kohn reformulèrent la DFT en 1964 dans leur article [6], cette reformulation est fondée sur les principes de la théorie de la fonctionnelle sous forme de deux théorèmes, par la suite Kohn et Sham présentèrent une approche sous forme d’une résolution analytique de l’équation de Schrödinger [4] :

a) Premier théorème :

«L’énergie totale de l’état fondamental E est une fonctionnelle unique de la densité des

particules ρ(r)pour un potentiel externe Vext(r) donné». L’énergie s’écrit comme suit:

16

(I.23)

Où :

∫ 𝝆(𝒓)𝑽𝒆𝒙𝒕(𝒓) : présente l’interaction noyau-électron.

F[ρ(r)] est la fonctionnelle de la densité ρ[r] indépendant du potentiel extérieur Vext , comporte les contributions cinétiques et coulombiennes à l’énergie :

(I.24)

Exc[ρ(r)] : est l’énergie d’échange et de corrélation.

EHartree[ρ(r)] : est la répulsion coulombienne électron-électron.

T [ρ(r)] : est l’énergie cinétique du système.

Le calculer d’énergie à l’état fondamental pour un potentiel externe donné, fait appel au principe variationnel, au lequel se fonde le deuxième théorème de Hohenberg et Kohn.

b) Deuxième théorème :

«La fonctionnelle de l'énergie totale de tout système a plusieurs particules possède un

minimum qui correspond à l'état fondamental et à la densité de particules de l'état fondamental».

Ce théorème indique le principe variationnel, où la fonctionnelle de l’énergie globale E[ρ(r)] est minimale, quand la densité électronique ρ(r) correspond à celle de l’état fondamental ρ0(r), ce qui donne:

(I.25)

La fonctionnelle de l’énergie totale de l’état fondamental s’écrit comme :

(I.26)

𝑬𝑯𝑭[𝝆(𝒓)] = 𝑭𝑯𝑭[𝝆(𝒓)] + ∫ 𝝆(𝒓)𝑽𝒆𝒙𝒕(𝒓)

𝑭[𝝆(𝒓)] = 𝑻[𝝆(𝒓)] + 𝑽é𝒍[𝝆(𝒓)] = 𝑻[𝝆(𝒓)] + 𝑬𝑯𝒂𝒓𝒕𝒓𝒆𝒆[𝝆(𝒓)] + 𝑬𝒙𝒄[𝝆(𝒓)]

𝑬(𝝆𝟎) = 𝒎𝒊𝒏 𝑬(𝝆)

17

Avec :

(I.27)

Le premier terme définit la valeur moyenne de l’énergie cinétique, le deuxième terme est l’interaction coulombienne de Hartree, et le troisième terme présente l’énergie d’échange et de corrélation.

Par conséquent l’équation fondamentale de la DFT s’écrit comme :

(I.28)

Avec :

(I.29)

F[ρ(r)] est la fonctionnelle universelle pour n’importe quel système à plusieurs électrons.

La résolution de l’équation (I.26) nécessite la connaissance de F[ρ(r)], malheureusement les théorèmes de Hohenberg et Kohn ne donnent aucun résultat.

I.6.2 Approche de Kohn et Sham :

L’approche de Kohn et Sham a été proposée en 1964 [7], suite aux travaux de Hohenberg et Kohn, son concept fondamental est de remplacer un système réel à N électrons en interaction dans un potentiel externe Veff(r), par un système auxiliaire fictif à N électrons (système de Kohn et Sham) d’électrons sans interaction mais de même densité électronique que le système réel. L’équation de Schrödinger dans le cadre de la théorie de Kohn et Sham est sous la forme

(I.30)

La résolution numérique de l’équation (I.30) est effectuée selon un processus itératif (Figure

I.1).

εi: est l’énergie d’une orbitale de Kohn-Sham,

Veff Le potentiel effectif s’écrit sous la forme suivante : [𝝏𝑭[𝝆(𝒓) 𝝏𝝆(𝒓) ]_{𝝆(𝒓)=𝝆} 𝟎(𝒓) = 𝟎 [𝝏𝑬[𝝆(𝒓) 𝝏𝝆(𝒓) ] = 𝑽𝒆𝒙𝒕[𝝆(𝒓)] + [ 𝝏𝑭[𝝆(𝒓) 𝝏𝝆(𝒓) ] 𝑭[𝝆(𝒓)] = 𝑻[𝝆(𝒓)] + ∫𝝆(𝒓)𝝆(𝒓′) |𝒓 − 𝒓′| 𝒅𝒓𝒅𝒓′+ 𝑬𝒙𝒄[𝝆(𝒓)] [−_𝟐𝒎ћ 𝛁_𝒊𝟐_{+ 𝑽} 𝒆𝒇𝒇(𝒓)] |𝝋𝒊(𝒓)⟩ = 𝜺𝒊|𝝋𝒊(𝒓)⟩

18

(I.31)

: Sont les interactions électron-noyau, et électron-électron respectivement

Le 𝑽̂ potentiel d’échange-corrélation donnée par la dérivée fonctionnelle de l’énergie E_𝒆𝒇𝒇 xc par rapport à la densité ρ

Vxc(r) : est le potentiel d’échange-corrélation donnée par la dérivée fonctionnelle de l’énergie

Excpar rapport à la densité ρ :

(I.32)

La fonctionnelle d’énergie est donnée par la relation suivante:

(I.33)

Où :

Eee[ρ(r)] : Est l’énergie potentielle de répulsion électron-électron 𝝐ext[ρ(r)] : L’énergie potentielle d’attraction noyau-électron

Tks[ρ(r)] : L’énergie cinétique de l’état fondamental du système fictif est :

(I.34)

: est un spin orbitale de Kohn-Sham.

𝝆 : Densité électronique peut être calculée à partir des orbitales Kohn-Sham comme la somme sur l’ensemble des orbitales occupées :

(I.35) ni : Occupation d’orbitale i. 𝝆(𝒓) = ∑ 𝒏𝒊|𝝋𝒊(𝒓)|² 𝑵 𝒊 𝑬[𝝆(𝒓)] = 𝑻𝒌𝒔[𝝆(𝒓)] + 𝑬𝒆𝒆[𝝆(𝒓)] + 𝝐𝒆𝒙𝒕[𝝆(𝒓)] + 𝑬𝒙𝒄[𝝆(𝒓)] 𝑻𝒌𝒔 = − ћ 𝟐𝒎∑⟨𝝋𝒊𝒌𝒙|𝜵𝟐|𝝋𝒊𝒌𝒙⟩ 𝑵 𝒊=𝟏 𝝋_𝒊𝒌𝒙 𝑽̂ = 𝑽_𝒆𝒇𝒇 ̂ + 𝑽_𝒏𝒆 ̂ + 𝑽_𝒆𝒆 ̂ _𝒙𝒄 𝑽̂ 𝒆𝒕 𝑽𝒏𝒆 ̂𝒆𝒆 𝑽_𝒙𝒄(𝒓) = 𝜹𝑬𝒙𝒄[𝝆(𝒓)] 𝜹𝝆(𝒓)

19

La méthode de Kohn et Sham donne des résultats exacts du problème à N électrons en interaction, mais le terme Vxc ne présente aucune formulation explicative [15], dont le calcul de la fonctionnelle d’échange et corrélation Exc est impossible, alors il est nécessaire d’aboutir à d’autres approximations.

20

21

I.6.3 Le potentiel de Coulomb :

Dans l’équation de Kohn-Sham, le potentiel V(c) utilisé comporte le potentiel de coulomb et potentiel d’échange et corrélation, défini comme suit :

(I.36)

Où :

VH,VN sont les potentiels de Hartree, et nucléaire respectivement.

Et Vc(r) est déterminé en fonction de la densité de charge par la résolution de l’équation de Poisson :

(I.37)

La résolution de cette

équation se fait dans un espace réciproque à l’espace réel, dont l’équation de Poisson est la diagonale, et la solution devient plus simple :

(I.38)

I.6.4 Potentiel d’échange-corrélation :

Le potentiel d’échange et de corrélation se présente de façon linéaire et se détermine dans l’espace diagonal. La représentation de la charge interstitielle dans l’espace réel est obtenue par la transformation de la série de Fourier. Afin de déterminer le potentiel d’échange et de corrélation plusieurs approximations étaient proposées.

I.7 Différents types de fonctionnelles d’échange et de corrélation :

I.7.1 Approximation de la densité locale (LDA) :

L’approximation de la densité locale (Local Density Approximation) LDA [16-17] fut introduite par Kohn et Sham en 1965, elle repose sur le fait que tous les termes d’échange-corrélation ne dépendent que de la valeur de la densité locale ρ(r), où la densité est traitée comme étant constante.

𝑽_𝒄(𝒓) = 𝑽_𝑯(𝒓) + 𝑽_𝑵(𝒓)

∆𝑽_𝒄(𝒓) = 𝟒𝝅𝝆(𝒓𝝆)

𝑽_𝒄(𝑮) = 𝟒𝝅 𝑮²

22

La LDA suppose que la densité électronique d’un gaz non uniforme est considérée comme uniforme de manière à ce qu’elle soit décomposée en tout point r de l’espace, l’énergie d’échange-corrélation par électron dans le gaz réel (inhomogène), est égale à l’énergie d’échange-corrélation par électron dans le gaz homogène de densité identique. Par conséquent, l’énergie totale d’échange et corrélation du gaz inhomogène s’écrit comme suit :

(I.39)

Où :

Est l’énergie d’échange-corrélation par particule du gaz homogène avec une densité constante [18]:

En combinant les équations (I.32) et (I.39), nous obtenons l’expression du potentiel d’échange-corrélation dans le cadre de la LDA comme :

(I.40)

La LDA suppose que 𝝐𝒙𝒄𝑳𝑫𝑨[𝝆(𝒓)] est purement local, donc cette énergie est divisée en deux

termes :

(I.41)

Les deux termes présentent les énergies de corrélation, et d’échange respectivement.

Cette fonctionnelle fut déterminée par Wigner [19], Ceperly-Alder [20], Perdew [21], Kohn-Sham [7], Hedin-Lundqvist [22] et Perdew-Wang [23].

La LDA était la fonctionnelle locale la plus utilisée jusqu’à 1992 avec l’apparition de la fonctionnelle de Perdew-Wang, mais elle est incapable de décrire correctement les systèmes fortement corrélés, en particulier les composantes des métaux de transitions de type isolant, ou isolant à transfert de charge. C’est pourquoi d’autre termes devraient être réintroduits dans l’expression d’échange et corrélation, c’est l’outil des méthodes dites GGA.

𝑬_𝑿𝑪𝑳𝑫𝑨_{[𝝆(𝒓)] = ∫ 𝝐} 𝒙𝒄 𝑳𝑫𝑨_{[𝝆(𝒓)] [𝝆(𝒓)]𝒅}𝟑_𝒓 𝑽𝒙𝒄𝑳𝑫𝑨(𝒓) = 𝜹𝝆(𝒓) 𝜹𝝐_𝒙𝒄𝑳𝑫𝑨_[𝝆(𝒓)] 𝜹𝝆(𝒓) 𝝐𝒙𝒄𝑳𝑫𝑨[𝝆(𝒓)] 𝝐𝒙𝒄[𝝆(𝒓)] = 𝝐𝒙[𝝆(𝒓)] + 𝝐𝒄[𝝆(𝒓)]

23

I.7.2 Approximation du gradient généralisé (GGA) :

La fonctionnelle du gradient généralisé (GGA) [14], est une suite et amélioration de la fonctionnelle de la densité locale (LDA). Les résultats de la LDA ne sont pas fiables dans tous les cas, en raison que la LDA se base sur le modèle du gaz de densité électronique homogène. Cependant la plupart des systèmes atomiques et moléculaires sont différent, et d’une manière générale, tous les systèmes réels sont inhomogènes, ça veut dire que la densité électronique contient une variation spatiale. D’où vient l’idée de la GGA pour corriger l’expression de l’énergie d’échange et corrélation qui se fonde uniquement sur la densité locale par une autre expression qui se base sur la densité et son gradient. En s’appuyant sur le gradient pour obtenir les propriétés électroniques désirées. L’énergie d’échange et de corrélation est décrite dans l’approximation GGA de la manière suivante :

(I.42)

Où :

𝝐𝒙𝒄𝑮𝑮𝑨[𝝆(𝒓), |𝜵𝝆(𝒓)|], étant la fonction d’échange et de corrélation dépendante de la densité

électronique et son gradient, et si on tient compte du spin, l’équation précédente devient :

(I.43)

Il existe plusieurs versions de la GGA, où les fonctionnelles de la GGA sont réalisées par deux façons : la première procédure est purement empirique, elle nécessite une interpolation numérique des résultats expérimentaux obtenus, la deuxième procédure admet des fonctionnelles fondées sur les principes de la mécanique quantique. Parmi ces versions celle de Perdew-Burk-Ernzerhof [24] qui ont exhibé une version développée sans paramètres empiriques. Elle est caractérisée par la densité électronique locale et son gradient du premier et second ordre inclus dans leur élément d’amélioration.

Malgré l’efficacité de l’approximation de la GGA, mais ces résultats ne sont pas souvent fiables, elles échouent toujours à calculer la largeur des bandes interdites, cela signifie que la DFT ne traite pas les états excités, autrement dit, l’approximation du gradient généralisé ne prend pas en considération la discontinuité du potentiel échange-corrélation.

𝑬𝒙𝒄𝑮𝑮𝑨[𝝆(𝒓)] = ∫ 𝝆(𝒓)𝝐𝒙𝒄𝑮𝑮𝑨[𝝆(𝒓), |𝜵𝝆(𝒓)|]𝒅𝟑𝒓

24

I.7.3 Approximation du gradient généralisé avec la correction de d’Hubbard

(GGA+U) :

Les approximations précédentes sont limitées, elles sont insuffisantes pour améliorer systématiquement le traitement d’énergie d’échange et corrélation. Le problème persiste dans quelques matériaux dont les électrons sont localisés fortement (orbitales d ou f), comme les oxydes des métaux de transition. Le problème peut être résolu en utilisant l’une des méthodes proposées qui est celle de la GGA+U, son principe est d’ajouter un Hamiltonien, qui définit l’interaction coulombienne entre les atomes fortement liée, de type Hubbard dite type de Hartree-Fock, traité dans un champ moyen, applicable aux orbitales d ou f, cela permet non seulement la correction des erreurs de la DFT, en plus l’ouverture des gaps de ces matériaux. En outre il est montré que les approches DFT+U [25] prennent en considération l’anisotropie orbitélaire de l’interaction coulombienne, ce qui conduit à décrire les effets de polarisation orbitale qui joue un rôle important sur l’anisotropie magnétique.

I.7.4 Potentiel de Becke et Johnson modifié mBJ :

Pour déterminer la structure électronique d’un système, il faut résoudre d’abord l’équation de Kohn et Sham. Plusieurs approximations de différents potentiels d’échange et corrélation ont été présentés. La version la plus récente a été proposée par Becke et Johnson [26] qui a été publiée par Tran et Blaha en 2009 [27]. La version du potentiel mBJ (modified Becke Johnson Potentiel), dite aussi TB : Tran-Blaha[27] a été implémentée dans le code ab initio Wien2k.

Tran et Blaha ont vérifié le potentiel d’échange et corrélation proposé par Becke et Johnson (BJ), ils ont découvert que le potentiel de corrélation LDA combiné au potentiel (BJ) donne des énergies de gap sous-estimées. Pour améliorer ces résultats Tran et Blaha ont introduit une simple modification du potentiel BJ. Le potentiel BJ modifié (mBJ) proposé par Tran et Blaha s’exprime par : (I.44) 𝑽_𝝈,𝝌𝒎𝑩𝑱(𝒓) = 𝒄 𝑽_𝝌,𝝈𝑩𝑹_{(𝒓) + (𝟑𝒄 − 𝟐)}𝟏 𝝅√ 𝟓 𝟏𝟐√ 𝟐𝒕𝝈(𝒓) 𝝆_𝝈(𝒓)

25

Où :

La densité des électrons est défini par :

Et la densité de l’énergie cinétique est donné par :

Le potentiel de Beck-Rossel [28] est donné par :

(I.45)

Ce potentiel a été proposé pour modéliser le potentiel coulombien crée par le trou d’échange. L’indice 𝜎 est la notation de spin.

Le terme 𝟀𝜎 est calculé par ρ0(r), 𝛻ρ𝜎(r), 𝛻²ρ𝜎(r), et t𝜎(r), et le terme b𝜎 est déterminé par la relation suivante :

(I.46)

Et le paramètre c sera calculé de façon dépendant linéairement de la racine moyenne de la

moyenne de 𝜵𝝆(𝒓)_𝝆(𝒓) [29].

(I.47)

𝞪 et 𝞫 sont deux coefficients indépendantes obtenus par l’ajustement aux résultats expérimentaux, donnés par (𝞪 = -0.012 et 𝞫= 1.023 Bohr1/2_{) et V}

cell le volume de la maille élémentaire.

Le coefficient c est nécessaire pour le calcul des propriétés électroniques et la structure de bande. Il dépend de l’énergie du gap, c’est-à-dire si ce coefficient diminue, l’énergie du gap diminuera. 𝝆_𝝈(𝒓) = ∑ |𝝋𝒏𝝈 _𝒊,𝝈|² 𝒊=𝟏 𝑻_𝝈(𝒓) =𝟏 𝟐∑ 𝜵𝝋𝒊,𝝈𝜵𝝋𝒊,𝝈 𝑵𝝈 𝒊=𝟏 𝑽_𝝈,𝝌𝒎𝑩𝑱(𝒓) = − 𝟏 𝒃𝝈(𝒓)[𝟏 − 𝒆 𝝌𝝈(𝒓)−𝟏 𝟐𝝌𝝈(𝒓)𝒆−𝝌𝝈(𝒓)] 𝒃𝝈 = [ 𝝌_𝝈𝟑_𝒆−𝝌𝝈 (𝟖𝝅𝝆𝝈)] 𝒄 = 𝜶 + 𝜷 (( 𝟏 𝑽𝒄𝒆𝒍𝒍∫ |𝜵𝝆(𝒓′_)| 𝝆(𝒓) 𝒅𝟑𝒓′)) 𝟏 𝟐

26

I.8 Méthodes des ondes planes linéarisées à Potentiel Total (FP-LAPW):

Le calcul d’énergie totale est conditionné par la connaissance de la densité électronique d’un système, en tenant compte de la formation des orbitales liantes et anti-liantes et la distribution orbitales des électrons, on génère les propriétés structurales des systèmes que nous désirons calculer, dans un code présenté dans cette thèse qui est le code Wien2k, ce qui conduit à utiliser une base d’ondes planes combinée à un potentiel total qui sert à résoudre l’équation de Kohn-Sham pour trouver la densité de l’état fondamental, l’énergie totale et les propres valeurs d’un système à N corps, au lieu d’utiliser la théorie de la fonctionnelle de la densité pour traiter les électrons de cœur (les états de cœurs, proches du noyau, fortement corrélés), et les états de valence. Et dans ce qui suit, nous allons brièvement présenter une des méthodes de résolution, qui est à la base de la méthode des ondes planes augmentées (APW) introduite par Slater [30-31], qui a remarqué que le potentiel et les fonctions d’ondes devraient être du genre ‘Muffin-Tin’ (sphère) situé près du noyau atomique, puis elle a été développée par Andersen [32] qui a utilisé les méthodes linéaires LAPW (Augmented Plane Wave), cette méthode s’avère performante pour calculer les propriétés structurales des matériaux, et donne des résultats fiables pour les ternaires des métaux de transition, et les oxydes binaires, surtout pour l’étude des propriétés des pérovskites et doubles pérovskites cubiques présentées dans ce travail, et la deuxième méthodes mathématiques de l’équation de Kohn-Sham, qui permettent d’accéder à

ρ(r) en appuyant sur leurs spécificités intrinsèques, consiste à éliminer le calcul du potentiel

dans la région de cœur :.

I.8.1 Méthode des ondes planes augmentées (APW) :

La méthode des ondes planes augmentées (APW) est une méthode développée par Slater [11] en 1937, sa notion décrit le potentiel cristallin et les fonctions d’onde au voisinage du noyau atomique sont sous la forme de Muffin-Tin (MT). Cette méthode consiste à sectionner la maille élémentaire en deux régions (Figure I.2) [33]:

27

Figure I.2 : Potentiel Muffin-Tin (MT)

 Une région de sphère atomique S de rayon Rmt, près du noyau, cette sphère dite Muffin-Tin, le potentiel et les fonctions d’onde sont identiques à ceux d’un atome isolé, d’où le potentiel a une symétrie sphérique, et les fonctions d’onde sont développées ; la solution de l’équation de Schrödinger est radiale.

 Une région interstitielle hors des sphères, le potentiel est considéré constant :

(I.48)

Où :

𝞨 : Le volume de la maille élémentaire.

K : le vecteur d’onde dans la zone de Brillouin irréductible.

CG,Alm : Les paramètres du développement en harmoniques sphériques Ylm.

G : Le vecteur du réseau réciproque.

Ul(r,l) : La solution radiale de l’équation de Schrödinger pour la section radiale, qui peut s’écrire de la forme :

(I.49)

V(r) présente le potentiel sphérique, U(r) sont des fonctions orthogonales à tout état propre

d’Hamiltonien identique qui disparait à la limite des sphères. 𝝋(𝒓) = { 𝟏 𝜴𝟏/𝟐∑ 𝑪𝑮𝒆𝒊(𝑮+𝑲).𝒓 𝑮 𝒓 < 𝑹𝒎𝒕 ∑ 𝑨𝒍𝒎𝑼𝒍(𝒓)𝒀𝒍𝒎(𝒓) 𝒍𝒎 𝒓 < 𝑹𝒎𝒕 Région interstitielle Sphère MT Sphère MT Rmt {− 𝒅𝟐 𝒅𝒓𝟐+ 𝒍(𝒍 + 𝟏) 𝒓𝟐 + 𝑽(𝒓) − 𝑬𝒍} 𝒓𝑼𝒍(𝒓, 𝑬𝒍) = 𝟎

28

En outre les modifications apportées par Slater [31]

,

L’approche de Muffin-Tin [36] donne des résultats exacts pour les matériaux hcp (héxagonal) et cfc (cubique à face centré). Les paramètres Alm sont déterminés en fonction des coefficients

CG des ondes planes existantes dans la région interstitielle pour assurer une suite à l’extrémité des sphères. Cependant, les coefficients Alm doivent être développés en fonction des paramètres

CG des ondes planes dans les régions interstitielles, après le calcul nous trouvons :

(I.50)

Où :

Jl est la fonction de Bessel d’ordre l, et l’origine est au centre de la sphère, donné par :

(I.51)

Les fonctions individuelles qui sont indiquées par C se comportent comme des ondes planes dans les régions interstitielles, et les fonctions radiales dans les sphères sont nommées ondes planes augmentées.

La convergence de cette base est contrôlée par deux coefficients : cut-off (RmtKmax), où le Rmt est le rayon atomique sphérique le plus petit dans la maille élémentaire, Kmax est la coupure des ondes planes dans la région interstitielle, et le deuxième coefficient Imax la coupure du moment angulaire dans les sphères Muffin-tin.

La méthode APW créée montre quelques complications de calcul, comme les coefficients Alm qui possèdent le terme Ul(Rmt) au dénominateur. Il est facile d’obtenir les valeurs de l’énergie

El dans lesquelles le terme Ul(Rmt) s’annule à la frontière de la sphère muffin tin, qui indique un problème d’asymétrie cela entraine des difficultés numériques quand les bandes apparaissent près de l’asymétrie.

Afin de surmonter ces problèmes, différentes modifications étaient introduites dans la méthode APW, comme celles présentées par Koelling [37] et Andersen [38].

𝑨𝒍𝒎= 𝟒𝝅𝒊 𝒍 𝜴𝟏𝟐𝑼𝒍(𝑹) ∑ 𝑪𝑮 𝑮𝑱𝒍(|𝒌 + 𝒈|𝑹)𝒀𝒍𝒎∗ (k+G) 𝑱𝒍(𝒓) = √ 𝝅 𝟐𝒙𝒋𝒍+𝟏_𝟐(𝒙)