Ministère de l’Enseignement Supérieur et de la Recherche
Scientifique
Université des Sciences et de la Technologie d’Oran
Thèse
Pour l’obtention du titre de
Docteur Es-Sciences
EnGénie mécanique
Option : Energétique
Présentée parMohammed BOUTABAA
Simulation numérique des Vortex de Dean dans un fluide
newtonien et un fluide viscoélastique en écoulement dans
des conduites courbes à sections carrée et rectangulaire
Soutenue le 30/09/2010 Devant le jury composé de:
Mr. Abbès Azzi Professeur, USTO Oran Président
Mr. Mohamed Bouzit Maitre de Conférences, USTO Oran Examinateur
Mr. Abdelkader Aris Maitre de conférences, ENSET Oran Examinateur
Mr. Driss. Nehari Maitre de Conférences, UAIB Mostaganem Examinateur
Mr. Ahmed Bettahar Professeur, UHB Chlef Examinateur
Rapporteur :
Mr. Abdelhamid Bounif, Professeur, USTO Oran Année : 2010
Résumé
La présente étude est consacrée à la simulation numérique tridimensionnelle des écoulements secondaires de Dean, au sein de l’écoulement non établi d’un fluide newtonien et d’un fluide viscoélastique de Phan-Thien-Tanner dans une conduite courbe à 180°. La section d’écoulement varie de la forme carrée à la forme rectangulaire dont le rapport d’aspect varie de 2 à 12. La méthode des volumes finis avec un maillage décalé est utilisée pour résoudre les équations de conservation de masse, de quantité de mouvement et l’équation constitutive de PTT écrites en coordonnées orthogonales généralisées.
Les simulations faites pour des nombres de Dean allant de 50 à 500, montrent que le champ dynamique et en particulier la vitesse axiale sont influencés par le nombre de Dean. L’étude met en évidence l’influence, d’une part, des effets de l’inertie et des forces centrifuges et d’autres part, les paramètres géométriques, sur la structure des vortex de Dean et les conditions d’apparition de vortex additionnels.
La présente étude montre également qu’aux nombres de Dean relativement faibles, l’élasticité anticipe la formation des vortex additionnels dans l’écoulement.
Mots clés : écoulement, conduite courbe, section carrée, section rectangulaire, fluide newtonien, fluide viscoélastique, vortex de Dean
Abstract
This study is devoted to the three-dimensional numerical simulation of developing flows of Newtonian and viscoelastic fluids through a curved duct of square cross-section and rectangular cross-section. The Phan-Thien-Tanner (PTT) model is used to represent viscoelastic effects. The numerical method uses a finite volume discretization with a staggered grid, and the equations are written in general orthogonal coordinates.
The numerical simulations produced for Dean numbers varying from 50 to 500 and aspect ratios varying from 2 to 12, show clearly the influence of the Dean number on the dynamic field and particularly on the axial velocity. The study shows the influence of inertial effects and centrifugal forces also the geometric parameters on the vortex structure and the onset of additional vortices.
The study shows that the transition from twin-cells to four-cells or more is anticipated for the viscoelastic fluids for relatively low range of Dean numbers.
Key words: Flow, curved duct, square cross-section, rectangular cross-section, Newtonian fluid, viscoelastic fluid, Dean Vortex.
Remerciements
Ce travail a été effectué sous la direction de Monsieur Abdelhamid Bounif, Professeur à l’UST Oran. Je tiens à lui exprimer ma reconnaissance. Il a contribué à l’amélioration de ce travail par ces insignes conseils.
Ce travail n’aurait pas vu le jour sans l’aide de Monsieur Gilmar Mompean, Professeur à l’Ecole Polytechnique de Lille, il m’a permis l’accès au Laboratoire de Mécanique de Lille (LML), et m’a autorisé à utiliser le code de calcul “Gilpol” développé par l’équipe de mécanique des fluides du LML. Qu’il trouve ici toute ma reconnaissance et ma gratitude. Je remercie également, Monsieur Laurent Thais, Maitre de conférences, à l’Ecole Polytechnique de Lille, pour sa disponibilité, son aide et ses précieux conseils.
Je remercie Monsieur Abbès Azzi, Professeur à l’UST Oran de bien vouloir accepter de présider le jury chargé d’examiner ce travail.
J’adresse également mes remerciements à Monsieur Mohamed Bouzit, Maitre de conférences à l’UST Oran, à Monsieur Abdelkader Aris, Maitre de conférences à l’ENSET Oran, à Monsieur Driss Nehari, Maitre de conférence à l’université de Mostaganem et à Monsieur Ahmed Bettahar, Professeur à l’université de Chlef, d’avoir accepté de faire partie du jury et d’examiner le présent travail.
Que Mr. Lionel Hellin, Docteur de l’Université de l’Ecole Polytechnique de Lille trouve ici l’expression de mes profonds remerciements pour son aide précieuse, sa convivialité et sa disponibilité pendant toute la période de mon stage au Laboratoire de Mécanique de Lille.
Un grand merci à ma mère, mon épouse et toute ma famille, qui m’ont toujours soutenu et aidé pendant l’accomplissement de cette thèse.
J’exprime aussi mes vifs remerciements à mes collègues enseignants, mes amis et mes proches qui m’ont soutenu et encouragé pendant l’élaboration de cette thèse.
Dédicaces
A feu mon père, que Dieu ait son âme et à ma mère en récompense pour leur éducation
A mon épouse, pour sa patience, son affection et son soutien A mes enfants, pour la simple raison que c’est de leur temps à partager
ensemble, que je puisais pour réaliser ce travail A mes sœurs et frères, pour leur soutien
i
Table des matières
Introduction 1
1 Généralités sur les fluides newtoniens et les fluides viscoélastiques 4
Introduction générale 4
1.1 Les fluides newtoniens 5
1.1.1 Prédiction du comportement des fluides newtoniens 5
1.2 Les fluides non newtoniens 6
1.2.1 Principales caractéristiques du comportement des fluides non-newtoniens 6
1.2.2 Les modèles de représentation des fluides non newtoniens 7
1.3 Les fluides viscoélastiques 10
1.3.1 Description phénoménologique des fluides viscoélastiques 10 1.3.2 Autres caractéristiques des fluides viscoélastiques 10
1.4 Modèles de représentation des fluides viscoélastiques 12
1.4.1 Modèle de Maxwell 12
1.4.2 Les Modèles différentiels constitutifs 13
1.4.3 Les modèles algébriques 21 2. Généralités et travaux sur les écoulements de Dean 22
Introduction 22
2.1 Généralités sur les écoulements de Dean 22 2.1.1 Mise en évidence des écoulements de Dean 22
2.1.2 Mécanisme de formation des vortex de Dean 23
2.1.3 Définition du nombre de Dean 24
2.1.4 Impact des écoulements de Dean 25
2.1.5 Historique des écoulements dans les conduites courbes 26
2.2 Travaux antérieurs sur les écoulements de Dean 26 2.3 Travaux sur les écoulements de Dean dans les conduites carrées et rectangulaires 28 2.3.1 Travaux concernant les fluides newtoniens 28 2.3.2 Travaux concernant les fluides non-newtoniens 31
ii
3 Méthode numérique 33
Introduction 33
3.1 Les équations gouvernantes 33 3.1.1 Equation de continuité 33
3.1.2 Equation de conservation de quantité de mouvement 33
3.1.3 Equation constitutive du fluide de Phan-Thien-Tanner 34
3.2 Les équations en coordonnées orthogonales généralisées 35 3.2.1 Transformation des coordonnées 35
3.2.2 Transformation des équations gouvernantes 38
3.2.3 Evaluation des contraintes et des vitesses dans le système cartésien 38 3.3 La formulation EVSS 39
3.4 Traitement numérique des équations gouvernantes 40 3.4.1 Equation de transport de la variable généralisée Φ 40
3.4.2 Discrétisation spatiale et temporelle de l’équation de transport 41
3.4.3 Volumes de contrôle et localisation des variables 41
3.4.4 Discrétisation spatiale des équations de transport 43
3.4.5 Discrétisation temporelle 51
3.4.6 Méthode de résolution 52
3.4.7 Equation constitutive de Phan-Thien-Tanner 54
3.5 Etude de l’écoulement dans la conduite courbe à 180° 54
3.5.1 Présentation de la géométrie 54 3.5.2 Maillage 56 3.5.3 Conditions aux limites 57 4 Résultats et interprétations 58
Introduction 58
4.1 Données générales 58
4.1.1 Données relatives aux configurations géométriques étudiées 58
4.1.2 Données relatives aux fluides et aux conditions d’écoulement 59
4.2 Etude de l’écoulement dans la conduite courbe à section carrée 60
4.2.1 Etude du champ dynamique de l’écoulement principal 60
4.2.3 Etude des vortex de Dean 78
4.3 Etude de l’écoulement dans la conduite courbe à section rectangulaire 83
iii
4.3.2 Rapport d’aspect Ar=4 88
4.3.3 Rapport d’aspect Ar=8 90
4.3.4 Rapport d’aspect Ar=12 91
4.4 Étude de l’effet de l’élasticité sur les vortex de Dean 94
4.5 Validation des résultats 95
4.5.1 Résultats relatifs à la section carrée 95 4.5.2 Résultats relatifs à la section rectangulaire 97 Conclusion générale 101
Références Bibliographiques 103 Publication
iv
Liste des figures
Figure 1.1 : Schéma unidimensionnel du modèle de Maxwell 13
Figure 1.2 : Représentation schématique du modèle élastique avec haltères 14 Figure 1.3 : Effet de l’anisotropie des contraintes normales: Ascension d’une solution de
Polyisobutylène le long d’un barreau tournant (Photographie : J. Bico) 21 Figure 1.4 : Effet de mémoire : Expansion d’un jet d’une solution de Polyacrylamide à la sortie
d’un orifice (Photographie : R. E. Evans) 21
Figure 2.1 : Représentation schématique de l’écoulement principal et de l’écoulement secondaire
au sein d’une conduite courbe à section rectangulaire 23
Figure 2.2 : Représentation qualitative des contours : (a) de la vitesse axiale, (b) de la pression,
dans une section droite de l’écoulement dans une conduite courbe 24
Figure 2.3 : Représentation schématique du mouvement tourbillonnaire dans une section droite de
l’écoulement dans une conduite courbe 24
Figure 3.1 : Représentation du système de coordonnées cartésiennes et du système de coordonnées
orthogonales généralisées 36
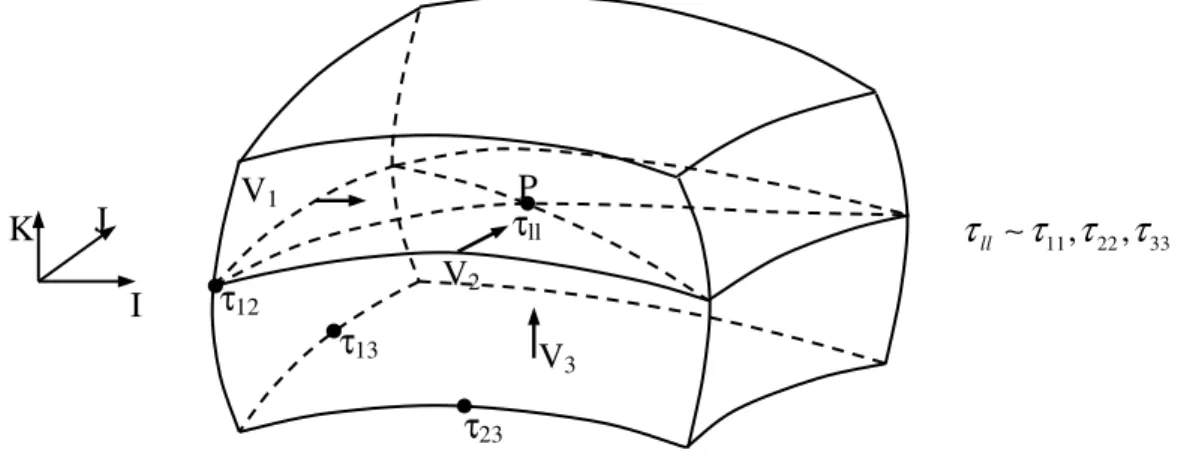
Figure 3.2 : Volume de contrôle et lieux de stockage et de traitement des variables 42 Figure 3.3 : Maillage entrelacé et volumes de contrôle p
V , VV1, VV2, VV3 42
Figure 3.4 : Vues de dessus (a) et de droite (b) du volume de contrôle VP et les variables associées 43
Figure 3.5 : Vues de dessus (a) et de face (b) du volume de contrôle VV1et les variables associées 43
Figure 3.6 : Vues de dessus (a) et de droite (b) du volume de contrôle VV2 et les variables associées 44
Figure 3.7 : Vues de face (a) et de droite (b) du volume de contrôle VV3 et les variables associées 44
Figure 3.8 : Géométrie de la conduite d’écoulement et conditions aux limites 55
Figure 3.9 : Vue globale du maillage de la conduite courbe 56
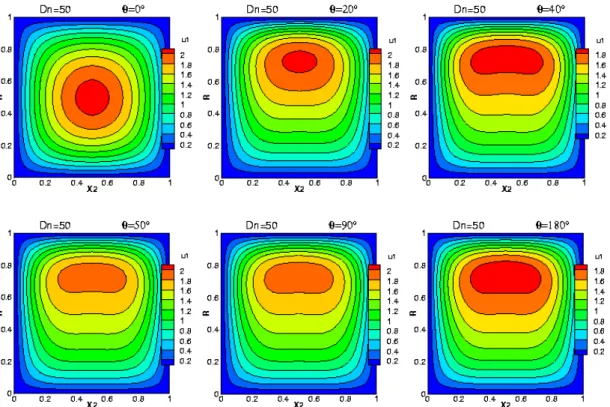
Figure 4.1 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°,
40°, 50°, 90° et 180°, à Dn=50. Pour un fluide newtonien 63
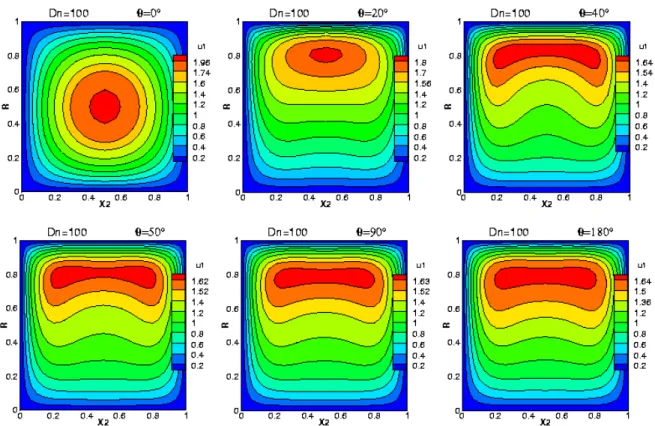
Figure 4.2 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
50°, 90° et 180°, à Dn=100. Pour un fluide newtonien 63
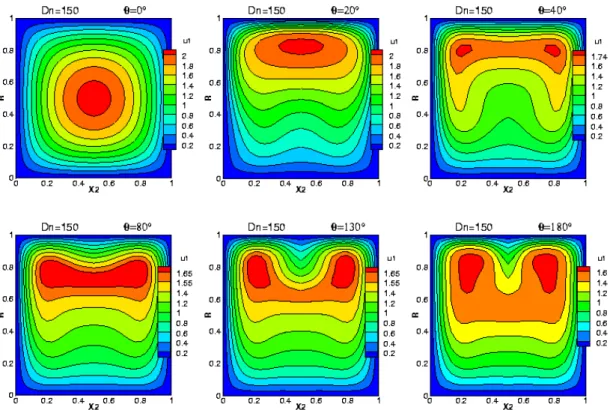
Figure 4.3 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
80°, 130° et 180°, à Dn=150. Pour un fluide newtonien 64
Figure 4.4 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
80°, 100° et 180°, à Dn=200. Pour un fluide newtonien 64
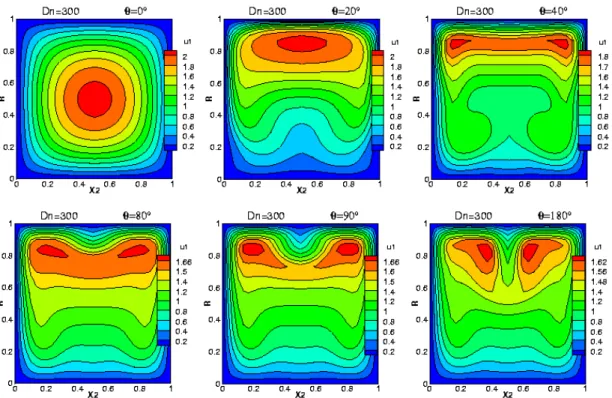
Figure 4.5 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
v
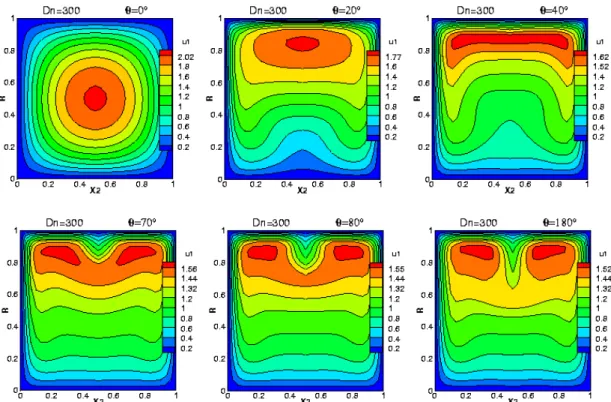
Figure 4.6 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
80°, 90° et 180°, à Dn=400. Pour un fluide newtonien 65
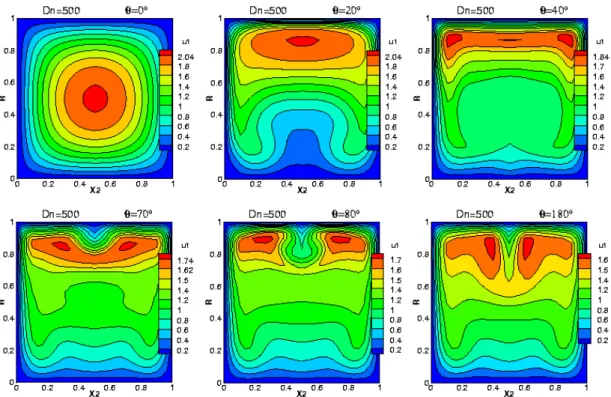
Figure 4.7 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
70°, 80° et 180°, à Dn=500. Pour un fluide newtonien 66
Figure 4.8 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
50°, 90° et 180°, à Dn=50. Pour un fluide viscoélastique PTT 66
Figure 4.9 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°,
50°, 90° et 180°, à Dn=100. Pour un fluide viscoélastique PTT 67
Figure 4.10 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°, 70°, 120° et 180°, à Dn=150. Pour un fluide viscoélastique PTT 67
Figure 4.11 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°, 70°, 90° et 180°, à Dn=200. Pour un fluide viscoélastique PTT 68
Figure 4.12 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°, 70°, 80° et 180°, à Dn=300. Pour un fluide viscoélastique PTT 68
Figure 4.13 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°, 70°, 80° et 180°, à Dn=400. Pour un fluide viscoélastique PTT 69
Figure 4.14 : Contours de la vitesse axiale aux positions angulaires θ respectivement de 0°, 20°, 40°, 60°, 70° et 180°, à Dn=500. Pour un fluide viscoélastique PTT 69
Figure 4.15 : Schéma d’une section d’écoulement et les directions des tracés des profils
horizontaux et verticaux de la vitesse axiale 70
Figure 4.16 : Profils horizontaux de la vitesse axiale aux positions angulaires θ respectivement de
0°, 40°, 90° et 180°, à Dn=50. Pour un fluide newtonien 72
Figure 4.17 : Profils horizontaux de la vitesse axiale aux positions angulaires θ respectivement de
40°, 90° et 180°, à Dn=100. Pour un fluide newtonien 72
Figure 4.18 : Profils horizontaux de la vitesse axiale aux positions angulaires et aux nombres de Dean simultanés de : 130°-150, 100°-200, 90°-300, 90°-400, 80°-500. Pour un fluide newtonien 73 Figure 4.19 : Profils verticaux de la vitesse axiale aux positions angulaires θ respectivement de 0°,
40°, 90° et 180°, à Dn=50. Pour un fluide newtonien 73
Figure 4.20 : Profils verticaux de la vitesse axiale aux positions angulaires θ respectivement de 40°,
90° et 180°, à Dn=100. Pour un fluide newtonien 74
Figure 4.21 : Profils verticaux de la vitesse axiale aux positions angulaires et aux nombres de Dean simultanés de 130°-150, 100°-200, 90°-300, 90°-400, 80°-500. Pour un fluide newtonien. 74 Figure 4.22 : Profils horizontaux de la vitesse axiale aux positions angulaires θ respectivement de 0°, 40°, 90° et 180°, à Dn=50. Pour un fluide viscoélastique de PTT 75
Figure 4.23 : Profils horizontaux de la vitesse axiale aux positions angulaires θ respectivement de
40°, 90° et 180°, à Dn=100. Pour un fluide viscoélastique de PTT 75
Figure 4.24 : Profils horizontaux de la vitesse axiale aux positions angulaires et aux nombres de Dean simultanés de 120°-150, 90°-200, 80°-300, 70°-400, 70°-500. Pour un fluide PTT. 76
vi
Figure 4.25 : Profils verticaux de la vitesse axiale aux positions angulaires θ respectivement de 0°,
40°, 90° et 180°, à Dn=50. Pour un fluide viscoélastique de PTT 76
Figure 4.26 : Profils verticaux de la vitesse axiale aux positions angulaires θ respectivement de 40°,
90° et 180°, à Dn=100. Pour un fluide viscoélastique de PTT 77
Figure 4.27 : Profils verticaux de la vitesse axiale aux positions angulaires et aux nombres de Dean simultanés de 120°-150, 90°-200, 80°-300, 70°-400, 70°-500. Pour un fluide viscoélastique de
PTT. 77
Figure 4.28 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=50. Pour un fluide newtonien 79
Figure 4.29 : Structure des vortex de Dean aux les positions angulaires θ respectivement de 40°,
90°, et 180°, à Dn=100. Pour un fluide newtonien 80
Figure 4.30 : Structure des vortex de Dean aux positions angulaires θ respectivement de 70°, 80°, 90°, 110°, 120°et 180° à Dn=150. Pour un fluide newtonien 80
Figure 4.31 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180° à Dn=200. Pour un fluide newtonien 80
Figure 4.32 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180°, à Dn=300. Pour un fluide newtonien 81
Figure 4.33 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180°, à Dn=400. Pour un fluide newtonien 81
Figure 4.34 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 80° et
180°, à Dn=500. Pour un fluide newtonien 81
Figure 4.35 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=50. Pour un fluide viscoélastique PTT 81
Figure 4.36 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=100. Pour un fluide viscoélastique PTT 82
Figure 4.37 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 70°, 80°, 100°, 120° et 180°, à Dn=150. Pour un fluide viscoélastique PTT 82
Figure 4.38 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180°, à Dn=200. Pour un fluide viscoélastique PTT 82
Figure 4.39 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180°, à Dn=300. Pour un fluide viscoélastique PTT 83
Figure 4.40 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180°, à Dn=400. Pour un fluide viscoélastique PTT 83
Figure 4.41 : Structure des vortex de Dean aux positions angulaires θ respectivement de 60°, 90° et
180°, à Dn=500. Pour un fluide viscoélastique PTT 83
Figure 4.42 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
vii
Figure 4.43 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=100. Pour un fluide newtonien 85
Figure 4.44 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=150. Pour un fluide newtonien 85
Figure 4.45 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=200. Pour un fluide newtonien 85
Figure 4.46 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=250. Pour un fluide newtonien 86
Figure 4.47 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=300. Pour un fluide newtonien 86
Figure 4.48 : Structure des vortex de Dean aux positions angulaires θ respectivement de 80°, 90° et
180°, à Dn=400. Pour un fluide newtonien 86
Figure 4.49 : Structure des vortex de Dean aux positions angulaires θ respectivement de 80°, 160°
et 180°, à Dn=500. Pour un fluide newtonien 86
Figure 4.50 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=50. Pour un fluide viscoélastique PTT 86
Figure 4.51 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=100. Pour un fluide viscoélastique PTT 87
Figure 4.52 : Structure des vortex de Dean aux positions angulaires θ respectivement de 40°, 90° et
180°, à Dn=150. Pour un fluide viscoélastique PTT 87
Figure 4.53 : Structure des vortex de Dean aux positions angulaires θ respectivement de 150°, 160°
et 180°, à Dn=200. Pour un fluide viscoélastique PTT 87
Figure 4.54 : Structure des vortex de Dean aux positions angulaires θ respectivement de 70°, 120°
et 180°, à Dn=300. Pour un fluide viscoélastique PTT 87
Figure 4.55 : Structure des vortex de Dean aux positions angulaires θ respectivement de 70°, 120°
et 180°, à Dn=400. Pour un fluide viscoélastique PTT 87
Figure 4.56 : Structure des vortex de Dean aux positions angulaires θ respectivement de 90°, 170°
et 180°, à Dn=500. Pour un fluide viscoélastique PTT 88
Figure 4.57 : Structure des vortex de Dean à la position angulaire 180°, aux nombres de Dean
respectivement de 50, 100, 150, 200, 300, 400 et 500. Pour un fluide newtonien 89 Figure 4.58 : Structure des vortex de Dean à la position angulaire 180°, aux nombres de Dean
respectivement de 50, 100, 150, 200, 300, 400 et 500. Pour un fluide viscoélastique PTT 89 Figure 4.59 : Structure des vortex de Dean à la position angulaire 180°, aux nombres de Dean
respectivement de 50, 100, 150, 200, 300, 400 et 500. Pour un fluide newtonien 90 Figure 4.60 : Structure des vortex de Dean à la position angulaire 180°, aux nombres de Dean
respectivement de 50, 100, 150, 200, 300, 400 et 500. Pour un fluide viscoélastique PTT. 91 Figure 4.61 : Structure des vortex de Dean à la position angulaire 180°, aux nombres de Dean
viii
Figure 4.62 : Structure des vortex de Dean à la position angulaire 180°, aux nombres de Dean
respectivement de 50 100 150 200 300 400 et 500. Pour un fluide viscoélastique PTT 93 Figure 4.63 : Vortex de Dean à la position angulaire 180°, aux nombres de Dean respectivement de 125, 137 et 150, et aux nombres de Deborah respectivement de 0.1, 0.3, 0.4 et 0.5 94
Figure 4.64 : Contours de la vitesse axiale (validation) 95
Figure 4.65 : Vortex de Dean (Ar=1) (validation) 96
Figure 4.66 : Vortex de Dean (Ar=1) (validation) 97
Figure 4.67 : Vortex de Dean (Ar=2) (validation) 97
Figure 4.68 : Vortex de Dean (Ar=4) (validation) 98
ix
Liste des tableaux
Tableau 1.1 : Les différents modèles de fluides viscoélastiques issus de la formulation globale en
fonction des valeurs des paramètres
λ
,ε
,ξ et β 19Tableau 3.1 : Expressions des grandeurs Φ, ,ϕ Λet SΦ de l’équation de transport en fonction de la
grandeur transportée. 41
Tableau 3.2 : Maillage utilisé en fonction du rapport d’aspect. 56
Tableau 4.1 : Valeurs du nombre de Reynolds en fonction du nombre de Dean pour le fluide
newtonien et le fluide viscoélastique PTT. 59
Tableau 4.2 : Position angulaire de l’apparition de la subdivision de la zone à forte quantité de
mouvement en fonction du nombre de Dean, pour le fluide newtonien 61
Tableau 4.3 : Position angulaire de l’apparition de la subdivision de la zone à forte quantité de
x
Glossaire
τ
Tenseur des extras-contraintes (N/m2, Pa)ij
τ Composantes du tenseur des extras-contraintes (N/m2, Pa)
σ
Tenseur des contraintes (contraintes totales de Cauchy)ij
σ Composantes du tenseur des contraintes totales
σ
u Vecteur vitesse
ui Composante i de la vitesse (m/s)
p Pression hydrostatique (Pa)
I Tenseur identité
∇ Opérateur nabla
η Viscosité dynamique (fluide newtonien)
ν
Viscosité cinématique&
γ Tenseur des vitesses de déformation
ij
γ& Composantes du tenseur des vitesses de déformation γ&
γ& Taux de cisaillement généralisé
(.)T Matrice transposée de la matrice (.)
ij
δ Composantes du tenseur de Kronecker
ρ La masse volumique
(.) /
D Dt Dérivée objective de (.)
1,3
( )xi i= Coordonnées d’un point dans le système cartésien ap
η Viscosité apparente
D Tenseur des taux de déformation
m Indice de consistance (modèle en loi de puissance
η
=mγ
&n) n Indice d’écoulement (modèle en loi de puissanceη
=mγ
&n)0
η
Valeur de la viscosité à un taux de cisaillement nulη
∞ Valeur de la viscosité à un taux de cisaillement infiniK, k Constantes empiriques relatives au modèle de Cross
sl
τ
Contrainte de seuil de plasticité (modèle de Bingham)pl
η Viscosité plastique (modèle de Bingham)
N1 Première différence des contraintes normales
N2 Seconde différence des contraintes normales
1, 2
ϕ ϕ
Coefficients d’anisotropieelast
τ
Tenseur des contraintes élastiquesvisq
τ Tenseur des contraintes visqueuses
E Module d’élasticité
γ Tenseur des déformations
λ
Temps de relaxation du fluide ou du matériau. /
d dt Dérivée matérielle
e
D Nombre de Deborah
We Nombre de Weissenberg
xi
p
τ Composante viscoélastique ou polymérique du tenseur
τ
s
τ
Composante visqueuse du tenseurτ
p
η Viscosité polymérique (non newtonienne)
s
η
Viscosité du solvant (newtonienne)1, 2
λ λ
Temps de relaxation et temps de retardation de la contrainteL Tenseur du gradient des vitesses généralisées ou effectives
{}
. Opérateur de tracem
η
Viscosité moléculaire du fluide0
m
η
Viscosité moléculaire au taux de cisaillement nulε
ε ξ β, , Paramètres liés au modèle MPTT de Phan-Thien-Tannere
R Nombre de Reynolds
Dn Nombre de Dean
Rc Rayon de courbure moyenne de la conduite
1,3
( )ψi i= Coordonnées dans le système orthogonal généralisé
J Matrice jacobienne de la transformation (xi→
ψ
i)i
d
ξ
Longueurs physiques infinitésimaleshj Facteurs d’échelle
ij
g Composantes du tenseur métrique
i
V Composantes de la vitesse contravariante physique
vi Composantes des vitesses contravariantes curvilignes
j i
H Facteurs d’étirement du maillage orthogonal
(
D Tenseur des taux de déformation généralisé
ij
D( Composantes du tenseur des taux de déformation généralisée
(
τ
Tenseur des extras-contraintes physiquesij
τ( Composantes physiques des extras-contraintes
(
Γ Tenseur physique des contraintes polymériques
ij
Γ( Composantes physiques des contraintes polymériques
Σ Tenseur des contraintes purement élastiques
(
Σ Tenseur physique des contraintes purement élastiques
ij
Σ( Composantes physiques des contraintes purement élastiques
VP Volume de contrôle de la pression p
VV1 Volume de contrôle de la vitesse V1
VV2 Volume de contrôle de la vitesse V2
VV3 Volume de contrôle de la vitesse V3
SPE,W,S,N,B,T Surfaces Est, Ouest, Sud, Nord, bas et haut du volume V P
SV1E,W,S,N,B,T Surfaces Est, Ouest, Sud, Nord, bas et haut du volume V V1
SV2E,W,S,N,B,T Surfaces Est, Ouest, Sud, Nord, bas et haut du volume V V2
SV3E,W,S,N,B,T Surfaces Est, Ouest, Sud, Nord, bas et haut du volume V V3
e
L Longueur des canaux droits d’entrée et de sortie de la conduite
T
M Transposée du tenseur M
c
U Vitesse débitante à la sortie de la conduite
R1, R2 Rayons de courbure interne et externe, de la conduite courbe
1
Introduction
Les écoulements dans les conduites courbes sont couramment rencontrés dans l’industrie, ils sont présents dans différentes applications industrielles telles que les échangeurs de chaleur, les canaux de refroidissement des aubes des turbines, des chambres de combustion des turboréacteurs et des moteurs de fusées, les installations thermo-hydrauliques des réacteurs nucléaires et les systèmes de mélange et de mixage.
Ces écoulements, sous l’effet de la force centrifuge résultant de la courbure de la conduite et - par conséquence - des lignes de courant, sont le siège d’un phénomène d’instabilité connu sous le nom d’instabilité de Dean, dont le résultat est l’apparition de deux ou plusieurs cellules tourbillonnaires contrarotatives (appelées Vortex de Dean) dans la conduite d’écoulement. Ces vortex modifient d’une façon substantielle, les caractéristiques de l’écoulement du fluide. Ils agissent sur la transition de l’écoulement du régime laminaire au régime turbulent, sur les taux de transfert de masse et de quantité de mouvement et les taux d’échanges thermiques. Et par conséquent, sur le mixage et sur le mélange au sein de l’écoulement.
De plus, les écoulements en conduites courbes sont fondamentalement différents des écoulements en conduites rectilignes, le champ dynamique est fortement influencé par la courbure de la conduite, les profils de vitesse présentent des comportements typiques, tels que l’aplatissement et le creusement des profils, et le décalage du maximum de la vitesse axiale vers la paroi externe de la conduite.
Les phénomènes constatés, lors des écoulements en conduites courbes, tels que la formation des vortex de Dean (cellules tourbillonnaires) et les variations du champ dynamique, sont exploités dans le domaine industriel, surtout dans les systèmes de mélange et de mixage, donnant naissance aux mélangeurs reposant sur le principe des écoulements de Dean alternés, connu souvent sous le nom du mélange chaotique. Dans le domaine des échangeurs de chaleur, ces constatations ont donné naissance à une famille d’échangeurs compacts reposant sur le principe d’utilisation des écoulements en conduites courbes.
2
Si, les premières études des écoulements en conduites courbes étaient exclusivement expérimentales, ils ont été suivies - peu de temps après - d’études analytiques qui ont donné une forte motivation à l’émergence d’une multitude d’études théoriques et expérimentales. Mais, ce sont les avancées dans les domaines du calcul numérique et de l’informatique qui ont donné un nouvel essor considérable aux études numériques des écoulements en conduites courbes.
Si les simulations numériques, les études théoriques et les études expérimentales des écoulements des fluides newtoniens dans les conduites courbes sont relativement nombreuses, il n’en n’est pas le cas pour les fluides viscoélastiques, et ce, malgré la diversité et l’abondance de ces fluides, qui sont souvent acheminés dans des conduites - simples ou complexes - présentant des courbures significatives.
L’extension de l’étude des écoulements de Dean aux fluides viscoélastiques est d’un intérêt certain et a généré un domaine d’étude et de recherche très actif. Cette importance s’est accrue au vu du grand nombre d’applications impliquant des fluides chargés, des suspensions aqueuses, des polymères et des solutions de polymères dans l’industrie.
Cependant, la simulation numérique de ces écoulements est assez délicate et difficile; la difficulté réside surtout dans la reproduction des écoulements secondaires et en particulier, les vortex de Dean. De plus, afin de satisfaire les besoins urgents des industriels, la majorité des modèles utilisés pour prédire le comportement des fluides s’écartant du modèle newtonien étaient des modèles empiriques ou grossiers, se limitant à introduire seulement les effets de la pseudoplasticité ou de la rhéoplasticité. Ces modèles nécessitaient souvent des itérations et des corrélations multiples.
Les percées récentes de la rhéologie, théorique, expérimentale et numérique ont permis l’émergence d’approches visant de plus en plus à reproduire fidèlement et avec justesse le comportement des fluides non newtoniens et en particulier, les fluides viscoélastiques, dans des configurations géométriques complexes et des conditions d’écoulement les plus divers, moyennant un temps de calcul et une capacité mémoire optimaux.
Cette motivation a encouragé aussi la production d’un nombre incessant de modèles et de lois de comportement.
3
La présente thèse a pour objectif d’étudier les vortex de Dean dans un écoulement d’un fluide newtonien et d’un fluide viscoélastique dans une conduite courbe en forme de “
⊃
” dont la section d’écoulement varie de la forme carrée à la forme rectangulaire.Dans le premier chapitre, nous présentons des généralités sur les fluides newtoniens et les fluides viscoélastiques. Les différentes lois constitutives des modèles les plus répandus sont présentées.
Le deuxième chapitre est consacré à l’étude des écoulements dans les conduites courbes, il comporte un bref aperçu sur les vortex de Dean et les mécanismes de leur apparition, ainsi qu’une synthèse des divers travaux concernant les écoulements en conduite courbes tant pour les fluides newtoniens que pour les fluides non newtoniens.
Le troisième chapitre est consacré à la méthode numérique qui est basée sur la théorie des volumes finis proposée par Spalding et Patankar, le traitement numérique des équations de mouvement et les équations constitutives. Notons qu’à cause de la forme géométrique de la conduite d’écoulement, les équations sont réécrites dans un système de coordonnées orthogonales généralisées.
Le dernier chapitre, regroupe les résultats des simulations numériques réalisées, pour le fluide newtonien et le fluide viscoélastique représenté par le modèle de Phan-Thien-Tanner. Les résultats sont suivis par des interprétations et des commentaires.
La conclusion générale présente une synthèse du travail effectué et fait apparaître les perspectives et les suggestions pour des éventuelles études qui pourraient être menées ultérieurement sur les écoulements en conduites courbes surtout pour les fluides viscoélastiques.
4
Chapitre I
Généralités
sur
les
fluides
newtoniens
et
viscoélastiques
Introduction généraleEn mécanique, il est souvent d’usage de classer les fluides, en fluides newtoniens et fluides non-newtoniens. Mais, cette classification -aussi sommaire soit-elle- est juste un moyen de scinder en deux grandes catégories, une multitude de groupes de fluides. Si le modèle du “fluide newtonien” décrit bien la très grande majorité des substances fluides à caractère moléculaire simple tels que les gaz, la vapeur, ou les liquides chimiquement simples (l’eau, l’air et quelques huiles simples en sont des exemples), il existe un bon nombre de fluides, dont certains, sont d’usage très courant, qui ont un comportement -sous écoulement plus complexe- qui ne peut être prédit par le modèle newtonien.
En effet, ces fluides -dont le comportement n’obéit pas au modèle newtonien- abondent dans la nature et les industries chimiques, agroalimentaires, papetières, de textile, etc. Le sang, le mucus des êtres vivants, une large gamme de produits alimentaires tels que les produits laitiers, les fromages fondus, le chocolat fondu, le miel, les huiles alimentaires, les pâtes de papier et le plastique fondu sont des exemples courants de fluides non newtoniens. Souvent, des produits ou matériaux d’intérêt industriel sont rendus non newtoniens par l’ajout de divers polymères à travers les processus d’extrusion, de moulage, de soufflage ou de filage. L’ajout de polymères aux détergents est souvent utilisé pour améliorer leurs propriétés rhéologiques. Les huiles multigrades ont des polymères comme additifs pour modifier le comportement de leur viscosité sous des contraintes de pression et de température extrêmes. Les huiles épaissies par ajout de polymères sont utilisées dans des roulements pour diminuer davantage les frottements plus que dans les huiles newtoniennes, sans pour autant réduire leur durée de vie.
Par ailleurs, si le fluide newtonien est décrit par une loi de comportement simple, les fluides non newtoniens échappent à cette règle et on observe l’émergence d’un grand nombre de lois de comportement qui ne cessent de se ramifier et de s’affiner pour donner naissance à une panoplie de lois de comportement dérivées.
5 1.1 Les fluides newtoniens
Les fluides newtoniens sont définis comme étant des fluides pour lesquels le tenseur des extras-contraintes
τ
est linéaire, isotrope, fonction du gradient de la vitesse∇
u
. En effet,en partant de la forme explicite du tenseur des contraintes
σ
, qui s’écrit:p
= − +
σ
Iτ
(1.1)Où p désigne la pression hydrostatique, I le tenseur identité et
τ
le tenseur desextras-contraintes ou le déviateur des extras-contraintes.
En faisant l’hypothèse que
τ
est symétrique, linéaire, isotrope et fonction du gradient de la vitesse∇
u
, et que le fluide vérifie la condition d’incompressibilité, on montre que :η
= &
τ
γ
(1.2)Où la constante
η
est la viscosité dynamique du fluide etγ
& est le tenseur des vitesses de déformation défini par :( )T
= ∇ + ∇
&
γ
u u (1.3)Les composantes du tenseur des contraintes
σ
sont alors données par :ij p ij ij p ij ij
σ = − δ +τ = − δ +ηγ& (1.4)
Remarque
La définition du fluide newtonien est très restrictive, les contraintes de cisaillement sont proportionnelles au gradient de vitesse, et par conséquent dans un écoulement cisaillé simple, la viscosité est indépendante de la vitesse de cisaillement, les seules contraintes créées par l’écoulement sont les contraintes de cisaillement.
1.1.1 Prédiction du comportement des fluides newtoniens
L’équation de conservation de la masse (ou condition d’incompressibilité) s’écrit :
. 0
∇ =u (1.5)
L’équation de quantité de mouvement de Cauchy s’écrit : .(
D
p Dt
ρ u= ∇ − I +τ ) (1.6)
En injectant les équations (1.1), (1.2) et (1.3), tenant compte de l’équation (1.5), et en adoptant la notation indicielle l’équation (1.6) s’écrit :
2 2 i i i j Du p u Dt x x ρ = − ∂ +η∂ ∂ ∂ (1.7)
6 Il faut remarquer que :
2 ( . ) 0 j j i i u x x x ∂ ∂ = ∇ = ∂ ∂ ∂ u (1.8)
On a donc sous forme vectorielle, les équations de Navier-Stokes pour un fluide newtonien incompressible : 2 D p Dt ρ η = −∇ + ∇ ∇ u u .u = 0 (1.9) La prédiction du comportement des fluides newtoniens incompressibles est assurée par la résolution des équations de Navier-Stokes, auxquelles s’ajoutent les conditions aux limites et les conditions initiales.
1.2 Les fluides non-newtoniens
Par opposition aux fluides newtoniens, les fluides non-newtoniens sont définis comme étant des fluides pour lesquels le tenseur des extras-contraintes ne peut pas être exprimé comme étant une fonction linéaire et isotrope des composantes du tenseur des vitesses de déformation.
En particulier, pour les fluides non-newtoniens en écoulement cisaillé, la relation entre la contrainte de cisaillement et la vitesse de cisaillement est non linéaire.
Dans ce cas, la contrainte de cisaillement est généralement écrite sous la forme : .
( )
τ η γ γ
= . (1.10)Où la viscosité apparente ou viscosité en cisaillement
η
est fonction deγ
& .Du fait, que le comportement des fluides non-newtoniens incompressibles ne peut être prédit par les équations de Navier-Stockes, il est donc nécessaire de coupler les équations de conservation de masse et de quantité du mouvement avec une autre relation afin d’assurer la fermeture du système.
Cette relation, qui est la loi de comportement ou la loi constitutive, est généralement formulée comme une relation entre les contraintes et le tenseur des taux de déformation, elle a pour but de modéliser les effets non-newtoniens du fluide.
1.2.1 Principales caractéristiques du comportement des fluides non-newtoniens
Le caractère non-newtonien le plus mentionné dans la littérature est la variation de la viscosité avec la vitesse de cisaillement.
7
La diminution de la viscosité avec l’augmentation du taux de cisaillement, (rhéofluidification), est observée pour la plupart des fluides non-newtoniens, ils sont appelés fluides pseudoplastiques ou fluides rhéofluidifiants, ce comportement très répandu, s’observe sur les solutions polymères et les suspensions aqueuses, les pétroles, le latex de caoutchouc, la pâte à papier, les colles, certaines peintures, etc.
On rencontre également le comportement inverse, (rhéoépaississement), où la viscosité augmente lorsqu’on augmente le taux de cisaillement, ces fluides sont appelés fluides rhéoépaississants ou fluides dilatants, ce comportement n’est observé que sur une plage limitée de taux de cisaillement pour certains fluides ou dans les suspensions fortement concentrées de particules solides tels que les solutions aqueuses d’amidon, le sable ou le quartz dans l’eau, les mélanges de farine et de mais.
Une autre catégorie de fluides importante qui mérite d’être citée est celle des fluides rhéoplastiques ou des fluides à seuil, pour lesquels, l’écoulement ne se produit qu’à partir d’un seuil minimal de contrainte
τ
sl appelé seuil de plasticité. Au delà de cette valeur, lefluide s’écoule, selon le modèle newtonien, le modèle pseudoplastique ou le modèle dilatant. Dans cette catégorie de fluides, on peut citer les peintures à l’huile, les dentifrices, les pommades et les gels, les boues de forage, etc.
1.2.2 Les modèles de représentation des fluides non-newtoniens
Une première approche simple pour modéliser les fluides non-newtoniens est de généraliser le modèle newtonien en introduisant une viscosité dite “apparente” ou “équivalente” dépendante de la vitesse de déformation ou du taux de cisaillement.
( )
ap f
η = γ& (1.11) Où
γ
&représente le taux de cisaillement généralisé1/ 2( )
γ
&= D.D (1.12)Dans ce cas, où la viscosité de cisaillement n’est pas indépendante du taux de cisaillement, il est nécessaire d’utiliser des modèles pour décrire le comportement mécanique de ces fluides.
Plusieurs modèles existent, dépendant essentiellement du nombre de paramètres qu’ils comportent. On distingue par exemple, les modèles à deux paramètres (le modèle
d’Oswald et Waele), ou à trois paramètres (le modèle de Carreau ou d’Ellis). Ces lois constitutives relativement simples et très utilisées dans l’industrie, permettent de
8
modéliser certains phénomènes importants des fluides non-newtoniens tels que la rhéofluidification ou le rhéoépaississement.
1.2.2.1 Le modèle dit “en loi de puissance”
Ce modèle a été proposé par Waele [1] et Ostwald [2], il a été largement utilisé de façon empirique dans l’industrie, il est donné par :
1
n
m
η
=γ
& − (1.13)Où m et n sont des constantes déterminées expérimentalement, appelées respectivement indice de consistance et indice d’écoulement.
Bien que ce modèle permette de résoudre un bon nombre de problèmes, il faut garder à l’esprit qu’il décrit très mal le comportement aux faibles taux de cisaillement.
Ce modèle est utilisé pour représenter simultanément les trois types de fluides (les fluides newtoniens pour
n
=
1
, les fluides pseudoplastiques pourn f
1
et les fluides dilatants pour1
n p
).1.2.2.2 Le modèle de Cross
Le modèle de Cross [3] est une extension du modèle en loi de puissance, il est donné par la formule suivante : . 0 1 1 ( )k K
η η
η η
∞∞γ
− = − + (1.14)Où K et k sont des constantes positives déterminées empiriquement,
η
0 est la valeur de la viscosité à un taux de cisaillement nul etη
∞ est la viscosité à un taux de cisaillement infini. 1.2.2.3 Le modèle de CarreauLe modèle de Carreau [4] est en réalité une variante du modèle de Cross, il est donné par : / 2 . 0 2 1 1 ( ) k K
η η
η η
∞∞γ
− = − + (1.15) RemarqueNotons, que par une simple réécriture de l’équation (1.14) définissant le modèle de Cross, on peut aboutir à l’équation (1.13) définissant le modèle dit en loi de puissance.
9 0 0(1 / )0 ( ) (1 / ) k K
η η η
η η
γ
η η
∞η
η η
∞ − = − = − − & (1.16)En supposant que
η
est la moyenne géométrique deη
0et deη
∞ c'est-à-dire que :0
η
η
η
=η
∞ (1.17) On a l’approximation suivante : 0 ( ) k Kη
γ
η
= & − (1.18)Qui est équivalente à la loi définissant le modèle en loi de puissance avec 0
k m =η K− et k=1-n .
1.2.2.4 Le modèle de Bingham
La représentation la plus simple des fluides rhéoplastiques ou fluides à seuil, est le modèle de Bingham [5], qui donne la relation entre la contrainte
τ
et le taux de cisaillementγ
&sous la forme suivante :
sl pl
τ τ= +η γ& (1.19)
Où
τ
sl est la contrainte de seuil ou seuil de plasticité et ηplest appelé la viscosité plastique.Remarques
• En réalité, les modèles de Cross, de Carreau, en loi de puissance et de Bingham modélisent la viscosité de cisaillement, de ce fait, ils sont utilisés surtout dans le cas des écoulements cisaillés. En outre, ces modèles s’avèrent insuffisants pour décrire d’autres comportements tels que la viscoélasticité des fluides non-newtoniens.
• Tous les fluides non-newtoniens ne présentent pas nécessairement un caractère pseudoplastique pour un écoulement simple de cisaillement en régime stationnaire. Certains fluides comme ceux dits de Boger [6] ont plus ou moins une viscosité constante sur une grande échelle de taux de cisaillement.
• Il existe aussi, des fluides où la viscosité de cisaillement -en plus de sa dépendance du taux de déformation-, dépend aussi du temps, c’est le cas des fluides thixotropes qui sont tels que, sous des conditions de taux de cisaillement constantes, présentent une décroissance de la viscosité dans le temps, l’effet est souvent réversible de sorte que si le matériau est laissé libre après la déformation, il regagnera sa viscosité initiale.
10
Le phénomène inverse est observé pour les fluides dits rhéopectiques ou anti-thixotropes qui sont tels que sous des conditions de cisaillement constantes la viscosité augmente dans le temps et décroît graduellement après.
1.3 Les fluides viscoélastiques
Un autre comportement non-newtonien très important est le caractère viscoélastique, très fréquent dans les suspensions, les solutions de polymères et dans les polymères fondus. Nous allons dans ce qui suit, présenter une étude détaillée sur les fluides non-newtoniens présentant ce caractère et qui sont appelés fluides viscoélastiques.
1.3.1 Description phénoménologique des fluides viscoélastiques
Un fluide viscoélastique est un fluide qui possède à la fois des propriétés de viscosité et d’élasticité. Ainsi, un fluide viscoélastique soumis à une déformation donnée, présente une réponse intermédiaire entre celle d’un solide hookéen classique purement élastique, pour lequel la contrainte est proportionnelle à la déformation, et celle d’un fluide newtonien classique purement visqueux caractérisé par une contrainte proportionnelle à la vitesse de déformation.
Cette réponse va dépendre en partie du rapport entre le temps de la sollicitation et le temps caractéristique (appelé aussi temps de relaxation) du matériau viscoélastique. Si le temps de sollicitation est petit devant le temps caractéristique du matériau, les composants élémentaires du matériau n’ont pas le temps de se déformer de manière importante et on observe une réponse élastique. Si le temps de sollicitation est grand devant le temps caractéristique, la réponse observée est du type visqueux.
Les polymères fondus et les solutions de polymères présentent généralement un comportement viscoélastique. Toutefois, l’utilisation de lois de comportement viscoélastique pour la modélisation des procédésde transformations des polymères s’avère difficile, et de ce fait, des modèles inélastiques ont presque exclusivement été pour longtemps utilisés lors des simulations d’écoulement d’importance industrielle.
1.3.2 Autres caractéristiques des fluides viscoélastiques 1.3.2.1 Anisotropie des contraintes normales
Dans un fluide newtonien soumis à un écoulement de cisaillement simple (ux =
γ
&y), seulela contrainte tangentielle σxyest modifiée par l’écoulement, les contraintes normales restent isotropes et égales à−p. Dans certains liquides, essentiellement des solutions
11
polymères de très grande masse moléculaire, l’écoulement de cisaillement induit également une différence entre les contraintes normales.
1( ) xx yy N σ −σ = γ& (1.20) 2( ) yy zz N σ −σ = γ& (1.21) L’anisotropie des contraintes normales est un effet non linéaire; à faible taux de cisaillement N1 et N2 sont des fonctions quadratiques de
γ
&.Pour refléter ce caractère non linéaire, on définit deux coefficients d’anisotropie
ϕ
1 etϕ
2 tels que : 2 1 1 N = −ϕ γ& (1.22) 2 2 2 N = −ϕ γ& (1.23)En général N1 est négatif et beaucoup plus grand en valeur absolue que N2qui est
généralement positif.
L’apparition de l’anisotropie des contraintes normales est lié au fait que l’écoulement de cisaillement modifie la microstructure du fluide et la rend anisotrope.
En résumé, pour un fluide newtonien la contrainte normale agissant sur la surface d’un élément fluide ne dépend pas de l’orientation de cette surface. Pour les fluides viscoélastiques, un matériau sollicité peut en effet engendrer une contrainte supplémentaire dans la direction de la sollicitation. Ceci provoque donc des différences entre les contraintes normales.
1.3.2.2 Effet Weissenberg
Un autre phénomène dit de “Weissenberg” est mis en évidence en remplissant un récipient d’un polymère mis en rotation par un barreau central. Le fluide remonte le long des parois du barreau central tournant. Cette propriété des fluides viscoélastiques est attribuée à l’anisotropie des contraintes normales. (Voir l’illustration de l’effet de Weissenberg sur la figure 1.3).
1.3.2.3 Relaxation de la contrainte et effet de mémoire
Toujours du fait que, les fluides viscoélastiques présentent des différences de contraintes normales non nulles, un autre phénomène s’observe lors d’un écoulement d’extrusion à la sortie d’une contraction, qui se caractérise par une expansion de la section d’écoulement à la sortie d’un confinement due à la relaxation des contraintes normales accumulées par le fluide pendant son trajet à l’intérieur du tube. Le fluide garde “une mémoire” de son état
12
initial. Cet effet d’expansion est très fréquent dans les procédés industriels d’extrusion de polymères fondus.
A titre d’exemple, pour un fluide newtonien l’expansion est de l’ordre de 1,12 à la sortie d’une filière, par contre pour un polymère fondu l’expansion peut atteindre 1,5 à 3 et dépend en outre des conditions expérimentales. (Voir l’illustration du phénomène de l’expansion et de la relaxation de la contrainte sur la figure 1.4).
1.4 Modèles de représentation des fluides viscoélastiques
Plusieurs modèles ont été élaborés pour représenter les effets de la viscoélasticité, le modèle le plus simple de fluide viscoélastique consiste à additionner les contraintes d’origine élastique et les contraintes d’origine visqueuse
elast visq E η
= + = + &
τ τ τ γ γ (1.24)
Où E est le module d’élasticité,
γ
est la déformation etγ
& la vitesse de déformation.On a souvent recours à des modèles analogiques de comportement. Il s’agit de disposer d’éléments mécaniques tels que les ressorts (contribution élastique) et les amortisseurs (contribution visqueuse) en série ou en parallèle afin d’obtenir une représentation la plus proche possible du comportement dynamique du fluide. L’utilisation des modèles analogiques est un moyen simple et relativement efficace pour bâtir la loi de comportement et constituent la base des modèles différentiels actuels. Plusieurs modèles analogiques sont utilisés, on peut citer à titre d’exemple, le modèle de Maxwell, le modèle de Kelvin, le Model de Jeffreys, etc.
1.4.1 Modèle de Maxwell
Le modèle de base pour les fluides viscoélastiques est le modèle de Maxwell. Il consiste à combiner un modèle d'élasticité linéaire et un modèle de viscosité linéaire. Pour le modèle d'élasticité linéaire, on postule que la contrainte est proportionnelle à la déformation (loi de Hooke), le coefficient de proportionnalité étant le module d'Young E et on associe à ce modèle un ressort hookéen. Pour le modèle de viscosité linéaire, on postule que la contrainte est proportionnelle à la vitesse de déformation (loi de Newton), le coefficient de proportionnalité étant la viscosité : on associe à ce modèle un amortisseur. En mettant en série un ressort hookéen et un amortisseur, on obtient le principe unidimensionnel du modèle de Maxwell (figure 1.1). Dans le cas unidimensionnel, si on note
τ
la contrainte et13
γ
& la vitesse de déformation, on obtient l’équation différentielle ordinaire suivante:1 d E dt
τ τ
γ
η
= + & (1.25)Qu’on peut réécrire sous la forme suivante :
d dt τ λ + =τ ηγ& (1.26) Où E η
λ= est un temps de relaxation du système.
Figure 1.1: Schéma unidimensionnel du modèle de Maxwell.
Remarque
Le modèle de Maxwell est limité quant aux types d’écoulements et de fluides qu’il peut représenter de manière adéquate, les modèles différentiels présentés dans le paragraphe qui suit sont les plus utilisés pour la modélisation des écoulements généraux des fluides viscoélastiques.
1.4.2 Les modèles différentiels constitutifs
De nombreux modèles dérivant de celui de Maxwell ont été proposés et employés pour décrire le comportement des fluides viscoélastiques et en particulier celui des fluides polymériques. Ils présentent tous des paramètres caractéristiques de temps
λ
dans le tenseur de contraintes. Ce temps caractéristique est lié au phénomène typique relatif aux fluides viscoélastiques qui est de la relaxation des contraintes.Cette constante
λ
a donné naissance à deux importants paramètres sans dimensions qui sont : le nombre de Deborah De =λ
/t0 où t0 est une échelle caractéristique de temps qui dépend de l’écoulement considéré, et le nombre de Weissenberg We =λγ
& qui relie le temps de relaxation à la vitesse de déformation, oùγ
& représente une vitesse dedéformation caractéristique de l’écoulement considéré.
Le modèle de base le plus simple, sensé capturer le phénomène important qui est la relaxation de la contrainte dans les fluides viscoélastiques est le modèle dit “modèle élastique avec haltères” (Elastic Dumbells Model), représenté par la figure 1.2, il est constitué de deux poids reliés par un ressort immergé dans un solvant newtonien, il a été
η
τ
E14
proposé par Kuhn en 1934. Depuis, et en se basant sur cette idée directrice, une multitude de modèles ont été mis au point.
En 1950, Oldroyd [7] transforme le modèle dit élastique avec haltères en introduisant une dérivation connue sous le nom de “la dérivée convective supérieure” pour assurer l’objectivité du tenseur des contraintes, et bâtit un premier modèlequi est le modèle UCM (Upper Convected Model). Après, Oldroyd introduit son équation constitutive appelée modèle d’Oldroyd-B où il combine les contributions du solvant et du polymère dans le tenseur des contraintes.
Par la suite, de nouveaux modèles ont été proposés, tels que le modèle de Phan-Thien-Tanner (PTT) [8, 9], le modèle de Giesekus [10,11] et les modèles FENE-P [12] (Finitely Extensible Non Linear Elastic) pour les chaines polymériques longues.
Notons que le domaine de la modélisation des fluides viscoélastiques est en continuel développement et la mise au point de nouveaux modèles est d’actualité.
Figure 1.2: Représentation schématique du modèle élastique avec haltères.
1.4.2.1 Le modèle de Maxwell surconvecté (UCM : Upper Convected Maxwell model) Le modèle de Maxwell surconvecté a fait son apparition dès l’introduction de la dérivée convective supérieure par Oldroyd.
Pour passer au modèle tensoriel surconvecté de Maxwell (UCM), il suffit de remplacer la dérivée temporelle de la contrainte
τ
dans l’équation (1.26) par une dérivée objective (dérivée convective supérieure) du tenseur des contraintesτ
.L’équation constitutive du modèle UCM s’écrit sous la forme tensorielle comme suit : 2
λ
∇η
+ =
τ
τ
D (1.27)τ
est le tenseur des extras-contraintes etτ
∇ est la dérivée supérieure convective ou dérivée d’Oldroyd deτ
, définie par :. . T. t ∇ =∂ + ∇ − ∇ − ∇ ∂ τ τ u τ τ u u τ (1.28) 2 rr 1 rr 2 F r 1 F r O k m2 1 m
15 Et D le tenseur des taux de déformation donné par :
1 ( ) 2 T = ∇ + ∇ D u u (1.29)
Où
u
est le vecteur vitesseλ
est le temps de relaxation de la contrainte etη
est la viscosité du fluide. 1.4.2.2 Le modèle d’Oldroyd-BParmi les équations constitutives les plus simples et les plus utilisées pour modéliser le comportement des solutions polymériques et les polymères fondus, dans des conditions générales d’écoulement, sont celles dites du type Oldroyd-B.
La loi de comportement d’Oldroyd-B découle de la dérivation du modèle moléculaire dit modèle élastique avec haltères. Elle s’écrit sous la forme suivante :
1 2 ( 2 )
λτ∇ + =τ η D+λ D∇ (1.30)
Où
η
désigne la viscosité totale,λ
1 le temps de relaxation de la contrainte etλ
2 le temps de retardation ou de ralentissement de la contrainte.Remarques
• Quand
λ
2 =0, l’équation (1.30) se réduit à l’équation constitutive du model UCM, et siλ λ
1 = 2 =0, l’équation (1.30) se réduit au cas d’un fluide newtonien de viscositéη
.• L’équation constitutive UCM représente une illustration d’un modèle et non pas le comportement réel d’un fluide. Par contre, l’équation constitutive d’Oldroyd-B peut représenter un certain nombre de fluides, en effet, elle décrit plusieurs caractéristiques des solutions diluées dans des solvants très visqueux tels que les fluides de Boger.
• Depuis leur introduction, ces deux modèles étaient impliqués dans plusieurs travaux relevant de disciplines diverses. Ces deux modèles (UCM et Oldroyd-B) restent toujours employés. Ils sont utilisés à des fins de validation de nouvelles approches et de nouvelles techniques. Néanmoins ces modèles ne peuvent simuler les écoulements complexes et se trouvent confrontés à deux problèmes majeurs : le premier étant le fait qu’ils prennent en compte une viscosité de cisaillement constante et le deuxième problème est le fait qu’ils prédisent une contrainte infiniepour un taux d’élongation fini, chose qui est physiquement irréaliste.
16
1.4.2.3 Réduction de l’équation constitutive d’Oldroyd-B
Pour les fluides viscoélastiques suivant la loi de comportement de type Oldroyd-B, le tenseur des extras-contraintes totales
τ
peut s’écrire comme étant la somme de la composante viscoélastique ou polymérique τp et de la composante purement visqueuseτ
s Doncs p = +
τ τ τ (1.31)
Avec τpqui doit satisfaire l’équation du modèle UCM (1.27) comme suit:
2 p p p
λ
τ
∇+ =τ
η
D (1.32) et 2 s =η
sτ
D (1.33)Où
η
s est la viscosité newtonienne du solvant et ηp est la viscosité polymérique ouplastique, qui sont liées par les relations suivantes :
s p η η η= + (1.34) Et 2 s 1
η
λ
λ
η
= (1.35)En substituant les équations (1.31), (1.33), (1.34) et (1.35) dans l’équation (1.30) et tenant compte de l’équation (1.32), l’équation constitutive d’Oldroyd-B se réduit sous la forme suivante :
2
p p p
λ
τ
∇+ =τ
η
D (1.36)
Qui ne s’exprime donc, qu’en fonction de la contrainte polymériqueτp. Où
λ
est le temps de relaxation et ηp est la viscosité polymérique.Remarque
Le modèle d’OLdroyd-B présente plusieurs défauts. En effet, avec ce modèle, on observe que :
• Dans les écoulements cisaillés simples stationnaires, la viscosité de cisaillement ne dépend pas du taux de cisaillement
γ
&• Dans les écoulements cisaillés simples stationnaires, la seconde différence de contraintes normales N2 est nulle.
17
• Et surtout dans les écoulements élongationnels stationnaires, la viscosité élongationnelle prend des valeurs infinies pour des taux élongationnels
ε
&
finis.Toutes ces prédictions sont en contradiction avec les résultats d’expériences menées sur la plupart des fluides polymériques.
1.4.2.4 Le modèle de Phan-Thien-Tanner
Des modèles macroscopiques permettant d’obtenir des résultats qualitativement plus en accord avec les expériences ont alors été développés. De manière générale, ces modèles présentent un terme additionnel par rapport à l’équation constitutive d’Oldroyd-B relatif à la contrainte polymérique, de façon à produire la pseudo-plasticité, une viscosité élongationnelle bornée et une seconde différence des contraintes normales non nulle. La forme générale de ces équations est :
( , )
p
λ
p f pη
p∇
+ + & = &
τ
τ
τ γ
γ
(1.37)Ce raisonnement a conduit à la naissance de plusieurs modèles, parmi eux, le modèle dit de Phan-Thien-Tanner qui est représenté par une équation de la forme :
({ })
p f p p p
λ
τ
∇+τ τ
=η
γ
& (1.38)En réalité, cette équation est une des formes simplifiées de l’équation du modèle PTT, où seulement la partie convective supérieure de la dérivée de Gordon-Schowalter est retenue. Deux formulations sont proposées pour la fonction f({ })
τ
:Une forme linéaire proposée dans [8], qui s’écrit :
({ }) 1p { }p p f
λε
η
= +τ
τ
(1.39)Et une forme exponentielle présentée ultérieurement dans [9], qui s’écrit :
({ }) exp[p { }]p p f
λε
η
=τ
τ
(1.40)λ
représente le temps de relaxationp
η la viscosité polymérique
ε
est un paramètre lié au comportement élongationnel du modèle PTT, appelé paramètred’extensibilité.
Si
ε
=
0
le modèle de PTT se réduit au modèle d’Oldroyd-BCe modèle a l’avantage de prédire pour un écoulement élongationnel simple, une viscosité élongationnelle croissante et présentant un plateau analogue à ce qui est observé sur les solutions polymères.