HAL Id: halshs-00173791
https://halshs.archives-ouvertes.fr/halshs-00173791
Submitted on 20 Sep 2007
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
Bernard Monjardet
To cite this version:
Maison des Sciences Économiques, 106-112 boulevard de L'Hôpital, 75647 Paris Cedex 13 http://mse.univ-paris1.fr/Publicat.htm
ISSN : 1624-0340
Modèles ordinaux de préférences
Bernard MONJARDET, CERMSEM
Modèles ordinaux de préférences
Bernard Monjardet
1Résumé
Dans ce texte à visée didactique on présente les principaux modèles d’ordres utilisés pour représenter les préférences d’un sujet sur un ensemble fini de biens de nature variée. On part du modèle d’ordre fort correspondant au cas où la préférence est représentée par une fonction d’utilité numérique, modèle qui implique que la relation d’indifférence du sujet est transitive. Les modèles d’ordre quasi-fort et d’ordre d’intervalles permettent de ne plus supposer l’indifférence transitive, tout en conservant des propriétés de représentation numériques avec l’introduction de seuils. Des résultats sur la caractérisation et la représentation numérique des relations de Ferrers, relations qui généralisent les relations d’ordres précédentes, permettent d’obtenir simplement les résultats sur ces relations d’ordres. Des compléments d’ordre historique ou mathématique sont proposés au lecteur.
1. Introduction
La classique fonction d’utilité des économistes qui représente les préférences d’un agent sur un ensemble -supposé ici fini- de biens, définit une relation de préférence: l’agent préfère (strictement) le bien y au bien x si u(x) < u(y). Cette relation de préférence est asymétrique et transitive, et est donc un ordre strict. De plus cet ordre n’est pas quelconque. En effet, dans cette modélisation des préférences par une fonction d’utilité, deux biens de même utilité sont considérés comme indifférents. La relation d’incomparabilité de l’ordre associé, qui correspond à la relation d’indifférence de l’agent, est donc transitive, ce qui fait de cet ordre un “ordre fort“. Or, on a constaté depuis longtemps que cette hypothèse de transitivité de l’indifférence n’est pas nécessairement vérifiée et l’on a défini d’autres modèles ordinaux pour la préférence qui, tout en ne la conservant pas permettent cependant une certaine représentation numérique. Ce sont ces modèles et leurs représentations numériques que nous allons présenter dans ce texte. Plusieurs points sont d’abord à mentionner ou préciser.
Les relations d’ordre que nous allons étudier sont utilisées dans les nombreux domaines où l’on a besoin de modéliser des préférences, c’est-à-dire non seulement en microéconomie, mais aussi par exemple dans les théories normatives ou descriptives de la décision et du choix (préférences d’un décideur sur des options, préférences d’un joueur sur des loteries) ou en théorie des votes (préférences d’un votant sur les candidats).
Dans ces modèles, on peut soit vouloir modéliser la préférence dite stricte (qui s’interprète comme “l’objet x est meilleur que l’objet y“) soit la préférence dite large (qui s’interprète comme “l’objet x est au moins aussi bon que l’objet y“). Nous ferons dans ce texte le premier choix qui conduit à modéliser la préférence par une relation O d’ordre strict, c’est-à-dire par une relation irréflexive et transitive (et donc asymétrique). Pour passer de cette modélisation à la seconde, il suffit de définir la préférence large R à partir de O, par (x,y) Œ R si et seulement si (y,x) œO. La relation de préférence large ainsi obtenue est totale et sa partie symétrique (xRy et yRx), qui modélise l’indifférence, est identique à la relation d’incomparabilité de l’ordre strict O (relation définie par (x,y) œ O et (y,x) œO). Dans ce texte, nous
1
CERMSEM, Université Paris I Panthéon Sorbonne, Maison des Sciences Économiques, 106-112 bd de l’Hopital 75647 Paris Cédex 13, FRANCE, monjarde@univ-paris1.fr
considérerons donc que la relation d’incomparabilité de l’ordre strict O modélise la relation d’indifférence. Nous reviendrons sur l'équivalence -en fait une dualité- entre ces deux classes de modèles à!la fin de ce texte.
Nous examinerons successivement aux sections 2,3 et 4 les classes d’ordres suivantes !: ordre strict fort, ordre strict quasi-fort et ordre strict d’intervalles (dans la suite nous omettrons généralement le qualificatif strict). Pour chacune de ces classes, nous donnerons plusieurs caractérisations des ordres de la classe ainsi que leurs propriétés de représentation numérique. La démonstration des résultats énoncés ne sera pas toujours faite immédiatement. En effet, il sera plus simple et surtout moins répétitif d’introduire à la section 5 une classe de relations binaires particulières appelées "relations de Ferrers" ou “biordres“. Les biordres ne sont pas en général des ordres, mais tous les ordres évoqués ci-dessus sont des biordres particuliers. Il suffira donc d’appliquer à ces différents cas les résultats généraux, d’ailleurs de démonstration simple, de caractérisation et de représentation numérique des biordres. On a toutefois une exception à cette démarche dans le cas de la représentation numérique “à seuil constant“ des ordres quasi-forts. Ce résultat, d’obtention beaucoup moins aisée, peut être prouvé au moyen de notions et résultats de la théorie des graphes dont l'exposé serait trop long ici ; nous nous contenterons donc de renvoyer à des références pour sa preuve.
Pour définir et caractériser les classes d’ordres évoquées ci-dessus, nous commençons à la section 2 par donner quelques définitions et notations générales sur les relations binaires et les relations d’ordre. La section 6 donne deux sortes de compléments!; les premiers sont des indications d’ordre historique sur les nombreux contextes où sont apparues les ordres étudiés ici, ainsi que des références à la littérature du sujet!; les seconds portent sur des résultats complémentaires présentés sous forme d’exercices.
2 Définitions et rappels
Soit X un ensemble fini ; le produit cartésien de X par X est l'ensemble de tous les couples (x,y), x Œ X, y Œ X ; on le note X 6 X ou X2 . On appelle relation binaire sur X (ou entre
éléments de X) toute partie R de ce produit cartésien ; on a donc R Õ X2. Si (x,y) Œ R, on dit que le couple (x,y) vérifie R, ou que x et y sont dans la relation R, ou que x et y sont en
relation (pour R) ; dans ce cas on écrit aussi xRy.
On pose :
xR = {y ΠX : xRy} Rx = {y ΠX : yRx}
Soit R une relation binaire sur un ensemble X. On note Rc la relation complémentaire de R
(xRcy si (x,y) œ R), et Rd la relation duale de R (xRdy si yRx). La relation (Rc)d (= (Rd)c) est notée Rcd et est égale à {(x,y) : (y,x) œ R} ; on l'appelle la coduale de R.
Les relations binaires étant des parties d'un ensemble, la relation d'inclusion et les opérations ensemblistes de réunion, intersection et complémentation sont définies sur elles. Ainsi
R Õ R' si xRy implique xR'y R Ã R' si xRy implique xR'y et R ≠ R'
Dans ces deux cas, on dit aussi que la relation R' est compatible avec la relation R ou que R' est une extension de R.
R»R' = {(x,y) Œ X 2 : (x,y) Œ R ou (x,y) Œ R'}
R«R' = {(x,y) Œ X 2 : (x,y) Œ R et (x,y) Œ R'}
Soient deux relations R et R' sur X ; le produit de R et R' est la relation sur X, notée RoR' ou RR', et définie par :
xRR'z s'il existe t ΠX tel que xRt et tR'z
entre parenthèses une expression algébrique ou/et ordinale de ces propriétés, où D = {(x,x) : x Œ X } désigne la relation égalité (dite aussi diagonale) sur X.
R réflexive : pour tout x Œ X, xRx (D Õ R) R irréflexive (ou antiréflexive) : pour tout x Œ X, xRcx (D Õ Rc) R symétrique : pour tous x, y Œ X, xRy fi yRx (R = Rd)
R antisymétrique : pour tous x, y Œ X, xRy et yRx fi x = y (R«Rd Õ D)
R asymétrique : pour tous x, y Œ X, xRy fi yRcx (R Õ Rdc)
R faiblement totale : pour tous x, y ΠX, xRcy et yRcx fi x = y
R totale (ou complète) : pour tous x, y Œ X, xRcy fi yRx (Rdc Õ R) R transitive : pour tous x, y, z Œ X, xRy et yRz fi xRz (R2 Õ R)
R négativement transitive : pour tous x, y, z Œ X, xRcy et yRcz fi xRcz ((Rc)2 Õ Rc)
Ces propriétés permettent de définir les relations particulières suivantes
Ordre strict O : relation asymétrique et transitive.
Ordre total strict (ou strictement total) L : relation asymétrique, faiblement totale et
transitive. Ordre O : relation réflexive, antisymétrique et transitive.
Ordre total (ou linéaire) L : relation antisymétrique, totale et transitive. Préordre total R : relation totale et transitive.
Équivalence E : relation réflexive, symétrique et transitive.
Dans le cas d’un ordre O, deux éléments x et y tels que xOy ou yOx sont dits comparables!; ils sont dits incomparables si xOcy et yOcx.
Un ordre total strict sur un ensemble X de cardinal k est un ordre où deux éléments distincts sont toujours comparables. Lorsque X est de cardinal k, on peut l’écrire x1 <...< xi...< xk où i est le rang de l’élément xi. Un tel ordre sera aussi noté k. Nous aurons besoin de considérer des ordres stricts particuliers obtenus en faisant la “somme cardinale“ d’ordres totaux stricts (c’est-à-dire l’union de deux tels ordres définis sur des ensembles disjoints). !On les note 1+2, 2+2et 1+3et ils sont représentés à la Figure 1.
1+2 2+2 1+3
FIGURE 1
Enfin nous définissons une notion de tableau d’une relation binaire qui va permettre des caractérisations intéressantes des ordres que nous étudions.
Un tableau d’une relation binaire R sur un ensemble X est la donnée d’un triplet (R, L1, L2)
où L1 et L2 sont deux ordres totaux sur X.
Un tableau (R, L1, L2) est en escalier si L1RL2 Õ R, i.e. si, pour tous x,y,z,t de X, xL1y, yRz
et zL2t impliquent xRt.
Un tableau où L1 = L2 = L est noté (R, L). Un tableau (R, L) en escalier est surdiagonal si R
Noter que dans ces définitions les ordres L1 et L2 sont des ordres réflexifs. Il s'ensuit que la
condition L1RL2 Õ R implique aussi L1R»RL2 Õ R.
Le fait qu'une relation R admette un tableau en escalier permet une représentation "en escalier" de la matrice d'incidence de cette relation, c'est-à-dire de la 0-1 matrice M à n = |X| lignes et n colonnes où mx,y = 1 (respectivement, 0) si (x,y) Œ R (respectivement, (x,y) œR).
Il suffit d'ordonner les lignes et les colonnes de cette matrice suivant les ordres L1 et L2. La
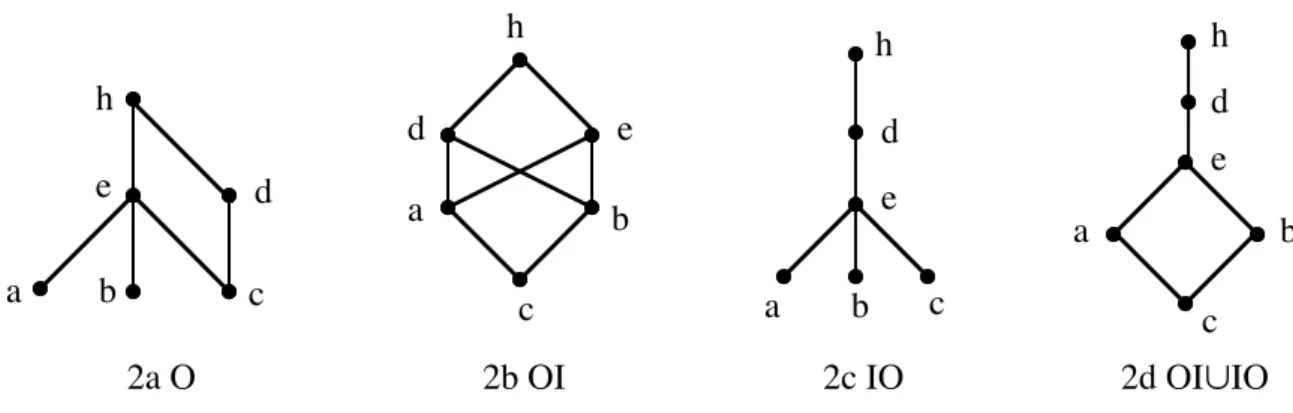
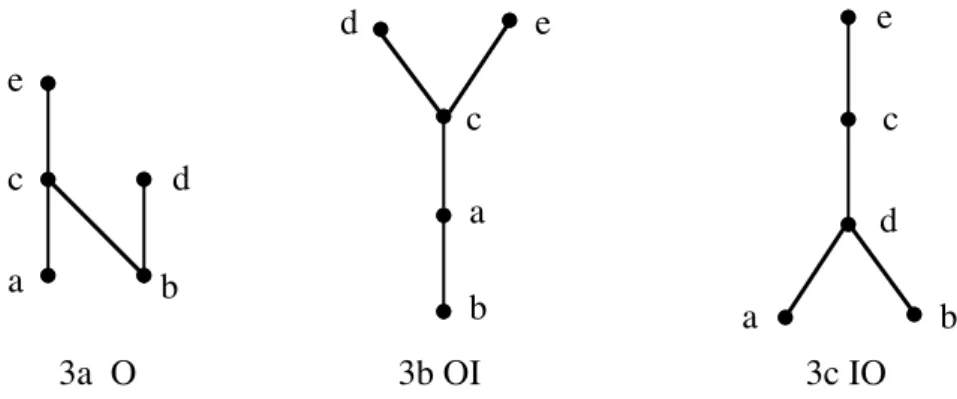
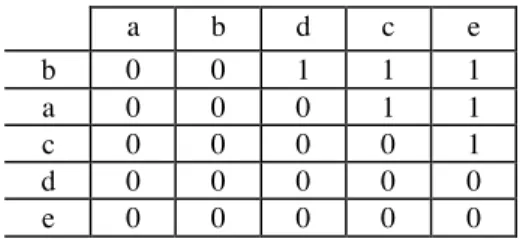
figure 2a donne un exemple de relation admettant un tableau en escalier pour le même ordre L = cabedh des lignes et des colonnes!; ce tableau est représenté à la Table 1. Comme de plus, tous les 1 de la 0-1 matrice d’incidence correspondant à ce tableau sont au dessus de la diagonale principale, ce tableau est surdiagonal. La relation de la figure 3a admet aussi un tableau en escalier représenté à la Table 2. Mais, contrairement aux apparences, ce n’est pas un tableau surdiagonal, car l’ordre bacde des lignes est différent de l’ordre abcde des colonnes.
2 Ordres forts
Dans cette section et les suivantes les ordres que nous étudions sont toujours stricts. Nous omettons donc en général le qualificatif strict pour les désigner.
Nous commençons par définir et caractériser les ordres forts qui sont les ordres associés au classique modèle de représentation des préférences par une fonction d’utilité numérique. Nous en donnons une définition purement ordinale, l’équivalence avec la propriété de représentation par une fonction numérique résultant de la caractérisation donnée au point (5) de la proposition ci-dessous. On peut la paraphraser en disant qu'à toute fonction numérique définie sur un ensemble X est associé naturellement l'ordre sur X induit par les valeurs strictement croissantes de cette fonction. Cet ordre est un ordre fort et inversement tout ordre fort peut être obtenu de cette manière. Cette propriété de représentation des ordres forts sera utilisée dans la suite pour obtenir d'autres types de représentations numériques pour des ordres plus généraux.
Définition 1.1
Un ordre fort est un ordre (strict) ne contenant pas comme sous-ordre l’ordre 1+2.
En d’autres termes, on ne peut jamais trouver dans un ordre fort deux éléments comparables qui soient tous les deux incomparables à un troisième élément. Des exemples d’ordre fort sont représentés aux Figures 2b, 2c, 2d, 3b et 3c. Dans ces figures, un ordre est représenté par son diagramme (de Hasse), où ne sont figurés que les couples de couverture de l’ordre, c’est-à-dire les couples xOy tels qu’il n’existe pas z avec xOz et zOy. Par exemple, dans la figure 2b, (c,a) et (a,d) sont des couples de couverture et le couple (c,d) déduit des précédents par transitivité n’est pas représenté.
Proposition 1.2
Soit O une relation binaire définie sur un ensemble X et soit I = Oc«Ocd. Les propriétés
suivantes sont équivalentes : (1) O est un ordre fort,
(2) O est asymétrique et négativement transitive, (3) O est un ordre strict et O = OI = IO,
(4) O est un ordre strict et I est une relation d'équivalence,
(5) il existe une fonction numérique u : X
Æ
„ telle que xOy ¤ u(x) < u(y). Preuve(1)
fi
(2) O étant un ordre fort est asymétrique. Si O n'est pas négativement transitive, il existe x,y et z avec xOcy, yOcz et xOz. yOx est impossible (puisque sinon l’on en déduiraityOz, une contradiction). On a de même zOcy. La restriction de O à {x,y,z} est alors
isomorphe à 1+2, ce qui est impossible.
(2)
fi
(3) La relation I étant réflexive, on a O Õ OI. Supposons OI Ú O ; il existe donc x,y et z avec xOy, yIz et xOcz. Mais xOcz, zOcy et O négativement transitive impliquent xOcy, une contradiction. On a donc O = OI et l’on montre de même O = IO.(3)
fi
(4) Puisque O est irréflexive, I est réflexive. Puisque (O c«Ocd)d = O cd«Oc, I estsymétrique. Soient x,y,z avec xIy et yIz. Si xIcz, on a soit xOz, soit zOx. Dans le premier cas,
yIx et xOz impliquent yOz, une contradiction. Le second cas conduit à une contradiction analogue. Donc I est transitive et est une équivalence.
(4)
fi
(5) Soit X/I l'ensemble quotient de X par l'équivalence I. Définissons une relation < sur cet ensemble quotient en posant pour deux classes C, C' Œ X/I , C<!C' s'il existe x Œ Cet y Œ C' avec xOy. On laisse au lecteur le soin de vérifier que cette relation peut aussi bien être définie par [pour tout x Œ Cet tout y Œ C', on a xOy] et que < est un ordre strict sur X/I. De plus cet ordre est strictement total. En effet, si pour deux classes C et C' différentes de X/I, il existe x Œ Cet y Œ C' avec xOcy et yOcx, on aurait xIy, une contradiction. L'ordre strictementtotal < peut donc être écrit dans l'ordre des rangs de ses éléments comme C1 <....< Ci....< Cp.
Définissons alors une application u de X dans „ en posant u(x) = i si x Œ Ci. Puisque xOy est
équivalent à x Œ Ci et y Œ Cj avec i < j, on a bien xOy équivalent à u(x) < u(y).
(5)
fi
(1) Soit u une fonction de X dans „ et O la relation définie par xOy si et seulement si u(x) < u(y). Il est immédiat de vérifier que O est irréflexive et transitive, i.e. un ordre strict. On a d'autre part xIy si et seulement si u(x) = u(y). L'existence de trois éléments x,y,z avec xOy, xIz et yIz est alors clairement impossible (puisqu'on aurait u(x) = u(z) = u(y) et u(x) < u(y)).L
orsqu'en microéconomie on définit la préférence d'un agent sur un ensemble X de biens au moyen d'une fonction d'utilité définie sur X, on suppose de ce fait que sa préférence (stricte) constitue un ordre fort. Il en résulte, comme nous l'avons déjà mentionné dans l'introduction, que sa relation d'indifférence est transitive ; en fait, on a x indifférent à y si et seulement si u(x) = u(y). Les notions d'ordre quasi-fort et d'ordre d'intervalles permettent des modélisations des préférences qui tout en ne supposant plus une indifférence transitive, conservent un certain type de représentation numérique que nous allons décrire ci-dessous.3 Ordres quasi-forts
Définition 1.3
Un ordre quasi- fort est un ordre (strict) ne contenant pas comme sous-ordre les ordres 1+3 et 2+2
En d’autres termes, on ne peut jamais trouver dans un ordre fort trois éléments comparables tous incomparables à un quatrième élément, ainsi que deux paires d’éléments comparables et incomparables aux éléments de l’autre paire. Un exemple d’ordre quasi-fort est représenté à la Figure 2a (par son diagramme).
h a b c d e a b c d h e e a b c d h e a b c d h 2a O 2b OI 2c IO 2d OI»IO Figure 2 Un ordre quasi-fort et les ordres forts associés
Proposition 1.4
Soit O une relation binaire définie sur un ensemble X et soit I = Oc«Ocd. Les propriétés
suivantes sont équivalentes : (1) O est un ordre quasi-fort,
(2) O est irréflexif et, pour tous x,y,z,t éléments de X, [xOy et zOt] impliquent [xOt ou zOy], et [xOy et yOz] impliquent [xOt ou tOz],
(3) O est un ordre strict et OI»IO est un ordre fort, (4) O admet un tableau en escalier (O, L) surdiagonal.
Comme annoncé plus haut , cette proposition sera prouvée à la section 5. La table 1 donne un tableau surdiagonal pour l’ordre quasi-fort de la Figure 2.a
c b a e d h c 1 1 1 b 1 1 a 1 1 e 1 d 1 h
Table 1 Tableau en escalier surdiagonal d’un ordre quasi-fort
Théorème 1.5 (représentation numérique des ordres quasi-forts)
Soit O une relation binaire définie sur un ensemble X et soit I = Oc«Ocd. Les propriétés
suivantes sont équivalentes : (1) O est un ordre quasi-fort,
(2) il existe une fonction numérique u : X
Æ
„ et un réel s tels que xOy ¤ u(x) + s < u(y),(3) il existe une fonction F de X dans l’ensemble des intervalles de longueur unité de „ telle que xOy si et seulement si F(x) < F(y) (l'ordre < sur les intervalles de „ étant pris au sens où, pour tous a Œ F(x), b Œ F(y), on a a<b).
La condition (2) ci-dessus montre le type de représentation numérique obtenu pour les ordres quasi-forts. Pour que y soit préféré à x, il faut que son "utilité" (pour adopter le terme utilisé en microéconomie) dépasse l'utilité de x d'une certaine quantité s. Celle-ci joue donc le rôle d'un "seuil" en dessous duquel x et y seront considérés comme indifférents. On notera que dans le modèle de l'ordre quasi-fort, ce seuil est constant, donc indépendant de l'utilité de x. Le modèle d'ordre d'intervalles permet d'obtenir un seuil variable, comme cela va apparaître dans les différentes caractérisations de ces ordres données dans la proposition 1.7 suivante (cf. condition (5)). Nous renvoyons à l'exercice 6 et à la section 6 pour des références où l'on trouvera la preuve de ce théorème ainsi que pour le problème voisin de l'introduction d'un seuil!d'indiscernabilité en psychophysique.
4 Ordres d’intervalles
Définition 1.6
Un ordre d’intervalles est un ordre (strict) ne contenant pas comme sous-ordre l’ordre 2+2.
En d’autres termes, on ne peut jamais trouver dans un ordre d’intervalles deux paires d’éléments comparables et incomparables aux éléments de l’autre paire. Un exemple d’ordre d’intervalles est représenté à la Figure 3a (par son diagramme).
a b c d e b c d b e a a c d e 3a O 3b OI 3c IO
Figure 3 Un ordre d’intervalles et les ordres forts associés
Proposition 1.7
Soit O une relation binaire définie sur un ensemble X et soit I = Oc«Ocd. Les propriétés suivantes sont équivalentes :
(1) O est un ordre d'intervalles,
(2) O est irréflexif et, pour tous x,y,z,t éléments de X, [xOy et zOt] impliquent [xOt ou zOy], (3) O est un ordre strict et OI est un ordre fort,
(4) O est irréflexive et admet un tableau en escalier (O, L1, L2),
(5) il existe deux fonctions numériques u!: X
Æ
„ et s : XÆ
„+ telles que xOy ¤ u(x) + s(x) < u(y),(6) il existe une fonction F de X dans l’ensemble des intervalles de „ telle que xOy ¤ F(x) < F(y).
Comme annoncé plus haut , cette proposition sera prouvée à la section 5.
Dans la condition (3) ci-dessus, "OI est un ordre fort" pourrait être remplacé par "IO est un ordre fort". On remarque que la condition (5) implique que x est indifférent à y dans ce modèle d'ordre d'intervalles si et seulement si [u(x) ≤ u(y) + s(y) et u(y) ≤ u(x) + s(x)]. Quant à la condition (6), elle implique que x est indifférent à y si et seulement si les deux intervalles
x et y ont une intersection non vide (cf. les compléments de la section 6 pour les graphes définis de cette manière).
Exemple
Nous illustrons les caractérisations précédentes des ordres d'intervalles sur l'ordre (strict) O dont le diagramme est donné à la figure 3a. C'est un ordre d'intervalles, puisqu'il ne contient pas 2+2. Les deux ordres forts OI et IO correspondants (condition (3)) sont représentés aux figures 3b et 3c par leurs diagrammes. Le tableau en escalier de O (condition (4)) est donné à la table 2. Pour obtenir la représentation numérique de la condition (5), on utilise l'algorithme donné dans la preuve de la proposition 1.9. Il permet d'abord de trouver deux fonctions f et g telles que xOy si et seulement si f(x) < g(y). Pour f on peut, par exemple, prendre la “fonction rang“ de l'ordre fort OI (= OOcd)!où le rang d’un élément est le rang de sa classe
d’équivalence dans l’ordre strict total défini entre ses classes (cf. la preuve de 4) implique 5) pour la proposition 1.2). On obtient ainsi f(b) = 1, f(a) = 2, f(c) = 3, f(d) = f(e) = 4. On a alors g(x) = Min{f(z) : xOcdz}, ce qui donne g(a) = g(b) = 1, g(c) = 3, g(d) = 2 et g(e) = 4. En prenant ensuite u = g et s = f-g, on obtient s(a) = 1, s(b) = s(c) = s(e) = 0 et s(d) = 2. Le lecteur vérifiera qu'on a bien alors xOy si et seulement si u(x) + s(x) < u(y). Pour obtenir l'application F de la condition (6), on pose F(x) = [u(x), u(x) + s(x)], ce qui donne F(a) = [1,2], F(b) = [1], F(c) = [3], F(d) = [2,4] et F(e) = [4]. On remarque que certains des intervalles permettant de représenter l'ordre O sont réduits à un seul nombre (mais il serait facile de déduire de cette représentation une autre sans intervalles triviaux).
a b d c e b 0 0 1 1 1 a 0 0 0 1 1 c 0 0 0 0 1 d 0 0 0 0 0 e 0 0 0 0 0
Table 2 Tableau en escalier d’un ordre d’intervalles
5 Relations de Ferrers
Afin de faciliter les preuves des propositions 1.4 et 1.7, nous introduisons maintenant la classe des relations de Ferrers (dites aussi biordres) et nous en donnons plusieurs caractérisations.
Définition 1.8
Une relation R sur un ensemble X est une relation de Ferrers (ou un biordre) si, pour tous x,y,z,t Œ X, on ne peut avoir simultanément xRy, zRt, xRct et zRcy.
On notera que cette définition implique que les éléments x et z d'une part, y et t d'autre part sont distincts, les autres éléments pouvant ne pas l'être. Par exemple, on ne peut avoir dans un biordre R la sous-relation formée de deux éléments x et y avec xRx, yRy, xRcy et yRcx.
Proposition 1.9
Soit R une relation binaire définie sur un ensemble X. Les propriétés suivantes sont équivalentes :
(1) R est une relation de Ferrers,
(2) pour tous x,y,z,t distincts de X, [xRy et zRt] impliquent [xRt ou zRy], (3) RRcd est un ordre fort,
(4) R admet un tableau en escalier (R, L1, L2),
(5) il existe deux fonctions f et g de X dans „ telles que xRy ¤ f(x) < g(y), (6) il existe deux fonctions u et s de X dans „ telles que
xRy ¤ u(x) + s(x) < u(y).
Nous commençons par prouver le lemme suivant portant sur une relation binaire R quelconque définie sur X. Pour x Œ X, on pose xR = {y Œ X : xRy} et Rx = {y Œ X : yRx}. Lemme 1.10
Soit R une relation binaire sur un ensemble X. On a alors :
a) pour x,y Œ X, xRRcdy ¤ xR Ú yR, xRcdRy ¤ Ry Ú Rx, x[(RRcd)cd]y ¤ xR ⊇ yR et
x[(RcdR)cd]y ¤ Rx Õ Ry,
b) RRcd et RcdR sont négativement transitives,
c) RRcd asymétrique ¤ RcdR asymétrique¤ RRcd ordre fort ¤ RcdR ordre fort,
d) Si R est un ordre strict noté O et I = Oc«Ocd, alors OI = OOcd et IO = OcdO.
Preuve
a) xRRcdy est équivalent à l'existence d'un élément t de X tel que xRt et yRct, ce qui est
équivalent à xR Ú yR. On en déduit immédiatement que x[(RRcd)cd]y est équivalent à xR
⊇ yR. Les deux autres équivalences se prouvent de manière identique.
b) puisque d'après a) x[(RRcd)c]y est équivalent à yR ⊇ xR, et x[(RcdR)c]y est équivalent à Ry Õ Rx, la transitivité négative de RRcd et de RcdR est évidente.
c) Supposons RRcd asymétrique et RcdR non asymétrique. Il existe donc x et y distincts avec
xRcdRy et yRcdRx, ce qui implique l'existence de z et t distincts avec zRy, zRcx, tRx et tRcy.
Avoir tRx et zRcx est équivalent à avoir tRRcdz , tandis qu'avoir zRy et tRcy est équivalent à
avoir zRRcdt, une contradiction avec RRcd asymétrique. On montre de même que RcdR
asymétrique implique RRcd asymétrique. Enfin puisque d'après b) RRcd est aussi
négativement transitive, cette relation est un ordre fort (proposition 1.2). De même pour RcdR.
d) Pour toute relation binaire O, on a évidemment OI Õ OOcd. Si O est un ordre strict et
xOOcdy, il existe t avec xOt et yOct. Si tOcy, on a tIy et donc xOIy. Si tOy, la transitivité de O implique xOy, et la réflexivité de I implique yIy, d'où xOIy. On a donc bien montré que OI = OOcd. On montre de même IO = OcdO.
Remarque 1.11
Il résulte immédiatement du point a) du lemme précédent que (RRcd)cd et (RcdR)cd sont des
préordres totaux (dont les ordres forts RRcd et RcdR sont les parties asymétriques). Ces préordres sont souvent appelés les préordres traces (à gauche, et à droite). L'exercice 3 permet de montrer quelques résultats complémentaires sur ces préordres (notés respectivement, T1 et T2) ou leur intersection (notée T).
Preuve de la proposition 1.9 (1)
fi
(2) évident.(2)
fi
(3) D'après le point c) du lemme 1.10 pour montrer que RRcd est un ordre fort il!suffitde montrer que cette relation est asymétrique. Sinon, il existe x,y Œ X avec xRRcdy et
yRRcdx. Ceci implique qu'il existe t et z avec xRt, yRct, yRz et xRcz, une contradiction avec
(2).
(3)
fi
(4) D'après le lemme 1.10, RRcd étant un ordre fort, RcdR est également un ordre fort.D'après un résultat classique (Szpilrajn,1930) qui dit que tout ordre (strict) est contenu dans un ordre total (strict), il existe donc deux ordres strictement totaux L1,s et L2,s tels que RRcd Õ
L1,s et RcdR Õ L2,s. Observons d'autre part que le codual d'un ordre strictement total Ls est
l'ordre total associé : (Ls)cd = Ls+{(x,x), x Œ X}. Notons L1 = (L1,s)cd et L2 = (L2,s)cd les
deux ordres totaux associés à L1,s et L2,s. On va montrer que (R, L1, L2) est un tableau en
escalier, i.e. que xL1y, yRz et zL2t impliquent xRt. Faisons d'abord une observation évidente : si R Õ R' on a Rcd ⊇ R'cd. En particulier, RRcd Õ L1,s implique L1 = (L1,s)cd Õ (RRcd)cd. Il
s'ensuit alors que xL1y implique x[(RRcd)cd]y, c'est-à-dire xR ⊇ yR (lemme 1.10). On montre
de même que zL2t implique Rz Õ Rt. Puisqu'on a yRz, on déduit alors xRz de la première
implication, ce qui avec la seconde implication, entraîne xRt.
(4)
fi
(1) Soient x,yz,t avec xRy et zRt . Puisque L1 est un ordre total, on a xL1z ou zL1x. Puisque R admet un tableau en escalier, alors L1R Õ R et l’on obtient dans le premier cas xRtet dans le second zRy, ce qui montre (1). (3)
fi
(5)RRcd étant un ordre fort, il existe d'après la proposition 1.2, une fonction f!: X
Æ
„ telle quexRRcdz si et seulement si f(x) < f(z). Posons alors pour tout y dans X
g(y) = Max{f(z), z Œ X} + 1, si yRcd = Ø(i.e. s'il n'existe pas z avec yRcd z),
g(y) = Min{f(z) : yRcdz}, si yRcd
≠
Ø. Soient x,y avec xRy :Si yRcd = Ø
,
f(x)≤
Max{f(z), z ΠX} < g(y).Si yRcd
≠
Ø,
soit z tel que yRcd z. xRy et yRcd z impliquent xRRcd z.On a donc f(x) < f(z) pour tout z Œ yRcd , d'où f(x) < Min{f(z) : yRcdz} = g(y).
Réciproquement, supposons f(x) < g(y). Que g(y) soit égal à Max{f(z), z Œ X} + 1 ou à Min{f(z) : yRcdz}, on a y(Rcd)cx, i.e. xRy.
(5)
fi
(6)Posons pour tout t dans X, u(t) = g(t) et s(t) = f(t) - u(t). Alors xRy si et seulement si f(x) = u(x) + s(x) < u(y).
(6)
fi
(1) Supposons qu'il existe x,y,z,t tels que xRy, zRcy, zRt et xRct. On a alors u(x) +s(x) < u(y), u(y) ≤ u(z) + s(z), u(z) + s(z) < u(t), et u(t) ≤ u(x) + s(x), ce qui est contradictoire.
Le lemme suivant nous permet de prouver facilement les propositions 1.7 et 1.4 (dans cet ordre).
Lemme 1.12 Soit O une relation binaire sur un ensemble X.
a) O est un ordre d'intervalles si et seulement si O est une relation de Ferrers irréflexive, b) O est un ordre quasi-fort si et seulement si O est une relation de Ferrers irréflexive et ne contenant pas 1+3.
Preuve
a) Si O est un ordre d'intervalles, il est irréflexif. De plus, puisqu'il ne contient pas 2+2, il vérifie la caractérisation (2) d'une relation de Ferrers (proposition 1.9). Inversement, si O est une relation de Ferrers irréflexive, elle est transitive car xOy, yOcy et yOt impliquent xOt
(point (2) de la proposition 1.9). O est donc un ordre strict qui ne peut contenir 2+2 puisque O est une relation de Ferrers. C'est donc un ordre d'intervalles.
b) Ceci résulte immédiatement de a) et du fait que, par définition, un ordre quasi-fort est un ordre d'intervalles ne contenant pas 1+3.
Preuve de la proposition 1.7
Appliquons la proposition 1.9 au cas où O est une relation de Ferrers irréflexive, et montrons que des conditions de cette proposition deviennent des conditions de la proposition 1.7, ce qui prouvera l'équivalence de ces dernières. C'est évident pour les conditions (2) et (4). Pour la condition (1), ceci résulte du lemme 1.12, énonçant que O est alors un ordre d'intervalles. La condition (3) implique que O est une relation de Ferrers, qui étant de plus irréflexive, est un ordre (d'intervalles) ; d'après le lemme 1.10, on a alors OOcd = OI, ce qui donne bien la
condition (3) de la proposition 1.7.
La condition (5) de cette dernière proposition est obtenue à partir de la condition (6) de la proposition 1.9. En effet, O étant irréflexive, on a u(x) + s(x) ≥ u(x), et donc s(x) ≥ 0. Considérons finalement la condition (6) de la proposition 1.7. Elle est évidemment impliquée par la condition (5) (de cette même proposition) : il suffit de poser F(x) = [u(x), u(x) + s(x)]. Inversement montrons que si (6) est vérifiée, O est un ordre d'intervalles en montrant que la condition (2) est vérifiée. D'abord, puisque F(x) n’est pas strictement inférieur à F(x), O est irréflexive. Soient x,y,z,t avec xOy, zOt et xOct ; on doit montrer zOy. Les deux premières
relations impliquent u(x) + s(x) < u(y) et u(z) + s(z) < u(t) et la troisième u(x) + s(x) ≥ u(t). On en déduit u(z) + s(z) < u(y), soit zOy.
Preuve de la proposition 1.4
(1)
fi
(2) Un ordre quasi-fort étant un ordre d'intervalles sans 1+3, il vérifie la première implication de (2) (proposition 1.7). Quant à la seconde, il!est clair que si elle n'était pas vérifiée la restriction de O à {x,y,z,t} serait isomorphe à 1+3, ce qui est impossible.(2)
fi
(3) D'après la proposition 1.7, O est un ordre d'intervalles et OI est un ordre fort ; il en est de même de IO (lemme 1.10d). Comme il est clair que l'union de deux relations négativement transitives est négativement transitive, OI«IO est négativement transitive. Pour montrer que cette relation est un ordre fort, il suffit donc de montrer qu'elle est asymétrique. Or, supposons qu'il existe x,y avec x(OI«IO)y et y(OI«IO)x ; OI et IO étant asymétriques, on aurait alors, par exemple, xOIy et yIOx. Ceci implique qu'il existe z et t avec xOz, zIy, yIt et tOx. Ces quatre éléments sont nécessairement différents (par exemple, t ≠ y, car sinon la transitivité de O implique yOz, une contradiction). Mais alors la restriction de O à {y,t, x,z} serait isomorphe à 1+3, ce qui est impossible.(3)
fi
(4) D'après le (lemme 1.10b) et d)), les relations OI et IO sont négativement transitives. Mais comme elles sont contenues dans l'ordre fort OI«IO, elles sont aussi asymétriques et donc des ordres forts. D'après l'implication de (4) par (3) établie à la proposition 1.7, O admet un tableau en escalier (O, L1, L2) où L1 et L2 sont deux ordressont contenus dans l'ordre fort OI«IO, on peut prendre L1 = L2 = L, ordre strictement total
contenant OI«IO. La relation I étant réflexive, on a O Õ OI«IO Õ L. Le tableau (O,L) est donc surdiagonal.
(4)
fi
(1). Puisque O admet un tableau en escalier (O, L), c'est un ordre d'intervalles (proposition 1.7). Soient x,y,z,t avec xOy, yOz (et donc xOz). Ce tableau (O,L) étant surdiagonal, on a O Õ L, donc xLy, yLz et xLz. Puisque LO Õ O et yOz, si on a tLy, on a tOz. De même, puisque OL Õ O et xOy, si yLt, on a xOt. Donc, la restriction de O à {x,y,z,t}ne peut être isomorphe à 1+3, ce qui montre que O est un ordre quasi-fort.
Pour terminer cette section, nous revenons sur la dualité entre les modélisations de la préférence stricte et de la préférence large d'un individu. Cette dualité est une conséquence du résultat élémentaire suivant.
Proposition 1.13
Les ensembles, ordonnés par inclusion, des relations asymétriques et des relations totales définies sur un ensemble X sont deux demi-treillis duaux, par l'application de codualité R
Æ
Rcd .Preuve
Il est évident que l'intersection (respectivement, l'union) de deux relations asymétriques (respectivement, totales) définies sur X est asymétrique (respectivement, totale).L'ensemble des relations asymétriques (respectivement, totales) définies sur X est donc un inf-demi-treillis (respectivement, un sup-demi-inf-demi-treillis). Comme une relation asymétrique R (respectivement totale) est caractérisée par R Õ Rcd (respectivement, R ⊇ Rcd), que de plus
(Rcd)cd = R, et qu’enfin R Õ R' si et seulement si Rcd ⊇ R'cd, on en déduit aisément que
l'application de codualité est un anti-isomorphisme entre ces deux demi-treillis.
Ainsi chaque fois que l'on définit une classe particulière de relations asymétriques, l'application de codualité la transforme en une classe duale de relations totales. La classe duale des ordres forts est celle des préordres totaux. Celle des ordres est la classe des relations totales dont la partie asymétrique est transitive, relations parfois appelées relations
quasi-transitives. Alors que les relations coduales d'un ordre d'intervalles n'ont pas reçues de nom
particulier, celles coduales d'un ordre quasi-fort ont été appelées quasi-ordres ou semiordres (il n'est pas inutile de signaler que le terme anglais de semiorder désigne selon les auteurs un ordre quasi-fort ou un quasi-ordre).
D'autre part la dualité entre deux de ces classes permet de transporter immédiatement tout résultat obtenu sur l'une en un résultat sur l'autre. Ainsi, il est complètement équivalent de modéliser la notion de préférence comme une préférence stricte, c'est-à-dire par un ordre strict, ou comme une préférence large c'est-à-dire par une relation quasi-transitive. Si, en microéconomie, le second choix est plus souvent fait, le choix du premier a au moins deux avantages : d'une part, il est plus conforme au principe de parcimonie (la coduale d'une relation asymétrique comporte beaucoup plus de couples) ; d'autre part, et surtout, il fait relever de la théorie des ensembles ordonnés l'étude des modèles mathématiques de la préférence
Remarque 1.14
Si O est une relation asymétrique et qu'on note R la relation totale coduale de O, on a R = Ocd
= O + I, avec I = Oc«Ocd = R«Rd. Ainsi, si O est un ordre modélisant la préférence stricte,
relation R modélisant la préférence large, c'est-à-dire la relation qui, classiquement, modélise l'indifférence.
6 Compléments
6-1 Compléments historiques et bibliographiques
Les ordres d'intervalles ont une longue histoire qui présente la particularité d'être discontinue. Cette histoire remonte au début du siècle dernier quand, à Cambridge, le jeune mathématicien prodige Norbert Wiener cherche à répondre à une question que lui a posée Bertrand Russel : comment obtenir la notion d'instant de temps (ou de point sur une droite) à partir de la notion de période de temps (ou d'intervalle sur une droite) ? Dans son article de 1914, Wiener définit une relation O de "complete succession" par les deux conditions que O est irréflexive et satisfait OIO ÕO (ce qui est l'une des caractérisations des ordres d'intervalles données à l'exercice 4). Deux papiers ultérieurs de Wiener (dont on trouvera l'essentiel du contenu traduit en notations modernes dans Fishburn et Monjardet,1992) contiennent des développements sur ces ordres. Ils sont motivés par le projet de fonder une théorie valable de la mesure de quantités comme la perception psychologique de la hauteur tonale, pour lesquelles on peut seulement définir une relation de "différence juste perceptible" (jnd) introduite par les psychophysiciens de la fin du 19ème siècle. Dans ce cas, comme l'avait fait observer Poincaré, la relation d'indiscernabilité entre deux quantités n'est plus une équivalence, puisqu'elle n'est pas nécessairement transitive.
Dans les années trente du siècle dernier, des économistes comme Goergescu-Roegen (1936) ou Armstrong (1939) remarquent un phénomène similaire pour les préférences : la relation d'indifférence peut ne pas être transitive. Et, vingt ans plus tard, le souci de construire un modèle de préférence individuelle rendant compte de cette intransitivité de l'indifférence conduit Luce à définir les quasi-ordres (qu'il dénomme "semiorders": Luce,1956). Alors que les papiers de Wiener étaient pratiquement tombés dans l'oubli, les ordres d'intervalles réapparaissent en 1970 dans un article de Fishburn généralisant les "semiorders" de Luce. Ils sont alors définis comme des relations O irréflexives vérifiant la condition que xOy et zOt impliquent xOt ou zOy.
Auparavant, pour un problème de génétique, Benzer avait considéré des "graphes (non orientés) d'intervalles" dont on observa ensuite qu'ils étaient exactement les complémentaires des graphes de comparabilité des ordres d'intervalles (en effet les sommets de ce graphe sont les éléments d'une famille d'intervalles, deux intervalles étant reliés par une arête si leur intersection est non vide).
Depuis, les ordres d'intervalles, les ordres quasi-forts, les graphes ou les hypergraphes d'intervalles, ou encore les graphes d'indifférence (qui sont les complémentaires des graphes de comparabilité des ordres quasi-forts) sont apparus (ou réapparus, car leurs redécouvertes ont été nombreuses) dans de multiples contextes de mathématiques "pures" ou "appliquées" et d'informatique : représentations ensemblistes et numériques de graphes, estimation statistique, sériation et archéologie, théorie de l'utilité en psychologie mathématique et microéconomie, aide à la décision, ordonnancements, classification, logique temporelle... De très nombreux résultats et références concernant ces structures peuvent être trouvé dans les ouvrages de Berge (1970), Golumbic (1980), Mirkin et Rodin (1984), Fishburn (1985), Pirlot et Vincke (1997), Aleskerov et Monjardet (2002) ou encore dans Monjardet (1978, 1988). Citons simplement un résultat intéressant notamment du point de vue de la reconnaissance algorithmique des ordres d'intervalles. Une antichaîne maximale d'un ordre O défini sur un ensemble X est une partie A de X formée d’éléments tous incomparables entre eux et maximale avec cette propriété. Considérons la relation suivante < entre les antichaînes maximales d'un ordre O : A < A' si, pour tout x dans A\A', il existe x' dans A' avec xOx'!; il
est facile de voir que cette relation < est un ordre strict sur l’ensemble les antichaînes maximales. Le résultat est alors qu'un ordre strict est un ordre d'intervalles si et seulement l'ordre < entre ses antichaînes maximales est un ordre strictement total. De plus, le nombre des antichaînes maximales d'un ordre d'intervalles est exactement le nombre de "marches" de son tableau en escalier. Signalons aussi deux références de base pour les aspects algorithmiques concernant ces structures, à savoir les deux synthèses de Möhring (1984, 1989).
La notion de relation de Ferrers a été introduite par Riguet en 1951, le nom de Ferrers étant dû au lien avec le graphe de Ferrers-Sylvester associé à une partition d'un entier. La représentation numérique associée n'est toutefois pas mentionnée et la notion ne suscite guère d'intérêt. Mais près de vingt ans plus tard, Ducamp et Falmagne (1969), motivés par l'étude de "l'échelle de Gutmann" en analyse des questionnaires, définissent la notion correspondante dans le cas d'une relation entre deux ensembles X et Y disjoints (et non nécessairement finis) et donnent le résultat de représentation : il existe deux fonctions f de X dans „ et g de Y dans „ telles que xRy si et seulement si f(x) < g(y). Ce même résultat est obtenu indépendamment par Bouchet (1971,1984) dans son étude des codages des relations binaires. Rebaptisées parfois "biordres", les relations de Ferrers ou leurs généralisations valuées (qui permettent, dans la théorie de la "consistance probabiliste", de modéliser les préférences variables dans le temps d'un sujet) ont fait l'objet de nombreux travaux, notamment à propos de la "dimension Ferrers" d'une relation (cf. par exemple, Monjardet (1976), Cogis, (1982), Ducamp, Doignon et Falmagne (1984) ou Doignon, Monjardet, Roubens et Vincke (1986) ainsi que le livre de Falmagne (1985).
6-2 Compléments mathématiques
Ils portent sur des exemples ou des résultats supplémentaires présentés sous forme d’exercices.
Exercice 1
Soit l'ensemble ordonné (X = {a,b,c,d,e,f,g,h,i, j}, O) dont l'ordre O est donné par la relation de couverture suivante : (a,b) (i.e. a est couvert par b dans O), (c,a),(c,d),(e,g),(g,a),(g,d),(g,f), (h,j),(j,c),(j,e) et (i,g). Représenter le diagramme de cet ensemble ordonné. Calculer les relations IO et OI et en déduire que O est un ordre d'intervalles. Donner le tableau en escalier et des représentations numériques par seuil et par intervalles de cet ordre. Comparer le nombre de "marches" du tableau en escalier de O et le nombre de ses antichaînes maximales (cf. section 6).
Exercice 2
Soit l'ensemble ordonné (X = {a,b,c,d,e,f,g,h,i,j}, O) dont l'ordre O est donné par la relation d e c o u v e r t u r e s u i v a n t e : (d,a),(e,a),(e,b),(e,c),(f,a),(f,b),(f,c),(g,b),(g,c),(h,d),(h,e),(h,f),(i,d),(i,e),(i,f), (h,j),(j,e),(j,g) et (j,f). Répondre aux mêmes questions qu'à l'exercice 1 et, en particulier, déterminer à quelle classe d'ordres appartient l'ordre O.
Exercice 3 (autour des préordres "traces" T1 et T2)
Soit R une relation binaire sur X. Pour x ΠX, on pose d+(x) = |xR| = |{y ΠX : xRy}|, d-(x)
=|Rx| = |{y Œ X : yRx}| et s(x) = d+(x) - d-(x). On définit les relations suivantes sur X : xT1y ¤ xR ⊇ yR ; xT2y ¤ Rx Õ Ry ; T = T1«T2 ;
xT+y ¤ d+(x) ≥ d+(y) ; xT-y ¤ d-(x) ≤ d-(y) ; xTsy ¤ s(x) ≥ s(y)
En décomposant ces relations en leurs parties asymétriques et symétriques, on écrit : T1 = F1 + E1 ; T2 = F2 + E2 ; T+ = F+ + E+ ; T- = F- + E- ; T= F+ E ; Ts = Fs+ Es
Montrer les relations suivantes :
a) T1 = (RRcd)cd Õ T+ ; T2 = (RcdR)cd Õ T- ; T Õ Ts.
b) F1 = (RRcd)cd«(RRcd) ; F2 = (RcdR)cd«(RcdR) ; F = (F1«T2)»(F2«T1).
Dans le cas où R est un ordre strict O et où I = Ocd«Oc, montrer les relations suivantes :
T1 = (OI)cd ; F1 = (OI)cd« OI ; T2 = (IO)cd ; F2 = (IO)cd«IO ; T = (OI)cd«(IO)cd =
(OI»IO)cd ; F = (OI«IO) « (OI«IO)cd ; E = (OI)c«(OI)cd«(IO)c«(IO)cd ; O = OE»EO ;
xEy ¤ [xO = yO et Ox = Oy] ¤ xI = yI.
Exercice 4 (multiples caractérisations des ordres d'intervalles)
Soit O un ordre strict sur un ensemble X.
Montrer que les propriétés suivantes sont équivalentes : a) O est un ordre d'intervalles,
b) OIO Õ O,
c) OI est sans circuit, d) OI est asymétrique, e) OI = F1,
f) T1 est un préordre total,
g) T1 = T+.
Montrer que dans les caractérisations b), c), f) et g) , on peut ne supposer que O est une relation irréflexive.
Donner d'autres caractérisations des ordres d'intervalles utilisant IO, T2 ou T-.
Exercice 5 (multiples caractérisations des ordres quasi-forts)
Soit O un ordre strict sur un ensemble X.
Montrer que les propriétés suivantes sont équivalentes : a) O est un ordre quasi-fort,
b) OIO Õ O et O2I Õ O, c) OI»IO est sans circuit, d) OI»IO est asymétrique, e) OI»IO = F,
f) T= OI»IO»E,
g) Test un préordre total, h) T = Ts.
g) O est un ordre d'intervalles vérifiant F1«(F2)d =
ø.
Montrer que dans ce cas , on a aussi T = T+«T-.
Montrer que dans les caractérisations b) e) et g), on peut ne supposer que O est une relation irréflexive.
Exercice 6 (Vers la preuve du théorème 1.5)
Soit O une relation binaire asymétrique sur un ensemble X et I = Ocd«Oc.
1) Montrer que O est un ordre d'intervalles si et seulement si tout circuit de la relation Ocd (= O + I) contient au moins deux couples consécutifs de la relation I.
2) Montrer que O est un ordre quasi-fort si et seulement si la relation Ocd est totale et tout
circuit de longueur 3 ou 4 de cette relation contient strictement plus de couples de la relation I que de couples de la relation O.
N.B. Cette caractérisation des ordres quasi-forts, utilisée avec un résultat sur l'existence d'une fonction potentiel pour une relation valuée, permet de donner une preuve du théorème 1.5 de
représentation numérique à seuil constant des ordres quasi-forts (cf. Pirlot et Vincke, 1997, ou Aleskerov et Monjardet, 2002)
Exercice 7 (les "S-ordres")
Soit O une relation binaire sur un ensemble X. On suppose que O est irréflexive et vérifie la condition (S) suivante : pour tous x,y,z,t Œ X, xOy et yOz
fi
xOt ou tOza) Montrer que O est une relation d'ordre strict. Un tel ordre est appelé un S-ordre.
b) Montrer qu'un ordre strict O est un S-ordre si et seulement si il n'existe pas x,y,z,t Œ X avec xOy, yOz, xIt, yIt et zIt (où I = Ocd«Oc).
Montrer que pour O relation binaire irréflexive sur un ensemble X, les trois conditions suivantes sont équivalentes :
a) O est un S-ordre.
b) pour tous x,y Œ X, xO ⊇ yO ou Oy Õ Ox
c) pour tous x,y Œ X, xO = yO, ou Ox = Oy, ou xO … yO et Ox à Oy, ou yO … xO et Oy à Ox.
NB. On observera qu'un ordre quasi-fort est un ordre d'intervalles qui est également un S-ordre. On trouvera une étude des S-ordres dans Monjardet (1978) et Doble, Doignon, Falmagne et Fishburn (2001).
REFERENCES
Aleskerov F.T. and Monjardet (2002) Utility Maximisation, Choice and Preference, Springer Verlag (Studies in Economic Theory,Volume 16).
W. Armstrong (1939) The dereminateness of the utility function, Economic Journal, 49, 453-467.
Berge C. (1970) Graphes et hypergraphes, Dunod, Paris.
A. Bouchet (1971) Etude combinatoire des ordonnés finis ; applications, thèse de doctorat d'état, Grenoble.
A. Bouchet (1984) Codages et dimensions de relations binaires, in Orders : Descriptions and
Roles, (éds. M. Pouzet, D. Richard) Annals of Discr. Math. 23, pp.387-396.
O. Cogis (1982) On the Ferrers dimension of a digraph, Discr. Math. 38, 47-52.
J.P. Doignon, B. Monjardet, M. Roubens et Ph. Vincke (1986) Biorders families, valued relations and preference modelling, J. Math. Psych. 30, 435-480.
A. Ducamp, J.C. Falmagne (1969) Composite measurement, J. Math. Psychol.6(3), 359-390. A. Ducamp, J.P. Doignon and J.C. Falmagne (1984) On realizable biorders and the biorder dimension of a relation, J. Math. Psychol.28(1), 73-109.
C.W. Doble, J.P. Doignon, J.C. Falmagne and P.C. Fishburn (2001) Almost connected orders,
Order 18, 295-311.
J.C. Falmagne (1985) Elements of psychophysical theory, Oxford University Press, Oxford. P.C. Fishburn (1985) Interval orders and interval graphs. A study of partially ordered sets,
Wiley, New York.
P.C. Fishburn and B. Monjardet (1992) Norbert Wiener on the theory of measurement, 1914, 1915, 1921, J. Math. Psychology, 36, 165-184.
Goergescu-Roegen, N. (1936) The pure theory of consumer's behavior, Quaterly Journal of
Economics, 50, 545-593.
M.C. Golumbic (1980) Algorithmic graph theory and perfect graphs, Academic Press.
R.D. Luce, (1956) Semiorders and theory of utility discrimination, Econometrica, 24(2), 178-191.
R.H. Möhring (1984) Algorithmic aspects of comparability graphs and interval graphs, in
Graphs and orders (ed. I.Rival), D.Reidel, Dordrecht, pp. 41-101.
R.H. Möhring (1989) Computationally tractable classes of ordered sets, in Algorithms and
orders (ed. I.Rival), D.Reidel, Dordrecht, pp.283-306.
B. Monjardet (1978) Axiomatiques et propriétés des quasi-ordres. Math. Sci. hum. 63, 51-82. B. Monjardet (1988) Intervals,intervals, Order,5,211-219.
M. Pirlot M et Ph.Vincke (1997) Semiorders. Properties, Representations, Applications, Kluwer, Dordrecht.
Riguet, J., (1951) Les relations de Ferrers, CRAS, 232, Paris.