Book Calculus Unllimited pdf - Web Education

Jerrold Marsden

University ofCalifornia, Berkeley

Alan Weinstein

University ofCalifornia, Berkeley

The Benjamin/Cummings Publishing Company, Inc.

Menlo Park. California - Reading, Massachusetts

Sponsoring Editor: Susan A. Newman Production Editor: Madeleine S. Dreyfack

To Alison, Christopher, Asha, and the future of calculus.

Copyright © 1981 by The Benjamin/Cummings Publishing Company, Inc. Philippines copyright© 1981 by The Benjamin/Cummings Publishing Company, Inc.

All rights reserved. No part of this pUblication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printedin the United States of America. Published simultaneously in Canada.

Library of Congress Cataloging in Publication Data

Marsden, Jerrold E. Calculus unlimited.

Includes index.

1. Calculus. I. Weinstein, Alan, 1943- joint author. II. Title.

QA303.M3374 515 80-24446 ISBN 0-8053-6932·5

ABCDEFGHIJ-AL-8321 0

The Benjamin/Cummings Publishing Company, Inc

2727 Sand Hill Road

.Preface

Purpose

This book is intended to supplement our text, Calculus (Benjamin! Cummings, 1980), or virtually any other calculus text (see page vii, How To Use This Book With Your Calculus Text). As the title Calculus Unlimited implies, this text presents an alternative treatment of calculus using the method of exhaustion for the derivative and futegral in place of limits.

With

the aid of this method, a definition of the derivative may be introduced in the first lecture of a calculus course for students who are familiar with functions and graphs.

Approach

Assuming an intuitive understanding of real numbers, we begin in Chapter 1 with the defmition of the derivative. The axioms for real numbers are pre-sented only when needed, in the discussion of continuity. Apart from this, the development is rigorous and contains complete proofs.

As you will note, this text has a more geometric flavor than the usual analytic treatment of calculus. For example, our definition of completeness is in terms of convexity rather than least upper bounds, and Dedekind cuts are replaced by the notion of a transition point.

Who Should Use This Book

This book is for calculus instructors and students interested in trying an alternative to limits. The prerequisites are a knowledge of functions, graphs, high school algebra and trigonometry.

How To Use This Book

Because the "learning-by-doing" technique introduced in Calculus has proved to be successful, we have adapted the same format for this book. The solutions to "Solved Exercises" are provided at the back of the book; however readers are encouraged to try solving each example before looking up the solution.

vi PREFACE

The Origin Of The Def"mition

or

The Derivative

Several years ago while reading Geometry and the Imagination, by Hilbert and Cohn-Vossen (Chelsea, 1952, p. 176), we noticed a defmition of the circle of curvature for a plane curve C. No calculus, as such, was used in this defmition. This suggested that the same concept could be used to defIne the tangent line and thus serve as a limit-free foundation for the differential calculus. We intro-duced this new defmition of the derivative into our class notes and developed it in our calculus classes for several years.Asfar as we know, the definition has not appeared elsewhere. If our presumption of originality is ill-founded, we welcome your comments.

Jerrold Marsden

Alan Weinstein

Berkeley, CA

How To Use This Book

With Your Calculus Text

There are two ways to use this book:

1. Itcan be used to take a second look at· calculus from a fresh point of view after completion of a standard course.

2. It can be used simultaneously with your standard calculus text ·as a supplement. Since tms book is theory oriented, it is meant for better students, although Chapter 1 is designed to be accessible toallstudents. The table below shows the chapters of this book that can be used to supplement sectionsinsome of the standard calculus texts.

Corresponding Chapters in Standard Texts' Chapters

in this Ellis/ Grossman Leithold Marsden/ Protterl Purcell Salas/ Shenk Swokowski Thomasl

Book Gulick Weinstein Morrey Hille Finney

1 3.2 2.10 3.3 R-3 4.3 4.3 3.1 3.1 3.::: 1.8 2 3.2 2.10 3.3 1.1 4.3 4.3 3.1 3.2 3.2 1.9 3 3.1 3.2 3.5 1.3 5.1 5.2 3.2 3.4 3.3 2.3 4 1.1 1.2 1.1 R-l A-4 1.3 1.5 U J.l 1.2 5 2.5 2.4/10.4 2.5/5.1 2.3 6.5 6.3 2.6(App. B 2.7/4.2 2.5/4.4 2.11(3.1 0 4.0 3.~ ~.2-~.~ 2.4 0.4 0.12 4.7 4.3 4.5 3.4 7 4.2 2.4/10.6 4.7 3.3 6.2 6.2 4.1 4.12 4.3 3.8 8 8.2 3.7(10.7 9.3/3.6 5.2 9.4/5.2 5.11(10.2 3.7 4.6 8.7 2.4 9 3.3 7.5 10.2 6.2 9.2 10.7 7.1 3.8 9.2 2.10 10 S4 63 91-95 7.2 99 103 6.4 7.5 8.4 6.8 II 5.3 4.3 7.3 4.1 7.3 8.3 5.2 5.1 5.2 4.8 12 5.4 4.5 7.6 4.2 7.5 8.4 5.3 5.2 5.5 4.8

13 6.5 10.8 3.4 12.2 4.6 8.4 App.B App. Ch. 5 App.lI Ch.4/Summary • See following list of references.

• R. Ellis and D. Gulick, Calculus with Analytic Geometry Harcourt, Brace, Jovanovich (1978)

• S. Grossman, Calculus Academic Press (1977)

• L. Leithold, Calculus, 3rd Ed., Harper and Row (1976)

• J. Marsden and A. Weinstein, Calculus, Benjamin/Cummings (1980) • M. Protter and C. B. Morrey, Calculus, 4th Ed., Addison-Wesley (1980) • E. J. Purcell Calculus with Analytic Geometry, 3rd Ed., Prentice-Hall

(1978)

• S. L. Salas and E. Hille, Calculus. One and Several Variables, 3rd Ed., Wiley (1978)

viii HOW TO USE THIS BOOK WITH YOUR CALCULUS TEXT

• A. Shenk,Calculus, Goodyear (1977)

• E.

W. Swokowski,

Calculus with Analytic Geometry, Second Edition, Prindle Weber and Schmidt, (1980)

• G. B. Thomas and R. L. Finney, Calculus and Analytic Geometry, 5th Ed., Addison-Wesley (1979)

Preview For The Instructor

This preview is intended for those who already know calculus. Others should proceed directly to Chapter 1.

The method of exhaustion of Eudoxus and Archimedes may be sum-marized as follows: Having defined and computed areas of polygons, one deter-mines the area of a curvilinear figureF using the principle that wheneverPI and P2 are polygons such that PI is inside F andF isinsideP2 , then Area (Pt)~ Area (F)~Area

(P

2 ).This approach appears. in modern mathematics in the form of Dedekind cuts, inner and outer measure, and lower and upper sums for integrals.

To apply the method of exhaustion to differentiation, we replace the relation of inclusion between figures by the relation ofovertaking defined as follows.

Definition Let / andgbe real-valued functions with domains contained in IR, andx

°

a real number. We say that / overtakesgat x

°

if there is an open intervalI containingXo such that

O. x EI andx=1=Xoimpliesx is in the domain of

f

andg.

1. x EI andx

<

Xoimplies/(x) <g(x). 2. x EIandx

>

Xo implies/ex)

>

g(x).

Given a function

f

and a numberXo in its domain, we may compare fwith the linear functions1_m(x)= f(xo)

+

rn(x - xo).

Definition Let / be a function defined in an open interval containingxo. Suppose that there is a numberrnosuch that:

1. rn

<

rnoimpliesfovertakes1_m atXo. 2. rn

>

rnoimplies1_m overtakes / atXo.

Then we say thatf is differentiable atXo, and thatrnois the derivativeof /atxo.

The following notion of transition occurs implicitly in both of the pre-ceding defmitions.

x PREVIEW FOR THE INSTRUCTOR

Definition LetA andBbe sets of real numbers, andXoa real number. We

say that Xo is a transition point from A to Bif there is an open intervalI containingXosuch that:

1. xElandx<xoimpliesxEA andx¢=B. 2. x Elandx >xoimpliesx EB andx¢A.

The preceding defInition of the derivative is equivalent to the usual limit approach, as we shall prove in Chapter 13. However, it is c·onceptually quite different, and for students who wish a logically complete defInition of the deri-vative, we believe that it is simpler and geometrically appealing.

Both Euclid and Archimedes probably employed the following defInition of tangent: "the tangent line touches the curve, and inthe space between the line and curve, no other straight line can be interposed".* This is in fact, a some-what loose way of phrasing the defInition of the derivative we have given here. Why, then, did Fermat, Newton, and I.eibniz change the emphasis from the method of exhaustion to the method of limits? The reason must lie in the computational power of limits, which enabled Newton and Leibniz to establish the rilles of calcillus, in spite of the fact that limits were not clearly understood for at least another century. However, there is nothing to prevent one from carrying out the same program using the method of exhaustion. We shall do so in this book.

In teaching by this approach, one may begin by defming transition points (with examples like birth, freezing, and sunset) and then go on to define over-taking and the derivative. (One must emphasize the fact that, in the defmition of a transition point, nothing is said about the numberXo itself.) The notion of

transition point occurs again in graphing, when we consider turning points and inflection points, so the computational techniques needed to determine over-taking are put to good use later.

Since the defInition of the derivative is so close to that of the integral (a transition point between lower and upper sums), the treatment of the funda-mental theorem of calculus becomes very simple.

For those courses in which the completeness of the real numbers is empha-sized, the following version of the completeness axiom is especially well suited tothe transitiollsapproach.

*c.

Boyer, The History of the Calculus and Its Conceptual Development,Dover (1959), p.57.

Definition A setA of real numbers is convex if, wheneverx andy are in A andx <z

<y,

then z is inA.

Compleleness Axiom Every convex set of real numbers is an interval.

With this axiom, the proofs of "hard" properties of continuous functions, such as their boundedness on closed intervals and their integrability, are within the reach of most fIrst-year students.

Although the transition-point approach has some computational disadvan-tages, it does enable one to present a logically complete defInition, with geome-tric and physical motivation at the end of only one hour of lecture. (Chapter 1is such a lecture.) Coupled with an early intuitive approach to limits for their com· putational power, this method allows one to delay rigorous limits until later in the course when students are ready for them, and when they are really needed for topics like L'Hopital's rille, improper integrals, and infinite senes.

limits are so importantinmathematics that they cannot be ignored in any calculus course.It is tempting to introduce them early because they are simple to use in calcillations, but the subtlety of the limit concept often causes beginning students to feel uneasy about the foundations of calcillus. Transitions, in contrast, provide conceptually simple definitions of the derivative and inte-gral, but they are quite complicated to use in calculations. Fortunately, one does not need to do many calculations directly from the definition. The great "machine" of Newton and Leibniz enables us to calculate derivatives by a proce-dure which is independent of the particular form of the defmition being used.

Although our reasons for using the method of transitions stem mostly from trying to make calcillus easier to learn, we have another reason as well. Many mathematicians have complained that calculus gives a distorted picture of modem mathematics, with total emphasis on "analysis." We hope that the use of transitionswillpartly answer this complaint.Itgives a better balance between the various disciplines of mathematics and gives the student a more accurate picture of what modem mathematics is all about.

We have mentioned that the concept of transition is importantinits own right, and we gave some nonmathematical examples involving sudden changes. Although the notion of transition is built into differential and integral calculus, the classical techniques of calculus (limits. the rilles of calculus. and so on) have proven insufficient as a tool for studying many discontinuous phenomena. Such phenomena are. of common occurrence in biology and the social sciences and include, for example, revolutions, birth, and death. They may all be described as transitions.

xii PREVIEW FOR THE INSTRUCTOR

Contemporary mathematicians have been paying more and more attention to discontinuous phenomena and a geometric or qualitative description of nature. In biology and sociology this aspect is an important complement to a quantitative analysis. OUf emphasis on transitions is inspired partly by the belief

that this concept

will

play an increasingly important role in the applications of mathematics.

*

*Of particular interest in this direction is the catastrophe theory introduced by the French

mathematician Rene Thornin his book Structural Btability and Morphogenesis (Benjamin, 1975). Thorn's book is somewhat philosophical in nature, but more concrete applications of catastrophe theory can be foundinthe books: E. C. Zeeman, Catastrophe Theory: Selected

Papers 1972-1977 (Addison-Wesley, 1977); T. Poston and I. Stewart, Catastrophe Theory

and its Applications (Fearon-Pitman, 1978). The applications to biological and social

sciences have received some rather sharp criticism; the main critical paper, by H. J. Sussmann and R. S. Zahler, is "Catastrophe theory as applied to the social and biological sciences: a critique," Synthese 37 (1978),117-216. A general account of the controversy is giveninA. Woodcock and M. Davis, Catastrophe Theory (Dutton, 1978).

Contents

Preface

v

How to use this book with your calculus text Vll

Preview for the instructor

ix

1

TIlE DERIVATIVE

1

2

TRANSmONSANDDERIVATIVES

16

3

ALGEBRAIC RULES FOR DIFFERENTIATION

31

4

TIlE REAL NUMBERS

45

5

CONTINUITY

54

6

GRAPIDNG

74

7

TIlE MEAN VALUE THEOREM

93

8

INVERSE FUNCTIONS AND THE CHAIN RULE

100

9

TIlE TRIGONOMETRIC FUNCTIONS

114

10

TIlE EXPONENTIAL AND LOGARITHM

FUNCTIONS

123

11

THEINTEGRAL

147

12

TIlE FUNDAMENTAL THEOREM OF CALCULUS

171

13

LIMITS AND THE FOUNDATIONS OF CALCULUS

180

Appendix:

solutions

194

Index

233

1

The Derivative

This chapter gives a complete definition of the derivative assuming a knowledge of high-school algebra, including inequalities, functions, and graphs. The next chapter will reformulate the defInition in different language, and in Chapter 13 wewillprove that it is equivalent to the usual definition in terms of limits.

The definition uses the concept of change of sign, so we begin with this.

Change of Sign

A function is said to change sign when its graph crosses from one side of the x axis to the other. We can defme this concept precisely as follows.

Definition Let

f

be afunction and Xo a real number. We say that

f

changes sign from negative to positive at Xo if there is

an

open interval (a,b) containing Xo such that

f

is defmed on (a,b) (except possibly at xo)and

j{x)

<0

ifa<x<xo and

f(x)

>

0 if Xo

<

x

<

b

Similarly, we say that f changes sign from positive to negative at Xo if there is an open interval (a,b) containing Xo such that

f

is defined on (a,b)(except possibly atxo) and

[(x)

>

0 ifa <x <xo and

f(x)

<0

ifxo<x<b

Notice that the interval (a,b) may have to be chosen small, since a func-tion which changes sign from negative to positive may later change back from positive to negative (see Fig. I-I).

v

fchanges from negative to positive here

bl

fchanges from positive to negative here x

Fig.1-1 Changeofsign.

Worked Example 1 Where does[(x) =x2

- 5x

+

6 change sign?

'!\olution We factorI and write I(x) = (x - 3)(x - 2). The function I changes sign whenever one of its factors does. This occurs at

x

= 2 and

x

= 3. The fac-tors have opposite signs for

x

between 2 and 3, and the same sign otherwise, so

f

changes from positive to negative at x = 2 and from negative to positive at

X

=

3. (See Fig.

1-2).

v

y = x2- 5x+ 6

x

Fig. 1-2 y

=

x2

- 5x+6 changes sign atx = 2 and

x=3.

We can compare two functions, [andg, by looking at the sign changes of the difference f(x) - g(x). The following example illustrates the idea.

Worked Example2 LetfVc)

=

tx3- 1 andg(x)

=

X2 - 1.

(a) Find the sign changes of f(x) - g(x).

(b) Sketch the graphs of[andgon the same set of axes.

(c) Discuss the relation between the results of parts (a) and (b).

Solution

(a) [(x) - g(x)

=

tx3

- 1 - (x2 - 1)= tx3 - x2 = tx2(x - 2). Since the factor x appears twice, there is no change of sign at x = 0(x2 is positive both for x

<

0 and for x> 0). There is a change of sign from negative to positive at x= 2.

CHANGE OF SIGN 3 fabove 9 here /" graphs ' / cross here ~fbelow 9 here x

~

Graphs touch here

Fig.1-3 f - 9changes sign when the graphs of f

and9cross.

(b) See Fig. 1-3.

(c) Since [(x) - g(x) changes sign from negative to positive at x = 2, we can say:

If x is near 2 and x

<

2, then f(x) - g(x)

<

0; that is,f(x) <g(x). and

Ifx is near 2 and x> 2, thenf(x) - g(x)

>

0; that is,f(x)

>

g(x). Thus the graph of [must cross the graph of g atx = 2, passing from below to above it as

x

passes 2.

Solved Exercises*

1. Iff(x)is a polynomial andf(xo)= O,must[necessarily change sign atxo? 2. For which positive integers n does[(x)

=

xrl change sign at zero?

3. If.rl

'*

'2,describe the sign change at'1 of f(x)= (x - '1)(X - '2)'

Exercises

1. Find the sign changes of each of the follOWing functions: (a) [(x)= 2x - 1

(c) f(x) = x2

*Solutions appear in the Appendix.

(b) f(x) = x2

- 1

2. Describe the change of sign at x =

°

of the function f(x) = mx for m = -2, 0,2.

3. Describe the change of sign at x =

°

of the function f(x) = mx - x2 for

1 1

m=-l,-2,0,2,1.

4. Let f(t) denote the angle of the sun above the horizon at time t. When does f(t) change sign?

Estimating Velocities

If the position of an object moving cU.ung a line changes linearly with time, the object is said to be in unifonn motion, and the rate of change of position with respect to time is called the velocity. The velocity of a uniformly moving object is a fixed number, independent of time. Most of the motion we observe in nature is not uniform, but we still feel that there is a quantity which expresses the rate of movement at any instant of time. This quantity, which we may call the instantaneous velocity, will depend on the time.

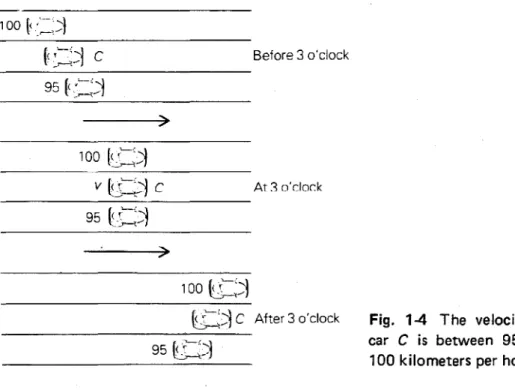
To illustrate how instantaneous velocity might be estimated, let us suppose that we are looking down upon a car C which is moving along the middle lane of a three-lane, one-way road. Without assuming that the motion of the car is uni-form, we wish to estimate the velocity Voof the car at exactly 3 o'clock.

100[<:~-~.::l 100

rS:l

v~ic 100

{i:.:l

Before 3 o'clock At 3 o'c1od

t:G::::i

C After 3 o'clock

---~---95U:~

Fig. 1-4 The velocity of car C is between 95 and 100 kilometers per hour.

ESTIMATING VELOCITIES 5

Suppose that we have the following information (see Fig. 1-4): A car

which was moving uniformly with velocity 95 kilometers per hour was passed by car Cat 30'clock, and a car which was moving uniformlywithvelocity 100

kilo-meters per hour passed car Cat 3 o'clock.

We conclude thatVo was at least 95 kilometers per hour and at most 100 kilometers per hour. This estimate of the velocity could be improved if we were to compare carxwith more "test cars."

In

general, let the variabley represent distance along a road (measured in kilometers from some reference point) and let

x

represent time (in hours from some reference moment). Suppose that the position of two cars travelingin.the positive direction is represented by functions flex) and fz(x). Then car 1 passes car 2 at time Xo if the function/l(x) - /2(x),which represents the ''lead'' of car lover car 2, changes sign from negative to positive at xo. (See Fig. 1-5.) When this happens, we expect car 1 to have a higher velocity than car 2 at time

xo.

y f1(x) - f2(x) positive here f1(x) - f2(x) negative here xo x Fig. 1-5

'1 - '2

changes sign from negative to posi-tive atxo.

Since the graph representing uniform motion with velocity v is a straight line with slope v, we could estimate the velocity of a car whose motion is nonuniform by seeing how the graph of the function giving its position crosses straight lines with various slopes.

Worked Example 3 Suppose that a moving object is at position y = I(x) =

tx

2

at timex.Show that its velocity atXo = 1 is at least

t.

Solution We use a "test object" whose velocity isv =

t

and whose position at time

x

is

tx.

When

x

=

Xo

= 1, both objects are aty

=

t.

When 0

<x

<

1, we have

x

2

<

x,

so

tx

2

<

tx;

when

x>

1, we have

tx

2

>

tx.

Itfollows that the difference

tx

2 -

tx

changes sign from negative to positive at 1, so the velocity

of our moving object is at least

t

(see Fig. 1-6).

Solved Exercise

4. Show that the velocity at

Xo

=

I of the object in Worked Example 3 is at most 2.

y = position 1 y= -x2 2 1 y=-x

2 Fig. 1-6 The graph ofy =

TX

is above that of y

=

x= time

TX

2 when 0<x

<

1 and is

below whenx

>

1.

Exercise

5. How does the velocity atXo

=

1 of the object in Worked Example 3

com-pare with

}?

With

t?

Definition of the Derivative

While keeping the idea of motion and velocity in mind, we will continue our dis-cussion simply in terms of functions and their graphs. Recall that the line through (xo,Yo) with slope m has the equationy - Yo = m(x - xo). Solving for y in terms ofx,we fmd that this line is the graph of the linear functionlex)= Yo

+

m(x - xo). We can estimate the "slope" of a given function I(x) atXoby

comparing I(x) and lex), Le. by looking at the sign changes atXo of I(x)

-lex)

=

I(x) - [f(xo)

+

m(x - xo)] for various values of m. Here is a precise formulation.

Definition Let f be a function whose domain contains an open interval about xo. We say that the number mo is the derivative of fat xo, pro-vided that:

1. For everym

<

mo,the function [(x) - [[(xo)

+

m(x -xo)]

changes sign from negative to positive atxo. 2. For everym

>

mo,the function

[(x) - [[(xo)

+

m(x -xo)]

DEFINITION OF THE DERIVATIVE 7

If such l1 number mo exists, we say thatf is diffen:ntiablc atxo, and we

write mo = f'(xo). If

f

is differentiable at each point of its domain, we just say thatf is differentiable. The process offmding the derivative of a function is calleddifferentiation.

Geometrically, the definition says that lines through(xo,/(xo)) with slope less than

f'

(xo) cross the graph of

f

from above to below, while lines with slope greaterthanf'(xo) cross from below to above. (See Fig. 1-7.)

y= f(xl

x

y = f(xo) +m, (x - xo); slopem1 < mo

Fig. '-7 Lines with slope different fromrnocross the curve.

Given

t

andxo, the number t'(xo) is uniquely detennined ifit exists. That is, at most one number satisfies the definition. Suppose that mo: and

m

_{o both} satisfied the definition, and mo

*

rno; say mo

<

mo.

Let m = (mo +mo)/2, so

mo

<

m

<

mo. By condition 1 for rno'/(x) - [f(xo)

+

m(x - xo)] changes sign from negative to positive atxo, and by condition 2for mo, it changes sign from positive to negative atxo. But it can't do both! Therefore mo

=

mo.

The line through (xo,/(xo)), whose slope is exactly !'(xQ) -is-phlched, together with the graph of

t,

between the "downcrossing" lines with slope less than !'(xo) and the "upcrossing" lines with slope greater than f'(xo). It is the line with slope['(xo), then, which must be tangent to the graph of fat (xo.Yo).

We may take this as ourdefinition of tangency. (See Fig. 1-8.)

y Line with slope>f' _{(x o)} Xo Line with slope< f' (x_o) x

Fig. '-8 The slope of the tangent line is the deriva-tive.

Definition Suppose that the function [is differentiable at Xo. The line y =f(xo)

+

['(xo)(x -xo) through (xo,f(xo» with slope['(xo) is called

thetangent line to the graph0[[at (x o,f(xo».

Following this defmition, we sometimes refer

to['(xo)

as theslope o[the curvey = [(x) at the point (xo,f(xo».Notethat the defmitions do not say

any-thing about how (or even whether) the tangent line itself crossesthegraph of a

function. (See Problem 7 at the end of this chapter.)

Recalling the discussion in which we estimated the velocity of a car by seeing which cars it passed, we can now give a mathematical defmition of velocity.

Definition Let y = [(x) represent the position at time x of a moving object.

If

f

is differentiable at xo, the number ['(xo) is called the (instan-taneous)velocity of the object at the timeXo.

More generally, we callf'(xo) the rate Of change ofy with respect tox at xo·

Worked Example 4 Find the derivativeof[(x)= x2atXo = 3. Whatis the

equa-tion of the tangent line to the parabolay = x2_{at the point (3, 9)?}

Solution According to the definition of the derivative -with[(x)= x2, X0= 3,

and[(xc)

=

9-we must investigate the sign change at3, for various values of m, of [(x) - [((xo)

+

m(x -xo)] = x 2 - [9

+

m(x - 3)] = x2 - 9 - m(x - 3) = (x+3)(x - 3) - m(x - 3) = (x - 3)(x+3 - m)

According to Solved Exercise 3, with71 = 3 and71. =m - 3, the sign change is:

1. From negative to positive ifm - 3

<

3; that is,m

<

6. 2. From positive to negativeif 3

<

m -

3;that is,

m

>

6.

We see that the number mo

=

6 fits the conditions in the defmition of the derivative, so ['(3)

=

6. The equation of the tangent line at (3,9) is therefore

DEFINITION OF THE DERIVATIVE 9 y

123

Solved Exercises

x Fig. 1-9 The equation of

the line tangent to y = x2 atXo = 3 isy = 6x - 9.

5. Letf(x)=x3

_What isf'(O)? What is the tangent line at (0, O)?

6. Let [be a function for which we know thatf(3)

=

2andf'(3)=

{I"i

Find they intercept of the line which is tangent to the graph of

fat

(3,2).

{

X ifx~O .

7. Let f(x)

=

Ixl

=

-x ifx

<

0 (the absolute value functIOn). Show by a geometric argument that [is not differentiable at zero.

8. The position of a moving object at time

x

is

x

2

•What is the velocity of the object when

x

=

3?

Exercises

6. Find the derivative of[(x)

=

x2 _at

x

=

4. What is the equation of the tan-gent line to the parabolay

=

x

2

at (4, 16)? 7. Iff(x) = x4•what is

f'

(O)?

y

x

y=((xl Fig. 1-10 Where ;s f

8. The position at time x of a moving object is x3

• What is the velocity at

x=O?

9. For which value of Xo does the function in Fig. 1-10 fail to be differentiable?

The Derivative as a Function

The preceding examples show how derivatives may be calculated directly from the defInition. Usually, we will not use this cumbersome method; instead, we will use differentiation rnles. These rules. once derived. enable us to differentiate many functions quite simply. In this section, we will content ourselves with deriving the rules for differentiating linear and quadratic functions. General rules will be introduced in Chapter 3.

The following theorem will enable us to fmd the tangent line to any para-bola at any point.

Theorem 1 Quadratic Function Rule. Let f(x) = ax2

+

bx

+

c, where a, b, and c are constants, and let Xo be any real number. Then [is differentiable at xo, and ['(xo) = 2ax_o

+

b.

Proof We must investigate the sign changes at Xo of the function

f(x) - [f(xo)+m(x - xo)]

=ax2

+

bx

+

c - [ax~

+

bxo

+

c

+

m(x - xo)]

= a(x2 - x~)+b(x - xo) - m(x - xo)

= (x -xo)[a(x

+

xo)

+

b

-m]

The factor [a(x

+

xo) + b - m] is a (possibly constant) linear function whose value at x = Xo is a(xo

+

xo) + b - m = 2ax_o

+

b -

m.

If m

<

2ax_o

+

b, this factor is positive at x

=

xo,and being a linear function it is also positive when x is near xo. Thus the product of [a(x+xo)

+

b -

m]

with (x - xo) changes sign from negative to positive at xo.1f m

>

2ax_o

+

b, then the factor [a(x +xo) + b - m] is negative when x is near xo, so its product with (x - xo) changes sign from positive to negative at xo.

Thus the number mo

=

2ax_o

+

bsatisfies the definition of the deriv-ative, and so ['(xo) = 2ax_o

+

b.

THE DERIVATIVE AS A FUNCTION 11

Solution Applying the quadratic. function rule with a= 3, b = 2, c= -1, and

Xo= -2,we findf'(---':2)= 2(3)(-2)+2= -10.

We can use the quadratic function rule to obtain quickly a fact which may be known to you from analytic geometry.

Worked Example 6 Suppose that a

*'

O. At which point does the parabolay=

ax2

+

bx

+

c have a horizontal tangent line?

Solution The slope of the tangent line through the point (xo,ax~

+

bxo

+

c) is 2axo

+

b. This line is horizontal when its slope is zero; that is, when 2axo

+

b

=

0,or Xo

=

-b/2a. The y value here is a(-b/2a?

+

b(-b/2a)

+

c

=

b2/4a_ b2

/2a

+

c= -(b2/4a)

+

c. The point (-b/2a, _b2

/4a

+

c) is called the vertex of the parabolay

=

ax2

₊

_bx

₊

_c.

In Theorem 1 we did not require that a::f= O.Whena= 0, the function f(x) = ax2

₊

_bx

₊

_c

_{is linear, so we have the following corollary:}

Coro/Iory Linear Function Rule. If f(x) = bx + c, and Xo is. any real number, then ['(xc) = b.

In particular, i[ f(x) = c, a constant function, then ['(xo) = 0 for allxo.

For instance,if[(x)

=

3x+4, then ['(xo)

=

3 for anyxo~ifg(x)

=

4, then g'(xo)= 0 for anyxo.

This corollary tells us that the rate of change of a linear function is just the slope of its graph. Note that it does not depend on Xo: the rate of change of a linear function isconstant. For a general quadratic function, though, the deriva-tive ['(xo) does depend upon the pointXo at which the derivative is taken. In fact, we can considerf' as a new function; writing the letter x instead of xo, we have['(x)= 2ax+b.

Definition Let f be any function. We define the function

1"',

with domain equal to the set of points at which [is differentiable, by setting

1"'

(x) equal to the derivative of[ atx. The function f' (x) is simply called the derivative off(x).

Worked Example 7 What is the derivative of [(x)= 3xz - 2x

+

I?

Writing X instead ofxo, we fmd that the derivative off(x) = 3x2 - 2x + 1 is f'(x) = 6x -2.

Remark When we are dealing with functions given by specific formulas, we often omit the function names. For example, we could state the result of Worked Example 7 as "the derivative of3x2 _{- 2x+1 is6x - 2."}

Since the derivative of a function [is another function [' , we can go on to differentiate j' again. The result is yet another function, called the second derivative of[and denoted by [".

Worked Example8 Find the second derivative of [(x)

=

3x2

- 2x+1.

Solution We must differentiate f'(x) = 6x - 2. This is a linear function;

applying the formula for the derivative of a linear function, we fmd["(x)= 6. The second derivative of 3x2 - 2x+1 is thus the constant function whose value

for every x is equal to6.

If [(x) is the position of a moving object at timex, then f'(x) is the veloc-ity, so f"(x) is the rate of change of velocity with respect to time. It is called "theaccelerationof the object.

We end with a remark on notation. It is not necessary to represent func-tions by

f

and independent and dependent variables by

x

andy;as long as we say what we are doing, we can use any letters we wish.

Worked Example 9 Letg(a)

=

4a2

₊

_{3a - 2. What isg'(a)? What isg'(2)?}

Solution If[ex)

=

4x2

+

3x - 2, we know that ['ex)

=

8x

+

3. Using g instead offandainstead of x, we haveg'(a)

=

8a

+

3. Finally,g'(2)

=

8·2

+

3

=

19. Solved Exercises

9. Let[(x)= 3x+1.What isf'(8)?

10. An apple falls from a tall tree toward the~arth.After t seconds, it has fallen 4.9t2 _{meters. What is the velocity of the apple when t}

₌

_{3? What is the}

acceleration?

11. Find the equation of the line tangent to the graph of f(x)

=

3x2

+

4x

+

2 at the point where Xo= 1.

12. For which functions f(x) = ax2

+

bx

+

C is the second derivative equal to

PROBLEMS FOR CHAPTER 1 13

Exercises

10. Differentiate the following functions: (a) I(x)=x2

+

3x - 1

(c) f(x)= -3x +

4

(b) I(x)= (x - l)(x

+

1) (d) get)

=

-4t2

+ 3t

+

6

11. A ball is thrown upward at t = 0; its height in meters until it strikes the ground is24.5t - 4.9t2_{where the time istseconds. Find:}

(a) The velocity att = 0,1,2,3,4,5.

(b) The time when the ball is at its highest point. (c) The time when the velocity is zero.

(d) The time when the ball strikes the ground.

12. Find the tangent line to the parabolay=x2 - 3x

+

1 whenxo = 2. Sketch.

13. Find the second derivative of each of the following:

(a) f(x)=x2 _{-5 (b) f(x)=x-2}

(c) A function whose derivative is 3x2 - 7.

Problems for Chapter 1 _

1. Find the sign changes of:

(a) f(x) = (3x2 - l)/(3x2+ 1) (b) f(x)= l/x

2. Where do the following functions change sign from positive to negative?

Ca) fCx)= 6 - SX (b) f(x)= 2x2 - 4x+2

(c) [(x)= 2x - x2 (d) [(x)= 6x+ I (e) [(x)= (x - l)(x+2)2(X+3)

3. The position at timex of a moving object is x3• Show that the velocity at time lUes between 2 and4.

4. Let[(x) = (x - rdn1(x - r2)n2 ... _{(x - rk)nk, wherer1 <r2 <···<rkare}

the roots of

f

and n1, .•• , nk are positive integers. Where doesI(x) change sign from negative to positive?

5. Using the definition of the derivative directly, find ['(2) if[(x)

=

3x2.

6. If [(x) = XS+x, is ['(0) positive or negative? Why?

7. Sketch each of the following graphs together with its tangent line at (0,0): (a) y = x 2 (b) y = x3 (c) Y = _x3•Must a tangent line to a graph always lie on one side of the graph?

8. Find the derivative atXo= 0 of I(x)= x3

+

X.

9. Find the following derivatives: (a) [(x) = x2 - 2;find ['(3). (b) [(x) = 1;find ['(7). (c) [(x) = -13x2

- 9xT 5; findt'(l). (d) g(s)= 0; findg'(3).

(e) k(y)= (y +4)(y - 7);find k'(-l).

(f) x(f)= 1 - [2;find x'(0).

(g) [(x) = -x+2; findf'(3.752764). 10. Find the tangent line to the curve y = x2

- 2x+1 whenx = 2. Sketch. 11. Let[(x) = 2x2 - 5x

+

2,k(x)= 3x - 4,g(x)

=

ix2

+

2x,lex)

=

-2x

+

3,

andhex)

=

-3x2

+

X

+

3.

(a) Find the derivative of[(x)

+

g(x) atx = 1. (b) Find the derivative of3[(x) - 2h(x)atx =

o.

(c) Find the equation of the tangent line to the graph of[(x) atx = 1. (d) Where does lex) change sign from negative to positive?

(e) Where doeslex) - [k(x) -;-k'(-l)](x + 1) change sign from positive to negative?

12. Find the tangent line to the curvey = -3x2

₊

2x

+

1 whenx = O. Sketch. 13. Let R be any point on the parabola y

=

x2

•(a) Draw the horizontal line

through R. (b) Draw the perpendicular to the tangent line atR.Show that the distance between the points where these lines cross they axis is equal to 1

2' regardless of the value of x. (Assume, however, that x =1= 0.)

14. Given a point (x,y), find a general rule for determining how many lines through the point are tangent to the parabolay= x2

•

15. If[(x)

=

ax2 +bx +c

=

a(x - r)(x - s) (r and s are the roots off),show that the values of

I'

(x) at r andsare negatives of one another. Explain this by appeal to the symmetry of the graph.

16. Let[(t)

=

2t2 - St + 2 be the position of object A and let h(t)= - 3t2 +

t

+

3 be the position of objectB.

(a) When isA moving faster thanB?

(b) How fastisBgoing whenA stops? (c) When doesB change direction? 17. Letf(x)

=

2x2 _+3x+1.

(a) For which values ofx is['(x)negative, positive, and zero? (b) Identify these points on a graph off.

PROBLEMS FOR CHAPTER 1 15

18. How do the graphs of functions ax2 + bx + c whose second derivative is positive compare with those for which the second derivative is negative and those for which the second derivative is zero?

19. Where does the functionf(x) = -21x - 11failto be differentiable? Explain your answer with a sketch.

.2

Transitions and Derivatives

In this chapter we reformulate the definition of the derivativein terms of the concept of transition point. Other concepts, such as change of sign, can also be expressed in 'terms of transitions. In addition to the new language, a few new basic properties of change of sign and overtaking will be introduced.

In what follows the reader is assumed to be familiar with the interval notation and the containment symbol E. Thus

x

E (0,b] means 0

<

x

~ b,

x E (-<Xl,b) means x

<

b, etc. Intervals of the form (a,b) are called open, while those of the form

[a,

b] are called closed.

Transition Points

Some changes are sudden, or defmitive, and are marked by a transition point. The time of sunrise marks the transition from night to day, and the summe~

solstice marks the transition from spring to summer. Not all transitions take place in time, though. For example, letTdenote the temperature of some water. For certain values ofT, the water is in a liquid state; for other values ofT, the water is in a solid state (ice) or a gaseous state (water vapor). Between these states are two transition temperatures, the freezing point and the boiling point.

Here is another example. A tortoise and a hare are running a race. Let T

denote the period of time during which the tortoise is in the lead; letHdenote the period of time during which the hare is ahead. A moment at which the hare overtakes the tortoise is a transition point from T to H. When the tortoise overtakes the hare, the transition is fromHtoT.

Inorder to do mathematics with the concept of transition, we must give a

formal defmition. The following defmition has been chosen for its intuitive con-tent and for technical convenience.

Definition Let A and B be two sets of real numbers. A number Xo is

called a transition point from A to B if there is an open interval I con-tainingXo such that

1. If xE I ami x <xo, then x isinA but notinB.

2. IfX EIand x> xo, then x is in B but not in A.

TRANSITION POINTS 17

There are several remarks to be made concerning this defmition. The first one concerns delmitions in general; the others concern the particular definition above.

Remark 1 DefInitions play an important role in mathematics. They set out in undisputable terms what is meant by a certain phrase, such as"xo is a transition point from A toB."Definitions are usually made to reflect some intuitive idea, and our intuition is usually a reliable guide to the use of the defmed expression. Still, if we wish to establish that"xo is a point of transition from A to B" in a given example, the defmition is the Imal authority; we must demonstrate that the conditions set out in the defmi-tion are met. Partial or approximate compliance is not acceptable; the conditions must be met fully and exactly.

There is no disputing the correctness of a defmition, but only its usefulness. Over a long period of mathematical history. the most useful defmitions have survived. Thousands have been discarded as inappropriate or useless.

Remark 2 There are a couple of specific points to be noted in the. defmi-tion above. First of all, we do not specify to what set the point Xo itself

belongs. It may belong to A, B, both, or neither. The second thing to notice is the role of the interval I. Its inclusion in the definition corre· sponds to the intuitive notion that transitional change may be temporary. For instance, in the transition from ice to water, the intervalI must be chosen so that its right-hand endpoint is lessthan or equal to the boiling point. Reread the defmition now to be sure that you understand this remark.

Remark 3 In the example of the tortoise and the hare, suppose that the tortoise is behind for t

<

tl , that they run neck and neck from t l to t2,

and that the tortoise leads for

t>

t2. There is no transition pointin this case, but rather a transition period. In our defmition, we are only con-cerned with transition points. In nonmathematical situations, it is not always clear when a transition is abrupt and when it occurs over a period. Consider, for example, the transition of power from one government to another, or the transition of an embryo from pre-life to life.

Worked Example 1 Let A be the set of real numbers, for which the point (1,2) lies outsidethe circle x2 ₊

y2 =

,2.

Let B be the set ofrfor which (1,2) lies insidex2₊

y2 =

r.

Find the transition pOint fromA toB. Does it belong to A, B,both, or neither?

Solution The point (1,2) lies at a distance

V

12

₊

₂2

_=.J5

_{from the origin, so} A

=

(0,

VS)

and B

=

(Aoo). The transition point is

-vs:

which belongs to

A B

~'<:~:\":\:'.\.\\~~*~<.<.~"<.<.(:~\;'~~*~~\\~

neitherA nor B. (The point (l,2) lies on the circle of radius

.J5,

not inside or outside it.)

If A and B are intervals, then a transition point from A to B must be a common endpoint. (See Fig. 2-1.) Notice that, whenA andBare intervals, there is at most one transition point between them, which mayor may not belong to

A orB. A B ~~'R\\\~~\\\$,\~\~\~~ \ - - - , - - Transition points

A

B

~\~~\~~~~~~\\~ v:! Transition A r--"--\ B period

~~~ ;''"'<,*,~<'"'''

I

J

!

..

.

Gap~ Notransition pOint

A ,..---'--'\ B

':fffffffffffffffffffff!H1!!11!!1M:~:',\~~\'::...\'®..\\"\z

~ ~Overlap

Fig.2-1 IfA andBare intervals, transition points are common endpoints.

~~...----::::_Inscribed polygons

I L - _ - ? 'Circumscribed polygons

A

B

~ffffffffffffffffffffffffffffffffff1(ffffiff:ffff#ffffffffffffffJ1fffffffffjfffff#ffffMffffff)

o

Areas of inscribed \ Areas of circumscribed

polygons polygons

Area of circle

TRANSITION POINTS 19

Some transitions. occur along curves or surfaces. For example, the

coast-line is the transition curve between land and sea, while your skin is the

transi-tion surface between your body and the atmosphere. We give a mathematical example of a transition curve in Chapter 6, but we will usually be dealing with transition points.

The notion of transition occurs in the answer given by the ancient Greeks to the question, "What is the area enclosed by a circle of radiusr?" We may con-sider the set A consisting of the areas of all possible polygons inscribed in the

circle and the setB consisting of the areas ofallpossible circumscribed polygons.

The transition point fromA to B is the area of the circle. (See Fig.2-2.)By using inscribed and circumscribed regular polygons with sufficiently many sides, Archimedes was able to locate the transition point quite accurately.

Solved Exercises....

1. Let B be the set consisting of those x for which x2

- I

>

0, and letA

=

(-1,1] . Find the transition points fromB toA and fromA toB.

2. Let A

=

(-00,-1/1000), B

=

0/1000,00), C

=

[-1/1000,1/1000]. Find the transition points from each of these sets to each of the others.

3. Let x be the distance from San Francisco on a road crossing the United States. If A consists of those x for which the road is in California at mile

x,

and B consists of those

x

for which the road is in Nevada at mile

x,

what is the transition point called?

Exercises

1. Describe the following as transition points: (a) Vernal equinox.

(c) A mountain top. (e) Outbreak of war. (g) A window shattering.

(b) Entering a house. (d) Zero.

(f) Critical mass. (h) Revolution.

2. What transition points can you identify in the following phenomena? De-scribe them.

(a) The movement of a pendulum. (c) A traffic accident.

(e) Drinking a glass of water.

*Solutions appear in the Appendix.

(b) Diving into water. (d) Closing a door. (f) Riding a bicycle.

3. For each of the following pairs of functions, f(x) and g(x), letA be the set of x where f(x)

>

g(x), and let B be the set of x where f(x)

<

g(x).Find the transition points, if there are any , fromA toB and fromB toA.

(a)f(x)=2x-l; g(x)=-x+2 (b)f(x)=x2+2; g(x)=3x+6 (c)f(x)=x3-x; g(x)=x (d)f(x)=x2- l ; g(x)=-x2_+l 4. Find the transition points from A to B and from B to A in each of the

fol-lowingcases:

(a) A = [1,3)

B = the setofxfor whichx2 - 4x

+

3

>

0

(b) A = the set ofx for which-3 <x~ lor 10 <x~ 15 B

=

the set ofx for which x

<

-3, 0~x ~10, or 16 <x

Change of Sign and Overtaking

The concept of change of sign was defmed in Chapter 1. Now we express it in terms of transitions. Let

f

be any function,N the set of

x

for which

x

is in the domain ofI andI(x)

<

0, andP the set ofx for whichx is in the domain ofI andf(x)

>

O.

Theorem 1 (a) Xo is a point of transition from N to P if and only iff changes sign from negative to positive at xo. (b)Xo is a point of transition from PtoNifand only iff changes sign from positive to negative at Xo.

Prool (a) Suppose that Xo is a transition point fromN toP. By defInition, there is an open intervalI containing Xo such that (i) if x EI and x

<

xo, then

x

is in N but not in P, and (ii) if

x

EI and

x

>

xo, then x is in P but not in N. Letting I = (a, b) and noting thatx E (a, b) and x

<

Xo is the same as saying a

<

x

<

xo, we see that (i) reads: if a

<

x

<

Xo then

x

is in the domain of

f

and f(x)

<

0; and (ii) reads: ifxo

<x <b

then

x

is in the domain of [and[(x)

>

O. Thus, by the defmition of change of sign given in Chapter 1,

f

changes sign from negative to positive. Conversely, we can reverse this argument to show that if

f

changes sign from negative to posi-tive, then Xo is a transition point from P to N.

The proof of (b) is similar.

Let us return to the race between the tortoise and the hare. Denote by

ICt)

the tortoise's position at time t and by get) the hare's position at time t.

The transition "the tortoise overtakes the hare at time to" means that there is an open intervalI about to such that:

CHANGE OF SIGN AND OVERTAKING 21

1. Ift EI and t

<

to, then/(t) <get). 2. IftEl and t> to, then I(t)

>

get).

If we graph

I

and g, this means that the graph ofllies below that ofg for t just to the left of to and above that of g for t just to the right of to. (See Fig. 2-3.) Notice the role of the interval!. (We could have taken a slightly larger one.) It appears in the defmition because the hare may overtake the tortoise at a later time tl.

Point at which the

tortoise overtakes the hare

\

I I I 1 I ~ H _t, f (t) (tortoise) H

Fig. 2-3 The tortoise overtakes the hare at to and the hare overtakes the tortoise at tl •

We now state the defmition of overtaking for general functions.

Definition Let

I

and g be two functions,A the set ofx(in the domain of I and of g) such that f(x)

<

g(x). andB the set ofx (in the domain of I and g) such that I(x)

>

g(x). If Xo is a transition point fromA to B, we say that

I

overtakes

gat

x

o.

In other words, I overtakes gat Xo if there is an interval I containing Xo such that

if

andg are defined onI,except possibly atxo) and

1. Forx inI andx <xo'/(x) <g(x). 2. Forx inI andx> Xo. I(x)

>

g(x).

We call an open intervalI aboutX(I for which conditions 1 and 2 are true

an interval which works for

I

and gatXo; Le., I is small enough so that inI to

the left ofxo,

I

is belowg, while in1to the right ofxo,

I

is aboveg. (See Fig. 2-4.) Clearly, if a certain interval I works for

I

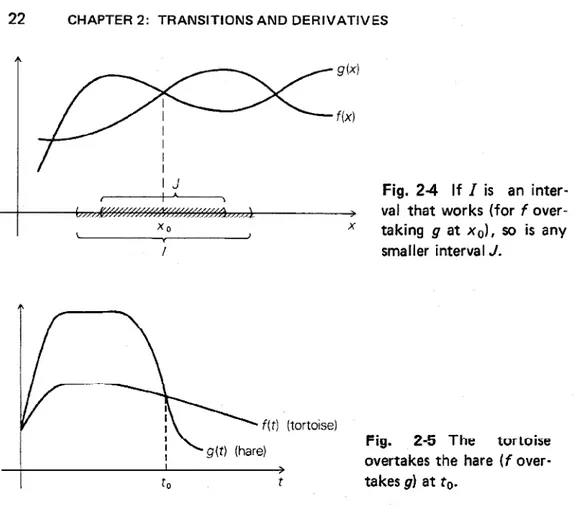
and g at xo, so does any open intervalJ contained inI, as long as it still containsXo.

If the tortoise and hare both fall asleep and start running the wrong way when they wake up, we still say that "the tortoise overtakes the hare" if the hare passes the tortoise when going in the wrong direction. (See Fig. 2-5.) In the general situation, when

I

overtakesgat xo, the graph ofImay actually be going downward. It is only the change in

I

as compared with the changeingwhich is important.

g(x) Xo

,

I f(xl x Fig. 2-4 If I is an inter-val that works (for f over-taking g at xo), so is any smaller intervalJ.

f(t) (tortoise)

t

Fig. 2·5 The tortoilie overtakes the hare (f over-takesg) atto.

Worked Example 2 For the functions

f

andg in Fig. 2-6, tell whether

f

over-takes g, g overtakes f; or neither, at each of the pointsXl, xz, XS, X4, and Xs·

When overtaking takes place, indicate an interval which works.

y= f(x)

'"

\

\ \

y=g(x)

Fig. 2-6 What overtakings occur at the indicated points?

Xs x,

y

Solution Neither function overtakes the other at Xl- In fact, in the interval

(O,xz) about Xl, g(x)

>

[(x) forX both to the right and to the left ofX1.AtX2,

[ overtakesg; an interval which works isI = (Xl> X3)' (Note that the numberXz

is what we called Xo in the defmition.) At X3, g overtakes [; an interval which

works is (X2, X4)' At X4, [overtakesg again; an interval which works is(X3.xs).

CHANGE OF SIGN AND OVERTAKING 23

The relations between the concepts of overtaking and change of sign are explored in Problems 8 and 9 at the end of the chapter.

If, while the tortoise is overtaking the hare atto, a snail overtakes the tor-toise at to, then we may conclude that the snail overtakes the hare atto. Let us state this as a theorem about functions.

Theorem 2 Supposef, g, and h are functions such that

f

overtakes g atXo and g overtakes hatXo. Then f overtakes h at xo.

Proof LetII be an interval which works for f and gat_{xo, and let 12 be an} interval which works for g and h atXo. That these intervals exist follows from the assumptions of the theorem. ChooseI to be any open interval about Xo which is contained in both I} and 12 • For instance, you could

choose I to consist of all points which belong to bothII and12 • (Study

Fig. 2-7, where a somewhat smaller interval is chosen. Although the three graphs intersect in a complicated way, notice that the picture looks quite simple in the shaded region above the intervalI.You should return to the figure frequently as you read the rest of this proof.)

Xo

I,

Fig. 2-7 f overtakesgandgovertakesh at x o.

We will show that the interval I works for

f

and h. We begin by assuming that

x.

EI and x <xo

SinceIis contained in bothI} and12 ,(A) implies:

X Ell and x<xo xEI2 and x <xo

SinceII works for

f

and gat Xo and12 works for g and hat xo, (AI) and

(A_z)imply

f(x) <g(x)(and x isin the domain off andg) g(x)

<

hex)(and x is in the domain of g and h)

(Bt ) and(Bz)together imply that

f(x)

<

h(x) (and x is in the domain of f and h)

(B₁₎ (B_{2 )}

(B)

This chain of reasoning began with (A) and concluded with (B), so we have

proven

that if xEI and x

<

xo,then [(x)

<

hex).

Similarly, one proves

that if x EI and x> Xo thenf(x)

>

hex),so I works.

The next result provides a link between the concepts of linear change and transition. We know that a faster object overtakes a slower one when they meet. Here is the formal version of that fact for uniform motion. Its proof is a good exercise in the algebra of inequalities.

Theorem 3 Let ft(x)

=

mtx +bt and fz(x)

=

mzx +bz be linear

func-tions whose graphs both pass through the point (xo,Yo). Ifm2

>

mt,then f2 overtakes fl at Xo·

Proof Since Yo = fl(XO) = mlxO

+

bl> we can solve for bl to get bl =

Yo - mtXo· Substituting this into the formula for ft(x), we have flex) =

mtx +Yo - mlxO, which we can rewrite as flex) = mt(x - xo) +Yo· Similarly, we have fz(x)

=

mz(x - xo) +Yo. From Fig. 2·8, we guess that it is possible to takeI = (-00,(0). To fmish the proof, we must show that x <xo impliesfz(x) <flex)and that x

>

Xoimplies fix)

>

fleX).

y

Fig. 2-8 fl and fz both pass through (x0,Yo) and

CHANGE OF SIGN AND OVERTAKING 25

Assume thatx

<

Xo. Then x - Xo

<

0. Since m2 - ml

>

0,x - Xo

andm2 - mI"have. opposite signs so that

so

so

and

which says exactlythatfz(x) <fl(X).

Ifx>xo,we havex -Xo

>

0, so(m2 - ml)(x -xo)

>

O. A chain of manipulations like the one above (which you should write out yourself) leads to the conc1usionf2(x)

>

flex). That finishes the proof.

Terminology It is useful to be able to speak of graphs overtaking one another. If G1 and G2 are curves in the plane. which are the graphs of

functions flex) and f2(x), we will sometimes say that G2overtakes. Gl at a

poin;t when what is really meant is thatf2 overtakes fl. Thus, Theorem 3 may be rephrased as follows (see Fig. 2-9):

. If the line /1 with slope m1 meets the line /z with slope mz at

(xo,Yo), and ifm2

>

mI,then12overtakesII at Xo·

c

Fig. 2-9 12 overtakes11 at Xl;12 overtakes C at xz;C overtakes12 atX3.

-~~+_-:--I,

y I

-I'---....L

_x-,- - - x... z---'-x-3

----,>;

(This statement only applies to those lines which are graphs of functions-we may not speak of a vertical line overtaking or being overtaken by any-thing.)

Solved Exercises

4. Where does l/x change sign?

5. LetI(x)

=

3x

+

2,g(x)

=

x

+

2. Show in two ways thatf overtakes gat 0: (a) by the defmition of overtaking; (b) by Theorem 3.

6. Letf(x)

=

-3 andg(x)

=

_x2

•At what point or points doesf overtake g?

Construct an interval which works. Sketch.

7. Let f(x)

=

2x2 _{and g(x)}

₌

_{5x - 3. Show that g overtakes I at x = 1. Is} (-oo,~) an interval which works? Is it the largest one?

Exercises

5. Describe the change of sign atx = 0 of the functionf(x) = mx for various values of

m.

Can you fmd a transition point on the

"m

axis" where a cer-tain change takes place?

6. Let f(x)

=

x2

- 2x - 3 andg(x)

=

2x - 2. Where doesg overtakef? Find an interval which works. Sketch.

7. Letf(x) = x3 - x and g(x) = 2x. At what point or points doesf overtake

g? Does (-3,0) work for any of these points?Ifnot, why not? Sketch. 8. Letf(x)

=

_x2 +4 andg(x)

=

3x - 2. At what point or points

doesfover-take g? Find the largest interval which works. Sketch. 9. Letf(x)=

I/CI

-x) andg(x)= -x

+

1.

(a) Show that

f

overtakesg atx = O. Find an interval which works. Sketch. (b) Show that

f

overtakes g at x = 2. Is (1,3) an interval which works?

What is the largest interval which works?

---~--~._----The Derivative

The derivative was defmed in Chapter 1. To rephrase that defmition using the language of transitions, we shall use the follOWing terminology. Letfbe a

func-THE DERIVATIVE 27

tion whose domain contains an open interval about xo. Let A be the set of numbers m such that the linear function f(xo)

+

m(x - xo) (whose graph is the line through (xo,f(xo)) with slope m) is overtaken by fat xo. LetB be the set of numbers m such that the linear functionf(xo) +m(x - xo) overtakesfat xo.

Theorem 4 A number mo is a transition point fromA toBif andonlyif mo is the derivative offat xo.

Proof First, suppose that mo is a transition point fromA toB.Thus there is an open intervalI about mo such that (i) if ml E I and ml

<

mo, then ml is in A but not in D, and (ii) if ml E I and ml

>

rna,

then ml is inB but not in A. Let m

<

mo. Choose m1E I such that m :::;;; m1

<

mo· (Why

can we do this?) By (i), the functionAxo) + ml(x - xo) is overtakenby fat xo. By Theorems 2 and 3, I(xo)

+

m(x - xo) is also overtaken by I at Xo; Le. I(x) - ff(xo)

+

m(x - xo)] changes sign from negative to positive at Xo- This gives condition 1 of the defInition of the derivative, and condition 2 is proved in the same way.

Conversely, if mo is the derivative of

I

at xo, then the defInition of the derivative shows thatA = (-"",mo) andB = (mo,=),and somo is the

transition point fromA toB.

In Chapter 1 we proved that the derivative is unique if it exists. In the pres-ent terminology, this means that there is at most one transition point fromA to B. (In Problems 18-20, the reader is invited to prove this directly from the defI-nition ofA and B).

Solved Exercise

8. Let I(x)

=

x2

+

tx

+

2 andXo

=

2. Construct the setsA andBand use them to calculatef'(O).

Exercises

10. Calculate the derivative of/ex)

=x

2

-x

atx= 1 using Theorem 4.

11. For each of the follOWing functions, fmd the sets A and B involved in Theorem 4 and show that the derivative does not exist at the specifIc point:

(a)

f(x)

=

{x

2x - 1

ifX~l}.,

ifx

>

1

{ 02X +4 (b) [(x) = 2x+3 { X'2 (c) [(x) = .. x

ifX~-l}.

' ifx>-1·

ifX~O},

if x

>

0 Xo =-1 Xo= 0

12. Is the following an acceptable defmition of the tangent line? "The tangent line through a point on a graph is the one line which neither overtakes nor is overtakenby the graph." If so, discuss. If not, give an example.

Problemsfor Chapter2 _

1. Describe the following as transition p.oints.

(a) Turning on alight. (b) 1000 Centigrade. (c) An aircraft landing. Cd) Signing a contract.

2. What transition points can you identify in the following phenomena? (a) Breathing. (b) A heart beating.

(c) Blinking. (d) Walking. (e) A formal debate. (f) Firefighting.

(g) Marriage. (h) Receiving exam results. (i) Solving homework problems.

3.. LetA be the set of areas of trianglesinscribed in a circle of radius 1,B the set of areas of circumscribed triangles. Is there a transition point fromA to

B? (You may assume that the largest inscribed and smallest circumscribed triangles are equilateral.) What happens if you use quadrilaterals instead of triangles? Octagons?

4. For each of the following pairs of sets, find the transition points fromA to

B and fromBtoA.

(a) A =(0,l);B=(-oo,t)and(l,3).

(b) A = those x for whichx2

<

3;B= those~ for which x2

>

3. (c) A = those x for which x3~4;B= those x for which x3~4.

(d) A = thosea fur which the equationx'2 -ra

=

0 has two real roots;

B= those a for which the equation x2

+

a = 0 has less than two real roots.

(e) A = those x for which

y'

x2

- 4 exists (as a real number):

B= those x for which.J x2 - 4 does not exist (as a real number). 5. For which values ofn(positive and negative) doesxn change sign at 07