Étude comparative par diffraction X et modélisation moléculaire de la structure d’un intermédiaire réactionnel d’un insecticide

Faculté des Sciences et de la Technologie

Département de Génie des Procédés

N° D’ORDRE : M …../2012

Mémoire

Présenté pour obtenir le

DIPLOME DE MAGISTER

En

Cristallographie et modélisation moléculaire

Par

Zahraoui Mehdi

Date de Soutenance : Membres du jury :

Président : M. Belhakem Pr. Université de Mostaganem

Examinateur : A. Zanoun Pr. ENSET – Oran

Examinateur : A. Feddag M.C.A. Université de Mostaganem

Encadreur : A. Chouaih M.C.A. Université de Mostaganem

Année universitaire : 2011 - 2012

Étude comparative par diffraction X et modélisation

moléculaire de la structure d’un intermédiaire

réactionnel d’un insecticide

UNIVERSITE

ABDELHAMIDE IBN BADIS DE MOSTAGANEM

Résumé

Le travail présenté dans ce mémoire est basé sur trois principaux axes :

 Le premier axe est consacré à la détermination de la structure d’un nouvel insecticide de la famille des pyréthroides – C21H16N2O4FClBr2– à partir d’un spectre de diffraction des

rayons X. Ces composés trouvent leurs applications dans le domaine agricole. Ainsi, une analyse structurale détaillée a été réalisée pour avoir la géométrie moléculaire et la disposition des atomes les uns par rapport aux autres.

 Le deuxième axe définit les concepts et les méthodes de la chimie théorique. Nous avons présenté les généralités relatives au traitement quantique non relativiste d’un système composé de plusieurs particules puis nous avons abordé les deux grandes familles de calculs quantiques: L’approximation de Hartree-Fock et la théorie de la fonctionnelle de densité.

 Le troisième axe présente l’aspect pratique des calculs pour détermination de la géométrie structurelle théorique à l’aide des calculs théoriques Ab-initio et DFT et une comparaison entre les résultats expérimentaux et calculus.

Abstract:

The work presented in this paper is based on three main axes:

 The first theme focuses on determining the structure of a new family of insecticidal pyrethroids - C21H16N2O4FClBr2 - from a spectrum of X-ray diffraction. These compounds

have applications in agriculture. Thus, a detailed structural analysis was performed for molecular geometry and arrangement of atoms to each other.

 The second line defines the concepts and methods of theoretical chemistry. We have presented the general for the treatment of non-relativistic quantum system consisting of several particles. Then we discussed the two main families of quantum calculations: the Hartree-Fock and the functional theory.

 The third presents the practical calculations for determining the structural geometry using theoretical calculations and theoretical ab-initio DFT.

صخهي : وذقًنا مًعنا ِذْ ًف ةٍسٍئر تلااجي ةثلاث ىنإ ىسقي ةحٔزطلأا :  يزشح ذٍبًن ةٌرٕهبنا ةٍُبنا ذٌذحج ىهع زكجزٌ لٔلأا لاجًنا دأزثٌزبنا ةهئاع ٍي C21H16N2O4FClBr2 ًف تاقٍبطج ّن يذنا ةعشلأا جازعَا ٍي قلاطَا ًعارزنا لاجًنا ةٍٍُسنا . بكزًنا اذٓن يٍُٕبنا مٍهححنا ٌإ ضعبنا آضعب عي تارذنا عضٕج ةٍفٍكٔ بكزًنا ةسذُْ ةفزعي ٍي اُُكًٌ  ذقٔ ةًٍكنا ةٍبسُنا ةجناعًنا ىهع ذًحعًنا ةًٍكنا ءاًٍٍكناب ظبجزًنا يزظُنا بَاجنا مثًٌ ًَاثنا لاجًنا ا ًف ثهًعحسا ةفاثكنا ةناد ةٌزظَ تاباسحن DFT ٔ Hartree – Fock  ةسذُْ ذٌذححن ةٍقٍبطحنا ةٍحاُناب ىُعٌ ثناثنا لاجًنا ءيزجنا آًٍُب ةَراقًنا ٔ اٍبٌزججٔ اٌزظَ

SOMMAIRE

INTRODUCTION GENERALE ... 1

Chapitre I –

ÉTUDE BIBLIOGRAPHIQUE

I.1. Principe de diffraction des rayons X par les cristaux ………... 5 I.2. Corrections apportées aux intensités mesurées ………. 13

I.3. Principe de la modélisation moléculaire ………. 20

Chapitre II -

DISPOSITIF EXPÉRIMENTAL ET TRAITEMENT DES DONNÉES

II.1. Diffractomètre automatique ……… 44 II.2. Choix du monocristal ……….. 50

II.3. Recherche de la maille 50

II.4. Enregistrement et collecte des données 53

Chapitre III -

DETERMINATION DE LA STRUCTURE DU COMPOSE C21H16N2O4FClBr2

III.1. Les insecticides de la famille des pyréthroïdes 56

III.2. Diffraction des rayons X 57

III.3. Modélisation Moléculaire 78

Chapitre IV -

ANALYSE STRUCTURALE DU COMPOSE C21H16N2O4FClBr2

IV.1. Analyse par diffraction X 82

IV.2. Calcul théorique 91

IV.3. Moment dipolaire 97

INTERPRETATION DES RESULTATS 99

CONCLUSION GÉNÉRALE 101

BIBLIOGRAPHIE 104

Liste des tableaux

N° Intitulé du tableau Page

III-1 Paramètres cristallographiques et conditions expérimentales de la molécule. 70

III-2 Coordonnées fractionnelles des atomes avec leur facteur de température isotrope équivalent.

78

III-3 Paramètres d’agitation thermique anisotrope de la molécule. 79

III-4 Coordonnées des atomes 87

IV.1 Distances expérimentales inter atomique 85

IV.2 Distances expérimentales inter atomique X – H 86

IV.3 Valeurs expérimentales des angles de valence 89

IV.4 Valeurs des angles de torsion 91

IV.5 Liaison hydrogène 93

IV.6 Distances interatomiques (en Å) obtenues par diffraction X en comparaison

avec les distances du calcul théorique.

96

IV.7 Angles de valence (en degré) théoriques en comparaison avec ceux de la diffraction X

97

IV.8 Liaison hydrogène 98

Liste des figures

N° Intitulé de la figure Page

I.1 Loi de Bragg 09

I.2 Représentation du facteur de structure dans le plan complexe Somme des contributions de chacun des atomes.

09

I.3 Interférence entre deux ondes diffusées en O et en O’. 11

I.4 Facteur de diffusion atomique 12

I.5 Polarisation des rayons X 16

I.6 Facteur de polarisation 17

I.7 Correction de Lorentz 18

I.8 Facteur de Lorentz 19

I.9 Extinction primaire 20

I.10 Extinction secondaire 21

I.11 Absorption des rayons X par la matière. 22

II.1 Diffractomètre automatique CAD4 Nonius 47

II.2 Les différentes rotations 48

II.3 Différentes rotations pour amener un vecteur en position de réflexion de Bragg.

49

II.4 Trièdre attaché au cristal. 50

II.5 Profil d’une réflexion 58

III.1 Pics de la densité 73

III.2 Squelette de la molécule C21H16N2O4FClBr2 après résolution 75 III.3 Représentation tridimensionnelle de la molécule C21H16N2O4FClBr2 80

IV.1 Distances inter atomiques 86

IV.2 Angles de valence 88

IV.3 Angles de torsion 90

IV.4 Liaisons hydrogène expérimentales entre deux molécules 94

IV.5 Empilement des molécules dans la maille 94

IV.6 Liaison hydrogène théorique entre deux molécules (dimer) 100

IV.7 Orientation du moment dipolaire 102

INTRODUCTION GENERALE

Parmi les millions d’espèces d’insectes qui fourmillent sur la planète, très peu peuvent être considérées comme nuisibles. De ce nombre, plusieurs vivent exclusivement en pays tropicaux. Que dire alors de ces insectes qui ont le malheur de menacer le bien-être de l’homme ! La lutte contre les insectes et leurs dangers ne cesse de se développer, à travers les recherches et les méthodes qui ont beaucoup changé avec le temps. D’où l’existence de deux types de traitement complémentaires : les mesures préventives et les mesures curatives. Les mesures curatives qui sont caractérisées par l’emploi de produits chimiques, dans lesquels on distingue les insecticides et les fumigènes.

Les structures des pyréthroïdes obtenus à partir des données expérimentales de diffraction des rayons X ont été étudiées par plusieurs auteurs [1-4]. Des progrès considérables ont été accomplis dans la structure relative des pyréthroïdes avec leur activité biologique, mais amélioration des concepts tels exige des renseignements fiables sur la forme de la molécule (configuration, les longueurs et les angles). L’activité biologique dans les pyréthroïdes est liée à la structure moléculaire et dépend fortement de la stéréochimie adoptée par les centres asymétriques [5-6]. Dans ce contexte, le composé C21H16N2O4FClBr2 apparait comme un intermédiaire utile dans la synthèse de certains insecticides de la famille des pyréthroïdes [7]. L'étude de la conformation de cette molécule peut donner des informations sur le mécanisme de son activité biologique [8,9].

Dans ce travail, nous nous intéressons au composé C21H16N2O4FClBr2 , un intermédiaire réactionnel d’un insecticide de synthèse dont l’objectif est de définir le type d’isomère, par détermination de la structure tridimensionnelle. La structure est déterminée en utilisant d’une part la technique de diffraction des rayons X sur monocristal et d’autre part les calculs ab initio. Nous allons aussi mettre en évidence la stéréochimie de l’atome de carbone asymétrique responsable de l’activité biologique de ce type de composés. A la fin, nous proposons une étude comparative entre les résultats expérimentales obtenus par diffraction des rayons X et ceux théoriques obtenus par les méthodes Ab initio.

Ce document est divisé en cinq parties de la manière suivante :

Dans la première partie de ce mémoire nous présentons des notions théoriques relatives à la détermination de structures à partir des données de diffraction des rayons X indispensables à la compréhension de ce travail. L’expérience de diffraction permet d’obtenir des facteurs de structure à partir des intensités diffractées. Avant d’utiliser cette information, l’ensemble des données doit subir quelques corrections. La réalisation de cette étude est faite par le package WINGX-32 qui regroupe les programmes nécessaires pour traiter la plupart des problèmes cristallographiques.

Par la suite, nous présentons les méthodes théoriques de la chimie quantique. La modélisation moléculaire est une application des méthodes théoriques et des méthodes de calcul pour résoudre des problèmes impliquant la structure moléculaire et la réactivité chimique [10]. Ces méthodes peuvent être relativement simples et utilisables rapidement ou au contraire elles peuvent être extrêmement complexes et demander des centaines d’heures de temps d’ordinateur, même sur un superordinateur. En plus, ces méthodes utilisent souvent des moyens infographiques très sophistiques qui facilitent grandement la transformation de quantités impressionnantes de nombres en quelques représentations graphiques facilement interprétables [11].

Dans le deuxième chapitre nous décrivons le dispositif expérimental nécessaire pour la collecte des intensités diffractées qui seront traitées en utilisant le formalisme de Blessing. Le troisième chapitre est consacré à la détermination de la structure tridimensionnelle du composé C21H16N2O4FClBr2 par diffraction des rayons X et modélisation moléculaire. Le dernier chapitre est consacré à l’analyse structurale où nous présentons les différents résultats théoriques et expérimentaux avec une étude comparative. Pour mettre en évidence le transfert de charge au sein de la molécule, le moment dipolaire a été calculé.

CHAPITRE I – ÉTUDE BIBLIOGRAPHIQUE

I.1. Principe de diffraction des rayons X par les cristaux :

L’interaction entre un faisceau de rayons X et la matière provoque une vibration des électrons des atomes. Cette vibration, qui due au champ électrique associe au faisceau incident, est caractérisée par la diffusion d’un rayonnement de même longueur d’onde.

Les nœuds du réseau cristallin constituent des sources cohérentes et les ondes diffusées interférentes, donnant ainsi des pics de diffraction dans des directions privilégiées (Figure. I.1).

Si on appelle et , les vecteurs unitaires portent respectivement par les directions des faisceaux diffusé et incident, on démontre que l’intensité diffractée par un cristal dans la direction s’écrit :

[I-1]

Relation dans laquelle x est le vecteur de diffusion :

Les grandeurs I0, ae et LP représentent respectivement l’intensité de l’onde incidente,

la longueur de diffusion de l’électron et le facteur de Lorentz-polarisation.

sont respectivement le facteur de structure et la fonction d’interférence. Cette dernière prend une valeur non nulle à l’intérieur d’un domaine centré sur un nœud du réseau réciproque tel que est un vecteur du réseau réciproque. prend alors sa valeur maximale égale à N (N étant le nombre total de mailles dans le cristal) [12].

[I-1’]

Figure. I.1 : Loi de Bragg

I.1.1.Facteur de structure :

Le facteur de structure constitue le concept fondamental des théories de diffraction. Il est défini comme étant la somme de toutes les contributions atomiques affectées chacune par son déphasage dépendant directement de la position de l’atome j dans la maille.

d   P2 P1   C 1 2 1’ 2’ B A O Atome 1 Atome 2 Atome 3 Atome 4 Réel Imaginair e

Figure. I.2 : Représentation du facteur de structure dans le plan complexe - somme des contributions de chacun des atomes.

[I-2]

N : Le nombre d’atomes par maille ; fj : Le facteur de diffusion de l’atome j ;

: Le déphasage entre les différents atomes de la maille formulée par : [I-3]

Le facteur de structure s’écrit :

[I-4] Ou encore : [I-5] [I-6] On a alors: [I-7]

On peut également écrire le facteur de structure sous la forme exponentielle, soit : [I-8]

I.1.2. Facteur de diffusion atomique :

L’interaction des photons avec la matière se fait essentiellement avec les électrons ainsi, pour une intensité incidente Ii, l’intensité diffusée Idiff par un électron par unité d’angle solide peut s’écrire :

P r I

Où ₂ 0 2 0 4 mc e r 

 est le rayon classique de l’électron, m et e étant la masse et charge

de l’électron, respectivement, et c la vitesse de la lumière ; P est un facteur de polarisation dépendant de la polarisation de l’onde incidente et de la direction de diffusion, relativement à la polarisation.

Pour calculer la diffusion en provenance d’un atome, il faut tenir compte des interférences entre les ondes diffusées par tous les électrons. Lorsque deux diffuseurs interfèrent (figure I.3), la différence de phase entre les deux intensités diffusées s’écrit :



s s



.r 2 0      [I-10]

Le vecteur de diffusion, qui indique dans l’espace réciproque de la direction de

diffusion, est alors défini par S 1



ss₀



ha*kb*lc*

 et nous pouvons donc écrire

r S. 2   [I-11] O’ B A O r s 0 s  2

Figure. I.3 : Interférence entre deux ondes diffusées en O et en O’.

Les s et s₀ sont respectivement les vecteurs unitaires définissant les ondes incidentes et diffusées et r_j x_ja*y_jb*z_jc* est un vecteur de position de O’.

L’intensité totale diffusée dans la direction Speut donc s’écrire sous la forme d’une

intégrale sur l’ensemble des électrons par exemple sur la densité électronique

I I r P

 

r e dr Iir P

 

r e i Srdr i i diff      . 2 2 0 2 0   _ 

_



  _[I-12]

Cette expression mathématiquement parlante, exprime que l’intensité diffusée est proportionnelle à la transformée de Fourier de la densité électronique, en fonction du vecteur S de l’espace réciproque considérée. Dans le cas d’un atome, la densité électronique possède en première approximation une symétrie sphérique, et l’intensité diffusée par un atome est appelée facteur de diffusion atomique f, et ne dépend que de

 

sin _{[voir annexe].}

Les atomes les plus lourds ont une décroissance du facteur de diffusion moins rapide, à cause de la plus grande densité électronique (relative) au centre de l’atome. On appelle facteur de diffusion d’un atome j, la somme des amplitudes diffusées par tous les électrons qui le constituent. Ce facteur dépend de la nature chimique des atomes, de la température et de l’angle de diffraction .

La figure I.4 montre que la contribution des électrons de l’atome j à la diffraction diminue quand l’angle de diffraction augmente. En pratique les réflexions à sont négligeables. L’agitation thermique est la cause de l’affaiblissement important des intensités de Bragg dans le domaine

Figure I.4 : Facteur de diffusion atomique. fJ ZJ 0 30° Atome au repos Atome au repos rerererrrrrrrre pos rerepos Atome en agitation aaAAaaqAQaaaagi tatiaenenenenaagit éqgitéagitation

I.1.2.1.Modèle de Pseudo-Atomes Rigides :

Modèle des atomes sphériques :

Les modèles des atomes sphériques sont le modèle de pseudo-atome le plus utilisé en cristallographie. Il définit le cristal comme un ensemble d’atomes ayant la structure électronique d’atomes isolés à symétrie sphérique, non déformés par les liaisons chimiques et centrés sur les positions des noyaux.

Dans ce modèle, les facteurs de diffusion des atomes libres sont incorrects à cause de la déformation. Toutefois, imperfection est en partie corrigée par les facteurs de température et on observe un assez bon accord entre facteurs de structures observées et calculées obtenues dans l’affinement par la méthode des moindres carrés [13,14].

I.1.3. Agitation thermique des atomes :

Le facteur de température joue un rôle essentiel dans la résolution de la structure cristalline, tout cristal présente à une température T un désordre dû à l’agitation thermique des atomes qui le constituent. Les vibrations de ces atomes autour de leur position d’équilibre au sein de la maille ont pour effet de diminuer l’amplitude du facteur de structure.

Le facteur de structure s’écrit alors:

[I-13]

Avec Tj le facteur de température donne par la moyenne :

[I-14]

Où représente le vecteur de déplacement instantané de l’atome j par rapport à sa position d’équilibre.

Dans l’hypothèse harmonique du mouvement des atomes (mouvement de faible amplitude), le facteur de température s’écrit :

[I-15]

Si U1, U2, U3 sont les composantes de dans le réseau direct, alors le terme en exponentiel s’exprime par :

[I-16]

[I-17]

[I-18]

Ou encore, en notation matricielle :

[I-19]

[I-20]

[I-21]

Si l’atome j possède une agitation thermique identique, dans les trois directions de la maille ( = = ), le tenseur est dit isotrope et s’écrit comme :

[I-22]

Alors l’atome j à un déplacement quadratique moyen isotrope (même agitation dans les différentes directions).

Le facteur de température s’écrit :

Si de plus Uj est le même pour l’ensemble des atomes de la maille du cristal alors, l’agitation thermique est représentée par un facteur de température globale B.

[I-24]

Ce qui a pour effet d’abaisser l’intensité diffractée. Ce phénomène étant d’autant plus marqué pour les grandes valeurs de comme présenté précédemment (figure. I.4).

I.2. Corrections apportées aux intensités mesurées :

Les intensités mesurées sont affectées d’un certain nombre d’erreurs. Les unes sont liées à l’angle de diffraction et conduisent à 2 types de corrections : la correction de polarisation et la correction de Lorentz. Les autres sont liées aux propriétés physiques et à la nature de cristal. Ce sont :

 La correction d’absorption ;  La correction d’extinction ;

I.2.1. Correction de polarisation :

La correction de polarisation dépend de l’état du faisceau incident des rayons X et l’angle de diffusion du faisceau diffracté (Figure. I.5). Quand un faisceau est diffracté par un cristal, l’intensité diffractée est affectée par un facteur, appelé facteur de polarisation P [15].

[I-25]

Pour une réflexion donnée, l’intensité diffracté se met alors, sous la forme suivante :

[I-26] Rayon X incident 2 2 B

A

Figure. I.5 : Polarisation des rayons X.

Fig.2.5 Polarisation des rayons X

L’angle varie entre les valeurs extrêmes 0 et varie entre les valeurs extrêmes 0 et 1. Par conséquent le facteur de polarisation P varie entre ½ et 1 (figure.I.5). Ainsi pour chaque réflexion, l’intensité mesurée est P fois l’intensité réelle. La correction de polarisation consiste à diviser l’intensité mesurée par le facteur P.

0 30 60 90 120 150 180 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 Coe ff ici en t de p olarisation P

I.2.2. Correction de Lorentz :

Dans un cristal réel, le réseau n’est pas infini. À cet effet, les nœuds du réseau réciproque ne sont plus ponctuels, et sont donc représentés par de petits volumes sphériques.

Dans le réseau direct, cela se traduit par un élargissement du faisceau diffracté. Étant donné son volume, le nœud de coordonnées (h k l) met un certain temps t pour traverser la sphère d’Ewald, ce temps dépend de la position du nœud par rapport à cette sphère, les différences de temps de diffraction entre les familles de plans réticulaires sont responsables d’erreurs systématiques dans les mesures d’intensités. La correction de Lorentz consiste à ramener tous les nœuds h k l au même temps de traversée de la sphère d’EWALD. On montre que le facteur de Lorentz L se réduit à l’expression suivante [16].

En pratique la correction de Lorentz est toujours associée à la polarisation. On parle couramment de la correction de Lorentz-polarisation désignée par le paramètre LP. La variation du coefficient de Lorentz en fonction de l’angle de diffraction est représentée sur la figure I.8.

I.2.3. Correction d’extinction :

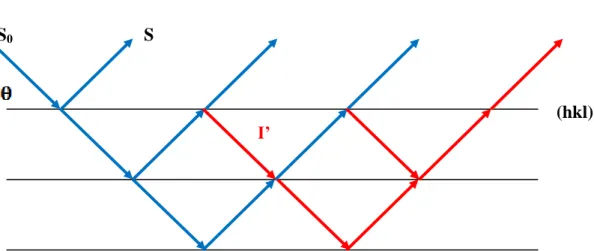
L’effet de l’extinction peut être décrit par un affaiblissement des intensités des réflexions fortes dues à une réduction de l’intensité du faisceau incident le long de son chemin à travers le cristal. Le concept du cristal mosaïque introduit la distinction entre deux types d’extinction : l’extinction primaire et l’extinction secondaire.

I.2.3.1. Extinction primaire :

Le phénomène d’extinction est associé au calcul du pouvoir réflecteur d’un cristal parfait, c'est-à-dire d’un cristal pour lequel les distorsions angulaires des plans réticulaires n’excédant pas quelques secondes d’arc. Pour un tel cristal, la théorie cinétique est remplacée par la théorie dynamique [17,18].

Dans la théorie cinétique, seule les ondes diffusées par les différents points du cristal interférent, alors que dans la théorie dynamique un état interférentiel s’installe entre les ondes incidentes et les ondes diffusées qui constituent un système couple (figure I.9).

Angle de diffraction Coe ff ici en t de L or en tz L 0 30 60 90 120 150 180 1 2 3 4 5

Figure I.9 : Extinction primaire.

Le coefficient d’extinction primaire est donné par :

[I-28]

Où Id est l’intensité intégrée fournit par la théorie dynamique et Ic celle fournie par la théorie cinétique. Ce coefficient Yp est en général très voisin de 1 et affecte principalement

les facteurs de structure de module élevé et à faible valeur de sin .

I.2.3.2. Extinction secondaire :

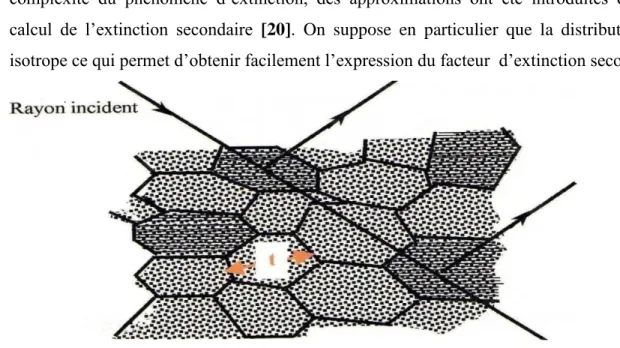
Ce phénomène est lié à l’extinction des défauts structuraux (délocalisations) dans un cristal, entrainant la rupture de la cohérence optique, d’où un phénomène d’interférence entre l’onde incidente et l’onde diffractée.

L’extinction secondaire ne peut être décrite qu’en considérant le cristal comme mosaïque, c'est-à-dire former de blocs parfaits, de dimension t, présentant de petites désorientations les uns par rapport aux autres (moins de 0.5 degré) (Figure I.10).

Dans la pratique, on peut rencontrer deux types de cristaux, les cristaux de type I dont l’extinction donnée par la largeur de la mosaïque, par contre dans les cristaux de type II, le phénomène d’extinction est dominé par la dimension moyenne t des domaines parfaits.

S0 S

I’

La plupart des cristaux étudiés actuellement sont de type I [19]. En raison de la complexité du phénomène d’extinction, des approximations ont été introduites dans le calcul de l’extinction secondaire [20]. On suppose en particulier que la distribution est isotrope ce qui permet d’obtenir facilement l’expression du facteur d’extinction secondaire.

Figure I.10 : Extinction secondaire.

I.2.4. Correction d’absorption :

Un faisceau de rayons X est absorbé par la matière. Dans l’approximation des interactions faibles, la variation d’intensité du faisceau sur une distance dl parcourue dans le cristal suit la loi de Beer-Lambert:

[I-29]

Où est le coefficient d’absorption linéaire. Il dépend de la longueur d’onde de la radiation utilisée et de la nature de l’échantillon traversé ; l est la longueur traversée.

En intégrant l’équation précédente, nous obtenons :

[I-30]

Cette dernière relation reflète la décroissance de l’intensité du faisceau incident en fonction du trajet l parcouru dans le cristal.

La correction d’absorption revient à ramener tous les trajets de rayonnement à l’intérieur de la matière à la même longueur.

La figure I-11 montre que les longueurs des trajets des rayonnements à l’intérieur de la matière dépendent de la position du point diffusant les rayons X et de la l’angle d’incidence et de diffusion [21].

Figure I.11 : Absorption des rayons X par la matière.

Les corrections de Lorentz-polarisation et d’extinction des tâches ont été appliquées à l’ensemble des réflexions.

O R

I.3. Principe de la modélisation moléculaire :

Introduction

Avec le début du vingtième siècle, les lois de la mécanique classique mise en œuvre par Isaac Newton ne permettent plus de décrire le comportement de petites particules [22], telles que les électrons, les noyaux. Afin de résoudre ce problème, la mécanique quantique est apparue permettant ainsi de calculer et par suite de comprendre, les propriétés physiques et chimiques de systèmes atomiques et moléculaires. En fait, ces propriétés trouvent leur origine dans le comportement des électrons présents au sein du système et leur évaluation se fait à l’aide des méthodes et d’outils numériques. Ces dernières sont maintenant au cœur de très nombreuses études en chimie, physique, sciences des matériaux et même en biologie. Cet essor remarquable est sans aucun doute dû à la conjonction de faits

i) la mise au point de nouvelles théories et méthodologies permettant des simulations

prédictives sur des systèmes réalistes,

ii) l’essor formidable des moyens informatiques

Les méthodes de calculs quantiques se basent sur divers formalismes mathématiques dans lesquels il s’agit d’appliquer l’équation de Schrödinger en prenant en compte toutes les interactions entre les particules constituant les systèmes étudiés. L’impossibilité d’atteindre les solutions de cette équation a incité les Chimistes et les Physiciens théoriciens (Kohn, Sham, Fermi, Born, Oppenheimer, Hartree) à développer un ensemble de méthodes se basant sur des formalismes mathématiques afin d’obtenir les observables de la mécanique quantique : tout progrès dans ces connaissances dépend essentiellement de l’élaboration de techniques d’approximation fiables.

I.3.1. Méthodes Ab initio :

I.3.1.1. Généralités :

Le cation de Schr dinger décrit une particule par sa fonction d’onde ( , )r t ( , ) ( , )r t ih r t t        

[I-31]

2 ( , ) 2m

V

r t       

[I-32]

Le premier terme correspond l’énergie cinétique, le deuxième au potentiel. Dans notre cas nous utiliserons l’équation de Schrdinger indépendante du temps (stationnaire) qui pour un système a N particules et M noyaux s’écrit sous la forme :

1 1 1 1 ( ... , ... ) ( ... , ... ) i N M i i N M H r r R R E r r R R     [I-33] H 

étant l’opérateur hamiltonien pour le système formé de M noyaux et de N électrons. Les

coordonnées ri _{regroupent les variables d’espace et de spin de l’électron i, les coordonnées}

i

R celles du noyau k. H



peut se décomposer ainsi :

[ 1-34]

Les deux premiers termes désignent respectivement l’énergie cinétique des électrons Te et celle des noyaux Tn Les termes restants désignent les énergies potentielles et qui se répartissent en trois sommations : un premier attractif du à l’interaction électrostatique entre

les noyaux et les électrons V_Ne



, deux autres répulsifs résultant des interactions

coulombiennes entre, l’un de type électron-électron V_ee



, l’autre attaché aux interactions

noyau-noyau V_NN



[23] Devant l’impossibilité à trouver une solution exacte de l’équation..[1,34]

Dans le cas des systèmes polyélectroniques à n corps il est nécessaire d’utiliser des approches simplificatrices

I.3.1.2. Approximation de Born Oppenheimer :

De nombreux calculs en physique de la matière sont basés sur cette approximation [24]. Partant du simple constat que les électrons sont beaucoup moins lourd que les noyaux et que leur mouvement est beaucoup plus rapide, une première approximation prend en compte une évolution des électrons dans un potentiel créé par des atomes fixes [25].

La fonction d’onde électronique_el( ,r R) dépend alors explicitement des coordonnées r

et paramétriquement des coordonnées. R La fonction d’onde totale se réduira au produit d’une fonction d’onde électronique par une fonction d’onde nucléaire :

( ,r R) n(R) e( ,r R)

    [1-35]

L’hamiltonien de l’équation (1.4) peut donc se réduire à un hamiltonien électronique :

e n

H

H

H

    

[1-36]

Les solutions de l’équation de Schrödinger avec e





sont des fonctions d’onde électroniques Ψe et des énergies électroniques Ee Comme pour l’hamiltonien, l’énergie totale se répartira en deux, l’énergie électronique et l’énergie nucléaire.

L’approximation de Born-Oppenheimer n’est valable que lorsque les couplages des mouvements électroniques et nucléaires sont négligeables

I.3.1.3. Approximation d’Hartree-Fock (HF):

Cette approximation est très fréquemment utilisée, dans la mesure où elle est à la base de presque toutes les méthodes ab initio. Une solution exacte de l’équation [1 .36]. n’est possible que dans le cas de l’atome d’hydrogène, en raison de l’absence des termes de répulsion coulombienne multiples présents dans les systèmes polyélectroniques. Afin de contourner cette difficulté, une première approximation, celle de Hartree, considère la fonction d’onde multiélectronique d’un système à N électrons comme étant le produit de fonctions à une particule (monoélectroniques), désignées par le terme « orbitale ». La fonction d’onde du système s’écrit sous la forme

1 2 1 2

( ,x x ...x_N) ( ) (x x ).... (x_N)

    

[1-37].

La fonction d’onde  est appelée « produit de Hartree ». La répulsion coulombienne est considérée comme un effet moyen. D’où le nom de cette approximation : principe du champ moyen. La méthode Hartree-Fock applique cette simplification aux électrons d’une molécule. Elle s’écrit sous la forme :

2 2 ( ) ( ) ( ) ( ) ( ) 2m Ve r j r K x i x i x _{    } _{  }     [1- 38]

Dans cette équation, on trouve successivement le terme d’énergie cinétique, les termes d’interaction coulombienne noyau v(r) et de répulsion coulombienne électron-électron j(r) , enfin le terme d’échange k (x) [27,28].

Il est à noter que la fonction d’onde  change de signe au cours de la permutation de deux électrons i et k : (...,x_i, ,x_k,....) (....,x_k, ,x_i,....)

(...,x_i, ,x_k,....)

 est une combinaison linéaire de fonctions monoélectroniques où les électrons, considérés comme des fermions, obéissent au principe d’exclusion de Pauli. Une approximation consiste à utiliser un déterminant dit de Slater [29]. Ce dernier est constitué de fonctions monoélectroniques nommées spin-orbitales pour les systèmes à couches fermées où les électrons sont tous appariés. Une fonction biélectronique écrite sous la forme



1 1 2 2 1 2 2 1



1 2 ( ) ( ) ( ) ( ) ( , ) 2 x x x x x x     

  génèrera une fonction générale à N

particules de la forme : 1 2





det ( ) ( , , , ) ! i k n x x x x n   

Ce déterminant de Slater conduit à une fonction d’onde multiélectronique et antisymétrique, respectant le principe d’exclusion de Pauli. La fonction d’onde entre les électrons de même spin est illustrée par un espace entourant l’électron dans la distribution de spins parallèles qualifié de trou d’échange appelé aussi « trou de Fermi ». Ce trou est représenté par une sphère de densité électronique constante et équivalente à la charge d’un électron. Il suit l’électron dans ses déplacements et, par conséquent, tient compte de l’échange : c’est là toute la différence entre la méthode HF et celle de Hartree.

L’équation [1. 38].sera résolue d’une manière auto-cohérente (SCF pour « Self Consistent

0

 donne une nouvelle fonction 1 et ainsi de suite jusqu’à l’obtention d’une fonction d’onde auto-cohérente à l’ordre n, lorsque   n n1

[30,31]. Après convergence, l’énergie est à son minimum et les orbitales génèrent un champ produisant les mêmes orbitales : d’où le nom de cette méthode. Celle-ci est également variationnelle, dans la mesure où elle permet d’affirmer que pour l’état fondamental, la valeur de l’énergie associée à n’importe quelle autre fonction sera toujours supérieure à l’énergie associée à la fonction d’onde exacte ₀:E( ) E₀( )

L’énergie totale est la somme de l’énergie cinétique et de trois termes d’énergie potentielle

tot cin ne coul X

E E E E E avec 2 2 1 ( ) ( ) 2 N cin i i i E r r dr m    



   [1- 39] ( ) ( ) ne E 



v r  r dr [1-40] 0 1 ( ) ( ) 4 coul r r E dr dr r r   



     [1-41] 2 , 0 ( ) ( ) ( ) ( ) 4 N i k i k x i k r r r r e E dr dr r r         



    [1-42].

Ene représente l’énergie potentielle classique d’une densité de charge ρ(r) dans un potentiel externe Vext( r ) . Ecoul à son tour est une énergie potentielle due à la répulsion électronique entre deux électrons occupant les positions r et r , La dernière contribution à l’énergie potentielle est un terme d’échange Ex inexistant en mécanique classique.

Dans cette méthode, la « self-interaction » désignant l’interaction de l’électron avec lui-même s’annule du fait de son inclusion dans le potentiel j(r) et dans l’opérateur d’échange k^ Les méthodes HF considèrent que l’électron est dans un champ moyen des N électrons [32,33]. Le fait d’annuler cette « self-interaction » est un avantage de la méthode Hartree-Fock par rapport à la DFT.

L’échange entre deux électrons de même spin est bien décrit par une séparation spatiale (répulsion coulombienne). De plus, deux électrons voisins peuvent être de spins opposés (up ↑ et down ↓). La méthode Hartree-Fock ne schématise pas la répulsion entre ces deux, par conséquent, il s’agit de la même interprétation pour les paires d’électrons de même spin et de spin différents. L’énergie se trouve généralement supérieure à la valeur exacte. De ce fait l’énergie de corrélation Ecorr , représentant la différence entre l’énergie exacte Eexacte et celle d’HF EHF , est une quantité négative :

corr exactes HF

E E E [1-43]

Ecorr sera considérée comme une mesure de l’erreur introduite par l’approximation HF. Comme il y a un trou d’échange excluant les électrons de même spin dans la même région d’espace, un autre trou peut aussi exister pour les électrons de spins opposés, et vu l’application du principe d’exclusion de Pauli, le trou de corrélation (« trou de Coulomb ») sera plus petit que celui d’échange.

Cependant, il existe deux types de corrélation, suivant la manière de séparer les électrons:

i) une corrélation dynamique à courte distance, due à la répulsion entre deux électrons

lors de leurs déplacements respectifs,

ii) une corrélation non dynamique, dite statistique, liée à l’existence de déterminants de

Slater relativement dégénérés en énergie. Cet effet est présent lorsque l’état fondamental d’un système électronique ne peut pas être décrit par un seul déterminant de Slater.

Les équations HF ne sont pas toujours faciles à résoudre. Aussi exprime-t-on les orbitales moléculaires (OM) comme des combinaisons linéaires de jeux prédéfinis de fonctions monoélectroniques. D’où le qualificatif de cette approximation : LCAO pour « Linear Combinaison of Atomic Orbitals ». À partir de l’équation des orbitales moléculaires :

1

k

i Ci 



Il s’agira de déterminer les coefficients C. Le déterminant de Slater, solution de l’équation à N électrons, est construit à partir des N/2 orbitales de plus basses énergies. La méthode HF peut être restreinte, RHF pour (« Restricted Hartree-Fock ») et concernera les systèmes à couches fermées, et contraignants les spin-orbitales appariés de spin différents à avoir la même partie spatiale. Une deuxième approche, dite non restreinte, UHF (pour « Unrestricted Hartree-Fock ») [34,35] s’appliquera aux systèmes dits à couches ouvertes. Elle consiste à traiter indépendamment les orbitales α et β. Les orbitales n’étant plus totalement occupées, le nombre des intégrales à calculer est doublé et demande plus de temps de calcul.

Dans la méthode HF, les électrons sont considérés comme indépendants les uns des autres et se déplace chacun dans un potentiel moyen créé par l’ensemble des électrons. L’électron se trouve sans interaction avec l’électron voisin, ce qui est un inconvénient de cette méthode. D’autres méthodes viennent remédier à ce problème de manque de corrélation

I.3.1.4. Approximation Post-Hartree-Fock (PHF):

Cette approximation propose des effets de corrélation qui ne sont pas pris en compte dans une approche de type HF. Elle fait appel à des fonctions d’ondes corrélées, solution du problème à N électrons sous la forme d’une combinaison linéaire de déterminants de Slater.

Les méthodes Post-HF se répartissent par ordre croissant en ressources informatiques d’abord la théorie de perturbation de Møller-Plesset au second ordre (MP2) ; puis viennent les méthodes MP3 et MP4 plus sophistiquées et par suite plus « gourmandes. Parmi ces méthodes, existent également les méthodes d’Interaction de Configuration (CI) et les méthodes MSCF (pour « Multi Configuration Self Consistent Field »).

Ces méthodes ne sont pas adaptées aux grands systèmes moléculaires tels que les complexes à transition de spin. Une solution tenant compte de la corrélation pour de tels composés, et qui permet de résoudre le système en fonction de sa densité monoélectronique, est apportée par la théorie de la fonctionnelle de densité DFT [36].

I.3.2. Théorie de la fonctionnelle de densité DFT :

Comme nous l’avons mentionné dans le paragraphe des méthodes Post Hartree-Fock, ces dernières sont lourdes et inapplicables dans les grands systèmes. Au cours des trente dernières années, la Théorie de la Fonctionnelle de la Densité DFT (« Density Functional Theory »), venant compléter les méthodes HF et Post-HF, s’est révélée comme particulièrement performante. Cette approche présente plusieurs avantages qui facilitent son utilisation dans différents domaines, surtout en chimie et science des matériaux.

 D’abord, elle inclut dans son formalisme une grande part de la corrélation électronique.

 Elle peut être appliquée à des systèmes aussi différents que les matériaux covalents, ioniques.

 L’aspect monoélectronique permet de donner une interprétation « chimique » de la fonction d’onde. Dans le cas des méthodes Hartree-Fock, il s’agissait d’exprimer l’énergie du système en fonction de la fonction d’onde , alors que dans le cas de la DFT, l’énergie sera une fonctionnelle de la densité électronique du système. Avant de passer aux fondements de la DFT, il nous faut d’abord définir ce qu’est la densité électronique (r).

I.3.2.1. Densité électronique :

Dans les sections précédentes, nous avions défini les électrons comme étant des particules indissociables. Or, en tant que particule isolée, l’électron ne peut pas être localisé : nous parlerons plutôt de sa probabilité de présence dans un élément de volume dr , définissant

ainsi la densité électronique (r). En fait, les électrons sont considérés dans leur ensemble (nuage électronique) et la densité électronique localisera les régions de l’espace où les électrons sont les plus probables. Cette probabilité de présence sera définie comme étant l’intégrale multiple du carré de la fonction d’onde.

Il s’agit d’une fonction positive dépendant uniquement des trois coordonnées spatiales (x,y,z). Cette quantité s’annule à l’infini ; intégrée sur tout l’espace, elle est égale au nombre total d’électrons N :

( ) 0 ( ) r r dr N      



[1-45].

Contrairement à la fonction d’onde, la densité électronique est une observable qui peut être mesurée par diffraction X. De ce fait, la densité électronique est riche d’informations : « La connaissance de la densité électronique est tout ce dont nous avons besoin pour une détermination complète des propriétés moléculaires » (E. Bright Wilson, 1965).

Vu l’importance de la densité électronique, plusieurs tentatives de mise en place d’un formalisme quantique basée sur cette quantité ont été proposées. Citons l’approche de Thomas-Fermi, consistant à exprimer toutes les contributions à l’énergie électronique totale en termes de densité électronique [37,38]. Le système inhomogène est subdivisé en volume élémentaires d r3 , dans lesquels les électrons ont un comportement d’un gaz homogène de densité constante : un tel gaz est appelé jellium.

I.3.2.2. Théorèmes de Honenberg-Kohn :

Premier théorème de Hohenberg-Kohn :

Le premier théorème de Hohenberg et Kohn [39] consiste à justifier théoriquement la relation entre le potentiel et la densité électronique. À une densité électronique donnée correspond un potentiel extérieur uniqueV ext (r) En fait, le potentiel est à une constante près, une fonctionnelle de la densité électronique (r) . Ainsi pour un système à N électrons (positions Rα , charges nucléaires Zα ), l’hamiltonien pourra être construit à partir de la densité électronique  (r) , permettant ainsi de connaitre la fonction d’onde Ψ fond et

l’énergie E fond fondamentales propres du système. L’énergie totale du système

Deuxième théorème de Hohenberg-Kohn :

Honenberg et Kohn ont montré que toute énergie E (Ψ), satisfaisant les limites nécessaires ( )r 0 et



( )r dr N et qui est associée à un potentiel extérieur V ext, est toujours supérieure ou égale à celle de l’état fondamental E



( )r



Dans ce cas, l’énergie

de l’état fondamental s’écrira sous la forme :













1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 i j XC ne i j ij r r E r T r E r V r r dr dr dr r          



 



[ 1 . 46 ].

Les termes :



V_ne( ) ( )r  r dr représentent l’interaction électrostatique électron-noyau alors que le terme 1 ( ) ( ) 2 i j i j ij r r dr dr r  



correspond à la répulsion électrostatique électron-électron.

T’

[

 (r)

]

représente l’énergie cinétique d’un gaz d’électrons en interaction répartie en:

 Échange dû à l’anti-symétrisation de la fonction d’onde,

 Corrélation « statistique » qui se définit comme étant l’échange des électrons de niveaux d’énergie quasi dégénérée,

 Corrélation « dynamique » qui consiste à minimiser l’énergie des électrons,

 Auto-interaction dépendant du terme de répulsion électron-électron.

I.3.2.3. Théorèmes de Kohn-Sham :

L’idée de Kohn et de Sham est d’utiliser un système fictif de N électrons non interagissant, de même densité électronique que le système en interaction, et de remplacer ainsi le terme



( )



T  r par le terme T



( )r



représentant l’énergie cinétique du gaz d’électron sans

interaction.

Cette correspondance entre un système d’électrons en interaction et un système sans interaction a en fait plusieurs conséquences, parmi lesquelles le passage d’une description, basée sur la fonction d’onde à N électrons, à une autre avec N fonctions d’ondes mono-électroniques.Pour décrire l’état fondamental électronique Kohn et Sham proposent de remplacer la fonctionnelle d’énergie de Honenberg et Kohn par un système d’équations autocohérentes à un électron [40].

La résolution de ces dernières, appelées équations de Kohn-Sham, permet par conséquent de minimiser l’énergie E



( )r



Elles sont couplées par la densité électronique

( ) _i( ) _i( )

i

r r r

 _



_{ }

inclue dans la solution obtenue d’une façon itérative.

Afin d’augmenter les orbitales en terme de base de fonction d’ondes, différentes bases peuvent être utilisées. Une fois ces dernières choisies, les orbitales sont utilisées pour déterminer la meilleure densité  au travers du cycle autocohérent.

I.3.2.4. Trou d’échange et de corrélation :

La densité de spin



₂( , )r r_{1 2} représente la probabilité de trouver deux électrons avec des spins

σ

1et

σ

2 quelconques dans deux éléments de volume dr1et dr2,

2

2( , )r r1 2 N N( 1) ... ( , ....r r1 2 rN dr dr1 2....drN

  

 

 [1-47]

Pour des fermions chargés tels que les électrons, la probabilité de trouver l’électron 1 en r1 est largement dépendante de la position de l’électron 2 : nous dirons que leurs mouvements sont corrélés. Mais la nature des fermions fait que les électrons se repoussent à cause de la répulsion Coulombienne. Le principe de Pauli ainsi que la corrélation inter-électronique interdisent la présence des électrons de spin (

σ

1 2 ) dans la même région de l’espace au moyen du trou d’échange-corrélation (XC). Le terme « trou » représente la diminution de la densité électronique en r2 liée aux interactions électron-électron non classiques. La

probabilité d’occupation spatiale s’écrit alors :

2 2 2 2 1 2 (r ,r ) (r )   [1-48] 1 1 2 1 2 1 2 (r ) ( )r ( )r _xctrou ( ) ( )r r ( )r _xctrou   _  _    [1-49]

Le premier terme correspond à l’interaction coulombienne, alors que le deuxième terme représente l’interaction d’une densité électronique avec celle d’un trou d’échange-corrélation.

La matrice densité est ainsi définie et normalisée pour les paires d’électrons r1 et r2 de spins respectifs σ1 et σ2 1 2 1 2 3 3 1 2 ( , ) ( 1) d r d r r r N N     

 

[1-50]

Cependant la densité d’échange-corrélation peut s’exprimer sous la formetrou_xc ( , )r r_{1 2} : 3 3 1 2 3 3 1 2 3 3 1 1 2 1 2 1 2 1 2 1 2 1 2 1 2 ( ) ( , ) ( , ) ( ) ( ) 1 1 1 2 2 2 trou xc ee ee X C r r r r r r r V d r d r d r d r d r d r r r r r r r V U E             







_[1-51]

U est le terme d’énergie électrostatique et E_XC celui d’échange corrélation définie comme étant l’interaction d’une densité électronique avec celle probabiliste d’un trou d’échange-corrélation. Un autre paramètre peut également être introduit qui permet de définir l’amplitude de la corrélation : λ[41] Pour λ = 0 , la corrélation est nulle et il n’y a pas d’interaction sur le système, alors que pour λ = 1, le système sera entièrement corrélé. La densité de probabilité s’écrira alors :

  

_(r_{1 1},r_{2 2})



_( )r n r_{1 }( ₁

 

₁,r_{2 2}) [1-52]

1 1 2 2

( , )

n r_

 

r est la probabilité de trouver un électron de spin σ2 dans le volume élémentaire

3 2

d r en r₂pourvu qu’un électron de spin σ1 soit dans le volume 3 1

d r enr₁

I.3.2.5. Approximations en DFT :

I.3.2.5.1. Approximation locale de la densité (LDA) :

La fonctionnelle d’échange-corrélation E xc est une grandeur physique dépendante de plusieurs paramètres comme la densité électronique, l’énergie cinétique, etc. Afin d’obtenir une bonne approximation de cette fonction, elle doit reproduire au mieux les caractéristiques physiques du trou d’échange-corrélation. Elle se base sur les propriétés d’un gaz homogène d’électrons ; la densité électronique et la fonction d’onde sont considérées localement comme constantes. La fonctionnelle d’échange-corrélation s’écrit :





3

( ) ( ) ( )

XC XC

Où



_{X C} représente la densité d’énergie d’échange-corrélation par quasi-particule. Elle se répartit en deux termes εx et εc qui désignent respectivement l’échange et la corrélation. Cette répartition permet d’utiliser l’énergie d’échange proposée par Dirac pour le gaz homogène d’électrons : 1 4 3 3 3 3 ( ) 4 XC







 

     [1-54]

Par le concept de LDA il est possible d’estimer l’énergie d’échange-corrélation d’un système inhomogène en utilisant les résultats d’un gaz homogène d’électrons de densité égale à la densité locale d’un système inhomogène. L’énergie de corrélation d’un gaz uniforme d’électrons n’est pas déterminée exactement. Cependant, certaines expressions approchées permettent de décrire les densités électroniques faibles ou élevées. Cette approximation considérée localement permet de décrire correctement les systèmes ayant une densité électronique variant faiblement dans l’espace. Par contre, la LDA, présente des inconvénients: certaines grandeurs sont surestimées, telles que les énergies de cohésion, d’autres sont sous-estimées, telles que les longueurs de liaisons [42]. Nous noterons que la LDA traite l’échange localement, alors que la méthode HF le traite sur tout le système rendant cette dernière mieux adaptée à ce genre de problème

I.3.2.5.2. Introduction du terme de spin :

L’introduction de la notion de spin dans l’approximation de la LDA conduit à la LSDA (« Local Spin Density Approximation »). La densité électronique se divisant en deux populations () et () , l’énergie sera alors :

hom 3

, ( ( ), ( )) ( )

LSDA

XC XC r r r r

( , )

LSDA XC



 

_{ } étant l’énergie d’échange-corrélation par particule du gaz d’électrons uniforme de densité (r). Elle se répartit en termes d’échange et en termes de corrélation :

( , ) ( , ) ( , )

LSDA

X C X C



 

_{ } 

 

_{ } 

 

_{ } [1-56]

L’avantage de cette approximation est qu’elle permet de décrire des systèmes placés dans un champ magnétique externe et d’accéder à la susceptibilité. La LSDA convient aussi bien aux systèmes dont la variation de la densité électronique est lente qu’aux systèmes dont la densité électronique varie rapidement, ce qui la rend d’un usage plus fréquent que la LDA [43]. Cependant, elle aussi surévalue les énergies de liaisons et donne des « gaps » trop faibles pour les semi-conducteurs et les composés isolants.

I.3.2.5.3. Introduction d’un gradient à l’approximation locale :

Afin de corriger les erreurs de la LDA (la sous-estimation de l’énergie d’échange d’un pourcentage de 10 à 15 %, alors que la corrélation était surestimée de presque 200 % [44]), d’autres approximations ont vu le jour. Dans un premier temps, les auteurs ont introduit un terme de gradient dans l’expression de l’énergie, en traitant la LDA comme le premier terme d’une série de Taylor :

 

4 3 ( ) ( ( )) ( ) ( ( )) ( ) .... GEA GEA XC XC XC r r r dr C r r E       dr   

_



_

 [1-57]

Cette forme de fonctionnelle constitue l’approximation du gradient GEA (« Gradient

Expansion Approximation »). Cette approximation donnant des résultats moins bons que la

LDA, la fonctionnelle GEA

 

X C

E  a été modifiée afin de respecter les principales conditions aux limites. L’approximation résultante est appelée GGA pour « Generalized Gradient

Approximation » :



,



( ( ), ( ))

GGA GGA

XC XC r r

Les contributions pour l’échange et la corrélation sont développées séparément :



,



( , ) ( , )

GGA GGA GGA

XC EX C

E      drE   [1-59]

Comme nous l’avons vu, le problème de la LDA était l’échange ; une attention particulière sera donnée au développement de cette partie :





4 3 , ( ( )) ( ) GGA GGA X EX F s r r dr E    



 [1-60]

F étant la fonction du gradient réduite :

4/3 ( ) ( ) ( ) r r s r    

Plusieurs fonctions se basant sur cette approximation ont été proposées : citons les fonctions de Becke 88 (B88) [45], la fonction de Perdew/Wang 86 (PW86) [46] :

o B88 : La fonctionnelle d’échange B88 est basée sur une analyse dimensionnelle de la densité d’échange : 2 88 1 ( ) 1 6 sin ( ) B _s s s h s F     

étant un paramètre empirique déterminé par analyse des moindres carrés des énergies d’échange des six atomes de gaz rares (de He à Rn) : la valeur

qui minimise l’erreur est égale à 0.0042 u.a.

o PW91 : Perdew et Wang [47] : celle-ci provient d’une modification de cette fonctionnelle F afin de satisfaire à d’autres conditions.

o PW86 : Cette fonctionnelle est basée sur une expansion du gradient du trou d’échange-corrélation autour de sa forme LSDA :

1/15 2 4 6 86 ( ) 1 1, 296 14 0, 2 PW s s s s p p p F    _{ }   _{ }   _{ }            avec

(24



2 1/3) Précisons que les fonctionnelles de corrélation ont des formes analytiques beaucoup plus compliquées et qui ne peuvent pas être comprises à l’aide de raisonnements physiques actuels simples.

I.3.2.5.4. Fonctionnelles hybrides pour le calcul moléculaire :

Quand Kohn et Sham proposèrent leur approche en 1965, ils avaient mentionné l’intérêt d’avoir un terme d’échange exact. Ils avaient déjà formalisé une expression formelle pour l’énergie d’échange-corrélation, basée sur l’approximation de Hartree-Fock, alors que le terme de corrélation restait inchangé par rapport à celui de la LDA. L’utilisation de cette fonctionnelle permettait au potentiel effectif d’avoir un comportement asymptotique correct. Bien que fonctionnant correctement sur les atomes, les résultats sont décevants pour les molécules. La GGA donne de meilleurs résultats. La raison en est le caractère artificiel de la séparation des termes d’échange et de corrélation : en combinant le terme d’échange non local provenant de l’équation HF, avec un trou de corrélation local (LDA), l’autocohérence de la description du trou local a été perdue. Pour cela, le choix de Becke était d’utiliser différemment l’échange exact, en incluant une partie de celle-ci dans l’expression de l’énergie d’échange-corrélation [48]. L’expression résultante se compose de trois paramètres ; par suite, elle est désignée par B3 [49] :

88 91

0( )

LDA exact LDA B PW

XC EXC a EX EX ax EX aC EC

E        [1-61]

Les coefficients a0 , a x et aCsont déterminés de manière semi-empirique par ajustement

sur les données expérimentalesE_{X C}exact représente ici l’énergie d’échange exacte obtenue à partir d’un calcul HF.

a

0 peut être reliée au caractère « particules indépendantes » du

système. a xet a c aident à optimiser les corrections du gradient pour l’échange et pour la

de la manière la plus simple et de retrouver la limite du gaz d’électrons uniforme. Un résultat intéressant de cette approximation est la précision améliorée sur les énergies, meilleure que celle obtenue en utilisant l’approximation GGA.

À titre d’exemple, l’énergie d’échange-corrélation dans le cas de la fonctionnelle hybride B3LYP (constituée de la fonctionnelle B88 à trois paramètres et de la fonctionnelle de corrélation LYP de Lee, Yang et Parr [50]) s’écrit sous la forme :

3 88 (1 ) (1 ) B LY P LSDA B LY P LSDA XC X XC X C C E  a E aE bE cE  c E [1-62] avec a = 0,2, b = 0,72 et c = 0,81.

Les paramètres a , b et c sont des quantités semiempiriques déterminées par un lissage des chaleurs de formation d’un ensemble standard de molécules. Cette fonctionnelle donne des résultats remarquablement précis sur un grand nombre de systèmes [51].

Notons qu’au cours de ce travail, nous avons utilisé essentiellement les fonctionnelles B3LYP.

I.3.2.5.5. Bases utilisées dans le calcul moléculaire :

Dans ce paragraphe, nous allons décrire les fonctions de base. Les quatre types de fonctions de base ou orbitales atomiques les plus utilisées sont :

o STO

Les orbitales de type Slater ou STO (« Slater Type Orbitals ») [52], o Les orbitales de type Gaussienne ou GTO (« Gaussian Type Orbitals ») [53], o Les fonctions de base numérique,

o Les ondes planes.

Les orbitales de type Slater s’écrivent en coordonnées sphériques sous la forme :

1 , ( , , ) STO n l m r r   NY r e 



_{ }   [1-63]

N étant le facteur de normalisation, n, l et m sont les nombres quantiques  et Y l ,msont

les fonctions harmoniques usuelles décrivant la partie angulaire de la fonction. Ces fonctions présentent une décroissance correcte avec r de type exponentiel.

Pour les orbitales de type gaussienne, chaque fonction est centrée sur un atome défini par sa position R A . Elle possède une certaine ressemblance avec les orbitales atomiques (OA) correspondant aux solutions des équations HF pour les atomes isolés.

) ( , ) ( , ) ( _{A A P p P A} P P r R d g r R r R _  _



 



 [1-64]

avec gP et P r définis par :

2 ( , ) r P r g  e

( )

n m l y z

P r



cx

Les gaussiennes de type s, p, d, etc. ... ne sont que les solutions du polynôme de degré 0,1, 2, etc. ... La partie angulaire p(r) de la fonction est constituée d’un polynôme de degré variable. La partie radiale de la fonction est une combinaison linéaire de gaussiennes primitives, notées gp . Selon que les différents paramètres nécessaires à l’expression des GTO, les coefficients d  p et les exposants α_{ p} de la contraction, ainsi que ceux du