Dissemblance et diversit´e

(1)

Dissemblance et diversit´e

D. Chessel Notes de cours cssb9

On aborde les bases d’un domaine plein d’avenir : celui de la mesure de la biodiversit´ e. Dissimilarit´ es m´ etriques, euclidiennes, ultram´ e- triques : d´ efinitions et mode de calcul. Leurs usages. Typologie et diversit´ e sont deux concepts indissociables.

Table des mati` eres

1 Introduction 2

2 Calcul des dissimilarit´ es 4

2.1 D´ efinitions . . . . 4

2.2 Distance de Mahalanobis . . . . 6

2.3 Dissimilarit´ es ´ ecologiques . . . . 7

2.4 Distances g´ en´ etiques, taxonomiques, phylog´ en´ etiques . . . . 8

3 Propri´ et´ es des dissimilarit´ es 10 3.1 Dissimilarit´ es euclidiennes . . . . 10

3.2 Que faire des distances non euclidiennes . . . . 13

3.3 Dissimilarit´ es ultram´ etriques . . . . 15

4 Des esp` eces aux communaut´ es 18 4.1 La question de la mesure de la diversit´ e . . . . 18

4.2 Diversit´ e et diff´ erences . . . . 23

4.3 Typologie sur diff´ erences . . . . 25

4.4 Maximiser la diversit´ e . . . . 30

R´ ef´ erences 35

(2)

1 Introduction

Nous partirons d’un probl` emes pos´ e par des ornithologues de renom [2] d´ ecrit dans :

http://pbil.univ-lyon1.fr/R/pps/pps023.pdf L’article contient toutes les donn´ ees consign´ ee dans l’objet ecomor :

library(ade4) data(ecomor)

Les donn´ ees originales, directement accessibles dans l’article et reproduites dans la liste ecomor pr´ esentent une petite erreur d’´ edition qui a une grande impor- tance s´ emantique. Les auteurs confrontent trois cort` eges faunistiques compl` ete- ment disjoints. Trois r´ egions soumis ` a un bioclimat m´ editerran´ een (Chili, Ca- lifornie et Provence) ont une avifaune nicheuse sans aucune esp` ece commune.

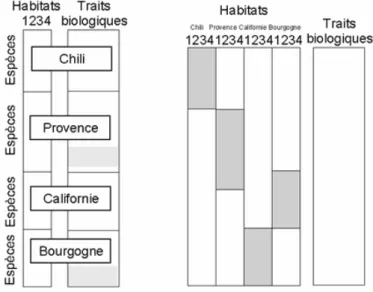
Elles sont cependant structur´ ees par le mˆ eme gradient d’ouverture du milieu (prairies, maquis, forˆ ets). La comparaison des trois univers conduit ` a la d´ efi- nition de 4 types d’habitats comparables. D’autre part un certain nombre de traits ´ ecologiques et de variables morphom´ etriques sont enregistr´ ees pour toutes les esp` eces nicheuses. Le sch´ ema de la structure des donn´ ees est :

Chaque tableau esp` eces-habitats est en pr´ esence-absence ce qui d´ efinit le pro- fil de chaque esp` ece du type 1000 pour les sp´ ecialistes des milieux ouverts ` a 0001 pour les foresti` eres strictes en passant par 1111 pour les esp` eces qu’on rencontre partout. Les auteurs ont rajout´ e une quatri` eme r´ egion de r´ ef´ erence non m´ editerran´ eenne (Bourgogne), pour comparaison. Mais le nouveau cort` ege a la propri´ et´ e d’avoir une partie de ses esp` eces en commun avec la Provence.

Dans l’article une ´ etoile indique qu’une esp` ece est commune au pool Provence et

au pool Bourgogne mais seul est mentionn´ e le profil en Provence ce qui laisse ` a

penser qu’il est le mˆ eme dans les deux r´ egions. Or ce n’est pas vrai et J. Blondel

m’a transmis les pr´ ecisions n´ ecessaires. La modification porte sur 13 des 129

esp` eces (et uniquement sur le profil d’habitat) mais oblige ` a choisir entre deux

sch´ emas :

(3)

A gauche, on a r´ ep´ et´ e les esp` eces en commun (la partie grise signale la r´ ep´ eti- tion). A droite on a utilis´ e leur profil global (la partie grise seule ne contient pas uniquement des 0). La perturbation est petite mais a grande signification car elle conduit ` a deux probl` emes diff´ erents. La forme de gauche est un ensemble de quatre couples de tableaux ´ ecologiques qui demande la comparaison de quatre

´

evolutions du contenu en traits biologiques entre les quatre types d’habitat. La forme de droite est un couple unique qui envisage la variation en traits biolo- giques soit entre r´ egions (analyse inter), soit entre strates d’une mˆ eme r´ egion (analyse intra), soit entre tous les ´ el´ ements (analyse simple). La situation est encore compliqu´ ee par le sch´ ema des hypoth` eses de l’article (figure 1). On y

Fig. 1 – 1 - Mod` ele de la convergence bioclimatique, 2/3 - Absence de conver- gence, 4 - Mod` ele phylog´ en´ etique, 5 - Convergence bioclimatique ajust´ ee (CAL Californie, CH Chili, PR Provence, BU Bourgogne)

voit une typologie de r´ egions soit faible (2) soit forte (3) soit organis´ ee (1, 4, 5)

mais sans r´ ef´ erence au gradient environnemental commun. Or comment s’int´ e-

resser ` a la variation entre r´ egions sans tenir compte que chacune d’entre elles est

(4)

elle-mˆ eme une structure (et bien connue pour ˆ etre forte) ? La question est donc tr` es ouverte. On a conserv´ e les donn´ ees sous la forme (A Lieu d’alimentation, B R´ egime alimentaire, C Morphom´ etrie) :

names(ecomor)

[1] "forsub" "diet" "habitat" "morpho" "taxo" "labels" "categ"

La question est comment mesurer, comparer, d´ ecrire des structures faunis- tiques avec des cort` eges sp´ ecifiques distincts. Peut-on sortir du comptage pur et simple des esp` eces pour mesurer et comparer la biodiversit´ e. Ces questions sont d’actualit´ e [9], c’est le moins qu’on puisse dire ! L’essentiel des questions introduites ici sont d´ evelopp´ ees dans la th` ese de S. Pavoine [21].

2 Calcul des dissimilarit´ es

Chacun sait qu’il y a plusieurs mani` eres de mesurer une distance, ` a vol d’oiseau, en kilom` etres d’autoroute ou en minutes de TGV. Il y en a encore bien plus de mani` eres de mesurer la dissimilarit´ e au sens large entre objets.

2.1 D´ efinitions

En math´ ematiques, on appelle distance d´ efinie sur un ensemble E une fonc- tion d de E × E dans R qui v´ erifie pour tout x, y et z ´ el´ ements de E :

d (x, y) ≥ 0 d (x, y) = 0 ⇒ x = y

d (x, y) = d (y, x) d (x, y) ≥ d (x, z) + d (z, y)

En statistique, on appelle dissimilarit´ e d´ efinie sur un ensemble fini I ` a n ´ el´ e- ments (num´ erot´ es 1, 2,. . ., i, ..., n) une fonction d de I × I dans R qui v´ erifie pour tout i et j :

d _ij ≥ 0

(5)

d ii = 0 d ij = d ji

La dissimilarit´ e est dite m´ etrique (d´ efinition 1 dans [8]) si pour tout i, j et k

´

el´ ements de I on a :

d _ij ≤ d _ik + d _kj

Une dissimilarit´ e est euclidienne (definition 2 dans [8]) si il existe n points dans un espace euclidien dont les distances deux a deux sont exactement les dissi- milarit´ es consid´ er´ ees. On parle aussi de distance euclidienne mais le terme est ambigu. Nous y reviendrons.

Une dissimilarit´ e est ultram´ etrique si pour tout i, j et k ´ el´ ements de I on a :

d ij ≤ max(d ik , d kj )

Nous verrons que cette notion est essentielle pour la mesure de la biodiversit´ e.

En biologie, on utilise le terme de distance pour d´ esigner la diff´ erence mesu- r´ ee entre deux individus, deux populations, deux sites, deux esp` eces, . . ., sans se pr´ eoccuper de d´ efinition. Pour suivre la coutume, on appellera matrice de distances une matrice contenant une dissimilarit´ e observ´ ee. Les matrices de dis- tances sont donc des matrices carr´ ees (n lignes et n colonnes), contenant des nombres positifs ou nuls, sym´ etriques et ayant des ´ el´ ements nuls sur la diago- nale. Ces objets sont stock´ es dans dans la classe dist sous la forme d’un vecteur avec des attributs :

x <- matrix(rnorm(100), nrow = 5) d <- dist(x)

d

as.matrix(d) unclass(d)

Le nombre d’indices de dissimilarit´ es propos´ es en ´ ecologie est proprement vertigineux. Calculer une dissimilarit´ e rel` eve de la partie exp´ erimentale (acqui- sition), s’en servir rel` eve de la partie statistique de l’exploitation des donn´ ees.

Quelques fonctions qui calcule des dissimilarit´ es :

– les distances directement import´ ees ou observ´ ees (as.dist) – les distances issues des tableaux (dist et dist.quant) – les distances issues des triplets statistiques (dist.dudi)

– Les distances issues des donn´ ees floro-faunistiques en pr´ esence-absence (dist.binary)

– Les distances g´ en´ etiques (dist.genet) – Les distances de voisinages (dist.neig) – les distances entre profils (dist.prop)

– Les distances phylog´ en´ etiques (newick2phylog) – les distances taxonomiques (dist.taxo)

Pour utiliser d’autres options, examiner les librairies qui sont orient´ ees ´ ecologie et qui sont cit´ ees dans :

http://cran.r-project.org/src/contrib/Views/Environmetrics.html

Quelques cas importants sont ` a connaˆıtre.

(6)

2.2 Distance de Mahalanobis

Pour les variables morphom´ etriques, la distance de Mahalanobis s’impose.

A l’origine [18] le nom d´ esigne la distance entre populations au sens de l’inverse de la matrice de covariance intra-classe. Par extension on utilise le terme pour d´ esigner la distance entre deux individus au sens de l’inverse de la matrice de co- variances totales. Les liens entre les deux est affaire de mod` ele mais l’utilisateur a besoin de connaˆıtre la fonction de cette id´ ee.

set.seed(29092006) par(mfrow = c(1, 3)) library(MASS)

s <- matrix(c(1, 0.8, 0.8, 1), 2) x1 <- mvrnorm(20, c(0.5, -0.5), s) x2 <- mvrnorm(20, c(-0.5, 0.5), s) x <- rbind.data.frame(x1, x2) row.names(x) <- as.character(1:40) fac <- factor(rep(1:2, rep(20, 2)))

s.class(x, fac, xlim = c(-3, 3), ylim = c(-3, 3), sub = "A", csub = 3) choix <- c(8, 24, 28)

s.label(x[choix, ], clab = 2, add.p = T) w <- dudi.pca(x, scan = F, scal = F)

s.class(w$li, fac, xlim = c(-3, 3), ylim = c(-3, 3), sub = "B", csub = 3)

s.label(w$li[choix, ], clab = 2, add.p = T)

s.class(w$l1, fac, xlim = c(-3, 3), ylim = c(-3, 3), sub = "C", csub = 3)

s.label(w$l1[choix, ], clab = 2, add.p = T)

d = 1

A

●

1 2

8 24

28

d = 1

B

●

● ●

●

● ●

●

1 2

8 24 28

d = 1

C

●

● ●

●

● ●

●

1 2

8 24 28

Utiliser la distance de Mahalanobis, c’est utiliser la distance euclidienne ordi- naire sur les coordonn´ ees normalis´ ees de l’ACP en lieu et place des donn´ ees.

On utilise des donn´ ees d´ ecorr´ el´ ees, en particulier en prenant en compte l’effet taille au niveau d’une seule variable (alors que cet effet compte dans la distance ordinaire comme 95 % des variables). Cette op´ eration est essentielle en morpho- m´ etrie et est malheureusement import´ ee dans bien d’autres domaines o` u elle ne sert que de perturbation.

as.matrix(dist(x))[choix, choix]

8 24 28

8 0.000000 1.282952 1.777313 24 1.282952 0.000000 1.294394 28 1.777313 1.294394 0.000000

as.matrix(dist(w$l1))[choix, choix]

8 24 28

8 0.000000 1.646473 2.180075 24 1.646473 0.000000 1.073575 28 2.180075 1.073575 0.000000

as.matrix(dist.quant(x, meth = 3))[choix, choix]

8 24 28

8 0.000000 1.646473 2.180075

24 1.646473 0.000000 1.073575

28 2.180075 1.073575 0.000000

(7)

2.3 Dissimilarit´ es ´ ecologiques

Pour les donn´ ees en pr´ esence-absence, les indices sont en grand nombre. Ce sont des indices de similarit´ e S compris entre 0 et 1 qu’on transforme en distance avec D = √

1 − S. Les donn´ ees propos´ ees par B. Hugueny et pr´ esent´ ees dans : http://pbil.univ-lyon1.fr/R/pps/pps050.pdf

posent clairement le probl` eme (pr´ esence-absence de n = 268 esp` eces dans p = 33 bassins cˆ otiers de l’Afrique de l’Ouest). Refaire la figure avec la fiche de documentation du dataset :

●

●●●●●●● ● ●● ● ●●

● ●

● ● ●

Senegal

Niger

Volta

Gambie Geba Corubal Konkoure Kolente Little Scarcies Rokel Jong Sewa Moa Mano Loffa Saint Paul Saint John Nipoue Cavally Tabou Dodo Nero San Pedro Mene Sassandra Boubo Bandama Agnebi Me Komoe Bia Tano Pra Mono Oueme Ogun

La distance entre deux bassins, du point de vue faunistique est une fonction du nombre d’esp` eces en commun a = n 11 et tient compte que du nombre d’esp` eces qui ne sont que dans le premier b = n 10 ou dans le second c = n 01 . Doit-on tenir compte du nombre d’esp` eces absentes dans les deux d = n 00 ?

Pour tous les couples on a en tout cas n = n 11 + n 10 + n 01 + n 00

La fonction dist.binary permet d’utiliser 10 indices indiqu´ es par :

1 = JACCARD index (1901) S3 coefficient of GOWER & LEGENDRE s1 = a/(a+b+c) --> d = sqrt(1 - s)

2 = SOCKAL & MICHENER index (1958) S4 coefficient of GOWER & LEGENDRE s2 = (a+d)/(a+b+c+d) --> d = sqrt(1 - s)

3 = SOCKAL & SNEATH(1963) S5 coefficient of GOWER & LEGENDRE s3 = a/(a+2(b+c)) --> d = sqrt(1 - s)

4 = ROGERS & TANIMOTO (1960) S6 coefficient of GOWER & LEGENDRE s4 = (a+d)/(a+2(b+c)+d) --> d = sqrt(1 - s)

5 = CZEKANOWSKI (1913) or SORENSEN (1948) S7 coefficient of GOWER & LEGENDRE s5 = 2a/(2a+b+c) --> d = sqrt(1 - s)

6 = S9 index of GOWER & LEGENDRE (1986) s6 = (a-(b+c)+d)/(a+b+c+d) --> d = sqrt(1 - s) 7 = OCHIAI (1957) S12 coefficient of GOWER & LEGENDRE s7 = a/sqrt((a+b)(a+c)) --> d = sqrt(1 - s)

8 = SOKAL & SNEATH (1963) S13 coefficient of GOWER & LEGENDRE

(8)

s8 = ad/sqrt((a+b)(a+c)(d+b)(d+c)) --> d = sqrt(1 - s) 9 = Phi of PEARSON = S14 coefficient of GOWER & LEGENDRE s9 = ad-bc)/sqrt((a+b)(a+c)(b+d)(d+c)) --> d = sqrt(1 - s) 10 = S2 coefficient of GOWER & LEGENDRE

s10 = a/(a+b+c+d) --> d = sqrt(1 - s) and unit self-similarity

2.4 Distances g´ en´ etiques, taxonomiques, phylog´ en´ etiques

Pour les donn´ ees g´ en´ etiques, les d´ efinitions des distances sont ind´ ependantes des modes d’utilisation. Elles sont associ´ ees aux m´ ecanismes temporels de la d´ erive des fr´ equences all´ eliques et de la s´ eparation des populations. Le pour- centage d’all` eles partag´ es est une mesure de la proximit´ e g´ en´ etique entre deux populations et ram` ene au cas pr´ ec´ edent.

Plus g´ en´ eralement, soit A un tableau de fr´ equences all´ eliques avec t popula- tions (lignes) et m all` eles (colonnes). Soit ν le nombre de loci. Le locus j donne m(j) all` eles.

m =

ν

X

j=1

m(j)

Pour la ligne i (1 ≤ i ≤ q) et l’all` ele k (1 ≤ k ≤ m(j)) du locus j (1 ≤ j ≤ ν ), on note a ^k _ij la valeur initiale dans le tableau (effectifs).

a ⁺ _ij =

m(j)

X

k=1

a ^k _ij p ^k _ij = a ^k _ij a ⁺ _ij Soit P le tableau de terme g´ en´ eral p ^k _ij . On a :

p ⁺ _ij =

m(j)

X

k=1

p ^k _ij = 1 p ⁺ _i+ =

ν

X

j=1

p ⁺ _ij = ν p ⁺ ₊₊ =

ν

X

j=1

p ⁺ _i+ = tnu

La fonction dist.genet propose les distances entre populations ` a partir des fr´ equences all´ eliques p ^k _ij les plus classiques :

Distance de Nei

D ₁ (a, b) = −ln(

P ν k=1

P m(k) j=1 p ^k _aj p ^k _bj q P ν

k=1

P m(k) j=1 (p ^k _aj ) ²

q P ν k=1

P m(k) j=1 (p ^k _bj ) ²

)

Distance angulaire d’Edwards

D 2 (a, b) = v u u t 1 − 1

ν

X

k=1 m(k)

X

j=1

q p ^k _aj p ^k _bj

Coefficient de coancestralit´ e ou distance de Reynolds

D ₃ (a, b) = v u u t

P ν k=1

P m(k)

j=1 (p ^k _aj − p ^k _bj ) ² 2 P ν

k=1 (1 − P m(k)

j=1 p ^k _aj p ^k _bj )

(9)

Distance euclidienne dite de Roger

D 4 (a, b) = 1 ν

nuy

X

k=1

v u u t 1 2

m(k)

X

j=1

(p ^k _aj − p ^k _bj ) ²

Distance absolue de Provesti

D 5 (a, b) = 1 2ν

ν

X

k=1 m(k)

X

j=1

|p ^k _aj − p ^k _bj |

Pour les donn´ ees spatiales, on utilise la distance ordinaire ou la distance de voisinage (longueur du plus court chemin d’un sommet ` a un autre) :

S01 S02

S03

S04 S05

S06

S07

S08

S09 S10 S11

S12 S13

S14 S15

S16 S17

S18 S19 S20

S21

S22 S23

S24 S25

data(irishdata)

area.plot(irishdata$area.utm, clab = 0) n0 <- neig(mat01 = irishdata$link > 0)

s.label(irishdata$xy.utm, lab = names(irishdata[[2]]), clab = 1, neig = n0, add.plot = T)

dist.neig(n0)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2 3

3 3 4

4 3 4 2

5 5 2 4 5

6 3 3 1 2 3

7 4 5 2 1 6 3

8 1 2 3 3 4 2 4

9 1 4 2 2 5 2 3 2

10 1 3 2 2 4 2 3 1 1

11 4 1 3 4 1 2 5 3 4 3

12 3 4 1 1 5 2 1 3 2 2 4

13 4 1 3 4 2 2 5 3 4 3 1 4

14 3 2 5 5 4 4 6 2 4 3 3 5 3

15 4 3 2 3 3 1 4 3 3 3 2 3 2 4

16 2 1 4 4 3 3 5 1 3 2 2 4 2 1 3

17 3 1 5 5 3 4 6 2 4 3 2 5 2 1 4 1

18 2 2 2 2 3 1 3 1 2 1 2 2 2 3 2 2 3

19 3 2 2 3 2 1 4 2 3 2 1 3 1 3 1 2 3 1

20 4 2 3 4 2 2 5 3 4 3 1 4 2 4 1 3 3 2 1

21 2 3 1 1 4 1 2 2 1 1 3 1 3 4 2 3 4 1 2 3

22 2 4 2 1 5 2 2 3 1 2 4 2 4 5 3 4 5 2 3 4 1

23 3 1 3 3 3 2 4 2 3 2 2 3 1 2 2 1 2 1 1 2 2 3

24 1 4 3 2 6 3 3 2 1 2 5 3 5 4 4 3 4 3 4 5 2 1 4

25 1 3 4 3 5 3 4 1 2 2 4 4 4 3 4 2 3 2 3 4 3 2 3 1

(10)

Pour les donn´ ees taxonomiques, on utilise la racine de la longueur du plus court chemin d’une esp` ece ` a un autre.

E3 E1 E2 E4 E5 E6 E7 E8 E9 E10 E11 E12 E13 E14 E15

●

● ●

●

● ●

●

● ●

●

data(taxo.eg) w <- taxo.eg[[1]]

names(w)

[1] "genre" "famille" "ordre"

row.names(w) <- sub("esp", "E", row.names(w)) w1 <- as.taxo(w)

wphy <- taxo2phylog(w1)

plot(wphy, cleaves = 2, cnod = 2) dist.taxo(w1)^2

E3 E1 E2 E4 E5 E6 E7 E8 E9 E10 E11 E12 E13 E14 E1 2

E2 2 2 E4 2 2 2 E5 2 2 2 2 E6 2 2 2 2 2 E7 2 2 2 2 2 2

E8 8 8 8 8 8 8 8

E9 8 8 8 8 8 8 8 4

E10 8 8 8 8 8 8 8 6 6 E11 8 8 8 8 8 8 8 6 6 4

E12 8 8 8 8 8 8 8 6 6 6 6

E13 8 8 8 8 8 8 8 6 6 6 6 4

E14 8 8 8 8 8 8 8 6 6 6 6 6 6

E15 8 8 8 8 8 8 8 6 6 6 6 6 6 2

Les distances phylog´ en´ etiques ont ´ et´ e abord´ ees dans la fiche cssb3 de la pr´ esente s´ erie. Chaque discipline utilise ou cr´ ee des dissimilarit´ es, par exemple l’analyse des donn´ ees textuelles :

http://www.cavi.univ-paris3.fr/lexicometrica/jadt/

On comprend que le passage par une matrice de dissimilarit´ e, est un outil puis- sant pour associer des informations de type vari´ e.

3 Propri´ et´ es des dissimilarit´ es

3.1 Dissimilarit´ es euclidiennes

La question est essentielle. Soient 4 points du plan :

(11)

A -1 -1

B 2 -1

C 2 1

D 1 2

Repr´ esenter ces 4 points et les distances qui les s´ eparent.

● ●

●

−1.0 −0.5 0.0 0.5 1.0 1.5 2.0

−1.0−0.50.00.51.01.52.0

X

Y

●

A B

C D

3 3.606 3.606

2 3.162 1.414

Oublier alors cette repr´ esentation et ne garder que les distances. Peut-on trouver 4 points sur un plan qui ont pour distances deux ` a deux les valeurs ci-dessous ?

A B C

B 3.000 C 3.606 2.000 D 3.606 3.162 1.414

Sans doute ! Mais si on ne connaˆıt que les distances, il peut ne pas y avoir de solutions. Le probl` eme et la solution sont de Gower [7]. En g´ en´ eral, la question est : ´ etant donn´ ee une matrice de distances D = [d ij ] entre n entit´ es existe t-il n points M i dans un espace euclidien de dimension p tels que :

d ² _ij = kM i − M j k ² ?

Si c’est le cas, l’espace poss` ede une base orthonorm´ ee dans laquelle le point M _i a des coordonn´ ees qu’on peut mettre sur la ligne i d’un tableau X. La matrice XX ^t contient alors les produits scalaires hM i | M _j i. Or :

d ² _ij = kM _i − M _j k ² = kM _i k ² + kM _j k ² − 2 hM _i | M _j i

Sans perte de g´ en´ eralit´ es on peut supposer que le centre de gravit´ e du nuage est

`

a l’origine (sinon on le translate) et donc que P n

i=1 M i = 0. On consid` ere alors la matrice des valeurs H =

− ¹ ₂ d ² _ij

. On calcule la moyenne par lignes m i , la moyenne par colonne m j et la moyenne g´ en´ erale m :

m _i = − 1

2 kM i k ² − 1 2n

X ⁿ

j=1 kM j k ² m _j = − 1

2 kM j k ² − 1 2n

X ⁿ

i=1 kM i k ² m = − 1

n X ⁿ

i=1 kM i k ²

(12)

La matrice H centr´ ee par ligne et par colonne vaut alors : H _•• =

− 1

2 d ² _ij − m i − m j + m

= XX ^t

Toutes ses valeurs propres sont positives ou nulles. R´ eciproquement si la matrice des carr´ es des distances doublement centr´ ees a toutes ses valeurs positives ou nulles :

H _•• =

− 1 2 d ² _ij

••

= UΛU ^t = UΛ

¹²

Λ

¹²

U ^t = XX ^t

Les carr´ es des distances entre les lignes de X sont les carr´ es des distances d’ori- gine. Donc pour une matrice de distance D quelconque de deux choses l’une : - ou bien

− ¹ ₂ d ² _ij

•• qui est sym´ etrique a toutes ses valeurs propres positives ou nulles. On dit qu’elle est euclidienne. La matrice X = UΛ

¹²

donne les co- ordonn´ ees d’un nuage de points dont les distances sont celles de d´ epart. X est dite repr´ esentation euclidienne de D. Ces coordonn´ ees sont rang´ ees par ordre d´ ecroissant de variance et si on utilise les premi` eres pour voir une projection du nuage sur ses axes principaux on dit qu’on fait une Analyse en coordonn´ ees prin- cipales (PCOA). - ou bien

− ¹ ₂ d ² _ij

•• qui est sym´ etrique a des valeurs propres n´ egatives. On dit qu’elle n’est pas euclidienne. La repr´ esentation euclidienne n’existe pas et la PCOA n’a pas lieu d’ˆ etre. En pratique on fait souvent ”comme si” en ignorant le probl` eme des valeurs propres n´ egatives. Gower et Legendre [8] ont ´ etudi´ e le caract` ere euclidien ou non de nombreuses distances et on sait souvent si on choisit une m´ ethode de calcul qui donnera ou non une matrice de distances euclidiennes. Par exemple toutes les distances bas´ ees sur des indices de similarit´ e sont euclidiennes alors que les distances les plus utilis´ ees en g´ en´ etique ne le sont pas.

data(yanomama)

geo <- as.dist(yanomama$geo) is.euclid(geo, T, T)

[1] 1.270026e+05 6.054361e+04 2.596671e+02 2.420916e+02 1.291763e+02 [6] 9.500950e+01 6.269167e+01 3.382556e+01 2.016325e+01 -2.469270e-13 [11] -1.318136e+01 -2.167582e+01 -2.942247e+01 -4.815153e+01 -7.937122e+01 [16] -1.178871e+02 -1.489993e+02 -1.755983e+02 -2.411742e+02

[1] FALSE

020000400006000080000100000

(13)

Cette matrice de dissimilarit´ es n’est pas euclidienne pour des raisons simples d’arrondis imp´ eratives lors de l’´ edition. Il s’agit de distances ` a vol d’oiseau, donc euclidienne par d´ efinition. On corrige le probl` eme par :

geo <- quasieuclid(geo)

s.label(dudi.pco(geo, scan = F)$li, sub = "Distances g´ eographiques", csub = 2, clab = 1.5)

d = 50

Distances géographiques

1 2 3 4 5 7 6

8 9

10 11 12 13

14 15

16 18 17 19

3.2 Que faire des distances non euclidiennes

Deux r´ esultats fondamentaux confortent l’int´ erˆ et des distances euclidiennes.

Quand une matrice de distances n’est pas euclidienne, on sait calculer [3] la plus petite constante c qui assure que la distance d ij +c ∀i 6= j est euclidienne.

L’exemple est d´ ecrit p. 435 dans l’ouvrage de r´ ef´ erence de P. et L. Legendre [15]. On consid` ere quatre points et les distances :

dmat

A B C

B 0.800 C 0.800 0.800 D 0.377 0.377 0.377

−0.5 0.5 1.0 1.5

−0.50.51.01.5

● ●

●

A B

C

Distances

−0.5 0.5 1.0 1.5

−0.50.51.01.5

● ●

●

A B

C

Distances + 0.1

−0.5 0.5 1.0 1.5

−0.50.51.01.5

● ●

●

A B

C

●

D

Distances +0.20083

−0.5 0.5 1.0 1.5

−0.50.51.01.5

● ●

●

A B

C

●

D

Distances +0.6

(14)

Il est impossible de construire une figure qui respecte ces distances. Si on ajoute 0.1 la figure grossit et on pense que c’est la voie d’une solution car la petite distance augmente relativement plus vite que la grande.

Il existe une valeur unique (0.20083) qui donne les quatre points dans un plan. Ensuite le quatri` eme point monte dans la troisi` eme dimension et la figure n’est plus plane mais la configuration encore euclidienne.

La fonction cailliez donne la constante avec la solution d´ ecrite dans [3].

gen <- as.dist(yanomama$gen) is.euclid(gen)

[1] FALSE

gen <- cailliez(gen)

s.label(dudi.pco(gen, scan = F)$li, sub = "Distances g´ en´ etiques", csub = 2, clab = 1.5)

d = 20

Distances génétiques

1 2 3 4

5

6

7

8 9 10

12 11 13

14 15

16 17 18 19

Quand une matrice de distances n’est pas euclidienne, on sait aussi calculer [16] la plus petite constante c qui assure que la distance q

d ² _ij + c ∀i 6= j est euclidienne.

ant <- as.dist(yanomama$ant) is.euclid(ant)

[1] FALSE

ant <- lingoes(ant)

s.label(dudi.pco(ant, scan = F)$li, sub = "Distances anthropom´ etriques",

csub = 2, clab = 1.5)

(15)

d = 100

Distances anthropométriques

1 3 2

4 5

6 7

8 10 9

11 12 13

14 15 16 17 18 19

On voit bien la question ainsi pos´ ee. Comment mesurer la ressemblance entre ces typologies faites par ces diff´ erentes distances ? La question ´ etait directement pos´ ee par R. Spielman, l’auteur des donn´ ees [31]. On trouvera un exemple de mˆ eme type dans un triplet spatial-environnemental et g´ en´ etique (typologie de sites) avec :

data(butterfly)

3.3 Dissimilarit´ es ultram´ etriques

Dans la classe des dissimilarit´ es euclidiennes, un sous-ensemble de grand int´ erˆ et ´ ecologique (voir ci-apr` es) est celui des distances ultram´ etriques. Les dis- similarit´ es peuvent ˆ etre m´ etrique :

d ac ≤ d ab + d bc

Les distances euclidiennes sont toujours m´ etriques. L’in´ egalit´ e pr´ ec´ edente est dite in´ egalit´ e triangulaire. Une distance euclidienne peut en plus v´ erifier l’in-

´

egalit´ e triangulaire ultram´ etrique :

d ac ≤ max (d ab , d bc )

La seconde est plus forte que la premi` ere. Les distances euclidiennes sont celles des nuages de points. Les distances ultram´ etriques sont celles des arbres de classification. On aura des d´ etails dans :

http://pbil.univ-lyon1.fr/R/stage/stage7.pdf

Il suffit ici de savoir qu’une dissimilarit´ es par le biais des m´ ethodes de classifica- tion hi´ erarchique ascendante (CHA) induit une hi´ erarchie de partitions valu´ ee qu’on voit par un dendrogramme. Les dendrogrammes sont des arbres (graphes sans cycles) dont toutes les feuilles sont ` a la mˆ eme distance de la racine. Les phylog´ enies historiques et les taxonomies en sont (autant dire que ce sont des inventions de biologistes !).

Inversement si on a un dendrogramme, la distance entre feuilles d´ efinies par

la hauteur du premier ancˆ etre commun est ultram´ etrique. En fait trouver un

dendrogramme, c’est trouver une hi´ erarchie de partition valu´ ee, c’est trouver

une distance ultram´ etrique.

(16)

library(clue)

x = c(0, 1, 1, 2, 1, 9, 9, 10, 4, 4, 6, 6, 8) y = c(1, 0, 1, 1, 2, 4, 5, 4, 8, 10, 8, 10, 10) xy = cbind.data.frame(x, y)

par(mfrow = c(2, 2)) s.label(xy, clab = 2) dxy <- dist(xy) print(dxy, dig = 2)

1 2 3 4 5 6 7 8 9 10 11 12

2 1.4 3 1.0 1.0 4 2.0 1.4 1.0 5 1.4 2.0 1.0 1.4 6 9.5 8.9 8.5 7.6 8.2 7 9.8 9.4 8.9 8.1 8.5 1.0 8 10.4 9.8 9.5 8.5 9.2 1.0 1.4 9 8.1 8.5 7.6 7.3 6.7 6.4 5.8 7.2 10 9.8 10.4 9.5 9.2 8.5 7.8 7.1 8.5 2.0 11 9.2 9.4 8.6 8.1 7.8 5.0 4.2 5.7 2.0 2.8 12 10.8 11.2 10.3 9.8 9.4 6.7 5.8 7.2 2.8 2.0 2.0 13 12.0 12.2 11.4 10.8 10.6 6.1 5.1 6.3 4.5 4.0 2.8 2.0

hsxy <- hclust(dxy, "complete") plot(hsxy, hang = -1)

ultrasxy <- cl_ultrametric(hsxy) print(ultrasxy, dig = 2)

Dissimilarities using Ultrametric distances:

[,1] [,2] [,3] [,4] [,5] [,6] [,7]

[1,] 1.414214

[2,] 1.000000 1.414214

[3,] 2.000000 2.000000 2.000000

[4,] 2.000000 2.000000 2.000000 1.414214

[5,] 12.206556 12.206556 12.206556 12.206556 12.206556

[6,] 12.206556 12.206556 12.206556 12.206556 12.206556 1.000000

[7,] 12.206556 12.206556 12.206556 12.206556 12.206556 1.414214 1.414214 [8,] 12.206556 12.206556 12.206556 12.206556 12.206556 8.485281 8.485281 [9,] 12.206556 12.206556 12.206556 12.206556 12.206556 8.485281 8.485281 [10,] 12.206556 12.206556 12.206556 12.206556 12.206556 8.485281 8.485281 [11,] 12.206556 12.206556 12.206556 12.206556 12.206556 8.485281 8.485281 [12,] 12.206556 12.206556 12.206556 12.206556 12.206556 8.485281 8.485281

[,8] [,9] [,10] [,11] [,12]

[1,]

[2,]

[3,]

[4,]

[5,]

[6,]

[7,]

[8,] 8.485281

[9,] 8.485281 2.000000

[10,] 8.485281 2.828427 2.828427

[11,] 8.485281 2.828427 2.828427 2.000000

[12,] 8.485281 4.472136 4.472136 4.472136 4.472136 plot(dxy, ultrasxy)

abline(c(0, 1))

z <- dudi.pco(ultrasxy, scan = F)$li z$A1 <- jitter(z$A1, amount = 0.2)

z$A2 <- jitter(as.numeric(z$A2), amount = 0.2)

s.label(z, clab = 0)

(17)

d = 2

1 2 3 4 5

6 7

8 9

10 11 12 13

2 1 3 4 5 8 6 7 13 9 10 11 12

04812

Cluster Dendrogram

hclust (*, "complete") dxy

Height

●●

●

●● ●

● ●● ● ●

●● ●

● ●●

● ● ●● ●

●

●● ●

● ●●● ●

●

●● ●

●●●● ●●● ●

● ●● ● ●

●●

● ●

● ●●

●

● ●

●●●●●●● ●

●

● ●

●

2 4 6 8 10 12

246810

dxy

ultrasxy

d = 2

●

●●●●

●●

●

●●

●

13 points sont dans un plan. On connait leurs coordonn´ ees. La matrice de dis- tances euclidiennes (au sens strict) :

d _ab = p

(x _a − x _b ) ² + (y _a − y _b ) ²

est envoy´ e dans une classification hi´ erarchique (se m´ efier, il y en a beaucoup !) qui donne un dendrogramme (classe hclust). La classification donne une dis- tance ultram´ erique, donc euclidienne et la repr´ esentation euclidienne de cette nouvelle distance est possible. Les CAH sont des pratiques qui concentrent l’as- pect classification alors que la PCO concentre l’aspect ordination. On m´ elange souvent les deux.

Noter que la nouvelle distance est sup´ erieure ou ´ egale ` a la premi` ere pour tous les couples (on dit qu’elle dominante) C’est la plus petite qui a cette propri´ et´ e.

On dit que c’est l’ultram´ etrique dominante minimale.

par(mfrow = c(1, 2))

hcxy <- hclust(dxy, "single") plot(hcxy, hang = -1)

ultracxy <- cl_ultrametric(hcxy) plot(dxy, ultracxy)

abline(c(0, 1))

(18)

5 4 2 1 3 8 6 7

13 12 11 9 10

1 4 7

Cluster Dendrogram

hclust (*, "single") dxy

Height

●

● ●●

●●●

●●●● ●

●●●

●●●● ●

●

●●●

●●●● ●

●

●●●

●●●● ●●● ●

●●●● ●

●

● ●

●●●

●

● ●

●●●●●●● ●

●

● ●● ●

● ●

●

2 4 6 8 10

1 3 5

dxy

ultracxy

Avec cette m´ ethode, la nouvelle distance est toujours plus petite. On dit qu’elle est sous-dominante. Mais c’est la plus grande qui a cette propri´ et´ e. On dit que c’est l’ultram´ etrique sous-dominante maximale. Dans la librairie de Kurt Hornik, on trouve une fonction qui donne l’ultram´ etrique la plus proche, au sens des moindres carr´ es (crit` ere L2) ou des moindres diff´ erences en valeurs absolues (crit` ere L1) :

par(mfrow = c(1, 2))

ultra2 <- ls_fit_ultrametric(dxy) plot(ultra2)

plot(dxy, ultra2) abline(c(0, 1))

0 4 8

5 1 3 2 4 8 6 7 13 9

10 11 12

●●●●

●●●

●●●● ●

●●●

●●●● ●

●●

●●●

●●●● ●

●

●●●

●●●● ●●● ●

●●●● ●

●●

● ●

●●●

●

● ●

●●●●●●● ●

●● ●

●

2 4 6 8 10

2 4 6 8

dxy

ultra2

Pour en savoir plus, voir l’ouvrage de r´ ef´ erence pour les ´ ecologues [14] ou les documents de cours [29] [1] [13] disponibles sur le r´ eseau. ¹ .

4 Des esp` eces aux communaut´ es

4.1 La question de la mesure de la diversit´ e

Elle se pose d` es que l’objet d’´ etude est une collection, collection d’arbres dans un forˆ et, d’individus dans une communaut´ e, collection de g` enes, de s´ equences, collection d’entit´ es non toutes identiques.

1

Acc` es :

www.imep-cnrs.com/mroux/algoclas.pdf

www.iup.univ-avignon.fr/Etudes/Master/TAIM//SupportsCours/Classification/

coursClassification.pdf

ses.enst.fr/lebart/DEA/CLassif.pdf

(19)

La figure est explicite. Que vaut la variabilit´ e des ´ el´ ements d’une collection pour une variable binaire (1 est-il plus divers que 2 ?) pour une variable quantitative (la diversit´ e est nulle en 4 mais, entre 3 et 5, lequel est-il le plus divers ?) pour une variable quantitative et deux variables qualitatives (6) pour un ensemble de variables complexes (7) pour des variables redondantes (8) pour des proportions

´

egales mais des effectifs diff´ erents (9-10) pour des choses non comparables (11) ou des objets spatialis´ es (12-13). La question n’est pas simple et la bibliographie associ´ ee est ´ enorme.

Parmi les bases solides on retient que la diversit´ e est une qualit´ e d´ efinie pour une distribution d’objets rang´ es par cat´ egories. On en a d’abord parl´ e pour les individus d’une communaut´ es rang´ es par esp` ece (diversit´ e taxonomique) ou pour les individus d’une soci´ et´ e rang´ es par cat´ egories de ressources (in´ egalit´ e sociale). Le nombre de cat´ egories (richesse) est l’indice le plus imm´ ediat mais quand les classes sont artificielles c’est le mode de distribution entre classes qui doit ˆ etre d´ ecrit :

Plus particuli` erement, le fait d’augmenter uniform´ ement de cinq se-

maines le nombre minimal de semaines d’admissibilit´ e exacerberait

(20)

le probl` eme de l’in´ egalit´ e des revenus entre les hommes et entre les m´ enages au Canada. L’indice de Gini pour les hommes passerait de 0,448 ` a 0,459 pour le revenu avant impˆ ot, . . . ²

Le coefficient de Gini [6] est celui de Simpson [30] en ´ ecologie et de Gini- Simpson pour les puristes. La diversit´ e est une valeur pour les ´ ecologues, l’in-

´

egalit´ e est une plaie pour les sociologues. Patil et Taillie ont synth´ etiser l’´ etat de l’art dans les ann´ ees 80 en parlant de fonction de la raret´ e.

Soit un relev´ e ´ ecologique contenant s esp` eces avec les proportions p = (p ₁ , · · · , p _i , · · · , p _s )

. Soit R une fonction caract´ eristique de la raret´ e de l’esp` ece du type : R : [0, 1] → R ⁺

La diversit´ e est la moyenne de la raret´ e des esp` eces du relev´ e. La raret´ e diminue quand p augmente et vaut 0 quand p vaut 1. On peut comprendre ainsi :

La richesse

R (p) = 1 p − 1 ⇒

s

X

i=1

p i

1 p _i − 1

= s − 1 L’indice de Simpson

R (p) = (1 − p) ⇒

s

X

i=1

p i (1 − p i ) = 1 −

s

X

i=1

p ² _i

L’indice de Shannon

R (p) = − ln (p) ⇒

s

X

i=1

p i ln (p i )

0.0 0.2 0.4 0.6 0.8 1.0

0 1 2 3 4 5

Proportion

Rareté

Richesse Shannon Simpson

2

L’assurance-chˆ omage et la redistribution du revenu - Aoˆ ut 1995 sur http://www11.hrsdc.

gc.ca/

(21)

D´ efinir la diversit´ e par la richesse, c’est donner une pr´ ef´ erence absolue aux es- p` eces rares (valeur suprˆ eme de la coche naturaliste). Le formalisme de Hill [11]

a enrichi la collection d’indices ` a partir de

N a = (p â ₁ + p â ₂ + · · · + p â _s )

^(1−a)¹

qui produit :

1 a = −∞ N _−∞ est l’inverse de la proportion de l’esp` ece la plus rare 2 a = 0 Richesse N ₀ est le nombre d’esp` eces

3 a = ¹ ₂

N

¹

2

= ( √ p 1 + √

p 2 + ... √ p s ) ² 4 a = 1 Shannon

N 1 = lim

a→1 (N a ) = exp −

s

X

i=1

p i ln (p i )

!

5 a = 2 Simpson inverse

N 2 = 1 P s

i=1 p ² _i

6 a = ∞ N _∞ est l’inverse de la proportion de l’esp` ece la plus abondante La critique radicale d’Hurlbert [12] et une multitude d’approches voisines ont montr´ e les difficult´ es d’installer des m´ ethodes canoniques. Par exemple : Rencontres the proportion of potential interindividual encounters which is in-

terspecific (as opposed to intraspecific), assuming avery individual in the collection can encounter all other individuals

∆ 1 = N

N − 1 "

1 − X ^s

i=1

N i

N ² #

Esp´ erance the expected number of species in a sample of n individuals selected at random from a collection containing N individuals, S species, and N _i individuals in the ith species

E (S n ) = X ^s

i=1





 1 −

N − N i

n N

n







[12] ∆ 1 = h

N N −1

i 1 − P s

i=1 p ² _i

∆ 2 = 1 − P s

i=1 p ² _i

∆ 3 = P

s

¹

i=1

p

²_i

∆ ₄ = ¹⁻

P

s i=1

p

²_i

P

s

i=1

p

²_i

−

_N¹

∆ ₅ = ¹⁻

P

s i=1

p

²_i

P

s

i=1

p

²_i

[17]

D = X ^s

i=1

n i (n i − 1) N (N − 1)

≈ X ^s

i=1 p ² _i [19]

E = 1 − pP s

i=1 p ² _i

1 − ^√ ¹ _s

(22)

[25]

D = 1 − pP s i=1 p ² _i 1 − ^√ ¹

N

On sait depuis longtemps que ces quantit´ es sont tr` es corr´ el´ ees et, globalement, explore le mˆ eme point de vue.

Une petite fonction pour choisir des couleurs :

editcolor <- function() { w <- matrix(0, 21, 21)

par(mar = c(0.1, 0.1, 0.1, 0.1)) plot(c(1, 22), c(1, 22), type = "n")

rect(col(w), row(w), col(w) + 1, row(w) + 1, col = couleurs) w <- as.numeric(locator(1))

w <- floor(w)

num <- (w[1] - 1) * 21 + w[2]

return(couleurs[num]) }

Implanter une petite fonction pour repr´ esenter un vecteur dans le plan d’ex- p´ erience qui nous concerne :

foo1 <- function(z = runif(16), sub = "") { sn1 <- c("I", "II", "III", "IV")

col1 <- c("chartreuse4", "steelblue2", "firebrick1", "springgreen") reg.num <- rep(1:4, rep(4, 4))

str.num <- rep(1:4, 4)

plot(str.num, z, type = "n", xlim = c(0.5, 4.5), ax = F, xlab = "Strates") axis(1, 1:4, sn1)

axis(2)

for (k in 1:4) lines(1:4, z[reg.num == k], type = "b", col = col1[k], lwd = 2)

s.label(cbind.data.frame(str.num, z), lab = names(ecomor$habitat), add.p = T)

title(main = sub, cex.main = 1.5) }

Repr´ esenter les mesures classiques de diversit´ e :

library(vegan) par(mfrow = c(2, 2))

foo1(apply(ecomor$habitat > 0, 2, sum), sub = "Richesse")

foo1(diversity(as.matrix(ecomor$habitat), index = "shannon", MARGIN = 2),

"Shannon")

foo1(diversity(as.matrix(ecomor$habitat), index = "simpson", MARGIN = 2),

"Simpson")

foo1(diversity(as.matrix(ecomor$habitat), index = "invsimpson",

MARGIN = 2), "Hill")

(23)

Strates

z

I II III IV

5102030

●

● Bu1 Bu2

Bu3 Bu4

Ca1 Ca2

Ca3 Ca4

Ch1 Ch2

Ch3 Ch4

Pr1 Pr2

Pr3 Pr4

Richesse

Strates

z

I II III IV

2.02.53.03.5

● ●

●

● Bu1 Bu2

Bu3 Bu4

Ca1 Ca2

Ca3 Ca4

Ch1 Ch2

Ch3 Ch4

Pr1 Pr2

Pr3 Pr4

Shannon

Strates

z

I II III IV

0.840.880.920.96

● ●

●

● Bu1 Bu2 Bu3 Bu4 ●

Ca1 Ca2

Ca3 Ca4

Ch1 Ch2

Ch3 Ch4

Pr1 Pr2

Pr3 Pr4

Simpson

Strates

z

I II III IV

5102030

●

● Bu1 Bu2

Bu3 Bu4

Ca1 Ca2

Ca3 Ca4

Ch1 Ch2

Ch3 Ch4

Pr1 Pr2

Pr3 Pr4

Hill

4.2 Diversit´ e et diff´ erences

Nous sommes ` a pied d’œuvre. Nous avons 16 habitats de 4 types dans 4 r´ egions. Nous voulons comparer les habitats, comparer leur contenu, leurs pro- pri´ et´ es. Nous voulons faire un bilan des ressemblances et des diff´ erences. Nous voulons comparer la variabilit´ e et faire un bilan typologique. Nous voulons avoir plusieurs points de vue. Vaste programme.

Nous avons besoin d’une th´ eorie g´ en´ erale pour rep´ erer les possibles : C.R.

Rao[26] [27] [28] nous la fournit. Les esp` eces sont diff´ erentes, plus ou moins. Les habitats sont diversifi´ es, plus ou moins en fonctions des diff´ erences des esp` eces qui y sont. Les habitats sont plus ou moins diff´ erents entre eux selon les diff´ e- rences qui existent entre les esp` eces de l’un et ceux de l’autre. S. Pavoine [, p.

46] montre la naissance de cette id´ ee en ´ ecologie [10] o` u elle sera confidentielle jusqu’` a sa mise en usage en biologie marine [32], puis en g´ en´ etique (les esp` eces sont remplac´ ees par des s´ equences nucl´ eotidiques) [20] qui conduira aux travaux de Rao.

On peut utiliser, comme on voudra :

– le langage ´ ecologique : un communaut´ e est une collection pond´ er´ ee d’es- p` eces ;

– le langage g´ en´ etique : une population est une collection pond´ er´ ee de g` enes ; – le langage statistique : une collection est une distribution pond´ er´ ee de

cat´ egories.

Les cat´ egories de la collection sont au nombre de s. Une collection est un ´ el´ ement de l’ensemble :

P = {p = (p 1 , · · · , p i , · · · , p s )

s

X

i=1

p i = 1}

(24)

Les cat´ egories montrent des diff´ erences consign´ ees dans une matrice de distances

`

a s lignes et s colonnes :

D = [d ij ] 1 ≤ i ≤ s 1 ≤ j ≤ s

La diversit´ e de p du point de vue de D est d´ efinie par la diversit´ e quadratique ou encore entropie quadratique :

div _D (p) = 1 2

X

i,j

p _i p _j d ² _ij

La seule contrainte impos´ ee pour que ce calcul ait un sens est que le m´ elange de deux collections soit plus diverses que chacune des deux, soit, pour deux nombres positifs quelconques :

α + β = 1 ⇒ div _D (αp + β q) ≥ αdiv _D (p) + βdiv _D (q)

Si l en est ainsi, non seulement la diversit´ e a un sens mais, l’augmentation de la diversit´ e par m´ elange est une mesure de distances entre collections :

δ _D (p, q) = √ 2

r

2div _D ( p + q

2 ) − div _D (p) − div _D (q)

Ces quelques ´ el´ ements d’introduction suffisent pour comprendre qu’il ne s’agit pas d’un bricolage mais d’une structure de raisonnement tr` es ouverte. En effet, supposons que toutes les esp` eces soient ´ egalement diff´ erentes entre elles :

i 6= j ⇒ d ij = √ 2 Alors la diversit´ e d’une collection est :

div(p) =

i=s

X

i=1 i=s

X

i=1

p i p j δ ij =

i=s

X

i=1

p i (1 − p i ) = 1 −

i=s

X

i=1

p ² _i

Et la distance entre deux collections est : δ ² (p, q) = 4(1 −

i=s

X

i=1

(p _i + q _i ) ²

4 ) − 2(1 −

i=s

X

i=1

p ² _i ) − 2(1 −

i=s

X

i=1

q ² _i ) =

i=s

X

i=1

(p i − q i ) ² Ce qui signifie que penser chaque esp` ece diff´ erente de chacune des autres exac- tement de la mˆ eme mani` ere, c’est mesurer la diversit´ e par l’indice de Simpson et assure la typologie des sites par une ACP centr´ ee.

d0 <- matrix(sqrt(2), nrow(ecomor$habitat), nrow(ecomor$habitat)) diag(d0) <- 0

d0 <- as.dist(d0)

quad1 <- divc(ecomor$habitat, d0)[, 1]

sim1 <- diversity(as.matrix(ecomor$habitat), index = "simpson", MARGIN = 2)

all(abs(quad1 - sim1) < 1e-14) [1] TRUE

La diff´ erence est vite compr´ ehensible. Dans l’indice classique, on ne fait aucune diff´ erence dans les diff´ erences entre esp` eces : un lion et deux impalas, c’est la mˆ eme chose qu’un gnou et deux z` ebres ou qu’un ´ eland et deux koudous.

On peut maintenant introduire des points de vue tr` es diff´ erents :

(25)

par(mfrow = c(2, 2))

d0 <- dist.quant(ecomor$morpho, 3) q0 <- divc(ecomor$habitat, d0)[, 1]

foo1(q0, sub = "Diversit´ e morphologique") d0 <- dist.taxo(ecomor$taxo)

q0 <- divc(ecomor$habitat, d0)[, 1]

foo1(q0, sub = "Diversit´ e taxonomique")

forsub <- data.frame(t(apply(ecomor$forsub, 1, function(x) x/sum(x)))) d0 <- dist(forsub)

q0 <- divc(ecomor$habitat, d0)[, 1]

foo1(q0, sub = "Diversit´ e comportementale") d0 <- dist(ecomor$diet)

q0 <- divc(ecomor$habitat, d0)[, 1]

foo1(q0, sub = "Diversit´ e alimentaire")

Strates

z

I II III IV

4681014

●

● ●

●

Bu1 Bu2

Bu3 Bu4 Ca1 Ca2

Ca3 Ca4 Ch1 Ch2

Ch3 Ch4 Pr1

Pr2 Pr3

Pr4

Diversité morphologique

Strates

z

I II III IV

2.42.83.2

●

● ●

●

● ● ●

●

● ●

Bu1 Bu2

Bu3 Bu4

Ca1

Ca2 Ca3 Ca4

Ch1 Ch2

Ch3 Ch4

Pr1 Pr2

Pr3 Pr4

Diversité taxonomique

Strates

z

I II III IV

0.10.20.30.40.5

● ●

●

● ●

●

● ●

●

Bu1 Bu2

Bu3 Bu4

Ca1 Ca2

Ca3 Ca4

Ch1 Ch2

Ch3 Ch4 Pr1 Pr2

Pr3 Pr4

Diversité comportementale

Strates

z

I II III IV

0.40.60.81.0

●

● ●

●

● ●

●

● ●

Bu1 ● Bu2

Bu3 Bu4

Ca1

Ca2 Ca3 Ca4 Ch1

Ch2 Ch3

Ch4 Pr1

Pr2 Pr3

Pr4

Diversité alimentaire

Un outil assainir le d´ ebat sur la biodiversit´ e ? C’est possible.

4.3 Typologie sur diff´ erences

La manipulation simultan´ ee des variabilit´ es intra communaut´ es (diversit´ e) et inter communaut´ es (typologie) est un ´ el´ ement fondamental de cette approche.

On trouvera dans la th` ese de S. Pavoine ³ une approche compl` ete de la d´ ecompo- sition de la diversit´ e dans des plans d’observations complexes, crois´ es ou hi´ erar- chiques. Cette introduction s’ach` evera sur deux questions importantes trait´ ees dans ce travail.

La premi` ere touche ` a l’usage de la distance induite sur les communaut´ es par une distance observ´ ee sur les esp` eces. L’exemple a ´ et´ e choisie parce que l’analyse du tableau esp` eces-sites n’a aucun sens sauf ` a enfoncer une porte ouverte : les cort` eges faunistiques n’ont aucun points communs d’un continent ` a l’autre. Mais

3

http://pbil.univ-lyon1.fr/R/liens/these_sp.pdf

(26)

en passant par des traits biologiques, on retrouve la possibilit´ e de comparer ce qui ne l’´ etait pas par la seule taxonomie.

Consid´ erons le lieu d’alimentation des esp` eces d’oiseaux. forsub signifie fo- raging substrate et contient des variables binaires (1 = oui, 0 = non) pass´ ees en pourcentage par lignes :

foliage alimentation dans le feuillage ground alimentation au sol

twig alimentation sur les rameaux bush alimentation dans les buissons trunk alimentation sur les troncs aerial alimentation a´ erienne

Les lieux d’alimentation font une typologie d’esp` eces, les esp` eces font une ty- pologie d’habitats : la question est comment faire une typologie d’habitats sur la base des comportements des esp` eces qu’on y trouve. Cette question est pro- prement ´ ecologique : expertiser un milieu par les esp` eces qui l’habitent est une activit´ e quotidienne. Pourtant la solution statistique est r´ ecente[22].

Les esp` eces font une typologie d’habitats, triviale, d` es qu’on la connaˆıt :

par(mfrow = c(2, 1))

wt <- as.data.frame(t(ecomor$habitat))

table.paint(wt, clabel.r = 1, clabel.c = 0.5, cleg = 0) a <- -ecomor$habitat

a <- t(apply(a, 1, cumsum))

w <- paste(a[, 1], a[, 2], a[, 3], a[, 4], a[, 5], a[, 6], a[, 7], a[, 8], a[, 9], a[, 10], a[, 11], a[, 12], a[, 13], a[, 14], a[, 15], a[, 16], sep = "")

table.paint(wt[, order(w)], clabel.r = 1, clabel.c = 0.5, cleg = 0)

Bu1Bu2 Bu3Bu4 Ca1Ca2 Ca3Ca4 Ch1Ch2 Ch3Ch4 Pr1Pr2 Pr3Pr4

E033 E034 E035 E070 E071 E001 E031 E100 E032 E069 E101 E102 E099 E030 E121 E048 E104 E057 E056 E127 E064 E025 E063 E098 E065 E066 E027 E026 E124 E067 E128 E129 E053 E051 E052 E094 E023 E024 E125 E093 E054 E055 E095 E050 E092 E126 E075 E076 E074 E077 E097 E061 E062 E096 E008 E106 E090 E045 E007 E105 E006 E029 E020 E021 E022 E049 E122 E058 E088 E047 E010 E044 E082 E078 E079 E080 E081 E083 E123 E028 E111 E015 E018 E019 E118 E119 E120 E016 E017 E112 E113 E114 E115 E116 E117 E046 E042 E009 E043 E089 E107 E108 E109 E011 E012 E013 E014 E091 E110 E084 E086 E040 E087 E041 E039 E085 E059 E060 E038 E073 E036 E002 E003 E004 E037 E072 E005 E103 E068

Bu1Bu2 Bu3Bu4 Ca1Ca2 Ca3Ca4 Ch1Ch2 Ch3Ch4 Pr1Pr2 Pr3Pr4

Les colonnes du tableau habitats-esp` eces sont ordonn´ ees, en haut, par la taxono- mie. En bas, c’est exactement le mˆ eme tableau ` a une permutation des colonnes pr` es.

Les cat´ egories de site d’alimentation font une typologie des esp` eces, simple

avec trois grands types et des nuances. Voir le tableau suffit ` a comprendre son

contenu :

(27)

par(mfrow = c(2, 1))

wt <- as.data.frame(t(forsub))

table.value(wt, clabel.r = 1, clabel.c = 0.5, cleg = 0, csi = 0.25) hc1 <- hclust(dist(forsub))

table.value(wt[, hc1$order], clabel.c = 1, cleg = 0, csi = 0.25)

foliage ground twig bush trunk aerial

foliage ground twig bush trunk aerial E117 E116 E115 E114 E113 E112 E017 E016 E111 E076 E088 E124 E123 E041 E119 E118 E018 E058 E029 E056 E061 E002 E004 E120 E098 E122 E072 E037 E003 E049 E036 E060 E059 E022 E021 E074 E020 E047 E086 E026 E027 E121 E048 E068 E073 E091 E109 E006 E105 E007 E096 E062 E092 E095 E055 E054 E093 E125 E052 E051 E053 E066 E025 E064 E104 E030 E099 E069 E100 E032 E038 E005 E103 E084 E110 E014 E013 E108 E107 E089 E043 E009 E015 E028 E083 E081 E080 E079 E078 E082 E010 E045 E090 E106 E008 E077 E050 E024 E023 E094 E067 E063 E127 E057 E101 E102 E011 E012 E126 E001 E031 E075 E046 E087 E044 E128 E065 E071 E035 E033 E034 E042 E129 E097 E019 E085 E039 E070 E040

Mais deux tableaux simples ne rendent pas simple la question de la typologie des colonnes du premier par la distance induite sur les lignes par le second ! Un tableau et une matrice de distance s’associe dans une double PCO :

d0 <- dist(forsub)

dpco1 <- dpcoa(ecomor$habitat, d0, scan = F) plot(dpco1)

L’essentiel est dans le fait que la distance entre esp` eces, quand elle est eucli- dienne, introduit une distance entre sites qui est aussi euclidienne. On peut alors faire une repr´ esentation euclidienne des esp` eces et des sites d’un seul coup.

Ils sont en effet dans un mˆ eme espace euclidien, parceque les esp` eces d´ efinissent cet espace par leur distance et parce que les sites sont des centres de gravit´ e (distributions de fr´ equences sur les esp` eces). On repr´ esente ainsi la typologie des sites induite par la distances entre esp` eces. Un exemple d’utilisation en mi- crobiologie est dans [5]. En fait, cette strat´ egie ici effleur´ ee recouvre une tr` es large gamme d’analyses connues (voir [22]).

Dissemblance et diversit´e