Clique-Stable Set Separation in Perfect Graphs with no Balanced Skew-Partitions

The results labeled with Clear-Scaling are obtained by first removing all those entries who do not participate in any matching of the undirected graph (due to Fact 10 the

ÆtnaNova’s users organize definitions, theorem statements, and proof specifica- tions, in files named scenarios 2 , which ÆtnaNova processes in order to establish whether or not

It is also easy to see that if the potential is not symmetric (in this case, meaning the values on the two vertices are distinct), then the eigenvectors will not have the form

On the other hand, it is shown in [20] that the restricted perfect matching problem is polynomial when G is a complete bipartite graph and k = 2.. Thus, we deduce that the L

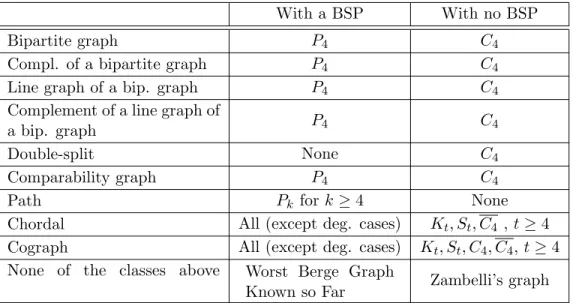
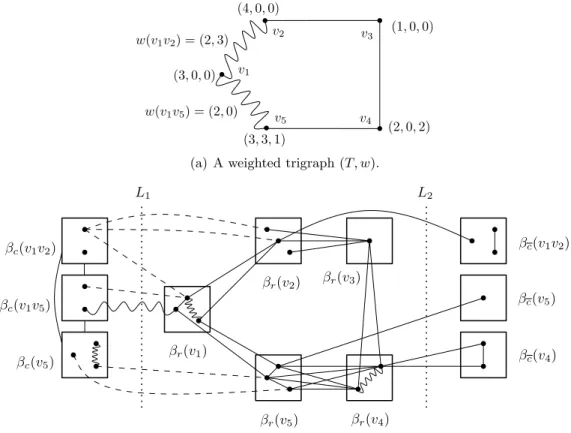
Lemma 4.1. Since the problem is auto-complementary, we consider only the cases of bipartite graphs, line trigraphs and doubled trigraphs. A clique in a bipartite trigraph is an edge,

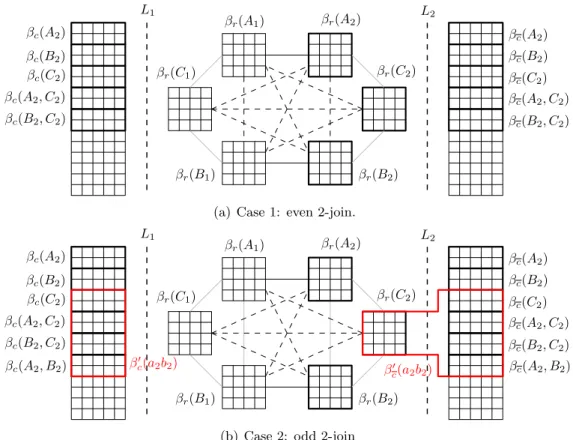
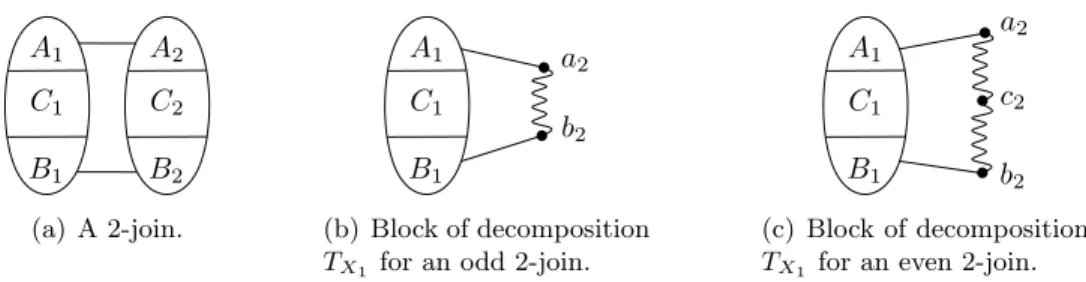
In fact, the method of contraction of a 2-join used in the previous subsection can easily be adapted to a generalized k-join. We only require that the basic class C of graphs

A graph is perfect if the chromatic number of every induced subgraph equals the size of its largest clique, and an algorithm of Gr¨ otschel, Lov´asz, and Schrijver [6] from 1988

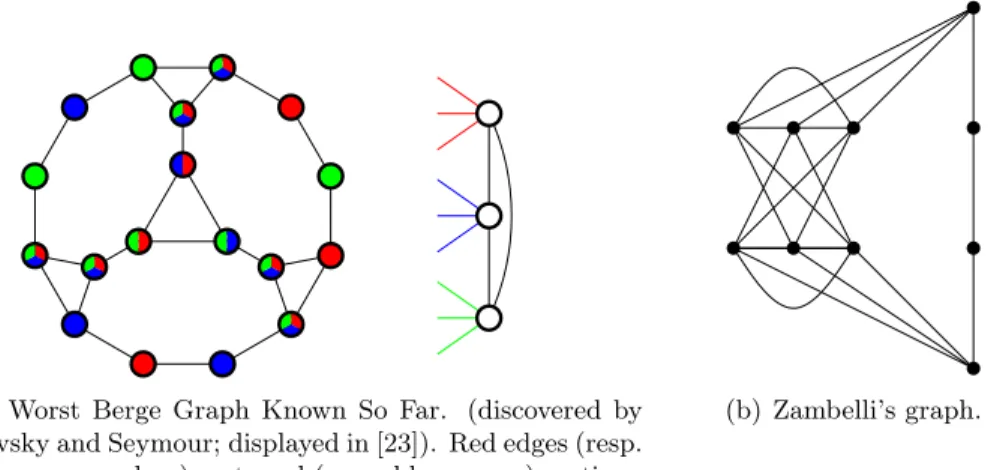
It follows that there are at most n 4 tight skew partitions in any n-vertex graph, because the corresponding cutset of each belongs to the list output by the Kennedy-Reed algorithm..